1 Introduction

In recent years, unmanned air vehicles (UAVs) have attracted considerable attention and unprecedented surge due to their potential in enormous applications including civilian and military operations [1]. Due to the latest innovations and upgradation in quadrotors, the micro-aerial vehicles have drastically increased the role of UAVs in applications such as law enforcement [2], battle damage assessment [3], agriculture services [4], photographing and live streaming [5] and surveillance over nuclear sites [6]. In comparison to other fixed-wing UAVs, a quadrotor is classified into the category of rotary-wings UAV and has distinguished features of vertical take-off and landing, high maneuverability and working in degraded environments that contribute some promising exceptions of using quadrotor instead of other UAVs [7].

Limited literature focus on the nature of the lumped disturbances torques caused by uncertainties and exogenous disturbances in quadrotor UAVs. To make sure stable and steady flights in the presence of exogenous disturbances, various control algorithms have been proposed in recent years. In Bouabdallah and Seigwart [8], a dynamic model for quadrotor was developed. After obtaining the model, research work was carried out to investigate control schemes for attitude and altitude tracking of the quadrotor. Control approaches based on linear techniques including proportional integral derivative and linear quadratic regulator were used to meet the challenges in quadrotor control algorithms [9]. Indubitably, their work added significant contribution in achieving desired control performances but their remained complications like deviation from initial conditions and tuning parameters of the controllers [10,11,12]. Nonlinear control schemes such as, LMI-based control approach [13], adaptive sliding mode control [14], back-stepping control [15], and integral sliding mode control [16, 17] are recently proposed to suppress the effect of mismatched disturbances in robust manner, but the nominal control performance is degraded at the cost of robustness.

To achieve better control performance, second order sliding mode control (SMC) was proposed in [18] to attain stable flight hovering for a quadrotor UAV. An adaptive control mechanism based on SMC was introduced to counteract the matched and mismatched perturbation in [19]. A robust finite time adaptive SMC was proposed in [20] for stabilization of quadrotor UAV. A global asymptotic convergent observer for attitude tracking of quadrotor UAV was introduced in [21]. Sliding mode control of quadrotor with disturbance observer was proposed in [22]. Moreover, a backstepping integral sliding mode control was proposed with disturbance rejection capability [23]. Therefore, it is imperative to achieve finite time convergence and further improve the robustness quality in terms of disturbances rejection and capability of compensating model parametric uncertainties to ensure safe within single control law without trading-off the nominal control performance.

Among the aforementioned control schemes, SMC has been widely employed in aviation industry due to the excellent features of conceptual simplicity and anti-disturbance capability. It is observed that traditional SMC remains robust to counteract matched disturbances only which means the disturbances coming through the same channel as that of the control input [24, 25]. However, the disturbance that can affect the flight control applications are usually the mismatched ones. The problem also becomes noticeable in the aircrafts control systems, where the lumped disturbances torques generated by modeling discrepancies, external winds, and uncertain varying inertial parameters directly influence the system states rather than through the control input channels [26]. In such systems, the sliding motion of the traditional SMC scheme is critically affected by the mismatched disturbances, eventually the control performance of SMC degrades as its robustness property is severely averted [27]. Therefore, to the author’s knowledge, in flight control systems the issues of mismatched disturbances and uncertain model parameters need to be addressed by modifying the control law of sliding mode scheme.

Motivated by the above-mentioned discussion, this paper proposes a novel composite control law NDOSMC, that combines SMC and nonlinear disturbance observer to stabilize the quadrotor in finite time in the presence of parametric variations and mismatched exogenous disturbances. The non-vanishing exogenous disturbances are considered in this study. Strong robustness and fast retrieval of nominal control performance are the prominent features of the proposed control strategy.

The layout of this paper is organized as follows: Sect. 2 gives a brief overview of nonlinear mathematical model of a quadrotor system. In Sect. 3 NDOSMC strategy is designed for tracking control of quadrotor. Numerical simulation results and discussion are presented in Sect. 4. Finally, conclusion is drawn in Sect. 5.

2 Mathematical Model

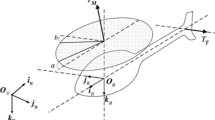
Quadrotor UAV is composed of four identical, equally spaced rotors [28], as shown in Fig. 1. The changes in the speed of the rotors generates aerodynamic moments of quadrotor. In Fig. 1, T1, T2, T3, and T4 represent corresponding thrusts generated by each rotor, θ, ϕ and \(\psi\) indicate roll, pitch and yaw angles, respectively. Quadrotor dynamics are portrayed both in frame and in inertial frame as shown in Fig. 2.

Fig. 1
figure 1

Quadrotor model in “X” configuration

Full size image
Fig. 2
figure 2

Body-fixed and inertial frame of reference

Full size image

The quadrotor model can be described into translational and rotational coordinates that denotes its linear and angular positions respectively [29]

$$\xi = (x,y,z) \in {\mathbb{R}}^{3} ,\quad \eta = (\phi ,\theta ,\psi ) \in {\mathbb{R}}^{3}$$
(1)

where \(\xi = (x,y,z),\eta = (\phi ,\theta ,\psi )\) gives linear and angular orientation of quadrotor in inertial frame respectively. The rotation matrix transforms the coordinates from body frame to the inertial frame is given by [28]

$$R_{\Omega } = \left[ {\begin{array}{*{20}l} {c_{\psi } c_{\theta } } \hfill &\quad {c_{\psi } s_{\theta } s_{\phi } } \hfill & \quad {c_{\psi } s_{\theta } c_{\phi } + s_{\psi } s_{\phi } } \hfill \\ {s_{\psi } c_{\theta } } \hfill & \quad {s_{\psi } s_{\theta } s_{\phi } + c_{\psi } c_{\theta } } \hfill & \quad {s_{\psi } s_{\theta } c_{\phi } - c_{\psi } s_{\phi } } \hfill \\ { - s_{\theta } } \hfill & \quad {s_{\phi } c_{\theta } } \hfill & \quad {c_{\phi } c_{\theta } } \hfill \\ \end{array} } \right]$$
(2)

where \(c(.)\) and \(s(.)\) denote \(\cos (.)\) and \(\sin (.)\) respectively. The quadrotor model can be presented in state space form as

$$\dot{X} = f(X,U)$$
(3)

where \(X\) and \(U\) represent state vectors, and control inputs respectively. The state vector and control input vector are given as follows

$$X = \left[ {\begin{array}{*{20}c} \phi & {\dot{\phi }} & \theta & {\dot{\theta }} & \psi & {\dot{\psi }} & z & {\dot{z}} & x & {\dot{x}} & y & {\dot{y}} \\ \end{array} } \right]^{T}$$
(4)
$$U = \left[ {\begin{array}{*{20}l} {U_{1} } \hfill & {U_{2} } \hfill & {U_{3} } \hfill & {U_{4} } \hfill \\ \end{array} } \right]^{T}$$
(5)

In this work we consider the attitude and altitude dynamics to simplify the control architecture. Let the attitude and altitude subsystem of the quadrotor model be represented as (6)

$$\left. {\begin{array}{*{20}l} {\dot{x}_{1} = x_{2} } \hfill \\ {\dot{x}_{2} = a_{1} f_{1} + b_{1} U_{1} + a_{2} \xi_{1} } \hfill \\ {\dot{x}_{3} = x_{4} } \hfill \\ {\dot{x}_{4} = a_{3} f_{1} + b_{2} U_{2} + a_{4} \xi_{2} } \hfill \\ {\dot{x}_{5} = x_{6} } \hfill \\ {\dot{x}_{6} = a_{5} f_{3} + b_{3} U_{3} } \hfill \\ {\dot{x}_{7} = x_{8} } \hfill \\ {\dot{x}_{8} = - g + b_{4} \cos x_{1} cosx_{3} U_{4} } \hfill \\ \end{array} } \right\}$$
(6)

where the model parameters are rewritten as

$$\begin{aligned} & \left[ {f_{1} ,f_{2} ,f_{3} ,f_{4} } \right] = \left[ {x_{2} x_{4} ,x_{2} x_{6} ,x_{2} x_{4} ,\cos x_{1} \sin x_{3} } \right] \\ & \left[ {\xi_{1} ,\xi_{2} } \right] = \left[ {x_{4} \omega_{r} ,x_{2} \omega_{r} } \right] \\ & \left[ {a_{1} ,a_{2} ,a_{3} ,a_{4} ,a_{5} } \right] = \left[ {\frac{{I_{yy} - I_{zz} }}{{I_{xx} }},\frac{{J_{r} }}{{I_{xx} }},\frac{{I_{zz} - I_{xx} }}{{I_{yy} }},\frac{{J_{r} }}{{I_{yy} }},\frac{{I_{xx} - I_{yy} }}{{I_{zz} }}} \right] \\ & \left[ {b_{1} ,b_{2} ,b_{3} ,b_{4} } \right] = \left[ {\frac{l}{{I_{xx} }},\frac{l}{{I_{yy} }},\frac{1}{{I_{zz} }},\frac{1}{m}} \right] \\ \end{aligned}$$

In (6), \(g\) is the gravitational acceleration, m is the mass of the vehicle, \(\left[ {I_{xx} ,I_{yy} ,I_{zz} } \right]\) represent the moment of inertia, \(J_{r}\) represents rotor inertia, and \(w_{r}\) is the angular rotation. The dynamic equations of the quadrotor manifest that the rotational dynamics are independent of the rotational dynamics while the translational dynamics depend upon the rotational dynamics (Euler angles).

Generally, the nominal system of quadrotor can be presented as

$$\begin{aligned} & \dot{x}_{in} = x_{(i + 1)n} \\ & \dot{x}_{(i + 1)n} = a_{in} f_{in} + b_{in} u_{in} + \xi_{in} \\ \end{aligned}$$
(7)

The subscript “n” with each state and system parameters indicates its nominal form. The actual model of the quadrotor, with exogenous disturbances is defined as

$$\begin{aligned} & \dot{x}_{i} = x_{(i + 1)} + d_{i} \\ & \dot{x}_{(i + 1)} = a_{i} f_{i} + b_{i} u_{i} + \xi_{i} + \Delta_{i} \\ \end{aligned}$$
(8)

where \(i = 1,3,5,7\) and \(\xi_{in} ,\xi_{i} = 0\) for \(i = 5,7.\)

The terms \(d_{i} ,\Delta_{i}\) represent the mismatched and matched uncertainties respectively. The nomenclature used in this paper and nominal values of the parameters are enlisted in Table 1.

Table 1 Model parameters of quadrotor system
Full size table

Assumption 1

The mismatched exogenous disturbances \(d_{i}\) and matched disturbances \(\Delta_{i}\) in system (8), are bounded, non-vanishing and defined by \(\left[ {\mathop d\limits^{ * }_{i} ,\mathop {\Delta_{i} }\limits^{ * } } \right] = \left[ {\sup \left| {d_{i} } \right|,\sup \left| {\Delta_{i} } \right|} \right].\)

Assumption 2

It is assumed that following inequalities hold valid \(\frac{1}{{b_{i} }} - \frac{1}{{b_{in} }} \ge \frac{1}{{b_{n} }},\frac{{a_{i} }}{{b_{i} }} - \frac{{a_{in} }}{{b_{in} }} \ge \frac{{a_{in} }}{{b_{in} }}.\) where \(a_{in} ,b_{in}\) are known positive constants denoting nominal values of the model parameters, and \(a_{i} ,b_{i}\) are unknown bounded time-varying uncertain parameters.

Remark 1

From (6), it is deduced that rotational dynamics of the quadrotor are not coupled, thus independent control inputs can be synthesized to stabilize each rotational moment.

3 Sliding Mode Control

SMC is a non-linear control methodology developed from the idea of defining a switching function and a control law that drives the system states towards the sliding manifold, thereby reducing the tracking error to zero. For robust controller designs, the system states once reach sliding surface stay within the neighborhood of the sliding manifold despite the existence of uncertainties in the system [30].

3.1 Controller Design for Nominal System

Let \(x_{dn} \in R^{4}\) defined as \(x_{dn} = [\phi_{d} ,\theta_{d} ,\psi_{d} ,z_{d} ]^{T}\) be the desired attitude and altitude states of the vehicle’s nominal model. The tracking error signals can be denoted as

$$e_{i} = x_{in} - x_{dn}$$
(9)

Consider the sliding surface for nominal system as

$$s_{i} = c_{i} e_{i} + \dot{e}_{i}$$
(10)

where \(c_{i} > 0,\quad {\text{for}}\quad i = 1,2,3,4\) are arbitrary control variables. Equation (10) can be expressed by substituting (9) as

$$s_{i} = c_{i} e_{i} + x_{{\left( {i + 1} \right)n}} - \ddot{x}_{dn}$$
(11)

The control inputs \(u_{in}\) must be synthesized such that they drive (11) to zero in finite time and eventually the tracking errors converge to zero in the presence of bounded disturbances. Taking time derivative of (11), and invoking (7) yields

$$\dot{s}_{i} = c_{i} \dot{e}_{i} + a_{in} f_{in} + b_{in} u_{in} + \xi_{in} - \ddot{x}_{dn}$$
(12)

Now driving \(\dot{s}_{i}\) to zero, the attitude and altitude dynamics can be stabilized on the defined sliding manifolds by synthesizing the control laws as follows

$$u_{in} = - b_{in}^{ - 1} \left\{ {\begin{array}{*{20}l} {c_{i} \dot{e}_{i} + a_{in} f_{in} + \xi_{in} - \ddot{x}_{dn} } \hfill \\ { - k_{i} s_{i} - \eta_{i} {\text{sgn}} \left( {s_{i} } \right)} \hfill \\ \end{array} } \right\}$$
(13)

where \(k_{i} ,\eta_{i} > 0{\text{ for(}}i = 1,2,3,4)\) represent the controller gains. Back-substituting (13) in (12), yields

$$\dot{s}_{i} = - k_{i} s_{i} - \eta_{i} sgn\left( {s_{i} } \right)$$
(14)

3.1.1 Stability Analysis

To validate the stability of system dynamics of (14) around \(s_{i} = 0\), Lyapunov candidate functions can be defined as

$$v_{i} = \frac{1}{2}s_{i}^{2}$$
(15)

Taking time derivative of (15) along (10), (12) and (13) yields

$$\dot{v}_{i} = - k_{i} s_{i}^{2} - \eta_{i} |s_{i} | < 0$$
(16)

By selecting the control gains \(k_{i} ,\eta_{i} > 0,\) that makes \(\dot{v}_{i} < 0\) to guarantee the stability. Taking condition \(s_{i} = 0,\) the surface solution can be evaluated as

$$e_{i} (t) = e_{i} (0)exp( - c_{i} t)$$
(17)

Remark 2

The error trajectories of the nominal attitude and altitude states approach the sliding manifold in finite time and the tracking errors remains zero afterwards. Our main objective is to control the actual states of UAV. In the next subsection, a controller is designed that makes the actual UAV behave like nominal model of UAV.

3.2 Controller Design for Actual System

As the actual UAV is subjected to external disturbances and parametric uncertainties. The conventional SMC does not work for such case causing a severe steady state error depending on the maximum bound of external disturbances. To deal the situation a novel NDOSMC is designed to make the response of actual model same as nominal model of UAV. The self-tuning introduced in the switching gain of control law adjust its value to compensate the parametric uncertainties. The disturbance observer estimates the influence of the disturbance and updates the sliding manifold and control law. Choose the sliding surface for actual system as

$$\delta_{i} = c_{i} z_{i} + \dot{z}_{i}$$
(18)

where \(z_{i} = x_{i} - x_{in}\) is the tracking error between actual and nominal states of UAV. By substituting (7) and (8), (18) can be expressed as

$$\delta_{i} = c_{i} z_{i} + x_{i + 1} + {\hat{d}}_{i} - x_{(i + 1)n}$$
(19)

In (19), while substituting (8) the disturbances term \(d_{i}\) is replaced by \({\hat{d}}_{i}\). The estimation of disturbances is provided in the Theorem 1. The time derivative of surface can be calculated by using (7) and (8) as

$$\begin{aligned} \dot{\delta }_{i} & = c_{i} (x_{i + 1} + d_{i} - x_{(i + 1)n} ) + a_{i} f_{i} + b_{i} u_{i} + \xi_{i} + \Delta_{i} + \dot{{\hat{d}}}_{i} \\ & \quad - a_{in} f_{in} - b_{in} u_{in} - \xi_{in} \\ \end{aligned}$$
(20)

The control law can be formulated as

$$\begin{aligned} u_{i} & = - \frac{{c_{i} (x_{i + 1} + {\hat{d}}_{i} - x_{(i + 1)n} )}}{{b_{in} }} - \frac{{a_{in} }}{{b_{in} }}f_{i} - \frac{{\xi_{i} }}{{b_{in} }} + \frac{{a_{in} }}{{b_{in} }}f_{in} \\ & \quad + \frac{{b_{in} }}{{b_{in} }}u_{in} + \frac{{\xi_{in} }}{{b_{in} }} - k_{i} {\text{sgn}} \left( {\delta_{i} } \right) - \eta_{i} \delta_{i} \\ \end{aligned}$$
(21)

Dividing surface dynamics by \(b_{i}\) and substituting (21) in (20) one can obtain

$$\begin{aligned} \frac{{\dot{\delta }_{i} }}{{b_{i} }} & = \left( {\frac{1}{{b_{i} }} - \frac{1}{{b_{in} }}} \right)\Gamma + \left( {\frac{{a_{i} }}{{b_{i} }} - \frac{{a_{in} }}{{b_{in} }}} \right)f_{i} - k_{i} {\text{sgn}} \left( {\delta_{i} } \right) \\ & \quad - \eta_{i} \delta_{i} + {\tilde{d}} + \frac{{\Delta_{i} }}{{b_{i} }} + \frac{{\dot{{\hat{d}}}_{i} }}{{b_{i} }} \\ \end{aligned}$$
(22)

where \(\Gamma = c_{i} \left( {x_{i + 1} - x_{(i + 1)n} } \right) + \xi_{i} - a_{in} f_{in} - \xi_{in} - b_{in} u_{in} ,\quad {\tilde{d}} = \frac{{c_{i} }}{{b_{i} }}d_{i} - \frac{{c_{i} }}{{b_{in} }}{\hat{d}}_{i} .\)

Remark 3

As the UAV is subjected to unknown exogenous disturbances. If the observed signal of disturbance profile is not available, then the surface (19) can be reduced by ignoring the \({\hat{d}}_{i}\) term. Recalling Assumption 1, the solution of the reduced surface can be written as

$$z_{i} (t) \le \frac{{d_{i}^{ * } }}{{c_{i} }}\left( {1 - e^{{ - c_{i} t}} } \right) + z_{i} (0)e^{{^{{ - c_{i} t}} }}$$
(23)

which shows that UAV trajectory tracking error cannot be reduced to zero, causing a fixed steady state error of \(\frac{{d_{i}^{ * } }}{{c_{i} }}\) as \(t \to \infty .\) To overcome the issue the NDO is designed in the following subsection.

3.2.1 Design of NDO

A nonlinear disturbance observer that estimates the exogenous disturbances in system (8) and update the surface manifold (19) and control input (21) is expressed as follows

$${{\hat{d}}}_{i} = p_{i} + h_{i} x_{i}$$
(24)
$${\dot{p}}_{i} = - h_{i} \left( {x_{i + 1} + {\hat{d}}_{i} } \right)$$
(25)

where \({\hat{d}}_{i} ,p_{i}\) and \(h_{i}\) for \(i = 1,2,3,4\) represent the estimation of disturbances, internal state observer and the observer gains to be designed respectively. The following assumption can be made.

Assumption 3

The disturbance estimation error given as \({\tilde{d}}_{i} = d_{i} - {\hat{d}}_{i}\) is bounded and defined by \(\mathop {{\tilde{d}}_{i} }\limits^{ * } = \sup \left| {{\tilde{d}}_{i} } \right|.\)

Assumption 4

The exogenous disturbances considered are slow time varying and their derivatives are assumed to be zero, \({\dot{d}}_{i} \approx 0.\)

Theorem 1

Suppose the Assumption4is satisfied for the system (8). The estimation of mismatched disturbance\({\hat{d}}_{i}\)precisely track the real disturbance\(d_{i} ,\)if the observer gain is selected as\(h_{i} > 0,\)which validates the exponential stability of the system as\(\dot{{\tilde{d}}}_{i} (t) + h_{i} {\tilde{d}}_{i} (t) = 0.\)

Proof of Theorem 1

Taking time derivative of estimation error, invoking (25) and (8) yields

$$\dot{{\tilde{d}}}_{i} = \dot{{\hat{d}}}_{i} - {\dot{p}}_{i} - h_{i} \left( {x_{i + 1} + d_{i} } \right)$$
(26)

Using \(d_{i} = {\tilde{d}}_{i} + {\hat{d}}_{i} ,\) (26) becomes

$$\dot{{\tilde{d}}}_{i} = - {\dot{p}}_{i} - h_{i} \left( {x_{i + 1} + {\hat{d}}_{i} } \right) - h_{i} {\tilde{d}}_{i}$$
(27)

The internal state of the disturbance observer is defined as

$${\dot{p}}_{i} = - h_{i} \left( {x_{i + 1} + {\hat{d}}_{i} } \right)$$
(28)

Incorporating (28) in (27) yields

$$\dot{{\tilde{d}}}_{i} = - h_{i} {\tilde{d}}_{i}$$
(29)

If \(h_{i} > 0,\) the solution of (29) becomes exponentially decaying.

3.2.2 Stability Analysis of the Proposed NDOSMC

To facilitate the stability analysis of NDOSMC, the following lemma is introduced.

Lemma 1

[20] Assume that a continuous positive-definite function \(V(t) = f(s) > 0\)with\(s(0) = s_{0}\) satisfy the subsequent differential inequality \(\dot{V}(t) + \beta_{1} V^{\alpha } (t) + \beta_{2} V(t) \le 0,\) where β1, β2and α are the positive constants. Based on which the functionV(t) converges to zero in finite time given as:

$$t_{s} = \frac{1}{{2\beta_{1} }}\ln \left( {\frac{{\beta_{1} v_{i}^{\frac{1}{2}} s_{i} \left( 0 \right) + \beta_{2} }}{{\beta_{2} }}} \right)$$
(30)

Theorem 2

Consider system (8). If the surface manifold and control law are chosen according to (19) and (21), then sliding mode enforcement along (19) can be validated. Resultantly, the system states will converge to the desired reference trajectories and tracking errors will converge to zero in finite time.

Proof of Theorem 2

Consider the Lyapunov candidate functions of the form as

$$v_{i} = \frac{1}{{2b_{i} }}\delta_{i}^{2}$$
(31)

Taking time derivative of (31), invoking (18), (21) following Assumptions 1, 2 and 3 yields

$$\begin{aligned} & \dot{v}_{i} = \delta_{i} \left\{ \begin{gathered} \left( {\frac{1}{{b_{i} }} - \frac{1}{{b_{in} }}} \right)\Gamma + \left( {\frac{{a_{i} }}{{b_{i} }} - \frac{{a_{in} }}{{b_{in} }}} \right)f_{i} - k_{i} {\text{sgn}} \left( {\delta_{i} } \right) \hfill \\ - \eta_{i} \delta_{i} + {\tilde{d}} + \frac{{\Delta_{i} }}{{b_{i} }} + \frac{{h_{i} {\tilde{d}}_{i} }}{{b_{i} }} \hfill \\ \end{gathered} \right\} \\ & \quad \le - \left| \begin{gathered} - \frac{1}{{b_{in} }}\Gamma - \frac{{a_{in} }}{{b_{in} }}f_{i} + k_{i} - {\tilde{d}}^{*} - \frac{{\Delta_{i}^{*} }}{{b_{i} }} \hfill \\ - \frac{{h_{i} \mathop {{\tilde{d}}}\limits^{*}_{i} }}{{b_{i} }} \hfill \\ \end{gathered} \right||\delta_{i} | - \eta_{i} \delta_{i}^{2} \\ \end{aligned}$$
(32)

The enforcement of sliding mode is guaranteed, if the following condition holds true

$$k_{i} = \left| {\frac{1}{{b_{in} }}\Gamma + \frac{{a_{in} }}{{b_{in} }}f_{i} + {\tilde{d}}^{*} + \frac{{\Delta_{i}^{*} }}{{b_{i} }} + \frac{{h_{i} \mathop {{\tilde{d}}}\limits^{*}_{i} }}{{b_{i} }}} \right| + \varepsilon$$

Thus \(\dot{v}_{i} \le - \varepsilon \left| {\delta_{i} } \right| - \eta \delta_{i}^{2} .\)

$$\dot{v}_{i} \le - \sqrt 2 \varepsilon v_{i}^{\frac{1}{2}} - 2\eta v_{i}$$
(33)

Let \(\lambda_{1} = \sqrt 2 \varepsilon ,\lambda_{2} = 2\eta .\) then (33) can be rewritten as

$$\dot{v}_{i} + \lambda_{1} v_{i}^{\frac{1}{2}} + \lambda_{2} v_{i} \le 0$$
(34)

Then according to Lemma 1, the differential inequality (34) yields the finite-settling time as

$$t_{f} = \frac{1}{{2\lambda_{1} }}\ln \left( {\frac{{\lambda_{1} v_{i}^{\frac{1}{2}} \delta_{i} \left( 0 \right) + \lambda_{2} }}{{\lambda_{2} }}} \right)$$
(35)

Remark 4

The designed NDO expressed in (24) and (25) makes the surface (19) and control input (21) practically realizable for the actual UAV. Thus, introducing improvement in the results stated in Remark 3 gives finite time convergence of the state variables. Recalling Assumption 1 the mathematical solution of (19) can be written as

$$z_{i} (t) \le \frac{{{\tilde{d}}_{i}^{ * } }}{{c_{i} }}\left( {1 - e^{{ - c_{i} t}} } \right) + z_{i} (0)e^{{^{{ - c_{i} t}} }}$$
(36)

The expression (36) shows that UAV trajectory tracking errors can be driven to origin. As the NDO has updated the control law by estimating the influence of disturbance. The exogenous disturbance estimation error \({\tilde{d}}_{i}\), which is likely to converge to zero and is also proved from (29).

4 Simulation Results and Discussion

In this section, numerical simulations are presented to validate the efficiency of proposed control schemes. The initial conditions \(\left( {\phi \left( {t_{0} } \right),\theta \left( {t_{0} } \right),\psi \left( {t_{0} } \right),z\left( {t_{0} } \right)} \right)\) are set as \(\left( {0,0,0,0} \right).\) The desired trajectory of the attitude and altitude \(\left( {\phi_{d} ,\theta_{d} ,\psi_{d} ,z_{d} } \right)\) of the quadrotor system are chosen as \((0.1cos(t), \, sin(0.15t),\)\(0.2sin(t), \, 2).\) Moreover, to obtain accurate disturbance estimation, initially the exogenous disturbance estimator is set to zero. The tuning gains of the designed control strategy are chosen as \(c_{1} = 20,c_{2} = c_{3} = c_{4} = 14,\)\(\eta_{1} = 2,\eta_{2} = 1,\eta_{3} = 1.8,\eta_{4} = 2\) and \(h_{i} = 30 \, (for_{{}} i = 1,2,3,4).\)

The flight control architecture based on proposed method is illustrated in Fig. 3 which is composed of composite control scheme.

Fig. 3
figure 3

Proposed DOSMC scheme for quadrotor

Full size image

The Non-vanishing exogenous disturbances assumed in the state model (8) at \(t = 6{\text{s}} ,\) is given for \(i = 1,2,3,4\) as

$$d_{i} (t) = \left[ {\begin{array}{*{20}l} {0.6\;\sin \;(0.4{\text{t}}),} \hfill & {0.5\;\sin \;(0.4{\text{t}})} \hfill \\ {1.5\;\sin \;(0.4{\text{t}}),} \hfill & {0.8\;\sin \;(0.4{\text{t}})} \hfill \\ \end{array} } \right]$$
(37)

Figures 4, 5, 6 and 7 validate that reference signals tracking remain unaffected during the first 6 s which validate Remark 2 that the nominal performance of SMC is retained in the absence of exogenous disturbances. Then at t = 6 s, sudden injection of mismatched disturbance occurs, and eventually the observer starts estimation of the influence caused by disturbances and update the control law to retrieve the nominal system performance. The recovery time of NDOSMC to mitigate the tracking error is phenomenally lower as within \(t = 0.3{\text{s}}\) the proposed controller resumes accurate tracking of nominal states. Thus, the proposed control law remarkably suppresses the influence of exogenous disturbances. Figures 8, 9, 10 and 11 validate the estimation accuracy of the observer and the phenomenal reduction of disturbance estimation errors.

Fig. 4
figure 4

Roll angle tracking

Full size image
Fig. 5
figure 5

Pitch angle tracking

Full size image
Fig. 6
figure 6

Yaw angle tracking

Full size image
Fig. 7
figure 7

Altitude trajectory tracking

Full size image
Fig. 8
figure 8

Disturbance observation in roll angle

Full size image
Fig. 9
figure 9

Disturbance observation in pitch angle

Full size image
Fig. 10
figure 10

Disturbance observation in yaw angle

Full size image
Fig. 11
figure 11

Disturbance observation in altitude state

Full size image

Additionally, in practice, the moment of inertia is time-variant. The time-varying parametric uncertainties incorporated in quadrotor system (8) are modeled as

$$diag\left( {I_{xx} ,I_{yy} ,I_{zz} } \right) + \alpha_{i} \sin \left( t \right)$$
(38)

where \(\alpha_{i} = (1,5,3,7)\) for \(i = 1,2,3,4\) represents the coefficients of time-varying uncertainty in moment of inertia. The states dependent gain-scheduling based SMC law compensate the uncertainty in the model parameters and make sure fast convergence of the states towards the desired trajectories. Simulation results in Figs. 4, 5, 6 and 7 show the efficacy of the proposed controller by validating the Assumption 1. The parametric uncertainties are efficiently compensated by the proposed control strategy thereby maintaining the stability of the vehicle.

The performance analysis given in Table 2 validate the effectiveness of the proposed control strategy. Thus, the proposed NDOSMC method guarantees the stability of the vehicle under the influence of exogenous disturbances and time varying parametric uncertainties.

Table 2 Control performance evaluation of NDOSMC
Full size table

5 Conclusion

Exogenous disturbance attenuation and robustness against parametric variations are the two crucial properties required for control designs in flight control applications. In this paper, a NDOSMC has been presented to achieve finite time tracking control performance for quadrotor UAV in the presence of parametric uncertainties and exogenous disturbances. The parametric uncertainties are compensated by incorporating gain scheduling in SMC law while the influence of exogenous disturbances is mitigated by integrating a nonlinear DOB with SMC scheme. The proposed NDOSMC scheme remarkably attenuate the influence of exogenous disturbances and retain nominal tracking performance.