Introduction

Hypotension during non-cardiac surgery is associated with increased mortality from complications in postoperative periods (Monk et al. 2015). In these cases, the risk of organ injuries increases when the MAP remains below 80 mmHg for more than 10 min or below 70 mmHg for less than 10 min (Wesselink et al. 2018).

Hypotension is often one of the complications in cesarean surgeries with spinal anesthesia (das Neves et al. 2010). The risk of postoperative acute kidney injury increase when intraoperative MAP is less than 60 mmHg for more than 20 min and less than 55 mmHg for more than 10 min (Sun et al. 2015). In vascular surgery for elderly patients, intraoperative hypotension is defined as a 40% reduction in pre inductive MAP for more than 30 min and is associated with postoperative myocardial injury (Van Waes et al. 2016). Intraoperative hypotension increases the risk of postoperative cerebrovascular accidents, especially when MAP values decrease by more than 30% of baseline MAP. The MAP value to initiate the use of vasopressors is set at 65 mmHg. However, it is possible to consider values slightly higher than this, especially when dealing with patients previously diagnosed with hypertension (Rhodes et al. 2017). The use of norepinephrine (NE), epinephrine (EPP), ephedrine (EPD), and phenylephrine (PHP) as a vasopressor drug is widely used to control hypotension, especially in surgeries that use spinal anesthesia (Lee et al. 2017). Although studies on MAP control began a long time ago, the current standard for guide vasopressor infusion is manual titration, in which the professional responsible for patient care set infusion rates in response to MAP variations (Rinehart et al. 2021). In part, this can be explained by the challenge to control MAP, when a large variability in parameters related to the pharmacological response of patients on the administration of vasopressors, e.g., NE and PHP. Researches have studied a wide range of control models as a proposals for solutions, including proportional-integral (PI) control and its alternatives, adaptive control, rule-based control, and intelligent control (Sathish and Nachiappan 2019). Table 1 presents the main articles about MAP control in hypotensive conditions (Davoud et al. 2020; Fung et al. 2004; Huang and Roy 1998; Kashihara et al. 2004; Kashihara 2018; Ngan Kee et al. 2007, 2012, 2017; Rinehart et al. 2017, 2018; Soltesz et al. 2017; Tasoujian et al. 2019, 2020).

Table 1 MAP hypotension controllers review
Full size table

In contrast with systems of MAP control for hypertension, in which the vasodilator drug sodium nitroprusside (SNP) presents a model already consolidated and referenced by (Slate and Sheppard 1982), the mathematical models suggested for vasopressor drugs response are not widely available. Among these models, those developed by Rinehart et al. (2011) and Luspay and Grigoriadis (2015) can be highlighted. We used the last one as the basis for patient simulation.

This paper describes the development and testing of an adaptive controller embedded in simple hardware considering the variabilities in the MAP response of patients in relation to PHP infusion, providing adaptability in the automatic MAP control system for different types of patients. The control type is composed of a PID controller, whose gain parameters are estimated from the identification system of the patient’s characteristics, using a recursive polynomial model estimator, autoregressive with exogenous input (ARX) using estimation algorithm by recursive least squares with forgetting factor.

Methods

Patient model

The mathematical model for the patient simulation presented in Fig. 1 is derived from the studies of Luspay and Grigoriadis (2015) and Wassar et al. (2014), considering the existence of a regressive nonlinear relationship between PHP injection defined as u(t) and MAP response as MAP(t) obtained in animal trials.

Fig. 1
figure 1

Patient simulation model

Full size image

Because variations were observed between animals, as well as variability during the infusion time, it was possible to verify that for step variation of PHP injection, the MAP response variation can be represented by a simplified first-order transfer function with time delay, as shown in Eq. (1).

$$\frac{\Delta P(s)}{{I(s)}} = \frac{K}{\tau s + 1}e^{ - Ts}$$
(1)

where.

ΔP = Mean arterial pressure variation (mmHg);

I = PHP infusion rate (mL/h);

K = Patient sensitivity (mmHg.h.mL−1);

τ = Time constant of drug application representing drug absorption, distribution and metabolism (s);

T = Delay time of the injection line (s).

The main transfer function is influenced by changes in its parameters during the time and intensity of the drug injection rate, thus allowing the simulation of the physiological response of different types of patients. The equations for the parameter variations are shown in (2) to (5).

$$G_{T} (s) = \left\{ \begin{gathered} \sigma \left[ {T_{\min } ,T_{\max } } \right]\left\{ {\frac{{b_{T1} s + b_{T0} }}{{a_{T2} s^{2} + a_{T1} s + a_{T0} }}} \right\}I(s) \to t \ge t_{0} \hfill \\ 0 \to otherwise \hfill \\ \end{gathered} \right\}$$
(2)
$$G_{K} (s) = K_{0} \times e^{{\left[ { - K_{1} \times I(s) \times \frac{1}{{a_{k0} s + 1}}} \right]}}$$
(3)
$$G_{\tau } (s) = \frac{{b_{\tau 0} }}{s} \times I(s)$$
(4)
$$G_{d} (s) = \frac{{b_{d} }}{{a_{d} s + 1}}$$
(5)

where I is the PHP infusion rate, T is the delay time of the injection, σ is a saturation function to limit its value between the bounds of Tmin and Tmax, K0 is the nominal sensitivity in relation to PHP, K1 is the dynamic sensitivity (mmHg/ml h−1), aK0 is the coefficient of the sensitivity transfer function fixed in 550, bτ0 is the integration coefficient of the time constant variation, ad = 40 and bd = 5 are coefficients of stochastic activity and the patient's breathing effects function and aT0 = 1, aT1 = 10, aT2 = 10, bT0 = 1, and bT1 = 100 are delay time coefficients of function. During simulation and testing, some parameters were maintained with constant values, such as aK0 = 550, ad = 40, bd = 5, aT0 = 1, aT1 = 10, aT2 = 10, bT0 = 1, and bT1 = 100.

The GT(s) block is responsible for the random variation of the delay time at the drug injection. The delay time has a short peak period during the initial injection of the drug, a value that gradually decreases with other injections. The GK(s) block is responsible for the dynamic variation of the patient’s sensitivity and shows that patients gradually lose sensitivity to a given vasoactive drug through their subsequent injection. The Gτ(s) block is responsible for the dynamic variation of the time constant in response to the injection of the drug. The time constant increases slowly from an initial value, according to the amount of injection of the drug. The Gd(s) block represents stochastic activity and the patient's breathing effects. The simulation allows the variation of all parameters between their limits. However, for this study, 10 types of patients were defined as presented in Table 2 (Coelho et al. 2020).

Table 2 Parameter for patients
Full size table

System identification

System identification is the technique for developing mathematical models of a dynamic system based on observed input and output data. It is a statistical method used to estimate unknown model parameters, i.e., the coefficients in the differential equation. The model identification approach is named Identification for Control (I4C) if the model applicability is valid under certain boundary conditions (De Carvalho et al. 2021).

A decisive step in the identification procedure is the appropriate model type selection (Aguirre 2015). The representation of the general linear model can be considered as follows:

$$y(k)=\frac{B(q)}{F(q)A(q)}u(k)+\frac{C(q)}{D(q)A(q)}\nu(k)$$
(6)

Considering \(q^{ - 1}\) as the time delay operator, then \(y(k){q}^{-1}=y(k-1)\), \(\nu (k)\) represents the noise, e \(A(q)\), \(B(q)\), \(C(q)\), \(D(q)\), \(F(q)\) represent polynomials functions defined as in Eqs. (7) and (11).

$$A(q) = 1 - a_{1} q^{ - 1} - \cdot \cdot \cdot - a_{ny} q^{ - ny}$$
(7)
$$B(q)=1-b_1q^{-1}-\cdot\cdot\cdot-b_{nu}q^{-nu}$$
(8)
$$C(q) = 1 - c_{1} q^{ - 1} - \cdot \cdot \cdot - c_{n\nu } q^{ - n\nu }$$
(9)
$$D(q) = 1 - d_{1} q^{ - 1} - \cdot \cdot \cdot - d_{nd} q^{ - nd}$$
(10)
$$F(q) = 1 - f_{1} q^{ - 1} - \cdot \cdot \cdot - f_{nf} q^{ - nf}$$
(11)

The general linear model representation can also be considered as

$$y(k) = G(q)u(k) + H(q)\nu (k)$$
(12)

In this representation, functions \(G(q)\) and \(H(q)\) are considered respectively process and noise functions, as shown in Fig. 2.

Fig. 2
figure 2

General representation of estimated model

Full size image

From the general linear model, several models can be derived with a few simplifications (Navrátil and Ivanka 2014). Two are particularly interesting, the ARX and the autoregressive model with moving average and exogenous inputs (ARMAX). The ARX model considers C(q) = D(q) = F(q) = 1 with A(q) and B(q) representing arbitrary polynomials to be estimated, resulting in the model according to Eq. (13) and Fig. 3.

$$y(k) = \frac{B(q)}{{A(q)}}u(k) + \frac{1}{A(q)}\nu (k)$$
(13)
Fig. 3
figure 3

ARX model representation

Full size image

From the ARX model, a linear differential equation can be obtained, relating the output to the inputs presented in Eq. (14) (Aruna and Jaya Christa 2020).

$$y(k) = a_{1} y(k - 1) + \cdot \cdot \cdot + a_{na} y(k - n_{a} ) + b_{1} u(k - 1) + \cdot \cdot \cdot + b_{nb} u(k - n_{b} ) + e(k)$$
(14)

From the ARX model, it is obtained \(\theta\) defined as the system parameter vector and \(\phi\) as the regressors vector.

$$\theta ={\left[{a}_{1}{a}_{2}\cdots {a}_{na} {b}_{1}{b}_{2}\cdots {b}_{nb}\right]}^{\mathrm{T}}$$
(15)
$$\phi \left(k-1\right)={\left[y\left(k-1\right)\dots y\left(k-{n}_{a}\right) u\left(k-1\right)\dots u\left(k-{n}_{b}\right)\right]}^{\mathrm{T}}$$
(16)

The ARMAX model assumes \(D(q) = F(q) = 1\), and \(A(q)\), \(B(q)\), and \(C(q)\) being the arbitrary polynomials to be estimated, resulting in the model according to Eq. (17) and Fig. 4.

$$y(k) = \frac{B(q)}{{A(q)}}u(k) + \frac{C(q)}{{A(q)}}\nu (k)$$
(17)
Fig. 4
figure 4

ARMAX model representation

Full size image

From ARMAX model a linear differential equation can be obtained, relating the output to the inputs, as shown in Eq. (18).

$$y(k) = a_{1} y(k - 1) + \cdot \cdot + a_{na} (k - n_{a} ) + b_{1} u(k - 1) + \cdot \cdot + b_{nu} u(k - n_{u} ) + e(k) + c_{1} e(k - 1) + \cdot \cdot + c_{nc} e(k - n_{c} )$$
(18)

Therefore, from the ARMAX model we can obtain \(\theta\) defined as the system parameter vector and \(\phi\) as the regressors vector.

$$\theta ={\left[{a}_{1}{a}_{2}\cdots {a}_{na} {b}_{1}{b}_{2}\cdots {b}_{nb} {c}_{1}{c}_{2}\cdots {c}_{nc}\right]}^{\mathrm{T}}$$
(19)

Adaptive PID controller design

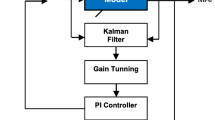
The adaptive PID MAP controller (PID-AD) was designed to perform patient identification during a predefined time of 200 s, and after this identification period, the system works in automatic control mode. The identification time has taken into account the variability of all possible patients, from the least sensitive to the most sensitive. The block diagram proposed for this controller is shown in Fig. 5.

Fig. 5
figure 5

Block diagram of the proposed controller

Full size image

We calculated the PID-AD gains considering two criteria for performance comparison. The criteria adopted in this development are the control algorithm methods from the study by (Ziegler and Nichols 1942) in their PI (ZN-PI) and PID (ZN-PID) versions, and also the method (Skogestad 2004) known as Skogestad internal model control (SIMC).

In this work, the proposal for real-time estimation of patient parameters and calculation of controller gains is based on an ARX model used to describe the dynamics of the patient response.

The identification method used for the patient parameters is based on an ARX model estimator using a recursive least squares with forgetting factor estimation algorithm.

This estimator allows obtaining a discrete transfer function of the patient response, according to Eq. (14). Considering that the main transfer function of the MAP variation of the patient relative to the FNF infusion rate is a first-order function (Luspay and Grigoriadis 2015), then the model generated by the estimator is shown in Eq. (20).

$$G(z) = \frac{Y(z)}{{U(z)}} = \frac{{b_{0} z^{1} + b_{1} z^{0} }}{{a_{0} z^{1} + a_{1} z^{0} }}$$
(20)

And consequently, the estimated coefficients \(a_{0}\), \(a_{1}\), \(b_{0}\), and \(b_{1}\) define the system response according to Eq. (21).

$$y(k) = \frac{{B(q^{ - 1} )}}{{A(q^{ - 1} )}}u(k) = \frac{{b_{0} q^{1} + b_{1} }}{{a_{0} q^{1} + a_{1} }}u(k)$$
(21)

The software implementation of the PID-AD controller is structured as shown in Fig. 6, using the polynomial recursive model estimator block available in the MATLAB® libraries and its Simulink® module.

Fig. 6
figure 6

Software implementation of PID-AD controller

Full size image

We developed the block for patient identification and PID gains to calculate the sensitivity, the delay time in the injection line, and the time constant of the drug application. The block also defines the values of the proportional gain (KP), integral gain (KI), and derivative gain (KD) of the controller. Equation (22) presents how the sensitivity is calculated. Equation (23) defines the time constant of drug application corresponding to drug absorption, distribution, and metabolism.

$$K = \frac{{\left( {b0 + b1} \right)}}{{\left( {a0 + a1} \right)}}$$
(22)
$$\tau = \frac{K}{{\left( {b1/Ts} \right)}}$$
(23)

The PID-CTRL block has one output tagged MV, corresponding to the PHP infusion rate. When the A_M input of the PID_CTRL block assumes a true status, defining that the PID is in automatic mode, the MV output is the result of the automatic calculation performed by the PID algorithm inside the block, as shown in Fig. 7. If the A_M input of the PID_CTRL block assumes a false state, defining that the PID is in manual mode, the MV output is a constant value.

Fig. 7
figure 7

Details of band-limited white noise block for persistent excitation

Full size image

In this study, the controller is in manual mode during the initial patient identification stage, with a fixed PHP rate of 20 mL/h provided by M_MV input. During this moment, a signal provided by the band-limited white noise block is added to the MV output signal of the PID-CTRL block. It generates a normally distributed random value, performing the persistent excitation function required for patient identification. Figure 7 shows these details inside the PID-CTRL control block.

In the block “recursive polynomial model estimator” shown in Fig. 6, the output error corresponds to the estimation error signal. This signal is sufficiently low when the estimation achieves success. In this work, any value of this signal less than 0.00001 is considered a level of success in patient estimation. If during the 200 s for patient identification this error signal reaches a level equal to or below the setpoint, the controller assumes automatic control mode. Otherwise, the controller remains in the manual, ensuring the safe operation of the system in manual mode.

The estimation success condition check was implemented within the Switcher block, shown in Fig. 6. This estimation failure status can be observed during system operation by warnings on a screen of the supervisory system integrated with the controller through the existing communication between controller and supervisory. Figure 10 shows the supervisory screen of this system.

The system set the controller gain for each identified patient case. To achieve the best performance, in this work, we used three heavily used methods for tuning gains in control systems, ZN-PI, ZN-PID, and SIMC control algorithms. Table 3 presents the equations relative to the three methods.

Table 3 PID gains forms
Full size table

We designed the switch block so that after the determined time for patient parameter identification, called the switching time, the patient parameter identification mode and the system control mode are switched automatically. At the instant that mode transfer is performed, the block responsible for patient identification and PID gains transfers the current values to the PID controller, which from that moment on uses them as parameters for the control. The PID control output set the PHP infusion rate in the control mode.

We performed the model implementation in a Windows PC i7 Desktop computer with 8 Gb of RAM with support from MATLAB/Simulink® (v. 2019a, license number 40686582). As shown in Fig. 8, the architecture of the computer simulation system has two blocks, the patient simulation unit and the adaptive PID controller block. Both were assembled in MATLAB/Simulink.

Fig. 8
figure 8

System architecture for adaptive PID controller software simulation

Full size image

Hardware implementation

The evaluation of the controller was performed using a real-time hardware-in-the-loop (HIL) simulation and compared to the software simulation. The hardware implementation to evaluate the system performance was embedded on two Arduino DUE boards with a 32-bit ARM Cortex-M3 Atmel SAM3X8E microcontroller, 512 Kb of Flash memory, 12-bit analog to digital converter, and 12-bit digital to analog converter. One of the boards simulates the dynamics of the patient in real-time while the other performs the controller functions, according to the architecture shown in Fig. 9. The algorithm was initially obtained by the MATLAB/Simulink® code generator using C +  + language from the software simulation. After this step, we treated the algorithm for the hardware board in the specific interface device environment program (IDE).

Fig. 9
figure 9

Hardware implementation of PID-AD controller

Full size image

We configured several parameters as constants during the software simulation. These parameters are configured in the hardware simulation from a supervisory system, as shown in Fig. 10. In hardware simulation, it allows adjusting the reference value of MAP, the initial value of the PHP infusion rate at any time. We designed the supervisory system using the free educational version of the Indusoft Web Studio software. The supervisory system communicates with the hardware through the MODBUS protocol at a rate of 1 sample every 0.5 s. This system collects and stores all data produced during the simulation.

Fig. 10
figure 10

Supervisory system for MAP PID-AD controller

Full size image

The test procedure consists of the MAP response analysis considering two main phases: patient identification and effective control. In the identification phase, the system injects PHP with a fixed rate of 20 ml/h during the first 200 s. After this phase, the system switches to the control phase, consisting of two stages. In the first stage, the PID-AD controller assumes the drug injection automatically. The PID-AD controller sets the SP value of MAP at 85 mmHg during 300 s. In the second stage, the SP changes to 93 mmHg maintaining this value for next 630 s. Therefore, the performance analysis of the controller occurred during the 930 s after the initial 200 s of identification, totalizing 1130 s of the test.

Results

Frequently, automatic MAP controllers are evaluated with patient parameters changing into three types: insensitive, nominal, and sensitive (Silva et al. 2019). In this study, we tested the control for ten different types of patients, according to Table 2. Tables 4, 5, and 6 present the values obtained for gain, time constant, and dead time of the patient response, calculated from Eqs. (22) and (23), and the controller gains KP, KI, and KD calculated by the equations in Table 3, immediately after the 200 s corresponding to the patient identification step. We collected the results in software and hardware simulation after the patient identification stage for an adaptive control system based on the ZN-PI, ZN-PID, and SIMC methods.

Table 4 Software and hardware simulation data for ZN-PI
Full size table
Table 5 Software and hardware simulation data for ZN-PID
Full size table
Table 6 Software and hardware simulation data for SIMC
Full size table

Figure 11 shows the MAP control response for type 1, 5, and 10 patients. This figure allows the comparison results of the computer simulation, with the architecture is already shown in Fig. 7, and the simulation of the embedded HIL model with architecture already shown in Fig. 8. The comparison shows the control phase, exactly after the initial 200 s used for patient identification. In the simulation, it is possible to verify that the steady-state error (SSE) was less than 0.21 mmHg for SIMC control, less than 0.31 mmHg for ZN-PID control, and less than 0.14 mmHg for ZN-PI control. The system achieved the desired MAP value of 93 mmHg with an overshoot value (OS) less than 0.06 mmHg for SIMC control, less than 5.53 mmHg for ZN-PID control and less than 4.34 mmHg for ZN-PI control. The settling time (ST) variation was from 143.5 to 175.5 s for the SIMC control, from 57.5 to 235 s for the ZN-PID control, and between 62.5 and 240.5 s for the ZN-PI control, according to Table 7.

Fig. 11
figure 11

MAP control response: a Patient 01, b Patient 05 and c Patient 10

Full size image
Table 7 Hardware performance results
Full size table

Discussion

We analyzed the controller performance in the three gain settings proposals for the PID algorithm, based on the ZN-PI, ZN-PID, and SIMC criteria. The analysis was carried out using the criteria defined as SSE, ST, OS, the absolute error integral (IAE) and the squared error integral (ISE), as shown in Table 8. The table shows the minimum and maximum simulation parameters performed on all ten patient types.

Table 8 Controller performance results for the patient in full range
Full size table

We compared the values obtained in the three controllers’ tests using performance criteria established by Luspay and Grigoriadis (2015). All three controllers showed a successful result, but the performance of the SIMC control type is particularly interesting, because of the low values for the OS and ST indexes, allowing a smoother control of the MAP control.

Despite the maximum IAE and ISE of the SIMC control type being higher than other control types, in 6 of the 10 simulated patients, these values were lower, which denotes SIMC performance was not worse compared to the other control types.

The proposed MAP PID-AD controller shows feasibility for implementation in clinical applications and aggregates value because it is a low-cost device and simple hardware. In this work, we did perform animal studies or human clinical trials. Therefore, more researches in future studies are requires to test and validate the controller in an ideal environment and a full range of variations.

Conclusion

This paper presents the development of two devices, first to simulate different patients and the other for MAP regulation. A simple physiological model expressed by a first-order function with varying parameters was used to characterize the MAP response as a function of PHP drug infusion, allowing the simulation of the patient’s response. The named PID-AD controller is a simple and low-cost alternative to identify and control the MAP for several types of patients in a hypotensive situation. PID-AD processes a real-time estimation of the pharmacological response of patients and utilizes this information to calculate in the control algorithm. The MAP regulation results achieved here suggest that the PID-AD, compared to other reference work in the literature is a simple, non-complex tool for controlling hypotension, showing feasibility for use in perioperative and intensive care units.