A theoretical liquid crystal elastomer model that mimics the elasticity of cat skin

Abstract

A mathematical model for nematic liquid crystal elastomers is proposed that mimics the elastic response of cat skin where reorientation of dermal fibres produces an increase in the thickness direction under tensile stretch. To capture this unusual effect, the uniaxial order parameter in the nematic elastomer model is allowed to decrease then increase again, and the critical stretch at which this change of monotonicity occurs and where the director also rotates suddenly is predicted. In addition, the model parameters are described by probability density functions and their uncertainty is propagated numerically to the predicted mechanical results.

“Of particular relevance here is the fact that technology of people must be different from that of nature simply because the two span different size scales [...] Everyday terms such as ‘assembly’, ‘polymer’, ‘blueprint’, ‘safety factor’, ‘design’, and ‘intended application’ were meant for our production systems, and we run considerable risk of self-deception when we use them for natural systems.” - S. Vogel [16]

1 Introduction

Extensive experimental programs have demonstrated the capability of a class of nematic liquid crystal elastomesr (LCEs) to present certain auxetic responses, while their volume is conserved under large elastic strain [8,9,10,11,12,13]. In particular, when a material sample is stretched longitudinally, its thickness, measured in the direction perpendicular to the sample’s plane, first decreases, then increases if the deformation is sufficiently large, then decreases again. Such mechanical behaviour is generated at a molecular level, without porosity emerging at macroscopic scale, and it is accompanied by a mechanical Fréedericksz transition whereby the nematic director, which is initially aligned within the sample’s plane and perpendicular to the longitudinal direction, rotates suddenly to become parallel with the applied force.

Auxetic materials that are simple to fabricate and avoid porosity-related weakening have long been sought for applications in a range of industries including sports equipment, aerospace, biomedical materials and architecture. Because of the intrinsic similarities between LCEs and conventional rubber [17], suitable descriptions can be achieved by adapting existing hyperelastic models for rubber-like solids [5]. Hyperelastic materials are the class of material models described by a strain-energy density function with respect to a fixed reference configuration.

In [6], a quantitative model is proposed and calibrated to available experimental data for auxetic LCEs. To analyse the effect of different model parameters on the predicted mechanical response, a simplified qualitative model is developed in [7]. The theoretical analysis suggests that auxeticity can be obtained by letting the uniaxial scalar order parameter decrease to a sufficiently low value then increase again. This is in agreement with the experimental observations where, in addition, mechanical biaxiality can also be observed that enhances the auxetic behaviour.

The purpose of this paper is to present a mathematical model for nematic LCEs that is capable of predicting a similar auxetic behaviour as that found in cat skin where reorientation of dermal fibres produces an increase in the thickness direction under tensile stretch. Cat skin thickening occurs first at small strain and continues at large strain until a maximum stretch is attained, after which the skin thickness begins to decrease. Both compressible and incompressible isotropic hyperelastic models are found acceptable within the range of experimental data, as reported in [15]. For the incompressible LCE model mimicking such behaviour, the uniaxial order parameter is allowed to decrease then increase again, and the critical stretch at which this change in monotonicity and where the director also rotates suddenly is predicted. In addition, a stochastic elasticity framework [5] is adopted where the model parameters are described by probability density functions, and the uncertainty in those parameters is propagated numerically to the predicted mechanical results. The theoretical model is described and explained in Section 2. This model is then calibrated to experimental data showing the auxeticity of cat skin in Section 3. The stochastic framework is summarised in the appendix.

2 Stochastic strain-energy function

In this paper, the model functions describing an incompressible nematic LCE satisfy the following assumptions [5]:

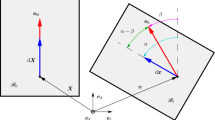
• Objectivity (frame-indifference). This condition states that the scalar strain-energy function is unaffected by a superimposed rigid-body transformation, which involves a change of position after deformation. As the nematic director n is defined with respect to the deformed configuration, it transforms when this configuration is rotated, whereas the nematic director n₀ for the reference configuration does not.

• Isotropy. This property requires that the strain-energy function is unaffected by a rigid-body transformation prior to deformation. As n is defined with respect to the deformed configuration, it does not change when the reference configuration is rotated, whereas n₀ does.

These fundamental assumptions underpin also the finite elasticity and liquid crystal theories [2, 14].

In particular, the following two-term strain-energy function is considered,

$$ W^{(lce)}=\frac{\mu_{1}}{2n^2}\left( \lambda_{1}^{2n}+\lambda_{2}^{2n}+\lambda_{3}^{2n}\right) +\frac{\mu_{2}}{2m^2}\left( \alpha_{1}^{2m}+\alpha_{2}^{2m}+\alpha_{3}^{2m}\right), $$

(1)

where μ₁,μ₂ > 0 and m,n are given parameters, with μ = μ₁ + μ₂ representing the shear modulus at infinitesimal strain, $\{\lambda _{1}^2,\lambda _{2}^2,\lambda _{3}^2\}$ denote the eigenvalues of the Cauchy-Green tensor FF^T, where F is the deformation gradient from the reference cross-linking state, satisfying $\det \mathbf {F}=1$, and $\{\alpha _{1}^2,\alpha _{2}^2,\alpha _{3}^2\}$ are the eigenvalues of AA^T, where $\mathbf {A}=\mathbf {G}^{-1}\mathbf {F}\mathbf {G}_{0}$ is the local elastic deformation tensor, such that $\det \mathbf {A}=1$, with G₀ and G representing the ‘natural’ deformation tensors due to the liquid crystal director in the reference and current configuration, respectively.

Given an intrinsically uniaxial LCE, the natural gradient tensor takes the form [7],

$$ \mathbf{G}=a^{-1/6}\mathbf{I}+\left( a^{1/3}-a^{-1/6}\right)\mathbf{n}\otimes\mathbf{n}, $$

(2)

where n is the nematic director, ⊗ denotes the tensor product of two vectors, I = diag(1,1,1) is the second order identity tensor, and

$$ a=\frac{1+2Q}{1-Q} $$

(3)

represents the anisotropy parameter, with Q the uniaxial scalar order parameter. In the reference configuration, G is replaced by G₀, with n₀ instead of n, a₀ instead of a, and Q₀ instead of Q.

The model function defined by equation (1) can be regarded as a slight generalisation of the strain-energy density proposed in [7] where m = −n. Similar but more general models were introduced and analysed in [6]. In addition, here, it is assumed that the shear modulus μ follows a Gamma probability density function (see Appendix A for details), while m,n are deterministic constants.

For the LCE sample, in a Cartesian system of coordinates (X₁,X₂,X₃), we designate the plane formed by the first two directions as the sample’s plane and the third direction as its thickness direction. The LCE is elastically deformed by application of a tensile force in the first (longitudinal) direction, while the nematic director is initially along the second (transverse) direction.

Setting the nematic director in the reference and current configuration, respectively, as follows,

$$ \mathbf{n}_{0}= \left[ \begin{array}{c} 0\\ 1\\ 0 \end{array} \right],\qquad \mathbf{n}= \left[ \begin{array}{c} \sin\theta\\ \cos\theta\\ 0 \end{array} \right], $$

(4)

where 𝜃 ∈ [0,π/2] is the angle between n and n₀, the deformation gradient takes the form

$$ \mathbf{F}=\text{diag}\left( \lambda_{1},\lambda_{2},\lambda_{3}\right), $$

(5)

such that $\det \mathbf {F}=\lambda _{1}\lambda _{2}\lambda _{3}=1$.

Assuming that the rotation of the nematic director within the plane formed by its initial orientation and the applied force from 𝜃 = 0 to 𝜃 = π/2 happens suddenly [6, 7], we denote by λ_crt the longitudinal stretch ratio λ₁ where the rotation occurs. In practice, although the angle 𝜃 may take intermediate values between 0 and π/2, the deformation interval for which the director rotation is observed can be very short, and its separate analysis will be omitted.

When the director for the reference and current configuration are given by (4), the associated natural deformation tensors are, respectively,

$$ \mathbf{G}_{0}=\text{diag}\left( a_{0}^{-1/6} ,a_{0}^{1/3} ,a_{0}^{-1/6}\right) $$

(6)

and

$$ \mathbf{G}= \left[ \begin{array}{ccc} a^{-1/6} +\left( a^{1/3}-a^{-1/6}\right)\sin^{2}\theta & \left( a^{1/3}-a^{-1/6}\right)\sin\theta\cos\theta & 0 \\ \left( a^{1/3}-a^{-1/6}\right)\sin\theta\cos\theta & a^{-1/6} +\left( a^{1/3}-a^{-1/6}\right)\cos^{2}\theta & 0 \\ 0 & 0 & a^{-1/6} \end{array} \right]. $$

(7)

The elastic deformation tensor $\mathbf {A}=\mathbf {G}^{-1}\mathbf {F}\mathbf {G}_{0}$ is then equal to

$$ \mathbf{A}=\left[ \begin{array}{ccc} \lambda_{1}a_{0}^{-1/6}\left( a^{-1/3}\sin^{2}\theta+a^{1/6}\cos^{2}\theta\right) & \lambda_{2}a_{0}^{1/3}\left( a^{-1/3}-a^{1/6}\right)\sin\theta\cos\theta & 0 \\ \lambda_{1}a_{0}^{-1/6}\left( a^{-1/3}-a^{1/6}\right)\sin\theta\cos\theta & \lambda_{2}a_{0}^{1/3}\left( a^{1/6}\sin^{2}\theta+a^{-1/3}\cos^{2}\theta\right) & 0 \\ 0 & 0 & \lambda_{3}a_{0}^{-1/6}a^{1/6} \end{array} \right]. $$

(8)

In particular:

• If 𝜃 = 0, then

  $$ \mathbf{G}=\text{diag}\left( a^{-1/6} ,a^{1/3} ,a^{-1/6}\right); $$

  (9)

• If 𝜃 = π/2, then

  $$ \mathbf{G}=\text{diag}\left( a^{1/3} ,a^{-1/6} ,a^{-1/6}\right) $$

  (10)

For the corresponding elastic Cauchy-Green tensor $\mathbf {A}^{T}\mathbf {A}=\text {diag}\left (\alpha _{1}^{2},\alpha _{2}^{2},\alpha _{3}^{2}\right )$, where “T” denotes the transpose (see also [6]), we have:

• If 𝜃 = 0, then

  $$ \alpha_{1}^{2}=\lambda_{1}^{2}a_{0}^{-1/6}a^{1/6} ,\qquad \alpha_{2}^{2}=\lambda_{2}^{2}a_{0}^{1/3}a^{-1/3},\qquad \alpha_{3}^{2}=\lambda_{3}^{2}a_{0}^{-1/6}a^{1/6}; $$

  (11)

• If 𝜃 = π/2, then

  $$ \alpha_{1}^{2}=\lambda_{1}^{2}a_{0}^{-1/6}a^{-1/3} ,\qquad \alpha_{2}^{2}=\lambda_{2}^{2}a_{0}^{1/3}a^{1/6},\qquad \alpha_{3}^{2}=\lambda_{3}^{2}a_{0}^{-1/6}a^{1/6}. $$

  (12)

Under the uniaxial deformation considered here, the second and third directions must be stress free. Then the corresponding principal Cauchy stresses, defined by

$$ T^{(lce)}_{i}=\frac{\partial W^{(lce)}}{\partial\lambda_{i}}\lambda_{i}-p,\qquad i=1,2,3, $$

(13)

with p denoting the usual Lagrange multiplier for the incompressibility constraint, take the form

$$ \begin{array}{@{}rcl@{}} T^{(lce)}_{i}&=&\frac{\mu_{1}}{n}\left( \lambda_{i}^{2n}-\lambda_{2}^{2n}\right) +\frac{\mu_{2}}{m}\left( \alpha_{i}^{2m}-\alpha_{2}^{2m}\right)\\ &=&\frac{\mu_{1}}{n}\left( \lambda_{i}^{2n}-\lambda_{3}^{2n}\right) +\frac{\mu_{2}}{m}\left( \alpha_{i}^{2m}-\alpha_{3}^{2m}\right),\qquad i=1,2,3. \end{array} $$

(14)

The associated first Piola-Kirchhoff stresses are equal to

$$ P^{(lce)}_{i}=T^{(lce)}_{i}\lambda_{i}^{-1},\qquad i=1,2,3. $$

(15)

Taking λ₁ = λ, we solve for λ₂ the equation

$$ T^{(lce)}_{2}-T^{(lce)}_{3}=0. $$

(16)

To capture the auxetic response while maintaining the continuum mechanics formulation tractable, we let the uniaxial scalar parameter Q > 0 decrease linearly with respect to the longitudinal stretch ratio λ from a given value Q₀ ∈ (0,1), at λ = 1, to a minimum value Q_crt ∈ (0,Q₀) that occurs at the critical stretch ratio λ = λ_crt, then increase again, also linearly, to a value Q₁ ∈ (Q_crt,Q₀), i.e.,

$$ Q(\lambda)=\left\{ \begin{array}{ll} C_{1}\lambda+D_{1} & \text{for}\ 1\leq\lambda\leq\lambda_{crt},\\ C_{2}\lambda+D_{2} & \text{for}\ \lambda_{crt}\leq\lambda\leq\lambda_{max}, \end{array} \right. $$

(17)

such that Q(1) = Q₀, Q(λ_crt) = Q_crt and Q(λ_max) = Q₁. Hence, C₁ = (Q₀ − Q_crt)/(1 − λ_crt), D₁ = (Q_crt − λ_crtQ₀)/(1 − λ_crt), C₂ = (Q_crt − Q₁)/(λ_crt − λ_max), D₂ = (λ_crtQ₁ − λ_maxQ_crt)/(λ_crt − λ_max).

When a is given by (3) and Q = Q(λ) is described by (17) , the energy function is equal to

$$ w(\lambda,\theta)=W^{(lce)}(\lambda_{1},\lambda_{2},\lambda_{3},a,\theta), $$

(18)

where W^(lce)(λ₁,λ₂,λ₃,a,𝜃) = W^(lce) is defined by equation (1).

Solving the equation

$$ w(\lambda,0)=w(\lambda,\pi/2) $$

(19)

gives the critical stretch ratio λ = λ_crt.

3 Numerical example

To illustrate the mechanical behaviour predicted by the theoretical LCE model, in the numerical example, we set n = 1 and m = − 1, and obtain:

• If 𝜃 = 0, then

  $$ \lambda_{2}=\lambda_{2}(\lambda,a)=\frac{1}{\sqrt{\lambda}}\left( \frac{\mu_{1}+\mu_{2}\lambda^{2}a_{0}^{-2/3}a^{2/3}}{\mu_{1}+\mu_{2}\lambda^{2}a_{0}^{1/3}a^{-1/3}}\right)^{1/4} $$

  (20)

  and

  $$ \lambda_{3}=\frac{1}{\lambda_{1}\lambda_{2}}=\frac{1}{\sqrt{\lambda}}\left( \frac{\mu_{1}+\mu_{2}\lambda^{2}a_{0}^{1/3}a^{-1/3}}{\mu_{1}+\mu_{2}\lambda^{2}a_{0}^{-2/3}a^{2/3}}\right)^{1/4}; $$

  (21)

• If 𝜃 = π/2, then

  $$ \lambda_{2}=\lambda_{2}(\lambda,a)=\frac{1}{\sqrt{\lambda}}\left( \frac{\mu_{1}+\mu_{2}\lambda^{2}a_{0}^{-2/3}a^{-1/3}}{\mu_{1}+\mu_{2}\lambda^{2}a_{0}^{1/3}a^{-1/3}}\right)^{1/4} $$

  (22)

  and

  $$ \lambda_{3}=\frac{1}{\lambda_{1}\lambda_{2}}=\frac{1}{\sqrt{\lambda}}\left( \frac{\mu_{1}+\mu_{2}\lambda^{2}a_{0}^{1/3}a^{-1/3}}{\mu_{1}+\mu_{2}\lambda^{2}a_{0}^{-2/3}a^{-1/3}}\right)^{1/4}. $$

  (23)

We further assume that μ follows a Gamma probability distribution with shape and scale parameters ρ₁ = 190 and ρ₂ = 0.01, respectively, while μ₁ follows a Beta distribution with hyperparameters ξ₁ = 90 and ξ₂ = 100. The mean values of the model parameters are then $\underline {\mu }=\rho _{1}\rho _{2}=1.9$, $\underline {\mu }_{1}=\underline {\mu }\xi _{1}/(\xi _{1}+\xi _{2})=0.9$, and $\underline {\mu }_{2}=\underline {\mu }-\underline {\mu }_{1}=1$. These mean values were calibrated to the experimental data for cat skin displayed in Table 1. Note that, under the incompressibility assumption, which is valid for LCEs, and considered acceptable for cat skin in [15], λ₂ = 1/(λ₁λ₃). Therefore, the behaviour of λ₂ can be calculated from the data for λ₃ as a function of λ₁. We also find Q₀ = 0.85, Q_crt = 0.001 and Q₁ = 0.1.

Table 1 Cat skin experimental values for stretch ratio λ₃ in the thickness direction vs. stretch ratio λ₁ in the longitudinal direction [15]

In Fig. 1(a), the auxetic response, showing how the stretch ratio corresponding to the thickness direction first increases then decreases, is captured. In the plots, as λ₃ records a change of monotonicity at λ₁ = λ_crt, a slight change in the gradient of λ₂ can also be observed, although this stretch ratio continues to decrease as λ₁ increases. Figure 1(b) depicts the associated deformation dependent uniaxial parameter Q given by equation (17). The energy function described by equation (18) is illustrated in Fig. 2(a). The corresponding first Piola-Kirchhoff stress defined by equation (15) is plotted in Fig. 2(b). The computer simulations were run in Matlab 2022a where inbuilt functions for random number generation were used.

Fig. 1

(a) Computed transverse stretch ratio λ₂ and thickness stretch ratio λ₃ for the LCE model, and the associated experimental values for the deformation of cat skin under uniaxial tensile load, and (b) the scalar uniaxial order parameter Q, respectively. The vertical lines correspond to the predicted longitudinal stretch ratio λ₁ = λ_crt where the director rotates suddenly. The dashed lines indicate mean values

Fig. 2

(a) Energy function and (b) computed first Piola-Kirchhoff stress (in MPa), respectively. The vertical lines correspond to the predicted longitudinal stretch ratio λ₁ = λ_crt where the director rotates suddenly. The dashed lines indicate mean values

4 Conclusion

Biomimetic materials are continuously sought in research fields such as biomedical engineering and regenerative medicine [1, 3]. This paper presents a hypothetical LCE model that mimics the unusual elastic response of cat skin examined experimentally and modelled within the theoretical framework of isotropic finite elasticity in [15]. Specifically, when a material sample is extended longitudinally, assuming that its volume is preserved, its thickness increases until a critical deformation is reached, then decreases. The hypothetical model suggests that LCEs could also be produced that exhibit such auxetic response, both under the small and large strain regimes. The present study may also reignite interest in the extraordinary mechanical behaviour of cat skin, which has been less investigated and discussed than other skin tissue types [4].

Appendix A: Stochastic model parameters

For the stochastic modelling of nematic LCEs adopted in this paper, the following hypotheses are required [5, Chapter 6]: For any given finite deformation, at any point in the material, the shear modulus μ > 0 and its inverse, 1/μ, are second order random variables, i.e., they have finite mean value and finite variance. This assumption is guaranteed by setting the following mathematical expectations:

$$ \left\{\begin{array}{ll} E\left[\mu\right]=\underline{\mu}>0,&\\ E\left[\log\ \mu\right]=\nu,& \text{such\ that} |\nu|<+\infty. \end{array}\right. $$

(A.1)

The first constraint in (A.1) specifies the mean value for the random shear modulus μ, and the second constraint provides a condition from which it follows that 1/μ is a second order random variable. By the maximum entropy principle, the shear modulus μ with mean value $\underline {\mu }$ and standard deviation $\|\mu \|=\sqrt {\text {Var}[\mu ]}$ (which is equal to the square root of the variance, Var[μ]) follows a Gamma probability distribution with shape and scale parameters ρ₁ > 0 and ρ₂ > 0, respectively, such that

$$ \underline{\mu}=\rho_{1}\rho_{2},\qquad \|\mu\|=\sqrt{\rho_{1}}\rho_{2}. $$

(A.2)

The resulting probability density function takes the form

$$ g(\mu;\rho_{1},\rho_{2})=\frac{\mu^{\rho_{1}-1}e^{-\mu/\rho_{2}}}{\rho_{2}^{\rho_{1}}{\Gamma}(\rho_{1})},\qquad\text{for}\ \mu>0\ \text{and}\ \rho_{1}, \rho_{2}>0, $$

(A.3)

where ${\Gamma }:\mathbb {R}^{*}_{+}\to \mathbb {R}$ is the complete Gamma function

$$ {\Gamma}(z)={\int}_{0}^{+\infty}t^{z-1}e^{-t}\text dt. $$

(A.4)

The word ‘hyperparameters’ is used for ρ₁ and ρ₂ to distinguish them from μ and other material constants.

When μ = μ₁ + μ₂, assuming μ_i > 0, i = 1, 2, we define the auxiliary random variable

$$ R_{1}=\frac{\mu_{1}}{\mu}, $$

(A.5)

such that 0 < R₁ < 1. Then, the random model parameters can be expressed equivalently as follows,

$$ \mu_{1}=R_{1}\mu,\qquad \mu_{2}=\mu-\mu_{1}=(1-R_{1})\mu. $$

(A.6)

It is reasonable to assume

$$ \left\{\begin{array}{ll} E\left[\log\ R_{1}\right]=\nu_{1},& \text{such\ that} |\nu_{1}|<+\infty,\\ E\left[\log(1-R_{1})\right]=\nu_{2},& \text{such\ that} |\nu_{2}|<+\infty, \end{array}\right. $$

(A.7)

in which case, the random variable R₁ follows a standard Beta distribution, with hyperparameters ξ₁ > 0 and ξ₂ > 0 satisfying

$$ \underline{R}_{1}=\frac{\xi_{1}}{\xi_{1}+\xi_{2}},\qquad \text{Var}[R_{1}]=\frac{\xi_{1}\xi_{2}}{\left( \xi_{1}+\xi_{2}\right)^2\left( \xi_{1}+\xi_{2}+1\right)}, $$

(A.8)

where $\underline {R}_{1}$ is the mean value and Var[R₁] is the variance of R₁. The associated probability density function is

$$ \beta(r;\xi_{1},\xi_{2})=\frac{r^{\xi_{1}-1}(1-r)^{\xi_{2}-1}}{B(\xi_{1},\xi_{2})},\qquad \qquad\text{for}\ r\in(0,1)\ \text{and}\ \xi_{1}, \xi_{2}>0, $$

(A.9)

where $B:\mathbb {R}^{*}_{+}\times \mathbb {R}^{*}_{+}\to \mathbb {R}$ is the Beta function

$$ B(x,y)={\int}_{0}^{1}t^{x-1}(1-t)^{y-1}dt. $$

(A.10)

For the random coefficients given by (A.6), the corresponding mean values are

$$ \underline{\mu}_{1}=\underline{R}_{1}\underline{\mu}, \qquad \underline{\mu}_{2}=\underline{\mu}-\underline{\mu}_{1}=(1-\underline{R}_{1})\underline{\mu}, $$

(A.11)

and the variances and covariance take the form, respectively,

$$ \begin{array}{@{}rcl@{}} \text{Var}\left[\mu_{1}\right] &=& (\underline{\mu}-2b)^2\text{Var}[R_{1}]+(\underline{R}_{1})^2\text{Var}[\mu]+\text{Var}[\mu]\text{Var}[R_{1}], \end{array} $$

(A.12)

$$ \begin{array}{@{}rcl@{}} \text{Var}\left[\mu_{2}\right] &=& (\underline{\mu}-2b)^2\text{Var}[R_{1}]+(1-\underline{R}_{1})^2\text{Var}[\mu]+\text{Var}[\mu]\text{Var}[R_{1}], \end{array} $$

(A.13)

$$ \begin{array}{@{}rcl@{}} \text{Cov}[\mu_{1},\mu_{2}] &=& \frac{1}{2}\left( \text{Var}[\mu]-\text{Var}[\mu_{1}]-\text{Var}[\mu_{2}]\right). \end{array} $$

(A.14)