Understanding temporal dynamics of jumps in cryptocurrency markets: evidence from tick-by-tick data

Abstract

Cryptocurrency markets have recently attracted significant attention due to their potential for high returns; however, their underlying dynamics, especially those concerning price jumps, continue to be explored. Building on previous research, this study examines the presence and clustering of jumps in an extensive tick data set covering six major cryptocurrencies traded against Tether on seven leading exchanges worldwide over nearly 2.5 years. Our analysis reveals that jumps occur on up to 58% of trading days, with negative jumps predominating in both frequency and size. Notably, we observe systematic clustering of jumps over time, especially in Bitcoin and Ethereum, indicating interconnected market dynamics and potential predictive power for market movements. By employing high-frequency econometric tools, we identify temporal patterns in jump occurrence, highlighting heightened activity during specific trading hours and days. We also find evidence of jumps influencing intraday returns, underscoring their significance in short-term price dynamics. Our findings enhance understanding of the cryptocurrency market microstructure and offer insights for risk management and predictive modeling strategies. Nevertheless, further research is needed to develop robust methodologies for detecting and analyzing co-jumps across multiple assets.

1 Introduction

It is clear to skeptics that cryptos are a Ponzi scheme, and even clearer for supporters that cryptos are the future. But scientific knowledge about this new asset class is still relatively scarce. Previous studies, such as those by Scaillet et al. (2020), have noted that Bitcoin experiences price jumps. This observation has been extended to include co-jumps with altcoins (Bouri et al., 2020) and is linked to phenomena such as self-excitation dynamics (Zhang et al., 2023) and spillover effects driven by market sentiment (Aysan et al., 2024). Alexander et al. (2023) find that informed traders are driving buying pressure in cryptocurrency (CC) markets. According to Barucci et al. (2023), Bitcoin/US Dollar Tether (USDT) and Ethereum/USDT are the markets to look at in order to capture sentiment and information flows, while US Dollar markets do not contain relevant information. Liu and Tsyvinski (2020) identified key predictors for cryptocurrency returns, such as investor attention and a propensity for extreme returns exceeding 5%, focusing on daily data. Aste (2019) found significant correlations between end-of-day prices and market sentiment, specifically analyzing positive sentiment indicators.

Our first main contribution is the extension of Scaillet et al. (2020) to investigate recent data that also includes altcoins and Tether trading pairs. To the best of our knowledge, this is the first investigation of jumps on a large panel of very recent tick-by-tick CC data from multiple markets traded against Tether. Previous analyses on jumps mostly use aggregated data provided by a single exchange. O’Hara (2015) has pointed out that changes in market microstructure due to high-frequency (HF) and algorithmic trading require that empirical analyses account for the interconnectedness of global markets due to cross-market arbitraging, and for the changes in time dimensions with respect to sampling frequency. We therefore consider tick-by-tick data spanning over almost 2.5 years from 7 of the largest crypto exchanges worldwide.

Second, while we find evidence similar to Aysan et al. (2024), who studied the relationship between news and jumps, we instead decompose how jumps are clustered in time systemically. We use the HF econometrics toolbox to not only look at jumps in CC markets, but specifically at what happens right after a jump is detected. This reveals the temporal dynamics of both positive and negative jumps in CCs at the highest possible frequency and addresses a gap highlighted by Zhang et al. (2022). More specifically, we show which CCs are prone to jumping simultaneously or multiple times within short time intervals. This helps increase the predictability of market movements. Given that investors observe important news or large market movements, knowledge about the effect of such movements on their portfolio helps them assess the risks related to the position they currently take in the market. We show specifically that jumps in BTC are often followed by jumps in other currencies, or further jumps of BTC itself, while altcoins both exhibit less frequent jumps, and their jumps are also less likely to happen along with jumps in other CCs.

Finally, we use this opportunity to compare how the results of commonly used jump tests change in CC markets that inhibit a very distinct market microstructure. This is due to their 24/7 trading nature, which disrupts traditional market patterns tied to exchange opening and closing times. Unlike traditional assets, news and regulatory changes in cryptocurrency markets can be immediately adopted, regardless of the time, due to the constant trading activity. This instantaneous adoption is particularly impactful as CC markets are heavily influenced by investor attention and sentiment, especially considering that trading volume fluctuates heavily in response to news and market sentiment. The autocorrelation present in CC price processes is magnitudes higher than that in traditional markets and this makes it difficult to narrow down exact jump timings. Also, the results on simultaneous jumps suggest that we possibly need to anchor co-jumps to more than two assets. However, there still exists a gap in noise-robust jump detection methods when several assets exhibit possible co-jumps.

Building upon previous high-frequency jump analyses, the very recent data acquired from the

captures the latest period of increased market activity of the largest CCs. We account for the interconnectedness of crypto markets by looking at some of the largest exchanges in North America, Europe and Asia. Our dataset consists of observations from April 12, 2019 until September 27, 2021. It consists of tick data collected from the exchanges Binance, Bitfinex, Bitstamp, Coinbase Pro, HitBTC, OKex and Poloniex and features the currencies Bitcoin (BTC), Bitcoin Cash (BCH), Ethereum Classic (ETC), Ethereum (ETH), Litecoin (LTC) and Ripple (XRP).

In total, we detected 1,392 jumps over all assets, of which approximately 61% were negative. Negative jumps dominate not only in quantity, but the overall distribution of jump sizes is also negatively skewed. This is partly due to the observed time frame including the effects of the recent Covid crisis, high volatility due to Elon Musk Tweets, and Chinese regulations. These results confirm findings on the number and distribution of jumps in earlier periods. While CCs tend to jump more than traditional assets, they still share some common properties: jumps seem to have a stronger impact during bull markets than during crashes. This becomes especially evident when linking jumps to important events and the results suggest that jumps are clustered around periods of high investor attention.

The largest assets BTC and ETH jump on 58% (32%) of all observed trading days. Some smaller currencies have slightly fewer testing days as they are sometimes too illiquid for a high-frequency evaluation which makes the interpretation of their test results more difficult. In general, currencies with higher market capitalizations tend to jump more, but more observations does not automatically mean more jumps. Next to the assumptions on high-frequency data, the theoretical properties of the methodologies we use have been derived from traditional assets. Consequently, jump detection in CCs is less accurate in terms of narrowing down exact jump times due to differences in market microstructure noise. This calls for new approaches for noise-robust volatility and jump estimators for CCs.

The jumps we detected show seasonal patterns. We detect more jumps in the middle of the week than on weekends, and most jumps are identified during 1 pm−5 pm UTC with a sharp drop from 1 am to 6 am UTC. This indicates that seasonality patterns in jumps are similar to seasonality patterns in volatility and trading volume and therefore a connection between these variables seems to exist. The lowest number of jumps coincides with the time when only Asian exchanges are open, from 12 am to 7 am UTC. As European exchanges open around 8−9 am UTC, there is a notable uptick in jump activity and the opening of American exchanges from 1 pm to 2:30 pm UTC leads to a pronounced increase in jumps, followed by a rapid decline with the closing of European exchanges at 4 pm UTC. Even though we observe several extreme jumps of more than $\pm 10\%$ in a single moment, small jumps of less than $\pm 2.5\%$ dominate and account for roughly 62% of all jumps. We observe only 24 positive and 23 negative extreme jumps, making these events very rare. Note that we distinguish between extreme jumps that are detected using HF econometrics tools, and extreme returns that are unprocessed log returns, either daily or in HF.

To investigate the relationship between jumps and returns, we run regressions where we introduce a dummy variable for separating days with and without jumps and additional dummy variables for days with positive (negative) jumps. These end-of-day returns are then regressed against those variables. We find a significant influence of these intraday jumps on end-of-day returns. In case of a positive jump on a specific trading day, the end-of-day return is also likely to be positive and vice versa. In case of an extreme intraday jump, it is likely that we will also observe an extreme return. Since CCs are traded 24/7, end-of-day returns are less meaningful, and therefore, we additionally regress intraday jumps against end-of-day returns of the following trading day and find no evidence for an effect on the following day. HF jumps are an important driver of CC prices in the short run and need to be accounted for in any meaningful option pricing model.

Our analysis additionally reveals that while the majority of clusters consist of single jumps, the presence of clusters with multiple jumps indicates periods of heightened market activity, aligning with prior research (Zhang et al., 2023) who find that self-exciting jumps in BTC predominantly follow medium-sized negative jumps, suggesting a negative asymmetry. While assets mostly jump alone, evidence of temporal clustering, self-excitation, and contamination effects emerges. Although we can observe the time structure of these jumps and further dissect these jump clusters, techniques for identifying co-jumps for multiple assets simultaneously would be required to robustify this analysis further. The frequency of single-asset jumps varies across cryptocurrencies, with BTC leading, followed by ETH, and all other altcoins making up the remaining jumps. This highlights the dominant role of the largest CCs. Negative jump clusters outnumber positive or mixed-direction clusters, which becomes particularly evident in BTC, ETH, and XRP. Additionally, the co-occurrence matrix indicates a notable association between jumps in BTC and ETH, suggesting market inter-dependencies. Further analysis of conditional probabilities reinforces Bitcoin’s influence, indicating higher probabilities of other cryptocurrencies following BTC jumps, which provides guidance for predictive modeling and risk management strategies.

The remainder of this paper is structured as follows: Sect. 2 discusses related literature and gives an overview of important events in the crypto universe. Section 3 describes the methodology, problem statement of jump detection in high-frequency markets, and describes the basic model and the applied jump-testing procedures. Section 4 describes the data and its properties. Section 5 discusses the empirical results, such as number of jumps, jump sizes, daily and weekly seasonality in jumps, and the effect of jumps on returns. Section 6 provides an overview over the temporal structure of jumps in cryptocurrencies. Section 7 concludes this paper.

2 Literature review

The widely unexplored properties of CCs have attracted the interest of researchers. CCs are distinct from other financial assets, commodities, or currencies: they can be traded 24/7, are largely unregulated, and currently highly speculative because the technology behind them is still in development. The promise of high returns in relatively short time frames, and the interest in their use case as a new digital currency, has led to increased market capitalization. Bitcoin alone has a market capitalization of almost $1.3 trillion (as of April 2024), and has grown bigger than high profile stocks in the S &P500 such as Tesla and Meta, only topped by the largest tech stocks Microsoft, Apple, Nvidia, Alphabet, and Amazon.

Researchers have analyzed the properties of cryptocurrencies, especially Bitcoin, by looking at correlations between sentiment and prices, including jumps (Aste, 2019; Aysan et al., 2024) and correlations between different CCs (Härdle et al., 2020), studying them from a monetary perspective (Yermack, 2015), or putting them into indices such as CRIX () (Trimborn & Härdle, 2018). Zhang et al. (2022) investigate the effect of the introduction of BTC futures on normal and jump volatility. Burnie et al. (2020) find that social media discussions can be the trigger for price shifts in CCs. Makarov and Schoar (2020) find that cross-country arbitrage opportunities frequently appear in cryptocurrencies; however, according to Crépellière et al. (2023), these opportunities have declined both in frequency and intensity since 2018. Menkveld and Yueshen (2018) study the connection of Flash-Crashes and cross-arbitraging in high frequency, but with the example of traditional assets, whereas Borri (2019) outlines the tail-risks of CCs. Trimborn et al. (2020) show that the risk-return trade-off can be improved by diversifying the digital asset portfolio. Giudici et al. (2020) discusses recent trends in academic discussions on digital assets. Certainly, a recent trend is to use available indices for building option pricing models (Madan et al., 2019). Analyses on the performance of indices such as in Chen et al. (2016) and Elendner et al. (2018) has helped researchers calibrate their models and portfolio composition. As new assets constantly emerge, Howell et al. (2020) explore the factors that lead to successful launches.

There have long been discussions whether to include a jump component to option pricing models, such as in Duffie et al. (2000). We make use of the HF econometrics toolbox and show that jumps are an essential component in the price process of CCs. This lays groundwork for the calibration of crypto option pricing models as employed, e.g., in Hou et al. (2020) and Matic et al. (2023).

Studying financial assets at high frequencies poses significant challenges that require familiarity with the growing body of HF econometrics literature. Aït-Sahalia and Jacod (2014) outline that HF data have unique properties due to irregularly spaced observations resulting in asynchronicity, market microstructure noise, and information loss if data are aggregated to 1-s intervals. Heavy tails, long memory in volatility, and intradaily and weekly seasonality, as observed in other financial assets, additionally result in non-normality. The concept of market microstructure noise as introduced, e.g., by Black (1986), and with respect to high frequency and algorithmic trading, as in O’Hara (1998) calls for robust volatility and jump devices. Econometric methods for determining the right sampling frequency were introduced and discussed, e.g., in Aït-Sahalia et al. (2005, 2011); Zhang et al. (2005); Liu et al. (2015); Jacod et al. (2017); Li et al. (2018) and important contributions to pre-averaging methods are Jacod et al. (2009, 2010) and Christensen et al. (2010) with the theory further developed by Hautsch and Podolskij (2013); Podolskij et al. (2017), and Li et al. (2020) among others. To estimate the variation in high-frequency data, Barndorff-Nielsen and Shephard (2004, 2006), and Barndorff-Nielsen et al. (2006) proposed the use of multi-power variation estimation. Robustifications can be found, e.g., in Vetter (2010). The advances in HF econometrics allow us thus to employ various techniques for handling the difficulties of our underlying data and to test for jumps in CCs.

Christensen et al. (2014) show a summary of recent approaches for jump detection methods. They find that, historically, jumps have been detected mainly in frequencies as low as daily. Even high-frequency analyses mostly looked at intervals like 1 or 5 min (Aysan et al., 2024; Scaillet et al., 2020), not at tick data. Possibly, this is because many assets are not assumed to be traded frequently enough to justify a HF analysis. Mukherjee et al. (2020) provide an overview of jump tests and also co-jump tests. In this paper, we employ Lee and Mykland (2012)’s methodology, which allows for moment-based detection of jumps and is robust against market microstructure noise. To lower the probability of spurious jump detection, we additionally test for jumps using the approach as proposed in Aït-Sahalia et al. (2012) and only accept jumps detected by Lee and Mykland on days where Ait-Sahalia, Jacod and Li also detected a jump. We address the issue of multiple testing using a Bonferroni correction on both tests.

Research on jumps has also suggested that correlated assets often jump together: see Aït-Sahalia et al. (2015) and Caporin et al. (2017). In addition, the jump sizes may be correlated in assets and in volatility, as indicated by Hou et al. (2020). Addressing such co-jumps further, Winkelmann and Yao (2020) extend Lee and Mykland (2012)’s approach to identifying jumps in two assets applied nominal and inflation indexed government bond yields at monetary policy announcements. Xu et al. (2022) study co-jumps between cryptocurrencies and blockchain related company stocks. Zhang et al. (2023) approach co-jumps from a network modeling perspective using 5 minute and daily intervals. Bouri et al. (2020) find evidence for co-jumping among the largest CCs, whereas Zhang et al. (2023) study self-excitation in Bitcoin returns.

The existing literature on CCs and jump detection raised several questions that we will address in the methodological part:

• 1. How does the methodology proposed by Lee and Mykland (2012) for jump detection perform when applied to high-frequency cryptocurrency market data, considering the unique microstructure of these markets?

• 2. What are the intradaily and weekly seasonality patterns of jumps in cryptocurrency markets, and how do they compare to patterns observed in volatility and trading volume, as indicated by Petukhina et al. (2021)?

• 3. Given the predictors for end-of-day returns of CCs discovered by Liu and Tsyvinski (2020), and the effect of sentiment (Aste, 2019) on daily returns, do jumps also predict end-of-day returns of CCs?

• 4. How do the results differ compared to Scaillet et al. (2020) when employing recent tick-by-tick data from several exchanges and how do other CCs behave?

• 5. What are the characteristics of jump clusters in HF CC markets, and how do they compare to the findings in of Zhang et al. (2022, 2023) and Aysan et al. (2024)?

• 6. Do cryptocurrency jumps exhibit self-excitation dynamics or spillover effects similar to those observed by Zhang et al. (2023) and Aysan et al. (2024)?

3 Methodology

3.1 Basic idea

Jumps are omnipresent in financial time series but have not been thoroughly explored in CC time series, particularly at high frequencies. For investors, it is essential to have reliable expectations regarding the frequency and size of jumps in order to minimize potential losses from significant downside risks and to capitalize on profitable bull runs. We employ the methodology described by Lee and Mykland (2012) to extract jumps from high-frequency CC time series. We keep only those jumps for which the methodology of Aït-Sahalia et al. (2012) also detected a jump on the same day. These methods utilize the pre-averaging approach to denoise the time series and provide jump- and noise-robust volatility estimates for typical variations in each sample.

Fig. 1

Bitcoin price, realized volatility and volume. (Source: Quandl)

The dataset captures a temporary market downturn during the COVID-19 crisis and a subsequent bull run, reaching new all-time highs for Bitcoin. Figure 1 shows the dynamics of Bitcoin prices, trading volume, and realized volatility both in 2011−2013 and 2019−2021. Price and volume have risen exponentially, while realized volatility has decreased. The red lines indicate a selection of important events in the crypto universe during our observation period:

• 1. Former US President Donald Trump releases a series of Tweets against BTC and other cryptos

• 2. Chinese President Xi Jinping announces his support for blockchain technology

• 3. In the course of the Covid crisis, US stock markets experienced so called Black Thursday, causing large sell-offs and trading got suspended for 15 min on NYSE. This affected the crypto market as well.

• 4. The third BTC halving comes into effect, which halves the reward for mining a BTC block. Historically, this event has led to major bull runs in the near future (

• 5. Notable movements to large exchanges could be observed, indicating that some whales sold significant amounts of Bitcoin at once

• 6. The SEC files a lawsuit against Ripple, arguing that XRP is a security. Consequently, major exchanges suspend trading activities for XRP

• 7. Tesla announces a $ 1.5 billion investment in Bitcoin and reveals plans to accept Bitcoin as a form of payment for its products

• 8. Coinbase announces effectiveness of registration statement and anticipated listing date of its Class A common stock on the Nasdaq Global Select Market

• 9. Bitcoin plunges 30% to $30,000 continuing a major sell-off in the cryptocurrency markets after Musk announced the suspension of vehicle purchases using Bitcoinb

We investigate how these events are related to the occurrence of jumps. Clearly, in terms of price, realized volatility and trading volume of these events had a significant influence on BTC and thus indicate a connectedness of jumps to important events, and with volatility and trading volume.

We test each currency on each exchange for every day separately using standard tools of HF econometrics and to address the issue of multiple testing we use a Bonferroni correction. The jumps in HF time series depicted in Fig. 1 are used to answer these questions.

3.2 Modeling jumps

Consider a complete probability space $(\Omega , {\mathcal {F}}_t, {\mathbb {P}})$ with $\Omega$ the set of all possible events, ${{\mathcal {F}}_t:t\in [0,T]}$ a right-continuous information filtration and ${\mathbb {P}}$ the probability measure. Now define the model

$$\begin{aligned} dX_{t} = \sigma dW_{t} + Z_{t}dJ_t, \end{aligned}$$

(1)

where $t\in [0,T]$ is an arbitrary point in time within one trading day. Here, T equals to one trading day of 24 h starting lasting from 00:00:00 UTC and ending at 23:59:59 UTC. t is any trade recorded within that interval. Note that timestamps are exact up to nanoseconds. $X_t$ is the log price at all times, $\sigma \in {\mathbb {R}}^+$ denotes a volatility estimate assumed to be constant over the observed period. $W_t$ is a Brownian motion, $J_t\in \left\{ 0,1 \right\}$ denotes the jump arrival indicator with jumps of size $Z_t$. Our objective is to estimate $J_t$ in a data driven way. While this is a fairly simple model, extensions like the SVCJ can be employed as, e.g., in Matic et al. (2023) and Hou et al. (2020), however, in this jump analysis, we follow the approach of the jump-testing methodologies that we discuss in the next sections.

3.3 Lee and Mykland jump test

To identify jumps in HF data, a common approach is to use a pre-averaging method to reduce noise and to calculate some multi-power variation to get an estimate of governing volatility in the observed process. This method allows for moment-based detection of intraday jumps. Due to market microstructure noise, it is impossible for us to observe the true price $X_t$, we can only observe

$$\begin{aligned} \tilde{P_{t}} = X_{t} + \epsilon _t, \end{aligned}$$

the price contaminated with noise $\epsilon _t \subset {\mathbb {R}}$ with standard deviation $q \in {\mathbb {R}}^+$. Denote as ${{\hat{\sigma }}} \in {\mathbb {R}}^+$ the empirically derived volatility estimate. The lag order of k is denoted by $k-1$, where $k \in {\mathbb {N}}$. This the lag order of the autocorrelation function of $\tilde{P_{t}}$ that is determined empirically. We fix the grid

$$\begin{aligned} {\mathcal {G}}^k_n = \left\{ 0 = t_{n,0}< t_{n,k}< t_{n,2k} < \cdots \right\} \end{aligned}$$

to get the subsampled price ${\tilde{P}}(t_{ik})$ consisting of only observations sampled at time points inside ${\mathcal {G}}^n_k$ and introduce

$$\begin{aligned} {\mathcal {G}}_n^{kM} = \left\{ t_n< t_{n,kM}< t_{n,2kM}< \cdots \right\} = \left\{ t_0< t_{kM}< t_{2kM} < \cdots \right\} \end{aligned}$$

in order to sample ${\hat{P}}(t_j)$ at every M observations from ${\mathcal {G}}^k_n$ with $t_j \in {\mathcal {G}}_n^{kM}$ for all j and $M \sim C\left\lfloor n/k \right\rfloor ^{\frac{1}{2}}$. $C \in {\mathbb {R}}^+$ is selected as per recommendation of Lee and Mykland (2012) and Jacod et al. (2009, 2010). Now, define

$$\begin{aligned} {\hat{P}}(t_j) \overset{\text {def}}{=} M^{-1}\sum _{i = \left\lfloor j/k\right\rfloor }^{\left\lfloor j/k\right\rfloor + M-1}{\tilde{P}}(t_{ik}) \end{aligned}$$

and calculate the returns of these pre-averaged prices

$$\begin{aligned} {\bar{P}}(t_j) \overset{\text {def}}{=} {{\hat{P}}(t_{j+kM})- {\hat{P}}(t_{j})} \end{aligned}$$

and scale these returns

$$\chi (t_{j} )\mathop = \limits^{{{\text{def}}}} \frac{{\sqrt M }}{{\sqrt {V_{n} } }}\bar{P}(t_{j} )$$

with $\chi (t_{j} )$ following a standard normal distribution, and

$$\begin{aligned} V_n \overset{\text {def}}{=} {\text{ Var }\left[ \sqrt{M}{\bar{P}}(t_j)\right] }. \end{aligned}$$

Note that $V_n$ has the limit

$$\begin{aligned} {{\,\textrm{plim}\,}}_{n \rightarrow \infty }V_n = \frac{2}{3}\sigma ^2C^2T+2q^2, \end{aligned}$$

where we estimate q with

$$\begin{aligned} {\hat{q}}^2=\frac{1}{2(n-k)}\sum ^{n-k}_{m=1}\{{\tilde{P}}(t_{m})-{\tilde{P}}(t_{m+k})\}^2 \end{aligned}$$

and ${{\hat{\sigma }}}$ are used to estimate noise variance and volatility respectively, s.t. we can calculate the test statistic

$$\begin{aligned} {\hat{\xi }}_{t_j} \overset{\text {def}}{=} {\frac{| \chi \left( t_j \right) | - A_n}{B_n}} \end{aligned}$$

for every ${\bar{P}}_{t_j}$. Using the result that

$$\begin{aligned} \frac{\max _{t_j\in {\mathcal {G}}_n^{kM}}| \chi \left( t_j \right) | - A_n}{B_n}\overset{{\mathcal {L}}}{\rightarrow }\xi \end{aligned}$$

asymptotically, where $\xi$ follows a standard Gumbel distribution, with the scaling terms

$$\begin{aligned}{} & {} A_n = \left( 2 \log \left\lfloor \frac{n}{kM} \right\rfloor \right) ^{1/2} - \frac{\log \pi +\log \left( \log \left\lfloor \frac{n}{kM} \right\rfloor \right) }{2\left( 2\log \left\lfloor \frac{n}{kM} \right\rfloor \right) ^{1/2}},\\{} & {} B_n = \frac{1}{\left( 2\log \left\lfloor \frac{n}{kM} \right\rfloor \right) ^{1/2}}, \end{aligned}$$

under the null hypothesis of no jumps we can then say that if, e.g., ${{\hat{\xi }}}>$ 99th percentile of the standard Gumbel distribution we observe a jump.

3.4 Aït-Sahalia, Jacod and Li jump test

This method again uses pre-averaging to obtain a noise-robust power variation ${\bar{V}}$ for any observed log return time series Z. The ratio of two differently weighted power variations converges to some finite limit under the null hypothesis of no jumps.

Recall the results of Aït-Sahalia and Jacod (2009). We have n observed increments of Y on [0, t]. For any integer $i \ge 1$ and $p \in {\mathbb {R}}^+$, we can write

$$\begin{aligned} \Delta _{i}^{n}Y = Y_{i\Delta _n } - Y_{(i-1)\Delta _n},\text { } B (Y,p,\Delta _n)_t = \sum _{i=1}^{[t/\Delta _n]}|\Delta _i^n|^{p}. \end{aligned}$$

(2)

For an integer $k \ge 2$, the test statistic is denoted as

$$\begin{aligned} S_J ( p,k,\Delta _n)_n = \frac{B(X,p ,k\Delta _n)_T}{B(X,p ,\Delta _n)_T}. \end{aligned}$$

with two possible cases. Let $\Omega _T^j$ be the collection of events where jumps are observed and $\Omega _T^c$ where a continuous path is observed. For $p>2$, the test statistic has the asymptotic behavior

$$\begin{aligned} S_J \left( p,k,\Delta _n \right) \overset{{\mathbb {P}}}{\rightarrow }\left\{ \begin{matrix} 1 &{} \text {on } \Omega _T^j \\ k^{p/2-1} &{} \text {on } \Omega _T^c \end{matrix}\right. \end{aligned}$$

Since this test statistic is not robust to noise, the construction of a robustified test statistic is necessary. This task makes again use of the results from Jacod et al. (2009, 2010). For defining a pre-averaging window, a sequence of integers $k_n$ needs to be chosen that satisfies:

$$\begin{aligned} k_n\sqrt{\Delta _n} = \theta + { \scriptstyle {\mathcal {O}}}(\Delta _n^{1/4}), \theta > 0. \end{aligned}$$

Weight functions $g \in {\mathbb {R}}$ are used to weigh observations within the pre-averaging window, where

$$\begin{aligned} \left. \begin{matrix} g \text { is continuous, piece-wise } C^1 \\ \text { with a Lipschitz derivative }g', \\ s \not \in (0,1) \Rightarrow g(s) =0, &{} \text { }\displaystyle \int g(s)^2ds >0, \end{matrix}\right\} , \end{aligned}$$

with which we can obtain the parameters

$$\begin{aligned} \left. \begin{matrix} g_i^n = g(i/k_n), &{} g_i^{'n}=g_i^n-g_{i-1}^n, \\ {\bar{g}}(p) = \displaystyle \int \left| g(s) \right| ^{p} ds, &{} {\bar{g}}^{'}(p) = \displaystyle \int \left| g(s)^{'} \right| ^{p} ds. \end{matrix}\right\} . \end{aligned}$$

Now, for any $Y = (Y_t)_{t \ge 0}$ we have the random variables

$$\begin{aligned} {\bar{Y}}(g)_i^{n}=\sum _{j=1}^{k_n -1}g_j^{n}\Delta _{i+j}^{n}Y, \text { } {\hat{Y}}(g)_i^{n}=\sum _{j=1}^{k_n}(g_j^{'n}\Delta _{i+j}^{n}Y)^2 \end{aligned}$$

as well as the processes

$$\begin{aligned} V(Y,g,q,r)_t^n = \sum _{i=0}^{[t/\Delta _n]-k_n}\left| {\bar{Y}}(g)_i^{n} \right| ^{q}\left| {\hat{Y}}(g)_i^{n} \right| ^r, \end{aligned}$$

and these processes implicitly depend on $\Delta _n$ and $k_n$.

Let $p\ge 4$ be an even integer, and define $(\rho (p)_j)_{j=0,...,p/2}$ as the unique numbers solving the triangular system of linear equations

$$\begin{aligned} \left. \begin{matrix} \rho (p)_0=1, \\ \sum _{l=0}^{j}2^{l}m_{2j-2l}C_{p-2l}^{p-2j}\rho (p)_{l}=0, j = 1,2,...,p/2, \end{matrix}\right\} , \end{aligned}$$

with $m_r$ the rth absolute moment of the law ${\mathcal {N}}(0,1)$. We follow the recommendation of the authors and set $p=4$, so that we obtain

$$\begin{aligned} \rho (4)_0=1, \text { } \rho (4)_1=-3, \text { } \rho (4)_2=0.75, \end{aligned}$$

fix $k_n =100$ and for any process Y we set

$$\begin{aligned} {\bar{V}}(Y,g,p)_t^n = \sum _{l=0}^{p/2}\rho (p)_{l}V(Y,g,p-2l,l)_t^n, \end{aligned}$$

which is a robustified version of the power variation in 2.

To compute the robustified test statistic for jumps, we set up the constants

$$\begin{aligned} \gamma = \frac{({{\bar{g}}})(2)}{({{\bar{h}}})(2)}, \gamma ^{'} = \frac{({{\bar{g}}})(p)}{({{\bar{h}}})(p)}, \gamma ^{''} = \frac{\gamma ^{p/2}}{\gamma ^{'}}, \end{aligned}$$

under the assumption that $\gamma ^{''} >1$. The robustified test statistic is

$$\begin{aligned} S_{RJ}(g,h,p)_n = \frac{{\bar{V}}(Z,g,p)_T^n}{{\bar{V}}(Z,h,p)_T^n}. \end{aligned}$$

Asymptotically, the test statistic has the following limit behavior:

$$\begin{aligned} S_{RJ} \left( p,k,\Delta _n \right) \overset{{\mathbb {P}}}{\rightarrow }\left\{ \begin{matrix} 1 &{} \text {on } \Omega _T^j \\ \gamma ^{''} &{} \text {on } \Omega _T^c \end{matrix}\right. . \end{aligned}$$

Introduce the variance scaling term

$$\begin{aligned} \sqrt{\Sigma _{RJ,n}^c} = \frac{M*(g,g,\phi ;p)_T^n-2\gamma ^{p/2}M*(g,h,\phi ,p)_T^n+\gamma ^{p}M*(h,h,\phi ;p)_T^n}{(\Delta _n^{1-p/4}{\bar{V}}(Z,g,p)_T^{n}/\gamma ^{''})^2}, \end{aligned}$$

then the critical value for rejecting the null hypothesis of no jumps is

$$\begin{aligned} C_n^c = \Bigl \{S_{RJ}(g,h,p)_n < \gamma ^{''}- z_{\alpha } \Delta _n^{1/4} \sqrt{\Sigma _{RJ,n}^c} \Bigr \}. \end{aligned}$$

with $z_{\alpha }$ the corresponding quantile of the standard normal distribution, s.t. the rejection region can be obtained by choosing a respective $\alpha$.

4 Data

We sampled price data from seven exchanges located across three regions: Europe, Asia, and the US; the data encompass six of the largest currencies by market capitalization. The dataset ${\mathcal {D}}$ ranges from April 12, 2019 to September 27, 2021. The dataset contains a total of 1,760,537,789 observations of ticks

$$\begin{aligned} (D, t, E, C, x) \in {\mathcal {D}}, \end{aligned}$$

where D denotes the calendar date, $0 \le t < 86,400$ is the time (in seconds) at which the tick was observed,

$$\begin{aligned} E \in \left\{ \text {Binance, Bitfinex, Bitstamp, Coinbase Pro, HitBTC, OKex, Poloniex} \right\} \end{aligned}$$

denotes a crypto exchange of interest,

$$\begin{aligned} C \in \left\{ \text {BCH, BTC, ETC, ETH, LTC, XRP} \right\} \end{aligned}$$

is the observed cryptocurrency, and $x \in {\mathbb {R}}$ is its observed log-value.

From this dataset, we extract one time series, denoted as $X_C$, for each cryptocurrency C on every observed date D. This time series serves as an estimate of the true price of cryptocurrency C on the observed trading day. For each cryptocurrency C, we first consider the set of ticks ${\mathcal {D}}_C$ observed in this currency on date D, i.e.,

$$\begin{aligned} {\mathcal {D}}_C = \bigcup _{E \in {\mathcal {E}}} \{(t,x) : (D,t,E,x,C) \in {\mathcal {D}}\} \end{aligned}$$

with the associated set of time points at which the currency was sampled at

$$\begin{aligned} {\mathcal {T}}_C = \{ t : (t,x) \in {\mathcal {D}}_C \}. \end{aligned}$$

To standardize the time steps, we aggregate these ticks into intervals of 1 s each and take averages over all tick values observed in the respective timespan to obtain a first estimate

$$\begin{aligned} {{\hat{X}}}_C :\{ 0,...,86,399 \} \rightarrow {\mathbb {R}}. \end{aligned}$$

If in second $0 \le s \le 86,399$, there are no observed ticks, we set

$$\begin{aligned} {{\hat{X}}}_C(s) = \text {n.a.n.}, \end{aligned}$$

else, we take an average

$$\begin{aligned} {{\hat{X}}}_C(s) = \frac{1}{n} \sum _{i=1}^n x_i \end{aligned}$$

over the set of ticks

$$\begin{aligned} \{(t,x) \in {\mathcal {D}}_C : s \le t \le s+1\} = \{(t_1,x_1),...,(t_n,x_n)\} \end{aligned}$$

occurring in second s. We then aggregate each resulting estimate ${{\hat{X}}}_C$ into frequency blocks, ensuring that each block contains at least 95% of the potential daily observations for that frequency. The result is our estimate $X_C$.

Therefore, let $\theta \in \{1,5,10,15\}$ be the highest frequency (in seconds) such that

$$\begin{aligned} |\{ s \in \{0,..., 86,399\}: {{\hat{X}}}_C(s) \ne \text {n.a.n.} \}| \ge 0.95 \cdot N_\theta , \end{aligned}$$

where $N_\theta = 3600/\theta$ denotes the maximum number of observations at frequency $\theta$. For example, a dataset aggregated to 1-s intervals would have to have at least $0.95 \cdot N_{\text {1}}=0.95 \cdot 86,400=82,080$ observations. If there are less than $0.95 \cdot N_{15} = 5472$ observations, we concluded that the respective data is not “high frequency" and therefore, omitted the data for this cryptocurrency and this date. We admit that this threshold seems arbitrary, but needed to decide on a cutoff point as there is no unique definition of what exactly determines a high-frequency dataset.

The resulting estimate $X_C :\{0,\theta , 2\theta ,..., N_\theta \theta - 1\} \rightarrow {\mathbb {R}}$ is then simply the last observed aggregated tick between $k\theta$ and $(k+1)\theta$ seconds, i.e.,

$$\begin{aligned} X_C(k\theta ) = {{\hat{X}}}_C(s_k), \end{aligned}$$

where $s_k$ is the largest number $k \theta \le s < (k+1)\theta$ with ${{\hat{X}}}_C(s_k) \ne \text {n.a.n.}$.

Additionally, we omit days where data is not available for all trading hours. These days are omitted to avoid evaluating incomplete days of data. We did not calculate a test statistic on the respective days in order to avoid violating the assumptions of HF data in the testing methodologies. In theory, certain edge cases may emerge, such as the scenario where there exists only a very low number of observations per hour. However, empirical evidence suggests that such instances are exceedingly rare and practically negligible. The aggregation of cross-market data further implies that the prices of an asset on different exchanges follow the same process. As Crépellière et al. (2023) pointed out, opportunities for cross-market arbitraging have diminished since 2018. We therefore make this simplifying assumption. Nevertheless, it would be an interesting area for future research to investigate the differences in market microstructure noise among exchanges. This would also shed light on the effect of pre-averaging and jump detection on different exchanges.

As usual in HF literature, we remove bounceback outliers and returns outside of a range of 10 standard deviations. In terms of the amount of standard deviations the literature varies. Lee and Mykland (2012) use for example a cutoff of 7 standard deviations. To account for the high volatility of CC we relax this cutoff further. To account for cross-market arbitraging, we aggregate the prices per symbol over the different exchanges and take the mean price for each point in time in case of simultaneous observations. The data are obtained from the .

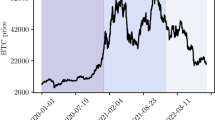
Figure 2 shows the aggregated daily prices of the six CCs on a log scale along with a selection of relevant events in the crypto universe. Recall that these are a series of Donald Trump Tweets attacking cryptos in July 2019, a pro-blockchain statement of Chinese President Xi Jinping in October 2019, the peak of the Covid crisis in March 2020, the third BTC halving in May 2020, large scale wallet movements to exchanges in September 2020, a lawsuit against Ripple in December 22, 2020, Tesla’s $1.5 billion investment in Bitcoin and announcement of plans to accept it as payment in February 2021, Coinbase’s registration statement effectiveness and Nasdaq listing date announcement in April 2021, and Bitcoin’s 30% plunge to $30,000 in May 2021. The plot indicates that these events have an influence not only on BTC, but also on other cryptos in the form of sudden price changes and increased volatility. To understand the nature of these price changes better, we will now give an overview of the data set and then turn to the summary statistics of daily and HF returns and to the frequency of extreme returns.

Fig. 2

Log price of and

Table 1a shows the number of observations per exchange. With roughly one billion observations, 56.9% of observations were collected from Binance. OKex and Coinbase Pro follow with large distance. In contrast, only less than 20 million (1.1%) observations were collected from the smallest exchange Poloniex. Since we collected all ticks, the number of observations resembles the frequency of trades happening on each market place. These differences have various reasons, e.g., not all symbols are traded on all exchanges, and some exchanges are more popular in certain countries. For example, Coinbase Pro and Bitstamp allow for trading CCs against EUR, thus making them more popular in Europe. As a consequence, we observe a high level of concentration on only few exchanges. In order to be able to make a fair comparison, we used cryptos traded against US Dollar (Tether).

Table 1 Data overview

Table 1b shows the number of observations per symbol in the raw dataset and after aggregation. Column two shows the total number of observations in the raw dataset. Column three shows the percentage of observations that each currency contributes to the total number of observations in the dataset. We observe that, similarly to the number of observations per exchange, the data is highly concentrated on a few currencies. In terms of currencies, the market is thus even more strongly concentrated. Columns four and five show the number and the percentage of observations after aggregation. Column six shows the percentage of observations that are left after aggregation. Since we aggregate prices over different exchanges and only on days with enough data, the amount of observations per symbol is reduced drastically. The data pool has then a total of 160,537,822 million observations on a total of 865 trading days. This is slightly lower than the full amount (878 days) caused by database outages or dropped data due to quality issues. After aggregation, the concentration reduces substantially, as we can have no more than 86,400 observations on a single trading day at the highest possible frequency of 1 s. Therefore, BTC is less dominant in the aggregated data, and while ETH and XRP gain in shares of observations, the smaller three currencies barely change in percentage share of total observations. We observe that no currency keeps more than roughly 25% of observations (ETH), while BTC only keeps slightly less than 5 % of observations after aggregation.

Table 2 shows the returns of aggregated CC prices at the corresponding frequencies. As often in financial data, the observed log returns are not normally distributed, as the higher moments show in the last two columns. The large kurtosis shows that there are many values close to zero. This is likely due to the presence of market microstructure noise in HF data, which can be eliminated, e.g., by sampling at lower frequencies or in many cases by means of using techniques such as pre-averaging. The strongly decreased kurtosis at a frequency of 15 s hints at this. The summary statistics indicate that even in very high-frequency large positive or negative returns of up to $\pm 48\%$ (BCH) and + 23% and - 24% (XRP) are observed. The minima and maxima seem symmetric. This is only partly due to the cutoff in the range of 10 standard deviations. In fact, only ETC and LTC are affected by this cutoff where a single return for ETC (LTC) goes up to $\pm 88\%$ ($\pm 81\%$). Unlike all other CCs with a positive skewness, ETC shows a negative skewness at a 1 s frequency. At 5 s, only XRP has a negative skewness. When the data gets aggregated to 10 or 15 s the return distribution is always skewed negatively. This is likely because liquidity is higher during bull runs than during downturns.

Table 2 Comprehensive summary of return statistics across different frequencies

Table 3a shows the statistics of the daily returns of CCs and Fig. 3 shows their histogram. In contrast to HF returns, we observe a negative skewness in all time series. The kurtosis values are much lower, as the daily frequency eliminates market microstructure noise. Furthermore, the minima and maxima have changed significantly. Both the minima and maxima become more extreme for some CCs, and less extreme for others. Thus, the extreme returns on a daily scale in comparison to HF returns seem to differ in some cases, but seem highly similar in others. Intuitively, such extreme events in HF should also have an influence on the price process in the longer run given their disruptive nature (they would be highly unlikely in a pure random walk model). These findings lead us to investigate whether extreme daily returns could be explained by intraday singularities. In such a scenario, only few large observations would cause extreme daily returns and we seek to identify these returns by means of a jump-testing procedure. The histogram shows that while these extreme minima are tail events that happened during the covid shock, there is a substantial amount of returns that are larger than $\pm 5\%$.

Fig. 3

Histogram of daily returns on all time series.

The data show that the characteristics of the different CCs are quite similar, despite their differences in technology and investor attention. The markets are highly concentrated, s.t. most observations are collected from big coins such as BTC and ETH and on big exchanges such as Binance, OKex, and Coinbase Pro. In both daily and in high-frequency time periods, extreme returns occur frequently. Whereas the unprocessed HF returns are difficult to interpret due to market microstructure noise, the daily returns are negatively skewed with long tails. Note that the results on returns differ from, e.g., Liu and Tsyvinski (2020) because we observe a much shorter time span in a later point in time that includes the effects of the Covid crisis in March 2020 and the latest bull run and volatility period in 2021. Indeed, for developing profitable trading strategies and reliable models, we need to account for these statistical properties. Given the high magnitude of returns even at tick level, we have to focus on HF events to preserve the information that this data contains, as we already see that events in HF and in daily frequency seem to be connected. If we want to model these dynamics we need to incorporate knowledge about jumps. In the following section we will show that daily dynamics are largely driven by the occurrence of jumps in high frequency.

Table 3 Return statistics on a daily frequency

5 Understanding CC jumps

5.1 Overview

We preprocess the data to investigate the occurrence of jumps in HF. Since the two testing methodologies differ, we preprocess the dataset differently for both methodologies. Lee and Mykland works best on processing ticks as it does not make any assumptions on the time between two observations. We determine consecutive jump detections by tagging jumps that were detected within 10 moments after initial detection and removing them from the data. Aït-Sahalia, Jacod and Li on the other hand works best on equi-spaced data. Hence, we sample data at a frequency of up to 15 s using the approach described in 4. To maintain a regular structure, we impute missing observations by inserting the last observed price. We set $\alpha = 0.999$ and apply a Bonferroni correction to minimize the detection of spurious jumps. In total, we observed 1,392 jumps on all assets; where Lee and Mykland detected a jump Aït-Sahalia, Jacod and Li detected the presence of jumps on the same day. Note that the method is robust to varying $\alpha$. With $\alpha = 0.99$, we detect 1,779 jumps, setting $\alpha = 0.95$ we detect 2,150 jumps, and with $\alpha = 0.9$ 2,330 jumps.

Figure 4 shows the number of jumps detected per day in all time series. Note that these jumps are always detected on the highest possible frequency, and only on days where the data can be aggregated to a maximum of 15 s. The exact frequency depends on the pre-averaging parameters k and M, which complicates obtaining equi-spaced jump-testing grids. Indeed, there is currently no one-fits-all approach to balance the highly time varying nature of CC price processes with some sort of stable set of parameters for anchoring co-jumps accurately.

We see that the number of jumps is varying over time, while prices and liquidity have largely increased both in comparison to the period of 2011-13 and 2019 vs 2021. The red vertical lines mark the same events as shown in Fig. 1. This not exhaustive list of events includes a series of Trump tweets (July 2019), bullish comments of Xi Jinping (October 2019), the Covid crisis (March 2020), the third BTC halving (May 2020), large transfers to exchange wallets (September 2020), the lawsuit against Ripple (December 2020), Tesla’s $1.5 billion investment in Bitcoin(February 2021), Coinbase’s Nasdaq listing date announcement (April 2021), and Bitcoin’s 30% plunge to $30,000 (May 2021). Although we focused only on a few key events in the crypto universe, these events appear to influence both prices and the number of detected jumps. Even though jumps are frequently occurring, they seem to be clustered in the neighborhood of these events. A higher frequency of jumps often persists over several days. Looking at the nature of price movements around these events, this finding is not surprising as these events were often preceded and/or followed by increased volatility.

Fig. 4

Number of observed jumps on all time series.

Table 4 Number of test days and jumps per asset

Table 4 shows the number of test days and the number of jumps detected. We observe that more testing days do not necessarily cause more jumps. This indicates that spurious jumps are not dominating the results. Moreover, larger CCs tend to jump more often, and the most jump were detected in the largest asset BTC. Most CCs tend to have more jump days than traditional assets, similarly to Scaillet et al. (2020) who find that BTC has an unusually high jump rate.

5.2 Crypto market microstructure and jump testing

Table 5 shows values for k and M, and the block size for jump detection $k*M$ when applying the methodology of Lee and Mykland. The block sizes tend to be quite high. Therefore, the exact moment of jump detection can often only be approximated. Even though we can sample data at the highest frequency, we often have to sub-sample to eradicate market microstructure noise. This is due to high values in the ACF test which serves as an indicator for dependent noise. In the original paper, the authors determine $k=3$ empirically, whereas we often have to choose values of $k\ge 14$. The theoretical properties of existing jump detection methods are not fully applicable to CCs.

Table 5 Summary statistics of k and M (rounded)

This highlights the differences in market microstructure compared to traditional assets. They arise from the 24/7 trading nature that eliminates many of the known patterns, e.g., on closing and opening of exchanges, as well as over the weekend. If, e.g., China announces a change in regulation, this may be well in the middle of the night for US and European based traders. In traditional asset exchanges, these effects are adopted by the market at opening time. However, in crypto markets, they can be adopted instantaneously. Recall Fig. 1, BTC trading volume is highly time varying. Trading volume is related to news regarding specific assets (Rognone et al., 2020), where news arrivals increase trading activity. This is even more so the case for a market that is heavily driven by investor attention (Alexander et al., 2023) and sentiment (Aysan et al., 2024). While trading volume for traditional exchange traded assets is also time varying, their trading is driven by fundamentals that don’t usually change significantly from one day to another with established companies. Also, their trading is contained to the opening hours of exchanges. In effect, the largest assets traded are truly “high frequency", whereas, e.g., ETH is the second largest cryptocurrency, but sometimes cannot be aggregated to a frequency of 1 s as the markets were not liquid enough. Together with the oftentimes large degree of autocorrelation in CC price processes, this raises the question how accurately we can really narrow down exact jump times.

5.3 Seasonality, size and direction of jumps

Fig. 5

Number of jumps per weekday and per hour (both aggregated). Timezone: UTC.

Fig. 6

Size of jumps.

Figure 5 shows the number of jumps aggregated per weekday and per hour. Looking at weekdays, the highest number of jumps is observed during the middle of the week, whereas the lowest values on are on Friday and Saturday. This is an interesting finding, as Petukhina et al. (2021) shows similar patterns in volatility and trading volume on different weekdays. We see a strong connection between volatility and trading volume, and the occurrence of jumps. Additionally, we find evidence for seasonality patterns in the detection of jumps per hour, as most jumps are detected around 13–17h UTC and the lowest number of jumps between 1 and 7 h UTC. This is an interesting finding as the time window of 13–17 h UTC is the one where it is plausible for people ranging from the US, to Europe, and East Asia to be awake (assuming that we could expect the majority of people to be awake between 8 am and 10 pm). The fewest jumps occur, when only Asian exchanges are open (between 12 am and 7 am UTC). When European exchanges are opening, the number of jumps rises (8–9 am UTC). The opening of American exchanges (1–2:30 pm UTC) causes a stark increase in jumps, and with closing of European exchanges (4 pm UTC) the number of jumps rapidly drops.

Figure 6 presents the histogram of jump sizes. It shows a large density of jumps in the area of $\pm 5\%$ and especially in the area of $\pm 2.5\%$, and a dominance of negative jumps. Furthermore, the distribution has heavy tails in both directions. This is a common property for asset returns as well, and provides further evidence for a relation between jumps and returns. Table 6a shows the according summary statistics on jumps, aggregated and separated by positive and negative jumps. Most jumps are rather small, and with roughly 2/3 of jumps being negative, the overall distribution of jumps is negatively skewed and the negative tail is heavier than the positive one.

Table 6 Descriptive statistics on jumps

In contrast to the common assumption that jumps happen mainly during flash crashes, the results indicate that prices do not seem to jump more heavily during bearish periods. It seems that crash patterns resemble a quick but steady sell-off, rather than concentrated, heavy movements. Bullish periods with large upwards price movements seem to create quite similar jumps, although fewer in overall quantity. While CCs undoubtedly have a large downside risk due to their large volatility, this risk was outweighed by the high rewards of the latest bull run. At least in the observed time frame, ETFs and investors may have largely profited from these characteristics of CCs. In addition to the many small jumps, few large jumps can be observed in the tails, as can be seen in Table 6b. Even though most jumps are in the area of $\pm 1\%$, we can observe almost 200 returns smaller than − 2.5% and 145 returns larger than + 2.5%. 71 observed HF returns are smaller than − 5% and 68 returns are larger than + 5%. Looking at jumps with magnitude of $\pm 10\%$, we still observe 23 (24) jumps, whereas 5 (5) returns are $\pm 20\%$. This is a result of the preprocessing done in the Lee and Mykland, as well as Aït-Sahalia, Jacod and Li jump methodology w.r.t. previously discussed challenges when working with HF data. While this clearly blurs the exact moment of an occurred jump, it also means that CCs are prone to jump by more than $\pm 20\%$ within few minutes or seconds during strongly bullish / bearish phases. Even though extreme jumps are much rarer than extreme returns, they still seem to be a reoccurring phenomenon. And despite the obvious differences, the statistical properties of extreme returns and actually detected jumps look similar. Therefore, we now turn to the relationship between jumps and returns. In comparison with Scaillet et al. (2020), we find that with the time being, the skewness of the jump distribution has become negative over all time series.

5.4 The effect of jumps on end-of-day returns

Liu and Tsyvinski (2020) have identified a series of predictors for daily CC returns. The goal of this section is to gain a better understanding of the predictive power that intraday jumps have on end-of-day returns. In other words, we are wondering if jumps have a persistent effect on the underlying price process. Therefore, we run a regression to understand the effect of intraday jumps on end-of-day returns. We first consider a regression of all jumps, then only positive (negative) jumps. We additionally test whether an intraday jump has an effect on the returns of the end of the next day.

Table 7 presents the results of the regression of daily returns against the occurrence of a jump on the same day, the occurrence of a jump on the previous day, and the occurrence of a positive (negative) jump on the same day. The regression tables show the slope estimates and the corresponding standard deviations in brackets below; end-of-day returns in this context refer to the end of any trading day which ends at 23:59:59 UTC. We report significant observations with three stars for a p-value $< 0.001$, two stars for $p <0.01$, and one star for $p < 0.05$. To guarantee robust estimates, we use a one-way fixed effects estimator with a within transformation to account for the differences between the different CCs. We use White standard errors for heteroscedasticity-consistency. We find that jumps significantly affect end-of-day returns as given the dominance of negative jumps in the dataset, the overall effect is negative on daily returns. Accordingly, when separating between positive and negative jumps, jumps either have a positive or negative effect on the return process. A jump on the previous day does not significantly affect daily returns in our dataset. The analysis shows that intraday detection of jumps has implications on end-of-day returns in the same direction as a detected jump, however, not on the following day. Since daily returns in our dataset were negatively skewed for all CCs and the vast majority of detected jumps was also negative, the skewness of a distribution seems to be related to the ratio of positive vs. negative jumps. However, judging from Table 6a this applies only to the number of jumps, but not to their respective size, as the jump size distribution is positively skewed despite having observed mostly negative jumps. Future research could extend this relatively simplistic regression model to study relationships with returns, trading volume and realized volatility among others in more preceding and following periods. It would be interesting to see what happens, e.g., in the first hour, 6, 12, 24, and 48 h and possibly the week before and after each jump. This would enhance our understanding of the exact relationship between high-frequency jumps and those market parameters, and possibly others.

Table 7 Relationship of jumps and daily returns

6 The role of jump clusters in high frequency

The heuristic for clustering jumps in trading data operates on the principle of temporal proximity within a dynamically defined window. This approach for identifying is described in Algorithms 1 and 2 and involves two steps:

• 1. Calculation of the Average Grid Size: The average time between consecutive pre-averaged returns is computed for each symbol. This is used to determine the grid size for that symbol.

• 2. Clustering Jumps: We use a rolling window, five times the average grid size, to determine clusters. A new cluster is initiated whenever the time gap between consecutive jumps exceeds the size of the rolling window.

Algorithm 1

Calculate average grid sizes

Algorithm 2

Cluster jumps based on proximity

There are some drawbacks to this approach. The heuristic assumes that each jump is independent of the others because the jump tests are univariate. A better way would be test for co-jumps, as, e.g., Winkelmann and Yao (2020) is doing on the example of two correlated assets. Pre-averaging trade times to compute the grid size can obscure exact jump times, introducing uncertainty about whether the timely order of jumps within a cluster truly is accurate. Also, if jumps are close to each other, it is unclear whether the jump really triggered another jump or whether this was just rooted in the uncertainty about the exact jump time caused by pre-averaging. Recall Table 5 where the jump could have happened at any point between two observations, but we can only observe a rather sparse grid due to pre-averaging. Since different cryptocurrencies have varying levels of liquidity and trading activity over time, the resulting grid sizes vary day by day. An alternative would be to fixate k and M over time to obtain equi-spaced grids, however, in a time span of two and a half years this approach will introduce some level of bias due to the time varying and especially speculative nature of crypto markets.

When speaking of clusters from here after, we mean that the jumps we identified independently of each other are clustered in time and refer strictly to the outlined heuristic. A more sophisticated approach would be to run a similar test as in Winkelmann and Yao (2020). However, co-jumps would have to be anchored to more than two assets, as we identified 85 clusters in the observed time period where at least 3 assets jumped within a short time period as can be seen in Table 8a. This would be an interesting direction of future research.

Table 8 Summary of jump statistics

While the majority of clusters consist of single jumps, the presence of clusters with multiple jumps indicates periods of heightened market activity, as observed in previous studies. Zhang et al. (2023) suggest self-exciting jumps in BTC, noting they mostly follow medium-sized jumps, and are triggered more by negative than positive jumps. We conclude that assets mostly jump alone, but there is evidence for temporal clustering, self-excitation and contamination effects. While we can observe the time structure of these jumps and will now further dissect these jump clusters, this analysis could be additionally robustified. To the best of our knowledge, noise robust techniques for identifying co-jumps in more than two assets would be required for that, but are currently not available.

Table 8b shows the jumps per single-asset cluster. BTC leads in the frequency of single-asset jumps, followed by ETH and BCH. These cryptocurrencies hold the highest value among the six examined. BTC and ETH notably boast significant trading volumes, emphasizing their importance and liquidity in the cryptocurrency market. It is important to note that the number of BTC jumps (338) is approximately twice that of ETC (158). The substantial difference in the number of jumps between BTC and other CCs suggests that BTC experiences more frequent pronounced jump patterns within the analyzed time frame.

The analysis of self-excitation within jump clusters offers insights into the directional consistency of jumps within the same cluster, as detailed in Table 9a. It is evident that negative jump clusters outnumber positive or mixed-direction clusters, aligning with the findings of Zhang et al. (2023), who suggest that negative jumps tend to trigger self-excitation more frequently than positive jumps on average. Additionally, the aftershocks of negative self-excitation persist longer compared to those of positive self-excitation. Notably, BTC, ETH, and XRP exhibit a higher number of exclusively negative jump clusters. Something we did not cover in this analysis due to the aggregation of data over different exchanges is whether it is possible to link the origin of a self-excitation cluster to a specific exchange. That is, if a jump occurs, e.g., in BTC, it would be interesting to know if the jump happens on all exchanges simultaneously, or if it originates from a specific exchanges. In case of any regularities in this, it would allow us to identify on which exchanges informed traders are active.

The co-occurrence matrix in Table 9b highlights how jumps in one cryptocurrency are associated with jumps in others, indicating potential market inter-dependencies. Specifically, we observe that jumps in one cryptocurrency often coincide with jumps in others. Our analysis reveals notable associations between jumps in Bitcoin (BTC) and Ethereum (ETH), suggesting a strong interconnection between the two leading CCs. This finding echoes the results of Aysan et al. (2024), who also identified significant spillover effects between BTC and altcoins, particularly in the context of positive jumps spilling over from altcoins to BTC. Aysan et al. (2024) find that positive jumps in altcoins can lead to positive jumps in Bitcoin, indicating a momentum effect in the crypto market during favorable conditions. Similarly, our co-occurrence matrix also highlights associations between jumps in different cryptocurrencies, particularly noting the frequent occurrence of jumps in both Bitcoin and Ethereum.

Table 9c presents the conditional probabilities of observing a jump in one cryptocurrency given a jump in another, offering insights into predictive relationships. The conditional probability values are computed based on the empirical likelihood of one cryptocurrency jumping on a day given that the other cryptocurrency has already jumped on the same day. The table presents the probability values for each cryptocurrency in each row, given that a jump has already happened in the cryptocurrency listed in the corresponding column. The conditional probabilities further emphasize Bitcoin’s influence, as the conditional probabilities suggest that in case there is a jump in BTC, there is a higher possibility that other cryptocurrencies will follow compared to other assets. This underscores the potential for predictive modeling and risk management strategies that account for the interconnected nature of cryptocurrency markets.

Table 9 Summary of jump statistics

While Aysan et al. (2024) examine the influence of news events, such as the TRMI occurrence, on jump occurrence in both Bitcoin and altcoins, our study primarily focuses on detecting and analyzing simultaneous jumps at high frequencies. Both results agree on the limited influence of altcoin news on Bitcoin jumps, suggesting that Bitcoin’s market dominance and popularity render it less sensitive to news events in altcoins. Similarly to self-excitation clusters, it would be interesting to further investigate the exact sequence of jumps across assets. In practice, it would be difficult though to perform such an investigating on markets other than BTC and ETH due to liquidity constraints.

7 Conclusion

In this study, we have made several contributions to the understanding of cryptocurrency markets, focusing on the detection and analysis of jumps and their impact on market dynamics. Our analysis spans a period of almost 2.5 years and includes tick-by-tick data from seven major cryptocurrency exchanges, covering a wide range of cryptocurrencies including Bitcoin (BTC), Ethereum (ETH), and Ripple (XRP).

First, we extended previous research on jumps in cryptocurrency markets to include altcoins and Tether trading pairs. To the best of our knowledge this is the first comprehensive investigation of jumps using tick-by-tick data from a large panel of cryptocurrencies traded against Tether. Our findings provide valuable insights into the dynamics of jumps in these markets, revealing both systematic clustering and asymmetries in the distribution of jumps.

Second, we decomposed the temporal dynamics of jumps, shedding light on how jumps are clustered in time and identifying patterns of co-jumps across different cryptocurrencies. Our analysis highlights the interconnectedness of cryptocurrency markets and the influence of major assets like Bitcoin on the behavior of other cryptocurrencies.

Third, we compared the performance of commonly used jump tests in cryptocurrency markets, emphasizing the need for new methodologies that account for the unique market microstructure of cryptocurrencies. Our findings underscore the challenges of accurately detecting jumps in the presence of market microstructure noise in these markets.

Overall, our analysis contributes to the growing body of knowledge on cryptocurrency markets and provides valuable insights for investors, researchers, and policymakers. By understanding the dynamics of jumps and their impact on market behavior, investors can better develop option pricing and predictive models, and implement effective risk management strategies in the still dynamically evolving cryptocurrency universe.