1 Introduction

Nowadays, the interest on noise pollution is quickly growing, due to the fact that sound disturbance made by transports can induce to health damages, such as annoyance, sleep disturbance, or even ischemic heart disease [1]. In general, the instrument to absorb noise is divided in two macro-categories: resonators [2] and porous media [3]. Acoustic resonators mainly include perforated panels [4] and Helmholtz resonators [5]. These solutions show great acoustic performance in correspondence of their resonance frequencies; they are generally tunable, but they perform narrow frequency band gaps of influence [6], thus becoming not useful far from their working frequency. Instead, porous media for acoustic purposes are materials made of channels, cracks, or cavities, which let the sound waves to enter the foam, thus dissipating their energy by viscous and thermal losses; these energy consumption dynamics allow sound absorption over wider frequency ranges [7, 8]. Anyway, porous media, designed standalone, are not so good at low frequencies [9]; this limitation is generally overcome through the use of solutions like multi-layer configurations [10], or porous media with embedded periodic inclusions [11, 12]. The latter is an interesting way to improve the efficiency of acoustic packages: porous media with embedded periodic inclusions exhibit proper dynamic filtering effects that could be advantageous both for the dynamics of the system and its manufacturing aspects. This approach may have several applications in energy, civil, and transportation (aerospace, automotive, and railway) engineering fields, where space, weight, and acoustic comfort still represent critical challenges [13, 14]. In the present work, a new configuration is numerically studied, starting from the state of the art regarding the acoustic packages based on porous meta-materials with embedded periodic inclusions. Its main improvements are represented by the disposition of the inclusions, remarking their positive effects in terms of noise suppression and doing several mass considerations. The sound transmission loss (TL) may be estimated through different approaches, such as the transfer matrix method (TMM) [3], the finite-element method (FEM) [15], the wave finite-element method (WFEM) [10], and the statistical energy analysis (SEA) [16, 17], all having their own advantages and limitations [18]. In the context of this research, TMM and FEM are used. In particular, for the purposes of the present work, the AcuH toolbox developed by WaveSet S.R.L. [19] is used to perform quick and efficient TMM-based calculations for multi-layered configurations.

In Sect. 2, the problem is explained, discussing about the materials used for the acoustic package and the geometrical properties of the analyzed configurations; then, the finite-element implementation is examined. In Sect. 3, the definition of TL is introduced, followed by the equation that is used for its evaluation and the Transfer Matrix Method, considered as an analytical reference with respect to the numerically analyzed homogeneous case. In Sect. 4, the analyses of the case are listed, and then, the results are plotted and discussed. Moreover, mass considerations are done in this section and an optimized configuration for aeronautical use, starting from the meta-core solution analyzed in this work, is investigated. In Sect. 5, the concluding considerations are developed.

2 Definition of the Problem

In this section, an acoustic package is numerically developed, considering a layer of glass wool, with embedded periodic inclusions with the shape of hollow cylinders made of balsa.

2.1 Material and Geometrical Properties

Glass wool is a low-density material that guarantees good acoustic performance; therefore, the addition of solid inclusions can be a problem in the contexts where weight requirements are particularly demanding, as in the case of aeronautic and space fields. With reference to this, a previous evaluation about the inclusion material is necessary: in this context, balsa wood can be an acceptable choice for improving the performance of the foam without experiencing huge mass issues. Balsa is a very soft and light lumber, with a coarse, open grain. Because of its high strength-to-density ratio, balsa is a very popular material for light, stiff structures in model bridge tests, model buildings, and construction of aircraft models.

The glass wool and balsa properties are, respectively, reported in Tables 1 and 2. The glass wool properties are useful to numerically simulate the foam behavior, according to Johnson–Champoux–Allard approach [20, 21], which models the foam as an equivalent fluid. The FE implementation and analysis of this kind of materials has already been validated by the authors in their previous works [22], as well as for more complicated di-phasic behaviors [23] through the use of Biot theory of poro-elasticity [24].

Table 1 Properties of balsa
Full size table
Table 2 Properties of glass wool
Full size table

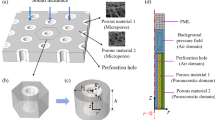
The package is formed by an array, where the single unit cell is a cube with dimension d, with an embedded cylinder with radius \(r = 0.2 d\) and length d (Fig. 1). The improvement developed in this paper is done considering the unit cell described above and changing the disposition of the inclusion inside it. For doing this, it is necessary to introduce \(\delta\) as a new parameter that characterizes the angular shift of the inclusions along the thickness. This is more clear thanks to Fig. 2b, defining \(\delta\) as the angle that rules the position shift of the inclusions with respect to the initial configuration, represented in (Fig. 2a).

Fig. 1
figure 1

Geometry of the cell made by glass wool with an embedded balsa cylinder

Full size image
Fig. 2
figure 2

a 2D representation of the Configuration 0 cell, with the inclusion placed in the vertical line of symmetry; b 2D representation of the cell with a pattern angle ruled by \(\delta\)

Full size image

This work is focused on TL, which can give a value of the quality of the meta-core solutions developed. A first configuration (named as Configuration 0) is built considering an unit cell like the one plotted in Fig. 1, and developing an array of four of those cells (Fig. 3a). The TL of such a configuration is well studied by Magliacano et al. [25]; here, the authors want to demonstrate how the performance of a similar meta-core solution can be further improved thanks to a specific pattern of inclusions. For each configuration, the inclusions are disposed one respect to the next in anti-symmetrical position (Fig. 3b), taking into account the proposed unit cell and the parameter \(\delta\) previously introduced and explained in Fig. 2b. It is reasonable to think that a pattern where the inclusions are disposed differently respect to Fig. 3a, where are one after the other along the same direction, can lead to positive dissipation effects and then higher values of TL. This may be physically explained by the fact that, for Configuration 0, while the sound wave is traveling through the sample, a part of it perceives the presence of the inclusions, but this does not happen in the zones of the foam that are far from the inclusions itself; instead, adopting an angle \(\delta\) different from \(0^{\circ }\) results in a wider fraction of the sound power being affected by the presence of the inclusions, and then by the periodic effect.

Fig. 3
figure 3

a Configuration 0: inclusions are placed in the plane of symmetry. b New meta-core solution, where the inclusions are disposed anti-symmetrically

Full size image

In the analyzed case with four cells, the first and the third inclusions are placed to the right of the center of symmetry, with an angle \(+\,\delta\), while the second and the fourth ones are on its left, with an angle \(-\,\delta\). The angle \(\delta\) is arbitrarily limited, such that the inclusions are always completely embedded in the cells; this is not mandatory, because this package can be periodically repeated in x and y directions. Anyway, it may still be convenient to operate as described, defining a limit angle \(\delta _{\text {lim}}\), such that

$$\begin{aligned} \delta _{\text {lim}} = \arctan \bigg ({1-\frac{2 r}{d}}\bigg ). \end{aligned}$$
(1)

In this case, the ratio between r and d is fixed, and then \(\delta _{\text {lim}}\) as well, with an angle equal to \(31^{\circ }\). An angle \(\delta > \delta _{\text {lim}}\) means an inclusion divided on the left and on the right side of the cell section (x-axis) because of the periodicity of the package; thus, a maximum angle \(\delta _{\text {lim}}\) is defined for numerical reasons and for reducing the complexity of the system.

Fig. 4
figure 4

3D model for one of the analyzed configurations

Full size image

2.2 Finite-Element Implementation

For what concerns the FE implementation, the module “Pressure Acoustics and Frequency Domain” of COMSOL MultiPhysics is used both as modeling environment and numerical solver.

The numerical model is developed as follows: a layer of air (blue color, with \(c_{\text {air}} = 343\) m/s and \(\rho _{\text {air}} = 1.2\) kg/m\(^3\)) is placed at the top to excite the system with a plane-wave radiation acting along the negative verse of z-axis. Then, the acoustic package is placed, consisting in four glass wool cells (yellow color) with embedded cylinders (red color), followed by another layer of air (blue color) with perfectly matching boundary conditions (Fig. 4). A perfectly matched layer (PML) represents an artificial absorbing layer for wave equations, commonly used to truncate computational regions in numerical methods to simulate problems with open boundaries; this allows the PML to strongly absorb outgoing waves from the interior of a computational region, without reflecting them back into the interior. The boundary conditions applied on faces normal to x- and y-axes are not relevant for analyses with the aforementioned kind of excitation, since under such condition, the waves do not have propagating components along those directions; thus, for the sake of computational simplicity, a sound hard boundary wall (SHBW) boundary condition is applied herein. Eventually, for different angles of excitation, proper periodic conditions should be used instead. A detailed description of classical FE formulation and equations can be easily found in the context of the relevant literature [26]. The resulting geometrical model is then represented in Fig. 4.

Table 3 Number of FE mesh elements for each of the studied configurations
Full size table
Fig. 5
figure 5

Examples of meshes for three configurations: a configuration 1, d = 12.5 mm, \(\delta = 10^{\circ }\), b configuration 4, d = 50.0 mm, \(\delta = 20^{\circ }\), c configuration 8, d = 100 mm, \(\delta = 15^{\circ }\)

Full size image

This study is developed for eight configurations, leading to 56 different tests (6 angles plus case without inclusions as reference per each of the eight configurations), where the main variable are represented by

  • the dimension of the unit cell d (and, as a consequence, the radius of the inclusion and the thickness of the inclusion walls);

  • the angle \(\delta\) from \(0^{\circ }\) to \(25^{\circ }\).

For all the considered meta-core solutions, the mesh consists of tetrahedral elements, generated through physics controlled algorithms that are pre-implemented in the software. The maximum element size is imposed lower than \(\frac{1}{5}\) of the minimum wavelength. The number of mesh elements changes with \(\delta\); then, for each configuration, the average number of domain, boundary, and edge elements is reported in Table 3, while in Fig. 5, there are some visual examples.

3 Methodological Framework

In this section, the authors present the methods adopted in the present work, aiming at the conceptualization and design of an innovative acoustic package for noise insulation.

3.1 Transmission Loss

The performance of each of the developed meta-core solution is evaluated in terms of TL, which can be defined as follows:

$$\begin{aligned} {\text {TL}} = 10 \log _{10}\frac{\varPi _{\text {incident}}}{\varPi _{\text {transmitted}}}, \end{aligned}$$
(2)

where \(\varPi _{\text {incident}}\) is the incident power and \(\varPi _{\text {transmitted}}\) is the transmitted one. TL values are generally plotted in the frequency domain. Taking into account a noise disturbance traveling through a panel that divides the source from the receiver, the TL represents the classical parameter used to evaluate how many dBs of the initial power are perceived by the receiver; it should be pointed out that this is an absolute value, while other measure scales are used to predict what a human can perceive with its ears, mainly related to psycho-acoustics.

3.2 Transfer Matrix Method

The TL of a homogeneous system, e.g., a homogeneous sample made of glass wool (which represents a basic attempt of acoustic solution, then improved with the meta-cores proposed in this work), has its analytical formulation, developed according to the TMM [3]. This TL solution is meaningful to validate FEM analyses and results, and can be written as follows:

$$\begin{aligned} {\text {TL}} = 10\log _{10}{\frac{1}{4} | T_{11} + \frac{T_{12}}{\rho _0 c_0} + \rho _0 c_0 T_{21} + T_{22}| }, \end{aligned}$$
(3)

where

$$\begin{aligned} \begin{bmatrix} T_{11} &{} T_{12} \\ T_{21} &{} T_{22} \end{bmatrix} = \begin{bmatrix} \cos (kd) &{} j\sin (kd)Z_c \\ j\sin (kd)/Z_c &{} \cos (kd) \end{bmatrix}. \end{aligned}$$
(4)

In this study, the analytical evaluation of the TL of an acoustic package is produced for a homogeneous glass wool layer, but also for a multi-layered model made of different materials, thus demonstrating the flexibility of this approach, which is very suitable for the validation of numerical models with an analytic reference related to homogeneous cases. In particular, for a multi-layered model, the matrix becomes

$$\begin{aligned} \begin{bmatrix} T_{11} &{} T_{12} \\ T_{21} &{} T_{22} \end{bmatrix} = \prod _{n} \begin{bmatrix} T_{11,n} &{} T_{12,n} \\ T_{21,n} &{} T_{22,n} \end{bmatrix}, \end{aligned}$$
(5)

where \(T_{ij,n}\) is the matrix coefficient in the ith row and jth column of the n-layer in a multi-layered model. Thus, for evaluating the TL of a complex system, it is necessary to perform the product of the TMM matrices related to each layer. Moreover, the TMM can be used for rigid materials as well, but with different matrix coefficients

$$\begin{aligned} \left\{ \begin{array}{l} T_{11,{\text {rigid}}} = 1 \\ T_{12,{\text {rigid}}} = i \omega m (1 - D \frac{ k_0^4}{\omega ^2 m}) \\ T_{21,{\text {rigid}}} = 0 \\ T_{22,{\text {rigid}}} = 1, \end{array}\right. \end{aligned}$$
(6)

where \(m = \rho t\), with: \(\rho\) is the density of the material, t is the thickness of the layer, and D is its flexural rigidity.

4 Analyses and Results

In this section, several meta-core solutions, listed in Table 3, are investigated, analyzed, and discussed. Once described the several obtained results, some important considerations about the mass increase are developed; then, the opportunity to introduce this class of meta-solutions for a realistic aeronautic application is considered.

4.1 Parametric Analyses About Dimension of the Unit Cells and Angular Shift of the Inclusions

These analyses are meant to highlight how a different angular pattern of the inclusions may influence the TL of this package, comparing the results of each configuration with two standard cases: the homogeneous one (obviously without inclusions), and the case with inclusions at \(\delta = 0^{\circ }\). To define a reference, the TL of each homogeneous case is evaluated making use of the TMM. Figure 6 stands as a starting point for each configuration; then, acoustic packages with meta-cores are considered advantageous if and only if their TL is greater than the respective homogeneous one in most of the audible frequency range, or at least in the frequency band of interest.

Fig. 6
figure 6

TL of homogeneous case for each configuration, evaluated through the TMM

Full size image

The TL of the eight analyzed configurations is plotted in Fig. 7, thus performing a comparison between the homogeneous case (evaluated with both TMM and FEM approaches), and the cases with \(\delta = 0^{\circ }\), \(\delta = 5^{\circ }\), \(\delta = 10^{\circ }\), \(\delta = 15^{\circ }\), \(\delta = 20^{\circ }\), and \(\delta = 25^{\circ }\). It is well known that the addition of periodic inclusion inside a homogeneous package brings to a high increase in terms of TL in the region where the half-wavelength is almost equal to the length of periodicity; then, known that the wavelength \(\lambda\) is equal to \(\frac{c}{f}\), before running the analyses, it is possible to suggest that the higher is the value of d, the lower is the range of frequency where the periodicity effect appears, since the wavelength is inversely proportional to the frequency itself.

It is evident that the increase in terms of TL caused by the effect of \(\delta\) is not negligible; in particular, this increase is higher for configurations with a lower value of d. This may represent an encouraging result, due to the fact that thinner configurations are often required in several applications where space and weight are strictly limited. Moreover, it is important to underline that a meta-core solution applied to a very thick layer of homogeneous foam may actually be unnecessary, since its acoustic performance would reasonably be already good enough. The effect of the dimension of the cell, combined with the pattern angle \(\delta\), is further clarified in Fig. 8, where the TL for each configuration is plotted, only considering the cases with \(\delta = 0^{\circ }\) and \(\delta = 25^{\circ }\).

Fig. 7
figure 7

TL of the analyzed configurations in the frequency range of interest

Full size image
Fig. 8
figure 8

TL for each configuration, considering the cases with \(\delta = 0^{\circ }\) and \(\delta = 25^{\circ }\)

Full size image

To better appreciate the produced TL improvements, the maximum values of TL for the studied configurations are reported in Table 4, comparing the maximums for \(\delta = 0^{\circ }\) with those for \(\delta = 25^{\circ }\); in a similar way, the respective percentage increases are shown in Table 5.

Table 4 TL comparison between the homogeneous case and the case with \(\delta = 0^{\circ }\) and \(\delta = 25^{\circ }\); \(f_{\text {res}}\) is the frequency where the transmission loss is maximum
Full size table
Table 5 TL percentage increases for \(\delta = 0^{\circ }\) respect to the homogeneous case; TL percentage increases for \(\delta = 25^{\circ }\) respect to the homogeneous case; TL percentage increases for \(\delta = 25^{\circ }\) respect to \(\delta = 0^{\circ }\)
Full size table
Fig. 9
figure 9

a Contour plot of the % increase of  TL, considering the eight configurations studied for six values of \(\delta\), evaluated respect to the homogeneous case; b contour plot of the % increase of TL, evaluated respect to the case with \(\delta = 0^{\circ }\)

Full size image

In conclusion, two contour plots are presented for the TL increase of the \(\delta = 25^{\circ }\) case respect to the homogeneous one (Fig. 9a), as well as, in the same way, for the TL increase of the \(\delta = 25^{\circ }\) case respect to the \(\delta = 0^{\circ }\) one (Fig. 9b).

4.2 Mass Considerations

The meta-core solutions modeled, investigated, and analyzed show remarkable performance in the ranges of frequency where the periodicity effect gives its influence. However, to reach this goal, periodic inclusions made of balsa are introduced, thus implying a non-negligible increase in terms of mass, due to the fact that the density of glass wool is 16 kg/m\(^3\), while that of balsa is 163 kg/m\(^3\). Considering that the ratio between the radius of the cylinder r and the dimension of the cubic cell d is unchanged, the increase in mass is always the same for any configuration, and its percentage value is equal to around 90%. With the scope of investigating a workaround for the aforementioned issue, the authors have examined the possibility to replace the plain cylindrical inclusions with hollow ones, with a limited wall thickness and air inside the cavities (Fig. 10). In particular, the thickness of the walls is chosen equal to \(t_{\text {walls}} = 0.05 d\), which corresponds to an increase of mass of about 44% compared to the homogeneous configuration, and a decrease of mass of about 33% respect to the configurations with plain inclusions, keeping almost the same performance in terms of TL. It should be noted that the increase/decrease in terms of mass are even more advantageous when such meta-core package is placed in a system with additional layers of solid materials, which contribute to increase the total base mass.

Fig. 10
figure 10

Representation of the configuration with hollow inclusions, for \(d = 50\) mm \(\delta = 0^{\circ }\), with solid (on the left) and transparent (on the right) views

Full size image

4.3 Design of an Optimized Configuration for Aeronautical Applications

A typical fuselage multi-layered panel section is analyzed herein; the developed acoustic package is placed in this complex system, characterized by:

  • the outer skin of the fuselage, made of carbon fiber;

  • the acoustic solution, made of glass wool and embedded periodic inclusions;

  • a sandwich representing the interior trim, whose skins are made of pre-preg epoxy and with a core made of Divinycell F50. Divinycell F is a class of polyethersulfone-based (PESU) recyclable foamed core materials, specifically developed for aircraft interior requirements. It combines lightweight characteristics [“50” represents its density expressed in (kg/m\(^3\))] [27].

The model characterization is clarified in Fig.11, while the material properties are reported in Tables 1, 2, and 6.

Fig. 11
figure 11

a Typical fuselage multi-layered panel section, improved with a meta-core solution with plain inclusions; b typical fuselage multi-layered panel section, improved with a meta-core solution with hollow inclusions

Full size image
Table 6 Material properties of the layers of a typical aircraft fuselage
Full size table

The acoustic package made of glass wool and four periodic inclusions is studied for both plain and hollow cylindrical inclusions. The thickness of the glass wool package is 75.00 mm, and thus that of the unit cell is 18.75 mm. The whole system is 84.95 mm thick, and it is analyzed to evaluate its TL in the range of \(\delta\) that goes from \(0^{\circ }\) to \(25^{\circ }\). As expected, the percentage mass increase is smaller than before:

  • for filled inclusions, there is a mass increment of 18% respect to the case without inclusions;

  • for hollow inclusions, there is a mass increment of 7% respect to the case without inclusions.

In Fig. 12, the TL results are reported in the frequency band of interest. The analyses are carried on for the configurations having hollow inclusions, and then compared with the TMM results related to package without inclusions for two different cases: the first one is the starting acoustic package without inclusions, while the second one is numerically developed simulating an increase in terms of mass of the whole system equal to the mass increment due to hollow inclusions (a system 7% heavier than the initial one). Then, it is possible to see that, even with the same mass, the system with hollow inclusions performs better in the band gap of interest.

Fig. 12
figure 12

TL of the system with embedded hollow inclusions, in the frequency range of interest

Full size image

5 Conclusions

In this work, a model with embedded inclusions inside an acoustic package is developed, considering the variation of the angular pattern of the inclusions. This approach is proposed for several configurations with different dimensions of the unit cell; the results are plotted and explained, showing the excellent performance of this innovative configuration, which exhibits better results for lower values of thickness; this is a positive result, since solutions with limited dimensions can be more suitable for several fields, from transport to civil applications. Moreover, a more lightweight solution is conceptualized and analyzed, adopting hollow inclusions instead of plain ones, leading to the same values in terms of TL performance. In conclusion, some mass considerations are presented, also for a case that estimates the mass increase of the new meta-core system in a more realistic way.