1 Introduction

With the rapid development of society and the continuous progress in modern science and technology, engineering structures closely related to people's lives, such as high-rise buildings, bridges, dams, and offshore platforms, are gradually evolving towards larger and more complex configurations [1, 2]. On one hand, factors such as overlooking certain influences on the actual behavior of engineering structures during design, the complexity of structural calculations for complex systems, design errors, and construction errors can lead to discrepancies between the actual behavior of engineering structures and their design objectives [3, 4]. On the other hand, during use structures are subject to environmental erosion, material aging, the long-term effects of loads, fatigue, as well as the sudden effects of natural disasters such as earthquakes, floods, and typhoons. This collective impact inevitably results in damage accumulation and resistance degradation, potentially leading to catastrophic accidents in extreme cases [5, 6]. Effective diagnosis and monitoring of structures can provide insights into their current condition, enabling timely repairs of damaged structures. This is crucial for enhancing the reliability of structural operations, ensuring production safety, effectively reducing maintenance costs, and guiding the rational use of structures [7,8,9].

Structural damage diagnosis technology aims to identify the actual behavior of structures and establish more accurate structural analysis models. Accurate structural models not only enable more precise predictions of the response of real systems but also provide references for potential failure paths and modes in structures [10,11,12]. The fundamental issues in structural damage diagnosis technology involve determining whether a structure has incurred damage, locating the damage, and assessing the extent of the damage. These aspects constitute quantitative evaluations of structural defects, integrity, functional use, and durability. Furthermore, by recognizing or detecting the behavior of structures at different times, long-term online monitoring of structural conditions can be achieved. This serves as the foundation for structural damage detection technology and provides a basis for the implementation of reinforcement measures [13,14,15].

The time-domain regression method (TDRM) is a commonly used approach in time series analysis. The basic idea is to establish an auto-regressive model based on the response data of the system. This model utilizes auto-regressive coefficients or residual quantities to construct damage indicators, achieving the goal of structural damage diagnosis [16]. Sohn et al. [17] proposed a two-stage AR-ARX model based on the acceleration response signals of the structure. They utilized the changes in the residuals of this model before and after damage to achieve structural damage diagnosis. Nair et al. [18] established an auto-regressive moving average time series model (ARMA) based on structural vibration response signals. They suggested using the first three coefficients of the AR model as damage indicators, and through testing and analysis of experimental results, they evaluated the effectiveness of this indicator, successfully achieving structural damage diagnosis and localization. Hu et al. [19] addressed the online structural damage diagnosis problem by establishing an auto-regressive moving average (ARMA) model. They defined a representative combination of the first three coefficients of the AR model as a damage-sensitive factor. Through numerical simulations on the ASCE benchmark standard structure, they demonstrated the feasibility and effectiveness of this method.

This study introduces a substructure identification regression method for frame structures, developed through the exploration of frame structure mechanics models and damage detection methods. The proposed method enables the direct detection of structural stiffness to identify the location and extent of structural damage.

The main advantages of the novel time-domain regression method (TDRM) over existing damage diagnostic methods are as follows:

  • (1) Simple modeling, easy computation, and effective identification.

  • (2) Sensitivity to minor structural damage, with good noise reduction capability.

  • (3) No need for known external excitation signals, relying solely on the structural output signals for damage identification, thus avoiding the need for external excitation acquisition.

  • (4) Utilizing its autoregressive coefficients not only allows for determining the occurrence of damage but also enables direct determination of damage location and severity.

2 Frame structure model simplification

2.1 Substructure analysis method

Large civil engineering structures pose increasing challenges for overall structural damage analysis as the number of degrees of freedom and unknown parameters increases. In recent years, scholars both domestically and internationally have proposed various methods to address this difficulty in conducting damage diagnosis for large civil engineering structures. In reality, when a structure undergoes damage, only specific local regions are affected while the majority of the structure remains undamaged. The substructure analysis method addresses this by dividing the entire structure into multiple substructures for local damage identification, offering an effective approach for damage detection and state assessment in large and complex structures. This method enables hierarchical and zonal identification, providing an effective solution for precise damage localization and reducing identification time [20].

We divides the frame structure into multiple substructures, and implements local damage identification within each substructure following the “divide and conquer” approach. As shown in Fig. 1, the framework structure is divided into substructures, with each substructure consisting of three nodes, overlapping one node with the next substructure. Within each substructure, a regression model is established using the structural acceleration response signals from adjacent floors to extract their autoregressive coefficients for identifying stiffness losses in the structure.

Fig. 1
figure 1

Frame structure model and its standard substructures

Full size image

2.2 Shear frame structure simplified model

As the number of degrees of freedom and unknown parameters increases, conducting overall structural damage analysis for large civil engineering structures becomes significantly challenging. Therefore, for complex large-scale structural systems, simplification of the model is often necessary to facilitate structural damage diagnosis. In recent years, scholars have proposed various methods to address this challenge in conducting damage diagnosis for large civil engineering structures. To simplify computations, existing frame structures are often simplified into shear frame structures that do not consider rotational degrees of freedom. The simplified model of a shear frame structure is depicted in Fig. 2.

Fig. 2
figure 2

Shear frame structure simplified model

Full size image

2.3 Improved simplified model of plane frame structures

For complex large-scale structures, simplification of models is often necessary for facilitating structural damage diagnosis. The prevalent simplified form of frame structures is the shear structure model. However, recent studies by some scholars indicate that replacing complex frame structures with shear model can result in overly simplistic models, leading to inaccuracies in damage localization [21]. To overcome this oversimplification issue, complex frame structures can be simplified to plane frame structures [22]. Koh et al. [23] proposed an improved condensation method (ICM) for plane frame structures and demonstrated through simulations and experimental results that, compared to shear-type frame structures, this simplified plane frame structure allows for more accurate damage localization. However, this method requires knowledge of the stiffness matrix and external excitation signals of the frame structure after damage has occurred, limiting its practical application in engineering projects.

This study employs a novel model reduction method [24] to transform complex frame structure into a simplified plane frame structure, where each level possesses one translational degree of freedom and two rotational degrees of freedom. This is done to overcome the drawbacks associated with shear structure model. In the simplified analysis of the frame structure, the complex frame structure is initially transformed into a plane frame structure. Figure 3 shows a schematic diagram of the frame structure with multi-story and multi-bay, and Fig. 4 shows a standard substructure mechanical model of frame structure.

Fig. 3
figure 3

Improved simplified model of plane frame structures

Full size image
Fig. 4
figure 4

Standard substructure mechanical model of frame structure

Full size image

Assumption: (1) The beam and column satisfy the Euler Bernoulli beam, and the cross-section of the beam perpendicular to the axis before deformation remains plane after deformation (assuming a rigid cross-section); (2) The plane after cross-section deformation remains perpendicular to the axis after deformation; (3) The floor slab is rigid within the plane.

3 A novel time-domain regression damage detection method

According to Newton’s Second Law, ignoring damping, the dynamic equation of layer \(i\) of the Fig. 4 substructure can be expressed as:

$$ m_{i} \ddot{x}_{i} = V_{i} + V_{i + 1} $$
(1)

Here, \(V_{i}\) represents the shear force induced by the lower part of the \(i\) th floor, and \(V_{i + 1}\) represents the shear force induced by the upper part of the \(i\) th floor. Figure 2 shows the frame divided into independent substructures, and individual analyses are performed on each of these substructures.

According to the Euler–Bernoulli beam theory, the shear force can be expressed as:

$$ V_{i} = \sum\limits_{j = 1}^{m + 1} \left[ - \frac{{12EI_{ij} }}{{H_{i}^{3} }}(x_{i} - x_{i - 1} ) - \frac{{6EI_{ij} }}{{H_{i}^{2} }}(\theta_{ij} + \theta_{(i - 1)j} )\right] $$
(2)
$$ V_{i + 1} = \sum\limits_{j = 1}^{m + 1} \left[ - \frac{{12EI_{(i + 1)j} }}{{H_{(i + 1)}^{3} }}(x_{i} - x_{i - 1} ) + \frac{{6EI_{(i + 1)j} }}{{H_{(i + 1)}^{2} }}(\theta_{ij} + \theta_{(i + 1)j} )\right] $$
(3)

Among them, \(\theta_{ij}\) represents the rotational degrees of freedom generated by the \(i\) th floor and \(j\) th column, \(x_{i}\) is the displacement response of the \(i\) th floor, \(EI_{ij}\) is the bending stiffness of the \(i\) th floor and \(j\) th columns, \(H_{i}\) is the height of the \(i\) th floor.

Let \({{EI_{ij} } \mathord{\left/ {\vphantom {{EI_{ij} } {EI}}} \right. \kern-0pt} {EI}} = \alpha_{j}\),\({{EI_{(i + 1)j} } \mathord{\left/ {\vphantom {{EI_{(i + 1)j} } {EI}}} \right. \kern-0pt} {EI}} = \beta_{j}\), where \(EI\) is the reference stiffness introduced for simplified calculation, and \(\alpha_{j}\) and \(\beta_{j}\) are the newly introduced stiffness coefficients. Equation (1) can be expressed as:

$$ \begin{gathered} m_{i} \ddot{x}_{i} = \sum\limits_{j = 1}^{m + 1} \big[ - \frac{12EI}{{H_{i}^{3} }}\alpha_{j} (x_{i} - x_{i - 1} ) - \frac{12EI}{{H_{i + 1}^{3} }}\beta_{j} (x_{i} - x_{i + 1} ) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - \frac{6EI}{{H_{i}^{2} }}\alpha_{j} (\theta_{ij} + \theta_{(i - 1)j} ) + \frac{6EI}{{H_{i + 1}^{3} }}\beta_{j} (\theta_{ij} + \theta_{(i + 1)j} )\big] \hfill \\ \end{gathered} $$
(4)

The deformation of the corner related term in Eq. (4) is:

$$ \begin{gathered} \sum\limits_{j = 1}^{m + 1} \big[ - \frac{6EI}{{H_{i}^{2} }}\alpha_{j} (\theta_{ij} + \theta_{(i - 1)j} ) + \frac{6EI}{{H_{i + 1}^{3} }}\beta_{j} (\theta_{ij} + \theta_{(i + 1)j} )\big] \hfill \\ = - \frac{{6EI_{ij} }}{{H_{i}^{2} }}\sum\limits_{k = 1}^{m + 1} {\alpha_{k} } \left\{ {{{\sum\limits_{j = 1}^{m + 1} {\left[ {\alpha_{j} (\theta_{ij} + \theta_{(i - 1)j} )} \right]} } \mathord{\left/ {\vphantom {{\sum\limits_{j = 1}^{m + 1} {\left[ {\alpha_{j} (\theta_{ij} + \theta_{(i - 1)j} )} \right]} } {\sum\limits_{k = 1}^{m + 1} {\alpha_{k} } }}} \right. \kern-0pt} {\sum\limits_{k = 1}^{m + 1} {\alpha_{k} } }}} \right\} \hfill \\ \,\,\,\, + \frac{{6EI_{ij} }}{{H_{i + 1}^{2} }}\sum\limits_{k = 1}^{m + 1} {\beta_{k} } \left\{ {{{\sum\limits_{j = 1}^{m + 1} {\left[ {\beta_{j} (\theta_{ij} + \theta_{(i + 1)j} )} \right]} } \mathord{\left/ {\vphantom {{\sum\limits_{j = 1}^{m + 1} {\left[ {\beta_{j} (\theta_{ij} + \theta_{(i + 1)j} )} \right]} } {\sum\limits_{k = 1}^{m + 1} {\beta_{k} } }}} \right. \kern-0pt} {\sum\limits_{k = 1}^{m + 1} {\beta_{k} } }}} \right\} \hfill \\ \end{gathered} $$
(5)

To simplify the calculations, introduce a new rotational response, namely the weighted average rotational response:

$$ {{\theta_{i - 1}^{ + } = \sum\limits_{j = 1}^{m + 1} {\big[\alpha_{j} \theta_{(i - 1)j} ]} } \mathord{\left/ {\vphantom {{\theta_{i - 1}^{ + } = \sum\limits_{j = 1}^{m + 1} {[\alpha_{j} \theta_{(i - 1)j} \big]} } {\sum\limits_{k = 1}^{m + 1} {\alpha_{k} } }}} \right. \kern-0pt} {\sum\limits_{k = 1}^{m + 1} {\alpha_{k} } }} $$
(6)
$$ {{\theta_{i}^{ - } = \sum\limits_{j = 1}^{m + 1} {[\alpha_{j} \theta_{ij} ]} } \mathord{\left/ {\vphantom {{\theta_{i}^{ - } = \sum\limits_{j = 1}^{m + 1} {[\alpha_{j} \theta_{ij} ]} } {\sum\limits_{k = 1}^{m + 1} {\alpha_{k} } }}} \right. \kern-0pt} {\sum\limits_{k = 1}^{m + 1} {\alpha_{k} } }} $$
(7)
$$ {{\theta_{i}^{ + } = \sum\limits_{j = 1}^{m + 1} {[\beta_{j} \theta_{ij} ]} } \mathord{\left/ {\vphantom {{\theta_{i}^{ + } = \sum\limits_{j = 1}^{m + 1} {[\beta_{j} \theta_{ij} ]} } {\sum\limits_{k = 1}^{m + 1} {\beta_{k} } }}} \right. \kern-0pt} {\sum\limits_{k = 1}^{m + 1} {\beta_{k} } }} $$
(8)
$$ {{\theta_{i + 1}^{ - } = \sum\limits_{j = 1}^{m + 1} {[\beta_{j} \theta_{(i + 1)j} ]} } \mathord{\left/ {\vphantom {{\theta_{i + 1}^{ - } = \sum\limits_{j = 1}^{m + 1} {[\beta_{j} \theta_{(i + 1)j} ]} } {\sum\limits_{k = 1}^{m + 1} {\beta_{k} } }}} \right. \kern-0pt} {\sum\limits_{k = 1}^{m + 1} {\beta_{k} } }} $$
(9)

Among them, \(\theta_{i}^{ - }\) is the weighted average rotational response caused by the lower column of the \(i\) th floor; \(\theta_{i}^{ + }\) is the weighted average rotational response caused by the upper column of the \(i\) th floor. By substituting the newly introduced weighted average rotational response into Eq. (5), Eq. (4) can be simplified as:

$$ \begin{gathered} m_{i} \ddot{x}_{i} = \sum\limits_{j = 1}^{m + 1} [ - \frac{12EI}{{H_{i}^{3} }}\alpha_{j} (x_{i} - x_{i - 1} ) - \frac{12EI}{{H_{i + 1}^{3} }}\beta_{j} (x_{i} - x_{i + 1} ){\kern 1pt} {\kern 1pt} {\kern 1pt} \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - \frac{6EI}{{H_{i}^{2} }}\alpha_{j} (\theta_{i}^{ - } + \theta_{i - 1}^{ + } ) + \frac{6EI}{{H_{i + 1}^{3} }}\beta_{j} (\theta_{i}^{ + } + \theta_{i + 1}^{ - } )] \hfill \\ \end{gathered} $$
(10)

The equivalent floor stiffness of the \(i\) th and \(i + 1\) th floors is defined as:

$$ k_{i,i - 1} = \sum\limits_{j = 1}^{m + 1} {\frac{12EI}{{H_{i}^{3} }}\alpha_{j} } $$
(11)
$$ k_{i,i + 1} = \sum\limits_{j = 1}^{m + 1} {\frac{12EI}{{H_{i + 1}^{3} }}\beta_{j} } $$
(12)

Define the new equivalent weighted average rotational response as:

$$ \delta_{i} = {{(\theta_{i}^{ - } + \theta_{i - 1}^{ + } )H_{i} } \mathord{\left/ {\vphantom {{(\theta_{i}^{ - } + \theta_{i - 1}^{ + } )H_{i} } 2}} \right. \kern-0pt} 2} $$
(13)
$$ \delta_{i} = {{(\theta_{i}^{ - } + \theta_{i - 1}^{ + } )H_{i} } \mathord{\left/ {\vphantom {{(\theta_{i}^{ - } + \theta_{i - 1}^{ + } )H_{i} } 2}} \right. \kern-0pt} 2} $$
(14)

By substituting Eq. (10):

$$ m_{i} \ddot{x}_{i} = - k_{i,i - 1} ({\kern 1pt} x_{i} - x_{i - 1} + \delta_{i} ){\kern 1pt} - k_{i,i + 1} (x_{i} - x_{i + 1} - \delta_{i + 1} ) $$
(15)

Similarly, considering structural damping and external forces, the dynamic equation of the \(i\) th floor can be expressed as:

$$ \begin{gathered} m_{i} \ddot{x}_{i} = - k_{i,i - 1} ({\kern 1pt} x_{i} - x_{i - 1} + \delta_{i} ){\kern 1pt} - c_{i,i - 1} ({\kern 1pt} \dot{x}_{i} - \dot{x}_{i - 1} + \dot{\delta }_{i} ) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - k_{i,i + 1} (x_{i} - x_{i + 1} - \delta_{i + 1} ) - c_{i,i + 1} ({\kern 1pt} \dot{x}_{i} - \dot{x}_{i + 1} - \dot{\delta }_{i + 1} ) + p_{i} \hfill \\ \end{gathered} $$
(16)

Convert inter-floor damping \(c_{i,i - 1}\) and \(c_{i,i - 1}\) to node damping \(c_{i - 1}\), \(c_{i}\), and \(c_{i + 1}\):

$$ c_{i} = c_{i,i - 1} + c_{i,i + 1} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} c_{i - 1} = - c_{i,i - 1} ,{\kern 1pt} {\kern 1pt} c_{i + 1} = - c_{i,i + 1} $$
(17)

The general expression of the dynamic equation for the ith floor can be obtained by substituting Eq. (17) into Eq. (16) and simplifying it as follows:

$$ \begin{gathered} m_{i} \ddot{x}_{i} = - k_{i,i - 1} ({\kern 1pt} x_{i} - x_{i - 1} + \delta_{i} ){\kern 1pt} - k_{i,i + 1} (x_{i} - x_{i + 1} - \delta_{i + 1} ) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - c_{i} \dot{x}_{i} - c_{i - 1} \dot{x}_{i - 1} - c_{i + 1} \dot{x}_{i + 1} + c_{i - 1} \dot{\delta }_{i} - c_{i + 1} \dot{\delta }_{i + 1} + p_{i} \hfill \\ \end{gathered} $$
(18)

Through the aforementioned simplification analysis, the frame structure can be simplified to a plane frame structure with three degrees of freedom per level, as shown in Fig. 5: one translational degree of freedom \(x_{i}\) and two rotational degrees of freedom \(\theta_{i}^{ - }\), \(\theta_{i}^{ + }\).

Fig. 5
figure 5

Reduced model for frame structures

Full size image

Multiplying both ends of Eq. (18) by \(\ddot{x}_{i} (t - \tau )\) and taking the expected value:

$$ \begin{gathered} m_{i} R_{{\ddot{x}_{i} }} (\tau ) = k_{i,i - 1} [R_{{\ddot{x}_{i} x_{i - 1} }} (\tau ) - R_{{\ddot{x}_{i} x_{i} }} (\tau ) - R_{{\ddot{x}_{i} \delta_{i} }} (\tau )] + k_{i,i + 1} [R_{{\ddot{x}_{i} x_{i + 1} }} (\tau ) - R_{{\ddot{x}_{i} x_{i} }} (\tau ) + R_{{\ddot{x}_{i} \delta_{i + 1} }} (\tau )] \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - c_{i} R_{{\ddot{x}_{i} \dot{x}_{i} }} (\tau ) - c_{i - 1} R_{{\ddot{x}_{i} \dot{x}_{i - 1} }} (\tau ) - c_{i + 1} R_{{\ddot{x}_{i} \dot{x}_{i + 1} }} (\tau ) + c_{i - 1} R_{{\ddot{x}_{i} \dot{\delta }_{i} }} (\tau ) - c_{i + 1} R_{{\ddot{x}_{i} \dot{\delta }_{i + 1} }} (\tau ) \hfill \\ \end{gathered} $$
(19)

Simplify the damping term as follows:

$$ R_{{\ddot{x}_{i} }} (\tau ) = {{k_{i,i - 1} } \mathord{\left/ {\vphantom {{k_{i,i - 1} } {m_{i} }}} \right. \kern-0pt} {m_{i} }}[R_{{\ddot{x}_{i} x_{i - 1} }} (\tau ) - R_{{\ddot{x}_{i} x_{i} }} (\tau ) - R_{{\ddot{x}_{i} \delta_{i} }} (\tau )] + {{k_{i,i + 1} } \mathord{\left/ {\vphantom {{k_{i,i + 1} } {m_{i} }}} \right. \kern-0pt} {m_{i} }}[R_{{\ddot{x}_{i} x_{i + 1} }} (\tau ) - R_{{\ddot{x}_{i} x_{i} }} (\tau ) + R_{{\ddot{x}_{i} \delta_{i + 1} }} (\tau )] $$
(20)

Converting Eq. (20) into the form of a regression equation, the time-domain regression method (TDRM) based on substructures can be expressed as:

The top floor(\(i = n\)):

$$ {\mathbf{Y}} = {\mathbf{R}}_{{\ddot{x}_{n} }} (\tau_{j} ),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} j = 1, \ldots ,N $$
(21)
$$ {\mathbf{X}} = [{\mathbf{R}}_{{\ddot{x}_{n} x_{n - 1} }} (\tau ) - {\mathbf{R}}_{{\ddot{x}_{n} x_{n} }} (\tau ) - {\mathbf{R}}_{{\ddot{x}_{n} \delta_{n} }} (\tau ){\kern 1pt} ] $$
(22)
$$ {{\varvec{\upbeta}}} = ({\mathbf{X^{\prime}X}})^{ - 1} {\mathbf{X^{\prime}Y}} = [{{k_{n,n - 1} } \mathord{\left/ {\vphantom {{k_{n,n - 1} } m}} \right. \kern-0pt} m}_{n} {\kern 1pt} ]^{T} $$
(23)

The middle floor(\(2 \le i \le n - 1\))

$$ {\mathbf{Y}} = {\mathbf{R}}_{{\ddot{x}_{i} }} (\tau_{j} ),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} j = 1, \ldots ,N $$
(24)
$$ {\mathbf{X}} = [{\mathbf{R}}_{{\ddot{x}_{i} x_{i - 1} }} (\tau ) - {\mathbf{R}}_{{\ddot{x}_{i} x_{i} }} (\tau ){\kern 1pt} - {\mathbf{R}}_{{\ddot{x}_{i} \delta_{i} }} (\tau ){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathbf{R}}_{{\ddot{x}_{i} x_{i + 1} }} (\tau ) - {\mathbf{R}}_{{\ddot{x}_{i} x_{i} }} (\tau ) + {\mathbf{R}}_{{\ddot{x}_{i} \delta_{i + 1} }} (\tau )] $$
(25)
$$ {{\varvec{\upbeta}}} = ({\mathbf{X^{\prime}X}})^{ - 1} {\mathbf{X^{\prime}Y}} = [{{k_{i,i - 1} } \mathord{\left/ {\vphantom {{k_{i,i - 1} } m}} \right. \kern-0pt} m}_{i} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{k_{i,i + 1} } \mathord{\left/ {\vphantom {{k_{i,i + 1} } m}} \right. \kern-0pt} m}_{i} {\kern 1pt} ]^{T} $$
(26)

The bottom floor(\(i = 1\))

$$ {\mathbf{Y}} = {\mathbf{R}}_{{\ddot{x}_{1} }} (\tau_{j} ),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} j = 1, \ldots ,N $$
(27)
$$ {\mathbf{X}} = [{\mathbf{R}}_{{\ddot{x}_{1} x_{g} }} (\tau ) - {\mathbf{R}}_{{\ddot{x}_{1} x_{1} }} (\tau ) - {\mathbf{R}}_{{\ddot{x}_{1} \delta_{1} }} (\tau ){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathbf{R}}_{{\ddot{x}_{1} x_{2} }} (\tau ) - {\mathbf{R}}_{{\ddot{x}_{1} x_{1} }} (\tau ) + {\mathbf{R}}_{{\ddot{x}_{1} \delta_{2} }} (\tau )] $$
(28)
$$ {{\varvec{\upbeta}}} = ({\mathbf{X^{\prime}X}})^{ - 1} {\mathbf{X^{\prime}Y}} = [{{k_{1,0} } \mathord{\left/ {\vphantom {{k_{1,0} } m}} \right. \kern-0pt} m}_{1} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{k_{1,2} } \mathord{\left/ {\vphantom {{k_{1,2} } m}} \right. \kern-0pt} m}_{1} {\kern 1pt} ]^{T} $$
(29)
$$ {\varvec{Y}} = \varvec{X}\boldsymbol{\beta} $$
(30)

In these equations, \({\varvec{Y}}\) represents the regression variable, \({\varvec{X}}\) stands for the regression factor, and \({\varvec{\beta}}\) denotes the regression coefficient. \({\varvec{R}}_{{\ddot{x}x}} (\tau )\) signifies the cross-correlation function between acceleration and displacement, \({\varvec{R}}_{{\ddot{x}\delta }} (\tau )\) represents the cross-correlation function between acceleration and angular displacement, and \({\varvec{R}}_{{\ddot{x}}} (\tau )\) indicates the autocorrelation function of acceleration. \(k_{i,j}\) denotes the stiffness value of the column between the \(i\) th and \(j\) th floor slabs, while \(j\) represents the number of sampling points.

Given the time-domain regression model with regression variables and factors, namely the structure's acceleration, displacement, and rotation displacement signals, the regression coefficients of this model can be determined. By extracting the stiffness-related terms from these regression coefficients, the objective of identifying the structural stiffness can be achieved.

4 Reconstruction of structural rotation information

In the above regression method, it is necessary to know the complete response information of the structure, including all joint rotations in the frame, as the input signal for identifying the inter-story column stiffness of the frame structure. This is a very demanding requirement in practice. In order to simplify the process of damage diagnosis and solve the problems in measuring structural rotational information. Static cohesion technology [25, 26] can be used to reconstruct the rotation response, to reconstruct the structural rotation information through the measured structural displacement response signal.

4.1 Force analysis

The displacement decomposition diagram of the beam element is shown in Fig. 6, with each node having two translational displacements and one rotational displacement.

Fig. 6
figure 6

Displacement decomposition diagram of beam element

Full size image

When the axial deformation of the beam is not considered, its element stiffness matrix is:

$$ {\mathbf{k}}_{1} = \left[ {\begin{array}{*{20}c} {\frac{12EI}{{l^{3} }}} & {\frac{6EI}{{l^{2} }}} & { - \frac{12EI}{{l^{3} }}} & {\frac{6EI}{{l^{2} }}} \\ {\frac{6EI}{{l^{2} }}} & \frac{4EI}{l} & { - \frac{6EI}{{l^{2} }}} & \frac{2EI}{l} \\ { - \frac{12EI}{{l^{3} }}} & { - \frac{6EI}{{l^{2} }}} & {\frac{12EI}{{l^{3} }}} & { - \frac{6EI}{{l^{2} }}} \\ {\frac{6EI}{{l^{2} }}} & \frac{2EI}{l} & { - \frac{6EI}{{l^{2} }}} & \frac{4EI}{l} \\ \end{array} } \right] $$
(31)

When the stiffness of the inter-story columns in the frame structure satisfies \({{k_{ij} } \mathord{\left/ {\vphantom {{k_{ij} } {\sum\nolimits_{j = 0}^{m} {k_{ij} } }}} \right. \kern-0pt} {\sum\nolimits_{j = 0}^{m} {k_{ij} } }} = {{k_{(i + 1)j} } \mathord{\left/ {\vphantom {{k_{(i + 1)j} } {\sum\nolimits_{j = 0}^{m} {k_{(i + 1)j} } }}} \right. \kern-0pt} {\sum\nolimits_{j = 0}^{m} {k_{(i + 1)j} } }}\), then the rotational displacement satisfies \(\theta_{i}^{ - } = \theta_{i}^{ + }\). Because in practical engineering, the stiffness distribution of columns on the same floor of the frame structure is basically the same, it can be considered that the rotational displacement of beam column nodes on the same floor is equal. Therefore, the standard substructure of the three degree of freedom frame structure shown in Fig. 6 can be simplified as shown in Fig. 7.

Fig. 7
figure 7

Simplified diagram of standard substructure for frame structure

Full size image

The stiffness matrix of each element in Fig. 7 can be represented as:

$$ {\mathbf{k}}_{x} = \left[ {\begin{array}{*{20}c} {\frac{{12EI_{x} }}{{H_{x}^{3} }}} & {\frac{{6EI_{x} }}{{H_{x}^{2} }}} & { - \frac{{12EI_{x} }}{{H_{x}^{3} }}} & {\frac{{6EI_{x} }}{{H_{x}^{2} }}} \\ {\frac{{6EI_{x} }}{{H_{x}^{2} }}} & {\frac{{4EI_{x} }}{{H_{x}^{{}} }}} & { - \frac{{6EI_{x} }}{{H_{x}^{2} }}} & {\frac{{2EI_{x} }}{{H_{x}^{{}} }}} \\ { - \frac{{12EI_{x} }}{{H_{x}^{3} }}} & { - \frac{{6EI_{x} }}{{H_{x}^{2} }}} & {\frac{{12EI_{x} }}{{H_{x}^{3} }}} & { - \frac{{6EI_{x} }}{{H_{x}^{2} }}} \\ {\frac{{6EI_{x} }}{{H_{x}^{2} }}} & {\frac{{2EI_{x} }}{{H_{x}^{{}} }}} & { - \frac{{6EI_{x} }}{{H_{x}^{2} }}} & {\frac{{4EI_{x} }}{{H_{x}^{{}} }}} \\ \end{array} } \right] $$
(32)

Let \(k_{x} = {{12EI_{x} } \mathord{\left/ {\vphantom {{12EI_{x} } {H_{x} }}} \right. \kern-0pt} {H_{x} }}\), Eq. (31) can be expressed as:

$$ {\mathbf{k}}_{x} = \left[ {\begin{array}{*{20}c} {k_{x} } & {\frac{{H_{x} }}{2}k_{x} } & { - k_{x} } & {\frac{{H_{x} }}{2}k_{x} } \\ {\frac{{H_{x} }}{2}k_{x} } & {\frac{{H_{x}^{2} }}{3}k_{x} } & { - \frac{{H_{x} }}{2}k_{x} } & {\frac{{H_{x}^{2} }}{6}k_{x} } \\ { - k_{x} } & { - \frac{{H_{x} }}{2}k_{x} } & {k_{x} } & { - \frac{{H_{x} }}{2}k_{x} } \\ {\frac{{H_{x} }}{2}k_{x} } & {\frac{{H_{x}^{2} }}{6}k_{x} } & { - \frac{{H_{x} }}{2}k_{x} } & {\frac{{H_{x}^{2} }}{3}k_{x} } \\ \end{array} } \right] $$
(33)

Therefore, the overall stiffness matrix of the standard substructure shown in Fig. 7 is composed of element stiffness matrices \({\mathbf{k}}_{{{\mathbf{i - 1}}}}\), \({\mathbf{k}}_{{\mathbf{i}}}\) and \({\mathbf{k}}_{{{\mathbf{i + 1}}}}\):

$$ {\mathbf{k}} = \left[ {\begin{array}{*{20}c} {k_{i - 1} + k_{i} } & { - \frac{{H_{i - 1} }}{2}k_{i - 1} + \frac{{H_{i} }}{2}k_{i} } & { - k_{i} } & {\frac{{H_{i} }}{2}k_{i} } & 0 & 0 \\ {} & {\frac{{H_{i - 1}^{2} }}{3}k_{i - 1} + \frac{{H_{i}^{2} }}{3}k_{i} } & { - \frac{{H_{i} }}{2}k_{i} } & {\frac{{H_{i}^{2} }}{6}k_{i} } & 0 & 0 \\ {} & {} & {k_{i} + k_{i + 1} } & { - \frac{{H_{i} }}{2}k_{i} + \frac{{H_{i + 1} }}{2}k_{i + 1} } & { - k_{i + 1} } & {\frac{{H_{i + 1} }}{2}k_{i + 1} } \\ {} & {} & {} & {\frac{{H_{i}^{2} }}{3}k_{i} + \frac{{H_{i + 1}^{2} }}{3}k_{i + 1} } & { - \frac{{H_{i + 1} }}{2}k_{i + 1} } & {\frac{{H_{i + 1}^{2} }}{6}k_{i + 1} } \\ {} & {} & {} & {} & {k_{i + 1} } & { - \frac{{H_{i + 1} }}{2}k_{i + 1} } \\ {} & {} & {} & {} & {} & {\frac{{H_{i + 1}^{2} }}{3}k_{i + 1} } \\ \end{array} } \right] $$
(34)

The overall stiffness matrix \({\mathbf{k}}\) is a symmetric matrix that can be transformed into rows and columns:

$$ {\mathbf{k}}^{*} = \left[ {\begin{array}{*{20}c} {k_{i - 1} + k_{i} } & { - k_{i} } & 0 &\vline & { - \frac{{H_{i - 1} }}{2}k_{i - 1} + \frac{{H_{i} }}{2}k_{i} } & {\frac{{H_{i} }}{2}k_{i} } & 0 \\ {} & {k_{i} + k_{i + 1} } & { - k_{i + 1} } &\vline & { - \frac{{H_{i} }}{2}k_{i} } & { - \frac{{H_{i} }}{2}k_{i} + \frac{{H_{i + 1} }}{2}k_{i + 1} } & {\frac{{H_{i + 1} }}{2}k_{i + 1} } \\ {} & {} & {k_{i + 1} } &\vline & 0 & { - \frac{{H_{i + 1} }}{2}k_{i + 1} } & { - \frac{{H_{i + 1} }}{2}k_{i + 1} } \\ \hline {} & {} & {} &\vline & {\frac{{H_{i - 1}^{2} }}{3}k_{i - 1} + \frac{{H_{i}^{2} }}{3}k_{i} } & {\frac{{H_{i}^{2} }}{6}k_{i} } & 0 \\ {} & {} & {} &\vline & {} & {\frac{{H_{i}^{2} }}{3}k_{i} + \frac{{H_{i + 1}^{2} }}{3}k_{i + 1} } & {\frac{{H_{i + 1}^{2} }}{6}k_{i + 1} } \\ {} & {} & {} &\vline & {} & {} & {\frac{{H_{i + 1}^{2} }}{3}k_{i + 1} } \\ \end{array} } \right] $$
(35)

4.2 Static condensation method

The static condensation method, also known as the master–slave degree-of-freedom method, was initially proposed by Guyna in 1965 [27]. This approach involves the partitioning of a structure's degrees of freedom into master and slave degrees of freedom [28]. It neglects the inertial forces on condensed degrees of freedom and employs the principle of potential energy invariance to condense the mass and stiffness matrices. Essentially, it is a form of static degree of freedom condensation technique. Serving as a simplified solution for dynamic systems with degrees of freedom, static condensation allows for the reconstruction of unknown rotational displacement information in a structure’s dynamic analysis. This is achieved by reconstructing the unknown rotational displacement information from known translational displacement information through the static condensation method.

The dynamic equation of the frame can be written (neglecting structural damping for simplicity) in block form as:

$$ \left[ {\begin{array}{*{20}c} {{\mathbf{M}}_{{{\mathbf{tt}}}} } & {{\mathbf{M}}_{{{\mathbf{tr}}}} } \\ {{\mathbf{M}}_{{{\mathbf{rt}}}} } & {{\mathbf{M}}_{{{\mathbf{rr}}}} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\mathbf{\ddot{X}}}_{{\mathbf{t}}} } \\ {{\mathbf{\ddot{X}}}_{{\mathbf{r}}} } \\ \end{array} } \right]{\mathbf{ + }}\left[ {\begin{array}{*{20}c} {{\mathbf{K}}_{{{\mathbf{tt}}}} } & {{\mathbf{K}}_{{{\mathbf{tr}}}} } \\ {{\mathbf{K}}_{{{\mathbf{rt}}}} } & {{\mathbf{K}}_{{{\mathbf{rr}}}} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\mathbf{X}}_{{\mathbf{t}}} } \\ {{\mathbf{X}}_{{\mathbf{r}}} } \\ \end{array} } \right]{\mathbf{ = }}\left[ {\begin{array}{*{20}c} {{\mathbf{F}}_{{\mathbf{t}}} } \\ {{\mathbf{F}}_{{\mathbf{r}}} } \\ \end{array} } \right] $$
(36)

Among them, the subscripts \(r\) represents the translational displacement of the node, and \(t\) represents the rotational displacement of the node.

Because the inertial force in the direction of the rotation can be ignored, so \({\mathbf{F}}_{{\mathbf{r}}} = 0\). Assumed the mass distribution of the framework structure is concentrated, so \({\mathbf{M}}_{{{\mathbf{rt}}}} = {\mathbf{M}}_{{{\mathbf{rr}}}} = 0\). Therefore, by expanding the second line of Eq. (36):

$$ {\mathbf{K}}_{{{\mathbf{rt}}}} {\mathbf{X}}_{{\mathbf{t}}} + {\mathbf{K}}_{{{\mathbf{rr}}}} {\mathbf{X}}_{{\mathbf{r}}} {\mathbf{ = 0}} $$
(37)

According to the above equation, the rotational displacement can be expressed as translational displacement:

$$ {\mathbf{X}}_{{\mathbf{t}}} = - {\mathbf{K}}_{{{\mathbf{rt}}}}^{ - 1} {\mathbf{K}}_{{{\mathbf{rr}}}} {\mathbf{X}}_{{\mathbf{r}}} $$
(38)

According to Eq. (35), the sub-stiffness coefficient matrices \({\mathbf{K}}_{{{\mathbf{rt}}}}\) and \({\mathbf{K}}_{{{\mathbf{rr}}}}\) can be expressed as:

$$ {\mathbf{K}}_{{{\mathbf{rt}}}} = \left[ {\begin{array}{*{20}c} { - \frac{{H_{i - 1} }}{2}k_{i - 1} + \frac{{H_{i} }}{2}k_{i} } & {\frac{{H_{i} }}{2}k_{i} } & 0 \\ { - \frac{{H_{i} }}{2}k_{i} } & { - \frac{{H_{i} }}{2}k_{i} + \frac{{H_{i + 1} }}{2}k_{i + 1} } & {\frac{{H_{i + 1} }}{2}k_{i + 1} } \\ 0 & { - \frac{{H_{i + 1} }}{2}k_{i + 1} } & { - \frac{{H_{i + 1} }}{2}k_{i + 1} } \\ \end{array} } \right] $$
(39)
$$ {\mathbf{K}}_{{{\mathbf{rr}}}} = \left[ {\begin{array}{*{20}c} {\frac{{H_{i - 1}^{2} }}{3}k_{i - 1} + \frac{{H_{i}^{2} }}{3}k_{i} } & {\frac{{H_{i}^{2} }}{6}k_{i} } & 0 \\ {\frac{{H_{i}^{2} }}{6}k_{i} } & {\frac{{H_{i}^{2} }}{3}k_{i} + \frac{{H_{i + 1}^{2} }}{3}k_{i + 1} } & {\frac{{H_{i + 1}^{2} }}{6}k_{i + 1} } \\ 0 & {\frac{{H_{i + 1}^{2} }}{6}k_{i + 1} } & {\frac{{H_{i + 1}^{2} }}{3}k_{i + 1} } \\ \end{array} } \right] $$
(40)

Therefore, given the known health condition of the frame structure and the inter-story stiffness values, the unknown rotational displacement values can be reconstructed through the aforementioned steps using the obtained translational displacement values. Then, calculate the equivalent weighted average rotational displacement response \(\delta_{i}\) (\(\delta_{i} = (\theta_{i} + \theta_{i - 1} )H_{i} /2\)) using the reconstructed rotational displacement \(\theta_{i}\), and use \(\delta_{i}\) as the input signal for the regression model.

5 Numerical simulation

5.1 Model introduction

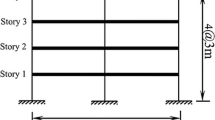
To demonstrate the effectiveness of the newly proposed model to improve the accuracy of damage detection, a numerical example of a five-story and two-bay plane frame is utilized herein. The parameters of the frame structure are as follows (shown in Fig. 8): the flexural rigidities \(EI_{ij}\) of all columns and beams are the same and equal to \(15 \times 10^{7} {\text{N}} \cdot {\text{m}}^{{2}}\); the height of each story of the structure is \(H_{i} = 3{\text{m}}\) (\(i = 1, \cdots ,5\)); the linear mass of beams and columns is 200 kg/m, the mass of each floor slab is \(m_{i} = 1 \times 10^{5} {\text{kg}}\), and the span of each bay is \(L_{j} = 4{\text{m}}\) (\(j\) = 1、2). Hence, the equivalent story stiffnesses of all stories in the frame are the same and equal to \(k_{i,i - 1} = k_{i - 1,i} = \sum\nolimits_{0}^{j} {{{12EI_{ij} } \mathord{\left/ {\vphantom {{12EI_{ij} } {H_{i}^{3} }}} \right. \kern-0pt} {H_{i}^{3} }}} = 160 \times 10^{7} {\text{N/m}}\).The damping matrix of the frame structure is proportional to the stiffness matrix; the damping ratio of the first mode of the structure is 2%.

Fig. 8
figure 8

Five-story two-span frame structure model

Full size image

5.2 Damage pattern setting

Damage Case 1: The stiffness value of the middle column on the first floor is reduced by 15%, that is 5% reduction of the equivalent story stiffness. \(k_{1} = 152MN/m\).

Damage Case 2: The stiffness value of the middle column on both the second and fourth floors is reduced by 15%, that is \(k_{2} = k_{4} = 152MN/m\).

Damage Case 3: Add 0.3 × 105 kg of concentrated mass on the fourth floor slab.

In this study, the stiffness values of the structure before and after damage were calculated as \(k_{i}\) and \(\hat{k}_{i}\). The damage index DF was established based on the percentage of stiffness loss:

$$ DF_{i} = \frac{{\left| {k_{i} } \right. - \left. {\hat{k}_{i} } \right|}}{{k_{i} }} \times 100\% $$
(41)

5.3 Numerical results

Random white noise signals with a mean value of 0 and a root mean square (RMS) value of 1 were applied as external excitations on the beam-column joints of each floor in the plane frame structure depicted in Fig. 5. The sampling frequency was set at 200Hz, and the sampling duration was 50s. To assess the performance of the damage detection method in resisting noise, random white noise with a root mean square (RMS) value of 10% was added to the acceleration response signals, and the results were compared with those obtained without noise.

Figure 9 presents the response time history of the first-floor beam-column joints without damage and noise. In this figure, subfigure (a) illustrates the time history of translational acceleration response for the first-floor beam-column joints in a healthy state. Subfigure (b) depicts the reconstructed translational displacement time history obtained through displacement reconstruction techniques applied to the translational acceleration response. Subfigure (c) shows the time history of the reconstructed rotational displacement obtained by further applying static condensation techniques to the reconstructed translational displacement response. Finally, subfigure (d) displays the time history of the reconstructed rotational acceleration obtained through static condensation techniques.

Fig. 9
figure 9

Time history response without damage and noise

Full size image

5.3.1 Damage case 1

From Figs. 10 and 11, it can be seen that the structure suffered approximately 5% damage on the first floor, which is consistent with the actual situation. The recognition error in the figure is due to the displacement and rotation signals in the model input values being obtained through reconstruction techniques, which amplify the system error. Overall, the TDRM detection method proposed in this paper still performs well under the influence of white noise, and can accurately determine the location and degree of damage.

Fig. 10
figure 10

Identification results for damage case 1 with no-noise

Full size image
Fig. 11
figure 11

Identification results for damage case 1 with 10% noise

Full size image

In the Figs. 10 and 11, the blue bar represents the identified value of equivalent story stiffness for a floor in its substructure, the green bar represents the identified value of equivalent story stiffness for the floor at the same location in its neighbouring substructure, and the red bar represents the theoretical value of equivalent story stiffness for the floor.

5.3.2 Damage case 2

Figures 12 and 13 show the numerical simulation results of damage case 2, with each element representing the same meaning as damage case 1. According to Figs. 12 and 13, the structure suffered approximately 5% damage in both second and fourth floors, which is consistent with the actual situation. The setting of this case indicates that the ADRM damage detection method proposed in this article is applicable to the diagnosis of multiple damage situations. From the diagnostic results of the above two cases, it can be seen that this method can accurately determine the occurrence, location, and quantitative analysis of damage. It can not only diagnose single damage, but also diagnose the occurrence of multiple damage situations, and has good noise resistance.

Fig. 12
figure 12

Identification results for damage case 2 with no-noise

Full size image
Fig. 13
figure 13

Identification results for damage case 2 with 10% noise

Full size image

5.3.3 Damage case 3

Damage condition 3 simulates damage by adding an additional concentrated mass to the fourth floor slab. At this time, the elastic stiffness of the structure remains unchanged, but the geometric stiffness below the fourth floor will be reduced due to the gravity P-△ effect. The setting of this damage condition is to determine whether the damage identification method proposed in this article can be used to distinguish the different structural damages caused by changes in mass and stiffness.

From Fig. 14, it can be seen that the additional mass on the fourth floor slab caused a reduction in the stiffness of the structure from 1st to 4th floors, while the stiffness value on the 5th floor remained unchanged. This case indicates that the damage detection method can not only identify damage caused by changes in structural mass, but also distinguish the differences in structural damage caused by changes in mass and stiffness.

Fig. 14
figure 14

Identification results for damage case 3 with no-noise

Full size image

In Fig. 14, the blue and green columns represent the same meanings as case 1 and case 2, respectively. The yellow column represents the theoretical value of the equivalent inter-story column stiffness for this floor when no damage has occurred.

6 Conclusion

This article considers the existence of rotational degrees of freedom in actual frame structures. Firstly, by simplifying the mechanical model of a multi-story multi-bay frame structure, a novel reduced model for the frame is proposed with three degrees of freedom for each node.

Secondly, an ADRM damage detection model was established based on the motion equation. The model takes the response signal of the structure as the known input and the equivalent story stiffness value as the output. The purpose of an inductive substructure identification method for frame structures considering node rotation has been achieved.

Finally, a two-span five-story frame structure was established to validate the damage detection method. It has been demonstrated through numerical calculations that this method can accurately diagnose single and multiple damages in frame structures, and can distinguish the differences in structural damage caused by changes in mass and stiffness.

Although this damage detection method has shown significant advantages in damage localization, damage degree judgment, and noise resistance. However, this method may increase system errors due to that displacement and rotation signals are obtained through reconstruction techniques during the modeling process. Therefore, reducing the error of signal reconstruction is the key issue to be addressed in the next step of work.

Next, on one hand, it is necessary to establish an experimental platform for experimental validation to further demonstrate the effectiveness and reliability of this method. We will design a plane frame structure to overcome the coupled motion in the x and y directions of three-dimensional frame structures under loading conditions, ensuring it possesses only one horizontal displacement degree of freedom and two rotational degrees of freedom within the plane. On the other hand, it is necessary to explore new damage diagnosis methods that can accurately locate and determine the degree of damage without relying on structural types, in order to overcome the constraints of structural types on loss diagnosis.