1 Introduction

Barium titanate and sodium bismuth titanate are good ceramic materials showing good properties like electrical, ferroelectric, piezoelectric and electromechanical coupling, etc. Generally solid solutions of above these two materials are investigated for the enhancement of these properties as reported by some researchers [1,2,3,4,5,6,7]. In our earlier studies, we have investigated the [Ba(NdxTi1−2xNbx)O3]1−y[Na0.5Bi0.5TiO3]y ceramics with x = 0.1 and varying y values. These materials showed good piezoelectric and electromechanical coupling conversion. In the present study, we have chosen the above ceramic materials with x = 0.1 and y = 0.60, 0.65 and 0.70 for the investigation of dielectric, DC and AC resistivity properties. In ferroelectrics, the variation of dielectric permittivity with temperature is usually indirectly characterized from ω and T by the Arrhenius law, modified Arrhenius law (also called Chen et al. law) [8] and by Vogel–Fulcher’s relation [9]. The Arrhenius relation is valid for solid materials in which the dipoles are free to rotate and the interaction between them is zero. However, in a real solid, the dipoles are not free and the material properties are dependent on the interaction among these dipoles. The Debye frequency is generally of the order of 1012 to 1015 Hz. In relaxor materials, Vogel–Fulcher relationship equation is used to characterize the materials. With this equation, one obtains physically reasonable parameters, i.e., ω0 < 1015 Hz. Though one gets physically reasonable parameters for Vogel–Fulcher law, as in the case of dipolar cluster glasses, Vogel–Fulcher temperature is found to depend on the range of ω values investigated and hence there is a whole range of activation energies and relaxation times. Considering the relaxor materials as an intermediate case between normal ferroelectrics and Debye medium, Chen et al. law, i.e., modified the Arrhenius law is used for describing the relaxation behavior of relaxors. Using these equations, information regarding the activation energy for relaxation and long-range interactions and dipolar freezing temperature can be obtained indirectly from angular frequency and Tmax. There also report studying the relaxation behavior of relaxor materials with statistical studies or modeling and also by using the Lorentz and Gaussian fitting [10,11,12,13]. In our earlier studies, we have proposed modified Lorentz equation which is very simplest and direct way to directly describe or model the temperature dependence of dielectric permittivity with T and ω simultaneously in terms of activation energy and relaxation times for relaxor ferroelectric materials [14, 15]. This modified Lorentz equation can also be used to model the anomalies observed in the temperature dependence of DC and AC resistivity plots. Modeling using this modified Lorentz equation is a new way to estimate the activation energy and relaxation times for conduction and relaxation process. In the present study, modeling has been carried out and is reported in this paper.

2 Experimental procedure

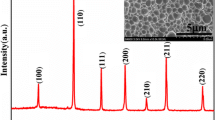
A new [Ba(Nd0.1Ti0.8Nb0.1)O3](1−y)[Na0.5Bi0.5TiO3]y dielectric relaxor ceramics with y = 0.60, 0.65 and 0.70 were prepared through a solid-state double sintering route. The calcination of powder was done at 900 °C for 5 h. Final sintering temperature of prepared ceramic disks were done at 1175 °C for 2 h. The measurements for temperature dependence of dielectric at different constant frequencies were taken using a HP4192A impedance analyzer. AC resistivity data were obtained using AUTOLAB PGSTAT 30 low-frequency analyzer from impedance/admittance measurements. DC resistivity data were obtained using Keithley 617 programmable electrometer. Modeling of dielectric, DC and AC resistivity data was carried out using ORIGIN 6.1 software.

3 Results and discussion

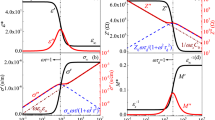
Figure 1a shows the temperature dependence of dielectric permittivity (ε′) for ceramics [Ba(Nd0.1Ti0.8Nb0.1)O3](1−y)[Na0.5Bi0.5TiO3]y at 10 kHz frequency. The room temperature ε′ for y = 0.60, 0.65 and 0.70 are 1441, 1701 and 1308, respectively. The temperature at which ε′ attains peak value (Tmax) is 367 K, 408 K and 452 K for ceramics with y = 0.60, 0.65 and 0.70, respectively [5]. Figure 1b shows the experimental and fitted curve of dielectric permittivity versus temperature plot for y = 0.70 using Lorentz equation for three dielectric peaks (Eq. 1). This equation fits well to the experimental dielectric data varying with temperature at 10 kHz frequency. Modeling using Lorentz equation only gives information about the area under the peak, width and peak positions. In our previous studies, we have proposed a modified Lorentz equation and by using this modified equation it is shown that we can obtain activation energy for relaxation and relaxation times from the dielectric data directly [10, 11]. This equation describes or models the dielectric data with temperature and angular frequency simultaneously. The modified Lorentz equation for the three anomalies observed in the dielectric data is as given in Eq. (2). Each term in equation has their usual meaning. It can be seen from Fig. 1c that this Eq. (2) fits well to the experimental dielectric data and with this equation activation energy for relaxation and relaxation times are evaluated and are shown in Table 1. Table 1 also shows the values evaluated for other compositions for which the figures are not shown here. The activation energy for the first anomaly (Eact1) is 27.10 meV, 24.53 meV and 24.15 meV for the ceramic compositions with y = 0.60, 0.65 and 0.70, respectively. The activation energy for the second and third anomalies observed at higher temperature is higher than that of first anomaly as shown in Table 1. This may be due to the more energy required for dipolar relaxation to occur due to greater thermal fluctuations at higher temperatures. The dipolar relaxation times for the first dielectric anomaly are 5.02 ms, 4.55 ms and 4.55 ms for y = 0.60, 0.65 and 0.70 ceramics, respectively. It shows higher values of relaxation times for the other two anomalies observed at higher temperature when compared to first anomaly. This may be because more time is needed for the dipoles to overcome the thermal fluctuations to attain a relaxed state.

$$y =\, y_{0} + \frac{{2A_{1} }}{\pi }\frac{{w_{1} }}{{4(x - x_{{{\text{c}}1}} )^{2} + w_{1}^{2} }} + \frac{{2A_{2} }}{\pi }\frac{{w_{2} }}{{4(x - x_{{{\text{c}}2}} )^{2} + w_{2}^{2} }} + \frac{{2A_{3} }}{\pi }\frac{{w_{3} }}{{4(x - x_{{{\text{c}}3}} )^{2} + w_{3}^{2} }}$$
(1)
$$\begin{aligned} \varepsilon ^{\prime} & = (\varepsilon_{{\text{s}}} - \varepsilon_{\infty } ) + \frac{{2A_{1} }}{\pi }\frac{{w_{1} }}{{4((T - T_{{{\text{c}}1}} )K_{B} /E_{{{\text{act}}1}} )^{2} *((\omega *\tau_{1} )^{2} + 1) + w_{1}^{2} }} \\ & \quad + \frac{{2A_{2} }}{\pi }\frac{{w_{2} }}{{4((T - T_{{{\text{c}}2}} )K_{{\text{B}}} /E_{{{\text{act}}2}} )^{2} *((\omega *\tau_{2} )^{2} + 1) + w_{2}^{2} }} \\ & \quad + \frac{{2A_{3} }}{\pi }\frac{{w_{3} }}{{4((T - T_{{{\text{c}}3}} )K_{{\text{B}}} /E_{{{\text{act}}3}} )^{2} *((\omega *\tau_{3} )^{2} + 1) + w_{3}^{2} }} \\ \end{aligned}$$
(2)
$$y = y_{0} + \frac{{2A_{1} }}{\pi }\frac{{w_{1} }}{{4(x - x_{{{\text{c}}1}} )^{2} + w_{1}^{2} }} + \frac{{2A_{2} }}{\pi }\frac{{w_{2} }}{{4(x - x_{{{\text{c}}2}} )^{2} + w_{2}^{2} }}$$
(3)
$$\begin{aligned} \rho ^{\prime}_{{{\text{ac}}}} & = (\rho ^{\prime}_{{\text{s}}} - \rho ^{\prime}_{\infty } ) + \frac{{2A_{1} }}{\pi }\frac{{w_{1} }}{{4((T - T_{{{\text{c}}1}} )K_{{\text{B}}} /E_{{{\text{act}}1}} )^{2} *((\omega *\tau_{1} )^{2} + 1) + w_{1}^{2} }} \\ & \quad + \frac{{2A_{2} }}{\pi }\frac{{w_{2} }}{{4((T - T_{{{\text{c}}2}} )K_{{\text{B}}} /E_{{{\text{act}}2}} )^{2} *((\omega *\tau_{2} )^{2} + 1) + w_{2}^{2} }} \\ \end{aligned}$$
(4)
$$\rho_{{{\text{DC}}}} = \rho_{0} + \frac{{2A_{1} }}{\pi }\frac{{w_{1} }}{{4((T - T_{{{\text{c}}1}} )K_{{\text{B}}} /E_{{{\text{a}}1}} )^{2} + w_{1}^{2} }} + \frac{{2A_{2} }}{\pi }\frac{{w_{2} }}{{4((T - T_{{{\text{c}}2}} )K_{{\text{B}}} /E_{{{\text{a}}2}} )^{2} + w_{2}^{2} }}$$
(5)
Fig. 1
figure 1

a Dielectric permittivity versus temperature at 10 kHz, b and c experimental and fitted dielectric permittivity curves using Eqs. (1) and (2), respectively

Full size image
Table 1 Parameters obtained by modeling the dielectric data at 10 kHz using Eq. (2)
Full size table

Figure 2a depicts the variation of AC resistivity with temperature at 10 kHz frequency for [Ba(Nd0.1Ti0.8Nb0.1)O3](1−y)[Na0.5Bi0.5TiO3]y ceramics. It can be seen that weak positive temperature coefficient of resistance (PTCR) effect was observed around the dielectric transition temperatures. The room temperature resistivity is around 1 MΩ cm. Negative temperature coefficient of resistance (NTCR) behavior was observed above the dielectric transition temperature. Similar to modeling of dielectric data, AC resistivity data are also modeled with Lorentz equation (Eq. 3) and modified Lorentz equation (Eq. 4) for two anomalies observed in the resistivity data as shown in Fig. 2b, c, respectively, for y = 0.65. The parameters obtained by fitting the modified Lorentz equation to experimental resistivity data are tabulated in Table 2. The activation energy for conduction for the first anomaly of resistivity data is 30.35 meV, 22.56 meV and 28.85 meV for ceramic composition with x = 0.60, 0.65 and 0.70 respectively, whereas for the second anomaly it has higher value as shown in Table 2.

Fig. 2
figure 2

a AC resistivity versus temperature at 10 kHz, b and c experimental and fitted AC resistivity curves using Eqs. (3) and (4), respectively

Full size image
Table 2 Parameters obtained by modeling the AC resistivity data at 10 kHz using Eq. (4)
Full size table

Figure 3a–c shows the AC resistivity data at 2 kHz and its modeling using Eqs. (3) and (4). The parameter obtained from the modeling is tabulated in Table 3. It can be seen from Tables 2 and 3 that the activation energy for conduction at 2 kHz frequency is of the order of few micro eV when compared to few meV at 10 kHz frequency. This means that lowering of frequency has resulted in lowering of activation energy by few orders of magnitude. Similar decrease was observed in relaxation times for conduction species with the lowering of frequency. This may be related to the least vibration of dipoles and conducting species at lower frequencies leading to lesser activation energy and relaxation times. At higher frequencies, the dipoles vibrate very fast and hence more activation energy is needed to attain relaxed state and contribute to the resistivity observed.

Fig. 3
figure 3

a AC resistivity versus temperature at 2 kHz, b and c experimental and fitted AC resistivity curves using Eqs. (3) and (4), respectively

Full size image
Table 3 Parameters obtained by modeling the AC resistivity data at 2 kHz using Eq. (4)
Full size table

Figure 4a shows the DC resistivity data as a function of temperature. Similar trend of PTCR behavior was observed as in the case of AC resistivity data. Figure 4b, c shows the modeling of experimental DC resistivity data for x = 0.70 ceramic using Lorentz (Eq. 3) and modified Lorentz equation (Eq. (5)) for two peaks, respectively. These equations are found to best fit to the experimental data as is evidenced by regression value which is tabulated in Table 4. Other parameters obtained from the fitting are also shown in Table 4. It is observed that the activation energy for conduction of charge carriers is 90 µeV irrespective of the ceramic sample under study and also same for the two anomalies observed in the DC resistivity plots. The activation energy for AC conduction is higher than that of DC conduction (Tables 2, 3, 4). At higher frequencies, the charged polar and conducting species vibrate very fast in response to the applied frequency and this has the effect for more activation energy for conduction species to relax. This explanation is in good agreement with the observed higher values of activation energy for AC conduction when compared to DC conduction.

Fig. 4
figure 4

a DC resistivity versus temperature, b and c experimental and fitted DC resistivity curves using Eqs. (3) and (5), respectively

Full size image
Table 4 Parameters obtained by modeling the DC resistivity data using Eq. (5)
Full size table

4 Conclusions

[Ba(Nd0.1Ti0.8Nb0.1)O3](1−y)[Na0.5Bi0.5TiO3]y dielectric relaxor ceramics with y = 0.60, 0.65 and 0.70 were prepared through a solid-state double sintering route. Modified Lorentz equations proposed by us are used to model the dielectric, AC and DC resistivity data. It is shown that these equations fit well to the experimental data and we can estimate the activation energy and relaxation times. These equations can be extended to study the dielectric relaxor, AC and DC resistivity of other ferroelectric materials.