1 Introduction

Hyper-redundant manipulators have more DOF than the minimum number of DOF that are required to perform a specific task. High DOF of redundant manipulators provides greater flexibility while working in narrow and cluttered environments. These manipulators are of great interest due to their applications in the fields of medical robotics, search and rescue during disaster relief, and space robotic systems. The inverse kinematics of hyper-redundant manipulators have become complicated and quite challenging because the IK is a nonlinear and configuration-dependent problem. The most popular approaches to resolve the solution of the IK problem are the geometric [1], analytical [2], and iterative approaches [3]. The geometrical approach has the advantage of good geometric intuition and low computational cost. Chirikjian and Burdick [4] proposed a geometric technique for solving the IK of hyper-redundant manipulators by modeling them as a characteristic curve of a robot called the backbone curve. Xu et al. [5] adopted a modified modal approach to determine the IK of hyper-redundant manipulators for orbit servicing applications, in which the 3D backbone of the robot is specified using mode function to represent the geometry of the manipulator. Menon et al. [6] proposed a geometric method for motion planning of hyper-redundant manipulators, in which the motion of the links was assumed as the motion of the tractrix curve. Sardana et al. [7] proposed an easy geometric technique for determining the IK of a four-link redundant manipulator of an in vivo robot for medical applications. The limitation with the geometrical approach is that a closed-form solution must exist geometrically for the first three joints, and the solutions for these joints are time-consuming.

Shimizu et al. [8] proposed an analytical approach for IK computation, in which solutions are determined by the joint angle parametrization method. The analytical methods are challenging to solve due to the involvement of multiple parameters, nonlinearity, and transcendental equations within the IK of serial manipulators. Though analytical approaches are accurate, they are highly configuration dependent and are computationally expensive with a high number of DOF.

The numerical iterative approach has been extensively utilized for IK of redundant manipulators for which explicit closed-form solutions do not exist. A popularly used iterative approach for the IK problem of serial manipulators is the cyclic coordinate descent (CCD) method [9]. It operates to reduce positional and orientation errors by moving a single joint at a time, starting from end-effector to base. Though this method is effective, it cannot deal with the global constraints of the manipulator. Ananthanarayanan and Ordonez [10] proposed a hybrid approach by combining analytical and numerical methods for solving the IK solution of generalized hyper-redundant manipulators, and this method significantly improves computational efficiency.

Numerous computational schemes have been adopted to take advantage of redundancy. Many researchers have used the idea of the pseudo-inverse technique [11] to obtain the joint velocities, which minimize the joint rates in the least square sense. This method is also utilized at the joint acceleration level by adding the null-space term to satisfy the additional secondary criteria such as obstacles [12], singularity [13], joint-limit avoidance [14], and joint torque minimization [15]. In general, Jacobian methods lack sensitivity at joint limits and have singularities. An optimization-based approach for IK solution of hyper-redundant manipulator avoiding obstacles and singularities [16] was implemented at a joint position level, and hence there is no need for Jacobian computation, thus reducing the computational burden for the solution.

Evolutionary methods have gained popularity and are widely implemented to solve IK problems. Parker et al. [17] used genetic algorithms to solve the IK problem while minimizing joint displacement. This method has a limitation of poor precision of solution. Koker [18] implemented neural networks and genetic algorithms together to determine the solution of the IK problem. Bingul et al. [19] implemented a neural network using a back-propagation algorithm to solve the IK problem of an industrial robot with an offset wrist. The neural network approach usually requires training sets whose size increases exponentially with the number of DOFs.

The modularity of robots has been practiced in the design of robot mechanisms for flexibility and ease in maintenance. A modular, reconfigurable robot consists of a set of standardized modules that can be arranged to different structures and DOFs for diverse task requirements [20]. The multimodal nature of the IK problem offers multiple solutions. Kalra et al. [21] used a real-coded genetic algorithm to obtain the solution of a multimodal IK problem of an industrial robot, which is a fitness sharing niching method. The limitation of this approach is to set more unknown parameters. These parameters rely significantly on the nature of search space, which makes this approach a configuration dependent. Tabandeh et al. [22] proposed an adaptive niching technique to solve the IK of a serial robotic manipulator with an application to modular robots, which was able to determine multiple IK solutions. Contrary to the other niching algorithms, this approach requires few parameters to be set. This feature allows the algorithm to be used for finding the IK solution of any robot configuration. The above literature proposed the use of the niching-based approach for determining the multiple IK solutions of industrial and redundant robots. Though the method is efficient, it is computationally expensive. In the proposed approach, classical optimization methods have been used for determining the global minimum and multiple IK solutions. This significantly reduces the time, and it can also be applied to a wide variety of robot configurations.

Collision avoidance is a crucial aspect to be considered in inverse kinematics and motion planning of robots. A wide variety of techniques have been adopted for collision avoidance. The most popular method proposed for obstacle avoidance is an artificial potential field approach [23]. For local optimal control of the redundant robot and collision avoidance, pseudo-inverse of Jacobian and its variants such as task priority [24] and extended Jacobian-based [25] methods have been extensively used. The main limitation of the Jacobian-based methods is that the algorithmic singularities need to be avoided. Chirikjian [26] proposed a discrete modal summation geometric approach to manipulate the robot in tunnels. The limitation with this approach is defining the modal functions, which requires several sets of modes to span the entire robot workspace, and proper mode switching mechanisms need to be implemented. Choset [27] proposed a follow-the-leader approach to serpentine motion planning.

Some of the obstacle avoidance methods were performed by using polyhedral collision detection. These approaches work based on computational geometry algorithms. The polyhedral interference-based approaches have been used for collision detection and computation of the distance between two objects [28]. Hubbard [29] proposed a method for approximating polyhedral objects with bounding spheres, which are hierarchically organized for the representation of the robot model. Collision detection in this approach was performed by checking the condition, such as the distance between the centers of two spheres is smaller than the sum of their radii. Here, the limitation is that the accuracy of collision detection can be improved by approximating the model with more number of spheres, which is computationally expensive. The bounding box approach is popularly used in collision detection. Van Henten [30] proposed a bounding box approach for modeling the links of the robot, and later the bounding boxes were converted into hierarchical bounding spheres with different levels of refinement. This approach is computationally fast but less accurate in collision interference. The collision avoidance schemes proposed in the literature are useful for different types of obstacles, but the obstacle modeling and collision detection techniques are quite complex.

Although the algorithms mentioned above proposed IK solutions and redundancy resolution in a cluttered environment, these methods are known to be expensive because of the use of evolutionary algorithms and intricate modeling of obstacles. By taking the limitations in the literature, such as Jacobian singularities and complex collision detection schemes, into account, this paper proposes a simple and efficient approach for the inverse kinematics of spatial hyper-redundant manipulators suitable to work in narrow regions and cluttered environments with different types of 3D obstacles. Spatial robots with two DOF at each joint are considered in this work, except for the first joint, which is a revolute joint. These robots offer higher flexibility while maneuvering in a cluttered workspace. A classical optimization algorithm has been implemented to solve the inverse kinematic solution of the manipulator in multiple obstacle environment. Redundancy resolution for such manipulators is carried out by using constrained optimization methods with an objective of minimization of joint rotation. The IK problem is characterized by the transcendental equations, which make it a non-convex optimization problem with multiple solutions. A global search optimization approach has been implemented to determine multiple IK solutions.

The remainder of the paper is organized as follows. Section 1 introduces the hyper-redundant manipulators and analyzes the forward kinematics of this manipulator. Section 2 explains the formulation of the IK problem, collision avoidance scheme, redundancy resolution, and optimization techniques implemented to determine the IK solution. Section 3 shows the simulation results of the manipulator. Section 4 describes the conclusion of the work.

1.1 Kinematic modeling of a hyper-redundant spatial manipulator

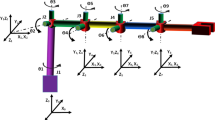
The position and orientation of the end-effector are required to perform the IK of hyper-redundant manipulators. The joints of the robot are modeled with universal joints for better accessibility and control in the workspace. These joints have two orthogonal DOF that are formed by pitch axis and yaw axis at all the joints except at joint 1, which is a revolute joint. A generalized spatial hyper-redundant manipulator is shown in Fig. 1.

Fig. 1
figure 1

D–H coordinate system of n-DOF hyper-redundant manipulator with 2-DOF universal joints

Full size image

The forward kinematic analysis begins with the assignment of coordinate frames at the robot joints, and these frames are used to describe the position and orientation of one frame relative to another frame. The frame assignment of the hyper-redundant manipulator is shown in Fig. 1. The Denavit–Hartenberg (D–H) parameters for the assigned frames are given as per the standard convention. The D–H parameters for the developed model of the 9-DOF hyper-redundant manipulator are listed in Table 1.

Table 1 D–H parameters of a 9-DOF hyper-redundant manipulator
Full size table

The transformation of the ith frame relative to the (i − 1)th frame is derived from the generalized homogeneous transformation matrix. It is given by

$$T_{i}^{i - 1} = \left[ {\begin{array}{*{20}c} {C\theta_{i} } & { - S\theta_{i} C\alpha_{i} } & {S\theta_{i} S\alpha_{i} } & {a_{i} C\theta_{i} } \\ {S\theta_{i} } & {C\theta C\alpha_{i} } & { - C\theta_{i} S\alpha_{i} } & {a_{i} S\theta_{i} } \\ 0 & {s\alpha_{i} } & {C\alpha_{i} } & {d_{i} } \\ 0 & 0 & 0 & 1 \\ \end{array} } \right]$$
(1)

For the robot shown in Fig. 1, the position of the end-effector with respect to the base frame is given by

$$T_{9}^{0} = T_{1}^{0} T_{2}^{1} T_{3}^{2} T_{4}^{3} T_{5}^{4} T_{6}^{5} T_{7}^{6} T_{8}^{7} T_{9}^{8}$$
(2)

From the above equation of the homogeneous transformation matrix, the final end-effector position and orientation can be determined. These are taken as the required inputs to perform the IK analysis.

2 The formulation of IK problem

The modules involved in the solution of IK problem are as follows:

  1. 1.

    Formulation of the IK as an optimization problem.

  2. 2.

    Method for efficient collision detection.

  3. 3.

    Approach to redundancy resolution scheme.

  4. 4.

    Choice of appropriate optimization techniques.

In the following sections, these four modules of the method are explained.

2.1 Problem formulation

The IK problem is formulated as an optimization problem, for which the objective function is the reachability of the manipulator in the task space. This is measured as the total Euclidean distance (D), i.e., the distance between the current position of the end-effector (E) and the task space location (P). As shown in Fig. 2, the vectorial representation of distance is given by Eq. (3). Though the robots considered in the present study are spatial, a planar robot is shown for easy understanding.

Fig. 2
figure 2

Schematic diagram of serial hyper-redundant manipulator

Full size image

The total Euclidean distance between E and P can be calculated as

$$D = \parallel E - P\parallel$$
(3)

For a given joint configuration (θ), the end-effector position E (Ex, Ey, Ez) can be calculated using Eq. (2). The current end-effector position is a function of joint angle (θ); hence, the distance in Eq. (3) can be represented as

$$D = \parallel E(\theta ) - P\parallel$$
(4)

where \(\varvec{\theta}= [\theta_{1} ,\theta_{2} ,\theta_{3} ,\theta_{4} , \ldots ,\theta_{n} ]\).

In order to reach the specified task space location, P (Px, Py, Pz) from the end-effector position (E), the distance between E and P should be zero. Hence, the problem is posed as minimization of a square of total Euclidean distance, which is shown as

$${ \text{Minimize: }} f = D^{2} = \left( {(E_{x} - P_{x} )^{2} + (E_{y} - P_{y} )^{2} + (E_{z} - P_{z} )^{2} } \right)$$
(5)

The kinematic configuration that results in minimum objective function value can be considered as an IK solution to the problem. The results of a few cases are reported using the formulation given in Sect. 3.1.

As the problem formulated is non-convex and multimodal in nature, multiple local solutions exist. The task of obtaining multiple IK solutions is performed using the multi-start framework. This approach uses a local nonlinear optimization solver with different start points. By using an objective function given in Eq. (5) and multi-start approach, multiple IK solutions of the spatial manipulator are obtained. The case studies and the corresponding IK results are reported in Sect. 2.4.2.

2.2 Obstacle avoidance

Redundant robots, while operating to perform the required task, need to avoid collisions with obstacles in the workspace. The collision avoidance requires collision detection, i.e., to find whether a robot is in a collision with any obstacle at a given configuration. The task of collision detection has been carried out by using a bounding box approach. In the present study, 3D obstacles such as spheres, cylinders, and cones were considered, and the boundaries of these solids are enveloped by a box. For generating bounding boxes, the obstacles were represented as a set of points on solid boundaries. From the point set, extremum coordinates of the points are determined. By using these coordinates, the vertices of the box are determined. The facet information, i.e., the vertices that are used to form a particular face, is computed using the convex hull algorithm. The facets and their corresponding vertices are used to model the bounding box around the 3D solids that are used in collision avoidance. Once the obstacles in 3D space were surrounded by a bounding box, the configurations that lead to collision need to be detected. The scheme is illustrated in Fig. 3. Several points that are uniformly distributed on the robot link are considered say P1, P2,…,Pn, and a check is performed whether these points lie within the bounding box of an obstacle. If any of these points lie in the bounding box, then the collision occurs. The algorithm for collision detection is shown in Table 2. This algorithm takes the extremum coordinates of the box as input and checks for a set of points on the links of the robot if they lie within the bounding box. In the algorithm, n represents the number of query points on each link for collision check.

Fig. 3
figure 3

Schematic representation of collision detection scheme

Full size image
Table 2 Algorithm for collision detection
Full size table

By using the above algorithm, configurations leading to the collision have been identified. These configurations need to be avoided, and the robot should move away from the obstacle. The penalty approach has been implemented for obstacle avoidance. The penalties are imposed for the configurations that are interfering with obstacles by augmenting them with the objective function. The modified statement of the optimization problem has been used when the workspace has obstacles, which is given by

$${\text{Minimize: }}f = \left( {(E_{x} - P_{x} )^{2} + (E_{y} - P_{y} )^{2} + (E_{z} - P_{z} )^{2} } \right) + \sum\limits_{i = 1}^{m} {C_{i} }$$
(6)

where ci is the ith penalty and m is the number of collisions.

A fixed penalty value of 100 is used, which is determined based on the score of the objective function.

2.3 Redundancy resolution

Redundant manipulators have multiple IK solutions. They provide a choice to select the best solution. The task of finding the best solution among the available solutions is called the redundancy resolution, which is performed based on certain optimization criteria. Here, the redundancy resolution has been formulated as a nonlinear constrained optimization problem. The optimization criterion used is the minimization of the sum of individual joint rotations between the home configuration, which is assumed as initial configuration and the configuration corresponding to end-effector task space location, i.e., final configuration, which is shown in Eq. (7). The reachability of the end-effector in task space is chosen as constraints of the problem given in Eq. (8):

$${\text{Minimize: }}f \, = \sum\limits_{j = 1}^{n} {(\theta_{{i_{j} }} } - \theta_{{f_{j} }} )^{2}$$
(7)

The optimization problem is stated as follows:

$${\text{Subjected to: }}g = \left( {(E_{x} - P_{x} )^{2} + (E_{y} - P_{y} )^{2} + (E_{z} - P_{z} )^{2} } \right) = 0$$
(8)

where \(\theta_{{i_{j} }}\) is the initial joint configuration of the corresponding jth joint and \(\theta_{{f_{j} }}\) is the final joint configuration of the corresponding jth joint.

The task of redundancy resolution was performed using the sequential quadratic programming technique, discussed in Sect. 2.4.3. It has been implemented for a spatial redundant manipulator, traversing specified paths with and without obstacles. The results are reported in Sects. 3.2 and 3.3. The task of collision avoidance has been carried out by imposing the penalties for the configurations violating the constraints in the workspace. The optimization criteria have been modified by adding the penalty term to the equation. The modified equation is given as

$${\text{Minimize: }}f = \sum\limits_{j = 1}^{n} {(\theta_{{i_{j} }} - \theta_{{f_{j} }} )^{2} } + \sum\limits_{i = 1}^{m} {C_{i} }$$
(9)

where Ci is the ith penalty and m is the number of collisions.

A fixed penalty value of 1000 is being used, which is determined based on the score of the objective function.

2.4 Optimization techniques for IK solutions

Three types of optimization methods are used to solve different formulations of IK problem:

  1. 1.

    IK problem formulated as an unconstrained optimization problem is solved using Nelder–Mead method.

  2. 2.

    IK problem formulated as an unconstrained optimization problem is also solved using multi-start algorithm to find multiple solutions.

  3. 3.

    IK problem with constraints is solved using SQP.

2.4.1 Nelder–Mead’s simplex search algorithm for an unconstrained optimization problem

Initially, the IK problem is considered as a nonlinear optimization problem without constraints. This problem is attempted with the Nelder and Mead simplex search method [31], which is a direct search method suitable for nonlinear and multivariable problems without constraints. This approach is a derivative-free method with good convergence. This method works by creating a geometric simplex, which is a geometric figure formed by (n + 1) vertices, where n is the number of variables of the optimization problem. In each iteration, the simplex method determines the reflected vertex of the worst vertex with the highest function value through a centroid vertex. According to the function value at this new vertex, the algorithm performs the operations such as reflection, extension, and contraction to form a new vertex. This process continues iteratively until the desired minimum was achieved. This method is used for the solution to the problem posed in Eq. (5), and the results are reported in Sect. 3.1.

2.4.2 Multi-start method for multiple optima

The optimization algorithms implemented for IK and redundancy resolution are local search algorithms. These algorithms often suffer from getting trapped in a local optimum point. Multimodal optimization deals with the task of evaluating multiple local optimal solutions while optimizing multimodal functions. Generally, global optimization algorithms are employed to determine multiple solutions, and these algorithms search through more than the single basin of attraction. In this approach, we have adopted the global search and multi-start framework, which performs the optimization process with the generation of a number of starting points and use local optimization solver to find the optimal solutions.

Multi-start method [32] has two phases: In the first phase, the solution is generated, and in the second phase, the solution is usually improved. Then, each iteration produces a solution, and the best of overall solutions is the output. The algorithm of the multi-start procedure is described in Table 3.

Table 3 Algorithm for multi-start procedure
Full size table

This method generates uniformly distributed points [33] within the search space (S) and starts a local solver from each of these points. In general, this approach converges to a global solution when there are a large number of start points in search space, and there is also a chance of arriving at the same local solution many times. To overcome this difficulty, some potential start points that are close to the previous solution have to be eliminated. The elimination procedure is performed by generating uniformly distributed start points in S, and the objective function value is evaluated at each point. The points are sorted according to their function value, and the best points are retained. A local solver starts from each point of the reduced sample, except if there is another sample point within a certain critical distance that has a lower function value. The local solver is not started from the sample points that are very close to a previously discovered local minimum. Then, again additional uniformly distributed points are generated, and the procedure is applied to all the points which are retained from previous iterations and newly generated set of points. The implementation of this algorithm provides multiple IK solutions. A few cases of multiple configurations were reported for a given task space location in Sect. 3.1.1. These multiple solutions can be considered as suitable kinematic configurations of a robot working in diverse environments.

To compare the solutions that are obtained through multi-start and are close to the global minimum, a global search algorithm has been implemented. This algorithm generates start points using a scatter search mechanism [34]. The main feature of this algorithm is that it analyzes start points and eliminates the points that are not likely to improve the function value. Initially, it generates potential start points and then it evaluates score function for a set of trial points. The points with the best score function have been chosen and used as initial point for the local solver. If the remaining trail points satisfy function score and constraint filters, global search runs local solver. Finally, this process creates a global optimum solution vector. Joint configurations corresponding to the global minimum for different task space locations are reported using this approach.

2.4.3 SQP approach for constrained optimization

Since the above technique deals with unconstrained problems, the optimization problem with constraints was handled by a nonlinear constrained optimization technique called sequential quadratic programming (SQP), which is a quadratic approximation of the Lagrangian function with linearization of constraints [35]. A quadratic subproblem is formulated and solved to develop a search direction. The line search can be performed with respect to two alternative merit functions, and a modified BFGS formula updates the Hessian matrix. By using this approach, a few simulation results of robot tracing a specified path are reported in Sect. 3.2.

3 Simulation results

In this paper, a classical nonlinear optimization approach has been implemented to determine the IK solution and redundancy resolution of a 9-DOF spatial robot in a cluttered workspace. This was performed using the optimization toolbox of the MATLAB, which uses the methods explained in Sect. 2.4. IK simulations were performed using MATLAB on a PC with Intel Xeon E5 processor @3.50 GHz with 32 GB RAM.

The results are reported for the following three situations:

  1. 1.

    Inverse kinematics and multiple solutions of spatial hyper-redundant manipulators without obstacles in the workspace.

  2. 2.

    Redundancy resolution of spatial hyper-redundant manipulators.

  3. 3.

    Inverse kinematics and redundancy resolution of spatial hyper-redundant manipulators with 3D obstacles in the workspace.

3.1 Inverse kinematics solution of the spatial hyper-redundant manipulator

The inverse kinematics of spatial hyper-redundant manipulator are determined for a 9-DOF manipulator at different task space locations. Here, the IK problem is posed as an optimization problem with the objective as minimization of total Euclidean distance shown in Eq. (5). Several sample target points have been chosen to evaluate the IK solutions. Table 4 shows the joint configurations of the 9-DOF robot for a set of six task space coordinates. The forward kinematic model of the end-effector as indicated in Eq. (2) describes that there are nine unknowns to be determined for each task space location specified in three-dimensional coordinates.

Table 4 Joint configurations corresponding to task space coordinates
Full size table

Here, the problem is posed using Eq. (5). The same is solved using Nelder and Mead simplex algorithm. The solution is obtained in the form of the joint configuration to reach the specified target location. Figure 4a–d shows the joint configurations of 9-DOF robot at task locations of (18, 18, 20), (38, 35, 25), (− 28, − 28, 20), and (− 38, − 35, 25) mm. The positional error obtained after the convergence is about 7.39e−11. The values of positional error for different task space coordinates are reported in Table 4.

Fig. 4
figure 4

IK solutions of spatial hyper-redundant manipulator. a Joint configuration for target point (18, 18, 20), b joint configuration for target point (20, 25, 25), c joint configuration for target point (− 28, − 28, 20), and d joint configuration for target point (− 38, − 35, 25)

Full size image

The positional error obtained has been compared with the existing literature [21], and it was observed that the order of positional error is negligible (10−11 times), as shown in Table 5. From the values of positional error, it was observed that the end-effector is precisely located at desired task space locations.

Table 5 Results of positional error comparing between SCARA and 9-DOF spatial hyper-redundant robot
Full size table

The convergence of function value during the optimization process is shown in Fig. 5. The number of iterations required to attain the minimum function value for a task coordinate of (18, 18, 20) mm starts at 900, which is shown in Fig. 5a. From Fig. 5b, it is observed that the convergence of function is achieved after 400 iterations for a task coordinate (38, 35, 25) mm. From the rate of convergence, it is inferred that the computational time for this simulation is smaller, and it is about 10 s. The computational time is less when compared to evolutionary-based approaches. The IK solution of robot without constraints and obstacles in workspace can be easily implemented using a Jacobian-based approach [36]. This approach offers a six-dimensional self-motion manifold of solutions in joint space without singularities. The existing method is likely to give an IK solution in self-motion manifold. But the proposed approach is implemented to show its effectiveness.

Fig. 5
figure 5

Function plots. a Convergence plot for target point (18, 18, 20) and b convergence plot for target point (38, 35, 25)

Full size image

3.1.1 Multiple IK solutions of redundant manipulators using the multi-start algorithm

Simulations were performed on a 9-DOF spatial manipulator to determine multiple IK solutions. A global search optimization algorithm discussed in Sect. 2.4.2 was implemented to evaluate multiple IK solutions of the robot for a given task space location. The objective function chosen for this simulation is similar to the function chosen for a general IK procedure discussed in Sect. 3.1. The multi-start framework has been adopted to determine the local optimum points of the problem. The procedure starts with the generation of ten start points in search space, and a nonlinear optimization solver was executed at each start point to evaluate optimal solutions using the algorithm shown in Table 3. Figure 6a–f shows six different kinematic configurations of the ten obtained for the same task space coordinate (18, 18, 20) mm. From Fig. 6a–f, it was observed that all kinematic configurations are distinct, and these can be a suitable candidate solution for reconfigurable spatial redundant manipulators.

Fig. 6
figure 6

a–f Multiple kinematic configurations of 9-DOF robot at end-effector position (18, 18, 20) mm

Full size image

All the local optimum solutions were visualized through basins of attraction shown in Fig. 7. Start points at which the optimization algorithm executes are represented as dots, and the basins of attractions are shown as stars. The dots that are converging to the basins of attraction represent the required solutions. Here, ten feasible kinematic configurations are obtained as optimal solutions.

Fig. 7
figure 7

Visualization of basins of attraction and multiple solutions for a task location (18, 18, 20) mm

Full size image

The computational time for attaining multiple IK solutions, i.e., 10 joint configurations of a redundant manipulator, is about 45 s. The solutions have converged quickly even with ten points when compared with the evolutionary techniques [22]. In the multimodal approach of industrial robots [21], a maximum of four different kinematic configurations have been obtained with a population size of 50. From the size of the population and number of iterations, the evolutionary algorithms are known to be computationally expensive. The proposed global optimization algorithm is able to achieve 10 distinct kinematic configurations for a 9-DOF spatial robot in less time. Table 6 shows ten distinct joint configurations corresponding to the task space location (18, 18, 20) mm. The positional error is also reported in Table 6, which is almost zero and ensures that the end-effector reaches the desired target precisely. From the joint configurations in Table 6, it was observed that the solutions were not repetitive, i.e., the same local solutions have not arrived. To show the efficacy of the approach, this algorithm has been implemented for different numbers of start points, and all the solutions have been interpreted. Figure 8a–d shows the minimized objective function values of multiple solutions for a range of 10–40 start points. It was observed that the least positional error is achieved with 40 start points, and it is in the order of 2.36e−13. From Fig. 8a–d, it was also observed that the magnitude of positional error was less at different start points range. The solutions are consistent even for less number of start points.

Table 6 Multiple kinematic configurations corresponding to the task space coordinate (18, 18, 20)
Full size table
Fig. 8
figure 8

a–d Plot showing converged function values with different numbers of start points

Full size image

To compare that the solutions obtained through the local search algorithm are close to the global optimal solution, a global search algorithm described in Sect. 2.4.2 has been implemented for different task space coordinates. In this algorithm, start points were generated using a scatter search mechanism. Local optimization solver runs based on the score of the start points, and this feature enables the algorithm to arrive at the global optimal solution without trapping at the local optimal point. Table 7 shows the joint configurations corresponding to a global minimum value at different task space coordinates. From the positional error reported in Table 7, it was observed that the magnitude of the converged objective function is almost the same with the positional error magnitudes reported in Tables 4, 5, and 6.

Table 7 Joint configurations corresponding to a global minimum at different task space coordinates
Full size table

3.2 Results for redundancy resolution using SQP

These simulations depict the redundancy resolution scheme of hyper-redundant manipulators. Here, the problem is to evaluate the best IK solution among the multiple solutions by considering the performance criterion of joint rotation minimization from the previous position, given in Eq. (7), and the corresponding task constraint is given in Eq. (8). Here, 9-DOF redundant manipulator was considered to trace two different paths, such as a straight-line and circular path in task space. The path in the task space is taken as a series of points, and the optimization algorithm is implemented at every point to determine the kinematic configuration at the corresponding point. Figure 9a shows the kinematic configurations of the robot while tracing a straight-line path, whereas Fig. 9b shows kinematic configurations while tracing a circular path. In both the cases, the accuracy in reaching the task space is ensured. The computational time for the simulation of the robot while tracing each path is about 90 s. The angular displacement at each DOF, while the manipulator is tracing a straight-line path in the task space, is shown in Fig. 10. As the objective, joint distance minimization is formulated, which provides the least movement of joints from the previous configurations. The variation of joint rotation at each DOF corresponding to task space coordinates is shown in Fig. 10a–f, and these variations are shown for both redundancy resolution and no redundancy resolution.

Fig. 9
figure 9

Joint configurations of a 9-DOF robot. a Joint configurations of robot for a straight-line path and b joint configurations of robot for a circular path

Full size image
Fig. 10
figure 10

Angle variation of a 9-DOF robot at task locations while tracing a straight-line path

Full size image

Figure 11a–f shows the angular displacement at each DOF while the robot is tracing a circular path in task space, with and without redundancy resolution. The variations in angular rotations are shown only for 6-DOF in a 9-DOF robot. The same trend has been followed in the remaining DOF. In both the cases, it is evident that the joint rotations were minimized with redundancy resolution along the defined path when compared with no redundancy resolution.

Fig. 11
figure 11

Angle variation of a 9-DOF robot at task locations while tracing a circular path

Full size image

From Figs. 10 and 11, it is also inferred that the joint angle variation between two task space coordinates is uniform, while the variation of joint rotation with no redundancy resolution is high and non-uniform. The task of redundancy resolution minimizes joint angle rotation, which in turn reduces the joint torque required to rotate a specific joint.

3.3 IK solutions of redundant robot in cluttered environment

This section presents the results of different IK simulations of the robot operation in the cluttered environment. A wide variety of 3D working environments are considered to simulate the robots working in real-time applications. For this simulation, a redundant robot with five links and 9-DOF is considered. All the links are of uniform length and are taken as 20 mm. The IK solutions of the robot are computed using optimization techniques discussed in Sect. 2.4. The collision detection scheme discussed in Sect. 2.2 has been implemented for different types of 3D obstacles using Eq. (6). To determine the collision of a specific link with any of the obstacle, the links of the robot have been modeled as line segments, which are discretized as a series of points. A set of points are chosen in a uniform manner along the link, so that all portions on the link are considered for collision avoidance. The number points generated on the link are proportional to the link length. As the link length considered is 20 mm, the number points chosen for discretization of link are also 20. In all the cases of simulations, a constant value of the penalty is being added to the objective function; this value is determined based on the value of the merit function which is used as the objective of the optimization problem. The value of penalty considered for simulation of redundant robot with multiple obstacles is 100.

Figure 12a shows robot configuration for a task space location (14, 14, 14) with three spherical obstacles in the workspace, while Fig. 12b depicts the IK solution of the robot with four spherical obstacles. The end-effector of the robot reached the task space location accurately, and the positional error is negligible. Robot configurations for different task space locations while avoiding 3D obstacles of different shapes in the workspace are shown in Fig. 13.

Fig. 12
figure 12

IK solution of spatial redundant robot with spherical obstacles a three spherical obstacles and b four spherical obstacles

Full size image
Fig. 13
figure 13

IK solution of spatial redundant robot with obstacles of different shapes a at task space location (5, 25, 25), (22, 15, 30) and b at task space location (10, 30, 30), (24, 12, 25)

Full size image

A workspace with cylindrical and conical obstacles has been considered, and kinematic configurations of the robot are shown while avoiding these obstacles. Figure 14a shows the joint configurations of the robot at task space locations (50, 20, 30) and (50, 15, 20), while Fig. 14b shows the configuration at task space location (46, 22, 30). To show the realistic model of the robot, the links of the robot are considered as cylinders. Collision detection scheme in Sect. 2.2 has been extended for cylindrical links. The line segment model of the robot link has been considered as an axis of the cylinder. The discretized points on the line segment are chosen as the center of the circles, and a series of circles are generated along the axis. The coordinates on the circle are the points on the surface of the cylindrical link. Collision detection has been performed by checking whether the points on the surface of the cylinder lie within the range of bounding box, which is implemented using an algorithm in Table 2.

Fig. 14
figure 14

IK solution of spatial redundant robot with cylindrical and conical obstacles a at task space location (50, 20, 30), (50, 15, 20) and b at task space location (10, 30, 30), (46, 22, 30)

Full size image

Figure 15a, b shows the joint configurations of the robot, whose links were modeled as cylinders at task space locations (35, 20, 30) and (46, 22, 30).

Fig. 15
figure 15

IK solution of redundant robot with cylindrical and conical obstacles when links of the robot modeled as cylinders a at task space location (35, 20, 30) and b at task space location (46, 22, 30)

Full size image

Narrow passages similar to ducts and frame cutouts were modeled in the workspace, and the task coordinates are chosen in a way that robot enters through those passages. Figure 16 shows the robot configuration while passing through the duct-like passage and reached the target location inside the duct without colliding the boundary of the duct. For clarity, Fig. 16 is shown in two different views. Figure 17 shows the IK solution of the robot at the task location of (20, 15, 13) entering through a frame. Two different views of Fig. 17 are shown. The computational time for single IK solution with multiple obstacles is less than 120 s.

Fig. 16
figure 16

IK solution of spatial redundant robot with a duct-shaped object as obstacle a front view and b side view

Full size image
Fig. 17
figure 17

IK solution of spatial redundant robot in a rectangular frame as obstacle at task space location (20, 15, 13) a front view and b side view

Full size image

Apart from the above results, some IK simulations of the robot have been performed while tracing a path in the 3D cluttered environment. Figure 18 shows a case with a circular path around the spherical obstacle. In this case, the robot configurations corresponding to the target points along the path are evaluated by applying the redundancy resolution scheme discussed in Sect. 2.3. The obstacle avoidance has been carried out by adding penalties to the optimization criteria given in Eq. (9). The value of penalty chosen for the IK simulation of robot tracing a path is 1000.

Fig. 18
figure 18

IK solution of spatial redundant robot while tracing a circular path around spherical obstacle

Full size image

From Fig. 18, it was observed that the joint displacements are reduced while tracing a path in the workspace. The path chosen was very close to the obstacle, and the IK solution in figure ensures no collision with the sphere.

Figure 19 shows the robot configurations while tracing a semicircular path behind the spherical obstacle. For better visibility of path in the workspace, a magnified view is shown in Fig. 19, which depicts the robot configurations along the path without colliding with the obstacle.

Fig. 19
figure 19

IK solution of spatial redundant robot while tracing a semicircular path around spherical obstacle

Full size image

Another case of IK simulation of a robot has been performed in the 3D environment similar to a closed chamber with a spherical obstacle resting on a support member. Here, the path is chosen in a confined area so that the robot should trace the path without colliding the walls of the chamber and sphere. The working environment and the path traced are similar to robots working in real-time applications like welding and painting. Figure 20 shows the IK solution of the robot while tracing a semicircular path in the 3D working environment. It was observed that all the robot configurations reaching the given task locations in the path are accurately reached without colliding the obstacles. From the magnified view of Fig. 20, all the robot configurations and path are clearly visible. The computational time for IK simulation of the robot while tracing a path shown in Fig. 20 is about 400 s.

Fig. 20
figure 20

IK solution of spatial redundant robot while tracing a semicircular path in a closed and cluttered environment

Full size image

4 Conclusions

In this paper, inverse kinematics of spatial hyper-redundant manipulators in multiple obstacle environment were performed by using a classical optimization approach. To improve the accessibility of the manipulator in a diverse task space environment, the joints of the robot were modeled with multi-DOF and considered as universal joints. The problem is of multimodal nature, which leads to multiple IK solutions. A classical global optimization approach has been implemented to determine multiple kinematic configurations of the 9-DOF spatial manipulator. A nonlinear optimization algorithm is used to perform the redundancy resolution of the spatial robot with and without obstacles in the workspace, resulting in the least joint rotation during travel of the path in the workspace. Thereby, joint torques required to move a specific joint can be lowered. Simulations were performed on the 9-DOF spatial redundant manipulator. The proposed approach is computationally efficient due to less computational burden involved in implementing the optimization algorithm and effective modeling of obstacles in the workspace. The problem of trapping the IK solutions in local regions was avoided with the use of a multi-start approach and obtained multiple solutions. The results show that the IK solutions were accurate, and the convergence rate was good. The simulation results of the IK solution of robots with obstacles of different shapes make the approach adaptable in a wide range of working environments. The effective kinematic modeling of the robot enables extending the implementation of the proposed approach to more number of DOF.