Modeling and Optimization of Electromagnetic Conversion Coupling Coefficient Based on Maxwell’s Magnetic Field Theory

Abstract

Purpose

Due to the difficulty of establishing an accurate analytical model of magnetic induction intensity in the case of multiple permanent magnet layouts, it is necessary to develop a mathematical model that can accurately describe the magnetic field distribution around multiple permanent magnets from the basic electromagnetic field theory. Optimization of permanent magnet arrangement and coil size parameters is a potential way to improve energy conversion efficiency.

Method

This work presents a mathematical model of the axial flux density distribution in a multiple permanent magnet configuration based on classical Maxwell's electromagnetic field theory. Theoretical calculations of the magnetic flux and its rate of change were completed and validated using ANSYS Maxwell software. In addition, the permanent magnet arrangement and coil parameters design were optimized to obtain the maximum induced electromotive force (EMF). Finally, the energy conversion performance was experimentally measured for different combinations of magnet and coil configurations.

Results

Theoretical studies have shown that the magnetic flux changes of three homopolar aligned magnets are more significant than that of their two-magnet counterparts. Simulation results show that there is an optimal value for the coil height which maximizes the output open circuit voltage when the number of Ampere-turns is kept constant. The results show that the theoretical and experimental induced voltages of the three heteropolar arrangements of permanent magnets are significantly higher than those of the same polarity arrangement.

Conclusion

The efforts of this work are expected to provide a sound fundamental theoretical reference for optimizing the configuration of electromagnetically coupled structures and improving the efficiency of vibration energy conversion.

Introduction

In recent decades, electromagnetic vibration energy harvesting technology has attracted extensive attention due to its advantages of high current, high power, high efficiency, low output impedance, and wide-band tuning. From the perspective of electromagnetic induction, abrupt changes in magnetic flux density can cause significant induced voltages. Staggered permanent magnets manipulated in translation and rotation achieve dramatic flux density abrupt changes [1, 2]. Electromagnetic conversion has developed into a high-efficiency energy conversion mechanism. Its advantages are that it does not involve smart materials, long life, and competitive high current output. Thereby, to improve the efficiency of energy harvesting from complex environmental excitation sources, various electromagnetic energy harvesting configurations are widely studied and utilized [3,4,5]. Sha et al. [6] proposed an electromagnetic tracking method based on the rapid determination of the maximum magnetic flux density vector (MMFDV) represented by two azimuth angles. Magnetic flux density has always been utilized to detect the texture of materials and to measure a number of physical parameters. The rapid growth in the field of microsensors for a variety of applications such as structural health monitoring, biochemical sensors, and pressure sensors has increased the demand for portable, low cost, and efficient energy harvesting devices. Bedekar et al. [7] described a self-powered pulse rate sensor within a vibration energy harvester integrated inside a pen commonly carried by humans in the pocket close to the heart. Williams and Yates [8] assessed the feasibility of a micro-electric generator for microsystems and optimize the design. El-hami et al. [9] designed and fabricated a new vibration-based electromechanical power generator using an electromagnetic transducer based on the relative motion of a magnet pole with respect to a coil. Glynne-Jones et al. [10] described the design of miniature generators capable of converting ambient vibration energy into electrical energy for use in powering intelligent sensor systems. The measurement and evaluation of magnetic flux density [11,12,13] is of great significance for the accuracy of magnetoelectric sensing devices. Torres et al. [14] determined the spatial distribution of the magnetic flux density of passive magnetic field sources most commonly used for magnetic stimulation of biological systems. Ouldhamrane et al. [15] developed a fast and accurate field calculation tool based on the original combination of the magnetic charge concept, image theory, and relative permeance function of an axial flux permanent magnet motor; moreover, they performed an experimental protocol that included measuring the global properties (electromotive force (EMF), Torque) and local field density measurements. Magnetic fields in the millitesla range influence mostly the electrons in the plasma while ions remain unmagnetized. Ehiasarian et al. [16] compared the ion flux, ion composition and time evolution of the cathode spot plasma in various magnetic field configurations where magnetoelectric conversion combinations of permanent magnet arrays and electromagnetic coils were used to alter the shape and intensity of the magnetic field on the cathode surface, ranging from through-field to arched. Takeyama and Kojima [17] proposed a copper-lined (CL) primary coil composed of steel and copper composite material for electromagnetic flux compression technology to generate ultra-high magnetic field, and the best seed field for obtaining the highest peak magnetic field was determined. However, an optimized calculation of the magnetic flux of multiple permanent magnets in different orientations has not been reported. Note that time-varying effects in the magnetic flux density convert the induced EMF apparently. Through the literature correlation study in recent years, we can get the current hot spots of electromagnetic power generation technology. Fig. 1 presents keywords literature retrieval from Web of Science by using CiteSpace, from which it can be easily seen that keywords such as magnetic flux, electromagnetic induction, energy harvester, finite element analysis, magnetic levitation, and frequency up-conversion are similar to neural network distribution. Enhancing the electromechanical coupling coefficient is a pivotal approach to enhancing the output performance of electromagnetic energy harvesters, since the magnetic energy conversion method is a contactless, high-efficiency renewable energy pathway.

Fig. 1

Keywords literature retrieval from Web of Science by using CiteSpace

Due to their simple structure, high output power, and low impedance, electromagnetic components are widely used in the field of vibration energy conversion. Wind energy is a green and sustainable source of energy that can be converted into electrical energy to support low-power electronic devices in wireless applications. To improve the performance of vortex-induced vibration (VIV) energy harvester, Hou et al. [18] proposed a broadband piezoelectric electromagnetic hybrid energy harvester, which is composed of piezoelectric patches and electromagnetic devices, and can scan vortex- and base-induced vibration energy simultaneously. Bjurstrom et al. [19] proposed a new concept to efficiently scavenge the vibrational energy of low frequency and very small dislocations. They described and evaluated an electromagnetic energy harvester whose energy is generated by changes in the air gap caused by motion in the magnetic circuit. Tao et al. [20] presented a micro-electromagnetic vibration energy harvester (VEH) that uses CMOS-compatible 3D MEMS coils and a ferromagnetic core to improve efficiency and output power, and they found there is an optimal initial magnet offset in relation to the air gap to maximize the output power of the system. Oh et al. [21] established an electromagnetic energy generator (EMG) device based on CoFe₂O₄ magnetic material, copper coil, and 3D printed tubular structure. The excitation source of the device is a manual or electromagnetic exciter, and its electrical output response is harvested. The device has considerable power generation capacity (up to 0.86 mW). Shen et al. [22] investigated the energy conversion performance of a new type of inertial electromagnetic damper, the tuned inertial mass electromagnetic damper (TIMED), which can convert cable vibration energy into electrical energy for harvesting. Magnetostrictive energy acquisition has attracted much attention due to its high energy conversion efficiency and environmental durability. Magnetostrictive harvester is mainly composed of giant magnetostrictive material (GMM), magnetic circuit, and circuit, which involves complex mechanical electromagnetic coupling problems. In many previous studies, magnetostrictive harvesters operate under constant prestress and magnetic bias imposed by small signal vibration. Mizukawa et al. [23] used the linearized constitutive equation to model the magnetostrictive energy harvester, and considered the energy loss caused by eddy currents in high-frequency applications. Based on the algebraic output power, the effect of parameter variations on the output power is investigated and the optimal design parameters for the resistors and capacitors in the circuit are given in the form of an algebraic solution. Wang and Zhu [24] investigated reducing the resonant frequency of a vibration energy harvester to accommodate low-frequency ambient vibrations by symmetrically placing magnetic springs with negative stiffness on both sides of the equilibrium point to reduce the corresponding resonant frequency. Huang and Yang [4] proposed a new prototype tunable bistable energy harvester (TBEH), which uses electromagnetic coils and permanent magnets to harvest the vibration energy of the host structure. They studied the effect of single and multiple repeated pulses on the vibration suppression and energy conversion performance of TBEH system. Park and Jang [25] proposed a design method and experimental validation of a two DOF electromagnetic energy harvester consisting of four tensile spring suspended rigid bodies and an electromagnetic transducer, and introduced a Helbach magnetic array to increase the power output, which locates two nearby resonances to give the harvester a larger frequency bandwidth.

Previous reports have demonstrated that the permanent magnet arrangement and coil parameter selection have a great influence on the conversion efficiency of electromagnetic energy harvesters. The main purpose of this paper is to facilitate the maximum energy capture efficiency by optimizing the configuration of permanent magnets and coils. The analytical mathematical model of the magnetic field intensity of multiple permanent magnets can provide guidance for the design of sophisticated magnetic field environments for innovative electromagnetic energy harvesters and enhance the efficiency of energy conversion between magnet energy and mechanical energy. Obtaining the maximum flux variation is the fundamental way to achieve satisfactory electromagnetic energy harvesting. In this paper, a simple theoretical calculation model is proposed to obtain the magnetic flux and its rate of change distribution for an arbitrary permanent magnet and coil layout. Theoretical estimation of magnetic induction intensity distribution and magnetic flux and its rate of change based on Maxwell's electromagnetic field theory can provide an important theoretical basis for size optimization of multiple permanent magnets and optimal design of energy harvesters based on electromagnetic vibrations. The multi-parameter structure optimization with the maximum output induced voltage as the optimization target can provide guidance for the structural and functional integration design of new electromagnetic energy converters. In this work, the axial magnetic flux density distribution in multiple combined permanent magnet configurations is derived based on the axial magnetic vector potential model. Furthermore, the two-dimensional transient magnetic field module of ANSYS Maxwell software is used to simulate and calculate the magnetic flux and its change rate under the multi-combination permanent magnet arrangement, and the accuracy of the theoretical model is verified by comparing with the theoretical calculation results. In addition, the maximum induced electromotive force can be obtained by optimizing the arrangement of permanent magnets and the coil structure for different combinations. Finally, the experimental verification is conducted to make the theoretical analysis sound, and the actual energy conversion performance of the permanent magnet–coil electromagnetic coupling mechanism is measured experimentally.

Mathematical Model

The electromagnetic coupling coefficient is related to the rate of change of the magnetic flux, which in turn is related to the magnetic induction strength of the permanent magnet. Therefore, the electromagnetic coupling coefficient can be evaluated by establishing a model for calculating the magnetic field strength, which can be obtained by the derivation of the magnetic vector potential. The derivation of the magnetic vector potential is shown in the Appendix. Thus, the radial and axial magnetic vector potentials can be expressed as

$$A_{r} \left( x \right) = A\left( x \right) \cdot \hat{r},\,A_{\phi } \left( x \right) = A\left( x \right) \cdot \hat{\Psi }$$

(1)

where $\hat{\Psi } = \,\, - \sin \left( \phi \right)\hat{x} + \cos \left( \phi \right)\hat{y}$ is a function of position; ${\hat{\mathbf{r}}}$ is the radial vector; ${\mathbf{A}}\left( {\mathbf{x}} \right)$ denotes magnetic vector potential.

Combining Eq. (A13) and Eq. (1), the specific forms of radial and axial magnetic vector potentials can be obtained by

$$A_{r} \left( {\mathbf{x}} \right) = \frac{{{\upmu }_{0} M_{s} }}{4\pi }\sum\limits_{j = 1}^{2} {\left( { - 1} \right)}^{j} \int_{{z_{1} }}^{{z_{2} }} {\int_{0}^{2\pi } {\left. {\frac{{\sin \left( {\phi - \phi^{\prime}} \right)}}{{\left| {{\mathbf{x - x^{\prime}}}} \right|}}} \right|} }_{{r^{\prime} = R_{c} \left( j \right)}} R_{c} \left( j \right){\text{d}}\phi^{\prime}{\text{d}}z^{\prime}$$

(2)

$$A_{\phi } \left( {\mathbf{x}} \right) = \frac{{{\upmu }_{{0}} M_{s} }}{4\pi }\sum\limits_{j = 1}^{2} {\left( { - 1} \right)}^{j} \int_{{z_{1} }}^{{z_{2} }} {\int_{0}^{2\pi } {\left. {\frac{{\cos \left( {\phi - \phi^{\prime}} \right)}}{{\left| {{\mathbf{x - x^{\prime}}}} \right|}}} \right|} }_{{r^{\prime} = R_{c} \left( j \right)}} R_{c} \left( j \right){\text{d}}\phi^{\prime}{\text{d}}z^{\prime}$$

(3)

where ${\upmu }_{0}$ is the free space permeability; $M_{s}$ is the saturation magnetization; ${\mathbf{x}}$ is the position vector; $R_{c} \left( j \right)$ is the boundary radius, $R_{c} \left( 1 \right) = R_{1} ,R_{c} \left( 2 \right) = R_{2}$.

Radial Field Component

The radial magnetic flux density is the first-order partial derivative of the radial magnetic vector potential with respect to the radial direction, namely:

$$B_{r} \left( x \right) = - \frac{\partial }{\partial z}A_{\phi } \left( x \right)$$

(4)

Combining Eqs. (3 and 4), the specific form of radial magnetic flux density can be obtained by

$$B_{r} \left( {r,\phi ,z} \right) = \frac{{\mu_{0} M_{s} }}{4\pi }\sum\limits_{j = 1}^{2} {\sum\limits_{k = 1}^{2} {\left( { - 1} \right)^{{\left( {j + k} \right)}} } } \times \int_{0}^{2\pi } {\cos \left( {\phi - \phi^{\prime}} \right)} g\left( {r,\phi ,z;R_{c} \left( j \right),\phi^{\prime},z_{k} } \right)R_{c} \left( j \right)d\phi^{\prime}$$

(5)

For the convenience of calculation, the above integral formula can be further processed, and the final radial magnetic flux density expression can be rewritten as

$$B_{r} \left( {r,\phi ,z} \right) = \frac{{{\upmu }_{0} M_{s} }}{4\pi }\sum\limits_{j = 1}^{2} {\sum\limits_{k = 1}^{2} {\left( { - 1} \right)^{{\left( {j + k} \right)}} R_{c} \left( j \right)} } \times \sum\limits_{m = 0}^{{N_{\phi } }} {S_{\phi } \left( m \right)} \cos \left( {\phi - \phi^{\prime}\left( m \right)} \right)g\left( {r,\phi ,z;R_{c} \left( j \right),\phi^{\prime}\left( m \right),z_{k} } \right)$$

(6)

where

$$z_{k} = \left[ {z_{1} \, z_{2} } \right]\mathop {\lim }\limits_{x \to \infty } ,\,\,g\left( {r,\phi ,z;r^{\prime},\phi^{\prime},z_{k} } \right) = \frac{1}{{\left[ {r^{2} + r^{{\prime}{2}} - 2rr^{\prime}\cos \left( {\phi - \phi^{\prime}} \right) + \left( {z - z_{k} } \right)^{2} } \right]^{1/2} }}$$

The remaining integral in $\phi^{\prime}$ can be written in terms of a discrete sum using a simple numerical scheme such as Simpson's method. $N_{\phi }$ denotes the number of mesh points in the $\phi^{\prime}$. $r^{\prime}\left( n \right),\phi^{\prime}_{s} \left( m \right)$ denotes the values at which the integrands are evaluated. The Simpson integration coefficients $S_{\phi } \left( m \right)$ and $\phi^{\prime}\left( m \right)$ are specified as follows:

$$\phi^{\prime}\left( m \right) = \frac{m}{{N_{\phi } }}2\pi \, \left( {m = 0,1,2,...,N_{\phi } } \right)$$

(7)

$$S_{\phi } \left( m \right) = \left\{ \begin{gathered} \frac{1}{3} \, \left( {m = 0} \right) \hfill \\ \frac{4}{3} \, \left( {m = 1,3,5,...} \right) \hfill \\ \frac{2}{3} \, \left( {m = 2,4,6,...} \right) \hfill \\ \frac{1}{3} \, \left( {m = N_{\phi } } \right) \hfill \\ \end{gathered} \right.$$

(8)

Applying these schemes to Eq. (6), the total radial field component can be calculated by

$$B_{r} \left( {r,\phi ,z} \right) = \frac{{\mu_{0} M_{s} }}{4\pi }\sum\limits_{j = 1}^{2} {\sum\limits_{k = 1}^{2} {\left( { - 1} \right)^{{\left( {j + k} \right)}} R_{c} \left( j \right)} } \times \sum\limits_{m = 0}^{{N_{\phi } }} {S_{\phi } \left( m \right)} \cos \left( {\phi - \phi^{\prime}\left( m \right)} \right)g\left( {r,\phi ,z;R_{c} \left( j \right),\phi^{\prime}\left( m \right),z_{k} } \right)$$

(9)

Figure 2 shows the radial magnetic flux density distribution of permanent magnets with different outer diameters. From Fig. 2, it can be seen that the radial flux density of cylindrical permanent magnets reaches its maximum value on the outer radius circles of the upper and lower surfaces and in opposite directions. The projected shape of the radial flux density is related to the ratio of the outer diameter to the height of the permanent magnet. It can be found that for a given height of the permanent magnet, the smaller the radius of the permanent magnet, the more elliptical the projected shape of the flux density peaks and valleys are in the vertical plane.

Fig. 2

Radial flux density distribution of permanent magnets with different outer diameters. a R₂ = 10 mm, h = 40 mm; b R₂ = 20 mm, h = 40 mm

Axial Field Component

Similarly, the axial magnetic flux density can be expressed as a function of the position function, which can be calculated by introducing the magnetic vector potential:

$$B_{z} \left( x \right) = \frac{1}{r}\left( {\frac{\partial }{\partial r}\left( {rA_{\phi } \left( x \right)} \right) - \frac{\partial }{\partial \phi }A_{r} \left( x \right)} \right)$$

(10)

The axial flux density can be simplified by referring to the same numerical format in the previous section. The axial magnetic flux intensity formula in the cylindrical coordinate system can be expressed as

$$\begin{gathered} B_{z} \left( {r,\phi ,z} \right) = \frac{{\mu_{0} M_{s} }}{4\pi }\sum\limits_{j = 1}^{2} {\left( { - 1} \right)}^{{\left( {j + 1} \right)}} \times \left\{ {\frac{2\pi }{{N_{\phi } }}\sum\limits_{m = 0}^{{N_{\phi } }} {\left[ {S_{\phi } \left( m \right)\left( {r\cos \left( {\phi - \phi^{\prime}\left( m \right)} \right) - R_{c} \left( j \right)} \right)R_{c} \left( j \right)} \right.} } \right. \hfill \\ \, \left. { \, \left. { \times \int_{{z_{1} }}^{{z_{2} }} {g^{3} \left( {r,\phi ,z;R_{c} \left( j \right),\phi^{\prime}\left( m \right),z^{\prime}} \right)dz^{\prime}} } \right]} \right\} \hfill \\ \end{gathered}$$

(11)

The integral form for g³ function can be evaluated analytically through considering the following relationship:

$$\int_{{z_{1} }}^{{z_{2} }} {g^{3} \left( {r,\phi ,z;r^{\prime},\phi^{\prime},z^{\prime}} \right){\text{d}}z^{\prime} = } \sum\limits_{k = 1}^{2} {\left( { - 1} \right)^{k + 1} } I\left( {r,\phi ,z;r^{\prime},\phi^{\prime},z_{k} } \right)$$

(12)

Accordingly, the axial magnetic flux intensity can be calculated by

$$\begin{gathered} B_{z} \left( {r,\phi ,z} \right) = \frac{{{\upmu }_{0} M_{s} }}{4\pi }\sum\limits_{j = 1}^{2} {\sum\limits_{k = 1}^{2} {\left( { - 1} \right)}^{{\left( {j + k} \right)}} } \times \left\{ {\frac{2\pi }{{N_{\phi } }}\sum\limits_{m = 0}^{{N_{\phi } }} {\left[ {S_{\phi } \left( m \right)\left( {r\cos \left( {\phi - \phi^{\prime}\left( m \right)} \right) - R_{c} \left( j \right)} \right)} \right.} } \right. \hfill \\ \, \left. {\left. { \times R_{c} \left( j \right)I\left( {r,\phi ,z;R_{c} \left( j \right),\phi^{\prime}\left( m \right),z_{k} } \right)} \right]} \right\} \hfill \\ \end{gathered}$$

(13)

where

$$I \equiv \left\{ \begin{gathered} F\left( {r,\phi ,z;r^{\prime},\phi^{\prime},z_{k} } \right) \, if \, r^{2} + r^{{\prime}{2}} - 2rr^{\prime}\cos \left( {\phi - \phi^{\prime}} \right) \ne 0 \hfill \\ - \frac{1}{{2\left( {z - z_{k} } \right)^{2} }} \, if \, r = r^{\prime},\cos \left( {\phi - \phi^{\prime}} \right) = 1,z \ne z_{k} \, \hfill \\ \end{gathered} \right.$$

(14)

$$F\left( {r,\phi ,z;r^{\prime},\phi^{\prime},z_{k} } \right) = \frac{{\left( {z - z_{k} } \right)g\left( {r,\phi ,z;r^{\prime},\phi^{\prime},z_{k} } \right)}}{{r^{2} + r^{{\prime}{2}} - 2rr^{\prime}\cos \left( {\phi - \phi^{\prime}} \right)}}$$

(15)

Figure 3 shows the axial magnetic flux density distribution of single permanent magnet with different outer diameters. It can be seen that the axial magnetic flux density of single permanent magnet is considerable inside the magnet, while the axial magnetic flux density of single permanent magnet is stable radially along the outer radius (r < R₂). Surprisingly, the axial magnetic flux density of single permanent magnet experiences a sudden reverse when the radial distance is greater than the outer radius decrease (r > R₂). Additionally, the axial flux density is symmetric about the z = 0 plane and decreases rapidly along the z-axis. It is also clear that the larger the outer radius of the permanent magnet, the smaller the maximum flux density. Therefore, to increase the axial flux density, it is crucial to determine a favorable outer radius and height.

Fig. 3

Axial magnetic flux density distribution of single permanent magnet with different outer diameters. a R₂ = 10 mm, h = 40 mm; b R₂ = 20 mm, h = 40 mm

Magnetic Field Calculation for Multiple Permanent Magnets

The theoretical calculations of the radial and axial magnetic flux densities of a single permanent magnet based on Maxwell’s electromagnetic field theory are presented above. In engineering practice, it is necessary to rationalize the arrangement of permanent magnets to increase the magnetic flux density. Therefore, it is of great significance to study the homopolar or heteropolar arrangement of multiple combined permanent magnets to improve the axial magnetic flux density. The formula for calculating the axial magnetic flux density for multiple combined permanent magnets in a co-polar or heteropolar arrangement is first derived, and then the magnetic field components for the case of two and three combined permanent magnets in a co-polar or heteropolar arrangement are presented in comparison. Figure 4 shows a schematic diagram of two and three combined permanent magnet configurations in a co-polar or heteropolar arrangement.

Fig. 4

Schematic diagram of two and three permanent magnets aligned with the same or different poles

For the combined configuration of two axially magnetized cylindrical permanent magnets with the same or different poles, the axial flux density can be calculated by the superposition of the axial magnetic fields generated by the two permanent magnets at different positions, and the integral expression can be written as

$$\begin{gathered} B_{z} \left( {r,\phi ,z} \right) = \frac{{{\upmu }_{0} M_{s} }}{4\pi }\sum\limits_{j = 1}^{2} {\left( { - 1} \right)}^{{\left( {j + 1} \right)}} \times \left\{ {\frac{2\pi }{{N_{\phi } }}\sum\limits_{m = 0}^{{N_{\phi } }} {\left[ {S_{\phi } \left( m \right)\left( {r\cos \left( {\phi - \phi^{\prime}\left( m \right)} \right) - R_{c} \left( j \right)} \right)R_{c} \left( j \right)} \right.} } \right. \hfill \\ \, \left. { \times \int_{{z_{1} }}^{{z_{2} }} {g^{3} \left( {r,\phi ,z;R_{c} \left( j \right),\phi^{\prime}\left( m \right),z^{\prime}} \right){\text{d}}z^{\prime}} } \right]{ + }\left( { - 1} \right)^{p} \left[ {S_{\phi } \left( m \right)\left( {r\cos \left( {\phi - \phi^{\prime}\left( m \right)} \right) - R_{c} \left( j \right)} \right)} \right. \hfill \\ \, \left. {\left. { \times R_{c} \left( j \right)\int_{{z_{3} }}^{{z_{4} }} {g_{1}^{3} \left( {r,\phi ,z;R_{c} \left( j \right),\phi^{\prime}\left( m \right),z^{\prime}} \right){\text{d}}z^{\prime}} } \right]} \right\} \hfill \\ \end{gathered}$$

(16)

where p = 1 denotes homopolar alignment layout, p = 2 denotes heteropolar alignment layout $z_{k} = \left[ {z_{1} \, z_{2} } \right]$, $z_{{k_{1} }} = \left[ {z_{3} \, z_{4} } \right]$.

$$g\left( {r,\phi ,z;r^{\prime},\phi^{\prime},z_{k} } \right) = \frac{1}{{\left[ {r^{2} + r^{{\prime}{2}} - 2rr^{\prime}\cos \left( {\phi - \phi^{\prime}} \right) + \left( {z - z_{k} } \right)^{2} } \right]^{1/2} }}$$

(17)

$$g_{1} \left( {r,\phi ,z;r^{\prime},\phi^{\prime},z_{{k_{1} }} } \right) = \frac{1}{{\left[ {r^{2} + r^{{\prime}{2}} - 2rr^{\prime}\cos \left( {\phi - \phi^{\prime}} \right) + \left( {z - z_{{k_{1} }} } \right)^{2} } \right]^{1/2} }}$$

(18)

$$\int_{{z_{3} }}^{{z_{4} }} {g_{1}^{3} \left( {r,\phi ,z;r^{\prime},\phi^{\prime},z^{\prime}} \right){\text{d}}z^{\prime} = } \sum\limits_{k = 1}^{2} {\left( { - 1} \right)^{k + 1} } I_{1} \left( {r,\phi ,z;r^{\prime},\phi^{\prime},z_{{k_{1} }} } \right)$$

(19)

$$I_{1} \equiv \left\{ \begin{gathered} F_{1} \left( {r,\phi ,z;r^{\prime},\phi^{\prime},z_{{k_{1} }} } \right) \, if \, r^{2} + r^{{\prime}{2}} - 2rr^{\prime}\cos \left( {\phi - \phi^{\prime}} \right) \ne 0 \hfill \\ - \frac{1}{{2\left( {z - z_{{k_{1} }} } \right)^{2} }} \, if \, r = r^{\prime},\cos \left( {\phi - \phi^{\prime}} \right) = 1,z \ne z_{{k_{1} }} \, \hfill \\ \end{gathered} \right.$$

(20)

$$F_{1} \left( {r,\phi ,z;r^{\prime},\phi^{\prime},z_{{k_{1} }} } \right) = \frac{{\left( {z - z_{{k_{1} }} } \right)g_{1} \left( {r,\phi ,z;r^{\prime},\phi^{\prime},z_{{k_{1} }} } \right)}}{{r^{2} + r^{{\prime}{2}} - 2rr^{\prime}\cos \left( {\phi - \phi^{\prime}} \right)}}$$

(21)

Therefore, the ultimate expression of axial magnetic flux density can be calculated by

$$\begin{gathered} B_{z} \left( {r,\phi ,z} \right) = \frac{{{\upmu }_{0} M_{s} }}{4\pi }\sum\limits_{j = 1}^{2} {\sum\limits_{k = 1}^{2} {\left( { - 1} \right)}^{{\left( {j + k} \right)}} } \times \left\{ {\frac{2\pi }{{N_{\phi } }}\sum\limits_{m = 0}^{{N_{\phi } }} {\left[ {S_{\phi } \left( m \right)\left( {r\cos \left( {\phi - \phi^{\prime}\left( m \right)} \right) - R_{c} \left( j \right)} \right)} \right.} } \right. \hfill \\ \, \left. { \times R_{c} \left( j \right)I\left( {r,\phi ,z;R_{c} \left( j \right),\phi^{\prime}\left( m \right),z_{k} } \right)} \right] - \left[ {S_{\phi } \left( m \right)\left( {r\cos \left( {\phi - \phi^{\prime}\left( m \right)} \right) - R_{c} \left( j \right)} \right)} \right. \hfill \\ \, \left. {\left. { \times R_{c} \left( j \right)I_{1} \left( {r,\phi ,z;R_{c} \left( j \right),\phi^{\prime}\left( m \right),z_{{k_{1} }} } \right)} \right]} \right\} \hfill \\ \end{gathered}$$

(22)

For the combined configuration of multiple axially magnetized cylindrical permanent magnets with the same or different poles, the axial flux density can be calculated by superimposing the axial magnetic fields generated by multiple permanent magnets at different positions, and the axial flux density can be expressed as

$$\begin{gathered} B_{z} \left( {r,\phi ,z} \right) = \frac{{{\upmu }_{0} M_{s} }}{4\pi }\sum\limits_{j = 1}^{2} {\left( { - 1} \right)}^{{\left( {j + 1} \right)}} \times \left\{ {\frac{2\pi }{{N_{\phi } }}\sum\limits_{m = 0}^{{N_{\phi } }} {\left[ {S_{\phi } \left( m \right)\left( {r\cos \left( {\phi - \phi^{\prime}\left( m \right)} \right) - R_{c} \left( j \right)} \right)R_{c} \left( j \right)} \right.} } \right. \hfill \\ \, \left. { \times \int_{{z_{1} }}^{{z_{2} }} {g^{3} \left( {r,\phi ,z;R_{c} \left( j \right),\phi^{\prime}\left( m \right),z^{\prime}} \right){\text{d}}z^{\prime}} } \right] + \left( { - 1} \right)^{{p_{1} }} \left[ {S_{\phi } \left( m \right)\left( {r\cos \left( {\phi - \phi^{\prime}\left( m \right)} \right) - R_{c} \left( j \right)} \right)R_{c} \left( j \right)} \right. \hfill \\ \, \left. { \times \int_{{z_{3} }}^{{z_{4} }} {g_{1}^{3} \left( {r,\phi ,z;R_{c} \left( j \right),\phi^{\prime}\left( m \right),z^{\prime}} \right){\text{d}}z^{\prime}} } \right] + \left( { - 1} \right)^{{p_{2} }} \left[ {S_{\phi } \left( m \right)\left( {r\cos \left( {\phi - \phi^{\prime}\left( m \right)} \right) - R_{c} \left( j \right)} \right)R_{c} \left( j \right)} \right. \hfill \\ \, \left. { \times \int_{{z_{5} }}^{{z_{6} }} {g_{2}^{3} \left( {r,\phi ,z;R_{c} \left( j \right),\phi^{\prime}\left( m \right),z^{\prime}} \right){\text{d}}z^{\prime}} } \right] + ... \hfill \\ \, \left. { + \left( { - 1} \right)^{{p_{{\text{n}}} }} \left[ {S_{\phi } \left( m \right)\left( {r\cos \left( {\phi - \phi^{\prime}\left( m \right)} \right) - R_{c} \left( j \right)} \right)R_{c} \left( j \right)\left. { \times \int_{{z_{2n + 1} }}^{{z_{2n + 2} }} {g_{n}^{3} \left( {r,\phi ,z;R_{c} \left( j \right),\phi^{\prime}\left( m \right),z^{\prime}} \right){\text{d}}z^{\prime}} } \right]} \right.} \right\} \hfill \\ \end{gathered}$$

(23)

where p_n = 1 denotes homopolar alignment layout, p_n = 2 denotes heteropolar alignment layout, $z_{k} = \left[ {z_{1} \, z_{2} } \right]$, $z_{{k_{1} }} = \left[ {z_{3} \, z_{4} } \right]$, $z_{{k_{2} }} = \left[ {z_{5} \, z_{6} } \right]$, $z_{{k_{n} }} = \left[ {z_{2n + 1} \, z_{2n + 2} } \right]$

$$g_{2} \left( {r,\phi ,z;r^{\prime},\phi^{\prime},z_{{k_{2} }} } \right) = \frac{1}{{\left[ {r^{2} + r^{{\prime}{2}} - 2rr^{\prime}\cos \left( {\phi - \phi^{\prime}} \right) + \left( {z - z_{{k_{2} }} } \right)^{2} } \right]^{1/2} }}$$

(24)

$$\int_{{z_{5} }}^{{z_{6} }} {g_{2}^{3} \left( {r,\phi ,z;r^{\prime},\phi^{\prime},z^{\prime}} \right){\text{d}}z^{\prime} = } \sum\limits_{k = 1}^{2} {\left( { - 1} \right)^{k + 1} } I_{2} \left( {r,\phi ,z;r^{\prime},\phi^{\prime},z_{{k_{2} }} } \right)$$

(25)

$$I_{2} \equiv \left\{ \begin{gathered} F_{2} \left( {r,\phi ,z;r^{\prime},\phi^{\prime},z_{{k_{2} }} } \right) \, if \, r^{2} + r^{{\prime}{2}} - 2rr^{\prime}\cos \left( {\phi - \phi^{\prime}} \right) \ne 0 \hfill \\ - \frac{1}{{2\left( {z - z_{{k_{2} }} } \right)^{2} }} \, if \, r = r^{\prime},\cos \left( {\phi - \phi^{\prime}} \right) = 1,z \ne z_{{k_{2} }} \, \hfill \\ \end{gathered} \right.$$

(26)

$$F_{2} \left( {r,\phi ,z;r^{\prime},\phi^{\prime},z_{{k_{2} }} } \right) = \frac{{\left( {z - z_{{k_{2} }} } \right)g_{2} \left( {r,\phi ,z;r^{\prime},\phi^{\prime},z_{{k_{2} }} } \right)}}{{r^{2} + r^{{\prime}{2}} - 2rr^{\prime}\cos \left( {\phi - \phi^{\prime}} \right)}}$$

(27)

$$g_{n} \left( {r,\phi ,z;r^{\prime},\phi^{\prime},z_{{k_{n} }} } \right) = \frac{1}{{\left[ {r^{2} + r^{{\prime}{2}} - 2rr^{\prime}\cos \left( {\phi - \phi^{\prime}} \right) + \left( {z - z_{{k_{n} }} } \right)^{2} } \right]^{1/2} }}$$

(28)

$$\int_{{z_{2n + 1} }}^{{z_{2n + 2} }} {g_{n}^{3} \left( {r,\phi ,z;r^{\prime},\phi^{\prime},z^{\prime}} \right)dz^{\prime} = } \sum\limits_{k = 1}^{2} {\left( { - 1} \right)^{k + 1} } I_{n} \left( {r,\phi ,z;r^{\prime},\phi^{\prime},z_{{k_{n} }} } \right)$$

(29)

$$I_{n} \equiv \left\{ \begin{gathered} F_{n} \left( {r,\phi ,z;r^{\prime},\phi^{\prime},z_{{k_{n} }} } \right) \, if \, r^{2} + r^{{\prime}{2}} - 2rr^{\prime}\cos \left( {\phi - \phi^{\prime}} \right) \ne 0 \hfill \\ - \frac{1}{{2\left( {z - z_{{k_{n} }} } \right)^{2} }} \, if \, r = r^{\prime},\cos \left( {\phi - \phi^{\prime}} \right) = 1,z \ne z_{{k_{n} }} \, \hfill \\ \end{gathered} \right.$$

(30)

$$F_{n} \left( {r,\phi ,z;r^{\prime},\phi^{\prime},z_{{k_{n} }} } \right) = \frac{{\left( {z - z_{{k_{n} }} } \right)g_{n} \left( {r,\phi ,z;r^{\prime},\phi^{\prime},z_{{k_{n} }} } \right)}}{{r^{2} + r^{{\prime}{2}} - 2rr^{\prime}\cos \left( {\phi - \phi^{\prime}} \right)}}$$

(31)

For two and three permanent magnets arranged with the same poles, their axial magnetic field components differ greatly. In Fig. 5, the three permanent magnets with the same pole arrangement will have two peaks and one valley, which causes the permanent magnets to move along the axis, resulting in a large variation in magnetic flux. Figure 6 shows the axial magnetic flux density distribution of the three permanent magnets with different outer radii. From Fig. 6, it can be seen that the axial magnetic induction intensity decreases with the increase of the outer diameter of the permanent magnets, and the magnetic field components along both axes decay significantly. Therefore, choosing a suitable outer diameter is the key to improve the axial magnetic induction strength of permanent magnets.

Fig. 5

The axial magnetic flux density distribution (R₂ = 10 mm, h = 20 mm, d_g = 5 mm). a Two PMs; b three PMs

Fig. 6

The axial magnetic flux density distribution of three PMs configuration (h = 20 mm, d_g = 5 mm). a R₂ = 10 mm; b R₂ = 12.5 mm; c R₂ = 15 mm; d R₂ = 20 mm

Theoretical Calculation of Magnetic Flux

According to Eqs. (A3 and 23), the magnetic flux over a certain cross-sectional area can be calculated, and then the rate of change of the flux can be obtained by taking its first-order derivative. Figure 7 shows the theoretical calculation of the flux and the rate of change for a single-turn coil with different combinations of permanent magnet configurations. From Fig. 7, it can be seen that the flux variation is larger for the triple permanent magnet configuration than for the double permanent magnet configuration as shown in Fig. 7a. From Fig. 7b, it can be seen that the flux variation rate is higher for the triple permanent magnet configuration than for the double permanent magnet configuration. Figure 8 shows the magnetic flux through the single-turn coils with different outer radii. From Fig. 8, it can be found the larger the outer radius of the permanent magnets, the larger the magnetic flux. Figure 9 shows the rate of change of magnetic flux for single-turn coils with different outer radii. From Fig. 9, it can be seen that the smaller the outer diameter of the permanent magnet, the greater the rate of change of magnetic flux on the same section of the permanent magnet.

Fig. 7

The calculated magnetic flux of a single-turn coil and its rate of change (R₂ = 10 mm, h = 20 mm, d_g = 5 mm, v = 1 m/s). a Magnetic flux of single-turn coil; b the rate of change of magnetic flux in a single-turn coil

Fig. 8

Magnetic flux of single-turn coil distribution under different external radius (h = 20 mm, d = 5 mm, d_g = 5 mm)

Fig. 9

The rate of change of magnetic flux in single-turn coil under different external radius (h = 20 mm, d = 5 mm, d_g = 5 mm, v = 1 m/s)

The height of the permanent magnet has a significant influence on its external magnetic field distribution, which in turn affects the flux distribution when traveling through the coil. Figure 10 shows the magnetic flux and the rate of change of flux through a single-turn coil, respectively, at different coil heights. From Fig. 10, it can be seen that the higher the height of the permanent magnet, the higher the corresponding flux fluctuation. Therefore, the higher the rate of flux change of the permanent magnet, the higher the peak height and valley depth of its flux.

Fig. 10

Magnetic flux and its change rate of single-turn coil distribution under different coil heights (R₂ = 10 mm, d = 5 mm, d_g = 5 mm). a Magnetic flux; b magnetic flux change rate

Magnetic Circuit Optimization Design

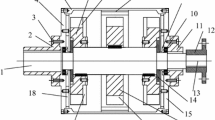
To improve the electromechanical conversion coefficient, it is essential to perform the design of the magnetic circuit of the electromagnetic induction loop. Hereby, the combined permanent magnet arrangement and coil sizes are optimized according to the principle of maximum variation of magnetic flux. First, to verify the accuracy of the theoretical analysis results, the magnetic field models of permanent magnets and coils are established using ANSYS Maxwell, as shown in Fig. 11. The transient magnetic field analysis module was used to simulate the whole process of the permanent magnets passing through the coil uniformly, and the magnetic field changes and induced voltage during the process were calculated and compared with the theoretical calculation results. In addition, the average induced voltage of three different combinations of permanent magnets with different configurations is parametrically processed using the optimization design module of ANSYS Maxwell software, which provides an important basis for extracting the optimal structural and dimensional parameters.

Fig. 11

Schematic diagram of three permanent magnets with homopolar facing configuration passing through a multi-turn coil

Verification of Theoretical Calculation

To verify the accuracy of the above magnetic field theory calculation, the magnetic flux and induced voltage distribution of three permanent magnets in the same polarity arrangement during the passage through the coil were calculated using ANSYS Maxwell. Figure 11 shows a schematic diagram of three homopolar aligned combined permanent magnets. To facilitate comparison with the theoretical analysis, it is assumed that the permanent magnet passes through the induction coil at a constant speed, i.e., the current position of the permanent magnet can be determined by calculating the time, where cap is the region of motion, i.e., the area where the moving grid is set up. Figure 12 shows a comparison of the analytical solution with the finite element method for three heteropolar combined permanent magnet arrangements. As can be seen in Fig. 12, the distribution trend of magnetic flux and the rate of change of magnetic flux in theory and simulation are basically the same. The mismatch between the theoretical and simulation results is mainly due to the horizontal coordinate transformation. In the ANSYS simulation, the motion time of the permanent magnet can be determined by giving the default constant velocity and stationary travel. However, in theoretical calculations, the rate of change of the magnetic flux can be expressed as the product of the derivative of the flux with respect to the displacement and the velocity of motion. Thus, when the velocity is constant, the rate of change of the magnetic flux is proportional to the derivative of the magnetic flux with respect to the displacement. In addition, using a theoretical method, the magnetic flux through the coil can be obtained by integrating the axial magnetic induction of the permanent magnet over a finite cross-sectional area. The theoretically calculated flux is smaller than the actual flux due to the omitted flux. Thereby, magnetic flux distribution computed by ANSYS is slightly larger than that of theoretical calculation, as shown in Fig. 12a. Accordingly, rate of change of magnetic flux calculated by ANSYS is likewise larger than the counterpart of theoretical estimation, as described in Fig. 12b. Therefore, without complex and time-consuming simulation analysis, the flux and induced voltage of multiple combined permanent magnets can be parameterized by a simple predictive theoretical model.

Fig. 12

The comparisons of analytical solutions and FEA method in three PMs configuration (R₂ = 10 mm, h = 20 mm, d_g = 5 mm, v = 1 m/s). a Magnetic flux of single-turn coil; b the rate of change of magnetic flux in a single-turn coil

The gap between the permanent magnet and the coil affects the loss of the magnetic field lines, which in turn affects the induced voltage. Figure 13 shows the relationship between the average induced voltage and the magnet–coil gap for the two combined permanent magnet arrangements. It is evident from Fig. 13 that the average induced voltage decreases as the permanent magnet–coil gap increases. Therefore, it is important to determine the appropriate small clearance. In addition, the structure of the coil also has a great influence on the induced voltage. Figure 14 shows the relationship between the average induced voltage and coil height for the two combined permanent magnet arrangements. From Fig. 14, it can be found that the coil height has a significant effect on the induced voltage, and there is an optimal coil height that maximizes the average induced voltage. The axial component of the magnetic field lines changes throughout the passing process. When the permanent magnet is located in the middle of the coil, the axial component of the magnetic field line is small, and the axial magnetic flux is accordingly small.

Fig. 13

The relationship between mean induced voltage and gap distance of permanent magnets and coil

Fig. 14

The relationship between the mean induced voltage and coil height

Combined Permanent Magnet Configuration and Coil Size Optimization Design

Based on the above analysis and simulation results, it can be concluded that three combined permanent magnet arrangements are better than two combined permanent magnet arrangements. Therefore, a comprehensive parametric analysis of the three combinatorial permanent magnet arrangements was carried out. First, three combinatorial PM arrangements with different magnetization directions were compared. The permanent magnet is a circular permanent magnet with an outer diameter of 12 mm, a number of Ampere-turns of 7500, an inner diameter of the coil of 35 mm, and an outer diameter of 55 mm. Figure 15 shows four different permanent magnet configuration modes. As can be seen in Fig. 15, Case.1 and Case.2 are in heteropolar and homopolar arrangements, respectively. The intermediate permanent magnets in Case.3 and Case.4 are magnetized horizontally. Figure 16 shows a schematic illustration of three permanent magnets of opposite polarity passing through a multi-turn coil.

Fig. 15

Schematic diagram of three different configurations of permanent magnets

Fig. 16

Schematic diagram of three permanent magnets with heteropolar facing configuration

Figure 17 compares the average induced voltages at different coil heights for these four combined permanent magnet arrangements. It can be seen from Fig. 17 that the average induced voltage in Case.1 is the largest and does not decrease with the change of coil height. Therefore, Case.1 is the preferred combination permanent magnet arrangement. Figure 20 shows the relationship between the average induced voltage and the coil height and diameter. In Fig. 18, the smaller the wire diameter, the greater the induced voltage, but the corresponding resistance is also greater. Therefore, the maximum power can be obtained by selecting the appropriate wire diameter. According to the engineering circumstances and the requirement of power maximization, a copper coil with a wire diameter of 0.2 mm and a suitable height was chosen here. It can also be seen from Fig. 18 that the correlation between the average induced voltage and the coil height is not monotonic, but increases and then decreases as the coil height increases. Therefore, there is an optimal coil height that maximizes the average induced voltage when the number of Ampere-turns of the coil is constant.

Fig. 17

Comparison of mean induced voltage in three different configurations

Fig. 18

Relationship between mean induced voltage and coil height and coil diameter (R₂ = 10 mm, h = 20 mm, N = 2000)

Figure 19 shows the effect of different coil heights on the average induced voltage for two combined permanent magnet arrangements with constant Ampere-turns. It can be seen from Fig. 19 that when the height of the induction coil is changed from 3 to 42 mm, the average induced voltage of the Case.1 permanent magnet configuration fluctuates slightly, while the average induced voltage of the Case.2 permanent magnet configuration fluctuates greatly, and the coil height increases to 12 mm. In addition, the average induced voltage of the permanent magnet configuration of Case.1 is 7.67 V when the coil height changes, which is almost twice that of Case.2. Therefore, choosing a permanent magnet heteropolar arrangement configuration can maximize the output induced voltage and obtain stable power generation performance.

Fig. 19

Comparison of average induced voltages for two combined permanent magnet arrangements (R₂ = 15 mm, R₁ = 3 mm h = 10 mm, N = 2000)

Experimental Verification

To verify the accuracy of the theoretical and simulation results, we experimentally investigated the induced voltage output of different configurations of permanent magnets. First, we experimentally evaluated the three permanent magnet homopolar arrangement configuration and the two permanent magnet homopolar arrangement configuration. Figure 20 shows the experimental verification of different combined permanent magnet configurations. It can be found that the induced voltage can be measured by the data acquisition system and that the induced voltage generated by random vibration undergoes high-frequency oscillations. From Fig. 20, it can be seen that the induced voltage fluctuation of three permanent magnets arranged with the same pole is larger than that of two permanent magnets. Figure 21 shows the induced voltage distributions for two configurations of the three combined permanent magnets, from which it can be found that the theoretical and experimental induced voltages for the three combined permanent magnets in the heteropolar arrangement are significantly higher than those for the corresponding monopolar arrangement. Figure 22 shows the measured RMS voltages for different combinations of permanent magnet configurations. From Fig. 22, it can be seen that the energy conversion efficiency of the heteropolar configuration of the three combined permanent magnets is the highest, and the measured RMS induced voltages of the three magnet configurations agree well with the theoretical and simulation results.

Fig. 20

Experimental verification of different permanent magnet configurations

Fig. 21

Induced voltage distribution for two configurations of three combined permanent magnets. a Analytic solutions; b experimental results

Fig. 22

The measured RMS voltage with different combined permanent magnet configurations

Concluding Remarks

In this paper, a mathematical model of axial magnetic flux density distribution for multiple permanent magnet configurations is proposed based on the classical Maxwell's electromagnetic theory. The model can be employed to calculate the axial and radial magnetic field components of circular permanent magnets, which provides a sound theoretical basis for effectively predicting the stacking of sophisticated magnetic fields. Furthermore, the theoretical calculation of the magnetic flux and its rate of change has been performed and verified by ANSYS Maxwell software. In addition, the arrangement of the combined permanent magnet and coil parameters has been designed and optimized to obtain the maximum induced electromotive force. Finally, the actual energy conversion performance of the magnet–coil electromagnetic coupling mechanism has been experimentally verified and measured. Theoretical studies show that the flux variation is more pronounced for three homopolar arrangements of combined permanent magnets than for two configurations. Simulation results show that for the same Ampere-turns, the smaller the coil diameter, the larger the output voltage. When the number of Ampere-turns is kept constant, there is an optimal coil height that maximizes the output voltage. The results show that the theoretical and experimental induced voltages for the three heteropolar arrays are significantly higher than those for the three homopolar arrays. The efforts of this work are expected to provide a potential design configuration reference for optimizing electromagnetic energy conversion layouts and maximizing energy conversion.

Appendices

Appendix

Modeling of Magnetic Field

Modeling the field component of a permanent magnet magnetized in the thickness direction is based on Maxwell’s equations. For axially magnetized cylindrical permanent magnets, the residual magnetic induction is equal around the circumference. Therefore, the radial and axial field components need to be considered and estimated (Fig. 

Fig. 23

Schematic diagram of magnetic field lines of a cylindrical permanent magnet

23).

To calculate the magnetic field distribution of axially magnetized permanent magnets, we need to mathematically describe and analyze the magnetic vector potential. Primarily, it is necessary to understand the differential form of the field equations given in Eq. (A1). Therefore, the field equation in integral form (Ampere's current law) can be represented by Eq. (A2).

$$\nabla \times {\rm H} = J,\,\,\nabla \cdot B = 0$$

(A1)

where J is free current density, A/m²; H is magnetic field intensity, A/m; B denotes magnetic flux density, T.

$$\oint_{C} {H \cdot {\text{d}}l = } \int_{S} {J \cdot {\text{d}}s} ,\,\oint_{S} {B \cdot {\text{d}}s} = 0$$

(A2)

where $B = \mu_{0} \left( {H + M} \right)$, for linear, homogeneous, and isotropic materials, B and M are proportional to H, namely, $B = \mu H$, $M = \chi_{m} H$. $\mu$ and $\chi_{m}$ denote the permeability and magnetic susceptibility of the material, respectively. The relationship between $\mu$ and $\chi_{m}$ is described by $\mu = {\upmu }_{0} \left( {\chi_{m} + 1} \right)$.

Magnetic Vector Potential

The magnetic flux through the surface S can be expressed as

$$\Phi = \int_{S} {B \cdot {\text{d}}{\mathbf{s}}}$$

(A3)

Considering a stationary, homogeneous, and isotropic material with linear constitutive relation, the vector potential A has the following relations:

$$\nabla \cdot B = 0 \Rightarrow B = \nabla \times A$$

(A4)

$$\nabla^{2} A - \nabla \left( {\nabla \cdot A} \right) = - \mu J$$

(A5)

By applying Coulomb gauge condition ($\nabla \cdot {\mathbf{A}} = 0$), Eq. (A5) can be rewritten as

$$\nabla^{2} A = - \mu J$$

(A6)

The above equation can be expressed as an integral form using Green's function in free space; thereby, the forms of magnetic vector potential and magnetic flux density can be calculated by

$$A\left( x \right) = \frac{\mu }{4\pi }\int {\frac{{J\left( {x^{\prime}} \right)}}{{\left| {x - x^{\prime}} \right|}}} {\text{d}}v^{\prime}$$

(A7)

$$B\left( x \right) = \frac{\mu }{4\pi }\int {\frac{{J\left( {x^{\prime}} \right) \times \left( {x - x^{\prime}} \right)}}{{\left| {x - x^{\prime}} \right|^{3} }}} dv^{\prime}$$

(A8)

where Green’s function in free space is expressed as $G\left( {x,x^{\prime}} \right) = - \left( {1/4\pi } \right)\left( {1/\left| {x - x^{\prime}} \right|} \right)$.

In terms of surface current density, since magnetization and surface normals are parallel or antiparallel to the upper and lower surfaces of the shell, it can be found that j_m = 0 on the upper and lower surfaces of the shell, and two more surfaces need to be considered:

$${\text{inner surface = }}\left\{ \begin{gathered} r^{\prime} = R_{1} \hfill \\ 0 \le \phi \le 2\pi \hfill \\ z_{1} \le z \le z_{2} \hfill \\ \end{gathered} \right.,\,\,{\text{outer surface = }}\left\{ \begin{gathered} r^{\prime} = R_{2} \hfill \\ 0 \le \phi \le 2\pi \hfill \\ z_{1} \le z \le z_{2} \hfill \\ \end{gathered} \right.$$

The unit normals of these surfaces can be expressed as

$$\hat{n} = \left\{ \begin{gathered} - \hat{r} \, ({\text{inner surface}}) \hfill \\ \, \hat{r} \, ({\text{outer surface}}) \hfill \\ \end{gathered} \right.$$

(A9)

Then the surface current density is

$$j_{m} = \left\{ \begin{gathered} - M_{s} \hat{\Psi } \, ({\text{inner surface}}) \hfill \\ \, M_{s} \hat{\Psi } \, ({\text{outer surface}}) \hfill \\ \end{gathered} \right.$$

(A10)

Therefore, the magnetic vector potential of a single permanent magnet can be expressed as

$$A\left( x \right) = \frac{{\mu_{0} }}{4\pi }\oint_{S} {\frac{{j_{m} \left( {x^{\prime}} \right)}}{{\left| {x - x^{\prime}} \right|}}} {\text{d}}s^{\prime}$$

(A11)

By substituting Eq. (A10) into Eq. (A11), it will yield:

$$A\left( x \right) = \frac{{\mu_{0} M_{s} }}{4\pi }\sum\limits_{j = 1}^{2} {\left( { - 1} \right)}^{j} \int_{{z_{1} }}^{{z_{2} }} {\int_{0}^{2\pi } {\left. {\frac{{\hat{\Psi }}}{{\left| {x - x^{\prime}} \right|}}} \right|} }_{{r^{\prime} = R_{c} \left( j \right)}} R_{c} \left( j \right){\text{d}}\phi^{\prime}{\text{d}}z^{\prime}$$

(A12)

where $R_{c} \left( 1 \right) = R_{1} ,R_{c} \left( 2 \right) = R_{2}$, $\hat{\Psi } = - \sin \left( \phi \right)\hat{x} + \cos \left( \phi \right)\hat{y}$ is the position function.

By employing the position function, the magnetic vector potential of a single permanent magnet can be given as

$$A\left( x \right) = \frac{{\mu_{0} M_{s} }}{4\pi }\sum\limits_{j = 1}^{2} {\left( { - 1} \right)}^{j} \left\{ { - \int_{{z_{1} }}^{{z_{2} }} {\int_{0}^{2\pi } {\left. {\frac{{\sin \left( {\phi^{\prime}} \right)\hat{x}}}{{\left| {x - x^{\prime}} \right|}}} \right|} }_{{r^{\prime} = R_{c} \left( j \right)}} R_{c} \left( j \right)d\phi^{\prime}dz^{\prime} + \int_{{z_{1} }}^{{z_{2} }} {\int_{0}^{2\pi } {\left. {\frac{{\cos \left( {\phi^{\prime}} \right)\hat{y}}}{{\left| {x - x^{\prime}} \right|}}} \right|} }_{{r^{\prime} = R_{c} \left( j \right)}} R_{c} \left( j \right){\text{d}}\phi^{\prime}{\text{d}}z^{\prime}} \right\}$$

(A13)