1 Introduction

Due to the stable meteorological conditions and electromagnetic properties of stratospheric space, the stratospheric flight platform has attracted the attention of many researchers in recent years. The stratospheric airship has set off a worldwide development boom because of its advantages of long residence time and low cost [13, 17], etc. However, from the perspective of control engineering, the control of stratospheric airships faces many challenges and difficulties compared with fixed-wing or rotorcraft. First, compared to fixed-wing aircraft or rotary-wing drones, the control challenges of stratospheric airships lie in their immense volume and considerable inertia, which significantly increase the difficulty of their control. Furthermore, due to their complex structure and operating environment, the dynamic characteristics of airships often exhibit multivariate, nonlinear, and uncertain traits. This makes it difficult to establish an accurate mathematical model for stratospheric airships, and traditional control methods are often not directly applicable to their control systems. Therefore, this research aims to explore the control strategies and methods of stratospheric airships from the perspective of control engineering, to provide new ideas and solutions for addressing their control challenges.

There has been significant progress in the research of trajectory tracking for stratospheric airships in recent years, and now there exist relatively mature research achievements. In [21], by redefining velocity and configuration errors and utilizing the dynamic characteristics of the error system, a state feedback control law is designed to enhance the stability of airship trajectory tracking. In [23], a control framework that includes predictive control and sliding mode control is proposed to solve the trajectory tracking problem of stratospheric airships under state constraints. In [4], the adaptive sliding mode attitude controller was used to track the attitude, and the problem of asymmetric error-constrained vector field path tracking was solved. In [5], a robust controller with an inner-outer loop structure is designed to solve the underactuated problem of stratospheric airships by proposing a new control tracking strategy. In [28], a multi-loop control system is designed to address the problem of planar trajectory tracking for underactuated stratospheric airships, and the simulation verification of classic path flight is achieved. Many other control strategies for airships have been extensively researched in addition to trajectory tracking control, such as path following control [29,30,31] and control of airships with special structures [3, 11].

The aforementioned control methods are only capable of ensuring asymptotic convergence, meaning that there is no constraint on the convergence time of errors. However, in practical airship operations, the convergence time is a crucial performance metric. To address this concern, fixed-time control schemes [16] can offer a faster convergence rate, ensuring that the system error converges within each fixed time interval. In [27], for incomplete systems, a fixed-time control strategy is proposed based on the concept of power integration. In [22], by designing an integral sliding surface, an adaptive fixed-time control system is derived, but it is not extended to higher-order systems. In [14], by transformation extension, the error system is transformed from a time-delay system to a non-delay system, and a non-singular sliding mode is designed to achieve fixed-time uniform convergence. In [34], a cascade control structure is constructed to achieve fixed-time tracking control under external disturbances.

However, emphasizing solely on enhancing the controller’s performance is insufficient from a broader perspective. In current technology level, stratospheric airships must adopt time-space energy storage strategies to achieve day-night cycling. Moreover, traditional onboard wind speed measurement equipment uses a Pitot tube [7]. For flights in the stratosphere with low air density and low power, the pressure changes caused by dynamic pressure cannot be accurately measured. Therefore, to meet the mission requirements, developing a control algorithm for stratospheric airships that can minimize energy consumption while effectively tracking trajectory in the absence of airspeed measurement has become an urgent problem to be solved.

During the long-term operation of the stratospheric airship, the duration of staying in the air is mainly affected by the battery power and the avionics equipment life, so the equipment loss should be reduced as much as possible. Therefore, event-triggered control can be utilized to decouple control tasks from time periodicity, thereby reducing the working frequency of the controller, achieving the goal of reducing energy consumption and improving the working lifespan. In [12], an event-triggered control based on fixed and variable thresholds is implemented for a suspension system using a radial basis function neural network. In [24], they proposed an event-triggered mechanism to address the issue of communication load between the controller and the actuator in dynamic positioning of marine surface ships with actuator faults. In [6], a robust fuzzy control scheme based on event-triggered was proposed to ensure the high fidelity of the path tracking control of underactuated ships. In [8], by employing guided control event-triggered, the number of controller executions for a ship is reduced. In [33], the communication and computation burden of the path tracking controller of a watercraft has been reduced by using an event-triggered mechanism.

To address the issue of unmeasurable airspeed, methods such as adaptive control [18, 32], fuzzy logic systems [15], and neural networks [9] can be utilized in the design of control algorithms. In [18], minimizing the performance index of unmanned aerial vehicles is achieved through the design of a strictly negative imaginary part adaptive controller. In [15], this study achieved the guidance and obstacle avoidance of robots in unknown disturbances by using singleton fuzzy control and fuzzy blending control. In [9], under non-extreme conditions, unknown variables can be estimated by analyzing ship wakes using convolutional neural networks.

This paper is inspired by the works of [1, 20], and we address the issue of trajectory tracking in stratospheric airships. The paper integrates a fixed-time convergence controller and a fixed-time extended state observer with event-triggered mechanism to achieve the airship control task.

The main contributions and characteristics of the proposed method in this paper can be summarized as follows:

  1. 1.

    Drawing on the actual characteristics of stratospheric airships and practical control challenges, including unknown individual differences of airships, external interference, and limited communication and computing resources, this study addresses the problem of trajectory tracking control for stratospheric airships when the airspeed is unmeasurable. Furthermore, this study investigates the implementation of an event-triggered mechanism to enhance the operational lifespan of stratospheric airships.

  2. 2.

    The backstepping method is utilized to design virtual control laws for achieving trajectory tracking tasks. A filter is also designed to estimate the derivative of virtual state variables to reduce complex computations. Additionally, a fixed-time extended state observer is firstly designed, and an adaptive law is introduced to eliminate unknown terms, ensuring that each term in the state space complies with engineering practice. These methods contribute to enhancing the control performance of the system while reducing computational complexity.

  3. 3.

    By designing an event-triggered mechanism, the controller calculations will only be performed when the set threshold conditions are met, significantly reducing the frequency of controller calculations and achieving the goal of saving computing resources.

This paper is arranged as follows. The mathematical model of the airship and the prior knowledge needed in the rest sections are shown in Sect. 2. The design of the observer and its convergence proof are shown in Sect. 3. In Sect. 4, the control law was designed by the backstepping method, and it was proved that the controller is semi-globally uniformly ultimately bounded. In Sect. 5, the paper presents simulation results. The full text is summarized, and the paper concludes by highlighting future work in Sect. 6.

2 Problem Formulation and Preliminaries

2.1 Problem Formulation

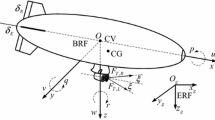
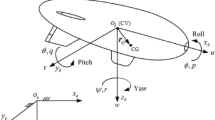
The stratospheric airship model in this paper is shown in Fig. 1.

Fig. 1
figure 1

Structure of the stratospheric airship

Full size image

The nonlinear mathematical model of the stratospheric airship with six DOF(degrees of freedom) is expressed as

$$\begin{aligned} \left\{ \begin{array}{l}\dot{\varvec{X}}_{\varvec{1}}= \varvec{TX_{2}} \\ \dot{\varvec{X}}_{\varvec{2}}=- \varvec{\chi } ^{-1} (\varvec{\Upsilon X_{2}}+ \varvec{\Gamma } (v_{a}))+ \varvec{\chi } ^{-1}\varvec{\tau } \end{array}, \right. \end{aligned}$$
(1)

where \(\varvec{X_{1}}=[x,y,z,\phi ,\theta ,\varphi ] ^{\textrm{T}}\)is the 6-DOF position attitude vector of the stratospheric airship, \(\varvec{X_{2}}=[u,v,w,p,q,r] ^{\textrm{T}}\)is the 6-DOF velocity and angular velocity information of the stratospheric airship. \(\varvec{\chi }\) is a constant value symmetric matrix, \(\varvec{\Upsilon } \) denotes the inertial matrix. \(v_a\) is the airspeed. \(\varvec{\tau } =\left[ \tau _{u},\tau _{v},\tau _{w},\tau _{p},\tau _{q},\tau _{r} \right] ^{\textrm{T}}\) corresponds to the forward thrust, lateral thrust, longitudinal thrust, roll adjustment moment, pitch adjustment moment, and yaw adjustment moment of the airship, respectively. T is the rotation matrix given as

$$\begin{aligned} \begin{aligned}&\varvec{T}=\begin{bmatrix}\varvec{R} & 0_{3\times 3}\\ 0_{3\times 3}& \varvec{K} \end{bmatrix},\\&\varvec{R} = \begin{bmatrix} c \theta c\psi & s\theta c\psi s\phi -s\psi c\phi & s\theta c\psi c\phi +s\psi s\phi \\ c \theta s\psi & s\theta s\psi s\phi +c\psi c\phi & s\theta s\psi c\phi -c\psi s\phi \\ -s\theta & c\theta s\phi & c\theta c\phi \end{bmatrix},\\&\varvec{K} = \begin{bmatrix} 1& s\phi t\theta & c\phi t\theta \\ 0 & c\phi & -s\phi \\ 0 & s\phi e\theta & c\phi e\theta \end{bmatrix},\\ \end{aligned} \end{aligned}$$
(2)

where \(s\cdot =\sin \cdot \),\(c\cdot =\cos \cdot \),\(t\cdot =\tan \cdot \),\(e\cdot =\sec \cdot \). Obviously can obtain that \(\left\| \varvec{T} \right\| =\frac{1}{\cos \theta }\ge 1 \) and \(\left\| \cdot \right\| \)means the determinant of a matrix.

Remark 1

Since the airspeed is unmeasurable, \(\Gamma (v_{a})\) in the Eq. (1) is an unknown quantity to be estimated, and the mathematical expression is

$$\begin{aligned} \varvec{\Gamma (v_{a})} =\begin{bmatrix}(G-B)\sin \theta -F_{ax} \\ (B-G)\cos \theta \sin \phi -F_{ay} \\ (B-G)\cos \theta \cos \phi -F_{az} \\ z_{C}G\cos \theta \sin \phi -y_{C}G\cos \theta \cos \phi -M_{ax} \\ z_{C}G\sin \theta +x_{C}G\cos \theta \cos \phi -M_{ay} \\ -x_{C}\cos \theta \sin \phi -y_{C}G\sin \theta -M_{az} \end{bmatrix}, \end{aligned}$$
$$\begin{aligned} \varvec{F_{a}}=\begin{bmatrix}-\frac{1}{2} \rho v_{a}^{2}S_{ref}C_{x}(\alpha _{angle},\beta _{sideslip},q,r) \\ frac{1}{2} \rho v_{a}^{2}S_{ref}C_{y}(\beta _{sideslip},q,r) \\ frac{1}{2} \rho v_{a}^{2}S_{ref}C_{z}(\alpha _{angle},q,r) \end{bmatrix}\Rightarrow \begin{bmatrix}F_{ax} \\ F_{ay} \\ F_{az} \end{bmatrix}, \end{aligned}$$
$$\begin{aligned} \begin{aligned} \varvec{ M_{a}}&=\begin{bmatrix}-\frac{1}{2} \rho v_{a}^{2}S_{ref}L_{ref}C_{l}(\alpha _{angle},\beta _{sideslip},p,\dot{p} ) \\ frac{1}{2} \rho v_{a}^{2}S_{ref}L_{ref}C_{m}(\alpha _{angle},\beta _{sideslip},p,\dot{p},q,\dot{q}) \\ frac{1}{2} \rho v_{a}^{2}S_{ref}L_{ref}C_{n}(\alpha _{angle},\beta _{sideslip},p,\dot{p},r,\dot{r}) \end{bmatrix}\\ &\Rightarrow \begin{bmatrix}M_{ax} \\ M_{ay} \\ M_{az} \end{bmatrix}, \end{aligned} \end{aligned}$$

where the gravity force on the airship is \(G=mg\), the buoyancy force is \(B=\rho g\nabla \), \(\nabla \) is the total volume of the airship, \(\rho \) is the atmospheric density at the altitude of the airship, g is the acceleration of gravity at the altitude of the airship. \(F_{ax},F_{ay},F_{az}\) and \(C_{x},C_{y},C_{z}\) are the drag, drag coefficient, lateral force, lateral force coefficient, lift, and lift coefficient of the airship, respectively. \(M_{ax},M_{ay},M_{az}\) and \(C_{l},C_{m},C_{n}\) are the roll moment, pitch moment, yaw moment and the corresponding coefficient of the airship, respectively. \(S_{ref}\) is the reference area, \(L_{ref}\) is the reference length.

The more detailed model derivation is given in [4].

Assumption 1

The control input \(\varvec{F_{T}}\) and \(\varvec{M_{T}}\) satisfies \(\varvec{F_{T,\min }}\le \varvec{F_{T}}\le \varvec{F_{T,\max }}\), \(\varvec{M_{T,\min }}\le \varvec{M_{T}}\le \varvec{ M_{T,\max }}\), It can be obtained that the control input t satisfies the input constraint as

$$\begin{aligned} \begin{aligned} \varvec{\tau }&= \textrm{sat}( \varvec{\tau _{0}})\\ &=\begin{Bmatrix} \varvec{\tau _{0,\max }},&\varvec{\tau _{0}}> \varvec{\tau _{0,\max }}\\ \varvec{\tau _{0}},&\varvec{\tau _{0,\min }}\le \varvec{\tau _{0}}\le \varvec{ \tau _{0,\max }}\\ \varvec{\tau _{0,\min }},&\varvec{\tau _{0}}< \varvec{\tau _{0,\min }} \end{Bmatrix} \\ &= \varvec{\tau _{0}}+\varvec{\delta _{\tau }}, \end{aligned} \end{aligned}$$
(3)

where \(\cdot _{\max }\) and \(\cdot _{\min }\) denote the maximum and minimum value of the control input, respectively.

Assumption 2

The desired position \(\varvec{X_{1d}}\) of an airship is bounded and differentiable second order.

Assumption 3

The airspeed of the airship is unmeasurable. Due to the thin air in the stratosphere, the vast majority of stratospheric airships cannot effectively measure airspeed. The target pose is artificially set, so the assumption is valid.

2.2 Preliminaries

For an n-dimensional vector \(\varvec{x}\) we have \(\textrm{sig}^{a}(\varvec{x})=[|x_{1}|^{a}\textrm{sign}(x_{1}),|x_{2}|^{a}\textrm{sign}(x_{2}), \ldots ,|x_{n}|^{a}\textrm{sign}(x_{n}) ]\), \(\textrm{sign}(\varvec{x})=[\textrm{sign}(x_1),\textrm{sign}(x_2),\cdots ,\textrm{sign}(x_n)]\), where a is an arbitrary real number, \(\textrm{sign}(\cdot )\) is the sign function as

$$\begin{aligned} \textrm{sign}(x)=\left\{ \begin{matrix}-1 & x<0 \\ 0 & x=0 \\ 1 & x>0 \end{matrix}. \right. \end{aligned}$$
(4)

For a nonlinear system \(\varvec{x(t)},\varvec{x}=[x_{1},x_{2},\cdots ,x_{n}]\) satisfies

$$\begin{aligned} \begin{aligned} \varvec{x}(t)=&f(\varvec{x}(t)),\\ \varvec{x}(0)=&\varvec{0}\\ f(0)=&\varvec{0},\varvec{x}\subset R^n, \end{aligned} \end{aligned}$$
(5)

where \(R^n\) is an n-dimensional vector.

\(\varvec{\theta }\) and \(\varvec{\theta ^k}\) are expressed as \(\varvec{\theta } = [\theta _1,\theta _2,...,\theta _n]^\textrm{T}\), \(\varvec{\theta ^k} = [\theta _1^k,\theta _2^k,...,\theta _n^k]^\textrm{T}\).

Lemma 1

[20] If Eq. (5) is satisfied as

$$\begin{aligned} \begin{aligned} \dot{\varvec{x}}&=-c_{1}\textrm{sig}^{\alpha }(\varvec{x})-c_{2}\textrm{sig}^{\beta }(\varvec{x}),\\ \varvec{x}(0)&=\varvec{0}, \end{aligned} \end{aligned}$$
(6)

where \(\alpha ,\beta ,c_{1},c_{2}\) are positive constants and satisfy \(0<\alpha <1,\beta >1\), then this nonlinear system is fixed-time convergent and the convergence time T is satisfied as

$$\begin{aligned} T\le \frac{1}{c_{1}(1-\alpha )} +\frac{1}{c_{2}(\beta -1)}. \end{aligned}$$
(7)

In addition, if there exist small perturbations such that the nonlinear system of equation (5) is satisfied as

$$\begin{aligned} \dot{\varvec{x}}=-c_{1}\textrm{sig}^{\alpha }(\varvec{x})-c_{2}\textrm{sig}^{\beta }(\varvec{x})+\varvec{\eta }, \varvec{x}(0)=\varvec{x_{0}}, \end{aligned}$$
(8)

where \(\varvec{\eta } \) is a vector of small positive real numbers, then this nonlinear system is semi-global fixed-time uniform ultimate boundedness(SGFTUUB), and it converges in the neighborhood of the origin, and the convergence time is satisfied as

$$\begin{aligned} T\le \frac{1}{c_{1}(1-\alpha )(2^{\alpha }-1)} +\frac{1}{c_{2}(\beta -1)}. \end{aligned}$$
(9)

3 Observer Design

3.1 Model Transformation

The paper’s proposed event-triggered mechanism \( \varvec{\bar{\tau }}=\mathrm sat(\varvec{\tau }_0)\), \(\varvec{\tau (t)} = \varvec{\bar{\tau }(t_k)}, \forall t\in [t_k,t_{k+1})\) is defined as

$$\begin{aligned} \begin{aligned} t_{k+1}=\textrm{inf}\left\{ t> t_{k} | |e_{1}(t)|\ge \zeta _{1}\left| \bar{\tau }_{1}(t_{k}) \right| +\varsigma _{1}\ or\right. \\ \left. |e_{2}(t)|\ge \zeta _{2}\left| \bar{\tau }_{2}(t_{k}) \right| +\varsigma _{2}\ or\right. \\ \left. \vdots \right. \\ \left. |e_{6}(t)|\ge \zeta _{6}\left| \bar{\tau }_{6}(t_{k}) \right| +\varsigma _{6}\right\} , \end{aligned} \end{aligned}$$

where \(e_i(t)=\tau _i(t)-\bar{\tau _i}(t_k)\) is the measurement error. \(0<\zeta _i<1\) and \(\varsigma _i>0\) are controller parameters.

Remark 2

Definition \(\varphi _i(t) = \frac{\bar{\tau }_i(t) -\tau _i(t)}{\zeta _i|\tau _i(t)|+\varsigma _i},i = 1,2,\cdots ,6\), according to the trigger condition, for any \(t\in [t_k,t_{k+1})\), there are \(\bar{\tau }_i(t) -\bar{\tau }_i(t_k) \le \zeta _i|\bar{\tau }_i(t_k)|+\varsigma _i\), and \(\tau _i(t) = \bar{\tau }_i(t_k)\), \(|\varphi _i(t)|\le 1,k = 0,1,2,\dots \) are attainable by definition \(t_0:=0\). The controller error caused by event-triggered mechanism is defined as \(\varrho _i(t):=\bar{\tau }_i(t)-\tau _i(t)\). From \(|\varphi _i(t)|\le 1\), \(\bar{\tau }_{i,\min }\le {\bar{\tau }}_i(t)\le {\bar{\tau }}_{i,\max }\), the error \(\varrho _i(t)\) is bounded.

From the event-triggered mechanism we have

$$\begin{aligned} \varvec{\bar{\tau }}(t)=\varvec{\varphi } (t)(\varvec{\zeta } |\varvec{\tau }(t)|+\varvec{\varsigma } )+\varvec{\tau }(t), \end{aligned}$$
(10)

where \(\varvec{\varphi }\), \(\varvec{\zeta }\),\(\varvec{\varsigma }\) are the parameters to be designed, and the bounded error \(\varvec{\varrho } (t)\) caused by event-triggered mechanism can be eliminated by the adaptive term.

For ease of calculation, let

$$\begin{aligned} \varvec{\delta ^*}= \varvec{ \chi ^{-1}\Gamma }(v_{a}) +\varvec{ f}+\varvec{\chi ^{-1}\varrho } + \varvec{\delta }_{\tau }, \end{aligned}$$
(11)

where \(\varvec{f}\) is the external disturbance.

Consider the (10) and (11), the observer model are expressed as

$$\begin{aligned} \left\{ \begin{array}{l}\dot{\varvec{X}}_{\varvec{1}}= \varvec{TX_{2}} \\ \dot{\varvec{X}}_{\varvec{2}}=- \varvec{\chi ^{-1} \Upsilon X_{2}}+\varvec{ \chi ^{-1}{\bar{\tau }}} + \varvec{\delta ^*}. \end{array}\right. \end{aligned}$$
(12)

Assumption 4

From Remark 2, the error \(\varvec{\varrho _i(t)}\) is bounded. The external disturbance terms \(\varvec{\Gamma }\) and \(\varvec{f}\) are continuous and bounded.

Assumption 5

Since the perturbation in the stratospheric environment is significantly smaller than that in the tropospheric environment, and the motor power is limited, the perturbation does not change much, there is a constant C such that \(||\dot{\varvec{\delta }}^{\varvec{*}}||\le C\) holds.

3.2 Fixed-Time Convergence Observer

The observer is designed as follows

$$\begin{aligned} \left\{ \begin{aligned}\dot{\hat{{\varvec{X}}_{\varvec{1}}}}=&\varvec{T\hat{X}_{2}}+\mu _{1}\textrm{sig}^{\alpha _{1}}(\varvec{X_{1}}-\hat{\varvec{X}}_{\varvec{1}})+\varepsilon _{1}\textrm{sig}^{\beta _{1}}(\varvec{X_{1}}-\hat{\varvec{X}}_{\varvec{1}}) \\ \dot{\hat{\varvec{X}}}_{\varvec{2}}=&-\varvec{ \chi ^{-1} \Upsilon X_{2}}+\varvec{ \chi ^{-1}{\bar{\tau }}} + \hat{\varvec{\delta }}^{\varvec{*}} +\mu _{2}\textrm{sig}^{\alpha _{2}}(\varvec{X_{1}}-\hat{\varvec{X}}_{\varvec{1}}) \\ &+\varepsilon _{2}\textrm{sig}^{\beta _{2}}(\varvec{X_{1}}-\hat{\varvec{X}}_{\varvec{1}}) \\ {\dot{\hat{\varvec{\delta }}}}^{\varvec{*}}=&\mu _{3}\textrm{sig}^{\alpha _{3}}(\varvec{X_{1}}-\hat{\varvec{X}}_{\varvec{1}})+\varepsilon _{3}\textrm{sig}^{\beta _{3}}(\varvec{X_{1}}-\hat{\varvec{X}}_{\varvec{1}}) \\ &+\gamma _{1}\textrm{sig}^{1/2}(\varvec{X_{1}}-\hat{\varvec{X}}_{\varvec{1}})+\varvec{\ell _{1}} \\ \varvec{{\dot{\ell }} _{1}}=&k_{1}\textrm{sign}(\varvec{X_{1}}-\hat{\varvec{X}}_{\varvec{1}}), \end{aligned}\right. \end{aligned}$$
(13)

where \(\ell _{1}\) is the adaptive term; \(\alpha _{i}\in (0,1),\beta _{i}> 1,i=1,2,3,4\); \(\mu _{i},\varepsilon _{i},\gamma _{1},k_{1}\) are positive constants; \(\hat{X_{1}},\hat{X_{2}},\hat{\delta ^* }\) are the observed values of the pose, velocity and disturbance, respectively.

The error of the observer is defined as

$$\begin{aligned} \left\{ \begin{array}{l}\varvec{\tilde{e}_{1}} =\varvec{X_{1}}-\hat{\varvec{X}}_{\varvec{1}} \\ \varvec{\tilde{e}_{2}} = \varvec{X_{2}}-\hat{\varvec{X}}_{\varvec{2}} \\ \varvec{\tilde{e}_{3}} =\varvec{\delta ^*} -\hat{\varvec{\delta }}^{\varvec{*}}, \end{array}\right. \end{aligned}$$
(14)

the derivative of Eq. (14) is as follows

$$\begin{aligned} \left\{ \begin{array}{l}\dot{\tilde{\varvec{e}}}_{\varvec{1}}=\varvec{T\tilde{e}_{2}}-\mu _{1}\textrm{sig}^{\alpha _{1}}(\varvec{\tilde{e}_{1}})-\varepsilon _{1}\textrm{sig}^{\beta _{1}}(\varvec{\tilde{e_{1}}}) \\ \dot{\tilde{\varvec{e}}}_{\varvec{2}}=\varvec{\tilde{e}_{3}} -\mu _{2}\textrm{sig}^{\alpha _{2}}(\varvec{\tilde{e_{1}}})-\varepsilon _{2}\textrm{sig}^{\beta _{2}}(\varvec{\tilde{e}_{1}}) \\ \dot{\tilde{\varvec{e}}}_{\varvec{3}}=\varvec{\dot{\delta }^*}-\mu _{3}\textrm{sig}^{\alpha _{3}}(\varvec{\tilde{e}_{1}})-\varepsilon _{3}\textrm{sig}^{\beta _{3}}(\varvec{\tilde{e}_{1}})-\gamma _{1}\textrm{sig}^{1/2}(\varvec{\tilde{e}_{1}})\\ \quad \quad -\varvec{\ell _{1}}. \end{array}\right. \end{aligned}$$
(15)

The parameters \(\alpha _i =i \bar{\alpha } -(i-1)\), \(\beta _i=i \bar{\beta }-(i-1)\), \(\bar{\alpha } \in (1-l_1)\), \(\bar{\beta } \in (1+l_2)\) with small constants \(l_1>0\), \(l_2>0\). The observer gain \(\mu _i, \varepsilon _i, i=1, 2, 3, 4\) are assigned such that the matrix \(\varvec{A_1}\), \(\varvec{A_2}\) is Hurwitzian

$$\begin{aligned} \varvec{A_1} = \begin{bmatrix} -\varepsilon _1 & 1 & 0 \\ -\varepsilon _2 & 0 & 1\\ -\varepsilon _3 & 0 & 0 \end{bmatrix}, \\ \varvec{A_2} = \begin{bmatrix} -\mu _1 & 1 & 0 \\ -\mu _2 & 0 & 1\\ -\mu _3 & 0 & 0 \end{bmatrix}. \end{aligned}$$

Firstly, consider the error system (15) separately with the new forms only

$$\begin{aligned} \left\{ \begin{array}{l}\varvec{\dot{\tilde{e}}_{1}}=\varvec{T\tilde{e}_{2}}-\mu _{1}\textrm{sig}^{\alpha _{1}}(\varvec{\tilde{e}_{1}})-\varepsilon _{1}\textrm{sig}^{\beta _{1}}(\varvec{\tilde{e}_{1}}) \\ \varvec{\dot{\tilde{e}}_{2}}=\varvec{\tilde{e}_{3}}-\mu _{2}\textrm{sig}^{\alpha _{2}}(\varvec{\tilde{e}_{1}})-\varepsilon _{2}\textrm{sig}^{\beta _{2}}(\varvec{\tilde{e}_{1}}) \\ \varvec{\dot{\tilde{e}}_{3}^*}=\varvec{\dot{\delta }^*}-\mu _{3}\textrm{sig}^{\alpha _{3}}(\varvec{\tilde{e}_{1}})-\varepsilon _{3}\textrm{sig}^{\beta _{3}}(\varvec{\tilde{e}_{1}}). \end{array}\right. \end{aligned}$$
(16)

Theorem 1

Based on Assumptions 1–4, the system (16) can converge to zero in finite time, and the convergence time is denoted as

$$\begin{aligned} T_1\le \frac{\lambda ^{1-\bar{\alpha }}_{\max }(\varvec{P_1})}{\gamma _1(1-\bar{\alpha })} +\frac{1}{\gamma _2(\bar{\beta }-1) \Psi ^{\bar{\beta }-1 }}, \end{aligned}$$
(17)

where \(\gamma _1 = \lambda _{\min }(\varvec{Q_1})/\lambda _{\max }(\varvec{P_1})\), \(\gamma _2 = \lambda _{\min }(\varvec{Q_2})/\lambda _{\max }(\varvec{P_2})\). \(\Psi \) is a positive number satisfied as \(\Psi \le \lambda _{\min }(\varvec{P_2})\). \(\varvec{P_1,P_2,Q_1,Q_2}\) are positive definite nonsingular symmetric matrices and satisfied as \( \varvec{P_1A_1} + \varvec{A_1^\textrm{T}P_1} = -\varvec{Q_1}\), \(\varvec{ P_2A_2} + \varvec{A_2^\textrm{T}P_2} = -\varvec{Q_2}\).

Proof

The main proof process refers to Theorem 2 of [1] and Theorem 1 of [25]. Consider two Lyapunov functions as \(V_1(\beta _1,\varvec{e} ) =\varvec{\kappa ^\textrm{T}P_1\kappa }\) and \(V _2(\alpha _1,\varvec{e } )=\varvec{\varpi ^\textrm{T}P_2\varpi } \), where \(\varvec{e}=[\varvec{\tilde{e_{1}},\tilde{e_{2}},\tilde{e_{3}}^*}]^\textrm{T}\), \(\varvec{\kappa } = [\varvec{e_1}^{1/r_1},\varvec{e_2}^{1/r_2},\varvec{e_3}^{1/r_3}]\), \(\varvec{\varpi } = [\varvec{e_1}^{1/s_1},...,\varvec{e_3}^{1/s_3}]\), \(s_i=(i-1)\bar{\alpha }-(i-2)\), \(r_i=(i-1)\bar{\beta }-(i-2);i=1,2,3\).

Derivation of \(V_1\) at gain of \(\beta _{1}=1\) as

$$\begin{aligned} \begin{aligned} \dot{V_1}(1,\varvec{e})&= \varvec{\dot{\kappa }^\textrm{T}P_1\kappa }+\varvec{\kappa P_1\dot{\kappa }^\textrm{T}}\\ &=\varvec{\dot{e}^\textrm{T}P_1e}+\varvec{e^\textrm{T}P_1\dot{e}}\\&=\varvec{e^\textrm{T}(P_1A_1} + \varvec{A_1^\textrm{T}P_1})\varvec{e}\\ &=-\varvec{e^\textrm{T}Q_1e}\\ &\le 0. \end{aligned} \end{aligned}$$
(18)

Remark 3

In Eq. (18), \(\varvec{\kappa }\) is regarded as a three-dimensional vector, but each element of it is also a three-dimensional vector. For the sake of mathematical rigor, the \(\varvec{P_1}\) matrix can be extended to a block diagonal matrix \(\varvec{P_1^*}\) with the same dimension as \(\varvec{K}\),

$$\begin{aligned} \varvec{P_1^*} =\begin{bmatrix}\varvec{P_1} & \varvec{0_{3\times 3}} & \varvec{0_{3\times 3}} \\ \varvec{0_{3\times 3}} & \varvec{P_1} & \varvec{0_{3\times 3}}\\ \varvec{0_{3\times 3}} & \varvec{0_{3\times 3}} & \varvec{P_1} \end{bmatrix}, \end{aligned}$$

which does not affect the subsequent operation. Besides that, the elements in the Hurwitz matrix \(\varvec{A}_1\) are the observer parameters to be set, and no other variables are involved, so Eq. (18) holds.

According to (18), if \(\varvec{e_i}=\varvec{0}\), there is \(\varvec{\dot{e}_i}=\varvec{0}\) and \(\dot{V_1}(1,\varvec{e}) = 0\), it is worth noting that if \(\beta _1 \in (1,1+\xi )\) where \(\xi \) is a small constant, there is \(\dot{V_1}(\beta _1,\varvec{e}) \le 0\), the error system for \(V_1\) is asymptotically stable.

Based on this thought, according to theorem 7.1 in [2] we have

$$\begin{aligned} \dot{V}_1(\beta _1,\varvec{e})\le -(\lambda _{\min }\varvec{Q_1}/\lambda _{\max }\varvec{P_1})V_1^{\bar{\beta }}(\beta _1,\varvec{e}). \end{aligned}$$
(19)

Similarly, the derivative of \(V_2(\alpha _1,\varvec{e})\) with respect to time will be obtained

$$\begin{aligned} \dot{V}_2(\alpha _1,\varvec{e})\le -(\lambda _{\min }\varvec{Q_2}/\lambda _{\max }\varvec{P_2})V_2^{\bar{\alpha }}(\alpha _1,\varvec{e}). \end{aligned}$$
(20)

From Rayleigh’s inequalities:

$$\begin{aligned} \begin{array}{c} \left\| \varvec{\varpi } \right\| \le \frac{V_2(\varvec{\varpi })}{\lambda _{\min }\varvec{P_2}}\le \frac{\Omega }{\lambda _{\min }\varvec{P_2}} \le 1\\ \textrm{and} \quad V_1(\varvec{\kappa })\le \lambda _{\max }\varvec{P_1}\left\| \varvec{\kappa } \right\| ^2 \end{array} \end{aligned}$$
(21)

applied to \(\left\| \varvec{\kappa } \right\| =1\). Take a number \(\Omega \) such that \(V_2(\varvec{\varpi (t_0)})>\Omega \), the full-time derivatives along the trajectory of the whole system (16) are calculated as

$$\begin{aligned} \dot{V_2}\le \dot{V_2}(\varvec{\varpi })+\sum _{i=1}^{n} \frac{ \partial (V_2)}{\partial x_i}(v_i(t))\le \dot{V_2}(\varvec{\varpi })\le -\gamma _2 V_2^{\bar{\alpha }}(\varvec{\varpi }),\nonumber \\ \end{aligned}$$
(22)

where \(\gamma _2=\lambda _{\min }\varvec{Q_2}/\lambda _{\max }\varvec{P_2}\), it is easy to prove that \(V_2\) convergence reaches \(\Omega \) in time no longer than \(T_2=1/(\gamma _2(\bar{\beta }-1)\Omega ^{\bar{\beta }-1})\) which independent of the initial conditions of the system (16).

The full-time derivative of \(V(\kappa )\) along system trajectory (16) is calculated as

$$\begin{aligned} \dot{V_1}\le \dot{V_1}(\varvec{\kappa })+\sum _{i=1}^{n} \frac{ \partial (V_1)}{\partial x_i}(\textrm{w} _1(t))\le \dot{V_1}(\varvec{\kappa })\le -\gamma _1V_1^{\bar{\beta }}, \end{aligned}$$
(23)

where \(\gamma _1=\lambda _{\min }\varvec{Q_1}/\lambda _{\max }\varvec{P_1}\).

For the term \(\varvec{\dot{ \delta ^ * }}\), which is regarded as a small quantity mentioned in Lemma 1, we can see that it does not affect the convergence of fixed time if \(\alpha \) is sufficiently close to 1. \(\square \)

Remark 4

This paper only discusses the bounded error of the observer at the initial time.

Therefore, it can be concluded that (16) converges in a fixed time \(T _ { 1 }\); according to the fixed-time convergence property, when \(t > T _ { 1 }\), the system is always in a convergent state, that is,1 \(\varvec{\dot{\tilde{e_{1}}}}=\varvec{\dot{\tilde{e_{2}}}}={\dot{\tilde{\varvec{e}_{\varvec{3}}}}}^{\varvec{*}}=\varvec{0}\); substitute this conclusion into Eq. (13) as follows

$$\begin{aligned} \left\{ \begin{array}{l}\varvec{\dot{\tilde{e_{1}}}}=\varvec{0} \\ \varvec{\dot{\tilde{e_{2}}}}=\varvec{0} \\ \varvec{\dot{\tilde{e_{3}}}}=-\gamma _{1}\textrm{sig}^{1/2}(\varvec{\tilde{e}_{1}})-\varvec{\ell _{1}} \end{array} \right\} t>T_{1}. \end{aligned}$$
(24)

Since \(\varvec{{\dot{\ell }} _{1}}=k_{1}\textrm{sign}(\varvec{\tilde{e}_{1}})\), the system converges in fixed time. The value of \(\varvec{\ell _{1}}\) as the integral term of the sign function of the converged system is equal to zero. So we have \(\varvec{\dot{\tilde{e}}_{1}}=\varvec{\dot{\tilde{e}}_{2}}=\varvec{\dot{\tilde{e}}_{3}}=\varvec{0}\) when \(t>T_{1} \).

The new state equation is obtained by replacing the observed values with the actual values as

$$\begin{aligned} \left\{ \begin{array}{l}\varvec{\dot{\hat{X}}_{1}}= \varvec{T\hat{X}_{2}} \\ \varvec{\dot{\hat{X}}_{2}}=- \varvec{\chi ^{-1} \Upsilon X_{2}}+\varvec{ \chi ^{-1}{\bar{\tau }}} + \hat{\varvec{\delta }}^{\varvec{*}}. \end{array}\right. \end{aligned}$$
(25)

4 Backstepping Controller Design

4.1 Control Law Design

Define two sliding surfaces \(s_{1}\) and \(s_{2}\)

$$\begin{aligned} & \left\{ \begin{array}{l}\varvec{s_{1}}=\varvec{e_{1}}+k_{1}\varvec{C_{1}} \\ \varvec{\dot{C}_{1}}= \gamma _{1}\textrm{sig}^{\alpha }(\varvec{e_{1}})+\eta _{1}\textrm{sig}^{\beta }(\varvec{e_{1}}), \end{array}\right. \end{aligned}$$
(26)
$$\begin{aligned} & \left\{ \begin{array}{l}\varvec{s_{2}}=\varvec{e_{2}}+k_{2}\varvec{C_{2}} \\ \varvec{\dot{C}_{2}}= \gamma _{2}\textrm{sig}^{\alpha }(\varvec{e_{2}})+\eta _{2}\textrm{sig}^{\beta }(\varvec{e_{2}}), \end{array}\right. \end{aligned}$$
(27)

where \(\varvec{e_{1}}=\hat{\varvec{X}}_{\varvec{1}}-\varvec{X_{1d}} \), \(\varvec{e_{2}}=\hat{\varvec{X}}_{\varvec{2}}-\varvec{X_{2d}}\); \(\varvec{C_{1}}\), \(\varvec{C_{2}}\) are synovial variables; \(\alpha ,\beta ,\gamma _{i},\beta _{i},k_{i},\eta _{i}\) are all positive constants and satisfy \(0<\alpha <1,\beta >1 \). \(\varvec{X_{2d}}\) is the newly introduced state variable whose expression will be derived by backstepping.

If the sliding mode surfaces \(\varvec{s_{1}}\) and \(\varvec{s_{2}}\) satisfy \(\varvec{\dot{s_{1}}}= \varvec{\dot{s_{2}}}=\varvec{0}\) then we have

$$\begin{aligned} \left\{ \begin{array}{l}\varvec{\dot{e}_{1}}=-k_{1}\gamma _{1}\textrm{sig}^{\alpha }(\varvec{e_{1}})-k_{1}\eta _{1}\textrm{sig}^{\beta }(\varvec{e_{1}}) \\ \varvec{\dot{e}_{2}}=-k_{2}\gamma _{2}\textrm{sig}^{\alpha }(\varvec{e_{2}})-k_{2}\eta _{2}\textrm{sig}^{\beta }(\varvec{e_{2}}). \end{array}\right. \end{aligned}$$
(28)

It follows from Lemma 1 that \(\varvec{e_{1},e_{2}}\) all converge in fixed time. Therefore, the design goal of the controller is to make the first derivative of the sliding mode surface zero.

Combine (25) to differentiate the two sliding mode surfaces separately

$$\begin{aligned} \left\{ \begin{aligned}\varvec{\dot{s}_{1}}=&\varvec{\dot{\hat{X}}_{1} }-\varvec{\dot{X}_{1d}}+k_{1}\varvec{\dot{C}_{1}}\\=&\varvec{T}(\varvec{s_{2}}-k_{2}\varvec{C_{2}}+\varvec{X_{2d}})-\varvec{\dot{X}_{1d}}+k_{1}\varvec{\dot{C}_{1}} \\=&\varvec{T}(\varvec{s_{2}}+\varvec{X}_c-k_{2}\varvec{C_{2}}+\varvec{X_{2d}}-\varvec{X}_c)\\ &-\varvec{\dot{X}_{1d}}+k_{1}\varvec{\dot{C}_{1}} \\ \varvec{\dot{s}_{2}} =&\varvec{\dot{\hat{X}}_{2} }-\varvec{\dot{X}_{2d}}+k_{2}\varvec{\dot{C}_{2}}\\=&-\varvec{ \chi ^{-1} \Upsilon X_{2}}+\varvec{ \chi ^{-1}{\bar{\tau }}} +\varvec{ \hat{\delta }^*}-\varvec{\dot{X}_{2d}}+k_{2}\varvec{\dot{C}_{2}} \end{aligned}\right. , \end{aligned}$$
(29)

where \(\varvec{X_{c}}\) is the virtual control input with the following expression, \(\lambda _{11},\lambda _{12}\) are positive constants

$$\begin{aligned} \begin{aligned} \varvec{X_{c}}=&k_{2}\varvec{C_{2}}-\varvec{T}^{-1} k_{1}\varvec{\dot{C_{1}}}+\varvec{T}^{-1}\varvec{\dot{X_{1d}}}\\ &-\lambda _{11}\textrm{sig}^{\alpha }(\varvec{s_{1}})-\lambda _{12}\textrm{sig}^{\beta }(\varvec{s_1}). \end{aligned} \end{aligned}$$
(30)

To reduce the computational burden caused by direct differentiation of dummy variables, the state variable \(\varvec{X_{2d}}\) is introduced [19], \(\varvec{X_{2d}}\) denotes the filtered value of \(\varvec{X_{c}}\) after passing a first-order low-pass filter at a time constant of \(\sigma \), and the expression as

$$\begin{aligned} \sigma \varvec{\dot{X}_{2d}}=\textrm{sig}^\alpha (\varvec{X_c}-\varvec{X_{2d}})+\textrm{sig}^\beta (\varvec{X_c}-\varvec{X_{2d}}). \end{aligned}$$
(31)

Combined with the control objective, the control rate of the designed system is

$$\begin{aligned} \begin{aligned} \varvec{\tau } =&\mathrm sat(\varvec{\tau }_0),\\ \varvec{\tau }_0=&\varvec{\chi } [\varvec{\chi ^{-1}\Upsilon X_2}-\hat{\varvec{\delta }}^{\varvec{*}}+\varvec{\dot{X}_{2d}} -k_2\varvec{\dot{C_2}} \\ &-\lambda _{21}\textrm{sig}^{\alpha }(\varvec{s_2}) -\lambda _{22}\textrm{sig}^{\beta }(\varvec{s_2})-\varvec{T s_1}], \end{aligned} \end{aligned}$$
(32)

where \(\lambda _{21},\lambda _{22}\) are positive constants.

For Eq. (25), under the premise of satisfying Assumptions 1–4, the closed-loop system of SGFTUUB can be obtained by designing the above virtual control rate and backstepping controller, combined with the nonlinear first-order low-pass filter and observer.

4.2 Stability Analysis

The Lyapunov function V is chosen as

$$\begin{aligned} V=\frac{1}{2} (\varvec{s}^2_1+\varvec{s}^2_2+\varvec{z}^2), \end{aligned}$$
(33)

where \(\varvec{z}=\varvec{X_{2d}}-\varvec{X_{c}}\) represents the filtering error. The first derivative is denoted as

$$\begin{aligned} \varvec{\dot{z}}=\varvec{\dot{X}_{2d}}-\varvec{\dot{X}_c}=-\frac{1}{\sigma } \textrm{sig}^\alpha (\varvec{z})-\frac{1}{\sigma } \textrm{sig}^\beta (\varvec{z})-\varvec{\dot{X}_c}. \end{aligned}$$
(34)

Remark 5

The stability of the observer has been proved in section III, so only the stability of the controller is discussed next.

Combining Eq. (30) and Assumption 2,3, we know that the first derivative of the virtual control rate \(\varvec{X_c}\) is bounded, that is, \(|\varvec{\dot{X}_c}|\le |\varvec{\delta _{X_c}}|\), where \(\varvec{\delta _{X_c}}\) s a positive constant vector.

Taking the derivative of Eq. (33) concerning time t and combining Eqs. (29), (32), (34) and \(||\varvec{T}||=\frac{1}{\cos \theta }\ge 1\) from (2), we have

$$\begin{aligned} \begin{aligned} \dot{V} =&\varvec{s_1\dot{s}_1}+\varvec{s_2\dot{s}_2}+\varvec{z\dot{z}} \\ \le&\varvec{s_1}\varvec{T}(\varvec{s_2}-\lambda _{11}\textrm{sig}^\alpha (\varvec{s_1})-\lambda _{12}\textrm{sig}^\beta (\varvec{s_1})+\varvec{z}) \\ &+\varvec{s_2}(-\varvec{T s_1}-\lambda _{21}\textrm{sig}^\alpha (\varvec{s_2})-\lambda _{22}\textrm{sig}^\beta (\varvec{s_2})) \\ &+\varvec{z}(-\frac{1}{\sigma } \textrm{sig}^\alpha (\varvec{z})-\frac{1}{\sigma } \textrm{sig}^\beta (\varvec{z})+\varvec{\delta _{X_c}}) \\ \le&-\lambda _{11}(\varvec{s^2_1})^{\frac{1+\alpha }{2} }-\lambda _{12}(\varvec{s^2_1})^{\frac{1+\beta }{2}}+\varvec{s_1z} -\lambda _{21}(\varvec{s^2_2})^{\frac{1+\alpha }{2}}\\ &-\lambda _{22}(\varvec{s^2_2})^{\frac{1+\beta }{2}} -\frac{1}{\sigma } (\varvec{z}^2)^{\frac{1+\alpha }{2}}-\frac{1}{\sigma } (\varvec{z}^2)^{\frac{1+\beta }{2}}+\varvec{z\delta _{X_c}}, \end{aligned} \end{aligned}$$
(35)

Young’s inequality \(2xy\le x^2+y^2\) can be further transformed into

$$\begin{aligned} \begin{aligned} \dot{V}\le&-\lambda _{11}(\varvec{s^2_1})^{\frac{1+\alpha }{2} }- \lambda _{12}(\varvec{s^2_1})^{\frac{1+\beta }{2} } -\lambda _{21}(\varvec{s^2_2})^{\frac{1+\alpha }{2} } \\ &-\lambda _{22}(\varvec{s^2_2})^{\frac{1+\beta }{2} }+\frac{1}{2}\varvec{s^2_1} +\varvec{z}^2-\frac{1}{\sigma }(\varvec{z}^2)^{\frac{1+\alpha }{2} } \\ &-\frac{1}{\sigma }(\varvec{z}^2)^{\frac{1+\beta }{2} } +\frac{1}{2}\varvec{\delta _{X_c}^2} \\ \le&-\lambda _{11}(\varvec{s^2_1})^{\frac{1+\alpha }{2} }-\lambda _{21}(\varvec{s^2_2})^{\frac{1+\alpha }{2} } -(\lambda _{12}-\frac{1}{2} )(\varvec{s^2_1})^{\frac{1+\beta }{2} }\\&-(\lambda _{22}-\frac{1}{2} )(\varvec{s^2_2})^{\frac{1+\beta }{2} } -\frac{1}{\sigma }(\varvec{z}^2)^{\frac{1+\alpha }{2} } \\ &-(\frac{1}{\sigma }-1)(\varvec{z}^2)^{\frac{1+\beta }{2} } +\frac{1}{2}\varvec{\delta _{X_c}^2}, \end{aligned}\nonumber \\ \end{aligned}$$
(36)

when the parameters of the designed controller satisfy \(\{\lambda _{11},\lambda _{21}>0; \lambda _{12},\lambda _{22}>\frac{1}{2}; \frac{1}{\sigma }>1\}\), let

$$\begin{aligned} \begin{aligned}&M=\min (\lambda _{11},\lambda _{21}), \\ &N=\min (\lambda _{12}-\frac{1}{2},\lambda _{22}-\frac{1}{2}), \\ &P=\frac{1}{\sigma }-1, \end{aligned} \end{aligned}$$
(37)

substitute in the above equation as

$$\begin{aligned} \begin{aligned} \dot{V}\le&-M\sum _{i=1}^{2}(\varvec{s^2_i})^{\frac{1+\alpha }{2} } -N\sum _{i=1}^{2}(\varvec{s^2_i})^{\frac{1+\beta }{2} } -P(\varvec{z}^2)^{\frac{1+\alpha }{2} } \\ &-P(\varvec{z}^2)^{\frac{1+\beta }{2} }+\frac{1}{2}\varvec{\delta _{X_c}^2}. \end{aligned} \end{aligned}$$
(38)

Lemma 2

[10] If there exists a positive real number \(x_1,x_2, \ldots ,x_n\ge 0 \) with exponent \(k>0\), then there is

$$\begin{aligned} & \max (n^{k-1},1)(x_1^k+x_2^k+\cdots +x_n^k)\nonumber \\ & \ge (x_1+x_2+\cdots +x_n)^k. \end{aligned}$$
(39)

By Lemma 2 we have

$$\begin{aligned} \begin{aligned} \dot{V} \le&-\min (M,P) \left( \sum _{i=1}^{2}(\varvec{s^2_i})^{\frac{1+\alpha }{2} }+(\varvec{z}^2)^{\frac{1+\alpha }{2} } \right) \\ &-\min (N,P)\left( \sum _{i=1}^{2}(\varvec{s^2_i})^{\frac{1+\beta }{2} }+(\varvec{z}^2)^{\frac{1+\beta }{2} } \right) +\frac{1}{2}\varvec{\delta _{X_c}^2} \\ \le&-\min (M,P)\left( \sum _{i=1}^{2}(\varvec{s^2_i})+\varvec{z}^2 \right) ^{\frac{1+\alpha }{2} } \\ &-\min (N,P)3^{\frac{1-\beta }{2} } \left( \sum _{i=1}^{2}(\varvec{s^2_i})+\varvec{z}^2 \right) ^{\frac{1+\beta }{2} }+\frac{1}{2}\varvec{\delta _{X_c}^2} \\ \le&-H_1V^{\frac{1+\alpha }{2}}-H_2V^{\frac{1+\beta }{2}}+\varvec{\Delta }, \end{aligned} \end{aligned}$$
(40)

where \(H_1=\min (M,P);H_2=3^{\frac{1-\beta }{2}}\min (N,P);\varvec{\Delta } =\frac{1}{2}\delta _{X_c}^2 \). When appropriate control parameters are chosen and M, N, P is positive, it follows from Lemma 1 that the Lyapunov function V is semi-global fixed-time uniform ultimate boundedness and has

$$\begin{aligned} T_V\le \frac{2}{H_1(2^{(1+\alpha )/{2} }-1)({1-\alpha } )} +\frac{2}{H_2({\beta -1} )}, \end{aligned}$$
(41)

where \(T_V\) is the convergence time of V, The convergence time \(T_t\) of Eq. (29) is satisfied as

$$\begin{aligned} T_t \le T_V + T_1. \end{aligned}$$
(42)

Theorem 2

The controller in this paper does not appear Zeno phenomenon during the whole control process.

Proof

Based on the measuring error \(\varvec{{e}}(t)=\varvec{\tau }(t)-\varvec{\bar{\tau }}(t_k)\) defined in event-triggered mechanism, \(\varvec{\bar{\tau }}(t_k)\) is a constant for \(t\in [t_k,t_{k+1})\), we have

$$\begin{aligned} \varvec{\dot{e}}(t)=\varvec{{\dot{\tau }}}(t)-\varvec{\dot{{\bar{\tau }}}}(t_k)=\varvec{{\dot{\tau }}}(t), \end{aligned}$$
(43)

which implies \({\dot{e}_i}(t)\le |{{\dot{\tau }}}_i(t)|\).

Taking the derivative of (32) we have

$$\begin{aligned} \begin{aligned} \varvec{{\dot{\tau }}} =&\varvec{\chi } [\varvec{\chi ^{-1}\Upsilon \dot{X}_2}-{\dot{{\hat{\varvec{\delta }}}}}^{\varvec{*}}+\varvec{\ddot{X}_{2d}} -k_2\varvec{\ddot{C_2}} \\ &-\lambda _{21}\alpha |\varvec{s_2}|^{\alpha -1 }\textrm{sign}(\varvec{s_2}) \\ &-\lambda _{22}\beta |\varvec{s_2}|^{\beta -1 }\textrm{sign}(\varvec{s_2})-\varvec{\dot{T} s_1}-\varvec{ T \dot{s}_1}]. \end{aligned} \end{aligned}$$
(44)

Given the continuity of \(\varvec{{\dot{\tau }}}\) and based on the Assumptions 1–4, Eq. (43) satisfies as

$$\begin{aligned} \exists \hbar >0,|\varvec{{\dot{\tau }}}|\le \hbar . \end{aligned}$$
(45)

Therefore, we obtain

$$\begin{aligned} \begin{aligned} \int _{t_k}^{t_{k+1}} \dot{{\varvec{\tau }}}(t)dt&={\varvec{\tau }}(t_{k+1})-{\varvec{\tau }}(t_{k}) \\ &\le \zeta |\varvec{\bar{\tau }}(t_k)|+\varsigma -\varvec{0} \\ &\le \hbar (t_{k+1}-t_k). \end{aligned} \end{aligned}$$
(46)

That means

$$\begin{aligned} t_{k+1}-t_k\ge \frac{\zeta |\varvec{\bar{\tau }}(t_k)|+\varsigma }{\hbar }\ge \frac{\varsigma }{\hbar }, \end{aligned}$$
(47)

it is proved that there is no Zeno phenomenon in the control process of the controller. \(\square \)

5 Simulation

In this section, the proposed algorithm is applied to the airship model proposed in Sect. 2 to verify the effectiveness of the control algorithm.

The airship modeling parameter values involved in the simulation in MATLAB are: \(m = 9.4\times 10^3\,\textrm{kg}\), \(\rho = 0.088\,\mathrm{kg/m}^3\), \(l = 38\,\textrm{m} \), \(C_d = 0.5\), \(L_{ref}=38\,\textrm{m} \), \(S_{ref}=1134\,\textrm{m}^2\), \([I_x,I_y,I_z]=10^6\times [2,5.5,5.5]\), \(x_c=y_c=0\), \(z_c=0.5\,\textrm{m}\), \(G=91556\,\textrm{N}\), \(B=91556\,\textrm{N}\), \(a_1=73.5\), \(a_2 =62.5 \), \(b=19\).

The controller parameters are set as follows: \(\zeta _1=\zeta _2=\zeta _3=\zeta _4=\zeta _5=\zeta _6=0.01\), \(\varsigma _1=\varsigma _2=\varsigma _3= \varsigma _4=\varsigma _5=\varsigma _6=5\), \(\alpha =0.8\), \(\alpha _1 =\alpha _2 =\alpha _3 =\alpha _4=0.6\), \(\beta =1.2\), \(\beta _1 =\beta _2 =\beta _3 =\beta _4 =1.5\), \(\mu _1 =\varepsilon _1= 1\), \(\mu _2=\varepsilon _2 = 0.01\), \(\mu _3 = \mu _4 =\varepsilon _3=\varepsilon _4= 0.001\), \(\gamma _1=\gamma _2=k_1=k_2=0.01\), \(\eta _1=\eta _2=0.01\), \(\sigma =0.6\), \(\lambda _{11}=\lambda _{21}=0.4\), \(\lambda _{12}=\lambda _{22}=0.6\).

The desired trajectory and the desired attitude are:

$$\begin{aligned} \begin{bmatrix} x_d \\ y_d\\ z_d\\ \phi _d\\ \theta _d\\ \psi _d \end{bmatrix}= \begin{bmatrix}2000\sin (0.005t) + 2000\cos (0.0025t) \\ 2000\sin (0.0025t) + 2000\cos (0.005t) \\ -0.1t -18930 \\ 0 \\ \arctan 2(0.1,\sqrt{\dot{x_d}^2+\dot{y_d}^2}) \\ \arctan 2(\dot{y_d},\dot{x_d}) \end{bmatrix}, \end{aligned}$$

the initial state is:

$$\begin{aligned} \begin{bmatrix}x_0 \\ y_0 \\ z_0 \\ \phi _0 \\ \theta _0 \\ \psi _0 \end{bmatrix}= \begin{bmatrix}2000\,\textrm{m} \\ 2040\,\textrm{m} \\ -\,18{,}900\,\textrm{m} \\ 0^{\circ } \\ 0^{\circ } \\ 30^{\circ } \end{bmatrix}, \end{aligned}$$

the unknown disturbance \(\varvec{ \chi ^{-1}\Gamma }(v_{a}) +\varvec{ f}\) from the environment where \(\varvec{ f}\) is set to:

$$\begin{aligned} f = -10^{-4}\times \begin{bmatrix} 2(1+0.1\sin (t/60)+0.2\cos (t/60)) \\ 0.1(0.5\sin (t/60)+\cos (t/60)) \\ 0.04(0.5\sin (t/60)+0.1\cos (t/60)) \\ 0.5(1+0.1\sin (t/60)+0.2\cos (t/60)) \\ 0.5(1+0.1\sin (t/60)+0.2\cos (t/60)) \\ 2(1+0.1\sin (t/60)+0.2\cos (t/60)) \end{bmatrix}. \end{aligned}$$

In this subsection, the simulation results of the control algorithm are mainly as follows.

Figures 2 and 3 show the trajectory tracking of the stratospheric airship in three-dimensional space and an x–y plane. It can be seen that the proposed controller can make the stratospheric airship travel along the desired trajectory. Figures 4 and 5 illustrate the trajectory tracking performance of the proposed controller, while Figs. 6, 7 and 8 demonstrate the stability of the closed-loop system under the proposed control algorithm. Specifically, Fig. 4 shows the tracking error between the actual trajectory and the desired trajectory, and Fig. 5 shows the state response of the sliding surface.

Fig. 2
figure 2

Three-dimensional trajectory of the stratospheric airship

Full size image
Fig. 3
figure 3

The trajectory of the stratospheric airship in x–y plane

Full size image
Fig. 4
figure 4

Observation error curves for the six state variables

Full size image
Fig. 5
figure 5

Sliding surface state response curve

Full size image
Fig. 6
figure 6

Angular velocity curves during trajectory tracking of stratospheric airships

Full size image
Fig. 7
figure 7

Velocity curves during trajectory tracking of stratospheric airships

Full size image
Fig. 8
figure 8

Attitude angle curves during trajectory tracking of stratospheric airships

Full size image

Combined with Figs.  2, 9 and 10, it can be seen that there is a large trajectory error at the initial time, which leads to a significant control input in a short time. The controller reaches a saturated state to maximize the use of thrusters to make the airship get the desired trajectory. However, they decrease rapidly after reaching the desired goal, which successfully indicates the effectiveness of the control algorithm in achieving the desired trajectory.

Fig. 9
figure 9

Control force curves during trajectory tracking of stratospheric airships

Full size image
Fig. 10
figure 10

Control moment curves during trajectory tracking of stratospheric airships

Full size image

To verify the effectiveness of the event-triggered mechanism used in this paper, the controller model proposed is compared with the periodic control model after eliminating the event-triggered mechanism. By changing the control mode of time continuity into highly discretization control of condition trigger, the actuation frequency is successfully reduced, it can be seen from Fig. 11 that the operating frequency of the actuator under the action of the event-triggered mechanism controller is about 1/5 of that under periodic control. Figure 12 compares the periodic controller with the event-triggered controller by \(\tau \) 6. It is evident from the results that the event-triggered mechanism effectively reduces the operating frequency of the closed-loop system, thereby reducing the actuator damage of the stratospheric airship and increasing its air operation time.

Fig. 11
figure 11

Comparison of sensor working times based on event triggered and cycle triggered

Full size image
Fig. 12
figure 12

Comparison of the influence of event triggering and no event triggering on control frequency

Full size image
Fig. 13
figure 13

Comparison of control errors for trajectory tracking of stratospheric airships with [26]

Full size image

To study the advantages of the controller in this paper, a comparative simulation is performed between different methods. The fixed-time trajectory tracking controller for multi-stratospheric airship formation in [26] is chosen as the comparison object. The controller parameters are \(k_{10}=k_{20}=k_{30} = \textrm{ diag}[0.0140, 0.0100, 0.1000, 0, 0.4000, 0.0120]^\textrm{T}\), \(k_{40}=k_{50}=k_{60} = \textrm{ diag}[0.0080, 0.0500, 0.1500, 0, 0.0080, 0.0500]^\textrm{T}\), \(k_{p0}=21\), \(k_{q0}=23\), which is consistent with the control parameters of our method.

Fig. 14
figure 14

Comparison of x–y plane control trajectories for trajectory tracking of stratospheric airships with [26]

Full size image
Fig. 15
figure 15

Comparison of y–z plane control trajectories for trajectory tracking of stratospheric airships with [26]

Full size image
Fig. 16
figure 16

Comparison of x–z plane control trajectories for trajectory tracking of stratospheric airships with [26]

Full size image

The results of the comparative simulation are shown in Figs. 13, 14, 15 and 16, where the comparison results of position variance error, pitch error, and yaw error are given in Fig. 13, and the trajectory in different directions is shown in Figs. 14, 15, and 16. It can be seen from Fig. 13 that the transient response time of the control algorithm in this paper is smaller. Still, the trajectory overshoot of the control algorithm in this paper is relatively significant in Figs. 14, 15 and 16. This is because the computational input of the fixed-time controller exceeds the constraints of the actuator, resulting in saturation, which in turn deteriorates the control performance. To alleviate the impact of input saturation, some compensation methods can be introduced in future work.

6 Conclusion

In this paper, we propose an event-triggered trajectory tracking controller to address the issue of the unmeasurable airspeed of a stratospheric airship under unknown disturbances. A fixed-time observer is employed to estimate unmeasurable wind speed and unknown disturbances. A fixed-time controller is devised to ensure rapid convergence of the algorithm, and an event-triggered mechanism is implemented to reduce the working frequency of the actuator. The simulation results illustrate the successful and rapid trajectory tracking achieved by the proposed control algorithm and the closed-loop system remains bounded without any occurrence of Zeno phenomenon. The paper does not address the actuator saturation problem and constrained control issues. In future studies, additional constrained issues, such as the actuator saturation problem, will be considered.