1 Introduction

Today, concerns about the lack of fossil fuels and environmental pollution are the main driving factors for research and development activities in the field of using renewable and clean fuels such as the sun, wind, ocean, and river. Among the clean energies, ocean energy has received more attention due to its availability most of the time as well as its high energy density. Oceans cover more than 70% of the earth's surface, and since the mass density of water is approximately 1000 times that of air, the energy density of ocean waves is also higher [2]. Tidal currents, geothermal energy, and water waves are energy sources of the ocean, each of which can be used in different ways. Unlike tidal currents that occur only during limited hours of the day, ocean waves are available most of the day and night. Wind losses are less at the surface of the ocean and the waves produced can often travel longer distances [3]. The energy density of wave farms is 2 to 3 kW/m2, which is higher than solar parks (0.1 to 0.2 kW/m2) and wind farms (0.4 to 0.6 kW/m2) [4]. In the United States, electricity generation from waves can reach more than 1170 TWh per year, which is approximately one-third of the 4000 TWh of electricity consumed in the United States each year [5]. The basis of wave energy conversion consists of two steps: converting wave energy into mechanical energy and then converting mechanical energy into electrical energy by the generator. Wave energy conversion systems can be divided into five general categories: underwater turbines, indoor systems, point absorbers, vibration-based systems, and oscillating water columns [6]. Vibration-based systems use a transducer to produce electrical energy, among these transducers, there are usually three types of transducers that are widely used: turbine transducers, piezoelectric transducers, and electromagnetic transducers. Piezoelectric is an interesting physical transformation that occurs by converting mechanical strain into electrical potential [7]. Common synthetic piezoelectric materials include polymers, ceramics, or lead [8]. Due to the low frequency of ocean waves, less attention has been paid to harvesting energy with vibration-based energy devices from the ocean. The costs of wave energy are very high compared to other renewable and superior technologies, and this is one of the biggest disadvantages of the commercialization of wave energy harvesting systems. For wave energy technology to reach its full potential, smaller, more economical, and more flexible harvesters must be introduced and optimized. [9]. One of the ways to optimize the design of a given harvesting system is to optimize its geometric shape or geometric configuration to achieve maximum efficiency in a certain way [10].

For thousands of years, mankind has sought to use ocean waves to do useful things. The world's first commercial wave farm with a capacity of 2.25 MW was built in Portugal in 2005 [11]. Researchers have always been looking for different ways to increase the efficiency of electric energy production, and we will mention some of them in the following. In 2012, Bachynski et al. investigated the effects of geometry and mass distribution on ideal energy absorption from irregular waves for safe and reliable use of wave energy sources for electricity generation [12]. In 2013, Cha et al. investigated different geometries of underwater piezoelectric composite beams under base excitation and it was observed that with the increase of immersion length due to the reduction of the resonance frequency of the structure, the lifting power decreases [13]. In 2015, Diamond et al. presented the experimental results of two mass modulation schemes and showed that one of them is more effective in improving the energy harvesting capabilities of the energy harvester [14]. In 2017, Saadatnia et al. designed a duck-shaped harvester that converted sea wave energy into electrical energy using triboelectric and electromagnetic generators [15]. In 2019, Jin et al. designed three different geometric models for an energy harvesting system and concluded that a 90° cone is better for energy harvesting than the other two types [16]. In 2019, Shi et al., numerically studied the movements of a float with a conical end, with different mass and cross-sectional areas. By conducting experiments and numerical calculations, it was determined that the average power output increased by reducing the ratio of the draft to the height of the cone and constant mass and also mass change alone is not effective [17]. In 2020, Erselcan and Kükner conducted research on the effect of the geometry and mass, and dimensions of the float and by estimating the costs, they concluded that the most cost-effective type of optimization of the extractors is based on changing their geometry [18].

In the present study, to optimize the energy harvester system, several different floating buoy models have been designed according to certain wave conditions, which can calculate the damping value, stiffness coefficient, and natural frequency of each floating buoy. Among the different generators, the piezoelectric generator has been chosen due to its small size and higher energy density than other generators. In the following, by comparing the damping and frequency of buoys with each other, a more suitable geometric model for energy harvesting will propose. It should be mentioned, previous studies have investigated the properties of mechanical energy harvesters, which are connected to buoys, as mechanical amplifiers. In this study, the buoy is utilized as the mechanical amplifier, and its geometry is optimized to maximize harvested energy.

2 Mathematical Modeling

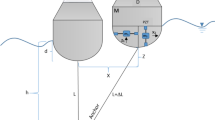
In this research, the piezoelectric transducer is modeled as a beam-column based on Euler–Bernoulli's law, which will be explained below (Fig. 1). Suppose a supporting column beam with length L, stiffness EI, and tip mass Mtip is connected to a moving mass Mbase and is also connected to a spring K and damper C and subjected to an external time-dependent force F, in following the schematic view of the system is shown.

Fig. 1
figure 1

Schematic of the piezoelectric transducer [19]

Full size image

According to Euler–Bernoulli's law, the potential and kinetic energy of this system are, respectively, as follows [19]:

$$\pi =\int_{0}^{L} \left({EI}_{b}+{EI}_{p}\right){\left(\frac{{\partial }^{2}w}{\partial {x}^{2}}\right)}^{2} dx-{\int }_{0}^{{L}_{e}}z{w}_{p}{V}_{e31}\left(\frac{{\partial }^{2}w}{\partial {x}^{2}}\right) dx+\frac{1}{2}K{Z}^{2},$$
(1)
$$\begin{aligned}T&={\int }_{0}^{L}({\rho }_{b}{t}_{b}{w}_{b}+({\rho }_{b}{t}_{p}{w}_{p}){\left(\frac{\partial w}{\partial \mathrm{t}}+\dot{Z}\right)}^{2}dx+\frac{1}{2}{\mathrm{M}}_{\mathrm{base}}{\dot{Z}}^{2}\\ &\quad +\frac{1}{2}{\mathrm{M}}_{\mathrm{tip}}{\left(\dot{Z}+\left(\frac{\partial w}{\partial \mathrm{t}}|x=L\right)\right)}^{2}.\end{aligned}$$
(2)

In the above relations, p index is related to piezoelectric and b index is related to the beam. Variable w represents the width, V represents the voltage and Le represents the effective length, and z is the distance from the neutral axis. The input electrical energy in this system is also calculated in the following relation:

$${W}_{ie}=-{\int }_{0}^{{L}_{e}} z{w}_{p}{e}_{31}V\frac{{\partial }^{2}w}{\partial {x}^{2}}dx-{\int }_{0}^{L}{w}_{p}{e}_{33} \frac{{V}^{2}}{{t}_{p}}dx,$$
(3)

where e33 is the constant strain transmittance component and the width of the piezoelectric layer. The displacement of the beam with the method of separation of variables is as follows:

$$w\left(x,t\right)=\sum_{i=1}^{n}{\varphi }_{i}(x){q}_{i}(t).$$
(4)

In the above equation, φ(x) represents the mode shape and q(t) represents the time response. By substituting Eq. (4) in Eqs. (1–3), leads to the following coupled differential equations of motion:

$${m}_{eq}{q}_{i}+{c}_{eq}\ddot{q}_{i}+\left({k}_{eq}+{k}_{g}\right){q}_{i}-\theta V=-{m}^{*}\ddot{Z},$$
(5)
$${M}_{eq}\ddot{Z}+c\dot{Z}+kz=F-{m}^{*}\ddot{q},$$
(6)
$${C}_{p}\dot{V}+\frac{V}{R}+\theta {\dot{q}}_{i}=0.$$
(7)

The equivalent mass and stiffness values in the above relations are also obtained with the help of the following relations:

$${m}_{eq}=2{\int }_{0}^{L}({\rho }_{b}{t}_{b}{w}_{b}+({\rho }_{b}{t}_{p}{w}_{p}){\varphi }^{2}dx+{\mathrm{M}}_{\mathrm{tip}}{\varphi }^{2}(L))dx,$$
(8)
$${c}_{eq}=2\zeta \sqrt{{k}_{eq}{m}_{eq}},$$
(9)
$${k}_{eq}=2{\int }_{0}^{L}\left({EI}_{b}+{EI}_{p}\right){\left(\frac{{\partial }^{2}\varphi }{\partial {x}^{2}}\right)}^{2}dx,$$
(10)
$${M}_{eq}={M}_{\mathrm{tip}}+{M}_{\mathrm{base}}+2\left\{{\rho }_{b}{t}_{b}{w}_{b}+{\rho }_{p}{t}_{p}{w}_{p}\right\},$$
(11)
$${m}^{*}=2{\int }_{0}^{L}({\rho }_{b}{t}_{b}{w}_{b}+({\rho }_{b}{t}_{p}{w}_{p})\varphi dx+{\mathrm{M}}_{\mathrm{tip}}\varphi (L))dx,$$
(12)
$${k}_{g}=N{\int }_{0}^{L}{\left(\frac{{\mathrm{d}}^{2}\varphi }{\mathrm{d}{x}^{2}}\right)}^{2}dx,$$
(13)
$${C}_{p}=2{\int }_{0}^{L}\frac{{w}_{p}{e}_{33}}{{t}_{p}}dx,$$
(14)
$$\theta =2{\int }_{0}^{{L}_{e}}z{w}_{p}{e}_{31}\left(\frac{{d}^{2}\varphi }{\mathrm{d}{x}^{2}}\right)dx,$$
(15)

where, ζ is the damping ratio. According to Euler–Bernoulli's equation, the mode shape for the system is as follows:

$$\begin{aligned}\varphi \left(x\right)&={C}_{i}\left\{{\mathrm{cos}}\left(\frac{{\lambda }_{i}x}{L}\right)-cosh \left(\frac{{\lambda }_{i}x}{L}\right)\right.\\&\left.\quad+{\sigma }_{i}(sin\left(\frac{{\lambda }_{i}x}{L}\right) -sinh\left(\frac{{\lambda }_{i}x}{L}\right)\right\},\end{aligned}$$
(16)

in which λi is the eigenvalue of the ith vibration mode shape, which is obtained from the characteristic equation, and σi is a coefficient that is presented in literature [19]. The characteristic equation can also be calculated according to the special function and boundary conditions. Substituting Eq. (16) into Eqs. (8–15), the mass and stiffness of the system can be calculated, and the natural frequency can be easily obtained from this equation:

$${\omega }^{2}=({k}_{eq}-{k}_{g})/{m}_{eq}.$$
(17)

For simplifying the following equation, the fundamental frequency is written as ω2 = α.(EIbp/L3mbp)—β.(g/L). For several mass ratios coefficients α and β are previously obtained [19] and presented in Table 1. These coefficients ate named as coefficients of the fundamental frequency.

Table 1 Coefficients of the fundamental frequency with varying the mass ratio
Full size table

3 Features of the Ocean Wave and Buoys

All around the world, the energy density and characteristics of ocean waves are unique, and this is considered as a reference for the design of floating vessels [10]. These characteristics depend on the climatic conditions and geographical location of the chosen place. Therefore, it is necessary to choose a suitable sea location and check the wave characteristics of that area before designing the floating vessels. In this article, the selected location is hypothetical and the characteristics of the waves are also hypothetical, which are described below. The main wave parameters include wavelength, wave speed, wave height, and other parameters such as wave frequency and wave number can be calculated from these parameters according to the relation obtained the following [20]:

$${\omega }_{w}=\sqrt{2\pi g/{L}_{w}},$$
(18)
$$k=2\pi /{L}_{w},$$
(19)

where Lw is the wavelength. Also, the encounter frequency can also be obtained from the following relation:

$${\omega }_{\mathrm{e}}={\omega }_{w}-\frac{{{\omega }_{w}}^{2}}{g}u\mathrm{cos}\mu, $$
(20)

where ωw is the wave frequency, u is the ship speed, and μ is the angle of ship travel. The parameters of the wave in this study are presented in Table 2. Note that these parameters are written based on the data presented in the previous study [20].

Table 2 Values of wave parameters
Full size table

4 Characteristics of buoys

The reduction of cost and economic profit can be related to the structure of the harvester device. It has revealed the need to include geometry optimization studies to help determine the shape of the device in the early stages of the design process [21]. To optimize the geometry of the buoys, several buoys with minor geometric changes and the same material and weight have been designed by 3D design software. The mass of all the buoys is 200 kg and their material is maple wood. In the first figure, which is a rectangular cube, after several steps of rounding the lower part, we reached a semi-cylindrical shape. Then a semi-cylinder volume is considered and stretched from both sides to make an oval-like shape. In the third figure, a hemisphere was stretched from two sides, and we obtained an oval, and in the last figure, a half cylinder was stretched from one side and a shape like a boat was obtained. Specifications of each shape are given in Table 3.

Table 3 Specifications of the dimensions of the buoys
Full size table

5 Heave motion

A float on the surface of the ocean is almost always oscillating, the three motions that are purely oscillating are heave, pitch and roll [22]. Heave movement is called the up and down swinging movements of the float. Heave's equation of motion can be expressed as follows:

$$a\ddot{z}+b\dot{z}+cz={F}_{0}\mathrm{cos}{\omega }_{e}t,$$
(21)

where a is the added mass, b is damping coefficient, c is the restoring force coefficient, and F0 is the amplitude of the buoyancy force. Because of the different geometries of the floaters the value of the dynamic coefficients will be different in each cross section. Therefore, the strip theory method is used to calculate the above-mentioned coefficient of the Heave equation of motion. Using this method, several cross-sections of the float are considered with the same distances and using formulas related to each dynamic coefficient, the value of each is calculated in each cross-section, and finally, it is integrated over the length of the float. In this theory, the mutual effects of adjacent sections are ignored, but the final results with this method are very close to the experimental results [20]. When the floater moves up and down in the water, it also moves a certain amount of water. It is the amount of added mass of each section, which can be calculated using the following relation:

$${a}_{n}=C\rho \pi {B}_{n}^{2}/8,$$
(22)

where Bn is the cross section of the floater, and C is the added mass factor. The following relation can be used to calculate the added mass of the entire floater:

$${a}_{z}={\int }_{-l/2}^{l/2}{a}_{n}dx.$$
(23)

The damping force always acts against the direction of the float and reduces the intensity of the movement, the amount of damping usually depends on the type of vibration movement, collision frequency and geometry of the float [20]. The following relationship is used to calculate the damping coefficient for the whole floater:

$$b={\int }_{-l/2}^{l/2}\frac{\rho {g}^{2}{\bar{A}}^{2}}{{{\omega }_{e}}^{3}}dx,$$
(24)

where Ᾱ is the amplitude ratio for a two-dimensional body in heaving motion. In the heaving motion, the restoring force enters the float as an additional buoyancy force. The restoring force coefficient or stiffness coefficient for any section can be calculated from the following equation and the stiffness coefficient for the whole floater is shown by c:

$$c={\int }_{-l/2}^{l/2}\rho g{B}_{n}dx.$$
(25)

The excitation force has a direct relationship with the characteristics of water waves, and water waves are the only source of propulsion for floats. In the heave motion, the excitation force is calculated from the integral of the buoyant force multiplied by the length of the float:

$${F}_{0}=2\rho g{\zeta }_{a}{\int }_{-L/2}^{L/2}y\mathrm{cos}{k}^{^{\prime}}xdx,$$
(26)

where k' = kxcosμ is the effective wave number.

6 Geometry of Buoy

By calculating the dynamic coefficients for each buoy and finding the natural frequency of the buoy in heave motion and comparing them, it is possible to choose the best and most suitable buoy for energy harvesting. The results of the calculations are given in Table 4 (Table 5).

Table 4 Dynamic properties of the floater designed based on rectangular cube and half cylinder
Full size table
Table 5 Dynamic properties of the floater designed based on the half sphere and half cylinder
Full size table

To maximize energy harvesting, the frequencies of the system should be close to the frequency of the ocean. On the other hand, lower damping of the floater results in higher oscillation amplitude. Therefore, to increase the efficiency of the energy harvester, the following parameter, which is simply named "Effectiveness" should be maximized:

$$\begin{aligned}\mathrm{Effectiveness} \left(\%\right)=\Big\{\Big(1-\frac{{\omega }_{n}-{\omega }_{\mathrm{ocean}}}{{\omega }_{n}}\Big)\times W{F}_{1}+\Big(\frac{{C}_{\mathrm{max}}-C}{{C}_{\mathrm{max}}}\Big)\times W{F}_{2}\Big\}\times 100,\end{aligned}$$
(27)

where WFi are the weight factors which are considered 0.5 in this study, and ωocean is the ocean frequency which is considered 1.3 rad/s. Variations of the natural frequency and damping coefficient for diffident floaters are shown in part (A) of Fig. 2. In part (B) of this figure, variation of the effectiveness for different floaters is shown. As shown in this figure, the 7th floater have maximum effectiveness and is good for energy harvesting.

Fig. 2
figure 2

Variation of the natural frequency and damping coefficient for diffident floaters (A); and variation of the effectiveness for different floaters (B)

Full size image

7 Result and discussion

In Fig. 3 a buoy and its equivalent vibratory system are schematically shown [19]. In this system vertical movement of the buoy (yb), leads to vertical oscillations of m1. Then the mass-less gear transmits the motion of m1 to the base mass (Mbase). It can easily be concluded that the displacement amplitude of both m1 and Mbase are the same. Based on the depicted equivalent lumped model of the system (Eq's 5–7) and the dynamic model of the buoy (Eq. 21), the coupled equations of motion for the whole ocean wave energy harvesting system can be obtained. The electromechanical equations of motion for the presented energy harvesting system can be obtained as follows:

$${m}_{eq}{q}_{i}+{c}_{eq}\ddot{q}_{i}+\left({k}_{eq}+{k}_{g}\right){q}_{i}-\theta V=-{m}^{*}\ddot{\beta },$$
(28)
$${J}^{*}\ddot{\beta }+{C}^{*}\dot{\beta }+{K}^{*}\beta =-{m}^{*}r\ddot{q}+Cr\dot{z}+Krz,$$
(29)
$${C}_{p}\dot{V}+V/R+\theta {\dot{q}}_{i}=0,$$
(30)

where J* = (Meq + m1)r2, C* = 3Cr2, K* = 3kr2, and other coefficients are previously presented. Considering Eqs. (21, 28–30) the output electrical voltage of the system will be obtained.

Fig. 3
figure 3

Schematic of the energy harvester and its equivalent vibratory model

Full size image

To show the effect of changing the floater on the amount of harvested energy, the best (7th floater) and worst (5th floater) floaters, as shown in part B of Fig. 2 are selected and the output electrical voltage by these systems is calculated. Figure 4 shows the output voltage of the energy harvester attached to the 5th floater and 7th floater as the worst and best system for energy harvesting is depicted. In this figure, the amplitude of output voltage for the best and worst floaters are, respectively, equal to 4.92 V and 3.14 V, which means, optimizing the floater can improve the amplitude of output voltage by more than 36%. Since the output power is related to the square of output voltage (P = V2/R), it can be concluded selecting the proper buoy can increase the output power by more than 59%.

Fig. 4
figure 4

Comparison of the harvested electrical voltage with varying the floater

Full size image

8 Conclusion

In this study, several floaters with the same weight and material and different geometry were studied to optimize the application of the ocean wave energy harvester. To do so, using the method of strip theory, added mass, damping, stiffness, excitation force and consequently natural frequencies of the floaters are obtained. Comparing the floaters, it is concluded that increasing the length-to-width ratio of the floater leads to an increase in the frequency. Furthermore, in the floaters with the same length-to-width ratio, those with a lower vertical radius-to-length ratio have higher natural frequencies. Regarding the damping of the floaters, it can be deduced in the floater with semi-circular cross sections, if the ratio of length to width of the floats is near one and two, the damping will significantly be decreased and increased, respectively. To maximize the harvested energy, the frequencies of the floater should be close to the frequency of the ocean. On the other hand, lower damping of the floater results in higher oscillation amplitude. Therefore, a parameter named Effectiveness is presented to combine both frequency and damping effects. It is shown that the Effectiveness can result in 36% improvement in the harvested voltage and consequently, it improves the output power by more than 59%.