1 Introduction

Spacecraft motion due to the interaction with internal payload motions has been an important issue in acquiring high-quality images from high-altitude Earth orbit. For imaging mission of spacecraft, the slewing mechanism with scanning optical mirror assemblies is a popular technique being employed in many spacecraft. For geostationary orbit spacecraft, it is important to obtain navigation information of ground targets on image detector plane. Also, it is necessary to keep a specific target object within a certain image pixel location. Such technique is named INR (image navigation and registration) in general [1, 2]. For the GOES spacecraft, INR is conducted by using gimballed mirror system, which can be steered in two axes [3,4,5]. The gimballed mirror motion is used to correct errors due to unwanted orbital and attitude disturbances called IMC (image motion compensation). Also, black-body calibration maneuver is employed periodically to calibrate IR (infrared) payloads during operation. The internal gimbal motion tends to produce reaction torque to the spacecraft main body.

The reaction torque disturbs spacecraft pointing, and such disturbing effects should be minimized by using active control techniques [6,7,8,9]. One representative approach is called MMC (mirror motion compensation) using feedforward control approach. The GOES spacecraft employs two scanning mirrors to provide east–west and north–south scans of imagers and sounders. The scan mirrors are also used to provide black-body calibration of the payload [2, 3].

The scanning payload motion creates internal disturbances, which perturb attitude motion of the main spacecraft body [6,7,8,9]. The spacecraft body typically being stabilized with its own attitude controller attempts to compensate for the perturbations due to payload motion. Due to the large difference in mass properties between spacecraft body and the payload, it is usually difficult to directly compensate the payload motion. However, the main controller performance could be improved if one can estimate the disturbance as accurate as possible in real time. Since the disturbance cannot be measured directly, it can be estimated by indirect methods such as disturbance observer technique.

The disturbance observer is used to estimate unknown disturbances in real time by using dynamic observer theory [10,11,12]. This approach has been used in many applications of robotics manipulators. As far as our understanding goes, the disturbance observer theory has not been employed in spacecraft disturbance estimation caused by payload motion. So, a disturbance observer proposed in [10] is modified to handle internal disturbance produced by the steerable payload motions. The estimated disturbance can be directly compensated in the form of a feedforward control. The traditional feedback control approaches, e.g., PD (proportional plus derivative) control with quaternion attitude and body angular velocity, could be further augmented such as a disturbance accommodation technique for better performance under internal payload motions. Dynamic observer can be designed independent of the controller design as it is called separation principle in control theory [13]. For fast convergence to true state, the observer design can be made with high observer gains [14, 15].

This paper is organized as follows. After the introduction, the governing equations of motion are presented in Sect. 2. The payload configuration and internal slew motion dynamics are described in Sect. 3, and controller design is presented in Sect. 4. Simulation study (Sect. 4) and conclusion of the study are followed thereafter.

2 Governing Equations of Motion

The spacecraft attitude dynamics are described by Eulers rotational equations of motion. First, we define angular momentum vectors of a spacecraft and reaction wheels such that [16]

$$\begin{aligned} {\mathbf {H}}_s= & {} {\mathbf {h}}_s + {\mathbf {h}}_{RW}, \end{aligned}$$
(1)
$$\begin{aligned} {\mathbf {h}}_s= & {} {\mathbf {J}}_s {\varvec{\omega }}, \end{aligned}$$
(2)
$$\begin{aligned} {\mathbf {h}}_{RW}= & {} {\mathbf {C}}(\beta ) {\mathbf {I}}_{RW} {\varvec{\omega }}_{RW}, \end{aligned}$$
(3)

for which the total angular momentum vector (\({\mathbf {H}}_s\)) of the system consists of that of spacecraft (\({\mathbf {h}}_s\)) and reaction wheel (\({\mathbf {h}}_{RW}\)). \({\mathbf {J}}_s\) is mass moment of inertia of the spacecraft and \({\varvec{\omega }}\) is angular velocity vector of the spacecraft. The reaction wheels in a pyramid configuration with skew angles \(\beta _i\) (\(i=1,2,3,4\)) are located in the spacecraft body frame with the following direction cosine matrix (DCM) (Fig. 1).

$$\begin{aligned} {\mathbf {C}}(\beta )= & {} \left[ \begin{array}{cccc} \cos \beta _1 &{} -\cos \beta _2 &{} \cos \beta _3 &{} -\cos \beta _4 \\ \sin \beta _1 &{} 0 &{} -\sin \beta _3 &{} 0 \\ 0 &{} -\sin \beta _2 &{} 0 &{} \sin \beta _4 \\ \end{array} \right] . \end{aligned}$$
(4)
Fig. 1
figure 1

A spacecraft configuration with a pyramid type of reaction wheels

Full size image

With such definitions of physical parameters, the governing equations of motion can be written as

$$\begin{aligned} {\mathbf {J}}_s \dot{{\varvec{\omega }}} + \dot{{\mathbf {h}}}_{RW} + {\varvec{\omega }} {\times } ({\mathbf {J}}_s {\varvec{\omega }} + {\mathbf {h}}_{RW}) = {\mathbf {M}}_p, \end{aligned}$$
(5)

where \({\mathbf {M}}_p\) represents disturbance torques due to internal and external sources. Using the definition in Eq. (3), it follows that [17]

$$\begin{aligned} {\mathbf {J}}_s \dot{{\varvec{\omega }}} + [{\varvec{\omega }}{\times }] {\mathbf {J}}_s {\varvec{\omega }} + [{\varvec{\omega }}{\times }] {\mathbf {C}}(\beta ) {\mathbf {h}}_{RW} {\varvec{\omega }}_{RW} = -{\mathbf {C}}(\beta ) {\mathbf {I}}_{RW} \dot{{\varvec{\omega }}}_{RW} + {\mathbf {M}}_p,\nonumber \\ \end{aligned}$$
(6)

where the vector multiplication notation for the angular velocity vector \([{\varvec{\omega }}{\times }]\) is defined as \([{\varvec{\omega }}{\times }] = \left[ \begin{array}{ccc} 0 &{} -\omega _3 &{} \omega _2 \\ \omega _3 &{} 0 &{} -\omega _1 \\ -\omega _2 &{} \omega _1 &{} 0 \end{array} \right] \).

Meanwhile, the attitude kinematics in terms of quaternion can be addressed by first introducing quaternion attitude parameters [16].

$$\begin{aligned} {\mathbf {q}} = \left[ \begin{array}{c} {\mathbf {q}}_{13} \\ q_4 \end{array} \right] . \end{aligned}$$
(7)

With the following definitions:

$$\begin{aligned} {\mathbf {q}}_{13}&= \left[ \begin{array}{c} q_1 \\ q_2 \\ q_3 \end{array} \right] = {\mathbf {n}} \sin \frac{{\varPhi }}{2}, \nonumber \\ q_4&= \cos \frac{{\varPhi }}{2}, \end{aligned}$$
(8)

where \({\varPhi }\), \({\mathbf {n}}\) represents Euler’s principal angle and principal axis, respectively. The quaternion kinematics is given by

$$\begin{aligned} \dot{{\mathbf {q}}} = \frac{1}{2} {\varvec{\Omega }}({\varvec{\omega }}) {\mathbf {q}}, \end{aligned}$$
(9)

where the following matrix parameters are used.

$$\begin{aligned} {\varvec{\Omega }}({\varvec{\omega }}) = \left[ \begin{array}{cc} -[{\varvec{\omega }}{\times }] &{} {\varvec{\omega }} \\ -{\varvec{\omega }}^\mathrm{{T}} &{} 0 \end{array} \right] . \end{aligned}$$
(10)

As it is well recognized, quaternion is a primary tool for large angle attitude maneuver feedback control law design. Also, feedback control for eigenaxis rotation can be made for improved maneuver performance [18]. Quaternion can be approximated as a half of Euler angles under small angular displacements.

3 Internal Slew Motion of Payload

The internal payload can be described as a steering mechanism with two degrees-of-freedom angular motion allowed.

Fig. 2
figure 2

A spacecraft payload with two-axis scan angles (east–west, north–south)

Full size image

As one can see in Fig. 2, the payload in two-axis angular motion produces reaction torques to the spacecraft body. The reaction torque as internal disturbance affects spacecraft attitude under control in turn. Such disturbance effects should be handled by compensation schemes.

The spacecraft attitude motion including internal payload dynamics can be formulated by ignoring the coupling term between reaction wheel actuator (\({\mathbf {u}}\)) and main body motion in the following form [19].

$$\begin{aligned} {\mathbf {J}}_s \dot{{\varvec{\omega }}} + {\varvec{\omega }} {\times } {\mathbf {H}}_s = {\mathbf {u}} + \sum _{i} {\mathbf {M}}^i_p, \end{aligned}$$
(11)

for which the internal torque (\({\mathbf {M}}^i_p\)) due to the \(i-th\) payload motion (\({\varvec{\omega }}^i_p\)) can be expressed such that

$$\begin{aligned} {\mathbf {M}}^i_p = {\mathbf {I}}^i_p {\dot{{\varvec{\omega }}}}^i_p + {\varvec{\omega }}^i_p {\times } {\mathbf {I}}^i_p {\varvec{\omega }}^i_p, \end{aligned}$$
(12)

which can be rewritten as

$$\begin{aligned} {\mathbf {M}}^i_p = \left[ \begin{array}{c} {\mathbf {I}}^p_{xx} {\dot{{\varvec{\omega }}}}_x \\ -{\mathbf {I}}^p_{xy} {\dot{{\varvec{\omega }}}}_x + {\mathbf {I}}^p_{xz} {\varvec{\omega }}^2_x \\ -{\mathbf {I}}^p_{xz} {\dot{{\varvec{\omega }}}}_x - {\mathbf {I}}^p_{xy} {\varvec{\omega }}^2_x \end{array} \right] , \end{aligned}$$
(13)

where \({\mathbf {I}}^p_{()}\) stands for moment of inertia of the payload, while \({\varvec{\omega }}^i_p = [{\varvec{\omega }}_x, {\varvec{\omega }}_y, {\varvec{\omega }}_z]^\mathrm{{T}}\) represents payload angular motion with respect to spacecraft body-axis motion. By substituting the payload angular displacement, Eq. (12) can be rewritten as [6]

$$\begin{aligned} {\mathbf {M}}^i_p = \left[ \begin{array}{c} {\mathbf {I}}^p_{xx} \ddot{\beta } \\ {\mathbf {I}}^p_{yy} \ddot{\alpha } + {\mathbf {I}}^p_{xz}({\dot{\beta }}^2 \cos \beta + \ddot{\beta } \sin \beta ) + {\mathbf {I}}^p_{xy}({\dot{\beta }}^2 \sin \beta - \ddot{\beta } \cos \beta ) \\ {\mathbf {I}}^p_{xz}({\dot{\beta }}^2 \sin \beta - \ddot{\beta } \cos \beta ) + {\mathbf {I}}^p_{xy}(-{\dot{\beta }} \cos \beta - \ddot{\beta } \sin \beta ) \end{array} \right] ,\nonumber \\ \end{aligned}$$
(14)

where \(\alpha \), \(\beta \) represent internal payload angular motion variables and moment of inertia terms with superscript p standing for the payload. Usually, the mass moments of inertia of the payload are much smaller than those of the spacecraft. The payload motions are prescribed as functions of time, so that they can be used to scan the images or black-body calibration maneuvers for payload.

4 Controller Design

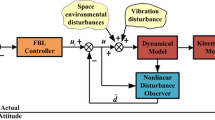
The attitude compensation techniques discussed in this study is explored by two types. The first one is a typical PD (proportional plus derivative) control and the other one is feedforward control using disturbance observer. As discussed in the previous section, the disturbance term appears in the form of reaction torque from payload motion. The PD control law can accommodate disturbances to a certain extent. But, under a circumstance of significant disturbing sources, the performance of the PD controller tends to be degraded. If the disturbance can be cancelled out similarly to feedback linearization, then the controller performance could be improved. Such characteristics become more evident as the disturbance size increases. For the problem at hand, the internal payload motion of spacecraft may have significant effect on the overall performance of attitude control system and attitude pointing requirements.

4.1 Conventional Feedback Control

The disturbance compensation can be made by a conventional attitude controller. It is assumed that the attitude controller employs reaction wheel actuators, which can produce control torque (\({\mathbf {u}}\)) as addressed in Eq. (6). The attitude controller can be made by a simple feedback (PD) structure using attitude error in quaternion (\({\mathbf {q}}_e\)) and body angular rates (\({\varvec{\omega }}\)) such that [16, 18]

$$\begin{aligned} {\mathbf {u}} = -{\mathbf {K}}_q {\mathbf {q}}_e - {\mathbf {K}}_v {\varvec{\omega }}, \end{aligned}$$
(15)

where \({\mathbf {K}}_q\), \({\mathbf {K}}_v\) represent positive definite feedback gain matrices, and \({\mathbf {q}}_e = [q_{1e},q_{2e},q_{3e},q_{4e}]^\mathrm{{T}}\) is quaternion error between commanded (\({\mathbf {q}}_c\)) and current (\({\mathbf {q}}\)) attitude quaternions such that

$$\begin{aligned} \left[ \begin{array}{c} q_{1e} \\ q_{2e} \\ q_{3e} \\ q_{4e} \end{array} \right] = \left[ \begin{array}{cccc} q_{4c} &{} q_{3c} &{} -q_{2c} &{} -q_{1c} \\ -q_{3c} &{} q_{4c} &{} q_{1c} &{} -q_{2c} \\ q_{2c} &{} q_{1c} &{} q_{4c} &{} -q_{3c} \\ q_{1c} &{} q_{2c} &{} q_{3c} &{} q_{4c} \end{array} \right] \left[ \begin{array}{c} q_1 \\ q_2 \\ q_3 \\ q_4 \end{array} \right] . \end{aligned}$$
(16)

For a regulation problem, it follows as \({\mathbf {q}}_e = [q_{1c},q_{2c},q_{3c},q_{4c}]=[0,0,0,1]\). The controller in Eq. (15) is well known and stabilizes the spacecraft dynamics model without disturbance.

$$\begin{aligned} {\mathbf {J}}_s \dot{{\varvec{\omega }}} + {\varvec{\omega }} {\times } {\mathbf {J}}_s {\varvec{\omega }} = {\mathbf {u}}, \end{aligned}$$
(17)

with the attitude kinematics in Eq. (9).

The stability of the PD controller has been thoroughly explored in a number of previous studies [20, 21]. The control command attempts to nullify disturbed attitude due to the internal payload motion. As mentioned previously, the disturbance due to internal payload motion may destabilize attitude pointing of the main spacecraft body. So, the conventional feedback law, which explicitly employs body angular information only may suffer from limited performance under large disturbance input. This is attributed to the typical nature of feedback control law in general.

4.2 Disturbance Compensation by Using Feedforward Control

Another disturbance compensation approach is direct control of the disturbance itself in the form of feedforward control. The internal disturbance effects cannot be directly quantified or measured. One promising approach, which has received significant attention recently, is the so-called disturbance observer. The disturbance is estimated online by an estimation update rule such that the state vector under control converges to a true state. The disturbance observer has been already investigated in many previous studies [10,11,12], especially in robotics manipulators. In this study, we seek to adopt the main approach proposed in [10]. The theory itself is not new, but as far as our best understanding goes, it is a new attempt to apply it to spacecraft internal disturbance estimation problem.

For theoretical development of the dynamic observer, let us consider a spacecraft under control (\({\mathbf {u}}\)) and disturbance input (\({\mathbf {d}}\)). The disturbance is caused by the internal payload motion as addressed in the previous section. The dynamic coupling between spacecraft main body and reaction wheels is ignored for simplicity of analysis.

$$\begin{aligned} {\mathbf {J}}_s \dot{{\varvec{\omega }}} + {\varvec{\omega }} {\times } {\mathbf {H}}_s = {\mathbf {u}} + {\mathbf {d}}. \end{aligned}$$
(18)

Then for the estimation of disturbance input, the following disturbance estimation observer can be proposed as [10]

$$\begin{aligned} \dot{\hat{{\mathbf {d}}}} = -L \hat{{\mathbf {d}}} + L ({\mathbf {J}}_s \dot{{\varvec{\omega }}} + {\varvec{\omega }} {\times } {\mathbf {H}}_s - {\mathbf {u}}), \end{aligned}$$
(19)

where L is a positive definite observer gain matrix. Upon making use of the governing equations of motion, it follows that

$$\begin{aligned} \dot{\hat{{\mathbf {d}}}} = -L \hat{{\mathbf {d}}} + L {\mathbf {d}} = L {\varDelta }{\mathbf {d}}, \end{aligned}$$
(20)

where \({\varDelta }{\mathbf {d}}={\mathbf {d}}-\hat{{\mathbf {d}}}\) is the estimation error in disturbance. By assuming the disturbance is constant (\(\dot{{\mathbf {d}}}\approx 0\)) over a short time period, for which convergence in observer is made using a high observer gain (L), Eq. (20) can be rewritten as [10]

$$\begin{aligned} {\varDelta }\dot{{\mathbf {d}}} = -L {\varDelta }{\mathbf {d}}. \end{aligned}$$
(21)

That is, the estimation error (\({\varDelta }{\mathbf {d}}\)) for the disturbance quickly converges. With a high observer gain, convergence can be achieved quickly enough. This is true also for the so-called separation principle, for which the observer design can be made independent of the controller design [11].

It is assumed that disturbance can be estimated by the update law in Eq. (19). With the disturbance update law enforced, the new control law for disturbance compensation can be proposed as

$$\begin{aligned} {\mathbf {u}} = {\mathbf {J}}_s (\dot{{\varvec{\omega }}}_d - {\mathbf {K}}_v {\varDelta }{\varvec{\omega }} - {\mathbf {K}}_q {\varDelta }{\mathbf {q}}) + {\varvec{\omega }} {\times } {\mathbf {H}}_s - \hat{{\mathbf {d}}}, \end{aligned}$$
(22)

where \({\varDelta }{\mathbf {q}} = {\mathbf {q}}_e\) is a quaternion attitude error, and \({\varDelta }{\varvec{\omega }} = {\varvec{\omega }} - {\varvec{\omega }}_d\) corresponds to angular velocity error between the present (\({\varvec{\omega }}\)) and desired angular velocities (\({\varvec{\omega }}_d\)), and \({\mathbf {K}}_v\), \({\mathbf {K}}_q\) are positive definite feedback gain matrices. As one can see, the control law consists of the conventional feedback control on \({\varDelta }{\varvec{\omega }}\), \({\varDelta }{\mathbf {q}}\) and feedforward terms (\({\varvec{\omega }}_d\), \({\mathbf {H}}_s\), \(\hat{{\mathbf {d}}}\)).

The acceleration term in Eq. (19) can be estimated and approximated as

$$\begin{aligned} \dot{{\varvec{\omega }}}(t) \approx \frac{{\varvec{\omega }}(t) - {\varvec{\omega }}(t-{\varDelta }t)}{{\varDelta }t}. \end{aligned}$$
(23)

Or, we can adopt the approach in [10], where a technique without using an acceleration term has been proposed. The issue of noise arising by the finite difference approach in Eq. (23) needs further investigation in the future.

Once the control law is implemented, the closed-loop system becomes

$$\begin{aligned} {\varDelta }\dot{{\varvec{\omega }}} + {\mathbf {K}}_v {\varDelta }{\varvec{\omega }} + {\mathbf {K}}_q {\varDelta }{\mathbf {q}} = {\mathbf {J}}^{-1}_s {\varDelta }{\mathbf {d}}. \end{aligned}$$
(24)

The stability of the closed-loop system has been investigated in [18] for a special case of regulator problem. It is assumed that the observer employs a high gain, for which the observer error converges quickly (\({\varDelta }{\mathbf {d}} \approx 0\)). Then the closed-loop system becomes

$$\begin{aligned} {\varDelta }\dot{{\varvec{\omega }}} + {\mathbf {K}}_v {\varDelta }{\varvec{\omega }} + {\mathbf {K}}_q {\varDelta }{\mathbf {q}} = 0. \end{aligned}$$
(25)

For stability proof, the following candidate Lyapunov function is proposed:

$$\begin{aligned} L = \frac{1}{2} {\varDelta }{\varvec{\omega }}^\mathrm{{T}} {\varDelta }{\varvec{\omega }} + {\varDelta }{\mathbf {q}}^\mathrm{{T}} {\mathbf {K}}_q {\varDelta }{\mathbf {q}}. \end{aligned}$$
(26)

For a diagonal feedback gain matrix (\({\mathbf {K}}_q = diag(k_q)\)) on the quaternion error term and regulation problem with \([q_{1c},q_{2c},q_{3c},q_{4c}]=[0,0,0,1]\), it follows that [18]

$$\begin{aligned} {\varDelta }{\mathbf {q}}^\mathrm{{T}} {\mathbf {K}}_q {\varDelta }{\mathbf {q}} = {\mathbf {K}}_q [q^2_1 + q^2_2 + q^2_3 + (1-q_4)^2], \end{aligned}$$
(27)

and by using the closed-loop dynamics in Eq. (25), (herein, the detailed information is shown in “Appendix”)

$$\begin{aligned} {\dot{L}} = - {\varDelta }{\varvec{\omega }}^\mathrm{{T}} {\mathbf {K}}_v {\varDelta }{\varvec{\omega }} \le 0. \end{aligned}$$
(28)

Therefore, stability is guaranteed with the proposed control law [20, 21] on the condition that the observer states (\(\hat{{\mathbf {d}}}\)) converge quickly to true states with a high observer gain (L).

5 Simulation Results

For simulation study, the following mass properties of the spacecraft are assumed as

$$\begin{aligned} {\mathbf {J}}_s = \left[ \begin{array}{ccc} 3,426 &{} 0 &{} 0 \\ 0 &{} 992 &{} 0 \\ 0 &{} 0 &{} 357 \end{array} \right] kg \cdot m^2. \end{aligned}$$

The mass moment of inertial of the payload for the gimbal and mirror is given by \({\mathbf {I}}^p_{xx} = 0.158\) kg m\(^2\), \({\mathbf {I}}^p_{xz} = 0.0186\) kg m\(^2\), \({\mathbf {I}}^p_{xy} \sim \varepsilon \), and \({\mathbf {I}}^p_{xx} = 0.0305\) kg m\(^2\) for mirror only. The initial body orientation attitude is set to \([80,-80,-50]^\mathrm{{T}}\) deg with the angular velocity \([0,0,0]^\mathrm{{T}}\) deg/s, respectively. The feedback gains (\({\mathbf {K}}_q\), \({\mathbf {K}}_v\)) are all given in the form of moment of inertia term (\({\mathbf {J}}_s\)) scaled by a constant (\(\alpha =100\)).

The disturbance is generated by, for instance, normal imaging motion as well as a black-body calibration motion so that resultant disturbance effects can be modeled about spacecraft body axes (Fig. 3). First, simulation results with real black-body calibration of payload are obtained. The simulation results are presented in Figs. 4, 5, and 6. Gimbal servo commanded attitude profiles from black-body calibration maneuver is presented in Fig. 4 [2]. The actual responses produce internal disturbance torque as addressed above.

Fig. 3
figure 3

Actual black-body calibration example gimbal servo command profiles

Full size image

On the other hand, Fig. 4 shows the estimated disturbance responses by the disturbance observer theory. The estimated disturbance matches fairly with the real disturbance torques in Fig. 3. This is due to the high-gain disturbance observer, which is designed to work independently of the control law.

Fig. 4
figure 4

Estimated black-body calibration example gimbal servo command profiles

Full size image

Both actual and estimated disturbance torque profiles are plotted together in Fig. 5 for comparison purpose. As one can see, they are well matched within the closed-loop observer dynamics and feedback control with feedforward compensation strategy.

Fig. 5
figure 5

Actual and estimated disturbance profiles due to internal gimbal motion

Full size image

Presented in Fig. 6 are Euler attitude angle responses with the closed-loop control implemented. Since the closed-loop control law is designed to compensate for the internal disturbance effect, the overall behavior seems to be quite satisfactory even under large initial spacecraft attitude errors. Especially, the attitude responses in Fig. 6 validates the stability proof with combined high-gain observer and attitude error feedback strategies in Eq. (22).

Fig. 6
figure 6

Euler attitude angles responses with the new control law proposed to compensate estimated disturbance effects

Full size image

Corresponding quaternion attitude responses over time are also presented in Fig. 7. The responses also exhibit a similar performance behavior to Euler angle responses in Fig. 6.

Fig. 7
figure 7

Quaternion attitude angles responses with the new control law proposed to compensate estimated disturbance effects

Full size image

The internal disturbance model in the previous simulation case could be regarded as a special one. So, this time we attempt to test another disturbance, to examine the feasibility of the proposed idea. For this purpose, a sharp step-input type disturbance is generated artificially as in Fig. 8.

Fig. 8
figure 8

A sharp step-input disturbance input due to internal payload motion

Full size image

The corresponding estimated disturbance (\(\hat{{\mathbf {d}}}\)) torques are displayed in Fig. 9, whereas the overlapped display for both real and estimated disturbance responses are presented in Fig. 10.

Fig. 9
figure 9

A sharp step-input disturbance input due to internal payload motion

Full size image
Fig. 10
figure 10

Overlapped display of step-input disturbance due to payload motion (actual vs. estimated)

Full size image

The estimated disturbance estimator works well in this case to successfully estimate sharp step-input type disturbance. One can better tune the observer dynamics with the gain matrix (L) for the closed-loop observer dynamics in Eq. (21).

On the other hand, attitude responses in Euler angles and quaternion under the sharp step-input disturbance are presented in Figs. 11 and 12, respectively.

Fig. 11
figure 11

Euler angle responses under sharp step-input disturbance with the compensation control law

Full size image
Fig. 12
figure 12

Quaternion attitude responses under step-input disturbance with compensation control law

Full size image

Through the simulation study made so far, one can arrive at the conclusion that the control law with the feedforward compensation of the estimated internal disturbance seems to be effective in dealing with unknown disturbance sources. The high-gain observer results in smooth and quick convergence of observed state, which could be a promising feature of the disturbance observer in general. The idea could be further extended to other spacecraft disturbance estimation techniques also. Even if the principal theoretical background and algorithm were adopted from robotics and references, we believe that the application to spacecraft image navigation and registration (INR) technology is rather new and may offer renewed interest and opportunities in this field.

6 Conclusion

In this study, a new control approach has been explored by handling disturbances due to internal payload motion for imaging geostationary satellites. Onboard mirror motion compensation (MMC) is formulated in terms of a combined feedback and feedforward control law design. The feedforward control directly compensates for internal disturbance by using so-called disturbance observer theory. The observer design can be done separate from the controller design to ensure quick convergence to true state by high-gain observer. It is expected that the proposed new control approach allows faster convergence and better control efficiency under internal payload motion of spacecraft. Further study could be considered to explore different disturbance estimation approaches to deal with various disturbance sources.