Characterization of hot deformation behavior of 30Si2MnCrMoVE low-alloying ultra-high-strength steel by constitutive equations and processing maps

Abstract

Isothermal compression tests of as-forged 30Si2MnCrMoVE low-alloying ultra-high-strength steel were carried out on a Gleeble 3500 thermal simulator at the deformation temperatures of 950–1150 °C and strain rates of 0.01–10 s⁻¹. Based on the classical stress–dislocation density relationship and the kinematics of the dynamic recrystallization, the constitutive equations of the work hardening dynamical recovery period and dynamical recrystallization period were developed by using the work hardening curve and Avrami equation, which shows good agreement with the experimental value. Processing maps at the strain of 0.90 were constructed based on dynamic material model and were analyzed combined with microstructure observation under different conditions. The optimum parameter based on the processing maps was obtained and verified by a supplementary experiment. The power dissipation maps and instability maps at strains of 0.05–0.90 were also constructed, and the evolution law was analyzed in detail. The established constitutive equation and hot processing maps can provide some guidance for hot working process.

1 Introduction

30Si2MnCrMoVE ultra-high-strength steel (UHSS) is a kind of low-alloying martensitic strengthened steel, which is widely used in the manufacture of solid rocket and missile engine shells because of its good combination of strength (R_m ≥ 1650 MPa), plasticity (δ ≥ 9%) and toughness (K_IC ≥ 80 MPa $\sqrt {\text{m}}$) and low cost. The dynamic evolution of microstructure and mechanical behavior during hot deformation under different thermodynamic parameters is crucial to the assessment of hot working performance of different metals and alloys [1]. However, coarse and inhomogeneous austenite grains often appear after forging, which are difficult to eliminate by simple quenching and tempering process. So far, no relevant reports have been found on the hot deformation behavior of 30Si2MnCrMoVE UHSS. To obtain the optimal thermodynamic processing parameters and improve the hot working process for 30Si2MnCrMoVE UHSS, it is necessary to study the constitutive models and processing maps. Generally, the hot deformation of an alloy depends mainly on dislocation movement and twinning during which process dynamic recovery (DRV) and dynamic recrystallization (DRX) perform. DRV and DRX process can eliminate the defects caused by the hot deformation. In most of the martensitic strengthened steels, hot deformation is usually carried out at the temperature range of austenite phase where DRX is the main microstructural modifying mechanism. It can act as a desirable process to utilize DRX to obtain uniform and fine austenite structure and to eliminate deformation defects prior to the austenite decomposition [2,3,4,5,6,7,8]. When the strain reaches the critical strain of recrystallization, softening rate is accelerated and flow stress decreases after reaching the peak value, and finally, softening effect and hardening effect balance each other leading to a steady state [9]. The steady-state flow dominated by DRX suppresses the plastic instabilities and facilitates microstructural modification [3, 10]. Raj [11] first proposed the approach of processing maps to characterize different regions of safe deformation and plastic instabilities under different processing conditions. The processing map is defined as a superimposition of the power dissipation and the instability map which are based on dynamic material model (DMM) [5]. Prasad and Seshacharyulu [5, 12, 13] have applied this approach to a variety of materials and demonstrated a high reliability.

In this study, the flow behavior of 30Si2MnCrMoVE UHSS was investigated by a series of isothermal compression tests at the deformation temperatures of 950–1150 °C and strain rates of 0.01–10 s⁻¹. The constitutive equations of the work hardening dynamic recovery period and dynamic recrystallization period were established based on the classical stress–dislocation density relationship and the kinematics of the dynamic recrystallization. Moreover, the processing maps of 30Si2MnCrMoVE UHSS at the strain of 0.90 were constructed based on DMM and were analyzed combined with microstructure observation. Meanwhile, the power dissipation maps and instability maps at strains of 0.05–0.90 of 30Si2MnCrMoVE UHSS were also constructed. It is expected that the results will offer some guidance for the hot working process of as-forged 30Si2MnCrMoVE UHSS.

2 Experimental procedures

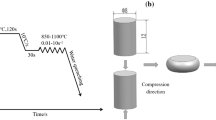
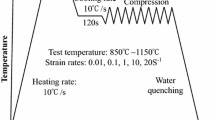
30Si2MnCrMoVE UHSS used in this investigation was cast by vacuum consumption and electroslag remelting technology and forged to round bar. The chemical composition is given in Table 1, and the original microstructure is shown in Fig. 1. Cylindrical compression samples of 12 mm in height and 8 mm in diameter were cut from a 300-mm-diameter bar. A series of isothermal compressions were carried out on a Gleeble 3500 simulator at deformation temperatures of 950, 1000, 1050, 1100 and 1150 °C, strain rates of 0.01, 0.1, 1 and 10 s⁻¹ and the height reduction of 60% (the true strain is 0.916). The specimens were heated at a speed of 10 °C/s and held for 10 min at the deformation temperatures prior to compression to obtain uniform temperature distribution and complete austenite microstructure. In order to reduce the friction between the anvils and samples, graphite sheets were padded between the samples and dies. K-type thermocouples were fixed at the surface of samples to trace and adjust the temperature. In order to retain the grain sizes of prior austenite, the specimens were quickly quenched in water after compression. Saturated picric acid solution with a small amount of detergent was adopted to reveal prior austenite grain boundaries. Olympus PM3 optical microscope was used to observe the deformed microstructure.

Table 1 Chemical composition of 30Si2MnCrMoVE UHSS (mass%)

Fig. 1

Original microstructure of 30Si2MnCrMoVE ultra-high-strength steel used in present study

3 Experimental results and analysis

3.1 Flow stress analysis

Figure 2 shows the obtained flow curves at different deformation temperatures and strain rates ($\dot{\varepsilon }$). Under the same conditions, like most metals, the stress decreases with increasing temperature and decreasing strain rate. It is worth noting that a strong strain rate dependence can be observed at all temperatures. All of the specimens at the strain rate of 0.01 and 0.1 s⁻¹ (Fig. 2a, b) exhibit the dynamic recrystallization softening effect after the flow stress reaches the peak value, while none of the specimens at 1 and 10 s⁻¹ (Fig. 2c, d) shows the same rule, which keeps a steady state after reaching the peak value. In general, the variation in flow stress at different strain rates can be attributed to the deformation mechanism, which can be divided into DRV type and DRV + DRX type [14]. When the strain rate is 1 and 10 s⁻¹, the deformation mechanism is mainly DRV. As shown in Fig. 2c, d, when the strain is very small, the stress increases rapidly with strain and work hardening starts to appear because of the dislocation multiplication. Then, with the strain increasing, the growth rate of true stress values slows down owing to softening effect of dynamic recovery, i.e., the opposite sign dislocations annihilate each other. However, work hardening still plays a dominant role at this stage. After reaching the peak value, the true stress keeps a steady state as softening and hardening effects are basically in balance. What is difference of the strain rate at 0.01 and 0.1 s⁻¹ is that a stress decreases before the steady state, which indicates that the softening mechanisms (DRV, DRX, etc.) are sufficient to balance work hardening.

Fig. 2

True stress–strain curves of 30Si2MnCrMoVE steel under hot compression at different strain rates. a 0.01 s⁻¹; b 0.1 s⁻¹; c 1 s⁻¹; d 10 s⁻¹

3.2 Establishment of constitutive equation for 30Si2MnCrMoVE UHSS

3.2.1 Hot deformation parameters

The effects of temperature and strain rate under hot working condition are often incorporated in the well-known Zener–Hollomon parameter, Z, as follows [15]:

$$Z = \dot{\varepsilon }{ \exp }\left( {\frac{Q}{RT}} \right)$$

(1)

where Q denotes the apparent activation energy; R is the gas constant, 8.314 J mol⁻¹ K⁻¹; and T is the absolute temperature. The flow stress of the materials deformed under different temperatures, strain rates and strains can be expressed by Arrhenius equation in three forms [16]:

$$A_{1} \exp \left( {\beta \sigma } \right) = Z,\;\;{\text{under}}\;{\text{lower}}\;{\text{stress}}\;(\beta \sigma < 0.8)$$

(2)

$$A_{2} \sigma^{{n_{1} }} = Z,\;\;{\text{under}}\;{\text{higher}}\;{\text{stress}}\;(\beta \sigma > 1.2)$$

(3)

$$A\left[ {\sinh \left( {\alpha \sigma } \right)} \right]^{n} = Z,\;\;{\text{under}}\;{\text{all}}\;{\text{stress}}\;{\text{levels}}$$

(4)

where A₁, $A_{2}$, $A$, $n_{1}$, $n$, β and α are constants determined by deformation. $\alpha = \beta /n_{1}$, and σ is the flow stress.

By substituting Eqs. (2)–(4) into Eq. (1), Eqs. (5)–(7) can be obtained:

$$\dot{\varepsilon } = A_{1} \sigma^{{n_{1} }} { \exp }\left( { - \frac{Q}{RT}} \right)$$

(5)

$$\dot{\varepsilon } = A_{2} { \exp }\left( {\beta \sigma } \right){ \exp }\left( { - \frac{Q}{RT}} \right)$$

(6)

$$\dot{\varepsilon } = A\left[ {\sinh \left( {\alpha \sigma } \right)} \right]^{n} { \exp }\left( { - \frac{Q}{RT}} \right)$$

(7)

Taking the logarithm of both sides of Eqs. (5) and (6), Eqs. (8) and (9) can be obtained:

$${\ln}\,\dot{\varepsilon } = { \ln }A_{1} + n_{1} { \ln }\sigma - \frac{Q}{RT}$$

(8)

$${\ln}\,\dot{\varepsilon } = { \ln }A_{2} + \beta \sigma - \frac{Q}{RT}$$

(9)

The deformation activation energy used in this work corresponds to the peak stress (σ_p). The values of $n_{1}$ and $\beta$ can be obtained by calculating the slope of ${ \ln }\dot{\varepsilon }$ versus ${ \ln }\sigma_{\text{p}}$ and ${ \ln }\dot{\varepsilon }$ versus $\sigma_{\text{p}}$, respectively, according to Eqs. (8) and (9). An illustration of such values is presented in Fig. 3 based on the peak stress at different temperatures. The mean value of $n_{1}$ and $\beta$ is 6.362 and 0.0609, respectively, and the value of α is 0.00958.

Fig. 3

Plot of lnσ (a) and σ (b) versus ln $\dot{\varepsilon }$ for obtaining $n_{1}$ and β, respectively

Taking the logarithm values of both sides of Eq. (7), n and Q can be expressed as follows:

$$\frac{1}{n} = \left. {\frac{{\partial \ln \left[ {\sinh \left( {\alpha \sigma_{\text{p}} } \right)} \right]}}{{\partial \ln \dot{\varepsilon }}}} \right|_{T}$$

(10)

$$Q = nkR = nR \cdot \left. {\frac{{\partial \ln \left[ {\sinh \left( {\alpha \sigma_{\text{p}} } \right)} \right]}}{{\partial \left( {1/T} \right)}}} \right|_{{\dot{\varepsilon }}}$$

(11)

where k is the slope of ln [sinh(ασ)] versus 1/T. The plots of ln [sinh(ασ_p)] versus $\ln \dot{\varepsilon }$ and ln [sinh(ασ)] versus 1/T are shown in Fig. 4a, b, according to which the average slope was used to calculate the values of n and Q, which were 4.64 and 362,482.78 J/mol, respectively. By inputting Q, R and $\dot{\varepsilon }$ into Eq. (1), Z parameter can be calculated.

Fig. 4

Plot of ln [sinh(ασ_p)] versus ln $\dot{\varepsilon }$ (a), ln [sinh(ασ_p)] versus 1/T (b) and ln [sinh(ασ_p)] versus lnZ (c)

Taking the logarithm values of both sides of Eq. (4), Eq. (12) can be obtained:

$$\ln Z = \ln A + n\ln \left[ {\sinh \left( {\alpha \sigma_{\text{p}} } \right)} \right]$$

(12)

The value of A was obtained as 1.23 × 10¹³ according to the intercept of the fitted line in Fig. 4c. Finally, the Arrhenius constitutive model of the studied steel at peak stress can be expressed as follows:

$$\dot{\varepsilon } = 1.23 \times 10^{13} \ln \left[ {\sinh \left( {0.00958\sigma_{\text{p}} } \right)} \right]^{4.64} { \exp }\left( { - \frac{362,482.78}{RT}} \right)$$

(13)

The peak stress can also be written as a function of Z parameter:

$$\sigma_{\text{p}} = \frac{1}{\alpha }\ln \left\{ {\left( {\frac{Z}{A}} \right)^{{\frac{1}{n}}} + \left[ {\left( {\frac{Z}{A}} \right)^{{\frac{2}{n}}} + 1} \right]^{{\frac{1}{2}}} } \right\} = \frac{1}{0.00958}\ln \left\{ {\left( {\frac{Z}{{1.23 \times 10^{13} }}} \right)^{{\frac{1}{4.64}}} + \left[ {\left( {\frac{Z}{{1.23 \times 10^{13} }}} \right)^{{\frac{2}{4.64}}} + 1} \right]^{{\frac{1}{2}}} } \right\}$$

(14)

3.2.2 Flow stress constitutive equation considering work hardening and DRV

In the initial stage of deformation, i.e., the main deformation mechanisms which are mainly work hardening (WH) and DRV, the variation in dislocation density with strain can be expressed as [17]:

$$\frac{{{\text{d}}\rho }}{{{\text{d}}\varepsilon }} = U - \varOmega \rho$$

(15)

where ${\text{d}}\rho /{\text{d}}\varepsilon$ is the increased rate of dislocation density with strain; U represents the WH and can be treated as constant with respect to strain; Ωρ is a term due to dynamic recovery by dislocation annihilation and rearrangement; and Ω is often termed the coefficient of dynamic recovery. By integrating the above equation and doing some algebraic operations, the flow stress during WH and DRV period can be expressed as [6]:

$$\sigma = \left[ {\sigma_{\text{sat}}^{2} - \left( {\sigma_{\text{sat}}^{2} - \sigma_{0}^{2} } \right)\exp \left( { - \varOmega \varepsilon } \right)} \right]^{0.5}\,\, (\varepsilon < \varepsilon_{\text{c}} )$$

(16)

where σ₀ and σ_sat are the yield stress and saturated stress, respectively, and ε_c is the critical strain for the occurrence of DRX. This equation characterizes the relationship between stress and strain during the period that has not yet undergone DRX.

Based on Eq. (16), there are three parameters (σ_sat, σ₀ and Ω) to be determined. Generally, the imaginary saturation stress, the steady-state stress and the peak stress can be obtained by plotting the work hardening rate–stress (θ − σ, $\theta = {\text{d}}\sigma /{\text{d}}\varepsilon$) curve, as shown in Fig. 5. The yield stress was identified on the flow curves in terms of 2% offset in total strain [7]. The variations in σ₀ and σ_sat with σ_p are shown in Fig. 6, and the relationships can be mathematically expressed by linear fitting method as:

$$\sigma_{0} = 0.5367\,\sigma_{\text{p}}$$

(17)

$$\sigma_{\text{sat}} = 1.076\,\sigma_{\text{p}}$$

(18)

Fig. 5

Work hardening rate versus flow stress at deformation temperature of 950 °C and strain rate of 0.01 s⁻¹. σ_ss Steady state stress

Fig. 6

Relationship between stress (σ_sat and σ₀) and peak stress

Substituting the experimental results into Eq. (16), the values of Ω can be easily calculated for different deformation conditions. Then, the relationship between Ω and Zener–Hollomon parameter can be expressed by power law equation as follows:

$$\varOmega = 183.1Z^{ - 0.11582}$$

(19)

Therefore, the constructive equation for the studied steel at DRX stage can be described as follows:

$$\begin{aligned} & Z = \dot{\varepsilon}\,{\exp }\left( {\frac{362,482.78}{RT}} \right) \\ & \sigma_{0} = 0.5367\sigma_{\text{p}} \\ & \sigma_{\text{sat}} = 1.076\sigma_{\text{p}} \\ & \varOmega = 263.288Z^{ - 0.13184} \\ & \sigma = \left[ {\sigma_{\text{sat}}^{2} - \left( {\sigma_{\text{sat}}^{2} - \sigma_{0}^{2} } \right)\exp \left( { - \varOmega \varepsilon } \right)} \right]^{0.5} \left( {\varepsilon < \varepsilon_{\text{c}} } \right) \\ & \sigma_{\text{p}} = 104.4{ \ln }\left\{ {\left( {\frac{Z}{{1.23 \times 10^{13} }}} \right)^{{\frac{1}{4.64}}} + \left[ {\left( {\frac{Z}{{1.23 \times 10^{13} }}} \right)^{{\frac{2}{4.64}}} + 1} \right]^{{\frac{1}{2}}} } \right\} \\ \end{aligned}$$

(20)

3.2.3 Flow stress constitutive equation considering DRX

In DRX region, the evolution of dislocation density depends on DRX kinetics, which can be characterized by the Avrami equation sufficiently as follows [18]:

$$X_{\text{d}} = 1 - { \exp }\left[ { - K_{\text{d}} \left( {\frac{{\varepsilon - \varepsilon_{\text{c}} }}{{\varepsilon_{\text{p}} }}} \right)^{{n_{\text{d}} }} } \right]$$

(21)

where X_d is the DRX fraction; n_d is the Avrami’s power; K_d is a constant; and ε_p is the strain corresponding to the peak stress. X_d can also be estimated by the following equation:

$$X_{\text{d}} = \frac{{\sigma_{\text{WH}} - \sigma }}{{\sigma_{\text{sat}} - \sigma_{\text{ss}} }}$$

(22)

where σ_WH is extension of the flow stress at the dynamic recovery stage. Then, the flow stress during DRX period can be expressed by combining Eqs. (21) and (22):

$$\sigma = \sigma_{\text{WH}} - \left( {\sigma_{\text{sat}} - \sigma_{\text{ss}} } \right)\left\{ {1 - { \exp }\left[ {K_{\text{d}} \left( {\frac{{\varepsilon - \varepsilon_{\text{c}} }}{{\varepsilon_{\text{p}} }}} \right)^{{n_{\text{d}} }} } \right]} \right\} \left( {\varepsilon \ge \varepsilon_{\text{c}} } \right)$$

(23)

According to Eq. (23), five parameters (σ_ss, ε_c, ε_p, K_d and n_d) should be determined. ε_p and σ_ss can be readily obtained from flow stress curves and θ − σ curves. The variations in ε_p and σ_ss with Zener–Hollomon parameter are shown in Figs. 7 and 8. The critical strain ε_c is usually equal to (0.5–0.8)ε_p, and in this study, ε_c = 0.8ε_p is selected. The relationships between the three parameters (ε_p, σ_ss and ε_c) and Zener–Hollomon parameter can be mathematically expressed as:

$$\varepsilon_{\text{p}} = 0.597Z^{0.12658}$$

(24)

$$\varepsilon_{\text{c}} = 0.8\varepsilon_{\text{p}} = 0.456Z^{0.12658}$$

(25)

$$\sigma_{\text{ss}} = 0.3263Z^{0.1805}$$

(26)

Fig. 7

Relationship between lnε_p and lnZ

Fig. 8

Relationship between lnσ_ss and lnZ

In order to determine the value of K_d and n_d, Eq. (21) can be rewritten in double natural logarithm form as follows:

$$\ln \left[ {- \ln \left( {1 - X_{\text{d}} } \right)} \right] = { \ln }K_{\text{d}} + n_{\text{d}} { \ln }\frac{{\varepsilon - \varepsilon_{\text{c}} }}{{\varepsilon_{\text{p}} }}$$

(27)

The value of K_d and n_d can be calculated as 0.864 and 1.5646 by linear regression between ln(−ln(1 − X_d)) and ln [(ε − ε_c)/ε_p], as is shown in Fig. 9.

Fig. 9

Relationship between ln[-ln(1 − X_d)] and ln [(ε − ε_c)/ε_p]

Therefore, the constructive equation for the studied steel at DRX stage can be described as follows:

$$\left\{\begin{aligned}\varepsilon_{\text{p}} &=0.597Z^{0.12658}\\ \varepsilon_{\text{c}} &= 0.8\varepsilon_{\text{p}} = 0.456Z^{0.12658} \\ \sigma_{\text{ss}} &= 0.3263Z^{0.1805} \\ \sigma_{\text{WH}} &= \left[ {\sigma_{\text{sat}}^{2} - \left({\sigma_{\text{sat}}^{2} - \sigma_{0}^{2} } \right){ \exp }\left( {- \varOmega \varepsilon } \right)} \right]^{0.5} \,\,\left( {\varepsilon \ge \varepsilon_{\text{c}} } \right) \\ \sigma &= \sigma_{\text{WH}} - \left( {\sigma_{\text{sat}} - \sigma_{\text{ss}} } \right)\left\{ {1 - { \exp }\left[ { - 0.864\left( {\frac{{\varepsilon - \varepsilon_{\text{c}} }}{{\varepsilon_{\text{p}} }}} \right)^{1.5646} } \right]} \right\} \left( {\varepsilon \ge \varepsilon_{\text{c}} } \right) \\ \end{aligned}\right.$$

(28)

According to Eqs. (20) and (28), comparisons between the experimental values and the predicted values under different conditions are plotted in Fig. 10, which demonstrates that the constitutive model can accurately predict the flow stress of the studied steel except for several points of high strain rates and large strains.

Fig. 10

Comparison between experimental and predicted flow stresses at different strains for strain rates of 0.01 s⁻¹ (a), 0.1 s⁻¹ (b), 1 s⁻¹ (c) and 10 s⁻¹ (d)

3.3 Processing map

3.3.1 Method of constructing processing map of 30Si2MnCrMoVE UHSS

It is well known that the energy dissipation of materials can be divided into two parts: potential energy and kinetic energy [19]. Potential energy is related to the relative position of atoms. The change of microstructures will inevitably lead to the change of atomic potential energy, which corresponds to the dissipative covalent (J). Kinetic energy is related to the movement of atoms, that is, dislocation motion. Kinetic energy conversion is dissipated in the form of thermal energy, which corresponds to dissipation (G). Moreover, the ratio of these two energies is determined by the strain rate sensitivity of flow stress, m. The efficiency of power dissipation η, whose physical meaning is the proportional relationship between the energy dissipated by the evolution of microstructures and the linear dissipative energy, is employed to express the power dissipation rate, which is defined as follows [20]:

$$\eta = \frac{J}{{J_{\text{max}} }} = \frac{2m}{2m + 1}$$

(29)

where J_max represents an ideal linear dissipator (m = 1), i.e., half of the total power is consumed by microstructural evolution. The variation in η at different temperatures and strain rates can constitute a power dissipation map. Moreover, according to the maximum entropy production rate principle proposed by Ziegler, Prasad et al. considered that the system is unstable if the dissipation function $D\left( {\dot{\varepsilon }} \right)$ satisfies the inequality with $\dot{\varepsilon }$:

$$\frac{{{\text{d}}D}}{{{\text{d}}\dot{\varepsilon }}} < \frac{D}{{\dot{\varepsilon }}}$$

(30)

and the criterion of material rheological instability is as follows [21]:

$$\xi \left( {\dot{\varepsilon }} \right) = \frac{{\partial \lg \left[ {m/\left( {m + 1} \right)} \right]}}{{\partial \lg \dot{\varepsilon }}} + m < 0$$

(31)

where $\xi \left( {\dot{\varepsilon }} \right)$ is a dimensionless instability parameter, and the flow instabilities may occur when $\xi \left( {\dot{\varepsilon }} \right)$ becomes negative. The variation in $\xi \left( {\dot{\varepsilon }} \right)$ at different temperatures and strain rates can constitute an instability map. According to irreversible thermodynamics, the relationship between logarithmic flow stress and logarithmic strain rate at a fixed temperature and strain rate can be fitted with a third-order polynomial as follows [22]:

$$\lg \sigma = a + b\lg \dot{\varepsilon } + c(\lg \dot{\varepsilon })^{2} + d\left( {\lg \dot{\varepsilon }} \right)^{3}$$

(32)

where a, b, c and d are material constants. Then, m value can be calculated as follows:

$$m = \frac{{\partial \left( {\lg \sigma } \right)}}{{\partial \left( {\lg \dot{\varepsilon }} \right)}} = b + 2c\lg \dot{\varepsilon } + 3d\left( {\lg \dot{\varepsilon }} \right)^{2}$$

(33)

The values of η and $\xi \left( {\dot{\varepsilon }} \right)$ can be obtained according to Eqs. (29) and (31), which constitute the power dissipation maps and instability maps, respectively, by superimposing in which the processing maps of the studied steel were constructed.

3.3.2 Processing map of 30Si2MnCrMoVE UHSS at strain of 0.90

Based on Eqs. (29) and (31), the processing map of 30Si2MnCrMoVE UHSS at the strain of 0.90 is shown in Fig. 11. The contour numbers display the value of η as percentage, where the green region corresponds to 0.30 < η < 0.40, the yellow region corresponds to 0.40 < η < 0.50, the white region corresponds to η < 0.30 and the grid region represents the regions of instability. A higher η indicates that more energy was consumed by the microstructural evolution during the hot working process. In this map, two instability regions were predicted at 950–1150 °C/3–10 s⁻¹ and 1120–1150 °C/0.01–0.03 s⁻¹.

Fig. 11

Processing map of 30Si2MnCrMoVE UHSS at strain of 0.90. Contour numbers display value of η as percentage

In terms of the value of η, the processing map at the strain of 0.90 can be divided into three domains marked A–C based on flow instability areas and η values. Domain A is flow instability regimes occurring at all temperatures and the strain rate of 3–10 s⁻¹, and the value of η is below 0.30. As manifested in Fig. 12a, it is easy to observe that flow localization occurs at the temperature of 950 °C and the strain rate of 10 s⁻¹. Some researchers have proved that when the material is deformed at high strain rates, the flow localization can be caused by localized slip due to the adiabatic temperature rise in various materials [1, 7, 10]. Furthermore, due to the deformation process being less than 0.1 s at the strain rate of 10 s⁻¹, there is no sufficient time for nucleation and grain growth. Domain B is safe regimes with a high η value of 0.30–0.50 at the temperature of 950–1150 °C and the strain rate of 0.05–3 s⁻¹. Previous reports have demonstrated that when the η value was between 0.30 and 0.50, DRX probably occurred for steel [8, 23, 24]. η values in this domain are just within the range above, revealing that DRX takes place when the studied steel is deformed under these conditions. Figure 12b presents the microstructure at the temperature of 1000 °C and the strain rate of 0.1 s⁻¹ with η value of 0.35, in which DRX deformed and grown grains coexist, which indicates that recrystallization was not complete. In contrast, homogeneous and equiaxed grains can be obtained at the temperature of 1150 °C and the strain rate of 1 s⁻¹ with higher η value of 0.40, as shown in Fig. 12c. Therefore, it can be inferred that the energy dissipation efficiency should be over 0.40 to obtain a homogeneous recrystallization structure for 30Si2MnCrMoVE UHSS. Domain C is regimes at the low strain rates with a low energy dissipation lower than 0.30, which indicates that it is not very suitable for the studied steel to deform under these conditions. It is worth noting that there is an instability area at the temperature of 1075–1150 °C and at the strain rate of 0.01–0.03 s⁻¹ with η value lower than 0.10. As shown in Fig. 12d, in the field of view, almost all the recrystallized grains are grown and coarsened, which could be ascribed to the low nucleation rate and promoted grain growth at high temperatures and low strain rates.

Fig. 12

Optical microstructure of studied steel deformed at a strain of 0.90. a 950 °C, 10 s⁻¹; b 1000 °C, 0.1 s⁻¹; c 1150 °C, 1 s⁻¹; d 1150 °C, 0.01 s⁻¹

According to the above analysis, for 30Si2MnCrMoVE UHSS, at the strain of 0.90, the hot deformation can be safely carried out at the temperature of 950–1150 °C and the strain rate of 0.05–3 s⁻¹. However, ideal uniform equiaxed recrystallized grains cannot be obtained by deformation under all these parameters. In order to obtain uniform equiaxed grains, the recommended optimum parameter is 1150 °C/10^−0.5 (~ 0.3) s⁻¹ with η value as high as 0.47.

In order to verify the optimum parameter based on processing map, another experiment was carried out at the temperature of 1150 °C and the strain rate of 0.3 s⁻¹. The low stress curve and optical microstructure are shown in Fig. 13a, b, respectively. The deformation mechanism is DRV + DRX type, which is similar to that at the strain rate of 0.01 and 0.1 s⁻¹, and the grains are homogeneous and equiaxed.

Fig. 13

Flow stress curve of 1150 °C, 0.3 s⁻¹ (a) and optical microstructure at strain of 0.90 (b)

3.3.3 Processing map at different strains

As described in Sect. 3.1, with the increase in strain, the variation in stress versus strain is changing, which can be attributed to different deformation mechanisms. And many researchers have demonstrated that the strain has a significant impact on the processing maps [21, 25]. Therefore, it is necessary to construct processing maps at different strains. As is shown in Fig. 14, the power dissipation maps of 30Si2MnCrMoVE UHSS at true strains of 0.05–0.90 at intervals of 0.05, total of 18 maps, were constructed. The contour numbers display the value of η as percentage, and the green regions correspond to 0.30 < η < 0.40, the yellow regions correspond to 0.40 < η < 0.50, the red regions correspond to 0.50 < η < 0.60, and the white regions correspond to η < 0.30. When strain is below 0.2, the green regions are mainly concentrated at the temperature of 975–1150 °C and the strain rate of 0.01–0.03 s⁻¹. With the strain increasing from 0.2 to 0.4, the green region expands and moves toward the regions of low temperature and high strain rate, during which process a yellow region appears at 1050–1150 °C/0.01 s⁻¹ when the strain is 0.25 and a red region appears at 1050–1100 °C/0.01 s⁻¹ when the strain is 0.35. Therefore, when the strain is small, in order to ensure high power dissipation efficiency, the medium/high temperature and low strain rate can be chosen for hot deformation for the studied steel. At the strain of 0.4, the green and yellow regions continue to move toward regions of low temperature and high strain and the yellow regions at 1050–1150 °C/0.01 s⁻¹ start to shrink until the complete disappearance at the strain of 0.7. When the strain is reaching 0.45, another yellow region appears at 1150 °C/0.1 s⁻¹ and a low power dissipation region (η < 0.3) appears at 1150 °C/0.01 s⁻¹, both of which expand with the increase in strain. At the strain of 0.55, the third yellow region appears at 950 °C/0.01 s⁻¹, which expands with the increasing strain. When the strain is 0.90, the yellow region is located at 975–1150 °C/0.1–1 s⁻¹ and 950 °C/0.01–0.1 s⁻¹ and low power dissipation efficiency (η < 0.3) and the low energy dissipation rate regions occupy most of the high strain rate and low strain rate domains.

Fig. 14

Power dissipation efficiency maps of 30Si2MnCrMoVE UHSS at strain of 0.05–0.90. Contour numbers display value of η as percentage

Figure 15 displays the power dissipation efficiency versus strain from 0.05 to 0.90 under the condition of 950 °C/10 s⁻¹, 1050 °C/0.01 s⁻¹ and 1150 °C/0.3 s⁻¹. Under different deformation conditions, the power dissipation efficiency varies differently with the strain. The power dissipation efficiency remains low (η < 0.3) or decreases slightly with the increase in strain under the condition of 950 °C/10 s⁻¹. The power dissipation efficiency first increases and decreases sharply at the strain of 0.4 under the condition of 1050 °C/10 s⁻¹, and the mechanism needs to be further investigated in future. The power dissipation efficiency increases monotonously with strain under the condition of 1150 °C/0.3 s⁻¹, and there is an upward trend when strain is 0.90. Therefore, the recommended process parameter is 1150 °C/0.3 s⁻¹.

Fig. 15

Power dissipation efficiency versus strain of 30Si2MnCrMoVE UHSS under condition of 950 °C/10 s⁻¹, 1050 °C/0.01 s⁻¹ and 1150 °C/0.3 s⁻¹

Figure 16 shows the instability maps of 30Si2MnCrMoVE UHSS at true strains of 0.05–0.90. When the strain is 0.05, the instability region is located at 1000–1100 °C/0.03–1 s⁻¹, which decreases gradually with the increase in strain until disappearing at the strain of 0.4. This may be ascribed to the high DRX activation energy at the strain below 0.4 under these conditions. At the same time, a new instability region appears at the high strain rate at the strain of 0.3 and gradually enlarges with strain increasing. Another instability region appears at high temperature and low strain rate and extends to low temperature region. The microstructure of the instability regions is shown in Fig. 12a, d, which exhibits flow instability at 950 °C/10 s⁻¹ and coarse austenite grains at 1150 °C/0.01 s⁻¹.

Fig. 16

Instability maps of 30Si2MnCrMoVE UHSS at strain of 0.05–0.90. Blue regimes represent instability (ξ < 0)

4 Conclusions

• 1. The constitutive model can accurately predict the flow stress of the work hardening dynamic recovery period and dynamic recrystallization period for 30Si2MnCrMoVE UHSS.

• 2. According to the processing map and microstructure observation at the strain of 0.90, the hot deformation of 30Si2MnCrMoVE UHSS could be safely carried out at the temperature of 950–1150 °C and the strain rate of 0.05–3 s⁻¹. In order to obtain uniform equiaxed grains, η value should be over 0.4 and the recommended optimum parameter is 1150 °C/0.3 s⁻¹ with a η value as high as 0.47.

• 3. The strain has a significant impact on the processing maps, and under different deformation conditions, the power dissipation efficiency varies differently with the strain. The instability regimes should be avoided and the parameters with high power dissipation efficiency should be selected when working out the hot working process for 30Si2MnCrMoVE UHSS.