Efficient path algorithms for clustered Lasso and OSCAR

Abstract

In high dimensional regression, clustering features according to their effects on outcomes is often as important as feature selection. For example, insurance premiums are set for each rate class pertaining to risk factors related to claim risk. To calculate reliable insurance premiums, it is often necessary to group the numerous rate classes into fewer classes. However, the combinations of ways to consolidate rate classes are vast, and it is computationally challenging to consider each combination individually. Under such circumstances, sparse regularization techniques for feature clustering are extremely useful as methods that automatically consolidate rate classes with no significant differences in risk levels during the estimation process. For this purpose, clustered Lasso and octagonal shrinkage and clustering algorithm for regression (OSCAR) can be used to generate feature groups automatically using pairwise $L_1$ norm and pairwise $L_\infty$ norm, respectively. This paper proposes efficient path algorithms for clustered Lasso and OSCAR to construct solution paths with respect to their regularization parameters. Despite the excessive terms in exhaustive pairwise regularization, their computational costs are reduced by using the symmetry of those terms. Simple equivalent conditions to check subgradient equations in each feature group are derived using the graph theory. The proposed algorithms are shown to be more efficient than existing algorithms via numerical experiments.

1 Introduction

With the recently increasing prevalence of high-dimensional data in many fields, feature selection and clustering have become increasingly important. For example, premium tariffs have long been used to reference general insurance premiums according to insured’s attribute information. In tariffs, the premium is referenced from the combination of classes to which factors related to insurance risks, such as the insured’s occupation for workers’ compensation insurance, belong. However, some factors, such as the insured’s occupation, age and address, often have too many categories to obtain reliable estimates for their individual categories. In such cases, rating categories are often grouped into fewer categories which have similar risk levels in practice. The grouping of rate categories simplifies the tariff, which reduces administrative risk on misapplication of premiums. Some sparse regularization techniques such as Lasso (Tibshirani, 1996) and its variants (Tibshirani et al., 2005) can be used to provide a simple and reliable tariff with grouped rating classes (Devriendt et al., 2021; Fujita et al., 2020).

This paper focuses on two types of feature-clustering regularization without any prior information on feature groups. One type is clustered Lasso (She, 2010), formulated by

$$\begin{aligned} \mathop {\mathrm {\text {minimize} \quad }}\limits _{\beta }\ \ \frac{1}{2} \left\| y-X\beta \right\| ^2 +\lambda _1 \sum _{i=1}^{p} | \beta _i | + \lambda _2 \sum _{j<k} \left| \beta _j - \beta _k \right| , \end{aligned}$$

(1)

where $y \in \mathbb {R}^n$ is a response vector, $X \in \mathbb {R}^{n\times p}$ is a design matrix, $\beta \in \mathbb {R}^p$ is a coefficient vector and $\lambda _{1}, \lambda _{2}$ are regularization parameters. The last term enforces coefficients to be similar or equal. The other type is octagonal shrinkage and clustering algorithm for regression (OSCAR) (Bondell & Reich, 2008), defined by

$$\begin{aligned} \mathop {\mathrm {\text {minimize} \quad }}\limits _{\beta }\ \ \frac{1}{2} \left\| y-X\beta \right\| ^2 + \lambda _1 \sum _{i=1}^{p} | \beta _i | + \lambda _2 \sum _{j<k} \max \left\{ | \beta _j |, | \beta _k | \right\} , \end{aligned}$$

(2)

where the pairwise $L_{\infty }$ norm encourages absolute values of highly correlated coefficients to be zero or equal. Note that the pairwise $L_{\infty }$ norm in (2) can be converted into the $L_1$ norm as $\max \left\{ | \beta _j |, | \beta _k | \right\} = (| \beta _j- \beta _k | + | \beta _j + \beta _k |)/2$; thus OSCAR and clustered Lasso can be regarded as special cases of generalized Lasso (Tibshirani & Taylor, 2011).

Fast methods to obtain a solution of coefficients $\beta$ with discrete points of $[\lambda _{1}, \lambda _{2}]$ have been developed for clustered Lasso (Lin et al., 2019) and OSCAR (Bao et al., 2020; Bogdan et al., 2015; Luo et al., 2019; Zhong & Kwok, 2012), and generalized Lasso (Gong et al., 2017; Xin et al., 2014) including them. However, on tuning the regularization parameters, a solution path of $\beta$ in a continuous range of $[\lambda _{1}, \lambda _{2}]$ is preferable over a grid search on discrete values of $[\lambda _{1}, \lambda _{2}]$. Algorithms to obtain such solution paths are called path algorithms and have been proposed for more general settings (Arnold & Tibshirani, 2016; Tibshirani & Taylor, 2011; Zhou & Lange, 2013) than clustered Lasso and OSCAR. However, because of $m = p(p-1)/2$ pairwise regularization terms in (1) and (2), applying those algorithms to clustered Lasso and OSCAR require excessive computational costs of the order of $\mathcal {O}(mn^2 + T m^2) = \mathcal {O}(p^2n^2 + T p^4)$ if $m\le n$ and otherwise $\mathcal {O}(m^2n + T n^2) = \mathcal {O}(p^4n + T n^2)$, where T is the number of iterations in the algorithms (see Section 8 of Tibshirani & Taylor, 2011). In some special cases where, say, $X=I_p$ and $\lambda _1=0$, the solution path becomes simple and can be obtained fast because the coefficients only merge in turn as $\lambda _2$ increases (Hocking et al., 2011). Those cases can be extended to the weighted clustered Lasso with distance-decreasing weights (Chiquet et al., 2017). An efficient path algorithm that obtains an approximate solution path with an arbitrary accuracy bound around a starting point has been proposed for OSCAR with a general design matrix (Gu et al., 2017).

In this article, we propose novel path algorithms for clustered Lasso and OSCAR with a general design matrix. The proposed algorithms can construct entire exact solution paths much faster than the existing ones can. The solution paths in clustered Lasso and OSCAR have two types of breakpoints; one is the fusing events in which some coefficients merge to form a new group, sharing the same coefficient values in the optimal solution. The other is the splitting event in which a coefficient group made by fusing events splits into the smaller groups with different coefficient values. To specify the occurrence times of those events in an efficient way, we derived equivalent simple optimality conditions of the solution from subgradient equations involving $\mathcal {O}(p^2)$ subgradients of the regularization terms. Because the derived optimality conditions involve only $\mathcal {O}(p)$ inequalities, the occurrence time of the next event can be specified in only $\mathcal {O}(np)$ time, which is significantly less than those of the existing algorithms solving optimization problems with $\mathcal {O}(p^2)$ constraints. We demonstrate the computational efficiency and accuracy of the proposed algorithm in numerical experience. Moreover, the proposed methods were applied to the real datasets including the automobile insurance claim datasets in Brazil.

2 Path algorithm for clustered Lasso

In this section, we propose a solution path algorithm for clustered Lasso (1) that yields a solution path $\beta (\eta )$ along regularization parameters $[\lambda _{1}, \lambda _{2}] = \eta [\bar{\lambda }_1, \bar{\lambda }_2]$ controlled by a single parameter $\eta > 0$ with a fixed direction $[\bar{\lambda }_1, \bar{\lambda }_2]$. Hereafter, we assume $n\ge p$ and ${\text {rank}}\left( X \right) = p$ to ensure that the objective function (1) is strictly convex. Otherwise, the solution path may not be unique and continuous, making it difficult to track. In such a case, a ridge penalty term $\varepsilon \left\| \beta \right\| ^2$ with a tiny weight $\varepsilon$ can be added to (1), which is equivalent to extending the response vector y and design matrix X into $y^* = [y^{\top },$ ${\textbf {0}}$$_p^{\top }]^{\top }$ and $X^* = [X^{\top },\sqrt{\varepsilon } I_p]^{\top }$ to make the problem strictly convex (Arnold & Tibshirani, 2016; Gaines et al., 2018; Hu et al., 2015; Tibshirani & Taylor, 2011).

In (1), the regularization terms encourage the coefficients to be zero or equal. Thus, from the solution $\beta (\eta )$ for a fixed regularization parameter $\eta > 0$, we define the set of fused groups ${\mathcal {G}}(\eta ) = \{G_{\underline{g}}, G_{\underline{g}+1}, \dots , G_{\overline{g}}\}$ and grouped coefficients $\beta ^{\mathcal {G}}(\eta ) = [\beta ^{\mathcal {G}}_{\underline{g}}, \beta ^{\mathcal {G}}_{\underline{g}+1},\dots ,\beta ^{\mathcal {G}}_{\overline{g}}]^\top \in \mathbb {R}^{\overline{g}-\underline{g}+1}$ to satisfy the following statements:

• $\bigcup _{g=\underline{g}}^{\overline{g}} G_g = \left\{ 1, \ldots , p \right\}$, where $G_0$ may be an empty set but others may not.

• $\beta ^{\mathcal {G}}_{\underline{g}}<\cdots< \beta ^{\mathcal {G}}_{-1}< \beta ^{\mathcal {G}}_0 = 0< \beta ^{\mathcal {G}}_1< \cdots < \beta ^{\mathcal {G}}_{\overline{g}}$ and $\beta _i = \beta ^{\mathcal {G}}_g$ for $i\in G_g$.

From this definition, $\underline{g}$ and $\overline{g}$ represent the numbers of groups with negative and positive grouped coefficients, respectively. Note that $\underline{g}\le 0 \le \overline{g}$ because the group $G_0$ exists as an empty set, even if no zeros exist in the entries of $\beta (\eta )$. Correspondingly, we introduce the grouped design matrix $X^{\mathcal {G}}= [x^{\mathcal {G}}_{\underline{g}}, x^{\mathcal {G}}_{\underline{g}+1},\dots ,x^{\mathcal {G}}_{\overline{g}}] \in \mathbb {R}^{n\times (\overline{g}-\underline{g}+1)}$, where $x^{\mathcal {G}}_g = \sum _{j \in G_g} x_j$ and $x_j$ is the j-th column vector of X.

2.1 Piecewise linearity

Because the objective function of (1) is strictly convex, its solution path would be a continuous piecewise linear function (Hoefling, 2010; Tibshirani & Taylor, 2011). Specifically, as long as the signs and order of the solution $\beta (\eta )$ are conserved as in the set ${\mathcal {G}}$ of fused groups defined above, the problem (1) can be reduced to the following quadratic programming problem:

$$\begin{aligned} \mathop {\mathrm {\text {minimize} \quad }}\limits _{\beta }\ \ \frac{1}{2} \left\| y - X^{\mathcal {G}}\beta ^{\mathcal {G}} \right\| ^2 + \eta \bar{\lambda }_1 \sum _{g=\underline{g}}^{\overline{g}} p_g {\text {sign}} ( \beta ^{\mathcal {G}}_g ) \beta ^{\mathcal {G}}_g + \eta \bar{\lambda }_2 \sum _{g=\underline{g}}^{\overline{g}} p_g r_g \beta ^{\mathcal {G}}_g, \end{aligned}$$

where $p_g$ is the cardinality of $G_g$, $q_g = p_{\underline{g}} + \cdots + p_{g-1}$ is the number of coefficients smaller than $\beta ^{\mathcal {G}}_g$, and $r_g = q_g - (p - q_{g+1})$. Hence, because $\beta ^{\mathcal {G}}_0$ is fixed at zero, the nonzero elements of the grouped coefficients $\beta ^{\mathcal {G}}_{-0}(\eta )= [\beta ^{\mathcal {G}}_{\underline{g}},\dots ,\beta ^{\mathcal {G}}_{-1},\beta ^{\mathcal {G}}_1,\dots ,\beta ^{\mathcal {G}}_{\overline{g}}]^\top$ are obtained by

$$\begin{aligned} \beta ^{\mathcal {G}}_{-0}(\eta ) = \left[ \left( X^{\mathcal {G}}_{-0} \right) ^\top X^{\mathcal {G}}_{-0} \right] ^{-1} \left[ \eta a +\left( X^{\mathcal {G}}_{-0} \right) ^\top y \right] , \end{aligned}$$

(3)

where $X^{\mathcal {G}}_{-0}= [x^{\mathcal {G}}_{\underline{g}},\dots ,x^{\mathcal {G}}_{-1},x^{\mathcal {G}}_1,\dots ,x^{\mathcal {G}}_{\overline{g}}]$ and $a = [a_{\underline{g}},\dots ,a_{-1},a_1,\dots ,a_{\overline{g}}]^\top \in \mathbb {R}^{\overline{g}-\underline{g}}$, $a_g = -\bar{\lambda }_1 p_g {\text {sign}} ( \beta ^{\mathcal {G}}_g ) - \bar{\lambda }_2 p_g r_g$. Thus, the solution path $\beta (\eta )$ moves linearly along $\beta ^{\mathcal {G}}(\eta )$ as defined above until the set ${\mathcal {G}}$ of fused groups changes.

2.2 Optimality condition

In this subsection, we show the optimality conditions of (1) and then derive a theorem to check them efficiently. Owing to $L_1$ norms, the optimality condition involves their subgradients as follows:

$$\begin{aligned} x_i^\top \left( X^{\mathcal {G}}\beta ^{\mathcal {G}}- y \right) + \tau _{i0} + \lambda _2 r_g + \sum _{j \in G_g \setminus \left\{ i \right\} } \tau _{ij} = 0, \qquad i \in G_g, \end{aligned}$$

(4)

where $\tau _{i0} \in [-\lambda _1,\lambda _1]$ is a subgradient of $\lambda _1 \left| \beta _i \right|$ which takes $\lambda _1 {\text {sign}} ( \beta ^{\mathcal {G}}_g )$ if $\beta ^{\mathcal {G}}_g \ne 0$, and $\tau _{ij} \in [-\lambda _2,\lambda _2] \; (i\ne j,\; i,j\in G_g)$ is subject to the constraint $\tau _{ij} = -\tau _{ji}$, which implies that $\tau _{ij}$ is a subgradient of $\lambda _2 \left| \beta _i - \beta _j \right|$ with respect to $\beta _i$ when $\beta _i = \beta _j$ (Hoefling, 2010). For an overview of subgradients, see  Bertsekas (1999).

Although it is not straightforward to check the optimality conditions including subgradients, we can derive their equivalent conditions, which are easier to verify. For the group $G_0$ of zeros, if we assume $m=p_0\ge 1$ and denote the sorted values of $x_i^\top (X^{\mathcal {G}}\beta ^{\mathcal {G}}- y) + \lambda _2 r_g$ over $i \in G_0$ by $f_1 \ge f_2 \ge \cdots \ge f_m$, we can propose the following theorem to check condition (4).

Theorem 1

There exist $\tau _{i0} \in \left[ -\lambda _1, \lambda _1 \right]$ and $\tau _{ij} = -\tau _{ji} \in \left[ -\lambda _2, \lambda _2 \right]$ such that

$$\begin{aligned} f_i + \tau _{i0} + \sum _{j \in \{1,\dots ,m\} \setminus \left\{ i \right\} }\tau _{ij} =0, \qquad i=1,\dots ,m, \end{aligned}$$

(5)

if and only if

$$\begin{aligned} \sum _{j=1}^{k} f_j&\le \lambda _1 k + \lambda _2k(m-k), \quad&k=1,\dots , m, \end{aligned}$$

(6)

and

$$\begin{aligned} \sum _{j=k+1}^{m} f_j&\ge -\lambda _1 (m-k) - \lambda _2 k(m-k), \quad&k=0,\dots , m-1. \end{aligned}$$

(7)

This theorem can reduce the optimality condition (4) into some inequalities which can be easily checked. The necessity of conditions (6) and (7) can be easily verified by summing Eq. (5) over $j=1,\dots ,k$ and $j=k+1,\dots ,m$, respectively, and bounding $\tau$s by $\tau _{i0} \in \left[ -\lambda _1, \lambda _1 \right]$ and $\tau _{ij} \in \left[ -\lambda _2, \lambda _2 \right]$, whereas proving the sufficiency of these conditions is not trivial. The proof of this theorem is provided in Appendix A. In the following subsection, we describe key ideas of the proof and introduce a relevant lemma.

For a nonzero group $G_g$, let $m=p_g$ and let $f_1 \ge f_2 \ge \cdots \ge f_m$ denote the sorted values of $x_i^\top (X^{\mathcal {G}}\beta ^{\mathcal {G}}- y) + \lambda _{1} {\text {sign}} ( \beta ^{\mathcal {G}}_g ) + \lambda _2 r_g$ over $i \in G_g$. Then, the following corollary of Theorem 1, which is derived by fixing $\lambda _1$ at zero, can be used to check optimality condition (4).

Corollary 1

There exist $\tau _{ij} = -\tau _{ji} \in \left[ -\lambda _2, \lambda _2 \right]$ such that

$$\begin{aligned} f_i + \sum _{j \in \{1,\dots ,m\} \setminus \left\{ i \right\} }\tau _{ij} =0, \qquad i=1,\dots ,m, \end{aligned}$$

(8)

if and only if

$$\begin{aligned} \sum _{j=1}^{k} f_j \le \lambda _2 k(m-k), \quad k=1,\dots ,m-1, \end{aligned}$$

(9)

and $\sum _{j=1}^{m} f_j = 0$.

2.3 Equivalent network flow problems for subgradient equations

This subsection provides key ideas to prove the Theorem 1. Some types of computations that appear in structured sparse models can be reduced to network flow problems (Hoefling, 2010; Jung, 2020; Mairal & Yu, 2013; Mairal et al., 2011; Xin et al., 2014), to which efficient algorithms are applicable. The main idea of our study is based on Theorem 2 in Hoefling (2010), which states that subgradient equations in a fused Lasso signal approximator (i.e. X is an identical matrix) without Lasso terms (i.e. $\lambda _1=0$) can be checked through a maximum flow problem on the underlying graph whose edges correspond to the pairwise fused Lasso penalties.

We extend the approach of Hoefling (2010) to the weighted clustered Lasso problem; this is formulated as

$$\begin{aligned} \mathop {\mathrm {\text {minimize} \quad }}\limits _{\beta }\ \ \frac{1}{2} \left\| y-X\beta \right\| ^2 + \sum _{i=1}^{p} \lambda _{i,0} | \beta _i | + \sum _{j<k} \lambda _{j,k} \left| \beta _j - \beta _k \right| . \end{aligned}$$

To demonstrate its equivalence to a maximum flow problem, we introduce the flow network $G=\{(V,E),c,r,s\}$ defined as follows:

Vertices::

Define the vertices by $V = \{0,1,\dots ,m\} \cup \{r,s\}$ where r and s are called the source and the sink, respectively.

Edges::

Define the edges by $E = \left\{ (i,j); i,j\in V, i\ne j \right\} \setminus \left\{ (r,s),(s,r) \right\}$, that is, all the pairs of vertices except for the pair of the source and sink are connected.

Capacities::

A flow network is a graph (V, E) attached with flows over respective edges. Each edge has a non-negative capacity, and the flow over the edge cannot exceed its capacity. Here, we define the capacities on the edges in E as

$$\begin{aligned} c(r,i)&= f_i^{-},\; c(i,r) = 0,&i = 0,\dots ,m, \\ c(i,s)&= f_i^{+},\; c(s,i) = 0,&i = 0,\dots ,m, \\ c(i,0)&= c(0,i) = \lambda _{i0},&i = 1,\dots ,m, \\ c(i,j)&= c(j,i) = \lambda _{ij},&1 \le i < j \le m, \end{aligned}$$

where $f_0 = -\sum _{j=1}^m f_j$, $f_i^{-} = \max \left\{ -f_i,0 \right\}$ and $f_i^{+} = \max \left\{ f_i,0 \right\}$. Note that $f_i = f_i^{+}-f_i^{-}$; therefore, $\sum _{j=0}^m f_j^{+} - \sum _{j=0}^m f_j^{-} = \sum _{j=0}^m f_j = 0$.

A flow on the flow network $G=\{(V,E),c,r,s\}$ is a set of values $\tau = \{ \tau _{ij};(i,j)\in E \}$ satisfying the following three properties:

Skew symmetry::

$\tau _{ij} = -\tau _{ji}$ for $(i,j) \in E$,

Capacity constraint::

$\tau _{ij} \le c(i,j)$ for $(i,j) \in E$,

Flow conservation::

$\sum _{j; (i,j) \in E} \tau _{ij} = 0$ for $i \in V\setminus \{r,s\}$.

From this definition, we can observe the equivalence of the flows between the vertices $\{0,1,\dots ,m\}$ with the subgradients of the regularization terms. Specifically, the flow $\tau _{ij}$ for $i,j \in \{1,\dots ,m\}$ is defined equivalently with the subgradient of $\lambda _{i,j} \left| \beta _i - \beta _j \right|$. The flow $\tau _{i0}$ for $i \in \{1,\dots ,m\}$ is also defined equivalently with the subgradient of $\lambda _{i,0} | \beta _i |$.

The value $| \tau |$ of a flow $\tau$ through r to s is the net flow out of the source r or that into the sink s formulated as follows:

$$\begin{aligned} | \tau | = \sum _{i; (r,i) \in E} \tau _{ri} = \sum _{i; (i,s) \in E} \tau _{is}, \end{aligned}$$

where the last equality holds from the flow conservation. The maximum flow problem on $G=\{(V,E),c,r,s\}$ is a problem to find the flow that attains the maximum value $\max _\tau | \tau |$, called the maximum flow. For an overview of the theory of the maximum flow problems, see e.g. Tarjan (1983).

Then, we obtain the following lemma relating the condition (5) to the maximum flow problem on $G=\{(V,E),c,r,s\}$.

Lemma 1

There exist $\tau _{i0} \in \left[ -\lambda _{i0}, \lambda _{i0} \right]$ and $\tau _{ij} = -\tau _{ji} \in \left[ -\lambda _{ij}, \lambda _{ij} \right]$ such that

$$\begin{aligned} f_i + \tau _{i0} + \sum _{j \in \{1,\dots ,m\} \setminus \left\{ i \right\} }\tau _{ij} =0, \qquad i=1,\dots ,m, \end{aligned}$$

(10)

if and only if the maximum value of a flow through r to s on $G=\{(V,E),c,r,s\}$ is $\sum _{i=0}^m f_i^{+} = \sum _{i=0}^m f_i^{-}$.

The proof of this lemma is given in Appendix A.

The Eq. (10) appears in subgradient equation within a fused group for the weighted clustered Lasso problem with penalty terms $\sum _{i=1}^m \lambda _{i0}|\beta _i| + \sum _{1 \le i < j \le m} \lambda _{ij}|\beta _i-\beta _j|$. Therefore, we can use Lemma 1 to check the subgradient equation by seeking the maximum flow on the corresponding flow network.

While it is generally difficult to find when the subgradient equations in the weighted clustered Lasso problem are violated as the regularization parameters grow, we can provide explicit conditions to check the violation of (5) for the ordinary clustered Lasso problem as in Theorem 1 by using the max-flow min-cut theorem. Here we consider the minimum cut problem on the flow network $G=\{(V,E),c,r,s\}$ where $\lambda _{i0} = \lambda _1$ and $\lambda _{ij}=\lambda _2$ for all $i\ne j \in \{1,\dots ,m\}$. A cut of the graph is a partition of the vertex set V into two parts $V_r$ and $V_s = V {\setminus } V_r$ such that $r\in V_r$ and $s\in V_s$. Then, the capacity of the cut is defined by the sum of capacities on edges $(i,j)\in E$ such that $i\in V_r$ and $j\in V_s$. The max-flow min-cut theorem (see e.g. Tarjan, 1983), states that the maximum value of a flow through r to s on $G=\{(V,E),c,r,s\}$ is equal to the minimum capacity of a cut of the same graph. Because the capacity of the cut attains $\sum _{i=0}^m f_i^{+} = \sum _{i=0}^m f_i^{-}$ for $V_r = \{r\},V_s = V{\setminus } \{r\}$ and $V_r=V{\setminus } \{s\},V_s=\{s\}$, the minimum capacity of a cut is at least $\sum _{i=0}^m f_i^{+} = \sum _{i=0}^m f_i^{-}$. Thus, from that theorem and Lemma 1, it suffices to prove that any other cuts have capacities not smaller than $\sum _{i=0}^m f_i^{+} = \sum _{i=0}^m f_i^{-}$ if and only if (6) and (7) hold.

Because all the pairs of the vertices in $\{1,\dots ,m \}$ are connected by edges with the same capacity, the capacity of a cut within those edges depends only on the numbers of the vertices $\{1,\dots ,m \}$ belonging to $V_s$ and $V_r$, respectively. With those numbers fixed at k and $m-k$, the capacity of a cut is minimized when $1,\dots ,k \in V_s$ selected by the descending order of capacities $f_1^+\ge f_2^+ \ge \cdots \ge f_m^+$ of the edges connecting to the sink node s, and $k+1,\dots ,m \in V_r$ selected by the descending order of capacities $f_m^-\ge f_{m-1}^- \ge \cdots \ge f_1^-$ of the edges connecting to the source node r. Then, evaluating the capacity of a cut in the cases $0 \in V_r$ and $0 \in V_s$ yields inequalities (6) and (7), respectively. For the detail of the proof, see Appendix A.

2.4 Events in path algorithm

In this subsection, we specify the events and their occurrence times in our path algorithm, whose outline is presented in Sect. 4. In the context of path algorithm, we define three types of events that influence the set ${\mathcal {G}}$ of fused groups: The first type is the fusing event, in which adjacent groups are fused when their coefficients collide. The second type is the splitting event, in which a group is split into smaller groups satisfying the optimality condition within each group when the condition is violated within the group. The last type is the switching event, in which the order of the partial derivative of the square-error term $\frac{1}{2} \left\| y-X\beta \right\| ^2$ for the coefficients within a group changes. Although the last one does not change the grouping of the coefficients, it affects the order of the coefficients in applying Theorem 1 and Corollary 1 to check the optimal condition.

Events in the path algorithm refer to moments when the optimality conditions (4) and the condition of $\beta$ being sorted in ascending order are violated. To denote the time of the last occurring event as $\eta$, we define the occurrence time of the next event as $\eta + \Delta$. This occurrence time is the minimum of the possible times for the fusing, splitting, and switching events, denoted respectively as $\eta + \Delta _g^{\text {fuse}}, \eta +\Delta _g^{\text {split}}$, and $\eta +\Delta _g^{\text {switch}}$. This section explains the methods for calculating the occurrence times of these events.

First, the occurrence time of the fusing event can be detected by following the changes in grouped coefficients according to (3) with their slopes $\frac{\textrm{d}\beta ^{\mathcal {G}}_{-0}}{\textrm{d}\eta } = [(X^{\mathcal {G}}_{-0})^{\top } X^{\mathcal {G}}_{-0}]^{-1}a$ for nonzero groups and $\frac{\textrm{d}\beta ^{\mathcal {G}}_{0}}{\textrm{d}\eta }= 0$ for $G_0$. If $\frac{\textrm{d}\beta ^{\mathcal {G}}_{g}}{\textrm{d}\eta } > \frac{\textrm{d}\beta ^{\mathcal {G}}_{g+1}}{\textrm{d}\eta }$, the coefficients of two adjacent groups $G_g$ and $G_{g+1}$ approach at a rate of $\frac{\textrm{d}\beta ^{\mathcal {G}}_{g}}{\textrm{d}\eta } - \frac{\textrm{d}\beta ^{\mathcal {G}}_{g+1}}{\textrm{d}\eta }$. Therefore, the gap of grouped coefficients, which is $\beta ^{\mathcal {G}}_{g+1}(\eta ) - \beta ^{\mathcal {G}}_{g}(\eta )$ at time $\eta$, shrinks to zero at time $\eta + \Delta ^{\text {fuse}}_g$, where

$$\begin{aligned} \Delta ^{\text {fuse}}_g = {\left\{ \begin{array}{ll} \frac{-\beta ^{\mathcal {G}}_{g+1}(\eta ) + \beta ^{\mathcal {G}}_{g}(\eta )}{\frac{\textrm{d}\beta ^{\mathcal {G}}_{g+1}}{\textrm{d}\eta } - \frac{\textrm{d}\beta ^{\mathcal {G}}_{g}}{\textrm{d}\eta }} & \quad \text {if} \frac{\textrm{d}\beta ^{\mathcal {G}}_{g+1}}{\textrm{d}\eta } < \frac{\textrm{d}\beta ^{\mathcal {G}}_{g}}{\textrm{d}\eta }, \\ \displaystyle \infty & \quad \text {otherwise}, \end{array}\right. } \end{aligned}$$

unless any other event occurs. At this time, the groups $G_g$ and $G_{g+1}$ have the same coefficients and, hence, have to be fused into one group. Note that, if $\frac{\textrm{d}\beta ^{\mathcal {G}}_{g}}{\textrm{d}\eta } \le \frac{\textrm{d}\beta ^{\mathcal {G}}_{g+1}}{\textrm{d}\eta }$, the adjacent groups $G_g$ and $G_{g+1}$ will never be fused at that rate, which is represented by $\Delta ^{\text {fuse}}_g = \infty$.

Next, the occurrence time of the splitting event on the group $G_g$ can be specified by the timing at which the optimality condition (4) gets violated. Let $o(j) \in \{1,\dots ,p\}$ denote the order of coefficients such that $G_g = \{ o(q_g+1),\dots ,o(q_{g+1}) \}$ and $x_{o(q_g+1)}^\top (X^{\mathcal {G}}\beta ^{\mathcal {G}}- y) \ge \cdots \ge x_{o(q_{g+1})}^\top (X^{\mathcal {G}}\beta ^{\mathcal {G}}- y)$. As $x_{i}^\top (X^{\mathcal {G}}\beta ^{\mathcal {G}}- y)$ is the partial derivative of the square error term $\frac{1}{2} \left\| y-X\beta \right\| ^2$ with respect to $\beta _i$, this ordering represents the order of the partial derivatives among the coefficients in a group. When a group is split into two groups, one group is composed of the coefficients with the larger partial derivatives than those in the other group and thus its grouped coefficient moves below that of the other group. Then, we can use Theorem 1 for $G_0$ and Corollary 1 for each nonzero group to check the optimality conditions.

From Corollary 1 with $m=p_g$ and $f_i = x_{o(q_g+i)}^\top (X^{\mathcal {G}}\beta ^{\mathcal {G}}- y) + \lambda _{1} {\text {sign}} ( \beta ^{\mathcal {G}}_g ) + \lambda _2 r_g$, the optimality condition (4) in a nonzero group $G_g$ holds if and only if

$$\begin{aligned} \sum _{j=1}^{k} f_j= & x_{\underline{o}(g,k)}^\top \left( X^{\mathcal {G}}\beta ^{\mathcal {G}}- y \right) + \lambda _{1} k {\text {sign}} ( \beta ^{\mathcal {G}}_g ) + \lambda _2 k r_g \le \lambda _2 k(p_g-k), \nonumber \\ & \quad k=1,\dots , p_g, \end{aligned}$$

(11)

where $x_{\underline{o}(g,k)} = \sum _{j=q_g+1}^{q_g+k} x_{o(j)}$. Because $[\lambda _{1}, \lambda _{2}] = \eta [\bar{\lambda }_1, \bar{\lambda }_2]$, the difference between the left and right sides of the inequality (11) changes at a rate of $\sigma (g, k)$, where

$$\begin{aligned} \sigma (g, k)= & \frac{\textrm{d}}{\textrm{d}\eta }\left[ \sum _{j=1}^{k} f_j - \lambda _2 k(p_g-k)\right] \\= & x_{\underline{o}(g,k)}^\top X^{\mathcal {G}}\frac{\textrm{d}\beta ^{\mathcal {G}}}{\textrm{d}\eta } + \bar{\lambda }_1 k {\text {sign}} ( \beta ^{\mathcal {G}}_g ) + \bar{\lambda }_2 k\left[ r_g-(p_g-k) \right] . \end{aligned}$$

Therefore, the gap of the inequality, which is $x_{\underline{o}(g,k)}^\top (y - X^{\mathcal {G}}\beta ^{\mathcal {G}}(\eta ))- \eta \bar{\lambda }_1 k {\text {sign}} ( \beta ^{\mathcal {G}}_g ) - \eta \bar{\lambda }_2 k\left[ r_g-(p_g-k) \right]$ at time $\eta$, goes below zero after time $\eta + \Delta _{g, k}^{\text {split}}$, where

$$\begin{aligned} \Delta _{g, k}^{\text {split}}= {\left\{ \begin{array}{ll} \frac{ x_{\underline{o}(g,k)}^\top (y - X^{\mathcal {G}}\beta ^{\mathcal {G}}(\eta ))- \eta \bar{\lambda }_1 k {\text {sign}} ( \beta ^{\mathcal {G}}_g ) - \eta \bar{\lambda }_2 k\left[ r_g-(p_g-k) \right] }{\sigma (g, k)} & \quad \text {if }\sigma (g, k) > 0, \\ \infty & \quad \text {otherwise}, \end{array}\right. } \end{aligned}$$

unless any other event occurs. After this time, the inequality (11) no longer holds for k and, hence, the optimality condition (4) for the group $G_g$ fails. In this case, if we regard $\{o(q_g+1),\dots ,o(q_g+k)\}$ and $\{o(q_g+k+1),\dots ,o(q_{g+1})\}$ in $G_g$ as two distinct groups with the relevant variables and constants redefined accordingly, the condition (9) in Corollary 1 and, hence, the optimality condition (4) are satisfied for each group. Therefore, the group $G_g$ has to be split into the two groups at time $\eta + \Delta _{g, k}^{\text {split}}$.

The timing of the splitting event in the group $G_0$ can be detected in a similar way. From Theorem 1 with $m=p_0$ and $f_i = x_{o(q_0+i)}^\top (X^{\mathcal {G}}\beta ^{\mathcal {G}}- y) + \lambda _2 r_0$, the optimality condition (4) in $G_0$ holds if and only if

$$\begin{aligned}&\sum _{j=1}^{k} f_j = x_{\underline{o}(0,k)}^\top \left( X^{\mathcal {G}}\beta ^{\mathcal {G}}- y \right) + \lambda _2 k r_0 \le \lambda _1 k + \lambda _2k(p_0-k),\quad k=1,\dots , p_0, \end{aligned}$$

(12)

$$\begin{aligned}&\sum _{j=k+1}^{p_0} f_j = x_{\overline{o}(0,k)}^\top \left( X^{\mathcal {G}}\beta ^{\mathcal {G}}- y \right) + \lambda _2 (p_0-k) r_0 \ge -\lambda _1 (p_0-k) - \lambda _2 k(p_0-k), \nonumber \\&\quad k=0,\dots , p_0-1, \end{aligned}$$

(13)

where $x_{\underline{o}(0,k)} = \sum _{j=q_0+1}^{q_0+k} x_{o(j)}$ and $x_{\overline{o}(0,k)} = \sum _{j=q_0+k+1}^{q_1} x_{o(j)}$. The difference between the left and right sides of the first inequality (12) changes at a rate of $\sigma (0, -k)$, where

$$\begin{aligned} \sigma (0, -k)= & \frac{\textrm{d}}{\textrm{d}\eta }\left[ \sum _{j=1}^{k} f_j - \lambda _1 k - \lambda _2k(p_0-k)\right] \\= & x_{\underline{o}(0,k)}^\top X^{\mathcal {G}}\frac{\textrm{d}\beta ^{\mathcal {G}}}{\textrm{d}\eta } - \bar{\lambda }_1 k + \bar{\lambda }_2 k \left[ r_0-(p_0-k) \right] . \end{aligned}$$

for $k = 1,\dots ,p_0$. Therefore, the gap of that inequality, which is $x_{\underline{o}(0,k)}^\top (y - X^{\mathcal {G}}\beta ^{\mathcal {G}}(\eta )) + \eta \bar{\lambda }_1 k - \eta \bar{\lambda }_2 k \left[ r_0-(p_0-k) \right]$ at time $\eta$, goes below zero after time $\eta + \Delta _{0,-k}^{\text {split}}$, where

$$\begin{aligned} \Delta _{0,-k}^{\text {split}}= {\left\{ \begin{array}{ll} \frac{x_{\underline{o}(0,k)}^\top (y - X^{\mathcal {G}}\beta ^{\mathcal {G}}(\eta )) + \eta \bar{\lambda }_1 k - \eta \bar{\lambda }_2 k \left[ r_0-(p_0-k) \right] }{\sigma (0, -k)} & \quad \text {if } \sigma (0, -k) > 0, \\ \infty & \quad \text {otherwise}, \end{array}\right. } \end{aligned}$$

for $k = 1,\dots ,p_0$, unless any other event occurs. The violation of the condition (12) with k means that the coefficients $\beta _{o(q_0+1)},\dots ,\beta _{o(q_0+k)}$ can no longer stay at zero but deviate from zero in the negative direction whereas the other coefficients $\beta _{o(q_0+k+1)},\dots ,\beta _{o(q_1)}$ remain in $G_0$.

Similarly, the difference between the left and right sides of the second inequality (13) changes at a rate of $\sigma (0, k)$, where

$$\begin{aligned} \sigma (0, k)= & \frac{\textrm{d}}{\textrm{d}\eta }\left[ \sum _{j=k+1}^{p_0} f_j + \lambda _1 (p_0-k) + \lambda _2 k(p_0-k)\right] \\= & x_{\overline{o}(0,k)}^\top X^{\mathcal {G}}\frac{\textrm{d}\beta ^{\mathcal {G}}}{\textrm{d}\eta } + \bar{\lambda }_1 (p_0-k) + \bar{\lambda }_2 (p_0-k)(r_0+k) \end{aligned}$$

for $k = 0,\dots ,p_0-1$. Therefore, the gap of that inequality, which is $x_{\overline{o}(0,k)}^\top (y - X^{\mathcal {G}}\beta ^{\mathcal {G}}(\eta ))- \eta \bar{\lambda }_1 (p_0-k) - \eta \bar{\lambda }_2 (p_0-k)(r_0+k)$ at time $\eta$, exceeds zero after time $\eta + \Delta _{0,k}^{\text {split}}$ where

$$\begin{aligned} \Delta _{0,k}^{\text {split}}= {\left\{ \begin{array}{ll} \frac{x_{\overline{o}(0,k)}^\top (y - X^{\mathcal {G}}\beta ^{\mathcal {G}}(\eta ))- \eta \bar{\lambda }_1 (p_0-k) - \eta \bar{\lambda }_2 (p_0-k)(r_0+k)}{\sigma (0, k)} & \quad \text {if }\sigma (0, k) < 0, \\ \infty & \quad \text {otherwise}, \end{array}\right. } \end{aligned}$$

for $k = 0,\dots ,p_0-1$ unless any other event occurs. The violation of the condition (13) with k means that the coefficients $\beta _{o(q_0+k+1)},\dots ,\beta _{o(q_1)}$ can no longer stay at zero but deviate from zero in the positive direction whereas the other coefficients $\beta _{o(q_0+1)},\dots ,\beta _{o(q_0+k)}$ remain in $G_0$.

In our path algorithm, it is necessary to define another internal event in which the order $o(1),\dots ,o(p)$ of indices changes within a group; we call this event the switching event. For $k \in \{1,\dots ,p-1\}{\setminus } \{q_{\underline{g}+1},\dots ,q_{\overline{g}}\}$, the indices assigned to o(k) and $o(k+1)$ are switched by the reversal of the inequality $x_{o(k)}^\top (X^{\mathcal {G}}\beta ^{\mathcal {G}}- y) \ge x_{o(k+1)}^\top (X^{\mathcal {G}}\beta ^{\mathcal {G}}- y)$. Because the gap of the inequality, which is $\left( x_{o(k)}^\top -x_{o(k+1)}^\top \right) \left[ y-X^{\mathcal {G}}\beta ^{\mathcal {G}}(\eta ) \right]$ at time $\eta$, changes at a rate of $\left( x_{o(k)}^\top -x_{o(k+1)}^\top \right) X^{\mathcal {G}}\frac{\textrm{d}\beta ^{\mathcal {G}}}{\textrm{d}\eta }$, the switching event on o(k) and $o(k+1)$ occurs at time $\eta + \Delta _{k}^\text {switch}$, where

$$\begin{aligned} \Delta _{k}^\text {switch} = {\left\{ \begin{array}{ll} \frac{\left( x_{o(k)}^\top -x_{o(k+1)}^\top \right) \left[ y-X^{\mathcal {G}}\beta ^{\mathcal {G}}(\eta ) \right] }{\left( x_{o(k)}^\top -x_{o(k+1)}^\top \right) X^{\mathcal {G}}\frac{\textrm{d}\beta ^{\mathcal {G}}}{\textrm{d}\eta }} & \quad \text {if } (x_{o(k)}^\top -x_{o(k+1)}^\top ) X^{\mathcal {G}}\frac{\textrm{d}\beta ^{\mathcal {G}}}{\textrm{d}\eta } < 0, \\ \infty & \quad \text {otherwise}, \end{array}\right. } \end{aligned}$$

unless any other event occurs.

3 Path algorithm for OSCAR

In this section, we propose a solution path algorithm for OSCAR (2) that is derived in a manner similar to that for clustered Lasso. We use the same symbols and variables as in the preceding section, which have similar but slightly different definitions. Our algorithm constructs a solution path of $\beta (\eta )$ along regularization parameters $[\lambda _{1}, \lambda _{2}] = \eta [\bar{\lambda }_1, \bar{\lambda }_2]$. We also assume $n\ge p$ and ${\text {rank}}\left( X \right) = p$ to ensure strict convexity.

In contrast to clustered Lasso, the regularization terms in (2) encourage the absolute values of the coefficients to be zero or equal. Hence, from the solution $\beta (\eta )$, we define the fused groups ${\mathcal {G}}(\eta ) = \left\{ G_0, G_1, \dots , G_{\overline{g}} \right\}$ and the grouped absolute coefficients $\beta ^{\mathcal {G}}(\eta ) = [\beta ^{\mathcal {G}}_0, \beta ^{\mathcal {G}}_1,\dots ,\beta ^{\mathcal {G}}_{\overline{g}}]^\top \in \mathbb {R}^{\overline{g}+1}$ to satisfy the following statements:

• $\bigcup _{g=0}^{\overline{g}} G_g = \left\{ 1, \ldots , p \right\}$, where $G_0$ may be an empty set but others may not.

• $\beta ^{\mathcal {G}}_0=0< \beta ^{\mathcal {G}}_1< \cdots < \beta ^{\mathcal {G}}_{\overline{g}}$ and $| \beta _i | = \beta ^{\mathcal {G}}_g$ for $i\in G_g$.

Correspondingly, we define the signed grouped design matrix $X^{\mathcal {G}}= [x^{\mathcal {G}}_0, x^{\mathcal {G}}_1,\dots ,x^{\mathcal {G}}_{\overline{g}}] \in \mathbb {R}^{n\times (\overline{g}+1)}$, where $x^{\mathcal {G}}_g = \sum _{j \in G_g} {\text {sign}} ( \beta _j ) x_j$.

3.1 Piecewise linearity

Because the objective function of (2) is strictly convex, its solution path would be a continuous piecewise linear function as well as that of clustered Lasso. As long as the grouping ${\mathcal {G}}$ of the solution $\beta (\eta )$ is conserved as defined above, the problem (2) can be reduced to the following quadratic programming problem:

$$\begin{aligned} \mathop {\mathrm {\text {minimize} \quad }}\limits _{\beta }\ \ \frac{1}{2} \left\| y - X^{\mathcal {G}}\beta ^{\mathcal {G}} \right\| ^2 + \eta \bar{\lambda }_1 \sum _{g=1}^{\overline{g}} p_g \beta ^{\mathcal {G}}_g + \eta \bar{\lambda }_2 \sum _{g=1}^{\overline{g}} p_g \left( q_g + \frac{p_g - 1}{2} \right) \beta ^{\mathcal {G}}_g, \end{aligned}$$

where $p_g$ is the cardinality of $G_g$ and $q_g = p_0 + \cdots + p_{g-1}$. Hence, because $\beta ^{\mathcal {G}}_0$ is fixed at zero, the nonzero elements of the absolute grouped coefficients $\beta ^{\mathcal {G}}_{-0}(\eta )= [\beta ^{\mathcal {G}}_1,\dots ,\beta ^{\mathcal {G}}_{\overline{g}}]^\top$ are obtained by

$$\begin{aligned} \beta ^{\mathcal {G}}_{-0}(\eta ) = \left[ \left( X^{\mathcal {G}}_{-0} \right) ^\top X^{\mathcal {G}}_{-0} \right] ^{-1} \left[ \eta b+\left( X^{\mathcal {G}}_{-0} \right) ^\top y \right] , \end{aligned}$$

(14)

where $X^{\mathcal {G}}_{-0}= [x^{\mathcal {G}}_1,\dots ,x^{\mathcal {G}}_{\overline{g}}]$ and $b= [b_1,\dots ,b_{\overline{g}}]^\top \in \mathbb {R}^{\overline{g}}$, $b_g = -\bar{\lambda }_1 p_g - \bar{\lambda }_2 p_g (q_g + \frac{p_g - 1}{2})$.

3.2 Optimality condition

In this subsection, we show the optimality conditions of (2) and then derive a theorem to check them efficiently. For a nonzero group $G_g \, (g\ne 0)$, the optimality condition can be described as follows:

$$\begin{aligned} s_i x_i^\top \left( X^{\mathcal {G}}\beta ^{\mathcal {G}}- y \right) + \lambda _{1} + \lambda _2 q_g + \sum _{j \in G_g \setminus \left\{ i \right\} } \left( \tau _{ij}+\frac{\lambda _2}{2} \right) = 0, \qquad i \in G_g, \end{aligned}$$

(15)

where $s_i = {\text {sign}} ( \beta _i )$ and $\tau _{ij}\in [-\lambda _2/2,\lambda _2/2]\; (i\ne j,\; i,j\in G_g)$ are subject to the constraints $\tau _{ij} + \tau _{ji} = 0$, which imply that $\tau _{ij}+\frac{\lambda _2}{2}$ is a subgradient of $\lambda _2 \max \left\{ | \beta _i |, | \beta _j | \right\} = \frac{\lambda _2}{2}(| s_i\beta _i - s_j\beta _j | + s_i\beta _i + s_j\beta _j)$ with respect to $s_i \beta _i$ when $s_i \beta _i = s_j \beta _j>0$. Then, if we denote the sorted values of $s_i x_i^\top (X^{\mathcal {G}}\beta ^{\mathcal {G}}- y) + \lambda _1 + \lambda _2 (q_g + \frac{p_g - 1}{2})$ over $i \in G_g$ by $f_1 \ge f_2 \ge \cdots \ge f_m$, we can apply Corollary 1 to the condition (15) to specify when it fails as in the next subsection.

For the group $G_0$ of zeros, the optimality condition is given by

$$\begin{aligned} x_i^\top \left( X^{\mathcal {G}}\beta ^{\mathcal {G}}- y \right) + \xi _{i0} + \sum _{j \in G_0 \setminus \left\{ i \right\} } \xi _{ij} = 0, \qquad i \in G_0, \end{aligned}$$

(16)

where $\xi _{i0} \in [-\lambda _1,\lambda _1]$ is a subgradient of $\lambda _1 \left| \beta _i \right|$ when $\beta _i=0$ and $\xi _{ij} \in [-\lambda _2,\lambda _2] \; (i\ne j,\; i,j\in G_0)$ are subject to the constraints $| \xi _{ij} | + | \xi _{ji} | \le \lambda _2$, which implies that $\xi _{ij}$ is a subgradient of the $L_{\infty }$ penalty $\lambda _2 \max \left\{ | \beta _i |, | \beta _j | \right\}$ with respect to $\beta _i$ when $\beta _i = \beta _j = 0$. When we assume $m=p_0\ge 1$ and let $f_1,\dots ,f_m$ denote the values of $x_i^\top (X^{\mathcal {G}}\beta ^{\mathcal {G}}- y )$ in $i \in G_0$ sorted as $| f_1 |\le | f_2 |\le \cdots \le | f_m |$, we can propose the following theorem to check condition (16).

Theorem 2

There exist $\xi _{i0} \in \left[ -\lambda _1, \lambda _1 \right]$ and $\xi _{ij} \in \left[ -\lambda _2, \lambda _2 \right]$ such that $| \xi _{ij} | + | \xi _{ji} | \le \lambda _2$ and

$$\begin{aligned} f_i + \xi _{i0} + \sum _{j \in \{1,\dots ,m\} \setminus \left\{ i \right\} }\xi _{ij} =0, \qquad i=1,\dots ,m, \end{aligned}$$

(17)

if and only if

$$\begin{aligned} \sum _{j=k+1}^{m} | f_j | \le \lambda _1 (m-k) + \lambda _2 \frac{(m-k)(m+k-1)}{2}, \qquad k=0,\dots , m-1. \end{aligned}$$

(18)

The proof of this theorem is provided in Appendix B.

3.3 Events in path algorithm

Our path algorithm for OSCAR has the fusing, splitting, and switching events defined similarly to those for the clustered Lasso. However, because OSCAR groups absolute values of the coefficients and uses $L_\infty$ norms, the timings of these events in OSCAR are obtained much differently from those in clustered Lasso. Hence, in this subsection, we derive the occurrence times of the respective type of events in OSCAR.

First, the occurrence time of the fusing event can be detected by following the changes in grouped absolute coefficients according to (14) with their slopes $\frac{\textrm{d}\beta ^{\mathcal {G}}_{-0}}{\textrm{d}\eta } = [(X^{\mathcal {G}}_{-0})^{\top } X^{\mathcal {G}}_{-0}]^{-1}b$ for nonzero groups and $\frac{\textrm{d}\beta ^{\mathcal {G}}_{0}}{\textrm{d}\eta }= 0$ for $G_0$. Because the gap of the grouped absolute coefficients, which is $\beta ^{\mathcal {G}}_{g+1}(\eta ) - \beta ^{\mathcal {G}}_{g}(\eta )$ at time $\eta$, changes at a rate of $\frac{\textrm{d}\beta ^{\mathcal {G}}_{g}}{\textrm{d}\eta } - \frac{\textrm{d}\beta ^{\mathcal {G}}_{g+1}}{\textrm{d}\eta }$, it shrinks to zero at time $\eta + \Delta ^{\text {fuse}}_g$ where

$$\begin{aligned} \Delta ^{\text {fuse}}_g(\eta ) = {\left\{ \begin{array}{ll} \frac{-\beta ^{\mathcal {G}}_{g+1}(\eta ) + \beta ^{\mathcal {G}}_{g}(\eta )}{\frac{\textrm{d}\beta ^{\mathcal {G}}_{g+1}}{\textrm{d}\eta } - \frac{\textrm{d}\beta ^{\mathcal {G}}_{g}}{\textrm{d}\eta }} & \quad \text {if }\frac{\textrm{d}\beta ^{\mathcal {G}}_{g+1}}{\textrm{d}\eta } < \frac{\textrm{d}\beta ^{\mathcal {G}}_{g}}{\textrm{d}\eta }, \\ \displaystyle \infty & \quad \text {otherwise}, \end{array}\right. } \end{aligned}$$

unless any other event occurs. At this time, groups $G_g$ and $G_{g+1}$ have the absolute values of the coefficients and, hence, have to be fused into one group.

Next, to specify the splitting events, let $o(j) \in \{1,\dots ,p\}$ denote the order of coefficients such that $G_g = \{ o(q_g+1),\dots ,o(q_{g+1}) \}$ and $s_{o(q_g+1)} x_{o(q_g+1)}^\top (X^{\mathcal {G}}\beta ^{\mathcal {G}}- y) \ge \cdots \ge s_{o(q_{g+1})} x_{o(q_{g+1})}^\top (X^{\mathcal {G}}\beta ^{\mathcal {G}}- y)$ for each group, where $s_i$ is defined by

$$\begin{aligned} s_i = {\left\{ \begin{array}{ll} {\text {sign}} ( \beta _i ) & \quad \text {if }\beta _i \ne 0, \\ - {\text {sign}} ( x_i^\top (X^{\mathcal {G}}\beta ^{\mathcal {G}}- y) ) & \quad \text {if } \beta _i = 0. \end{array}\right. } \end{aligned}$$

If $\beta _i \ne 0$, $s_{i} x_{i}^\top (X^{\mathcal {G}}\beta ^{\mathcal {G}}- y)$ stands for the directional derivative of the square-error term $\frac{1}{2} \left\| y - X^{\mathcal {G}}\beta ^{\mathcal {G}} \right\| ^2$ along the direction in which the absolute value of $\beta _i$ increases with no change in any other coefficients in $\beta$. If $\beta _i = 0$, $s_i$ indicates the sign of the direction of $\beta _i$ to which the square error term $\frac{1}{2} \left\| y - X^{\mathcal {G}}\beta ^{\mathcal {G}} \right\| ^2$ decreases. As $s_{i} x_{i}^\top (X^{\mathcal {G}}\beta ^{\mathcal {G}}- y) = -| x_{i}^\top (X^{\mathcal {G}}\beta ^{\mathcal {G}}- y) |$ for $i\in G_0$, $o(1),\dots ,o(p_0)$ represents the ascending order of the absolute values of the partial derivatives of the square error term $\frac{1}{2} \left\| y - X^{\mathcal {G}}\beta ^{\mathcal {G}} \right\| ^2$ in $G_0$. Note that, when $\beta _i$ arrives at or leaves zero, the value of $s_i$ does not change although its definition changes.

The occurrence time of the splitting event on a nonzero group $G_g$ can be specified by the timing at which the optimality condition (15) gets violated. From Corollary 1 with $m=p_g$ and $f_i = s_{o(q_g+i)} x_{o(q_g+i)}^\top \left( X^{\mathcal {G}}\beta ^{\mathcal {G}}- y \right) + \lambda _{1} + \lambda _2 \left( q_g + \frac{p_g - 1}{2} \right)$, the optimality condition (15) in a nonzero group $G_g$ holds if and only if

$$\begin{aligned} & \sum _{j=1}^{k} f_j = x_{\underline{o}(g,k)}^\top \left( X^{\mathcal {G}}\beta ^{\mathcal {G}}- y \right) + \lambda _{1} k + \lambda _2 k \left( q_g + \frac{p_g - 1}{2} \right) \le \frac{\lambda _2}{2} k(p_g-k), \nonumber \\ & \qquad k=1,\dots , p_g, \end{aligned}$$

(19)

where $x_{\underline{o}(g,k)} = \sum _{j=q_g+1}^{q_g+k} s_{o(j)} x_{o(j)}$. Because $[\lambda _{1}, \lambda _{2}] = \eta [\bar{\lambda }_1, \bar{\lambda }_2]$, the difference between the left and right sides of the inequality (19) changes at a rate of $\sigma (g, k)$, where

$$\begin{aligned} \sigma (g, k)= & \frac{\textrm{d}}{\textrm{d}\eta }\left[ \sum _{j=1}^{k} f_j - \frac{\lambda _2}{2} k(p_g-k)\right] \\= & x_{\underline{o}(g,k)}^\top X^{\mathcal {G}}\frac{\textrm{d}\beta ^{\mathcal {G}}}{\textrm{d}\eta } + \bar{\lambda }_1 k + \bar{\lambda }_2 k\left( q_g + \frac{k-1}{2} \right) \end{aligned}$$

for $k=1,\dots , p_g$. Therefore, the gap of that inequality, which is $x_{\underline{o}(g,k)}^\top (y - X^{\mathcal {G}}\beta ^{\mathcal {G}}(\eta ))- \eta \bar{\lambda }_1 k - \eta \bar{\lambda }_2 k\left( q_g + \frac{k-1}{2} \right)$ at time $\eta$, goes below zero after time $\eta + \Delta _{g, k}^{\text {split}}$, where

$$\begin{aligned} \Delta _{g, k}^{\text {split}}= {\left\{ \begin{array}{ll} \frac{ x_{\underline{o}(g,k)}^\top (y - X^{\mathcal {G}}\beta ^{\mathcal {G}}(\eta )) - \eta \bar{\lambda }_1 k - \eta \bar{\lambda }_2 k (q_g + \frac{k-1}{2})}{\sigma (g, k)} & \quad \text {if } \sigma (g, k) > 0, \\ \infty & \quad \text {otherwise}, \end{array}\right. } \end{aligned}$$

unless any other event occurs. After this time, the inequality (19) no longer holds for k and, hence, the optimality condition (15) for the group $G_g$ fails. In this case, if we regard $\{o(q_g+1),\dots ,o(q_g+k)\}$ and $\{o(q_g+k+1),\dots ,o(q_{g+1})\}$ in $G_g$ as two distinct groups with the relevant variables and constants redefined accordingly, the condition (9) in Corollary 1 and, hence, the optimality condition (15) are satisfied for each group. Therefore, the group $G_g$ has to be split into the two groups at time $\eta + \Delta _{g, k}^{\text {split}}$.

The timing of the splitting event in the group $G_0$ can be detected in a similar way. From Theorem 2 with $f_i = s_{o(i)}x_{o(i)}^\top (X^{\mathcal {G}}\beta ^{\mathcal {G}}- y)$, the optimality condition (16) in $G_0$ holds if and only if

$$\begin{aligned} & \sum _{j=k+1}^{p_0} f_j = x_{\overline{o}(0,k)}^\top \left( X^{\mathcal {G}}\beta ^{\mathcal {G}}- y \right) \ge - \lambda _1(p_0-k) - \lambda _2\frac{(p_0-k)(p_0 + k - 1)}{2}, \nonumber \\ & \qquad k=0,\dots , p_0-1, \end{aligned}$$

(20)

where $x_{\overline{o}(0,k)} = \sum _{j=k+1}^{p_0} s_{o(j)}x_{o(j)}$. The difference between the left and right sides of the inequality (20) changes at a rate of $\sigma (0, k)$, where

$$\begin{aligned} \sigma (0, k) = x_{\overline{o}(0,k)}^\top X^{\mathcal {G}}\frac{\textrm{d}\beta ^{\mathcal {G}}}{\textrm{d}\eta } + \bar{\lambda }_1 (p_0-k) + \bar{\lambda }_2 \frac{(p_0-k)(p_0 + k - 1)}{2} \end{aligned}$$

for $k = 0,\dots ,p_0-1$. Therefore, the gap of the inequality, which is $x_{\overline{o}(0,k)}^\top (y - X^{\mathcal {G}}\beta ^{\mathcal {G}}(\eta ))- \eta \bar{\lambda }_1 (p_0-k) - \eta \bar{\lambda }_2 \frac{(p_0-k)(p_0 + k - 1)}{2}$ at time $\eta$, exceeds zero after time $\eta + \Delta _{0, k}^{\text {split}}$, where

$$\begin{aligned} & \Delta _{0,k}^{\text {split}} \\ & = {\left\{ \begin{array}{ll} \frac{x_{\overline{o}(0,k)}^\top (y - X^{\mathcal {G}}\beta ^{\mathcal {G}}(\eta ))- \eta \bar{\lambda }_1 (p_0-k) - \eta \bar{\lambda }_2 \frac{(p_0-k)(p_0 + k - 1)}{2}}{\sigma (0, k)} & \quad \text {if } \sigma (0, k) < 0, \\ \infty & \quad \text {otherwise}, \end{array}\right. } \end{aligned}$$

for $k = 0,\dots ,p_0-1$, unless any other event occurs. The violation of condition (20) with k implies that the coefficients $\beta _{o(k+1)},\dots ,\beta _{o(p_0)}$ can no longer remain at zero but must deviate from zero in the directions indicated by the signs $s_{o(k+1)}, \ldots , s_{o(p_0)}$, while the other coefficients $\beta _{o(1)},\dots ,\beta _{o(k)}$ continue to stay in $G_0$.

The switching event of the order $o(1),\dots ,o(p)$ is needed for OSCAR as well. For $k \in \{1,\dots ,p-1\}{\setminus } \{q_1,\dots ,q_{\overline{g}}\}$, the indices assigned to o(k) and $o(k+1)$ are switched by the reversal of the inequality $s_{o(k)} x_{o(k)}^\top (X^{\mathcal {G}}\beta ^{\mathcal {G}}- y) \ge s_{o(k+1)} x_{o(k+1)}^\top (X^{\mathcal {G}}\beta ^{\mathcal {G}}- y)$. Because the gap of the inequality, which is $\left( s_{o(k)}x_{o(k)}^\top -s_{o(k+1)}x_{o(k+1)}^\top \right) \left[ y-X^{\mathcal {G}}\beta ^{\mathcal {G}}(\eta ) \right]$ at time $\eta$, changes at a rate of $\left( s_{o(k)}x_{o(k)}^\top -s_{o(k+1)}x_{o(k+1)}^\top \right) X^{\mathcal {G}}\frac{\textrm{d}\beta ^{\mathcal {G}}}{\textrm{d}\eta }$, the switching event on o(k) and $o(k+1)$ occurs at time $\eta + \Delta _{k}^\text {switch}$, where

$$\begin{aligned} & \Delta _{k}^\text {switch} \\ & = {\left\{ \begin{array}{ll} \frac{(s_{o(k)} x_{o(k)}^\top -s_{o(k+1)} x_{o(k+1)}^\top ) [y-X^{\mathcal {G}}\beta ^{\mathcal {G}}(\eta )]}{(s_{o(k)} x_{o(k)}^\top -s_{o(k+1)} x_{o(k+1)}^\top ) X^{\mathcal {G}}\frac{\textrm{d}\beta ^{\mathcal {G}}}{\textrm{d}\eta }} & \quad \text {if } (s_{o(k)} x_{o(k)}^\top -s_{o(k+1)} x_{o(k+1)}^\top ) X^{\mathcal {G}}\frac{\textrm{d}\beta ^{\mathcal {G}}}{\textrm{d}\eta } < 0, \\ \infty & \quad \text {otherwise} \end{array}\right. } \end{aligned}$$

unless any other event occurs.

Additionally, when the inequality $0 \ge s_{o(1)} x_{o(1)}^\top (X^{\mathcal {G}}\beta ^{\mathcal {G}}- y)$ within the zero group $G_0$ is violated, we can define another case of a switching event where the sign $s_{o(1)}$ reverses. This switching event for the sign reversal of $\beta _{o(1)}$, with $s_{o(1)} = - {\text {sign}} ( x_{o(1)}^\top (X^{\mathcal {G}}\beta ^{\mathcal {G}}- y) )$, occurs at time $\eta + \Delta _{0}^{\text {switch}}$, where

$$\begin{aligned} \Delta _{0}^\text {switch} = {\left\{ \begin{array}{ll} \frac{x_{o(1)}^\top \left[ y-X^{\mathcal {G}}\beta ^{\mathcal {G}}(\eta ) \right] }{x_{o(1)}^\top X^{\mathcal {G}}\frac{\textrm{d}\beta ^{\mathcal {G}}}{\textrm{d}\eta }} & \quad \text {if }\, s_{o(1)} x_{o(1)}^\top X^{\mathcal {G}}\frac{\textrm{d}\beta ^{\mathcal {G}}}{\textrm{d}\eta } > 0, \\ \infty & \quad \text {otherwise}. \end{array}\right. } \end{aligned}$$

unless any other event occurs.

4 Path algorithm and complexity

The outlines of our path algorithms for clustered Lasso and OSCAR are shown in Algorithm 1. Although the variables are defined differently for clustered Lasso and OSCAR, both algorithms have the same types of events and thus can be described in a common format.

As for the computational cost, $\mathcal {O}(np^2)$ time is required to obtain the initial solution $\beta ^{(0)} = (X^\top X)^{-1}X^\top y$. By using a block matrix computation to update $[(X^{\mathcal {G}}_{-0})^\top X^{\mathcal {G}}_{-0}]^{-1}$, each iteration where a fusing/splitting event occurs requires $\mathcal {O}(np)$ time. The complexity of each iteration where a switching event occurs is even smaller (only $\mathcal {O}(n)$) because we only need to update the event times for the indices switched by the event. For more detail, see Appendix C. Thus, Algorithm 1 requires $\mathcal {O}(np^2 + (T_\text {fuse}+ T_\text {split})np + T_\text {switch} n)$ time where $T_\text {fuse}$, $T_\text {split}$ and $T_\text {switch}$ are the numbers of fusing, splitting, and switching events that occur until the algorithm ends, respectively.

It is difficult to assess the number of iteration theoretically. Even for the lasso, the complexity of regularization path is $\mathcal {O}(3^p)$ in the worst case (Mairal & Yu, 2012). We show ordinary evolution of the number of events in the numerical studies.

Algorithm 1

Path algorithm for clustered Lasso and OSCAR

5 Numerical experiment

In this section, we evaluate the processing time and accuracy of our path algorithms using synthetic and real data.

5.1 Computational efficiency for synthetic data

First, we compare the processing time and the number of iterations on synthetic datasets between our algorithms implemented in R and the dual path algorithm (DPA) (Arnold & Tibshirani, 2016; Tibshirani & Taylor, 2011) which is designed to estimate generalized Lasso problems, including clustered Lasso and OSCAR.¹ This experiment was conducted on a Windows 10 64-bit machine with an Intel i7-8665U CPU at 1.90 GHz and 16 GB of RAM, using R.

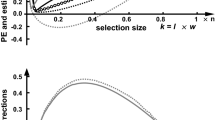
The synthetic datasets are generated from the model $y=X\beta + e$, where $e \sim N(0, I_n)$. The covariates in X are generated as independent and identical standard normal variables. The true coefficients are given by $\beta = [\theta ^\top ,\theta ^\top ,-\theta ^\top ,-\theta ^\top ,{\textbf {0}}_{0.2p}^\top ]^\top \in \mathbb {R}^p$ where $\theta \sim N(0, I_{0.2p})$. We set four levels of the problem size $[n,p]\in \{[20, 10], [60, 30], [100, 50], [200, 100]\}$ and two directions of tuning parameters $[\bar{\lambda }_{1}, \bar{\lambda }_{2}]\in \{[0, 1], [1, 1]\}$ in the path algorithms for clustered Lasso and OSCAR, respectively. Figure 1 shows the average running time over 10 simulated datasets for each case. As the problem size increases, our algorithms become much faster than the DPA (Arnold & Tibshirani, 2016; Tibshirani & Taylor, 2011). When we count the number of iterations as in Fig. 2, it appears to increase rapidly with the problem size. The number of iterations in our method is approximately doubled by the switching events but still less than that in the DPA, which includes events occurring only in the dual problem.

Fig. 1

Running time on synthetic data

Fig. 2

Number of iterations on synthetic data

5.2 Numerical results for real data

We also conduct experiments on real datasets: the splice dataset from LIBSVM data (Chang & Lin, 2011) and the brvehins2 dataset of automobile insurance claims from ‘CASdatasets’.² This experiment was conducted on a Windows 10 64-bit machine with an Intel i7-8665U CPU at 1.90 GHz and 16 GB of RAM, using MATLAB. Each dataset includes training and test data whose sizes are shown in Table 1. Each data point in the splice dataset represents a segment of a DNA sequence, with a dummy variable indicating the type of splice site used as the response variable, and a sequence of nucleotides used as predictors. For brvehins2 data, we calculate the mean amount of robbery claims in each policy as a response variable, set 341 dummy variables for the cities where 10+ robbery claims occurred as predictors, and divide their records into training and test data evenly as $n_{\text{ train }} = n_{\text{ test }}$. For each dataset, we run 5-fold cross validation (CV) to tune $\eta$ and select $\bar{\lambda }_{1}$ from $\{0,0.5,1,2 \}$ while $\bar{\lambda }_{2}$ is fixed at 1. We compare two tuning methods for $\eta$: one is a path-based search from all the event times in 5 entire solution paths of CV trials, and the other is a grid search from 100 grid points $\eta = 10^{-\frac{4i}{99}}\eta _{\max }$ $(i=0,\dots ,99)$, where $\eta _{\max }$ is the terminal point of the solution path. The solution paths are obtained by our methods implemented in MATLAB, and the solution for each grid point is given by the accelerated proximal gradient (APG) algorithms for clustered Lasso (Lin et al., 2019) and OSCAR (Bogdan et al., 2015).³

In Table 1, we evaluate the CV errors and test errors by using the mean squared error (MSE). Our path-based tuning of $\eta$ performs slightly better than or equally to the grid search in CV errors. Their test errors are also slightly different. The number of nonzero groups (gnnz) in ${\mathcal {G}}(\eta )$ with $\eta$ selected by the path and grid search is also shown in Table 1. The gnnz is sensitive to the value of $\eta$ and also differs between the path and grid search. In Table 2, we compare the running time per iteration with respect to event types and that per grid point in the grid search with the APG algorithms. Our path algorithms can update solution by path events much faster than the APG algorithms. As described in the previous section, a switching event requires much less time than a fusing/splitting event.

Table 1 Cross validation errors, test errors and number of nonzero groups (gnnz)

Table 2 Running time (s) per iteration of each event type in our algorithm and per grid point in APG

5.3 Application in automobile insurance rating

In the application of our methods to the real dataset brvehins1 from the ‘CASdatasets’ package in R, which consists of automobile insurance claims in Brazil, the experiments were conducted on a Windows 10 64-bit machine with an Intel i7-8665U CPU at 1.90 GHz and 16 GB of RAM. We used the following variables in the dataset:

• Car model (e.g. Citroen C3). We extracted the 77 car models whose total exposures exceeds 10,000 years.

• State in Brazil (e.g. Acre).

• Exposure or duration of insurance policy.

• Total claim amount of vehicle fire.

The purpose of this analysis is to estimate the expected claim amounts per exposure by car model and state as the pure premium of automobile fire insurance. In Japanese voluntary automobile insurance, all the car models are classified into 17 grades of insurance premium rating. In addition, the claim risk in fire insurance generally depends on the location of the insured property. Therefore, we applied clustered Lasso and OSCAR to the dataset to group the car models and states to apply the insurance premium.

First, we randomly divided this dataset into five for the use of the 5-fold CV. Then, we aggregated claim amounts of fire incidents and exposures by state and car model, and calculated the claim amount per exposure as the response variable of this analysis. We also created dummy variables for the 77 car-model groups and the 27 states in Brazil, respectively, and used them as the predictors.

We ran 5-fold CV to tune $\eta$ and select $\bar{\lambda }_{1}$ from $\{0,0.5,1,2,5,10,50,100 \}$ with $\bar{\lambda }_{2}$ fixed at 1 for clustered Lasso and OSCAR, respectively. As a result, the minimum CV MSE was obtained for clustered Lasso with $\eta = 10.79$ and $\bar{\lambda }_{1} = 50$, that is, $[\lambda _1,\lambda _2]=\eta [\bar{\lambda }_{1},\bar{\lambda }_{2}]=(539.50,10.79)$. The solution for the clustered Lasso with the optimal values of $\lambda _1, \lambda _2$ contains 28 fused groups. Table 3 presents the grouped coefficients, which are considered as the relative difference in pure premium in BRL, and the numbers of car models and states that belong to the fused groups. The largest fused group with coefficient $-1.6866$ contains 55 car models and 5 states. There are no car models but 13 states with coefficients less than $-1.6866$, each forming an isolated group. The group with zero coefficient is the second largest and includes 10 car models and three states. Each of the seven car models and the three states with positive coefficients forms an isolated group. A few car models have large coefficients, which implies relatively high risk of vehicle fire.

Table 3 Coefficients and numbers of members of the fused groups in the clustered Lasso solution for automobile fire insurance rating

6 Conclusion

We proposed efficient path algorithms for clustered Lasso and OSCAR. For both problems, there are only two types of events that make change-points in solution paths, namely fusing and splitting events. By using symmetry of regularization terms, we derived simple conditions to monitor the violation of optimal conditions that causes a split. Specifically, we showed that a group can be split only along a certain order of indices determined by the first derivative of the square loss. Numerical experiments demonstrated that our algorithms are much faster than the existing methods. Although our algorithms require an enormous number of iterations for large problems to obtain entire solution paths, they can be modified to generate a partial solution path within an arbitrary interval of $\eta$, which may be determined by a coarse grid search with fast solvers (Lin et al., 2019; Luo et al., 2019; Zhong & Kwok, 2012).

Although OSCAR and Clustered Lasso were proposed over a decade ago, the demand for high-dimensional data analysis remains high, and some relevant sparse regularization methods such as SLOPE (Bogdan et al., 2015) and network lasso (Hallac et al., 2015) have been proposed. Recently, Dupuis and Tardivel (2024) expanded our techniques to SLOPE (Bogdan et al., 2015), and further removed the assumption $\textrm{ker}(X) = {0}$ for the design matrix.

The scarcity of research on path algorithms can be attributed to analytical challenges, the increasing complexity of modern models, the high computational cost in high dimensions, and numerical instability. However, these issues can be addressed by combining path algorithms with methods like grid search. By analyzing points with grid search and applying path algorithms over specific intervals, both computational cost and numerical instability can be mitigated.

Our algorithms construct one-dimensional solution paths along $[\lambda _{1}, \lambda _{2}] = \eta [\bar{\lambda }_1, \bar{\lambda }_2]$ driven by a single parameter $\eta$. When the design matrix is a unit matrix, we can obtain the solution with $[\lambda _{1}^\prime , \lambda _{2}]$ such that $\lambda _{1}^\prime < \lambda _{1}$ by soft-thresholding the solution with $[\lambda _{1}, \lambda _{2}]$ (Friedman et al., 2007; Hoefling, 2010). Therefore, our algorithms can be extended to obtain solution maps over the two-dimensional domain of $[\lambda _{1}, \lambda _{2}]$ in such cases. Existing algorithms including ours cannot provide such solution maps with a general design matrix, which can be studied in the future.

Appendices

Proofs of Theorem 1, Corollary 1 and Lemma 1

In this section, we give proofs of Theorem 1, Corollary 1 and Lemma 1 that is shown in Sect. 2.2 and 2.3.

Proof of the Lemma 1

Consider a flow $\tau = \{ \tau _{ij}; (i,j)\in E\}$ on the flow network $G=\{(V,E),c,r,s\}$ defined above. From the capacity constraint, the value $| \tau | = \sum _{i=0}^m \tau _{ri} = \sum _{i=0}^m \tau _{is}$ of the flow cannot be more than $\sum _{i=0}^m c(r,i) = \sum _{i=0}^m c(i,s) = \sum _{i=0}^m f_i^{+} = \sum _{i=0}^m f_i^{-}$. Therefore, this value of the flow is attained if and only if $\tau _{ri} = c(r,i) = f_i^{-}, \tau _{is} = c(i,s) = f_i^{+}$ for all $i=0,\dots ,m$, and hence

$$\begin{aligned} \sum _{j\in V\setminus \{i\}} \tau _{ij} = f_i + \tau _{i0} + \sum _{j \in \{1,\dots ,m\} \setminus \left\{ i \right\} }\tau _{ij} = 0, \qquad i = 1,\dots ,m, \end{aligned}$$

(21)

from the flow conservation where $\tau _{i0} \in \left[ -\lambda _{i0}, \lambda _{i0} \right]$ and $\tau _{ij} = -\tau _{ji} \in \left[ -\lambda _{ij}, \lambda _{ij} \right]$ from the skew symmetry and the capacity constraint. Furthermore, the flow conservation at the vertex zero $\sum _{i\in V{\setminus } \{0\}} \tau _{0i} = f_0 + \sum _{i=1}^m \tau _{0i} = - \sum _{i=1}^m f_i - \sum _{i=1}^m \tau _{i0} = 0$ follows from the sum of (21) over $i \in \{1,\dots ,m\}$, completing the proof. $\square$

Proof of Theorem 1

From the max-cut min-flow theorem and Lemma 1 in Sect. 2.3, it suffices to prove that the minimum capacity of a cut of $G=\{(V,E),c,r,s\}$ is just $\sum _{i=0}^m f_i^{+} = \sum _{i=0}^m f_i^{-}$ if and only if (6) and (7) hold.

For $V_r = \{r\},V_s = V{\setminus } \{r\}$ and $V_r=V{\setminus } \{s\},V_s=\{s\}$, the capacity of the cut attains $\sum _{i=0}^m f_i^{+} = \sum _{i=0}^m f_i^{-}$, which is supposed to be the minimum capacity of a cut. For the other cuts, let k and $m-k$ denote the cardinality of $\tilde{V}_s = V_s \cap \{1,\dots ,m\}$ and $\tilde{V}_r = V_r \cap \{1,\dots ,m\}$, respectively. Then, the capacity of the cut $C(V_r,V_s)$ is obtained by, if $0\in V_s$,

$$\begin{aligned} C(V_r,V_s)&= \sum _{i\in V_r, j\in V_s, (i,j)\in E} c(i,j) \nonumber \\&= \sum _{i \in \tilde{V}_r} c(i,s) + \sum _{i \in \tilde{V}_s} c(r,i) + c(r,0) + \sum _{i \in \tilde{V}_r} c(i,0) + \sum _{i \in \tilde{V}_r, j\in \tilde{V}_s} c(i,j)\nonumber \\&= \sum _{i \in \tilde{V}_r} f_i^{+} + \sum _{i \in \tilde{V}_s} f_i^{-} + f_0^{-} + \sum _{i \in \tilde{V}_r} \lambda _1 + \sum _{i \in \tilde{V}_r, j\in \tilde{V}_s} \lambda _2\nonumber \\&= \sum _{i \in \tilde{V}_r} f_i^{+} + \sum _{i \in \tilde{V}_s} f_i^{-} + f_0^{-} + (m-k)\lambda _1 + k(m-k)\lambda _2, \end{aligned}$$

(22)

and otherwise

$$\begin{aligned} C(V_r,V_s)&= \sum _{i \in \tilde{V}_r} c(i,s) + \sum _{i \in \tilde{V}_s} c(r,i) + c(0,s) + \sum _{i \in \tilde{V}_s} c(0,i) + \sum _{i \in \tilde{V}_r, j\in \tilde{V}_s} c(i,j)\nonumber \\&= \sum _{i \in \tilde{V}_r} f_i^{+} + \sum _{i \in \tilde{V}_s} f_i^{-} + f_0^{+} + \sum _{i \in \tilde{V}_s} \lambda _1 + \sum _{i \in \tilde{V}_r, j\in \tilde{V}_s} \lambda _2\nonumber \\&= \sum _{i \in \tilde{V}_r} f_i^{+} + \sum _{i \in \tilde{V}_s} f_i^{-} + f_0^{+} + k\lambda _1 + k(m-k)\lambda _2. \end{aligned}$$

(23)

Therefore, since $f_1 \ge f_2 \ge \cdots \ge f_m$, $C(V_r,V_s)$ is bounded by

$$\begin{aligned} C(V_r,V_s) \ge \sum _{i=k+1}^m f_i^{+} + \sum _{i=1}^k f_i^{-} + f_0^{-} + (m-k)\lambda _1 + k(m-k)\lambda _2, \end{aligned}$$

(24)

from (22) and

$$\begin{aligned} C(V_r,V_s) \ge \sum _{i=k+1}^m f_i^{+} + \sum _{i=1}^k f_i^{-} + f_0^{+} + k\lambda _1 + k(m-k)\lambda _2, \end{aligned}$$

(25)

from (23). The equalities in both (24) and (25) hold when $\tilde{V}_s = \{1,\dots ,k\}$ and $\tilde{V}_r = \{k+1,\dots ,m\}$. Thus, $C(V_r,V_s) \ge \sum _{i=0}^m f_i^{+} = \sum _{i=0}^m f_i^{-}$ for any cut if and only if (6) and (7) hold, completing the proof. $\square$

Corollary 1 is derived from Theorem 1 as follows.

Proof of Corollary 1

By taking $\lambda _1=0$ in Theorem 1, the Eq. (5) reduces to (8) and the inequality (6) reduces to (9). Furthermore, combining the inequalities (6) for $k=m$ and (7) for $k=0$, we obtain $\sum _{j=1}^{m} f_j = 0$. Then, the inequality (7) for $k=1,\dots ,m-1$ holds because

$$\begin{aligned} \sum _{j=k+1}^{m} f_j = \sum _{j=1}^{m} f_j - \sum _{j=1}^{k} f_j = - \sum _{j=1}^{k} f_j \ge -\lambda _2 k(m-k), \end{aligned}$$

from (9), completing the proof. $\square$

Proof of Theorem 2

This section provide a proof of Theorem 2. For the proof of Theorem 2, we introduce the following flow network $G=\{(V,E),c,r,s\}$ defined differently from that in Theorem 1.

Vertices::

Define the vertices by $V = U \cup W \cup \{r,s\}$ where $U = \{u_1,\dots ,u_m\}$ and $W=\{ w_{ij}; 1\le i < j \le m \}$.

Edges::

Define the edges by $E = \left\{ (r,u_i); i =1,\dots ,m \right\} \cup \left\{ (u_i,s); i =1,\dots ,m \right\} \cup$ $\left\{ (u_i,w_{jk}); i\in \{j,k\},1\le j< k \le m \right\} \cup \left\{ (w_{ij},s); 1\le i < j \le m \right\}$.

Capacities::

Define the capacities on the edges in E by

$$\begin{aligned} c(r,u_i)&= | f_i |,&i=1,\dots ,m, \\ c(u_i,s)&= \lambda _{i0},&i=1,\dots ,m, \\ c(u_i,w_{ij})&= c(u_j,w_{ij}) = \lambda _{ij},&1\le i< j \le m, \\ c(w_{ij},s)&= \lambda _{ij},&1\le i < j \le m, \end{aligned}$$

and, for convenience, $c(v,v^\prime ) = 0$ if $(v,v^\prime ) \notin E$ but $(v^\prime ,v) \in E$.

Then, we obtain the following lemma relating the condition (17) to the maximum flow problem on $G=\{(V,E),c,r,s\}$.

Lemma 2

There exist $\xi _{i0} \in \left[ -\lambda _{i0}, \lambda _{i0} \right]$ and $\xi _{ij},\xi _{ji} \in \left[ -\lambda _{ij}, \lambda _{ij} \right]$ such that $| \xi _{ij} | + | \xi _{ji} | \le \lambda _{ij}$ and

$$\begin{aligned} f_i + \xi _{i0} + \sum _{j \in \{1,\dots ,m\} \setminus \left\{ i \right\} }\xi _{ij} =0, \qquad i=1,\dots ,m, \end{aligned}$$

(26)

if the maximum value of a flow through r to s on $G=\{(V,E),c,r,s\}$ is $\sum _{i=1}^m | f_i |$.

Proof

Let $\tau _{ij}$ and $\tau _{ji}$ denote the flows from $u_i$ and $u_j$ to $w_{ij}$, respectively, bounded by $0\le \tau _{ij}, \tau _{ji}\le \lambda _{ij}$ from their capacity constraints. Then, from the flow conservation at $w_{ij}$, the flow from $w_{ij}$ to the sink s must be $\tau _{ij} + \tau _{ji}$, which is also bounded by $0\le \tau _{ij} + \tau _{ji}\le \lambda _{ij}$. We also denote by $\tau _{i0}$ a flow from $u_i$ to s, bounded by $0 \le \tau _{i0} \le \lambda _{i0}$ from its capacity constraint. From the capacity constraint, the value of a flow cannot be more than $\sum _{i=1}^m | f_i |$, which is attained if and only if the flows from the source r to $u_i$ is $| f_i |$ for all $u_i\in U$ and hence, from the flow conservation at $u_i\in U$, $-| f_i | + \tau _{i0} + \sum _{j \in \{1,\dots ,m\} {\setminus }\left\{ i \right\} }\tau _{ij} =0$. If such a flow exist, (26) is satisfied by setting $\xi _{ij} = s_i\tau _{ij}$ for $i \in \{1,\dots ,m\}, j\in \{0,\dots ,m\}{\setminus } \{i\}$ where $s_i = -{\text {sign}} ( f_i )$. $\square$

Note that the Eq. (26) appears in the subgradient equation within the fused group of zeros for the weighted OSCAR problem with penalty terms $\sum _{i=1}^m \lambda _{i0}|\beta _i| + \sum _{1 \le i < j \le m} \lambda _{ij}\max \{|\beta _i|,|\beta _j|\}$. We can use Lemma 2 to check the subgradient equation by seeking the maximum flow on the corresponding flow network. However, in the weighted OSCAR problem, it is generally difficult to find when the subgradient equation is violated as the regularization parameters grow. We can only provide the explicit condition to check the violation of (5) for the ordinary OSCAR problem as in Theorem 2, whose proof is provided as follows.

Proof of Theorem 2

First, it is easy to verify that (17) implies (18) as follows:

$$\begin{aligned} \begin{aligned} \sum _{i=k+1}^{m} | f_i |&\le \sum _{i=k+1}^{m}\left( | \xi _{i0} | + \sum _{j\ne i}| \xi _{ij} | \right) \\&= \sum _{i=k+1}^{m} | \xi _{i0} | + \sum _{k+1\le i<j\le m}(| \xi _{ij} |+| \xi _{ji} |) + \sum _{i=k+1}^{m} \sum _{j=1}^{k} | \xi _{ij} | \\&\le \lambda _1(m-k) + \lambda _2 \frac{(m-k)(m-k-1)}{2} + \lambda _2 k(m-k). \end{aligned} \end{aligned}$$

Consider the minimum cut problem on the same flow network $G=\{(V,E),c,r,s\}$ where $\lambda _{i0} = \lambda _1$ and $\lambda _{ij}=\lambda _2$ for all $i\ne j \in \{1,\dots ,m\}$. Let $V_r, V_s \subset V$ denote a cut of the graph such that $V_r \cup V_s = V$, $V_r \cap V_s = \emptyset$, $r\in V_r$, $s\in V_s$. We also denote $U_r = V_r \cap U$, $U_s = V_s \cap U$, $W_r = V_r \cap W$ and $W_s = V_s \cap W$. From the max-flow min-cut theorem and Lemma 2, the minimum capacity of a cut of $G=\{(V,E),c,r,s\}$ has to be just $\sum _{i=1}^m | f_i |$. When $V_r = \{r\}$ and $V_s = V{\setminus } \{r\}$, the capacity of the cut attains $\sum _{i=1}^m | f_i |$. Thus, it suffices to prove that capacity of any other cuts of the graph cannot be less than $\sum _{i=1}^m | f_i |$ if (18) holds.

The capacity $C(V_r,V_s)$ of the cut can be decomposed as follows:

$$\begin{aligned} C(V_r,V_s)&= \sum _{v\in V_r, v^\prime \in V_s, (v,v^\prime )\in E} c(v,v^\prime ) \nonumber \\&= \sum _{u \in U_s} c(r,u) + \sum _{u \in U_r} c(u,s) + \sum _{u\in U_r, w\in W_s, (u,w)\in E} c(u,w) + \sum _{w \in W_r} c(w,s). \end{aligned}$$

(27)

Since $| f_1 |\le | f_2 | \le \cdots \le | f_m |$, the first and second terms in (27) are bounded by

$$\begin{aligned} \sum _{u \in U_s} c(r,u) + \sum _{u \in U_r} c(u,s) \ge \sum _{i=1}^k | f_i | + \lambda _1 (m-k), \end{aligned}$$

where k is the cardinality of $U_s$. To bound the rest terms in (27), let $C(V_r,V_s;w_{ij})$ denote the capacity of the cut within the edges including $w_{ij}$ formulated as follows:

$$\begin{aligned} C(V_r,V_s;w_{ij}) = {\left\{ \begin{array}{ll} c(w_{ij},s) & \quad \text {if } w_{ij} \in W_r, \\ \sum _{u\in \{u_i,u_j\} \cap U_r} c(u,w_{ij}) & \quad \text {if } w_{ij} \in W_s. \end{array}\right. } \end{aligned}$$

Then, the third and fourth terms in (27) are represented by $\sum _{u\in U_r, w\in W_s, (u,w)\in E} c(u,w) + \sum _{w \in W_r} c(w,s) = \sum _{w\in W} C(V_r,V_s;w)$. Furthermore, $C(V_r,V_s;w_{ij})$ can be evaluated as follows:

• (i) If $u_i, u_j \in U_r$, we have

  $$\begin{aligned} C(V_r,V_s;w_{ij}) = {\left\{ \begin{array}{ll} \lambda _2 & \quad \text {if } w_{ij} \in W_r, \\ 2\lambda _2 & \quad \text {if } w_{ij} \in W_s. \end{array}\right. } \end{aligned}$$

• (ii) If $u_i, u_j \in U_s$, we have

  $$\begin{aligned} C(V_r,V_s;w_{ij}) = {\left\{ \begin{array}{ll} \lambda _2 & \quad \text {if } w_{ij} \in W_r, \\ 0 & \quad \text {if } w_{ij} \in W_s. \end{array}\right. } \end{aligned}$$

• (iii) Otherwise, we have $C(V_r,V_s;w_{ij}) = \lambda _2$ whichever $w_{ij} \in W_r$ or $w_{ij} \in W_s$.

Thus, since we have $\frac{(m-k)(m-k-1)}{2}$, $\frac{k(k+1)}{2}$ and $k(m-k)$ cases for (i), (ii) and (iii), respectively, the capacity $C(V_r,V_s)$ of the cut is bounded by

$$\begin{aligned} C(V_r,V_s) \ge \sum _{i=1}^k | f_i | + \lambda _1 (m-k) + \lambda _2 \frac{(m-k)(m-k-1)}{2} + \lambda _2 k(m-k), \end{aligned}$$

where the equality holds when we set, for example, $U_s = \{u_1,\dots ,u_k\}$ and $W_s=\{ w_{ij}; 1\le i<j\le k \}$. Therefore, $C(V_r,V_s) \ge \sum _{i=1}^m | f_i |$ for any cut if (18) holds, completing the proof. $\square$

Complexity of the path algorithms

The total computational cost of our path algorithms for clustered Lasso and OSCAR is $\mathcal {O}(np^2 + (T_\text {fuse}+ T_\text {split})np + T_\text {switch} n)$ time where $T_\text {fuse}$, $T_\text {split}$ and $T_\text {switch}$ are the numbers of iterations in which fusing, splitting and switching events occur, respectively. The first term $\mathcal {O}(np^2)$ is required to obtain the initial solution $\beta ^{(0)} = (X^\top X)^{-1}X^\top y$. In the following subsections, we derive the complexity per iteration for each event type.

1.1 Complexity per iteration for fusing/splitting events

In this subsection, we discuss the complexity of the iteration where a fusing/splitting event occurs. More specifically, we evaluate the computational cost of updating ${\mathcal {G}}$, $\beta ^{\mathcal {G}}$, $X^{\mathcal {G}}$, $o(\cdot )$, $[(X^{\mathcal {G}}_{-0})^\top X^{\mathcal {G}}_{-0}]^{-1}$, $\frac{\textrm{d}\beta ^{\mathcal {G}}}{\textrm{d}\eta }$ and $\frac{\textrm{d}\beta }{\textrm{d}\eta }$ by the fusion/split of the groups and then calculating the next timings of the events.

First, we focus on the update of $[(X^{\mathcal {G}}_{-0})^\top X^{\mathcal {G}}_{-0}]^{-1}$ where a few columns in $X^{\mathcal {G}}_{-0}$ are replaced by a fusing/splitting event. When the set $\mathcal {G}$ of fused groups is changed into $\mathcal {\tilde{G}}$ by a fusing/splitting event, let $X^{\mathcal {G}} = [X_{(1)},X_{(2)}]$ and $X^{\mathcal {\tilde{G}}} = [X_{(1)},\tilde{X}_{(2)}]$ denote the grouped design matrices sharing some columns $X_{(1)} \in \mathbb {R}^{n\times p_{(1)}}$ but having different ones $X_{(2)}\in \mathbb {R}^{n\times p_{(2)}}$ and $\tilde{X}_{(2)}\in \mathbb {R}^{n\times \tilde{p}_{(2)}}$, respectively. We can permute the columns of $X^{\mathcal {G}}$ and $X^{\mathcal {\tilde{G}}}$ to apply those notations and recover their original orders after the update. Note that, because at most two groups are involved in a fusing/splitting event, the number of columns replaced by a fusing/splitting event cannot exceed two, that is, $p_{(2)},\tilde{p}_{(2)}\le 2$. Moreover, because we assume $n\ge p$ and ${\text {rank}}\left( X \right) = p$, we have $n > p_{(1)}$ and the inverse of $(X^{\mathcal {G}}_{-0})^\top X^{\mathcal {G}}_{-0}$ always exists.

Then, we can update $Z = [(X^{\mathcal {G}}_{-0})^\top X^{\mathcal {G}}_{-0}]^{-1}$ into $\tilde{Z} = [(X^{\mathcal {\tilde{G}}}_{-0})^\top X^{\mathcal {\tilde{G}}}_{-0}]^{-1}$ by using the following lemma:

Lemma 3

Given $X_1,X_2,\tilde{X}_2$ and $Z = [(X^{\mathcal {G}}_{-0})^\top X^{\mathcal {G}}_{-0}]^{-1}$ decomposed in a block matrix

$$\begin{aligned} Z = \begin{bmatrix} Z_{11} & \quad Z_{12} \\ Z_{21} & \quad Z_{22} \end{bmatrix}, \end{aligned}$$

with $Z_{11} \in \mathbb {R}^{p_{(1)}\times p_{(1)}}$, $Z_{12}=Z_{21}^\top \in \mathbb {R}^{p_{(1)}\times p_{(2)}}$ and $Z_{22} \in \mathbb {R}^{p_{(2)}\times p_{(2)}}$. Then, $\tilde{Z} = [(X^{\mathcal {\tilde{G}}}_{-0})^\top X^{\mathcal {\tilde{G}}}_{-0}]^{-1}$ is obtained by

$$\begin{aligned} \tilde{Z} = \begin{bmatrix} U+UVWV^\top U & \quad -UVW \\ -WV^\top U & \quad W \end{bmatrix}, \end{aligned}$$

(28)

where $U = Z_{11}-Z_{12}Z_{22}^{-1}Z_{21}$, $V = X_{(1)}^\top \tilde{X}_{(2)}$ and $W = (\tilde{X}_{(2)}^\top \tilde{X}_{(2)}- V^\top UV)^{-1}$. Moreover, the computation of (28) requires $\mathcal {O}(np_{(1)})$ time.

Proof

From block matrix inversion of $\tilde{Z} = [(X^{\mathcal {\tilde{G}}}_{-0})^\top X^{\mathcal {\tilde{G}}}_{-0}]^{-1} = ([X_{(1)},\tilde{X}_{(2)}]^\top [X_{(1)},\tilde{X}_{(2)}])^{-1}$, we yield

$$\begin{aligned} \tilde{Z} = \begin{bmatrix} A & \quad V \\ V^\top & \quad D \end{bmatrix}^{-1}=\begin{bmatrix} A^{-1}+A^{-1}VS^{-1}V^\top A^{-1} & \quad -A^{-1}VS^{-1} \\ -S^{-1}V^\top A^{-1} & \quad S^{-1} \end{bmatrix}, \end{aligned}$$

(29)

where $A = X_{(1)}^\top X_{(1)}$, $V=X_{(1)}^\top \tilde{X}_{(2)}$, $D = \tilde{X}_{(2)}^\top \tilde{X}_{(2)}$ and $S=D-V^\top A^{-1}V$. Since we also obtain $A = X_{(1)}^\top X_{(1)} = (Z_{11}-Z_{12}Z_{22}^{-1}Z_{21})^{-1}$ from block matrix inversion of $Z = [(X^{\mathcal {G}}_{-0})^\top X^{\mathcal {G}}_{-0}]^{-1} = ([X_{(1)},X_{(2)}]^\top [X_{(1)},X_{(2)}])^{-1}$, we yield (28) by substituting $U = A^{-1}$ and $W = S^{-1}$ into (29).

Using $p_{(2)},\tilde{p}_{(2)}\le 2$, U, V and W can be obtained in $\mathcal {O}(p_{(1)}^2)$ time, $\mathcal {O}(np_{(1)})$ time and $\mathcal {O}(p_{(1)}^2)$ time, respectively. Therefore, because $n > p_{(1)}$, the computation of $\tilde{Z}$ requires $\mathcal {O}(np_{(1)})$ time. $\square$

From Lemma 3, $[(X^{\mathcal {G}}_{-0})^\top X^{\mathcal {G}}_{-0}]^{-1}$ can be updated in $\mathcal {O}(n| {\mathcal {G}} |)$ time where $| {\mathcal {G}} |$ is the number of fused groups which is equal to the number of columns in $X^{\mathcal {G}}$. Moreover, because $n\ge p$, the complexity of updating the other variables ${\mathcal {G}}$, $\beta ^{\mathcal {G}}$, $X^{\mathcal {G}}$, $o(\cdot )$, $\frac{\textrm{d}\beta ^{\mathcal {G}}}{\textrm{d}\eta }$ and $\frac{\textrm{d}\beta }{\textrm{d}\eta }$ is no more than that of updating $[(X^{\mathcal {G}}_{-0})^\top X^{\mathcal {G}}_{-0}]^{-1}$. Thus, updating those variables when a fusing/splitting event occurs requires $\mathcal {O}(n| {\mathcal {G}} |)$ time.

After updating those variables, the computational cost to calculate the next timings of events $\Delta _{g}^\text {fuse}, \Delta _{g, k}^\text {split}$ and $\Delta _{k}^\text {switch}$ is evaluated as follows:

• All the timings of fusing events $\Delta _{g}^\text {fuse}$ can be obtained in $\mathcal {O}(| {\mathcal {G}} |)$ time.

• To obtain the timings of splitting/switching events, we need to calculate $X^{\mathcal {G}}\beta ^{\mathcal {G}}$ and $X^{\mathcal {G}}\frac{\textrm{d}\beta ^{\mathcal {G}}}{\textrm{d}\eta }$ which requires $\mathcal {O}(n | {\mathcal {G}} |)$ time. Then, given $X^{\mathcal {G}}\beta ^{\mathcal {G}}$ and $X^{\mathcal {G}}\frac{\textrm{d}\beta ^{\mathcal {G}}}{\textrm{d}\eta }$, each timing of splitting/switching events can be obtained in $\mathcal {O}(n)$ time. Thus, the computation of all the timings of splitting events $\Delta _{g, k}^\text {split}$ and switching events $\Delta _{k}^\text {switch}$ requires $\mathcal {O}(np)$ time.

Above all, it requires $\mathcal {O}(np)$ time to update all the variables and the next timings of events for a fusing/splitting event.

1.2 Complexity per iteration for switching events

Next, we discuss the complexity of the iteration where a switching event occurs.

When the switching event which swaps the indices assigned to o(k) and $o(k+1)$ in a group $G_g$ occurs, the other variables ${\mathcal {G}}$, $\beta ^{\mathcal {G}}$, $X^{\mathcal {G}}$, $[(X^{\mathcal {G}}_{-0})^\top X^{\mathcal {G}}_{-0}]^{-1}$, $\frac{\textrm{d}\beta ^{\mathcal {G}}}{\textrm{d}\eta }$ and $\frac{\textrm{d}\beta }{\textrm{d}\eta }$ than o(k) and $o(k+1)$ are preserved as before the event. As for the next timings of events, we need to calculate the following ones by their definition using $x_{o(k)}$, $x_{o(k+1)}$, $x_{\underline{o}(g,k)}$ and $x_{\overline{o}(g,k)}$ updated in the switching event.

• $\Delta _{g,k}^{\text {split}}$ and, for $g=0$ in clustered Lasso, $\Delta _{g,-k}^{\text {split}}$.

• $\Delta _{k-1}^\text {switch}$, $\Delta _{k}^\text {switch}$ and $\Delta _{k+1}^\text {switch}$.

Each of them can be obtained in $\mathcal {O}(n)$ time. The remainder of the next timings of events can be updated by only subtracting the step size $\Delta _{k}^\text {switch}$ of the current switching event from them, which only requires $\mathcal {O}(p)$ time.

Thus, it requires $\mathcal {O}(n)$ time to update the variables and the next timings of events for a switching event of a pair of indices. Similarly, the computation for the switching event which flips the sign of $s_1$ in OSCAR also requires $\mathcal {O}(n)$.

Accuracy of clustered Lasso and OSCAR in numerical experience

In this section, we compare the estimation accuracy of clustered Lasso, OSCAR, and other sparse regularization techniques (Ridge, Lasso, and Elastic Net) using synthetic data under various experimental conditions. These simulations were conducted on a Macbook Pro (15-inch, 2017), MacOS Monterey version 12.6, with an Intel i7-7920HQ at 3.1 GHz and 16 GB of RAM, using MATLAB. The five simulation examples used in this study are the same as those in Bondell and Reich (2008), which were modified from the simulation study in Zou and Hastie (2005).

In each example, data were generated from the following regression model:

$$\begin{aligned} y = X\beta +\epsilon , \ \ \epsilon \sim N(0, \sigma ^2). \end{aligned}$$

For each example, 500 datasets were generated. Each dataset consisted of a training set of size n and an independent validation set of size n used only for selecting the tuning parameters. For each dataset, our path algorithms were applied to the training data with tuning direction $[\bar{\lambda }_{1}, \bar{\lambda }_{2}]\in \{[0, 1], [0.25, 1], [0.5, 1], [1, 1], [2, 1], [4, 1], [8, 1], [16, 1]\}$, respectively. After yielding the solution paths with these tuning directions, the optimal values of $[\lambda _1, \lambda _2]$ were selected from them based on the mean squared prediction error in the validation data. For Ridge, Lasso, and Elastic Net,⁴ the regularization parameter was tuned via a grid search over $\lambda = 10^{-3 + \frac{i}{100}} (i=0,\ldots , 5000)$ based on the mean squared prediction error in the validation data.

After obtaining the estimate $\hat{\beta }$ with the optimal regularization parameter, we evaluated the estimation accuracy by the mean squared error (MSE) whose formula is introduced by Tibshirani (1996) as

$$\begin{aligned} \text {MSE} = (\hat{\beta } - \beta )^T V (\hat{\beta } - \beta ), \end{aligned}$$

where V is the population covariance matrix of X.

The five simulation scenarios are described as follows:

• Example 1: The dataset size is set to $n=20$ and the dimension of predictors is set to $p=8$. The true parameters are set to $\beta = (3,2,1.5,0,0,0,0,0)^T$ and $\sigma =3$, and the covariance matrix is given by $\textrm{Cov}\left[ x_i, x_j \right] = 0.7^{| i-j |}$

• Example 2: This example has the same settings as Example 1, except for $\beta =(3,0,0,1.5,0,0,0,2)^T$.

• Example 3: This example has the same settings as Example 1, except that $\beta _j = 0.85$ for all j.

• Example 4: The dataset size is set to $n=100$ and the dimension of predictors is set to $p=40$. The true parameters are set to

  $$\begin{aligned} \beta = (\underbrace{0, \ldots , 0}_{10}, \underbrace{2, \ldots , 2}_{10}, \underbrace{0, \ldots , 0}_{10}, \underbrace{2, \ldots , 2}_{10})^T \end{aligned}$$

  and $\sigma = 15$, and the covariance matrix is given by $\textrm{Cov}\left[ x_i, x_j \right] = 0.5$ for $i\ne j$ and $\textrm{Var} \left[ x_i \right] = 1$.

• Example 5: The dataset size is set to $n=50$ and the dimension of predictors is set to $p=40$. The true parameters are set to

  $$\begin{aligned} \beta = (\underbrace{3, \ldots , 3}_{15}, \underbrace{0, \ldots , 0}_{25}) ^ T \end{aligned}$$

  and $\sigma = 15$. The predictors are generated as follows:

  $$\begin{aligned} x_i&= Z_1 + \epsilon _i^x, Z_1 \sim N(0, 1)\ \ (i = 1, \ldots 5) \\ x_i&= Z_2 + \epsilon _i^x, Z_2 \sim N(0, 1)\ \ (i = 6, \ldots 10) \\ x_i&= Z_3 + \epsilon _i^x, Z_3 \sim N(0, 1)\ \ (i = 11, \ldots 15) \\ x_i&\sim N(0, 1) \ \ (i = 16, \ldots 40), \\ \end{aligned}$$

  where $\epsilon _i^x$ is independently distributed as $N(0, 0.16), i= 1, \ldots , 15$. In this model, each of the top three groups has pairwise correlation $\rho \approx 0.85$, and the remaining 25 predictors are pure noise features.

Table 4 Median values of the MSE and number of nonzero groups (gnnz) from 500 replications. The values in parentheses represent the standard errors estimated using the bootstrap method with 500 resamplings

Table 4 summarizes the MSEs and the number of nonzero groups (gnnz), which indicates the complexity of the model in terms of the number of unique non-zero coefficients. According to the MSEs, clustered Lasso and OSCAR are highly competitive in prediction. Clustered Lasso achieves the lowest MSE in all examples, whereas OSCAR attains the second lowest MSE, except for Example 4. As seen from the gnnz in Table 4, clustered Lasso provides the least complex model. Particularly in Example 3, the median gnnz for clustered Lasso is only two, which contributed to the considerably lowest MSE in clustered Lasso. OSCAR also yields the second or third least gnnz in all example. Although the gnnz values for clustered Lasso and OSCAR are larger than those of the true coefficients in most cases, both methods demonstrate a significant reduction in model complexity.