1 Introduction

Arc welding is accompanied by generation of the welding fumes, which have toxicological and ecological danger. Welding fume is formed as a mixture of high-temperature metal vapors (where iron is a predominate component) from the arc and shielding gas, in the case if the gas metal arc welding (GMAW) is used. Initial vapor temperature \(T_{0} \sim 3000\,\mathrm{K}\), therefore, electron–atom collisions cause the vapor–gas mixture partial ionization, i.e. the plasma formation.

Ionization balance in the complex thermal plasma, which consists of the electrons, ions and atoms, is determined by the atoms’ impact ionization and electron–ion recombination and is described by well-known Saha equation (Mitchner and Kruger 1973).

The vapor–gas mixture cools down in the form of a divergent flow into air. The vapor supersaturation growth under cooling leads to vapor condensation, which begins for iron at the temperature \(T\sim 2700\)–\(2800\,\mathrm{K}\) (Vishnyakov et al. 2013). Initial iron atom number density \(n_{\mathrm{A}} \sim 10^{18}\,\text{cm}^{-3}\). Iron ionization potential \(I = 7.9\,\mathrm{eV}\) and for the temperature of 2700 K Saha equation gives the electron and ion number density \(n_{\mathrm{e}} = n_{\mathrm{i}} \sim 10^{13}\,\text{cm}^{-3}\). Condensation of the iron vapor provides the nucleus number density \(n_{\mathrm{n}} \sim 10^{16}\)–\(10^{17}\,\text{cm}^{-3}\). Condensations occurs as a heterogeneous ion-induced nucleation, therefore, initial nuclei have the positive charge. In these conditions, electrons are captured by nuclei and ionization balance cannot be described by Saha equation.

For the first time, the effect of dust particles on plasma ionization balance was observed by Calcote (1948), later by Sugden and Thrush (1951), and Shuler and Weber (1954). It was assumed that the source of excess electrons is the thermionic emission from the particles’ surface. Gibson (1966) has considered in details how the thermionic emission from particle surface influence the plasma ionization balance. Further investigations were devoted, basically, to the determination of electron number density and particle charges (Goree 1994; Shukla and Mamun 2002; Sodha and Kaw 1968; Sodha and Mishra 2011; Yakubov and Khrapak 1989). Ionization balance in the dusty plasma was studied insufficiently. The systems, in which it was possible to neglect electrons, were not considered at all.

The two-component plasmas was considered earlier as a dust-electron plasma, in which ionization balance is ensured by equality between thermionic flux from particle and the electron–particle collision backflow (Vishnyakov and Dragan 2004; Vishnyakov 2016). In the nucleation zone of the welding fume, another kind of the two-component plasma takes place, which can be named as a dust-ion plasma.

Such a dust–ion plasma is considered in the present paper. The consideration is based on the modeling of a single gas parcel evolution. Each moment of the gas parcel evolution corresponds to some plasma space volume, because vapor–gas mixture is the flow. Therefore, such consideration allows studying all processes in the welding fume.

2 Ionization Balance in Complex Plasmas with UV Source

The welding fume plasma is affected by UV-radiation from electric arc, which provides the photon flux as a function of photon energy, determined by Planck’s law (Pohl 1963):

$$\begin{aligned} j_{\mathrm{ph}}(h\nu ) = {\frac{2 (h\nu )^2}{c^2 h^3}} {\frac{1}{\exp {\frac{h\nu }{k_\mathrm{B} T_{\mathrm{arc}}}}-1}}, \end{aligned}$$
(1)

where c is the light velocity, h is the Planck constant, \(T_{\mathrm{arc}} \) is the arc effective temperature, \(k_{\mathrm{B}} \) is the Boltzmann constant.

Effective temperature \(T_{\mathrm{arc}} = 5000\,\mathrm{K}\) corresponds to arc UV-radiation power of \(5\,\mathrm{W}\mathrm{/} \mathrm{m}^{\mathrm{2}}\), which is observed in GMAW, and provides the photon flux with energy higher than atom ionization potential \(h\nu \ge I = 7.9\,\mathrm{eV}\) (for iron) \(j_{\mathrm{ph}} \sim 10^{16}\,\text{cm}^{-2}\, \text{s}^{-1}\) .

The photoionization cross section in the Kramers–Heisenberg approach (Zel’dovich and Raizer 1966):

$$\begin{aligned} \sigma _{\mathrm{ph}}(h\nu ) = {\frac{8h^3}{3 \sqrt{3} \pi ^2 c e^2 m_\mathrm{e}^2}} \left( {\frac{I}{h\nu }} \right) ^3. \end{aligned}$$

Thus, electron/ion generation via UV ionization is determined by the following equation:

$$\begin{aligned} {\frac{{\mathrm{d}n_{\mathrm{e(i)}}}}{{\mathrm{d}t}}}= & {} n_{\mathrm{a}} {\frac{16 I^3}{3 \sqrt{3} \pi ^2 c^3 e^2 m_\mathrm{e}^2}}{\int \limits _{I /k_{\mathrm{B}} T_{\mathrm{arc}}} ^{\infty } {\frac{\mathrm{d}x}{x (\exp {x} - 1)}}}\nonumber \\= & {} \frac{n_\mathrm{a}}{\tau _{\mathrm{UV}}} \equiv Q_{\mathrm{UV}} , \end{aligned}$$
(2)

where \(n_\mathrm{a} \) is the atom number density, \(\tau _\mathrm{UV} \sim 0.1\, \mathrm{s}\) is the photoionization time constant.

Ionization rate via electron–atom collisions is described by following equation (Mitchner and Kruger 1973):

$$\begin{aligned} Q_{\mathrm{V}}^{\mathrm{ion}} = n_{\mathrm{e}} n_{\mathrm{a}} k_{\mathrm{ion}} , \end{aligned}$$
(3)

where \(k_{\mathrm{ion}} = \pi r_{\mathrm{a}}^{2} v_{\mathrm{Te}} \) is the ionization rate constant, \(v_{\mathrm{Te}} = \sqrt{8k_{\mathrm{B}} T / \pi m_{\mathrm{e}}} \) is the electron thermal velocity.

Recombination rate is described as:

$$\begin{aligned} Q_{\mathrm{V}}^{\mathrm{rec}} = n_{\mathrm{e}}^{2} n_{\mathrm{i}} k_{\mathrm{rec}} , \end{aligned}$$
(4)

where \(k_{\mathrm{rec}} = k_{\mathrm{ion}} / K_{\mathrm{S}} \) is the recombination rate constant, \(K_{\mathrm{S}} \) is the Saha constant:

$$\begin{aligned} K_{\mathrm{S}} = \frac{\varSigma _\mathrm{i}}{\varSigma _\mathrm{a}} \nu _\mathrm{e} \exp {\frac{ -I}{k_\mathrm{B} T}}, \end{aligned}$$

where \(\varSigma _{\mathrm{i}} \) and \(\varSigma _{\mathrm{a}} \) are the statistical weights for ions and atoms, respectively, \(\nu _{\mathrm{e}} = 2(2\pi m_{\mathrm{e}} k_{\mathrm{B}} T / h^{2})^{3 /2}\) is the electron states’ effective density.

The balance of Eqs. (3) and (4) leads to Saha equation for usual thermal ionization:

$$\begin{aligned} {\frac{{n_{\mathrm{e}} n_{\mathrm{i}}}}{{n_{\mathrm{a}}}} } = K_{\mathrm{S}} . \end{aligned}$$
(5)

Ionization balance in the thermal plasma with UV-radiation is determined by equation:

$$\begin{aligned} Q_{\mathrm{UV}} + Q_{\mathrm{V}}^{\mathrm{ion}} = Q_{\mathrm{V}}^{\mathrm{rec}} . \end{aligned}$$
(6)

In this case, equilibrium ionization is described as:

$$\begin{aligned} {\frac{{n_{\mathrm{e}} n_{\mathrm{i}}}}{{n_{\mathrm{a}}}} } = K_{\mathrm{S}} \left( {1 + {\frac{1}{n_{\mathrm{e}} k_{\mathrm{ion}}\tau _{\mathrm{UV}}}}} \right) . \end{aligned}$$
(7)

Electrical neutrality in the plasma without dust component is described as \(n_{\mathrm{e}} = n_{\mathrm{i}} = n_{0} \), where \(n_{0} \) is the unperturbed number density, which, as it follows from Eq. (7), is determined by solution of the equation

$$\begin{aligned} n_{0}^{3} + K_{\mathrm{S}} n_{0}^{2} - K_{\mathrm{S}} \left( {n_{\mathrm{A}} - {\frac{{1}}{{k_{\mathrm{ion}}\tau _{\mathrm{UV}}}} }} \right) n_{0} - {\frac{K_{\mathrm{S}} n_{\mathrm{A}}}{k_{\mathrm{ion}}\tau _{\mathrm{UV}}} } = 0; \end{aligned}$$

and in the temperature range \(T > 2000\,\mathrm{K}\) this solution differs little from the value \(n_{0} \), which is solution of Eq. (5).

Thus, the influence of ionization by UV-radiation can be neglected at the plasma temperature \(T > 2000\,\mathrm{K}\) and photon flux \(j_{\mathrm{ph}} \sim 10^{16}\,\text{cm}^{-2}\,\text{s}^{-1}\) (volume ionization time constant is \((n_0 k_{\mathrm{ion}})^{-1} \sim 5\,\upmu \)s at the temperature of 3000 K). This influence becomes appreciable at the temperature \(T < 1900\,\mathrm{K}\).

3 Nucleation

The metal vapors with initial temperature \(T_{0} \sim 3000\,\mathrm{K}\) mix with shielding gas with temperature \(T_{\mathrm{sg}} \sim 300\,\mathrm{K}\) and cools down. The vapor–gas mixture temperature in the gas parcel is described by the following equation (Vishnyakov et al. 2017b, 2018a):

$$\begin{aligned} T = T_{\mathrm{sg}} + (T_{0} - T_{\mathrm{sg}} )\exp {\frac{{ - t}}{{\tau _{\mathrm{mix}}}} }, \end{aligned}$$
(8)

where \(\tau _{\mathrm{mix}} \) is the mixing time scale, which is defined experimentally. In the system under consideration \(\tau _{\mathrm{mix}} = 1.7\,\mathrm{ms}\), that has been determined by coincidence via the calculated and measured condensed particles’ chemical composition (Vishnyakov et al. 2018b).

Temperature time dependency determines the change in number densities of the condensable atoms:

$$\begin{aligned} n_{\mathrm{Aj}} = {\frac{{P}}{{k_{\mathrm{B}} T}}}g_\mathrm{{i}} , \quad g_\mathrm{{j}} = {\frac{{g_\mathrm{{j0}}}}{{\mu _\mathrm{{j}} {\sum \nolimits _{j} {{\frac{{g_\mathrm{{j0}} }}{{\mu _{\mathrm{j}}}} } + {\frac{{\mu _{\mathrm{j}}}}{{\mu _{\mathrm{sg}}}} }\exp {\frac{{t}}{{\tau _{\mathrm{mix}}}} }}}} }}, \end{aligned}$$
(9)

where P is the atmospheric pressure, \(g_{{\mathrm{j0}}} \) is the initial mass fraction of the component in vapors, \(\mu \) is the molecular (atom) mass.

In the multicomponent systems, Saha equation should be solved for each component, and then unperturbed number density is determined as a sum of individual solutions. The initial iron mass fraction \(g_{\mathrm{Fe0}} = 0.97\) in the system under consideration, which at the temperature 3000 K provides initial iron number density \(n_{\mathrm{A}} = 2.4\times 10^{18}\,\text{cm}^{-3}\) and unperturbed number density \(n_{0} = 1.4\times 10^{13}\,\text{cm}^{-3}\).

The vapor–gas mixture cooling provides the increase of vapor supersaturation: \(S_{\mathrm{j}} = P_{\mathrm{j}} / P_{\mathrm{j,sat}} \), where \(P_{\mathrm{j}} = g_{\mathrm{j}} P\) is the partial pressure, \(P_{\mathrm{j,sat}} \) is the saturated vapor pressure, \(P_{\mathrm{sat}} = A\exp ( - B / T)\), A and B are the Antoine constants. In the system under consideration, the iron supersaturation at the temperature \(\sim 2780\,\mathrm{K}\) reaches such value when nucleation starts (Vishnyakov et al. 2011). The nucleus number density is determined by following equation (Vishnyakov et al. 2013):

$$\begin{aligned} n_{\mathrm{n}} = {\frac{{n_{\mathrm{a0}}}}{{N_{\mathrm{an}} + N_{\mathrm{an}}^{ - 3 / 2} \exp {\frac{{\varDelta G(r_{\mathrm{n}} )}}{{k_{\mathrm{B}} T}}}}}}, \end{aligned}$$
(10)

where \(n_{\mathrm{a0}} = n_{\mathrm{A}} - n_{0} \) is the iron atom number density before nucleation, \(N_{\mathrm{an}} = 4\pi r_{\mathrm{n}}^{3} \rho / 3m_{\mathrm{a}} \) is the average atoms’ number in the single nucleus, \(r_{\mathrm{n}} \) is the average nucleus radius, \(\rho \) is the density, \(m_{\mathrm{a}} \) is the iron atomic mass, \(\varDelta G(r_{\mathrm{n}} )\) is the change in Gibbs free energy under formation of equilibrium nucleus with radius \(r_{\mathrm{n}} \).

The nucleus number density under existing conditions is \(n_{\mathrm{n}} \sim 10^{16}\,\text{cm}^{-3}\) that is much greater equilibrium (Saha) electron number density, which is \(\sim 4\times 10^{12}\,\text{cm}^{-3}\) in the nucleation region. The iron atom number density decreases down to \(n_{\mathrm{A}} = 1.8\times 10^{18}\,\text{cm}^{-3}\), because part of atoms transfers into liquid phase of nuclei.

4 Surface Ionization

Appearance of the large number of nuclei in the system leads to creation of the new additional ionization/recombination channel, which is caused by the atoms and ions interaction with nucleus surface. Surface atom ionization degree is described by well-known Saha–Langmuir equation (Dresser 1968):

$$\begin{aligned} \alpha _{\mathrm{s}} = {\frac{{n_{\mathrm{is}}}}{{n_{\mathrm{as}}}} } = {\frac{{\varSigma _{\mathrm{i}}}}{{\varSigma _{\mathrm{a}}}} }\exp {\frac{{W_{\mathrm{n}} - I}}{{k_{\mathrm{B}} T}}}, \end{aligned}$$
(11)

where \(n_{\mathrm{is}} \) is the ion number density near nucleus surface, \(n_{\mathrm{as}} \) is the atom number density as a result of ionization near nucleus surface, \(W_{\mathrm{n}} \) is the electron work function for nucleus, which differs from the work function for flat surface (Smirnov 1997): \(W_{\mathrm{n}} = W + 0.39e^{2} / r_{\mathrm{n}} \).

Surface atom ionization rate is described by following equation

$$\begin{aligned} Q_{_{\mathrm{s}}} ^{\mathrm{ion}} = n_{\mathrm{a}} n_{\mathrm{n}} v_{\mathrm{Ta}} \sigma _{\mathrm{an}} \beta _{\mathrm{s}} , \end{aligned}$$
(12)

where \(v_{\mathrm{Ta}} \) is the atom thermal velocity, \(\sigma _{\mathrm{an}} = \pi r_{\mathrm{n}}^{2} \) is the atom-nucleus collision cross section, \(\beta _{s} = \alpha _{\mathrm{s}} / (1 + \alpha _{\mathrm{s}} )\) is the surface ionization coefficient with neglected desorption energy (Vishnyakov 2007).

Surface ion recombination rate is:

$$\begin{aligned} Q_{_{\mathrm{s}}} ^{\mathrm{rec}} = n_{\mathrm{i}} n_{\mathrm{n}} v_{\mathrm{Ti}} \sigma _{\mathrm{in}} \gamma _{\mathrm{s}} , \end{aligned}$$
(13)

where \(v_{\mathrm{Ti}} \cong v_{\mathrm{Ta}} \) is the ion thermal velocity,

$$\begin{aligned} \sigma _{\mathrm{in}} = \pi r_{\mathrm{n}}^{2} \left( {1 - {\frac{{e^{2}Z_{\mathrm{n}}}}{{r_{\mathrm{n}} k_{\mathrm{B}} T}}}} \right) \end{aligned}$$

is the ion-nucleus collision cross section (Fortov et al. 2004), \(eZ_{\mathrm{n}} \) is the nucleus charge, \(\gamma _{\mathrm{s}} = 1 / (1 + \alpha _{\mathrm{s}} )\) is the surface recombination coefficient.

The thermoelectric and photoelectric emissions from nucleus surface should be also taken into account. Thermionic emission is determined by Richardson equation:

$$\begin{aligned} j_{\mathrm{e}}^{\mathrm{T}} = {\frac{{4\pi m_{\mathrm{e}} (k_{\mathrm{B}} T)^{2}}}{{(2\pi \hbar )^{3}}}}\exp {\frac{{ - W_{\mathrm{n}}}}{{k_{\mathrm{B}} T}}} = {\frac{{1}}{{4}}}\nu _{\mathrm{e}} v_{\mathrm{Te}} \exp {\frac{{ - W_{\mathrm{n}}}}{{k_{\mathrm{B}} T}}}, \end{aligned}$$

and thermionic emission rate is

$$\begin{aligned} Q_{_{\mathrm{em}}} ^{\mathrm{T}} = \pi r_{\mathrm{n}}^{2} n_{\mathrm{n}} \nu _{\mathrm{e}} v_{\mathrm{Te}} \exp {\frac{{ - W_{\mathrm{n}} }}{{k_{\mathrm{B}} T}}}. \end{aligned}$$
(14)

UV electron emission rate is:

$$\begin{aligned} Q_{\mathrm{em}}^{\mathrm{ph}} = \pi r_{\mathrm{n}}^{2} n_{\mathrm{n}} j_{\mathrm{ph}} Y_{\mathrm{n}} , \end{aligned}$$
(15)

where \(Y_{\mathrm{n}} \sim 0.1\) is the quantum yield.

Electron adsorption rate via sporadically collisions:

$$\begin{aligned} Q_{\mathrm{e}}^{\mathrm{ads}} = n_{\mathrm{e}} n_{\mathrm{n}} \sigma _{\mathrm{en}} v_{\mathrm{Te}} , \end{aligned}$$
(16)

where electron–nucleus collision cross section is

$$\begin{aligned} \sigma _{\mathrm{en}} = \pi r_{\mathrm{n}}^{2} \left( {1 + {\frac{{e^{2}Z_{\mathrm{n}}}}{{r_{\mathrm{n}} k_{\mathrm{B}} T}}}} \right) . \end{aligned}$$

Thus, it is possible to describe ionization balance by separate equations for electrons and ions, considering the volume [Eqs. (1), (3), (4)] and surface [Eqs. (12)–(16)] processes:

$$\begin{aligned}&Q_{\mathrm{UV}} + Q_{_{\mathrm{V}}} ^{\mathrm{ion}} + Q_{\mathrm{em}}^{\mathrm{T}} + Q_{\mathrm{em}}^{\mathrm{ph}} = Q_{\mathrm{V}}^{\mathrm{rec}} + Q_{e}^{\mathrm{ads}} , \end{aligned}$$
(17)
$$\begin{aligned}&Q_{\mathrm{UV}} + Q_{_{\mathrm{V}}} ^{\mathrm{ion}} + Q_{\mathrm{s}}^{\mathrm{ion}} = Q_{\mathrm{V}}^{\mathrm{rec}} + Q_{\mathrm{s}}^{\mathrm{rec}} . \end{aligned}$$
(18)
Fig. 1
figure 1

Evolution of ionization, recombination and emission rates

Full size image

Evolutions of the values of ionization, recombination and emission rates during nucleation are presented in Fig. 1 The equilibrium nucleus is in potential well and some activation energy is necessary for the nucleus growth. This activation energy decreases down to zero with the vapor–gas mixture cooling. After that, nucleation transfers into unrestricted growth of nuclei.

Solution of Eqs. (17) and (18) gives greater values of ion number density, than for electron number density. The surface ionization rate is increased and volume ionization rate is decreased in the nucleation region. Thus, the basic ionization mechanism in the nucleation region is the surface ionization.

5 Discussion

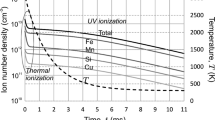
Calculated evolution of the number densities of iron atoms, charge carriers and nuclei are presented in Fig. 2 from the beginning of vapor-shielding gas mixing at temperature 3000 K to nucleation stopping at temperature 2680 K. Evolution of the nucleus average radius and charge during nucleation are presented in Fig. 3.

Fig. 2
figure 2

Evolution of the number densities

Full size image
Fig. 3
figure 3

Evolution of the nucleus radius and charge during nucleation

Full size image

Plasma ionization balance is described by Saha equation before nucleation starts (\(t = 0{-}0.14\,\mathrm{ms})\). Nucleation creates new ionization and recombination channels, that leads to expansive growth of the ion number density. Equilibrium nucleus number density remains much greater than ion number density; however, ions are the centers of ion-induced nucleation and their number should correspond to nuclei number. When nucleation occurs, ions disappear from gas phase and electron–ion recombination is replaced by the neutralization of nuclei with greater collision cross section. As a result, the balance between ionization and recombination is broken in favor of ionization, and new electrons and ions appear in the plasma via impact atom ionization, until electrons are being captured by nuclei. Therefore, achievement of equilibrium nucleus number is the time-phased process, which includes additional atom ionization and formation of additional nuclei until equilibrium will be reached.

This process lasts about 100 nanoseconds. Evolution of the number densities of iron atoms, charge carriers, nuclei and nucleus charge during stabilization are presented in Fig. 4. Vapor condensation occurs on the positive charged ions; therefore, nucleus has initial positive charge. However, large electron–nucleus collision frequency causes rapid nucleus neutralization.

Fig. 4
figure 4

Evolution of number densities and nucleus charge during stabilization

Full size image

6 Conclusion

The volume thermal ionization is the basic process of plasma formation in the mixing zone of welding fume before nucleation. Ionization balance in this zone is described by Saha equation, because photoionization by UV-radiation from arc can be neglected.

When nucleation starts, the ionization mechanism is changed and ionization balance becomes determined by interphase interaction, because thermodynamics requires nucleus number density, that is much greater than ion number density. At same time the electrons are captured by nuclei.

Thus, the dust–ion plasma, which has the ions and charged nuclei as the base components in the buffer gas, is formed. The ionization balance in such a plasma is determined by the atom and ion interaction with surface of the particles, which are the nuclei in the system under consideration.

The dust–ion plasma exists during nucleation. When nucleation terminates and nucleus growth begins, requirement to number of nuclei disappears. The intense Brownian collisions and coagulation leads to the nucleus number density decrease, and accordingly, to the decrease of surface interaction.

It should be taken into account that such a change of the ionization mechanism can occur only if the alkali metal additional agents are absent in the plasma, because their presence leads to ion number density increase and nucleus number density decrease, that was demonstrated experimentally by Vishnyakov et al. (2017a).