1 Introduction

We live in a world of (at least) three spatial dimensions. However, for some physical systems, a two-dimensional description appears to provide a suitable approximation for the dynamics involved. This happens when one dimension is highly compactified like in thin films or due to some other physical mechanisms, like rotation or strong magnetic fields, that prevents variations along one dimension. In fluid dynamics, such a dimension reduction is met in a variety of systems from molecular to astrophysical scales. At the smallest scales, such a reduction is met in the dynamics of electrons in ultra-pure materials such as graphene that display two-dimensional hydrodynamic behavior (Narozhny 2022; Aharon-Steinberg et al. 2022; Bandurin et al. 2018). In an equally exotic case, two-dimensional flows are met in fluids of light (Abobaker et al. 2022; Ferreira et al. 2022). Two-dimensional flows have also been observed in Bose–Einstein condensates in liquid Helium (Seo et al. 2017; Gauthier et al. 2019; Johnstone et al. 2019). Furthermore, two-dimensional dynamics are shown to be a good approximation for the motion of bacteria in films or thin layers (Sokolov et al. 2007; Kurtuldu et al. 2011; Wu and Libchaber 2000; Wei et al. 2023) and for the flow in soap films (Martin et al. 1998; Rivera et al. 1998; Vorobieff et al. 1999; Kellay and Goldburg 2002). Increasing in scale, plasma flows in the presence of strong magnetic fields, such as in Tokamak devices are also known to display close to two-dimensional dynamics (Xia and Shats 2003; Fujisawa 2008). Finally, at the planetary scale, flows are very often constrained to two-dimensional motions due to the presence of rotation, stratification, and geometrical constraints (Young and Read 2017; Byrne and Zhang 2013; King et al. 2015; Siegelman et al. 2022a).

In the systems above, despite being close to two-dimensional, variations along the third direction cannot always be disregarded, and some times play an important role in the energy balance relation. This is in particular true for the turbulent case where the dynamics of the flow drastically differ in two and in three dimensions. Turbulence is realized both in three and in two dimensions when the Reynolds number Re (the ratio of the viscous time scale to the to eddy turn-over time) attains large values. In three-dimensional turbulence, the self-interaction between eddies generates smaller and smaller eddies transferring energy toward the smallest scales where it is dissipated effectively by viscosity, independently of how small it is. In two dimensions, the opposite behavior is observed. Eddies self-organize to generate larger eddies and thus transfer energy to larger scales. Unlike the three-dimensional case, in two dimensions, because energy is transferred upscale, viscosity is not efficient at dissipating it and energy piles up at the largest scale of the system. The dynamics of flows in three and in two dimensions are thus fundamentally different.

This brings out the question: what happens when a flow is only approximately two-dimensional and the flow lies between the two extreme situations? On the one hand, if two-dimensional motions dominate energetically, one can expect that flow dynamics will not be far from those of two dimensions and the transfer of energy will be towards the large scales. On the other hand, the inverse transfer of energy can be proved only if enstrophy (the mean square of vorticity) is conserved exactly, which is only true in two-dimensional flows. Three-dimensional perturbations, even if subdominant, will break enstrophy conservation and the upscale transfer of energy is questioned. This question for the behavior of quasi-two-dimensional flows has been around for a long time (Danilov and Gurarie 2000). What has been revealed in the last years is that a hybrid state of turbulence exists where transfer to larger and to smaller scales coexist, building what is referred to as a bidirectional or split cascade.

This review deals with when, how, and in what sense can a flow transition from three-dimensional to two-dimensional behavior as a control parameter is varied. We will give a phenomenological description of the different phases of turbulence that are observed and describe their behavior close to the critical points where phase transitions are observed. The richness of behaviors observed in quasi-two-dimensional turbulence surpassed all expectations leading to the discovery in the last years of new phenomena that challenge our mathematical and physical understanding of fluid turbulence. These new discoveries are reviewed and categorized in order to give direction to future research. Furthermore, the appearance of quasi-two-dimensional turbulence in a variety of different systems is also reviewed by mentioning key works in the different systems. Finally, an attempt is made to note the many questions that are open in the field, stressing the need for further studies. Throughout the text, the mathematical formalism is made as light as possible in favor of readability and give references for more formal descriptions.

The rest of this review is structured as follows. In Sect. 2, three- and two-dimensional turbulence are briefly reviewed. Then in Sect. 3, thin-layer turbulence is discussed, and a detailed description of the transition from three-dimensional (3D) to two-dimensional (2D) dynamics is given. In Sect. 4, some recent results in other quasi-2D systems like rotating and magneto-hydrodynamic flows are given. In Sect. 5, conclusions are drawn, and open questions in the field are presented.

2 Two- and three-dimensional turbulence

Turbulence in three and two dimensions has been a subject of study for well over a century, earning itself the title of the last unsolved problem of classical physics. Some excellent books on three-dimensional turbulence can be found in Frisch and Kolmogorov (1995), Pope and Pope (2000), Davidson (2015), Davidson et al. (2011) while reviews on three- and two-dimensional turbulence can be found in Alexakis and Biferale (2018), Zhou (2021), Tabeling (2002), Boffetta et al. (2012), Pandit et al. (2017). The present review is limited in presenting some basic results that are indispensable for the discussion that follows and refer the reader to the former mentioned reviews for any further information.

2.1 Three-dimensional turbulence

In its simplest form, turbulence in three and two dimensions of a unit density fluid, is described by the evolution of the incompressible velocity field \(\textbf{u}\) that follows the Navier–Stokes equation

$$\begin{aligned} \partial _t \textbf{u}+ \textbf{u}\cdot \nabla \textbf{u}= - \nabla P + \nu \nabla ^2 \textbf{u}-\alpha \overline{\textbf{u}}+ \textbf{f} \end{aligned}$$
(1)

where P is the pressure imposing the incompressibility condition \(\nabla \cdot \textbf{u}=0\), \(\nu \) is the viscosity and \(\textbf{f}\) is an external force assumed to act on a length scale \(\ell _f\) and inject energy at a rate \(\mathcal {I} _\mathcal {E} \). The term \(-\alpha \overline{\textbf{u}}\) (where \(\overline{\textbf{u}}\) stands for the vertically averaged velocity) is an additional drag term that models the effect of boundaries and is added here to make contact later on with 2D turbulence. We will consider as domain an orthogonal box of dimensions \(L\times L \times H\) with H being the height along the direction which fluctuations are suppressed. For simplicity, we consider here only periodic boundary conditions. For a given functional form of the forcing and non-dimensionalizing using \(\ell _f\) and \(\mathcal {I} _\mathcal {E} \), the resulting non-dimensional numbers of the system are (i) the Reynolds number is given by \(\textrm{Re}=\frac{\mathcal {I} _\mathcal {E} ^{1/3}\ell _f^{4/3}}{\nu }\) (ii) the large scale Reynolds number \(\textrm{Re}_\alpha = \frac{\mathcal {I} _\mathcal {E} ^{1/3}}{\ell _f^{2/3}\alpha }\) (iii) the length scale ratio \(L/\ell _f\) and (iv) the normalized height \(H/\ell _f\). In what follows, all quantities will be non-dimensionalized using the forcing length scale \(\ell _f\) and the energy injection rate \(\mathcal {I} _\mathcal {E} \) (thus setting \(\ell _f=1\) and \(\mathcal {I} _\mathcal {E} =1\)).

In three dimensions, the inviscid unforced system 1 for smooth flows, conserves two quadratic invariants. The first is energy \(\mathcal {E} =\frac{1}{2} \left\langle \vert \textbf{u}\vert ^2 \right\rangle \) where the angular brackets stand for volume average. The second is helicity \(\mathcal {H} =\frac{1}{2} \left\langle \textbf{u}\cdot \textbf{w} \right\rangle \) (where \(\textbf{w}=\nabla \times \textbf{u}\) is the vorticity) that is not going to be discussed here but refer the reader to Alexakis and Biferale (2018), Pouquet and Yokoi (2022). In the presence of a forcing and dissipation, the following energy balance relation holds

$$\begin{aligned} \mathcal {I} _\mathcal {E} = \epsilon _{\nu } + \epsilon _{\alpha } \end{aligned}$$
(2)

where \(\mathcal {I} _\mathcal {E} = \left\langle \textbf{u}\cdot \textbf{f} \right\rangle \) is the time and volume averaged energy injection rate, \(\epsilon _{\nu } =\nu \left\langle \vert \nabla \textbf{u}{\vert } ^2 \right\rangle \) is the energy dissipation rate due to viscosity and \(\epsilon _{\alpha } =\alpha \left\langle \vert \overline{\textbf{u}}{\vert } ^2 \right\rangle \) is the energy dissipation rate due to the drag term.

To express the notion of scale, we are going to use the Fourier-transformed fields \(\hat{\textbf{u}}_\textbf{k}\) such that

$$\begin{aligned} \hat{\textbf{u}}_\textbf{k}= \left\langle e^{-i\textbf{k}\cdot \textbf{x}} \textbf{u} \right\rangle \quad \mathrm \quad \textbf{u}= \sum _\textbf{k}e^{i\textbf{k}\cdot \textbf{x}} \hat{\textbf{u}}_\textbf{k}\end{aligned}$$
(3)

where \(\ell =1/k\) gives a natural definition of scale. Using this, we can define the spherically averaged energy spectrum as

$$\begin{aligned} E(k)= \frac{L}{2} \sum _{k\le \vert \textbf{q}\vert < k+1/L} \vert \hat{\textbf{u}}_\textbf{q}\vert ^2 \end{aligned}$$
(4)

where the sum is over all wavenumbers \(\textbf{q}\) that satisfy \(k\le \vert \textbf{q}\vert <k+1/L\). Note that we have normalized E(k) by L so that it has dimensions of energy per unit of wavenumber.

It was the pioneering work of last century that led to the understanding that it was the flux of energy through scales that controlled the statistical properties of high Re flows. Early work of Kolmogorov (1941) argued the existence of a constant flux of energy in scale space from the large to the small dissipative scales such that in the infinite \(\textrm{Re},\textrm{Re}_\alpha \) limit (in our notation)

$$\begin{aligned} \epsilon _\nu = \mathcal {I} _\mathcal {E} , \quad \textrm{and} \quad \epsilon _\alpha =0 \end{aligned}$$
(5)

so that all of the injected energies arrive at small scales and dissipate by viscosity. Further assuming that this process is self-similar in scale, led to the prediction of the famous Kolmogorov energy spectrum

$$\begin{aligned} E(k) = c_{_K} \epsilon _\nu ^{2/3} k^{-5/3}, \quad k_f<k<k_\nu \end{aligned}$$
(6)

for wavenumbers larger than \(k_f=1/\ell _f\) where \(c_{_K}\) is a non-dimensional order one constant. His prediction is valid up to what is now known as the Kolmogorov wavenumber \(k_\nu =1/\ell _\nu = \epsilon _\nu ^{1/4}/\nu ^{3/4}\simeq k_f\textrm{Re}^{-3/4}\). For wavenumbers smaller than \(k_f\), since there is no flux of energy, these scales are expected to reach a thermal equilibrium state with an equipartition of energy among modes leading to

$$\begin{aligned} E(k) = c_{_T} \mathcal {I} _\mathcal {E} ^{2/3} \ell _f^{11/3} \,\, k^2, \quad k<k_f \end{aligned}$$
(7)

where \(c_{_T}\) is an other non-dimensional constant (Dallas et al. 2015; Alexakis and Brachet 2019; Gorce and Falcon 2022).

Later research showed that the forward cascade is not self-similar and the distributions of velocity differences develop stronger tails as smaller scales are examined. As a result, there is a small correction to the exponent of the energy spectrum. This phenomenon referred to as intermittency has been the study of numerous studies in order to quantify and understand these corrections, that however is not going to be discussed here.

2.2 Two-dimensional turbulence

Despite the fact that two-dimensional flows obey the same equation as three-dimensional flows, they do not display the same dynamic properties. In two dimensions, the Navier–Stokes equation (1) can be written in terms of the out-of-plane vorticity as

$$\begin{aligned} \partial _t w + \textbf{u}\cdot \nabla w = \nu \nabla ^2 w -\alpha w + f_w \end{aligned}$$
(8)

where \(w=\mathbf{e_z}\cdot \textbf{w}\) (where \(\mathbf{e_z}\) is the unit vector along z taken to be the out-of-plane direction), \(f_w = \mathbf{e_z}\cdot \nabla \times \textbf{f}\) and we have added the drag force \(-\alpha w\) often met in two-dimensional systems due to bottom friction. There are two quadratic invariants in two dimensions the energy \(\mathcal {E} =\frac{1}{2} \left\langle \vert \textbf{u}\vert ^2 \right\rangle \) and the enstrophy \(\Omega =\frac{1}{2} \left\langle \vert \textbf{w}\vert ^2 \right\rangle \). Their balance relations read

$$\begin{aligned} \mathcal {I} _\mathcal {E} = \epsilon _{\nu } + \epsilon _\alpha , \quad \mathcal {I} _\Omega = \eta _{\nu } + \eta _\alpha \end{aligned}$$
(9)

where \(\mathcal {I} _\mathcal {E} \) is again the energy injection rate, \(\mathcal {I} _\Omega = \left\langle wf_w \right\rangle \simeq k_f^2 \mathcal {I} _\mathcal {E} \) is the enstrophy injection rate. The energy dissipation terms at small and large scales are given by \(\epsilon _{\nu } = \nu \left\langle \vert \textbf{w}\vert ^2 \right\rangle \) and \(\epsilon _{\alpha } = \alpha \left\langle \vert \textbf{u}\vert ^2 \right\rangle \) respectively and the enstrophy dissipation rates by \(\eta _{\nu } = \nu \left\langle \vert \nabla \textbf{w}\vert ^2 \right\rangle \) and \(\eta _{\alpha } = \alpha \left\langle \vert \textbf{w}\vert ^2 \right\rangle \).

It was first realized by Onsager (1949) using a point vortex model that in two dimensions’ negative “temperature" states can exist where the flow self-organizes to generate large scale structures. Later on, the work of Kraichnan, Leith, and Batchelor (Kraichnan 1967, 1971; Leith 1968; Batchelor 1969), led to what is known as the KLB dual cascade picture of two-dimensional turbulence. Their work argued that a constant forward flux of energy is incompatible with a constant flux of enstrophy. In spectral space, the energy spectrum E(k) is related to the enstrophy spectrum \(E_\Omega (k)=k^2E(k)\). This implies that a constant forward energy flux would imply an ever larger flux of enstrophy that is inconsistent with the enstrophy conservation. As a result, the only possibility is that enstrophy cascades forward toward the small scales while energy cascades inversely in the large scales. Therefore, at infinite domains and in the infinite \(\textrm{Re},\textrm{Re}_\alpha \) limit

$$\begin{aligned} \epsilon _\alpha \simeq \mathcal {I} _\mathcal {E} , \quad \epsilon _\nu \simeq 0 \quad \textrm{and} \quad \eta _\alpha \simeq 0, \quad \eta _\nu \simeq \mathcal {I} _\Omega . \end{aligned}$$
(10)

The presence of this dual cascade picture has been verified in numerical simulations (Boffetta and Musacchio 2010; Lilly 1969, 1972) and experiments (Byrne et al. 2011; von Kameke et al. 2011; Kelley and Ouellette 2011). Same arguments as in the three-dimensional cascade lead to the prediction of an \(E(k)\propto k^{-5/3}\) energy spectrum for the range of wavenumbers that an inverse cascade of energy is present \(k_\alpha \ll k\ll k_f\) while the steeper spectrum \(E(k)\propto k^{-3}\) is predicted for the range of wavenumbers \(k_f\ll k\ll k_\nu \) that a forward enstrophy cascade is observed. Here \(k_\nu = \eta _\nu ^{1/6}/\nu ^{1/2} \simeq k_f Re^{1/2}\) while \(k_\alpha = \epsilon _\alpha ^{1/2}/\alpha ^{3/2} = k_f Re_\alpha ^{-3/2} \). Note that the viscous wavenumber \(k_\nu \) has a different scaling in 2D than 3D. We have also introduced a new cut-off wavenumber \(k_\alpha \) (and length scale \(L_\alpha =1/k_\alpha \)) such that wavenumbers with \(k<k_\alpha \) are severely damped by the drag force. The inverse cascade of energy is shown not to be intermittent (Boffetta et al. 2000) unless energy is injected in a fractal set (Sofiadis et al. 2023).

Unlike the the small-scale viscous cut-off \(\ell _\nu =1/k_\nu \) that can become arbitrarily small as \(\textrm{Re}\rightarrow \infty \), the large scale cut of \(L_\alpha =1/k_\alpha \) is limited by the domain size L. Thus, while for \(L_\alpha \ll L\) the aforementioned inverse cascade and power laws will be present, when \(L\ll L_\alpha \), the inverse cascade will reach the domain size scale before the drag coefficient \(\alpha \) becomes effective. In the latter case, energy that arrives at the large scales will pile up at the domain size in what is known as a spectral condensate (Falkovich 1992). In square periodic domains, this condensate takes the form of two large counter-rotating vortexes with large enough amplitude for the dissipation to balance the energy arriving from the small scales. This leads to the estimate for the energy of the condensate to be

$$\begin{aligned} \mathcal {E} \simeq \frac{\mathcal {I} _\mathcal {E} }{\alpha + \nu L^2}. \end{aligned}$$
(11)

This energy can be very large in particular in the \(\alpha =0\) case that we will examine later on. The cascade picture described before is then altered, and steeper power laws are observed. The amplitude of the velocity fluctuations is so large that it brings the system to a quasi-equilibrium state that merits various equilibrium statistical approaches (Onsager 1949; Kraichnan 1975; Robert and Sommeria 1991; Naso et al. 2010; Bouchet and Venaille 2012; Laurie et al. 2014; Frishman and Herbert 2018; van Kan et al. 2022). Figure 1 shows two vorticity visualizations of two-dimensional flows such that on the left \(L_\alpha < L\) while on the right \(L_\alpha \gg L\). The condensate state has been realized in various experiments (Byrne et al. 2011; Francois et al. 2013). The statistical properties of the inverse cascade case \(L_\alpha \ll L\) and the condensate case \(L_\alpha \gg L \) are so different that we are going to treat them separately for the quasi-2D case.

Fig. 1
figure 1

Visualization of vorticity for the turbulent state \(L\gg L_\alpha \) (left) and for the condensate state \(L_\alpha \gg L\) (right). In both cases, the forcing scale \(\ell _f\) was 80 times smaller than the domain size L

Full size image

3 Thin-layer turbulence

Turbulent flows confined in thin layers are perhaps the simplest and most intuitive flows that can display split energy cascades. It is thus an optimal choice for the study of quasi-two-dimensional flows. Furthermore, such anisotropic domains are very relevant for the atmosphere whose horizontal direction is of the order of 1000 km, while the pressure scale height of the order of 10 km. As such they have been extensively studied in the literature.

Here we will discuss how the cascade properties of thin-layer turbulence change as the layer height is varied in the limit of large \(\textrm{Re},\textrm{Re}_\alpha \). We will distinguish between two cases: (i) cases that the drag is efficient at absorbing the large scale energy that arrives in the presence of an inverse cascade so that \(L_\alpha \ll L\) and (ii) cases that the a large-scale drag is very weak or absent so that a condensate is formed so that \(L_\alpha \gg L\). In the first case, we will quantify the forward and inverse flux of energy using \(\epsilon _\alpha \) and \(\epsilon _\nu \) (measured in units of \(\mathcal {I} _\mathcal {E} \)) that express the fraction of energy that is transferred in the large and the small scales respectively. In the infinite \(\textrm{Re},\textrm{Re}_\alpha \) limit \(\epsilon _\alpha =0, \epsilon _\nu =1\) for three-dimensional turbulence while \(\epsilon _\alpha =1, \epsilon _\nu =0\) for two-dimensional turbulence.

In the condensate case, we will typically consider \(\alpha =0\) so that \(\epsilon _\alpha ,\epsilon _\nu \) are not suitable to quantify the state of the flow. Instead we will use the energy of the largest-scale modes \(\mathcal {E} _C\) defined as

$$\begin{aligned} \mathcal {E} _C =\frac{1}{2} \sum _{\vert \textbf{k}\vert < c/L} \vert \hat{\textbf{u}}_\textbf{k}\vert ^2 \end{aligned}$$
(12)

with \(c>2\pi \) an order one number. Finally, we will also consider the energy of 3D fluctuations as

$$\begin{aligned} \mathcal {E} _{3\textrm{D}} =\frac{1}{2} \left\langle \vert \textbf{u}-\overline{\textbf{u}}\vert ^2 \right\rangle . \end{aligned}$$
(13)

In what follows, we describe the behavior of \(\epsilon _\alpha ,\epsilon _\nu ,\mathcal {E} _C,\mathcal {E} _{3\textrm{D}}\) as the height of the layer is varied for the turbulent and the condensate case.

3.1 From 3D turbulence to 2D turbulence

First, the case \(L_\alpha \ll L \) (that no condensate forms) is considered. The first work that made the remark that flows in thin layers can cascade energy to both large and small scales was Smith et al. (1996). Since then a series of more systematic works followed that measured the fraction of energy that cascaded to that large scales as the height was varied (Celani et al. 2010; Musacchio and Boffetta 2017; Benavides and Alexakis 2017; van Kan and Alexakis 2019; Poujol et al. 2020) whose results will be described in this section.

We begin the presentation of thin-layer turbulence by considering first a layer of height H much larger than the forcing scale and then gradually decreasing it. For \(H\gg \ell _f\), the flow displays three-dimensional turbulence with only forward cascade observed at scales \(\ell \) smaller than \(\ell _f\) forming a \(k^{-5/3}\) energy spectrum. At scales larger than \(\ell _f\), energy is expected to reach a thermal equilibrium state with equipartition of energy among modes. An argument can be made that if one considers horizontal scales \(\ell _\perp \gg H \gg \ell _f\) where the flow is constrained to move primarily in two dimensions, an inverse cascade can build up. However, the primary interactions at such scales are not with same scale two-dimensional eddies but rather directly with the forcing scale modes that are more energetic and act as a turbulent diffusion. Thus, even at these scales, the cascade will be strictly forward. This is a conjecture however that needs to be verified.

The strictly forward cascade behavior changes as smaller layer heights are considered. Eventually a critical height \(H_{3\textrm{D}}\) is reached such that for heights \(H<H_{3\textrm{D}}\), a new phase of turbulence appears that a bidirectional cascade is present. Numerical simulations indicate that the fraction of the energy that cascades inversely \(\epsilon _\alpha \) is gradually increasing from zero as a power law (Benavides and Alexakis 2017; van Kan and Alexakis 2019)

$$\begin{aligned} \epsilon _\alpha \propto (H_{3\textrm{D}}-H)^{\beta _1} \end{aligned}$$
(14)

where \(\beta _1\) is measured to be close to unity but its precise value has yet to be determined. The presence of this critical point is not trivial nor fully understood. The only evidence we have are from numerical simulations (Benavides and Alexakis 2017; van Kan and Alexakis 2019) that however can be questioned because unavoidably they suffer from limited resolution. Further investigations would be required both numerical and theoretical to investigate this point and conclude its presence and on the universality class of this transition.

As H is decreased further than \(H_{3\textrm{D}}\), the fraction of energy that cascades to the small scales is decreased. For \(H \ll H_{3\textrm{D}}\), all scales \(\ell >H\) have a two-dimensional behavior with an inverse cascade of energy and a forward cascade of enstrophy. This however does not imply that no energy arrives at scales close to the height \(\ell \sim H\). Along with the enstrophy cascade, some energy has to be transported to the small scales as well, so at scale H, the flux of energy is \(\epsilon _\nu \propto \eta _\nu H^2\) (Boffetta et al. 2011). This energy is then transported to even smaller scales \(\ell <H\) by three-dimensional interactions. Note that at the limit \(H\rightarrow 0\), the fraction of energy transported to the small scales also goes to zero \(\epsilon _\nu \rightarrow 0\) and 2D behavior is recovered. Given that \(\eta _\nu \sim \mathcal {I} _\Omega \simeq \mathcal {I} _\mathcal {E} /\ell _f^2\) implies that

$$\begin{aligned} \epsilon _\nu \propto H^2 \end{aligned}$$
(15)

This behavior was first predicted in Boffetta et al. (2011) and verified using a shell model. This scaling however has never been tested using numerical simulations and it is something future research needs to confirm.

The scaling in 15 does not continue for arbitrarily small H. If \(H\sim \ell _\nu \), then a new transition is observed toward a third phase of turbulence where all three-dimensional perturbations are damped out. In particular in the case that the forcing is two-dimensional, the transition to exactly 2D behavior occurs in a critical way: there is a second critical height \(H_{2\textrm{D}}\) such that for all \(H<H_{2\textrm{D}}\), the flow becomes exactly two-dimensional. A very interesting dynamical behavior is observed for layer heights slightly larger than \(H_{2\textrm{D}}\). If we denote as \(\mathcal {E} _{3\textrm{D}}\), the energy contained in 3D modes alone, then it is measured that close to this new critical height \(\mathcal {E} _{3\textrm{D}}\) scales like

$$\begin{aligned} \mathcal {E} _{3\textrm{D}} \propto (H-H_{2\textrm{D}})^{\beta _2} \end{aligned}$$
(16)

where \(\beta _2\) is an exponent larger than one (Benavides and Alexakis 2017; Alexakis et al. 2021). This exponent is linked to the fact that as \(H_{2\textrm{D}}\) is approached from above 3D fluctuations grow or decay with growth that is randomly distributed in space and time. As a result, not only the amplitude of 3D perturbations depends on \(H-H_{2\textrm{D}}\) but also the fraction of area that is occupied by them. In Alexakis et al. (2021), this behavior was linked to the universality class observed in the presence of multiplicative noise in extended systems (Tu et al. 1997; Genovese et al. 1998) that is related to the KPZ equation (Kardar et al. 1986). This leads to the prediction that \(\beta _2\simeq 1.7\dots \) compatible with present data but further work is needed to draw firm conclusions.

Finally, for \(H\ll \ell _\nu \), all three-dimensional fluctuations are severely damped and the flow can be proven to become exactly two-dimensional (Gallet and Doering 2015; Gallet 2015) and thus all properties mentioned in Sect. 2.2 are recovered. A sum-up of all the different phases of thin-layer turbulence and their transitions in the \(L_\alpha \ll L\) case is sketched in Fig. 2 and reported in Table 1.

Fig. 2
figure 2

A sketch of the qualitative behavior of \(\epsilon _\alpha \) (top panel, blue line), \(\epsilon _\nu \) (top panel red line) and \(\mathcal {E} _{3\textrm{D}}\) (bottom panel red line) as a function of the layer height H

Full size image

3.2 From 3D turbulence to a 2D condensate

In finite domains when the drag coefficient is very small (or even zero), even a weak inverse cascade will lead to the formation of a large-scale condensate at long times. The study of condensates is costly with numerical simulations due to the very long times that are involved. For this reason, such studies always come after studies without the condensate. Nonetheless, various numerical studies of thin-layer turbulence exist in the literature (van Kan and Alexakis 2019; Musacchio and Boffetta 2019). On the contrary to the numerical simulations, laboratory experiments do not have such time limitations and various studies of thin-layer flows have been investigated in the literature although with limited separation between the forcing scale and the domain height (Xia et al. 2009, 2011; Francois et al. 2013; Shats et al. 2010).

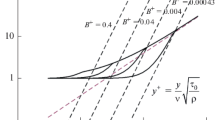
As in the previous section, we begin with a layer that has a height H much larger than the forcing scale \(H\gg \ell _f\) so that no inverse cascade and no condensate is formed, and gradually reduce this height. As H is reduced beyond the critical height \(H_{3\textrm{D}}\) (discussed in the previous section), a weak inverse cascade starts to build up leading to the formation of a condensate of energy \(\mathcal {E} _C\). If the drag coefficient \(\alpha \) is finite, the increase of \(\mathcal {E} _C\) is gradual. For \(\alpha =0\) however, even a small inverse cascade can lead to a large value of \(\mathcal {E} _C\). In fact, studies very close to \(H_{3\textrm{D}}\) showed that the transition to the condensate state is discontinuous (van Kan and Alexakis 2019). In more detail, it was shown that for H larger than \(H_{3\textrm{D}}\), the large-scale energy remained small \(\mathcal {E} _C=\mathcal {O}(1/L^2)\), but as soon as it became slightly smaller than \(H_{3\textrm{D}}\), a condensate formed and \(\mathcal {E} _C\) jumped to a finite value \(\mathcal {E} _C=\mathcal {O}(1)\). Furthermore, it was shown in van Kan and Alexakis (2019) that if H was gradually increased again to values larger than \(H_{3\textrm{D}}\), the condensate state remained with \(\mathcal {E} _C=\mathcal {O}(1)\) up to some second critical value \(H'_{3\textrm{D}}>H_{3\textrm{D}}\). Thus for values of H in the range \(H_{3\textrm{D}}<H< H'_{3\textrm{D}}\), two steady states (two different attractors) exist for the same value of H, and a hysteresis diagram was constructed (van Kan and Alexakis 2019) as shown in Fig. 3.

Further investigations of this system van Kan et al. (2019) revealed that if run for a long time, there are random jumps from one attractor to the other. The time distribution of these random jumps follows an exponential distribution indicating a memory-less process (van Kan et al. 2019). It was also shown that as the Reynolds number and the domain size are increased, this range of H where both attractors are stable increases (de Wit et al. 2022b). This bistability is thus a behavior that is expected to survive in the large Re limit.

Fig. 3
figure 3

A sketch of the qualitative behavior of \(\mathcal {E} _C\) (blue line), and \(\mathcal {E} _{3\textrm{D}}\) (red line) as a function of the layer height H in the condensate state

Full size image

As H is decreased significantly from \(H_{3\textrm{D}}\), \(\ell _f\gg H\) the condensate becomes stable and its amplitude depends on the principal mechanism that saturates the inverse cascade. If the Reynolds number is moderate, viscous dissipation will provide the main saturation mechanism and \(\mathcal {E} _C \propto \mathcal {I}_\mathcal {E} L^2/\nu \) (van Kan and Alexakis 2019). For large Reynolds numbers however, a new mechanism for saturation is present that originates from an eddy-viscosity effect due to the small 3D eddies at scales \(\ell <H\). These 3D eddies extract energy from the condensate scales. A flux loop mechanism thus is present in which energy injected at \(\ell _f\) moves up scale to the condensate scale L through 2D motions and then back to smaller scales \(\ell <H\) through interactions with the forcing scale 3D eddies. The condensate energy then in this case is not inversely proportional to viscosity but rather reaches a viscosity-independent scaling \(\mathcal {E} _C\propto (\mathcal {I}_\mathcal {E} \ell _f)^{2/3}\) (Musacchio and Boffetta 2019; van Kan and Alexakis 2019). A simple model that captures this behavior was proposed in van Kan and Alexakis (2019).

At even smaller layer heights, such that \(H\sim \ell _\nu \), a new transition appears again towards a state where 3D perturbations are damped as in the previous section. The case of the condensate however is significantly different from the turbulent case. While in the former, turbulence was unstructured and uniform in space allowing 3D perturbations to grow anywhere in the domain, in the condensate state, the flow is still chaotic but self-organized in coherent structures of high concentration of vorticity and strain in small regions of space. In Seshasayanan and Gallet (2020), Lohani et al. (2023), the evolution of infinitesimal 3D perturbations in a two-dimensional flow in the condensate state was followed. This study revealed that \(\mathcal {E} _{3\textrm{D}}\) in this limit followed a random behavior with long periods of decay and very short periods of very large exponential increase. The periods of increase were shown to appear when the extreme of vorticity or the strain of a flow crossed a certain threshold. The statistics of these extremes were studied in detail recently in Seshasayanan (2023). Using a point vortex model that was coupled to point like 3D perturbations in van Kan et al. (2021a) showed that the instantaneous growth rate of the energy of the 3D perturbations displayed power law distributions that were linked to the power law distribution of strain in space. As such the logarithm of the energy of the perturbations followed a Lévy random walk that explains the sudden jumps in the growth of energy observed in Seshasayanan and Gallet (2020). This leads to a new type of intermittency the Lévy-On-Off intermittency that was described and studied in detain in van Kan et al. (2021b), van Kan and Pétrélis (2023). This also leads to new power law behavior for the 3D energy

$$\begin{aligned} \mathcal {E} _{3\textrm{D}} \propto (H-H_{2\textrm{D}}^*)^{\beta _3} \end{aligned}$$
(17)

where \(H_{2\textrm{D}}^*\) is the critical value of H below which all 3D perturbation are damped and \(\beta _3\) is an other exponent that depends on the Lévy noise parameters (see van Kan et al. 2021b; van Kan and Pétrélis 2023). This behavior suggested by the model is yet to be confirmed by direct numerical simulations.

Finally, for \(H\ll \ell _\nu \), all 3D perturbations are damped and the systems recover its exact two-dimensional behavior. The different stages of thin-layer condensates are shown in Fig. 3 and summed up in Table 1 along with the turbulent case.

Table 1 Table with the different phases and critical behaviors observed in thin layer turbulence
Full size table

4 Other examples of quasi-2D flows

Similar transitions to the ones observed in thin-layer turbulence are expected to be found in other quasi-two-dimensional flows. However, due to the increased numerical cost or the technical difficulties in constructing laboratory experiments has limited their study. In what follows we mention a few of these systems focusing on the additional phenomena that are present.

4.1 Rotating turbulence

Rotating turbulence is perhaps the simplest system after thin layers that displays quasi-2D behavior and split cascades. It deals with turbulence in a rotating reference frame of rotation \(\Omega \) quantified here by the Rossby number \(Ro=\mathcal {I} _\mathcal {E} ^{1/3} /(\Omega \ell _f)^{2/3}\). The transition from 3D turbulence to a 2D inverse cascade has been investigated in Deusebio et al. (2014) and Pestana and Hickel (2019). The critical layer height \(H_{3\textrm{D}}\) was shown to increase with the rotation rate from the weak rotation value \(H_{3\textrm{D}}\propto \ell _f\) to a value that was shown to increase as

$$\begin{aligned} H_{3\textrm{D}} \propto \ell _f /Ro. \end{aligned}$$
(18)

This scaling was confirmed in van Kan and Alexakis (2020) using an asymptotic model of the rotating Navier–Stokes equation for fast-rotating turbulence within highly elongated domains.

Although, rotating turbulence appeared to have the same phenomenological description as in thin layers for the 3D to 2D transition in the large Ro and small Ro limit, at intermediate values of Ro, a new state of turbulence was discovered in Di Leoni et al. (2020) at which the flow formed a crystal of co-rotating vortexes at scales larger than the forcing scale. This state of turbulence occurs close to the \(H_{3\textrm{D}}\) transition height at which the co-rotating 2D vortexes are stable while counter-rotating 2D vortexes decay due to 3D fluctuations. The remaining co-rotating vortexes form crystals as have been seen in point vortex models (Aref and Vainchtein 1998) and experiments on magnetized electron columns (Fine et al. 1995). This new state of turbulence is supported by a flux loop mechanism and was shown to be metastable that reduced to an inverse cascade if a strong perturbation is applied. Such vortex crystals have been observed in the North pole of Jupiter by the Juno spacecraft mission (Adriani et al. 2018) and have been interpreted by quasi-geostrophic dynamics in a curved domain (Siegelman et al. 2022b). The results of Di Leoni et al. (2020) could provide an alternative explanation. We note that in both models, a segregation between co-rotating and counter-rotating vortexes led to the formation of the crystal.

Condensates in rotating turbulence have been studied in Seshasayanan and Alexakis (2018), Alexakis (2015), Yokoyama and Takaoka (2017) where a discontinuous transition and hysteresis were also found close to \(H_{3\textrm{D}}\). However, the significant larger complexity of rotating turbulence did not allow a thorough investigation. However, recently new experimental platforms have been built that have been able to quantify the formation of large scales in rotating turbulence and disentangle the forward and inverse transfers as well as the presence of wave turbulence (Lamriben et al. 2011; Campagne et al. 2014; Gallet et al. 2014; Machicoane et al. 2016; Yarom and Sharon 2014; Kolvin et al. 2009; Brunet et al. 2020; Monsalve et al. 2020). These experiments are very suitable in studying the long-term behavior of rotating turbulence close to critical points and future work is expected to verify numerical observations as well as reveal new interesting physics.

4.2 Stratified turbulence

By stratified, we refer to turbulence in the presence of gravity \(-\textbf{e}_z g\) and a mean stable density gradient \(S=-\rho _0^{-1}d\rho /dz\). Unlike rotation, stratification works against the two-dimensionalization of turbulence by leading to the formation of strong vertical gradients, despite the fact that it suppresses vertical motions it. In Sozza et al. (2015), it was shown that the critical height \(H_{3\textrm{D}}\) that the inverse cascade appears is decreased with stratification as

$$\begin{aligned} H_{3\textrm{D}} \propto \ell _f Fr, \end{aligned}$$
(19)

where \(Fr=\mathcal {I} _\mathcal {E} ^{1/3} /(gS)^{1/2}\ell _f^{2/3}\) is the Froude number. As a result, in strongly stratified flows, deviations from two-dimensional turbulence can appear at much thinner layers than in the absence of stratification.

Little or no work has been done for the other critical points in strongly stratified turbulence or in the presence of a condensate.

4.3 Rotating and stratified turbulence

Rotating and stratified turbulence provides perhaps the simplest model of a dry atmosphere, and various studies have been devoted to its cascade properties directly from the Navier–Stokes (Bartello 1995; Marino et al. 2013; Pouquet et al. 2017; Herbert et al. 2016) or from reduced models (Xie 2020). It combines both the effect of two-dimensionalization of rotation and the suppression of vertical motions of stratification. The resulting complexity however is larger than the sum of its parts. In van Kan and Alexakis (2022) using an asymptotic model for strong rotation and long boxes, it was shown that in this limit, the parameter space split in three different phases, one with no inverse cascade, one rotating dominated regime with an inverse cascade due to a two-dimensionalization and a third strongly stratified regime with an inverse cascade corresponding to quasi-geostrophic dynamics. It seems thus the phase space of rotating and stratified turbulence is far more complex than anticipated and a careful exploration of it and its asymptotic limits is needed.

4.4 Convection

Although convection involves inherently 3D motions in the presence of strong rotation or vertical confinement, it can lead to quasi-2D behavior. There have been numerous reports in the last years of an inverse cascade and the formation of coherent large-scale quasi-2D vortices in rotating Rayleigh–Benard convection that coexists with 3D eddies that extract energy from the unstable stratification (Guervilly et al. 2014; Favier et al. 2014; Maffei et al. 2021). The behavior of the large-scale vortices form resembles the ones observed in thin-layer turbulence and rotating turbulence displaying a discontinuous transitions and a hysteresis (Favier et al. 2019; de Wit et al. 2022a).

Finally, inverse cascade has been reported in Vieweg et al. (2022) for very horizontally extended domains even in the absence of rotation.

4.5 Magnetohydrodynamic turbulence

Like strong rotation for ordinary fluids , a strong uniform magnetic field is also capable of bi-dimensionalizing electrically conducting fluids. Within the Magneto-Hydro-Dynamic (MHD) approximation, two particular limits are of interest. First, the high conductivity limit (corresponding to the large magnetic Reynolds number limit) relevant to astrophysical plasmas and tokamak devices. The transition to a two-dimensional behavior in this limit has been investigated in Alexakis (2011), Sujovolsky and Mininni (2016) see also the review of Oughton et al. (2017). Second, for low magnetic Reynolds numbers (low conductivity), the magnetic field acts as a damping mechanism for all velocity fluctuations varying along the direction of the magnetic field. This so-called quasi-static MHD with relation to the transition to 2D flow has been studied in Favier et al. (2011), Reddy and Verma (2014), Verma (2017). This limit is suitable for liquid metals and has been investigated in some innovating experiments (Pothérat and Klein 2014; Pothérat et al. 2000; Xia et al. 2011; Xia and Shats 2003; Gallet et al. 2012).

Just like in the previous examples, MHD transitions from a three-dimensional forward cascade to a bidirectional cascade and two-dimensional cascade are observed. However, the presence of additional invariants both in 3D and 2D makes the phase space of MHD turbulence sufficiently more complex such that even in pure 2D MHD such transitions can be observed (Seshasayanan et al. 2014; Seshasayanan and Alexakis 2016).

4.6 Quantum turbulence

Quantum turbulence refers to turbulent flow of quantum fluids, where vortex are quantized. There are various models used to describe such flows that is beyond the purpose of this work to describe. We will however mention the experiments in Seo et al. (2017), Johnstone et al. (2019), Gauthier et al. (2019) where quasi-two-dimensionalization in super-fluids is observed and the formation of large-scale vortices. Numerically, such bi-dimensionalization has been observed in thin superfluid layers (Müller et al. 2020) using the Gross–Pitaevskii equation and in the two fluid description of superfluid turbulence in the presence of a counter-flow (Polanco and Krstulovic 2020).

5 Conclusions

If something is kept from this review, it should be the plethora of new dynamic phenomena that appear in quasi-2D turbulence when it is pushed to the right limits. To begin with, even in the simplest case of a thin-layer flow, different phases of turbulence are observed in the infinite Re limit. Unlike the commonly accepted expectations for homogeneous and isotropic turbulence for which a universal behavior is expected, in the presence of confinement and anisotropy, distinct phases of turbulence are present such that in one phase, there is large-scale energy transfer and self-organization while in the other disorder and efficient energy dissipation. These phase are separated by critical points that display continuous or discontinuous phase transitions. Near these critical points, novel dynamical behaviors are observed that include the appearance of hysteresis diagrams and new critical exponents that are summed up in the Table 1. As the complexity of the system is increased further, new phases are discovered like the vortex-crystal meta-stable phase observed in rotating turbulence.

Recent research has only scratched the surface of these new phenomena and a lot of further work is required. In particular, investigating the behavior of the flows close to criticality and classifying them in universality classes is a much-needed direction for the field. Theoretical, numerical, and experimental investigations need to proceed in parallel in this direction in order to establish a clear and quantitative understanding of these transitions.

Furthermore, expanding the system complexity including more physical effects would allow us to make contact with with physical and industrial systems. Here, only idealized situations were examined with a well-defined injection and dissipation scale. Reality is far more complex, with forcing mechanisms that span a wide range of scales (like convection, planetary scale baroclinic instabilities, etc.) and large-scale dissipation much more complex than the linear drag force assumed here. However, if we cannot understand this behavior in the idealized models, what hope do we have to understand the more complex physical systems? Progress in both directions and a connection between the the idealized and more physical case would be required in order to obtain accurate predicting models.

Finally, I would would like to note that we live in a world that climate gradually changes and an atmosphere belongs to the wider class of quasi-two-dimensional flows. It is thus important to understand how this system responds to variations of parameters. For this reason, studies of fundamental questions along the directions reviewed in this work are imperative.

On behalf of all authors, the corresponding author states that there is no conflict of interest.