1 Introduction

The 11-year sunspot cycle is one of the most intriguing natural cycles known to mankind. Let us begin by looking at Fig. 1, which shows how the number of sunspots seen over the Sun’s surface varied with time during the last four centuries. Galileo and some of his contemporaries were among the first to study sunspots systematically in the beginning of the seventeenth century by using the newly-discovered telescope. The first entries in Fig. 1 in the years after 1610 are based on the records left by them. Then there was a period of about 70 years—known as the Maunder minimum—during which sunspots were rarely seen. After that, the sunspot number has gone up and down in a roughly periodic manner, with a period of about 11 years, although there have been lots of irregularities.

Fig. 1
figure 1

The yearly averaged sunspot number plotted against time since the invention of the telescope. Credit: David Hathaway

Full size image

The sunspot cycle was discovered by Schwabe (1844). A first clue about the physical nature of sunspots came with the discovery by Hale (1908) of Zeeman splitting in the spectra of sunspots, from which it can be concluded that sunspots are regions of strong magnetic field of about 3000 gauss (or 0.3 tesla)—approximately 5000 times stronger than the magnetic field near the geomagnetic poles. The discovery of magnetic fields in sunspots was a momentous discovery in the history of physics, since this was the first time that somebody conclusively established the existence of magnetic fields outside the Earth’s environment. Now we know that magnetic fields are ubiquitous in the astronomical universe, with many planets, stars and galaxies having magnetic fields.

With the discovery of the magnetic fields in sunspots, it became clear that the 11-year sunspot cycle is essentially the magnetic cycle of the Sun. Since the Sun is made of matter in the plasma state, one can presume that this magnetic cycle is due to some plasma processes. The earliest model of the sunspot cycle given by Parker (1955a) and developed further by Steenbeck et al. (1966) is now referred to as the \(\alpha \Omega\) dynamo model. With new observational and theoretical discoveries coming along, there was need to suitably modify and upgrade this model to a more comprehensive model known as the flux transport dynamo model. Although there may still be some critics unwilling to accept the flux transport dynamo as the appropriate theoretical model for the sunspot cycle, this model has emerged as the currently favoured theoretical model of the sunspot cycle and undoubtedly deserves a careful consideration. The present author was lucky that the most crucial years of growth of this model roughly coincided with his scientific career and our group could make some key contributions to the development of this model.

The aim of this presentation is to introduce the flux transport dynamo model to plasma physicists who may not have much familiarity with the phenomenology of the sunspot cycle, highlighting some of the contributions from our group. This is not a comprehensive review of the whole field. The choice of topics has been, to some extent, guided by the research interests of our group. We refer the readers to several reviews of the solar dynamo in which the flux transport dynamo model has been discussed extensively (Charbonneau 2010, 2014; Choudhuri 2011; Karak et al. 2014a). We may also mention that increasingly more data are coming about spots and cycles of other solar-like stars, making it clear that the Sun is not an unusual star in having magnetic activities. Whether the solar dynamo models can be readily extrapolated to explain the cycles of all solar-like stars is an important question on which the last word has not been said yet (Choudhuri 2017). For a non-technical introduction to the sunspot cycle and dynamo theory, readers may look at the popular science book by Choudhuri (2015).

After summarizing the relevant observational data in Sect. 2, we shall discuss the theory of sunspot formation in Sect. 3. Then Sect. 4 will be devoted to introducing the basics of the flux transport dynamo model and discussing how this model explains the regular periodic features of the sunspot cycle. The question of how the irregularities of the sunspot cycles arise will be briefly discussed in Sect. 5. Then our conclusions will be summarized in Sect. 6.

2 Relevant observational data

About a decade after Hale’s famous discovery of magnetic fields in sunspots (Hale 1908), Hale et al. (1919) made another important discovery. Often two sunspots are seen side by side, although sometimes both the sunspots in a pair may not be equally well formed. Hale et al. (1919) found that usually the two sunspots occurring in a pair have opposite magnetic polarities. The occurrence of such bipolar sunspot pairs suggests the existence of a sub-surface strand of magnetic flux which presumably occasionally breaks through the solar surface as shown in Fig. 2. If the two intersections of the strand of magnetic flux with the surface become the two sunspots, then magnetic field lines would come out of one sunspot (making its polarity positive) and would go down into the other sunspot (making its polarity negative).

Fig. 2
figure 2

A magnetic flux tube piercing through the solar surface and giving rise to two sunspots of opposite magnetic polarity

Full size image

Figure 3 shows a magnetogram map of the solar surface in which white and black colours respectively indicate regions of positive and negative magnetic polarities, whereas grey colour is put in the regions where the magnetic field is too weak to be detected by the magnetogram. In the magnetogram map, a bipolar sunspot pair appears as a white patch and a black patch side by side. We see in Fig. 3 that the right sunspots in the sunspot pairs in the northern hemisphere are positive (white patches), whereas the right sunspots in the sunspot pairs in the southern hemisphere are negative (black patches). This is the case for a particular 11-year cycle. In the next cycle, the polarity reverses. The right sunspots in the northern hemisphere would become negative in the next cycle and the right sunspots in the southern hemisphere would become positive.

Fig. 3
figure 3

A magnetogram map of the solar disk, with white, black and grey indicating regions of positive, negative and very weak magnetic field. Note that a magnetogram gives the line-of-sight component of the magnetic field. A standard convention in magnetogram maps is that the rotation axis of the Sun is in the vertical (up-down) direction

Full size image

We point out another thing in Fig. 3. The line joining the centres of the two sunspots in a bipolar sunspot pair tends to be nearly parallel to the solar equator. Hale’s co-worker Joy, however, noted that there is a systematic tilt of this line with respect to the equator (the right sunspot in a pair usually appearing closer to the equator) and that this tilt of sunspot pairs increases with latitude (Hale et al. 1919). This result is usually known as Joy’s law. The tilts, however, show a considerable amount of scatter around the mean given by Joy’s law. As we shall see later, this law of tilts of sunspot pairs plays a very important role in solar dynamo theory.

Fig. 4
figure 4

The two possible components of the solar magnetic field: a the toroidal component and b the poloidal component

Full size image

For the time being, if we ignore the tilts of bipolar sunspots and assume that these appear at the same latitude, then Fig. 3 suggests the possible existence of a sub-subsurface magnetic field as shown in Fig. 4(a). The magnetic field with this type of configuration is known as the toroidal field. If some parts of this field are to rise and look as sketched in Fig. 2, then we would get a distribution of sunspots as seen in Fig. 3. On the other hand, Fig. 4(b) shows what is called the poloidal field—looking like what the geomagnetic field is expected to be. Dynamo theory developed historically by following the mean field approach in which we do an ensemble average of various physical quantities. When we carry on this kind of averaging, the mean magnetic field can often be regarded as axi-symmetric, i.e. independent of \(\phi\) in spherical coordinates. We can write this mean magnetic field as

$$\begin{aligned} \mathbf{B}= B_{\phi } (r, \theta , t) \mathbf{e}_{\phi }+ \nabla \times [A (r, \theta , t) \mathbf{e}_{\phi }]. \end{aligned}$$
(1)

The toroidal field is given by \(B_{\phi } (r, \theta , t) \mathbf{e}_{\phi }\), whereas \(\nabla \times [A (r, \theta , t) \mathbf{e}_{\phi }]\) gives the poloidal field of which the components are given by

$$\begin{aligned} B_r = \frac{1}{r \sin \theta } \frac{\partial }{\partial \theta } (\sin \theta A), \; \; B_{\theta } = - \frac{1}{r} \frac{\partial }{\partial r} (r A). \end{aligned}$$
(2)

It is easy to check that the contours of constant \(r \sin \theta A\) give the magnetic field lines of the poloidal field in the poloidal plane (i.e. the meridional plane).

In the fundamental paper on dynamo theory, Parker (1955a) suggested that the sunspot cycle is produced by an oscillation between the toroidal magnetic field of the Sun and a poloidal field of the type shown in Fig. 4(b). The proper observational proof for the existence of such oscillations came only several decades later, when solar astronomers had gathered sufficient data for the polar magnetic field of the Sun. The upper part of Fig. 5 shows the temporal variation of the poloidal field at the two poles of the Sun, whereas the lower part shows the sunspot number, which is a proxy of the toroidal magnetic field intensity. Note that the polar field, first discovered by Babcock and Babcock (1955), is of order a few gauss (keep in mind that 1 gauss = \(10^2\) \(\mu\)T)—much weaker than the 3000-gauss field in the interiors of sunspots. We see a clear oscillation between the toroidal and the poloidal fields: when one of them is strong, the other one is weak.

Fig. 5
figure 5

The variation with time of the magnetic field at the two poles of the Sun, along with the sunspot number shown at the bottom. Credit: Gopal Hazra

Full size image

Let us now say a few words about the appearance of the poloidal field on the solar surface. At a particular time, it is found that there would be a latitude belt over which this field at the surface would have a particular sign. These latitude belts shift towards the poles with the progress of the sunspot cycle. This is in contrast to sunspots, which appear at lower and lower latitudes with the progress of the cycle. Figure 6 is a time-latitude plot in which the shaded regions indicate the latitudes where sunspots appeared at a particular time, whereas the colours indicate the longitude-averaged poloidal field at the surface. During a sunspot cycle, the shades appear closer to the equator with time, indicating that sunspots appear at lower latitudes with the progress of the cycle. On the other hand, the colours indicating the longitude-averaged poloidal field show a trend of poleward migration. Since the shaded regions in Fig. 6 look like a pattern of repeated butterflies, they make up what is called the butterfly diagram. We note that the polar field is strongest at the time of the sunspot minimum and reverses at the time of the sunspot maximum. A reversal of the polar field at the time of a sunspot maximum was first observed by Babcock (1959). The theoretical explanation of Fig. 6 should be a major goal of a theoretical model of the sunspot cycle.

Fig. 6
figure 6

The time-latitude plot of the longitude-averaged radial magnetic field at the solar surface superposed on the butterfly diagrams of sunspots indicating the latitudes where sunspots are seen at a particular time

Full size image

For the sake of completeness, it may be mentioned that the surface poloidal field has been found to be confined in small flux tubes having diameter of the order of a few hundred km with magnetic field of order 1000 gauss (Stenflo 1973; Tsuneta et al. 2008). Early magnetograms did not resolve these small flux tubes and gave what would be the average value of the poloidal magnetic field if magnetic fields inside the flux tubes were spread over the solar surface. The colours in Fig. 6 correspond to such average values.

3 Theory of sunspot formation

Before discussing the theory of how sunspots form, let us make a few comments about the interior structure of the Sun according to what is often called the standard model of the Sun. The energy generated by nuclear fusion in the central region of the Sun is transported outward by radiative transfer till a radius of \(0.7 R_{\odot }\), where \(R_{\odot }\) is the solar radius. The region from \(0.7 R_{\odot }\) to the solar surface turns out to be unstable to convection, where heat is transported by convection. It is this region, known as the solar convection zone, where the dynamo action takes place. Sunspots are concentrations of magnetic field sitting at the top of this turbulent convection zone.

Fig. 7
figure 7

A plasma with vertical magnetic field heated from below. a The initial configuration. b The likely appearance of the magnetic field after convection starts (the dashed lines indicating the convective motions in the plasma)

Full size image

Why do magnetic fields remain concentrated within the sunspots instead of filling up all space? To address this question, we need to consider the interaction between the magnetic field and the convection. This subject is known as magnetoconvection. Chandrasekhar (1952) worked out the linear theory of this subject. Simulations to study the nonlinear evolution of the system were carried out later (Weiss 1981). Consider that a plasma with a vertical magnetic field is heated from below, as sketched in Fig. 7(a). The magnetic tension tries to oppose convection. Eventually, when convection is initiated by making the vertical temperature gradient sufficiently strong, space gets divided into two kinds of regions, as shown in Fig. 7(b). From some regions, the magnetic field lines are expelled and convection can take place freely. In other regions, the magnetic field lines are concentrated and convection gets suppressed. Sunspots are presumably such regions of concentrated magnetic field—known as magnetic flux tubes—within which the convective heat transport is inhibited. The tops of such regions appear darker compared to the surroundings because of the decreased heat transport.

Fig. 8
figure 8

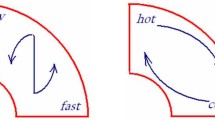
The generation of the toroidal field by the stretching of a poloidal field line by differential rotation. a An initial poloidal field line, with small arrows indicating rotation varying with latitude. b A sketch of the field line after it has been stretched by the faster rotation near the equatorial region

Full size image

The Sun does not rotate like a solid body, the equatorial region having a higher angular velocity. It has been realized from the early years of MHD research that magnetic field lines would be nearly “frozen” in the plasma in a large astrophysical body like the Sun (see, for example, Choudhuri (1998), section 14.2) and that the differential rotation would stretch out a poloidal field to produce a produce a toroidal field, as sketched in Fig. 8. It should be apparent from this figure that the toroidal field will have opposite signs in the two hemispheres. If parts of this toroidal field rise to the surface, then we would have bipolar sunspot pairs with opposite polarity in the two hemispheres, in agreement with observations presented in Fig. 3. Parker (1955b) realized that the pressure of the magnetic field may cause a region of plasma with strong magnetic field to expand, giving rise to what is called magnetic buoyancy. If the magnetic field exists in the form of a magnetic flux tube, then the pressure balance condition between its inside and outside would give

$$\begin{aligned} p_e = p_i + \frac{B^2}{2 \mu _0}, \end{aligned}$$
(3)

where \(p_e\) and \(p_i\) are the gas pressures in the exterior and the interior of the flux tube, while B is the magnetic field inside the flux tube. It follows from (3) that \(p_i < p_e\), which implies that the interior and exterior densities also may often, though not always, satisfy the relation \(\rho _i < \rho _e\). We shall not get into a discussion of the circumstances under which this may happen. If the interior density in some regions of the flux tube becomes less than the exterior density, then those regions of the flux tube become buoyant and rise against gravity, eventually taking up the kind of configuration shown in Fig. 2.

Fig. 9
figure 9

The map of angular velocity distribution in a poloidal plane inside the Sun, as obtained by helioseismology. From Howe et al. (2005), as given in Basu (2016)

Full size image

One of the major breakthroughs in modern astrophysics is that helioseismology—the study of solar oscillations—has succeeded in mapping the differential rotation in the interior of the Sun. Figure 9 shows the map of angular velocity distribution found by helioseismology. It can be seen in this map that the bottom of the convection zone at \(0.7 R_{\odot }\) indicated by the dashed circle is a region of concentrated differential rotation, where the angular velocity changes rather sharply in the radial direction. We believe that the toroidal magnetic field is primarily generated at the bottom of the convection zone and then parts of it rise to the surface due to magnetic buoyancy, as shown in Fig. 10. The Coriolis force due to the rotation of the Sun may act on the rising part of the flux tube and make it tilted, in accordance with Joy’s law.

Fig. 10
figure 10

The production of a tilted bipolar sunspot pair on the solar surface by the buoyant rise of a part of the toroidal field. From Dikpati and Gilman (2006)

Full size image

The rise of flux tubes due to magnetic buoyancy was first studied by doing simulations on the basis of the thin flux tube equation (Spruit 1981; Choudhuri 1990). The first such simulation in a 2D planar geometry was carried out by Moreno-Insertis (1986). We were the first to study the buoyant rise of flux tubes in a spherical geometry by incorporating the Coriolis force (Choudhuri 1989) and gave a theoretical explanation of Joy’s law (D’Silva and Choudhuri 1993) about three-quarters of a century after its observational discovery (Hale et al. 1919). We found that the effect of the Coriolis force is much stronger than what was suspected before (Choudhuri and Gilman 1987) and its effects would have been much larger than what is seen in observations unless the magnetic field inside the buoyant flux tubes was sufficiently strong. By requiring that theory matches observations, we were able to conclude that the magnetic field at the bottom of the convection zone has to be as strong as \(10^5\) gauss (D’Silva and Choudhuri 1993). This result was confirmed by the simulations of other groups (Fan et al. 1993; Caligari et al. 1995). As we shall point out in Sect. 4, this value of the toroidal field was crucial in constraining some aspects of the dynamo process.

As the results obtained by early thin flux tube simulations of sunspot formation played a key role in the growth of the flux transport dynamo model, we have presented a summary of these early simulations. Over the years, very impressive simulations of the buoyant rise of flux tubes going beyond the thin flux tube approach and using the full MHD equations have been carried out. Readers can get an idea of the level of sophistication reached in these simulations by looking at the work of Chen et al. (2017). Since this subject is beyond the scope of the present paper, we do not get into a discussion of it here and refer the excellent review by Fan (2009, 2021) for a discussion of this subject with full bibliography.

4 The basics of the flux transport dynamo model

We have discussed how the poloidal field can be stretched by differential rotation to produce the toroidal field, from which sunspots form. To explain the observed oscillation between the poloidal and the toroidal fields as seen in Fig. 5, we need a mechanism for producing back the poloidal field from the toroidal field. We invoke the idea of Babcock (1961) and Leighton (1969) on how the poloidal field can be generated from the decay of a tilted bipolar sunspot pair, like the pair shown in Fig. 10. Suppose the sunspot at the higher latitude in a pair has positive (negative) polarity. Typical sunspots live for a few days. When this sunspot pair decays, more positive (negative) polarity is spread around at the higher latitude and the opposite polarity at the lower latitude. It may be noted that this process would produce surface fields of opposite polarity on the two sides of the solar equator, leading to the annihilation of these fields by cross-equatorial diffusion. What we thus get is a poloidal field. This Babcock–Leighton mechanism for the generation of the poloidal field is somewhat different from the \(\alpha\)-effect (Parker 1955a; Steenbeck et al. 1966), in which helical turbulence twists the toroidal field to produce the poloidal field. If the toroidal field is as strong \(10^5\) gauss, as suggested by buoyancy simulations, then such twisting is not possible and we believe that the Babcock–Leighton mechanism is the dominant mechanism for generating the poloidal field in the Sun. It is possible that the \(\alpha\)-effect is also present in the regions of weak magnetic field along with the dominant Babcock–Leighton mechanism. The \(\alpha\)-effect may be necessary for the dynamo to recover from grand minima like the Maunder minimum when sunspots disappear and the Babcock–Leighton mechanism may be absent (Karak and Choudhuri 2013; Passos et al. 2014).

We now can think of a minimalistic dynamo model in which the toroidal and poloidal magnetic fields sustain each other through a feedback loop: differential rotation producing the toroidal field from the poloidal field and the Babcock-Leighton mechanism producing the poloidal field back from the toroidal field (which is responsible for the tilted bipolar sunspots). It turns out that this minimalistic model leads to a dynamo wave propagating poleward, in accordance with what is known as the Parker–Yoshimura sign rule (Parker 1955a; Yoshimura 1975). This means that sunspots should appear at higher latitudes with the progress of the cycle, opposite of what is observed (Choudhuri et al. 1995). It is clear that we need something else to turn things around. The meridional circulation of the Sun to be discussed in the next paragraph turns out to be this ‘something else’.

The Sun is known to have a plasma flow at the surface from the equator to the poles, the maximum amplitude of the flow at mid-latitudes being about 20 m s\(^{-1}\). As we do not expect the plasma to pile up near the solar poles, this poleward plasma flow must be a part of a larger meridional circulation pattern having an equatorward return flow somewhere below the surface bringing back the plasma that has flown to the poles. Since the turbulent stresses in the convection zone are responsible for the large-scale flows there (Choudhuri 2021b), we expect the meridional circulation to be confined within the convection zone. Dynamo models are found to give best results if the return flow of the meridional circulation is at the bottom of the convection zone, although some studies have been done with more general kinds of flows (Hazra et al. 2014). Within the last few years, helioseismology has confirmed the existence of the return flow at the bottom of the convection zone (Rajaguru and Antia 2015; Gizon et al. 2020), validating different theoretical groups who have been constructing dynamo models assuming such a flow for many years.

Fig. 11
figure 11

A cartoon indicating the essential ingredients of the flux transport dynamo model

Full size image

Figure 11 shows a cartoon summarizing what is called the flux transport dynamo model. The green colour indicates the region at the bottom of the convection zone where differential rotation produces the strong toroidal field. The red arrows represent magnetic buoyancy due to which the toroidal field rises to the solar surface to produce sunspots. The brown region near the surface is where the poloidal field is produced by the Babcock-Leighton mechanism. The blue curves indicate the all-important meridional circulation. The toroidal field produced at the bottom of the convection zone is advected equatorward by the meridional circulation there, ensuring that sunspots appear closer to the equator with the progress of the sunspot cycle. On the other hand, the poleward meridional circulation near the surface advects the poloidal field generated there, in agreement with observations.

The essential ideas of this model were presented in an early paper by Wang et al (1991) on the basis of a 1D model, which led to partial differential equations in \((\theta , t)\) for various relevant quantities. The first 2D calculations of the flux transport dyanamo model, involving partial differential equations in \((r, \theta , t)\), were done in the mid-1990s (Choudhuri et al. 1995; Durney 1995). The paper by Choudhuri et al. (1995), perhaps the most important paper in the present author’s scientific career, convincingly showed that the meridional circulation can indeed turn things around and make sunspots appear at lower latitudes with the progress of the cycle rather than at higher latitudes which would happen in the absence of the meridional circulation. This established the flux transport dynamo as a promising model of the solar dynamo and several groups started studying different aspects of this model within the next few years (Durney 1997; Dikpati and Charbonneau 1999; Küker et al. 2001; Dikpati and Gilman 2001; Nandy and Choudhuri 2001, 2002; Bonanno et al. 2002; Guerrero and Muñoz 2004; Chatterjee et al. 2004).

The flux transport dynamo model was first developed by doing calculations with the help of mean field equations obtained by averaging over the turbulence in the convection zone. The mean field equation for the evolution of the magnetic field is the famous dynamo equation

$$\begin{aligned} \frac{\partial \mathbf{B}}{\partial t} = \nabla \times (\mathbf{v}\times \mathbf{B}) + \nabla \times (\alpha \mathbf{B}) + \lambda _T \nabla ^2 \mathbf{B}, \end{aligned}$$
(4)

where \(\lambda _T\) is the turbulent diffusivity inside the convection zone and \(\alpha\) is the parameter which governs the generation of the poloidal field (see, for example, Moffatt (1978), Chapters 7–9; Parker (1979), Chapters 18–19; Choudhuri (1998), Chapter 16). The parameter \(\alpha\) for the Babcock–Leighton mechanism has to be specified somewhat differently compared to the classical \(\alpha\)-effect proposed by Parker (1955a) and Steenbeck et al. (1966). It may be mentioned that (4) is a simple version of the dynamo equation obtained on the basis of several simplifying assumptions. This particular version of the dynamo equation has been used widely in the mean field models of the solar dynamo. If we do not make some of these simplifying assumptions, then we end up with a more complicated version of the dynamo equation with additional terms which we shall not discuss here.

The mean magnetic field written in the form (1) can be substituted in (4), whereas the velocity has to be written as

$$\begin{aligned} \mathbf{v}= \mathbf{v}_m+ r \sin \theta \, \Omega (r, \theta ) \mathbf{e}_{\phi }, \end{aligned}$$
(5)

where \(\Omega (r, \theta )\) is the angular velocity in the interior of the Sun and \(\mathbf{v}_m\) is the velocity of meridional circulation having components in r and \(\theta\) directions. On substituting (1) and (5) into (4), some reasonable assumptions lead to the following coupled equations for the poloidal and the toroidal fields

$$\begin{aligned} \frac{\partial A}{\partial t} + \frac{1}{s}(\mathbf{v}_m.\nabla )(s A)= & {} \lambda _T \left( \nabla ^2 - \frac{1}{s^2} \right) A + \alpha B, \end{aligned}$$
(6)
$$\begin{aligned} \frac{\partial B}{\partial t} + \frac{1}{r} \left[ \frac{\partial }{\partial r} (r v_r B) + \frac{\partial }{\partial \theta }(v_{\theta } B) \right]= & {} \lambda _T \left( \nabla ^2 - \frac{1}{s^2} \right) B + s(\mathbf{B}_p.\nabla )\Omega + \frac{1}{r}\frac{d\lambda _T}{dr} \frac{\partial }{\partial {r}}(r B), \end{aligned}$$
(7)

where \(s = r \sin \theta\) and \(\mathbf{B}_p\) is the poloidal field with the components given by (2). To understand the behaviour of the flux transport dynamo, we have to solve (6) and (7) simultaneously after suitably specifying the various parameters \(\Omega\), \(\mathbf{v}_m\), \(\lambda _T\) and \(\alpha\).

Fig. 12
figure 12

A theoretical time-latitude plot from Chatterjee et al. (2004) based on their dynamo calculation. The time on the horizontal axis is indicated in years since the starting of the code. The shaded regions indicate the latitudes where sunspots are seen at different times, whereas the contours indicate the values of the radial magnetic field at the solar surface

Full size image

One of the aims of the flux transport dynamo model would be to explain surface observations such as what are presented in time-latitude plots like Fig. 6. Even the early 1D model of Wang et al (1991) produced remarkable matches with observational data. To give an idea of the success of 2D models in matching surface observational data, we show Fig. 12 taken from Chatterjee et al. (2004), which can be directly compared with the observational plot shown in Fig. 6. The shaded regions in both these time-latitude plots indicate sunspots. The contours of constant radial field at the surface seen Fig. 12 have to be compared with the colours in Fig. 6. Given the fact that Fig. 12 was one of the first such theoretical plots produced from the 2D flux transport dynamo model, hopefully all readers will agree that the fit between theory and observations was commendable.

We have pointed out in Sect. 1 about the evidence of magnetic cycles in other solar-like stars. The difficulty of making models of these stellar dynamos is that we do not have any detailed information about the differential rotation \(\Omega\) or the meridional circulation \(\mathbf{v}_m\) for other stars besides the Sun. However, these large-scale fluid flows can be calculated from mean field models of the large-scale flows (Kitchatinov and Ruediger 1995; Kitchatinov and Olemskoy 2012) and then used for constructing flux transport dynamo models of solar-like stars (Karak et al. 2014b). Such models can match many aspects of observational data. However, there are still doubts whether the flux transport dynamo model is universally applicable to all solar-like stars (Choudhuri 2017).

5 Modelling irregularities of the sunspot cycle

We have given some idea of how the regular periodic features of the sunspot cycle are explained with the flux transport dynamo model. A look at Fig. 1 makes it clear that the sunspot cycle is only approximately periodic. We shall now turn our attention to the question of how the flux transport dynamo model can be applied to explain the observed irregularities of the sunspot cycle. See a review by Choudhuri (2014) on this subject. An early idea was that the irregularities of the sunspot cycle are manifestations of chaos resulting from the nonlinearities of the dynamo problem (Weiss et al 1984). However, it appears that the most obvious kinds of nonlinearities would not produce the sustained irregularities we observe, and some stochastic fluctuations may be the more appropriate cause of the cycle irregularities (Choudhuri 1992; Hoyng 1993). We should point out that there are some irregularities which possibly result from nonlinear chaos. For example, the Gnevyshev–Ohl effect—the fact that the odd-numbered cycle was stronger than the previous even-numbered cycle for several cycles—is probably a manifestation of period doubling due to nonlinear chaos (Charbonneau et al. 2005, 2007). Since stochastic fluctuations are likely to be the more important source for sunspot cycle irregularities, let us now discuss how these fluctuations arise.

As we have pointed out, a crucial ingredient of the flux transport dynamo is the Babcock–Leighton mechanism, which involves the tilts of bipolar sunspot pairs as given by Joy’s law. However, Joy’s law happens to be a law of statistical averages, there being a random distribution of tilt angles around the average given by Joy’s law (Stenflo and Kosovichev 2012). This randomness presumably arises due to the effect of turbulence on the magnetic flux tubes rising through the convection zone (Longcope and Fisher 1996; Longcope and Choudhuri 2002) and introduces fluctuations in the Babcock–Leighton mechanism. Choudhuri et al. (2007) identified these fluctuations in the Babcock–Leighton mechanism arising out of the randomness in the sunspot tilt angles as the main source of irregularities in the sunspot cycle and developed a method for predicting the next upcoming cycle.

Different methods have been suggested over the years for the prediction of a sunspot cycle before its onset, perhaps the most popular method being the use of the polar field strength at the end of the previous cycle as the predictor (Schatten et al. 1978). After the initial development of the flux transport dynamo model during the solar cycle 23, whether it was possible to predict the next cycle 24 based on this theoretical dynamo model became an important question. There were sceptics (Tobias et al. 2006) who doubted the feasibility of such predictions at all. Dikpati and Gilman (2006) proposed a method of making such predictions by feeding some appropriate data of the past cycles into the dynamo code. They concluded that the upcoming cycle 24 would be a very strong cycle, in contrast to the prediction of a weak cycle by Schatten (2005) and Svalgaard et al. (2005), who had used the weak polar field at the end of the cycle 23 as the predictor. Choudhuri et al. (2007) and Jiang et al. (2007) pointed out several logical flaws in the Dikpati–Gilman arguments and developed an alternative methodology for predicting the next cycle based on the version of the flux transport dynamo model they had developed. They predicted a rather low value for the peak of the sunspot cycle 24, which turned out to be the first successful dynamo-based prediction of a sunspot cycle before its onset. Figure 13 is a plot of observed sunspot number along with the two theoretical predictions of cycle 24 due to Dikpati and Gilman (2006) and Choudhuri et al. (2007). The theoretical justification behind using the polar field strength at the end of the previous cycle as the predictor was provided by Jiang et al. (2007). They found that a correlation between the polar field at the end of a cycle and the strength of the next cycle arises if the turbulent diffusivity within the convection zone is assumed to have a value of \(10^{12}\) cm\(^2\) s\(^{-1}\) or higher. Jiang et al. (2007) gave several arguments in favour of such a value of turbulent diffusivity. Dikpati and Gilman (2006) had taken a lower value of turbulent diffusivity and did not get this correlation.

Fig. 13
figure 13

The predictions for the peak of cycle 24 by Dikpati and Gilman (2006) and Choudhuri et al. (2007) are indicated respectively by the upper star and the lower star in this plot showing the variation of sunspot number with time during that era. The circle of the horizontal axis indicates the time when these predictions were made

Full size image

We now realize that, apart from the fluctuations in the Babcock–Leighton mechanism, fluctuations in the meridional circulation also can be an additional source of irregularities in the sunspot cycles. The period of the flux transport dynamo depends on the strength of the meridional circulation, periods becoming shorter when the circulation is stronger (Dikpati and Charbonneau 1999; Nandy and Choudhuri 2001). If there are fluctuations in the meridional circulation, that would certainly introduce irregularities in the sunspot cycle (Karak 2010). Especially, durations of different cycles would vary due to such fluctuations. From the historical data of past cycles, Karak and Choudhuri (2011) indeed found indirect evidence for fluctuations in the meridional circulation in the past. Diffusion acting on longer cycles may make them weaker, giving rise to an anti-correlation between the cycle duration and strength. This anti-correlation readily leads to an explanation of the Waldmeier effect that stronger cycles rise faster, because they are shorter due to this anti-correlation (Karak and Choudhuri 2011). The recent work of Biswas et al. (2022), however, indicates that more careful investigation of this subject is needed.

Taking the fluctuations in the Babcock–Leighton mechanism and the fluctuations in the meridional circulation as the two main sources of irregularities in the sunspot cycles, Choudhuri and Karak (2012) developed a comprehensive model of grand minima like the Maunder minimum during the seventeenth century, which can be seen in Fig. 1. There is now indirect evidence (from the analysis of polar ice cores) that there have been about 27 grand minima in the last 11,000 yr (Usoskin et al. 2007). The results of Choudhuri and Karak (2012) are in broad agreement with this. With the realization that the fluctuations in the meridional circulation are so important in producing irregularities in the sunspot cycle, it is clear that these fluctuations have to be taken into consideration along with the fluctuations in the Babcock–Leighton mechanism for the prediction of future cycles. How this can be done has been discussed by Hazra and Choudhuri (2019).

Lastly, we may mention that two papers from our group—Choudhuri et al. (2007) on the prediction of sunspot cycles and Choudhuri and Karak (2012) on the grand minima—were selected as “Editors’ suggestion” in Physical Review Letters, showing that the subject of irregularities of the sunspot cycle is of considerable interest to the physics community.

6 Concluding remarks

The basic idea of the solar dynamo is that the sunspot cycle is produced by an oscillation between the toroidal and poloidal components of the solar magnetic field. The toroidal field, from which the sunspots arise due to magnetic buoyancy, is generated by the stretching of the poloidal field by differential rotation. How the poloidal field arises from the toroidal field is less certain. The current flux transport dynamo models invoke the Babcock–Leighton mechanism in the place of the older \(\alpha\)-effect which can work only if the toroidal field is much weaker what we now believe it to be. The meridional circulation, which is poleward at the surface and was expected to be equatorward at the bottom of the convection zone, plays a crucial role in the flux transport dynamo model in ensuring that the solar magnetic fields are transported in agreement with observations. We have also discussed how the irregularities in the Babcock–Leighton mechanism and in the meridional circulation may give rise to the observed irregularities in the sunspot cycle.

The flux transport dynamo model developed historically by following the mean field approach, in which we average over turbulence in the convection zone. Equation (4), which leads to Eqs. (6) and (7), is based on such mean field approach. Using the observational input for the solar differential rotation \(\Omega\) and the meridional circulation \(\mathbf{v}_m\) in Eq. (5), we can specify the velocity field \(\mathbf{v}\) and follow the kinematic approach of solving our equations only for the magnetic field. As we have already pointed out in Sect. 4, we have to go beyond the kinematic approach in modelling stellar dynamos for which we do not have information about the large-scale flows. Even for the Sun, we have to go beyond the kinematic approach if we want to study the observed variations of the large-scale flows with the cycle due to the back-reaction of the dynamo-generated magnetic field (Rempel 2006; Choudhuri 2021b). How the observed cyclic variation of the differential rotation, known as torsional oscillations, arises in the flux transport dynamo model has been studied by Chakraborty et al. (2009). The meridional circulation is found to become weaker at the time of the sunspot maximum (Hathaway and Rightmire 2010). While the variation of meridional circulation can be included in the dynamo model by introducing a simple quenching by the magnetic field (Karak and Choudhuri 2012), a proper theory requires the solving of the equation for meridional circulation along with the dynamo equations. Hazra and Choudhuri (2017) studied this problem by solving the perturbed part of the meridional circulation equation which incorporates the Lorentz force due to the dynamo-generated magnetic field. It may noted that the mean field models of the differential rotation and the meridional circulation show them to be intimately connected with each other. For example, to explain the shear layer of differential rotation just below the solar surface seen in Fig. 9, we need to analyze the thermal wind balance equation arising in the theory of the meridional circulation (Choudhuri 2021a; Jha and Choudhuri 2021). For alternative theoretical viewpoints about the near surface shear layer, the readers are referred to Hotta et al. (2015) and Matilsky et al. (2019).

Within the last few decades, tremendous advances have been made in the direct numerical simulation (DNS) of the geodynamo starting with the path-breaking work by Glatzmaier and Roberts (1995). While the mean field models played a historically important role in the growth of the flux transport dynamo model, often a question is asked whether these models still remain relevant in the present era of DNS. After a pioneering early DNS of the solar dynamo (Gilman 1983) failed to produce results in agreement with observations, this field remained dormant for a few years. Then, from about 2010 onwards, some impressive DNS calculations of the solar dynamo have been done (Ghizaru et al. 2010; Brown et al. 2010). However, simulating the solar dynamo is much more challenging than simulating the geodynamo because of the wide ranges of length and time scales involved. Also, the stratification of the convection zone within which the density and pressure vary by several orders of magnitude makes realistic simulations very difficult. Additionally, in a kinematic mean field model, one can specify the differential rotation and meridional circulation from observational data. In contrast, in a DNS, these large-scale flows have to come out of the simulations and, until one gets the large-scale flows correctly, there is no hope of building a realistic model of the dynamo. Because of these reasons, simulations of the solar dynamo are still of rather exploratory nature. We still have to depend on the mean field model for providing detailed explanations of different aspects of observational data.

One limitation of 2D mean field models is that the Babcock–Leighton mechanism is an inherently 3D mechanism and can be included in 2D models only through crude approximations. There has been some debate about the best way handling the Babcock–Leighton mechanism within the framework of 2D models (Durney 1997; Nandy and Choudhuri 2001; Muñoz-Jaramillo et al. 2010). Rather than going all the way to full 3D simulations, one can think of constructing 3D kinematic models (Yeates and Muñoz-Jaramillo 2013; Miesch and Dikpati 2014; Hazra et al. 2017). In such models, the large-scale flows are specified on the basis of the observational data, whereas the evolution of the magnetic field is treated in 3D so that the Babcock–Leighton mechanism is modelled realistically by considering the decay of tilted bipolar sunspots. It may be noted that over the years the surface flux transport models, which solve the advection–diffusion equation in \((\theta , \phi )\) coordinates with the magnetic fields of sunspots as sources, have been used for studying the Babcock–Leighton process on the solar surface (Wang et al 1989; Cameron et al. 2010; Jiang et al. 2014).

While 2D kinematic mean field models have provided explanations for many aspects of the sunspot cycle, we certainly need to go beyond them if we want our solar dynamo models to be sufficiently realistic. Perhaps 3D kinematic models happen to be the next important step. Ultimately our goal should be to carry on 3D simulations of the large-scale flows and the solar dynamo together. However, we probably have to wait for a few years before fully realistic simulations of this kind can be carried out in a self-consistent manner.

7 A personal note

Let me end by mentioning that this paper is based on my lecture given on the occasion of the Subrahmanyan Chandrasekhar Prize of Plasma Physics being bestowed on me. A Prize named after Professor Chandrasekhar has a special personal significance for me, since I am presumably the first recipient of this Prize who had Chandrasekhar himself as a professor at the University of Chicago. As a first-year graduate student there, I took a course on general relativity taught by him.

Fig. 14
figure 14

The Laboratory for Astrophysics and Space Research (LASR) in the University of Chicago campus, as it was in the 1980s. The upper left corner room was Parker’s office, whereas the room next to it was my office. The upper right corner room was Chandrasekhar’s office

Full size image

I dedicate this paper to the memory of my PhD supervisor E.N. (Gene) Parker, who first initiated me to the field of plasma astrophysics. He passed away a few months ago. Figure 14 shows the Laboratory for Astrophysics and Space Research in the University of Chicago campus, where we all had our offices. The left corner room in the upper floor was Parker’s office and the right corner room was Chandrasekhar’s office. My office was next to Parker’s office. Working in that office for four years, I had the rare privilege of observing these two giants of theoretical astrophysics closely.

Whatever little I have achieved in science during the last few years has been possible because of the succession of exceptionally brilliant students who decided to work under my supervision for their PhD—Sydney D’Silva, Mausumi Dikpati, Dibyendu Nandy, Piyali Chatterjee, Jie Jiang, Bidya Karak, Gopal Hazra. I am grateful to my colleague Rahul Pandit who insisted on nominating me for the Chandrasekhar Prize against my initial hesitation. I thank Eric Priest, Kazunari Shibata, Paul Charbonneau, Jie Jiang and Durgesh Tripathi for their support letters.

Apart from those who helped me professionally in my scientific career, my journey has been possible due to the support and encouragement of many others—family members, teachers, friends. My parents encouraged me from my childhood to take up an academic career. I would not have reached here today without the strong support of my wife Mahua.