Abstract
The main objective of this paper is to extend Morse–Forman theory to vector-valued functions. This is mostly motivated by the need to develop new tools and methods to compute multiparameter persistence. To generalize the theory, in addition to adapting the main definitions and results of Forman to this vectorial setting, we use concepts of combinatorial topological dynamics studied in recent years. This approach proves to be successful in the following ways. First, we establish a result which is more general than that of Forman regarding the sublevel sets of a multidimensional discrete Morse function. Second, we find a way to induce a Morse decomposition in critical components from the critical points of such a function. Finally, we deduce a set of Morse equation and inequalities specific to the multiparameter setting.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Discrete Morse theory (DMT) introduced by Forman (1998), Forman (2002) has proven to be extremely useful in a panoply of applications where the topological processing of data is a key ingredient. Many domains such as visualization, molecular biology, computer vision, computational geometry, to name but a few, that rely on point cluster generation and meshing techniques have already used Forman’s theory very successfully. Moreover, this theory has become central in the emerging and fast-growing field called topological data analysis (TDA) which aims at providing efficient topological and geometrical tools to extract and organize relevant qualitative information about given data. DMT can be used directly for discrete data processing or as a procedure that simplifies and reduces the computation of Persistent Homology (PH), another very popular and very efficient tool used in TDA.
In this paper, we focus exclusively on the discrete Morse theory developed by Forman since the work undertaken is based to some extent on the ideas from Allili et al. (2019), which were developed and expressed using the Forman framework. Nonetheless, there are alternative discrete Morse theories available with equivalent potential than the Forman’s approach (Fugacci et al. 2020; Scoville 2019). One version that has gained prominence in literature is the piecewise-linear (PL) Morse theory introduced by Banchoff (1967). Recent additions to this approach made notably by Bloch (2013) and Grunert et al. (2023) provide an insight about the possibility of using it to develop a framework for persistent homology of spaces and maps similar to the one achieved by Forman’s theory.
PH has been introduced in (Edelsbrunner et al. 2002) as a tool for the analysis of homologies of spaces which can be given in terms of meshes or cluster of points by means of a filtration defined on the space. This theory constitutes a reliable and efficient method to track the evolution of topological features in data. Its key properties that make it important in TDA are the robustness to noise, the independence of dimension, and its computability and algorithmic framework.
In the standard setting, PH is defined on a nested growing sequence, often called a filtration, of sublevel sets of a function \(f: |S| \rightarrow {\mathbb {R}}\) where S is typically a simplicial complex built from data and f is a continuous function on |S|, usually called a filtering function. It provides topological invariants of the filtration known as barcodes or persistence diagrams which measure the persistence of topological features of the data at different resolutions and scales in the space as encoded by the filtration. In this context, the filtration is indexed by a totally ordered set T and hence it is called a single-parameter filtration and it gives rise to the single-parameter PH. However, in many applications the data is best described using multiple parameters and using single-parameter filtrations can result in missing important information about the data. This is particularly the case for spatial complex and heterogeneous noisy data whose topological structure can depend on several parameters such as the scale, the density, the presence of outliers and other artifacts (Vipond et al. 2021; Xia and Wei 2015).
These shortcomings triggered the development of multiparameter persistence homology (MPH) defined on a multiparameter filtration of the sublevel sets of a one-parameter family of functions \(f_t: |S| \rightarrow {\mathbb {R}}\) (Carlsson and Zomorodian 2009). Typically, the parameter t is taken in some continuous interval such as [0, 1]. However when the number of used parameters is finite, the family of functions can be replaced by a function \(f: |S| \rightarrow {\mathbb {R}}^k\), for some positive integer k. The topological information provided by MPH can be encoded as multiparameter persistence modules (Carlsson et al. 2010) which do not possess a simple representation comparable to that of the persistence diagrams in the PH case. The rank invariant introduced by Carlsson et al. (2010) is an alternative invariant that contains the same information as the persistence diagram in the one parameter case. Software for visualizing the rank invariant of the two-parameter persistent homology (RIVET) is provided by Lesnick and Wright (2015). There are also efforts to find invariants that can be combined with statistical and machine learning tools such as the persistent landscapes (Bubenik 2015; Vipond 2020). However the extraction of multiparameter persistent information remains a hard task in the general case and the existing methods for the computation of MPH are computationally expensive due to the considerable size of complexes built from data.
One direction explored in some recent works consists in designing algorithms to reduce the original complexes generated from data to enough smaller cellular complexes, homotopically equivalent to the initial ones by means of acyclic partial matchings of discrete Morse theory. This approach used initially for the one-parameter filtrations has been extended to the multiparameter case for the first time by Allili et al. (2017). More efficient algorithms based on a similar idea are obtained by Allili et al. (2019), Scaramuccia et al. (2020). Even though the designed algorithms make use of the idea of discrete Morse pairings, the works did not provide a systematic extension of the Forman’s discrete Morse theory to the multiparameter case although a serious attempt was made by Allili et al. (2019) to achieve this goal. Indeed, new definitions of a multidimensional discrete Morse function, of its gradient field, its regular and critical cells are proposed. Moreover, it was proved that given a filtering function \(f: |S| \rightarrow {\mathbb {R}}^k\), there exists a multidimensional discrete Morse (mdm) function g with the same order of sublevel sets and the same acyclic partial matching as the one associated with f.
In this paper, the combinatorial vector fields framework is used to further develop the concept and the properties of the mdm theory. Many notions of the classical discrete Morse theory are extended to the mdm case. The relationship between a mdm function and its components functions are investigated and the handle decomposition and collapsing theorems are established. Moreover, results on Morse inequalities and Morse decompositions are proved for the first time. An additional contribution achieved in this work consists of a method that allows to partition critical cells of a mdm function into connected critical components. It is known from smooth singularity theory that the criticalities of smooth vector-valued functions are generally sets and not insolated points. Experimentations (Allili et al. 2019) suggest that it is also the case for a mdm function where each criticality is given as a component that may consist of several cells. We refer the reader to (Budney and Kaczynski 2023; Smale 1975; Wan 1975) and references therein for the classical singularity theory setting. In particular, the recent work of Budney and Kaczynski (2023) has been largely motivated by the call coming from Allili et al. (2019) for providing an adequate application-driven smooth background and geometric insight that would help us in understanding the discrete counterpart.
The partition of critical cells in components proposed in this work is a first step in this direction with the goal of linking mdm theory to the smooth singularity theory mentioned above and the piecewise linear setting (Edelsbrunner et al. 2008; Huettenberger et al. 2014), in which criticalities of vector-valued functions also appear in the form of sets.
The paper is organized as follows. In Sect. 2, we recall useful definitions and terminology about simplicial complexes and combinatorial vector fields. Section 3 is devoted to introduce and discuss notions of combinatorial dynamics on simplicial complexes which provide a framework to represent discrete vector fields and discrete Morse functions in terms of discrete dynamical systems and flows. This allows to associate to combinatorial vector fields the concepts of isolated invariant sets, Conley index, Morse decompositions and Morse inequalities which is achieved in Corollary 3.12. Some new results about Morse decompositions are also discussed. In Sect. 4, we build on preliminary results of Allili et al. (2019) and define multidimensional, or multiparameter, discrete Morse functions and outline many of their properties. In the sections that follow, many classical results of Forman’s theory for real-valued functions are extended to vector-valued functions. One of the difficulties in the study of mdm functions is the classification of their criticalities. Unlike real-valued discrete Morse functions for which each criticality is represented by a single cell, experimentations (Allili et al. 2019) and the smooth theory of singularity both suggest that a criticality of a mdm function is a component that may contain several cells. In Sect. 7, a method to group critical cells to form critical components is proposed in Definition 7.3. This leads to Theorem 7.7 on Morse decompositions and acyclicity. Our final result concerning Morse inequalities is stated in Theorem 7.8.
Concluding remarks and future work directions are proposed at the end of the paper.
2 Preliminaries
2.1 Maps and relations
Consider two sets X and Y. A partial map \(f:X\nrightarrow Y\) is a function whose domain \({{\,\textrm{dom}\,}}f\) is a subset of X. We note \({{\,\textrm{im}\,}}f:= f(X)\) the image of f and \({{\,\textrm{Fix}\,}}f:= \left\{ x\in {{\,\textrm{dom}\,}}f\ |\ f(x) = x\right\} \) the set of fixed points of f.
Moreover, a multivalued map \(F:X\multimap Y\) is a function which associates each \(x\in X\) to a non-empty subset \(F(x)\subseteq Y\). For every \(y\in Y\), we write \(F^{-1}(y):=\left\{ x\in X\ |\ y\in F(x) \right\} \) and for subsets \(A\subseteq X\) and \(B\subseteq Y\), we define \(F(A):= \bigcup _{x\in A}F(x)\) and \(F^{-1}(B):= \bigcup _{y\in B}F^{-1}(y)\).
Furthermore, for a binary relation \(R\subseteq X\times X\), we write xRy when \((x,y)\in R\). We define the transitive closure \({\bar{R}}\subseteq X\times X\) of R as the relation such that \(x{\bar{R}}y\) if there exists a sequence \(x=x_0,x_1,\ldots ,x_n=y\) in X such that \(n\ge 1\) and \(x_{i-1}Rx_i\) for each \(i=1,\ldots ,n\). The relation \({\bar{R}}\cup {{\,\textrm{id}\,}}_X\), where \({{\,\textrm{id}\,}}_X\) is the identity relation on X, is both reflexive and transitive, making it a preorder, which we call the preorder induced by R. Note that the preorder induced by a reflexive relation is simply its transitive closure.
2.2 Simplicial complexes
In the context of this article, we consider a simplicial complex K to be a finite collection of non-empty finite sets such that for all \(\sigma \in K\) and \(\tau \subseteq \sigma \), we have \(\tau \in K\). An element of a simplicial complex is called a simplex. The dimension of a simplex \(\sigma \) is \(\dim \sigma = {{\,\textrm{card}\,}}\sigma -1\), and we note \(K_p\) the set of simplices in K of dimension p. The superscript \(\sigma ^{(p)}\) is sometimes used to specify a simplex \(\sigma \) is of dimension p.
Furthermore, if \(\tau \subseteq \sigma \in K\), we say that \(\tau \) is a face of \(\sigma \) and \(\sigma \) a coface of \(\tau \). If, in addition, we have \(\dim \tau =\dim \sigma -1\), then \(\tau \) is said to be a facet of \(\sigma \) and, conversely, \(\sigma \) a cofacet of \(\tau \).
There are many ways to endow an abstract simplicial complex with a topology. When considering a simplicial complex as a combinatorial or discrete object, the Alexandrov topology is quite convenient (McCord 1966; Stong 1966). In this topology, the closure of a set of simplices \(A\subseteq K\), which we note \({{\,\textrm{Cl}\,}}A\), is the set of all faces of all simplices in A. We also call \({{\,\textrm{Ex}\,}}A:= {{\,\textrm{Cl}\,}}A\backslash A\) the exit set of A. Otherwise, since a simplicial complex is a particular case of a CW-complex, we may also identify each simplex \(\sigma ^{(p)}\in K\) with a cell of dimension p, which is homeomorphic to an open ball, in a Hausdorff space. In practice, this Hausdorff space is generally \({\mathbb R}^d\) and each p-cell is the convex hull of \(p+1\) affinely independent points. This point of view will prove itself to be particularly useful to generalize some of Forman’s classical results. We then note \({{\,\textrm{cl}\,}}A\) and \({{\,\textrm{ex}\,}}A:= {{\,\textrm{cl}\,}}A\backslash A\) respectively the closure and exit set of A in K considered as a CW-complex. When using the operators \({{\,\textrm{Cl}\,}}\), \({{\,\textrm{Ex}\,}}\), \({{\,\textrm{cl}\,}}\) or \({{\,\textrm{ex}\,}}\) with a singleton, we omit the braces.
We call \(\sigma \in K\) a free face of a simplicial complex K if it has a unique cofacet \(\tau \supset \sigma \). When K has a free face \(\sigma \) with cofacet \(\tau \supset \sigma \), then we call an elementary collapse the operation of removing \(\sigma \) and \(\tau \) to obtain a smaller subcomplex \(K\backslash \{\sigma ,\tau \}\). We say that K collapses onto a subcomplex L, noted \(K\searrow L\), if L can be obtained from K by doing a sequence of elementary collapses. Collapsing a simplicial complex onto a subcomplex may be seen as a deformation retraction. More precisely, if \(K\searrow L\), then L is a deformation retract of K, thus K and L are homotopy equivalent spaces when endowed with the topology of CW complexes, and we note \(K\simeq L\).
2.3 Combinatorial vector fields
We now introduce the concept of discrete vector fields on simplicial complexes. They were first used within the framework of discrete Morse theory by Forman (1998), Forman (2002), who defined them as collections of pairs of simplices. Here, we use the definition proposed by Batko et al. (2020), Kaczynski et al. (2016), which is better suited in our context. Also, note that a discrete vector field is a particular case of a multivector field, as defined by Mrozek (2017) (see Fig. 1).
Definition 2.1
(Discrete vector field) A discrete vector field, or a combinatorial vector field, on a simplicial complex K is an injective partial self-map \(\mathcal {V}:K\nrightarrow K\) such that
-
(1)
for each \(\sigma \in {{\,\textrm{dom}\,}}\mathcal {V}\), either \(\mathcal {V}(\sigma ) = \sigma \) or \(\mathcal {V}(\sigma )\) is a cofacet of \(\sigma \);
-
(2)
\({{\,\textrm{dom}\,}}\mathcal {V}\cup {{\,\textrm{im}\,}}\mathcal {V}= K\);
-
(3)
\({{\,\textrm{dom}\,}}\mathcal {V}\cap {{\,\textrm{im}\,}}\mathcal {V}= {{\,\textrm{Fix}\,}}\mathcal {V}\).
In (a), a discrete vector field \(\mathcal {V}\). The dots identify the fixed points of \(\mathcal {V}\), while the arrows show the pairs of simplices \((\sigma ,\tau )\) such that \(\mathcal {V}(\sigma ) = \tau \). In (b), the induced flow \(\Pi _\mathcal {V}\). In (c), a continuous flow on the underlying space which mimics the dynamics of the combinatorial flow
For some discrete vector field \(\mathcal {V}\) on K, we call a \(\mathcal {V}\)-path a sequence
of simplices in K such that \(\alpha _i\in {{\,\textrm{dom}\,}}\mathcal {V}\), \(\mathcal {V}(\alpha _i) = \beta _i\) and \(\beta _i\supset \alpha _{i+1}\ne \alpha _i\) for each \(i=0,\ldots ,n-1\). A \(\mathcal {V}\)-path is closed if \(\alpha _0=\alpha _n\) and nontrivial if \(n\ge 1\). A discrete vector field \(\mathcal {V}\) is said to be acyclic if there is no nontrivial closed \(\mathcal {V}\)-path.
Finally, we define the notion of \(\mathcal {V}\)-compatibility as introduced by Mrozek (2017) using the notation of Batko et al. (2020), Kaczynski et al. (2016). Note that this is unrelated to the compatibility of a discrete field with a multifiltration as defined by Scaramuccia et al. (2020).
Definition 2.2
(\(\mathcal {V}\)-compatibility) Let \(\mathcal {V}\) be a combinatorial vector field on a simplicial complex K. We say that \(A\subseteq K\) is \(\mathcal {V}\)-compatible if for all \(\sigma \in K\), we have \(\sigma ^-\in A\Leftrightarrow \sigma ^+\in A\) where
For all \(\sigma \in K\), can see that \(\sigma ^-=\sigma =\sigma ^+\) when \(\sigma \in {{\,\textrm{Fix}\,}}\mathcal {V}\), \(\sigma ^-\subsetneq \sigma =\sigma ^+\) when \(\sigma \in {{\,\textrm{im}\,}}\mathcal {V}\backslash {{\,\textrm{Fix}\,}}\mathcal {V}\) and \(\sigma ^-=\sigma \subsetneq \sigma ^+\) when \(\sigma \in {{\,\textrm{dom}\,}}\mathcal {V}\backslash {{\,\textrm{Fix}\,}}\mathcal {V}\).
3 Combinatorial dynamics
Many concepts of dynamical systems theory, notably elements of Conley index theory (Conley 1978), can defined in the combinatorial setting. In this section, we recall such notions, which were mainly discussed in (Batko et al. 2020; Kaczynski et al. 2016; Mrozek 2017). We also prove some new results, notably Propositions 3.14 and 3.15, regarding acyclic combinatorial vector fields and their induced flows, and Theorem 3.24.
3.1 Flows
We define the flow induced by a combinatorial vector field as in (Batko et al. 2020; Kaczynski et al. 2016). It is worth noting that this definition coincides with the one given in (Mrozek 2017) for combinatorial multivector fields when applied to vector fields.
Definition 3.1
(Flow associated to a discrete vector field) Given a combinatorial vector field \(\mathcal {V}\) on a simplicial complex K, the associated flow \(\Pi _\mathcal {V}\) is the multivalued map \(\Pi _\mathcal {V}:K\multimap K\) such that
Notice that \(\Pi _\mathcal {V}(\sigma ) = \{\mathcal {V}(\sigma )\}\) when \(\sigma \in {{\,\textrm{dom}\,}}\mathcal {V}\backslash {{\,\textrm{Fix}\,}}\mathcal {V}\) and \(\Pi _\mathcal {V}(\sigma )\subseteq {{\,\textrm{Cl}\,}}\sigma \) otherwise. An example of a flow is illustrated in Fig. 1.
A solution of a flow \(\Pi _\mathcal {V}\) is a partial map \(\varrho :{\mathbb Z}\nrightarrow K\) such that \({{\,\textrm{dom}\,}}\varrho \) is an interval of \({\mathbb Z}\) and, whenever \(i,i+1\in {{\,\textrm{dom}\,}}\varrho \), we have \(\varrho (i+1)\in \Pi _\mathcal {V}(\varrho (i))\). A solution is full when \({{\,\textrm{dom}\,}}\varrho ={\mathbb Z}\). We note \({{\,\textrm{Sol}\,}}(\sigma ,A)\) the set of full solutions \(\varrho :{\mathbb Z}\rightarrow A\) for which \(\sigma \in {{\,\textrm{im}\,}}\varrho \).
Moreover, a solution \(\varrho \) with \({{\,\textrm{dom}\,}}\varrho = \{m,m+1,\ldots ,m+n\}\) is nontrivial if \(n \ge 1\) and it is closed if \(\varrho (m) = \varrho (m+n)\). We note \(\sigma \rightarrowtriangle _{\mathcal {V}}\tau \) or  if there exists a nontrivial solution going from \(\sigma \) to \(\tau \). Similarly, for \(A,B\subset K\), we write
if there exists a nontrivial solution going from \(\sigma \) to \(\tau \). Similarly, for \(A,B\subset K\), we write
-
\(A\rightarrowtriangle _{\mathcal {V}}\tau \) if \(\sigma \rightarrowtriangle _{\mathcal {V}}\tau \) for some \(\sigma \in A\);
-
\(\sigma \rightarrowtriangle _{\mathcal {V}} B\) if \(\sigma \rightarrowtriangle _{\mathcal {V}}\tau \) for some \(\tau \in B\);
-
\(A\rightarrowtriangle _{\mathcal {V}} B\) if \(\sigma \rightarrowtriangle _{\mathcal {V}}\tau \) for some \(\sigma \in A\) and \(\tau \in B\).
Conversely, we use the symbol  if there exists no nontrivial solution going from a simplex (or a set) to another simplex (or set).
if there exists no nontrivial solution going from a simplex (or a set) to another simplex (or set).
From the definition of a flow, we can make the following observations, which will be useful in Sect. 6 to deduce properties of a subcomplex \(L\subseteq K\) from \(\Pi _\mathcal {V}\).
Lemma 3.2
Let \(\Pi _\mathcal {V}:K\multimap K\) be a flow and consider \(\alpha \subset \sigma \in K\). If  , then \(\sigma \in {{\,\textrm{im}\,}}\mathcal {V}\backslash {{\,\textrm{Fix}\,}}\mathcal {V}\) and \(\alpha =\mathcal {V}^{-1}(\sigma )\).
, then \(\sigma \in {{\,\textrm{im}\,}}\mathcal {V}\backslash {{\,\textrm{Fix}\,}}\mathcal {V}\) and \(\alpha =\mathcal {V}^{-1}(\sigma )\).
Proof
If \(\sigma \in {{\,\textrm{Fix}\,}}\mathcal {V}\), then \(\Pi _\mathcal {V}(\sigma )={{\,\textrm{Cl}\,}}\sigma \ni \alpha \), so \(\sigma \rightarrowtriangle _{\mathcal {V}}\alpha \). If \(\sigma \in {{\,\textrm{dom}\,}}\mathcal {V}\backslash {{\,\textrm{Fix}\,}}\mathcal {V}\), then \(\Pi _\mathcal {V}(\sigma )=\{\mathcal {V}(\sigma )\}\) and \(\Pi _\mathcal {V}\left( \mathcal {V}(\sigma )\right) = {{\,\textrm{Ex}\,}}\mathcal {V}(\sigma )\backslash \{\sigma \}\ni \alpha \), so \(\sigma \rightarrowtriangle _{\mathcal {V}}\mathcal {V}(\sigma )\rightarrowtriangle _{\mathcal {V}}\alpha \). Finally, suppose \(\sigma \in {{\,\textrm{im}\,}}\mathcal {V}\backslash {{\,\textrm{Fix}\,}}\mathcal {V}\) but \(\alpha \ne \mathcal {V}^{-1}(\sigma )\). Then, \(\Pi _\mathcal {V}(\sigma ) = {{\,\textrm{Ex}\,}}\sigma \backslash \{\mathcal {V}^{-1}(\sigma )\}\ni \alpha \) so, again, \(\sigma \rightarrowtriangle _{\mathcal {V}}\alpha \). \(\square \)
Lemma 3.3
Let \(\Pi _\mathcal {V}:K\multimap K\) be a flow and consider \(\sigma ,\tau \in K\) such that \(\sigma \rightarrowtriangle _{\mathcal {V}}\tau \).
-
(1)
For all \(\beta \supset \sigma \), we have \(\beta \rightarrowtriangle _{\mathcal {V}}\tau \).
-
(2)
For all \(\alpha \subset \tau \), we have \(\sigma \rightarrowtriangle _{\mathcal {V}}\alpha \).
Proof
To prove (1), let \(\beta \supset \sigma \rightarrowtriangle _{\mathcal {V}}\tau \). If \(\beta \rightarrowtriangle _{\mathcal {V}}\sigma \), the result is obvious. Otherwise, by Lemma 3.2, we have \(\beta \in {{\,\textrm{im}\,}}\mathcal {V}\backslash {{\,\textrm{Fix}\,}}\mathcal {V}\) and \(\sigma =\mathcal {V}^{-1}(\beta )\). Hence, \(\Pi _\mathcal {V}(\sigma )=\{\beta \}\) so every solution going from \(\sigma \) to \(\tau \) necessarily goes through \(\beta \), thus \(\beta \rightarrowtriangle _{\mathcal {V}}\tau \).
To prove (2), consider \(\sigma \rightarrowtriangle _{\mathcal {V}}\tau \supset \alpha \). Again, if \(\tau \rightarrowtriangle _{\mathcal {V}}\alpha \), we have the result. Otherwise, let \(\varrho \) be a nontrivial solution with \(\varrho (0)=\sigma \) and \(\varrho (n)=\tau \). By Lemma 3.2, we have \(\tau \in {{\,\textrm{im}\,}}\mathcal {V}\backslash {{\,\textrm{Fix}\,}}\mathcal {V}\) and \(\alpha =\mathcal {V}^{-1}(\tau )\), so \(\varrho (n-1)\ne \tau \).
-
If \(\varrho (n-1)\in {{\,\textrm{Fix}\,}}\mathcal {V}\), then \(\Pi _\mathcal {V}(\varrho (n-1)) = {{\,\textrm{Cl}\,}}\varrho (n-1)\supset {{\,\textrm{Cl}\,}}\tau \ni \alpha \), so \(\varrho ':{\mathbb Z}\nrightarrow K\) such that \(\varrho '(i)=\varrho (i)\) for \(i=0,\ldots ,n-1\) and \(\varrho '(n)=\alpha \) is a solution going from \(\sigma \) to \(\alpha \). Hence, \(\sigma \rightarrowtriangle _{\mathcal {V}}\alpha \).
-
If \(\varrho (n-1)\in {{\,\textrm{im}\,}}\mathcal {V}\backslash {{\,\textrm{Fix}\,}}\mathcal {V}\), since \(\mathcal {V}(\alpha )=\tau \ne \varrho (n-1)\), we can again verify that \(\alpha \in \Pi _\mathcal {V}(\varrho (n-1))\), so \(\varrho '\) as defined previously is still a solution going from \(\sigma \) to \(\alpha \). An example of such \(\varrho '\) is shown in Fig. 2.
-
If \(\varrho (n-1)\in {{\,\textrm{dom}\,}}\mathcal {V}\backslash {{\,\textrm{Fix}\,}}\mathcal {V}\), we then have \(\tau \in \Pi _\mathcal {V}(\varrho (n-1))=\{\mathcal {V}(\varrho (n-1))\}\), so \(\mathcal {V}(\varrho (n-1))=\tau =\mathcal {V}(\alpha )\), hence \(\varrho (n-1)=\alpha \) by the injectivity of \(\mathcal {V}\). Thus, \(\varrho \) restricted to \([0,n-1]\) is a solution going from \(\sigma \) to \(\alpha \).
\(\square \)
In red, a solution \(\varrho \) from a simplex \(\sigma \) to another simplex \(\tau \). In part (2) of Lemma 3.3, we see that if \(\varrho \) does not go through \(\alpha =\tau ^-\), then we can adapt it to define a new solution \(\varrho '\), shown in blue, which goes from \(\sigma \) to \(\alpha \) (color figure online)
As we will see in this section, many concepts of combinatorial dynamics rely on the idea of solutions between or contained inside sets. In particular, consider a subset A of a simplicial complex K. In (Batko et al. 2020; Kaczynski et al. 2016), the simplices \(\sigma \in A\) for which \({{\,\textrm{Sol}\,}}(\sigma ,A)\ne \emptyset \) are often considered. In the context of multivector fields (Mrozek 2017), simplices \(\sigma \in A\) for which \({{\,\textrm{Sol}\,}}(\sigma ^+,A)\ne \emptyset \) are mostly of interest. In our context, when A is \(\mathcal {V}\)-compatible, we prove that both ideas are equivalent.
Lemma 3.4
Let \(\Pi _\mathcal {V}\) be a flow on a simplicial complex K and consider \(\sigma \in A\subseteq K\). If A is \(\mathcal {V}\)-compatible, then the following statements are equivalent
-
(1)
\({{\,\textrm{Sol}\,}}(\sigma ^-,A)\ne \emptyset \)
-
(2)
\({{\,\textrm{Sol}\,}}(\sigma ^+,A)\ne \emptyset \)
-
(3)
\({{\,\textrm{Sol}\,}}(\sigma ,A)\ne \emptyset \).
Proof
We first show that \({{\,\textrm{Sol}\,}}(\sigma ^-,A)\ne \emptyset \Leftrightarrow {{\,\textrm{Sol}\,}}(\sigma ^+,A)\ne \emptyset \). The result is obvious if \(\sigma ^-=\sigma ^+\). Let \(\sigma ^-\ne \sigma ^+\), hence \(\sigma ^-\in {{\,\textrm{dom}\,}}\mathcal {V}\backslash {{\,\textrm{Fix}\,}}\mathcal {V}\) and \(\mathcal {V}(\sigma ^-)=\sigma ^+\). If \(\varrho :{\mathbb Z}\rightarrow A\) is a full solution with \(\varrho (n) = \sigma ^-\) for some \(n\in {\mathbb Z}\), then \(\varrho (n+1) = \sigma ^+\), so \(\varrho \) is a full solution with \(\sigma ^+\in {{\,\textrm{im}\,}}\varrho \), thus \({{\,\textrm{Sol}\,}}(\sigma ^+,A)\ne \emptyset \). Conversely, suppose \(\varrho :{\mathbb Z}\rightarrow A\) is a full solution with \(\varrho (n) = \sigma ^+\) for \(n\in {\mathbb Z}\). By definition of \(\Pi _\mathcal {V}\), we have
-
If \(\varrho (n-1)\in {{\,\textrm{Fix}\,}}\mathcal {V}\), then \(\sigma ^-\subset \sigma ^+\in {{\,\textrm{Cl}\,}}\varrho (n-1)=\Pi _\mathcal {V}(\varrho (n-1))\), so \(\sigma ^-\in \Pi _\mathcal {V}(\varrho (n-1))\). Thus, the map \(\varrho ':{\mathbb Z}\rightarrow K\) such that
$$\begin{aligned} \varrho '(i) = {\left\{ \begin{array}{ll} \varrho (i+1) &{}\text { if } i < n-1\\ \sigma ^- &{}\text { if } i=n-1\\ \varrho (i) &{} \text { if } i \ge n \end{array}\right. } \end{aligned}$$is a full solution with \(\sigma ^-\in {{\,\textrm{im}\,}}\varrho '\subseteq A\) because \({{\,\textrm{im}\,}}\varrho '={{\,\textrm{im}\,}}\varrho \cup \{\sigma ^-\}\) and \(\sigma ^-\in A\) by the \(\mathcal {V}\)-compatibility hypothesis on A.
-
If \(\varrho (n-1)\in {{\,\textrm{im}\,}}\mathcal {V}\backslash {{\,\textrm{Fix}\,}}\mathcal {V}\), then \(\sigma ^-\subset \sigma ^+\subset \varrho (n-1)\), so \(\sigma ^-\in {{\,\textrm{Ex}\,}}\varrho (n-1)\). Since \(\mathcal {V}(\sigma ^-)=\sigma ^+\ne \varrho (n-1)\), it follows that \(\sigma ^-\ne \mathcal {V}^{-1}(\varrho (n-1))\) and \(\sigma ^-\in {{\,\textrm{Ex}\,}}\varrho (n-1)\backslash \{\mathcal {V}^{-1}(\varrho (n-1))\}=\Pi _\mathcal {V}(\varrho (n-1))\). Thus, the map \(\varrho '\) as defined above is again a full solution with \(\sigma ^-\in {{\,\textrm{im}\,}}\varrho '\subseteq A\).
-
If \(\varrho (n-1)\in {{\,\textrm{dom}\,}}\mathcal {V}\backslash {{\,\textrm{Fix}\,}}\mathcal {V}\), then \(\mathcal {V}(\sigma ^-) = \sigma ^+ = \mathcal {V}(\varrho (n-1))\), so \(\sigma ^-=\varrho (n-1)\) by injectivity of \(\mathcal {V}\). Hence, \(\varrho \in {{\,\textrm{Sol}\,}}(\sigma ^-,A)\ne \emptyset \).
This shows that \({{\,\textrm{Sol}\,}}(\sigma ^-,A)\ne \emptyset \Leftrightarrow {{\,\textrm{Sol}\,}}(\sigma ^+,A)\ne \emptyset \). It follows that \({{\,\textrm{Sol}\,}}(\sigma ,A)\ne \emptyset \Leftrightarrow {{\,\textrm{Sol}\,}}(\sigma ^+,A)\ne \emptyset \). Indeed, we have either \(\sigma =\sigma ^+\) or \(\sigma =\sigma ^-\): the first case is obvious and we have just proven the second. \(\square \)
3.2 Isolated invariant sets and Conley index
Definition 3.5
((Isolated) invariant set) Let \(\Pi _\mathcal {V}\) be a flow on a simplicial complex K and consider \(S\subseteq K\).
-
(1)
We say that S is an invariant set if for every \(\sigma \in S\), we have \({{\,\textrm{Sol}\,}}(\sigma ,S)\ne \emptyset \).
-
(2)
An invariant set S is isolated if \({{\,\textrm{Ex}\,}}S\) is closed and there is no solution \(\varrho :\{-1,0,1\}\rightarrow K\) such that \(\varrho (-1),\varrho (1)\in S\) and \(\varrho (0)\in {{\,\textrm{Ex}\,}}S\).
Example 3.6
Consider \(\mathcal {V}\) as in Fig. 3. The set \(\{B, AB, BD, ABD\}\), shown in red, is not invariant since every solution that goes through it necessarily exits the set. The orange set \(\{C, CD, ACD\}\) is invariant, but not isolated since its exit set is not closed and the map \(\varrho :\{-1,0,1\}\rightarrow K\) such that \(\varrho (-1)=ACD\), \(\varrho (0) = AC\) and \(\varrho (1)=C\) is a solution that violates the definition of isolated set. The blue set \(\{C, AC, CD, ACD\}\) is also invariant, its exit set is closed, but it is not isolated because there is a map \(\varrho :\{-1,0,1\}\rightarrow K\), namely the one such that \(\varrho (-1)=ACD\), \(\varrho (0) = A\) and \(\varrho (1)=AC\), which violates the definition. Finally, we can see that the green set \(\{A, C, D, AC, AD, CD, ACD\}\) verifies both conditions to be an isolated invariant set.
The definition of an invariant set and that of an isolated invariant set given here come from (Batko et al. 2020; Kaczynski et al. 2016). In the context of multivector fields, Mrozek (2017) defines a set \(S\subseteq K\) as invariant if for all \(\sigma \in S\), we have \({{\,\textrm{Sol}\,}}(\sigma ^+,S_\mathcal {V})\ne \emptyset \), where \(S_\mathcal {V}\) is the maximal subset of S which is \(\mathcal {V}\)-compatible. In the context of vector fields, we show that these definitions follow the same idea.
Lemma 3.7
Let \(\Pi _\mathcal {V}\) be a flow on a simplicial complex K.
-
(1)
A subset of K is invariant in the sense of Mrozek (2017, Section 6.4) if and only if it is \(\mathcal {V}\)-compatible and invariant in the sense of Definition 3.5(1).
-
(2)
A subset of K is an isolated invariant set in the sense of Mrozek (2017, Section 7.1) if and only if it is isolated invariant in the sense of Definition 3.5(2).
Proof
If S invariant in the sense of Mrozek (2017), then it is \(\mathcal {V}\)-compatible (Mrozek 2017, Proposition 6.4) and since \(S_\mathcal {V}=S\), it follows from Lemma 3.4 that S is invariant in the sense of Definition 3.5(1). Conversely, if S is \(\mathcal {V}\)-compatible and invariant in the sense of Definition 3.5(1), we again have \(S_\mathcal {V}=S\) and the invariance of S in the sense of Mrozek (2017) follows from Lemma 3.4.
The second part of the lemma is shown as follows. From Theorem 7.1 in (Mrozek 2017), \(S\subseteq K\) is an isolated invariant set in the sense of Mrozek (2017) if and only if S is invariant in the sense of Mrozek (2017) and \({{\,\textrm{Ex}\,}}S\) is closed. From part (1) of the lemma, S is invariant in the sense of Mrozek (2017) if and only if it is \(\mathcal {V}\)-compatible and invariant in the sense of Definition 3.5(1). Finally, Proposition 3.4 in (Batko et al. 2020) states that S is \(\mathcal {V}\)-compatible, S is invariant in the sense of Definition 3.5(1) and \({{\,\textrm{Ex}\,}}S\) is closed if and only if S is isolated invariant in the sense of Definition 3.5(2), hence the result. \(\square \)
From Lemma 3.7, it follows that most results from the combinatorial dynamics theory defined by Mrozek (2017) may be directly applied within the framework of this article as long as the invariant sets considered here are \(\mathcal {V}\)-compatible. In particular, we can define the Conley index of an isolated invariant set.
Definition 3.8
Let S be an isolated invariant set of a flow. The Conley index of S, noted \({{\,\textrm{Con}\,}}(S)\), is the (singular) homology of \({{\,\textrm{Cl}\,}}S\) relative to \({{\,\textrm{Ex}\,}}S\) and the \(p^{\text {th}}\) Conley coefficient \(\beta _p(S)\) of S is the rank of the \(p^{\text {th}}\) homology group of \({{\,\textrm{Con}\,}}(S)\). We call
the Conley polynomial of S.
Notice that when considering a flow on a finite simplicial complex K, then K is trivially an isolated invariant set and \({{\,\textrm{Con}\,}}(K)\) is simply the homology of K. The Conley coefficients of K thus coincide with its Betti numbers and its Conley polynomial equals its Poincaré polynomial.
3.3 Morse decompositions
For a full solution \(\varrho :{\mathbb Z}\rightarrow K\) of a flow \(\Pi _\mathcal {V}\) on K, define the \(\alpha \)-limit and the \(\omega \)-limit sets of \(\varrho \) as
Definition 3.9
(Morse decomposition) Let \(\Pi _\mathcal {V}\) be a flow on a simplicial complex K. Consider a collection \(\mathcal {M}= \{M_r\subseteq K\ |\ r\in {\mathbb P}\}\) indexed by a poset \(({\mathbb P},\le )\). We say \(\mathcal {M}\) is a Morse decomposition of \(\Pi _\mathcal {V}\) if the following conditions are satisfied:
-
(1)
\(\mathcal {M}\) is a collection of mutually disjoint isolated invariant subsets of K;
-
(2)
for every full solution \(\varrho \) of \(\Pi _\mathcal {V}\), there are some \(r,r'\in {\mathbb P}\) such that \(r\le r'\) for which \(\alpha (\varrho )\subseteq M_{r'}\) and \(\omega (\varrho )\subseteq M_r\);
-
(3)
if there exists a full solution \(\varrho \) of \(\Pi _\mathcal {V}\) such that \(\alpha (\varrho )\cup \omega (\varrho )\subseteq M_r\) for some \(r\in {\mathbb P}\), then \({{\,\textrm{im}\,}}\varrho \subseteq M_r\).
Essentially, the sets \(M_r\) of a Morse decomposition \(\mathcal {M}\) are the starting and ending sets of every solution of \(\Pi _\mathcal {V}:K\multimap K\). Thus, we can see a Morse decomposition as an object describing the different connections that exist in a flow.
Example 3.10
Consider the combinatorial field \(\mathcal {V}\) from Fig. 4a. Then, the collection
indexed by \(({\mathbb P},\le )\) as depicted in Fig. 4b is a Morse decomposition of \(\Pi _\mathcal {V}\).
In (a), a discrete vector field \(\mathcal {V}\). The dots identify the fixed points of \(\mathcal {V}\), and each color represents a Morse set of \(\mathcal {M}\) as defined in Example 3.10. In (b), the Hasse diagram of the poset \({\mathbb P}\) used to index \(\mathcal {M}\) (color figure online)
Moreover, information on the homology of a simplicial complex K can be deduced from a Morse decomposition defined on K. Indeed, a Morse decomposition leads to a Morse equation, from which are derived the famous Morse inequalities. The following proposition is an adaptation of Theorem 9.11 in (Mrozek 2017).
Proposition 3.11
Let \(\mathcal {M}=\{M_r\ |\ r\in {\mathbb P}\}\) be a Morse decomposition of a simplicial complex K. Then,
for some polynomial Q(t) with non-negative coefficients.
Corollary 3.12
Let \(\mathcal {M}=\{M_r\ |\ r\in {\mathbb P}\}\) be a Morse decomposition of a simplicial complex K with \(\dim K = n\). Let
For all \(p=0,1,\ldots ,n\), we have
-
(1)
the strong Morse inequalities:
$$\begin{aligned} m_p - m_{p-1} + \cdots +(-1)^p m_0 \ge \beta _p(K) - \beta _{p-1}(K) + \cdots +(-1)^p \beta _0(K); \end{aligned}$$ -
(2)
the weak Morse inequalities:
$$\begin{aligned} m_p \ge \beta _p(K); \end{aligned}$$ -
(3)
an alternative expression for the Euler characteristic \(\chi (K)\) of K:
$$\begin{aligned} m_0 - m_1 + \cdots +(-1)^n m_n = \beta _0(K) - \beta _1(K) + \cdots +(-1)^n \beta _n(K) = \chi (K) \end{aligned}$$
Proof
The proof is similar to that of Theorem 9.12 in (Mrozek 2017). Recall that \(P_K(t)=\sum _{p=0}^n\beta _p(K)t^p\). To prove the strong Morse inequalities, it suffices to compare the coefficients of the polynomials obtained by multiplying each side of the equation in Proposition 3.11 by \((1+t)^{-1} = 1-t+t^2-\cdots \). The weak Morse inequalities follow. Also, we have the last equality by substituting \(t=-1\) in the equation of Proposition 3.11. \(\square \)
3.4 Basic sets and acyclic flows
Let \(\Pi _\mathcal {V}:K\multimap K\) be a flow on a simplicial complex and for two simplices \(\sigma ,\tau \in K\), we write
 when
\(\sigma \rightarrowtriangle _{\mathcal {V}}\tau \) and
when
\(\sigma \rightarrowtriangle _{\mathcal {V}}\tau \) and
 . Consider the chain recurrent set of
\(\Pi _\mathcal {V}\) defined as
. Consider the chain recurrent set of
\(\Pi _\mathcal {V}\) defined as

In \(\mathcal {R}\),  may be seen as an equivalence relation. A basic set of \(\Pi _\mathcal {V}\) is an equivalence class of
may be seen as an equivalence relation. A basic set of \(\Pi _\mathcal {V}\) is an equivalence class of  in \(\mathcal {R}\).
in \(\mathcal {R}\).
Theorem 3.13
(Theorems 9.2 and 9.3 in (Mrozek 2017)) Let \(\mathcal {B}\) be the collection of basic sets of a flow \(\Pi _\mathcal {V}:K\multimap K\). Consider the relation \(\le \) on \(\mathcal {B}\) such that for all \(B,B'\in \mathcal {B}\),

The relation \(\le \) is a partial order on \(\mathcal {B}\) making it a Morse decomposition.
Moreover, \(\mathcal {B}\) is the finest Morse decomposition of \(\Pi _\mathcal {V}\), meaning that for any Morse decomposition \(\mathcal {M}\) of \(\Pi _\mathcal {V}\), for each \(B\in \mathcal {B}\), there exists a \(M\in \mathcal {M}\) such that \(B\subseteq M\).
The Morse decomposition of a flow in basic sets essentially consists of fixed points and cycles. For instance, the Morse decomposition from Example 3.10 is the finest that exists for the given flow. Hence, we deduce that the basic sets for a flow \(\Pi _\mathcal {V}\) with no cycle are exactly the fixed points of \(\mathcal {V}\).
More formally, we say a flow \(\Pi _\mathcal {V}:K\multimap K\) is acyclic if, for all \(\sigma ,\tau \in K\),  implies \(\sigma = \tau \). When \(\Pi _\mathcal {V}\) is acyclic, we see that \(\mathcal {R}={{\,\textrm{Fix}\,}}\mathcal {V}\) and the following result is shown in a straightforward manner.
implies \(\sigma = \tau \). When \(\Pi _\mathcal {V}\) is acyclic, we see that \(\mathcal {R}={{\,\textrm{Fix}\,}}\mathcal {V}\) and the following result is shown in a straightforward manner.
Proposition 3.14
Let \(\Pi _\mathcal {V}:K\multimap K\) be an acyclic flow. The collection \(\mathcal {B}\) of basic sets of \(\Pi _\mathcal {V}\) is
Furthermore, it is worth noting that the acyclicity of \(\mathcal {V}\) is equivalent to that of the associated flow \(\Pi _\mathcal {V}\). Indeed, we know that gradient fields of discrete Morse functions are acyclic (Forman 1998), so this result implies that acyclic combinatorial flows play an essential role in the study of the dynamics of these functions. This next proposition was not shown explicitly in previous works, but it follows from results in (Desjardins Côté 2020).
Proposition 3.15
A discrete vector field \(\mathcal {V}:K\nrightarrow K\) is acyclic if and only if its associated flow \(\Pi _\mathcal {V}:K\multimap K\) is also acyclic.
Proof
If \(\mathcal {V}\) is not acyclic, there must exist a \(\mathcal {V}\)-path \(\alpha _0^{(p)},\beta _0^{(p+1)},\alpha _1^{(p)},\ldots ,\beta _{n-1}^{(p+1)},\alpha _n^{(p)}\) where \(\alpha _0=\alpha _n\) and \(n\ge 1\). We can easily verify that this path forms a solution in \(\Pi _\mathcal {V}\) going from \(\alpha _0\) to \(\alpha _n\). Hence, we have \(\alpha _0\rightarrowtriangle _{\mathcal {V}}\beta _0\rightarrowtriangle _{\mathcal {V}}\alpha _n=\alpha _0\), so  . Thus, \(\Pi _\mathcal {V}\) is not acyclic.
. Thus, \(\Pi _\mathcal {V}\) is not acyclic.
Conversely, suppose that \(\Pi _\mathcal {V}\) is not acyclic, meaning that there exists two simplices \(\sigma ,\tau \in K\) such that  and \(\sigma \ne \tau \). We can show there exists a nontrivial closed \(\mathcal {V}\)-path going from \(\sigma \) to \(\tau \). Indeed, since \(\sigma \rightarrowtriangle _{\mathcal {V}}\tau \rightarrowtriangle _{\mathcal {V}}\sigma \), we know there is a solution \(\varrho :\{0,1,\ldots ,m\}\rightarrow K\) with \(m\ge 2\) such that \(\varrho (0)=\varrho (m)=\sigma \). We also know from Desjardins Côté (2020, Proposition 5.3, Lemma 5.4) that \({{\,\textrm{im}\,}}\varrho \) contains no fixed point of \(\mathcal {V}\) and that, for some \(p\in {\mathbb N}\), the sequence \(\varrho (0),\varrho (1),\ldots ,\varrho (m)\) alternates between simplices in \({{\,\textrm{dom}\,}}\mathcal {V}\) of dimension p and simplices in \({{\,\textrm{im}\,}}\mathcal {V}\) of dimension \(p+1\). Thus, \(m=2n\) for some \(n\in {\mathbb N}\). Assuming, without loss of generality, that \(\varrho (0)\in {{\,\textrm{dom}\,}}\mathcal {V}\), we can define a nontrivial closed \(\mathcal {V}\)-path \(\alpha _0^{(p)},\beta _0^{(p+1)},\alpha _1^{(p)},\ldots ,\beta _{n-1}^{(p+1)},\alpha _n^{(p)}\) by considering \(\alpha _i:=\varrho (2i)\) and \(\beta _i:=\varrho (2i+1)\) for each \(i=0,\ldots ,n-1\) as well as \(\alpha _n:=\varrho (2n)=\varrho (0)\). Therefore, \(\mathcal {V}\) is not acyclic. \(\square \)
and \(\sigma \ne \tau \). We can show there exists a nontrivial closed \(\mathcal {V}\)-path going from \(\sigma \) to \(\tau \). Indeed, since \(\sigma \rightarrowtriangle _{\mathcal {V}}\tau \rightarrowtriangle _{\mathcal {V}}\sigma \), we know there is a solution \(\varrho :\{0,1,\ldots ,m\}\rightarrow K\) with \(m\ge 2\) such that \(\varrho (0)=\varrho (m)=\sigma \). We also know from Desjardins Côté (2020, Proposition 5.3, Lemma 5.4) that \({{\,\textrm{im}\,}}\varrho \) contains no fixed point of \(\mathcal {V}\) and that, for some \(p\in {\mathbb N}\), the sequence \(\varrho (0),\varrho (1),\ldots ,\varrho (m)\) alternates between simplices in \({{\,\textrm{dom}\,}}\mathcal {V}\) of dimension p and simplices in \({{\,\textrm{im}\,}}\mathcal {V}\) of dimension \(p+1\). Thus, \(m=2n\) for some \(n\in {\mathbb N}\). Assuming, without loss of generality, that \(\varrho (0)\in {{\,\textrm{dom}\,}}\mathcal {V}\), we can define a nontrivial closed \(\mathcal {V}\)-path \(\alpha _0^{(p)},\beta _0^{(p+1)},\alpha _1^{(p)},\ldots ,\beta _{n-1}^{(p+1)},\alpha _n^{(p)}\) by considering \(\alpha _i:=\varrho (2i)\) and \(\beta _i:=\varrho (2i+1)\) for each \(i=0,\ldots ,n-1\) as well as \(\alpha _n:=\varrho (2n)=\varrho (0)\). Therefore, \(\mathcal {V}\) is not acyclic. \(\square \)
3.5 Coarsening a Morse decomposition
We saw how to find the finest Morse decomposition associated to some flow, but a coarse decomposition may also be useful to describe the dynamics of the flow in a more global manner. Thus, considering a fine enough Morse decomposition \(\mathcal {M}\), we show here under which conditions we can group together some elements of \(\mathcal {M}\) to obtain a coarser one.
Consider a flow \(\Pi _\mathcal {V}:K\multimap K\). For \(A,A'\subseteq K\), define the connecting set \(C(A',A)\) as the set of simplices \(\sigma \in K\) for which there exists a full solution \(\varrho :{\mathbb Z}\rightarrow K\) with \(\sigma \in {{\,\textrm{im}\,}}\varrho \), \(\alpha (\varrho )\subseteq A'\) and \(\omega (\varrho )\subseteq A\). A slightly different definition is proposed in (Mrozek 2017), but we could verify that, in our context, it is equivalent to this one. Also, if \(A=\{\sigma \}\) and \(A'=\{\sigma '\}\), we simply write \(C(\sigma ',\sigma ):= C(\{\sigma '\},\{\sigma \})\). When A and \(A'\) are invariant, we can show that
From the definitions of connecting sets and of a Morse decomposition, the next result follows (see Mrozek 2017, Proposition 9.1).
Proposition 3.16
Let \(\mathcal {M}= \{M_r\ |\ r\in {\mathbb P}\}\) be a Morse decomposition of a flow \(\Pi _\mathcal {V}:K\multimap K\). For all \(r,r'\in {\mathbb P}\), the following statements are true.
-
(1)
\(C(M_{r'},M_r)\ne \emptyset \Leftrightarrow M_{r'}\rightarrowtriangle _{\mathcal {V}}M_r\).
-
(2)
\(C(M_{r'},M_r)\) is \(\mathcal {V}\)-compatible.
-
(3)
\(C(M_r,M_r) = M_r\).
-
(4)
If \(C(M_{r'},M_r) \ne \emptyset \), then \(r\le r'\). From the contrapositive, it follows that \(r'<r\) implies \(C(M_{r'},M_r) = \emptyset \).
The connecting sets can also be used to define Morse sets.
Definition 3.17
(Morse sets) Let \(\mathcal {M}= \{M_r\ |\ r\in {\mathbb P}\}\) be a Morse decomposition of a flow \(\Pi _\mathcal {V}:K\multimap K\) and consider \(I\subseteq {\mathbb P}\). The Morse set associated to I is
Proposition 3.18
(Theorem 9.4 in (Mrozek 2017)) Every Morse set M(I) is an isolated invariant set.
Note that Proposition 3.18 implies that Conley indexes are well defined for Morse sets M(I). Also, it suggests that Morse sets make good candidates to build a Morse decomposition \(\mathcal {M}'\) from a finer decomposition \(\mathcal {M}= \{M_r\ |\ r\in {\mathbb P}\}\). Theorem 3.24 establishes the necessary and sufficient conditions for a partition \(\{I_s\subseteq {\mathbb P}\ |\ s\in {\mathbb S}\}\) of \({\mathbb P}\) to induce a Morse decomposition \(\mathcal {M}' = \{M(I_s)\ |\ s\in {\mathbb S}\}\). Before stating and proving it formally, we give the intuition of the theorem with the two following examples.
Example 3.19
Consider the Morse decomposition \(\mathcal {M}\) from Example 3.10 and the partition \(\big \{\{1,3,4,6\}, \{2,5,8\}, \{7\}\big \}\) of its index set \({\mathbb P}=\{1,\ldots ,8\}\). The three induced Morse sets are shown in Fig. 5a. The connections between each of these Morse sets are summarized by the directed graph in Fig. 5b. Since this graph is not acyclic, it does not represent a partial order on \(\big \{\{1,3,4,6\}, \{2,5,8\}, \{7\}\big \}\). In other words, the connections between the induced Morse sets do not describe a partial order on the given partition of \({\mathbb P}\). Hence, from Theorem 3.24, it follows that the collection \(\mathcal {M}'\) of Morse sets induced by the partition \(\big \{\{1,3,4,6\}, \{2,5,8\}, \{7\}\big \}\) is not a Morse decomposition.
In (a), the discrete vector field \(\mathcal {V}\) from example 3.10 and the induced Morse sets \(M(\{1,3,4,6\})\) in red, \(M(\{2,5,8\})\) in blue and \(M(\{7\})\) in green. In the directed graph in (b), there is an arrow between two nodes iff there is a solution going from one of the associated Morse sets to the other (color figure online)
Example 3.20
Consider again the Morse decomposition \(\mathcal {M}\) from Example 3.10 and, this time, the partition \(\big \{\{1,3,6\}, \{2,8\}, \{4\}, \{5,7\}\big \}\) of \({\mathbb P}=\{1,\ldots ,8\}\). The induced Morse sets are shown in Fig. 6a and their connections are as in Fig. 6b. The directed graph obtained here is acyclic, which means it represents a partial order on \(\big \{\{1,3,6\}, \{2,8\}, \{4\}, \{5,7\}\big \}\). The existence of this partial order is necessary and sufficient to deduce that the induced Morse sets from Fig. 6a form a Morse decomposition of the given flow.
In (a), the discrete vector field \(\mathcal {V}\) from example 3.10 and the induced Morse sets \(M(\{1,3,6\})\) in red, \(M(\{2,8\})\) in blue, \(M(\{4\})\) in yellow and \(M(\{5,7\})\) in green. In the directed graph in (b), there is an arrow between two nodes iff there is a solution going from one of the associated Morse sets to the other (color figure online)
In order to prove Theorem 3.24, the following lemmas are needed.
Lemma 3.21
Let \(\mathcal {M}= \{M_r\ |\ r\in {\mathbb P}\}\) be a Morse decomposition and consider a partition \(\{I_s\subseteq {\mathbb P}\ |\ s\in {\mathbb S}\}\) of \({\mathbb P}\). If \(r\in I_s\) for some \(s\in {\mathbb S}\), then \(M_r\subseteq M(I_s)\). Moreover, when the Morse sets in \(\mathcal {M}' = \{M(I_s)\ |\ s\in {\mathbb S}\}\) are mutually disjoint, we have \(M_r\cap M(I_{s'})=\emptyset \) for all \(s'\in {\mathbb S}\) such that \(r\notin I_{s'}\).
Proof
From Proposition 3.16(3), we know that \(M_r = C(M_r,M_r)\), so if \(r\in I_s\),
It follows that \(M_r\cap M(I_{s'})\subseteq M(I_s)\cap M(I_{s'}) = \emptyset \) for all \(s'\ne s\) when the sets in \(\mathcal {M}'\) are mutually disjoint. \(\square \)
Lemma 3.22
Let \(\mathcal {M}= \{M_r\ |\ r\in {\mathbb P}\}\) be a Morse decomposition of a flow \(\Pi _\mathcal {V}\) and consider a partition \(\{I_s\subseteq {\mathbb P}\ |\ s\in {\mathbb S}\}\) of \({\mathbb P}\). For all \(s,s'\in {\mathbb S}\), we have
Proof
If \(M_{r'}\rightarrowtriangle _{\mathcal {V}}M_r\) for some \(r\in I_s\) and \(r'\in I_{s'}\), then obviously \(M(I_{s'})\rightarrowtriangle _{\mathcal {V}}M(I_s)\) from Lemma 3.21. Now, suppose \(M(I_{s'})\rightarrowtriangle _{\mathcal {V}}M(I_s)\). Then, there exists some \(\sigma \in M(I_s)\) and some \(\sigma '\in M(I_{s'})\) such that \(\sigma '\rightarrowtriangle _{\mathcal {V}}\sigma \). Also, by definition of a Morse set, \(\sigma \in C(M_{r_1},M_{r_2})\) and \(\sigma '\in C(M_{r_1'},M_{r_2}')\) for some \(r_1,r_2\in I_s\) and \(r_1',r_2'\in I_{s'}\), meaning that \(M_{r_1}\rightarrowtriangle _{\mathcal {V}}\sigma \rightarrowtriangle _{\mathcal {V}}M_{r_2}\) and \(M_{r_1'}\rightarrowtriangle _{\mathcal {V}}\sigma '\rightarrowtriangle _{\mathcal {V}}M_{r_2'}\). Hence,
Since \(M_{r_1'}\subseteq M(I_{s'})\) and \(M_{r_2}\subseteq M(I_s)\) by Lemma 3.21, we have the result. \(\square \)
We are now ready to state Theorem 3.24. It is proven in a general setting, but will be particularly useful in Sect. 7 to determine under which conditions the critical components of a mdm function form a Morse decomposition.
Definition 3.23
Let \(\Pi _\mathcal {V}:K\multimap K\) and consider a collection \(\mathcal {M}=\{M_r\ |\ r\in {\mathbb P}\}\) of subsets of K. A \(\mathcal {M}\)-path is a sequence \(r_0,r_1,\ldots ,r_n\in {\mathbb P}\) such that \(M_{r_0}\rightarrowtriangle _{\mathcal {V}}M_{r_1}\rightarrowtriangle _{\mathcal {V}}\cdots \rightarrowtriangle _{\mathcal {V}} M_{r_n}\) and a \(\mathcal {M}\)-cycle is a \(\mathcal {M}\)-path for which \(r_0=r_n\). We say a \(\mathcal {M}\)-path or a \(\mathcal {M}\)-cycle is trivial if \(r_0=r_1=\cdots =r_n\).
Theorem 3.24
Let \(\mathcal {M}= \{M_r\ |\ r\in {\mathbb P}\}\) be a Morse decomposition of a flow \(\Pi _\mathcal {V}:K\multimap K\). Consider a partition \(\{I_s\subseteq {\mathbb P}\ |\ s\in {\mathbb S}\}\) of \({\mathbb P}\) and the induced collection \(\mathcal {M}' = \{M(I_s)\ |\ s\in {\mathbb S}\}\). The three following statements are equivalent:
-
(a)
There exists a partial order on \({\mathbb S}\) for which \(\mathcal {M}'\) is a Morse decomposition.
-
(b)
There exists no nontrivial \(\mathcal {M}'\)-cycle.
-
(c)
The preorder induced by the relation R defined on \({\mathbb S}\) such that
is a partial order.
Proof
We will prove that (a) \(\Rightarrow \) (b) \(\Rightarrow \) (C) \(\Rightarrow \) (a).
First, we see that the proof of (a) \(\Rightarrow \) (b) follows from statements (1) and (4) of Proposition 3.16. Indeed, if \(\mathcal {M}'\) is a Morse decomposition for some partial order \(\le \) on \({\mathbb S}\) and \(s_0,s_1,\ldots ,s_n\subseteq {\mathbb S}\) is a sequence such that \(s_0=s_n\) and
then \(s_n\le s_{n-1}\le \cdots \le s_1\le s_0 = s_n\), thus \(s_0=s_1=\cdots =s_n\).
We now show (b) \(\Rightarrow \) (C). Since each \(M(I_s)\) is invariant, we can easily see that R is reflexive, meaning that the preorder induced by R is its transitive closure \({\bar{R}}\). To prove that it is a partial order, we only have to show that \({\bar{R}}\) is antisymmetric. Let \(s,s'\in {\mathbb S}\) be such that \(s{\bar{R}}s'\) and \(s'{\bar{R}}s\). Then, there exists two sequences \(s=s_0,s_1,\ldots ,s_m=s'\) and \(s'=s_m,s_{m+1},\ldots ,s_{m+n}=s\) in \({\mathbb S}\) such that \(s_{i-1}Rs_i\) for each \(i=1,\ldots ,m+n\). By definition of R and by (b), it follows that \(s_0 = s_1 =\cdots = s_{m+n}\) and, in particular, \(s=s'\).
We finally prove that (C) \(\Rightarrow \) (a). Consider the collection \(\mathcal {M}'\) indexed by the set \({\mathbb S}\) partially ordered by \({\bar{R}}\). We show that the three conditions of Definition 3.9 of a Morse decomposition are satisfied.
-
(1)
We know that \(M(I_s)\) is an isolated invariant set by Proposition 3.18. Thus, we only have to show that \(M(I_s)\cap M(I_{s'})=\emptyset \) for all \(s,s'\in {\mathbb S}\) such that \(s\ne s'\). Suppose \(\sigma \in M(I_s)\cap M(I_{s'})\). Then, there exists \(r_1,r_2\in I_s\) and \(r_1',r_2'\in I_{s'}\) such that \(\sigma \in C(M_{r_1},M_{r_2})\cap C(M_{r_1'},M_{r_2'})\), meaning that \(M_{r_1}\rightarrowtriangle _{\mathcal {V}}\sigma \rightarrowtriangle _{\mathcal {V}} M_{r_2}\) and \(M_{r_1'}\rightarrowtriangle _{\mathcal {V}}\sigma \rightarrowtriangle _{\mathcal {V}} M_{r_2'}\). Hence, \(M_{r_1}\rightarrowtriangle _{\mathcal {V}}\sigma \rightarrowtriangle _{\mathcal {V}} M_{r_2'}\) and \(M_{r_1'}\rightarrowtriangle _{\mathcal {V}}\sigma \rightarrowtriangle _{\mathcal {V}} M_{r_2}\). From Lemma 3.22, it follows that \(M(I_s)\rightarrowtriangle _{\mathcal {V}} M(I_{s'})\) and \(M(I_{s'})\rightarrowtriangle _{\mathcal {V}} M(I_s)\). By the definition of the partial order on \({\mathbb S}\), we have \(s'\le s\) and \(s\le s'\), thus \(s=s'\).
-
(2)
For any solution \(\varrho :{\mathbb Z}\rightarrow K\) of \(\Pi _\mathcal {V}\), since \(\mathcal {M}=\{M_r\ |\ r\in {\mathbb P}\}\) is a Morse decomposition, there are some \(r\le r'\in {\mathbb P}\) such that \(\alpha (\varrho )\subseteq M_{r'}\) and \(\omega (\varrho )\subseteq M_r\). Consider the unique indexes \(s,s'\in {\mathbb S}\) such that \(r\in I_s\) and \(r'\in I_{s'}\). From Lemma 3.21, we see that \(\alpha (\varrho )\subseteq M_{r'}\subseteq M(I_{s'})\) and \(\omega (\varrho )\subseteq M_{r}\subseteq M(I_{s})\), where \(s\le s'\) since we then have \(M(I_{s'})\rightarrowtriangle _{\mathcal {V}}M(I_s)\).
-
(2)
Now, consider a solution \(\varrho :{\mathbb Z}\rightarrow K\) such that \(\alpha (\varrho )\cup \omega (\varrho )\subseteq M(I_s)\) for some \(s\in {\mathbb S}\). Since \(\mathcal {M}\) is a Morse decomposition, we know there exists some \(r\le r'\in {\mathbb P}\) such that \(\alpha (\varrho )\subseteq M_{r'}\) and \(\omega (\varrho )\subseteq M_r\). Also, we have \({{\,\textrm{im}\,}}\varrho \subseteq C(M_{r'}, M_r)\) by definition of a connecting set. Moreover, we see that \(M_r\cap M(I_s)\supseteq \omega (\varrho )\ne \emptyset \). Since the sets in \(\mathcal {M}'\) are mutually disjoint, as shown in (1), it follows from Lemma 3.21 that \(r\in I_s\). Similarly, \(r'\in I_s\). We conclude that \({{\,\textrm{im}\,}}\varrho \subseteq C(M_{r'}, M_r)\subseteq M(I_s)\) by definition of a Morse set.
\(\square \)
Furthermore, from Lemma 3.22, we see that \(\mathcal {M}'\)-cycles can be characterized as follows.
Proposition 3.25
Let \(\mathcal {M}= \{M_r\ |\ r\in {\mathbb P}\}\) be a Morse decomposition. Consider a partition \(\{I_s\subseteq {\mathbb P}\ |\ s\in {\mathbb S}\}\) of \({\mathbb P}\) and the collection \(\mathcal {M}'=\{M(I_s)\ |\ s\in {\mathbb S}\}\). The sequence \(s_0,s_1,\ldots ,s_n\in {\mathbb S}\) is a \(\mathcal {M}'\)-path if and only if there exists a sequence \(r_0',r_1,r_1',r_2,r_2',\ldots ,r_{n-1}',r_n\in {\mathbb P}\) such that
-
\(r_0'\in I_{s_0}\), \(r_i,r_i'\in I_{s_i}\) for each \(i=1,\ldots ,n-1\) and \(r_n\in I_{s_n}\);
-
\(M_{r_{i-1}'}\rightarrowtriangle _{\mathcal {V}}M_{r_i}\) for each \(i=1,\ldots ,n\).
Moreover, the sequence \(s_0,s_1,\ldots ,s_n\in {\mathbb S}\) is a \(\mathcal {M}'\)-cycle iff there exists such a sequence \(r_0',r_1,r_1',r_2,r_2',\ldots ,r_{n-1}',r_n\in {\mathbb P}\) and \(s_0=s_n\).
4 Multidimensional discrete Morse functions
In this section, many notions of Morse–Forman theory (Forman 1998, 2002) are extended to vector-valued functions \(f:K\rightarrow {\mathbb R}^k\). A few concepts on multidimensional discrete Morse (mdm) functions discussed by Allili et al. (2019), which we also call multiparameter in reference to multiparameter persistence, are first presented. The gradient vector field of a mdm function is then defined and some of its properties are outlined.
4.1 Main definitions
For the remaining of the article, we note \(\preceq \) the partial order on \({\mathbb R}^k\) such that, for any \(a=(a_1,\ldots ,a_k)\) and \(b=(b_1,\ldots ,b_k)\) in \({\mathbb R}^k\),
We also write \(a\precneqq b\) whenever \(a\preceq b\) and \(a\ne b\). Moreover, for \(f:K\rightarrow {\mathbb R}^k\) and \(\sigma \in K_p\), consider
When \(f_1,\ldots ,f_k:K\rightarrow {\mathbb R}\) are clear from the context, we also write
We immediately see that for all \(f=(f_1,\ldots ,f_k):K\rightarrow {\mathbb R}^k\) and \(\sigma \in K\), we have
thus \(H_f(\sigma )\subseteq H_i(\sigma )\) and \(T_f(\sigma )\subseteq T_i(\sigma )\) for all \(i=1,\ldots ,k\). Those observations will come in handy later in this section.
Definition 4.1
(Multidimensional discrete Morse function) A multiparameter or multidimensional discrete Morse function (or simply a mdm function) defined on a simplicial complex K is a function \(f:K\rightarrow {\mathbb R}^k\) such that, for all \(\sigma \in K_p\):
-
(1)
\({{\,\textrm{card}\,}}H_f(\sigma ) \le 1\);
-
(2)
\({{\,\textrm{card}\,}}T_f(\sigma ) \le 1\);
-
(3)
if \(\beta ^{(p+1)}\supset \sigma \) is not in \(H_f(\sigma )\), then \(f(\beta )\succneqq f(\sigma )\);
-
(4)
if \(\alpha ^{(p-1)}\subset \sigma \) is not in \(T_f(\sigma )\), then \(f(\alpha )\precneqq f(\sigma )\).
Conditions (1) and (2) are analogous to those of a one-dimensional discrete Morse function. Conditions (3) and (4), on the other hand, need to be added in the multidimensional setting to ensure the values of f are comparable at least for simplices that are facets and cofacets of each other.
Furthermore, a key concept in discrete Morse theory is that of critical points. They can be defined just as in the original setting.
Definition 4.2
(Critical point) Let \(f:K\rightarrow {\mathbb R}^k\) be mdm. A simplex \(\sigma \in K_p\) is said to be a critical simplex or a critical point of index p of f if
A simplex that is not critical is regular.
It was shown by Allili et al. (2019) that, as in the one-dimensional setting, for all mdm function \(f:K\rightarrow {\mathbb R}^k\) and all \(\sigma \in K\), one of the sets \(H_f(\sigma )\) or \(T_f(\sigma )\) must have cardinality zero. The next result follows.
Proposition 4.3
Let \(f:K\rightarrow {\mathbb R}^k\) be mdm. Every \(\sigma \in K\) verifies exactly one of these conditions:
-
\(\sigma \) is critical;
-
\({{\,\textrm{card}\,}}H_f(\sigma ) =0\) and \({{\,\textrm{card}\,}}T_f(\sigma ) = 1\);
-
\({{\,\textrm{card}\,}}H_f(\sigma ) =1\) and \({{\,\textrm{card}\,}}T_f(\sigma ) = 0\).
This last observation leads to the definition of the gradient vector field of a mdm function.
Definition 4.4
(Gradient vector field) The gradient vector field, or simply the gradient, of a mdm function \(f:K\rightarrow {\mathbb R}^k\) is the discrete vector field \(\mathcal {V}\) such that \({{\,\textrm{dom}\,}}\mathcal {V}= \left\{ \sigma \in K\ |\ {{\,\textrm{card}\,}}T_f(\sigma ) = 0\right\} \) and, for all \(\sigma \in {{\,\textrm{dom}\,}}\mathcal {V}\),
We could easily verify that a gradient vector field \(\mathcal {V}\) of a mdm function f as defined above is indeed a discrete vector field. Moreover:
-
the fixed points of \(\mathcal {V}\) are the critical points of f;
-
\({{\,\textrm{im}\,}}\mathcal {V}\backslash {{\,\textrm{Fix}\,}}\mathcal {V}= \left\{ \sigma \in K\ |\ {{\,\textrm{card}\,}}T_f(\sigma )=1\right\} \);
-
\({{\,\textrm{dom}\,}}\mathcal {V}\backslash {{\,\textrm{Fix}\,}}\mathcal {V}= \left\{ \sigma \in K\ |\ {{\,\textrm{card}\,}}H_f(\sigma )=1\right\} \).
Thus, we can see that the gradient vector field defined here, although it is seen as a partial map \(\mathcal {V}:K\nrightarrow K\), follows the idea of the gradient of a real-valued discrete Morse function as defined by Forman (1998). Indeed, every \(\sigma \in K\) such that \({{\,\textrm{card}\,}}T_f(\sigma )=1\) is at the head of an arrow of \(\mathcal {V}\) (the element of \(T_f(\sigma )\) being at the tail of that arrow) while every \(\sigma \in K\) such that \({{\,\textrm{card}\,}}H_f(\sigma )=1\) is at the tail of an arrow (the element of \(H_f(\sigma )\) being at the head of that arrow). The main difference here is that the critical points of f are considered as fixed points of its gradient field, whereas they were simply not included in the original definition.
Example 4.5
Consider \(f=(f_1,f_2):K\rightarrow {\mathbb R}^2\), the function defined as in Fig. 7. We could verify that it is mdm and that its gradient field is as represented in the figure. Notice that \(f_2\) is not discrete Morse. Indeed, we can see that there are some \(\sigma \in K\) for which \({{\,\textrm{card}\,}}H_2(\sigma ) = 2\) or \({{\,\textrm{card}\,}}T_2(\sigma ) = 2\).
4.2 Vector-valued functions with discrete Morse components
Consider a vector-valued function \(f=(f_1,\ldots ,f_k):K\rightarrow {\mathbb R}^k\). From Example 4.5, we can see that f being mdm does not guarantee each \(f_i\) is discrete Morse. Conversely, f is not always mdm even if all its components are discrete Morse. Indeed, if each \(f_i\) is discrete Morse, we could easily verify that f satisfies conditions (1) and (2) of the definition of a mdm function, but not necessarily conditions (3) and (4). Actually, we could show that \(k\) discrete Morse functions \(f_1,\ldots ,f_k\) form a mdm function \(f=(f_1,\ldots ,f_k)\) if and only if for every pair of facet and cofacet \(\alpha ^{(p)}\subset \beta ^{(p+1)}\), the vectors \(f(\alpha )\) and \(f(\beta )\) are comparable in the partial order \(\preceq \).
Whenever a mdm function \(f=(f_1,\ldots ,f_k)\) is such that each of its component \(f_i\) is discrete Morse, we have the following result on the gradient vector fields of f and each \(f_i\).
Proposition 4.6
Let \(f=(f_1,\ldots ,f_k):K\rightarrow {\mathbb R}^k\) be mdm and each \(f_i\) be discrete Morse. Consider \(\mathcal {V}\) and \(\mathcal {V}_i\), the gradient vector fields of f and \(f_i\), respectively, for each \(i=1,\ldots ,k\). Then, \({{\,\textrm{dom}\,}}\mathcal {V}= \left\{ \sigma \in K\ |\ {{\,\textrm{card}\,}}\left( \bigcap _{i=1}^kT_i(\sigma )\right) = 0 \right\} \) and
Proof
First, for each \(\sigma \in K\), we know that \(T_f(\sigma ) = \bigcap _{i=1}^kT_i(\sigma )\). Hence, by definition of \({{\,\textrm{dom}\,}}\mathcal {V}\), we have directly \({{\,\textrm{dom}\,}}\mathcal {V}= \left\{ \sigma \in K\ |\ {{\,\textrm{card}\,}}\left( \bigcap _{i=1}^kT_i(\sigma )\right) = 0\right\} \).
Now, consider \(\sigma \in {{\,\textrm{dom}\,}}\mathcal {V}\). By definition of the gradient \(\mathcal {V}\), we have that \(\mathcal {V}(\sigma )~=~\beta \) if \(H_f(\sigma )~=~\{\beta \}\) for some \(\beta \supset \sigma \) and \(\mathcal {V}(\sigma )=\sigma \) otherwise. Also, we know that \(H_f(\sigma )=\bigcap _{i=1}^kH_i(\sigma )\) and \({{\,\textrm{card}\,}}H_i(\sigma )\le 1\) for each \(i=1,\ldots ,k\), so \(H_f(\sigma )=\{\beta \}\) if and only if \(H_i(\sigma )=\{\beta \}\) for each \(i=1,\ldots ,k\). Hence, by definition of each \(\mathcal {V}_i\), we have \(\mathcal {V}(\sigma )=\beta \) for some \(\beta \supset \sigma \) if and only if \(\mathcal {V}_i(\sigma )=\beta \) for each \(i=1,\ldots ,k\). \(\square \)
Put simply, this last result states that, for a mdm function f with discrete Morse components \(f_1,\ldots ,f_k\), there is an arrow in \(\mathcal {V}\) going from a simplex \(\sigma \) to its cofacet \(\beta \) if and only if there is an arrow in each \(\mathcal {V}_i\) going from \(\sigma \) to \(\beta \).
Example 4.7
Assume \(f=(f_1,f_2)\) is mdm and its components \(f_1\) and \(f_2\) are discrete Morse. Suppose the gradient vector fields of \(f_1\) and \(f_2\) are the ones represented in orange and blue in Fig. 8a, where the dots represent fixed points. Then, the gradient of f has to be the one shown in Fig. 8b, where the critical simplices are shown in red.
4.3 Acyclicity of a gradient vector field
As in the one-dimensional setting, gradient vector fields of mdm functions are necessarily acyclic and, conversely, every acyclic vector field represents the gradient of some mdm function.
Lemma 4.8
Let \(f_1,\ldots ,f_k:K\rightarrow {\mathbb R}\) be discrete Morse functions. If \(f_1,\ldots ,f_k\) have identical gradient vector fields \(\mathcal {V}_1 = \mathcal {V}_2 = \cdots = \mathcal {V}_k=:\mathcal {V}\), then \(f=(f_1,\ldots ,f_k)\) is mdm and its gradient is \(\mathcal {V}\).
Proof
Let \(\sigma \in K\). Notice that if \(\mathcal {V}_1 = \mathcal {V}_2 = \cdots = \mathcal {V}_k\), then we must have \(H_1(\sigma )~=~H_2(\sigma )~=~\cdots ~=~H_k(\sigma )\) and \(T_1(\sigma ) = T_2(\sigma ) = \cdots = T_k(\sigma )\). Indeed, if \(H_j(\sigma )=\{\beta \}\) for some \(j=1,\ldots ,k\), then \(\mathcal {V}_j(\sigma ) = \beta \), so \(\mathcal {V}_i(\sigma ) = \beta \) for all \(i=1,\ldots ,k\). It follows that \(H_1(\sigma ) = H_2(\sigma ) = \cdots = H_k(\sigma )\). Moreover, if \(T_j(\sigma ) = \{\alpha \}\) for some \(j=1,\ldots ,k\), then \(H_j(\alpha ) = \{\sigma \}\). Thus, \(H_i(\alpha ) = \{\sigma \}\) and \(T_i(\sigma ) = \{\alpha \}\) for all \(i=1,\ldots ,k\), hence \(T_1(\sigma ) = T_2(\sigma ) = \cdots = T_k(\sigma )\).
From these observations and using Proposition 4.6, assuming f is indeed mdm, we easily see that the gradient \(\mathcal {V}\) of f is such that \({{\,\textrm{dom}\,}}\mathcal {V}={{\,\textrm{dom}\,}}\mathcal {V}_i\) for all \(i=1,\ldots ,k\) and \(\mathcal {V}(\sigma )=\mathcal {V}_i(\sigma )\) for all \(\sigma \in {{\,\textrm{dom}\,}}\mathcal {V}\), so \(\mathcal {V}=\mathcal {V}_1=\mathcal {V}_2=\cdots =\mathcal {V}_k\).
All that is left to prove now is that f is a mdm function. Because \(H_f(\sigma ) = \bigcap _{i=1}^kH_i(\sigma )\) and \(T_f(\sigma ) = \bigcap _{i=1}^kT_i(\sigma )\) for all \(\sigma \in K\), we see that \(H_f(\sigma ) = H_i(\sigma )\) and \(T_f(\sigma ) = T_i(\sigma )\) for every \(i=1,\ldots ,k\), so the four conditions of a mdm function follow.
-
(1) \({{\,\textrm{card}\,}}H_f(\sigma ) = {{\,\textrm{card}\,}}H_i(\sigma )\le 1\) for any \(i\in \{1,\ldots ,k\}\).
-
(2) \({{\,\textrm{card}\,}}T_f(\sigma ) = {{\,\textrm{card}\,}}T_i(\sigma )\le 1\) for any \(i\in \{1,\ldots ,k\}\).
-
(3) If \(\beta ^{(p+1)}\supset \sigma \) is not in \(H_f(\sigma )\), since \(H_f(\sigma )=H_i(\sigma )\) for each \(i=1,\ldots ,k\), it follows that \(\beta \notin H_i(\sigma )\) for each \(i=1,\ldots ,k\). Consequently, \(f_i(\beta ) > f_i(\sigma )\) for all \(i=1,\ldots ,k\), so \(f(\beta )\succneqq f(\sigma )\).
-
(4) Is shown similarly to (3).
\(\square \)
Proposition 4.9
Let \(\mathcal {V}\) be a discrete vector field on a simplicial complex K. The field \(\mathcal {V}\) is acyclic if and only if \(\mathcal {V}\) is the gradient of some mdm function \(f:K\rightarrow {\mathbb R}^k\).
Proof
First, suppose \(\mathcal {V}\) is acyclic. It is known that for any acyclic discrete vector field \(\mathcal {V}\), there exists a discrete Morse function \(g:K\rightarrow {\mathbb R}\) for which \(\mathcal {V}\) is the gradient (Forman 1998). From Lemma 4.8, it follows that \(f=(g,g,\ldots ,g):K\rightarrow {\mathbb R}^k\) is mdm and its gradient vector field is \(\mathcal {V}\).
Now, let \(\mathcal {V}\) be the gradient of some mdm function \(f:K\rightarrow {\mathbb R}^k\). For all \(\mathcal {V}\)-path \(\alpha _0^{(p)},\beta _0^{(p+1)},\alpha _1^{(p)},\ldots ,\beta _{r-1}^{(p+1)},\alpha _r^{(p)}\), we see that
If this \(\mathcal {V}\)-path is non-trivial, i.e. \(r\ge 1\), it follows that \(f(\alpha _0)\ne f(\alpha _r)\), thus \(\alpha _0\ne \alpha _r\). Hence, a non-trivial \(\mathcal {V}\)-path cannot be closed, meaning that \(\mathcal {V}\) is acyclic. \(\square \)
This last proposition is well known in the one-dimensional setting. Actually, the reasoning used in the second part of the previous proof is also used to prove the analogous result in the original theory.
Furthermore, notice that there is no restriction on the dimension of the codomain \({\mathbb R}^k\) of the mdm function in Proposition 4.9. Therefore, for any integers \(k,k'\ge 1\), there exists a mdm function \(f:K\rightarrow {\mathbb R}^k\) having \(\mathcal {V}\) as a gradient field if and only if \(\mathcal {V}\) is acyclic if and only if there exists a mdm function \(g:K\rightarrow {\mathbb R}^{k'}\) having \(\mathcal {V}\) as a gradient field, thus the following corollary.
Corollary 4.10
Let \(f:K\rightarrow {\mathbb R}^k\) be mdm. For all integer \(k'\ge 1\), there exists a mdm function \(g:K\rightarrow {\mathbb R}^{k'}\) which has the same gradient vector field, hence the same critical points, as f.
In particular, we see from this result that for any mdm function, there exists a real-valued discrete Morse function having the same gradient vector field.
5 Flow of a multidimensional discrete Morse function
Here, we outline some results on the flow associated to the gradient field of a mdm function. We first present some direct consequences of the acyclicity of a gradient field, including the Morse inequalities which are central in other variants of Morse theory. Then, we show some interesting properties of the image of a solution for such a flow.
5.1 Gradient flow and finest Morse decomposition
Let \(\mathcal {V}\) be the gradient field of a mdm function \(f:K\rightarrow {\mathbb R}^k\). We note \(\Pi _f:=\Pi _\mathcal {V}\) the gradient flow of f. Similarly, we write \(\sigma \rightarrowtriangle _{f}\tau \) rather than \(\sigma \rightarrowtriangle _{\mathcal {V}}\tau \) when there is a solution in \(\Pi _f\) going from \(\sigma \) to \(\tau \). From the definition of a flow, we find directly the following characterization of \(\Pi _f\).
Proposition 5.1
Let \(f:K\rightarrow {\mathbb R}^k\) be mdm. The gradient flow of f is
For a gradient flow, we see that \(\Pi _f(\sigma ) = H_f(\sigma )\) when \({{\,\textrm{card}\,}}H_f(\sigma )=1\) and \(\Pi _f(\sigma )\subseteq {{\,\textrm{Cl}\,}}\sigma \) otherwise. Moreover, we know from Proposition 4.9 that the gradient of a mdm function is always acyclic and from Proposition 3.15 that a discrete vector field is acyclic if and only if its associated flow also is. The next result follows.
Proposition 5.2
The gradient flow \(\Pi _f\) of a mdm function \(f:K\rightarrow {\mathbb R}^k\) is always acyclic.
Also, the following proposition is a direct consequence of Theorem 3.13 and Proposition 3.14.
Proposition 5.3
Let \(f:K\rightarrow {\mathbb R}^k\) be mdm. The collection of basic sets of \(\Pi _f\) is
Therefore, \(\mathcal {M}\) is the finest Morse decomposition of \(\Pi _f\).
For any critical point \(\sigma ^{(p)}\in K\) of a mdm function \(f:K\rightarrow {\mathbb R}^k\), we can verify that the Poincaré polynomial of \(\{\sigma \}\) is simply \(P_{\{\sigma \}}(t) = t^p\). Hence, using Proposition 3.11 and Corollary 3.12, we see that this Morse decomposition leads to the following Morse equation and inequalities.
Proposition 5.4
Let \(f:K\rightarrow {\mathbb R}^k\) be mdm with \(\dim K = n\). Let \(m_p\) be the number of critical points of index p of f. We have the following Morse equation:
for some polynomial Q(t) with non-negative coefficients.
Corollary 5.5
Let \(f:K\rightarrow {\mathbb R}^k\) be mdm with \(\dim K = n\). Let \(m_p\) be the number of critical points of index p of f. For all \(p=0,1,\ldots ,n\), we have
-
(1)
the strong Morse inequalities:
$$\begin{aligned} m_p - m_{p-1} + \cdots +(-1)^p m_0 \ge \beta _p(K) - \beta _{p-1}(K) + \cdots +(-1)^p \beta _0(K); \end{aligned}$$ -
(2)
the weak Morse inequalities:
$$\begin{aligned} m_p \ge \beta _p(K); \end{aligned}$$ -
(3)
the following equality linking the Euler characteristic \(\chi (K)\) of K and the critical points of f:
$$\begin{aligned} m_0 - m_1 + \cdots +(-1)^n m_n = \beta _0(K) - \beta _1(K) + \cdots +(-1)^n \beta _n(K) = \chi (K) \end{aligned}$$
These Morse inequalities are completely analogous to those from the classical and discrete Morse theories. In Sect. 7, we will see that there also exists other inequalities which are specific to the multiparameter extension.
5.2 Properties of the image of a solution
As mentioned in the proof of Proposition 4.9, given a mdm function \(f:K\rightarrow {\mathbb R}^k\) with gradient \(\mathcal {V}\), it is clear that for all \(\mathcal {V}\)-path \(\alpha _0^{(p)},\beta _0^{(p+1)},\alpha _1^{(p)},\ldots ,\beta _{r-1}^{(p+1)},\alpha _r^{(p)}\), we have
We could think a similar property exists for solutions of \(\Pi _f\). For instance, we could expect that \(f(\sigma )\succeq f(\tau )\) for all \(\sigma \in K\) and all \(\tau \in \Pi _f(\sigma )\). However, it is not always the case, not even in the one-dimensional setting, as shown in Fig. 9.
Indeed, let \(f:K\rightarrow {\mathbb R}\) be the discrete Morse function defined in Fig. 9 and note \(\sigma ,\tau _1,\tau _2\in K\) the simplices for which \(f(\sigma ) = 3\), \(f(\tau _1) = 4\) and \(f(\tau _2) = 5\). We see that for \(i=1,2\), we have \(\tau _i\in \Pi _f(\sigma )\) but \(f(\sigma ) < f(\tau _i)\).
Nonetheless, we can prove that, in most cases, \(\sigma \rightarrowtriangle _{f}\tau \) implies \(f(\sigma )\succeq f(\tau )\).
Lemma 5.6
Let \(f:K\rightarrow {\mathbb R}^k\) be mdm and consider two simplices \(\sigma ,\tau \in K\) such that \(\tau \in {{\,\textrm{Cl}\,}}\sigma \backslash {{\,\textrm{Cl}\,}}T_f(\sigma )\). Necessarily, we have \(f(\sigma )\succeq f(\tau )\), and the equality is only verified when \(\sigma =\tau \).
Proof
Let \(\tau \in {{\,\textrm{Cl}\,}}\sigma \backslash {{\,\textrm{Cl}\,}}T_f(\sigma )\) and write \(\dim \tau =p\) and \(\dim \sigma =p+q\). The result is shown by induction on \(q = \dim \sigma -\dim \tau \). For \(q=0\), we obviously have \(\sigma =\tau \), so \(f(\sigma )=f(\tau )\). For \(q=1\), \(\tau \) is then a facet of \(\sigma \) such that \(\tau \notin T_f(\sigma )\), so \(f(\sigma )\succneqq f(\tau )\) by definition of a mdm function.
When \(q>1\), we could show there are two different simplices \(\beta _1,\beta _2\in K_{p+1}\) such that \(\tau \subset \beta _1\subset \sigma \) and \(\tau \subset \beta _2\subset \sigma \). By definition of a mdm function, at least one \(\beta \in \{\beta _1,\beta _2\}\) is such that \(\beta \notin H_f(\tau )\), so \(f(\beta )\succneqq f(\tau )\). Moreover, since \(\tau \subset \beta \) and \(\tau \notin {{\,\textrm{Cl}\,}}T_f(\sigma )\), we see that \(\beta \notin {{\,\textrm{Cl}\,}}T_f(\sigma )\), meaning that \(\beta \in {{\,\textrm{Cl}\,}}\sigma \backslash {{\,\textrm{Cl}\,}}T_f(\sigma )\). By the induction hypothesis, we then have \(f(\sigma )\succneqq f(\beta )\), so
\(\square \)
Lemma 5.7
Let \(f:K\rightarrow {\mathbb R}^k\) be mdm and consider \(\sigma ,\tau \in K\) such that \(\tau \in \Pi _f(\sigma )\). Suppose at least one of the following conditions is satisfied:
-
((a))
\({{\,\textrm{card}\,}}T_f(\sigma )=0\);
-
((b))
\(\tau \notin {{\,\textrm{Ex}\,}}T_f(\sigma )\);
-
((c))
for every \(\beta ^{(p+1)}\supset \tau ^{(p)}\) such that \(\beta \in {{\,\textrm{Cl}\,}}\sigma \backslash {{\,\textrm{Cl}\,}}T_f(\sigma )\), we have \(\beta \notin H_f(\tau )\).
We then have \(f(\sigma )\succeq f(\tau )\), where the equality \(f(\sigma )=f(\tau )\) can only hold if either \(\sigma =\tau \) or \(H_f(\sigma )=\{\tau \}\).
Proof
First, suppose \({{\,\textrm{card}\,}}T_f(\sigma )=0\). In the case where \({{\,\textrm{card}\,}}H_f(\sigma )=1\), we have \(\tau \in \Pi _f(\sigma )=H_f(\sigma )\) by Proposition 5.1, hence \(f(\sigma )\succeq f(\tau )\) by definition of \(H_f(\sigma )\). In the case \({{\,\textrm{card}\,}}H_f(\sigma )=0\) (\(\sigma \) is then critical), we have \(\tau \in \Pi _f(\sigma )={{\,\textrm{Cl}\,}}\sigma \) by Proposition 5.1 and \({{\,\textrm{Cl}\,}}\sigma ={{\,\textrm{Cl}\,}}\sigma \backslash {{\,\textrm{Cl}\,}}T_f(\sigma )\) because \(T_f(\sigma )=\emptyset \). Thus, from Lemma 5.6, we see that \(f(\sigma )\succeq f(\tau )\) and \(f(\sigma )=f(\tau )\Rightarrow \sigma =\tau \). This proves (a).
We now show that (b) implies \(f(\sigma )\succeq f(\tau )\) assuming (a) is not true, meaning that \({{\,\textrm{card}\,}}T_f(\sigma )=1\). From Proposition 5.1, we see that \(\tau \in \Pi _f(\sigma )={{\,\textrm{Ex}\,}}\sigma \backslash T_f(\sigma )\subset {{\,\textrm{Cl}\,}}\sigma \backslash T_f(\sigma )\). Since \(\tau \notin {{\,\textrm{Ex}\,}}T_f(\sigma )\) by hypothesis, it follows that \(\tau \in {{\,\textrm{Cl}\,}}\sigma \backslash {{\,\textrm{Cl}\,}}T_f(\sigma )\). The result follows from Lemma 5.6.
Finally, suppose that (a) and (b) are false and condition (c) is satisfied. Let \(\tau \in K_p\) and \(\sigma \in K_{p+q}\). Since \(\tau \in {{\,\textrm{Ex}\,}}T_f(\sigma )\) by hypothesis, we can deduce that \(q \ge 2\). From the definition of a simplicial complex, we could show that there exists a \(\beta \in K_{p+1}\) such that \(\tau \subset \beta \subset \sigma \) and \(\beta \notin {{\,\textrm{Cl}\,}}T_f(\sigma )\). In other words, \(\beta \in {{\,\textrm{Cl}\,}}\sigma \backslash {{\,\textrm{Cl}\,}}T_f(\sigma )\). From Lemma 5.6, it follows that \(f(\sigma )\succeq f(\beta )\). Moreover, by hypothesis (c), \(\beta \notin H_f(\tau )\), so \(f(\beta )\succneqq f(\tau )\) by definition of a mdm function. Also, it follows from Lemma 5.6 that \(f(\sigma )\succeq f(\beta )\). Hence, \(f(\sigma )\succeq f(\beta )\succneqq f(\tau )\). \(\square \)
Proposition 5.8
Let \(f:K\rightarrow {\mathbb R}^k\) be mdm and consider \(\sigma ,\tau \in K\) such that \(\sigma \rightarrowtriangle _{f}\tau \). Consider the three conditions from Lemma 5.7:
-
((a))
\({{\,\textrm{card}\,}}T_f(\sigma )=0\);
-
((b))
\(\tau \notin {{\,\textrm{Ex}\,}}T_f(\sigma )\);
-
((c))
for every \(\beta ^{(p+1)}\supset \tau ^{(p)}\) such that \(\beta \in {{\,\textrm{Cl}\,}}\sigma \backslash {{\,\textrm{Cl}\,}}T_f(\sigma )\), we have \(\beta \notin H_f(\tau )\).
If at least one of these conditions is satisfied, then \(f(\sigma )\succeq f(\tau )\), where the equality can only hold if either \(\sigma =\tau \) or \(H_f(\sigma )=\{\tau \}\).
Proof
First, we see that when \(\tau \in {{\,\textrm{Cl}\,}}\sigma \backslash {{\,\textrm{Cl}\,}}T_f(\sigma )\), the result is obvious from Lemma 5.6. Now, suppose \(\tau \in {{\,\textrm{Cl}\,}}T_f(\sigma )\). We see that \(\tau \in {{\,\textrm{Ex}\,}}\sigma \). Also, \(\tau \notin T_f(\sigma )\): otherwise, it would imply that \(\Pi _f(\tau )=\{\sigma \}\) and we would have a cycle  . Thus, \(\tau \in {{\,\textrm{Ex}\,}}\sigma \backslash T_f(\sigma )\) and we see from Proposition 5.1 that \(\tau \in \Pi _f(\sigma )\), so the result follows from Lemma 5.7.
. Thus, \(\tau \in {{\,\textrm{Ex}\,}}\sigma \backslash T_f(\sigma )\) and we see from Proposition 5.1 that \(\tau \in \Pi _f(\sigma )\), so the result follows from Lemma 5.7.
All that is left to show is the case \(\tau \notin {{\,\textrm{Cl}\,}}\sigma \). Since \(\sigma \rightarrowtriangle _{f}\tau \), there exists a solution \(\varrho :{\mathbb Z}\nrightarrow K\) with \({{\,\textrm{dom}\,}}\varrho =\{0,1,\ldots ,n\}\) where \(n\ge 1\) such that \(\varrho (0)=\sigma \) and \(\varrho (n)=\tau \). This part of the proposition is proved by induction on n.
For \(n=1\), we have \(\tau \in \Pi _f(\sigma )\) and the result is straightforward from Lemma 5.7. When \(n>1\), notice that \(\tau \notin {{\,\textrm{Cl}\,}}\sigma \) implies \(\tau \notin {{\,\textrm{Ex}\,}}T_f(\sigma )\) where \(\sigma =\varrho (0)\). Thus, let \(i_0\) be the greatest \(i=0,1,\ldots ,n-1\) such that \(\tau \notin {{\,\textrm{Ex}\,}}T_f(\varrho (i))\) and consider \(\upsilon :=\varrho (i_0)\). We make the following statement:
Indeed:
-
If \(i_0=n-1\), then \(\tau \in \Pi _f(\upsilon )\) and statement 1 follows from Lemma 5.7 because condition (b) is verified by definition of \(\upsilon \).
-
If \(i_0<n-1\), since \(i_0\) is the greatest \(i=0,1,\ldots ,n-1\) for which \(\tau \notin {{\,\textrm{Ex}\,}}T_f(\varrho (i))\), necessarily, \(\tau \in {{\,\textrm{Ex}\,}}T_f(\varrho (i_0+1))\).
-
When \({{\,\textrm{card}\,}}H_f(\upsilon )=1\), then \(\Pi _f(\upsilon )= H_f(\upsilon ) = \{\varrho (i_0+1)\}\), thus \(T_f(\varrho (i_0+1)) = \{\upsilon \}\) and \(\tau \in {{\,\textrm{Ex}\,}}\upsilon \subset {{\,\textrm{Cl}\,}}\upsilon \). Also, \({{\,\textrm{card}\,}}T_f(\upsilon )\) must be zero, so \(\tau \in {{\,\textrm{Cl}\,}}\upsilon = {{\,\textrm{Cl}\,}}\upsilon \backslash {{\,\textrm{Cl}\,}}T_f(\upsilon )\).
-
When \({{\,\textrm{card}\,}}H_f(\upsilon )=0\), then \(\varrho (i_0+1)\in \Pi _f(\upsilon )\subseteq {{\,\textrm{Cl}\,}}\upsilon \) and, because \(\tau \in {{\,\textrm{Ex}\,}}T_f(\varrho (i_0+1))\subset {{\,\textrm{Cl}\,}}\varrho (i_0+1)\), we deduce \(\tau \in {{\,\textrm{Cl}\,}}\upsilon \). Also, \(\tau \notin {{\,\textrm{Ex}\,}}T_f(\upsilon )\) by definition of \(\upsilon \) and \(\tau \notin T_f(\upsilon )\): otherwise, we would have a cycle
 , which would contradict the acyclicity of \(\Pi _f\). Hence, \(\tau \notin {{\,\textrm{Cl}\,}}T_f(\upsilon )\), so \(\tau \in {{\,\textrm{Cl}\,}}\upsilon \backslash {{\,\textrm{Cl}\,}}T_f(\upsilon )\).
, which would contradict the acyclicity of \(\Pi _f\). Hence, \(\tau \notin {{\,\textrm{Cl}\,}}T_f(\upsilon )\), so \(\tau \in {{\,\textrm{Cl}\,}}\upsilon \backslash {{\,\textrm{Cl}\,}}T_f(\upsilon )\).
-
We now show this second statement, still considering \(\upsilon \) as defined above and \(\tau \notin {{\,\textrm{Cl}\,}}\sigma \):
This follows from the induction hypothesis, which can be used since \(\sigma \rightarrowtriangle _{f}\upsilon \) and at least one of the conditions (a), (b) or (c) is verified for \(\sigma \) and \(\upsilon \). Indeed, suppose all three conditions are false, meaning that \(\upsilon \in {{\,\textrm{Ex}\,}}T_f(\sigma )\) and there exists a \(\beta \in H_f(\upsilon )\) such that \(\beta \in {{\,\textrm{Cl}\,}}\sigma \backslash T_f(\sigma )\). Then, we have \(\Pi _f(\upsilon ) = H_f(\upsilon ) = \{\beta \}\), so \(\varrho (i_0+1) = \beta \). Also, by definition of \(i_0\), we see that \(\tau \in {{\,\textrm{Ex}\,}}T_f(\beta ) = {{\,\textrm{Ex}\,}}\upsilon \subset {{\,\textrm{Cl}\,}}\upsilon \). Since \(\upsilon \in {{\,\textrm{Ex}\,}}T_f(\sigma )\) implies \(\upsilon \in {{\,\textrm{Cl}\,}}\sigma \), we find \(\tau \in {{\,\textrm{Cl}\,}}\sigma \), a contradiction.
The proposition follows from statements 1 and 2. \(\square \)
In particular, since \(T_f(\sigma )=H_f(\sigma )=\emptyset \) when \(\sigma \) is critical, we can deduce the following.
Corollary 5.9
Let \(f:K\rightarrow {\mathbb R}^k\) be mdm and consider \(\sigma ,\tau \in K\) such that \(\sigma \rightarrowtriangle _{f}\tau \) and \(\sigma \ne \tau \). If either \(\sigma \) or \(\tau \) is critical, then \(f(\sigma )\succneqq f(\tau )\).
6 Morse theorems
Here, we explain how the main theorems from Morse–Forman theory (see Forman 1998, Section 3) generalize in the multiparameter setting. A theorem extending some of those results is also proposed.
6.1 Classical results
One of the main theorems in both classical and discrete Morse theory is that a given topological space on which is defined a Morse function f is always homotopy equivalent to a CW complex having \(m_p(f)\) cells of dimension p for each \(p=0,1,2,\ldots \), where \(m_p(f)\) is the number of critical points of f of index p. This still holds in this setting.
Proposition 6.1
Let K be a simplicial complex. Suppose there exists a mdm function \(f:K\rightarrow {\mathbb R}^k\) and let \(m_p(f)\) be the number of critical points of index p of f. The complex K is homotopy equivalent to a CW complex with exactly \(m_p(f)\) cells of dimension p.
Proof
From Corollary 4.10, if there exists a mdm function \(f:K\rightarrow {\mathbb R}^k\), we know there exists a discrete Morse function \(g:K\rightarrow {\mathbb R}\) having the same gradient field as f, meaning that \(m_p(f) = m_p(g)\). Since Proposition 6.1 is well known for \(k=1\) (Forman 1998, Corollary 3.5), we have the result. \(\square \)
Note that, from this proposition, we could find an alternative proof to the famous Morse inequalities from Corollary 5.5.
Furthermore, Forman’s results on the homotopy type of a sublevel set still hold in the multiparameter setting. For a mdm function \(f:K\rightarrow {\mathbb R}^k\) and a vector \(a\in {\mathbb R}^k\), the sublevel set K(a) is the smallest subcomplex of K containing all \(\sigma \in K\) for which \(f(\sigma )\preceq a\):
We could easily show that, if we note \(\mathcal {V}\) the gradient field of f, K(a) is \(\mathcal {V}\)-compatible for all \(a\in {\mathbb R}^k\). Moreover, we see that a simplex \(\sigma \in K_p\) is in K(a) when either \(f(\sigma )\preceq a\) or \(f(\tau )\preceq a\) for some \(\tau \supset \sigma \). To check if the second condition is true, it is sufficient to consider cofacets \(\tau ^{(p+1)}\supset \sigma \), as suggests the next lemma. It is proven similarly to its one-dimensional analogue (Forman 1998, Lemma 3.2).
Lemma 6.2
Let \(f:K\rightarrow {\mathbb R}^k\) be mdm and \(\sigma \in K_p\). For all \(\tau \supset \sigma \), there exists a \(\beta \in K_{p+1}\) such that \(\sigma \subset \beta \subseteq \tau \) and \(f(\beta )\preceq f(\tau )\).
To state Propositions 6.3 and 6.4, which are analogous to Theorems 3.3 and 3.4 in (Forman 1998), we consider the following subset of \({\mathbb R}^k\):
Proposition 6.3
Let \(f:K\rightarrow {\mathbb R}^k\) be mdm and consider \(a\precneqq b\in {\mathbb R}^k\). If there is no critical simplex \(\sigma \in K\) such that \(f(\sigma )\in Q_a^b\), then
Proposition 6.4
Let \(f:K\rightarrow {\mathbb R}^k\) be mdm and consider \(a\precneqq b\in {\mathbb R}^k\). Suppose \(\sigma \in K_p\) is the only critical simplex of f with \(f(\sigma )\in Q_a^b\), then
where \(e^p\) is a cell of dimension p.
The proofs of these two propositions are omitted: Proposition 6.3 is a direct consequence of Lemma 6.6 whereas Proposition 6.4 is a particular case of Theorem 6.7. Both of these results will be proved hereafter.
6.2 Extended Morse theorem
In the one-dimensional setting, the last two propositions suffice to describe all changes in homotopy type of the sublevel set K(a) as a increases. Indeed, for a discrete Morse function \(f:K\rightarrow {\mathbb R}\), consider a critical simplex \(\sigma \). From Corollary 5.9, we see that for any critical simplex \(\alpha \subsetneq \sigma \), we have \(f(\alpha ) < f(\sigma )\) and conversely, for any critical simplex \(\beta \supsetneq \sigma \), we have \(f(\sigma ) < f(\beta )\). Hence, we can always choose parameters a large enough and b small enough so that, at least locally, \(\sigma \) is the unique critical simplex with \(f(\sigma )\in Q_a^b\).
When \(f:K\rightarrow {\mathbb R}^k\) is mdm with \(k>1\), we can see that this is not necessarily true by considering the following very simple example. Let \(f:K\rightarrow {\mathbb R}^2\) be as defined in Fig. 10 and consider the critical edge \(\sigma \) with \(f(\sigma )=(1,1)\). If we choose \(a\in {\mathbb R}^2\) so that \(f(\alpha )\preceq a\) for each (critical) vertex \(\alpha \subset \sigma \), we then have \((1,1)\preceq a\), so \(f(\sigma )\notin Q_a^b\) for all \(b\in {\mathbb R}^2\). Thus, in order to have \(f(\sigma )\in Q_a^b\), we must have at least one vertex \(\alpha \) with \(f(\alpha )\in Q_a^b\) as well. Consequently, the hypotheses of Proposition 6.4 may not be verified for \(\sigma \).
To overcome this gap, we come up with an additional result, Theorem 6.7, for which no hypothesis on the number of critical simplices \(\sigma \) with \(f(\sigma )\in Q_a^b\) is needed. To prove it, preliminary results are necessary.
Lemma 6.5
Let \(\Pi _\mathcal {V}:K\multimap K\) be a flow. A \(\mathcal {V}\)-compatible subset \(L\subseteq K\) is a subcomplex of K if and only if \(\Pi _\mathcal {V}(L)\subseteq L\).
Proof
Assume L is a subcomplex of K, meaning that \({{\,\textrm{Cl}\,}}\sigma \subseteq L\) for all \(\sigma \in L\). For all \(\sigma \in L\), by definition of \(\Pi _\mathcal {V}\), we have either \(\Pi _\mathcal {V}(\sigma )\subseteq {{\,\textrm{Cl}\,}}\sigma \), which is a subset of L because it is a subcomplex, or \(\Pi _\mathcal {V}(\sigma )=\{\mathcal {V}(\sigma )\}\subset L\) because L is \(\mathcal {V}\)-compatible.
Now, suppose \(\Pi _\mathcal {V}(L)\subseteq L\). Let \(\sigma \in L\) and consider \(\alpha \in {{\,\textrm{Cl}\,}}\sigma \). If \(\sigma \rightarrowtriangle _{\mathcal {V}}\alpha \), it is easy to verify that \(\alpha \in L\). Otherwise, if  , we have by Lemma 3.2 that \(\sigma \in {{\,\textrm{im}\,}}\mathcal {V}\backslash {{\,\textrm{Fix}\,}}\mathcal {V}\) and \(\alpha =\mathcal {V}^{-1}(\sigma ) = \sigma ^-\). By the \(\mathcal {V}\)-compatibility of L, it follows that \(\alpha \in L\), so L is a subcomplex of K. \(\square \)
, we have by Lemma 3.2 that \(\sigma \in {{\,\textrm{im}\,}}\mathcal {V}\backslash {{\,\textrm{Fix}\,}}\mathcal {V}\) and \(\alpha =\mathcal {V}^{-1}(\sigma ) = \sigma ^-\). By the \(\mathcal {V}\)-compatibility of L, it follows that \(\alpha \in L\), so L is a subcomplex of K. \(\square \)
Lemma 6.6
Let \(\Pi _\mathcal {V}:K\multimap K\) be an acyclic flow and consider a \(\mathcal {V}\)-compatible subcomplex \(L\subseteq K\). If \({{\,\textrm{Fix}\,}}\mathcal {V}\subseteq L\), then \(K\searrow L\).
Proof
If \(K\backslash L\) contains no fixed point of \(\mathcal {V}\), then \({{\,\textrm{card}\,}}K\backslash L=2n\) for some \(n\ge 0\). We prove the result by induction on n. If \(n=0\), it is obvious since \(L=K\).
When \(n\ge 1\), we first show that there exists a \(\sigma \in K\backslash L\) such that \(\Pi ^{-1}_\mathcal {V}(\sigma )=\emptyset \). Indeed, consider the preorder \(\le _\mathcal {V}\) induced by the relation  on K, i.e. \(\sigma \le _\mathcal {V}\tau \) iff \(\sigma =\tau \) or
on K, i.e. \(\sigma \le _\mathcal {V}\tau \) iff \(\sigma =\tau \) or  . By the acyclicity of \(\Pi _\mathcal {V}\), we see that \(\le _\mathcal {V}\) is actually a partial order on K. Hence, because \(K\backslash L\) is finite, we can choose \(\sigma \) maximal in \(K\backslash L\) relatively to \(\le _\mathcal {V}\). In other words, we can choose \(\sigma \in K\backslash L\) so that
. By the acyclicity of \(\Pi _\mathcal {V}\), we see that \(\le _\mathcal {V}\) is actually a partial order on K. Hence, because \(K\backslash L\) is finite, we can choose \(\sigma \) maximal in \(K\backslash L\) relatively to \(\le _\mathcal {V}\). In other words, we can choose \(\sigma \in K\backslash L\) so that  for all \(\tau \in K\backslash L\) such that \(\tau \ne \sigma \). Moreover, since \(\Pi _\mathcal {V}(L)\subseteq L\) by Lemma 6.5, we see that
for all \(\tau \in K\backslash L\) such that \(\tau \ne \sigma \). Moreover, since \(\Pi _\mathcal {V}(L)\subseteq L\) by Lemma 6.5, we see that  also holds for \(\tau \in L\), so
also holds for \(\tau \in L\), so  for all \(\tau \in K\backslash \{\sigma \}\). Finally, since \(\sigma \notin {{\,\textrm{Fix}\,}}\mathcal {V}\subseteq L\) by hypothesis, we have
for all \(\tau \in K\backslash \{\sigma \}\). Finally, since \(\sigma \notin {{\,\textrm{Fix}\,}}\mathcal {V}\subseteq L\) by hypothesis, we have  , thus \(\Pi _\mathcal {V}^{-1}(\sigma )=\emptyset \).
, thus \(\Pi _\mathcal {V}^{-1}(\sigma )=\emptyset \).
We now assume that \(\sigma \in K\backslash L\) is such that \(\Pi _\mathcal {V}^{-1}(\sigma )=\emptyset \). We can easily check that \(\sigma \in {{\,\textrm{dom}\,}}\mathcal {V}\backslash {{\,\textrm{Fix}\,}}\mathcal {V}\): if \(\sigma \) were in \({{\,\textrm{im}\,}}\mathcal {V}\), we would have \(\mathcal {V}^{-1}(\sigma )\in \Pi ^{-1}_\mathcal {V}(\sigma )\), a contradiction. Also, \(\sigma \) is a free face of \(\mathcal {V}(\sigma )\in K\backslash L\). Indeed, suppose \(\sigma \subset \beta \) for some \(\beta \in K\). We know that  because \(\Pi _\mathcal {V}^{-1}(\sigma )=\emptyset \). Hence, from Lemma 3.2, we necessarily have \(\mathcal {V}(\sigma ) = \beta \), so \(\sigma \) is a free face of \(\mathcal {V}(\sigma )\), which is in \(K\backslash L\) by the \(\mathcal {V}\)-compatibility of L.
because \(\Pi _\mathcal {V}^{-1}(\sigma )=\emptyset \). Hence, from Lemma 3.2, we necessarily have \(\mathcal {V}(\sigma ) = \beta \), so \(\sigma \) is a free face of \(\mathcal {V}(\sigma )\), which is in \(K\backslash L\) by the \(\mathcal {V}\)-compatibility of L.
Finally, we see that \(K\searrow K\backslash \{\sigma ,\mathcal {V}(\sigma )\}\) and, using the induction hypothesis, we then have that \(K\backslash \{\sigma ,\mathcal {V}(\sigma )\}\searrow L\), which concludes the proof. \(\square \)
Before we present the main theorem of this section, recall from Proposition 5.3 that
is a Morse decomposition of \(\Pi _f\), so by considering a set I of critical simplices of f, we can define the Morse set
for which \({{\,\textrm{Con}\,}}(M(I))\) is defined from Proposition 3.18, where
Theorem 6.7
Let \(f=(f_1,\ldots ,f_k):K\rightarrow {\mathbb R}^k\) be mdm and consider \(a,b\in {\mathbb R}^k\) such that \(a\precneqq b\). Let
Then,
Proof
Here is the idea of the proof. Consider the following subsets of K(b):

We will show that A, M(I) and B are mutually disjoint and, using Lemma 6.5, that they form the following nested sequence of subcomplexes of K(b):
Finally, after proving that A and B do not contain any critical points, it will follow from Lemma 6.6 that \(K(b)\searrow K(a)\cup A\cup M(I)\) and \(K(a)\cup A\searrow K(a)\).
First, recall that K(a), K(b) and M(I) are all \(\mathcal {V}\)-compatible sets, where \(\mathcal {V}\) is the gradient field of f. Also, we could easily show that \(\sigma ^+\rightarrowtriangle _{f}I\Leftrightarrow \sigma ^-\rightarrowtriangle _{f}I\). Using this argument, it would be straightforward to verify the \(\mathcal {V}\)-compatibility of A and B. Moreover, from the definitions of A, B and M(I), it is obvious that they are mutually disjoint sets.
Now, we show that \(K(b)\backslash K(a)= A\cup M(I)\cup B\). Verifying the inclusion from left to right is straightforward: if \(\sigma \in K(b)\backslash K(a)\) is not in M(I), then \(\sigma \in A\) if  and \(\sigma \in B\) if \(\sigma \rightarrowtriangle _{f}I\). We now prove \(A\cup M(I)\cup B \subseteq K(b)\backslash K(a)\).
and \(\sigma \in B\) if \(\sigma \rightarrowtriangle _{f}I\). We now prove \(A\cup M(I)\cup B \subseteq K(b)\backslash K(a)\).
-
By definition of A, we have \(A\subseteq K(b)\backslash K(a)\).
-
If \(\sigma \in M(I)\), by definition of a Morse set, there exists critical simplices \(\tau ,\tau '\in I\) such that \(\tau '\rightarrowtriangle _{f}\sigma \rightarrowtriangle _{f}\tau \). By definition of \(Q_a^b\), we thus have \(f(\tau ')\preceq b\) and \(f_i(\tau )>a_i\) for some \(i=1,\ldots ,k\). By Corollary 5.9, it follows that \(b\succeq f(\tau ')\succeq f(\sigma )\), so \(\sigma \in K(b)\). Moreover, we also have by Corollary 5.9 that \(f(\sigma )\succeq f(\tau )\), so \(f_i(\sigma )\ge f_i(\tau ) > a_i\) for some \(i=1,\ldots ,k\). In addition, for all coface \(\beta \supset \sigma \), we know from Lemma 3.3(1) that \(\beta \rightarrowtriangle _{f}\tau \), so \(f_i(\beta )>a_i\) by a similar reasoning. Hence, \(\sigma \notin K(a)\).
-
If \(\sigma \in B\), by definition of B, we have \(\sigma \in K(b)\). Also, there exists a critical \(\tau \in I\) such that \(\sigma \rightarrowtriangle _{f}\tau \). Hence, from Corollary 5.9, we see that \(f(\sigma )\succneqq f(\tau )\), thus \(f_i(\sigma )\ge f_i(\tau )>a_i\) for some \(i=1,\ldots ,k\) because \(f(\tau )\in Q_a^b\). From Lemma 3.3(1), we also have \(\beta \rightarrowtriangle _{f}\tau \) for all coface \(\beta \supset \sigma \), hence \(f_i(\beta )>a_i\). We conclude that \(\sigma \notin K(a)\).
Consequently, K(b) is the union \(K(a)\cup A\cup M(I)\cup B\) of mutually disjoint \(\mathcal {V}\)-compatible sets.
Next, we prove that \(K(a)\cup A\) and \(K(a)\cup A\cup M(I)\) are subcomplexes of K(b) using Lemma 6.5. To do so, we have to show that \(\Pi _f(K(a)\cup A)\subseteq K(a)\cup A\) and \(\Pi _f(K(a)\cup A\cup M(I))\subseteq K(a)\cup A\cup M(I)\). Since K(a) is a subcomplex of K(b), we already know that \(\Pi _f(K(a))\subseteq K(a)\) by Lemma 6.5. Thus, it suffices to show that \(\Pi _f(A)\subseteq K(a)\cup A\) and \(\Pi _f(M(I))\subseteq K(a)\cup A\cup M(I)\).
-
Let \(\sigma \in A\) and \(\gamma \in \Pi _f(\sigma )\) and suppose \(\gamma \in M(I)\cup B\). By definition of M(I) and B, we have \(\gamma \rightarrowtriangle _{f}\tau \) for some \(\tau \in I\), hence \(\sigma \rightarrowtriangle _{f}\gamma \rightarrowtriangle _{f}\tau \), which is a contradiction since
 by definition of A. Thus, \(\gamma \notin M(I)\cup B\), meaning that \(\gamma \in K(a)\cup A\).
by definition of A. Thus, \(\gamma \notin M(I)\cup B\), meaning that \(\gamma \in K(a)\cup A\). -
Let \(\sigma \in M(I)\) and \(\gamma \in \Pi _f(\sigma )\). By definition of M(I), there exists a \(\tau \in I\) such that \(\tau \rightarrowtriangle _{f}\sigma \rightarrowtriangle _{f}\gamma \). If there exists a \(\tau '\in I\) such that \(\gamma \rightarrowtriangle _{f}\tau '\), then \(\gamma \in M(I)\). Otherwise, if
 , then \(\gamma \notin B\), so \(\gamma \in K(a)\cup A\cup M(I)\). Either way, we have the desired result.
, then \(\gamma \notin B\), so \(\gamma \in K(a)\cup A\cup M(I)\). Either way, we have the desired result.
We now show that all critical points of f in \(K(b)\backslash K(a)\) are necessarily in I. To do so, we verify that \(f(\sigma )\in Q_a^b\) for all critical \(\sigma \in K(b)\backslash K(a)\). Since \(\sigma \notin K(a)\), we obviously have \(f_i(\sigma )>a_i\) for some \(i=1,\ldots ,k\). Also, \(\sigma \in K(b)\) implies that either \(f(\sigma )\preceq b\) or \(f(\gamma )\preceq b\) for some coface \(\gamma \supset \sigma \). When \(f(\sigma )\preceq b\), we immediately have \(f(\sigma )\in Q_a^b\). When \(f(\gamma )\preceq b\) for some coface \(\gamma \supset \sigma \), we see from Lemma 6.2 that there exists a cofacet \(\beta \) of \(\sigma \) such that \(f(\beta )\preceq f(\gamma )\preceq b\). It follows from the definition of a critical point that \(f(\sigma )\precneqq f(\beta )\preceq b\), so \(f(\sigma )\in Q_a^b\).
We deduce that the sets A and B do not contain any critical points of f. Also, recall from Proposition 5.2 that a gradient flow is always acyclic. Hence, from Lemma 6.6, it follows that \(K(b)= K(a)\cup A\cup M(I)\cup B\searrow K(a)\cup A\cup M(I)\) and \(K(a)\cup A\searrow K(a)\). By endowing K with the topology of a CW-complex, we conclude that
where M(I) is attached to K(a) along its exit set \({{\,\textrm{ex}\,}}M(I)\). \(\square \)
We want to emphasize the fact that Theorem 6.7 is a generalization of both Proposition 6.3 and Proposition 6.4. Indeed, when \(I=\emptyset \), then \(M(I)=\emptyset \) and we see from the proof that \(K(b)\searrow K(a)\), which proves Proposition 6.3. Then, when \(I=\{\sigma ^{(p)}\}\), we have \(M(I)=\{\sigma ^{(p)}\}\), which is homeomorphic to a cell of dimension p, and \({{\,\textrm{ex}\,}}M(I) = {{\,\textrm{cl}\,}}\sigma \backslash \sigma ={{\,\textrm{bd}\,}}\sigma \), so Proposition 6.4 follows.
6.3 Morse set examples
We conclude this section with a few examples to illustrate Theorem 6.7.
Example 6.8
Let K and \(f:K\rightarrow {\mathbb R}^2\) be as defined in Fig. 11. We could show that f is mdm and that the red simplices are critical.
For \(a = (0,5)\) and \(b= (1,5)\), we see in Fig. 12, as defined in the proof of Theorem 6.7, the sets K(a), A, M(I) and B. Here, notice that \({{\,\textrm{Con}\,}}(M(I))\) is trivial and \(K(b)\searrow K(a)\).
Example 6.9
Consider the (1-dimensional) simplicial complex K and the mdm function \(f:K\rightarrow {\mathbb R}^2\) defined in Fig. 13a.
-
If \(a = (2,0)\) and \(b=(2,1)\), we have \(K(b) = K(a)\cup M(I)\) as in Fig. 13b. More precisely, \(I = M(I) = \{f^{-1}(1,1), f^{-1}(2,1)\}\). We could show that \({{\,\textrm{Con}\,}}(M(I))\) is trivial and, although K(b) is obtained by adding two critical simplices to K(a), we have \(K(b)\searrow K(a)\).
-
If \(a = (2,1)\) and \(b=(2,2)\), we have \(K(b) = K = K(a)\cup M(I)\) as in Fig. 13c. Here, \(I = M(I) = \{f^{-1}(1,2)\}\). Since a unique critical simplex of dimension 1 is added to K(a) to obtain K(b), we see from either Proposition 6.4 or Theorem 6.7 that \(K(b)\simeq K(a)\cup e^1\), where \(e^1\) is a cell of dimension 1.
Example 6.10
Finally, consider K and \(f:K\rightarrow {\mathbb R}^2\) in Fig. 14a, where the red simplices are critical.
In (a), a mdm function, with critical simplices in red. In (b) and (c), the sets K(a) (black), A (blue) and M(I) (orange) as defined in the proof of Theorem 6.7 are represented, in (b), for parameters \(a=(2,1)\) and \(b=(2,2)\) and, in (c), for \(a=(1,2)\) and \(b=(2,2)\) (color figure online)
-
Let \(a=(2,1)\) and \(b=(2,2)\). We have \(K(b) = K(a)\cup A\cup M(I)\) as in Figure (b) where M(I) contains only one critical simplex.
-
Now, consider \(a=(1,2)\) and \(b=(2,2)\). We then have \(K(b)=K(a)\cup M(I)\) as in Fig. 14c. Here, we see that M(I) contains three critical simplices.
In both examples from Fig. 14b and c, even though the sets M(I) do not have the same number of critical simplices, we see that the homology change from K(a) to K(b) is the same because \(K(b)\simeq K(a)\cup e^1\) in both cases.
From the previous examples, we see that critical simplices can, more or less, interact with each other. In particular, notice that when \(I=\{\sigma ^{(p)},\tau ^{(p+1)}\}\) and there exists a unique path in the gradient field going from \(\tau \) to \(\sigma \), then \({{\,\textrm{Con}\,}}(M(I))\) is trivial and \(K(b)\searrow K(a)\). This is a consequence of a well-known result of Forman (1998) which states that, under these conditions, we can find another acyclic field in which \(\sigma \) and \(\tau \) are not critical by reversing the arrows along the unique path going from \(\tau \) to \(\sigma \). Informally, we could say that the two critical simplices cancel each other out.
7 Critical components of a multidimensional discrete Morse function
In the original Morse theory, which studies smooth real-valued Morse functions defined on smooth manifolds, it is well known that critical points are isolated. However, when extending the theory either by considering multiple Morse functions (Edelsbrunner and Harer 2004; Smale 1975; Wan 1975) or a vector-valued function (Budney and Kaczynski 2023), we see that the set of critical points obtained is separated in connected components. Experimentally, it seems that critical points of a mdm function form clusters much like the critical components that appear in the smooth setting (Allili et al. 2019).
In this section, we propose a way to partition the critical simplices of a mdm function as introduced in Sect. 4 in order to define such critical components in the discrete setting. Moreover, we establish acyclicity conditions under which this partition induces a Morse decomposition introduced in Sect. 3 and studied further in Sect. 5. That enables us to extend results on the Poincaré polynomial and Morse inequalities to our acyclic mdm function setting in Theorem 7.8. This result complements the theoretical goals of Allili et al. (2019) which provided the main motivation for our work.
7.1 Partitioning the critical points
Let \(f:K\rightarrow {\mathbb R}^k\) be mdm and consider \(\mathcal {C}\), the set of critical points of f. Since, in the smooth setting, the critical components of either multiple Morse functions or a vector-valued function are the connected components formed by the critical points, we could simply define the critical components of f as the connected components of \(\mathcal {C}\). However, it seems that the topological connectedness is neither a necessary nor a sufficient criteria to define the critical components of f. Indeed, we can see in (Allili et al. 2019) that, in practice, the clusters formed by critical simplices are not necessarily connected. Also, Example 7.1 shows that \(\mathcal {C}\) may be connected even though we could expect f to have multiple critical components.
Example 7.1
Consider the inclusion map \(\iota :S^1\hookrightarrow {\mathbb R}^2\) and the mdm function \(f:K\rightarrow {\mathbb R}^2\) defined as in Fig. 15b. We see that f is a discretization of \(\iota \), in the sense that every vertex \(v\in K\) is a point of \(S^1\) and \(f(v)=\iota (v)\). Moreover, we could show that the set of points in \(S^1\) which are critical for \(\iota \) is the one in red in Fig. 15a. This is the Pareto set of \(\iota \), which we will discuss below. Here, the Pareto set clearly has two connected components. However, the critical points of f are all connected.
We consider another approach to partition \(\mathcal {C}\). We still want the critical simplices in a same component to be connected in some way, but it should not necessarily be topologically. Hence, we consider the dynamical connections between the critical simplices, meaning that we consider \(\sigma ,\tau \in \mathcal {C}\) to be neighbors if either \(\sigma \rightarrowtriangle _{f}\tau \) or  .
.
Moreover, in (Allili et al. 2019), where mdm functions were first introduced, an algorithm to generate gradient fields was developed and it was noticed that the sets of critical simplices found computationally resembled Pareto sets, which were studied in the setting of smooth Morse theory (Smale 1975; Wan 1975). Since the concepts of Pareto sets and optima are widely used in the literature, many different variants exist: here, for a smooth vector-valued function \(g:M\rightarrow {\mathbb R}^k\), we see a local Pareto optimum as a point \(x\in M\) such that for all y in a small enough neighborhood of x, we have \(g_i(y) \le g_i(x)\) for at least one \(i=1,\ldots ,k\).
Following this idea, for a mdm function \(f:K\rightarrow {\mathbb R}^k\), we could require that for two neighboring (i.e. dynamically connected) critical simplices \(\sigma ,\tau \in \mathcal {C}\) to belong in the same component, they should be such that \(f_i(\sigma )\le f_i(\tau )\) and \(f_j(\sigma )\ge f_j(\tau )\) for some \(i,j=1,\ldots ,k\). Since, from Corollary 5.9, \(\sigma \rightarrowtriangle _{f}\tau \) implies that \(f(\sigma )\succneqq f(\tau )\), it follows that \(f_j(\sigma )\ge f_j(\tau )\) is trivial and \(f_i(\sigma )\le f_i(\tau )\) implies \(f_i(\sigma ) = f_i(\tau )\). Similarly,  implies that \(f(\sigma )\precneqq f(\tau )\), so in this case \(f_i(\sigma )\le f_i(\tau )\) is trivially true and \(f_j(\sigma ) = f_j(\tau )\). This leads to the following relation.
implies that \(f(\sigma )\precneqq f(\tau )\), so in this case \(f_i(\sigma )\le f_i(\tau )\) is trivially true and \(f_j(\sigma ) = f_j(\tau )\). This leads to the following relation.
Proposition 7.2
Let \(f:K\rightarrow {\mathbb R}^k\) be mdm and consider \(\mathcal {C}\), the set of critical points of f. Consider the relation R defined on \(\mathcal {C}\) as follows:

The transitive closure of R is an equivalence relation.
Proof
We easily see that R is both reflexive and symmetric, which makes it straightforward to verify that its transitive closure is an equivalence relation. \(\square \)
Definition 7.3
(Critical components) A critical component of a mdm function \(f:K\rightarrow {\mathbb R}^k\) is a class of the equivalence relation on \(\mathcal {C}\) defined in Proposition 7.2, which we note \(\sim \). We use the standards notations regarding equivalence relations, meaning that the partition of \(\mathcal {C}\) in critical components is \(\mathcal {C}/{\sim }\) and the critical component in which some \(\sigma \in \mathcal {C}\) belongs is \([\sigma ]\in \mathcal {C}/{\sim }\).
Here are a few interesting consequences of Definition 7.3. First, for \(k=1\), so when \(f:K\rightarrow {\mathbb R}\) is discrete Morse, \(\sigma \sim \tau \) if and only if \(\sigma = \tau \). Indeed, when \(\sigma ,\tau \in \mathcal {C}\) are such that \(\sigma \ne \tau \) and \(\sigma \rightarrowtriangle _{f}\tau \), we know from Corollary 5.9 that \(f(\sigma )>f(\tau )\), and we deduce that \(\sigma \not \sim \tau \). Hence, the critical components defined by \(\sim \) are just the isolated critical points. This agrees with the original smooth and discrete Morse theories.
Furthermore, using \(\sim \), it is possible for \(\mathcal {C}/{\sim }\) to have multiple components even if \(\mathcal {C}\) is connected, as shown in Example 7.4(a). Moreover, it is possible to find critical components which are not necessarily connected, as in Example 7.4(c).
In (a), the two critical components of \(\iota :S^1\rightarrow {\mathbb R}^2\) are shown in red and orange. In (b), the corresponding critical components of the mdm function discretizing \(\iota \) from Fig. 15b (color figure online)
Example 7.4
Each mdm function below has two distinct critical components, which are colored in red and orange.
-
((a))
In Fig. 16, we see the components of the mdm function considered in Example 7.1.
-
((b))
In Fig. 17, we have a mdm function \(f:K\rightarrow {\mathbb R}^2\) such that for each vertex \(v\in K\), \(f(v)=\iota (v)\) where \(\iota :S^1\hookrightarrow {\mathbb R}^2\) is the inclusion on the circle and, for each edge \(\sigma =\{v_1,v_2\}\), \(f(\sigma ) = \left( \max \{f_1(v_1),f_1(v_2)\},\max \{ f_2(v_1),f_2(v_2)\}\right) \).
-
((c))
We have in Fig. 18 the same mdm function that was considered in Example 6.8. Notice that the orange critical component is disconnected.
-
((d))
The function in Fig. 19 is mdm. Notice that there is a connection going from the red component to the orange one and vice versa.
The gradient field and critical components, in red and orange the mdm function from Example 7.4(b) (color figure online)
Critical components, in red and orange, of the mdm function from Example 6.8. Note that the red component contains only the critical vertex in the lower left part of the complex (color figure online)
7.2 Acyclicity of a mdm function
This last example shows that the suggested definition of critical components is not sufficient to induce a Morse decomposition for any mdm function \(f:K\rightarrow {\mathbb R}^k\). Indeed, if \(\mathcal {C}\) is the set of critical points of f, we know that \(\mathcal {M}=\{\{\sigma \}\in \mathcal {C}\}\) is a Morse decomposition of \(\Pi _f\) by Proposition 5.3 but, from Theorem 3.24, \(\mathcal {M}'=\left\{ M([\sigma ])\ |\ [\sigma ]\in \mathcal {C}/{\sim }\right\} \) is only a Morse decomposition when there exists no \(\mathcal {M}'\)-cycle.
Using Theorem 3.24, we establish here some necessary and sufficient conditions for the critical components to induce a Morse decomposition. To do so, we first characterize a \(\mathcal {M}'\)-cycle in terms of a mdm function f. This characterization follows directly from Proposition 3.25.
Proposition 7.5
Let \(f:K\rightarrow {\mathbb R}^k\) be mdm, \(\mathcal {C}\) be the set of critical points of f. Consider the collection
A sequence \([\sigma _0],[\sigma _1],\ldots ,[\sigma _n]\in \mathcal {C}/{\sim }\) is a \(\mathcal {M}\)-path if and only if there exists a sequence \(\tau _0',\tau _1,\tau _1',\tau _2,\tau _2',\ldots ,\tau _{n-1}',\tau _n\in \mathcal {C}\) such that
-
\(\tau _0'\in [\sigma _0]\), \(\tau _i,\tau _i'\in [\sigma _i]\) for each \(i=1,\ldots ,n-1\) and \(\tau _n\in [\sigma _n]\);
-
\(\tau _{i-1}'\rightarrowtriangle _{f}\tau _i\) for each \(i=1,\ldots ,n\).
Moreover, \([\sigma _0],[\sigma _1],\ldots ,[\sigma _n]\in \mathcal {C}/{\sim }\) is a \(\mathcal {M}\)-cycle iff there exists such a sequence \(\tau _0',\tau _1,\tau _1',\tau _2,\tau _2',\ldots ,\tau _{n-1}',\tau _n\in \mathcal {C}\) and \([\sigma _0]=[\sigma _n]\).
This leads to the following definition.
Definition 7.6
(f-cycle) Let \(f:K\rightarrow {\mathbb R}^k\) be mdm. A f-cycle is a sequence of critical components \([\sigma _0],[\sigma _1],\ldots ,[\sigma _n]=[\sigma _0]\in \mathcal {C}/{\sim }\) such that, for each \(i=1,\ldots ,n\), there exists some \(\tau '\sim \sigma _{i-1}\) and \(\tau \sim \sigma _i\) such that \(\tau '\rightarrowtriangle _{f}\tau \). We say that f is acyclic if there exists no f-cycle.
The next theorem is a direct consequence of Theorem 3.24 and Proposition 7.5.
Theorem 7.7
Let \(f:K\rightarrow {\mathbb R}^k\) be mdm. The collection
is a Morse decomposition if and only if f is acyclic.
Thus, when a mdm function is acyclic, its critical components induce another set of Morse equation and inequalities. This follows from Proposition 3.11 and Corollary 3.12.
Theorem 7.8
Let \(f:K\rightarrow {\mathbb R}^k\) be mdm with \(\dim K=n\) and
where \(\beta _p(M([\sigma ]))\) is the \(p^\text {th}\) Conley coefficient of \(M([\sigma ])\). If f is acyclic, then
for some polynomial Q(t) with non-negative coefficients. Thus, for all \(p=0,1,\ldots ,n\), we have
-
(1)
strong Morse inequalities:
$$\begin{aligned} m_p - m_{p-1} + \cdots + (-1)^p m_0 \ge \beta _p(K) - \beta _{p-1}(K) + \cdots (-1)^p \beta _0(K); \end{aligned}$$ -
(2)
weak Morse inequalities:
$$\begin{aligned} m_p \ge \beta _p(K); \end{aligned}$$ -
(3)
an alternative expression for the Euler characteristic \(\chi (K)\) of K:
$$\begin{aligned} m_0 - m_1 + \cdots (-1)^n m_n = \beta _0(K) - \beta _1(K) + \cdots (-1)^n \beta _n(K) = \chi (K). \end{aligned}$$
Theorem 7.8 is analogous to Theorem 6.2 in (Wan 1975). In this work, the author studies the singularities of smooth functions \(f:M\rightarrow {\mathbb R}^2\) on a manifold M and, in order to prove the existence of Morse inequalities relating the homology of M to the critical components of f, a no cycle property needs to be introduced.
This suggests the acyclicity of a vector-valued Morse function, whether it is discrete or smooth, is an essential property to establish Morse inequalities using the set of critical components of the function. Nonetheless, similar results could seemingly be found using the concept of persistence paths studied by Budney and Kaczynski (2023) without assuming acyclicity.
8 Conclusion and future work
The main achievement of this paper is the use of the framework of combinatorial vector fields and topological dynamics to provide a more complete definition of the multidimensional discrete Morse function (mdm) and the study of its properties. Building on preliminary results in (Allili et al. 2019) and based on the new framework, a reformulation of the definition of the mdm has allowed to establish key properties such as the handle decomposition and collapsing theorems and more importantly results on Morse inequalities and Morse decompositions. Moreover, a method of classification of critical cells of mdm functions into critical components is proposed and conditions for obtaining Morse decompositions and Morse inequalities taking into account the critical components are specified.
The results above suggest the possibility of undertaking future works in the following directions.
First, even though we only defined the mdm theory for simplicial complexes, it would be of interest to extend it to more general complexes or spaces. In particular, many of the results on combinatorial flows used in this article generalize to finite \(T_0\)-spaces (Lipiński et al. 2023), which are strongly related to simplicial complexes (McCord 1966; Stong 1966), thus suggesting the mdm theory itself could be extended to those spaces.
Furthermore, the notion of persistence paths, as studied by Budney and Kaczynski (2023), could also be defined in our context and potentially lead to both theoretical and practical results. On the one hand, we could link the critical components of a mdm function f to the homology of its domain without presuming the acyclicity of f as in Theorem 7.8. On the other hand, this could be used to find an alternative method to simplify the computation of multipersistent homology.
Experimental results validating this approach are a work in progress.
References
Allili, M., Kaczynski, T., Landi, C.: Reducing complexes in multidimensional persistent homology theory. J. Symb. Comput. 78, 61–75 (2017). https://doi.org/10.1016/j.jsc.2015.11.020
Allili, M., Kaczynski, T., Landi, C., Masoni, F.: Acyclic partial matchings for multidimensional persistence: algorithm and combinatorial interpretation. J. Math. Imaging Vis. 61(2), 174–192 (2019). https://doi.org/10.1007/s10851-018-0843-8
Banchoff, T.: Critical points and curvature for embedded polyhedra. J. Differ. Geom. 1(3–4), 245–256 (1967). https://doi.org/10.4310/jdg/1214428092
Batko, B., Kaczynski, T., Mrozek, M., Wanner, T.: Linking combinatorial and classical dynamics: Conley index and Morse decompositions. Found. Comput. Math. 20(5), 967–1012 (2020). https://doi.org/10.1007/s10208-020-09444-1
Bloch, E.D.: Polyhedral representation of discrete Morse functions. Discrete Math. 313(12), 1342–1348 (2013). https://doi.org/10.1016/j.disc.2013.02.020
Bubenik, P.: Statistical topological data analysis using persistence landscapes. J. Mach. Learn. Res. 16(3), 77–102 (2015)
Budney, R., Kaczynski, T.: Bifiltrations and persistence paths for 2-Morse functions. Algebr. Geom. Topol. 23(6), 2895–2924 (2023). https://doi.org/10.2140/agt.2023.23.2895
Carlsson, G., Singh, G., Zomorodian, A.: Computing multidimensional persistence. J. Comput. Geom. 1(1), 72–100 (2010). https://doi.org/10.20382/jocg.v1i1a6
Carlsson, G., Zomorodian, A.: The theory of multidimensional persistence. Discrete Comput. Geom. 42(1), 71–93 (2009). https://doi.org/10.1145/1247069.1247105
Conley, C.: Isolated invariant sets and the Morse index. Number 38 in CBMS Regional Conference Series in Mathematics, American Mathematical Society, Providence, Rhode Island (1978). https://doi.org/10.1090/cbms/038
Desjardins Côté, D.: Les systèmes dynamiques combinatoires. Master’s thesis, Université de Sherbrooke, Canada (2020). https://hdl.handle.net/11143/16458
Edelsbrunner, H., Harer, J.: Jacobi Sets of Multiple Morse Functions, volume 312 of London Mathematical Society Lecture Note, chapter 2. Cambridge University Press (2004), pp. 37–57. https://doi.org/10.1017/CBO9781139106962.003
Edelsbrunner, H., Harer, J., Patel, A.K.: Reeb spaces of piecewise linear mappings. In: SCG ’08: Proceedings of the Twenty-Fourth Annual Symposium on Computational Geometry (2008), pp. 242–250. https://doi.org/10.1145/1377676.1377720
Edelsbrunner, H., Letscher, D., Zomorodian, A.: Topological persistence and simplification. Discrete Comput. Geom. 28, 511–533 (2002). https://doi.org/10.1109/SFCS.2000.892133
Forman, R.: Morse theory for cell complexes. Adv. Math. 134(1), 90–145 (1998). https://doi.org/10.1006/aima.1997.1650
Forman, R.: A user’s guide to discrete Morse theory. Séminaire Lotharingien de Combinatoire, 48(B48c) (2002). https://www.mat.univie.ac.at/~slc/wpapers/s48forman.html
Fugacci, U., Landi, C., Varlı, H.: Critical sets of PL and discrete Morse theory: a correspondence. Comput. Graph. 90, 43–50 (2020). https://doi.org/10.1016/j.cag.2020.05.020
Grunert, R., Kühnel, W., Rote, G.: PL Morse theory in low dimensions. Adv. Geom. 23(1), 135–150 (2023). https://doi.org/10.1515/advgeom-2022-0027
Huettenberger, L., Heine, C., Garth, C.: Decomposition and simplification of multivariate data using Pareto sets. IEEE Trans. Vis. Comput. Graph. 20(12), 2684–2693 (2014). https://doi.org/10.1109/TVCG.2014.2346447
Kaczynski, T., Mrozek, M., Wanner, T.: Towards a formal tie between combinatorial and classical vector field dynamics. J. Comput. Dyn. 3(1), 17–50 (2016). https://doi.org/10.3934/jcd.2016002
Lesnick, M., Wright, M.: Interactive visualization of 2-D persistence modules (2015). https://doi.org/10.48550/arXiv.1512.00180
Lipiński, M., Kubica, J., Mrozek, M., Wanner, T.: Conley-Morse-Forman theory for generalized combinatorial multivector fields on finite topological spaces. J. Appl. Comput. Topol. 7(2), 139–184 (2023). https://doi.org/10.1007/s41468-022-00102-9
McCord, M.C.: Singular homology groups and homotopy groups of finite topological spaces. Duke Math. J. 33(3), 465–474 (1966). https://doi.org/10.1215/S0012-7094-66-03352-7
Mrozek, M.: Conley-Morse-Forman theory for combinatorial multivector fields on Lefschetz complexes. Found. Comput. Math. 17(6), 1585–1633 (2017). https://doi.org/10.1007/s10208-016-9330-z
Scaramuccia, S., Iuricich, F., De Floriani, L., Landi, C.: Computing multiparameter persistent homology through a discrete Morse-based approach. Comput. Geom. 89, 101623 (2020). https://doi.org/10.1016/j.comgeo.2020.101623
Scoville, N.A.: Discrete Morse Theory, volume 90 of Student mathematical library. American Mathematical Society, Providence, Rhode Island (2019), ISBN 9781470453794
Smale, S.: Global analysis and economics: Pareto optimum and a generalization of Morse theory. Synthese 31(2), 345–358 (1975). https://doi.org/10.1007/BF00485983
Stong, R.E.: Finite topological spaces. Trans. Am. Math. Soc. 123(2), 325–340 (1966). https://doi.org/10.2307/1994660
Vipond, O.: Multiparameter persistence landscapes. J. Mach. Learn. Res. 21(61), 1–38 (2020)
Vipond, O., Bull, J.A., Macklin, P.S., Tillmann, U., Pugh, C.W., Byrne, H.M., Harrington, H.A.: Multiparameter persistent homology landscapes identify immune cell spatial patterns in tumors. Proc. Natl. Acad. Sci. 118(41), e2102166118 (2021). https://doi.org/10.1073/pnas.2102166118
Wan, Y.-H.: Morse theory for two functions. Topology 14(3), 217–228 (1975). https://doi.org/10.1016/0040-9383(75)90002-6
Xia, K., Wei, G.-W.: Multidimensional persistence in biomolecular data. J. Comput. Chem. 36(20), 1502–1520 (2015). https://doi.org/10.1002/jcc.23953
Funding
Guillaume Brouillette was supported by the Natural Sciences and Engineering Council of Canada (NSERC) under grant number 569623 and the Fonds de recherche du Québec – Nature et technologies (FRQNT) under grant number 289126. Tomasz Kaczynski was supported by a Discovery Grant from the NSERC.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
On behalf of all authors, the corresponding author states that there is no Conflict of interest. Apart from the funding above, the authors have no relevant financial or non-financial interests to disclose.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Brouillette, G., Allili, M. & Kaczynski, T. Multiparameter discrete Morse theory. J Appl. and Comput. Topology (2024). https://doi.org/10.1007/s41468-024-00176-7
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s41468-024-00176-7
Keywords
- Discrete Morse theory
- Multiparameter persistent homology
- Discrete gradient field
- Combinatorial dynamics
- Morse decomposition
- Singularity theory



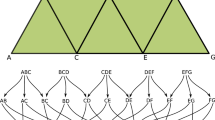










 , which would contradict the acyclicity of
, which would contradict the acyclicity of 
 by definition of A. Thus,
by definition of A. Thus,  , then
, then 







