1 Introduction

Linear accelerators (linacs) have been investigated for many applications. The design of linear accelerators potentially benefits from the use of X-band high-gradient accelerating structures to shorten the accelerator design [1]. Normal-conducting X-band technologies have been developed for future lepton linear collider projects over the several past decades [2,3,4]. Recent experiments have demonstrated that a gradient of 100 MV/m is achievable for X-band structures with a radio frequency (RF) breakdown rate of less than 10−5/pulse/m [5,6,7].

The power consumption is proportional to the square of the accelerating gradient. High-gradient accelerating structures consequently require more input power and increased investment in RF power sources. The RF pulse compressor alleviates the need for power source investments [8]. It converts the long pulse from the power generator to a short pulse with a higher power level. In several applications, such as the free electron laser (FEL) [9] and the Thomson scattering source [10], the linacs are operated in single-bunch mode and require a short pulse length. Therefore, the use of a RF pulse compressor is preferable in these single-bunch applications.

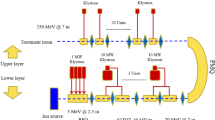
The present work is motivated by the design and optimization of such a X-band (11.424 GHz) linac with a SLED-I type pulse compressor. This X-band linac will be used in the injector of the Tsinghua Thomson scattering X-ray (TTX) facility [11]. It will boost the electron beam from the current 50 meV to 150 meV, as shown in Fig. 1.

Fig. 1
figure 1

Layout of TTX facility

Full size image

Given the space limitation in the bunker, the active length of this X-band structure should not be greater than 1.3 m, and a gradient of 80 MV/m is required. Such a X-band structure demands a RF input power greater than 120 MW. The RF pulse compressor has a power gain of more than 3, so a 50 MW X-band klystron suffices as the power supply. The RF pulse compressor used in this work was obtained from Ref.[12] and is a SLED-I type compressor with a compact and easily operated design. The compressed RF pulse shape is not flat, i.e., the power varies over time, as shown in Fig. 2. The facility is operated in single-bunch mode, and the electron bunch will be accelerated at the maximum voltage point in every RF pulse. However, the time-varying RF power travels through the structure at a limited speed (group velocity); thus, the upstream and downstream cells in the structure experience different input powers, thereby changing the distribution of the gradient. Detailed discussions will be presented in Sect. 2.

Fig. 2
figure 2

Schematic diagram of the RF pulse shape before and after the compressor

Full size image

The geometry of the X-band structure is optimized in this work to minimize the RF power required from the generator. This optimization is important in the TTX facility for 2 reasons: the klystron is more stable at lower power levels, and the spare power can be used to operate other X-band devices such as a RF photocathode gun [13], a deflecting cavity [14, 15], or a linearizer [16]. Section 3 analytically explores the optimum solution for the accelerating structure. The study shows that the compressed RF pulse results in a near-optimum solution for the constant-impedance structure. The constant-impedance structure uses an identical structure geometry for each regular cell. It is more easily fabricated than the common traveling wave (TW) structure with varying iris apertures. The study in Sect. 3 demonstrates that a constant-impedance structure is favorable for the linac design if a SLED-I type RF pulse compressor is used. The concept of utilizing a constant-impedance structure as a near-optimum solution was also presented in Ref.[17].

We implemented this concept to develop the RF design of the X-band linac in the TTX facility, which uses a constant-impedance structure as the nominal accelerating structure design. Another design using varying iris apertures is also discussed and compared with the nominal design. Further details will be presented in Sect. 4. The study in this work will be useful for designing linacs operated in single-bunch mode for other similar applications [18,19,20], such as X-band FEL sources [21,22,23,24,25,26,27] and Thomson sources [28]. In the two-beam acceleration scheme, the RF pulse generated by the drive beam delivered in single-bunch mode [29,30,31,32] has a shape similar to that produced by the SLED-I type RF pulse compressor. The discussion in this work is hence also helpful in studying two-beam acceleration.

2 Compressed RF pulse in the TW structure

The principle of the SLED-I type RF pulse compressor is described in Ref.[8]. The pulse shape of the compressed output RF power (dashed line in Fig. 2) can be expressed by the following formulas:

$$P(t) = P_{0} ((A - \Gamma ){\text{e}}^{ - \mu t} + \Gamma )^{2},$$
(1)
$$\mu = \omega \frac{1 + \beta }{2Q_{\text{s}}},$$
(2)
$$\Gamma = \frac{1 - \beta }{1 + \beta },$$
(3)

where t is the time from the peak power point, P0 is the klystron input power, A is the field amplitude at the peak power point, ω is the angular frequency, and β and Qs are the coupling and quality factors of the storage cavity, respectively. The power gain factor A2 is determined by the shape of the filling pulse and the time of the phase switching (see Fig. 2). In the ideal case, where the filling pulse is rectangular-shaped with a length of Tp and the phase is switched instantaneously, A can be analytically expressed as:

$$A = \Gamma + \frac{2\beta }{1 + \beta }(2 - {\text{e}}^{ - \mu T_{p}} ).$$
(4)

Figure 3a shows that the compressed RF power flows from the upstream cells to successive downstream cells in the X-band structure at a speed equal to the group velocity of the structure. The maximum accelerating voltage is achieved when the wave front of the peak RF power and the electron bunch arrive simultaneously at the end of structure, as shown in Fig. 3b.

Fig. 3
figure 3

a Power flow in the traveling wave structure at different times; b Accelerating voltage of the structure versus time

Full size image

The wall loss in the structure attenuates the RF power traveling within it. The RF power versus the longitudinal position z and the time t are expressed in the formulas below:

$$P(z,t) = P(0,t - T(z)){\text{e}}^{ - \alpha (z)},$$
(5)
$$T(z) = \int_{0}^{z} {\frac{{\text{d}}s}{{v}_{\text{g}}}},$$
(6)
$$\alpha (z) = \int_{0}^{z} {\frac{\omega }{Q{v}_{\text{g}}}}{\text{d}}s,$$
(7)

where T(z) is the filling time, α(z) is the attenuation factor, vg is the group velocity, and Q is the quality factor. The detailed derivation of Eqs. (5–7) is shown in Refs.[33, 34]. Assuming that the electron bunch passes through the structure at the speed of light, the gradient of each cell is expressed as:

$$ G(z) = G \left(z,t_{0} + \frac{z}{c} \right) = \sqrt {\omega \frac{R}{Q}\frac{{P \left(z,t_{0} + \frac{z}{c} \right)}}{{{\text{v}}_{g} }}}, $$
(8)

where R is the shunt impedance per unit length and t0 is the time point at which the beam enters the inlet of the structure.

To obtain the maximum voltage, the peak RF power and the electron bunch should arrive at the end of the structure simultaneously, such that

$$t_{0} + \frac{L}{c} = T(L) = T_{\text{f}},$$
(9)

where L is the length of one structure unit and Tf is the filling time. From Eqs. (1), (5), and (8), the gradient as a function of z can be given as:

$$\begin{gathered} G(z) = \sqrt {\omega \frac{R}{Q}\frac{{P\left(z,T(L) - \frac{L}{c} + \frac{z}{c}\right)}}{{{{v}}_\text{g} }}} \\ = \sqrt {\omega \frac{R}{Q}\frac{{P\left(0,T(L) - T(z) - \frac{L}{c} + \frac{z}{c}\right){\text{e}}^{ - \alpha (z)} }}{{{{v}}_{\text{g}} }}} \\ = \sqrt {\omega \frac{R}{Q}\frac{{P_{0} {\text{e}}^{ - \alpha (z)} }}{{{{v}}_{\text{g}} }}} F, \\ \end{gathered}$$
(10)
$$F = (A - \Gamma ){\text{e}}^{{ - \mu \left(T(L) - \frac{L}{c}\right) + \mu \left(T(z) - \frac{z}{c}\right)}} + \Gamma,$$
(11)

where the coefficient F represents the gradient gain due to the RF pulse compressor. According to Eqs. (1) and (4), A > Γ; thus, F is an increasing function of z. Figure 4 shows an example of the gradient distribution with and without the RF pulse compressor.

Fig. 4
figure 4

Change of distribution gradient by the RF pulse compressor

Full size image

3 Analytical optimization of the gradient distribution

This section explores the optimum solution that minimizes the input power for a given gradient. This optimization is equivalent to maximizing the effective shunt impedance Reff of the whole system [17], which is defined by the ratio of the average gradient \(\overline{G}\) and the required input power from the klystron:

$$R_{{{\text{eff}}}} = \frac{{\overline{G}^{2} L}}{{P_{0} }},$$
(12)
$$\overline{G} = \frac{1}{L}\int_{0}^{L} {G(z){\text{d}}z}.$$
(13)

For large accelerator projects such as linear colliders, the AC power consumption is significant. Thus, the optimization of these applications should also consider additional parameters such as the RF pulse length and the beam current. The study in this work will focus on maximizing Reff because the investment in the power sources is much more expensive than the electricity in our application.

Equation (8) indicates that the gradient is calculated from R, Q, and vg. Traveling wave accelerating structures usually have iris apertures that are tapered from the upstream cells to the downstream cells. The tapering results in the variation of vg from cell to cell, but the variations of R and Q are insignificant compared to that of vg. R and Q are assumed to be constant functions of z in this section. In this case, the distribution of the gradient is determined by vg = vg(z), which needs to be solved in the design work of the accelerating structure. If a RF pulse compressor is not used (F in Eq. (10) is 1), the integral of the square of the gradient can be written in a simple form:

$$\begin{gathered} \left\| {G(z)} \right\|^{2} = \frac{1}{L}\int_{0}^{L} {G^{2} (z){\text{d}}z} = \int_{0}^{L} {\frac{{P_{0} R\omega }}{{LQ{{v}}_\text{g} }}{\text{e}}^{ - \alpha (z)} {\text{d}}z} \\ = \int_{0}^{L} {\frac{{P_{0} }}{L}{{Re}}^{ - \alpha (z)} {\text{d}}\alpha (z)} = \frac{{P_{0} }}{L}R\left(1 - {\text{e}}^{ - \alpha (L)} \right) ,\\ \end{gathered}$$
(14)

From Eqs. (6) and (7), α(L) is equal to ωTf/Q. For a given P0, R, and Tf, the right side of Eq. (14) has a constant value regardless of the form of vg(z). In the calculus of variations, G(z) is an element or vector in a Banach space. Equation (14) provides the Euclidean norm of G(z). According to the Cauchy–Schwarz inequality \(\overline{G} = \left\langle {G(z),1} \right\rangle \le \left\| {G(z)} \right\|\left\| 1 \right\| = \left\| {G(z)} \right\|\). From Eqs. (12) and (14), we have

$$R_{{{\text{eff}}}} = \frac{{\overline{G}^{2} L}}{{P_{0} }} \le \frac{{\left\| {G(z)} \right\|^{2} L}}{{P_{0} }} = R\left( {1 - {\text{e}}^{{ - \frac{\omega }{Q}{{T}}_\text{f} }} } \right).$$
(15)

The two sides of Eq. 15 are equal when G(z) is equal to 1, which means that Reff reaches its maximum when G(z) is a constant function. This indicates that the optimum solution is a constant-gradient structure. From Eq. (14), \({\text{e}}^{ - \alpha \left( z \right)}\) should be a linear function of z. The form of vg(z) is given by the following equation, which is also a linear function of z:

$${{v}}_{\text{g}} (z) = \frac{\omega }{{Q\frac{{{\text{d}}\alpha (z)}}{{{\text{d}}z}}}} = \frac{\omega }{Q}\left( {\frac{L}{{1 - {\text{e}}^{{ - \frac{\omega }{Q}T_{\text{f}} }} }} - z} \right),$$
(16)

If the RF pulse compressor is used, then Eq. (15) can be rewritten as:

$$\begin{gathered} R_{{{\text{eff}}}} \le \frac{{\left\| {G(z)} \right\|^{2} L}}{{P_{0} }} = \int_{0}^{L} {\frac{R\omega }{{Q{{v}}_{\text{g}} }}{\text{e}}^{ - \alpha (z)} F^{2} (z){\text{d}}z} \\ = R\frac{\omega }{Q}\int_{0}^{{T_{\text{f}} }} {{\text{e}}^{{ - \frac{\omega }{Q}T(z)}} F^{2} (T(z)){\text{d}}T(z)} \\ \end{gathered},$$
(17)

where another assumption was made that the group velocity is much slower than the speed of light, i.e., T(z) = z/vg ≫ z/c; thus, the z/c and L/c terms in Eq. (10) can be ignored. Equation (17) indicates that if the filling time Tf is fixed, then the Euclidean norm of G(z) does not depend on the specific form of vg(z). Therefore, the conclusion remains that the optimum solution is a uniformly distributed gradient when a RF pulse compressor is used. With a constant function as the gradient, vg can be solved as a function of the filling time T(z) based on Eq. (10):

$${{v}}_{\text{g}} (T(z)) = \frac{{\omega RP_{0} {\text{e}}^{{ - \frac{\omega }{Q}T(z)}} }}{{QG^{2} }}F^{2} (T(z)).$$
(18)

One additional term F is included in the equation. It represents the effect of the pulse compressor on the solution of vg. F is an increasing function of T(z) such that the optimum solution of vg decreases more slowly than the solution without the RF pulse compressor. Figure 5 shows the solutions of vg with different parameters of the RF pulse compressor as examples. For a number of parameter sets, the solutions of vg approximate constant functions, as shown in the second and fourth curves in Fig. 5. The constant vg allows all the structure cells to use identical geometries, which is called the constant-impedance structure. Compared to a structure using linearly tapering iris apertures, the constant-impedance structure is significantly easier to fabricate and reduces the total cost of the accelerator.

Fig. 5
figure 5

(Color online) Optimum solution of group velocity vg versus the filling time T(z)

Full size image

However, the constant vg solution requires particular parameters of the RF pulse compressor that are inconsistent with the global optimum for maximizing Reff. The upper limit of Reff given by Eq. (17) can be written as:

$${\text{Max}}(R_{\text{eff}} ) = R\int_{0}^{{\tau_{\text{f}} }} {{\text{e}}^{ - \tau } F^{2} (\tau ){\text{d}}\tau },$$
(19)

where

$$\begin{gathered} \tau = \frac{\omega }{Q}T(z), \\ F(\tau ) = (A - \Gamma ){\text{e}}^{{ - \mu (T_{\text{f}} - \tau )}} + \Gamma = \frac{2\beta }{{1 + \beta }}\left( {2 - {\text{e}}^{{ - \frac{Q(1 + \beta )}{{2Q_{\text{s}} }}\tau_{\text{p}} }} } \right){\text{e}}^{{ - \frac{Q(1 + \beta )}{{2Q_{\text{s}} }}(\tau_{\text{f}} - \tau )}} + \frac{1 - \beta }{{1 + \beta }}, \\ \tau_{\text{f}} = \frac{\omega }{Q}{{T}}_{\text{f}} = \frac{\omega L}{{Q{{v}}_{\text{g}} }} , \\ \tau_{\text{p}} = \frac{\omega }{Q}T_{\text{p}} . \\ \end{gathered}$$
(20)

From Eqs. (10), (12), and (13), the effective shunt impedance of the constant-impedance structure is written as:

$$R_{{{\text{eff}}}}^{*} = \frac{R\omega }{{QL}}\left( {\int_{0}^{L} {\frac{{{\text{e}}^{{ - \frac{\omega z}{{2Qv_{\text{g}} }}}} }}{{\sqrt {{{v}}_{\text{g}} } }}F(z){\text{d}}z} } \right)^{2} = \frac{R}{{\tau_{\text{f}} }}\left( {\int_{0}^{{\tau_{\text{f}} }} {{\text{e}}^{{ - \frac{\tau }{2}}} F(\tau ){\text{d}}\tau } } \right)^{2}.$$
(21)

The expressions of Max(Reff) and \(R_{{{\text{eff}}}}^{*}\) contain 4 parameters: τf, β, Q/Qs, and τp. All 4 parameters are dimensionless parameters, so the discussion here applies for all RF frequencies. The parameter Q/Qs is the ratio of the quality factors in the regular accelerating cavities and the storage cavity of the pulse compressor, and τp represents the length of the filling pulse. These 2 parameters are usually given as numbers. The other 2 parameters τf and β can be optimized for the given τp and Q/Qs. Figure 6 plots 2 effective shunt impedances for different τp and Q/Qs with the optimum τf and β in each case. The discrepancy between Max(Reff) and \(R_{{{\text{eff}}}}^{*}\) is less than 1%, which indicates that the constant-impedance structure performs similarly to the global optimum solution. The optimum τf and β that maximize the effective shunt impedance \(R_{{{\text{eff}}}}^{*}\) of the constant-impedance structure shown in Fig. 6b when the RF pulse compressor is used is presented in Fig. 7.

Fig. 6
figure 6

(Color online) a Max(Reff) and b \(R_{{{\text{eff}}}}^{*}\) versus τp and Q/Qs at the optimum τf and β

Full size image
Fig. 7
figure 7

Optimum a τf and b β for different τp and Q/Qs

Full size image

If the RF pulse compressor is not used, F(τ) in Eqs. (19) and (21) is 1. In this case, the maximum \(R_{{{\text{eff}}}}^{*}\) for the constant-impedance structure is 0.81R when τf = 2.51. The effective shunt impedance Max(Reff) for the constant-gradient structure approximates R if τf is sufficiently large, as shown in Fig. 8. Note that a larger τf results in a longer filling time, which reduces the efficiency from the AC power to the beam. This calculation proves that the RF pulse compressor further optimizes the constant-impedance structure.

Fig. 8
figure 8

Max(Reff) and \(R_{{{\text{eff}}}}^{*}\) versus τf without RF pulse compressor

Full size image

4 RF design of X-band linac for TTX facility

Section 3 analytically explored the optimum RF design of a traveling wave accelerating structure. The analysis was performed with the assumption that R and Q are constant values for all the cells in the structure. However, this assumption leads to inaccuracies if the structure cells have differing geometries. In this section, the RF parameters for 2 designs, namely the optimized constant-impedance structure and the optimized structure using varying iris apertures, are numerically calculated.

The cut view of a traveling wave accelerating structure cell is shown in Fig. 9. The phase advancement per structure cell is 2π/3. The study of short-range wakefields requires the average radius of the iris aperture to not be less than 3.5 mm and the minimum radius to be larger than 3 mm [35, 36]. With this aperture, the average group velocity is approximately 2.3% of the speed of light, and the quality factor Q is approximately 7200. The parameters of the RF pulse compressor in this work are similar to those in Refs.[12, 44]. The quality factor of the storage cavity Qs is approximately 100,000. The total pulse length is approximately 1.5 μs; thus, τp is less than 14. According to Fig. 7a, the optimum τf is approximately 1.2, and thus the optimum filling time is given by Tf = τf Q/ω = 120 ns. The optimum active length of the structure is calculated as vg × Tf ≈ 0.8 m. The required total active length of the X-band structure for the TTX facility is 1.3 m. The structure is hence divided into 2 identical structure units. Each structure unit has 72 structure cells and an active length of 0.63 m. Under these conditions, the optimum Tf is approximately 95 ns, and the optimum τf is approximately 1. These optimum parameters facilitate the RF design of the linac.

Fig. 9
figure 9

Geometric sketch of a single cell

Full size image

In actual operation, the phase switching takes time. This results in the factor A becoming less than the value obtained through the theoretical calculation in Eq. (4). This effect is not considered in this work because it complicates the estimation. The actual required power should be scaled by a factor that considers the phase switching effect as well as the losses in the power transmission system.

The nominal RF design of the linac for TTX uses a constant-impedance structure. The design has three parameters for investigation: the iris thickness d, the ratio of the major radius to the minor radius in the elliptical iris e, and the coupling factor of the pulse compressor storage cavity β. Here, the radius of the iris aperture a is 3.5 mm, and the rounding in the wall R0 is 2.5 mm. We calculated the RF parameters R, Q, and vg of a single cell using the CST code [37]. The total required input power for the 2 structural units was calculated using Eq. (10) for average gradients of 80 MV/m.

Figure 10 plots the RF parameters of the structure versus β. The RF parameters include the required input power from the klystron, the maximum surface electric field Es, and the maximum modified Poynting vector Sc [38] in the structure. The maximum surface fields were calculated from the gradient when the peak of the compressed power propagates in the cell. Figure 10a shows that β for the minimum input power is 5. A larger value of β, however, induces a larger power flow in the upstream of the structure, which consequently increases the maximum surface field Es, and thus, Sc. According to a study on high-power tests of X-band accelerating structures, the RF breakdown rate is lower than 10−5/pulse/m when the structure operates at a pulse length of 100 ns, Es < 200 MV/m, and Sc < 5 MW/mm2 [7, 39]. Finally, β was set to 3.5 considering both the input power and the maximum surface fields. Figure 11 shows the RF parameters versus d and e. The optimum solution is d = 1.8 mm and e = 1.3 for the minimum input power under the condition that the maximum surface fields are below the limit set by the RF breakdown rate. The distributions of the normalized fields in the optimized single cell are shown in Fig. 12.

Fig. 10
figure 10

(Color online) a RF parameters versus β; b Distribution of gradient seen by beam for different β

Full size image
Fig. 11
figure 11

(Color online) a Input power versus d and e; b RF parameters versus e

Full size image
Fig. 12
figure 12

(Color online) The distributions of normalized a electric field and b modified Poynting vector in the single cell

Full size image

Another structure design with varying iris apertures, which often uses linear tapering on the iris apertures, is also discussed here. In this setup, the upstream cells have a large aperture such that the group velocity of these cells is higher than the average. This will reduce the gradient in the upstream cells to decrease the maximum surface fields in the structure. The strategy in this structure design uses the optimum value of β = 5 to minimize the input power, as shown in Fig. 13a. Figure 13b shows the maximum surface fields versus the tapering parameter ∆a, which is the difference between the aperture radii of the first and the last cells. The optimum ∆a for the minimum input power is 0.2 mm, and this ∆a also has a flat gradient distribution as shown in Fig. 14, in agreement with the analytical results in Sect. 3. However, a ∆a of 0.8 mm was finally selected to satisfy the criteria of the maximum surface fields. The optimization of d and e is similar to that of the constant-impedance structure design.

Fig. 13
figure 13

(Color online) a Input power versus β and ∆a; b Maximum surface fields versus ∆a

Full size image
Fig. 14
figure 14

(Color online) Distribution of gradient seen by beam for different ∆a

Full size image

The final parameters of this structure are listed in Table 1 along with the parameters of the constant-impedance structure. Both designs satisfy the criteria of maximum surface fields with a low breakdown rate. The tapering iris aperture design has a slightly lower input power than that of the nominal design using a constant-impedance structure. This phenomenon occurs because the value of β for the nominal design is not optimal with respect to the maximum surface fields.

Table 1 RF parameters of two designs
Full size table

The final design of the constant-impedance structure has a total length of 0.7 m, as shown in Fig. 15. This structure is named as “TTX-XC72”. The input and output couplers are both well matched to the WR90 waveguides with reflections of below −45 dB. The electric field along the beam path is simulated in CST [37] and shown in Fig. 16. The RF design of the SLED-I type RF pulse compressor using a corrugated circular cavity with a coupling coefficient of 3.5 has also been completed, as reported in Ref.[44]. The distribution of the field parameters in the accelerating structure operating with the compressed pulse is calculated analytically based on the parameters Q, R, vg, and β listed in Table 1 and presented in Fig. 17.

Fig. 15
figure 15

Assembly of the constant-impedance accelerating structure for the TTX facility

Full size image
Fig. 16
figure 16

Magnitude of electric field along the beam path at 1 W input power

Full size image
Fig. 17
figure 17

Distribution of field parameters for 80 MV/m gradient along the structure under the compressed pulse

Full size image

The modulation of the output pulse shape of the SLED-I pulse compressor to reduce the peak output power for lower surface fields while retaining the same average output power (the gradient is the same) will be considered in future studies. Two ways of modulating the output pulse shape using correction cavities [40,41,42] or the phase modulating SLED mode [43] will be studied for this application.

In conclusion, the constant-impedance structure design with its advantage of much easier fabrication is preferable for upgrades of the TTX facility. A structure prototype based on this constant-impedance structure design will be manufactured and tested in the near future.

5 Conclusion

The RF design of a X-band linac for the TTX source facility was discussed in this work. The linac was designed to boost the energy of the electron beam in the TTX facility from 50 to 150 meV. A SLED-I type RF pulse compressor is used to increase the obtained peak power such that a single 50 MW X-band klystron can support the operation of this structure at a gradient of 80 MV/m. The compressed RF pulse has an unflattened pulse shape, which changes the gradient distribution along the structure cells. The study showed that the gradients in the downstream cells increase more significantly than the gradients in the upstream cells.

The structure was optimized with the aim of reducing the required input power from the power source, so that the power source can operate more stably and provide spare power to feed other X-band devices. The analytical work proved that the optimum solution is a uniform distribution of the accelerating gradient. If the input RF pulse is flat, then the optimum solution is a constant-gradient structure. However, because the SLED-I type RF pulse compressor changes the RF shape, the constant-impedance structure is a near-optimum solution.

Two designs, a nominal design using the constant-impedance structure and a structure with varying iris apertures, were optimized in this work. Both designs have similar input power requirements and satisfy the criteria of generating the maximum surface field at a low breakdown rate. The constant-impedance structure design is more easily fabricated and therefore favorable for the X-band linac of the TTX facility.