1 Introduction

A 2-DoF hybrid robotic arm is developed based on a planar hybrid mechanism in Ref. (Liu et al. 2015). In industry, robots based on parallel or hybrid mechanisms have been widely used because of their advantages like low inertia, high stiffness and quick dynamic response (Xie et al. 2015; Bi et al. 2019). Many efforts have also been devoted to their theoretical analysis as well (Luo et al. 2019; Chen et al. 2015). In the development of a hybrid robot, the structure influences the performance greatly from the aspect of stiffness, inertia, dynamic performance, and etc. (Jin et al. 2018). Since the robotic arm has time-varying kinematic configurations and joint forces during its motion, optimization for a single load case or several load cases cannot guarantee global validity. In addition, the computational expense is normally high for the optimization of a hybrid robotic arm, how to reduce computational time is still challenging (Wang et al. 2019). Therefore, the topology optimization of the 2-DoF hybrid robotic arm with global validity and high computational efficiency is worth investigating.

Since time-varying configurations influence the load cases of each link in the workspace, the topology optimization of the robotic arm is more complicated than topology optimization of structures under static or vibrating loads (Smyl 2018). Early studies mainly optimize the structure of robotic arms for a single configuration or load case which cannot guarantee the validity in the whole workspace. Robust topology optimization (RTO) (Ben-Tal and Nemirovski 1997) and reliability based topology optimization (RBTO) (Kharmanda et al. 2004) are representative methods considering uncertainties. Due to the fact that these two methods require iterative calculation of additional function, the computational efficiency is normally unsatisfactory. In efficient topology optimization of the robotic arm, identifying the worst case is an essential step. For linear structural performance functions, the worst case can be identified using the anti-optimization technique (Lombardi and Haftka 1998). However, the identification of the worst-case is not so straightforward for a nonlinear performance and some effective methods have been proposed (Luo et al. 2009). For the topology optimization of the hybrid robotic arm, taking the kinematic characteristics into consideration is an ideal method to improve efficiency. Therefore, the worst case of each link will be identified based on force analysis to realize global validity within allowable computational time in this paper. On the basis of the identified worst case, the topology optimization can be carried out for each link.

The research on continuum-based topology optimization problem construction started with the pioneering works of homogenization method (Bendsøe and Kikuchi 1988). Sequentially, several representative methods like the evolutionary structural optimization (ESO) method (Xie and Steven 1993), the density-based method (Bendsøe 1989), the level set method (Sethian and Wiegmann 2000) and the independent continuous mapping (ICM) method (Sui et al. 2000) are proposed. Among them, the density-based method is widely used because of its generality and easy implementation. In this method, the integer 0–1 variables are replaced by continuous variables ranging from 0 to 1 to simplify the problem. Proper penalty is normally introduced to eliminate elements with intermediate density values, and the penalty method is often called interpolation scheme. Solid isotropic material with penalization (SIMP) method and rational approximation of material properties (RAMP) method (Stolpe and Svanberg 2001) are two typical interpolation schemes. Besides, meshless density variable approximation methods are frequently used in density-based topology optimization as well (Matsui and Terada 2004). In this paper, the SIMP interpolation method, which is a widely used scheme, will be used to construct the optimization problem. Besides, the objective function construction for links with multiple worst cases is essential for global validity, which requires further investigation in this paper.

Normally, the solving strategy of topology optimization can be summarized into three categories including the optimality criteria (OC) methods (Rozvany and Zhou 1991), the mathematical programming (MP) methods (Bruyneel et al. 2002) and the heuristic methods (Silva Smith 1997). In OC methods, certain criteria or optimal conditions in mathematical programming must be derived. OC methods are widely used in engineering because they are not sensitive to the quantity of variables. However, OC methods demand different criteria for different formulations, which limits its generality in topology optimization. MP methods have been applied in different kinds of optimization problems and has shown many advantages such as high accuracy, wide availability, and etc. In order to improve computational efficiency, the approximation technique and dual method are employed to transform the original optimization problem into a separable convex approximate problem. The methods like SLP (Fujii and Kikuchi 2000), SQP (Sedaghati et al. 2000), SCP (Zillober et al. 2004), CONLIN (Fleury and Braibant 1986) and MMA (Svanberg 1987) are commonly used and representative in the realization of this transformation. In general, heuristic methods include Particle Swarm Optimization (PSO) (Luh and Lin 2011), Genetic Algorithm (GA) (Essiet et al. 2019), Differential Evolution Algorithm (DEA) (Panagant and Bureerat 2018), and etc. Heuristic methods have shown great advantages in optimization with strong nonlinearity, however the convergence to the global optimal solution cannot be guaranteed. The guide-weight method was first proposed in the optimal design of antenna structures (Chen and Ye 1984, 1986). Thereafter, the modified guide-weight method is extended into continuum topology optimization and good results have been obtained (Liu et al. 2014; Xu et al. 2013). As mentioned in Ref. Xu et al. (2013), since the required iteration steps of modified guide-weight is normally far less than representative methods, this method will be used to solve the topology optimization in this paper for fast convergence. Normally, the mesh dependence and checkerboard problem influence the optimal topology greatly and there have been a number of research efforts applied to overcome these problems like variant finite element methods (Diaz and Sigmund 1995), constraint methods (Haber et al. 1996) and filtering techniques (Sigmund 2007). In this work, inspired by sensitivity filtering techniques, a guide-weight filtering method will be proposed to cope with these problems in modified guide-weight method.

The remainder of this paper is organized as follow: In Sect. 2, the workspace with good transmissibility is identified through kinematics analysis. Thereafter, the external forces of each link is analyzed in the workspace. On the basis of force analysis, the effect of axial load and shear is evaluated through the equivalent external load. Sequentially, the worst case is identified efficiently by locating the load case with maximum equivalent external load. In Sect. 3, for links with multiple worst cases, the SIMP interpolation scheme is utilized to construct the optimization problem and the objective function is formulated as the weighted sum of compliance under each worst case. Thereafter, the modified guide-weight method is used to solve the problem and a guide weight filtering method is proposed. Lastly, the CAD model of the hybrid robotic arm is presented based on the derived topology. Section 4 concludes the paper.

2 Worst case identification of the 2-DoF hybrid robotic arm

Topology optimization of the hybrid robotic arm aims to derive the topologies of each link with global validity in the workspace. Therefore, efficiently identifying the worst case in the workspace is an essential step. The computational efficiency of existing worst case identification method is normally unsatisfactory. The worst case identification considering the kinematic characteristics and compliance is a possible method and the computational efficiency is expected to be higher. In this section, the workspace with good transmissibility will be identified first. The effect of shear and axial load will be unified from the aspect of compliance, then the worst case with maximum compliance can be located efficiently.

2.1 Kinematic analysis and workspace identification

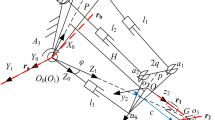
The kinematic scheme of the 2-DoF hybrid robotic arm is shown in Fig. 1a. Link HCE is shared by parallelogram mechanisms CFGH and ODEC. CB and CF are two edges of the triangle link BFC. OABC, ODEC and CFGH share a revolute center at point C. OABC and ODEC share a revolute center at point O. OA is fixed to the base and two coaxial actuating joints are located at point O. When OC and OD are driven, the end-effector can follow an arbitrary curve within the workspace and maintain a definite posture. The angle between OA and the x-axis is defined as \(\beta\). \(\delta\) represents the vertex angle between CF and CB. The lengths of OC, CE and HC are \(R_{1}\), \(L_{2}\) and \(R_{3}\), respectively. \(\theta_{1}\) is the driven angle between OC and the x-axis. \(\theta_{2}\) represents the other driven angle between OD and the x-axis.

Fig. 1
figure 1

The 2-DOF hybrid robotic arm: a kinematic scheme; b GTW and LTI distribution

Full size image

The position of the end-effector (denoted by H) in coordinate system O-xy can be expressed as:

$$\left\{ {\begin{array}{*{20}l} {X_{{\text{H}}} = R_{1} \cos \theta_{1} + R_{3} \cos (\theta_{2} + \varphi )} \hfill \\ {Y_{{\text{H}}} = R_{1} \sin \theta_{1} + R_{3} \sin (\theta_{2} + \varphi )} \hfill \\ \end{array} } \right.$$
(1)

Normally, the transmissibility influences the overall performance of the robotic arm greatly. The local transmission index (LTI) is widely used to evaluate the transmissibility, and its definition is:

$$\kappa {\text{ } = \text{ LTI}} = \min \left\{ {\sin \gamma_{1} ,\sin \varepsilon_{1} ,\sin \gamma_{2} ,\sin \varepsilon_{2} ,\sin \gamma_{3} ,\sin \varepsilon_{3} } \right\}$$
(2)

The driven angles of the robotic arm are defined as \(\theta_{1} \in \left[ {90^\circ ,180^\circ } \right]\), \(\theta_{2} \in \left[ {0^\circ , \, 90^\circ } \right]\) to avoid interference and singularity, and the ranges of the driven angles constitute the driving space of the robotic arm. When the driven angles vary in the driving space, all reachable positions of the end-effector constitute the workspace. In this work, the good transmission workspace (GTW) is defined as the area in which the LTI is large than 0.5. Based on the parameter optimization in Ref. Liu et al. (2015), the optimal parameters are derived as: \(\beta = 45^\circ\), \(\delta = 45^\circ\), \(R_{1} = 1000{\text{mm}}\), \(R_{3} = 1300{\text{mm}}\), \(L_{2} = 400{\text{mm}}\) and \(\varphi = 135^\circ\) by considering transmission and workspace requirement. The identified GTW and distribution of LTI are shown in Fig. 1b.

2.2 Force analysis under external load

The external load \({\mathbf{F}}_{e}\) is the payload, and its axis goes along the direction of link GH. Under this external load, the internal force of link GF can be derived through the equilibrium equation of link GH. Specifically, since the axis of the external load goes along the direction of link GH, the moment of internal force of link GF on joint H should be zero. When robotic arm is in non-singular configuration, the internal force of link GF should be zero. Similarly, the internal force of link AB can be derived as zero through the equilibrium equation of link CFB. Therefore, the internal force of link CFB is zero. The force diagrams of links HCE, OC and OD are shown in Fig. 2. For link HCE, \({\mathbf{F}}_{2i}\) denotes the internal force of link DE; \({\mathbf{F}}_{31x}\) and \({\mathbf{F}}_{31y}\) represent the reaction forces of joint C along the x- and y- axes. The equilibrium equations are derived as shown in Eqs. (3)–(5).

$$\sum {{\mathbf{F}}_{x} } = {\mathbf{F}}_{2i} \cos \theta_{1} - {\mathbf{F}}_{31x} = 0$$
(3)
$$\sum {{\mathbf{F}}_{y} = {\mathbf{F}}_{31y} - {\mathbf{F}}_{2i} } \sin \theta_{1} - {\mathbf{F}}_{e} = 0$$
(4)
$$\sum {{\mathbf{M}}_{C} } = {\mathbf{F}}_{e} R_{3} \cos ({{\pi - }}\varphi { - }\theta_{2} ) - {\mathbf{F}}_{2i} L_{2} \sin \gamma_{1} = 0$$
(5)
Fig. 2
figure 2

Force diagram: a link HCE; b link OC; c link OD

Full size image

Similarly, the equilibrium equations of OC are shown in Eqs. (6)–(8). \({\mathbf{F}}_{13x}\) and \({\mathbf{F}}_{13y}\) are the reaction forces of joint C along the x- and y- axes; \({\mathbf{F}}_{3x}\) and \({\mathbf{F}}_{3y}\) denote the reaction forces of joint O along the x- and y- axes; \({\mathbf{M}}_{3}\) is the driving torque provided by the actuator.

$$\sum {\mathbf{F}}_{x} = {\mathbf{F}}_{13x} - {\mathbf{F}}_{3x} = 0$$
(6)
$$\sum {{\mathbf{F}}_{y} } = {\mathbf{F}}_{3y} - {\mathbf{F}}_{13y} = 0$$
(7)
$$\sum {{\mathbf{M}}_{O} = - {\mathbf{F}}_{13y} R_{1} \cos \theta_{1} } - {\mathbf{F}}_{13x} R_{1} \sin \theta_{1} - {\mathbf{M}}_{3} = 0$$
(8)

The additional equations can be derived as follow:

$${\mathbf{F}}_{13x} = {\mathbf{F}}_{31x} , \, {\mathbf{F}}_{13y} = {\mathbf{F}}_{31y}$$
(9)

The equilibrium equations of link OD can be written as:

$$\sum {{\mathbf{F}}_{x} } = {\mathbf{F}}_{4x} + {\mathbf{F}}_{2i}^{\prime } \cos \theta_{1} = 0$$
(10)
$$\sum {{\mathbf{F}}_{y} } = {\mathbf{F}}_{2i}^{\prime } \sin \theta_{1} - {\mathbf{F}}_{4y} = 0$$
(11)
$$\sum {{\mathbf{M}}_{O} } = {\mathbf{F}}_{2i}^{\prime } L_{2} \sin \varepsilon_{1} - {\mathbf{M}}_{4} { = 0}$$
(12)

where, \({\mathbf{F}}_{4x}\) and \({\mathbf{F}}_{4y}\) are the reaction forces of joint O in the x- and y- axes direction; \({\mathbf{M}}_{4}\) represents the driving torque provided by the actuator and \({\mathbf{F}}_{2i}^{\prime }\) denotes the internal force of link DE.

Since the hybrid robotic arm is non-redundant, the forces can be uniquely determined when the configuration and external load are given.

2.3 Worst case identification

For a link under two external loads, the distribution of shear and bending-moment need to be further analyzed. Link IJK (Fig. 3a) is under two vertical loads at I and K, and the beam is in static equilibrium. Then the shear and bending-moment diagrams can be derived as shown in Fig. 3b, c, respectively. The shear and bending-moment diagrams of beams IJ and JK are the same as that of cantilever beams fixed at joint J. As to axial loads, similar results can be obtained as well. Since the joints’ positions of the hybrid robotic arm are determined when the location of the end-effector is given. In the following optimization, HCE is divided into cantilever beams HC and CE fixed at point C. While OC and OD are two cantilever beams fixed at point O.

Fig. 3
figure 3

Analysis of a typical link: a force diagram; b shear diagram; c bending-moment diagram

Full size image

For each link, both the magnitude and direction of the external load varies with different configurations. To simplify subsequent calculation, the external loads should be decomposed. Due to the fact that the external loads can be regarded as pure concentrated forces acting at the joint, the external loads of each beam can always be decomposed as axial load and shear as shown in Fig. 4.

Fig. 4
figure 4

Load decomposition schematic diagram

Full size image

\({\mathbf{F}}_{1tc}\) and \({\mathbf{F}}_{1s}\) represent axial load and shear of beam HC; \({\mathbf{F}}_{2tc}\) and \({\mathbf{F}}_{2s}\), \({\mathbf{F}}_{3tc}\) and \({\mathbf{F}}_{3s}\), \({\mathbf{F}}_{4tc}\) and \({\mathbf{F}}_{4s}\) represent axial loads and shears of CE, OC and OD, respectively. The values can be calculated through Eqs. (13)–(16).

$${\mathbf{F}}_{1tc} = - {\mathbf{F}}_{e} \sin (\varphi + \theta_{2} ), \, {\mathbf{F}}_{1s} = {\mathbf{F}}_{e} \cos (\varphi + \theta_{2} )$$
(13)
$${\mathbf{F}}_{2tc} = - {\mathbf{F}}_{2i} \cos \gamma_{1} , \, {\mathbf{F}}_{2s} = {\mathbf{F}}_{2i} \sin \gamma_{1}$$
(14)
$${\mathbf{F}}_{3tc} = {\mathbf{F}}_{13x} \cos \theta_{1} - {\mathbf{F}}_{13y} \sin \theta_{1} , \, {\mathbf{F}}_{3s} = - {\mathbf{F}}_{13y} \cos \theta_{1} - {\mathbf{F}}_{13x} \sin \theta_{1}$$
(15)
$${\mathbf{F}}_{4tc} = - {\mathbf{F}}_{2i}^{\prime } \cos \varepsilon_{1} , \, {\mathbf{F}}_{4s} = {\mathbf{F}}_{2i}^{\prime } \sin \varepsilon_{1}$$
(16)

Normally, a cantilever beam under shear is more fragile. However, when a cantilever beam is under both axial load and shear with changing magnitude, the destructive effect is hard to evaluate perceptually. How to unify the effect of axial load and shear quantitatively is the key to identify the worst cases of each beam. In general, the strain energy can be used to evaluate the closeness to structure failure. In topology optimization, the compliance, which characterizes the internal strain energy, is often used as the objective function to be minimized. Thus, evaluating the effect of axial load and shear from the aspect of compliance is an ideal choice. In topology optimization, the structural compliance is defined as:

$$C = {\mathbf{F}}^{{\text{T}}} {\mathbf{U}} = {\mathbf{U}}^{{\text{T}}} {\mathbf{KU}}$$
(17)

where \({\mathbf{F}}\) is the external load, \({\mathbf{U}}\) is the displacement vector and \({\mathbf{K}}\) is the stiffness matrix.

For a cantilever beam (Fig. 4) with both axial load and shear, under the assumption of small elastic deformation, the compliance C can be expressed as:

$$C = ({\mathbf{F}}_{tc} + {\mathbf{F}}_{s} )^{{\text{T}}} ({\mathbf{U}}_{tc} + {\mathbf{U}}_{s} ) = {\mathbf{F}}_{tc}^{{\text{T}}} {\mathbf{U}}_{tc} + {\mathbf{F}}_{s}^{{\text{T}}} {\mathbf{U}}_{s} = C_{tc} + C_{s}$$
(18)

where, \(C_{s}\) is the compliance when only shear is applied; while \(C_{tc}\) represents compliance under pure axial load. Therefore, the compliance of the cantilever beam is the sum of compliance caused by axial load and shear. Based on Eq. (17), the following equation can be derived:

$$C = {\mathbf{F}}^{{\text{T}}} {\mathbf{U}} = {\mathbf{F}}^{{\text{T}}} {\mathbf{K}}^{ - 1} {\mathbf{F}}$$
(19)

Therefore, the compliance under pure axial load or shear can be derived as follow:

$$C_{tc} = \eta_{1} {\mathbf{F}}_{tc}^{2} , \, C_{s} = \eta_{2} {\mathbf{F}}_{s}^{2}$$
(20)

In Eq. (21), \(C_{s - s}\) and \(C_{tc - s}\) represent compliance under pure shear or axial load with the same magnitude, respectively and \(\eta\) is defined as the equivalent coefficient of axial load with respect to shear.

$$\eta = \sqrt {{{C_{tc - s} } \mathord{\left/ {\vphantom {{C_{tc - s} } {C_{s - s} }}} \right. \kern-\nulldelimiterspace} {C_{s - s} }}} , \, \left\| {{\mathbf{F}}_{tc - s} } \right\| = \left\| {{\mathbf{F}}_{s - s} } \right\|$$
(21)

Based on Eqs. (17)–(21), the relation between compliance and external load can be expressed as:

$$C = \eta_{1} {\mathbf{F}}_{s}^{{2}} + \eta_{2} {\mathbf{F}}_{tc}^{{2}} = \eta_{1} ({\mathbf{F}}_{s}^{{2}} + \frac{{\eta_{2} }}{{\eta_{1} }}{\mathbf{F}}_{tc}^{{2}} ) = \eta_{1} ({\mathbf{F}}_{s}^{{2}} + \eta^{2} {\mathbf{F}}_{tc}^{{2}} ) = \eta_{1} ({\mathbf{F}}_{s} + \eta {\mathbf{F}}_{tc} )^{{\text{T}}} ({\mathbf{F}}_{s} + \eta {\mathbf{F}}_{tc} )$$
(22)

To evaluate the overall effect of external load, the equivalent external load is defined as:

$$F_{{{\text{eq}}}} = \left\| {{\mathbf{F}}_{s} + \eta {\mathbf{F}}_{tc} } \right\|$$
(23)

The worst cases of each link are identified by locating the maximum equivalent external load. The computational efficiency is higher because iterative calculation is avoided. The identification can be expanding into three-dimension by calculating the equivalent coefficient of moments as well. In this situation, the dimension of equivalent coefficient of moment with respect to force is reciprocal to length. In finite element analysis (FEA), the compliance can be calculated through Eq. (24). \({\mathbf{u}}_{i}\) represents the displacement vector of the ith element; \({\mathbf{k}}_{i}\) is the stiffness matrix of the ith element and \(N\) is the number of elements.

$$C = {\mathbf{U}}^{{\text{T}}} {\mathbf{KU}} = \sum\limits_{i = 1}^{N} {{\mathbf{u}}_{i}^{{\text{T}}} {\mathbf{k}}_{i} {\mathbf{u}}_{i} }$$
(24)

Since the hybrid robotic arm is developed based on a planar mechanism, the topology optimization will be carried out as a 2D problem. Based on the parameters of each link, the design domain of beam HC is determined as a 1300 mm × 200 mm rectangle, which is discreted into 130 × 20 elements; the design domain of beams CE and OD are 400 mm × 200 mm rectangles, which is discreted into 40 × 20 elements; and the design domain of beam OC is determined as a 1000 mm × 300 mm rectangle, which is discreted into 100 × 30 elements. The external load is applied to cantilever beams at the center of the right boundary line, and the left boundary is constrained. The derived equivalent coefficients of each beam are listed in Table 1. A smaller coefficient indicates that the beam is more sensitive to shear. It is shown that a slender cantilever beam (like HC) possess smaller coefficient, which is consistent with the principal of mechanics as well.

Table 1 Equivalent coefficients of each beam
Full size table

When the external load \({\mathbf{F}}_{e} = 2000{\text{N}}\), the equivalent external load distribution in the driving space is shown in Fig. 5, and the equivalent load distribution is plotted in task workspace as well (Fig. 6). Based on the distribution, the locations and the external loads of the identified worst cases are listed in Table 2. The equivalent external load distribution of beam OD is the same as that of beam CE. Therefore, the optimal topology of beam OD should be the same as that of beam CE as well.

Fig. 5
figure 5

Equivalent external load distribution atlases: a beam HC; b beams CE and OD; c beam OC

Full size image
Fig. 6
figure 6

Equivalent load distribution in task workspace: a beam HC; b beams CE and OD; c beam OC

Full size image
Table 2 Worst case of the hybrid robotic arm
Full size table

3 Topology optimization under the worst case

Since the worst cases of each link are identified, how to construct and solve the topology optimization is the main challenge encountered. In the formulation of the optimization problem, all worst cases should be taken into consideration for global validity, and the solving process is expected to converge as quickly as possible. In topology optimization, the mesh dependence and checkerboard problem are non-negligible problems as well. The methods to solve the aforementioned problems will be presented in this section.

3.1 Topology optimization problem and guide weight filtering method

The topology optimization of minimum compliance under a certain weight constraint can be expressed as:

$$\left\{ {\begin{array}{*{20}l} {{\text{find}}: \, {{\varvec{\uprho}}} = [\rho_{1} ,\rho_{2} , \cdots ,\rho_{N} ]^{{\text{T}}} \in R^{N} } \hfill \\ {\min : \, C({{\varvec{\uprho}}})} \hfill \\ {{\text{s.t.}}\, M \le fM_{0} } \hfill \\ { \, 0 < \rho_{\min } \le \rho_{i} \le 1 \quad i = 1,2, \cdots N} \hfill \\ \end{array} } \right.$$
(25)

In the density-based method, the design variable \(\rho_{i}\) is the relative density of the ith element in FEA; \(\rho_{\min }\) is the minimum value of the design variables to avoid singularity; N is the quantity of the elements; C is the structural compliance; \(M\) and \(M_{0}\) represent the actual and initial weight of the structure, respectively; f is the weight fraction. Based on the SIMP method, the following equation can be derived.

$${\mathbf{k}}_{i} = \rho_{i}^{p} {\mathbf{k}}_{io}$$
(26)

where p is the penalty factor; \({\mathbf{k}}_{i}\) and \({\mathbf{k}}_{io}\) are the actual and initial stiffness matrices of the ith element, respectively. Substituting Eq. (26) into Eq. (24), it leads to:

$$C = \sum\limits_{i = 1}^{N} {\rho_{i}^{p} {\mathbf{u}}_{i}^{{\text{T}}} {\mathbf{k}}_{io} {\mathbf{u}}_{i} }$$
(27)

From Eq. (27), we can get

$$\frac{\partial C}{{\partial \rho_{i} }}{ = }{\mathbf{F}}^{{\text{T}}} \frac{{\partial {\mathbf{U}}}}{{\partial \rho_{i} }}{ + }\left( {\frac{{\partial {\mathbf{F}}}}{{\partial \rho_{i} }}} \right)^{{\text{T}}} {\mathbf{U}}$$
(28)

Based on \({\mathbf{F}} = {\mathbf{KU}}\), it leads to:

$$\frac{{\partial {\mathbf{F}}}}{{\partial \rho_{i} }} = {\mathbf{K}}\frac{{\partial {\mathbf{U}}}}{{\partial \rho_{i} }}{ + }\frac{{\partial {\mathbf{K}}}}{{\partial \rho_{i} }}{\mathbf{U}}$$
(29)

The derivative of the nodal displacement vector \({\mathbf{U}}\) can be expressed as:

$$\frac{{\partial {\mathbf{U}}}}{{\partial \rho_{i} }} = {\mathbf{K}}^{ - 1} \left(\frac{{\partial {\mathbf{F}}}}{{\partial \rho_{i} }} - \frac{{\partial {\mathbf{K}}}}{{\partial \rho_{i} }}{\mathbf{U}}\right )$$
(30)

Substituting Eq. (30) into Eq. (28),

$$\frac{\partial C}{{\partial \rho_{i} }} = 2\frac{{\partial {\mathbf{F}}}}{{\partial \rho_{i} }}{\mathbf{U}}^{{\text{T}}} - {\mathbf{U}}^{{\text{T}}} \frac{{\partial {\mathbf{K}}}}{{\partial \rho_{i} }}{\mathbf{U}}$$
(31)

Neglecting the variation of load vector F, the formula can be derived as:

$$\frac{\partial C}{{\partial \rho_{i} }} = - \sum\limits_{j = 1}^{N} {{\mathbf{u}}_{j}^{{\text{T}}} \frac{{\partial {\mathbf{k}}_{j} }}{{\partial \rho_{i} }}} {\mathbf{u}}_{j} = - p\rho_{i}^{p - 1} {\mathbf{u}}_{i}^{{\text{T}}} {\mathbf{k}}_{io} {\mathbf{u}}_{i}$$
(32)

The weight of the design domain can be derived as:

$$M = \sum\limits_{i = 1}^{N} {\rho_{i} \rho_{m} v_{i} }$$
(33)

where \(v_{i}\) is the volume of the ith element and \(\rho_{m}\) is the density of the material. Then

$$\frac{\partial M}{{\partial \rho_{i} }} = \rho_{m} v_{i}$$
(34)

According to the modified guide-weight method (Liu et al. 2011), the proportional weight \(H_{i}\), the generalized weight \(W_{i}\), the guide weight \(G_{i}\) and the total guide weight \(G\) can be derived as follow:

$$\left\{ {\begin{array}{*{20}l} {H_{i} = \frac{\partial M}{{\partial \rho_{i} }} = \rho_{m} v_{i} } \hfill \\ {W_{i} = \rho_{i} H_{i} = \rho_{i} \rho_{m} v_{i} } \hfill \\ {G_{i} = - \rho_{i} \frac{\partial C}{{\partial \rho_{i} }} = p\rho_{i}^{p} {\mathbf{u}}_{i}^{T} {\mathbf{k}}_{io} {\mathbf{u}}_{i} } \hfill \\ {G = \sum\limits_{i = 1}^{N} {G_{i} = } \sum\limits_{i = 1}^{N} {p\rho_{i}^{p} {\mathbf{u}}_{i}^{T} {\mathbf{k}}_{io} {\mathbf{u}}_{i} = p} C} \hfill \\ \end{array} } \right.$$
(35)

The iterative formula can be written as:

$$x_{i}^{(k + 1)} = \left\{ {\begin{array}{*{20}l} {1{\text{ if }}\rho_{i} \ge 1} \hfill \\ {\alpha \left( {\frac{{p\rho_{i}^{p} {\mathbf{u}}_{i}^{T} {\mathbf{k}}_{io} {\mathbf{u}}_{i} }}{{\lambda \rho_{m} v_{i} }}} \right)^{(k)} { + }\left( {{1 - }\alpha } \right)\rho_{i}^{(k)} {\text{ if }}\rho_{\min } < \rho_{i} < 1 \quad i = 1,2, \cdots N} \hfill \\ {\rho_{\min } {\text{ if }}\rho_{i} \le \rho_{\min } } \hfill \\ \end{array} } \right.$$
(36)

The Lagrange multiplier can be derived as:

$$\lambda = \frac{pC}{{fM_{0} }}$$
(37)

There are more than one worst case for beams HC, CE and OD (as shown in Table2). If the objective function only considers one worst case, the derived topology can be fragile under other worst cases. In this paper, objective function is formulated as the weighted sum of compliance under each worst case to cope with the topology optimization under multiple worst cases. The optimization problem can be written as:

$$\left\{ {\begin{array}{*{20}l} {{\text{find}}: \, {{\varvec{\uprho}}} = [\rho_{1} ,\rho_{2} , \cdots ,\rho_{N} ]^{{\text{T}}} \in R^{N} } \hfill \\ {\min : \, C_{{{\text{sum}}}} ({{\varvec{\uprho}}}) = \sum\limits_{j = 1}^{S} {w_{j} C_{j} ({{\varvec{\uprho}}})} } \hfill \\ {{\text{s.t.}}\, M \le fM_{0} } \hfill \\ { \, 0 < \rho_{\min } \le \rho_{i} \le 1 \quad i = 1,2, \cdots N} \hfill \\ \end{array} } \right.$$
(38)

where \(S\) is the number of worst cases; \(w_{j}\) is the weight coefficient of the jth worst case; \(C_{j}\) is the compliance under the jth worst case.

Then, the following formula can be derived:

$$\frac{{\partial C_{{{\text{sum}}}} }}{{\partial \rho_{i} }} = - p\rho^{p - 1} \sum\limits_{j = 1}^{S} {w_{j} {\mathbf{u}}_{ij}^{{\text{T}}} {\mathbf{k}}_{io} {\mathbf{u}}_{ij} }$$
(39)

where \({\mathbf{u}}_{ij}\) is the displacement vector of the ith element under the jth load case. For beams HC, CE and OD, \(S = 2\) and \(w_{j} = 0.5\) considering the probability of occurrence of each worst case.

The guide weight, the total guide weight and the Lagrange multiplier can be derived as:

$$G_{i} = - \rho_{i} \frac{{\partial C_{{{\text{sum}}}} }}{{\partial \rho_{i} }} = p\sum\limits_{j = 1}^{S} {w_{j} \rho_{i}^{p} {\mathbf{u}}_{ij}^{{\text{T}}} {\mathbf{k}}_{io} {\mathbf{u}}_{ij} }$$
(40)
$$G = \sum\limits_{i = 1}^{N} {G_{i} = } p\sum\limits_{i = 1}^{N} {\sum\limits_{j = 1}^{S} {w_{j} \rho_{i}^{p} {\mathbf{u}}_{ij}^{{\text{T}}} {\mathbf{k}}_{io} {\mathbf{u}}_{ij} } = p} C_{{{\text{sum}}}}$$
(41)
$$\lambda = \frac{{pC_{sum} }}{{fM_{0} }}$$
(42)

In optimization, the mesh dependency and checkerboard problem will deteriorate the optimal topology. To address these non-negligible problems, a guide weight filtering method is proposed. This method modifies the guide weight of an element based on the guide weight in a fixed neighborhood.

This filtering formula of the ith element can be derived as:

$$\hat{G}_{i} = \frac{1}{{\rho_{k} \sum\limits_{i = 1}^{N} {\hat{L}_{i} } }}\sum\limits_{i = 1}^{N} {\hat{L}_{i} } \rho_{i} G_{i}$$
(43)

where N is the total number of elements in FEA. The convolution operator \(\hat{L}_{i}\) is written as:

$$\hat{L}_{i} = r_{\min } - {\text{dist}}(k,i), \, \left\{ {i \in N|{\text{dist}}(k,i) \le r_{\min } } \right\},\quad k = 1, \ldots N$$
(44)

The operator \({\text{dist}}(k,i)\) is defined as the distance between the center of element k and the center of element i. The convolution operator \(\hat{L}_{i}\) is zero outside the filter area. In the design variables updating process, the value of \(\hat{G}_{i}\) will replace the value of \(G_{i}\). In this method, the guide weight of an element is modified as the weighted average guide weight in the neighborhood. Through this filtering method, the mesh dependency and checkerboard problem can be eliminated.

3.2 Optimization of the 2-DoF hybrid robotic arm

In this section, the topology optimization of each link is carried out in MATLAB environment and the optimization procedure is shown in Fig. 7. The worst case will be identified first by searching the maximum equivalent external loads of each link in the workspace. Thereafter, the design variables will be optimized based on the iterative criterion presented in Sect. 3.1 and the structure will be updated.

Fig. 7
figure 7

Flowchart of topology optimization procedure

Full size image

All necessary parameters in topology optimization are listed in Table 3. The post process is executed when convergence is reached.

Table 3 Parameters for topology optimization
Full size table

The iteration processes and the final results of three cantilever beams are shown in Figs. 7, 8, 9. As shown in Fig. 8, the optimization procedure of beam HC converges within 60 steps and the final topology has a clear boundary.

Fig. 8
figure 8

Topology optimization of beam HC: a iteration process; b optimal topology

Full size image
Fig. 9
figure 9

Topology optimization of beam CE: a iteration process; b optimal topology

Full size image

As shown in Figs. 9 and 10, the optimal topology of beams CE and OC can be derived within 40 steps, which proves the fast convergence of modified guide-weight method.

Fig. 10
figure 10

Topology optimization of beam OC: a iteration process; b optimal topology

Full size image

3.3 Performance comparison

Based on the derived topologies of each beam, the CAD model of the optimized hybrid robotic arm is shown in Fig. 11a. To validate the effect of the topology optimization, the performance comparison is carried out based on finite element analysis. To make the comparison unbiased, the weight and shape of the baseline robotic arm is the same with the optimized one and the CAD model is shown in Fig. 11b.

Fig. 11
figure 11

CAD model of the robotic arm: a the optimized one; b the baseline one

Full size image

The vertical stiffness and natural frequencies under three typical configurations are compared using ANSYS 15.0 Workbench. The simulation results are listed in Table 4 and the selected configurations are shown in Fig. 12. The three configurations correspond to the end-effector location at the lower, higher and middle part of the task workspace. The vertical stiffness refers to the stiffness of the end-effector along the vertical direction. Based on the simulation result, the vertical stiffness of the optimized robotic arm can achieve two times of that of the baseline one. Besides, the first natural frequency can be improved more than 50% after the optimization. Therefore, the optimization method proposed in this paper is an effective way to improve the performance of the robotic arm.

Fig. 12
figure 12

Selected typical configurations: a Configuration I; b Configuration II; c Configuration III

Full size image
Table 4 the performance comparison of two robotic arms
Full size table

4 Conclusion

In this paper, the topology optimization of the 2-DoF hybrid robotic arm is accomplished based on efficient worst case identification. On the basis of forward and inverse kinematics analysis, the good transmission workspace is identified under the constraint of LTI. By analyzing the external forces of each link in the workspace, the equivalent external load is proposed to evaluate the effect of axial load and shear from the aspect of compliance. By searching for the maximum equivalent external load, the worst case with maximum compliance in the workspace is efficiently identified. Since the identification requires no iterative calculation, the computational efficiency is expected to be higher. Thereafter, the SIMP interpolation scheme is used to construct the optimization problem. By formulating the objective function as the weighted sum of compliance under each worst case, global validity can be further improved. For fast convergence, the modified guide-weight method is utilized as the iterative criterion and a guide weight filtering method is proposed to eliminate the mesh dependence and checkerboard problem. Based on the derived optimal topology, the CAD model of the hybrid robotic arm is presented. The effect of the optimization method has been testified through performance comparison between the optimized robotic arm and the baseline one based on finite element analysis. The derived CAD model is very helpful to the development of the 2-DoF robotic arm and the optimization approach can be further applied to other hybrid robotic arms as well.