Abstract
The concept of a neutrosophic set is an extension of a fuzzy set that uses indeterminacy. Similarly, an intuitionistic set has an extension, which is known as a single-valued neutrosophic set. The extension of intuitionistic fuzzy graphs and fuzzy graphs is single-valued neutrosophic fuzzy graphs (SVNF-graphs), which is the new component of graph theory. These versions of graph theory play an important role in many real-world problems, like medical diagnoses, law, engineering, finance, and industry. SVNF-graphs play an important role in linguistics, genetics, networking, sociology, computer technology, economics, and communication. The topological graph parameter gives a real number to the associated graph. There are numerous topological graph parameters proposed in the literature. In topological graph parameters, some uncertainty exists. Rosenfeld, Atanssov, and Smarandache introduced the concepts of a fuzzy graph, intuitionistic fuzzy graph (IFG), and SVNF-graph to overcome these uncertainties. SVNF-graph, IFG, and FG have vital roles in solving world-life problems. In this research work, we proposed a pythonic environment for the single-value neutrosophic fuzzy topological graph parameters. We introduced for the very first time some SVNF-graph parameters, like the Sombor graph parameter: the third and fourth versions of the SVNF-Sombor graph parameters for the SVNF-graph framework. Also, we have proved some characteristics and bounds of these topological graph parameters. We have discussed the social media application for the SVNF-Sombor graph parameter and its third and fourth versions. Under consideration application, We have shown that deleting a person (vertex) in the network can increase or decrease the chances of sending friend requests to other people of artificial intelligence.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Al-Zadeh gave the concept of a fuzzy set. A fuzzy set (FS) describes the components of an ordinary (crisp) set using membership values ranging from 0 to 1. The researcher extends the concept of the operations of a crisp set to a fuzzy set in Zadeh (1965), Chen et al. (2009) and Chen and Jian (2017). The reader can found more results in the citations (Flores and Srirama 2013; Karwowski and Mital 1986; Klir and Yuan 1996), for more information on the application of FSs (Ghoushchi et al. 2023; Yüksel et al. 2024; Fatima et al. 2024; Liu 2024).
In Atanassov and Atanassov (1999), Chen et al. (2019) and Chen and Wang (1995) developed the concept of an intuitionistic fuzzy set (IFS) using the extension of a fuzzy set. In this research paper, authors used the method of normalized Euclidean distance to develop an application for career determination in Ejegwa et al. (2014) and Horng et al. (2005). In this article, the authors established the application of IFS in medical diagnosis in Khatibi and Montazer (2009), Ahmad and Sabir (2023), Akram et al. (2022), and Palanisamy and Periyasamy (2023).
Neutrosophic set (NS) originated by Smarandache (2006) is a useful mathematical tool for handling inconsistent, ambiguous, and incomplete data in the real world. He presented the three components of Ns as truth membership (T), neutrality (N), and falsity (F) values, respectively, within the nonstandard interval \(\left] 0^-, 1^+ \right[\). The researcher produced a few operations on Ns, such as Cartesian product, complement, union, etc. The researchers also utilized the idea of the Ns cube to produce the concept of the geometric interpretation of Ns in Smarandache (2011) and Banitalebi and Borzooei (2023). Ns is an extension of the fuzzy set and intuitionistic fuzzy set. The application of Ns exists in many fields, such as data sciences, information systems, semantic web services, new economy growth, and information technology (El-Hefenawy et al. 2016; Das et al. 2021; Koundal et al. 2016).
Neutrosophic graphs were proposed by Vasantha Kandasamy and Ilanthenral (2015), Padma (2022) and Khalaf and Padma (2022) and developed using the concept of graph theory. Single-value neutrosophic fuzzy sets (SVNFs) were initiated by the researchers in Wang et al. (2012), Mahapatra et al. (2022) and Dey et al. (2023) as subclasses of Ns. The SVNFS is an extension of the IFS, which has three independent membership values, and these values are from the interval \([0, 1]\). Riaz et al. provided the notion of the topological structure of SVNFS and its application as a supply chain in Riaz et al. (2022). In this article, Jin et al. established the notion of a novel distance measure for SVNFS in Jin et al. (2022) and also developed the algorithm for MGDMP. In Akram and Adeel (2017), the authors developed some interesting properties and applications in the decision-making of neutrosophic graphs.
Single-valued neutrosophic fuzzy graphs were initiated by Broumi et al. (2016), and also, they have established their properties. The authors presented the novel idea of SVNF-graph and also developed their bounds in Mehra and Singh (2017). Krishnaraj et al. (2017) proposed the distance, median, status, total status, diameter, radius, eccentricity, and central vertex, and also examined the few properties of self-centered SVNF-graph. Researchers Akram and Sitara (2017) utilized the idea of NFS to structure graphs, and they also determined the characteristics of SVNF-graph. In this paper, authors provided the notation of some operations, such as lexicographic products, direct products, strong products, and degrees of a vertex, and gave an application of SVNF-graph (Naz et al. 2017; Akram and Sitara 2017).
The researchers provided the derivable single-valued neutrosophic graph notion, which is utilized as an instrument in wireless sensor networks and is perceived as these networks’ energy clustering in Hamidi and Borumand Saeid (2018). In Akram and Shahzadi (2017), authors provided innovative ways to use single-valued neutrosophic networks in decision-making scenarios. Finally, they constructed the algorithms for that. Researchers presented a decision-making technique that uses a single-valued neutrosophic graph and also provided the algorithmic process for the suggested technique in Akram et al. (2018). The ideas of degree of a vertex and total degree of a vertex in SVNF-graph are also presented by the concepts of the salient characteristics of the new operations, such as the SVNF-graph residue product, symmetric difference, maximal product, and rejection (Zeng et al. 2021).
A fuzzy set has expanded for the topological indices, which is a numeric value that describes the structural properties of a graph on the structure of a molecule. TIs have numerous characteristics. In one of them, the values of all the isomorphic graphs are the same (Kalathian et al. 2020; Liu et al. 2022; Majeed and Arif 2023). Fuzzy F-indexes and their properties are proposed by Islam and Pal (2023). Ahmad et al. (2023) established the upper bounds of various TIs and different products for fuzzy graphs and their application in cybercrime. In Islam and Pal (2021), investigated the bounds of the fuzzy hyper-wiener index and its application in shares of the market. Researchers (Binu et al. 2020) presented the relations between the fuzzy wiener index and fuzzy connectivity index and also discussed an illegal immigration network. Harold Wiener described the concept of TI known as the first Zagreb index by Balaban (1983) and Nadeem et al. (2021), Wiener index by Graovac and Pisanski (1991), Ismail et al. (2023) and different versions of the Sombor index by Gutman (2022), like the second, third, and fourth versions (Imran et al. 2022).
In this article, we have established the basic definitions and some operations of the SVNF-Sombor graph parameter, as well as the third and fourth invariants of the SVNF-Sombor graph parameters. We have developed the bounds for these graph theoretic parameters as well. Also, discuss applications of these invariants of the SVNF-Sombor graph parameters. Under consideration application, we have shown that deleting a person (vertex) in the network can increase or decrease the chances of sending friend requests to other people of artificial intelligence.
1.1 Motivation and research gap
An SVNF gave us three types of opinions: truth membership, neutrality, and falsity. Like FG, it is limited to one degree only and does not cover the non-membership. Similarly, IFG is limited to membership and non-membership degree facilities in decision-making. Therefore, SVNFS is very important for real-world problems. Similarly, after-sets, fuzzy graphs, IFG, and SVNFG are also very helpful tools in decision-making and expert systems. Along with the physical and chemical properties of complex networks, topological indices help to give output similar results to lab research-heavy experiments. With an amalgamation of fuzzy set environments, fuzzy graph theory, and topological indices, it covers three major fields in one package: computer science, chemistry, and mathematics.
In this paper, we will discuss the Sombor graph parameter and its third and fourth versions, and we will also discuss some of the basic operations and bounds of these indices as well. Moreover, we will discuss applications of the Sombor graph parameter and its third and fourth versions.
There is no work done on the SVNFG concerning graph operations in coordination with Sombor graph parameters. We have these Sombor graph parameters designed for SVNFG, and we checked the application of these newly developed Sombor graph parameters concerning SVNFG and some graph operations. There are many articles on Sombor indices (Das et al. 2021; Imran et al. 2023), but they are computed only for the crisp graph. In this article, we introduced all those Sombor versions for SVNFG
1.2 Framework
In the fragment of the research work 2, we provided the elementary definitions. We developed the definitions of the SVNF-Sombor graph parameter, third, and fourth invariants of the SVNF-Sombor graph parameters for the SVNF-Sombor graph parameters for the SVNF-graph framework in Sect. 3, and their bounds are provided. In Sect. 4, we construct the algorithm and application via the invariant of the SVNF-Sombor graph parameters. In Sect. 5, the conclusion is presented.
2 Preliminary
In this fragment of the research work, we will discuss some definitions of single-valued neutrosophic sets, fuzzy graphs, SVNF-graph, and intuitionistic fuzzy graphs, related to the consideration research work.
Definition 2.1
Let \(\Gamma\) be a space of an object with generated elements in \(\Gamma\) represented by \(\gamma .\) A single-valued neutrosophic set \(\Psi\) (SVNS \(\Psi\)) is associated an neutral value \(N_{\psi }(\gamma )\), and a falsity value \(F_{\psi }(\gamma ),\) by truth value \(T_{\psi }(\gamma )\), For each object of \(\gamma\) in \(\Gamma\) \(T_{\psi }(\gamma ),\) \(N_{\psi }(\gamma ),\) and \(F_{\psi }(\gamma )\) \(\in [0, 1].\) A SVNFS written as
Definition 2.2
Let \(G=(\Upsilon , \Box )\) be a fuzzy graph, where \(\Upsilon\) is an Fs of a non-empty space and \(\Box\) is a symmetric function relation on \(\Upsilon .\) \(\Upsilon : V\rightarrow [0. 1]\) and \(\Box : V\times V \rightarrow [0, 1]\), such that \(\Upsilon (uv)\le \Upsilon (u) \wedge \Upsilon (v)\) \(v\in V.\) \(\Upsilon\) is called the fuzzy vertex set of V and \(\Box\) is called the fuzzy edge set of E.
Definition 2.3
Consider \(G=(\Upsilon , \tilde{\Box })\) be an intuitionistic fuzzy graphs IFG.
-
1.
\(\Upsilon =\{{\gamma _{1}}, {\gamma _{2}}, {\gamma _{3}} {\dots }, {\gamma _{n}}\}\), such that \({\zeta _{1}}: \Upsilon \rightarrow [0, 1]\) represent the degree of membership and \({\nu _{1}}: \Upsilon \rightarrow [0, 1]\) expressed for the non-membership of the point \({\gamma _{i}} \in {\Upsilon } (i=1, 2, 3, \dots , n),\) respectively.
$$\begin{aligned} 0 {\le } {\zeta _{1}}(\gamma _{i}) + {\nu _{1}}(\gamma _{i}) {\le } 1. \end{aligned}$$(2) -
2.
\(\Gamma \subseteq \Upsilon \times \Upsilon ,\) where \({\zeta _{2}}: \Upsilon \times \Upsilon \rightarrow [0, 1]\) and \({\nu _{2}}: \Upsilon \times \Upsilon \rightarrow [0, 1],\) such that
$$\begin{aligned}&{\zeta _{2}}(\gamma _{i}, \gamma _{j}) {\le } \min [{\zeta _{1}}(\gamma _{i}) , {\zeta _{1}}(\gamma _{j})] \end{aligned}$$(3)$$\begin{aligned}&{\nu _{2}}(\gamma _{i}, \gamma _{j}) {\ge } \min [{\nu _{1}}(\gamma _{i}) , {\nu _{1}}(\gamma _{j})], \end{aligned}$$(4)\(0 {\le } {\zeta _{2}}(\gamma _{i}, \gamma _{j}) + {\nu _{2}}(\gamma _{i}, \gamma _{j}) {\le } 1,\) for each \((\gamma _{i}, \gamma _{j}) \in \Gamma\) or \(E=(i, j=1, 2, 3, \dots , n).\)
Definition 2.4
\(G=(\Lambda , \tilde{\Lambda })\) be the single-valued neutrosophic fuzzy graph, where
-
1.
The degree of truth membership \(T_{\Lambda }: V \rightarrow [0, 1],\) the degree of neutral (indeterminacy) membership \(N_{\Lambda }: V \rightarrow [0, 1],\) and the degree of falsity membership \(F_{\Lambda }: V \rightarrow [0, 1],\) of the component \(v_{i} \in V,\) respectively
$$\begin{aligned} 0 {\le } {T_{\Lambda }}(\gamma _{i}) + {N_{\Lambda }}(\gamma _{i})+{F_{\Lambda }}(\gamma _{i}) {\le } 3, \end{aligned}$$for all \(v_{i} \in V.\)
-
2.
The degree of truth membership \(T_{\tilde{\Lambda }}: E \subseteq V\times V \rightarrow [0, 1],\) the degree of neutral (indeterminacy) membership \(N_{\tilde{\Lambda }}: E \subseteq V\times V \rightarrow [0, 1],\) and the degree of falsity membership \(F_{\tilde{\Lambda }}: E \subseteq V\times V \rightarrow [0, 1],\) are defined as \(T_{\tilde{\Lambda }}(\gamma _{i}, {\gamma _{j}})\le \min \left[ T_{\Lambda }(\gamma _{i}), T_{\Lambda }(\gamma _{j}) \right] ,\) \(N_{\tilde{\Lambda }}(\gamma _{i}, {\gamma _{j}})\ge \max \left[ N_{\Lambda }(\gamma _{i}), N_{\Lambda }(\gamma _{j}) \right] ,\) and \(F_{\tilde{\Lambda }}(\gamma _{i}, {\gamma _{j}})\ge \max \left[ F_{\Lambda }(\gamma _{i}), F_{\Lambda }(\gamma _{j}) \right]\) of the edge \(({\gamma _{i}}, {\gamma _{j}}) \in E,\) respectively
$$\begin{aligned} 0 {\le } T_{\tilde{\Lambda }}(\gamma _{i}, {\gamma _{j}}), N_{\tilde{\Lambda }}(\gamma _{i}, {\gamma _{j}}), F_{\tilde{\Lambda }}(\gamma _{i}, {\gamma _{j}}) {\le } 3, \end{aligned}$$for all \(({\gamma _{i}}, {\gamma _{j}}) \in E(i, j= 1, 2, 3, \dots , n).\)
Definition 2.5
If we delete a vertex from the vertex set of the single-valued neutrosophic graph G, then we get a new graph \(G-v,\) with order of the SVNF-graph is
and size of the new single-valued neutrosophic graph is
If we delete an edge from the edge set of a single-valued neutrosophic fuzzy graph, then we obtained a new SVNF-graph (G-e), with the same order and its size is
3 Our proposed work
In this fragment of the paper, we will discuss our proposed work concerning the SVNF-graphs. defined the third, and fourth invariants of the fuzzy Sombor graph parameter for the SVNF-framework.
Definition 3.1
The fuzzy Sombor graph parameter for the SVNF-framework is defined as
where \({T}_{\tau _{(i)}},\) \({N}_{\tau _{(i)}},\) \({F}_{\tau _{(i)}},\) and \(d_(\tau _{i})\) are the truth membership, neutral membership, falsity value of node, and degree of a node.
Example 3.1
Let G be an \(SVNF-graph\) with {x, y, z} set of vertices and {xy, yz} are the set of edges, respectively. Suppose that truth membership degree, neutral value, and falsity degree of a vertex as follows: \(\{{T_{x}}, {N_{x}}, {F_{{x}}} \}=(0.2, 0.5, 0.8),\) \(\{{T_{y}}, {N_{y}}, {F_{y}} \}=(0.9, 0.7, 0.1),\) and \(\{{T_{z}}, {N_{z}}, {F_{z}} \}=(0.4, 0.6, 0.3),\) are illustrated in Fig. 1.
Solution 1
Consider G have with 3 vertices and 2 edges, respectively. Degree of the vertices are the following: \({\Psi }({x})=(0.2, 0.7, 0.8),\) \({\Psi }({y})=(0.6, 1.4, 1.1),\) and \({\Psi }({z})=(0.4, 0.7, 0.3).\) Now, we compute square of degree of vertices are the following: \({\Psi }^{2}({x})=(0.04, 0.49, 0.64),\) \({\Psi }^{2}({y})=(0.20, 0.98, 0.73),\) and \({\Psi }^{2}({z})=(0.16, 0.49, 0.09).\)
Using the mathematical Eq. (5) of SVNFSO-graph parameter
Definition 3.2
The third version of the fuzzy Sombor graph parameter for SVNF-framework is defined as
where \({T}({u_{i}}),\) \({N}({u_{i}}),\) \({F}({u_{i}}),\) and \(d({u_{i}})\) are the truth membership, neutral membership, falsity value of node, and degree of a node.
Example 3.2
Let G be an SVNF-graph with {x, y, z} set of vertices and {xy, yz} are the set of edges, respectively. Suppose that truth membership degree, neutral value, and falsity degree of a vertex as following: \(\{{T_{x}}, {N_{x}}, {F_{{x}}} \}=(0.2, 0.5, 0.8),\) \(\{{T_{y}}, {N_{y}}, {F_{y}} \}=(0.9, 0.7, 0.1),\) and \(\{{T_{z}}, {N_{z}}, {F_{z}} \}=(0.4, 0.6, 0.3),\) are illustrated in Fig. 1.
Solution 2
Consider G have with 3 vertices and 2 edges, respectively. Degree of the vertices are the following: \({\Psi }({x})=(0.2, 0.7, 0.8),\) \({\Psi }({y})=(0.6, 1.4, 1.1),\) and \({\Psi }({z})=(0.4, 0.7, 0.3).\) Now, we compute square of degree of vertices are the following: \({\Psi }^{2}({x})=(0.04, 0.49, 0.64),\) \({\Psi }^{2}({y})=(0.20, 0.98, 0.73),\) and \({\Psi }^{2}({z})=(0.16, 0.49, 0.09).\)
Using the mathematical Eq. (6) of third version of the SVNFSO-graph parameter
Definition 3.3
The fourth version of the fuzzy Sombor graph parameter for SVNF-framework is defined as
where \({T}({u_{i}}),\) \({N}({u_{i}}),\) \({F}({u_{i}}),\) and \(d(u_{i})\) are the truth membership, neutral membership, falsity value of node, and degree of a node.
Example 3.3
Let G be an \(SVNF-graph\) with {x, y, z} set of vertices and {xy, yz} are the set of edges, respectively. Suppose that truth membership degree, neutral value, and falsity degree of a vertex as following: \(\{{T_{x}}, {N_{x}}, {F_{\mathfrak {x}}} \}=(0.2, 0.5, 0.8),\) \(\{{T_{y}}, {N_{y}}, {F_{y}} \}=(0.9, 0.7, 0.1),\) and \(\{{T_{z}}, {N_{z}}, {F_{z}} \}=(0.4, 0.6, 0.3),\) are illustrated in Fig. 1.
Solution 3
Consider G have with 3 vertices and 2 edges, respectively. Degree of the vertices are the following: \({\Psi }({x})=(0.2, 0.7, 0.8),\) \({\Psi }({y})=(0.6, 1.4, 1.1),\) and \({\Psi }({z})=(0.4, 0.7, 0.3).\) Now, we compute square of degree of vertices are the following: \({\Psi }^{2}({x})=(0.04, 0.49, 0.64),\) \({\Psi }^{2}({y})=(0.20, 0.98, 0.73),\) and \({\Psi }^{2}({z})=(0.16, 0.49, 0.09).\)
Using the mathematical Eq. (7) of fourth version of \(SVNFSO-\)graph parameter
3.1 Bounds on the SVNF-Sombor graph parameter for SVNF-graphs
In this fragment, we will investigate the upper bounds on the single-valued neutrosophic fuzzy Sombor graph parameter by utilizing the edge and vertex deletion of the SVNF-graph.
Theorem 3.1
Let G be an SVNF-graph with order n and size m. Then, we derived the following results:
- (i):
-
Supposed that \({\tilde{\lambda }}\) be a vertex is deleted from the SVNF-graph. Then, we have
$$\begin{aligned}&SVNFSO(G)>SVNFSO(G-{\tilde{\lambda }}). \end{aligned}$$ - (ii):
-
Supposed that \({{\tilde{\gamma }}{\tilde{\upsilon }}}\) be an edge is deleted from the SVNF-graph. Then, we have
$$\begin{aligned}&SVNFSO(G)>SVNFSO(G-{{\tilde{\gamma }}{\tilde{\upsilon }}}). \end{aligned}$$
Proof
-
(i)
Let G be an SVNF-graph of vertex \(\aleph\) is deleted from G. Then, we have
$$\begin{aligned} SVNFSO(G)&\\ {}&= \displaystyle \sum _{{\tau }_{i}{{\tau }_j} \in E(G)} \sqrt{(T({\tau }_{i}), N({\tau _{i}}), F({\tau }_{i}))d^2({\tau }_{i})+(T({\tau }_{j}), N({\tau _{j}}), F({\tau }_{j}))d^2({\tau }_{j})}.\\&=\displaystyle \sum _{ \begin{array}{c} {\lozenge }{\Phi } \in E(G)\\ {{\aleph }}{\lozenge },{{\aleph }}{\Phi } \notin E(G)\\ {\lozenge }, {\Phi }\ne {{\aleph }} \end{array}}\sqrt{(T({\lozenge }), N({\lozenge }), F({\lozenge }))d^2({\lozenge })+(T(\Phi ), N(\Phi ), F(\Phi ))d^2({\Phi })} +\\&\quad \displaystyle \sum _{ \begin{array}{c} {\lozenge }^{\prime }{\Phi }^{\prime } \in E(G)\\ {{\aleph }}{\lozenge }^{\prime } \notin E(G),{{\aleph }}{\Phi }^{\prime } \in E(G)\\ {\lozenge }^{\prime }, {\Phi }^{\prime }\ne {{\aleph }} \end{array}} \sqrt{ (T({\lozenge }^{\prime }), N({\lozenge }^{\prime }), F({\lozenge }^{\prime }))d^2({{\lozenge }^{\prime }})+(T({\Phi }^{\prime }), N({\Phi }^{\prime }), F({\Phi }^{\prime }))d^2({{\Phi }^{\prime }})}\\&\quad +\displaystyle \sum _{ \begin{array}{c} {\zeta ^{\prime }}{{\aleph }}^{\prime } \in E(G)\\ {{\aleph }}{\zeta }^{\prime } \in E(G),{{\aleph }}{{\aleph }}^{\prime } \in E(G)\\ {{\aleph }}^{\prime } \ne {{\aleph }} \end{array}} \sqrt{(T({\zeta }^{\prime }), N({\zeta }^{\prime }), F({\zeta }^{\prime }))d^2({\zeta }^{\prime })+(T({\aleph }^{\prime }), N({\aleph }^{\prime }), F({\aleph }^{\prime }))d^2({\aleph }^{\prime })}\\&>\displaystyle \sum _{ \begin{array}{c} {\lozenge }{\Phi } \in E(G)\\ {{\aleph }}{\lozenge },{{\aleph }}{\Phi } \notin E(G)\\ {\lozenge }, {\Phi }\ne {{\aleph }} \end{array}}\sqrt{(T(\ell ), N(\ell ), F(\ell ))d^2({\lozenge })+(T(\Phi ), N(\Phi ), F(\Phi ))d^2({\Phi })} +\\&\quad \displaystyle \sum _{ \begin{array}{c} {\lozenge }^{\prime }{\Phi }^{\prime } \in E(G)\\ {{\aleph }}{\lozenge }^{\prime } \notin E(G),{{\aleph }}{\Phi }^{\prime } \in E(G)\\ {\lozenge }^{\prime }, {\Phi }^{\prime }\ne {{\aleph }} \end{array}} \sqrt{ (T({\lozenge }^{\prime }), N({\lozenge }^{\prime }), F({\lozenge }^{\prime }))d^2({{\lozenge }^{\prime }})+(T({\Phi }^{\prime }), N({\Phi }^{\prime }), F({\Phi }^{\prime })) (K_m)}\\&\quad +\displaystyle \sum _{ \begin{array}{c} {\zeta ^{\prime }}{{\aleph }}^{\prime } \in E(G)\\ {{\aleph }}{\zeta }^{\prime } \in E(G),{{\aleph }}{{\aleph }}^{\prime } \in E(G)\\ {{\aleph }}^{\prime } \ne {{\aleph }} \end{array}} \sqrt{(T({\zeta ^{\prime }}), N({\zeta ^{\prime }}), F({\zeta ^{\prime }}), (K_r))+(T({\aleph }^{\prime }), N({\aleph }^{\prime }), F({\aleph }^{\prime })(K_p))}\\&=SVFSO(G-{\aleph }), \end{aligned}$$where \(K_m=\left( d({{\Phi }^{\prime }})-({T(\aleph , {\Phi }^{\prime }), N(\aleph , {\Phi }^{\prime })}, F(\aleph , {\Phi }^{\prime }))\right) ^{2},\) \(K_r=\left( d({\zeta ^{\prime }})-({T(\aleph , {\zeta ^{\prime }}), N(\aleph , {\zeta ^{\prime }})}, F(\aleph , {\zeta ^{\prime }}))\right) ^{2},\) and \(K_p=\left( d({{\aleph }^{\prime }})-({T(\aleph , {\aleph }^{\prime }), N(\aleph , {\aleph }^{\prime })}, F(\aleph , {\aleph }^{\prime }))\right) ^{2}.\) Therefore
$$\begin{aligned}&SVNFSO(G)>SVNFSO(G). \end{aligned}$$ -
(ii)
Let G be an SVNF-graph has an edge \(e={\imath }{\jmath },\) which is deleted from G. Then, we have
$$\begin{aligned} SVNFSO(G)&\\ {}&= \displaystyle \sum _{\tau _{i}{\tau _j} \in E(G)} \sqrt{(T({\tau _{i}}), N({\tau _{i}}), F({\tau _{i}}))d^2({\tau }_{i})+{(T({\tau _{j}}), N({\tau _{j}}), F({\tau _{j}}))d^2({\tau }_{j})}}\\&=\displaystyle \sum _{ \begin{array}{c} {\phi }{\daleth } \in E(G)\\ {\imath }{\phi },{\phi }{{\jmath }} \notin E(G)\\ {\daleth }{\imath },{\daleth }{{\jmath }} \notin E(G) \end{array}}\sqrt{(T({\phi }), N({\phi }), F({\phi }))d^2({\phi })+(T({\daleth }), N({\daleth }), F({\daleth }))d^2({\daleth })} +\\&\quad \displaystyle \sum _{ \begin{array}{c} {\lozenge }^{\prime \prime }{\Phi }^{\prime \prime } \in E(G)\\ {\imath }{\lozenge }^{\prime \prime } \in E(G),{{\jmath }}{\Phi }^{\prime \prime } \notin E(G)\\ {\lozenge }^{\prime \prime } \ne {\imath } \end{array}} \sqrt{(T({\lozenge }^{\prime \prime }), N({\lozenge }^{\prime \prime }), F({\lozenge }^{\prime \prime }))d^2({\lozenge }^{\prime \prime })+(T({\Phi }^{\prime \prime }), N({\Phi }^{\prime \prime }), F({\Phi }^{\prime \prime }))d^2({\Phi }^{\prime \prime })}\\&\quad + \displaystyle \sum _{ \begin{array}{c} {\lozenge }^{\prime \prime }{\Phi }^{\prime \prime } \in E(G)\\ {\imath }{\lozenge }^{\prime \prime } \notin E(G),{{\jmath }}{\Phi }^{\prime \prime } \in E(G)\\ {\Phi }^{\prime \prime } \ne {{\jmath }} \end{array}} \sqrt{(T({\lozenge }^{\prime \prime }), N({\lozenge }^{\prime \prime }), F({\lozenge }^{\prime \prime }))d^2({\lozenge }^{\prime \prime })+(T({\Phi }^{\prime \prime }), N{\Phi }^{\prime \prime }, F{\Phi }^{\prime \prime } )d^2({\Phi }^{\prime \prime })}\\&\quad +\displaystyle \sum _{ \begin{array}{c} {\intercal }{\curlyvee } \in E(G)\ {\intercal } \ne {\curlyvee } \end{array}} \sqrt{(T({\intercal }), N({\intercal }), F({\intercal }))d^2({\intercal })+(T({\curlyvee }), N({\curlyvee }), F({\curlyvee }))d^2({\curlyvee })}\\ \\&>\displaystyle \sum _{ \begin{array}{c} {\phi }{\daleth } \in E(G)\\ {\imath }{\phi },{\phi }{{\jmath }} \notin E(G)\\ {\daleth }{\imath },{\daleth }{{\jmath }} \notin E(G) \end{array}}\sqrt{(T({\phi }), N({\phi }), F({\phi }))d^2({\phi })+(T({\daleth }), N({\daleth }), F({\daleth }))d^2({\daleth })} +\\&\quad \displaystyle \sum _{ \begin{array}{c} {\lozenge }^{\prime \prime }{\Phi }^{\prime \prime } \in E(G)\\ {\imath }{\lozenge }^{\prime \prime } \in E(G),{{\jmath }}{\Phi }^{\prime \prime } \notin E(G)\\ {\lozenge }^{\prime \prime } \ne {\imath } \end{array}} \sqrt{(T({\lozenge }^{\prime \prime }), N({\lozenge }^{\prime \prime }), F({\lozenge }^{\prime \prime }))(\lambda )+(T({\Phi }^{\prime \prime }), N({\Phi }^{\prime \prime }), F({\Phi }^{\prime \prime }))d^2({\Phi }^{\prime \prime })}\\&\quad + \displaystyle \sum _{ \begin{array}{c} {\lozenge }^{\prime \prime }{\Phi }^{\prime \prime } \in E(G)\\ {\imath }{\lozenge }^{\prime \prime } \notin E(G),{{\jmath }}{\Phi }^{\prime \prime } \in E(G)\\ {\Phi }^{\prime \prime } \ne {{\jmath }} \end{array}} \sqrt{(T({\lozenge }^{\prime \prime }), N({\lozenge }^{\prime \prime }), F({\lozenge }^{\prime \prime }))d^2({\lozenge }^{\prime \prime })+(T({\Phi }^{\prime \prime }), N{\Phi }^{\prime \prime } , F{\Phi }^{\prime \prime } )(\lambda _{1})}\\&\quad +\displaystyle \sum _{ \begin{array}{c} {\intercal }{\curlyvee } \in E(G)\\ {\intercal } \ne {\curlyvee } \end{array}} \sqrt{(T({\intercal }), N({\intercal }), F({\intercal }))(\lambda _{2})+(T({\curlyvee }), N({\curlyvee }), F({\curlyvee }))d^2({\curlyvee })}.\\&=SVNFSO(G-{\imath }{{\jmath }}). \end{aligned}$$
\({\lambda }_{1}=\left( d({\Phi }^{\prime \prime })-\left( T{\imath } {\jmath }, N({\imath }{\jmath }), F({\imath }{\jmath })\right) \right) ^2,\) \({\lambda }_{2}=\left( d^2({\intercal })-(T({\imath }{\jmath }), N({\imath }{\jmath }), F({\imath }{\jmath }))\right) ^2,\)
and \(\lambda =\left( d({\lozenge }^{\prime \prime })-\left( T(\imath \jmath ), N({\imath }{\jmath }), F({\imath }{\jmath })\right) \right) ^{2}.\)
Therefore
\(\square\)
Theorem 3.2
The bounds on the second version of the SVNF-Sombor graph parameter for a simple and connected SVNF-framework are given as
if \({\alpha }={\beta },\) then it is equal to zero.
Proof
Using the formulation of the second version of the SVNF-Sombor graph parameter
where \((T_{\mu })\) truth degree, \((N_{\mu })\) neutral degree, and \((F_{\mu })\) falsity degree are not same.
Assume that G is an SVNF-graph with order \(\left( \displaystyle \displaystyle \sum _{{\eta }, {\hat{\eta }}\in V(G)}(T), \displaystyle \sum _{{\eta }, {\hat{\eta }}\in V(G)}(N), \displaystyle \displaystyle \sum _{{\eta }, {\hat{\eta }}\in V(G)}(F)\right)\) and size is
\(\left( \displaystyle \displaystyle \sum _{{\eta }{\hat{\eta }}\in E(G)}(T), \displaystyle \sum _{{\eta }{\hat{\eta }}\in E(G)}(N), \displaystyle \sum _{{\eta }{\hat{\eta }}\in E(G)}(F)\right) ,\) respectively. Then, \(T({\hat{\eta }})<\displaystyle \displaystyle \sum _{{\eta }, {\hat{\eta }}\in V(G)}(T),\) \(N({\hat{\eta }})<\displaystyle \displaystyle \sum _{{\eta }, {\hat{\eta }}\in V(G)}(N),\) and \(F({\hat{\eta }})<\displaystyle \displaystyle \sum _{{\eta }, {\hat{\eta }}\in V(G)}(F).\) Now, compute the degree of any vertex of G, as: \(d({\hat{\eta }})=\left( \displaystyle \displaystyle \sum _{{\hat{\eta }}\sim {\eta }{\hat{\eta }}\in E(G)}(T_{\hat{\eta }}({\eta }{\hat{\eta }})),\right. \left. \displaystyle \sum _{{\hat{\eta }}\sim {\eta }{\hat{\eta }}\in E(G)}(N_{\hat{\eta }}({\eta }{\hat{\eta }})), \displaystyle \sum _{{\hat{\eta }}\sim {\eta }{\hat{\eta }}\in E(G)}(F_{\hat{\eta }}({\eta }{\hat{\eta }}))\right) .\) Also, \(\displaystyle \displaystyle \sum _{{\hat{\eta }}\sim {\eta }{\hat{\eta }}\in E(G)}(T_{\hat{\eta }}({\eta }{\hat{\eta }}))<\displaystyle \displaystyle \sum _{{\eta }, {\hat{\eta }}\in V(G)}(T),\) \(\displaystyle \displaystyle \sum _{{\hat{\eta }}\sim {\eta }{\hat{\eta }}\in E(G)}(N_{\hat{\eta }}({\eta }{\hat{\eta }}))<\displaystyle \displaystyle \sum _{{\eta }, {\hat{\eta }}\in V(G)}(N),\) and \(\displaystyle \displaystyle \sum _{{\hat{\eta }}\sim {\eta }{\hat{\eta }}\in E(G)}(F_{\hat{\eta }}({\eta }{\hat{\eta }}))<\displaystyle \displaystyle \sum _{{\eta }, {\hat{\eta }}\in V(G)}(F).\) Compute the square of the degree of any vertex of G as:
\(d^2({\hat{\eta }})=\left( \displaystyle \displaystyle \sum _{{\hat{\eta }}\sim {\eta }{\hat{\eta }}\in E(G)}(T^2({\eta }{\hat{\eta }})), \displaystyle \displaystyle \sum _{{\hat{\eta }}\sim {\eta }{\hat{\eta }}\in E(G)}(N^2({{\eta }}{\hat{\eta }})), \displaystyle \sum _{{\hat{\eta }}\sim {\eta }{\hat{\eta }}\in E(G)}(F^2({\eta }{\hat{\eta }}))\right) .\) Also, \(\displaystyle \displaystyle \sum _{{\hat{\eta }}\sim {\eta }{\hat{\eta }}\in E(G)}(T_{\hat{\eta }}^2({\eta }{\hat{\eta }}))<\displaystyle \displaystyle \sum _{{\eta }, {\hat{\eta }}\in V(G)}(T)^2,\) \(\displaystyle \displaystyle \sum _{{\hat{\eta }}\sim {\eta }{\hat{\eta }}\in E(G)}(N_{\hat{\eta }}^2({\eta }{\hat{\eta }}))<\displaystyle \displaystyle \sum _{{\eta }, {\hat{\eta }}\in V(G)}(N)^2,\) and \(\displaystyle \displaystyle \sum _{{\hat{\eta }}\sim {\eta }{\hat{\eta }}\in E(G)}(F_{\hat{\eta }}^2({\eta }{\hat{\eta }}))<\displaystyle \displaystyle \sum _{{\eta }, {\hat{\eta }}\in V(G)}(F)^2.\)
Using these inequalities, we get
and
Adding above three inequalities. 8, 9, and 10
Similarly
Adding both inequalities, 11, and 12. Then, we get
Thus
\(\square\)
3.2 Bounds on the third version of the SVNF-Sombor graph parameter for the SVNF-graphs
Theorem 3.3
Let G be an SVNF-graph with order n and size m. Then, we derived the following results.
- (i):
-
Suppose that \({\tilde{\lambda }}\) be a vertex deleted from the SVNF-graph. Then, we have
$$\begin{aligned}&SVNFSO_{3}(G)>SVNFSO_{3}(G-{\tilde{\lambda }}). \end{aligned}$$ - (ii):
-
Suppose that \({{\tilde{\gamma }}{\tilde{\upsilon }}}\) be an edge deleted from the SVNF-graphs. Then, we have
$$\begin{aligned}&SVNFSO_{3}(G)>SVNFSO_{3}(G-{{\tilde{\gamma }}{\tilde{\upsilon }}}). \end{aligned}$$
Proof
-
(i)
Let G be an SVNF-graph having vertex \({\tilde{\lambda }}\) is deleted from G
$$\begin{aligned}&SVNFSO_{3}(G)\\&\quad = \displaystyle \sum _{u_{i}{u_j} \in E(G)} \sqrt{2}\left( \frac{(T({u}_i), N({u}_i), F({u}_i))d^2(u_i)+(T({u}_j), N({u}_j), F({u}_j))d^2(u_j)}{(T({u}_i), N({u}_i), F({u}_i))d(u_i)+(T({u}_j), N({u}_j), F({u}_j))d{(u_j)}}\right) \pi . \\&\quad =\sqrt{2}\left( \displaystyle \sum _{ \begin{array}{c} {\tilde{h}}{\tilde{y}} \in E(G)\\ {{\tilde{\lambda }}}{\tilde{h}},{{\tilde{\lambda }}}{\tilde{y}} \notin E(G)\\ {\tilde{h}}, {\tilde{y}}\ne {{\tilde{\lambda }}} \end{array}}\left( \frac{(T({\tilde{h}}), N({\tilde{h}}), F({\tilde{h}}))d^2({\tilde{h}})+(T({\tilde{y}}), N({\tilde{y}}), F({\tilde{y}}))d^2({\tilde{y}})}{(T({\tilde{h}}), N({\tilde{h}}), F({\tilde{h}}))d({\tilde{h}})+(T({\tilde{h}}), N({\tilde{h}}), F({\tilde{h}}))d({\tilde{y}})}\right) + \right. \\&\qquad \left. \displaystyle \sum _{ \begin{array}{c} {\tilde{h}}^{\prime }{\tilde{y}}^{\prime } \in E(G)\\ {{\tilde{\lambda }}}{\tilde{h}}^{\prime } \notin E(G),{{\tilde{\lambda }}}{\tilde{y}}^{\prime } \in E(G)\\ {\tilde{h}}^{\prime }, {\tilde{y}}^{\prime }\ne {{\tilde{\lambda }}} \end{array}} \left( \frac{(T({\tilde{h}^{\prime }}), N({\tilde{h}^{\prime }}), F({\tilde{h}^{\prime }}))d^2({\tilde{h}^{\prime }})+{\tilde{\gamma }_{*}}}{(T({\tilde{h}^{\prime }}), N({\tilde{h}^{\prime }}), F({\tilde{h}^{\prime }}))d({\tilde{h}}^{\prime })+{\tilde{\gamma }_{44}}}\right) \right. \\&\qquad \left. +\displaystyle \sum _{ \begin{array}{c} {{\tilde{\zeta }^{\prime }}}{{\tilde{\lambda }}}^{\prime } \in E(G)\\ {{\tilde{\lambda }}}{\zeta }^{\prime } \in E(G),{{\tilde{\lambda }}}{{\tilde{\lambda }}}^{\prime } \in E(G)\\ {{\tilde{\lambda }}}^{\prime } \ne {{\tilde{\lambda }}} \end{array}} \left( \frac{(T(({\zeta }^{\prime })), N({\zeta }^{\prime }), F({\zeta }^{\prime }))d^2({\zeta }^{\prime })+(T({{\tilde{\lambda }}}^{\prime }), N({{\tilde{\lambda }}}^{\prime }), F({{\tilde{\lambda }}}^{\prime }) )d^2({{\tilde{\lambda }}}^{\prime })}{(T(({\zeta }^{\prime })), N({\zeta }^{\prime }), F({\zeta }^{\prime }))d({\zeta }^{\prime })+(T({{\tilde{\lambda }}}^{\prime }), N({{\tilde{\lambda }}}^{\prime }), F({{\tilde{\lambda }}}^{\prime }) )d({{\tilde{\lambda }}}^{\prime })}\right) +\right. \\&\left. \displaystyle \sum _{ \begin{array}{c} {\chi }{{\tilde{\lambda }}} \in E(G)\\ {\chi ^{\prime }}{{\tilde{\lambda }}} \in E(G) \end{array}} \left( \frac{(T({\chi }), N({\chi }),F({\chi }))d^2({\chi })+{\tilde{\gamma }_{5}}}{(T({\chi }), N({\chi }),F({\chi }))d({\chi })+{\tilde{\gamma }_{55}}}\right) \right. \\&\qquad \left. >\displaystyle \sum _{ \begin{array}{c} {\tilde{h}}{\tilde{y}} \in E(G)\\ {{\tilde{\lambda }}}{\tilde{h}},{{\tilde{\lambda }}}{\tilde{y}} \notin E(G)\\ {\tilde{h}}, {\tilde{y}}\ne {{\tilde{\lambda }}} \end{array}}\left( \frac{(T({\tilde{h}}), N({\tilde{h}}), F({\tilde{h}}))d^2({\tilde{h}})+(T({\tilde{y}}), N({\tilde{y}}), F({\tilde{y}}))d^2({\tilde{y}})}{(T({\tilde{h}}), N({\tilde{h}}), F({\tilde{h}}))d({\tilde{h}})+(T({\tilde{h}}), N({\tilde{h}}), F({\tilde{h}}))d({\tilde{y}})}\right) \right. \\&\qquad \left. +\displaystyle \sum _{ \begin{array}{c} {\tilde{h}}^{\prime }{\tilde{y}}^{\prime } \in E(G)\\ {{\tilde{\lambda }}}{\tilde{h}}^{\prime } \notin E(G),{{\tilde{\lambda }}}{\tilde{y}}^{\prime } \in E(G)\\ {\tilde{h}}^{\prime }, {\tilde{y}}^{\prime }\ne {{\tilde{\lambda }}} \end{array}} \left( \frac{(T({\tilde{h}^{\prime }}), N({\tilde{h}^{\prime }}), F({\tilde{h}^{\prime }}))d^2({\tilde{h}}^{\prime })+{{\tilde{\gamma }_{*}}}}{(T({\tilde{h}^{\prime }}), N({\tilde{h}^{\prime }}), F({\tilde{h}^{\prime }}))d({\tilde{h}}^{\prime })+{{\tilde{\gamma }}_{**}}}\right) \right. \\&\qquad \left. +\displaystyle \sum _{ \begin{array}{c} {{\tilde{\zeta }^{\prime }}}{{\tilde{\lambda }}}^{\prime } \in E(G)\\ {{\tilde{\lambda }}}{\zeta }^{\prime } \in E(G),{{\tilde{\lambda }}}{{\tilde{\lambda }}}^{\prime } \in E(G)\\ {{\tilde{\lambda }}}^{\prime } \ne {{\tilde{\lambda }}} \end{array}} \left( \frac{(T(\tilde{\zeta }^{\prime }), N(\tilde{\zeta }^{\prime }),F(\tilde{\zeta }^{\prime })){{\tilde{\gamma }}_{1}}+(T(\tilde{\lambda }^{\prime }), N(\tilde{\lambda }^{\prime }),F(\tilde{\lambda }^{\prime })){{\tilde{\gamma }}_{2}}}{(T(\tilde{\zeta }^{\prime }), N(\tilde{\zeta }^{\prime }), F(\tilde{\zeta }^{\prime })){{\tilde{\gamma }}_{11}}+(T(\tilde{\lambda }^{\prime }), N(\tilde{\lambda }^{\prime }), F(\tilde{\lambda }^{\prime })){{\tilde{\gamma }}_{22}}}\right) \right) \pi ,\\&=SVNFSO_{3}(G-{\tilde{\lambda }}), \end{aligned}$$where \({\tilde{\gamma }_{*}}=\left( T({\tilde{y}^{\prime }}), N({\tilde{y}^{\prime }}), F({\tilde{y}^{\prime }})\right) \left( d({\tilde{y}}^{\prime })-\left( T({{\tilde{\lambda }},{\tilde{y}}^{\prime }}), N({{\tilde{\lambda }},{\tilde{y}}^{\prime }}), F({{\tilde{\lambda }},{\tilde{y}}^{\prime }})\right) \right) ^{2},\) \({\tilde{\gamma }}_{**}=\left( T({\tilde{y}^{\prime }}), N({\tilde{y}^{\prime }}), F({\tilde{y}^{\prime }})\right) \left( d({\tilde{y}}^{\prime })-\left( T({{\tilde{\lambda }},{\tilde{y}}^{\prime }}), N({{\tilde{\lambda }},{\tilde{y}}^{\prime }}), F({{\tilde{\lambda }},{\tilde{y}}^{\prime }})\right) \right) ,\) \({\tilde{\gamma }}_{1}=\left( d({{\tilde{\zeta }^{\prime }}})-\left( T({\tilde{\lambda }}, {\tilde{\zeta }^{\prime }}), N({\tilde{\lambda }}, {\tilde{\zeta }^{\prime }}), F({\tilde{\lambda }}, {\tilde{\zeta }^{\prime }})\right) \right) ^{2},\) \({\tilde{\gamma }}_{11}=\left( d({{\tilde{\zeta }^{\prime }}})-\left( T({\tilde{\lambda }}, {\tilde{\zeta }^{\prime }}), N({\tilde{\lambda }}, {\tilde{\zeta }^{\prime }}), F({\tilde{\lambda }}, {\tilde{\zeta }^{\prime }})\right) \right) ,\) \({\tilde{\gamma }}_{2}=\left( d({{\tilde{\lambda }}}^{\prime })-\left( T({\tilde{\lambda }}, {\tilde{\lambda }}^{\prime }), N({\tilde{\lambda }}, {\tilde{\lambda }}^{\prime }), F({\tilde{\lambda }}, {\tilde{\lambda }}^{\prime })\right) \right) ^{2},\) \({\tilde{\gamma }}_{22}=\left( d({{\tilde{\lambda }}}^{\prime })-\left( T({\tilde{\lambda }}, {\tilde{\lambda }}^{\prime }), N({\tilde{\lambda }}, {\tilde{\lambda }}^{\prime }), F({\tilde{\lambda }}, {\tilde{\lambda }}^{\prime })\right) \right) ,\) \(\tilde{\gamma }_4=(T({\tilde{y}}^{\prime }), N({\tilde{y}}^{\prime }), F({\tilde{y}}^{\prime }))d^2({\tilde{y}}^{\prime }),\) \(\tilde{\gamma }_{44}=(T({\tilde{y}}^{\prime }), N({\tilde{y}}^{\prime }), F({\tilde{y}}^{\prime }))d_{\partial }({\tilde{y}}^{\prime }),\) \({\tilde{\gamma }_{5}}=(T({{\tilde{\lambda }}}), N({{\tilde{\lambda }}}), F({{\tilde{\lambda }}}) )d^2({{\tilde{\lambda }}}),\) and \({\tilde{\gamma }_{55}}=(T({{\tilde{\lambda }}}), N({{\tilde{\lambda }}}), F({{\tilde{\lambda }}}) )d({{\tilde{\lambda }}}).\) Therefore
$$\begin{aligned} SVNFSO_{3}(G)>SVNFSO_{3}(G-{\tilde{\lambda }}). \end{aligned}$$ -
(ii)
Let G be an SVNF-graph with an edge \(e={{\tilde{\gamma }}{\tilde{\upsilon }}},\) which is deleted from G. Then, we have
$$\begin{aligned}&SVNFSO_{3}(G)\\&\quad = \displaystyle \sum _{u_{i}{u_j} \in E(G)} \sqrt{2}\left( \frac{\left( T({u}_i), N({u}_i), F({u}_i)\right) d^2(u_i)+\left( T({u}_j), N({u}_j), F({u}_j)\right) d^2(u_j)}{\left( T({u}_i), N({u}_i), F({u}_i)\right) d(u_i)+\left( T({u}_j), N({u}_j), F({u}_j)\right) d(u_j)}\right) \pi . \\&\quad =\sqrt{2}\left( \displaystyle \sum _{ \begin{array}{c} {\phi }{\daleth } \in E(G)\\ {{\tilde{\gamma }}}{\phi },{\phi }{{\tilde{\upsilon }}} \notin E(G)\\ {\daleth }{{\tilde{\gamma }}},{\daleth }{{\tilde{\upsilon }}} \notin E(G) \end{array}}\left( \frac{\left( T({\phi }), N({\phi }), F({\phi })\right) d^2({\phi })+\left( T({\daleth }), N({\daleth }), F({\daleth })\right) d^2({\daleth })}{\left( T({\phi }), N({\phi }), F({\phi })\right) d_{\partial }({\phi })+\left( T({\daleth }), N({\daleth }), F({\daleth })\right) d({\daleth })}\right) + \right. \\&\qquad \left. \displaystyle \sum _{ \begin{array}{c} {\tilde{h}}^{\prime \prime }{\tilde{y}}^{\prime \prime } \in E(G)\\ {{\tilde{\gamma }}}{\tilde{h}}^{\prime \prime } \in E(G),{{\tilde{\upsilon }}}{\tilde{y}}^{\prime \prime } \notin E(G)\\ {\tilde{h}}^{\prime \prime } \ne {{\tilde{\gamma }}} \end{array}} \left( \frac{\left( T({\tilde{h}}^{\prime \prime }), N({\tilde{h}}^{\prime \prime }), F({\tilde{h}}^{\prime \prime })\right) d^2({\tilde{h}}^{\prime \prime })+{\tilde{\lambda }_{66}}}{\left( T({\tilde{h}}^{\prime \prime }), N({\tilde{h}}^{\prime \prime }), F({\tilde{h}}^{\prime \prime })\right) d({\tilde{h}}^{\prime \prime })+{\tilde{\lambda }_{6}}}\right) \right. \\&\qquad +\left. \left( \frac{\left( T({\tilde{\gamma }}), N({\tilde{\gamma }}), F({\tilde{\gamma }})\right) d^2({{\tilde{\gamma }}})+{\beta }{\partial }_{n}({{\tilde{\upsilon }}})d^2({{\tilde{\upsilon }}})}{\left( T({\tilde{\gamma }}), N({\tilde{\gamma }}), F({\tilde{\gamma }})\right) d({\tilde{\gamma }})+{\beta }{\partial }_{n}({{\tilde{\upsilon }}})d_{\partial }({{\tilde{\upsilon }}})}\right) >\right. \\&\qquad \left. \displaystyle \sum _{ \begin{array}{c} {\phi }{\daleth } \in E(G)\\ {{\tilde{\gamma }}}{\phi },{\phi }{{\tilde{\upsilon }}} \notin E(G)\\ {\daleth }{{\tilde{\gamma }}},{\daleth }{{\tilde{\upsilon }}} \notin E(G) \end{array}}\left( \frac{\left( T({\phi }), N({\phi }), F({\phi })\right) d^2({\phi })+\left( T({\daleth }), N({\daleth }), F({\daleth })\right) d^2({\daleth })}{\left( T({\phi }), N({\phi }), F({\phi })\right) d({\phi })+\left( T({\daleth }), N({\daleth }), F({\daleth })\right) d({\daleth })}\right) \right. \\&\qquad \left. +\displaystyle \sum _{ \begin{array}{c} {\tilde{h}}^{\prime \prime }{\tilde{y}}^{\prime \prime } \in E(G)\\ {{\tilde{\gamma }}}{\tilde{h}}^{\prime \prime } \in E(G),{{\tilde{\upsilon }}}{\tilde{y}}^{\prime \prime } \notin E(G)\\ {\tilde{h}}^{\prime \prime } \ne {{\tilde{\gamma }}} \end{array}} \left( \frac{\left( T({\tilde{h}}^{\prime \prime }), N({\tilde{h}}^{\prime \prime }), F({\tilde{h}}^{\prime \prime })\right) {\tilde{\lambda }_{7}}\left( T({\tilde{y}}^{\prime \prime }), N({\tilde{y}}^{\prime \prime }), F({\tilde{y}}^{\prime \prime })\right) d^2({\tilde{y}}^{\prime \prime })}{\left( T({\tilde{h}}^{\prime \prime }), N({\tilde{h}}^{\prime \prime }), F({\tilde{h}}^{\prime \prime })\right) {\tilde{\lambda }_{77}}+\left( T({\tilde{y}}^{\prime \prime }), N({\tilde{y}}^{\prime \prime }), F({\tilde{y}}^{\prime \prime })\right) d({\tilde{y}}^{\prime \prime })}\right) \right) \pi ,\\&\quad =SVNFSO_{3}(G-{{\tilde{\gamma }}}{{\tilde{\upsilon }}}), \end{aligned}$$where \({\tilde{\lambda }_{7}}=\left( d({\tilde{h}}^{\prime \prime })-\left( T({{\tilde{\gamma }}}, {\tilde{\upsilon }}), N({{\tilde{\gamma }}}, {\tilde{\upsilon }}), F({{\tilde{\gamma }}}, {\tilde{\upsilon }})\right) \right) ^{2},\) \({\tilde{\lambda }_{77}}=\left( d({\tilde{h}}^{\prime \prime })-\left( T({{\tilde{\gamma }}}, {\tilde{\upsilon }}), N({{\tilde{\gamma }}}, {\tilde{\upsilon }}), F({{\tilde{\gamma }}}, {\tilde{\upsilon }})\right) \right) ,\) \({\tilde{\lambda }_{6}}=\left( T({\tilde{y}}^{\prime \prime }), N({\tilde{y}}^{\prime \prime }), F({\tilde{y}}^{\prime \prime })\right) d({\tilde{y}}^{\prime \prime }),\) and \({\tilde{\lambda }_{66}}=\left( T({\tilde{y}}^{\prime \prime }), N({\tilde{y}}^{\prime \prime }), F({\tilde{y}}^{\prime \prime })\right) d^2({\tilde{y}}^{\prime \prime }).\) So,
$$\begin{aligned} SVNFSO_{3}(G)>SVNFSO_{3}(G-{{\tilde{\gamma }}{\tilde{\upsilon }}}). \end{aligned}$$
\(\square\)
Theorem 3.4
The bounds on the third version of the SVNF-Sombor graph parameter for a simple and connected SVNF-graph are given as
if \({\alpha }={\beta },\) then it is equal to zero.
Proof
Using the formulation of the third version of the SVNF-Sombor graph parameter
where \((T_{\mu })\) truth degree, \((N_{\mu })\) neutral degree, and \((F_{\mu })\) falsity degree are not same.
Assume that G is a SVNF-graph with order \(\left( \displaystyle \displaystyle \sum _{{\eta }, {\hat{\eta }}\in V(G)}(T), \displaystyle \sum _{{\eta }, {\hat{\eta }}\in V(G)}(N), \displaystyle \displaystyle \sum _{{\eta }, {\hat{\eta }}\in V(G)}(F)\right)\) and size is
\(\left( \displaystyle \displaystyle \sum _{{\eta }{\hat{\eta }}\in E(G)}(T), \displaystyle \sum _{{\eta }{\hat{\eta }}\in E(G)}(N), \displaystyle \sum _{{\eta }{\hat{\eta }}\in E(G)}(F)\right) ,\) respectively. Then, \(T({\hat{\eta }})<\displaystyle \displaystyle \sum _{{\eta }, {\hat{\eta }}\in V(G)}(T),\) \(N({\hat{\eta }})<\displaystyle \displaystyle \sum _{{\eta }, {\hat{\eta }}\in V(G)}(N),\) and \(F({\hat{\eta }})<\displaystyle \displaystyle \sum _{{\eta }, {\hat{\eta }}\in V(G)}(F).\) Now, compute the degree of any vertex of G, as:
Also, \(\displaystyle \displaystyle \sum _{{\hat{\eta }}\sim {\eta }{\hat{\eta }}\in E(G)}(T_{\hat{\eta }}({\eta }{\hat{\eta }}))<\displaystyle \displaystyle \sum _{{\eta }, {\hat{\eta }}\in V(G)}(T),\) \(\displaystyle \displaystyle \sum _{{\hat{\eta }}\sim {\eta }{\hat{\eta }}\in E(G)}(N_{\hat{\eta }}({\eta }{\hat{\eta }}))<\displaystyle \displaystyle \sum _{{\eta }, {\hat{\eta }}\in V(G)}(N),\) and \(\displaystyle \displaystyle \sum _{{\hat{\eta }}\sim {\eta }{\hat{\eta }}\in E(G)}(F_{\hat{\eta }}({\eta }{\hat{\eta }}))<\displaystyle \displaystyle \sum _{{\eta }, {\hat{\eta }}\in V(G)}(F).\) Compute the square of the degree of any vertex of G as:
Also, \(\displaystyle \displaystyle \sum _{{\hat{\eta }}\sim {\eta }{\hat{\eta }}\in E(G)}(T_{\hat{\eta }}^2({\eta }{\hat{\eta }}))<\displaystyle \displaystyle \sum _{{\eta }, {\hat{\eta }}\in V(G)}(T)^2,\) \(\displaystyle \displaystyle \sum _{{\hat{\eta }}\sim {\eta }{\hat{\eta }}\in E(G)}(N_{\hat{\eta }}^2({\eta }{\hat{\eta }}))<\displaystyle \displaystyle \sum _{{\eta }, {\hat{\eta }}\in V(G)}(N)^2,\) and \(\displaystyle \displaystyle \sum _{{\hat{\eta }}\sim {\eta }{\hat{\eta }}\in E(G)}(F_{\hat{\eta }}^2({\eta }{\hat{\eta }}))<\displaystyle \displaystyle \sum _{{\eta }, {\hat{\eta }}\in V(G)}(F)^2.\) Using these inequalities and we get,
and
Adding above three inequalities 15, 16, and 17
Similarly
Adding both inequalities, 18, and 19. Then, we get
Also
From above inequalities 21 and 22. Then
where
and
Thus
\(\square\)
3.3 Bounds on the fourth version of the SVNF-Sombor graph parameter for the linear diophantine fuzzy graphs
Theorem 3.5
Let G be an SVNF-graph with order n and size m. Then, we derived the following results.
-
(i)
Suppose that \({\tilde{\lambda }}\) be a vertex deleted from the SVNF-graph. Then, we have
$$\begin{aligned}&SVNFSO_{4}(G)>SVNFSO_{4}(G-{\tilde{\lambda }}). \end{aligned}$$ -
(ii)
Suppose that \({{\tilde{\gamma }}{\tilde{\upsilon }}}\) be an edge deleted from the SVNF-graphs. Then, we have
$$\begin{aligned}&SVNFSO_{4}(G)>SVNFSO_{4}(G-{{\tilde{\gamma }}{\tilde{\upsilon }}}). \end{aligned}$$
Proof
-
(i)
Let G be an SVNF-graph having vertex \({\tilde{\lambda }}\) is deleted from G
$$\begin{aligned}&SVNFSO_{4}(G)\\&\quad = \displaystyle \sum _{u_{i}{u_j} \in E(G)} \frac{1}{2}\left( \frac{(T({u}_i), N({u}_i), F({u}_i))d^2(u_i)+(T({u}_j), N({u}_j), F({u}_j))d^2(u_j)}{(T({u}_i), N({u}_i), F({u}_i))d(u_i)+(T({u}_j), N({u}_j), F({u}_j))d{(u_j)}}\right) ^2\pi . \\&\quad =\frac{1}{2}\left( \displaystyle \sum _{ \begin{array}{c} {\tilde{h}}{\tilde{y}} \in E(G)\\ {{\tilde{\lambda }}}{\tilde{h}},{{\tilde{\lambda }}}{\tilde{y}} \notin E(G)\\ {\tilde{h}}, {\tilde{y}}\ne {{\tilde{\lambda }}} \end{array}}\left( \frac{(T({\tilde{h}}), N({\tilde{h}}), F({\tilde{h}}))d^2({\tilde{h}})+(T({\tilde{y}}), N({\tilde{y}}), F({\tilde{y}}))d^2({\tilde{y}})}{(T({\tilde{h}}), N({\tilde{h}}), F({\tilde{h}}))d({\tilde{h}})+(T({\tilde{h}}), N({\tilde{h}}), F({\tilde{h}}))d({\tilde{y}})}\right) ^2 + \right. \\&\qquad \left. \displaystyle \sum _{ \begin{array}{c} {\tilde{h}}^{\prime }{\tilde{y}}^{\prime } \in E(G)\\ {{\tilde{\lambda }}}{\tilde{h}}^{\prime } \notin E(G),{{\tilde{\lambda }}}{\tilde{y}}^{\prime } \in E(G)\\ {\tilde{h}}^{\prime }, {\tilde{y}}^{\prime }\ne {{\tilde{\lambda }}} \end{array}} \left( \frac{(T({\tilde{h}^{\prime }}), N({\tilde{h}^{\prime }}), F({\tilde{h}^{\prime }}))d^2({\tilde{h}^{\prime }})+{\tilde{\gamma }_{*}}}{(T({\tilde{h}^{\prime }}), N({\tilde{h}^{\prime }}), F({\tilde{h}^{\prime }}))d({\tilde{h}}^{\prime })+{\tilde{\gamma }_{44}}}\right) ^2 \right. \\&\qquad \left. +\displaystyle \sum _{ \begin{array}{c} {{\tilde{\zeta }^{\prime }}}{{\tilde{\lambda }}}^{\prime } \in E(G)\\ {{\tilde{\lambda }}}{\zeta }^{\prime } \in E(G),{{\tilde{\lambda }}}{{\tilde{\lambda }}}^{\prime } \in E(G)\\ {{\tilde{\lambda }}}^{\prime } \ne {{\tilde{\lambda }}} \end{array}} \left( \frac{(T(({\zeta }^{\prime })), N({\zeta }^{\prime }), F({\zeta }^{\prime }))d^2({\zeta }^{\prime })+(T({{\tilde{\lambda }}}^{\prime }), N({{\tilde{\lambda }}}^{\prime }), F({{\tilde{\lambda }}}^{\prime }) )d^2({{\tilde{\lambda }}}^{\prime })}{(T(({\zeta }^{\prime })), N({\zeta }^{\prime }), F({\zeta }^{\prime }))d({\zeta }^{\prime })+(T({{\tilde{\lambda }}}^{\prime }), N({{\tilde{\lambda }}}^{\prime }), F({{\tilde{\lambda }}}^{\prime }) )d({{\tilde{\lambda }}}^{\prime })}\right) ^2+\right. \\&\qquad \left. \displaystyle \sum _{ \begin{array}{c} {\chi }{{\tilde{\lambda }}} \in E(G)\\ {\chi ^{\prime }}{{\tilde{\lambda }}} \in E(G) \end{array}} \left( \frac{(T({\chi }), N({\chi }),F({\chi }))d^2({\chi })+{\tilde{\gamma }_{5}}}{(T({\chi }), N({\chi }),F({\chi }))d({\chi })+{\tilde{\gamma }_{55}}}\right) ^2\right. \\&\qquad \left. >\displaystyle \sum _{ \begin{array}{c} {\tilde{h}}{\tilde{y}} \in E(G)\\ {{\tilde{\lambda }}}{\tilde{h}},{{\tilde{\lambda }}}{\tilde{y}} \notin E(G)\\ {\tilde{h}}, {\tilde{y}}\ne {{\tilde{\lambda }}} \end{array}}\left( \frac{(T({\tilde{h}}), N({\tilde{h}}), F({\tilde{h}}))d^2({\tilde{h}})+(T({\tilde{y}}), N({\tilde{y}}), F({\tilde{y}}))d^2({\tilde{y}})}{(T({\tilde{h}}), N({\tilde{h}}), F({\tilde{h}}))d({\tilde{h}})+(T({\tilde{h}}), N({\tilde{h}}), F({\tilde{h}}))d({\tilde{y}})}\right) ^2\right. \\&\qquad \left. +\displaystyle \sum _{ \begin{array}{c} {\tilde{h}}^{\prime }{\tilde{y}}^{\prime } \in E(G)\\ {{\tilde{\lambda }}}{\tilde{h}}^{\prime } \notin E(G),{{\tilde{\lambda }}}{\tilde{y}}^{\prime } \in E(G)\\ {\tilde{h}}^{\prime }, {\tilde{y}}^{\prime }\ne {{\tilde{\lambda }}} \end{array}} \left( \frac{(T({\tilde{h}^{\prime }}), N({\tilde{h}^{\prime }}), F({\tilde{h}^{\prime }}))d^2({\tilde{h}}^{\prime })+{{\tilde{\gamma }_{*}}}}{(T({\tilde{h}^{\prime }}), N({\tilde{h}^{\prime }}), F({\tilde{h}^{\prime }}))d({\tilde{h}}^{\prime })+{{\tilde{\gamma }}_{**}}}\right) ^2 \right. \\&\qquad \left. +\displaystyle \sum _{ \begin{array}{c} {{\tilde{\zeta }^{\prime }}}{{\tilde{\lambda }}}^{\prime } \in E(G)\\ {{\tilde{\lambda }}}{\zeta }^{\prime } \in E(G),{{\tilde{\lambda }}}{{\tilde{\lambda }}}^{\prime } \in E(G)\\ {{\tilde{\lambda }}}^{\prime } \ne {{\tilde{\lambda }}} \end{array}} \left( \frac{(T(\tilde{\zeta }^{\prime }), N(\tilde{\zeta }^{\prime }),F(\tilde{\zeta }^{\prime })){{\tilde{\gamma }}_{1}}+(T(\tilde{\lambda }^{\prime }), N(\tilde{\lambda }^{\prime }),F(\tilde{\lambda }^{\prime })){{\tilde{\gamma }}_{2}}}{(T(\tilde{\zeta }^{\prime }), N(\tilde{\zeta }^{\prime }), F(\tilde{\zeta }^{\prime })){{\tilde{\gamma }}_{11}}+(T(\tilde{\lambda }^{\prime }), N(\tilde{\lambda }^{\prime }), F(\tilde{\lambda }^{\prime })){{\tilde{\gamma }}_{22}}}\right) ^2\right) \pi ,\\&\quad =SVNFSO_{4}(G-{\tilde{\lambda }}). \end{aligned}$$where \({\tilde{\gamma }_{*}}=\left( T({\tilde{y}^{\prime }}), N({\tilde{y}^{\prime }}), F({\tilde{y}^{\prime }})\right) \left( d({\tilde{y}}^{\prime })-\left( T({{\tilde{\lambda }},{\tilde{y}}^{\prime }}), N({{\tilde{\lambda }},{\tilde{y}}^{\prime }}), F({{\tilde{\lambda }},{\tilde{y}}^{\prime }})\right) \right) ^{2},\) \({\tilde{\gamma }}_{**}=\left( T({\tilde{y}^{\prime }}), N({\tilde{y}^{\prime }}), F({\tilde{y}^{\prime }})\right) \left( d({\tilde{y}}^{\prime })-\left( T({{\tilde{\lambda }},{\tilde{y}}^{\prime }}), N({{\tilde{\lambda }},{\tilde{y}}^{\prime }}), F({{\tilde{\lambda }},{\tilde{y}}^{\prime }})\right) \right) ,\) \({\tilde{\gamma }}_{1}=\left( d({{\tilde{\zeta }^{\prime }}})-\left( T({\tilde{\lambda }}, {\tilde{\zeta }^{\prime }}), N({\tilde{\lambda }}, {\tilde{\zeta }^{\prime }}), F({\tilde{\lambda }}, {\tilde{\zeta }^{\prime }})\right) \right) ^{2},\) \({\tilde{\gamma }}_{11}=\left( d({{\tilde{\zeta }^{\prime }}})-\left( T({\tilde{\lambda }}, {\tilde{\zeta }^{\prime }}), N({\tilde{\lambda }}, {\tilde{\zeta }^{\prime }}), F({\tilde{\lambda }}, {\tilde{\zeta }^{\prime }})\right) \right) ,\) \({\tilde{\gamma }}_{2}=\left( d({{\tilde{\lambda }}}^{\prime })-\left( T({\tilde{\lambda }}, {\tilde{\lambda }}^{\prime }), N({\tilde{\lambda }}, {\tilde{\lambda }}^{\prime }), F({\tilde{\lambda }}, {\tilde{\lambda }}^{\prime })\right) \right) ^{2},\) \({\tilde{\gamma }}_{22}=\left( d({{\tilde{\lambda }}}^{\prime })-\left( T({\tilde{\lambda }}, {\tilde{\lambda }}^{\prime }), N({\tilde{\lambda }}, {\tilde{\lambda }}^{\prime }), F({\tilde{\lambda }}, {\tilde{\lambda }}^{\prime })\right) \right) ,\) \(\tilde{\gamma }_4=(T({\tilde{y}}^{\prime }), N({\tilde{y}}^{\prime }), F({\tilde{y}}^{\prime }))d^2({\tilde{y}}^{\prime }),\) \(\tilde{\gamma }_{44}=(T({\tilde{y}}^{\prime }), N({\tilde{y}}^{\prime }), F({\tilde{y}}^{\prime }))d_{\partial }({\tilde{y}}^{\prime }),\) \({\tilde{\gamma }_{5}}=(T({{\tilde{\lambda }}}), N({{\tilde{\lambda }}}), F({{\tilde{\lambda }}}) )d^2({{\tilde{\lambda }}}),\) and \({\tilde{\gamma }_{55}}=(T({{\tilde{\lambda }}}), N({{\tilde{\lambda }}}), F({{\tilde{\lambda }}}) )d({{\tilde{\lambda }}}).\) Therefore
$$\begin{aligned}&SVNFSO_{4}(G)>SVNFSO_{4}(G-{\tilde{\lambda }}). \end{aligned}$$ -
(ii)
Let G be an SVNF-graph with an edge \(e={{\tilde{\gamma }}{\tilde{\upsilon }}},\) which is deleted from G. Then, we have
$$\begin{aligned}&SVNFSO_{4}(G)\\&\quad = \displaystyle \sum _{u_{i}{u_j} \in E(G)} \frac{1}{2}\left( \frac{\left( T({u}_i), N({u}_i), F({u}_i)\right) d^2(u_i)+\left( T({u}_j), N({u}_j), F({u}_j)\right) d^2(u_j)}{\left( T({u}_i), N({u}_i), F({u}_i)\right) d(u_i)+\left( T({u}_j), N({u}_j), F({u}_j)\right) d(u_j)}\right) ^2\pi . \\&\quad =\frac{1}{2}\left( \displaystyle \sum _{ \begin{array}{c} {\phi }{\daleth } \in E(G)\\ {{\tilde{\gamma }}}{\phi },{\phi }{{\tilde{\upsilon }}} \notin E(G)\\ {\daleth }{{\tilde{\gamma }}},{\daleth }{{\tilde{\upsilon }}} \notin E(G) \end{array}}\left( \frac{\left( T({\phi }), N({\phi }), F({\phi })\right) d^2({\phi })+\left( T({\daleth }), N({\daleth }), F({\daleth })\right) d^2({\daleth })}{\left( T({\phi }), N({\phi }), F({\phi })\right) d_{\partial }({\phi })+\left( T({\daleth }), N({\daleth }), F({\daleth })\right) d({\daleth })}\right) ^2+ \right. \\&\qquad \left. \displaystyle \sum _{ \begin{array}{c} {\tilde{h}}^{\prime \prime }{\tilde{y}}^{\prime \prime } \in E(G)\\ {{\tilde{\gamma }}}{\tilde{h}}^{\prime \prime } \in E(G),{{\tilde{\upsilon }}}{\tilde{y}}^{\prime \prime } \notin E(G)\\ {\tilde{h}}^{\prime \prime } \ne {{\tilde{\gamma }}} \end{array}} \left( \frac{\left( T({\tilde{h}}^{\prime \prime }), N({\tilde{h}}^{\prime \prime }), F({\tilde{h}}^{\prime \prime })\right) d^2({\tilde{h}}^{\prime \prime })+{\tilde{\lambda }_{66}}}{\left( T({\tilde{h}}^{\prime \prime }), N({\tilde{h}}^{\prime \prime }), F({\tilde{h}}^{\prime \prime })\right) d({\tilde{h}}^{\prime \prime })+{\tilde{\lambda }_{6}}}\right) ^2\right. \\&\qquad +\left. \left( \frac{\left( T({\tilde{\gamma }}), N({\tilde{\gamma }}), F({\tilde{\gamma }})\right) d^2({{\tilde{\gamma }}})+{\beta }{\partial }_{n}({{\tilde{\upsilon }}})d^2({{\tilde{\upsilon }}})}{\left( T({\tilde{\gamma }}), N({\tilde{\gamma }}), F({\tilde{\gamma }})\right) d({\tilde{\gamma }})+{\beta }{\partial }_{n}({{\tilde{\upsilon }}})d_{\partial }({{\tilde{\upsilon }}})}\right) ^2>\right. \\&\qquad \left. \displaystyle \sum _{ \begin{array}{c} {\phi }{\daleth } \in E(G)\\ {{\tilde{\gamma }}}{\phi },{\phi }{{\tilde{\upsilon }}} \notin E(G)\\ {\daleth }{{\tilde{\gamma }}},{\daleth }{{\tilde{\upsilon }}} \notin E(G) \end{array}}\left( \frac{\left( T({\phi }), N({\phi }), F({\phi })\right) d^2({\phi })+\left( T({\daleth }), N({\daleth }), F({\daleth })\right) d^2({\daleth })}{\left( T({\phi }), N({\phi }), F({\phi })\right) d({\phi })+\left( T({\daleth }), N({\daleth }), F({\daleth })\right) d({\daleth })}\right) ^2\right. \\ \\&\qquad \left. +\displaystyle \sum _{ \begin{array}{c} {\tilde{h}}^{\prime \prime }{\tilde{y}}^{\prime \prime } \in E(G)\\ {{\tilde{\gamma }}}{\tilde{h}}^{\prime \prime } \in E(G),{{\tilde{\upsilon }}}{\tilde{y}}^{\prime \prime } \notin E(G)\\ {\tilde{h}}^{\prime \prime } \ne {{\tilde{\gamma }}} \end{array}} \left( \frac{\left( T({\tilde{h}}^{\prime \prime }), N({\tilde{h}}^{\prime \prime }), F({\tilde{h}}^{\prime \prime })\right) {\tilde{\lambda }_{7}}\left( T({\tilde{y}}^{\prime \prime }), N({\tilde{y}}^{\prime \prime }), F({\tilde{y}}^{\prime \prime })\right) d^2({\tilde{y}}^{\prime \prime })}{\left( T({\tilde{h}}^{\prime \prime }), N({\tilde{h}}^{\prime \prime }), F({\tilde{h}}^{\prime \prime })\right) {\tilde{\lambda }_{77}}+\left( T({\tilde{y}}^{\prime \prime }), N({\tilde{y}}^{\prime \prime }), F({\tilde{y}}^{\prime \prime })\right) d({\tilde{y}}^{\prime \prime })}\right) ^2 \right) \pi ,\\&\quad =SVNFSO_{4}(G-{{\tilde{\gamma }}}{{\tilde{\upsilon }}}), \end{aligned}$$where \({\tilde{\lambda }_{7}}=\left( d({\tilde{h}}^{\prime \prime })-\left( T({{\tilde{\gamma }}}, {\tilde{\upsilon }}), N({{\tilde{\gamma }}}, {\tilde{\upsilon }}), F({{\tilde{\gamma }}}, {\tilde{\upsilon }})\right) \right) ^{2},\) \({\tilde{\lambda }_{77}}=\left( d({\tilde{h}}^{\prime \prime })-\left( T({{\tilde{\gamma }}}, {\tilde{\upsilon }}), N({{\tilde{\gamma }}}, {\tilde{\upsilon }}), F({{\tilde{\gamma }}}, {\tilde{\upsilon }})\right) \right) ,\) \({\tilde{\lambda }_{6}}=\left( T({\tilde{y}}^{\prime \prime }), N({\tilde{y}}^{\prime \prime }), F({\tilde{y}}^{\prime \prime })\right) d({\tilde{y}}^{\prime \prime }),\) and \({\tilde{\lambda }_{66}}=\left( T({\tilde{y}}^{\prime \prime }), N({\tilde{y}}^{\prime \prime }), F({\tilde{y}}^{\prime \prime })\right) d^2({\tilde{y}}^{\prime \prime }).\) Therefore
$$\begin{aligned}&SVNFSO_{4}(G)>SVNFSO_{4}(G-{{\tilde{\gamma }}{\tilde{\upsilon }}}). \end{aligned}$$
\(\square\)
Theorem 3.6
The bounds on the fourth version of the SVNF-Sombor graph parameter for a simple and connected SVNF-graph are given as
if \({\alpha }={\beta },\) then it is equal to zero.
Proof
Using the formulation of the fourth version of the SVNF-Sombor graph parameter
where \((T_{\mu })\) truth degree, \((N_{\mu })\) neutral degree, and \((F_{\mu })\) falsity degree are not same.
Assume that G is an SVNF-graph with order \(\left( \displaystyle \displaystyle \sum _{{\eta }, {\hat{\eta }}\in V(G)}(T), \displaystyle \sum _{{\eta }, {\hat{\eta }}\in V(G)}(N), \displaystyle \displaystyle \sum _{{\eta }, {\hat{\eta }}\in V(G)}(F)\right)\) and size is
\(\left( \displaystyle \displaystyle \sum _{{\eta }{\hat{\eta }}\in E(G)}(T), \displaystyle \sum _{{\eta }{\hat{\eta }}\in E(G)}(N), \displaystyle \sum _{{\eta }{\hat{\eta }}\in E(G)}(F)\right) ,\) respectively. Then, \(T({\hat{\eta }})<\displaystyle \displaystyle \sum _{{\eta }, {\hat{\eta }}\in V(G)}(T),\) \(N({\hat{\eta }})<\displaystyle \displaystyle \sum _{{\eta }, {\hat{\eta }}\in V(G)}(N),\) and \(F({\hat{\eta }})<\displaystyle \displaystyle \sum _{{\eta }, {\hat{\eta }}\in V(G)}(F).\) Now, compute the degree of any vertex of G, as:
Also, \(\displaystyle \displaystyle \sum _{{\hat{\eta }}\sim {\eta }{\hat{\eta }}\in E(G)}(T_{\hat{\eta }}({\eta }{\hat{\eta }}))<\displaystyle \displaystyle \sum _{{\eta }, {\hat{\eta }}\in V(G)}(T),\) \(\displaystyle \displaystyle \sum _{{\hat{\eta }}\sim {\eta }{\hat{\eta }}\in E(G)}(N_{\hat{\eta }}({\eta }{\hat{\eta }})) <\displaystyle \displaystyle \sum _{{\eta }, {\hat{\eta }}\in V(G)}(N),\) and \(\displaystyle \displaystyle \sum _{{\hat{\eta }}\sim {\eta }{\hat{\eta }}\in E(G)}(F_{\hat{\eta }}({\eta }{\hat{\eta }}))<\displaystyle \displaystyle \sum _{{\eta }, {\hat{\eta }}\in V(G)}(F).\) Compute the square of the degree of any vertex of G as:
Also, \(\displaystyle \displaystyle \sum _{{\hat{\eta }}\sim {\eta }{\hat{\eta }}\in E(G)}(T_{\hat{\eta }}^2({\eta }{\hat{\eta }}))<\displaystyle \displaystyle \sum _{{\eta }, {\hat{\eta }}\in V(G)}(T)^2,\) \(\displaystyle \displaystyle \sum _{{\hat{\eta }}\sim {\eta }{\hat{\eta }}\in E(G)}(N_{\hat{\eta }}^2({\eta }{\hat{\eta }}))<\displaystyle \displaystyle \sum _{{\eta }, {\hat{\eta }}\in V(G)}(N)^2,\) and \(\displaystyle \displaystyle \sum _{{\hat{\eta }}\sim {\eta }{\hat{\eta }}\in E(G)}(F_{\hat{\eta }}^2({\eta }{\hat{\eta }}))<\displaystyle \displaystyle \sum _{{\eta }, {\hat{\eta }}\in V(G)}(F)^2.\) Using these inequalities and we get
and
Adding above three inequalities 23, 24, and 25
Similarly
Adding both inequalities, 26, and 27. Then, we get
Also
From above inequalities 29 and 30. Then
where,
and
Thus
\(\square\)
4 Algorithm
Consider \(SVNF-graph\) to be two graphs; each vertex or node shows people, and their fuzzy values have three components, such that \(T_{f}, N_{f},\) and \(F_{f}\) are the truth value, neutral value, and falsity fuzzy value. Similarly, every edge has \(T_{f}, N_{f},\) and \(F_{f}\) for consideration of \(SVNF-\)graphs. To obtain the desired result, we computed the fuzzy value individually for every vertex (people) using the dot product method and also for edges and then added them. Consider the graph \(SVNF-graph=(V, E).\) To determine the value of the Sombor graph parameter, third, and fourth invariants of the SVNF-Sombor graph parameters. We construct the following algorithm:
- Step 1::
-
Compute the membership value for each vertex (People).
- Step 2::
-
Compute the neutral membership value for each vertex (People).
- Step 3::
-
Compute the falsity degree for each vertex (People).
- Step 4::
-
Compute the \(d(v)-degrees\) for each vertex (peoples).
- Step 5::
-
Compute the \(d^{2}(v)-degrees\) for each vertex (peoples) using the concept of a dot product.
- Step 6::
-
Compute the SVNF-Sombor graph parameter for peoples.
- Step 7::
-
Sum up the value of membership values neural values, and also falsity values.
Similarly, we work for the third and fourth versions of the fuzzy Sombor indices. Also, flowchart of the article in 2
Where SVNFSO, SVNFSO3, and SVNFSO4 are the versions of the single-valued neutrosophic fuzzy Sombor graph parameters
4.1 Application
In this fragment of the article, we will give an application of a social network in which the Sombor, third, and fourth versions of the SVNF-Sombor graph parameter are used. In the presented application, we consider a social network in which artificial intelligence sends a friend request to people who know each other automatically. With the help of that application, we considered five people: \(\tau _{1}, \tau _{2},\) \(\tau _{3}, \tau _{4},\) \(\tau _{5}, \tau _{6},\) and \(\tau _{7 },\) are connected between them by different relational (friendship) routes or paths. \(\tau _{1}\) is a friend of the \(\tau _{2}, \tau _{6},\) and \(\tau _{6}. \tau _{7}\) is the friend of the \(\tau _{1}, \tau _{2},\) \(\tau _{3}, \tau _{4}, \tau _{5},\) and \(\tau _{6}.\) Will artificial intelligence send friend requests to \(\tau _{3},\) \(\tau _{4},\) \(\tau _{5},\) through \(\tau _{7}\) of \(\tau _{1}.\) We show that if we remove \(\tau _{7}\) or people, then what will be the effect on the environment of a particular area? or How many chances does an artificial intelligence send the friend request of \(\tau _{1}\) to \(\tau _{3},\) \(\tau _{4},\) and \(\tau _{5}\) or suggest a friend request to this vertex or people? Using the definition of the single-valued neutrosophic Sombor graph parameter of the third and fourth versions, we determine how many chances there are to send a friend suggestion to other people in social networking after removing the path (edge) or locking (deleting) the person (people) (vertex). By this time, consumption will decrease due to the improvement of the system.
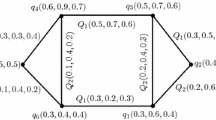
Assumed an SVN fuzzified social network or connection between the peoples \(\tau _{1},\) \(\tau _{2},\) \(\tau _{3},\) \(\tau _{4},\) \(\tau _{5},\) \(\tau _{6},\) and \(\tau _{7}\), respectively, in particular social media network, as shown in Fig. 3. The vertices of graphs are known as people or persons, and the edges are related to the network.
First, we calculate the degree of every vertex or person (people) of \(G_{1}\)
Now, we compute the square degree of every vertex
Here, we are working on the SVNF-Sombor graph parameter
We compute the value of the third invariant of the SVNF-Sombor graph parameter. By utilizing the formulation of the third invariant of the SVNF-Sombor graph parameter
Compute the value of the SVNF-Sombor graph parameter in the fourth version:
By applying the formulation of the fourth version of the SVNF-Sombor graph parameter
By removing the vertex (people) from the connecting network. Then, will AI send a friend suggestion to other people who do not know the considerable person? We determined the methodology for that situation using the SVNF-graph parameters:
If we delete the vertex or person (people) from the vertices or person (people)s A \(\tau _{7},\) from the \(G_1.\) Then, we established a new SVN graph \((G_{2}),\) as shown in Fig. 4.
First, we calculate the degree of every person (people). When we delete a vertex
Now, we compute the square degree of every person (people)
Here, we are working on the SVNF-Sombor graph parameter
We compute the value of the third invariant of the SVNF-Sombor graph parameter. By utilizing the formulation of the third invariant of the SVNF-Sombor graph parameter
We compute the value of the fourth invariant of the SVNF-Sombor graph parameter. By utilizing the formulation of the fourth invariant of the SVNF-Sombor graph parameter
Now, we studied both graphs \(G_{1}\) and \(G_{2}\) for SVNFSO, \(SVNFSO_{3},\) and \(SVNFSO_{4},\) Then, we construct a Table 1 for comparative study.
4.2 Comparative analysis
Sombor topological index and their invariants were proposed by Gutman (2022). He gave equal weight to every edge, vertex, or person (people), which is called a crisp graph. Here, we gave the weight to every edge or person (people) between 0 and 3, which is more generalized. A single-valued neutrosophic is more generalized than a fuzzy framework for graphs, crisp graphs.
We also observe that for the whole networks, the artificial intelligence has maximum chance to send friend request to the other people by the SVNFSO-graph parameter and the third and fourth versions of the SVNFSO-graph parameter. On behalf of human opinion when deleting a vertex (person), then artificial intelligence has minimum chances to send friend request to other people. Therefore, our method is more liable than other existing methods or fuzzy topological graph parameters
5 Conclusion and further discussion
In this research work, we proposed some new TIs for the frame of a SVNF-graph. The main outcomes of our research work are: We introduced the idea of the Sombor version of the SVNF-Sombor graph parameter for SVNF-graph and determined its bounds and their properties. We defined the concept of the third version of the SVNF-Sombor graph parameter in the SVNF-graph framework and also determined its bounds and properties. We defined the concept of the fourth invariant of the Sombor graph parameter in the SVNF-graphs framework and also determined their bounds and properties. An application of TIs to the graph structure of the social network friend suggestion via artificial intelligence between the person (people)s is given. In this application, we have shown that by deleting (blocking) person (people)s or vertex \(\tau _{7},\) how much chance does artificial intelligence have to send friend suggestions to other people?
The trajectory of future investigations emanating from this study lies in the cultivation of a deeper understanding of the intricate interplay between novel single-value neutrosophic fuzzy topological graph parameters and their application in the realm of social media dynamics. Subsequent endeavors should delve into the refinement and extension of these parameters, exploring their adaptability to evolving structures within online networks. The integration of machine learning methodologies to predict and analyze social interactions could unlock unprecedented insights. Furthermore, the elucidation of the broader implications on information dissemination and influence dynamics within social media ecosystems stands as an imperative avenue for exploration. In navigating this complex terrain, a synthesis of mathematical rigor and computational methodologies will be instrumental in shaping the future discourse in this burgeoning interdisciplinary domain. We are providing the path to the researchers for the future to investigate the properties of several topological graph parameters in different environments like picture fuzzy graph and Pythagorean fuzzy graph.
The proposed model, while pioneering in its exploration of novel single-value neutrosophic fuzzy topological graph parameters, is not immune to inherent limitations. The abstraction and quantification of nuanced social interactions within the confines of a mathematical framework inherently grapple with the intricacies of human behavior, yielding a model susceptible to oversimplification. Additionally, the efficacy of the model is contingent upon the fidelity of data sources, introducing a potential limitation rooted in the veracity and completeness of the social media datasets. The adaptability of the proposed parameters to dynamic shifts in online discourse and the evolving nature of social networks warrants further scrutiny, as the model may encounter challenges in capturing the temporal nuances inherent in social media dynamics.
Data availability
No datasets were generated or analyzed during the current study.
References
Ahmad U, Sabir M (2023) Multicriteria decision-making based on the degree and distance-based indices of fuzzy graphs. Granular Comput 8(4):793–807. https://doi.org/10.1007/s41066-022-00354-x
Ahmad U, Khan NK, Saeid AB (2023) Fuzzy topological indices with application to cybercrime problem. Granular Comput. https://doi.org/10.1007/s41066-023-00365-2
Akram M, Adeel A (2017) m-Polar fuzzy graphs and m-polar fuzzy line graphs. J Discrete Math Sci Cryptogr 20(8):1597–1617. https://doi.org/10.1080/09720529.2015.1117221
Akram M, Sitara M (2017) Single-valued neutrosophic graph structures. Appl Math E-Notes 17:277–296
Akram M, Sitara M (2018) Novel applications of single-valued neutrosophic graph structures in decision-making. J Appl Math Comput 56:501–532. https://doi.org/10.1007/s12190-017-1084-5
Akram M, Siddique S, Davvaz B (2018) New concepts in neutrosophic graphs with application. J Appl Math Comput 57:279–302. https://doi.org/10.1007/s12190-017-1106-3
Akram M, Sattar A, Saeid AB (2022) Competition graphs with complex intuitionistic fuzzy information. Granular Comput. https://doi.org/10.1007/s41066-020-00250-2
Akram M, Shahzadi G (2017) Operations on single-valued neutrosophic graphs. Inf Study 11(1):1–26
Atanassov KT, Atanassov KT (1999) Intuitionistic fuzzy sets. Physica-Verlag HD:1-137, https://doi.org/10.1007/978-3-7908-1870-3
Balaban AT (1983) Topological indices based on topological distances in molecular graphs. Pure Appl Chem 55(2):199–206. https://doi.org/10.1351/pac198855020199
Banitalebi S, Borzooei RA (2023) Domination in Pythagorean fuzzy graphs. Granular Comput. https://doi.org/10.1007/s41066-023-00362-5
Binu M, Mathew S, Mordeson JN (2020) Wiener index of a fuzzy graph and application to illegal immigration networks. Fuzzy Sets Syst 384:132–147. https://doi.org/10.1016/j.fss.2019.01.022
Broumi S, Talea M, Bakali A, Smarandache F (2016) Single valued neutrosophic graphs. J New Theory 10:86–101
Chen SM, Jian WS (2017) Fuzzy forecasting based on two-factors second-order fuzzy-trend logical relationship groups, similarity measures and PSO techniques. Inf Sci 391:65–79. https://doi.org/10.1016/j.ins.2016.11.004
Chen SM, Wang JY (1995) Document retrieval using knowledge-based fuzzy information retrieval techniques. IEEE Trans Syst Man Cybern 25(5):793–803. https://doi.org/10.1109/21.376492
Chen SM, Ko YK, Chang YC, Pan JS (2009) Weighted fuzzy interpolative reasoning based on weighted increment transformation and weighted ratio transformation techniques. IEEE Trans Fuzzy Syst 17(6):1412–1427. https://doi.org/10.1109/TFUZZ.2009.2032651
Chen SM, Zou XY, Gunawan GC (2019) Fuzzy time series forecasting based on proportions of intervals and particle swarm optimization techniques. Inf Sci 500:127–139. https://doi.org/10.1016/j.ins.2019.05.047
Cruz R, Gutman I, Rada J (2021) Sombor index of chemical graphs. Appl Math Comput 399:126018
Das KC, Cevik AS, Cangul IC, Shang Y (2021) On Sombor Index. Symmetry 13(1):140. https://doi.org/10.3390/sym13010140
Das R, Mukherjee A, Tripathy BC (2022) Application of neutrosophic similarity measures in Covid-19. Ann Data Sci 9(1):55–70. https://doi.org/10.1007/s40745-021-00363-8
Dey A, Mohanta K, Bhowmik P, Pal A (2023) A study on single valued neutrosophic graph and its application. https://doi.org/10.21203/rs.3.rs-2421528/v1
Ejegwa PA, Akubo AJ, Joshua OM (2014) Intuitionistic fuzzy set and its application in career determination via normalized Euclidean distance method. Eur Sci J 10(15):1857–7431
El-Hefenawy N, Metwally MA, Ahmed ZM, El-Henawy IM (2016) A review on the applications of neutrosophic sets. J Comput Theor Nanosci 13(1):936–944. https://doi.org/10.1166/jctn.2016.4896
Fatima A, Ashraf S, Jana C (2024) Approach to multi-attribute decision making based on spherical fuzzy Einstein Z-number aggregation information. J Oper Intell 2(1):179–201. https://doi.org/10.31181/jopi21202411
Flores H, Srirama S (2013) Adaptive code offloading for mobile cloud applications: exploiting fuzzy sets and evidence-based learning. In Proceeding of the fourth ACM workshop on Mobile cloud computing and services, pp 9–16. https://doi.org/10.1145/2497306.2482984
Ghoushchi NG, Ahmadzadeh K, Ghoushchi SJ (2023) A new extended approach to reduce admission time in hospital operating rooms based on the FMEA method in an uncertain environment. J Soft Comput Dec Anal 1(1):80–101. https://doi.org/10.31181/jscda11202310
Graovac A, Pisanski T (1991) On the Wiener index of a graph. J Math Chem 8(1):53–62. https://doi.org/10.1007/BF01166923
Gutman I (2022) Sombor indices-back to geometry. Open J Discrete Appl Math 5(2):1–5
Gutman I (2022) TEMO theorem for Sombor index. Open J Discrete Appl Math 5(1):25–28
Hamidi M, Borumand Saeid A (2018) Achievable single-valued neutrosophic graphs in wireless sensor networks. New Math Nat Comput 14(02):157–185. https://doi.org/10.1142/S1793005718500114
Horng YJ, Chen SM, Chang YC, Lee CH (2005) A new method for fuzzy information retrieval based on fuzzy hierarchical clustering and fuzzy inference techniques. IEEE Trans Fuzzy Syst 13(2):216–228. https://doi.org/10.1109/TFUZZ.2004.840134
Imran M, Luo R, Jamil MK, Azeem M, Fahd KM (2022) Geometric perspective to Degree-Based topological indices of supramolecular chain. Results Eng 16:100716
Imran M, Ismail R, Azeem M, Jamil MK, Al-Sabri EHA (2023) Sombor topological indices for different nanostructures. Heliyon 9(10):e20600
Islam SR, Pal M (2023) F-index for fuzzy graph with application. J Appl Eng Math 3(2):517–530
Islam SR, Pal M (2021) Hyper-Wiener index for fuzzy graph and its application in share market. J Intell Fuzzy Syst 41(1):2073–2083. https://doi.org/10.3233/JIFS-210736
Ismail R, Azeem M, Shang Y, Imran M, Ahmad A (2023) A unified approach for extremal general exponential multiplicative Zagreb indices. Axioms 12(7):675. https://doi.org/10.3390/axioms12070675
Jin Y, Kamran M, Salamat N, Zeng S, Khan RH (2022) Novel distance measures for single-valued neutrosophic fuzzy sets and their applications to multicriteria group decision-making problem. J Funct Spaces 2022:1–11. https://doi.org/10.1155/2022/7233420
Kalathian S, Ramalingam S, Raman S, Srinivasan N (2020) Some topological indices in fuzzy graphs. J Intell Fuzzy Syst 39(5):6033–6046. https://doi.org/10.3233/JIFS-189077
Karwowski W, Mital A (1986) Potential applications of fuzzy sets in industrial safety engineering. Fuzzy Sets Syst 19(2):105–120. https://doi.org/10.1016/0165-0114(86)90031-X
Khalaf AB, Padma P (2022) On certain types of neutrosophic fuzzy graphs. Pan-Am J Math. https://doi.org/10.28919/cpr-pajm/1-8
Khatibi V, Montazer GA (2009) Intuitionistic fuzzy set vs. fuzzy set application in medical pattern recognition. Artif Intell Med 47(1):43–52. https://doi.org/10.1016/j.artmed.2009.03.002
Klir GJ, Yuan B (1996) Fuzzy sets and fuzzy logic: theory and applications. Possibility Theory versus Probab. Theory 32(2):207–208
Koundal D, Gupta S, Singh S (2016) Applications of neutrosophic sets in medical image denoising and segmentation. Inf Study 257–275
Krishnaraj V, Vikramaprasad R, Dhavaseelan R (2017) Self-centered single valued neutrosophic graphs. Inf Study 12(24):15536–15543
Liu Z (2024) A distance measure of fermatean fuzzy sets based on triangular divergence and its application in medical diagnosis. J Oper Intell 2(1):167–178. https://doi.org/10.31181/jopi21202415
Liu JB, Nadeem MF, Azeem M (2022) Bounds on the partition dimension of convex polytopes. Comb Chem High Throughput Screen 25(3):547–553. https://doi.org/10.2174/1386207323666201204144422
Mahapatra R, Samanta S, Pal M (2022) Edge colouring of neutrosophic graphs and its application in detection of phishing website. Discret Dyn Nat Soc. https://doi.org/10.1155/2022/1149724
Majeed AS, Arif NE (2023) Topological indices of certain neutrosophic graphs. In AIP Conference Proceedings 2845(1). https://doi.org/10.1063/5.0157832
Mehra S, Singh M (2017) Single valued neutrosophic signed graphs. Inf Study 157(9):31–34
Nadeem MF, Azeem M, Siddiqui HMA (2021) Comparative study of Zagreb indices for capped, semi-capped, and uncapped carbon nanotubes. Polycyclic Aromat Compd 42(6):3545–3562. https://doi.org/10.1080/10406638.2021.1890625
Naz S, Rashmanlou H, Malik MA (2017) Operations on single valued neutrosophic graphs with application. J Intell Fuzzy Syst 32(3):2137–2151. https://doi.org/10.3233/JIFS-161944
Padma P (2022) On certain types of neutrosophic fuzzy graphs. https://doi.org/10.21203/rs.3.rs-1367362/v1
Palanisamy S, Periyasamy J (2023) Algebraic structure through interval-valued fuzzy signature based on interval-valued fuzzy sets. Granular Comput. https://doi.org/10.1007/s41066-023-00372-3
Riaz M, Almalki Y, Batool S, Tanveer S (2022) Topological structure of single-valued neutrosophic hesitant fuzzy sets and data analysis for uncertain supply chains. Symmetry 14(7):1382,7. https://doi.org/10.3390/sym14071382
Smarandache F (2006) Neutrosophic set-a generalization of the intuitionistic fuzzy set. In 2006 IEEE international conference on granular computing, pp 38–42. https://doi.org/10.1109/GRC.2006.1635754
Smarandache F (2011) A geometric interpretation of the neutrosophic sets. Granular Computing, In IEEE international conference 602606
Smarandache F, Kandasamy WB, Ilanthenral K (2015) Neutrosophic graphs: a new dimension to graph theory. In: Hong T-P, Kudo Y, Kudo M, Lin T-Y, Chien B-C, Wang S-L, Inuiguchi M, Liu GL (eds) Presented at 2011 IEEE International Conference on Granular Computing, 8–10 November 2011. IEEE Computer Society, National University of Kaohsiung, Taiwan, pp 602–606
Vasantha Kandasamy WB, Ilanthenral K (2015) Neutrosophic graphs: a new direction to graph theory. EuropaNova
Wang H, Smarandache F, Zhang Y, Sunderraman R (2010) Single valued neutrosophic sets. Inf Study 12:10–14
Wang H, Smarandache F, Zhang Y, Sunderraman R (2012) Single valued neutrosophic sets. Technical Sciences and Applied Mathematics
Yüksel S, Eti S, Dinçer H, Gökalp Y (2024) Comprehensive risk analysis and decision-making model for hydroelectricity energy investments. J Soft Comput Dec Anal 2(1):28–38. https://doi.org/10.31181/jscda21202421
Zadeh LA (1965) Fuzzy sets. Inf Control 8(3):338–353
Zeng S, Shoaib M, Ali S, Smarandache F, Rashmanlou H, Mofidnakhaei F (2021) Certain properties of single-valued neutrosophic graph with application in food and agriculture organization. Int J Comput Intell Syst 14(1):1516–1540. https://doi.org/10.2991/ijcis.d.210413.001
Author information
Authors and Affiliations
Contributions
M. I. and M. A.: the main manuscript text. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Imran, M., Azeem, M., Jamil, M.K. et al. Exploring innovative single-value neutrosophic fuzzy topological graph parameters. Granul. Comput. 9, 37 (2024). https://doi.org/10.1007/s41066-024-00454-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s41066-024-00454-w