1 Introduction

Bus network design problem (BNDP) is commonly divided into four consecutive aspects, namely; bus routing, frequency design, timetable setting, vehicle, and crew scheduling [1–6]. Although they are interrelated aspects of design, they are usually handled separately to alleviate the problem inherent complexity. Recently, a focus has been given on solving the first two aspects simultaneously [7, 8].

Generally speaking, two partners are involved in the BNDP, namely; operator and users. Operator makes necessary decisions on the four planning aspects to balance between the total; operation cost; and users cost to achieve a desired level of service. User cost is always calculated in equivalent time units. It can be easily expressed by the following expression:

$${\text{UC}}_{k} = \, \varphi_{\text{a}} ({\text{AT}}) \, + \, \varphi_{\text{w}} ({\text{WT}}) \, + \, \varphi_{B/A} (B/A) \, + \, \varphi_{\text{v}} ({\text{IVT}}),$$
(1)

where UC k is user cost associated with mode (k) of travel. The other four terms are access time, waiting time, boarding/alighting time, and in-vehicle time. Φ i is a weight factor to reflect the relative importance of the terms in the model [9–13].

Each term of UC k is controlled by a corresponding aspect of the BNDP. For instance, IVT is a direct reflection to transit route network design. Frequency design (bus headway inverse) is responsible for WT values. AT depends on bus stops location and spacing. B/A times are controlled by bus operational aspects.

User (passenger) route choice is a fundamental element in evaluating the UC (The subscript k is omitted in the rest of paper due to the type singularity of used mode). The determination of this choice is a very complicated process which depends on many factors. To get a solid grasp of the problem complexity, let us consider a simple transit network given in Fig. 1. The network is built of two nodes (origin–destination) connected by two lines. The first line (express line) is lower than the second line (regular line) in IVT value.

Fig. 1
figure 1

Simple transit network

Full size image

Intuitively, passengers would consider line 1 (the express line) in their route choice when boarding at node i. Line 2 (the slow line in IVT) would be considered in their attractive set, if only it minimizes the total travel time (both WT and IVT). In that case, passengers would board the first incoming bus of the two lines. Let us assume another situation, where line 1 is much faster than line 2 (i.e., line 2 is no longer attractive to passengers). All passengers would board line 1 leaving line 2. The determination of line 2 usage is called common lines or optimal strategies problem [14, 15].

More complexity is added when lines capacity are considered. Even if line 1 is the only attractive choice, some passengers may fail to board the first incoming bus of line 1 due to insufficient capacity. Logically, they would change from line 1 to line 2. However, they may find it is more profitable to wait more until they board in a vacant bus of line 1. Therefore, line 1 may exceed its capacity in the dynamic action.

The whole choice problem is determined within transit assignment process [16]. Transit assignment techniques are classified into two main groups, namely; schedule-based (SB) and frequency-based (FB) models. SB models depend mainly on representing transit network as time expanded (diachronic) graph, in which each node is copied several times to represent each bus departure [17]. Therefore, they are able to simulate passenger real-time route choice. However, they have restrictions in dealing with real-size networks due to the exponential increase in their graph representation [17–24]. Unlike SB models, FB models deal with aggregated frequency on bus lines. They are interested in calculating the share percentage of each line according to predefined assumptions about passengers’ behavior. They are appreciated due to their capability of performing assignment on real-size transit networks in tractable execution time. However, they have difficulties in representing the aforementioned line capacity (congestion) effect on passenger route choice [25–35].

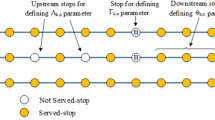
As stated before, transit assignment models concern with passenger route (path) choice. Since IVT is commonly assumed constant (flow independent), WT plays the pivotal role in route choice. WT is a function of line(s) frequency; therefore its estimation (as a tactical planning term) is done in the frequency design stage. Line frequency is calculated according to flow values on bus lines (transit assignment results) to provide a certain level of service. Bus stop is the place where these problems interact, see Fig. 2. Modeling the waiting time at bus stops is very important means to break the non-convergent loop.

Fig. 2
figure 2

Bus stop problem

Full size image

In this study, we try to decompose the transit assignment problem into two stages; the first stage deals with a separate bus stop modeling (simulation based), in which an attempt to capture the real experienced waiting time by users regarding different situations. The second stage uses the simulation results to feed a proposed heuristic transit assignment algorithm to obtain transit lines flow based on the Wardrop equilibrium principle.

The rest of paper is organized as follows: Sect. 2 reviews the problem state-of-art. Section 3 describes the methodology. Section 4’s numerical example is given to validate the contribution of the study. Section 5 gives the conclusion.

2 State-of-Art

The state-of-art is twofold; 1—reviewing waiting time estimation models, 2—reviewing transit assignment models. It is worth noting that any assignment model must define a way to estimate waiting time to complete the assignment task.

Average waiting time is a function of passenger and bus arrivals distribution, see Fig. 3. Here, ω max and ω avg represent the maximum and the average waiting time experienced by passengers, respectively, H is the bus headway [36].

Fig. 3
figure 3

Waiting time at bus stop

Full size image

Under the assumption of irregular buses arrival with headway standard deviation (σ H ), Holroyd and Scraggs developed a statistical model in Eq. (2) for calculating (ω avg) derived from central London off peak data [37]

$$\omega_{\text{avg}} = \, {\raise0.7ex\hbox{${0.5H}$} \!\mathord{\left/ {\vphantom {{0.5H} {\left[ {1 + \sigma_{H} /H^{2} } \right]}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\left[ {1 + \sigma_{H} /H^{2} } \right]}$}}.$$
(2)

Equation (3) is a general waiting model for random passengers’ arrival, and is as follows:

$$\omega_{\text{avg}} = \int\limits_{0}^{\infty } {t \times f_{\text{w}} } (t){\text{d}}t.$$
(3)

where f w(t) is waiting time distribution as a function in bus headway distribution. It could be relaxed into Eq. (4) formulation, where α is a parameter which depends on bus arrival distribution.

$$\omega_{\text{avg}} = \alpha {\text{H}} .$$
(4)

Bowman and Turnquist developed a model in Eq. (5) for estimating the expected waiting time in association with the passenger arrival time,

$$\omega_{\text{avg}} \left( t \right) = \left[ {1 - P\left( t \right)} \right] \times \, \omega \left( t \right) \, + \, P\left( t \right) \, \times \, \omega^{\prime}\left( t \right),$$
(5)

where ω avg(t) = the expected waiting time for an arrival at t; P(t) = probability that the intended bus arrives before t; ω(t) = the expected waiting time given the bus arrives after t; ω′(t) = the expected wait given the bus arrived before t. The model considers the aware passenger who adjusts his arrival according to the schedule reliability. This model would be more applicable with declared time table and high headways [38].

These models are categorized under free-congestion models, in which bus capacity is not considered, in other words, passengers are not assumed to wait more to find available space. More sophisticated models are introduced to tackle the congestion effect. The most widely used model is the one developed in [26] by De Cea and Fernandez. In Eq. (6), the effect of congestion on waiting time is taken similar to the Bureau of Public Roads (BPR) link congestion function, in which waiting time is monotone increasing with congestion,

$$\omega_{\text{avg}} = \, \alpha H \, + \, \beta \times (\vartheta { / }K_{\text{C}} )^{n} ,$$
(6)

where ϑ is the demand [number of passengers intended to ride buses of certain line(s)] and K C is the total line(s) capacity. The model does not consider the strict capacity of line (i.e., flow may exceed the line capacity).

Gendreau proposed a waiting model in Eq. (7) which depends on queuing theory. Passengers are lined in the bus stop and waiting time is calculated as the time spent in the queue system [39].

$$\omega_{\text{avg}} = \, 0.5H \, \left[ {1 + 1 /\gamma \left( {1 - \rho } \right) \, + \, \rho / {\text{HK}}_{\text{C}} \left( {1 - \, \rho } \right) \, {-} \, \rho \left( {1 - 1 / {\text{ HK}}_{\text{C}} } \right)} \right] \times \left[ {\left( {Z_{\gamma } + \, 1/ \, \gamma } \right) \, + \, \left( {Z_{\gamma } - \, 1 / { }\gamma } \right) \, \rho^{2} } \right],$$
(7)

where γ is a vector of shape parameters representing bus headway distribution, ρ = ϑ/K C, and Zγ is the random variable describing the interval separating the arrival of a passenger demand and the arrival of the first bus of type γ.

Considering the static assignment models (dynamic models are not in the scope of this study), the pioneer work is first presented in [14]. It introduced the common lines concept as alternative to shortest transit path which was commonly used. A better reformulation of the problem is developed in [15, 25]. They used optimal strategies concept to imitate passengers’ behavior. Their formulation has a linear relaxed version which is widely used in the BNDP solution approaches [40]. The optimal strategies could be represented by a graph theory model called hyper-path [41]. Equation (6) is used in [26] to model the effect of congestion on waiting times and consequently users’ optimal strategies. A variational inequality formulation is used to reach the equilibrium state. Recent assignment formulations depend on developing a graph representation to model congestion by bus seat allocation [33].

The paper contribution proposes a new methodology for the transit assignment problem to capture the line capacity effect, in its dynamic interpretation, on route choice regarding the ordinary network representation. It would help in increasing the route choice realism of FB models while conserving the simplicity of static network representation.

3 The Methodology

Unlike the literature, a different approach is given to model both the waiting time at bus stops and the transit assignment problem. A simple simulation algorithm is developed to model bus stop waiting time. Users’ real-waiting times are easily predicted considering each vehicle strict capacity. Then, a heuristic assignment model is provided with the obtained waiting time values as exogenous input.

3.1 Bus Stop Modeling

Provided that the load profile at bus stop is given as in Fig. 4, the service is based on the first come—first served (FCFS) order. Each step increase represents passengers’ arrival. On contrary, each step decrease denotes bus arrival with spare capacity (C). Points i and ii represent, respectively, the total demand (ϑ) and the maximum number of passengers queued at bus stop. All bus arrivals represent line total capacity (K C). When demand exceeds the arrival bus with spare capacity (C), some passengers may fail to board the first incoming bus and wait their turn to board. Demand, which is not served in congestion part, is postponed until they are served in discharge part.

Fig. 4
figure 4

Bus stop load profile of both passenger and bus arrivals

Full size image

We would simulate passenger arrival patterns and their waiting time in Algorithm (1). It evaluates the average waiting time ω avg experienced by passengers at the stop. It is worth noting that different preconditions are used to simulate different cases which may occur at a bus stop during the assignment process.

figure a

3.2 Assignment Model

The proposed assignment model is categorized under capacitated assignment models, because user travel time (UC) on certain route is a function of the transit network line capacity and flow. This leads the problem to resemble the urban transportation assignment problem. To solve the assignment problem, Wardrop equilibrium principle is commonly used. Equilibrium is reached when the total travel times in all routes (paths) actually used are equal or less than those which would be experienced by a passenger on any unused route.

The assignment could be formulated into a version of variational inequality as follows:

$$UC \, \left( {X^{*}} \right) \times \left( {X \, {-} \, X^{*}} \right) \, \ge \, 0\quad \forall \;X \in K$$
(8)

where X represents path flow vector, X* is the equilibrium path flow vector, K is the space of all feasible values of paths flow, and UC (X) denotes user’s path travel time as a monotone increasing function of path flow.

To trade-off the computational time and quality in solving the assignment model in Eq. (8) along with the proposed bus modeling, we would adopt the incremental assignment technique as used in [42]. When the OD matrix is divided into proper portions, the result of incremental assignment method is approximate to the one of the equilibrium assignment variational inequalities. The basic idea of incremental assignment method is to divide the OD matrix into several equal portions (increment size) and then assigns each portion to the transit route network according to shortest path method recurrently. After each portion assignment, travel time in transit route network should be updated, i.e., the minimum hyper-path is changed between the origin and destination due to the new value of waiting time (flow dependant).

The process of the transit assignment is illustrated in the following steps:

  • Step 1: Dividing the OD matrix into several equal portions

  • Step 2: Assigning one portion to the minimum hyper-path

    • Step 2.1: Select a pair of terminals (the origin terminal and the destination terminal) of the current portion

    • Step 2.2: Search the minimum hyper-path between the origin and the destination under the current conditions. The travel time of the minimum hyper-path contains the in-vehicle, waiting time that is recalled from bus modeling results

    • Step 2.3: Assign the passenger demand between the pair of terminals to the minimum hyper-path

  • Step 3: Repeat Step 2 until the whole OD matrix is assigned.

4 Numerical Experiment

To illustrate the basic purpose of this paper, we would assume a case of regular bus and passengers’ arrival (any real load profiles could be used in Algorithm 1). Different preconditions were used to simulate the expected situations in the assignment process. H takes values (2, 4, 5, 6, 12, 15, and 20 min), C ranges from 10 to 20 seats (load factor = 1), and ϑ takes (50, 100, 150, 200 and 250 pax. (passenger)/stop/h). The analysis period (t) is fixed at 60 min with time step (T) 1 min.

Algorithm 1 was written in MATLAB (Appendix) and run on a PC with Intel (R), Core (TC) I7, 2.8 GHz processor, and six gigs of RAM. More than 500 cases are obtained. For each case, ω avg is calculated exactly in minutes. Different relationships between the average waiting time and preconditions could be drawn, see some examples in Figs. 5, 6, and 7. It is obvious that average waiting time is affected by the three elements: ϑ, H, and C. The algorithm results are saved to be recalled within the assignment process.

Fig. 5
figure 5

Average waiting time in minutes versus the bus spare capacity at H = 20 min

Full size image
Fig. 6
figure 6

Average waiting time in minutes versus the demand at C = 10 seats

Full size image
Fig. 7
figure 7

Average waiting time in minutes versus headway in minutes at C = 10 seats

Full size image

4.1 Illustrative Example

An illustrative example of simple transit networks is given in Fig. 8. It comprises of three lines and three nodes. The in-vehicle time of lines is given on arcs in minutes. The network demand is as follows: ϑ 1–2 = 100 pax./h, ϑ 1–3 = 80, and ϑ 2–3 = 40. The available bus capacity is 10 seats. The headways of three lines are, respectively; 10, 6, and 5 min with lines capacity (K C): 60, 100, and 120 pax./h.

Fig. 8
figure 8

Illustrative example

Full size image

For the given example transit network, it is required to predict the patterns of network usage by passengers. A preliminary task of transit assignment problem is to enumerate available paths for each demand pattern. Available paths for the given demand are given in Table 1. Each demand pattern is faced by alternative paths.

Table 1 Path enumeration for the given network
Full size table

In Table 2, the implementation of Algorithm 1 results in the proposed assignment model is illustrated. The incremental assignment procedure is used with increment flow 20 passenger (Pax.). At first, all alternative paths are numerated. The least path in total travel time for each demand is determined. The portion of demand of the determined increment is assigned to the least travel time path. According to each line loaded demand and its capacity, the new waiting time from the simulation results is calculated. The new least path for each demand is recalculated for the next iteration. This process is repeated for each iteration until all demands are assigned (satisfied).

Table 2 Incremental assignment process
Full size table

At iteration 1, regarding the first increment for ϑ 1–2, the user would take the least cost path (line 1). Line 1 capacity is exhausted in iteration 2; however, it is still attractive for ϑ 1–3 demand portion to board. Although they would not ride the first incoming bus due to insufficient line capacity, they do not change to the alternative path 2 (line 2–line 3). This leads to the case discussed before, in which the line may exceed its capacity even if strict capacity is considered, see Fig. 9.

Fig. 9
figure 9

Proposed transit assignment methodology results

Full size image

In Fig. 10, when the strict line capacity is added to the assignment model, the exceeding demand of line 1 is moved to other lines (line 2 and line 3), which does not catch the actual behavior of transit users in dealing with the network congestion.

Fig. 10
figure 10

Transit assignment results with strict line capacity

Full size image

Obviously, in the strict capacity assignment, some demand would be classified as unsatisfied demand (i.e., demand originating from 1 is 180 pax./h, while lines capacity is 160 pax./h). Therefore, the proposed incorporation of bus stop simulation has the advantage over strict capacity assignment in reflecting a more realistic case at node 1. First, even if line 1 has reached its capacity, it may be still attractive to users. Second transit network capacity could be over capacitated with larger waiting times.

4.2 Benchmark Network

To demonstrate the effectiveness of the solution methodology proposed in this study, a benchmark network is solved. Figure 11 shows the network taken from De Cea and Fernandez [26] that has been utilized by many researchers as a benchmark network to compare their results with it [21, 27, 34, 43].

Fig. 11
figure 11

Benchmark network alignment

Full size image

The network consists of A and B demand node pair with ϑ A–B = 240 pax./h and two transfer nodes, X and Y. There are four transit lines serving the network; line 1 is an express line going directly from A to B, with service frequency 10 buses per hour and in-vehicle time equals 25 min. Line 2 is going from A to Y with an intermediate stop at X. Travel times on each line segment are 7 and 6 min, respectively, and frequency 10. Line 3 is going from X to B with an intermediate stop at Y. Travel times are 4 min on each segment with frequency 4. Line 4 is running only between Y and B with frequency of 20 and travel time of 10 min.

In Table 3, we compared our methodology with the results reported by De Cea and Fernandez [26]. In case (1), waiting times which come from Eq. (6) (as used by De Cea and Fernandez in their model) are used to feed our assignment model. There is a notable agreement in the results, regarding the congestion case of their work. This validates the proposed assignment model to converge at the equilibrium state by Eq. (8). It is worth noting that decreasing the increment step causes an increase in the algorithm accuracy; however, determining the increment size depends mainly on the network scale to reduce the number of iteration and, consequently, the running time.

Table 3 Benchmark results comparison
Full size table

In case (2), waiting times from the proposed simulation results are used in the assignment model. The results, regarding the comparison, show a new tendency of passengers’ behavior. More users leave Line 1 (the direct line) and wait more for Line 2 to benefit from the reduction of line 4 in their total travel time. In case (2), Line 3 has managed to take a fare number of passengers compared with case (1) (Line 2 flow splits between Line 3 and 4). The real representation of passengers waiting time in the simulation stage may give more realistic results for their true line choice and, consequently, more accurate transit assignment results than the classical static assignment techniques.

Now and simply, for any network scale, the proposed methodology can model all bus stops (each bus stop separately) according to passengers arriving distribution, different bus frequencies, and, consequently, line capacities, then store this data set as input to the proposed heuristic assignment model.

5 Conclusion

Transit assignment is fundamental input for justifying resource allocation in transport planning. Waiting time is a key element in transit assignment solution. A novel methodology is given for incorporating bus stop waiting time simulation into ordinary transit assignment problem. The methodology is built on two main steps; first, simulation is conducting regarding each stop condition. The simulation should consider different cases which bus stop may phase within the assignment process. Second the static assignment model is applied considering equilibrium principles. The illustrative example denotes the usefulness of proposed methodology. It combines the merits of both dynamic and static assignment approaches in simple framework. Also, the simulation may incorporate any load profile of passenger and bus arrivals into the static assignment model. Consequently, real profiles obtained from actual observed data may be used for the first time in the transit assignment problem solution. Regarding the benchmark problem, it may be noticed a new representation is given for users’ movement in the transit network that may give more realistic results for the line choice problem and consequently more accurate transit assignment results than the classical static assignment techniques. Moreover, the proposed approach still has the advantage to tackle the large-scale problems due to its heuristic manner.