1 Introduction

Meeting the energy needs of low-power applications like wireless sensor networks, medical devices, robotic systems, and self-sustaining autonomous units through the utilization of ambient energy sources, particularly vibrational energy, has garnered notable interest in contemporary times. This growing demand has prompted researchers to delve into the creation of energy harvesting technologies. Consequently, a substantial portion of these endeavors has been directed towards vibrational energy extraction employing piezoelectric materials, chosen for their advantageous frequency response and remarkable efficiency (Aridogan et al. 2014; Muthalif and Nordin 2015; Shaikh and Zeadally 2016; Wei and Jing 2017; Ravi and Zilian 2019; Liu et al. 2018; Fan 2018; Mobarakia et al. 2021; Mohamad Hossein Fatahi 2021; Ray and Jha 2022; Song et al. 2022; Cao and Huang 2022; Askari et al. 2022; Rakesh Ranjan Chand 2022).

The analysis focuses on a multi-layered configuration featuring a concentrated mass positioned at the beam's extremity. It has been established that reducing the thickness of the piezoelectric layer while augmenting the mass at the beam's tip contributes to a lowered resonance frequency and an enhanced output power (Johnson et al. 2006). Exploring the impact of mass dimensions, Anderson and Sexton (2006) examined how output power varies with mass length and width. Certain studies have demonstrated that integrating a proof mass at the harvester's tip yields satisfactory precision when utilizing a single-degree-of-freedom (SDOF) model, particularly when the system's vibrations closely align with one of its resonance frequencies. Additionally, Erturk and Inman (2008), Abdelkefi et al. (2013) (Sodano et al. 2004) proposed the incorporation of an end-tip mass to shift the system's inherent frequencies towards the operating frequency of the vibration source.

A cantilever-type piezomagnetoelastic energy harvester with two magnets to increase the efficiency and the output power presented by Tahmasbi et al. (2021). Chand and Tyagi’s (2022) work on a parabolic tapering piezoelectric rotational energy harvester provided numerical analysis with experimental validation. A low frequency piezoelectric energy harvester using secondary excitation of pressured fluid is proposed by Zhang et al. (2023) to scavenge low frequency vibration energy in ambient environments.

Bai et al. (2018) investigated energy harvesting resulting from human motion, employing a cantilever-structured piezoelectric energy harvester exposed to random vibration inputs. To this end, three distinct conceptual bimorph designs underwent ANSYS simulations to predict performance and optimize system parameters. In a separate endeavor, Li et al. (2019) validated a multi-mode piezoelectric energy harvester through analytical modeling. The configuration is tailored to generate multiple closed resonance peaks across a frequency spectrum, rendering it well-suited for broad-spectrum energy harvesting. This validation process was executed using ANSYS simulations.

Piezoelectric ceramics exhibit brittleness and susceptibility to fractures, which can arise from interface or through-the-thickness cracks. These cracks lead to undesirable declines in both electrical and mechanical performance. As the use of piezoelectric smart devices continues to grow, the potential for multiple failures and the associated concerns with piezoelectric material breakdown have garnered substantial attention from researchers in recent times (Lei and Chen 2019). Moreover, since piezoelectric components are also employed for assessing the failure and health status of other structures (Balamonica et al. 2020; Ezzat et al. 2020; Na 2022), it becomes crucial to discern the signs of their own failures to prevent confusion with performance alterations in distinct structures. Elevated stress levels, fatigue, and repetitive manufacturing procedures are primary factors that initiate and propagate cracks within structures. The progressive advancement of cracks and their eventual attainment of a critical size can ultimately lead to abrupt failure in MEMS devices (Shoaib et al. 2016). Shoaib et al. (2017) explored the effects of surface cracks on the dynamic behavior of an unimorph piezoelectric sensor cantilever beam. The investigation encompassed the tip displacement and output voltage of a beam incorporating a piezoelectric layer. The findings indicated that well-defined surface cracks amplify both displacement and output voltage, implying that increased voltage serves as a failure indicator. It should be noted that the breathing edge cracks are not a significant issue for this specific energy harvester design in relation to mid-layer cracks, since they are easier to detect. The similar cases have been considered in Shoaib et al. (2017). Given the intricate nature of the physics involved at the crack level, distinctive methodologies are applied to model simplified and specific crack types and scenarios (Wang 2000). Interlayer cracks, occurring parallel and perpendicular to the polarization axis, have been scrutinized (Gao and Noda 2004). It has been demonstrated that in bilayers exhibiting certain symmetries, cracks between layers do not exhibit oscillatory behavior. Additionally, the electrical displacement resulting from crack presence remains constant at crack levels and is solely contingent on the applied stress field. The examination of piezoelectric material failures extends beyond mechanical concerns; certain studies have delved into electrical failures within piezoelectric structures. Beom et al. (2009) numerically calculated the critical J integral at the onset of fracture and breakdown through finite element analysis. They explored the impact of both electric field direction and poling direction on fracture and breakdown resistance. Zhang et al. (2004) investigated the fracture mechanics problem of a crack within a two-dimensional magnetoelectric composite material subjected to coupled mechanical, electric, and magnetic loads at infinity. Viun et al. (2018) explored the influence of poling direction on fracture parameters for a limited permeable interface crack within a piezoelectric bi-material. Sladek et al. (2020) conducted an investigation into crack analysis within piezoelectric materials, taking into account the electric field and strain gradient. Their research delved into the behavior of cracks within two-dimensional piezoelectric materials. Gao et al. (2004) examined periodic permeable interface cracks within piezoelectric materials. This study readdressed the generalized 2D problem of electrically permeable collinear interface cracks present in piezoelectric materials. Their findings revealed that exclusively under electric loading, electric fields remain uniform not only within the materials but also within the cracks, while stress remains absent throughout. The topic of interface cracks within piezoelectric materials has been a focal point in numerous publications due to its significance (Fang and Liu 2013; Govorukha et al. 2016). These investigations have involved an analysis of the electrical field within the cracks, revealing its dependence on material constants and the applied load. Zhang et al. (2016) explored the impact of crack surface electrostatic tractions on the fracture behavior of magnetoelectric composite materials. Their study indicated that electrostatic tractions on the crack surfaces tend to close the cracks, consequently retarding the propagation of cracks. It was demonstrated that the traditional traction-free crack model consistently overestimates the influence of applied magnetoelectric loads on the intensity factors of crack tip fields. Lastly, Ayatollahi et al. (2018) examined the presence of multiple interfacial cracks across distinct piezoelectric layers subjected to time-harmonic loadings. Observations of straight and sharp cracks have been documented in silicon 100 (Nam et al. 2012). The extension of crack length was noted to correlate with the crystal coordinates of the structure. Furthermore, direct cracks propagating in the 100 and 110 directions were also evident due to fatigue loading (Ikehara and Tsuchiya 2016).

The motivation behind this study is to analyze how mid-layer cracks impact the operational performance of bimorph piezoelectric energy harvesters. The proposed research aims to address a critical gap in the current understanding of damages in the piezoelectric energy harvesters especially mid layer cracks. Despite the significant progress made in the field, there remains a lack of comprehensive understanding of the underlying mechanisms and key factors that influence damage phenomenon. This knowledge gap hinders the development of effective applications/interventions that can significantly improve relevant outcomes.

The significance lies in understanding the effects of cracks on stiffness, resonance frequency, voltage, and output power, which can lead to device malfunction. This research can aid in detecting defects in MEMS by monitoring the harvester's performance, potentially improving the reliability of micro-electromechanical systems. Upon reviewing the aforementioned investigations and based on the available knowledge, a comprehensive exploration encompassing the impacts of crack formation within the mid-layer of bimorph piezoelectric energy harvesters constructed with a silicon substrate is currently lacking. The presence of mid-layer cracks in bimorph piezoelectric energy harvesters holds the potential to influence their operational performance via two distinct mechanisms: reduction in structural stiffness and alteration of capacitance. This study addresses these aspects by conducting simultaneous analytical and numerical examinations, aiming to ascertain which factor exhibits greater significance in shaping the harvester's response when subjected to mid-layer cracks. Furthermore, the variation in output voltage of the bimorph piezoelectric energy harvester in the presence of mid-layer cracks is a topic of discussion. The subsequent sections will provide comprehensive insights into these methodologies and their findings.

2 Model of the Piezoelectric Energy Harvesting System

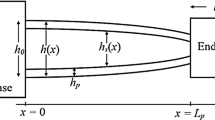
This section will outline the mathematical formulations corresponding to a bimorph configuration coupled with a silicon substrate. The substrate employed is silicon 100, characterized by anisotropic properties, which is sandwiched between two layers of PZT material. The energy harvesting system under scrutiny is a piezoelectric beam, as illustrated in Fig. 1. It is noteworthy that the bimorph piezoelectric cantilever beam presented here has been extensively examined in the literature and is recognized as one of the most effective platforms for energy harvesting. The structure features a composite cantilever beam comprised of three layers, housing a proof mass at the free end, strategically positioned to enable the adjustment of the natural frequency. The beam's length-to-thickness ratio is sufficiently large to satisfy the conditions stipulated by the Euler–Bernoulli beam theory. As depicted in Fig. 1, \(h_{p}\) and \(h_{s}\) represent the thickness of the piezoelectric and substrate layers, respectively. Additionally, \(q\) denotes the tip displacement, and \(u\left( t \right)\) signifies the harmonic excitation displacement. Direction 1 lies along beam length (longitude direction) and direction 3 is in the direction of polarization in the beam equilibrium condition.

Fig. 1
figure 1

Piezoelectric energy harvester and cross-sectional view

Full size image

The top and bottom surfaces of the piezoelectric layer are equipped with electrodes, facilitating the induction of a transverse mode, specifically the \(d_{31}\) mode. In this transverse mode, the piezoelectric components experience displacement perpendicular to the direction of lamination. As the beam structure is subjected to an external load, inducing transverse bending, the piezoelectric effect comes into play. This effect causes electric charges to accumulate on the opposing surfaces, thereby generating the resultant output voltage.

2.1 Governing Equations

One extremity of the bimorph, as illustrated in Fig. 1, is securely fixed to a wall and exhibits harmonic vibrations aligned with the vertical axis. To fine-tune the vibration characteristics of the beam, a mass denoted as \(m_{0}\). can be attached to the bimorph's terminus. The electrodes positioned on both the upper and lower surfaces of the bimorph can be configured in either a parallel or serial arrangement. Polarity alignment of the piezoelectric layers in the same orientation yields electric flds with opposing directions. Conversely, the piezoelectric layers oriented in opposite directions lead to electric fields aligned in the same direction. These respective configurations are referred to as serial and parallel connections.

The excitation of the structure is done by an external harmonic displacement and is expressed as

$$u\left( t \right) = u_{0} \exp (i\omega t)$$
(1)

where \(u_{0}\) is the amplitude of the displacement excitation and \(\omega\) ie eation fquency. The reduced form of piezoelectric constitutive equations for calculation of the axial stress and the transverse electric displacement is given by Jiang et al. (2005)

$$S_{1} = { }c_{11}^{E - 1} T_{1} + d_{31} E_{3}$$
(2)
$$D_{3} = d_{31} T_{1} + \varepsilon_{33} E_{3}$$
(3)

where \(S_{1}\). corresponds to the axial strain, \(T_{1}\). represents the axial stress, \(D_{3}\). signifies the electric displacement, \(E_{3}\). denotes the electric field directed through the thickness, \(c_{11}^{E}\). stands for the axial elastic stiffness under a constant electric field, \(d_{31}\). symbolizes the transverse-axial piezoelectric constant, and \(\varepsilon_{33}\) signifies the permittivity at a consistent strain level. In the context of the structure's linear analysis, the constant damping ratio option is implemented, designed to suit linear analytical approaches. The amplitude of excitation is very low and the behavior of the system is within the linear regime. It should be noted also the selected configuration is a commonly used interface for linear piezoelectric energy harvesters that linear energy harvesting circuit elements such as resistor is used in this study. Incorporating damping in piezoelectric ceramics often involves the introduction of complex values for the elastic constants. Therefore, in numerical computations, the axial elastic compliance, \(s_{11}^{E}\), is adjusted to \(s_{11}^{E} \left( {1 - iQ^{ - 1} } \right)\), with Q representing the material's quality factor (Jiang et al. 2005). The axial elastic compliance calculation method is shown by this equation which finally leads to axial stiffness component. Equation (2) can be reformulated as (Jiang et al. 2005)

$$T_{1} = c_{11}^{E} S_{1} - c_{11}^{E} d_{31} E_{3}$$
(4)

Substituting (4) into (3) results

$$D_{3} = d_{31} c_{11}^{E} S_{1} + E_{3} (\varepsilon_{33} - c_{11}^{E} d_{31}^{2} )$$
(5)

The piezoelectric capacitance, \(C_{p}\) is introduced as (Jiang et al. 2005)

$$C_{p} = \varepsilon_{33} \left( {1 - k_{31}^{2} } \right)\frac{bL}{{h_{p} }} = K_{eq} \frac{bL}{{h_{p} }}$$
(6)

where

$$k_{31} = \frac{{c_{11}^{E} d_{31}^{2} }}{{\varepsilon_{33} }}$$
(7)

Ttrain in the axial direction is represented in terms of deflection \(u_{3} \left( {x_{1} ,t} \right)\) as (Jiang et al. 2005)

$$S_{1} = - x_{3} u_{3,11}$$
(8)

where the second partial derivation of deflection is indicated by \(u_{3,11}\). In addition, the mid-layer is made of silicon, and its constitutive relation can be written as (Jiang et al. 2005)

$$\left[ {\begin{array}{*{20}c} {T_{1} } \\ {T_{2} } \\ {T_{12} } \\ \end{array} } \right]_{s} = \left[ {\begin{array}{*{20}c} {\overline{Q}_{11} } & {\overline{Q}_{12} } & {\overline{Q}_{16} } \\ {\overline{Q}_{16} } & {\overline{Q}_{22} } & {\overline{Q}_{26} } \\ {\overline{Q}_{16} } & {\overline{Q}_{26} } & {\overline{Q}_{66} } \\ \end{array} } \right]_{s} \left[ {\begin{array}{*{20}c} {S_{1} } \\ {S_{2} } \\ {S_{12} } \\ \end{array} } \right]_{s}$$
(9)

In which the subscript ‘s’ corresponds to silicon layer. Having the strain value in the silicon-made layer, the stress value corresponding to this layer is determined from Eq. (9) as (Jiang et al. 2005)

$$T_{1 - s} = Q_{11} S_{1}$$
(10)

where

$$Q_{11} = \frac{{E_{{11{\prime} s}} }}{{1 - \nu_{12} \nu_{21} }}$$
(11)

The formulation of the electric field within the piezoelectric layer, dependent on the arrangement of electrodes, can be expressed as follows:

$$E_{3} = - \frac{{V_{p} \left( t \right)}}{{h_{p} }}$$
(12)

For calculation of the bending moment, the axial stress relations in (4) and (10) can be employed as

$$\begin{aligned} M = & \iint {x_{3} T_{1} dx_{2} dx_{3} } = 2\mathop \int \limits_{0}^{c} \mathop \int \limits_{0}^{b} x_{3} \left( {Q_{11} } \right)\left( { - x_{3} u_{3,11} } \right)dx_{2} dx_{3} \\ & + 2\mathop \int \limits_{c}^{{c + h_{p} }} \mathop \int \limits_{0}^{b} x_{3} \left[ {c_{11} \left( { - x_{3} u_{3,11} } \right) - c_{11} d_{31} E_{3} } \right]dx_{2} dx_{3} \\ = & - \frac{2}{3}b\frac{{E_{{11{\prime} s}} }}{{1 - \nu_{12} \nu_{21} }}u_{3,11} c^{3} - \frac{2b}{3}u_{3,11} c_{11} \left[ {\left( {c + h_{p} } \right)^{3} - c^{3} } \right] \\ & - bc_{11} d_{31} E_{3} \left( {2c + h_{p} } \right)h_{p} \\ \end{aligned}$$
(13)

where \(c = h_{s} /2\) Furthermore, having the bending moment, the shear force is obtained as

$$N = \frac{dM}{{dx_{1} }} = - \frac{2}{3}b\frac{{E_{{11{\prime} s}} }}{{1 - \nu_{12} \nu_{21} }}u_{3,111} c^{3} - \frac{2b}{3}u_{3,111} c_{11} \left[ {\left( {c + h_{p} } \right)^{3} - c^{3} } \right]$$
(14)

Employing Euler–Bernoulli beam theory, the equation of motion given by

$$m\ddot{u}_{3} = M_{11}$$
(15)

where m is the linear mass density. Substituting M from (13) into (15) results

$$m\ddot{u}_{3} = - \frac{2}{3}b\frac{{E_{11\prime s} }}{{1 - \nu_{12} \nu_{21} }}u_{3,1111} c^{3} - \frac{2b}{3}u_{3,1111} c_{11} \left[ {\left( {c + h_{p} } \right)^{3} - c^{3} } \right]$$
(16)

The electrical charge at the electrode of the piezoelectric layer at (\(x_{3} = c + h_{p}\)) is denoted by \(Q_{p}\) and can be calculated as

$$\begin{aligned} Q_{p} = & - \iint {D_{3} dx_{1} dx_{2} } = - b\mathop \int \limits_{0}^{L} d_{31} c_{11}^{E} \left( { - x_{3} u_{3,11} } \right) + E_{3} (\varepsilon_{33} - c_{11}^{E} d_{31}^{2} )dx_{1} \\ = & - b\left[ {d_{31} c_{11}^{E} \left( {c + h_{p} } \right)\left[ {u_{3,1} \left( {L,t} \right) - u_{3,1} \left( {0,t} \right)} \right] + E_{3} (\varepsilon_{33} - c_{11}^{E} d_{31}^{2} } \right) L] \\ \end{aligned}$$
(17)

This alternating electric charge creates alternating current \(I_{p}\) at each electrode that can be obtained as (Jiang et al. 2005)

$$I_{p} = - \dot{Q}_{p}$$
(18)

From the calculated value for current, the output voltage can be determined as

$$V_{p} = 2RI_{p}$$
(19)

where R is the resistance load.

On the beam's left side, the conditions at the boundary are such that (Jiang et al. 2005)

$$u_{3} \left( t \right) = u_{0} \exp (i\omega t)$$
(20)
$$u_{3,1} \left( {0,t} \right) = 0$$
(21)

At the free end of the harvester, the bending moment is zero, but there is a shear force at \(x = 0\) that can be calculated as (Jiang et al. 2005)

$$M\left( {L,t} \right) = 0$$
(22)
$$N\left( {0,t} \right) = - m_{0} \ddot{u}_{3} \left( {L,t} \right)$$
(23)

By using the complex notation for the harmonic motion, we have (Jiang et al. 2005)

$$\left\{ {u_{3} \left( x \right),V_{p} ,Q_{p} ,I_{p} } \right\} = Re\left\{ {U\left( x \right),\overline{{V_{p} }} ,\overline{{Q_{p} }} \overline{,I}_{p} \} {\text{exp}}\left( {i\omega t} \right)} \right\}$$
(24)

Then Eq. (15) becomes

$$- \omega^{2} mU = U_{,1111} \left( { - \frac{2}{3}b\frac{{E_{{11{\prime} s}} }}{{1 - \nu_{12} \nu_{21} }}c^{3} - \frac{2b}{3}c_{11} \left[ {\left( {c + h_{p} } \right)^{3} - c^{3} } \right]} \right)$$
(25)

The general solutions of Eq. (25) can be written as (Jiang et al. 2005)

$$U = C_{1} sin\alpha x_{1} + C_{2} cos\alpha x_{1} + C_{3} sinh\alpha x_{1} + C_{4} cosh\alpha x_{1}$$
(26)

where “α” can be obtained as \({\alpha } = \left( {\frac{{{m}}}{{{D}}}{\omega }^{2} { }} \right)^{1/4}\) from Eq. (25) and ω is the excitation frequency. Through the process of reconfiguring Eqs. (20) to (23) via complex notation and substitution of (26) within the boundary conditions and voltage equation, a set of five equations emerges with five unknowns. By concurrently solving these derived equations, the output voltage can be ascertained. Upon solving Eqs. (18) and (19) and utilizing the determined electric current, \(I_{p}\), along with the voltage, \(V_{p}\), the resulting electrical power output, \(P\), can be computed. It's worth mentioning that Liao and Sodano (Liao and Sodano 2008) introduced an innovative approach to deduce a closed-form solution for the output power of bimorph piezoelectric energy harvesters. Their method employs fundamental circuit theories applied to a system subject to harmonic base excitation with an amplitude of \(u_{0}\), enabling the computation of power extracted in the resistive component (Liao and Sodano 2008) as

$$P = \frac{{D_{e}^{2} u_{0}^{2} }}{{\sqrt {MK} }}\frac{{k^{2} r^{2} \gamma }}{{\left( {2dr + \left( {1 + k^{2} - r^{2} } \right)r\gamma } \right)^{2} + \left( {1 - r^{2} - 2dr^{2} \gamma } \right)^{2} }}$$
(27)

Here, the quantities \(M, K, \theta\), \(C_{p}\), and \(D_{e}\) represent the effective mass, stiffness, electromechanical coupling coefficient, equivalent capacitance, and equivalent mass, respectively. These parameters are determined as follows (Qian et al. 2021):

$$M = \left( {\rho_{s} t_{s} + 2\rho_{p} t_{P} } \right) b$$
(28)
$$K = \left[ {1.0302E_{s} \left( {\frac{{h_{s}^{3} }}{{L^{4} }}} \right) + 2.0604E_{p} \left( {\frac{{3h_{s}^{2} h_{p} + 6h_{s} h_{p}^{2} + 4h_{p}^{3} }}{{L^{4} }}} \right)} \right]b$$
(29)
$$\theta = - 2.753d_{31} E_{p} b\left( {\frac{{h_{s} + h_{p} }}{{\sqrt {L^{3} } }}} \right)$$
(30)
$$C_{p} = 2K_{3} \varepsilon_{0} b\left( {\frac{L}{{h_{p} }}} \right)$$
(31)
$$D_{e} = - 0.783b\left( {\rho_{s} h_{s} + 2\rho_{p} h_{p} } \right)\sqrt L$$
(32)

These terms are the parameters of a symmetric bimorph beam harvester in the closed form (Qian et al. 2021). Furthermore, the electromechanical coupling coefficient \(k^{2}\). and frequency ratio are defined as follows (Qian et al. 2021)

$$k^{2} = \frac{{\theta^{2} }}{{C_{p} K}} , r = \frac{w}{{w_{n} }}$$
(33)

where \(w_{n}\) is the short-circuit natural frequency, and the dimensionless electrical resistance is defined as

$$\gamma = w_{n} C_{p} R$$
(34)

Notably, the aforementioned model possesses the capability to compute the output power for an intact bimorph piezoelectric energy harvester, free from any cracks. To explore the implications of mid-layer cracks, an examination of alterations in both mechanical and electral attributes becomes pivotal. This encompasses the assessment of stiffness reduction, alongside an exploration of shifts in the equivalent electrical circuit of the harvester in both parallel and series configurations. Additionally, potential adjustments in the equivalent capacitance will be scrutinized. Ultimately, the introduced relationships will facilitate the computation of the rate of alteration in output voltage, along with other pertinent performance parameters. This circuit configuration has been selected as it is a commonly used interface for piezoelectric energy harvesters and allows for the study of the electrical output characteristics.

3 Impact of Mid-Layer Transverse Cracks on the Mechanical Characteristics of the Bimorph Piezoelectric System

In order to ensure the secure operation of a piezoelectric energy harvester, a comprehensive comprehension of plausible damage patterns that could arise during operational usage is imperative. Apart from piezoelectric material failure, which lies beyond the scope of this study, one of the most prominent and recurrent forms of damage within the mid-layer—such as transverse cracks—holds paramount significance. These forms of damage not only alter stress distribution but also significantly impact the structural stiffness. Extended operational cycles can exacerbate the occurrence of such cracks. The impairment to the mid-layer can induce substantial deterioration in structural properties, influencing the system's response and potentially culminating in failure. Transverse cracks occurring within the mid-layer frequently constitute the principal mode of failure and possess the propensity to amass in significant densities under escalating loads. These cracks generally traverse the entire layer thickness, aligning themselves nearly parallel. Due to the likelihood of mid-layer transverse cracks forming in multilayer composites during loading, detecting their occurrence during operation is crucial. The present investigation employs a micromechanics approach to assess the stiffness decline of the mid-layer in the bimorph energy harvester. The characteristics of the bimorph energy harvester are tabulated in Table 1.

Table 1 PZT and silicon properties
Full size table

It is worth mentioning that silicon, which is the most common single material used in microelectromechanical systems, is an inhomogeneous crystalline material whose properties depend on the positional coordinates relative to the crystal lattice. Due to the complexity of the subject, many researchers have used inaccurate values for design and analysis by simplifying the elastic properties of silicon. Estimations with isotropic consideration of silicon are mainly done in the initial design calculations (McCarter and Paquin 2013).

3.1 Stiffness Reduction Calculation Using an Analytical Approach

To explore the influence of mid-layer cracks on the dynamic response and power output of a piezoelectric material-based beam, the analysis can employ a micromechanical perspective utilizing the crack density-driven stress transfer technique pioneered by Farrokhabadi et al. (2019). Unlike methods confined to specific layer arrangements, this technique offers a comprehensive exploration of mid-layer crack effects, encompassing multilayer stiffness degradation. There are various methods for analyzing the effect of mid-layer cracks on multilayer stiffness reduction, including the shear log, variational approach, and stress transfer method. However, these methods have limitations in terms of the type of loading and stacking sequence they can handle. In contrast, the micromechanical method used in this study is not limited to a specific arrangement of layers and can comprehensively analyze the effect of mid-layer cracks. This method considers the layers as orthotropic and accurately satisfies the equations of equilibrium, compatibility, continuity conditions for forces and displacements, and external boundary conditions, making it a more versatile approach compared to the other techniques mentioned.

This methodology treats the layers as orthotropic and rigorously satisfies equations of equilibrium, compatibility, force and displacement continuity conditions, and external boundary prerequisites. Stiffness reduction resulting from mid-layer crack formation is determined through the micromechanics model. Employing the approach introduced by Farrokhabadi et al. (2010), the mechanical attributes of the impaired layer, such as \(E_{1} \left( \rho \right), E_{2} \left( \rho \right), G_{12} \left( \rho \right)\), etc., can be ascertained as functions of crack density. This involves the definition of three independent constants—namely, \(k, k^{\prime}, \text{and}\ D\). Notably, constants \(k\) and \(k^{\prime}\) exhibit dependency on the damage parameter. Leveraging these constants, the altered material properties can be computed as follows:

$$\frac{{\nu_{21} }}{{E_{2} }} - k\frac{D\left( \rho \right)}{{E_{2} }} = \frac{{\nu_{21} \left( \rho \right)}}{{E_{2} \left( \rho \right)}} , D\left( \rho \right) = \frac{{E_{2} }}{{E_{2} \left( \rho \right)}} - 1,$$
(35)
$$\frac{{\nu_{23} }}{{E_{2} }} - k^{\prime}\frac{D\left( \rho \right)}{{E_{2} }} = \frac{{\nu_{23} \left( \rho \right)}}{{E_{2} \left( \rho \right)}} , \frac{1}{{E_{1} }} - k^{2} \frac{D\left( \rho \right)}{{E_{2} }} = \frac{1}{{E_{1} \left( \rho \right)}}$$
$$\frac{{\nu_{13} }}{{E_{1} }} - kk{\prime} \frac{D\left( \rho \right)}{{E_{2} }} = \frac{{\nu_{13} \left( \rho \right)}}{{E_{1} \left( \rho \right)}} , \frac{1}{{E_{3} }} - k^{{\prime}{2}} \frac{D\left( \rho \right)}{{E_{2} }} = \frac{1}{{E_{3} \left( \rho \right)}}$$

In the provided equations, the values of \({{E}}_{1} \left( {\rho } \right),{{ E}}_{2} \left( {\rho } \right),{{ G}}_{12} \left( {\rho } \right)\), and so forth represent the elastic constants of the affected layer, which remain undetermined and are evaluated based on the damage parameter \(D\left( \rho \right)\).

The stiffness reduction results from the above relations are used as equivalent properties in Eq. (27) of the analytical method and the numerical method for calculating output voltage.

4 Impact of Mid-Layer Cracks on Electrical Characteristics

Upon the emergence of transverse cracks within the silicon layer of a bimorph piezoelectric energy harvester, two scenarios concerning the generation of an electric field within these cracks become plausible. In cases where the crack is electrically impermeable, no electric field manifests within the crack, whereby only the impact of stiffness reduction influences the alteration in output electrical power. In more critical instances, if an electric field takes shape within the crack, this phenomenon—alongside stiffness reduction—exerts an influence on the electrical power output. For instance, instances such as the detachment or separation of layers, coupled with crack extension within the electrode segment, lead to the removal of barriers between differing layer poles, resulting in their direct alignment. This occurrence triggers the creation of an electric field or force within the crack section, contingent upon the manner of connection.

Taking into account the Euler–Bernoulli assumptions and the large magnitude of the length-to-thickness ratio of the beam, it is possible to determine the equivalent capacitance capacity for every individual piezoelectric layer, as follows:

$$C = \frac{{AK\varepsilon_{0} }}{d}$$
(36)

here A represents the cross-sectional area of the piezoelectric layers and serves as a parameter for computing the current flowing through this particular surface.

$$A = bL$$
(37)
$$Q_{t} = \sigma A$$
(38)

Also, the flux passing through the surface is constant and can be calculated as

$$\sigma = \frac{{Q_{t} }}{A} = \frac{{Q_{crack} }}{{A_{crack} }}$$
(39)

To calculate the amount of current passing through the surface of the cracked section, in the first step, the area of its cross-sectional area is obtained, and then the current passing through the surface of the cracked part can be calculated.

$$A_{crack} = bt_{crack} = b \frac{{h_{s} }}{20}$$
(40)

ere the crack thickness with an engineering assumption is considered as \(\frac{{{{h}}_{{{s}}} }}{20}\). According to the above relations, we have:

$$Q_{crack} = \frac{{\left( {h_{s} /20} \right)}}{L}Q_{t} = \frac{{h_{s} }}{20L}Q_{t}$$
(41)

The crack position in the structure can be seen in Fig. 2. It should be noted that a "stress transfer technique based on crack density” has been used in the analysis. This suggests that we did not model the specific locations or positions of individual cracks. Instead, a more generalized approach based on the overall crack density within the mid-layer of the device has been used. The assumptions made about the crack distribution and density to enable the semi-analytical modeling approach, without going into the details of the exact crack locations. This simplified approach focuses more on the overall impact of the cracks on device performance, such as the reduction in stiffness and variations in capacitance, rather than providing an explicit detailed model of the crack geometry and its analysis.

Fig. 2
figure 2

The cracks position in the structure

Full size image

Considering the type of the connection, mid-layer cracks can yield distinct outcomes in serial and parallel configurations, which are elaborated upon in the subsequent sections.

4.1 Serial Connection

In situations where piezoelectric layers are connected in series, a crack within the mid-layer prompts the creation of an electric field. This phenomenon arises from the alignment of opposing poles within the crack, as depicted in Fig. 3.

Fig. 3
figure 3

Electric field creation inside the mid-layer in the case of a crack in the piezoelectric serial connection

Full size image

The configuration of the piezoelectric energy harvester's equivalent circuit undergoes alteration, as illustrated in Fig. 4. Making the assumption of ideal capacitors, the equivalent capacitance for each segment—encompassing both the piezoelectric layer and the crack section—can be computed according to the following method (Han et al. 2008).

$$C = \frac{{bLK\varepsilon_{0} }}{{h_{p} }}$$
(42)
$$C^{\prime} = \frac{{bh_{c} K^{\prime}\varepsilon_{0} }}{{h_{s} }}$$
(43)
Fig. 4
figure 4

The equivalent circuit of the piezoelectric energy harvester with a crack in the mid-layer in the serial connection

Full size image

In the equation provided, \(h_{c}\) represents the thickness of the crack, \(K\) stands for the dielectric coefficient within the piezoelectric material, and \(K^{\prime}\) denotes the dielectric coefficient in the crack section. The crack section has the potential to be occupied by intermediary substances such as air, silicone oil, or water. Consequently, it is prudent to account for the characteristics of these intermediaries.

As the quantity of cracks within the mid-layer of the bimorph increases, the equivalent circuit undergoes corresponding modifications, leading to the calculation of equivalent capacitance for each scenario. This can be expressed using the formula

$$C_{eq} = \frac{C}{2} + nC^{\prime}$$
(44)

where n signifies the count of cracks. Given that the capacitance of each individual piezoelectric layer is established, the equivalent capacitance for the crack section can be ascertained using the following procedure (Covaci et al. 2020).

$$\frac{{C^{\prime}}}{C} = \frac{{h_{c} K^{\prime}}}{{h_{s} }}\frac{{h_{p} }}{LK}$$
(45)

The effect of the silicon layer's thickness on the ratio of crack section capacitance to piezoelectric layer capacitance is shown in Fig. 5. It's evident that, even with an increased thickness, the capacitance of the crack section remains notably inferior to that of the piezoelectric layer capacitance.

Fig. 5
figure 5

The ratio of crack section capacitance to piezoelectric layer capacitance

Full size image

4.2 Parallel Connection

In the case of parallel connection, the presence of cracks (Fig. 6) causes the poles of the same name to face each other, and no electric field is formed. But it causes repulsive force in this section. The formation of the force is shown in Fig. 7.

Fig. 6
figure 6

Repulsive force Creation inside the mid-layer in the case of a crack in the piezoelectric parallel connection

Full size image
Fig. 7
figure 7

Formation of repulsive force at the crack site in the case of parallel connection of piezoelectric layers

Full size image

In this case, the capacitance in the cracked section is zero, and the equivalent capacity is calculated as

$$C_{eq} = 2C$$
(46)
$$C_{crack} = 0$$
(47)

Since the electric field does not form in the crack section of parallel connection mode, similar to the impermeable cracking mode, only stiffness reduction will affect the output electrical power, and the results are the same as for impenetrable cracks.

5 Finite Element Model for the Voltage Calculation of Bimorph Energy Harvester

The verification of the derived relationships in this paper is conducted through finite element analysis of the bimorph piezoelectric energy harvester, utilizing ANSYS software. The model consists of three distinct element types: 640 solid226 elements representing the piezoelectric components, and 320 solid186 elements representing the structural aspects. The allocation of these elements is determined via a convergence test, as depicted in Fig. 8. Introducing the simulation of resistance between the upper and lower electrodes is achieved using a single CIRCU94 element with two nodes, aptly interfacing with the piezoelectric elements. The diagram further illustrates the voltage interaction between the piezoelectric layers and the circuit element, exemplifying an FE model for a bimorph configured in serial connection.

Fig. 8
figure 8

Finite element model of the bimorph energy harvester: a base excitation direction, b the voltage coupling between the piezoelectric and circuit element

Full size image

The output voltage, amplitude and phase angle are obtained from the finite element analysis. To investigate the behavior of the harvester in the presence of cracks in the substrate section, a continuum model has been used, and the equivalent properties of the damaged layer, such as stiffness and capacitance obtained from previous analyses, have been employed.

6 Results and Discussion

Prior to commencing the damage analysis, an examination of the analytical approach for voltage and power calculation is undertaken. Figure 9 presents a comparison of the output voltage against excitation frequency for the intact bimorph energy harvester, as obtained from both the analytical solution and finite element analysis.

Fig. 9
figure 9

Output voltage of the bimorph energy harvester vs. excitation frequency from Analytical solution and FEA

Full size image

The analytical solution is compared with finite element analysis. It shows a good agreement between the voltage spectrum by the analytical model and finite element results with an approximately 5.7% difference in the resonance frequency. The analytical and FEA models predict the resonance frequency as 83.5 Hz and 78.8 Hz, respectively. The slight difference is mainly due to the Euler–Bernoulli beam theory assumptions, while the continuous physical system is considered in the finite element analysis.

Since the piezoelectric energy harvester investigated in this study operates in the \(d_{31}\) mode, the axial stiffness is contributed to calculating the output voltage, and the changes of this parameter should be considered. It is obvious that all stiffness components are the same in isotropic materials, which is not an issue. To investigate the effects of damage in the other operating modes of energy harvesting by using piezoelectric materials such as \(d_{33}\) mode, the related stiffness component changes should be considered, and its effects should be investigated.

The micromechanical approach allows for the determination of the axial stiffness of the damaged layer, as demonstrated in Table 2 across varying quantities of cracks. This micromechanical approach allowed for a comprehensive analysis of the impact of mid-layer cracks on the overall stiffness reduction of the multilayer composite, without being limited to specific layer arrangements or loading conditions. The methodology provides a detailed, physics-based framework for predicting the degradation in structural performance due to the presence of mid-layer cracks.

Table 2 Calculated axial stiffness of mid-layer using micromechanics approach
Full size table

Furthermore, the outcomes of the analysis conducted on the bimorph piezoelectric employing this technique are presented in Table 3. The relationship between the axial stiffness of the impaired layer and the bimorph beam concerning the count of cracks, as determined through the micromechanics approach, is visualized in Fig. 10. The values presented in Tables 2 and 3 were obtained through the application of the micromechanical method described earlier in the manuscript. This method considers the multilayer structure as a series of orthotropic layers and accurately satisfies the equations of equilibrium, compatibility, continuity conditions for forces and displacements, and external boundary conditions.

Table 3 Calculated axial stiffness of bimorph piezoelectric using micromechanics approach
Full size table
Fig. 10
figure 10

The results of the micromechanics approach: a axial stiffness of silicon layer, b axial stiffness of bimorph

Full size image

The findings derived from the micromechanics methodology demonstrate that an escalation in the count of cracks within the mid-layer corresponds to a reduction in the axial stiffness of the bimorph piezoelectric energy harvester. Furthermore, to validate the outcomes obtained through the analytical method, the finite element approach has been employed. Utilizing the finite element method, the strain energy within a bimorph piezoelectric energy harvester afflicted with transverse cracks within the mid-layer can be assessed for a specific applied load, as represented by the equation:

$$SE = \frac{{\sigma_{1}^{2} V}}{{2E_{1} }}$$
(48)

Then, the axial modulus can be obtained as (Rahmani and Farrokhabadi 2018)

$$E_{1} = \frac{{\sigma_{1}^{2} V}}{2SE}$$
(49)

To assess the mesh independency, different numbers of mesh discretization are examined, and the best result has been achieved. The mesh study and convergence test determine the final numbers of elements and nodes.

Upon imposing a designated load, the strain energy is measured. Subsequently, under identical loading circumstances, a transverse crack is induced, and the strain energy is recalculated. An illustrative representation of the simulation depicting the corresponding crack and the mesh configuration surrounding the cracks can be found in Fig. 11.

Fig. 11
figure 11

a Strain energy distribution and b mesh configuration around the crack

Full size image

The obtained strain energy and the resultant axial stiffness from the finite element analysis for each case are shown in Table 4. The strain energy and the axial stiffness of the undamaged structure and damaged structure with different numbers of cracks in the mid-layer from 1 to 5 are also shown in Fig. 12.

Table 4 Calculated strain energy and axial stiffness from finite element analysis
Full size table
Fig. 12
figure 12

The results of FEA: a Strain energy of bimorph, b axial stiffness of bimorph

Full size image

The finite element analysis reveals that an increase in the count of cracks within the mid-layer of the bimorph piezoelectric energy harvester leads to heightened strain energy and diminished axial stiffness. A comparison between the stiffness reduction outcomes obtained through the micromechanics approach and finite element analysis underscores the high accuracy of the theoretical model, thus establishing its suitability for further investigations. The impact of silicon layer thickness on the natural frequency of the bimorph piezoelectric energy harvester is visualized in Fig. 13, whereas the overall structural natural frequency is presented in Fig. 14. Evident from the acquired results is the proportional relationship between the thickness of mid-layers and the rising natural frequency of the bimorph. Consistently, the anticipated outcome emerges that an increase in crack numbers leads to a decline in the natural frequency, a plausible consequence due to the bimorph energy harvester's reduced stiffness.

Fig. 13
figure 13

Effect of the mid-layer thickness on the natural frequency

Full size image
Fig. 14
figure 14

Effect of different mid-layer crack numbers on the Natural frequency

Full size image

Upon comparing the values in Table 3, obtained through the micromechanical analysis, and Table 4, which presents the results from the Finite Element Method (FEM) analysis, it can be observed that the FEM-derived values in Table 4 are consistently lower than the corresponding values documented in Table 3 from the micromechanical approach. This discrepancy can be attributed to the inherent differences between the two analysis methods. The micromechanical approach relies on a set of analytical equations that make simplifying assumptions, such as considering the layers as orthotropic materials. In contrast, the FEM analysis provides a more detailed, numerical solution that can capture the complex stress distributions and deformations within the multilayer structure more accurately.

As the quantity of mid-layer cracks increases, the disparity between the predicted values in Tables 3 and 4 diminishes. This observation suggests that the simplified assumptions used in the micromechanical analysis become more accurate as the degree of cracking in the multilayer structure increases. When there are fewer cracks, the stress distributions and deformations are more sensitive to the specific crack patterns and layer interactions, which the FEM analysis can capture more precisely. However, as the number of cracks increases, the overall structural behavior becomes more dominated by the average, homogenized properties of the cracked layers, which the micromechanical model can represent more effectively.

In summary, the differences between the two analysis methods highlight the trade-offs between the analytical rigor of the FEM approach and the computational efficiency of the micromechanical method. The converging results as the crack density increases indicate that the micromechanical model becomes a more reliable and practical tool for predicting the stiffness degradation in highly cracked multilayer composites.

Figures 15 and 16 display the variations in output electrical power and voltage as derived from the analytical method, across distinct crack numbers. Meanwhile, Figs. 17 and 18 depict the output voltage concerning excitation frequency, as determined by finite element analysis, for different crack quantities. Notably, the forecasted output voltage stemming from the analytical method concurs with results obtained from finite element analysis in relation to the propagation of transverse cracks. Both approaches affirm that augmenting the number of cracks corresponds to an approximate 0.2% increase in output voltage.

Fig. 15
figure 15

Effect of mid-layer cracks on the output power from analytical method

Full size image
Fig. 16
figure 16

Effect of mid-layer cracks on the voltage from analytical method

Full size image
Fig. 17
figure 17

Effect of mid-layer cracks on the voltage from finite element analysis

Full size image
Fig. 18
figure 18

Voltage-Frequency for cracks in the mid-layer of bimorph piezoelectric from finite element analysis

Full size image

With an increase in the count of cracks within the mid-layer of the bimorph, noticeable trends emerge: the natural frequency of the bimorph piezoelectric energy harvester diminishes, and concurrently, both voltage and output power augment. This relationship is evident when examining the influence of varying mid-layer crack quantities on the Phase angle and Impedance amplitude of the bimorph energy harvester, depicted in Figs. 19 and 20 correspondingly. The data illustrates that as the number of cracks rises, the impedance amplitude experiences a corresponding increase, while the phase angle demonstrates a converse decrease. These shifts signify additional indications of potential impairments within devices of this nature.

Fig. 19
figure 19

Effect of different mid-layer crack numbers on the Phase Angle

Full size image
Fig. 20
figure 20

Effect of different mid-layer crack numbers on the Impedance Amplitude

Full size image

The results of Fig. 20 reveal that the impedance amplitudes of the energy harvester will increase with an average rate of 0.8% by growing the number of mid-layer cracks. It should be noted that the reported changes in the parameters, including the amplitude and voltage depend on the dimensions and size of the cracks as well as the material of the mid-layer. Furthermore, since the crack density-based method is employed to calculate stiffness reduction due to crack formation, the present study can be used for mid-layer cracks analysis of bimorph piezoelectric energy harvesters even when cracks of mid-layer are not uniformly distributed.

As a verification study, it should be noted that this method was employed in another published paper (Jamshiddoust et al. 2023) with a composite substrate. A comparison of the natural frequencies and output voltage obtained from Ref. Jamshiddoust et al. (2023) and the current study, using the properties of the composite substrate, is shown in Table 5.

Table 5 Effect of mid-layer cracks on the natural frequency and output voltage of bimorph with composite substrate
Full size table

As can be seen from Table 5, using the properties of the composite substrate, the results from Reference Jamshiddoust et al. (2023) can be obtained.

In summary, underlying mechanisms can be categorized as effect on Natural Frequency, effect on Output Voltage and effect on Output Power. The presence of mid-layer cracks in the bimorph structure leads to a reduction in the overall structural stiffness of the device. According to the Euler–Bernoulli beam theory, the natural frequency of a cantilever beam is directly proportional to the square root of the bending stiffness. As the mid-layer cracks decrease the bending stiffness of the bimorph structure, the natural frequency of the energy harvester decreases accordingly. The more the number of mid-layer cracks, the greater the reduction in the overall stiffness, and consequently, the lower the natural frequency of the device.

The mid-layer cracks can affect the equivalent capacitance of the bimorph piezoelectric energy harvester, as discussed earlier. For a serial connection of the piezoelectric layers, the cracks create an electric field within the crack region, altering the effective capacitance. For a parallel connection, the cracks change the cross-sectional area of the piezoelectric layers, which also affects the overall capacitance. According to the governing equations of piezoelectric energy harvesters, the output voltage is inversely proportional to the device capacitance. Therefore, the presence of mid-layer cracks, which reduce the effective capacitance, leads to an increase in the output voltage of the energy harvester. The more the number of mid-layer cracks, the greater the reduction in capacitance, and consequently, the higher the output voltage of the device. The output power of the piezoelectric energy harvester is determined by the product of the output voltage and the current. As the mid-layer cracks increase the output voltage (due to capacitance reduction), and the current remains relatively unaffected, the overall output power of the device increases. The more the number of mid-layer cracks, the higher the output voltage, and consequently, the greater the output power of the energy harvester.

For a composite with active layers, the constitutive relations involve elastic, electro-elastic, and dielectric terms, and it is necessary to consider appropriate changes in all of these terms in the presence of damages such as cracks or delamination. By this research, it is shown that mid-layer crack causes a change in elastic stiffness and does not alter the electromechanical coupling terms. However, it should be remembered that the mid-layer crack-induced delamination between the piezoelectric layer and the substrate causes a reduction in the electromechanical coupling coefficients, i.e., reduces its load-carrying ability and its active effects. In such cases, it will be necessary to study the reduction of these parameters, which is one of the ongoing studies by the authors.

7 Conclusions

This paper introduces a semi-analytical solution to analyze transverse cracks within the mid-layer of a bimorph piezoelectric energy harvester, exploring both serial and parallel configurations. The novelty of this research primarily stems from its consideration of both stiffness reduction and changes in capacitance on the response of the proposed energy harvester. This study uncovers new insights into physical phenomena previously unreported. As anticipated, these cracks induce a reduction in structural stiffness. However, in the most severe cases, they can also induce alterations in the bimorph's capacitance. The introduction of multiple mid-layer cracks modifies both stiffness and the equivalent circuit. Consequently, in addition to stiffness reduction, the electric field within the crack may impact electrical power output. To address this, a micromechanics approach is employed to compute mid-layer stiffness reduction. This entails deriving coupled mechanical and electrical differential equations, followed by their solution. Changes in the equivalent circuit and equivalent capacitance of the piezoelectric energy harvester are investigated. With the formation of cracks, the voltage and output power of the piezoelectric energy harvester increase, indicative of failure. Results emphasize that stiffness reduction primarily influences output power. The effect of changes in equivalent capacitance and potential electric field within transverse cracks on output power is relatively minor compared to stiffness reduction. Overall, the close alignment between analytical model and numerical outcomes validates the reliability of this approach. The current study thus proposes a dependable method for analyzing mid-layer cracks in bimorph piezoelectric energy harvesters, applicable even when cracks are non-uniformly distributed. While silicon is the substrate examined in this study, the proposed crack analysis approach extends to all orthotropic materials, not solely limited to silicon.