1 Introduction

Single-walled carbon nanotubes (SWCNTs) have attracted widespread attention within the scientific and engineering communities, owing to their exceptional physical and chemical properties. In the growth of SWCNTs, various multiterminal junctions such as T-, Y-, X- and H-shaped junctions have been observed (Terrones et al. 2002; Park et al. 2006; Liu et al. 2011). These junctions suggest the possibility of the construction of stable nano-architected metamaterials comprising SWCNTs (Romo-Herrera et al. 2007; Zhou et al. 2011). These metamaterials have high strength and low density (Coluci et al. 2007; Li et al. 2009), and so the carbon nanotube super-architectures can be ideal candidates for designing the high sensitivity sensors and the CNT-reinforced composites. Recently, a novel face-centered cubic (FCC) nano-truss has been proposed by Zhang et al. (2018). They estimated both mechanical and thermal properties of the FCC nano-trusses by using the molecular dynamics simulation. Their results revealed that the proposed nano-trusses can be used as a lightweight and mechanically robust element with tunable Young’s modulus and high thermal stability.

The carbon nanotube super-architectures are encountered to various uncertainties such as inherent variability in material and geometrical properties, and external loads (Pedrielli et al. 2017). It was shown that the uncertainties could affect the mechanical behavior of the nanoscopic structures (Ghanipour and Ghavanloo 2019; Ghavanloo and Fazelzadeh 2015; Liu and Lv 2018; Ghanipour et al. 2018; Oktem and Adali 2018). Therefore, structural reliability analysis is necessary when new carbon nanotube super-architectures are proposed. The structural reliability analysis provides a useful framework for considering the uncertainties and is used to evaluate the ability of components or systems to remain safe during their lifecycle (Keshtegar 2016; Wang et al. 2017). Generally, the probabilistic reliability analysis is studied by various methods, such as the Monte Carlo (MC) simulation (Zhu and Du 2016), the first-order reliability method (FORM) (Zhou et al. 2017) and the second-order reliability method (SORM) (Der Kiureghian and Stefano 1991). For solving some reliability problems, the probabilistic reliability is not applicable because of inadequate data (Chen et al. 2017). However, nonprobabilistic reliability can effectively deal with reliability problems when only a few statistical data can be obtained (Wang et al. 2019a, b, c). Unfortunately, only a few results are available in the literature related to the structural reliability analysis of the nanoscopic structures. In the year 2016, the reliability analysis of composite beams reinforced with carbon nanotubes was investigated by using the FORM (Keshtegar et al. 2016). In another study, the first-order second-moment method was used for the reliability analysis of the composite plates reinforced with carbon nanotubes (Hussein and Mulani 2018). Recently, Esbati and Irani (2018) have proposed a procedure for evaluating the structural reliability of carbon nanotubes using the stochastic finite element methods. However, the reliability analysis of the carbon nanotube super-architectures has not been investigated so far.

In view of the above remarks, the main objective of this study is to present the reliability analysis of the carbon nanotube-based FCC nano-truss under two loading conditions including tension and shear. Here, we assume that the architecture of FCC nano-truss is designed such that the internal SWCNTs are only loaded in tension or compression. It should be noted that the reliability of nano-truss directly depends on the reliability of SWCNTs and their junctions. In this study, the FORM and the Crude Monte Carlo (CMC) method are employed to calculate the reliability of the internal SWCNTs. Furthermore, the reliability of the nano-truss is evaluated by using the reliability matrix method. Although high technological equipment is required to synthesize this nano-truss, our investigation can shed some light on the application of these novel nanoscopic structures.

The paper is organized as follows: In Sect. 2, we briefly review the main concepts of the reliability analysis. In Sect. 3, the reliability analysis of the carbon nanotube-based FCC nano-truss under two loading conditions is carried out. Finally, the conclusions of this study are summarized in Sect. 4.

2 Brief Review of Reliability Analysis

Generally, for a system comprising several components, both component reliability analysis and system reliability analysis are important. The component reliability refers to the probability of satisfying a performance criterion in a specific component of the system while the system reliability analysis refers to the probability of satisfying a performance criterion at a whole of the system (Haldar and Mahadevan 2000). As stated above, we use both the FORM and the CMC methods to evaluate the component reliability.

It is well known that the ultimate strength of the SWCNT, \(\sigma_{U}\), and the induced stress in each SWCNT, \(\sigma\), are uncertain variables. To investigate the performance of the SWCNT under tension or compression loads, a desirable limit state function (LSF) must be defined in terms of uncertain variables. The LSF can be expressed as:

$$g\left( {\tilde{\varvec{U}}} \right) = \sigma_{U} - \sigma \left( {\tilde{\varvec{U}}} \right)$$
(1)

where \(\tilde{\varvec{U}} = \left[ {u_{1} , u_{2} , \ldots , u_{n} } \right]^{T}\) is a vector of uncertain variables. Generally, failure surface is obtained by solving \(g\left( {\tilde{\varvec{U}}} \right) = 0\), while \(g\left( {\tilde{\varvec{U}}} \right) > 0\) represents the safe region and \(g\left( {\tilde{\varvec{U}}} \right) < 0\) corresponds to the failure region. The main objective of the component reliability analysis is the estimation of the failure probability of a component, \(p_{\text{f}}\). The probability of failure is estimated as:

$$p_{\text{f}} = {\text{Prob}}\left( { g\left( {\tilde{\varvec{U}}} \right) < 0} \right) = \mathop \int \limits_{{g\left( {\tilde{\varvec{U}}} \right) < 0}} f\left( {\tilde{\varvec{U}}} \right)d\tilde{\varvec{U}}$$
(2)

where \(f\) denotes the probability density function. In addition, the reliability of the component is obtained by:

$$R = 1 - p_{\text{f}}$$
(3)

It should be noted that the integration of Eq. (2) in most cases cannot be performed analytically. Therefore, various approximation methods such as the FORM and CMC methods can be used to evaluate Eq. (2). These methods are described briefly in the next subsections.

2.1 First-Order Reliability Methods (FORM)

The FORM is usually used to estimate the failure probability by approximating the LSF by a hyperplane tangent to the failure surface at the most probable point (MPP) (Li et al. 2018). It should be noted that the normal standard space is more desirable to solve the reliability problem. Therefore, the space of the basic random variables can be transformed into a space of standard normal variables by various transformation techniques such as the Rosenblatt transformation (Rosenblatt 1952) and the Nataf transformation (Lebrun and Dutfoy 2009). The transformation of a variable \(u_{i} \varvec{ }\) with an arbitrary distribution into \(x_{i}\) with a standard normal distribution is:

$$\Phi \left( {x_{i} } \right) = F_{i} \left( {u_{i} } \right)$$
(4)

where \(F_{i}\) and \(\varPhi\) are the cumulative distribution function (CDF) of the random variable and the cumulative distribution function of the standard normal variable, respectively. In accordance with the concept of CDF, the failure probability can be estimated as follows:

$$p_{\text{f}} = \varPhi \left( { - \beta } \right) = \frac{1}{{\sqrt {2\pi } }}\mathop \int \limits_{ - \infty }^{ - \beta } \exp \left( { - \frac{{t^{2} }}{2}} \right){\text{d}}t$$
(5)

where \(\beta\) is known as a reliability index which is the smallest distance between the origin and the LSF in the standard normal space \(G\). To calculate the failure probability by using FORM, it is necessary to find the MPP by solving the following constrained optimization problem:

$$x^{*} = \hbox{min} \{ \left\| {\tilde{\varvec{x}} } \right\||G\left( {\tilde{\varvec{x}}} \right) = 0\}$$
(6)

where \(x^{*}\) denotes the MPP. Therefore, according to definition of the reliability index, we have:

$$\beta = \left\| {\varvec{x}^{\varvec{*}} } \right\|$$
(7)

To find the design point, the improved Hasofer–Lind–Rackwitz–Fiessler (iHLRF) algorithm can be used (Liu and Der 1991). In this iterative algorithm, every new iteration of the design point is determined from the previous point. After finding the design point, the reliability of the component is obtained by:

$$R = 1 - \varPhi \left( { - \left\| {x^{*} } \right\|} \right)$$
(8)

2.2 Crude Monte Carlo (CMC) Method

Another important simulation method for estimating the probability of failure is the Monte Carlo method. According to the Monte Carlo simulation method, the probability of failure is expressed as (Azimi et al. 2018):

$$p_{\text{f}} = \mathop \int \limits_{ - \infty }^{ + \infty } \ldots \mathop \int \limits_{ - \infty }^{ + \infty } I\left( {\tilde{\varvec{U}}} \right)f\left( {\tilde{\varvec{U}}} \right){\text{d}}\tilde{\varvec{U}}$$
(9)

where \(I\left( {\tilde{\varvec{U}}} \right)\) denotes the indicator function and is defined as:

$$I\left( {\tilde{\varvec{U}}} \right) = \left\{ {\begin{array}{*{20}c} 1 &\quad {{\text{if}}\;g\left( {\tilde{\varvec{U}}} \right) < 0} \\ 0 &\quad {{\text{if}}\;g\left( {\tilde{\varvec{U}}} \right) > 0} \\ \end{array} } \right.$$
(10)

In addition, for the CMC method, the probability of failure in Eq. (9) is approximated as (Verhoosel et al. 2009):

$$p_{\text{f}} = \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} I\left( {u_{i} } \right)$$
(11)

where N is the number of simulations and \(u_{i}\) is one out of N random realizations of the vector \(\tilde{\varvec{U}}\). The simulation number can be determined by the following relation (Lemaire 2013):

$$N = \frac{1}{{\delta_{{P_{\text{f}} }}^{2} }}\left( {\frac{{1 - p_{\text{f}} }}{{p_{\text{f}} }}} \right)$$
(12)

where \(\delta_{{P_{\text{f}} }}\) is the coefficient of variation. This coefficient is usually set to 0.05.

2.3 System Reliability Matrix

System reliability is of critical importance for a complex system consisting of several components. Therefore, various techniques have been proposed to estimate the system reliability. In this study, the reliability of the system is calculated by using the reliability matrix method. This method is explained briefly as follows.

Consider a system S consisting of N components Ci, and assume the reliability of ith component is Ri. Furthermore, let us denote the physical interconnection between components Ci and Cj by \(\omega_{i,j}\), such that \(\omega_{i,j} = 0\) if the component Ci is not connected to the component Cj. Since a component cannot be connected to itself, we have also \(\omega_{ii} = 0\). Therefore, the component reliability matrix RC and the component connection matrix \({\varvec{\Omega}}\) are defined as (Tang 2001):

$${\mathbf{R}}_{{\mathbf{C}}} = \left[ {\begin{array}{*{20}l} {R_{1} } \hfill & 0 \hfill & \ldots \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & {R_{2} } \hfill & \ldots \hfill & 0 \hfill & 0 \hfill \\ \vdots \hfill & \vdots \hfill & \ddots \hfill & \vdots \hfill & \vdots \hfill \\ 0 \hfill & 0 \hfill & \ldots \hfill & {R_{N - 1} } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & \ldots \hfill & 0 \hfill & {R_{N} } \hfill \\ \end{array} } \right]$$
(13)
$${\varvec{\Omega}} = \left[ {\begin{array}{*{20}l} 0 \hfill & {\omega_{1,2} } \hfill & \ldots \hfill & {\omega_{1,N - 1} } \hfill & {\omega_{1,N} } \hfill \\ {\omega_{1,2} } \hfill & 0 \hfill & \ldots \hfill & {\omega_{2,N\_1} } \hfill & {\omega_{2,N} } \hfill \\ \vdots \hfill & \vdots \hfill & \ddots \hfill & \vdots \hfill & \vdots \hfill \\ {\omega_{1,N - 1} } \hfill & {\omega_{2,N\_1} } \hfill & \ldots \hfill & 0 \hfill & {\omega_{N - 1,N} } \hfill \\ {\omega_{1,N} } \hfill & 0 \hfill & \ldots \hfill & {\omega_{N - 1,N} } \hfill & 0 \hfill \\ \end{array} } \right]$$
(14)

Note that the matrix \({\varvec{\Omega}}\) is symmetric. The system reliability matrix is then expressed as:

$${\mathbf{R}} = {\mathbf{R}}_{{\mathbf{C}}} - {\varvec{\Omega}}$$
(15)

Finally, the system reliability is determined by calculating the determinant of the system reliability matrix R.

3 Reliability Analysis of FCC Nano-Truss

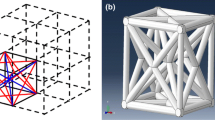
As mentioned in Zhang et al. (2018), the carbon nanotube-based nano-truss is built from the SWCNTs connected by multiterminal junctions. The atomistic structure of carbon nanotube-based nano-truss and its equivalent FCC truss are shown in Fig. 1. Here, the following assumptions were considered for reliability analysis:

Fig. 1
figure 1

Schematic illustration of nano-truss: a atomistic structure and b unit cell of equivalent FCC truss

Full size image
  1. (a)

    The tensile and the compressive yield strength of SWCNTs are taken to be the same.

  2. (b)

    The buckling does not occur in the SWCNTs.

  3. (c)

    The SWCNTs and the multiterminal junctions are, respectively, modeled by linear elastic struts and ball and socket joints.

According to the above assumptions, the reliability of carbon nanotube-based nano-truss in the uniaxial tensile and compressive forces is equal. Therefore, to illustrate the effects of loading condition on the failure probability of the FCC nano-truss, we assume that the structure is subjected to two loading conditions including uniaxial tension and shear loads.

The schematic illustration of loading conditions is depicted in Fig. 2. As depicted in Fig. 2, the load with magnitude P is applied at the junctions 2, 5, 7, 10 and 11, while the junctions 3, 4, 8, 9 and 13 are kept fixed. In addition, it can be observed that the FCC nano-truss consists of fourteen junctions (components) and thirty-six SWCNTs (links). The system graph of the nano-truss is shown in Fig. 3. Based on the system graph and using Eqs. (13–15), the system reliability matrix can be written as:

$${\mathbf{R}} = \left[ {\begin{array}{*{20}l} {R_{1} } \hfill & { - \omega_{1,2} } \hfill & { - \omega_{1,3} } \hfill & { - \omega_{1,4} } \hfill & { - \omega_{1,5} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & { - \omega_{1,11} } \hfill & { - \omega_{1,12} } \hfill & { - \omega_{1,13} } \hfill & { - \omega_{1,14} } \hfill \\ { - \omega_{1,2} } \hfill & {R_{2} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & { - \omega_{2,11} } \hfill & { - \omega_{2,12} } \hfill & 0 \hfill & 0 \hfill \\ { - \omega_{1,3} } \hfill & 0 \hfill & {R_{3} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & { - \omega_{3,12} } \hfill & { - \omega_{3,13} } \hfill & 0 \hfill \\ { - \omega_{1,4} } \hfill & 0 \hfill & 0 \hfill & {R_{4} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & { - \omega_{4,13} } \hfill & { - \omega_{4,14} } \hfill \\ { - \omega_{1,5} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {R_{5} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & { - \omega_{5,11} } \hfill & 0 \hfill & 0 \hfill & { - \omega_{5,14} } \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {R_{6} } \hfill & { - \omega_{6,7} } \hfill & { - \omega_{6,8} } \hfill & { - \omega_{6,9} } \hfill & { - \omega_{6,10} } \hfill & { - \omega_{6,11} } \hfill & { - \omega_{6,12} } \hfill & { - \omega_{6,13} } \hfill & { - \omega_{6,14} } \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & { - \omega_{6,7} } \hfill & {R_{7} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & { - \omega_{7,11} } \hfill & { - \omega_{7,12} } \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & { - \omega_{6,8} } \hfill & 0 \hfill & {R_{8} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & { - \omega_{8,12} } \hfill & { - \omega_{8,13} } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & { - \omega_{6,9} } \hfill & 0 \hfill & 0 \hfill & {R_{9} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & { - \omega_{9,13} } \hfill & { - \omega_{9,14} } \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & { - \omega_{6,10} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {R_{10} } \hfill & { - \omega_{10,11} } \hfill & 0 \hfill & 0 \hfill & { - \omega_{10,14} } \hfill \\ { - \omega_{1,11} } \hfill & { - \omega_{2,11} } \hfill & 0 \hfill & 0 \hfill & { - \omega_{5,11} } \hfill & { - \omega_{6,11} } \hfill & { - \omega_{7,11} } \hfill & 0 \hfill & 0 \hfill & { - \omega_{10,11} } \hfill & {R_{11} } \hfill & { - \omega_{11,13} } \hfill & 0 \hfill & { - \omega_{11,14} } \hfill \\ { - \omega_{1,12} } \hfill & { - \omega_{2,12} } \hfill & { - \omega_{3,12} } \hfill & 0 \hfill & 0 \hfill & { - \omega_{6,12} } \hfill & { - \omega_{7,12} } \hfill & { - \omega_{8,12} } \hfill & 0 \hfill & 0 \hfill & { - \omega_{11,12} } \hfill & {R_{12} } \hfill & { - \omega_{12,13} } \hfill & 0 \hfill \\ { - \omega_{1,13} } \hfill & 0 \hfill & { - \omega_{3,13} } \hfill & { - \omega_{4,13} } \hfill & 0 \hfill & { - \omega_{6,13} } \hfill & 0 \hfill & { - \omega_{8,13} } \hfill & { - \omega_{9,13} } \hfill & 0 \hfill & 0 \hfill & { - \omega_{12,13} } \hfill & {R_{13} } \hfill & { - \omega_{13,14} } \hfill \\ { - \omega_{12,13} } \hfill & 0 \hfill & 0 \hfill & { - \omega_{4,14} } \hfill & { - \omega_{5,14} } \hfill & { - \omega_{6,14} } \hfill & 0 \hfill & 0 \hfill & { - \omega_{9,14} } \hfill & { - \omega_{10,14} } \hfill & { - \omega_{11,14} } \hfill & 0 \hfill & { - \omega_{13,14} } \hfill & {R_{14} } \hfill \\ \end{array} } \right]$$
(16)

where Ri is the reliability of ith junction. The next step is to calculate the physical interconnection \(\omega_{i,j}\). Here we assume that the interconnection coefficient is equal to the probability of failure of each link, i.e., \(\omega_{i,j} = 1 - R_{i,j}\), because the interconnection between two components is proportional to its failure probability. Therefore, it is necessary to evaluate the reliability of each SWCNT. In this way, it is supposed that the failure of the SWCNT occurs when the internal force exceeds the ultimate stress of SWCNT. As a result, the LSF for each link is expressed as:

$$g_{i,j} = \sigma_{U} - \frac{{F_{i,j} }}{2\pi rt}$$
(17)

where \(\sigma_{U}\) is the ultimate stress of the SWCNT. In addition, \(r\) and \(t\) are the radius and the effective thickness of the SWCNT, and \(F_{i,j}\) denotes the internal force between junctions i and j. The internal force ratio of different links, \(f_{i,j} = \left| {F_{i,j} /P} \right|\), is listed in Table 1. In addition, the statistical information of input random variables is reported in Table 2. It is assumed that the correlation between the random variables is zero, and so they are independent. It should also be noted that the ultimate stress is the only deterministic variable and its value is 90 GPa.

Fig. 2
figure 2

Nano-truss under various loading conditions: a uniaxial tension, b shear

Full size image
Fig. 3
figure 3

Graph of FCC truss

Full size image
Table 1 Force ratio of different links
Full size table
Table 2 Statistical properties of the basic random variables for the nano-truss
Full size table

To achieve enough accuracy of the results obtained from the CMC, Shooman’s equation (Eq. 12) is used. The main procedure for computing the total number of simulation trials using Shooman’s equation can be summarized as follows:

  1. (a)

    The initial number of simulations must be specified.

  2. (b)

    The probability of failure is calculated using Eq. (11)

  3. (c)

    The total number of simulations is updated from Eq. (12).

  4. (d)

    The above procedure is repeated until the probability of failure converges to the constant value.

The mentioned procedure is used for each link. Figure 4 displays the variations in the probability of failure of one link with the number of simulations. It can be seen that 16,000 simulations are sufficient to get convergence in the determination of the probability of failure.

Fig. 4
figure 4

Variations in probability of failure of one link with number of simulations

Full size image

The results obtained from the FROM and the CMC methods for the reliability of each SWCNT are presented in Table 3. As can be inferred from this table, the results obtained from the FORM technique are in good agreement with those obtained from the CMC method. The flowchart of the FORM method is provided in Fig. 5.

Table 3 Estimated reliability of each link in nano-truss by FORM and CMC methods
Full size table
Fig. 5
figure 5

Flowchart of the FORM

Full size image

To determine the reliability of nano-truss subjected to various loads, we need to give appropriate values for the reliability of junctions. Since the reliability of junctions in the nano-truss is not accessible, we study the effect of these parameters on the total reliability of the FCC nano-truss. To elucidate the effect of the junction reliability, the estimated values of the reliability of the nano-truss for two types of loads are listed in Table 4 for different values of junction reliability. For numerical calculation in this table, it is assumed that the reliability of all junctions is equal. In addition, the results obtained from the FORM method for the reliability of the SWCNTs are used. The first observation made here is the difference between the reliability of the nano-truss under uniaxial tension and shear loads. Comparing the reliability of nano-truss under various loading conditions indicates that this structure is more proper under uniaxial tension load. The second observation is the influence of junction reliability. It is shown that the reliability of junctions has an outstanding effect on the reliability of the nano-truss. For example, for uniaxial tension load, one percent change in the reliability of junctions leads to a change of more than ten percent in the reliability of nano-truss.

Table 4 Reliability of nano-truss subjected to various loading conditions for different values of junction reliability
Full size table

As the final numerical study, the variations in the reliability of the nano-truss subjected to uniaxial tension as a function of the ultimate strength of the SWCNT are shown in Fig. 6. For calculating the numerical results, we use the FORM approach and we take Ri = 0.999. As expected, the reliability of the system increases with increasing the ultimate strength.

Fig. 6
figure 6

Variations in the reliability of the nano-truss under uniaxial tension as a function of the ultimate strength of SWCNT

Full size image

4 Conclusion

The reliability analysis of the FCC nano-truss in both tensile and shear regimes was investigated. In this way, the FORM and CMC approaches were employed to calculate the component reliability and the reliability matrix method was used to estimate the system reliability. Based on the numerical results, the following conclusions can be drawn:

  1. 1.

    The reliability of the SWCNTs and junctions can affect the reliability of the FCC nano-truss.

  2. 2.

    The reliability of the nano-truss decreases with decreasing the reliability of junctions.

  3. 3.

    The performance of the nano-truss in the uniaxial tension load is much better than that in shear load.

  4. 4.

    System reliability increases as the ultimate strength of SWCNT increases.

Although the reliability analysis was only implemented for the FCC nano-truss, the extension of the proposed procedure for analyzing the reliability of other carbon nanotube super-architectures is straightforward. Finally, it should be noted that the research on the structural reliability of nanoscopic structures is still in the primary stages and further work is required in this field.