1 Introduction

Systems modeled with fractional-order calculus have led to the new developments and results which are applied in several fields such as mechanics, biology, economics, biophysics, aerodynamics, signal and image processing. The applications of fractional calculus in viscoelasticity and electrical circuits with fractance have found in literature, see for instance (Debnath 2003; Miller and Ross 1993; Lakshmikantham 2008; Tabouche 2021) and references therein. Particularly, results on some physical problems using fractional-order dynamics found in nonlinear regularized long-wave model (Yavuz and Abdeljawad 2020), Schrodinger–KdV equation (Yavuz et al. 2021), circulant Halvorsen system (Hammouch et al. 2021), and option pricing models (Yavuz 2022). Recently, Naik et al. (2020) studied the COVID-19 model using fractional-order operator and discussed the average absolute relative error between actual cases and the model’s solution for infectious class, also discussed the impact of alternative drugs applied for treating the infected individuals. Fractional-order dynamics based susceptible-infected-recovered epidemic model for predicting the spread of an infectious disease were studied in Dasbasi (2021).

It is noted that when dealing with dynamical systems using varity of differential equations, the first and foremost one is existence of solution (Deep and Tunc 2020). Bohner et al. (2021) studied the fractional Volterra integro-differential equation with multiple kernels and delays. Yavuz et al. (2018) derived the approximate analytical solution for fractional partial differential equations with singular and nonsingular kernels using the Atangana–Baleanu and Liouville–Caputo fractional operators. On the other hand, impulses in differential equations reflects the dynamics of real world problems with unexpected discontinuities and rapid changes at certain instants such as blood flows, heart beats and so on, see Guo and Jiang (2012), Stamova and Tr (2016), & Area and Nieto (2021). Slynko and Tunc (2019) studied the Lyapunov stability of impulsive linear switched systems by constructing an equivalent impulsive system without switching.

In literature, the concepts of stability analysis of impulsive FOS are studied by various approaches; in this paper, we made an attempt to study MLS analysis for nonlinear impulsive FOS with time delays. Stability of solutions is essential one in the qualitative theory of dynamical systems as it addresses the system trajectories under small perturbations of initial conditions. The stability analysis of FOS is more difficult than the classical ones because the derivative of fractional-order is nonlocal and has infirm singular kernels (Agarwal et al. 2015, 2007; Arthi et al. 2019; Baleanu and Wu 2019; Yunquan and Chunfang 2016; Arthi et al. 2021). Recently, many authors focused on the various types of stability analysis for FOS, for example, the q-MLS and direct Lyapunov method for q-FOS was discussed in Li et al. (2018). Hyers-Ulam stability of nonlinear fractional system with delays has been analysed in Khan et al. (2020). Stability of fractional predator-prey system with harvesting rate was presented in Yavuz and Sene (2020). The Mittag–Leffler input stability of FOSs with exogenous disturbances using the Lyapunov characterization were studied in Sene (2020). The finite-time stability results for discrete-time FOSs using Gronwall inequality have been investigated in Wu et al. (2018a). The exponential stability of nonlinear FOS using Hurwitz state matrix and Lyapunov direct method was established in Sene (2019).

Among the different approaches MLS which is generally characterised by Mittag–Leffler functions holds the features of power-law convergence. So, compared to the other methods MLS is more useful in FOSs because the Mittag–Leffler functions are commonly used in fractional calculus. Li et al. (2010) proposed the MLS using fractional Lyapunov direct method. MLS and uniform asymptotic stability of nonlinear impulsive FOS were obtained in Stamova (2015). The MLS of nonlinear FOS with impulses was analysed in Yang et al. (2017). The MLS for impulsive FOSs with instantaneous and non-instantaneous impulses are studied in Agarwal et al. (2017). The MLS of nonlinear FOS by extended the Lyapunov direct method has been studied in Li et al. (2009). The MLS for linear impulsive fractional delayed difference equations was discussed in Wu et al. (2018b). The MLS for coupled system of FOS with impulses were investigated in Li (2015). The MLS and generalized MLS for fractional genetic regulatory networks using the fractional Lyapunov method has been established in Ren et al. (2015).The MLS for nonlinear fractional neutral singular systems were obtained by Li et al. (2012). The finite time stability of delayed FOSs by Mittag–Leffler functions was analyzed in Li and Wang (2018). MLS estimator for nonlinear FOS using linear quadratic regulator approach has been studied in Martnez-Fuentes and Martnez-Guerra (2018).

To the best of our knowledge, MLS of FOS with time delays has not yet been fully analyzed, which motivates our present study. There are few results available in the literature for MLS of FOS with impulsive effects that could not be suitable for impulsive FOSs with time delays. With this motivation, the existence and uniqueness of solutions, MLS analysis of the impulsive nonlinear FOS with time delays are established using the well-known fixed point theorems and Mittag–Leffler approach. Further the main contributions of this paper are outlined as:

  • The existence and uniqueness of solutions for the FOS is discussed with help of fixed point theory.

  • Some novel conditions for MLS of FOS are established for the considered nonlinear system is with time delays and impulses.

  • Further the results are extended to finite-time MLS of considered systems.

Finally, few examples are provided to validate the advantages and effectiveness of the proposed results.

2 Problem Description

Consider the impulsive fractional-order nonlinear system with constant time delay given by

$$\begin{aligned} _{0}D^{\nu }_{t} x(t)= \;& {} f(t,x(t))+Ax(t)+Bx(t-\sigma ),\; t\in J/{t_{1},t_{2},\dots t_{m}},\nonumber \\ x(t)=\; & {} \phi (t),\; t \in [- \sigma ,0], \nonumber \\ \Delta x(t_k)=\; & {} x(t^{+}_{k})-x(t^{-}_{k})=I_{k}x(t^{-}_{k}), \;k=1,2,\dots m, \end{aligned}$$
(1)

where \(_{0}D^{\nu }_{t}\) denotes the operator Caputo fractional derivative of \(\nu\)-order (\(0<\nu <1\)), \(f(\cdot )\) is a nonlinear function assumed to be Lipshitz continuous, A and B are constant matrices, \(\sigma\) is the constant time delay, \(J=[0,T]\), \(T\in R\), \(0<t_{1}<t_{2}\dots<t_{m}<T\), \(I_k:R^n \rightarrow R^n\) are continuous for \(k=1,2,\dots m\), \(x(t_k^+)= \lim \limits _{\epsilon \rightarrow 0^+}x(t_k+\epsilon )\) and \(x(t_k^-)= \lim \limits _{\epsilon \rightarrow 0^-} x(t_k+\epsilon )\). \(PC^1([-\sigma , T], \;R^n)\) be the Banach space of all piecewise continuous functions from \([-\sigma , T]\) into \(R^n\).

Before presenting our main results, the following hypotheses are introduced.

\((H_1)\):

\(PC^1([-\sigma , T])(\rho )=\left\{ x\in PC^1([-\sigma , T], R^n):\;\left\| x\right\| _\infty \le \rho \right\}\) and \(PC^1(\rho )=\left\{ \phi \in PC^1: \left\| \phi \right\| _1\ \le \rho \right\}\), \(\forall \rho > 0\).

\((H_2)\):

There exists a constant \(l>0\), such that \(\left\| f(t,\psi )\right\| \le l\left\| \psi (t)\right\|\), for almost every \(t\in J\) and all \(\psi \in PC^1(\rho )\).

\((H_3)\):

There exists a constant \(\mu >0\), such that \(\left\| f(t,\psi _1)-f(t,\psi _2)\right\| \le \mu \left\| \psi _1-\psi _2\right\| _1\), for almost every \(t\in J\) and all \(\psi _1,\psi _2 \in PC^1(\rho )\).

\((H_4)\):

Let \(I_k \in C(R^n,R^n)\) maps bounded set into bounded set, for a constant \(M>0\), such that \(\Vert I_k(x(t^{-}_{k}))-I_k(y(t^-_k))\Vert \le M\left\| x-y\right\| _\infty\) for each \(x,y \in PC^1([-\sigma , T])(\rho )\) for \(k=1,2,\ldots m\).

Let us recall some basic definitions and lemmas which are useful in deriving the main results.

Definition 1

(Li et al. 2010) The solution x(t) of system (1) is said to be Mittag–Leffler stable, if

$$\begin{aligned} \Vert x(t)\Vert \le {{m[x(t_{0})] E_{\nu }(-\lambda (t-t_{0})^{\nu })}}^{b}, \end{aligned}$$

where \(t_{0}\) is the initial time, \(\nu \in (0,1)\), \(b>0\), \(m(0)=0\), \(m(x)\ge 0\) and m(x) is locally lipshitz on \(x(t)\in PC^1([-\sigma , T], R^n)\) with lipshitz constant \(m_{0}\).

Definition 2

(Hei and Wu 2016) The system (1) is finite time stable with respect to \(\left\{ \delta ,\epsilon ,J\right\}\), for \(\delta < \epsilon\), if and only if \(\Vert \phi \Vert< \delta \; \; \Rightarrow \;\; \Vert x(t) \Vert < \epsilon ,\; \forall t \in J\), where \(x(t)\in PC^1([-\sigma , T], R^n)\), \(\Vert \phi \Vert = \sup \limits _{-\sigma \le t \le 0} \Vert \phi \Vert\).

3 Main Results

3.1 Existence and Uniqueness Results

Before discussing the stability results, we discuss the existence, uniqueness for system (1).

Lemma 1

(Lazarevic and Spasic 2009) Let \(0<\nu <1\) and let \(f:J \rightarrow R\) be continuous, the initial value problem

$$\begin{aligned} _{0}D^{\nu }_{t}x(t)= \;& {} f(t,x(t))+Ax(t)+ Bx(\theta -\sigma ),\;\; t\in [0,T], \nonumber \\ x(0)= & {} \phi (0), \end{aligned}$$
(2)

has the following Volterra fractional integral

$$\begin{aligned}&x(t)= \phi (0)+\frac{1}{\Gamma (\nu )}\int ^{t}_{0}(t-\theta )^{\nu -1}\left[ f(\theta , x(\theta ))+Ax(\theta )\right. \nonumber \\&\qquad \left. + Bx(\theta -\sigma )\right] d\theta , t\in [0,T]. \end{aligned}$$
(3)

Then, every solution of (3) is also a solution of (2) and conversely.

Lemma 2

(Feckan et al. 2012) Let \(\nu \in (0,1)\) and \(f:J \rightarrow R\) be continuous. A function \(x\in C(J,R)\) is given by

$$\begin{aligned} x(t)= \;& {} x_0-\frac{1}{\Gamma (\nu )}\int ^{t_0}_{0}(t_{0}-\theta )^{\nu -1}(f(t,x(t))+Ax(t)\\&+ Bx(\theta -\sigma ))d\theta \\&+\frac{1}{\Gamma (\nu )}\int ^{t}_{0}(t-\theta )^{\nu -1}(f(t,x(t))+Ax(t)\\&+ Bx(\theta -\sigma ))d\theta , \end{aligned}$$

is only solution of fractional Cauchy problem

$$\begin{aligned} ^cD^{\nu }_{t}x(t)= f(t,x(t))+Ax(t) + Bx(\theta -\sigma ),\quad t\in J, \quad x(t_0)=x_0, \quad t_0 > 0. \end{aligned}$$

Theorem 3

Let \(0<\nu <1\) and \(f:J\times PC^1 \rightarrow R^n\) be Lebesgue measurable function with respect to t on J. A function \(x(t)\in PC^1\left( [-\sigma ,T],R^n\right)\) is a solution of the system (1), if and only if, \(x(t) \in PC^1\left( [-\sigma ,T],R^n\right)\) is a solution of the fractional-order integral equations given by

$$\begin{aligned} x(t)={\left\{ \begin{array}{ll} \phi (t),&{} t \in [-\sigma ,0], \\ \phi (0)+\frac{1}{ \Gamma (\nu )} \int ^t_0 (t-\theta )^{\nu -1} [f(\theta , x(\theta ))+ Ax(\theta )+ Bx(\theta -\sigma )]d\theta ,&{} t\in [0,t_{1}),\\ \phi (0)+I_1(x(t^-_1)+\frac{1}{ \Gamma (\nu )} \int ^t_0 (t-\theta )^{\nu -1} [f(\theta , x(\theta ))+ Ax(\theta )+ Bx(\theta -\sigma )]d\theta ,&{} t\in [t_1,t_2),\\ \vdots &{}\vdots \\ \phi (0)+\sum \limits ^{m}_{k=1}I_{k}x(t^{-}_{k})+\frac{1}{ \Gamma (\nu )} \int ^t_0 (t-\theta )^{\nu -1} [f(\theta , x(\theta ))+ Ax(\theta )+ Bx(\theta -\sigma )]d\theta ,&{} t\in [t_m,T]. \end{array}\right. } \end{aligned}$$
(4)

Proof

Assume x(t) satisfies the system (1). If \(t \in [0,t_1)\) then

$$\begin{aligned} _{0}D^{\nu }_{t}x(t)= & {} f(t,x(t))+Ax(t)\nonumber \\&+Bx(t-\sigma ),\;\; t\in [0,t_1), \end{aligned}$$
(5)

with \(x(0)=\phi (0)\). Integrating (5) from 0 to \(t_1\) then

$$\begin{aligned} x(t)=\phi (0)+\frac{1}{\Gamma (\nu )}\int ^{t_1}_{0}(t-\theta )^{\nu -1}\left[ f(\theta ,x(\theta ))+Ax(\theta )+Bx(\theta -\sigma ) \right] d\theta . \end{aligned}$$

Suppose \(t \in [t_1,t_2)\), then

$$\begin{aligned} _{0}D^{\nu }_{t}x(t)=f(t,x(t))+Ax(t)+Bx(t-\sigma ),\; \;\; t\in [t_1,t_2), \end{aligned}$$

with \(x(t_1^+)=x(t^1_-)+I_1(x(t_1^-))\). Then, by Lemma 2, we get

$$\begin{aligned} x(t)= & {} x(t_1^+)-\frac{1}{\Gamma (\nu )}\int ^{t_1}_{0}(t_1-\theta )^{\nu -1}\left[ f(\theta , x(\theta ))\right. \\&\qquad \left. +Ax(\theta )+Bx(\theta -\sigma )\right] d\theta \\&\qquad +\frac{1}{\Gamma (\nu )}\int ^{t}_{0}(t-\theta )^{\nu -1}\left[ f(\theta , x(\theta ))+Ax(\theta )+Bx(\theta -\sigma )\right] d\theta \\= & {} x(t_1^-)+I_{1}x(t_1^-)-\frac{1}{\Gamma (\nu )}\int ^{t_1}_{0}(t_1-\theta )^{\nu -1}\left[ f(\theta ,x(\theta ))\right. \\&\qquad \left. +Ax(\theta )+Bx(\theta -\sigma )\right] d\theta \\&\qquad +\frac{1}{\Gamma (\nu )}\int ^{t}_{0}(t-\theta )^{\nu -1}\left[ f(\theta ,x(\theta ))+Ax(\theta )+Bx(\theta -\sigma )\right] d\theta \\= & {} \phi (0)+I_{1}x(t_1^-)+\frac{1}{\Gamma (\nu )}\int ^{t}_{0}(t-\theta )^{\nu -1}\left[ f(\theta ,x(\theta ))\right. \\&\qquad \left. +Ax(\theta )+Bx(\theta -\sigma )\right] d\theta . \end{aligned}$$

Suppose \(t\in [t_2,t_3)\), by Lemma 2, we have

$$\begin{aligned} x(t)= \;& {} x(t_2^+)-\frac{1}{\Gamma (\nu )}\int ^{t_2}_{0}(t_2-\theta )^{\nu -1}\left[ f(\theta , x(\theta ))\right. \\&\left. +Ax(\theta )+Bx(\theta -\sigma )\right] d\theta \\&+\frac{1}{\Gamma (\nu )}\int ^{t}_{0}(t-\theta )^{\nu -1}\left[ f(\theta ,x(\theta ))+Ax(\theta )+Bx(\theta -\sigma )\right] d\theta \\= \;& {} x(t_2^-)+I_{2}x(t_2^-)-\frac{1}{\Gamma (\nu )}\int ^{t_2}_{0}(t_2-\theta )^{\nu -1}\left[ f(\theta ,x(\theta ))\right. \\&\left. +Ax(\theta )+Bx(\theta -\sigma )\right] d\theta \\&+\frac{1}{\Gamma (\nu )}\int ^{t}_{0}(t-\theta )^{\nu -1}\left[ f(\theta ,x(\theta ))+Ax(\theta )+Bx(\theta -\sigma )\right] d\theta \\= \;& {} \phi (0)+I_{1}x(t_1^-)+I_{2}x(t_2^-)\\&+\frac{1}{\Gamma (\nu )}\int ^{t}_{0}(t-\theta )^{\nu -1}\left[ f(\theta , x(\theta ))+Ax(\theta )+Bx(\theta -\sigma )\right] d\theta . \end{aligned}$$

By similar arguments, for \(t\in [t_m,T]\), one can have

$$\begin{aligned} x(t)=\; & {} \phi (0)+\sum \limits ^m_{k=1}I_kx(t^-_k)+\frac{1}{\Gamma (\nu )}\int ^{t}_{0}(t-\theta )^{\nu -1}\left[ f(\theta ,x(\theta ))\right. \\&\left. +Ax(\theta )+Bx(\theta -\sigma )\right] d\theta . \end{aligned}$$

Conversely, let x(t) satisfies (4). If \(t\in [0,t_1)\) then using the fact that \(_0D^\nu _t\) is the left inverse of \(I^\nu _t\), we have (5). If \(t \in [t_k,t_{k+1})\),\(k=1,2,\ldots m\) then using the ideas of the Caputo derivative, we obtain

$$\begin{aligned} _{0}D^{\nu }_{t}=f(t,x(t))+Ax(t)+Bx(t-\sigma ),\; t\in [t_k,t_{k+1}), \end{aligned}$$

and \(\Delta x(t^-_k)=I_k(x(t^-_k))\).

Next, to discuss the uniqueness of system (1), define a mapping for \(x\in PC^1\left( [-\sigma ,T],R^n\right)\) as

$$\begin{aligned} Fx(t)={\left\{ \begin{array}{ll} \phi (t),&{} t \in [-\sigma ,0], \\ \phi (0)+\frac{1}{ \Gamma (\nu )} \int ^t_0 (t-\theta )^{\nu -1} [f(\theta , x(\theta ))+ Ax(\theta ) Bx(\theta -\sigma )]d\theta ,&{} t\in [0,t_{1}),\\ \phi (0)+I_1(x(t^-_1)+\frac{1}{ \Gamma (\nu )} \int ^t_0 (t-\theta )^{\nu -1} [f(\theta , x(\theta ))+ Ax(\theta )+Bx(\theta -\sigma ) ]d\theta ,&{} t\in [t_1,t_2),\\ \vdots &{}\vdots \\ \phi (0)+\sum \limits ^{m}_{k=1}I_{k}x(t^{-}_{k})+\frac{1}{ \Gamma (\nu )} \int ^t_0 (t-\theta )^{\nu -1} [f(\theta , x(\theta ))+ Ax(\theta ) + Bx(\theta -\sigma ) ]d\theta ,&{} t\in [t_m,T]. \end{array}\right. } \end{aligned}$$

Theorem 4

Assume (\(H_1\)), (\(H_2\)), (\(H_3\)) and (\(H_4\)) hold, then the system (1) has at least one solution on J provided that

$$\begin{aligned} \frac{\left\| \phi (0)\right\| +\frac{1}{\Gamma (\nu +1)}\left[ \left\| B\right\| \left\| \phi \right\| \sigma ^\nu +(l+\left\| A\right\| +\left\| B\right\| )T^\nu \rho \right] +mM}{\rho } \le 1, \end{aligned}$$
(6)

where \(M=\max \left\{ \left\| I_k(x(t_k^-))\right\| : \left\| x\right\| _{\infty } \le \rho \right\} , \;k=1,2,\ldots m.\)

Proof

From Assumption (\(H_1\)) it is clear that \(PC^1([-\sigma , T])(\rho )\) is a closed, bounded and convex subset of \(PC^1([-\sigma , T], R^n)\). Now, we use Schauder fixed point theorem to prove that F in (6) has a fixed point.

Step 1. F maps \(PC^1([-\sigma , T])(\rho )\) into \(PC^1([-\sigma , T])(\rho )\).

According to Holder inequality and the condition (\(H_2\)), for \(t\in [0,t_1)\)

$$\begin{aligned} \left\| (Fx)(t)\right\|\le & {} \left\| \phi (0)\right\| +\frac{1}{\Gamma (\nu )}\int ^{t}_{0}\left( t-\theta \right) ^{\nu -1}\left\| f(\theta , x(\theta ))\right\| d\theta \nonumber \\&+\frac{1}{\Gamma (\nu )}\int ^{t}_{0}\left( t-\theta \right) ^{\nu -1}\left\| Ax(\theta )\right\| d\theta \nonumber \\&+\frac{1}{\Gamma (\nu )}\int ^{t}_{0}\left( t-\theta \right) ^{\nu -1}\left\| Bx(\theta -\sigma )\right\| d\theta \nonumber \\\le & {} \left\| \phi (0)\right\| +\frac{1}{\Gamma (\nu )}\int ^t_{0}\left( t-\theta \right) ^{\nu -1}\left\| f(\theta , x(\theta ))\right\| d\theta \nonumber \\&+\frac{1}{\Gamma (\nu )}\int ^t_{0}(t-\theta )^{\nu -1}\left\| Ax(\theta )\right\| d\theta \nonumber \\&+\left\| B\right\| \frac{1}{\Gamma (\nu )}\int ^{t-\sigma }_{-\sigma }(t-\sigma -s)^{\nu -1}\left\| x(\theta )\right\| d\theta \nonumber \\\le & {} \left\| \phi (0)\right\| +\frac{1}{\Gamma (\nu )}\int ^t_{0} \left( t-\theta \right) ^{\nu -1}\left\| f(\theta , x(\theta ))\right\| d\theta \nonumber \\&+\frac{1}{\Gamma (\nu )}\int ^{t}_{0}(t-\theta )^{\nu -1}\left\| Ax(\theta )\right\| d\theta \nonumber \\&+\left\| B\right\| \frac{\left\| \phi \right\| }{\Gamma (\nu +1)}\left[ \left( t-\sigma \right) ^\nu -t^\nu \right] \nonumber \\&+\left\| B\right\| \frac{1}{\Gamma (\nu )}\int ^{t}_{0}(t-\theta )^{\nu -1}\left\| x(\theta )\right\| d\theta \nonumber \\\le & {} \left\| \phi (0)\right\| +\frac{1}{\Gamma (\nu +1)}\left[ \left\| B\right\| \left\| \phi \right\| \sigma ^\nu \right. \nonumber \\&\left. +(l+\left\| A\right\| +\left\| B\right\| )t_1^\nu \rho \right] \nonumber \\\le & {} \rho . \end{aligned}$$
(7)

Similarly, for \(t \in [t_k, t_{k+1}),\; k=1,2,\ldots m\)

$$\begin{aligned} \left\| (Fx)(t)\right\|\le & {} \left\| \phi (0)\right\| +mM \nonumber \\&+\frac{1}{\Gamma (\nu +1)}\left[ \left\| B\right\| \left\| \phi \right\| \sigma ^\nu +(l+\left\| A\right\| +\left\| B\right\| )T^\nu \rho \right] \nonumber \\\le & {} \rho . \end{aligned}$$
(8)

Combining (7), (8) and noting that \(\left\| (Fx)(t)\right\| =\left\| \phi (t)\right\| \le \left\| \phi \right\| _1 \le \rho ,\) for \(t \in [-\sigma , 0],\) it yields \(\left\| (Fx)(t)\right\| _\infty \le \rho .\) Hence \(F:PC^1([-\sigma , T])(\rho ) \rightarrow PC^1([-\sigma , T])(\rho ).\)

Step 2. F is continuous.

Let \({x_l}\) be a sequence such that \(x_l \rightarrow x\) on \(PC^1([-\sigma , T])(\rho )\), by the continuity of \(f(t,\psi )\) with respect to \(\psi\), \(I_k(\gamma )\) with respect to \(\gamma\) and \(x(\zeta )\) with respect to \(\zeta\), respectively, it is easy to see that \(f(t,x_l(t)) \rightarrow f(t, x(t))\), \(t \in J\), \(I_k(x_l) \rightarrow I_k(x)\), \(k=1,2,\ldots m\) on \(PC^1([-\sigma , T])(\rho )\) and \(x_l(t) \rightarrow x(t)\), \(t \in J\) as \(l \rightarrow \infty\).

For \(t \in [0, t_1)\)

$$\begin{aligned} \left\| (Fx_l)(t)-(Fx)(t)\right\|= \;& {} \frac{1}{\Gamma (\nu )}\| \int ^{t}_{0}(t-\theta )^{\nu -1}[f(\theta ,x_l(\theta )) \\&\left. -f(\theta , x(\theta ))]d\theta \right\| \\&+\frac{1}{\Gamma (\nu )}\| \int ^{t}_{0}(t-\theta )^{\nu -1}[Ax_l(\theta ) \\&\left. -Ax(\theta )]d\theta \right\| \\&+\frac{1}{\Gamma (\nu )}\| \int ^{t}_{0}(t-\theta )^{\nu -1}[Bx_l(\theta -\sigma ) \\&\left. -Bx(\theta -\sigma )]d\theta \right\| . \end{aligned}$$

Using Step 1, we get

$$\begin{aligned}\le & {} \frac{\left\| B\right\| \left\| \phi \right\| \sigma ^\nu }{\Gamma (\nu +1)}+\frac{t_1^\nu }{\Gamma (\nu +1)}\sup _{s\in J}\left\| f(\theta ,x_l(\theta ))-f(\theta ,x(\theta ))\right\| \nonumber \\&+\frac{t_1^\nu }{\Gamma (\nu +1)}\sup _{s\in J}\left\| Ax_l(\theta )-Ax(\theta )\right\| \nonumber \\&+\frac{t_1^\nu }{\Gamma (\nu +1)}\sup _{s\in J}\left\| Bx_l(\theta )-Bx(\theta )\right\| . \end{aligned}$$
(9)

By similar arguments, for \(t \in [t_k,t_{k+1}),\; k=1,2,\ldots m\)

$$\begin{aligned} \left\| (Fx_l)(t)-(Fx)(t)\right\|= & {} \left\| \sum _{i=1}^{k}\left\| I_{i}(x_l(t^-_i))-I_{k}(x(t^-_i))\right\| \right\| \nonumber \\&+\frac{1}{\Gamma (\nu )}\left\| \int ^{t}_{0}(t-\theta )^{\nu -1}[f(\theta ,x_l(\theta ))-f(\theta , x(\theta ))]d\theta \right\| \nonumber \\&+\frac{1}{\Gamma (\nu )}\left\| \int ^{t}_{0}(t-\theta )^{\nu -1}[Ax_l(\theta )-Ax(\theta )]d\theta \right\| \nonumber \\&+\frac{1}{\Gamma (\nu )}\left\| \int ^{t}_{0}(t-\theta )^{\nu -1}[Bx_l(\theta -\sigma )-Bx(\theta -\sigma )]d\theta \right\| \nonumber \\\le & {} \sum _{i=1}^{k}\left\| I_{i}(x_l(t^-_i))-I_{i}(x(t^-_i))\right\| +\frac{\left\| B\right\| \left\| \phi \right\| \sigma ^\nu }{\Gamma (\nu +1)}\nonumber \\&+\frac{T^\nu }{\Gamma (\nu +1)}\sup _{s\in J}\left\| f(\theta ,x_l(\theta ))-f(\theta ,x(\theta ))\right\| \nonumber \\&+\frac{T^\nu }{\Gamma (\nu +1)}\sup _{s\in J}\left\| Ax_l(\theta )-Ax(\theta )\right\| \nonumber \\&+\frac{T^\nu }{\Gamma (\nu +1)}\sup _{s\in J}\left\| Bx_l(\theta )-Bx(\theta )\right\| . \end{aligned}$$
(10)

Since \(l \rightarrow \infty\), \(f(t,x_l(t))\) convergent to f(t, x(t)), \(I_k(x_l)\) is convergent to \(I_k(x)\), \(k=1,2,\ldots m\) and \(x_l(t)\) is convergent to x(t) for \(t \in J\). Combining (9) and (10), noting that \(\left\| (Fx_l)(t)-(Fx)(t)\right\| =\left\| \phi (t)-\phi (t)\right\| =0\) for \(t \in [-\sigma , 0]\), it yields \(\left\| (Fx_l)(t)-(Fx)(t)\right\| _\infty \rightarrow 0\) as \(l \rightarrow \infty\). Therefore F is continuous.

Step 3. F maps bounded sets into equicontinuous sets of \(PC^1([-\sigma , T],R^n)\).

Since \(PC^1([-\sigma , T])(\rho )\) be a bounded set and \(x \in PC^1([-\sigma , T])(\rho )\), obviously Fx is equicontinuous on \([-\sigma ,0]\). For any arbitrary \(\theta _1\), \(\theta _2 \in [0,t_1)\), \(\theta _1 < \theta _2\), based on the Holder inequality and Step 1, we have

$$\begin{aligned} \left\| (Fx)(\theta _2)-(Fx)(\theta _1)\right\|\le & {} \frac{\left\| B\right\| \left\| \phi \right\| \sigma ^\nu }{\Gamma (\nu +1)}\\&+\frac{1}{\Gamma (\nu )}\int ^{\theta _1}_{0}\left\| [(\theta _2-\theta )^{\nu -1}-(\theta _1-\theta )^{\nu -1}]f(\theta , x(\theta ))\right. \\&\left. +Ax(\theta )+Bx(\theta )\right\| d\theta \\&+\frac{1}{\Gamma (\nu )}\int ^{\theta _2}_{\theta _1}\left\| [(\theta _2-\theta )^{\nu -1}]f(\theta , x(\theta ))+Ax(\theta )+Bx(\theta )\right\| d\theta \\\le & {} \frac{\left\| B\right\| \left\| \phi \right\| \sigma ^\nu }{\Gamma (\nu +1)}+\frac{l\rho +\left\| A\right\| \rho +\left\| B\right\| \rho }{\Gamma (\nu +1)}[\theta _1^\nu +(\theta _2-\theta _1)^\nu -\theta _2^\nu ]\\&+\frac{l\rho +\left\| A\right\| \rho +\left\| B\right\| \rho }{\Gamma (\nu +1)}[(\theta _2-\theta _1)^\nu ] \\\le & {} \frac{\left\| B\right\| \left\| \phi \right\| \sigma ^\nu +2[l\rho +\left\| A\right\| \rho +\left\| B\right\| \rho ]}{\Gamma (\nu +1)}(\theta _2-\theta _1)^\nu , \end{aligned}$$

as \(\theta _2 \rightarrow \theta _1\), the RHS of above inequality tends to zero. Then Fx is equicontinuous on \([0,t_1)\).

By similar arguments, for the time interval \([t_k,t_{k+1})\), we obtain

$$\begin{aligned}&\left\| (Fx)(\theta _2)-(Fx)(\theta _1)\right\| \\&\le \frac{\left\| B\right\| \left\| \phi \right\| \sigma ^\nu +2[l\rho +\left\| A\right\| \rho +\left\| B\right\| \rho ]}{\Gamma (\nu +1)}(\theta _2-\theta _1)^\nu \rightarrow 0, \end{aligned}$$

as \(\theta _2 \rightarrow \theta _1\). This shows that Fx is equicontinuous on \([t_k,t_{k+1})\) for \(k=1,2,\ldots m.\)

In other words, since \(F(PC^1([-\sigma , T]))(\rho ) \subset PC^1([-\sigma , T])(\rho )\) is uniformly bounded according to Step 1, then \(A(PC^1([-\sigma , T]))(\rho )\) is a relatively compact subset of \(PC^1([-\sigma , T], R^n)\). Thus

\(F:PC^1([-\sigma , T])(\rho ) \rightarrow PC^1([-\sigma , T])(\rho )\) is completely continuous.

Therefore, in the view of Steps 1-3 and by Schauder fixed point theorem, one can conclude that F has a fixed point in \(PC^1([-\sigma , T])(\rho )\) and which is a solution of system (1) on J. \(\square\)

Theorem 5

Assume (\(H_1\)), (\(H_2\)), (\(H_3\)) and (\(H_4\)) hold, then the system (1) has a unique solution on J, provided the following inequality holds

$$\begin{aligned} c=\frac{1}{\Gamma (\nu +1)}\left[ \left\| B\right\| \left\| \phi \right\| \sigma ^\nu +(\mu +\left\| A\right\| +\left\| B\right\| )T^\nu \right] +mM < 1. \end{aligned}$$
(11)

Proof

Let F be a function defined by (6). Then \(F:PC^1([-\sigma ,T])(\rho ) \rightarrow PC^1([-\sigma ,T])(\rho )\).

Now, we apply the Banach contraction principle to prove F has a unique fixed point.

According to the condition (\(H_3\)) and inequality (11), for arbitrary \(x_1, x_2 \in PC^1([-\sigma ,T])(\rho ),\) for \(t \in [-\sigma ,0]\)

$$\begin{aligned} \left\| (Fx_1)(t)-(Fx_2)(t)\right\| =\left\| \phi (t)-\phi (t)\right\| =0. \end{aligned}$$

Suppose \(t \in [0,t_1)\)

$$\begin{aligned}&\left\| (Fx_1)(t)-(Fx_2)(t)\right\| = \frac{1}{\Gamma (\nu )}\left\| \int ^t_0(t-\theta )^{\nu -1}[f(\theta ,x_1(\theta ))\right. \\&\quad \left. -f(\theta ,x_2(\theta ))]d\theta \right\| \\&\quad +\frac{1}{\Gamma (\nu )}\left\| \int ^t_0(t-\theta )^{\nu -1}[Ax_1(\theta )-Ax_2(\theta )]d\theta \right\| \\&\quad +\frac{1}{\Gamma (\nu )}\left\| \int ^t_0(t-\theta )^{\nu -1}[Bx_1(\theta -\sigma )-Bx_2(\theta -\sigma )]d\theta \right\| \\&\le \frac{1}{\Gamma (\nu )}\mu \int ^t_0(t-\theta )^{\nu -1}d\theta \sup _{s\in [0,t]}\left\| x_1-x_2\right\| _1 \\&\quad +\frac{1}{\Gamma (\nu )}\left\| A\right\| \int ^t_0(t-\theta )^{\nu -1}d\theta \sup _{s\in [0,t]}\left\| x_1-x_2\right\| _1 \\&\quad +\frac{\left\| B\right\| \left\| \phi \right\| \sigma ^\nu }{\Gamma (\nu +1)}+\frac{1}{\Gamma (\nu )}\left\| B\right\| \int ^t_0(t-\theta )^{\nu -1}d\theta \sup _{s\in [0,t]}\left\| x_1-x_2\right\| _1 \\&\le \frac{t_1^\nu \mu }{\Gamma (\nu +1)}\left\| x_1-x_2\right\| _\infty +\frac{t_1^\nu \left\| A\right\| }{\Gamma (\nu +1)}\left\| x_1-x_2\right\| _\infty \\&\quad +\frac{\left\| B\right\| \left\| \phi \right\| \sigma ^\nu }{\Gamma (\nu +1)}+\frac{t_1^\nu \left\| B\right\| }{\Gamma (\nu +1)}\left\| x_1-x_2\right\| _\infty \\&\le c\left\| x_1-x_2\right\| _\infty . \end{aligned}$$

By similar arguments for \(t \in [t_k,t_{k+1})\), \(k=1,2,\ldots m,\) we have

$$\begin{aligned}&\left\| (Fx_1)(t)-(Fx_2)(t)\right\| \le \frac{T^\nu \mu }{\Gamma (\nu +1)}\left\| x_1-x_2\right\| _\infty \\&\quad +\frac{T^\nu \left\| A\right\| }{\Gamma (\nu +1)}\left\| x_1-x_2\right\| _\infty \\&\quad +\frac{\left\| B\right\| \left\| \phi \right\| \sigma ^\nu }{\Gamma (\nu +1)}\\&\quad +\frac{T^\nu \left\| B\right\| }{\Gamma (\nu +1)}\left\| x_1-x_2\right\| _\infty +mM\left\| x_1-x_2\right\| _\infty \\\le & {} c\left\| x_1-x_2\right\| _\infty . \end{aligned}$$

Since \(c<1\), it follows that F is strict contraction. Hence by Banach fixed point theorem it can be concluded that there exists a unique fixed point and which is the unique solution of system (1). \(\square\)

3.2 Mittag–Leffler Stability

In this section, we prove the MLS of system (1) by using Laplace transform.

Theorem 6

Let \(x(t) \in PC^{1} ([-\sigma , T], R^{n})\) in (4) is a solution of the system (1) and satisfies

$$\begin{aligned} \left\| x(t)\right\| \le \left( 1-nM\right) ^{-1}\left\| \phi \right\| \left[ 1+\frac{\left\| B\right\| \sigma ^\nu }{\Gamma (\nu +1)}\right] E_\nu \left( \eta t^\nu \right) ,\;\; t\in \left[ t_m,T\right] , \end{aligned}$$

where \(\eta\) =\(\frac{ l+\left\| A\right\| +\left\| B\right\| }{1-nM}\), then the system (1) is Mittag–Leffler stable.

Proof

In general, let \(t\in \left. \left[ t_k,t_{k+1}\right. \right)\) then

$$\begin{aligned} x(t)= & {} \phi (0)+\sum _{k=1}^{m}I_k(x(t^-_k))+\frac{1}{ \Gamma (\nu )} \int ^t_0 (t-\theta )^{\nu -1} [f(\theta , x(\theta ))\\&+ Ax(\theta )+Bx(\theta -\sigma )]d\theta , \end{aligned}$$

taking norm on both sides

$$\begin{aligned} \left\| x(t)\right\|\le & {} \left\| \phi (0)\right\| +\sum _{k=1}^{m}\left\| I_k(x(t^-_k)\right\| \\&+\frac{1}{\Gamma (\nu )}\int ^t_{0}\left( t-\theta \right) ^{\nu -1}\left\| f(\theta ,x(\theta ))\right\| \\&+\frac{1}{\Gamma (\nu )}\int ^t_{0}(t-\theta )^{\nu -1}\left\| Ax(\theta )\right\| d\theta \\&+\left\| B\right\| \frac{1}{\Gamma (\nu )}\int ^{t-\sigma }_{-\sigma }(t-\sigma -\theta )^{\nu -1}\left\| x(\theta )\right\| d\theta \\\le & {} \left\| \phi (0)\right\| +\sum _{k=1}^{m}\left\| I_k(x(t^-_k))\right\| \\&+\frac{1}{\Gamma (\nu )}\int ^t_{0}\left( t-\theta \right) ^{\nu -1}\left\| f(\theta ,x(\theta ))\right\| d\theta \\&+\frac{1}{\Gamma (\nu )}\int ^{t}_{0}(t-\theta )^{\nu -1}\left\| Ax(\theta )\right\| d\theta \\&+\left\| B\right\| \frac{1}{\Gamma (\nu )}\int ^{0}_{-\sigma }(t-\sigma -\theta )^{\nu -1}\left\| x(\theta )\right\| d\theta \\&+\left\| B\right\| \frac{1}{\Gamma (\nu )}\int ^{t-\sigma }_{0}(t-\sigma -\theta )^{\nu -1}\left\| x(\theta )\right\| d\theta \\\le & {} \left\| \phi (0)\right\| +\sum _{k=1}^{m}\left\| I_k(x(t^-_k))\right\| \\&+\frac{1}{\Gamma (\nu )}\int ^t_{0} \left( t-\theta \right) ^{\nu -1}\left\| f(\theta , x(\theta ))\right\| \\&+\frac{1}{\Gamma (\nu )}\int ^{t}_{0}(t-\theta )^{\nu -1}\left\| Ax(\theta )\right\| d\theta \\&+\left\| B\right\| \frac{\left\| \phi \right\| }{\Gamma (\nu +1)}\left[ \left( t-\sigma \right) ^\nu -t^\nu \right] +\left\| B\right\| \frac{1}{\Gamma (\nu )}\int ^{t}_{0}\left\| x(\theta )\right\| d\theta . \end{aligned}$$

By Assumptions (\(H_2\)) and (\(H_4\)), we have

$$\begin{aligned} \left\| x(t)\right\|\le & {} \left\| \phi \right\| +nM\left\| x(t)\right\| +l\;_{0}D^{-\nu }_{t}\left\| x(t)\right\| +\left\| A\right\| \;_{0}D^{-\nu }_{t}\left\| x(t)\right\| \nonumber \\&+\frac{\left\| B\right\| \left\| \phi \right\| \sigma ^\nu }{\Gamma (\nu +1)}\nonumber \\&+\left\| B\right\| \;_{0}D^{-\nu }_{t}\left\| x(t)\right\| . \end{aligned}$$
(12)

For any function \(Q(t)>0\), (12) becomes

$$\begin{aligned} \left\| x(t)\right\|= & {} \left\| \phi \right\| +nM\left\| x(t)\right\| +l\;_{0}D^{-\nu }_{t}\left\| x(t)\right\| \\&+\left\| A\right\| \;_{0}D^{-\nu }_{t}\left\| x(t)\right\| +\frac{\left\| B\right\| \left\| \phi \right\| \sigma ^\nu }{\Gamma (\nu +1)}\\&+\left\| B\right\| \;_{0}D^{-\nu }_{t}\left\| x(t)\right\| -Q(t). \end{aligned}$$

Taking Laplace transform on both sides

$$\begin{aligned} \left\| x(\theta )\right\|= & {} \frac{\left\| \phi \right\| }{s}+nM\left\| x(\theta )\right\| +l\ s^{-\nu }\left\| x(\theta )\right\| \\&+\left\| A\right\| s^{-\nu }\left\| x(\theta )\right\| +\frac{\left\| B\right\| \left\| \phi \right\| \sigma ^\nu }{s\Gamma (\nu +1)}+\\&\left\| B\right\| s^{-\nu }\left\| x(\theta )\right\| -Q(s).\\ (1-nM)\left\| x(\theta )\right\|= & {} \frac{s^{\nu -1}\left\| \phi \right\| \left[ 1+\frac{\left\| B\right\| \sigma ^\nu }{\Gamma (\nu +1)}\right] -s^\nu Q(s)}{s^\nu -\eta }, \end{aligned}$$

where \(\eta = \frac{ l+\left\| A\right\| +\left\| B\right\| }{1-nM}\). Next, taking Inverse Laplace transform on both sides, one can have

$$\begin{aligned} (1-nM)\left\| x(t)\right\|= & {} \left\| \phi \right\| \left[ 1+\frac{\left\| B\right\| \sigma ^\nu }{\Gamma (\nu +1)}\right] E_\nu \left( \eta t^\nu \right) \\&-Q(t)*t^{-1}E_{\nu }\left( \eta t^\nu \right) , \end{aligned}$$

where \('*'\) denotes the convolution operator and the term \(t^{-1}E_\nu \left( \eta t^\nu \right) \ge 0\).

Then, it then follows that

$$\begin{aligned} \left\| x(t)\right\| \le (1-nM)^{-1}\left\| \phi \right\| \left[ 1+\frac{\left\| B\right\| \sigma ^\nu }{\Gamma (\nu +1)}\right] E_\nu (\eta t^\nu ),\;t\in \left. \left[ t_n,t_{n+1}\right. \right) . \end{aligned}$$

Therefore, from Definition 1, the solution of the system (1) is Mittag–Leffler stable. \(\square\)

It is well-known that the concept of short time stability (or) finite-time stability has attracted much attention because it has a special property that for given bounded initial condition, the system state does not exceeds some bounds during the time interval. Considering this, now the above MLS is extended to finite-time MLS using the following corollary.

Corollary 1

The system (1) is finite time stale with respect to \(\left\{ \delta ,\epsilon ,J\right\}\), \(\delta < \epsilon ,\) if and only if, the conditions

(\(S_1\)) There exists a constant \(M>0\), such that \(\left\| I_k(x(t^-_k))\right\| \le M\epsilon\), for \(k=1,2,\ldots m\) and any \(x\in PC^1\left( [-\sigma ,T],R^n\right)\),

(\(S_2\))\(\ \left\{ nM\epsilon +\delta \left[ 1+\frac{\left\| \phi \right\| \sigma ^\nu }{\Gamma (\nu +1)}\right] E_\nu (\eta t^\nu )\right\} < \epsilon\), where \(\eta\) =\(\frac{ l+\left\| A\right\| +\left\| B\right\| }{1-nM}\)

hold.

Proof

Under the condition (\(S_1\)) and by Theorem 6, we have

$$\begin{aligned}&\left\| x(t)\right\| \le \left\| \phi \right\| +nM\epsilon +\frac{1}{\Gamma (\nu )}\int ^t_{0}(t-\theta )^{\nu -1}\left\| f(\theta , x(\theta ))\right. \\&\left. +Ax(\theta )+Bx(\theta -\sigma )\right\| d\theta . \end{aligned}$$

Now, it is easy to see that

$$\begin{aligned} \left\| x(t)\right\| \le \left\{ nM\epsilon +\delta \left[ 1+\frac{\left\| B\right\| \sigma ^\nu }{\Gamma (\nu +1)}\right] \right\} E_\nu (\eta t^\nu ). \end{aligned}$$

By Definition 2, the solution of the system (1) is finite-time Mittag–Leffler stable. \(\square\)

Remark 1

It is noted that the core ideas and proof process in deriving the results in Theorem’s 4 & 5 on the existence and uniqueness of solutions of the considered time-delay system is followed from the similar ideas used in Guo and Jiang (2012) for a system without time-delay. Also, the MLS results proposed in Theorem 6 are new and different from the finite-time stability results discussed for an evolution system in Hei and Wu (2016). So this paper discloses the new results for time-delay systems which are not discussed in the existing literature.

4 Numerical Examples

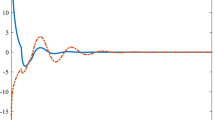
4.1 Example 1

Consider the following impulsive time delay fractional-order system

$$\begin{aligned}&\left. \begin{array}{ll} _0D^{0.5}_{t}x_1(t)= \tanh x_1(t)+0.2x_1(t)+0.02x_1(t-0.04)-0.01x_2(t-0.04), \\ _0D^{0.5}_{t}x_2(t)= \tanh x_2(t)+0.2x_2(t)-0.01x_1(t-0.04)+0.02x_2(t-0.04), \end{array}\right\} , \; t \in J/{t_1, t_2, \ldots t_m},\\&x_1(t)= 0.1, \;\; \ x_2(t)= 0.2, \;\; t\in [-0.04, \; 0],\\&\Delta x_1(t_k)= x_1(t_k)-x_2(t-k) = 0.05,\ \ \Delta x_2(t_k)= x_1(t_k)-x_2(t-k) = 0.05. \end{aligned}$$

It is easy to see \(f(t,x(t))=\begin{bmatrix} \tanh x_1(t) \\ \tanh x_2(t)\end{bmatrix}\) with \(l=\mu =1\), \(A=\begin{bmatrix} 0.2 &{} 0\\ 0&{} 0.2\end{bmatrix}\) with \(\Vert A\Vert =0.2\),

\(B=\begin{bmatrix} 0.02 &{} -0.01\\ -0.01&{} 0.02\end{bmatrix}\) with \(\Vert B\Vert =0.0224\), \(\sigma =0.04\).

It is easy to see that all Assumptions (\(H_1\)), (\(H_2\)), (\(H_3\)) and (\(H_4\)) are hold. Now, for the choice of \(n=10\), \(\delta = 0.5\), \(\epsilon = 1\), it is easy to see the proposed conditions in Theorems 4–6 are satisfied. Hence, it can conclude that the unique solution of above system exist and which is MLS.

4.2 Example 2

Consider the impulsive time delay fractional-order system

$$\begin{aligned} D^{0.5}_{0}x(t)= \;& {} 0.04x(t)-0.2x(t-0.05)+0.06 \;\; t \in J/{t_1,\; t_2, \;\ldots t_m}\\ x(t)= \;& {} 0.15 \;\; t\in [-0.05, \; 0]\\ \Delta x(t_k)= \;& {} x(t_k)-x(t-k) = 0.007. \end{aligned}$$

Let \(n=10\), \(\delta = 0.3\), \(\epsilon = 0.4\), then we can verify that \((S_1)\) in Corollary 1 is satisfied for the considered system. So we can calculate that the above system is finite-time MLS and by solving the inequality in (\(S_2\)), the estimated time is obtained as \(T\approx 0.3719\).

5 Conclusion

The qualitative analysis of nonlinear impulsive FOSs with time delays has been investigated, particularly on the existence, uniqueness and MLS of considered systems. The proposed results are new and have some novel ideas as the delay dependent conditions were established using the Laplace transforms and fractional-order calculus. Further, the results are extended to finite-time MLS of the considered FOSs. Finally, some examples are provided to validate the theoretical analysis. In practice the delay in the system design will be of time-varying in nature and also the nonlocal conditions in the initial data gives the better approximation in many physical problems, extending the results for these cases will be our future research directions.