Salience or event-splitting? An experimental investigation of correlation sensitivity in risk-taking

Abstract

Salience theory relies on the assumption that not only the marginal distribution of lotteries, but also the correlation of payoffs across states impacts choices. Recent experimental studies on salience theory seem to provide evidence in favor of such correlation effects. However, these studies fail to control for event-splitting effects (ESE). In this paper, we seek to disentangle the role of correlation and event-splitting in two settings: (1) the common consequence Allais paradox as studied by Bordalo et al. (Q J Econ 127:1243–1285, 2012), Frydman and Mormann (The role of salience in choice under risk: An experimental investigation. Working Paper, 2018), and Bruhin et al. (J Risk Uncertain 65:139–184, 2022); (2) choices between Mao pairs as studied by Dertwinkel-Kalt and Köster (J Eur Econ Assoc 18:2057–2107, 2020). In both settings, we find evidence suggesting that recent findings supporting correlation effects are largely driven by ESE. Once controlling for ESE, we find no consistent evidence for correlation effects. Our results thus shed doubt on the validity of salience theory in describing risky behavior.

1 Introduction

Due to its strong psychologic appeal and its ability to rationalize behavior in such diverse areas as finance, industrial organization, advertising, and politics, salience theory (Bordalo et al., 2012) has become increasingly popular in recent years.¹ Salience theory builds on the premise that outcome comparisons within states of nature are an important driver of decision making under risk. In particular, states with a higher outcome contrast attract the decision maker’s attention and receive greater decision weights. This assumption implies that decisions are not only driven by the marginal distributions of the lotteries, but also by the correlation of payoffs across states. A few recent experimental studies aim to test the key assumption of salience theory, and report correlation effects as predicted by salience theory (Bordalo et al., 2012; Bruhin et al., 2022; Dertwinkel-Kalt & Köster, 2020; Frydman & Mormann, 2018).

However, a potential issue arises due to the experimental design of these studies. In the experiments, participants had to choose between two lotteries. Participants were presented with these choices under different correlation structures. However, as the correlation of outcomes changed, so did the number of states that was displayed to subjects. Under salience theory such changes to the visual presentation of the choice task should not impact behavior. However, in the literature of testing regret theory (Bell, 1982; Loomes & Sugden, 1982), which is very similar to salience theory (Herweg & Müller, 2021; Lanzani, 2022), Starmer and Sugden (1993) provide evidence that such seemingly benign changes in the presentation of the choice problem can have a tremendous effect on decisions, even when the correlation of payoffs remains constant. Following Starmer and Sugden (1993), we refer to such effects as Event-splitting-Effects (ESE). Any correlation effects claimed in recent studies on salience theory could be attributed to ESE.

In this paper, we aim to disentangle correlation effects from ESE in settings considered in recent studies on salience theory. We take up key aspects of Bordalo et al. (2012), Frydman and Mormann (2018) and Bruhin et al. (2022) who study correlation effects in the context of the common consequence Allais paradox (Allais, 1953). We also consider the experimental set-up adopted by Dertwinkel-Kalt and Köster (2020) who use specific lottery pairs—Mao pairs (Mao, 1970).² In order to cleanly disentangle ESE and correlation effects, we implement a between-subject design inspired by Starmer and Sugden (1993). For subjects in the replication treatment, correlation effects and ESE are introduced at the same time. For subjects in the control group, ESE are well controlled for, which allows observing pure correlation effects.

Our findings suggest that the effects ascribed to changes in correlation described in recent studies (Bordalo et al., 2012; Bruhin et al., 2022; Dertwinkel-Kalt & Köster, 2020; Frydman & Mormann, 2018) might be attributable changes in the choice display, rather than changes in the correlation structure. Once we control for ESE, we find no evidence for systematic correlation effects. The ESE we document can be mostly explained by a tendency to overweight payoffs that are displayed in multiple states, even if the probability of the payoffs remains constant.

Our paper naturally relates to the literature on salience and regret theory. Within the framework of salience theory (Bordalo et al., 2012; Dertwinkel-Kalt & Köster, 2020), joint realizations characterized by substantial differences in payoffs tend to capture more attention due to their heightened salience, consequently leading to an uneven distribution of decision weight. Regret theory, on the other hand, operates on the premise that a decision maker’s utility is shaped by the comparative analysis of payoffs resulting from different choices. When a decision maker comes to realize that an alternative choice could have yielded a superior payoff, a sensation of regret is triggered (Bell, 1982; Loomes & Sugden, 1982). Despite the distinctly different ideas behind the two theories, Herweg and Müller (2021) show that in binary choice situations, regret theory, as proposed by Loomes and Sugden (1982), is a special case of salience theory (Bordalo et al., 2012), which in turn is a special case of generalized regret theory (Loomes & Sugden, 1987). Within the specific framework of our experiments, participants were tasked with making binary choices. This particular experimental setup aligns seamlessly with the decision paradigm outlined by Herweg and Müller (2021) and Lanzani (2022). Consequently, their assertion that both theories yield congruent predictions remains applicable.³

Despite the lively interest in regret and salience theory, the current experimental evidence remains inconclusive. Starmer and Sugden (1993) showed that the results of a series of earlier publications that seemed to provide evidence for correlation effects as predicted by regret theory were confounded by ESE, similar to the more recent studies on salience theory (Bordalo et al., 2012; Bruhin et al., 2022; Dertwinkel-Kalt & Köster, 2020; Frydman & Mormann, 2018). Once controlling for ESE, Starmer and Sugden (1993) report that correlation effects as predicted by regret theory are considerably weakened and not statistically significant. There are experimental studies that report evidence in line with regret or salience theory that do not rely on manipulations of the correlation of payoffs (e.g., Bleichrodt et al., 2010; Königsheim et al., 2019). However, these studies do not test the key behavioral assumption made in regret or salience theory in the way studies on correlation effects do. Consistent with Starmer and Sugden (1993)’s findings on regret theory, we find no evidence that correlation between acts matters as advocated by salience theory. An independent study conducted by Ostermair (2021) also suggests that ESE play a significant role in the prior empirical evidence supporting salience theory, although our results differ in certain aspects due to the distinct implementation of our experiments, as will be discussed later on. Taken together, these studies cast doubt on the descriptive ability of salience and regret theory. Notably, in a more recent investigation, Ostermair (2022) demonstrates that ESE persist under subjective uncertainty when testing the skew-symmetric property imposed by regret and salience theory within the context of the Allais paradox. Similarly, Leland et al. (2019) observe that transparent and non-transparent framings of choices can have substantial effects on risk behavior. As noted by the authors, the model of Bordalo et al. (2012) does not anticipate framing effects between minimal and transparent frames. Our study supplements their findings with additional evidence, emphasizing that controlling for decision framing is crucial when conducting experimental tests of theories.

The remainder of this paper is organized as follows. Section 2 briefly discusses salience theory. In Sect. 3, we detail our experimental design. In Sect. 4, we present our results. Section 5 concludes.

2 Salience theory

In this section we provide a brief summary of salience theory (Bordalo et al., 2012). Consider a situation in which a decision maker has to choose between two lotteries, A and B. There are S states of nature denoted by $s=1,...,S$, each with an associated probability given by $p_{s}$. Each of the lotteries $\theta \in \{ A, B \}$ assigns a payoff $x^{\theta }_{s}$ to each possible state of nature. The key feature of salience theory is a function $\sigma (x^{A}_{s},x^{B}_{s})$ that measures the salience of the different states. The salience function, for positive payoffs, satisfies the following conditions.⁴

Definition 1

A salience function is a continuous and bounded function $\sigma (x^{A}_{s},x^{B}_{s})$ that satisfies the following conditions.

• 1. Ordering: Consider two states $s, \tilde{s}$. Denote $x_{s}^{min}=min\{x_{s}^{A}, x_{s}^{B} \}$ and $x_{s}^{max}=max\{x_{s}^{A}, x_{s}^{B} \}$. If $[x_{s}^{min}, x_{s}^{max}] \subset [x_{\tilde{s}}^{min}, x_{\tilde{s}}^{max}]$, then $\sigma (x_{s}^{A}, x_{s}^{B})<\sigma (x_{\tilde{s}}^{A}, x_{\tilde{s}}^{B})$.

• 2. Diminishing sensitivity: For two payoffs $x_{s}^{A}$ and $x_{s}^{B}$, and any $\epsilon >0$, $\sigma (x_{s}^{A} + \epsilon , x_{s}^{B} +\epsilon )<\sigma (x_{s}^{A}, x_{s}^{B})$.

As Dertwinkel-Kalt and Köster (2020) argued, the ordering property can be intuitively understood as a contrast effect. The higher the contrast between two payoffs in the same state is, the more salient the state becomes. For instance, a state with payoffs of 100 and 0, which has an outcome contrast of 100, is more salient than a state with payoffs of 10 and 0, which has an outcome contrast of 10. The property of diminishing sensitivity can be understood as a level effect (Dertwinkel-Kalt & Köster, 2020). The same contrast in payoffs will be perceived as more salient for lower levels. For instance, the difference between 0 and 10 is more salient than the difference between 100 and 110.

The salience function establishes a salience ranking $k_s \in \{1,..., |S| \}$ which denotes the rank of state s, with lower ranks indicating greater salience. If two states receive the same salience, they obtain the same rank. There are no jumps in the ranking. State s then receives a decision weight $\pi _{s}$ according to its ranking, i.e.,

$$\begin{aligned} \pi _s=p_s\frac{\delta ^{k_s}}{\sum _{j=1}^{S}\delta ^{k_j} p_j} \end{aligned}$$

where $\delta \in (0,1]$ is the degree of local thinking that measures to which extent salient payoffs are overweighted by the decision maker. Thus, the most salient states are overweighted, whereas the least salient states are underweighted, relative to their probabilities of occurring. Finally, the decision maker evaluates lottery A and B based on these decision weights and chooses lottery A if and only if

$$\begin{aligned} \sum _{s \in S}\pi _{s}\left[ v\left( x_s^{A}\right) - v\left( x_s^{B}\right) \right] >0 \end{aligned}$$

Dertwinkel-Kalt and Köster (2020) introduced a continuous version of salience theory and demonstrated that salience theory induces a preference for skewness, not in an absolute, but in a relative sense. As a measure for a lottery’s absolute skewness, Dertwinkel-Kalt and Köster (2020) considered the third standardized central moment. The relative skewness is defined as the third centralized moment of the difference in the payoffs between lottery A and B in a given state, $\Delta _{A}=X^{A}-X^{B}$. Since $\Delta _{B}=-\Delta _{A}$, it follows that $S(\Delta _{B}) = -S(\Delta _{A})$. Lottery A is said to be positively skewed relative to lottery B if $S(\Delta _{A})>0$. Intuitively, whenever a decision maker chooses between two lotteries, the salience of the payoffs of a lottery depends on the context, that is on the payoffs that co-occur in the same state.⁵ A lottery with a positive relative skewness has an upside that stands out in comparison to the alternative lottery.

As preferences for absolute skewness are implied by many other theories such as prospect theory (Kahneman & Tversky, 1979), establishing that salience theory induces a preference for relative skewness greatly clarifies what distinguishes salience theory from other decision theories under uncertainty. In a controlled lab experiment, one can manipulate a lottery’s relative skewness by changing its correlation while leaving its marginal distribution constant. Therefore, testing for correlation effects allows to test the core assumptions of salience theory in a very clean way.

3 Experimental design

In this section, we detail our experimental design, the predictions made by salience theory in the considered settings, and, where applicable, how ESE might impact choices.

3.1 Setting I: common consequence Allais paradox

3.1.1 Salience theory and the common consequence Allais paradox

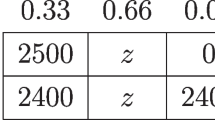
Experiments that demonstrate the common consequence Allais paradox commonly invoke two choices between a relatively riskier lottery A of the form $(a_h, p_h; z, p_z; a_l, p_l)$ and a safer lottery B of the form $(b, p_h; z, p_z; b, p_l)$, where $a_h>b>a_l$.⁶ In expected utility theory, the common consequence $z \in \{a_l, b \}$ is irrelevant to choices. However, a common observation is that participants in lab experiments express a preference for the safer option if $z=b$ but for the riskier option if $z=a_l$ (Allais, 1953).

Salience theory can explain this pattern if participants perceive the lotteries as independent (Bordalo et al., 2012). Moreover, salience theory implies that the Allais paradox can be turned off when payoffs are perfectly positively correlated. To see how salience theory can explain the Allais paradox if lottery A and B are independent, consider Table 1 for a visual representation of the choice under different correlation structures. Consider first the case in which $z=b$ (see Table 1i). Intuitively, the state $(a_l, b)$ is the most salient one. Consequently, the low payoff of lottery A and the high payoff of lottery B are overweighted. This makes lottery A relatively unattractive when $z=b$. Now, consider the case in which $z=a_l$. When lotteries are independent (see Table 1iii), the state in which lottery A yields the high payoff $a_h$ and lottery B yields the low payoff $a_l$ is the most salient one. Consequently, the high payoff of lottery A and the low payoff of lottery B are overweighted. As a result, the riskier lottery A becomes more attractive when $z=a_l$. To understand why salient theory predicts that the Allais paradox does not occur under positive correlation, consider Table 1i and 1ii. Note that, irrespective of the value of z, whether it is b or $a_l$, the state (z, z) is simply disregarded by the decision-maker. Therefore, altering z cannot impact lottery choices when payoffs are perfectly positively correlated.

Table 1 Experimental tasks on the Allais paradox

To see more clearly how alterations in the correlation structure impact the occurrence of the Allais paradox with a common consequence, consider the case where $z=b$. In this scenario, lottery B guarantees a payoff of b, implying a fixed correlation structure (see Table 1i). Consequently, any changes in the frequency of the Allais paradox, resulting from changes in the correlation structure, must arise from choices when $z=a_l$. Under maximally positive correlation, the most salient state is when lottery A yields the low payoff $a_l$, and lottery B yields the medium payoff b (see Table 1ii). Transitioning to the case of independent lotteries, the state $(a_h, a_l)$ becomes the most salient (see Table 1iii). Thus, the shift from maximally positive correlation to independence enhances the perceived attractiveness of lottery A compared to lottery B. This shift may lead to a preference change from the safer lottery B to the riskier lottery A.

3.1.2 ESE and the Allais paradox

In the experimental tests of correlation effects in the Allais paradox (Bordalo et al., 2012; Bruhin et al., 2022; Frydman & Mormann, 2018), choice tasks are often displayed in a state of the world representation that makes the correlation structure evident to subjects. Bruhin et al. (2022) additionally employ a different choice display that does not make the correlation structure evident when lotteries are independent. In the following, we show how ESE confound results in both types of choice displays.

In studies using the state of the world display, event-splitting tends to occur when choices between lotteries are displayed in the minimal state space. Consider again Table 1. Whenever payoffs are maximally positively correlated, the choice problem can be displayed in a matrix with 3 states (see Table 1i, ii). Note that this is always true for $z=b$. However, when $z=a_l$ and the lotteries are independent, the choice problem must be displayed in a matrix with at least four states (see Table 1iii). ESE occur if this difference in the number of displayed states and their probability of occurring, independent of the change in the correlation structure, impacts lottery choices.

To see how ESE might impact choices, note first that the minimal state space does not change for $z=b$. As a result, in the considered studies, no event-splitting occurs for $z=b$. Consider therefore the case in which $z=a_l$. Intuitively, changing the correlation structure from maximally positive to independent, the high payoff of lottery A ($a_h$) and the low payoff of lottery B ($a_l$) appear in one additional state. If decision makers attach more weight to payoffs that are displayed more often, irrespective of their probability, decision makers might attach more weight to the high payoff of lottery A and the low payoff of lottery B when lotteries are independent. This would render lottery A more attractive but lottery B less attractive. Thus, in the considered setting, ESE could induce similar effects as predicted by salience theory.

We now turn to the alternative choice display used by Bruhin et al. (2022). Whenever lotteries are maximally positively correlated, choices are displayed as illustrated in Table 1i and 1ii. However, when lotteries are independent, choices are in the “canonical" display as illustrated in Table 2. When $z=b$, three payoffs are displayed for lottery A, and lottery B is displayed as having one outcome (see Table 2i). When payoffs are maximally positively correlated, three payoffs are displayed for both lotteries (see Table 1ii). Thus, for lottery A, ESE do not occur. For lottery B, the same payoff b is displayed thrice instead of once. However, since lottery B is degenerate, ESE are unlikely to exert significant influence on choices.

Consider now the case when $z=a_l$. In the canonical display, when lotteries are independent, the high and the low payoff of lottery A and B occur once each (see Table 2ii). However, when payoffs are positively correlated, the low payoff of the risky lottery A ($a_l$) is displayed twice, and the high payoff of the safer lottery B (b) is also displayed twice (see Table 1ii). If decision makers attach more weight to payoffs that are displayed more often, ESE could once again cause behavior similar to that predicted by salience theory.

Table 2 “Canonical" display in Bruhin et al. (2022)

3.1.3 Experimental design and hypotheses

To disentangle correlation effects from ESE, we employ two between-subjects treatments. In the replication treatment,.⁷ for $z=a_l$, whenever the correlation structure is changed from positive to independent, the number of states changes from three to four (i.e., Table 1ii, iii). For $z=b$, there are always three states. In our second treatment, the correlation effects only (CEO) treatment, subjects face the presentation formats in Table 1iv, v. In this treatment, there are always five states and the displayed probabilities of each payoff stay constant when changing the correlation structure.⁸ This design controls for ESE and thus allows testing for correlation effects in a clean way. This design is inspired by Starmer and Sugden (1993) who employ treatments similar to our replication and CEO treatment to disentangle correlation effects from ESE using different choice tasks.

Each subject faces choices for 3 parameter sets (see Table 3) that might elicit behavior typical of the common consequence Allais paradox. For $z=a_l$, each subject faces the choice task for the two different correlation structures. For $z=b$, each subject faces only one choice. This results in $3*(2+1)=9$ decisions for each subject.

Table 3 Parameter values for the common consequence Allais paradoxes

Our main hypotheses for setting I are summarized in Hypothesis 1. As discussed above, changing the correlation structure from independent to maximally positive should eliminate choice patterns in line with the Allais paradox (Bordalo et al., 2012). This motivates Hypothesis 1.1. If effects found in previous studies are indeed driven by correlation effects, we should expect this prediction to hold true also in the CEO treatment. This motivates Hypothesis 1.2. Finally, if ESE and correlation effects are additively separable, comparing choices in the two treatments allows disentangling the effects of ESE and correlation effects. This motivates Hypothesis 1.3.

Hypothesis 1

• (1) In the replication treatment, when lotteries are independent, choices will exhibit a pattern consistent with the common consequence Allais paradox more frequently than when choices are maximally positively correlated.

• (2) Hypothesis 1.1 will also be confirmed in the CEO treatment.

• (3) The effects found in the replication treatment are largely driven by ESE.

3.2 Setting II: Mao pairs

3.2.1 Salience theory and preferences for relative skewness

Dertwinkel-Kalt and Köster (2020) test the prediction that salience theory induces a preference for relative skewness in the context of choices between two lotteries of a Mao pair (Mao, 1970), denoted $M(E, V, S, \eta )$. Mao pairs are pairs of lotteries $L(E,V, -S)$ and L(E, V, S) that share the same expected value E and variance V. Their skewnesses are of equal size but different sign (i.e., $-S$ and S). Since the first two moments are held constant, Mao pairs are particularly well suited to investigate (relative) skewness preferences. The joint distribution of the two lotteries is described by a parameter $\eta$. $\eta =0$ corresponds to the perfectly negative correlation and $\eta =1$ corresponds to the maximally positive correlation.

In Dertwinkel-Kalt and Köster (2020)’s second experiment, subjects decide between the six Mao pairs displayed in Table 4. Two of the Mao pairs each have the same variance, with one of these two Mao pairs being more symmetric (corresponding to $S=0.6$ in Table 4) than the other. To each subject, each Mao pair was presented in two correlation structures, maximally positively and perfectly negatively correlated. Consider Table 5. Moving from the maximally positive correlation structure to the perfectly negative one, i.e., moving from Table 5i to iii, increases the relative skewness of the right-skewed lottery. Moreover, for the symmetric Mao pairs, changing the correlation structure induces a sign change in the relative skewness of the lotteries. When $\eta =1$, it is the left-skewed lottery that is positively skewed relative to the right skewed lottery. When $\eta =0$, this relationship is reversed. For the asymmetric Mao pairs, the right-skewed lottery is always the lottery with a positive relative skewness, regardless of the correlation structure.

Salience theory predicts that the share of subjects choosing the right skewed lottery (weakly) increases when changing the correlation of the lotteries from maximally positive to perfectly negative. Moreover, this effect is predicted to be larger for the symmetric Mao pairs. In their experiment, Dertwinkel-Kalt and Köster (2020) confirm both hypotheses.

Table 4 Mao pairs used in Dertwinkel-Kalt and Köster (2020)

3.2.2 ESE in Dertwinkel-Kalt and Köster (2020)

To see how ESE can account for these findings, consider Table 5. In Dertwinkel-Kalt and Köster (2020), subjects are confronted with choices analogous to Table 5i and 5iii. When moving from Table 5i to iii, the correlation is increased from $\eta =0$ to $\eta =1$. However, the number of displayed states also changes from two to three. The high payoff of the left skewed lottery $L(E,V,-S)$ and the low payoff of the right skewed lottery are displayed once under negative correlation but twice under positive correlation. Therefore, if multiply displayed states receive a higher decision weight, these changes in the presentation of the choice problem might induce choice patterns similar to those predicted by salience theory.

Table 5 Reducing relative skewness

3.2.3 Experimental design and hypotheses

We again introduce two treatments. In the replication treatment,⁹ whenever the correlation structure is changed from perfectly negative to maximally positive, we also introduce ESE (see Table 5i, iii). In the correlation effects only (CEO) treatment, we control for ESE and only correlation effects are present (see Table 5ii, iii). Each subject faces 6*2=12 decisions in setting II.

We test Hypothesis 2 summarized below. Hypothesis 2.1 states that in the replication treatment we expect to replicate the findings of Dertwinkel-Kalt and Köster (2020). If the effects reported in Dertwinkel-Kalt and Köster (2020) are driven by correlation effects, we should expect to find choice patterns in line with Hypothesis 2.1 also in the CEO treatment. This motivates Hypothesis 2.2. Further, comparing choices in the two treatment will allow to disentangle ESE from correlation effects. This motivates Hypothesis 2.3.

Hypothesis 2

Consider two Mao pairs $M(E, V, S', \eta )$ and $M(E, V, S'', \eta )$ with $S'<S''$.

• (1) In the replication treatment, (a) for each of the Mao pairs the share of subjects choosing the right-skewed lottery is larger for $\eta =0$ (i.e., the perfectly negative correlation) than for $\eta =1$ (i.e., the maximal positive correlation). (b) The correlation effect described in (a) is larger for the more symmetric Mao pair $M(E, V, S^{'}, \eta )$.

• (2) Hypothesis 2.1 will also be confirmed in the CEO treatment.

• (3) The effects found in the replication treatment are largely driven by ESE.

3.3 Procedures

The experiment was conducted in Beijing at Renmin University of China. We preregistered our main experimental hypotheses with the AEA social science registry under the ID of AEARCTR-0007239. A total of 15 experimental sessions were conducted in March 2021, with a total of 296 Chinese undergraduate students participating.

The experiment was programmed with oTree (Chen et al., 2016) and conducted in Chinese and in a physical lab. The instructions and display of the choice tasks were modeled on Dertwinkel-Kalt and Köster (2020). Payoffs were displayed in an experimental currency that was translated into Yuan at a rate of 0.5. Tasks were presented in a matrix form. See Fig. 1 for an example. The presentation of choice tasks closely follows that of Dertwinkel-Kalt and Köster (2020). The order in which states appear, as well as which lottery was labeled option A and B, was randomized at the subject level. Participants received tasks in random order.

Our experiment used a between-subjects design. Participants in both the replication and CEO treatments decided on a total of 35 choice tasks.¹⁰ They read that for each choice task, there were two options with payoffs that depend on the turn of a wheel of fortune.¹¹ One of these tasks was randomly selected and paid out at the end of the experiment. In addition, participants received a show-up fee of 10 Yuan. Participants took about 30 min to complete the experiment and received an average payment of around 41 Yuan.

Fig. 1

Example of a decision screen. Figure notes: “Fields” refers to the fields of a wheel of fortune

4 Results

In this section, we present the results of the experiment. We start with the setting of the Allais paradox and then move on to the setting of Mao pairs. For both settings, our findings suggest that existing evidence for salience theory is mainly driven by ESE.

4.1 Setting I: common consequence Allais Paradox

Since we find that the occurrence of the common consequence Allais paradox varies significantly between our three parameter sets, we present results for each lottery separately.¹² We begin with the replication treatment. Figure 2a displays the occurrence of the Allais paradox choice pattern, net of the reverse choice pattern, for the three parameter sets for both the positive correlation structure and the case of independence. For all three parameter sets, we find that changing the correlation structure from positive to independent leads to a significant ($p<0.01$ for each choice task, two-sided t-test¹³) and large increase in choice patterns consistent with the Allais paradox. These patterns are generally in line results reported in recent studies (Bordalo et al., 2012; Bruhin et al., 2022; Frydman & Mormann, 2018).

Fig. 2

Frequency of the Allais paradox (net of the reverse choice pattern). There are 149 subjects in the replication treatment and 147 subjects in the CEO treatment. Values of parameter sets can be found in Table 3

To investigate the role of pure correlation effects, we next turn to the frequency of Allais-consistent choice pattern in the CEO treatment. See Fig. 2b. For parameter set 1, changing the correlation of the lotteries from positive to independent increases the occurrence of the Allais paradox significantly ($p=0.049$) from about 16–27%. This finding is in line with the predictions of salience theory. For parameter set 2, we observe that 11% (9.5%) of subjects exhibit a choice pattern in line with the Allais paradox when lotteries are positively correlated (independent). This difference is not statistically significant ($p=0.79$). Finally, for parameter set 3, changing the correlation structure from positive to independent reduces the occurrence of the Allais paradox significantly ($p=0.012$) from about 16% to 3%. This effect goes in the opposite direction as predicted by salience theory.

Comparing Fig. 2a, b, it is evident that the reactions to changes in the correlation structure are much more pronounced but also more systematic in the replication treatment than in the CEO treatment. This indicates that in our experiment, ESE are a much more important driver of behavior than correlation effects.

Now we test Hypothesis 1 more formally. We define a variable shift as $R(a_l \mid independent) - R(b \mid independent) - \big ( R(a_l \mid positive) - R(b\mid positive)\big )$, where $R(z \mid cs)$ is a dummy that equals 1 if a subject chose the risky option for common consequence $z \in \{ a_l, b\}$ under correlation structure $cs \in \{ independent, positive \}$, and 0 zero otherwise. For a given correlation structure, $R(a_l \mid cs ) - R(b\mid cs) = 1$ indicates the classical Allais choice pattern, whereas a value of – 1 indicates the reverse choice pattern and a value of 0 indicates behavior consistent with expected utility theory. Since the correlation structure does not change when $z=b$, i.e., $R(b \mid independent) =R(b \mid positive)$, the expression of shift boils down to $R(a_l \mid independent ) - R(a_l \mid positive)$. That is, changes in the frequency of the occurrence of the Allais paradox due to changes in the correlation structure must therefore stem from correlation effects in the case in which $z=a_{l}$. On the aggregate, the variable shift measures the increase in Allais paradox compatible behavior as a result of changing the correlation structure as predicted by salience theory, net of the reverse choice pattern. Notice that by netting out behavior consistent with the reverse Allais choice pattern, we are able to control for choice reversals that stem from decision noise.

We run a linear regression of the variable shift on a constant and a dummy that is equal to one if a given subject was in the replication treatment.¹⁴ The constant provides an estimate of the change in the frequency of the Allais paradox that is due to correlation effects. The coefficient on the replication dummy provides an estimate of the additional ESE. Since we find different choice patterns for the different parameter sets, we run this regression for all three parameter sets separately, as well as jointly.

Table 6 Relative impacts of ESE and correlation effects in the setting of the Allais paradox

We report our regression results in Table 6. We find that for the first parameter set, changing the correlation from positive to independent (controlling for ESE) induces an increase in the frequency of Allais compatible behavior by about 11 percentage points. The coefficient is significant at the 5% level. ESE induce a further increase in the frequency of Allais consistent behavior by around 35 percentage points ($p<0.01$). For the second parameter set, we find no evidence that the frequency of Allais compatible behavior is influenced by changing the correlation of the lotteries from positive to independent. The point estimate of the constant is $-$0.01 ($p=0.79$). The coefficient on the replication dummy is estimated at 0.255 ($p<0.01$), which implies that ESE lead to an increase in the frequency of the Allais paradox of around 26 percentage points. Finally, for the third parameter set, we find that changing the correlation of the lotteries from positive to independent (controlling for ESE) leads to a decrease in the occurrence of Allais compatible choice patterns by about 14 percentage points ($p=0.01$). We estimate that ESE lead to an increase in the frequency of Allais compatible behavior by around 42 percentage points. Finally, pooling the data from all three parameter sets, we find an estimate of the average correlation effect for our three decision tasks that is close to zero and not statistically different from zero ($p=0.64$). On average, ESE induce a large and significant increase in the Allais paradox by 34 percentage points ($p<0.01$). We summarize our results as follows:

Result 1

On the Allais paradox:

• (1) In the replication treatment, changing the correlation structure from maximally positive to independent increases the frequency of the common consequence Allais paradox for all three parameter sets. We confirm Hypothesis 1.1.

• (2) In the CEO treatment, we observe the above pattern for parameter set 1. For parameter set 2, no evidence of correlation effects is found. For parameter set 3, we find that changing the correlation from maximally positive to independent reduces the frequency of the common consequence Allais paradox. As we do not find consistent evidence for correlation effects as predicted by salience theory, we reject Hypothesis 1.2.

• (3) The effects in the replication treatment are largely driven by ESE. This result confirms Hypothesis 1.3.

4.2 Setting II: Mao pairs

We begin the exposition of our findings with the replication treatment, where both ESE and correlation effects are introduced at the same time. For the asymmetric Mao pairs,¹⁵ 90% of choices were for the right skewed option when the correlation was maximally positive. When the correlation was changed to negative, this hardly impacted choices. See Fig. 3. These findings are very much in line with the results of Dertwinkel-Kalt and Köster (2020), both with respect to the choice frequencies and the lack of reaction to changes in the correlation structure. For the more symmetric Mao pairs, changing the correlation structure from positive to negative decreases the choice frequency of the positively skewed option from 56 to 42%. This difference is significant at the 1% level. However, the effect goes in the opposite direction as predicted by salience theory and as the effect reported by Dertwinkel-Kalt and Köster (2020).

Fig. 3

Frequency of choices of the right-skewed option. There are 149 subjects in the replication treatment and 147 subjects in the CEO treatment. For each type of Mao pair, there are three Mao pairs. The parameters for the Mao pairs can be found in Table 4

We next turn to the CEO treatment, in which ESE are well controlled for. For the asymmetric Mao pairs, 94% of choices are for the positively skewed option when the correlation is positive. When lotteries are negatively correlated, 91% of choices are for the positively skewed lottery. This difference is marginally statistically significant ($p=0.08$) and goes in the opposite direction as predicted by salience theory. Turning to the more symmetric Mao pairs, 53% of choices were for the positively skewed option when the correlation was positive. This number is equal to 51% when the correlation is changed to negative. This difference is not statistically significant at any conventional significance level ($p=0.38$). When ESE are controlled for, we find no evidence that changing the correlation structure induces systematic and meaningful changes in lottery choices.

Comparing the choice patterns in the replication and the CEO treatment suggest that the effects we observe in the replication treatment are mainly driven by event-splitting, and not changes in the correlation structure. To test Hypothesis 2 more formally, we follow the analysis of Dertwinkel-Kalt and Köster (2020) closely. We construct a variable shift that is equal to one if a given subject chose the left skewed option for the maximally positive correlation but shifted to the right skewed option under negative correlation. For the reverse choice pattern, $shift =-1$. Finally, $shift =0$ when a subject chose the same lottery for both correlation structures. For each treatment, we then regress shift on a constant and dummy that is equal to 1 if a given Mao pair is asymmetric, and 0 otherwise.

Table 7 summarizes our regression results. In column 1, we report results for the replication treatment. The constant is estimated to be $-$0.14 and is statistically significant at the 1% level. In line with the exposition above, this suggests that changing the correlation structure from positive to negative induces subjects to switch away from the right skewed option. The estimate for the coefficient of the dummy indicating the asymmetric Mao pairs is 0.125 and is statistically significant at the 1% level. This implies that the effect of changing the correlation structure is negated for the asymmetric Mao pairs.

Table 7 Relative impacts of ESE and correlation effects in the setting of Mao pairs

In column 2, we report the estimates reported by Dertwinkel-Kalt and Köster (2020) for reference. Contrary to our findings, Dertwinkel-Kalt and Köster (2020) reported a positive constant of 0.127 and a negative coefficient for the dummy indicating the asymmetric Mao pairs of $-$0.118. As we do not observe the same choice patterns in our data as in Dertwinkel-Kalt and Köster (2020), we reject Hypothesis 2.1. Since our experimental design followed that of Dertwinkel-Kalt and Köster (2020) closely, this result is rather surprising. In column 3, we report the estimates for the CEO treatment. Here, the estimates for the constant and the dummy are both not significantly different from zero. As we find no evidence for correlation effects once ESE are controlled for, our results confirm Hypothesis 2.2.

Finally, in column 4, we pool the data of both treatments. We regress the variable shift on a constant, a dummy indicating an asymmetric Mao pair, a dummy indicating the replication treatment, and an interaction between the two dummy variables. The constant and the dummy indicating an asymmetric Mao pair provide an estimate of the frequency of preference reversals due to a change in the correlation structure. Both these coefficient are not significantly different from zero, which confirms our previous analysis. The replication dummy provides an estimate of the preference reversals that are due to ESE, net of correlation effects. This coefficient is estimated at $-$0.11 and is statistically significant at the 5% level. The coefficient of the interaction term is estimated at 0.13 and is statistically significant at the 5% level, which negates the ESE for the asymmetric Mao pairs. These results suggest that in our setting preference reversals are mainly driven by ESE and not by correlation effects. We therefore conclude that our results provide evidence in favor of Hypothesis 2.3. We summarize our results as follows:

Result 2

On Mao Pairs:

• (1) In the replication treatment, participants chose the right skewed lottery more often under the maximally positive than under the maximally negative correlation structure. This effect was observed only for the symmetric Mao pairs but not for the asymmetric ones. This contradicts the findings reported by Dertwinkel-Kalt and Köster (2020). We reject Hypothesis 2.1.

• (2) Once ESE are controlled for, we do not find evidence of correlation effects. We reject Hypothesis 2.2.

• (3) The effects found in the replication treatment seem to be largely driven by ESE. We confirm Hypothesis 2.3.

Our failure to replicate the results of Dertwinkel-Kalt and Köster (2020) is somewhat surprising. Although our experimental design was close to that of the original paper, there are notable differences, such as the subject pool (Chinese versus German students),.¹⁶ the display of choice tasks,¹⁷ the number of choice tasks, the incentive structure,¹⁸ and how uncertainty was resolved.¹⁹ However, none of these differences seems able to explain the differences between our findings. In this context, it is worth mentioning that by now three sets of authors, Dertwinkel-Kalt and Köster (2021), Ostermair (2021), and ourselves, have implemented their version of our experiment on ESE for the Mao pairs.²⁰ All three implementations yielded somewhat different results, despite all studies being reasonably powered. Ostermair (2021) and Dertwinkel-Kalt and Köster (2021) replicate the original findings of Dertwinkel-Kalt and Köster (2020), whereas we do not. The choice patterns reported by Dertwinkel-Kalt and Köster (2021) for their and our respective CEO treatment are qualitatively similar in that no consistent evidence for correlation effects is found, whereas Ostermair (2021) documents significant correlation effects contradicting regret and salience theory. Taken together, these results suggest that behavior in the considered setting might be either noisy or driven by subtle differences in design. Importantly, none of the three studies finds evidence for correlation effects as predicted by salience theory once ESE are controlled for.

5 Conclusion

In this paper, we report on an experiment conducted to study correlation effects in risk taking in both the setting of the Allais paradox and of Mao pairs, while controlling for ESE. In the setting of the Allais paradox, our results indicate that alterations in the choice display, rather than shifts in the correlation structure, may be responsible for the outcomes observed in prior studies by Bordalo et al. (2012), Frydman and Mormann (2018), and Bruhin et al. (2022). In the setting of Mao pairs, the picture is less clear since the results of our replication treatment contradict the results of (Dertwinkel-Kalt & Köster, 2020). However, our failure to replicate their results, together with our null findings on correlation effects once controlling for ESE, do shed considerable doubt on the experimental results of Dertwinkel-Kalt and Köster (2020). Overall, our study questions the validity of salience theory in describing risky behavior. Finally, given its substantial impact on risk behavior, researchers should be well aware of it when designing experiments involving event-splitting. Further research might be needed to better understand the mechanisms behind ESE. In the setting considered here and in other studies (Starmer & Sugden, 1993; Ostermair, 2021, 2022), ESE could be driven both by the change in the displayed number of states as well as the change in the displayed probabilities.²¹ Future research could aim at disentangling these mechanisms.