1 Introduction

Passive source localization technology has been a research hotspot in underwater acoustic community. The conventional matched field processing (MFP) has been studied widely, but it needs to solve the problem of sound field model and actual environment adaptation, which is difficult to use effectively in complex deep-sea environments [1,2,3]. Multipath phenomenon is obvious in deep water, and localization with feature parameters of multipath propagation has attracted much attention in recent years [4,5,6]. The performance of source localization using time-arrival structure in time domain is always limited by the accuracy of multipath time delay estimation [7,8,9,10,11]. To avoid this problem, many scholars convert time-domain signal into frequency domain and utilize characteristics of interference pattern for source localization.

Actually, in shallow water, sound intensity in the two-dimensional plane of frequency and distance presents a stable interference structure, and the positioning methods using interference pattern are widely studied [12,13,14]. While in deep water, interference striation is complex, and waveguide invariant (WI) varies greatly at different distances [15]. Li et al. [16] pointed out that in the deep-sea convergence zone, WI tends to infinity, and tends to 1 in the shadow zone. Therefore, the localization methods using interference pattern or WI in shallow water are difficult to apply in deep-water environments. It is necessary to develop new source localization methods according to the characteristics of sound interference structure in deep water.

There are typical interference structures in the both direct arrival zone and shadow zone. The former is mainly caused by the interaction between direct and surface-reflected arrivals [17], and the latter mainly resulted by the interaction of multiple bottom-reflected arrivals [18], which lead to different source localization methods. Based on the relation between the source depth and the interference structure in the direct arrival zone, McCargar and Zurk [19] proposed a source depth estimation method using the modified Fourier transform with vertical array line (VAL). Kniffin et al. [20] analyzed the limitations of the method and gave a simplified depth estimation method based on the observed spacing of deep-harmonic interference nulls. Duan et al. [21] proposed two source depth estimation (matched-interference-structure and matched-frequency-spacing) methods based on interference striation trace estimation. Wei et al. [22] used interference striations obtained by VAL to extract grazing angles of multipath eigenrays and estimated the source depth by the geometric structure. Apart from VAL, utilizing a single hydrophone to receive signal is also a common method for source localization [23]. In the direct arrival zone, Yang et al. [24] studied a single hydrophone target localization method based on interference characteristics of cross-correlated broadband fields and extracted target depth information through Fourier transform of interference striations. While in the shadow zone, Weng et al. [18] discussed the relation among the sound field interference pattern, propagation range, source depth and receiver depth, and proposed a passive source localization method using a single hydrophone. In addition to the above reception methods, horizontal array line (HLA) is also a good receiving approach, which can obtain stable interference pattern and has high array gain [25]. Recently, Emmetière et al. [26] proposed a source depth discrimination method based on deep-water WI with HLA. However, the maximum immersion depth of HLA is about a few hundred meters, making it difficult to deploy in practical applications. Until now, there has been little work on source localization through interference structure obtained by HLA. Besides, most of above methods are applicable for deep water with a complete sound channel (like the West Pacific Ocean and Mediterranean Sea), where the sound velocity of seawater near the bottom is higher than that near the surface. For shallower ocean waveguide with an incomplete sound channel (like the South China Sea), these methods are no longer applicable or require to be adjusted, so we still need to develop other source localization methods.

Considering the above problems about source localization in deep water, we propose a source depth discrimination method using a bottomed HLA suitable for deep-water environment with an incomplete channel. This method regards source depth identification as a binary classification problem and achieves depth discrimination by comparing the energy ratio of different modal interference groups on the interference spectrum. Therefore, the method mainly includes two aspects. Firstly, the interference spectrum is obtained through two-dimensional Fourier transform (2-D FT) of the interference pattern received by the HLA on the bottom of deep water. Based on the characteristics of incomplete channels, the interference striations can be divided into different types, called modal interference groups, and the corresponding interference spectral peaks also have different types. Differences in interference spectrums at different source depths can be used for source depth discrimination. Secondly, dividing the interference spectrum into subspaces and calculating the energy ratio between different subspaces can yield energy ratio of different modal interference groups. Then, source depth discrimination can be achieved through comparing the energy ratio with the given judgment threshold.

The remainder of the paper is organized as follows. In Sect. 2, the source depth discrimination method based on interference spectrum and related concepts are presented. Numerical simulations and experimental data are used to validate the effectiveness of the proposed method in Sect. 3. The conclusion and discussion are given in Sect. 4.

2 Principle and Method

2.1 Normal Modes of Acoustic Field and Modal Classification

According to the normal mode theory, underwater sound field can be represented by a set of normal modes. In the range-independent environment, the pressure received at range r and depth zr from a point source at depth zs is [27],

$$ p(z_s ,z_r ,r,f) = \sum_{m = 1}^M {\psi_m (z_s ,f)\psi_m (z_r ,f)\frac{{e^{ik_m (f)r} }}{{\sqrt {k_m (f)r} }}} = \sum_{m = 1}^M {A_m (z_s ,z_r ,r,f)e^{i\phi_m (r,f)} } $$
(1)

where f is the source frequency, M is the total order of propagation modes, and ψm, km, Am and ϕm are the eigenfunction, horizontal wavenumber, amplitude and phase of mode m. Note that the constant term is ignored in Eq. (1). As can be seen from Eq. (1), the complex exponential term changes significantly with the range, while the cylindrical expansion loss changes very slowly and can be ignored in the short-distance observation window. In the ideal waveguide, the amplitude is usually regarded as a constant independent of frequency [27]. Therefore, the amplitude can be considered independent of the range and frequency. Then, the signal intensity I is given by,

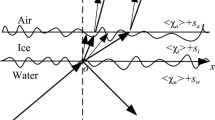
$$ \begin{gathered} I(z_s ,z_r ,r,f) = \left| {p(z_s ,z_r ,r,f)} \right|^2 \hfill \\ { = }\sum_{m = 1}^M {|} A_m (z_s ,z_r ){|}^{2}\hfill \\ \quad { + }\sum_{m,n = 1,m \ne n}^M {A_m (z_s ,z_r )A_n (z_s ,z_r )\cos (\Delta k_{mn} (f)r)} \hfill \\ \end{gathered} $$
(2)

where Δkmn = km–kn is the wavenumber difference between modes m and n. The first term in Eq. (2) is the direct current (DC) term, which does not produce interference patterns, and the second term contains a cosine function, which causes interference structures in the r-f image, as shown in Fig. 1. We can see that the interference term contains the source depth from Eq. (2), so it can be used to extract the source depth information.

Fig. 1
figure 1

Interference pattern I (r, f) of a source at zs = 50 m recorded by a 1.2 km long horizontal line array at zr = 1750 m. The source-to-array range is 27.5 km

Full size image

From the normal mode theory, the eigenfunction oscillates between the upper and lower turning point (at depths z +m and z −m , respectively) and the amplitude beyond these points shows exponential attenuation [27]. For a given sound speed profile (SSP) c(z), turning points satisfy,

$$ c(z_m^\pm ) = V_{p,m}^h = \frac{2\pi f}{{k_m }} $$
(3)

where V hp,m is the phase velocity of the mode m. Then modes can be divided into different types according to the depth of eigenfunctions oscillating. Here, we take the SSP measured by the conductivity-temperature-depth (CTD) during a South China Sea (SCS) experiment in 2022 as an example, as shown in Fig. 2. Considering that the deep-water waveguides in the SCS are mainly incomplete channels, there are three main types of sound ray propagation in water, pure refracted rays, bottom-reflected rays and surface-reflected-bottom-reflected rays, as shown in Fig. 3, which is calculated by BELLHOP code [28]. Therefore, similar to the case of sound rays, modes within different phase velocity ranges have different interactions with the boundary. We can ultimately divide the modes into following types:

Fig. 2
figure 2

Sound speed profile and bottom parameters in the experimental sea area

Full size image
Fig. 3
figure 3

Sound rays for an underwater source with SSP shown in Fig. 2. Three types of sound ray: pure refracted rays (in red line), bottom-reflected rays (in blue line) and surface-reflected-bottom-reflected rays (in black line)

Full size image

Trapped Mode (TM) The modal phase velocity satisfies,

$$ c_{\min } < V_{p,m}^h < c_{bottom} $$
(4)

where cmin is the minimum value of sound velocity in the waveguide, which is usually the sound velocity at the sound channel axis, and cbottom is the sound velocity of seawater near the sea bottom.

Bottom Interacting Mode (BIM) The modal phase velocity satisfies,

$$ c_{bottom} < V_{p,m}^h < c_{surface} $$
(5)

where csurface is the sound velocity of seawater near the sea surface.

Surface Interacting-Bottom Interacting Mode (SIBIM) The modal phase velocity satisfies,

$$ c_{surface} < V_{p,m}^h < c_{\max } $$
(6)

where cmax is the maximum value of sound velocity in the waveguide, which is usually the sound velocity of seabed.

Figure 2 also shows the phase velocity ranges corresponding to different modal types. It is worth noting that if the environment is a complete channel, the corresponding modal types will change and further research is needed. From Eq. (2), it can be seen that interference striation is caused by the interaction of different modes. After classifying modes, there are six types of possible interferences: TM–TM, TM-BIM, TM-SIBIM, BIM-BIM, BIM-SIBIM, and SIBIM-SIBIM, and we call them modal interference groups. In the following paper, we can see that the type of interference is dependent on source depth.

2.2 Interference Spectrum

In order to better illustrate the interference structure changes caused by different source depths, we analyze the 2-D FT of the interference pattern. The signal interference pattern of bandwidth B and central frequency f0 is obtained by the HLA laid on the seabed. The array length and central range of HLA is L and r0, respectively. Then, the 2-D FT of the interference pattern is defined by,

$$ \tilde{I}(\kappa ,t) = \int_{f_0 - \frac{B}{2}}^{f_0 + \frac{B}{2}} {\int_{r_0 - \frac{L}{2}}^{r_0 + \frac{L}{2}} {I(z_s ,z_r ,r,f)e^{ - i2\pi (\kappa r + tf)} drdf} } $$
(7)

where κ and t are the Fourier transform variables conjugate to range and frequency, respectively. After removing DC components, substituting Eq. (2) into Eq. (7) yields [15],

$$ \begin{gathered} \tilde{I}(\kappa ,t) = \sum_{m,n = 1,m \ne n}^M A_m (z_s ,z_r )A_n (z_s ,z_r )\hfill \\\sin c(\pi \kappa L)\sin c(\pi tL)\hfill \\ \, \ast [\delta (\kappa - \kappa_{mn} ,t - t_{mn} ) + \delta (\kappa + \kappa_{mn} ,t + t_{mn} )] \hfill \\ \end{gathered} $$
(8)

where * represents convolution, δ is the Dirac delta function, and the pair (κmn, tmn) is the Fourier coordinates of interference striation formed by modes m and n. Following formulas can be obtained according to the phase part of Eq. (1) [29],

$$ \kappa_{mn} (f) = \frac{{\partial (\Delta k_{mn} (f)r)}}{2\pi \partial r} = \frac{{\Delta k_{mn} (f)}}{2\pi } $$
(9)
$$ t_{mn} (r,f) = \frac{{\partial (\Delta k_{mn} (f)r)}}{2\pi \partial f} = r\frac{{\partial \Delta k_{mn} (f)}}{2\pi \partial f} $$
(10)

The modal phase slowness and group slowness can be calculated by taking the reciprocal of phase velocity and group velocity, respectively, as shown in following formulas:

$$ S_{p,m}^h = \frac{1}{{V_{p,m}^h }} = \frac{k_m }{{2\pi f}} $$
(11)
$$ S_{g,m}^h = \frac{1}{{V_{g,m}^h }} = \frac{\partial k_m }{{2\pi \partial f}} $$
(12)

where S hp,m and S hg,m are phase slowness and group slowness of mode m, respectively. By using Eqs. (9–12), it can be obtained that

$$ \kappa_{mn} (f) = f\Delta S_{p,mn}^h (f) $$
(13)
$$ t_{mn} (r,f) = r\Delta S_{g,mn}^h (f) $$
(14)

where ΔS hp,mn  = S hp,m − S hp,n and ΔS hg,mn = S hg,m − S hg,n are phase slowness difference and group slowness difference, respectively. An example of interference spectrum is displayed by Fig. 4, which is the 2-D FT of the intensity shown in Fig. 1. Through the spectral peaks on the interference spectrum, we can get the oscillation period of the interference striation along the range axis and frequency axis. For instance, Fig. 4 shows spectral peaks located at (± 5 km−1, ∓ 0.6 s) and the interference striation corresponding to the oscillation period (0.2 km, 1.7 Hz) can be observed in Fig. 1. Besides, the interference spectrum is symmetric about the origin center, so only the right half of the spectrum (κ ≥ 0) is considered in this paper.

Fig. 4
figure 4

Interference spectrum of interference pattern shown in Fig. 1. The spectral peaks marked by the black cross correspond to the observable interference striation in Fig. 1

Full size image

The expression of the deep-water WI is given in Reference [27],

$$ \beta_{mn} (r,f) = - \frac{{\Delta k_{mn} (f)}}{{f\frac{{\partial \Delta k_{mn} (f)}}{\partial f}}} = - \frac{{\Delta S_{p,mn}^h (f)}}{{\Delta S_{g,mn}^h (f)}} $$
(15)

The WI is used to characterize the slope of the interference striation, which is independent of the source depth and receiver depth, and only depends on the interfering modes m and n. Substitute Eqs. (13) and (14) into Eq. (15) to obtain,

$$ \beta_{mn} (r,f) = - \frac{r}{f}\frac{{\kappa_{mn} (f)}}{{t_{mn} (r,f)}} $$
(16)

This equation means the coordinate position of interference spectrum is associated with the WI. Furthermore, if two modes belong to the same type (TMs, BIMs or SIBIMs), the WI is roughly the same, which can be seen by plotting the phase slowness and group slowness, as shown in Fig. 5, which is calculated by KRAKEN code [30]. The image slope is basically consistent in same modal type, and the WIs corresponding to different types are defined here as follows: βmn ≈ -4 (if m and n are TMs), βmn ≈ 1.5 (if m and n are BIMs) and βmn ≈ 0.8 (if m and n are SIBIMs). In subsequent description, the WI is rewritten as βN and its value depends on which modal type N belongs to.

Fig. 5
figure 5

Phase slowness and group slowness of each mode calculated at a frequency of 355 Hz

Full size image

2.3 Dominant Modes and Spectral Peak Prediction

Different modes contribute differently to the sound field, with only a small number of modes playing a major role, which are called the dominant modes. Actually, the interference striations corresponding to the spectral peaks are caused by the interacting of different dominant modes, and can be clearly observed. While other striations are difficult to observe. According to Eq. (1), when the phase difference of adjacent normal modes satisfies,

$$ \Delta \phi_{m,m + 1} (r,f) = 2p\pi , \, p \in {\bf{\mathbb{Z}}} $$
(17)

the adjacent modes are called dominant modes [31], where m and m + 1 represent any two adjacent mode orders, Δϕm,m+1 is phase difference of adjacent mode, and p is any integer. The order of the dominant mode is usually a non-integer. In practice, we regard p as a discrete function of m (p(m), m = 1, 2, ···, M), and by linear interpolation, we obtain the continuous function (p(i), i ∈ [1, M]). Then, we can find the index i corresponding to the integer p(i). And dominant mode order md is defined as the intermediate value i + 0.5 between index i and i + 1. The phase slowness and group slowness of dominant mode can be calculated by interpolation. If acoustic field contains more than two dominant modes, the mode md and nd will form visible interference striation and the corresponding WI is

$$ \beta_{m_d n_d } (r,f) = - \frac{{\Delta S_{p,m_d n_d }^h (f)}}{{\Delta S_{g,m_d n_d }^h (f)}} $$
(18)

In the previous derivation, it is believed that the amplitude is approximately independent of the frequency, so it has no effect on the phase. However, Emmetière et al. [15] pointed out that in the deep-water case, the eigenfunction changes significantly with the frequency due to the strong refraction effect of the SSP. Therefore, it is necessary to consider the impact of the eigenfunction on the modal phase. According to Wentzel–Kramers–Brillouin (WKB) normal mode theory [28], the eigenfunction can be decomposed with an up-going wave Ψ −m (z, f) and a down-going wave Ψ +m (z, f),

$$ \psi_m (z,f) = \Psi_m^- (z,f) + \Psi_m^+ (z,f) $$
(19)

Represent the up-going and down-gong waves in phase integral form,

$$ \Psi_m^- (z,f) = \frac{C^- }{{\sqrt {{k_{zm} (z,f)}} }}e^{ - i\int_{z_m^- }^z {k_{zm} (Z,f)} dZ} $$
(20)
$$ \Psi_m^+ (z,f) = \frac{C^+ }{{\sqrt {{k_{zm} (z,f)}} }}e^{i\int_{z_m^+ }^z {k_{zm} (Z,f)} dZ} $$
(21)

where C∓ are constants, z∓ m and kzm are depths of turning points and vertical wave number of the mode m, respectively. The vertical wave number is calculated by,

$$ k_{zm} (z,f) = \sqrt {(2\pi f)^2 /c^2 (z) - k_m^2 } $$
(22)

where km is horizontal wavenumber of mode m. Beyond the turning depth, kzm is a pure imaginary number. The amplitude of the eigenfunction decays exponentially and its phase effect can be ignored. While between the upper and lower turning point, the influence of eigenfunction needs to be taken into account for the normal mode phase, so the modal phase is rewritten as [15],

$$ \phi_m^{\xi \varepsilon } (z_s ,z_r ,r,f) = k_m (f)r + \xi \int_{z_m^\xi }^{z_s } {k_{zm} (z,f)} dz + \varepsilon \int_{z_m^\varepsilon }^{z_r } {k_{zm} (z,f)} dz $$
(23)

where (ξ, ε) = (± 1, ± 1), representing the superscript of turning point. So that there are four different phase terms of each mode. Specifically, when (ξ, ε) = (0, 0), the phase term degenerates to the form before correction, as shown in Eq. (1). By taking the derivative of Eq. (23), the delay the mode m can be obtained [32],

$$ \begin{gathered} t_m^{\xi \varepsilon } (z_s ,z_r ,r,f) = r\frac{\partial k_m (f)}{{2\pi \partial f}} + \xi \int_{z_m^\xi }^{z_s } {\frac{{\partial k_{zm} (z,f)}}{2\pi \partial f}} dz \hfill \\+ \varepsilon \int_{z_m^\varepsilon }^{z_r } {\frac{{\partial k_{zm} (z,f)}}{2\pi \partial f}} dz \hfill \\ \, = rS_{g,m}^h + \xi \int_{z_m^\xi }^{z_s } {S_{g,m}^v } dz + \varepsilon \int_{z_m^\varepsilon }^{z_r } {S_{g,m}^v } dz \hfill \\ \end{gathered} $$
(24)

where S vg,m is the vertical group slowness of the mode m, which can be determined by the formula,

$$ S_{g,m}^v (z,f) = \frac{{\partial k_{zm} (z,f)}}{2\pi \partial f} = \frac{{\frac{2\pi f}{{c^2 (z)}} - k_m S_{g,m}^h (f)}}{{k_{zm} (z,f)}} $$
(25)

Then, we can define the effective group slowness as [32],

$$ S_{g,m}^{\xi \varepsilon } = \frac{{t_m^{\xi \varepsilon } (z_s ,z_r ,r,f)}}{r} = S_{g,m}^h + \frac{\xi }{r}\int_{z_m^\xi }^{z_s } {S_{g,m}^v } dz + \frac{\varepsilon }{r}\int_{z_m^\varepsilon }^{z_r } {S_{g,m}^v } dz $$
(26)

Through Eq. (26), the original horizontal group slowness formula is modified by considering the influence of the eigenfunction. Specifically, when (ξ, ε) = (0, 0), the effective group slowness degenerates to the general horizontal group slowness. After phase correction, Eq. (17) is rewritten as,

$$ \Delta \phi_{ww^{ + 1} } (z_s ,z_r ,r,f) = 2p\pi , \, p \in {\mathbb{Z}} $$
(27)

where w = (m, ξ, ε) and w+1 = (m + 1, ξ, ε) are adjacent modes. As mentioned before, there are four possibilities for corrected phase term, so there are also four corresponding phase differences. Then, the dominant mode order can be obtained according to Eq. (27), and other modal quantity can be evaluated by interpolation.

We know that the spectral peaks on the interference spectrum are the results of dominant modal interactions. To predict the spectral peaks, we replace the modes (m and n) in Eq. (8) with dominant modes (wd = (md, ξ, ε) and vd = (nd, μ, υ)) and yield [15],

$$ \begin{gathered} \tilde{I}(\kappa ,t) = \sum_{w_d ,v_d ,w_d \ne v_d } {A_{w_d } A_{v_d } \sin c(\pi \kappa L)\sin c(\pi tL)} \hfill \\ \, \quad \ast [\delta (\kappa - \kappa_{w_d v_d } ,t - t_{w_d v_d } ) + \delta (\kappa + \kappa_{w_d v_d } ,t + t_{w_d v_d } )] \hfill \\ \end{gathered} $$
(28)

where

$$ \kappa_{w_d v_d } (f) = f\Delta S_{p,w_d v_d }^h (f) $$
(29)
$$ t_{w_d v_d } (r,f) = r\Delta S_{g,w_d v_d } (f) $$
(30)

where \( \Delta S_{g,\varvec{w}_d \varvec{v}_d } = S_{g,m_d }^{v}-S_{g,n_d}^{v}\) is effective group slowness difference. Through Eqs. (29) and (30), the spectral peaks in the interference spectrum can be predicted, as shown in Fig. 6.

Fig. 6
figure 6

Spectral peaks prediction on interference spectrum shown in Fig. 4

Full size image

We have classified the modes in Sect. 2.1, so the dominant mode can also be divided into different types according its phase velocity. Then, it can be determined which two type modes interact to cause the spectral peak, or which modal interference group corresponds to. Figure 7 displays an example of Ĩ (κ, t) for (a) surface source and (b) underwater source, from which we can see significant differences in the positions and types of spectral peaks. It can be clearly observed that Fig. 7(b) contains an additional spectral peak compared with Fig. 7(a), and the dominant modes include BIMs. The reason is that underwater source can excite more BIMs and TMs, so that the modal interference groups contain more components including these two types, while most of the modes excited by surface source are SIBIMs and corresponding interference group is mainly SIBIM-SIBIM. Therefore, we can define subspaces of Ĩ (κ, t) that are associated to a given type of interference and calculate the energy of modal interference groups in these subspaces. Through subspace energy ratio, source depth discrimination can be realized.

Fig. 7
figure 7

Ĩ (κ, t) of a 20 Hz bandwidth (345 Hz-365 Hz) acoustic intensity simulated over a 1.2 km HLA, (a) for a surface source zs = 50 m and (b) for an underwater source zs = 200 m, and the modal interference group corresponding to the spectral peak has been marked

Full size image

2.4 Subspaces Definition of Interference Spectrum

As stated before, there are six types of possible interference. For underwater source with an incomplete channel, TM and BIM play a major role in interference structures. So, we are interested in modal interference group that contains at least one TM or one BIM (TM–TM, TM-BIM, TM-SIBIM, BIM-BIM, and BIM-SIBIM). Once we partition the interference spectrum into subspaces and calculated the energy ratio of modal interference group which we are interested. The source depth discrimination can be realized. According to the method in Reference [26], we can obtain the boundary of the subspace through the following steps.

For interference striation formed by modes m and n, we assume that n ∈ N. Then for arbitrary mode m, the corresponding Fourier coordinate relation is given by Eq. (16). Considering that Eq. (14) is linear, so one can decompose Eq. (16) by selecting an arbitrary mode l as,

$$ t_{mn} = t_{ml} + t_{ln} = - \frac{r}{f}\left( {\frac{{\kappa_{ml} }}{{\beta_{ml} }} + \frac{{\kappa_{ln} }}{{\beta_{ln} }}} \right) $$
(31)

To simplify Eq. (31), we choose the mode l ∈ N and let βml =  + ∞, then using the linearity of Eq. (13) to rewrite Eq. (31),

$$ t_{mn} = - \frac{r}{f}\frac{{\kappa_{ln} }}{\beta_N } = - \frac{r}{f}\frac{1}{\beta_N }(\kappa_{mn} - \kappa_{ml} ) $$
(32)

Note that the interferences caused by mode m and all the modes of the subset N satisfy Eq. (32), then one can obtain a generalized linear formula [26],

$$ t(\kappa ) = - \frac{r}{f}\frac{1}{\beta_N }(\kappa - \kappa_{ml} ),\kappa \in [f\Delta S_{p,\min }^h ,f\Delta S_{p,\max }^h ] $$
(33)

where ΔS hp,min and ΔS hp,max are the minimum and maximum horizontal phase slowness difference between the mode m and the subset N, respectively. Equation (33) gives the position of the modal interference group on the Ĩ (κ, t), and formula parameters can be estimated based on Fig. 5. For example, if m and N belong to same type like TMs, then βml =  + ∞ only if ΔS hg,ml  = 0. As a result, m = l and thus κml = 0. For the mode of TMs, the phase slowness is displayed in Fig. 5, and we can know that ΔS hp,min  = 0 and ΔS hp,max  = 1/cmin–1/cbottom. Other cases are similar, and the results are shown in Table 1. It is noted that the table does not give the corresponding parameters of the TM-SIBIM because these two types do not have equal slowness mode. Actually, these boundaries are not used in the subsequent subspace definition, so it has no impact on the results of the proposed method.

Table 1 Parameters of different types of interferences
Full size table

We can obtain the approximate positions of different modal interference groups on the spectrum through the boundaries in Table 1, for example, spectral peaks formed by BIM and SIBIM exist between or near the boundaries determined by BIM-SIBIM. Then using other bounds obtained in Table 1, two subspaces can be defined as shown in Fig. 8, in which D0 gathers all possible modal interference groups and D1 gathers only modal interference groups involving at least one TM or one BIM. Note that not all bounds are used to determine subspaces. To include the main lobe in subspaces, some bounds have been stretched out. Additionally, considering that the WIs vary due to the SSP errors and environment fluctuations, the left borders (SIBIM-SIBIMs) of D0 and D1 are defined with βN = 0.4 (instead of 0.8 in Table 1) in order to gather all modal interference groups as much as possible.

Fig. 8
figure 8

Subspaces defined by Table 1. The bounds of subspace D1 are superimposed with dashed orange lines, whereas the bounds of D0 are displayed in blue line

Full size image

After the subspaces are defined, energy ratio of different modal interference groups can be calculated by,

$$ \tau = \frac{{\int_{D_1 } {\tilde{I}(\kappa ,t)d\kappa dt} }}{{\int_{D_{0} } {\tilde{I}(\kappa ,t)d\kappa dt} }} $$
(34)

where τ is energy ratio, D1 and D0 are areas surrounded by straight line segments of the same color in Fig. 8. An example of the defined subspaces superimposing on the interference spectrum for surface source and underwater source is shown in Fig. 9(a) and (b), respectively. For surface source, it excites more SIBIMs and spectral peak concentrates in D0 not in D1, so τ is lower. While the underwater source excites more TMs and BIMs, so τ is relatively higher, which can be distinguished from surface source.

Fig. 9
figure 9

Ĩ (κ, t) (a) for surface source and (b) for underwater source with subspaces superimposed on

Full size image

3 Simulations and Experimental Results

3.1 Experiment Review

An acoustics experiment was conducted in the deep-water area of the SCS during September 2022. The objective is to study characteristics of the sound propagation in deep water. The experiment layout is displayed in Fig. 10. The 74 wide band signals (WBSs) charged with 100 g or 1000 g TNT are dropped from Research Vessel (R/V) at different ranges with the explosion depths are 50 and 200 m, and the signals are received by the HLA placed on the seabed. The SSP and bottom parameters near the HLA are shown in Fig. 2. The HLA is 1.2 km long with receivers spaced 15 m apart and placed at 1750 m on the seabed. The sensitivity for each hydrophone assumed on HLA is −170 dB (reference level is 1 V/μPa), and the sampling rate of hydrophone is 24 kHz. The distance between the source and HLA can be calculated based on their longitude and latitude, which is obtained from the onboard Global Positioning System (GPS). The interference structures of sources at different depths can be obtained through the HLA and are used for subsequent source depth discrimination.

Fig. 10
figure 10

Experimental configuration

Full size image

3.2 Numerical Simulations

According to the previous methodology, we can consider source depth discrimination as a binary classification problem. By comparing the energy ratio calculated from Eq. (34) with a classification threshold ν, one can get the decision result. To distinguish between two different source depths in the experiment, we choose discrimination depth zlim = 65 m, and there are two possibilities for judgment,

$$ \begin{gathered} H_0 :0 < z_s \le z_{lim} \, (if \, \tau \le \nu ) \hfill \\ H_1 :z_s > z_{lim} \, (if \, \tau > \nu ) \hfill \\ \end{gathered} $$
(35)

where H0 and H1 are the corresponding results for surface source and underwater source, respectively. The performance of a binary problem can be evaluated by calculating the detection probability PD and false alarm probability PFA of the classifier. Here, PD is the probability of classifying an underwater source to H1, and PFA is the probability of classifying a surface source to H1. We select the decision threshold based on the PFA and PD from simulation analysis. The parameters of the HLA in simulation are consistent with the experiment. For the source, the bandwidth B = 20 Hz and the central frequency f0 = 355 Hz. Then, calculate sound field for range from 1 to 50 km with 0.5 km steps, and for depth from 1 to 300 m with 1 m steps. Use the presented method to get energy ratio τ and finally obtain the receiver operating characteristic (ROC) curve, as shown by the black line in Fig. 11(a). For the target false alarm probability PFA = 10%, the corresponding decision threshold ν is 0.642. After getting the appropriate threshold, one can achieve source depth discrimination by using Eq. (35). Figure 11(b) displays the classification results of simulation data. The sources classified under H1 are shown in black color, whereas the ones associated with H0 are in white. We should note that the method cannot effectively distinguish between two source depths at ranges of 0–5 km, 12–22 km and 36–39 km. This phenomenon can be explained through sound ray diagrams. According to Snell’s law, the critical grazing angle α0 of the refracted sound ray satisfies,

$$ \alpha_0 = \arccos \left( {\frac{c_0 }{{c_{surface} }}} \right) $$
(36)

where c0 is the sound velocity at source. Then, we can obtain that α0 gradually increases with source depth from 1 to 300 m, so that the range of distances where refracted sound rays can be received gradually increases. We consider trace of refracted sound ray for zs = 300 m calculated by BELLHOP code [28], as shown in Fig. 12. Obviously, the array does not receive refracted sound rays at distances of 0–5 km, 12–22 km and 36–39 km. So, for all sources with depth from 1 to 300 m, the HLA at these distances cannot receive refracted sound rays. Therefore, SIBIMs dominate receiving signal for both surface and underwater source, resulting in poor classification performance. Remove these ranges and recalculate the ROC curve, as shown by blue line in Fig. 11(a). It can be seen that the performance of the method has improved, and the detection probability and decision threshold are 71.46% and 0.654. Besides above distances, the performance at 26–28 km is also poor. At these distances, although the HLA can receive BIM or TM, SIBIMs have main contribution to the signal. Therefore, the energy ratios are lower than the threshold at different depths, making it difficult to distinguish at this range.

Fig. 11
figure 11

(a) The ROC curve of simulation results. The black line is calculated for the whole propagation path, while blue line is calculated for the distances where can receive refracted sound rays. (b) Classification results of simulation data using decision threshold with a false alarm probability of 10%. The sources classified under H1 (underwater sources) are shown in black color, whereas the ones associated with H0 (surface sources) are in white. The depth corresponding to the red dashed line is the discrimination depth zlim

Full size image
Fig. 12
figure 12

Surface-refracted-bottom-reflected sound rays for source depth zs = 300 m

Full size image

3.3 Experimental Results

In this section, we validate the effectiveness of the method using data from a SCS experiment. Two signal processing results are shown in Fig. 13, where the first row corresponds to a source at 50-m depth and 9.63-km range, and the second row corresponds to a source at 200-m depth and 9.94-km range. According to the previously proposed method, transform the time-domain signal received by HLA into frequency domain to obtain interference pattern, as shown in Fig. 13(a) and (d). Then, the interference spectrum can be gained by performing 2-D FT on the interference pattern, as shown in 13(b) and (e). Due to the problem of environmental noise during the experiment, the interference spectrum usually has many side lobes, which affects the calculating of energy ratio. The Richardson–Lucy deconvolution algorithm [33] is used for image processing to remove the side lobes and make energy be concentrated in the position of the main lobe. The processed interference spectrum is shown in Fig. 13(c) and (f), leaving only some major spectral peaks. The energy ratios of different modal interference groups for the received signals are calculated by using Eq. (34), and the results are 0.562 (50 m) and 0.733 (200 m), respectively. According to the decision threshold in Sect. 3.2, accurate depth discrimination of two sources can be achieved.

Fig. 13
figure 13

Interference patterns and interference spectrums of experimental data. Panels (a–c) correspond to 50-m source depth and 9.63-km source range. Panels (d–f) correspond to 200-m source depth and 9.94-km source range. Panels (a) and (d) are interference patterns. Panels (b) and (e) are interference spectrums. Panels (c) and (f) are interference spectrums after removing sidelobes

Full size image

Similar processing is performed on other signals, and the final depth discrimination results at different ranges are shown in Fig. 14(a). Similar to the previous simulation analysis, at distances of 0–5 km and 12–22 km, HLA cannot receive refracted sound rays for both sources and the discrimination performance is poor. Figure 14(b) displays the results after removing the above ranges with better classification performance left. Near a range of 25 km, the energy ratio calculated for two source depths is relatively close and smaller than threshold. This is consistent with the analysis of the results in simulation. At other ranges, the depth discrimination can be achieved between two explosion depths, indicating the effectiveness of this method. And the detection probability PD is 76.19% in Fig. 14(b), which is close to the simulation results.

Fig. 14
figure 14

(a) Classification results of experimental data for the whole propagation path. (b) The classification results of experimental data at the distances where refracted sound rays can be received

Full size image

One difference between simulation and experimental results is that the energy ratio of experimental data at 35–39 km is relatively high, as shown in Fig. 15. From numerical simulation analysis, the refracted sound line cannot be received at these distances for both source depths (50 m and 200 m) and SIBIMs dominate receiving signal, as shown in Fig. 16(a) and (b), so the corresponding energy ratio should be near or below the threshold, while the experimental results are opposite. This may be caused by variations in bottom topography. In fact, the water depth in the sea area 40 km away from HLA is 1360 m, so the water depth in actual experimental sea area is not constant. Considering the difference in water depth between the receiving and sending positions, we assume the bottom with a slight slope. The water depth increases linearly from 1360 m at range 0 km to 1760 m at range 40 km. Then recalculate the sound ray trajectory for different source depths, as shown in Fig. 16(c) and (d). Due to the effect of bottom slope, the distances where refracted sound rays can be received move toward the source. For instance, for source depth of 50 m, when the bottom is flat, refracted sound rays is received at distances of 42–48 km. But for the bottom with a slope, this range shifts toward the source and becomes 35–41 km. Therefore, the HLA can receive refracted sound rays at 35–39 km for both surface and underwater source in seabed and the energy ratio increases, being higher than the threshold. This explains why underwater sources at these distances can be identified in experimental data.

Fig. 15
figure 15

Energy ratios of simulations and experiment data at distance from 35 to 39 km for source depths of 50 m and 200 m

Full size image
Fig. 16
figure 16

Sound rays with different source depths and bottom topography. Flat bottom (a) for a surface source zs = 50 m and (b) for an underwater source zs = 200 m. Bottom with a slope (c) for a surface source zs = 50 m and (d) for an underwater source zs = 200 m

Full size image

4 Conclusion and Discussion

This paper reports a method to distinguish the surface source and underwater source based on interference spectrum using a bottom-mounted HLA in deep water with an incomplete channel. Theoretical analysis and simulation results indicate that the interference structure is closely related to the source depth, manifested as difference in peak positions in the interference spectrum. Considering the characteristics of incomplete channel, the normal modes can be divided into TMs, BIMs and SIBIMs. Through using modal classification and dominant mode, the spectral peak can be predicted and further explain the reasons for difference in spectral peaks between different source depths. By defining subspaces of interference spectrum and calculating energy ratio of different modal interference groups to realize depth discrimination. The effectiveness of the proposed depth discrimination method has been validated using numerical simulations and experimental data.

As modal classification is foundation of this method, there is a certain demand for SSP. It is usually required that the SSP has only an extreme value (minimum value) and the sound velocity of seabed is greater than that in seawater, otherwise modal types are not easily divided. Besides, we only discuss the incomplete channel and modal types are TM, BIM and SIBIM. For the complete channel, it is necessary to change the type of mode division, as there is no modal type of BIM in the complete channel. This situation can refer to the modal types in the literature [26]. For some special channels, such as a surface channel, due to its SSP having two channel axes, further research on modal classification is needed.

The proposed method utilizes a bottom-mounted HLA to obtain interference patterns, so the aperture and position of the HLA has an impact on the effectiveness of the method. Because of the large aperture of the long array, an appropriate low-frequency source is needed to ensure the correlation of the received signal and the integrity of the interference spectrum. In addition, as discussed in Sect. 3, it is necessary to place the HLA at a range that can receive the refracted sound rays for receiving TMs or BIMs as much as possible, otherwise the discrimination performance will be poor. From Fig. 12, it can be seen that placing the HLA at a shallower depth can receive more refracted rays, but the difficulty of placement increases accordingly. Therefore, more theoretical and experimental work, including modal classification under other channels and HLA position selection, should be studied in the future to improve the applicability of source depth discrimination method.