MacWilliams Identities of the Linear Codes Over ${\mathbb {F}}_q\times ({\mathbb {F}}_q+v{\mathbb {F}}_q)$

Abstract

Let R be the ${\mathbb {F}}_q$-algebra ${\mathbb {F}}_q\times ({\mathbb {F}}_q+v{\mathbb {F}}_q)$ of order $q^3$ where $v^2=v$ and ${\mathbb {F}}_q$ is a finite field of q elements. We study the MacWilliams identities of the linear codes over R related to complete, Hamming, symmetric, Gray and Lee weight enumerators.

1 Introduction

Since the seminal paper [8] of linear codes over ${\mathbb {Z}}_4$, codes over finite rings have been attracting attention. Linear codes over rings with few elements are already studied much (see for instance [2,3,4, 6, 12]), including linear codes over commutative semisimple rings isomorphic to ${\mathbb {Z}} _{2} \times {\mathbb {Z}} _2$ and ${\mathbb {Z}} _2 \times {\mathbb {Z}}_ 2 \times {\mathbb {Z}}_ 2$ [1, 5, 14]. In [11] we generalize some of the previous papers by studying linear codes over the more general semisimple ring ${\mathbb {F}}_q\times ({\mathbb {F}}_q+v{\mathbb {F}}_q),$ isomorphic to ${\mathbb {F}}_q\times {\mathbb {F}}_q\times {\mathbb {F}}_q,$ where q is any prime power. We study in [11] the standard form of the generator and parity check matrices, free codes and cyclic codes. To reduce its length we skip examining weight enumerators in [11]. Some of the weight enumerators for codes over the rings ${\mathbb {F}}_2\times ({\mathbb {F}}_2+v{\mathbb {F}}_2)$ and ${\mathbb {F}}_q+v{\mathbb {F}}_q$ are studied in [5] and [9], respectively. The aim of the current paper is to study the MacWilliams identities related to almost all frequently used weight enumerators of linear codes over the finite ${\mathbb {F}}_q$-algebra $R:={\mathbb {F}}_q\times ({\mathbb {F}}_q+v{\mathbb {F}}_q)$ where ${\mathbb {F}}_q+v{\mathbb {F}}_q:={\mathbb {F}}_q[v]$ is a ring extension of ${\mathbb {F}}_q$ obtained by adjoining a root v of the polynomial $x^2-x$ not in ${\mathbb {F}}_q$ (i.e., ${\mathbb {F}}_q[v]\cong {\mathbb {F}}_q[x]/(x^2-x)$). Throughout the paper, we let R be the ring ${\mathbb {F}}_q\times ({\mathbb {F}}_q+v{\mathbb {F}}_q)$ and q be a power of any prime. Any R-submodule of $R^n$ is called a linear code over R of length n.

2 Preliminaries

In this section we collect some preliminary results from [11]. The ring R is the direct product of the rings ${\mathbb {F}}_q$ and ${\mathbb {F}}_q[v]:={\mathbb {F}}_q+v{\mathbb {F}}_q,$ where ${\mathbb {F}}_q[v]$ is isomorphic to the ring ${\mathbb {F}}_q[x]/(x^2-x)$ via the ${\mathbb {F}}_q$-linear function mapping v to $x+(x^2-x).$ So, $v^2=v$ in the ring

$$\begin{aligned} {\mathbb {F}}_q[v]=\{b+vc\mid b,c\in {\mathbb {F}}_q\}. \end{aligned}$$

Moreover, ${\mathbb {F}}_q[v]$ is a vector space over ${\mathbb {F}}_q$ with basis $\{1,v\},$ and the multiplication on ${\mathbb {F}}_q[v]$ is extended by linearity so that $(b_1+vc_1)(b_2+vc_2)=b_1b_2+v(b_1c_2+c_1b_2+c_1c_2).$ The ring R is a vector space over ${\mathbb {F}}_q$ of dimension 3, with basis $\{(1,0),(0,1),(0,v)\},$ where ${\mathbb {F}}_q$-action on R is given by $\lambda (a,b+vc)=(\lambda a,\lambda b+v\lambda c).$

For any ring S and positive integer n the Euclidean inner product on $S^n$ is defined to be the map $[{\ },{\ }]_E:S^n\times S^n\rightarrow S$ given by the rule

$$\begin{aligned} [(s_1,s_2,...,s_n),(t_1,t_2,...,t_n)]_E=\sum _{i=1}^ns_it_i \end{aligned}$$

for all $(s_1,s_2,...,s_n),(t_1,t_2,...,t_n)\in S^n.$ If further S has an automorphism of order 2, then we may define a Hermitian inner product on $S^n.$ As $x^2-x$ has two roots v and $1-v$ not in ${\mathbb {F}}_q,$ the ${\mathbb {F}}_q$-linear map $\sigma$ fixing elements of ${\mathbb {F}}_q$ and interchanging v and $1-v$ is an ${\mathbb {F}}_q$-algebra automorphism of ${\mathbb {F}}_q[v]$ of order 2. So $\sigma :{\mathbb {F}}_q[v]\rightarrow {\mathbb {F}}_q[v]$ is given by the rule

$$\begin{aligned} \sigma (b+vc)=b+c-vc \end{aligned}$$

for all $b+vc\in {\mathbb {F}}_q[v].$ Being an analogue of the complex conjugation, $\sigma$ can be used to define a Hermitian inner product over $R^n.$ For any $s=(a,b+vc)\in R$ we let ${\overline{s}}:=(a,\sigma (b+vc))=(a,b+c-vc).$ The Hermitian inner product on $R^n$ is defined to be the map $[{\ },{\ }]_H:R^n\times R^n\rightarrow R$ given by the rule

$$\begin{aligned} [(s_1,s_2,...,s_n),(t_1,t_2,...,t_n)]_H=\sum _{i=1}^ns_i\overline{t_i} \end{aligned}$$

for all $(s_1,s_2,...,s_n),(t_1,t_2,...,t_n)\in R^n.$ For any linear code C over R of length n,  we use the notations $C^{\perp }$ and $C^{*}$ for the duals with respect to the Euclidean and the Hermitian inner products, respectively. Therefore,

$$\begin{aligned} C^{\perp }=\left\{ {\varvec{x}}\in R^n\mid \left[ {\varvec{x}},{\varvec{c}}\right] _E=0_R{\ }\forall {\varvec{c}}\in C\right\} ,{\ }{\ }C^{*}=\left\{ {\varvec{x}}\in R^n\mid \left[ {\varvec{x}},{\varvec{c}}\right] _H= 0_{R} {\ }\forall {\varvec{c}}\in C\right\} . \end{aligned}$$

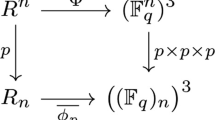
We consider the following two Gray maps $\phi ,\psi :R\rightarrow {\mathbb {F}}_q^3,$ allowing us to obtain q-ary linear codes of length 3n from linear codes over R of length n,  given by

$$\begin{aligned} \phi (a,b+vc)=(a,b,b+c),{\ }{\ }{\ }{\ }\psi (a,b+vc)=\left[ \begin{array}{ccc} a & b & b+c \\ \end{array} \right] \varvec{A^T} \end{aligned}$$

for any $(a,b+vc)\in R$ where

$$\begin{aligned} {\varvec{A}}=\left[ \begin{matrix} 1& 1& 0 \\ s& s& 1\\ -1& 0& s\\ \end{matrix} \right] {\ }(\text {if }p\not \equiv 3\text { mod 4}),{\ }{\ }{\ }{\ }{\ }{\varvec{A}}=\left[ \begin{matrix} 0& -1& 1 \\ -l& t& t\\ t& l& l\\ \end{matrix} \right] {\ }(\text {if }p\equiv 3\text { mod 4}), \end{aligned}$$

p is the characteristic of ${\mathbb {F}}_q,$ and s, l, t are any elements of the prime subfield ${\mathbb {Z}} _p$ of ${\mathbb {F}}_q$ satisfying $s^2=l^2+t^2=-1.$ See [11, Remark 2.4]. For any tuple ${\varvec{x}}=(x_1,x_2,...,x_n)$ and any i,  we let $({\varvec{x}})_i$ be the i th component $x_i$ of ${\varvec{x}}.$ Any element

$$\begin{aligned} {\varvec{x}}=(x_1,x_2,...,x_n)=\big ((a_1,b_1+vc_1),(a_2,b_2+vc_2),...,(a_n,b_n+vc_n)\big ) \end{aligned}$$

of $R^n$ is written simply as ${\varvec{x}}=({\varvec{a}},{\varvec{b}}+v{\varvec{c}})$ where ${\varvec{a}},{\varvec{b}},{\varvec{c}}\in {\mathbb {F}}_q^n$ are given by $({\varvec{a}})_i=a_i,({\varvec{b}})_i=b_i$ and $({\varvec{c}})_i=c_i$ for each i. We let $\Phi ,\Psi : R^n \rightarrow {\mathbb {F}}_q^{3n}$ be the following maps obtained from $\phi ,\psi$ as

$$\begin{aligned} \Phi ({\varvec{x}})=({\varvec{a}},{\varvec{b}},{\varvec{b}}+{\varvec{c}}),{\ }{\ }{\ }\Psi ({\varvec{x}})=(\varvec{a'},\varvec{b'},\varvec{c'}) \end{aligned}$$

for any ${\varvec{x}}=(x_1,x_2,...,x_n)=({\varvec{a}},{\varvec{b}}+v{\varvec{c}})\in R^n$ where $\left( (\varvec{a'})_i,(\varvec{b'})_i,(\varvec{c'})_i\right) =\psi (x_i).$

Remark 1

([11])

• (a) The maps $\phi :R\rightarrow {\mathbb {F}}_q^3$ and $\Phi :R^n\rightarrow {\mathbb {F}}_q^{3n}$ are both ring isomorphisms and ${\mathbb {F}}_q$-module isomorphisms.

• (b) The maps $\psi :R\rightarrow {\mathbb {F}}_q^3$ and $\Psi :R^n\rightarrow {\mathbb {F}}_q^{3n}$ are ${\mathbb {F}}_q$-module isomorphisms.

• (c) For any linear code C over R, 

  $$\begin{aligned} & \Phi (C^{\perp })=\Phi (C)^{\perp },\; \; \Psi (C^{*})=\Psi (C)^{\perp },\; \; (C^{\perp })^{\perp }=C,\; \; (C^{*})^{*}=C, \\ & (C^{\perp })^{*}=(C^{*})^{\perp },\; \; C^{\perp }=\sigma _n (C^{*}) =\sigma _n (C)^{*}, \; \; C^{*}=\sigma _n (C^{\perp })=\sigma _n (C)^{\perp }, \end{aligned}$$

  where the ${\mathbb {F}}_q$-algebra automorphism $\sigma _n:R^n\rightarrow R^n$ is given for any $(x_1,...,x_n)\in R^n$ by $\sigma _n(x_1,...,x_n)=\left( \overline{x_1},...,\overline{x_n}\right) .$

3 MacWilliams Identities

In this section we consider several weight enumerators of a linear code C over R and relate them to the weight enumerators of the dual of C.

One of the classic proofs of the MacWilliams identities for linear codes over finite fields uses group characters and the discrete Fourier transformation [7]. Let S be a finite commutative ring with unity. Assume that there is a group homomorphism $\chi :(S,+)\rightarrow {\mathbb {C}}^{\times }$ whose kernel does not contain any nonzero ideal of S. In this case, the aforementioned classic proof of the MacWilliams identities works almost verbatim for linear codes over S and shows that there are similar identities for linear codes over S. For the convenience of the reader we collect below key results that make the classic proof works over S. Its proof is almost same with the classic proof and hence omitted.

Remark 3.1

Let S be a ring satisfying the conditions in the above paragraph. Let C be a linear code over S of length n. Then,

• (a) $\sum _{a\in I}\chi (a)=0$ for any nonzero ideal I of S.

• (b) $\sum _{a\in I}\chi (sa)=0$ for any nonzero ideal I of S and any $s\in S$ that is not in the annihilator of I in S.

• (c) For any ${\varvec{w}}\notin C^{\perp },$ the set $J=\left\{ [{\varvec{v}},{\varvec{w}}]_E\mid {\varvec{v}}\in C\right\}$ is a nonzero ideal of S and

  $$\begin{aligned} \sum _{{\varvec{v}}\in C }\chi \left( [{\varvec{v}},{\varvec{w}}]_E\right) =k\sum _{a\in J }\chi \left( a\right) =0 \end{aligned}$$

  where k is an integer, $[{\ },{\ }]_E$ is the Euclidean inner product on $S^n$ and $C^{\perp }$ is the Euclidean dual of C.

• (d)
  $$\begin{aligned} \sum _{{\varvec{v}}\in C}{\hat{f}}({\varvec{v}})=|C|\sum _{{\varvec{w}}\in C^{\perp }}f({\varvec{w}}) \end{aligned}$$

  for any vector space V over ${\mathbb {C}}$ and for any function $f:S^n\rightarrow V$ where

  $$\begin{aligned} {\hat{f}}({\varvec{v}})=\sum _{{\varvec{w}}\in S^n}\chi \left( [{\varvec{v}},{\varvec{w}}]_E\right) f({\varvec{w}}). \end{aligned}$$

For instance, if we let V be the set of polynomials over ${\mathbb {C}}$ in the commuting variables X and Y and let $f({\varvec{v}})=X^{w_H({\varvec{v}})}Y^{n-{w_H({\varvec{v}})}}$ where $w_H({\varvec{v}})$ denotes the Hamming weight, then we see that ${\hat{f}}({\varvec{v}})=(Y-X)^{w_H({\varvec{v}})}\left( Y+(|S|-1)X\right) ^{n-{w_H({\varvec{v}})}}$ and Remark 3.1 shows that the MacWilliams identity for the Hamming weight distribution remains true for linear codes over S.

We observe below that our ring R satisfies the conditions on S. The rings with the conditions on S are called finite commutative Frobenius rings and the group homomorphism $\chi$ is called a generating character of the ring. More generally, for finite rings not necessarily commutative, it is proved in [13] that the MacWilliams identities can be extended to linear codes over the ring if and only if the ring is Frobenius. In this general case, one needs to change duals with certain one sided duals and annihilators. Being direct product of finite fields, it is well known that R is a finite Frobeniuos ring whose generating character is the product of generating characters of the field.

As our ring R is commutative, the results of this section may be justified by Remark 3.1 without consulting [13]. Although most of the results of this section may be seen as consequences of those of [13], they are not immediate consequences. The results of [13] depend on an ordering of the elements of the ring and we here need to choose an appropriate ordering of the elements of R to prevent our results being cumbersome..

Throughout this section, $[{\ },{\ }]$ is the Euclidean inner product on $R^n$, $w({\varvec{v}})$ is the Hamming weight of ${\varvec{v}}\in R^n,$ and $q=p^m$ where p is a prime. We consider the trace map $\textrm{Tr}:{\mathbb {F}}_q\rightarrow {\mathbb {Z}} _p$ of the field extension ${\mathbb {Z}} _p\subseteq {\mathbb {F}}_q.$ It is well known in the case of finite extensions of finite fields that $\textrm{Tr}$ is an onto ${\mathbb {Z}} _p$-linear transformation and

$$\begin{aligned} \textrm{Tr}(\alpha )=\alpha +\alpha ^p+\alpha ^{p^2}+\cdots +\alpha ^{p^{m-1}} \end{aligned}$$

for any $\alpha \in {\mathbb {F}}_q.$ See for instance [10] for the properties of the trace function. We define

$$\begin{aligned} \chi :R\rightarrow {\mathbb {C}} ^{\times },{\ }{\ }{\ }{\ }\chi \left( a,b+vc\right) =\zeta ^{\textrm{Tr}(a+2b+c)} \end{aligned}$$

where $\zeta =e^{2\pi i/p}$ is a primitive p th root of unity in ${\mathbb {C}}.$

Remark 3.2

The ring R is a Frobenius ring and $\chi$ is a generating character of R (i.e., $\chi :(R,+)\rightarrow {\mathbb {C}} ^{\times }$ is a group homomorphism and the kernel of $\chi$ does not contain a nonzero ideal of R).

Proof

Let $\chi _F:{\mathbb {F}}_q\rightarrow {\mathbb {C}} ^{\times }$ be the map given for any $\alpha \in {\mathbb {F}}_q$ by $\chi _F(\alpha )=\zeta ^{\textrm{Tr}(\alpha )}.$ As $\textrm{Tr}$ is additive, $\chi _F:({\mathbb {F}}_q,+)\rightarrow {\mathbb {C}} ^{\times }$ is a group homomorphism. As $\textrm{Tr}$ is onto, $\chi _F$ is nontrivial so that the only nonzero ideal ${\mathbb {F}}_q$ of the field ${\mathbb {F}}_q$ is not in the kernel of $\chi _F.$ Hence, $\chi _F$ is a generating character of ${\mathbb {F}}_q.$ We easily see that the map $\prod \chi _F:{\mathbb {F}}_q\times {\mathbb {F}}_q\times {\mathbb {F}}_q\rightarrow {\mathbb {C}} ^{\times },$ given by $(\prod \chi _F)(a,b,c)=\chi _F(a)\chi _F(b)\chi _F(c)$ is a group homomorphism. Note that $\chi =(\prod \chi _F)\circ \phi .$ As $\phi$ is a ring homomorphism, $\chi$ is a group homomorphism. Suppose for a moment that there is a nonzero ideal I of R in the kernel of $\chi .$ As ideals of a direct product of rings are direct product of ideals, $\phi (I)=A\times B\times C$ for some ideals A, B, C of ${\mathbb {F}}_q$ that are not all zero. Assume for instance $B\ne 0.$ Then $B={\mathbb {F}}_q.$ As $\textrm{Tr}$ is onto, there is a $b\in B$ such that $\textrm{Tr}(b)=1.$ Now $r=(0,b-vb)=\phi ^{-1}(0,b,0)\in I$ but $\chi (r)=\zeta \ne 1.$ $\square$

For any $r\in R$ and any ${\varvec{v}}=(v_1,v_2,...,v_n)\in R^n$ we let $c_r({\varvec{v}})=|\{i\mid v_i=r\} |$ be the number of components of ${\varvec{v}}$ equal to r. Note that $n-c_0({\varvec{v}})=w({\varvec{v}}).$ For any linear code C over R of length n the complete weight enumerator $KW _C\left( (Z_r)_{r\in R}\right)$ of C is the polynomial

$$\begin{aligned} KW _C\left( (Z_r)_{r\in R}\right) =\sum _{{\varvec{c}}\in C}\prod _{r\in R}Z_r^{c_r({\varvec{c}})}=\sum _{{\varvec{c}}\in C}\prod _{i=1}^nZ_{c_i} \end{aligned}$$

over ${\mathbb {C}}$ with $|R|$ variables $Z_r$ indexed by the elements r of R where $c_i$ denotes the i th component of ${\varvec{c}}.$ The following result is a special case of [13, Theorem 8.1], and it can also be proved by using Remark 3.1 (with $S=R,$ V is the space of polynomials over ${\mathbb {C}}$ in the commuting variables $Z_{r_i}$ and $f({\varvec{v}})=\prod _{i=1}^nZ_{v_i}$).

Theorem 3.3

[13] Let C be a linear code over R of length n and let $R=\{r_1,r_2,...,r_s\}$ be an ordering of the elements of R. Then,

$$\begin{aligned} |C|KW _{C^{\perp }}\left( Z_{r_1},Z_{r_2},...,Z_{r_s}\right) =KW _{C}\left( T_{r_1},T_{r_2},...,T_{r_s}\right) \end{aligned}$$

where

$$\begin{aligned} \left[ \begin{array}{c} T_{r_1},T_{r_2},...,T_{r_s} \\ \end{array} \right] =\left[ \begin{array}{c} Z_{r_1},Z_{r_2},...,Z_{r_s} \\ \end{array} \right] \varvec{M^T} \end{aligned}$$

and ${\varvec{M}}$ is the $|R|\times |R|$ matrix over ${\mathbb {C}}$ whose rows and columns are indexed by the elements of R in the given order and whose $(r_i,r_j)$ th entry is $\chi (r_ir_j).$

By identifying certain variables $Z_r$ in the complete weight enumerator we may obtain other weight enumerators. Let $r_1=0.$ Letting all the variables $Z_r$ indexed by nonzero elements $r\in R$ be X and letting $Z_0$ be Y we obtain the Hamming weight enumerator $HW_C(X,Y)$ of C. Therefore,

$$\begin{aligned} HW_C(X,Y)=KW_C(Y,X,X,...,X)=\sum _{{\varvec{c}}\in C}X^{w({\varvec{c}})}Y^{n-w({\varvec{c}})}. \end{aligned}$$

Using part (b) of Remark 3.1 (with $S=I=R$) and Theorem 3.3, we can justify the following.

Corollary 3.4

[13] Let C be a linear code over R of length n. Then

$$\begin{aligned} |C|HW _{C^{\perp }}\left( X,Y\right) =HW _{C}\big (Y-X,Y+(|R|-1)X\big ). \end{aligned}$$

Ordering the elements of R in a certain way we may force the matrix ${\varvec{M}}$ in Theorem 3.3 to be simpler to handle. We first order the elements of ${\mathbb {F}}_q^3$ and use the bijection $\phi :R\rightarrow {\mathbb {F}}_q^3$ to order the elements of R so that $\phi$ is order preserving. Fix an ordering $<_F$ of the elements of ${\mathbb {F}}_q=\{u_0,u_1,...,u_k\}$ such that $u_0=0_{{\mathbb {F}}_q}.$ For simplicity of notations we let ABC be the subset $A\times B\times C$ of ${\mathbb {F}}_q^3$ for any nonempty subsets A, B, C of ${\mathbb {F}}_q.$ If one of A, B, C is $\{0_{{\mathbb {F}}_q}\}$ then we write it in ABC as 0. Let $U={\mathbb {F}}_q-\{0\}.$ Using this notation of subsets of ${\mathbb {F}}_q^3$ we may partition ${\mathbb {F}}_q^3$ into the following mutually disjoint subsets

$$\begin{aligned} & S_1=000,{\ }S_2=00U,{\ }S_3=0U0,{\ }S_4=0UU, \\ & {\ }S_5=U00,{\ }S_6=U0U,{\ }S_7=UU0,{\ }S_8=UUU \end{aligned}$$

We first assume that, for any $i<j,$ every element of $S_i$ is smaller than every element of $S_j.$ To order the elements in an $S_i$ we use the dictionary order induced by the order on ${\mathbb {F}}_q.$ That is, for instance, for any $(f_1,f_2,f_3),(g_1,g_2,g_3)\in S_8$ we let $(f_1,f_2,f_3)\le (g_1,g_2,g_3)$ if and only if

$$\begin{aligned} & f_1<_Fg_1{\ }{\ }{\ }{\ }\text {or}{\ }{\ }{\ }{\ }(f_1=g_1{\ }\text {and}{\ } f_2<_Fg_2 ){\ }{\ }{\ }{\ }\text {or}{\ }{\ }{\ }{\ } \\ & (f_1=g_1{\ }\text {and}{\ }f_2=g_2{\ }\text {and}{\ } f_3\le _Fg_3 ). \end{aligned}$$

We now order the elements of R such that $\phi$ is order preserving where the order on ${\mathbb {F}}_q^3$ is the order described above.

Example 3.5

Let $q=3.$ Suppose we order ${\mathbb {F}}_q$ as ${\mathbb {F}}_q=\{0,2,1\}.$ Then $U=\{2,1\}$ and we order the elements of $S_i$ as

$$\begin{aligned} & S_1=\{000\},{\ }S_2=\{002,001\},{\ }S_3=\{020,010\},{\ }S_4=\{022,021,012,011\},{\ } \\ & S_5=\{200,100\}, S_6=\{202,201,102,101\},{\ }S_7=\{220,210,120,110\}, \\ & S_8=\{222,221,212,211,122,121,112,111\}. \end{aligned}$$

Writing elements of $S_1,S_2,...,S_8$ together in the given orders we order the elements of ${\mathbb {F}}_q^3.$ The preimages under $\phi$ of the elements in this ordering of ${\mathbb {F}}_q^3$ is the required order of the elements of R.

Using the order on R we may write the matrix ${\varvec{M}}$ in Theorem 3.3 as a $8\times 8$ block matrix. We first need a simple result. Recall that if ${\varvec{A}}$ is an $m \times n$ matrix and ${\varvec{B}}$ is a $p \times q$ matrix, then the Kronecker product ${\varvec{A}} \otimes {\varvec{B}}$ is the $pm \times qn$ block matrix given by

$$\begin{aligned} {\varvec{A}}\otimes {\varvec{B}}=\begin{bmatrix} a_{11}{\varvec{B}} & \dots & a_{1n}{\varvec{B}}\\ \vdots & \ddots & \vdots \\ a_{m1}{\varvec{B}} & \dots & a_{mn}{\varvec{B}} \end{bmatrix}. \end{aligned}$$

For any matrix ${\varvec{A}}$ we let $a_{i,j}$ be the (i, j) the entry of ${\varvec{A}}.$

Lemma 3.6

Let I, J, K, L be finite ordered sets, and let ${\varvec{A}}$ be an $|I |\times |J |$ matrix over ${\mathbb {C}}$ and ${\varvec{B}}$ be a $|K|\times |L |$ matrix over ${\mathbb {C}}.$ Assume that the rows and the columns of ${\varvec{A}}$ and ${\varvec{B}}$ are indexed by the elements of the ordered sets I, J, K, L. Let C be a $|I\times K|\times |J\times L |$ matrix whose rows and columns are indexed by the elements ordered sets $I\times K$ and $J\times L$ where the orders on $I\times K$ and $J\times L$ are the dictionary orders induced by the orders on I, J, K, L. If $c_{(i,k),(j,l)}=a_{i,j}b_{k,l}$ for all $(i,j)\in I\times J$ and $(k,l)\in K\times L$ then ${\varvec{C}}={\varvec{A}}\otimes {\varvec{B}}.$

Proof

Suppose that the ordered sets I, J, K, L are

$$\begin{aligned} I=\{i_1,i_2,...,i_a\},{\ }{\ }{\ }J=\{j_1,j_2,...,j_b\},{\ }{\ }{\ }K=\{k_1,k_2,...,k_c\},{\ }{\ }{\ }L=\{l_1,l_2,...,l_d\}. \end{aligned}$$

Writing the indexes of its rows and columns outside of the matrix we easily see that ${\varvec{C}}$ is given by

$\square$

Proposition 3.7

Assume the notations and the order on R fixed after Corollary 3.4. Let ${\varvec{A}}$ be the $k\times k$ matrix over ${\mathbb {C}}$ whose rows and columns are indexed by the elements of the ordered set $U=\{u_1,u_2,...,u_k\}$ and whose $(u_i,u_j)$ th entry is $\chi _F(u_iu_j)=\zeta ^{\textrm{Tr}(u_iu_j)}.$ Then the matrix ${\varvec{M}}$ in Theorem 3.3 becomes

where $\varvec{\mathbbm {1}}$’s denote the matrices of appropriate sizes all of whose entries are 1 and where we write the sets $S_i$ instead of $\phi ^{-1}(S_i)$ to label the rows and columns for simplicity of notations. More practically, for any $E,F,G,H,K,L\in \{0,U\},$ the block of ${\varvec{M}}$ corresponding to $EFG\times HKL$ is the matrix $[EH]\otimes [FK]\otimes [GL]$ where

$$\begin{aligned} [00]=1,{\ }{\ }{\ }[0U]=\varvec{\mathbbm {1}}_{1\times k},{\ }{\ }{\ }[U0]=\varvec{\mathbbm {1}}_{k\times 1},{\ }{\ }{\ }[UU]={\varvec{A}}. \end{aligned}$$

Proof

We justify it only for one of 64 blocks of ${\varvec{M}}.$ Consider for instance the block ${\varvec{B}}$ corresponding to $0UU\times UU0.$ By the definition of ${\varvec{M}}$ the entries of ${\varvec{B}}$ are $\chi (r_ir_j)$ where $\phi (r_i)\in 0UU$ and $\phi (r_j)\in UU0.$ Therefore, $\chi (r_ir_j)=\chi _F(0\lambda )\chi _F(\alpha \mu )\chi _F(\beta 0)=1\chi _F(\alpha \mu )1$ where $\phi (r_i)=(0,\alpha ,\beta )\in 0UU$ and $\phi (r_j)=(\lambda ,\mu ,0)\in UU0.$ Let $\varvec{\mathbbm {1}} _{1\times k}$ be the $|0|\times |U |$ matrix all of whose entries are 1 and $\varvec{\mathbbm {1}} _{k\times 1}$ be the $|U |\times |0 |$ matrix all of whose entries are 1 where their rows and columns are indexed by the elements of the ordered sets 0 and U. As the rows and columns of ${\varvec{B}}$ are indexed by the elements of the ordered sets 0UU and UU0 and as $b_{(0,\alpha ,\beta ),(\lambda ,\mu ,0)}=\chi (r_ir_j)=\mathbbm {1} _{0,\lambda }a_{\alpha ,\mu }\mathbbm {1} _{\beta ,0},$ Lemma 3.6 implies that ${\varvec{B}}=\varvec{\mathbbm {1}} _{1\times k}\otimes {\varvec{A}}\otimes \varvec{\mathbbm {1}} _{k\times 1}.$ The other blocks can be found similarly where we also use the equity $\varvec{\mathbbm {1}}\otimes \varvec{\mathbbm {1}} =\varvec{\mathbbm {1}}$ to simplify the blocks. $\square$

Example 3.8

Let $q=2$ and $C=\left<(1,1+v)(1,v),(1,0)(0,v)\right>,$ which is a linear code over R of length 2. The elements of R ordered as explained above are

$$\begin{aligned} R=\{r_1,r_2,...,r_8\}=\{(0,0),(0,v),(0,1+v),(0,1),(1,0),(1,v)(1,1+v),(1,1) \}. \end{aligned}$$

We easily find the elements of C and its Euclidean dual $C^{\perp }$ as follows

$$\begin{aligned} C=&\{(1,0)(1,v),(1,0)(1,0),(1,0)(0,v),(1,0)(0,0),(1,1+v)(1,v), (1,1+v)(1.0), \\ &(1,1+v),(0,v),(1,1+v)(0,0),(0,0)(1,v),(0,0)(1,0), (0,0)(0,v),(0,0)(0,0), \\ &(0,1+v)(1,v),(0,1+v)(1,0), (0,1+v)(0,v),(0,1+v)(0,0)\} \\ C^{\perp }&=\{(0,0)(0,0),(0,v)(0,1+v),(0,v)(0,0),(0,0)(0,1+v) \}. \end{aligned}$$

Letting $x_i=Z_{r_i}$ we see by the definition that the complete weight enumerators of C and $C^{\perp }$ are

$$\begin{aligned} & KW_C(x_1,x_2,x_3,x_4,x_5,x_6,x_7,x_8)=x_1^2+x_1x_2+x_1x_3+2x_1x_5+x_1x_6+x_1x_7 \\ & +x_2x_3+ x_2x_5+x_2x_7+x_3x_5+x_3x_6+x_5^2+x_5x_6+x_5x_7+x_6x_7, \\ & KW_{C^{\perp }}(x_1,x_2,x_3,x_4,x_5,x_6,x_7,x_8)=x_1^2+x_1x_2+x_1x_4+x_2x_3. \end{aligned}$$

The generating character of R is given by $\chi \left( a,b+vc\right) =(-1) ^{ a+2b+c}=(-1) ^{ a+c},$ and the matrix ${\varvec{M}}$ in Theorem 3.3 becomes

$$\begin{aligned} {\varvec{M}}=\left[ \begin{matrix} 1& 1& 1& 1& 1& 1& 1& 1 \\ 1& 1& -1& -1& 1& 1& -1& -1\\ 1& -1& -1& 1& 1& -1& -1& 1\\ 1& -1& 1& -1& 1& -1& 1& -1\\ 1& 1& 1& 1& -1& -1& -1& -1\\ 1& 1& -1& -1& -1& -1& 1& 1\\ 1& -1& -1& 1& -1& 1& 1& -1\\ 1& -1& 1& -1& -1& 1& -1& 1 \end{matrix} \right] . \end{aligned}$$

Now one may easily check that the MacWilliams identity

$$\begin{aligned} 16KW_{C^{\perp }}(x_1,x_2,x_3,x_4,x_5,x_6,x_7,x_8)=KW _{C}(y_1,y_2,y_3,y_4,y_5,y_6,y_7,y_8) \end{aligned}$$

in Theorem 3.3 related to complete weight enumerator is satisfied where $\left[ \begin{array}{c} y_1,y_2,...,y_8 \end{array} \right] =\left[ \begin{array}{c} x_1,x_2,...,x_8 \end{array} \right] \varvec{M^T}.$

Example 3.9

Assume the notations of Example 3.8. It follows from the definition that the Hamming weight enumerators are

$$\begin{aligned} HW_C(X,Y)=Y^2+6XY+9X^2, {\ }{\ }{\ }{\ } HW_{C^{\perp }}=Y^2+2XY+X^2. \end{aligned}$$

Now one may easily check that the MacWilliams identity

$$\begin{aligned} 16HW_{C^{\perp }}(X,Y)=HW_C(Y-X,Y+7X) \end{aligned}$$

in Corollary 3.4 is satisfied.

If a fixed coordinate of each codeword of a code is multiplied by a unit, then we get a monomially equivalent code. Therefore, it is reasonable to identify the variables $Z_r,Z_s$ in the complete weight enumerator whenever r is a unit multiple of s. The resulting weight enumerator is called the symmetrized weight enumerator. If we consider being a unit multiple of each other as a relation on R,  then it will be an equivalence relation whose equivalence classes are the sets $\phi ^{-1}(S_1),\phi ^{-1}(S_2),...,\phi ^{-1}(S_8).$ Denoting by $X_i$ each variable $Z_r$ with $\phi (r)\in S_i$ in the complete weight enumerator of a linear code C over R we obtain the symmetrized weight enumerator $SW_C(X_1,X_2,...,X_8)$ of C. Therefore,

$$\begin{aligned} SW_C(X_1,X_2,...,X_8)=KW_C(X_1,X_2,...,X_2,...,X_8,....,X_8)=\sum _{{\varvec{c}}\in C}\prod _{i=1}^8X_i^{w_i^{+}({\varvec{c}})} \end{aligned}$$

where $w_i^{+}({\varvec{c}})=|\{j\mid \phi (c_j)\in S_i\}|.$ If we choose one element $r_i$ from each $\phi ^{-1}(S_i),$ then $w_i^{+}({\varvec{c}})$ is the number of coordinates $c_j$ of ${\varvec{c}}$ that is a unit multiple of the element $r_i.$ In the definition of $SW_C$ above each variable $X_i$ occurs $|S_i |$ times in $KW_C.$ To simplify the notations we use the vector notation $\varvec{X_i}$ to denote $X_i,X_i,...,X_i$ ($|S_i |$ times). Therefore, $SW_C(X_1,X_2,...,X_8)=KW_C(X_1,\varvec{X_2},...,\varvec{X_8}).$

Corollary 3.10

Let C be a linear code over R of length n. Then

$$\begin{aligned} |C|SW _{C^{\perp }}\left( X_1,X_2,...,X_8\right) =SW _{C}\left( T_1,T_2,...,T_8\right) \end{aligned}$$

where $k=q-1$ and

Proof

It is clear from its definition that if the sum of each row of a matrix U is u and the sum of each row of a matrix V is v,  then the sum of each row of the matrix $U\otimes V$ is uv. It follows from part (b) of Remark 3.1 that the sum of each row of the matrix ${\varvec{A}}$ in Proposition 3.7 is $-\chi _F(su_0)=-\chi _F(0)=-1.$ Consider the matrix ${\varvec{M}}$ in Proposition 3.7. It has 64 blocks and we see that for any block the sum of each row is the same and the sum can be calculated easily. Consider for instance the block $\varvec{\mathbbm {1}}_{1\times k}\otimes {\varvec{A}}\otimes \varvec{\mathbbm {1}}_{k\times 1}$ corresponding to $0UU\times UU0.$ The sum of each row of this block is $(k)(-1)(1)=-k.$ We may find the row sums of each block similarly. By Theorem 3.3

$$\begin{aligned} |C|SW _{C^{\perp }}\left( X_1,X_2,...,X_8\right) =&|C |KW_{C^{\perp }}(X_1,{\varvec{X}}_2,...,{\varvec{X}}_8) \\ =&KW _{C}\left( T_1,T_{21},...,T_{2k},...,T_{81},...,T_{8k^3}\right) \\&\text {where} \left[ \begin{array}{c} T_1,T_{21},...,T_{2k},...,T_{81},...,T_{8k^3} \\ \end{array} \right] =\left[ \begin{array}{c} X_1,X_2,....,X_2,....,X_8,....,X_8 \\ \end{array} \right] \varvec{M^T}. \end{aligned}$$

Note first that $T_{21}=\cdots =T_{2k},$...., $T_{81}=\cdots =T_{8k^3}$ because for any block the sum each row is the same. Therefore,

$$\begin{aligned} |C|SW _{C^{\perp }}\left( X_1,X_2,...,X_8\right) =SW _{C}\left( T_1,T_2,...,T_8\right) \end{aligned}$$

where $T_2=T_{21},$..., $T_8=T_{81}.$ Finding the row sums of each block of M we easily find the required matrix relating $X_1,...,X_8$ and $T_1,,...,T_8.$ $\square$

We may also want to identify the variables $Z_r,Z_s$ in the complete weight enumerator whenever $\phi (r),\phi (s)\in {\mathbb {F}}_q^3$ have the same Hamming weights. The resulting weight enumerator is called the Gray weight enumerator. Considering the Hamming weights of elements of $S_i$ we see that the Gray weight enumerator can be obtained from the symmetric weight enumerator by substituting $Y_0=X_1,$ $Y_1=X_2=X_3=X_5,$ $Y_2=X_4=X_6=X_7$ and $Y_3=X_8.$ Therefore, the Gray weight enumerator of a linear code C over R of length n is defined to be

$$\begin{aligned} GW_C(Y_0,Y_1,Y_2,Y_3)=SW_C(Y_0,Y_1,Y_1,Y_2,Y_1,Y_2,Y_2,Y_3)=\sum _{{\varvec{c}}\in C}\prod _{i=0}^3Y_i^{w_i(\phi ({\varvec{c}}))} \end{aligned}$$

where $w_i(\phi ({\varvec{c}}))=|\{ j\mid w_H(\phi (c_j))=i \}|$ is the number of components $c_j\in R$ of ${\varvec{c}}$ such that $\phi (c_j)\in {\mathbb {F}}_q^3$ has Hamming weight i. Note that monomially equivalent linear codes over R must have the same Gray enumerators.

Corollary 3.11

Let C be a linear code over R of length n. Then

$$\begin{aligned} |C|GW _{C^{\perp }}\left( Y_0,Y_1,Y_2,Y_3\right) =GW _{C}\left( T_0,T_1,T_2,T_3\right) \end{aligned}$$

where $k=q-1$ and

$$\begin{aligned} \left[ \begin{array}{c} T_{0}\\ T_{1}\\ T_{2} \\ T_{3} \\ \end{array} \right] =\left[ \begin{array}{cccc} 1 & 3k & 3k^2 & k^3 \\ 1 & 2k-1& k^2-2k& -k^2 \\ 1 & k-2 & 1-2k & k \\ 1 & -3 & 3 & -1 \\ \end{array} \right] \left[ \begin{array}{c} Y_{0}\\ Y_{1}\\ Y_{2} \\ Y_{3} \\ \end{array} \right] \end{aligned}$$

Proof

Follows from Corollary 3.10. $\square$

Example 3.12

Assume the notations of Example 3.8. As $|R|=8,$ the complete and the symmetric weight enumerators of any linear code over R are the same. It follows from the definition that the Gray weight enumerators are

$$\begin{aligned} & GW_C(Y_0,Y_1,Y_2,Y_3)=Y_0^2+4Y_0Y_1+2Y_0Y_2+4Y_1^2+4Y_1Y_2+Y_2^2, \\ & GW_{C^{\perp }}(Y_0,Y_1,Y_2,Y_3)=Y_0^2+2Y_0Y_1+Y_1^2. \end{aligned}$$

The matrix in Corollary 3.11 becomes

$$\begin{aligned} {\varvec{N}}=\left[ \begin{matrix} 1& 3& 3& 1 \\ 1& 1& -1& -1\\ 1& -1& -1& 1\\ 1& -3& 3& -1\\ \end{matrix} \right] . \end{aligned}$$

Now one may easily check that the MacWilliams identity

$$\begin{aligned} 16GW _{C^{\perp }}\left( Y_0,Y_1,Y_2,Y_3\right) =GW _{C}(T_0,T_1,T_2,T_3) \end{aligned}$$

in Corollary 3.11 is satisfied where $\left[ \begin{array}{c} T_0,T_1,T_2,T_3 \end{array} \right] =\left[ \begin{array}{c} Y_0,Y_1,Y_2,Y_3 \end{array} \right] \varvec{N^T}.$

The Lee weight $w_L({\varvec{c}})$ of any ${\varvec{c}} \in R^n$ is defined to be $w_L({\varvec{c}})=n_1({\varvec{c}})+2n_2({\varvec{c}})+3n_3({\varvec{c}})$ where $n_i({\varvec{c}})=w_i(\phi ({\varvec{c}})).$ The Lee weight enumerator of a linear code C over R is defined to be

$$\begin{aligned} LW_C(X,Y)=\sum _{{\varvec{c}}\in C}X^{w_L({\varvec{c}})}Y^{3n-w_L({\varvec{c}})} \end{aligned}$$

Lemma 3.13

Let C be a linear code over R. Then

$$\begin{aligned} LW_C(X,Y)=GW_C(Y^3,XY^2,X^2Y,X^3). \end{aligned}$$

Proof

For simplicity we write $w_L,n_i,w_i$ for $w_L({\varvec{c}}),n_i({\varvec{c}}),w_i(\phi ({\varvec{c}})).$ Noting that $n_0+n_1+n_2+n_3=n$ and $n_i=w_i,$ we see

$$\begin{aligned} LW_C(X,Y)= & \sum _{{\varvec{c}}\in C}X^{w_L}Y^{3n-w_L} \\= & \sum _{{\varvec{c}}\in C}X^{n_1+2n_2+3n_3}Y^{3n_0+2n_1+n_2}\\= & \sum _{{\varvec{c}}\in C}(Y^3)^{n_0}(XY^2)^{n_1}(X^2Y)^{n_2}(X^3)^{n_3}\\= & GW_C(Y^3,XY^2,X^2Y,X^3) \end{aligned}$$

$\square$

Proposition 3.14

Let C be a linear code over R of length n. Then

$$\begin{aligned} |C|LW_{C^{\perp }}(X,Y)=LW_C(Y-X,Y+kX) \; \text {where} \; k=q-1 \end{aligned}$$

Proof

We will use Lemma 3.13 and Corollary 3.11. Now

$$\begin{aligned} |C|LW_{C^{\perp }}(X,Y)= & |C|GW_{C^{\perp }}(Y^3,XY^2,X^2Y,X^3) \\= & GW _{C}\left( \left[ Y^3, XY^2, X^2Y, X^3\right] \varvec{M^T}\right) \end{aligned}$$

where ${\varvec{M}}$ is the matrix in Corollary 3.11. The result follows because we easily see that $\left[ Y^3, XY^2, X^2Y, X^3\right] \varvec{M^T}$ is equal to

$$\begin{aligned} \left[ (Y+kX)^3, (Y-X)(Y+kX)^2, (Y-X)^2(Y+kX), (Y-X)^3\right] . \end{aligned}$$

$\square$

Example 3.15

Assume the notations of Example 3.8. We see that the Lee weight enumerators are

$$\begin{aligned} LW_C(X,Y)=Y^6{+}4XY^5{+}6X^2Y^4{+}4X^3Y^3{+}X^4Y^2,{\ }{\ }LW_{C^{\perp }}=Y^6{+}X^2Y^4{+}2XY^5. \end{aligned}$$

We may easily check that the MacWilliams identity

$$\begin{aligned} 16 LW_{C^{\perp }}(X,Y)=LW_C(Y-X,Y+X) \end{aligned}$$

in Proposition 3.14 is satisfied.

Using Remark 1 we may obtain similar results for the Hermitian dual $C^{*}.$

Theorem 3.16

Let C be a linear code over R of length n. Then,

• (a) Let $R=\{r_1,r_2,...,r_s\}$ be an ordering of th elements of R and $\theta$ be the permutation of $\{1,2,...,s\}$ defined for any i by $\sigma _1(r_i)=r_{\theta (i)}.$ Then,

  $$\begin{aligned} & KW_{\sigma _n(C)}(Z_{r_1},Z_{r_2},...,Z_{r_s})=KW_{C}(Z_{r_{\theta (1)}},Z_{r_{\theta (2)}},...,Z_{r_{\theta (s)}}), \\ & |C |KW _{C^{*}}\left( Z_{r_1},Z_{r_2},...,Z_{r_s}\right) =KW _{C}\left( T_{r_{\theta (1)}},T_{r_{\theta (2)}},...,T_{r_{\theta (s)}}\right) \end{aligned}$$

  where

  $$\begin{aligned} \left[ \begin{array}{c} T_{r_1},T_{r_2},...,T_{r_s} \\ \end{array} \right] =\left[ \begin{array}{c} Z_{r_1},Z_{r_2},...,Z_{r_s} \\ \end{array} \right] \varvec{M^T} \end{aligned}$$

  and ${\varvec{M}}$ is the matrix in Theorem 3.3.

• (b) $HW_{\sigma _n(C)}(X,Y)=HW_C(X,Y)$ and

  $$\begin{aligned} |C |HW _{C^{*}}\left( X,Y\right) =HW _{C}\big (Y-X,Y+(|R|-1)X\big ). \end{aligned}$$

• (c) $SW_{\sigma _n(C)}\left( X_1,X_2,X_3,X_4,X_5,X_6,X_7,X_8\right) =$ $SW_{C}\left( X_1,X_3,X_2,X_4,X_5,X_7,X_6,X_8\right)$ and

  $$\begin{aligned} |C|SW _{C^{*}}\left( X_1,X_2,X_3,X_4,X_5,X_6,X_7,X_8\right) & =SW _{C}\left( T_1,T_3,T_2,T_4,T_5,T_7,\right. \\ & \quad \left. T_6,T_8\right) \end{aligned}$$

  where $T_i$ are given as in Corollary 3.10.

• (d) $GW_{\sigma _n(C)}\left( Y_0,Y_1,Y_2,Y_3\right) =GW_{C}\left( Y_0,Y_1,Y_2,Y_3\right)$ and

  $$\begin{aligned} |C|GW _{C^{*}}\left( Y_0,Y_1,Y_2,Y_3\right) =GW _{C}\left( T_0,T_1,T_2,T_3\right) \end{aligned}$$

  where $T_i$ are given as in Corollary 3.11.

• (e) $LW_{\sigma _n(C)}(X,Y)=LW_C(X,Y)$ and $|C |LW _{C^{*}}\left( X,Y\right) =LW_C(Y-X,Y+kX)$

Proof

(a): Note for any $r\in R$ and any ${\varvec{c}}=(c_1,c_2,...,c_n)\in C$ that $c_i=r$ if and only if $\sigma _1(c_i)=\sigma _1(r).$ Thus, for any $(k_1,k_2,...,k_s)\in {\mathbb {N}}^s$ with $k_1+k_2+\cdots +k_s=n$ where ${\mathbb {N}}$ is the set of nonnegative integers, we see that the coefficient of $\prod Z_{r_i}^{k_i}$ in $KW_{\sigma _n(C)}\left( Z_{r_1},Z_{r_2},...,Z_{r_s}\right)$ is equal to the coefficient of $\prod Z_{r_i}^{k_{\theta (i)}}$ in $KW_{C}\left( Z_{r_1},Z_{r_2},...,Z_{r_s}\right) .$ This justifies the first equation. As $|\sigma _n(C)|=|C|$ and $\sigma (C)^{\perp }=C^{*},$ the second equation follows by putting $C=\sigma _n(C)$ in Theorem 3.3.

(b): As $\sigma _1:R\rightarrow R$ is an ${\mathbb {F}}_q$-algebra automorphism, we se that $w({\varvec{r}})=w(\sigma _n({\varvec{r}}))$ for any ${\varvec{r}}\in R^n.$ So $HW_{\sigma _n(C)}(X,Y)=HW_C(X,Y).$ The rest follows from Corollary 3.4.

(c): Note for instance that $\phi (r)\in S_2$ if and only if $\phi (\sigma _1(r))\in S_3.$ This implies that $w_2^{+}({\varvec{r}})=w_3^{+}(\sigma _n({\varvec{r}}))$ for any ${\varvec{r}}\in R^n.$ Similarly, we may justify that $w_6^{+}({\varvec{r}})=w_7^{+}(\sigma _n({\varvec{r}}))$ and $w_i^{+}({\varvec{r}})=w_i^{+}(\sigma _n({\varvec{r}}))$ for $i=1,4,5,8.$ Also as $\sigma _1^2$ is the identity, we see that $w_3^{+}({\varvec{r}})=w_2^{+}(\sigma _n({\varvec{r}}))$ and $w_7^{+}({\varvec{r}})=w_6^{+}(\sigma _n({\varvec{r}})).$ The first equation follows. The rest follows from Corollary 3.10.

(d) and (e): Maybe justified similarly. $\square$

Imitating the proof of Theorem 3.3 we easily see that the matrix ${\varvec{A}}$ in Proposition 3.7 is related to the weight enumerators of codes over ${\mathbb {F}}_q.$

Remark 3.17

Let ${\varvec{A}}$ be the $k\times k$ matrix over ${\mathbb {C}}$ whose rows and columns are indexed by the elements of the ordered set $U=\{u_1,u_2,...,u_k\}$ and whose $(u_i,u_j)$ th entry is $\chi _F(u_iu_j)=\zeta ^{\textrm{Tr}(u_iu_j)}.$ For any linear code D over ${\mathbb {F}}_q$ Then,

$$\begin{aligned} |D |KW _{D^{\perp }}\left( Z_{u_0},Z_{u_1},...,Z_{u_k}\right) =KW _{D}\left( T_{u_0},T_{u_1},...,T_{u_k}\right) \end{aligned}$$

where

$$\begin{aligned} \left[ \begin{array}{c} T_{u_0},T_{u_1},...,T_{u_k} \\ \end{array} \right] =\left[ \begin{array}{c} Z_{u_0},Z_{u_1},...,Z_{u_k} \\ \end{array} \right] \left[ \begin{array}{cc} 1 & \varvec{\mathbbm {1}} \\ \varvec{\mathbbm {1}} & \varvec{A^T} \\ \end{array} \right] . \end{aligned}$$