Bounds on Zero Forcing Using (Upper) Total Domination and Minimum Degree

Abstract

While a number of bounds are known on the zero forcing number Z(G) of a graph G expressed in terms of the order of a graph and maximum or minimum degree, we present two bounds that are related to the (upper) total domination number $\gamma _t(G)$ (resp. $\Gamma _t(G)$) of G. We prove that $Z(G)+\gamma _t(G)\le n(G)$ and $Z(G)+\frac{\Gamma _t(G)}{2}\le n(G)$ holds for any graph G with no isolated vertices of order n(G). Both bounds are sharp as demonstrated by several infinite families of graphs. In particular, we show that every graph H is an induced subgraph of a graph G with $Z(G)+\frac{\Gamma _t(G)}{2}=n(G)$. Furthermore, we prove a characterization of graphs with power domination equal to 1, from which we derive a characterization of the extremal graphs attaining the trivial lower bound $Z(G)\ge \delta (G)$. The class of graphs that appears in the corresponding characterizations is obtained by extending an idea of Row for characterizing the graphs with zero forcing number equal to 2.

1 Introduction

Given any real symmetric matrix M, one can associate M with the adjacency matrix of an undirected graph by concentrating solely on the positions of the nonzero entries of M. Fixing the positions of non-zero values and considering all possible values, the concepts of maximum nullity and minimum rank of the corresponding graph arise. The zero forcing number was introduced in [1] as a useful (and often attained) upper bound on the maximum nullity of a graph. (See [5, 6] and the recent monograph [21] surveying inverse problems and zero forcing in graphs.) Zero forcing is defined by the following process, which starts by choosing a set S of vertices of a graph G and coloring them blue. The color-change rule consists of identifying a blue vertex having only one non-blue neighbor and coloring that neighbor blue. The color-change rule is performed as long as possible. If at the end of the process all vertices become blue, then the initial set S is a zero forcing set of G. The minimum cardinality of a zero forcing set in G is the zero forcing number, Z(G), of G.

Several bounds are known for the zero forcing number, where the trivial lower bound $Z(G)\ge \delta (G)$ involves the minimum degree of a graph. Many authors studied upper bounds on Z(G) involving the order and the maximum degree of G, and considered also extremal families of graphs attaining the bounds [3, 15, 17]. For instance, the most recent such bound is $Z(G)\le \frac{n(\Delta - 2)}{\Delta - 1}$, which holds when G is a connected graph with maximum degree $\Delta \ge 3$ and G is not isomorphic to one of the five sporadic graphs [16]. Bounds on the zero forcing number expressed in terms of order, maximum and minimum degree were also proved [12] and the extremal graphs have recently been characterized [23]. We remark that good upper bounds on Z(G) are particularly interesting, because they also present upper bounds on the maximum nullity of a graph.

Domination in graphs is one of the most studied topics in graph theory; see a recent monograph [19] surveying core concepts of domination theory. Upon first sight, domination does not seem related to maximum nullity and zero forcing, yet there are some surprising connections. Notably, the concept of power domination, which was introduced in [18] as a model for monitoring electrical networks, has a very similar definition to that of zero forcing. In particular, the corresponding graph invariant $\gamma _P(G)$ is a lower bound for Z(G) in all graphs G [7]. Moreover, the so-called Z-Grundy domination number $\gamma _{\textrm{gr}}^{\textrm{Z}}(G)$ of G, as introduced in [9], is dual to the zero forcing number of G. In particular, $Z(G)=n(G)-\gamma _{\textrm{gr}}^{\textrm{Z}}(G)$ holds for every graph G (where n(G) is the order of G).

In this paper, we further relate zero forcing with domination. In particular, we prove an upper bound on the zero forcing number of a graph G, expressed in terms of the total domination number $\gamma _t(G)$ of G. (The latter invariant is one of the central concepts of graph domination, cf. [19] and the book [20] surveying total domination in graphs). We prove that for any graph G with no component isomorphic to a complete graph, we have $Z(G)\le n(G)-\gamma _t(G)$ and $Z(G)\le n(G)-\frac{\Gamma _t(G)}{2}$ where $\Gamma _t(G)$ is the upper total domination number of G. We prove that both of these bounds are sharp, present several properties of the two families of extremal graphs, and prove that any graph is an induced subgraph of a graph G with $Z(G)= n(G)-\frac{\Gamma _t(G)}{2}$. We also show that the ratio $\frac{n-Z(G)}{\Gamma _t(G)}$ can be arbitrarily large (which implies that the ratio $\frac{n-Z(G)}{\gamma _t(G)}$ can also be arbitrarily large). In the proofs, we are often using the language of Z-Grundy domination, which we present in the next section. We are also studying the graphs G with $Z(G)=\delta (G)$, that is, achieving the trivial lower bound. We prove a characterization of these graphs by widely extending a characterization of the graphs G with zero forcing number equal to 2 due to Row [25]. The result is obtained from a characterization of the graphs with power domination equal to 1, which we also prove.

We denote the degree of a vertex v in a graph G by $\deg _G(v)$. An isolated vertex is a vertex of degree 0, and an isolate-free graph is a graph with no isolated vertices. Hence if G is an isolate-free graph, then $\deg _G(v) \ge 1$ for all vertices $v \in V(G)$. In the following section, we present main definitions used in the paper. In particular, we recall the definition of the Z-Grundy domination number, $\gamma _{\textrm{gr}}^{\textrm{Z}}(G)$, and the equality $Z(G)=n(G)-\gamma _{\textrm{gr}}^{\textrm{Z}}(G)$ which holds in all graphs G (note that in the seminal paper [9] Z-Grundy domination number was introduced for isolate-free graphs, but our definition presented in the next section, allows also isolated vertices). In Sect. 3, we are concerned with total domination, we prove the bound $\gamma _{\textrm{gr}}^{\textrm{Z}}(G)\ge \gamma _t(G)$, and present several properties of graphs G that attain the equality $\gamma _{\textrm{gr}}^{\textrm{Z}}(G)=\gamma _t(G)$. In Sect. 4, we prove the mentioned results involving the upper total domination number. Finally, in Sect. 5, we prove the characterization of the graphs G with power domination 1 and the graphs G with $Z(G)=\delta (G)$. Several open problems are posed throughout the paper.

2 Definitions and Notation

For graph theory notation and terminology, we generally follow [19]. Specifically, let G be a graph with vertex set V(G) and edge set E(G), and of order $n(G) = |V(G)|$ and size $m(G) = |E(G)|$. If G is clear from the context, we simply write $V = V(G)$ and $E = E(G)$. The open neighborhood of a vertex v in G is $N_G(v) = \{u \in V \, :\, uv \in E\}$ and the closed neighborhood of v is $N_G[v] = \{v\} \cup N_G(v)$. We denote the degree of v in G by $\deg _G(v)$, and so $\deg _G(v) = |N_G(v)|$. Two vertices are neighbors if they are adjacent. For a set $X \subseteq V(G)$ and a vertex $v \in V(G)$, we denote by $\deg _X(v)$ the number of neighbors of v in G that belong to the set X, that is, $\deg _X(v) = |N_G(v) \cap X|$. In particular, if $X = V(G)$, then $\deg _X(v) = \deg _G(v)$. The subgraph of G induced by a set $D \subseteq V$ is denoted by G[D]. For $k \ge 1$ an integer, we let [k] denote the set $\{1,\ldots ,k\}$.

A vertex $x \in V$ dominates a vertex y if $y\in N_G[x]$, and we say that y is dominated by x. If $D \subseteq V$, then a vertex y in G is dominated by D if there exists $x \in D$ that dominates y. A set D is a dominating set of a graph G if every vertex in G is dominated by D.

A set D is a total dominating set (or shortly, a TD-set) of G if every vertex in G has a neighbor in D. The minimum cardinality of a TD-set of G is the total domination number of G, denoted $\gamma _t(G)$. A TD-set D in G is said to be a minimal TD-set of G if each $S \subsetneq D$ is not a TD-set of G. The maximum cardinality of a minimal TD-set in G is the upper total domination number, $\Gamma _t(G)$, of G. A $\gamma _t$-set of G is a TD-set of G of cardinality $\gamma _t(G)$, while a $\Gamma _t$-set of G is a minimal TD-set of G of cardinality $\Gamma _t(G)$.

For a set $D \subseteq V$ and a vertex $v \in D$, the open D-private neighborhood of v, denoted by $\textrm{pn}(v,D)$, is the set of vertices that are in the open neighborhood of v but not in the open neighborhood of the set $D \setminus \{v\}$. Equivalently, $\textrm{pn}(v,D) = \{w \in V \, :N(w) \cap D = \{v\}\}$. The D-external private neighborhood of v is the set $\textrm{epn}(v,D) = \textrm{pn}(v,D) \setminus D$, and its open D-internal private neighborhood is the set $\textrm{ipn}(v,D) = \textrm{pn}(v,D) \cap D$. We note that $\textrm{pn}(v,D) = \textrm{ipn}(v,D) \, \cup \, \textrm{epn}(v,D)$. A vertex in $\textrm{epn}(v,D)$ is a D-external private neighbor of v, and a vertex in $\textrm{ipn}(v,D)$ is a D-internal private neighbor of v. Hence, if $w \in \textrm{epn}(v,D)$, then $w \notin D$ and w is not dominated by $D \setminus \{v\}$, while if $w \in \textrm{ipn}(v,D)$, then $w \in D$ and w has no neighbor in $D \setminus \{v\}$. A fundamental property of minimal TD-sets (see [19, Lemma 4.25]) is that D is a minimal TD-set in G if and only if $|\textrm{epn}(v,D)| \ge 1$ or $|\textrm{ipn}(v,D)| \ge 1$ holds for every vertex $v \in D$.

The concept of Grundy domination can be presented by a sequence of vertices in a graph. The first type of the corresponding graph invariant, the so called Grundy domination number, was defined in [10] with a motivation coming from the domination game. A few years later, the Grundy total domination number [11] and the Z-Grundy domination number [9] were introduced. A sequence $S=(v_1,\ldots ,v_k)$ of vertices in a graph G is a Z-sequence if for every $i\in \{2,\ldots ,k\}$,

$$\begin{aligned} N_G(v_i) \setminus \bigcup _{j=1}^{i-1}N_G[v_j] \ne \emptyset . \end{aligned}$$

(1)

The corresponding set of vertices from the sequence S will be denoted by $\widehat{S}$. The maximum length $|\widehat{S}|$ of a Z-sequence S in a graph G is the Z-Grundy domination number, $\gamma _{\textrm{gr}}^{\textrm{Z}}(G)$, of G. (The definition of Grundy total domination number of a graph G, $\gamma _\textrm{gr}^t(G)$, is similar, one just needs to change the closed neighborhood symbol in (1) with the open neighborhood symbol.) If $(v_1,\ldots ,v_k)$ is a Z-sequence, then we say that $v_i$ footprints the vertices from $N_G[v_i] \setminus \cup _{j=1}^{i-1}N_G[v_j]$, and that $v_i$ is the footprinter of every vertex $u\in N_G[v_i] \setminus \cup _{j=1}^{i-1}N_G[v_j]$, for any $i\in [k]$ (where $[k]=\{1,\ldots ,k\}$). Note that if S is a Z-sequence, $x\in \widehat{S}$ may footprint itself, but it must footprint (also) a vertex y distinct from x. For a sequence $S=(u_1,\ldots , u_k)$ and a vertex $x \notin \widehat{S}$, we use the following notation: $S\oplus (x)=(u_1,\ldots , u_k,x)$.

As it turns out, the Z-Grundy domination number is dual to the zero forcing number. Moreover, a sequence S is a Z-sequence if and only if the set of vertices outside S forms a zero forcing set [9]. In particular, this implies that

$$\begin{aligned} Z(G)=n(G)-\gamma _{\textrm{gr}}^{\textrm{Z}}(G) \end{aligned}$$

(2)

for every graph G. In a subsequent paper, Lin presented a natural connection between four variants of Grundy domination and four variants of zero forcing [24]. The connections show that all versions of Grundy domination can be applied in the study of different types of minimum rank parameters of symmetric matrices.

Given a graph G, a complete subgraph is a clique in G. Similarly, a complete graph may also be called a clique. A vertex of degree 1 in G is called a leaf of G. A vertex $v \in V$ is a simplicial vertex of G, if $N_G(v)$ induces a clique. The graph G is chordal if it contains no induced cycles of length more than 3. Two vertices u and v in G are closed twins if $N_G[u] = N_G[v]$ and open twins if $N_G(u)=N_G(v)$. Vertices u and v in G are twins if they are either open or closed twins. A vertex $v \in V$ is called a twin vertex if there exists $u \in V(G)$, such that u and v are twins.

In all notations presented in this section, index G may be omitted if the graph G is understood from the context.

3 Zero Forcing and Total Domination

If G is an isolate-free graph and D is a TD-set of G, then the induced subgraph G[D] is isolate-free. In addition, the following observation is easy to see.

Observation 1

Let G be an isolate-free graph and let D be a minimal TD-set of G. If x belongs to a component C of G[D] such that x is not adjacent to a vertex $y\in V(C)$ with $\deg _C(y)=1$, then x has an external private neighbor with respect to D.

We will also make use of the following notation. Let D be a TD-set of G, and let $C_1(D),\ldots , C_{\ell }(D)$ be the components of G[D], which are isomorphic to $K_2$; possibly $\ell =0$ when there are no such components. If $\ell \ge 1$, then for each $i\in [\ell ]$, let $A_i(D)$ denote the set of vertices $x \in V(G)$ such that x has a neighbor in $V(C_i(D))$ and x has no neighbor in $D\setminus V(C_i(D))$. When D is clear from the context, we write $C_i$ and $A_i$. In particular, $V(C_i)\subset A_i$ for all $i\in [\ell ]$, since both vertices in $C_i$ are (internal) private neighbors to each other.

Theorem 2

If G is a graph such that no component of G is a clique, then $\gamma _{\textrm{gr}}^{\textrm{Z}}(G) \ge \gamma _t(G)$.

Proof

In the proof, we will construct a Z-sequence S of G, with $|\widehat{S}|\ge |D|$, where D is a $\gamma _t$-set of G. Among all $\gamma _t$-sets of G, let D be chosen in such a way that G[D] has the smallest possible number of $K_2$-components. In addition if G[D] has $\ell \ge 1$ $K_2$-components $C_1,\ldots , C_{\ell }$ with $V(C_i)=\{x_i,y_i\}$ for all $i\in [\ell ]$, then we choose D among all $\gamma _t$-set of G restricted as above in such a way that the number of $K_2$-components in G[D] for which $(N(x_i)\cap A_i)\setminus \{y_i\}=(N(y_i)\cap A_i)\setminus \{x_i\}$ is as small as possible.

First, consider the components of G[D] that are not isomorphic to $K_2$. For each such component C, first add to S all vertices u in G[D] such that u is adjacent to a vertex $v\in V(C)$ with $\deg _C(v)=1$. Each such vertex u footprints a corresponding vertex v noting that v is a D-internal private neighbor of u. Thereafter, we add to S all the remaining vertices in C. By Observation 1, every such vertex x, since it has no D-internal private neighbor, has a D-external private neighbor y. Therefore, x footprints y, and so the resulting sequence S, constructed so far, is a Z-sequence. Note that the number of vertices added to S from C is |V(C)| since all vertices of C have been added to S. Thus we constructed a Z-sequence of cardinality $|D|-2\ell$. If $\ell =0$, then the proof is complete. Thus let $\ell \ge 1.$

We are left with the components $C_1,\ldots , C_{\ell }$ of G[D], where $V(C_i)=\{x_i,y_i\}$ for all $i\in [\ell ]$. Without loss of generality, we may choose the indices of the components $C_i$ in such a way that there exists $k\in \{0\}\cup [\ell ]$ such that for all $i\le k$, we have

$$\begin{aligned} (N(x_i)\cap A_i)\setminus \{y_i\} = (N(y_i)\cap A_i)\setminus \{x_i\}, \end{aligned}$$

(3)

while for $i\ge k+1$, components $C_i$ do not have this property; that is, $(N(x_i)\cap A_i)\setminus \{y_i\} \ne (N(y_i)\cap A_i)\setminus \{x_i\}$. If $k < \ell$, then for each $i \in \{k+1,\ldots , \ell \}$ we proceed as follows. Renaming vertices if necessary, we may assume without loss of generality that

$$\begin{aligned} \bigl (N(x_i)\setminus N[y_i]\bigr )\cap A_i\ne \emptyset , \end{aligned}$$

and let $a_i\in \bigl (N(x_i)\setminus N[y_i]\bigr )\cap A_i$. For each $i\ge k+1$, we first add to S the vertex $y_i$, and then the vertex $x_i$. In this way, $y_i$ footprints $x_i$, while $x_i$ footprints $a_i$ and thus the so extended sequence S is still a Z-sequence. We note that we have added two vertices to S from each component $C_i$, where $|V(C_i)|=2$.

Finally, if $k \ge 1$, we deal with components $C_1,\ldots ,C_k$ in the following way. We claim that for every $i \in [k]$, the set $A_i$ does not induce a complete graph. Suppose, to the contrary, that $G[A_i]$ is a clique. Since no component of G is a clique, there exists a vertex $a\in A_i$, which is adjacent to a vertex $b\notin A_i$. We note that $b\notin D$, and by the definition of sets $A_i$, the vertex b is dominated by a vertex $c\in D\setminus V(C_i)$. Now, $D'=(D\setminus \{x_i,y_i\})\cup \{a,b\}$ is a TD-set of G. Since $|D'| = |D| = \gamma _t(G)$, the TD-set $D'$ is therefore a $\gamma _t$-set of G. Further vertex a is a $D'$-internal private neighbor of vertex b and vertices in $A_i$ are $D'$-external private neighbors of vertex a. Now, $G[D']$ has fewer $K_2$-components as G[D], which is a contradiction to the initial assumption on D. Therefore, no set $A_i$ induces a clique for $i\le k$. Thus, for each $i\le k$, there exists a vertex $a_i \in A_i \setminus \{x_i,y_i\}$ such that $a_i$ is not adjacent to a vertex $b_i \in A_i\setminus \{x_i,y_i\}$.

Next, we claim that for $i \in [k]$, no vertex in $V(C_i)$ has a neighbor in $V(G) \setminus A_i$. Assume that this is not true, and assume without loss of generality that $x_i \in V(C_i)$ has a neighbor $v \in V(G) \setminus A_i$. Clearly, $v\notin D$ and v is dominated by $u \in D\setminus V(C_i)$. Hence $D'=(D\setminus \{y_i\}) \cup \{v\}$ is a $\gamma _t$-set of G such that $G[D']$ has less $K_2$-components as G[D], a contradiction. Thus for every $i \in [k]$ it holds that all neighbors of $x_i$ (and $y_i$) are in $A_i$.

Now, we prove that for any $i,j \in [k],i \ne j$, there are no edges between $A_i$ and $A_j$. Suppose that $x \in A_i$ is adjacent to $y \in A_j$. Hence $D'=(D\setminus \{y_i,y_j\}) \cup \{x,y\}$ is a $\gamma _t$-set of G such that $G[D']$ has less $K_2$-components as G[D], a contradiction.

Finally, we extend a Z-sequence S as follows. For all $i \in [k]$, first add to S vertex $a_i$ (which footprints $x_i$) and then vertex $x_i$ (which footprints $b_i$). Combining this with all previous observations, we derive that S is a Z-sequence of cardinality |D|, and thus $\gamma _{\textrm{gr}}^{\textrm{Z}}(G)\ge |D|=\gamma _t(G)$. $\square$

Translated to the zero forcing number, Eq. (2) and Theorem 2 imply the following bound on the zero forcing number, where a clique component of a graph is a component of the graph that is a clique.

Corollary 3

If G is a graph with no clique component, then $Z(G)\le n(G)-\gamma _t(G)$.

The difference between the total domination number and the Z-Grundy domination number of a graph can be arbitrarily large. Moreover, the ratio $\frac{\gamma _{\textrm{gr}}^{\textrm{Z}}(G)}{\gamma _t(G)}$ can be arbitrarily large. For instance, let $G_k$, where $k\in \mathbb {N},$ be the graph obtained from the disjoint union of two copies of the complete graph $K_k$ by adding edges that form a perfect matching of $G_k$. Clearly, $\gamma _{\textrm{gr}}^{\textrm{Z}}(G_k)=k$ and $\gamma _t(G_k)=2$.

On the other hand, the bound in Theorem 2 is sharp. For instance, for the star $K_{1,\ell }$ we have $\gamma _{\textrm{gr}}^{\textrm{Z}}(K_{1,\ell })=2=\gamma _t(G)$. In the remainder of this section, we study properties of graphs whose Z-Grundy domination number equals the total domination number.

Since $\gamma _t(G) \le \gamma _{\textrm{gr}}^{\textrm{Z}}(G) \le \gamma _\textrm{gr}^t(G)$ holds for any graph G with no component isomorphic to a complete graph, any graph G with $\gamma _t(G)=\gamma _\textrm{gr}^t(G)$ also satisfies $\gamma _t(G)=\gamma _{\textrm{gr}}^{\textrm{Z}}(G)$. Graphs with $\gamma _t(G)=\gamma _\textrm{gr}^t(G)=k$, which are known under the name total k-uniform graphs, were studied in [4, 11, 13]. In these papers, bipartite graphs with $\gamma _t(G)=\gamma _\textrm{gr}^t(G)=4$ and with $\gamma _t(G)=\gamma _\textrm{gr}^t(G)=6$ were characterized. It was also shown that all connected total k-uniform graphs having no open twins are regular, and some examples of non-bipartite total k-uniform graphs, for even k, were also presented. Moreover, chordal total k-uniform graphs were characterized. (In particular, for $k \ge 3$ no such connected graphs exist). By the above observation, all total k-uniform graphs are also graphs with $\gamma _t(G)=\gamma _{\textrm{gr}}^{\textrm{Z}}(G)$, but this property holds also for many other graphs. For instance, while complete multipartite graphs are the only connected totally 2-uniform graphs (see [11]), we have the following characterization of connected graphs with $\gamma _t(G)=\gamma _{\textrm{gr}}^{\textrm{Z}}(G)=2$.

Proposition 4

Let G be a connected graph not isomorphic to a complete graph. Then $\gamma _t(G)=\gamma _{\textrm{gr}}^{\textrm{Z}}(G)=2$ if and only if $N[x] \cup N[y]=V(G)$ holds for any non-twin vertices x and y.

Proof

First let $N[x] \cup N[y]=V(G)$ hold for any non-twin vertices x and y. Suppose that there is a Z-sequence (u, v, w) in G, implying that $N(w)\setminus (N[u] \cup N[v]) \ne \emptyset$. Since $N[x] \cup N[y]=V(G)$ holds for any non-twin vertices x and y of G, u and v must be twins. Hence $N(v) \setminus N[u]=\emptyset$, a contradiction. Hence, $\gamma _{\textrm{gr}}^{\textrm{Z}}(G) \le 2$ and since G is not complete, $\gamma _{\textrm{gr}}^{\textrm{Z}}(G)=2$. By Theorem 2, $\gamma _t(G)=2$.

For the converse, let $\gamma _t(G)=\gamma _{\textrm{gr}}^{\textrm{Z}}(G)=2$. Suppose that there exists non-twin vertices u and v with $N[u] \cup N[v] \ne V(G)$. Since G is connected, there exists $w \in N(u) \cup N(v)$ such that w has a neighbor $w' \in V(G) \setminus (N[u] \cup N[v])$. Then (u, v, w) or (v, u, w) is a Z-sequence of G and hence $\gamma _{\textrm{gr}}^{\textrm{Z}}(G)\ge 3$, a contradiction. $\square$

By the results proved in [4] we know that there are no total k-uniform graphs for odd k. We can easily find graphs with $\gamma _t(G)=\gamma _{\textrm{gr}}^{\textrm{Z}}(G)=k$ for some odd k. For example, $C_5$ has both Z-Grundy domination number and total domination number equal to 3. We prove next that there are no chordal graphs with $\gamma _t(G)=\gamma _{\textrm{gr}}^{\textrm{Z}}(G)=3$. To prove this we first need the following observation, where statement (a) was proved in [22], while statement (b) is straightforward to verify.

Observation 5

If G is a graph and u a simplicial vertex of G, then

• (a) $\gamma _{\textrm{gr}}^{\textrm{Z}}(G)-1 \le \gamma _{\textrm{gr}}^{\textrm{Z}}(G-u) \le \gamma _{\textrm{gr}}^{\textrm{Z}}(G)$, and

• (b) $\gamma _t(G)-1 \le \gamma _t(G-u) \le \gamma _t(G)$.

Theorem 6

If G is a connected graph that contains a simplicial vertex, then $\gamma _t(G) \ne 3$ or $\gamma _{\textrm{gr}}^{\textrm{Z}}(G) \ne 3$.

Proof

Suppose, to the contrary, that there are connected graphs having simplicial vertices with both Z-Grundy domination number and total domination number equal to 3. Among all such graphs G that contain a simplicial vertex and satisfy $\gamma _t(G)=\gamma _{\textrm{gr}}^{\textrm{Z}}(G)=3$, let G be chosen to have minimum order. Clearly, G is not a complete graph. Let x be a simplicial vertex of G, and let $X=N[x]$, and so X induces a clique. Let $x_1,x_2$ be two arbitrary vertices from $X \setminus \{x\}$.

If $(x,x_1,x_2)$ is a Z-sequence of G, then since $\gamma _{\textrm{gr}}^{\textrm{Z}}(G)=3$ we infer that $N[x] \cup N[x_1] \cup N[x_2] = V(G)$, implying that $\{x_1,x_2\}$ is a TD-set of G, a contradiction. Hence, $(x,x_1,x_2)$ is not a Z-sequence of G. Since $x_1$ and $x_2$ were arbitrary, neither $(x,x_1,x_2)$ nor $(x,x_2,x_1)$ is a Z-sequence of G. Thus since X induces a clique, we infer that $N[x_1]=N[x]$ or $N[x_1]=N[x_2]$. We can therefore partition X into two sets, $A=\{a \in X \, :N[a]=N[x]\}$ and $B=X\setminus A$. Since G is not complete, the set B is not empty. If $|B| \ge 2$, then choosing $\{x_1,x_2\} \subseteq B$, the sequence $(x,x_2,x_1)$ is not a Z-sequence of G, implying that $N[x_1]=N[x_2]$, and so $x_1$ and $x_2$ are twins in G. Thus if $|B| \ge 2$, then any two vertices of B are twins in G. Let $b \in B$ and let $C = N(b) \setminus N[x]$, which is clearly non-empty. By our earlier observations, $X = A \cup B$ is a clique, $N[a] = X$ for all $a \in A$, and $N[b] = A \cup B \cup C$ for all $b \in B$.

Let $H = G-x$. By our earlier properties, the graph H is a connected isolate-free graph. Further, H is not a complete graph. Hence by Theorem 2, $\gamma _{\textrm{gr}}^{\textrm{Z}}(H) \ge \gamma _t(H) \ge 2$. By Observation 5, we have $\gamma _t(H) \le 3$ and $\gamma _{\textrm{gr}}^{\textrm{Z}}(H) \le 3$. If $\gamma _t(H) = 3$, then $\gamma _{\textrm{gr}}^{\textrm{Z}}(H) = 3$, contradicting the minimality of G. Hence, $\gamma _t(H) = 2$ and either $\gamma _{\textrm{gr}}^{\textrm{Z}}(H) = 2$ or $\gamma _{\textrm{gr}}^{\textrm{Z}}(H) = 3$. Let $\{u_1,u_2\}$ be an arbitrary $\gamma _t$-set of H. If $\{u_1,u_2\} \cap X \ne \emptyset$, then $\{u_1,u_2\}$ is a TD-set of G, and so $\gamma _t(G) = 2$, a contradiction. Hence, every $\gamma _t$-set of H has an empty intersection with X. Therefore, $A = \{x\}$, and $\{b,c\}$ is not a TD-set of H for any $b \in B$ and $c \in C$. We now select $b \in B$. Since $N[b] = B \cup C$ for all $b \in B$ and since $\{b,c\}$ is not a TD-set of H for any $b\in B$ and $c\in C$, we can select $c \in C$ in such a way that $D = N[c] \setminus (B \cup C)$ is non-empty. Hence there exists $d \in D$. If $A \cup B \cup C \cup D=V(G)$, then $\{b,c\}$ is a TD-set of G, a contradiction. Since H is connected, there exists $e \in V(H)\setminus (B \cup C \cup D)$ that has a neighbor $v \in C \cup D$. Therefore, (x, b, c, v) is a Z-sequence, where vertex x footprints b, vertex b footprints c, vertex c footprints d, and, finally, vertex v footprints e. Hence, $\gamma _{\textrm{gr}}^{\textrm{Z}}(G) \ge 4$, a contradiction. $\square$

Since every chordal graph which is not complete has a simplicial vertex, as an immediate consequence of Theorem 6 we have the following result.

Corollary 7

There is no connected chordal graph G such that $\gamma _t(G) = \gamma _{\textrm{gr}}^{\textrm{Z}}(G) = 3$.

We already know [4] that there are no connected total k-uniform chordal graphs for $k \ge 3$. This raises the following question.

Problem 1

Is there a connected chordal graph G with $\gamma _t(G)=\gamma _{\textrm{gr}}^{\textrm{Z}}(G)=k$ for $k \ge 4$?

We end the section with the following problem that arises from the above discussion.

Problem 2

Characterize the extremal graphs attaining the bound in Theorem 2.

From earlier papers one can suspect that finding a characterization of graphs G with $\gamma _\textrm{gr}^t(G)=\gamma _t(G)$ should be difficult. Thus we expect that Problem 2 will also not be easy.

4 Zero Forcing and Upper Total Domination

Comparing the Z-Grundy domination number with the upper total domination number of a graph, we note that the inequality in Theorem 2 cannot be improved by replacing $\gamma _t$ with $\Gamma _t$. In other words, there exist graphs such that the upper total domination number is larger than the Z-Grundy domination number, and the difference can even be arbitrarily large. For instance, the windmill graph $\textrm{Wd}(k,n)$, where $k \ge 3$ and $n\ge 2$, is obtained by taking n vertex disjoint copies of the complete graph $K_k$, selecting one vertex from each copy, and identifying these n selected vertices into one new vertex (that is a universal vertex of degree $n(k-1)$). The resulting windmill graph $G = \textrm{Wd}(k,n)$ satisfies $\gamma _{\textrm{gr}}^{\textrm{Z}}(G)=n$ and $\Gamma _t(G)=2n$. This yields the following result.

Observation 8

There exists an infinite family of connected isolate-free graphs G satisfying $\Gamma _t(G) = 2\gamma _{\textrm{gr}}^{\textrm{Z}}(G)$.

By Observation 8, if G is a connected isolate-free graph, then the ratio $\frac{\Gamma _t(G)}{\gamma _{\textrm{gr}}^{\textrm{Z}}(G)}$ can be as large as 2. However, we next prove that this ratio cannot exceed 2.

Theorem 9

If G is an isolate-free graph, then $\Gamma _t(G) \le 2\gamma _{\textrm{gr}}^{\textrm{Z}}(G)$.

Proof

We will use (a simplified version of) the setting described in the proof of Theorem 2. Let D be a $\Gamma _t$-set of G, and so D is a minimal TD-set of G of cardinality $\Gamma _t(G)$, and consider the components of the induced subgraph G[D]. We will construct a Z-sequence S of G, with $|\widehat{S}| \ge |D|/2$.

Let $\mathcal{C}_1$ be the set of all components of G[D] with more than two vertices, and let $\mathcal{C}_2$ be the set of all $K_2$-components of G[D]. Note that $\sum _{C\in \mathcal{C}_1\cup \mathcal{C}_2 }{|V(C)|}=|D|$.

If $C\in \mathcal{C}_1$ then, in the same way as in the proof of Theorem 2, we can add |V(C)| vertices to S (by first adding to S all vertices of C that are neighbors of leaves of C, and then all other vertices of C). After dealing in this way with all components from $\mathcal{C}_1$, we focus on the remaining components of G[D] (having two vertices). From each $C\in \mathcal{C}_2$, we can add at least one vertex to the sequence S in such a way that the added vertex footprints its neighbor in D. The resulting sequence S is a Z-sequence, and so $\gamma _{\textrm{gr}}^{\textrm{Z}}(G)\ge |\widehat{S}|$. On the other hand,

$$ |\widehat{S}| = \sum _{C\in \mathcal{C}_1}{|V(C)|} + \sum _{C\in \mathcal{C}_2}{\frac{|V(C)|}{2}} \ge \sum _{C\in \mathcal{C}_1\cup \mathcal{C}_2 }{\frac{|V(C)|}{2}} = \frac{|D|}{2} = \frac{\Gamma _t(G)}{2}. $$

This implies that $\gamma _{\textrm{gr}}^{\textrm{Z}}(G)\ge \frac{1}{2}\Gamma _t(G)$, as claimed. $\square$

As an immediate consequence of Theorem 9, we have the following corollary.

Corollary 10

If G is an isolate-free graph, then $Z(G)\le n(G)-\frac{\Gamma _t(G)}{2}$.

By the example leading to Observation 8, the windmill graphs $G = \textrm{Wd}(k,n)$ where $k \ge 3$ and $n\ge 2$ attain the upper bound in Theorem 9. Next, we present some properties of graphs G with $\Gamma _t(G) = 2\gamma _{\textrm{gr}}^{\textrm{Z}}(G)$. We will again use the following notation.

Let D be a $\Gamma _t$-set of an isolate-free graph G, and let $C_1,\ldots ,C_\ell$ be the $K_2$-components of G[D] where $V(C_i) = \{x_i,y_i\}$ for $i \in [\ell ]$. For each $i\in [\ell ]$, let $A_i(D)$ denote the set of vertices that are dominated by $V(C_i)$ and are not dominated by $D\setminus V(C_i)$. In particular, $V(C_i) \subseteq A_i(D)$ for all $i\in [\ell ]$, since both vertices in $V(C_i)$ are D-internal private neighbors to each other. From the proof of Theorem 2 and Theorem 9, we immediately get the following.

Lemma 11

If G is a graph with $\Gamma _t(G)=2\gamma _{\textrm{gr}}^{\textrm{Z}}(G)$ and D is a $\Gamma _t$-set of G, then each component of G[D] is isomorphic to $K_2$ and $N[x_i] \cap A_i(D)=N[y_i] \cap A_i(D)$ for all $i\in [\ell ]$.

We note that Lemma 11 implies that $V(C_1) \cup \cdots \cup V(C_\ell )=D$.

Lemma 12

If G is a graph with $\Gamma _t(G)=2\gamma _{\textrm{gr}}^{\textrm{Z}}(G)$ and D is a $\Gamma _t$-set of G, then the following properties hold.

• (a) $A_i(D)$ induces a clique for all $i \in [\ell ]$, and

• (b) there are no edges between $A_i(D)$ and $A_j(D)$ for all i and j where $1 \le i < j \le \ell$.

Proof

Let G be a graph with $\Gamma _t(G) = 2\gamma _{\textrm{gr}}^{\textrm{Z}}(G)$ and let D be a $\Gamma _t$-set of G. It follows from Lemma 11 that each component $C_i$ of G[D] is a $K_2$-component, implying that $\Gamma _t(G)=2\ell$. Further, $N[x_i] \cap A_i(D)=N[y_i] \cap A_i(D)$ for all $i \in [\ell ]$. Suppose that there exist $a,b \in A_i(D)$ such that $ab \notin E(G)$. Renaming components if necessary, we may assume that $i = 1$. Thus, $(a,x_1,x_2,\ldots , x_\ell )$ is a Z-sequence of G, since vertex a footprints $x_1$, vertex $x_1$ footprints b, and vertex $x_j$ footprints $y_j$ for all $j \ge 2$. Thus, $\gamma _{\textrm{gr}}^{\textrm{Z}}(G) \ge \ell + 1$, and so, $\gamma _t(G) = 2\ell < 2\gamma _{\textrm{gr}}^{\textrm{Z}}(G)$, a contradiction. Hence, $A_i(D)$ induces a clique for all $i \in [\ell ]$. This proves part (a).

To prove part (b), suppose that there exists an edge $e=ab$ between $A_i(D)$ and $A_j(D)$ for some i and j where $1 \le i < j \le \ell$, where $a \in A_i(D)$ and $b \in A_j(D)$. Since $A_i(D)$ is, by definition, the set of neighbors of $\{x_i,y_i\}$ that are not dominated by $D\setminus \{x_i,y_i\}$, no vertex from the set $\{x_i,y_i,x_j,y_j\}$ is incident with the edge e. Hence, $(x_1,\ldots ,x_i,a, x_{i+1},\ldots , x_\ell )$ is a Z-sequence of G, since each vertex $x_p$ footprints $y_p$ for $p \in [\ell ]$ and vertex a footprints vertex b. Thus, $\gamma _{\textrm{gr}}^{\textrm{Z}}(G) \ge \ell +1$, a contradiction. $\square$

In the rest of this section we will denote by H the subgraph $G-(A_1(D) \cup \cdots \cup A_\ell (D))$. If there is a vertex $v \in V(G)$ such that v is adjacent to all vertices of a set $X \subset V(G)$, then we will use the notation $v \sim X$.

Lemma 13

If G is a graph with $\Gamma _t(G)=2\gamma _{\textrm{gr}}^{\textrm{Z}}(G)$ and D is a $\Gamma _t$-set of G, then the vertices in $A_i(D)$ are closed twins for all $i \in [\ell ]$.

Proof

Let G be a graph with $\Gamma _t(G) = 2\gamma _{\textrm{gr}}^{\textrm{Z}}(G) = 2\ell$ and let D be a $\Gamma _t$-set of G. Suppose that there exist $a,b \in A_i(D)$, for some $i \in [\ell ]$, such that $N[a] \ne N[b]$. Renaming components if necessary, we may assume that $i = 1$. By Lemma 12, the set $A_1(D)$ induces a clique. Hence renaming the vertices a and b if necessary, we may assume without loss of generality that there exists a vertex $u \notin A_1(D)$ such that $u \in N[a] \setminus N[b]$. By Lemma 12, we also infer that $u \in V(H)$. If $\ell = 1$, then (b, a) is a Z-sequence in G noting that vertex b footprints $A_1(D)$ and vertex a footprints u, implying that $\gamma _{\textrm{gr}}^{\textrm{Z}}(G) \ge 2 = \ell + 1$, a contradiction. Hence, $\ell \ge 2$. In this case, $(b,a,x_2,\ldots , x_\ell )$ is a Z-sequence in G, noting that vertex b footprints $A_1(D)$, vertex a footprints u, and vertex $x_p$ footprints $A_p(D)$ for all $p \in [\ell ] \setminus \{1\}$. This produces a Z-sequence of length $\ell +1$, implying that $\gamma _{\textrm{gr}}^{\textrm{Z}}(G) \ge \ell +1$, a contradiction. $\square$

We note that by Lemma 13 and by definition of the sets $A_i(D)$, for every vertex $u \in V(H)$ there exist two distinct indices in $[\ell ]$, say i, j,  such that $u \sim A_i(D)$ and $u \sim A_j(D)$. Indeed, since $u \notin \cup _{i \in [\ell ]} A_i(D)$, the definition of $A_i(D)$ implies that there exist $i,j \in [\ell ], i\ne j$ such that u is dominated by a vertex in $C_i(D)$ and also by a vertex in $C_j(D)$. Since $C_i(D)\subset A_i(D)$ and all vertices of $A_i(D)$ are twins (by Lemma 13), $u\sim A_i(D)$ and similarly $u\sim A_j(D)$.

Lemma 14

If G is a graph with $\Gamma _t(G)=2\gamma _{\textrm{gr}}^{\textrm{Z}}(G)$ and D is a $\Gamma _t$-set of G, then for any adjacent vertices $u,v \in V(H)$ it holds that $|\{i \, :\, u\sim A_i(D) \text { and } v\sim A_i(D)\}| \ge 1$.

Proof

Let G be a graph with $\Gamma _t(G)=2\gamma _{\textrm{gr}}^{\textrm{Z}}(G)$ and let D be a $\Gamma _t$-set of G. Let $R = V(G) \setminus V(H)$. Suppose that there exist adjacent vertices $u,v \in V(H)$ with $N_R(u) \cap N_R(v) = \emptyset$. Let $i_1,\ldots , i_k$ be the indices for which $u \sim A_i(D)$ holds and let $\{j_1,\ldots , j_{\ell -k}\} = [\ell ] \setminus \{i_1,\ldots , i_k\}$. By supposition the vertex v has no neighbors in $A_{i_1}(D) \cup \cdots \cup A_{i_k}(D)$. Thus, $(x_{i_1},\ldots , x_{i_k},u,x_{j_1},\ldots , x_{j_{\ell -k}})$ is a Z-sequence of G of cardinality $\ell +1$, implying that $\gamma _{\textrm{gr}}^{\textrm{Z}}(G) \ge \ell +1$, a contradiction. $\square$

Lemma 15

If G is a graph with $\Gamma _t(G)=2\gamma _{\textrm{gr}}^{\textrm{Z}}(G)$ and D is a $\Gamma _t$-set of G, then for any non-adjacent vertices $u,v \in V(H)$ it holds that $|\{i \, :\, u\sim A_i(D) \text { and } v\sim A_i(D)\}| \ne 1$.

Proof

Let G be a graph with $\Gamma _t(G)=2\gamma _{\textrm{gr}}^{\textrm{Z}}(G)$ and let D be a $\Gamma _t$-set of G. Suppose that there exist non-adjacent vertices $u,v \in V(H)$ such that the only common neighbors of u and v in $V(G) \setminus V(H)$ are vertices of $A_{i_1}(D)$ for some $i_1 \in [\ell ]$. Let $i_1,\ldots , i_k$ be the indices for which $u \sim A_i(D)$ holds and let $\{j_1,\ldots , j_{\ell -k}\}=[\ell ] \setminus \{i_1,\ldots , i_k\}$. By supposition, the vertex v has no neighbors in $A_{i_2} \cup \cdots \cup A_{i_k}$. Then $(x_{i_2},x_{i_3},\ldots , x_{i_k},u,x_{i_1},x_{j_1},\ldots , x_{j_{\ell -k}})$ is a Z-sequence. Indeed, for $i \ne i_1$, the vertex $x_i$ footprints $A_i(D)$, the vertex u footprints $A_{i_1}(D)$, and the vertex $x_{i_1}$ footprints v. Thus, $\gamma _{\textrm{gr}}^{\textrm{Z}}(G) \ge \ell +1$, a contradiction. $\square$

Let G be a graph with $\Gamma _t(G)=2\gamma _{\textrm{gr}}^{\textrm{Z}}(G)$ and let D be a $\Gamma _t$-set of G. For a subset $B \subseteq V(H)$, we will denote by $X_{B}(D)$ the set

$$ X_B(D)=\{i\in [\ell ] \, :\, u\sim A_i(D) \text { for some } u\in B\}. $$

We will denote by $m_{B}(D)$ the largest cardinality of a minimal subset $X \subseteq X_B(D)$ such that

$$ B \subseteq \bigcup _{i \in X} N(x_i). $$

With this notation, we introduce the following lemma.

Lemma 16

If G is a graph with $\Gamma _t(G)=2\gamma _{\textrm{gr}}^{\textrm{Z}}(G)$ and D is a $\Gamma _t$-set of G, then for every $B \subseteq V(H)$ we have

$$ \gamma _{\textrm{gr}}^{\textrm{Z}}(G[B{\setminus } B'])+m_{B'}(D)\le |X_B(D)|, $$

where $B'=\{u\in B \, :\, u\text { is an isolated vertex of }G[B]\}$.

Proof

Let G be a graph with $\Gamma _t(G)=2\gamma _{\textrm{gr}}^{\textrm{Z}}(G)=2\ell$ and let D be a $\Gamma _t$-set of G. Let $B \subseteq V(H)$ and $B'=\{u\in B \, :\, u\text { is an isolated vertex of }G[B]\}$. Renaming vertices in D if necessary, we may assume without loss of generality that $X_{B}(D) = [k]$. Suppose, to the contrary, that $\gamma _{\textrm{gr}}^{\textrm{Z}}(G[B\setminus B']) + m_{B'}(D) > k$. Let $S=(a_1,\ldots ,a_s)$ be a $\gamma _{\textrm{gr}}^{\textrm{Z}}$-sequence of $G[B\setminus B']$ and let $X=\{i_1,\ldots ,i_m\}\subseteq X_{B'}(D)$ be a minimal subset of cardinality $m=m_{B'}(D)$ such that the vertices in $\{A_i(D) \, :\, i\in X\}$ dominate $B'$. We now consider the sequence given by

$$ S'=(a_1,\ldots ,a_s,x_{i_1},\ldots ,x_{i_m},x_{k+1},\ldots ,x_{\ell }). $$

The sequence $S'$ is a Z-sequence of G. To see this, note that the vertex $a_i$ footprints some vertex of $G[B\setminus B']$ for all $i \in [s]$ since S is a $\gamma _{\textrm{gr}}^{\textrm{Z}}$-sequence of $G[B\setminus B']$. By our choice of X, the vertex $x_{i_j}$ footprints some $u\in B'$. Finally, since $B \cap N(x_i)=\emptyset$, the vertex $x_{i}$ footprints the vertices in $A_i(D)$ for all $i\ge k+1$. Thus, $S'$ is a Z-sequence of G of length

$$ \underbrace{\gamma _{\textrm{gr}}^{\textrm{Z}}(G[B{\setminus } B'])+m_{B'}(D)}_{>k}+(\ell -k)>\ell =\gamma _{\textrm{gr}}^{\textrm{Z}}(G), $$

which gives rise to a contradiction. $\square$

We summarize the above lemmas into the following result in which we adopt the notation established in this section.

Proposition 17

If G is a graph with $\Gamma _t(G)=2\gamma _{\textrm{gr}}^{\textrm{Z}}(G)$ and D is a $\Gamma _t$-set of G, then the following properties hold.

• (i) each component of G[D] is isomorphic to $K_2$ and so $|D|=2\ell$, for some integer $\ell$;

• (ii) $N[x_i] \cap A_i(D)=N[y_i] \cap A_i(D)$, for each $i\in [\ell ]$;

• (iii) $A_i(D)$ induces a clique, for each $i \in [\ell ]$;

• (iv) there are no edges between $A_i(D)$ and $A_j(D)$, for each $\{i,j\}\subset [\ell ]$;

• (v) vertices in $A_i(D)$ are closed twins, for each $i \in [\ell ]$;

• (vi) for every adjacent vertices $u,v \in V(H)$, we have

  $$ |\{i:\, u\sim A_i(D) \text { and } v\sim A_i(D)\}| \ge 1; $$

• (vii) for every non-adjacent vertices $u,v \in V(H)$ it holds that

  $$ |\{i:\, u\sim A_i(D) \text { and } v\sim A_i(D)\}| \ne 1; $$

• (viii) for every $B\subset V(H)$, if $B'=\{u\in B:u\text { is an isolated vertex of }G[B]\}$, we have

  $$ \gamma _{\textrm{gr}}^{\textrm{Z}}(G[B{\setminus } B'])+m_{B'}(D)\le |X_B(D)|. $$

We do not think that the combination of properties in Proposition 17 is sufficient for an isolate-free connected graph G to satisfy $\Gamma _t(G)=2\gamma _{\textrm{gr}}^{\textrm{Z}}(G)$. Therefore, we pose the following problem.

Problem 3

Determine if the properties in Proposition 17 are sufficient for an isolate-free connected graph G to satisfy $\Gamma _t(G)=2\gamma _{\textrm{gr}}^{\textrm{Z}}(G)$. If not, then extend these properties to obtain a characterization of graphs G with $\Gamma _t(G)=2\gamma _{\textrm{gr}}^{\textrm{Z}}(G)$.

Now, we present a large family of graphs achieving the bound from Theorem 9. Let H be an arbitrary graph with $\gamma _{\textrm{gr}}^{\textrm{Z}}(H) \le \ell$. Let G be the graph obtained from H by adding $\ell$ disjoint cliques $K_{n_1},\ldots , K_{n_\ell }$, each of order at least 2, and then connecting by an edge every $u \in V(H)$ with every vertex of $K_{n_1} \cup \cdots \cup K_{n_\ell }$. The resulting graph G satisfies $\Gamma _t(G)=2\ell$ and $\gamma _{\textrm{gr}}^{\textrm{Z}}(G)=\ell$. Since H is an induced subgraph of G, we can formulate this observation as follows.

Observation 18

Every graph H is an induced subgraph of a graph G with ${\Gamma _t(G)}=2\gamma _{\textrm{gr}}^{\textrm{Z}}(G)$.

We note that in many graphs the Z-Grundy domination number is (much) bigger than the upper total domination number, and the ratio ${\gamma _{\textrm{gr}}^{\textrm{Z}}(G)}/{\Gamma _t(G)}$ can be arbitrarily large. Indeed, let G be an arbitrary graph, and let $G^*$ be obtained from the disjoint union of G and the complete graph T of order 2 with $V(T)=\{a,c\}$ by adding the edges from the set $\{ax \, :\,x\in V(G)\}$. Every TD-set of $G^*$ has to contain the vertex a in order to dominate the vertex c. However, any minimal TD-set containing a can only have two vertices, which yields $\Gamma _t(G^*)=2$. On the other hand, we observe that $\gamma _{\textrm{gr}}^{\textrm{Z}}(G^*) \ge \gamma _{\textrm{gr}}^{\textrm{Z}}(G)+1$, which can be arbitrarily large.

5 Graphs with $Z(G)=\delta (G)$ and Power Domination

A trivial lower bound on the zero forcing number in terms of the minimum degree came from the original paper on zero forcing due to the AIM-Group [1], which showed that

$$\begin{aligned} Z(G)\ge \delta (G) \end{aligned}$$

(4)

holds for all graphs G. Simple examples where the bound is attained are paths, since $Z(P_n)=1$. In this section, we will characterize the graphs G that attain the bound, which is equivalent to satisfying $\gamma _{\textrm{gr}}^{\textrm{Z}}(G)=n(G)-\delta (G)$, using a connection with the concept of power domination. Furthermore, we find a characterization of all graphs with power domination equal to 1.

As remarked earlier, the concept of power domination was introduced in [18], where it was motivated by the problem of monitoring an electrical power network. Next, we present its definition.

Power domination is a graph searching process which starts by placing phase measurement units on a set S of vertices in the power network, which are then labeled as observed (for the purpose of relating the process with zero forcing we will call these vertices blue). Now, the searching process consists of the following two steps, where the Propagation Step can be repeated:

• (1) Initialization Step (Domination Step): All vertices in S as well as all neighbors of vertices in S are observed (i.e., colored blue).

• (2) Propagation Step (Zero Forcing Step): Every vertex which is the only unobserved (i.e., non-blue) neighbor of some observed (i.e., blue) vertex becomes observed (i.e., blue).

If eventually the whole network is observed (that is, all vertices become blue), S is called a power dominating set. The minimum cardinality of a power dominating set of a graph G is the power domination number, and is denoted by $\gamma _P(G)$.

The following lemma provides an interesting relation between certain extremal families of graphs in power domination and in zero forcing.

Lemma 19

If G is a graph of order n with minimum degree $\delta$, then $Z(G)=\delta$ if and only if $\gamma _P(G)=1$ and there exists a power dominating set $\{x\}$ such that $\deg _G(x)=\delta$.

Proof

First, assume that $Z(G)=\delta$. Therefore, there exists a zero forcing set S with $\delta$ vertices, and let $x\in S$ be the vertex with which the color-change rule starts. Clearly, x has $\deg _G(x)$ neighbors, and exactly one neighbor of x, say y, needs to be non-blue before the propagation process starts. Since $|S|=\delta$, this implies that $\deg _G(x)=\delta$ and $S\subset N_G[x]$. In addition, $S'=\{x\}$ is a power dominating set, since once the initialization step is over, $N_G[x]$ is dominated, and the process of propagation in power domination is the same as the zero forcing process.

Conversely, let $S'=\{x\}$ be a power dominating set of G, where $\deg _G(x)=\delta$. Clearly, $N_G[x]$ is a zero forcing set. In addition, after removing a neighbor y of x from $N_G[x]$, the set $S=N_G[x]\setminus \{y\}$ is also a zero forcing set of G. Indeed, the color-change rule can be applied on the blue vertex x with only one non-blue neighbor, which is vertex y, after which the same propagation rules can be used (in either power domination and zero forcing). This implies that $Z(G)\le |N_G[x]|-1=\delta$, and we know that $Z(G)\ge \delta$ in any graph G. Thus $Z(G)=\delta$ as claimed. $\square$

Graphs G with power domination number $\gamma _P(G)=1$ were studied in [26], where many families of such graphs were presented, within the class of regular graphs of high degree (at least $n(G)-4$). Next, we give a complete characterization of graphs G with $\gamma _P(G)=1$. The idea for the class of graphs that characterizes these graphs was inspired by Row’s construction [25], where graphs with zero forcing number equal to 2 were characterized. First, we introduce the following notations. For a path $P :a_1,a_2,\ldots , a_k$ and vertex $a_i$ of the path P we denote the subpath of P from $a_{i+1}$ to $a_k$ by $^{a_i}\!P:a_{i+1},a_{i+2},\ldots , a_k$.

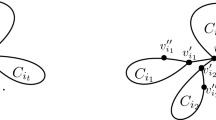
A graph G is a graph of k internally parallel paths if there exists $x \in V(G)$, which is an end-vertex of each of k internally pairwise disjoint induced paths $Q_1,\ldots , Q_k$, where $V(G)=\cup _{i=1}^{k}{V(Q_i)}$, and $V(Q_i) \cap V(Q_j)=\{x\}$ for any $i \ne j$, by possibly adding any number of edges between different paths, provided that the following property holds:

• for every set of $\ell$ vertices, $x_{i_1} \in V(Q_{i_1}),\ldots , x_{i_\ell } \in V(Q_{i_\ell })$, where $\ell \le k$, each belonging to distinct paths and none of them being an end-vertex of the corresponding path, it holds that there exists a vertex $x' \in \{x_{i_1},\ldots , x_{i_\ell }\}$ with $\deg _Y(x')=1$, where $Y=V(^{x_{i_1}}\!Q_{i_1})\cup \cdots \cup \, V(^{x_{i_\ell }}\!Q_{i_\ell })$.

For example, the graph G illustrated in Fig. 1 is a graph of three internally parallel paths.

Fig. 1

A graph G of three internally parallel paths

Theorem 20

Let G be a graph. Then $\gamma _P(G)=1$ if and only if G is a graph of k internally parallel paths for some k.

Proof

Let G be a graph with $\gamma _P(G)=1$, and let $\{x\}$ be a power dominating set of G. Let $k=\deg (x)$, and $N(x)=\{v_1^1,\ldots ,v_1^k\}$. We have that N[x] is a zero forcing set. So, in every propagation step, an uncolored vertex w is turned into blue, where w is the only uncolored vertex of a blue vertex. Note that if $N[x]=V(G)$, then G is a graph with k internally parallel graphs, where each one of these paths is $Q_i :x,v_1^i$. Hence we may assume that $N[x] \ne V(G)$, for otherwise the desired result hold.

Let $X=\{v_1^1,\ldots ,v_1^k\}$. Let w be the vertex colored in the first propagation step. Thus, there exist some $v_1^i$ such that w is the only uncolored neighbor of $v_1^i$. We let $v_2^i=w$, and update X to be $X=(X\setminus \{v_1^i\})\cup \{v_2^i\}$. We note that all the vertices in X are blue and the blue vertices that are not in X have all their neighbors colored blue at this point. This property will be maintained throughout the process.

We continue the process in the following way. In any propagation step we have a set $X=\{v_{i_1}^1,\ldots ,v_{i_k}^k\}$, and let w be the vertex that turns into blue in the present step. Then, there is a blue vertex for which w is the only uncolored neighbor. Since, by assuming the mentioned property, any blue vertex that is not in X has all its neighbors colored blue, then w is the only uncolored vertex of some $v_{i_j}^{j}\in X$. We let $v_{i_j+1}^{j}=w$ and update X to be $X=(X\setminus \{v_{i_j}^j\})\cup \{v_{i_j+1}^j\}$. We note that X has k blue vertices, and the blue vertices that are not in X have all their neighbors colored blue, thus the desired property is maintained. We continue until all the vertices of G are turned into blue.

At the end of the process, paths $Q_i :x,v_1^i,\ldots ,v_{n_i}^i$, where $i\in [k]$, have been determined. To prove that G is a graph of k internally parallel paths, we need to verify the additional condition that these paths must satisfy.

Now, let $\{v_{i_1}^{j_1},v_{i_2}^{j_2},\ldots ,v_{i_\ell }^{j_\ell }\}$, where $\ell \le k$, be a set of vertices each belonging to pairwise distinct paths and $i_m<n_m$ for each $m\in [\ell ]$. Let us assume, without loss of generality, that they were used to color an uncolored neighbor in the order $v_{i_1}^{j_1},v_{i_2}^{j_2},\ldots ,v_{i_\ell }^{j_\ell }$. We remark that in the propagation step in which $v_{i_1}^{j_1}$ is chosen to color a neighbor, $v_{i_1+1}^{j_\ell }$ is the only uncolored neighbor of $v_{i_1}^{j_1}$. Moreover, all the vertices $v_{i_m}^{j_m}$ with $m>1$ are uncolored at this point. We note also that if $v_i^j$ is uncolored, then all the vertices in $^{v_{i}^j}Q_j$ are uncolored. As a consequence of these observations, all the vertices in $^{v_{i_m}^{j_m}}Q_{j_m}$ are uncolored for $m\ge 1$. So, we have that $v_{i_1+1}^{j_1}$ is the only neighbor of $v_{i_1}^{j_1}$ in

$$ Y=\bigcup _{m\in [\ell ]} V(^{v_{i_m}^{j_m}}Q_{j_m}). $$

Therefore, G is a graph of k internally parallel paths. Now, let G be a graph of k internally parallel paths with paths $Q_1 :x,v_1^1,\ldots ,v_{n_1}^1$ through to $Q_k :x,v_1^k, \ldots ,v_{n_k}^k$. We will prove that $\{x\}$ is a power dominating set. Equivalently, we need to prove that $\{x,v_1^1,\ldots ,v_1^k\}$ is a zero forcing set. If $N[x]=V(G)$, we are done. Otherwise, let $X=\{v_1^1,\ldots ,v_1^k\}\setminus \{v_{n_1}^1,\ldots ,v_{n_k}^k\}$. Since G is a graph of k internally parallel paths, there is a vertex $v_{1}^i$ such that $\deg _Y(v_1^i)=1$, where

$$ Y=\bigcup _{j\in [k]}{V(^{v_1^j}Q_j)}, $$

and the neighbor is $v_2^i$. Then, we color $v_2^i$ blue, since it is the only uncolored neighbor of $v_1^i$. We continue this propagation process as follows. Let $X'$ be the set of the last colored vertices in each path $Q_i$, and $X=X'\setminus \{v_{n_1}^1,\ldots ,v_{n_k}^k\}=\{v_{i_1}^{j_1},\ldots ,v_{i_\ell }^{j_\ell }\}$. If $X\ne \emptyset$, since G is a graph of k internally parallel paths, there is a vertex $v_{i_m}^{j_m}$ such that $\deg _Y(v_{i_m}^{j_m})=1$, where

$$ Y=\bigcup _{t\in [\ell ]}{V(^{v_{i_t}^{j_t}}Q_{j_t})}, $$

and the neighbor is $v_{i_m+1}^{j_m}$. Thus, since it is the only uncolored neighbor of $v_{i_m}^{j_m}$, we turn it into blue. We can continue until all the vertices in G are blue, and therefore $\{x\}$ is a power dominating set and $\gamma _P(G)=1$. $\square$

Extremal graphs for the bound (4) are known for graphs with minimum degree 1 or 2. The only graphs with $\delta (G)=1$ and $Z(G)=1$ are paths [14]. It was proved in [25] that $Z(G)=2$ if and only if G is a graph of two parallel paths, or, equivalently, G is an outerplanar graph with the path cover number equal to 2.

For graphs G with $\delta (G) \ge 3$, it is worth noting that the idea arising from graphs with two parallel paths is extended by the definition of graphs with k internally parallel paths, where k can be arbitrarily large.

From the proof of Theorem 20, it follows that G is a graph of k internally parallel paths if and only if $\gamma _P(G)=1$ and there exists a power dominating set $\{x\}$ with $\deg (x)=k$, and in consequence $Z(G)\le k$. Combining this with Lemma 19, we have a characterization of graphs with $Z(G)=\delta (G)$, or, equivalently $\gamma _{\textrm{gr}}^{\textrm{Z}}(G)=n(G)-\delta (G)$.

Corollary 21

Let G be a graph. Then $Z(G)=\delta (G)$ if and only if G is a graph of $\delta (G)$ internally parallel paths.