The Threshold of a Stochastic SIRS Epidemic Model with a General Incidence

Abstract

In this article, a SIRS epidemic model with a general incidence rate is proposed and investigated. We briefly verify the global existence of a unique positive solution for the proposed system. Moreover, and unlike other works, we were able to find the stochastic threshold $\mathcal {R}_s$ of the proposed model which was used for the discussion of the persistence in mean and extinction of the disease. Moreover, we utilize stochastic Lyapunov functions to show under sufficient conditions the existence and uniqueness of stationary distributions of the solution. Lastly, numerical simulation is executed to conform our analytical results.

1 Introduction

In order to face different diseases, people are desirous to understand the mechanism of epidemics and try to prevent their occurrence and spread by effective and affordable measures and means. For this, several works have proposed deterministic and stochastic mathematical models to study the dynamics of transmission of infectious diseases such as Ebola, MERS, N1H1, Coronavirus, etc.(see for instance Casagrandi et al. [5]; McCluskey and van den Driessche [22]; Hethcote [10]; Taki et al. [24] and the references cited therein).

Mathematical models for epidemics have been evolving in complexity and realism, Kermack and McKendrick investigated the classical deterministic SIRS (susceptible-infected-removed) which divides the total population into susceptible individuals (S), infective individuals (I) and recovered individuals (R) describes the transmission of a contagious disease with recovered individuals lose immunity and return to the susceptible class. For several years, many studies on susceptible-infected-recovered-susceptible stochastic models have been published (see e.g. [1, 2, 17, 20, 23, 25, 27]). We consider the following deterministic SIRS model

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{dS}{dt}= &{} {\mu -\mu S- \beta S I+\gamma R ,} \\ \frac{dI}{dt}= &{} {\beta S I -(\lambda + \mu ) I ,} \\ \frac{dR}{dt}= &{} {\lambda I -(\mu + \gamma ) R.} \end{array}\right. } \end{aligned}$$

(1)

where the constants $\mu , \beta ,\lambda$ and $\gamma$ are positive. The basic reproduction number of the system (1) is defined by $\mathcal {R}_0 = \frac{\beta }{\lambda + \mu }$. In the paper [9], Hethcote showed that the free-disease equilibrium state $E_0(1, 0,0)$ is globally asymptotically stable if $\mathcal {R}_0 \le 1$. However, if $\mathcal {R}_0 > 1$ ; $E_0$ becomes unstable and the endemic equilibrium state $\Bigg (\frac{1}{\mathcal {R}_0}, \frac{(\mu +\gamma )(\mathcal {R}_0-1)}{( \mu +\gamma +\lambda )\mathcal {R}_0},\frac{\lambda (\mathcal {R}_0-1)}{( \mu +\gamma +\lambda )\mathcal {R}_0} \Bigg )$ is globally asymptotically stable.

In order to idealize the deterministic model approximation to the reality, we suppose that the noise has the main effect on the contact rate involved in the deterministic model we can change randomly by $\tilde{\beta } dt = \beta dt + \sigma dB_t$, where $\sigma$ is the standard deviation of the noise. The stochastic model resulting from (1) can be described by the system as follows

$$\begin{aligned} {\left\{ \begin{array}{ll} dS= &{} {( \mu -\mu S(t)- \beta S(t)I(t)+\gamma R(t)) dt - \sigma S(t) I(t) dB(t) ,} \\ dI= &{} {(\beta S(t) I(t)-(\lambda + \mu ) I(t)) dt + \sigma S(t) I(t) dB(t) ,} \\ dR= &{} {(\lambda I(t) -(\mu + \gamma ) R(t)) dt.} \end{array}\right. } \end{aligned}$$

(2)

where $B = (B_1, B_2, B_3)$ is a four-dimensional Brownian motion with independent components defined on a complete probability space $(\Omega ,\mathcal {F},\mathcal {P})$ with a natural filtration $\{\mathcal {F}_t\}_{t\ge 0}$(i.e. it is increasing and right continuous while $\mathcal {F}_0$ contains all P-null sets).

In 2009, Qiuying Lu in [21] proved that the stochastic SIRS system (1) is asymptotically stable if $\beta < \lambda +\mu -\sigma ^2/2$. In 2012, a more general SIR model has also been studied by Chunyan .Ji et al in [13], and they found the same result as Qiuying Lu.R [21] by normalizing this model. In 2014, Lahrouz and Settati in [15] proved the global asymptotical stablility of the system (1) under a condition $\mathcal {R}_s < 1$ and $\sigma ^2 \le \beta < \lambda +\mu +\sigma ^2/2$ where $\mathcal {R}_s =\frac{\beta }{\frac{\sigma ^2}{2}+\lambda + \mu }$; in the same year, Zhao and Jiang in [28] studied the threshold of the model (1) by choosing another incidence function of the form $\beta SI / (1+ \alpha I )$ and adding the death rate due to disease, except that the extinction was discussed by the authors in their article [28] by adding more conditions on the parameters of the proposed model. In 2015 Dan Li et al. in [16], using the same condition as [15] or $\sigma ^2 \le \beta < \sigma \sqrt{2(\lambda +\mu )}$ they proved the global asymptotic stability for the stochastic model, except that these last two works( [15] and [16]) did not start the case where $\beta \in ]\sigma \sqrt{2(\lambda +\mu )}, \lambda +\mu +\sigma ^2/2 [$ to complete the proof for all $\beta > 0$.

The speed of propagation of a disease is measured by its incidence wich plays an important role in the study of mathematical epidemiology and has an effect on the dynamical behavior of the epidemiological model. Mathematically, the incidence rate represents the number of new cases per unit time wich has taken a lot of form in previous works like $\beta S I$, $\beta S I / (S+I)$, $\beta I^p S^q$, $\beta S I^p/ (1+ \alpha I^q)$ , $\beta S I^p/ (1+ \alpha S)$. Let us point out that according to past work we notice that the epidemic models with the epidemic models with nonlinear incidences have more complicated dynamics than those with bilinear or standard incidence.

Based on the above discussion, in this paper, we propose a stochastic SIRS model with a general incidence rate where the transmission of the disease is governed by the general nonlinear saturated incidence rate $\beta S g(I)$. Note, that the incidence function $(I \rightarrow g(I))$ can be used in some specific forms for the incidence rate that have been used before with several papers ( for instance: [3, 4, 6, 7, 11, 18]).

The deterministic system of our model can be expressed by the following ordinary differential equations:

$$\begin{aligned} \left\{ \begin{array}{ll} dS(t)= &{} ({\Lambda -\mu _1S(t)+\tau R(t)-\beta S(t)g(I(t))) dt,} \\ dI(t)= &{} ({\beta S(t)g(I(t))-\lambda I(t)-\mu _2I(t))dt,} \\ dR(t)= &{} ({\lambda I(t)-\tau R(t) -\mu _3R(t))dt.} \end{array} \right. \end{aligned}$$

(3)

The function g(I) is assumed to be nonnegative, continuously differentiable, and $\frac{g(I)}{I}$ is monotonically decreasing on $(0,\infty )$, with $g(0) = 0$ and $g'(0) > 0$ which leads to $\frac{g(x)}{x}<g'(0)$ for any $x > 0$.

The parameters involved in the system (3) are positive constants, and it is natural to assume that $\mu _1 < \min (\mu _2; \mu _3)$. The characteristics of the parameters appearing in the system are as follows:

Symbol	Description
$\Lambda$	the influx of individuals into the susceptible
$\mu _i, i=1,2,3$	the natural death rate respectively of S, I and R compartments,.
$\lambda$	the recovery rate of the infective individuals.
$\tau$	the rate at which recovered individuals lose immunity and return to the susceptible class.
$\beta$	the transmission rate .

For system (3), Li.et.al [19] obtained a threshold dynamics completely determined by $\mathcal {R}_0$ is given by:

$$\begin{aligned} \mathcal {R}_0 =\frac{\beta \Lambda g'(0)}{\mu _1(\mu _2+\lambda )}. \end{aligned}$$

If $\mathcal {R}_0 < 1$, then system (3) has only the disease-free equilibrium $E_0 = (S_0, 0, 0) = (\frac{\Lambda }{\mu _1}, 0, 0)$ and it is globally asymptotically stable. This shows that the disease will die out and the entire population will be susceptible. If $\mathcal {R}_0 > 1$, then $E_0$ is unstable and system (3) has a unique positive endemic equilibrium $E^*= (S^*, I^*, R^*)$ which is globally asymptotically stable, where $S^*> 0$, $I^*> 0$, $R^*> 0$. This means that the disease will prevail and persist in a population.

To make the system (3) close to reality, our approach is to introduce fluctuations in the environment and to suppose that the transmission rate $\beta$ is non-deterministic, so we can add randomly fluctuation affecting directly the deterministic model. Then corresponding to model 3, we can establish the stochastic SIRS model as follows :

$$\begin{aligned} {\left\{ \begin{array}{ll} dS(t)= (\Lambda -\mu _1S(t)+\tau R(t)-\beta S(t)g(I(t)))dt+\sigma _1S(t)dB_1(t); \\ dI(t)=(\beta S(t)g(I(t))-\lambda I(t)-\mu _2I(t))dt+\sigma _2I(t)dB_2(t);\\ dR(t)= (\lambda I(t) -\tau R(t)-\mu _3R(t))dt+\sigma _3R(t)dB_3(t). \end{array}\right. } \end{aligned}$$

(4)

where $\sigma _i^2, i = 1, 2, 3$ are the intensities of white noise.

This paper is arranged as follows. In Section 2, we prove the global existence of a unique positive solution for the proposed system. The condition for the disease being persistent is given in Section 3. In Section 4, for the system (4), we proposed a sufficient condition of the disease extinction. In the last section,some conclusions are stated and the results are illustrated by numerical simulations.

We define the differential operator L; associated with the following general d-dimensional stochastic differential equation (SDE)

$$\begin{aligned} \textrm{d}X(t)=f(X(t),t)\textrm{d}t+g(X(t),t)\textrm{d}B(t), \end{aligned}$$

(5)

with the initial value $X_0 \in \mathbb {R}^d$. Where the mappings $f:\mathbb {R}^d\times [t_0;+\infty [ \rightarrow \mathbb {R}^d$,   $g: \mathbb {R}^d\times [t_0;+\infty [ \rightarrow \mathcal {M}_{d,m}(\mathbb {R})$, f and g are locally Lipschitz functions in x and B(t) is an d-dimensional Wiener process Brownian motion defined on the probability space $(\Omega , \mathcal {F}, \mathcal {P})$ with the filtration $\{\mathcal {F}_{t} \}_{t\ge 0}$ satisfying the usual condition. Let $S_h= \{ x \in \mathbb {R}^d : |x| < h \}$, where |x| denotes the Euclidean norm on $\mathbb {R}^d$. The differential operator L associated with the above equation is given by

$$\begin{aligned} L=\frac{\partial }{\partial t}+\sum _{i=1}^df_i(X,t)\frac{\partial }{\partial X_i}+\frac{1}{2}\sum _{i,j=1}^d[g^T(X,t)g(X,t)]_{ij}\frac{\partial ^2}{\partial X_iX_j} \end{aligned}$$

(6)

L acts on a function $V \in C^{2,1}(\mathbb {R}^d \times [t_0,\infty ];\mathbb {R}_+)$ as follows:

$$\begin{aligned} L V (x,t)= & {} V_t (x,t) + V_x (x,t)f(x,t) +\dfrac{1}{2}\text {trace}\left[ g^T(x,t)V_{xx }(x, t)g(x,t)\right] . \end{aligned}$$

(7)

By Itô’s formula, we have:

$$\begin{aligned} dV(X(t), t)= & {} L V (X(t), t) \textrm{d} t + V_x (X(t), t)\textrm{d} B(t). \end{aligned}$$

(8)

where:

$$\begin{aligned} V_t=\dfrac{\partial V}{\partial t}, \quad V_x=\left( \dfrac{\partial V}{\partial x_1}, \,\dfrac{\partial V}{\partial x_2},\dots ,\dfrac{\partial V}{\partial x_d} \right) \quad V_{xx} =\left( \dfrac{\partial V^2}{\partial x_i \partial x_j}\right) _{d\times d}. \end{aligned}$$

(9)

2 Existence and Uniqueness of the Positive Solution

In this section, we prove that the model (4) has a local positive solution. Then we investigate the global positivity of the solution.

Lemma 1

For any initial value $(S(0),I(0),R(0))\in \mathbb {R}^3_+$, there exists a unique positive solution to system (4) on $t\ge 0$, and the solution will remain in $\mathbb {R}^3_+$ with probability one.

Proof

Since the coefficients of system (4) are locally Lipschitz continuous, for any given initial value $(S(0),I(0),R(0))\in \mathbb {R}^3_+$, then there is a unique local solution positive (S(t), I(t), R(t)) on $[0, \tau _e)$, where $\tau _e$ is the explosion time [26]. Now, we show that the solution is global. We have only to prove that $\tau _e = \infty$ a.s. Consider an $\xi _0\ge 0$ be sufficiently large so that $S_0,I_0,R_0$ are all lie within the interval $[\frac{1}{\xi _0}; \xi _0]$. For each integer $k\ge \xi _0$, then we define the following stopping time :

$$\begin{aligned} \tau _k = \inf \left\{ t\in [0,\tau _e) :S(t)\not \in \Big (\frac{1}{k}, k\Big ) \;\;\;or\;\;\; I(t)\not \in \Big (\frac{1}{k}, k\Big )\;\;\;or\;\;\;R(t)\not \in \Big (\frac{1}{k}, k\Big )\right\} \end{aligned}$$

In the following, we set $\inf \emptyset = \infty$ ($\emptyset$ denotes the empty set). Clearly, $\tau _k$ is increasing as $k\uparrow \infty$. Let $\displaystyle \tau _\infty = \lim _{k\rightarrow \infty }\tau _k$ , then we have $\tau _\infty \le \tau _e$ a.s. Next, we will prove that $\tau _\infty =\infty$ a.s. Suppose not. There exist a constant $T > 0$ and $\epsilon \in (0,1)$ such that $P\{\tau _\infty \le T\}>\epsilon$. Therefore, there exists an integer $k_1\ge \xi _0$ so that

$$\begin{aligned} {P\{\tau _k \le T\}\ge \epsilon }\;\;\;\;\; \forall k\ge k_1 \end{aligned}$$

(10)

Define the $C^2$-function $V_1: \mathbb {R}^3_+\rightarrow \mathbb {R}^+$ by:

$$\begin{aligned} V_1(S,I,R ) = (S -1-\ln S) + (I-1-\ln I) + (R-1-\ln R) \end{aligned}$$

(11)

By using Itô’s formula and taking into consideration that $\frac{g(I)}{I}\le g'(0)$, we have

$$\begin{aligned} \begin{aligned} LV_1(S,I,R)=&\Lambda +\lambda +\tau +\mu _1+\mu _2+\mu _3+\frac{\sigma _2^2}{2}+\frac{\sigma _1^2}{2}+\frac{\sigma _3^2}{2}-\mu _2I\\&-\mu _1S-\mu _3R-\frac{\Lambda }{S}-\tau \frac{ R}{S}-\beta g(I)-\beta S\frac{g(I)}{I}-\lambda \frac{I}{R}\\ \le&M_0 \end{aligned} \end{aligned}$$

(12)

where $M_0 =\Lambda +\lambda +\mu _1+\mu _2+\mu _3+\tau +\frac{\sigma _1^2}{2}+\frac{\sigma _2^2}{2}+\frac{\sigma _3^2}{2}.$

Using the expectation (see [26]), we obtain for all $k \ge k_1$

$$\begin{aligned}{} & {} \mathbb {E}V_1(X(T\wedge \tau _k)) =V_1(X(0))\nonumber \\ {}{} & {} +\mathbb {E}\int _0^{T\wedge \tau _k}LV_1(X(t\wedge \tau _k),t\wedge \tau _k)dt\le V_1(X(0)) + M_0 T \end{aligned}$$

(13)

Denote $\Omega _k = \{\tau _k\le T\}$. By (10) we have $P(\Omega _k)\ge \epsilon$, for $k\ge k_1$. On the other hand, we have $V_1(X(T\wedge \tau _k))\ge 0$, thus

$$\begin{aligned} \begin{aligned} \mathbb {E}[V_1(X(T\wedge \tau _k))]=&\mathbb {E}[1_{\Omega _k}V_1(X(T\wedge \tau _k))]+\mathbb {E}[1_{\Omega ^c_k}V_1(X(T\wedge \tau _k))]\\ \ge&\mathbb {E}[1_{\Omega _k}V_1(X(\tau _k))], \end{aligned} \end{aligned}$$

where $1_{\Omega _k}$ represent the indicator function of $\Omega _k$. For every $\omega \in \Omega _k$ , one or more of $S(\tau _k,\omega )$, $I(\tau _k,\omega )$ , $R(\tau _k,\omega )$ equal to $\frac{1}{k}$ or k, thus

$$\begin{aligned} V(S(\tau _k,\omega ); I(\tau _k,\omega ); R(\tau _k,\omega ))\ge (k-1-\ln k ) \wedge ( \frac{1}{k}-1-\ln \frac{1}{k}) \end{aligned}$$

some component of $X(\tau _k,\omega ) =(S(\tau _k,\omega ), I(\tau _k,\omega ),R(\tau _k,\omega ))$ are equal either $\frac{1}{k}$ or k. As a result $V_1(X(T\wedge \tau _k))$ is no less then $k-1-\ln k$ or $\frac{1}{k}-1-\ln \frac{1}{k}$ . Therefore

$$\begin{aligned} V_1(X(\tau _k,\omega ))\ge \Big ((k-1-\ln k)\wedge (\frac{1}{k}-1-\ln \frac{1}{k})\Big ) \end{aligned}$$

(14)

Combining (13)-(14) yields

$$\begin{aligned} \begin{aligned} V_1(X(0))+ M_0 T \ge&\mathbb {E}V_1(X(\tau _k,\omega ))\\ \ge&\mathbb {E}[1_{\Omega _k}V_1( S(T\wedge \tau _k),I(T\wedge \tau _k),R(T\wedge \tau _k) )]\\ \ge&\Big ((k-1-\ln k)\wedge (\frac{1}{k}-1+\ln k)\Big ) \epsilon \end{aligned} \end{aligned}$$

Letting $k \longrightarrow \infty$ leads to the contradiction $\infty > V_1(X(0)+ M_0 T = \infty$. So we must have $\tau _\infty =\infty$ a.s, which means that the solution of the model (4) is positive and global.

Consequently, the proof of Lemma 1 is completed. $\square$

To show that the solution of system (4) is bounded, we need the following Lemma.

Lemma 2

[26] Let A(t) and U(t) be two continuous adapted increasing process on $t\ge 0$ with $A (0) = U(0) = 0$ a.s. Let M(t) be a real-valued continuous local martingale with $M(0)= 0$ a.s.

Let $X_0$ be a nonnegative $\mathcal {F}_0-measurable$ random variable such that $EX_0<\infty$.

Define $X(t)=X_0+A(t)-U(t)+M(t)$ for all $t\ge 0$ .

If X(t) is nonnegative,then $\displaystyle \lim _{t\rightarrow \infty }A(t)< \infty$ implies $\displaystyle \lim _{t\rightarrow \infty }U(t) <\infty ,$  

$\displaystyle \lim _{t\rightarrow \infty }X(t) <\infty$ and $\displaystyle -\infty< \lim _{t\rightarrow \infty }M(t) <\infty$ hold with probability one.

Lemma 3

Let (S(t), I(t), R(t)) be the solution of system (4) with initial value $(S(0),I(0),R(0))\in R^3_+,$ then $\displaystyle \limsup _{t\rightarrow \infty }[S(t)+I(t)+R(t)] <\infty ,$ a.s.

Proof

From the system (4) , we get

$$\begin{aligned}{} & {} d(S(t)+I(t)+R(t))\le [\Lambda -\mu _1(S(t)+I(t)+R(t))dt+\sigma _1 Sd B_1 ( t ) \\ {}{} & {} +\sigma _2 Id B_2 ( t ) +\sigma _3 Rd B_3 ( t ) \end{aligned}$$

Hence by stochastic comparison theorem we have

$$\begin{aligned} S(t)+I(t)+R(t)\le \frac{\Lambda }{\mu _1}+\bigg (S(0)+I(0)+R(0)-\frac{\Lambda }{\mu _1}\bigg ) \text {e}^{-\mu _1t} +M ( t ) \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} M ( t ) =&\sigma _1\int _0^t\text {e}^{-\mu _1(t-u)} S(u)dB_1(u)+\sigma _2\int _0^t\text {e}^{-\mu _1(t-u)} I(u)dB_2(u)\\&+\sigma _3\int _0^t\text {e}^{-\mu _1(t-u)} R(u)dB_3(u) \end{aligned} \end{aligned}$$

M(t) is a continuous local martingale with $M(0) = 0$ a.s.

Define $X(t)=X(0)+A(t)-U(t)+M(t)$, with $X(0)=S(0)+I(0)+R(0)$,

$A(t)=\frac{\Lambda }{\mu _1}(1-e^{-\mu _1t} )$, and $U(t)=(S(0)+I(0)+R(0))(1-e^{-t\mu _1})$ for all $t\ge 0$

And consequently, from the comparison theorem we deduce that $S(t)+I(t)+R(t)\le X(t)$ a.s. Note that A(t) and U(t) are continuous adapted increasing processes on $t\ge 0$ with $A (0) = U(0) = 0$ . By the Lemma 2, we deduce that $\displaystyle \lim _{t\rightarrow \infty } X ( t ) < \infty$ a.s . Thus, the proof has been completed. $\square$

3 Persistence in Mean

In general, for epidemiological models, we are interested in two things. One is when the disease will die out; the other is when the disease will prevail. In this section, we investigate the condition for the persistence of the disease.

Define the number $\mathcal {R}_s$ as follows:

$$\begin{aligned} \mathcal {R}_s= \mathcal {R}_0 - \frac{\sigma _2^2}{2( \lambda + \mu _2)} \end{aligned}$$

(15)

Definition 1

System (4), is said to be persistent in the mean if

$$\begin{aligned} \liminf _{t\rightarrow \infty }\left\langle I \right\rangle _t> 0, \; \; \liminf _{t\rightarrow \infty }\left\langle S \right\rangle _t> 0, \;\text {and} \; \liminf _{t\rightarrow \infty }\left\langle R \right\rangle _t > 0, \; \; a.s \end{aligned}$$

Here and in the sequel, we set $\left\langle x \right\rangle _t= \frac{1}{t} \int _0^t x(r) dr$

We will establish sufficient conditions to discuss persistence in mean , we also need the following lemma presented in [12]

Lemma 4

[12] Let $f \in \mathcal {C}[[0;\infty )\times \Omega ; (0;\infty ) ]$. If there exist positive constants $\lambda _0, \; \lambda$ such that

$$\begin{aligned} \ln f(t)\ge \lambda t - \lambda _0 \int _0^t f(s) ds +F(t) \quad a.s. \end{aligned}$$

for all $t \ge 0$ where $F \in \mathcal {C}[[0;\infty )\times \Omega ; \mathbb {R}]$ and $\displaystyle \lim _{t\rightarrow \infty }\frac{F(t)}{t}=0 \quad a.s.$ Then

$$\begin{aligned} \displaystyle \liminf _{t\rightarrow \infty }\left\langle f \right\rangle _t \ge \frac{\lambda }{\lambda _0} \quad a.s. \end{aligned}$$

Theorem 1

If $\mathcal {R}_s > 1$, then for any initial value $(S(0), I(0), R(0))\in \mathbb {R}_+^3$, the solution (S(t), I(t), R(t)) of system (4) has the following properties:

$$\begin{aligned} \lim _{t\rightarrow \infty }\left\langle S \right\rangle _t= & {} \frac{\Lambda }{\mu _1}>0\,\,\text {a.s.}, \nonumber \\ \liminf _{t\rightarrow \infty }\left\langle I \right\rangle _t\ge & {} \frac{(\lambda +\mu _2 )}{\beta g'(0)(\lambda +\mu _2 )}(\mathcal {R}_s-1)> 0 \,\,\text {a.s.},\nonumber \\ \liminf _{t\rightarrow \infty }\left\langle R \right\rangle _t\ge & {} \frac{(\lambda +\mu _2 )\lambda }{\beta g'(0)( \tau +\mu _3)(\lambda +\mu _2 )}(\mathcal {R}_s-1)> 0 \,\,\,a.s. \end{aligned}$$

(16)

Proof

• First we prove the assertion (16). Define the function $\phi (t)=x S(t)+y I(t)+z R(t).$ From the system (4), we have

  $$\begin{aligned} \begin{aligned} d\phi (t)&=\Big [x(\Lambda -\mu _1 S)+ [z \lambda - y( \mu _2+\lambda ) ]I(t)\Big ]dt\\&+\Big [ \big ( x \tau - z(\tau +\mu _3) \big )R(t)+(y-x)\beta S(t) g(I(t)) \Big ]dt+ dM(t) \end{aligned} \end{aligned}$$

  (17)

  where $M(t)=x\sigma _1\int _0^t S(u) dB_1(u)+y \sigma _2\int _0^t I(u) dB_2(u)+ z \sigma _3 \int _0^t R(u) dB_3(u)$ Let $x=y=1-a$ and $z=1-b$. Define $\phi$ as follows

  $$\begin{aligned} \begin{aligned} d\phi (t)&=\Big [(1-a)(A-\mu _1 S(t))+ (a+ b -1)\mu _2I(t)\\&+ \big ( b(\tau +\mu _3 )-a \tau -\mu _3 \big )R(t)\Big ]dt+ dM(t). \end{aligned} \end{aligned}$$

  Choose a and b such that

  $$\begin{aligned} \left\{ \begin{array}{lrl} b+a&{}= &{} 1 \\ b( \tau +\mu _3 )- a\tau &{}= &{}\mu _3 \end{array} \right. \end{aligned}$$

  (18)

  It’s easy to see that $a=\frac{\tau }{2\tau + \mu _3}\ne 1$ and $b=1-a$ is the unique solution of system (18). Then we have

  $$\begin{aligned} \begin{aligned} d\phi (t)=&(1-a)(A-\mu _1 S(t)) dt+ dM(t). \end{aligned} \end{aligned}$$

  (19)

  By integrating the above equation from 0 to t and dividing by t, we obtain:

  $$\begin{aligned} \left\langle S \right\rangle _t= \frac{A}{\mu _1}+ \frac{\phi (0)-\phi (t)}{(1-a)t}+\frac{M(t)}{(1-a)t}. \end{aligned}$$

  By the Lemma 3 and the law of large numbers we deduce that

  $$\begin{aligned} \lim _{t\rightarrow \infty }\left\langle S \right\rangle _t= \frac{A}{\mu _1}. \end{aligned}$$

  (20)

• First we prove the assertion (16). Define the function $\phi (t)= S(t)+ I(t).$ From the system (4), we have

  $$\begin{aligned} \begin{aligned} d\phi (t)&=\Big [(\Lambda -\mu _1 S) - (\mu _2+\lambda ) I(t)\Big ]dt+ dM(t) \end{aligned} \end{aligned}$$

  (21)

  where $M(t)=\Big [\sigma _1\int _0^t S(u) dB_1(u)\Big ]+\Big [\sigma _2\int _0^t I(u) dB_2(u)\Big ]$

  $$\begin{aligned} \begin{aligned} d\phi (t)&=\Big [(\Lambda -\mu _1 S(t))\Big ]dt+ dM(t). \end{aligned} \end{aligned}$$

  so, we get

  $$\begin{aligned} \begin{aligned} d\phi (t)=&(\Lambda -\mu _1 S(t)) dt+ dM(t). \end{aligned} \end{aligned}$$

  (22)

  By integrating the above equation from 0 to t and dividing by t, we obtain:

  $$\begin{aligned} \left\langle S \right\rangle _t= \frac{\Lambda }{\mu _1}+ \frac{\phi (0)-\phi (t)}{t}+\frac{M(t)}{t}. \end{aligned}$$

  By the Lemma 3 and the law of large numbers we deduce that

  $$\begin{aligned} \lim _{t\rightarrow \infty }\left\langle S \right\rangle _t= \frac{\Lambda }{\mu _1}. \end{aligned}$$

  (23)

• In view of the Itô’s formula,

  $$\begin{aligned} \begin{aligned} \ln I(t)-\ln I(0)=&\int _0^t\Big [\beta S(u)\frac{g(I(u))}{I(u)}-\Big (\lambda +\mu _2+\frac{1}{2}\sigma _2^2\Big )\Big ]du\\&+\sigma _2B_2(t). \end{aligned} \end{aligned}$$

  Integrating both sides from 0 to t and dividing by t gives

  $$\begin{aligned} \begin{aligned} \frac{\ln I(t)}{t}=-\Big (\lambda +\mu _2+\frac{1}{2}\sigma _2^2\Big )+\beta \left\langle S\frac{g(I)}{I}\right\rangle _t + \frac{M_1(t)}{t}, \end{aligned} \end{aligned}$$

  (24)

  where $\displaystyle M_1(t)=\sigma _2B_2(t)+\ln I(0).$ Using the fact that $\frac{g(I)}{I}<g'(0)$, the law of large numbers and the lemma 3 we have

  $$\begin{aligned} \lim _{t\rightarrow \infty }\frac{M_1(t)}{t} = 0. \end{aligned}$$

  (25)

  Moreover we have

  $$\begin{aligned} \begin{aligned} \frac{\ln I(t)}{t}\geqslant -\Big (\lambda +\mu _2+\frac{1}{2}\sigma _2^2\Big )+\beta \left\langle S\frac{g(I)}{I}\right\rangle _t + \frac{M_1(t)}{t}. \end{aligned} \end{aligned}$$

  (26)

  From the two first equations of system (4) we deduce that

  $$\begin{aligned} \begin{aligned}&d(S+I)=[\Lambda -\mu _1 S-(\lambda +\mu _2)I+ \tau R(t)] dt \\ {}&\quad +\sigma _1 S(t) dB_1(t) +\sigma _2 I(t) dB_2(t) \end{aligned} \end{aligned}$$

  (27)

  using the fact that $\frac{g(I)}{I} < g'(0)$ and $R(t)\ge 0$ we conclude that

  $$\begin{aligned} \begin{aligned}&d(S+I)\ge \Big [\Lambda - \dfrac{\mu _1}{g'(0)} S(t) \frac{g(I(t))}{I(t)}-(\lambda +\mu _2)I(t)\Big ] dt \\ {}&\quad +\sigma _1 S(t)dB_1(t) +\sigma _2 I(t) dB_2(t) \end{aligned} \end{aligned}$$

  (28)

  Consequently, we have

  $$\begin{aligned} \begin{aligned} S(t)+I(t) \ge \Lambda t- \frac{\mu _1}{g'(0)} \int _0^t S(u) \frac{g(I(u))}{I(u)}du-(\lambda +\mu _2)\int _0^t I(u)du + M_3(t) \end{aligned}\nonumber \\ \end{aligned}$$

  (29)

  where $M_3(t)=\sigma _1 \int _0^t S(u)dB_1(u)+\sigma _2 \int _0^tI(u) dB_2(u)+ S(0)+I(0).$ By the Lemma 3 and the law of large numbers we have

  $$\begin{aligned} \lim _{t\rightarrow \infty }\frac{M_3(t)}{t} = 0 \end{aligned}$$

  (30)

  Now let us define V by $V(t)=\ln (I(t)) +\frac{\beta g'(0)}{\mu _1}(S(t)+I(t)).$ Using Itô’s formula, and combining (29) and (32) we obtain

  $$\begin{aligned} \begin{aligned} \frac{V(t)-V(0)}{t}&\ge \frac{\Lambda \beta g'(0)}{\mu _1}- \frac{\beta g'(0)}{\mu _1}(\lambda +\mu _2)\left\langle I \right\rangle _t - (\lambda +\mu _2 + \frac{\sigma _2^2}{2} )\\ {}&+ \frac{M_4(t)}{t} \end{aligned} \end{aligned}$$

  (31)

  where $M_4(t)=M_1(t)+\frac{\beta g'(0)}{\mu _1} M_3(t).$ From (23), we deduce that

  $$\begin{aligned} \begin{aligned} \frac{\ln I(t)}{t} \ge&\frac{\Lambda \beta g'(0)}{\mu _1}- (\lambda +\mu _2 + \frac{\sigma _2^2}{2} ) -\frac{\beta g'(0)(\lambda +\mu _2 )}{\mu _1}\left\langle I \right\rangle _t + \frac{M_5(t)}{t}. \\ =&(\lambda +\mu _2 )(\mathcal {R}_s-1)-\frac{\beta g'(0)(\lambda +\mu _2 )}{\mu _1}\left\langle I \right\rangle _t + \frac{M_5(t) }{t}, \end{aligned} \end{aligned}$$

  (32)

  where $M_5(t)=M_4(t)+V(0)-\frac{\beta g'(0)}{\mu _1} (S(t)+I(t)).$ Making use of (25) and (30), and by lemma 3, one can obtain that

  $$\begin{aligned} \lim _{t\rightarrow \infty }\frac{M_5(t)}{t} = 0. \end{aligned}$$

  (33)

  This, yields by Lemma 4 that

  $$\begin{aligned} \displaystyle \liminf _{t\rightarrow \infty }\left\langle I \right\rangle _t \ge \frac{(\lambda +\mu _2 )}{\beta g'(0)(\lambda +\mu _2 )}(\mathcal {R}_s-1) \,\,a.s. \end{aligned}$$

• The third equation of system (4) gives $\left\langle R(t) \right\rangle _t= \frac{\lambda }{\tau + \mu _3}\left\langle I(t) \right\rangle _t+\frac{\overline{F}(t)}{t}$ , where $\overline{F}(t)=\frac{\sigma _3}{\tau +\mu _3}\int ^t_0R(u)dB_3(u)du-\frac{R(t)-R(0)}{\tau +\mu _3}.$ From the large number theorem for martingales, and using the Theorem 2, we deduce that $\displaystyle \lim _{t\rightarrow \infty }\frac{\overline{F}(t)}{t} = 0$. Thus the proof of Theorem 1 is completed.

$\square$

4 Extinction of the Disease

In this section, we investigate sufficient conditions for the extinction of the disease of the system (4).

Theorem 2

Let (S(t), I(t), R(t)) be the solution of system (4) with initial value $(S(0), I(0), R (0))\in \mathbb {R}^3_+$. If $\mathcal {R}_s< 1$, then

$$\begin{aligned} \displaystyle \limsup _{t\rightarrow \infty } \frac{\ln (I (t))}{t} \le (\lambda +\mu _2) (\mathcal {R}_s-1) < 0\;\;\;\;a.s., \end{aligned}$$

thus I(t) tends to zero exponentially almost surely.

Proof

From (24) it is easy to obtain

$$\begin{aligned} \frac{\ln I(t)}{t}=-\Big (\lambda +\mu _2+\frac{1}{2}\sigma _2^2\Big )+\beta \left\langle S\frac{g(I)}{I}\right\rangle _t + \frac{M_1(t)}{t}. \end{aligned}$$

(34)

where $\displaystyle \lim _{t\rightarrow \infty }\frac{M_1(t)}{t} = 0$.

On the other hand, using (23) and the fact that $\displaystyle \frac{g(I)}{I} < g'(0)$ we have

$$\begin{aligned} \displaystyle 0 \le {\limsup _{t\rightarrow \infty }\left\langle S\frac{g(I)}{I} \right\rangle _t} \le \frac{\Lambda g'(0)}{\mu _1}. \end{aligned}$$

Let us consider the function f by $f(x)=\beta x -\Big (\lambda +\mu _2+\frac{1}{2}\sigma _2^2\Big )$, for all x in $[0,\frac{\Lambda g'(0)}{\mu _1}]$.

Since f is increasing on $\left[ 0; \frac{\Lambda g'(0)}{\mu _1}\right]$, so by taking $\displaystyle x={ \limsup _{t\rightarrow \infty }\left\langle S(u)\frac{g(I)}{I} \right\rangle _t}$ we notice that

$$\begin{aligned} f(x) \le f\left( \frac{\Lambda g'(0)}{\mu _1}\right) . \end{aligned}$$

(35)

By letting t goes to $\infty$ in (34),and using (35),we derive that

$$\begin{aligned} \displaystyle \limsup _{t\rightarrow \infty }\frac{\ln I(t)}{t} \le \Big (\lambda +\mu _2\Big ) ( \mathcal {R}_s -1)\quad \text {a.s.} \end{aligned}$$

wich indicates that if $\mathcal {R}_s< 1$ the disease will die out exponentially with probability one.

This finishes the proof of Theorem 2. $\square$

5 Existence of Ergodic Stationary Distribution

Since stochastic systems have no endemic equlibria then we are led to use the theory of existence/uniqueness of the stationary distribution which is in some sense a tool for studying the disease persistence. Thus, we referred in this part to Hasminskii’s result in [8] to give sufficient conditions for the existence of a unique ergodic stationary distribution.

Now, let X(t) be a homogeneous Markov process in $\mathbb {R}^d$, and satisfy the following equation stochastic differential equation

$$\begin{aligned} dX(t)=f(X)dt+\sum ^l_{r=1}g_r(X)dW_r(t) \end{aligned}$$

then the diffusion matrix is defined as

$$\begin{aligned} \Lambda (x)=(\lambda _{i,j}(x)),\;\;\;\;\;\;\; \lambda _{i,j}(x)=\sum ^l_{r=1}g^i_r(x)g^j_r(x) \end{aligned}$$

Thus, we have the lemma as follows

Lemma 5

[8] The Markov process X(t) has a unique ergodic stationary distribution $\pi (.)$ if a bounded domain $D \subset \mathbb {R}^d$ with regular boundary $\Gamma$ exist and

• 1. There exists a constant M satisfying $\displaystyle \sum ^d_{i,j=1}\lambda _{i,j}(x)\xi _i\xi _j\ge M|\xi |^2,\;x\in D, \; \xi \in \mathbb {R}^d$

• 2. There exist nonnegative $C^2 -$function $V:D^c\rightarrow \mathbb {R}$, such that LV is negative for any $x\in D^c=\mathbb {R}^3\setminus D$. Here L is the operator defined in (6).Then

$$\begin{aligned} P_x\left\{ \underset{T\rightarrow \infty }{lim}\frac{1}{T}\int _0^Tf(X(t))dt=\int _{\mathbb {R}^d}f(x){\pi }(dx) \right\} =1,\;\;\;\;\forall x\in \mathbb {R}^d \end{aligned}$$

for any $x\in \mathbb {R}^d$, where f(.) is an integrable function with respect to the measure $\pi$.

Define a parameter

$$\begin{aligned} R_0^s=\frac{\Lambda \beta g'(0)}{\mu _1(\lambda +\Lambda +\mu _2) }-\frac{\frac{\sigma _2^2}{2}}{(\lambda +\Lambda +\mu _2)} \end{aligned}$$

Theorem 3

Assume that $R_0^s>1$, then system (4) has a unique stationary distribution and it has the ergodic property.

Proof

To prove Theorem 3, we need to check that each condition of Lemma 5 is satisfied.

Next, we tend to prove the second condition in Lemma 5 by constructing suitable Lyapunov function.

Let (S(t); I(t); R(t)) be a solution of system (4) with any given initial value (S(0); I(0); R(0)) . Then we construct a $C^2$-function $\widehat{V} : \mathbb {R}^3_+\rightarrow \mathbb {R}$ as following:

$$\begin{aligned} \widehat{V}=\widehat{M}(S+I+R-c_1\ln S-\ln I)-\ln S-\ln R+\frac{1}{\theta +2}(S+I+R)^{\theta +2} \end{aligned}$$

More simply we write $\widehat{V}:=\widehat{M}V_4+V_5+V_6$, where $V_4=S+I+R-c_1\ln S-\ln I$, $V_5=-\ln S-\ln R$, $V_6=\frac{1}{\theta +2}(S+I+R)^{\theta +2}$.

where $c_1$ the positive constant and need to be determined later on, $\theta$ is a constant satisfying $0<\theta <\frac{\mu _1}{\frac{(\sigma _1^2\vee \sigma _2^2\vee \sigma _3^2)}{2}}-1$, the $\widehat{M}$ is a positive constant and satisfies the following condition

$$\begin{aligned} -\widehat{M}\lambda +C\le -2 \end{aligned}$$

(36)

where $\lambda =(\gamma +\beta +\mu _2)(R_0^s-1)>0$ , and

$$\begin{aligned} C=\sup _{(S,I,R)\in \mathbb {R}^3_+} \Big \{-\frac{1}{2}(\mu _1-\frac{(\theta +1)}{2}(\sigma _1^2\vee \sigma _2^2 \vee \sigma _3^2))(S+I+R)^{\theta +2}-\frac{\Lambda }{S} \nonumber \\ -\lambda \frac{I}{R} +\widehat{M}c_1(\mu _1+\frac{\sigma _1^2}{2})+\mu _1+\mu _3+\tau +\frac{\sigma _1^2}{2}+\frac{\sigma _3^2}{2} +B \Big \} \end{aligned}$$

(37)

where

$$\begin{aligned}{} & {} B=\sup _{(S,I,R)\in \mathbb {R}^3_+}\Big \{ \Lambda (S+I+R)^{\theta +1} \nonumber \\ {}{} & {} -\frac{1}{2}(\mu _1-\frac{(\theta +1)}{2}(\sigma _1^2\vee \sigma _2^2 \vee \sigma _3^2))(S+I+R)^{\theta +2} \Big \}<\infty \end{aligned}$$

(38)

It is easy to check that

$$\begin{aligned} \liminf _{k\rightarrow \infty ,(S,I,R)\in \mathbb {R}_+^3\backslash D_k} \widehat{V}(S,I,R)=+\infty \end{aligned}$$

where $D_k =(\frac{1}{k},k)\times (\frac{1}{k},k)\times (\frac{1}{k},k)$. Furthermore, $\widehat{V} (S, I, R)$ is a continuous function, which exists a minimum point $(\bar{S}_0,\bar{I}_0,\bar{R}_0)$ in the interior of $\mathbb {R}_+^3$. Then we define a nonnegative $C^2$-function $V : \mathbb {R}_+^3\longrightarrow \mathbb {R}_+$ as follows

$$\begin{aligned} V(S,I,R)=\widehat{V}(S,I,R)-\widehat{V}(\bar{S}_0,\bar{I}_0,\bar{R}_0) \end{aligned}$$

Applying Itô’s formula for $V_4$, we can see

$$\begin{aligned} \begin{aligned} LV_4=&\Lambda -\mu _1S-\mu _2I-\mu _3R+ c_1( -\frac{\Lambda }{S}+\beta g(I)-\tau \frac{R}{S}+\mu _1+\frac{\sigma _1^2}{2}) -\beta \frac{g(I)}{I}S\\&+\lambda +\mu _2+\frac{\sigma _2^2}{2}\\ \le&-c_1\frac{\Lambda }{S}-\mu _1S+\lambda +\mu _2+\Lambda +\frac{\sigma _2^2}{2}+ c_1\mu _1+c_1\frac{\sigma _1^2}{2}+c_1\beta g(I)-c_1\frac{\tau R}{S}\\ \le&-2(\Lambda \mu _1 c_1)^{\frac{1}{2}}+\lambda +\mu _2+\Lambda +\frac{\sigma _2^2}{2}+ c_1\mu _1+c_1\frac{\sigma _1^2}{2}+c_1\beta g'(0) I \end{aligned} \end{aligned}$$

Remark that $-c_1\frac{\Lambda }{S}-\mu _1S\le -2(\Lambda \mu _1 c_1)^{\frac{1}{2}}$.

Let

$$\begin{aligned} c_1=\frac{\Lambda \beta ^2 g'(0)^2}{4\mu _1^\frac{3}{2}} \end{aligned}$$

Consequently

$$\begin{aligned} \begin{aligned} LV_4\le&- \Big [(\lambda +\Lambda +\mu _2)\Big (\frac{\beta \Lambda g'(0)}{\mu _1(\lambda +\Lambda +\mu _2) }-\frac{\frac{\sigma _2^2}{2}}{(\lambda +\Lambda +\mu _2)}-1 \Big )\Big ]+ c_1\mu _1\\&+c_1\frac{\sigma _1^2}{2}+c_1\beta g'(0) I \\ \le&-(\gamma +\beta +\mu _2)(R_0^s-1)+ c_1\mu _1+c_1\frac{\sigma _1^2}{2}+c_1\beta g'(0) I \end{aligned} \end{aligned}$$

In addition, we can obtain

$$\begin{aligned} \begin{aligned} LV_5=&-\frac{\Lambda }{S}-\tau \frac{R}{S} -\lambda \frac{I}{R}+\mu _1+\mu _3+\tau +\frac{\sigma _1^2}{2}+\frac{\sigma _3^2}{2} +\beta g(I) \\ \le&-\frac{\Lambda }{S}-\lambda \frac{I}{R}+\beta g'(0) I+\mu _1+\mu _3+\tau +\frac{\sigma _1^2}{2}+\frac{\sigma _3^2}{2} \end{aligned} \end{aligned}$$

Similarly, we have

$$\begin{aligned} \begin{aligned} LV_6=&(S+I+R)^{\theta +1}(\Lambda -\mu _1S-\mu _2I-\mu _3R)\\ {}&\quad +\frac{1}{2}(\theta +1)(S+I+R)^{\theta }(\sigma _1^2 S^2+\sigma _2^2 I^2+\sigma _3^2R^2) \\ \le&(S+I+R)^{\theta +1}(\Lambda -\mu _1(S+I+R))\\ {}&\quad +\frac{1}{2}(\theta +1)(\sigma _1^2\vee \sigma _2^2 \vee \sigma _3^2)(S+I+R)^{\theta +2} \\ \le&\Lambda (S+I+R)^{\theta +1}-\mu _1(S+I+R)^{\theta +2}\\ {}&\quad +\frac{1}{2}(\theta +1)(\sigma _1^2\vee \sigma _2^2 \vee \sigma _3^2)(S+I+R)^{\theta +2} \\ \le&B-\frac{1}{2}(\mu _1-\frac{(\theta +1)}{2}(\sigma _1^2\vee \sigma _2^2 \vee \sigma _3^2))(S+I+R)^{\theta +2} \end{aligned} \end{aligned}$$

because $\mu _1 < min(\mu _2; \mu _3)$ where

$$\begin{aligned}{} & {} B=\sup _{(S,I,R)\in \mathbb {R}^3_+}\Big \{ \Lambda (S+I+R)^{\theta +1} \\ {}{} & {} -\frac{1}{2}(\mu _1-\frac{(\theta +1)}{2}(\sigma _1^2\vee \sigma _2^2 \vee \sigma _3^2))(S+I+R)^{\theta +2} \Big \}<\infty \end{aligned}$$

The differential operator L acting on the function V yields

$$\begin{aligned} \begin{aligned} LV\le&\widehat{M} \Big \{-(\gamma +\beta +\mu _2)(R_0^s-1)+ c_1\mu _1+c_1\frac{\sigma _1^2}{2}+c_1\beta g'(0) I \Big \} \\&-\frac{\Lambda }{S}-\lambda \frac{I}{R}+\beta g'(0) I+\mu _1+\mu _3+\tau +\frac{\sigma _1^2}{2}+\frac{\sigma _3^2}{2} +B\\&-\frac{1}{2}(\mu _1-\frac{(\theta +1)}{2}(\sigma _1^2\vee \sigma _2^2\vee \sigma _3^2))(S+I+R)^{\theta +2} \\ =&(\widehat{M}c_1\beta +\beta )g'(0)I+ \widehat{M}c_1(\mu _1+\frac{\sigma _1^2}{2}) -\lambda \frac{I}{R}\\&+\mu _1+\mu _3+\tau +\frac{\sigma _1^2}{2}+\frac{\sigma _3^2}{2} -\frac{\Lambda }{S}\\&+B-\frac{1}{2}(\mu _1-\frac{(\theta +1)}{2}(\sigma _1^2\vee \sigma _2^2 \vee \sigma _3^2))(S+I+R)^{\theta +2} \end{aligned} \end{aligned}$$

Now we are in the position to construct a compact subset D such that the condition 2 in Lemma 5 holds. Define the following bounded closed set

$$\begin{aligned} D=\Big \{\epsilon \le S\le \frac{1}{\epsilon },\epsilon \le I\le \frac{1}{\epsilon },\epsilon ^2\le R\le \frac{1}{\epsilon ^2}\Big \} \end{aligned}$$

where $\epsilon > 0$ is sufficiently small constant . In the set $\mathbb {R}^3_+\backslash D$, we can choose $\epsilon >0$ satisfying the following inequalities (39)-(44)

$$\begin{aligned}{} & {} \quad \quad \quad \widehat{K}_1-\frac{\Lambda }{\epsilon }\le -1 \end{aligned}$$

(39)

$$\begin{aligned}{} & {} \quad \quad \quad (\widehat{M}c_1\beta +\beta )g'(0)\epsilon +C \le -1 \end{aligned}$$

(40)

$$\begin{aligned}{} & {} \quad \quad \quad \widehat{K}_1-\frac{\lambda }{\epsilon }\le -1 \end{aligned}$$

(41)

$$\begin{aligned}{} & {} \widehat{K}_2-\frac{1}{4}(\mu _1-\frac{(\theta +1)}{2}(\sigma _1^2\vee \sigma _2^2 \vee \sigma _3^2))\frac{1}{\epsilon ^{\theta +2}}\le -1 \end{aligned}$$

(42)

$$\begin{aligned}{} & {} \widehat{K}_3-\frac{1}{4}(\mu _1-\frac{(\theta +1)}{2}(\sigma _1^2\vee \sigma _2^2 \vee \sigma _3^2))\frac{1}{\epsilon ^{\theta +2}}\le -1 \end{aligned}$$

(43)

$$\begin{aligned}{} & {} \widehat{K}_4-\frac{1}{4}(\mu _1-\frac{(\theta +1)}{2}(\sigma _1^2\vee \sigma _2^2 \vee \sigma _3^2))\frac{1}{\epsilon ^{2\theta +4}}\le -1 \end{aligned}$$

(44)

where $\widehat{K}_i (i = 1, 2, 3, 4)$ are positive constants which can be found from the following inequations (5.11), (5.15), (5.17) and (5.19). For convenience, we divide $\mathbb {R}^3_+\backslash D$ into the following six domains,

$$\begin{aligned} \begin{array}{lll} D_1=\{ (S,I,R)\in \mathbb {R}^3_+,0<S<\epsilon \}, &{} D_2=\{ (S,I,R)\in \mathbb {R}^3_+,0<I<\epsilon \}, \\ D_3=\{ (S,I,R)\in \mathbb {R}^3_+,0<R<\epsilon ^2,I\ge \epsilon \}, &{} D_4=\Big \{(S,I,R)\in \mathbb {R}^3_+,S>\frac{1}{\epsilon }\Big \},\\ D_5=\Big \{(S,I,R)\in \mathbb {R}^3_+,I>\frac{1}{\epsilon }\Big \}, &{} D_6=\Big \{(S,I,R)\in \mathbb {R}^3_+,R>\frac{1}{\epsilon ^2}\Big \}. \end{array} \end{aligned}$$

Clearly, $D^C=D_1\cup D_2\cup D_3\cup D_4\cup D_5\cup D_6$. Thus, we only need to prove $LV (S, I, R) <-1$ on the above six domains.

Next we will show that on $D^C$ .

• Case 1. If $(S, I, R)\in D_1$, we have

  $$\begin{aligned} \begin{aligned} LV\le&-\frac{\Lambda }{S}+(\widehat{M}c_1\beta +\beta )g'(0)I+ \widehat{M}c_1(\mu _1+\frac{\sigma _1^2}{2}) -\lambda \frac{I}{R}\\ {}&+\mu _1+\mu _3+\tau +\frac{\sigma _1^2}{2}+\frac{\sigma _3^2}{2} \\&+B-\frac{1}{2}(\mu _1-\frac{(\theta +1)}{2}(\sigma _1^2\vee \sigma _2^2 \vee \sigma _3^2))(S+I+R)^{\theta +2} \\ \le&\widehat{K}_1-\frac{\Lambda }{\epsilon } \end{aligned} \end{aligned}$$

  (45)

  where

  $$\begin{aligned}{} & {} \widehat{K}_1=\sup _{(S,I,R)\in \mathbb {R}^3_+} \Big \{ B-\frac{1}{2}(\mu _1-\frac{(\theta +1)}{2}(\sigma _1^2\vee \sigma _2^2 \vee \sigma _3^2))(S+I+R)^{\theta +2}\nonumber \\{} & {} \quad +(\widehat{M}c_1\beta +\beta )g'(0)I+\widehat{M}c_1(\mu _1+\frac{\sigma _1^2}{2})+\mu _1+\mu _3+\tau +\frac{\sigma _1^2}{2}+\frac{\sigma _3^2}{2} \Big \}\nonumber \\ \end{aligned}$$

  (46)

  In view of (39), we get $LV \le -1$ for any $(S, I, R)\in D_1$.

• Case 2. If $(S, I, R)\in D_2$, one can see that

  $$\begin{aligned} \begin{aligned}&LV \le (\widehat{M}c_1\beta +\beta )g'(0)I+ \widehat{M}c_1(\mu _1+\frac{\sigma _1^2}{2})-\frac{\Lambda }{S} -\lambda \frac{I}{R}\\&+\mu _1+\mu _3+\tau +\frac{\sigma _1^2}{2}+\frac{\sigma _3^2}{2} \\&+B-\frac{1}{2}(\mu _1-\frac{(\theta +1)}{2}(\sigma _1^2\vee \sigma _2^2 \vee \sigma _3^2))(S+I+R)^{\theta +2}\\&\le (\widehat{M}c_1\beta +\beta )g'(0)I+C \end{aligned} \end{aligned}$$

  (47)
  $$\begin{aligned} LV \le (\widehat{M}c_1\beta +\beta )g'(0)\epsilon +C \end{aligned}$$

  (48)

  According to (36),(40), one can obtain that $LV \le -1$ for any $(S, I, R)\in D_2$.

• Case 3. If $(S, I, R)\in D_3$, we obtain

  $$\begin{aligned} \begin{aligned} LV\le&-\lambda \frac{I}{R}+(\widehat{M}c_1\beta +\beta )g'(0)I+ \widehat{M}c_1(\mu _1+\frac{\sigma _1^2}{2}) \\ {}&+\mu _1+\mu _3+\tau +\frac{\sigma _1^2}{2}+\frac{\sigma _3^2}{2} \\ {}&+B-\frac{1}{2}(\mu _1-\frac{(\theta +1)}{2}(\sigma _1^2\vee \sigma _2^2 \vee \sigma _3^2))(S+I+R)^{\theta +2}\\ \le&\widehat{K}_1-\lambda \frac{ 1}{\epsilon } \end{aligned} \end{aligned}$$

  (49)

  Together with (41), we can deduce that $LV \le -1$ for any $(S, I, R)\in D_3$.

• Case 4. If $(S, I, R)\in D_4$, one can derive that

  $$\begin{aligned} \begin{aligned} LV\le&-\frac{1}{4}(\mu _1-\frac{(\theta +1)}{2}(\sigma _1^2\vee \sigma _2^2 \vee \sigma _3^2))S^{\theta +2} \\ {}&-\frac{1}{4}(\mu _1-\frac{(\theta +1)}{2}(\sigma _1^2\vee \sigma _2^2 \vee \sigma _3^2))S^{\theta +2}\\ {}&-\frac{1}{2}(\mu _1-\frac{(\theta +1)}{2}(\sigma _1^2\vee \sigma _2^2 \vee \sigma _3^2))(I+R)^{\theta +2}+(\widehat{M}c_1\beta +\beta )g'(0)I\\ {}&+ \widehat{M}c_1(\mu _1+\frac{\sigma _1^2}{2})-\frac{\Lambda }{S} -\lambda \frac{I}{R} +\mu _1+\mu _3+\tau +\frac{\sigma _1^2}{2}+\frac{\sigma _3^2}{2} +B\\ \le&\widehat{K}_2-\frac{1}{4}(\mu _1-\frac{(\theta +1)}{2}(\sigma _1^2\vee \sigma _2^2 \vee \sigma _3^2))S^{\theta +2}\\ \le&\widehat{K}_2-\frac{1}{4}(\mu _1-\frac{(\theta +1)}{2}(\sigma _1^2\vee \sigma _2^2 \vee \sigma _3^2))\frac{1}{\epsilon ^{\theta +2}} \end{aligned} \end{aligned}$$

  (50)

  where

  $$\begin{aligned}{} & {} \widehat{K}_2=\sup _{(S,I,R)\in \mathbb {R}^3_+} \Big \{-\frac{1}{4}(\mu _1-\frac{(\theta +1)}{2}(\sigma _1^2\vee \sigma _2^2 \vee \sigma _3^2))S^{\theta +2}\nonumber \\ {}{} & {} +\widehat{M}c_1(\mu _1+\frac{\sigma _1^2}{2})+\mu _1+\mu _3 \nonumber \\ {}{} & {} +\tau +\frac{\sigma _1^2}{2}+\frac{\sigma _3^2}{2} +B +(\widehat{M}c_1\beta +\beta )g'(0)I\nonumber \\ {}{} & {} -\frac{1}{2}(\mu _1-\frac{(\theta +1)}{2}(\sigma _1^2\vee \sigma _2^2 \vee \sigma _3^2))(I+R)^{\theta +2} \Big \} \end{aligned}$$

  (51)

  In view of (42) and , we can conclude that $LV \le -1$ on $D_4$.

• Case 5. If $(S, I, R)\in D_5$, one can obtain that

  $$\begin{aligned} \begin{aligned} LV\le&-\frac{1}{4}(\mu _1-\frac{(\theta +1)}{2}(\sigma _1^2\vee \sigma _2^2 \vee \sigma _3^2))I^{\theta +2} \\ {}&-\frac{1}{4}(\mu _1-\frac{(\theta +1)}{2}(\sigma _1^2\vee \sigma _2^2 \vee \sigma _3^2))I^{\theta +2} \\ {}&-\frac{1}{2}(\mu _1-\frac{(\theta +1)}{2}(\sigma _1^2\vee \sigma _2^2 \vee \sigma _3^2))(S+R)^{\theta +2} \\ {}&-\frac{\Lambda }{S}+(\widehat{M}c_1\beta +\beta )g'(0)I\\ {}&+ \widehat{M}c_1(\mu _1+\frac{\sigma _1^2}{2})-\lambda \frac{I}{R} +\mu _1+\mu _3+\tau +\frac{\sigma _1^2}{2}+\frac{\sigma _3^2}{2}+B \\ \le&\widehat{K}_3-\frac{1}{4}(\mu _1-\frac{(\theta +1)}{2}(\sigma _1^2\vee \sigma _2^2 \vee \sigma _3^2))I^{\theta +2}\\ \le&\widehat{K}_3-\frac{1}{4}(\mu _1-\frac{(\theta +1)}{2}(\sigma _1^2\vee \sigma _2^2 \vee \sigma _3^2))\frac{1}{\epsilon ^{\theta +2}} \end{aligned} \end{aligned}$$

  (52)

  where

  $$\begin{aligned}{} & {} \widehat{K}_3=\sup _{(S,I,R)\in \mathbb {R}^3_+} \Big \{ -\frac{1}{4}(\mu _1-\frac{(\theta +1)}{2}(\sigma _1^2\vee \sigma _2^2 \vee \sigma _3^2))I^{\theta +2} \nonumber \\ {}{} & {} +(\widehat{M}c_1\beta +\beta )g'(0)I+\mu _1+\mu _3 \nonumber \\ {}{} & {} +\tau +\widehat{M}c_1(\mu _1+\frac{\sigma _1^2}{2})+\frac{\sigma _1^2}{2}+\frac{\sigma _3^2}{2} +B\nonumber \\ {}{} & {} -\frac{1}{2}(\mu _1-\frac{(\theta +1)}{2}(\sigma _1^2\vee \sigma _2^2 \vee \sigma _3^2))(S+R)^{\theta +2} \Big \} \end{aligned}$$

  (53)

  Combining with (43) we have $LV \le -1$ on $D_5$.

• Case 6. If $(S, I, R)\in D_6$, one can see that

  $$\begin{aligned} \begin{aligned} LV\le&-\frac{1}{4}(\mu _1-\frac{(\theta +1)}{2}(\sigma _1^2\vee \sigma _2^2 \vee \sigma _3^2))R^{\theta +2} \\ {}&\quad -\frac{1}{4}(\mu _1-\frac{(\theta +1)}{2}(\sigma _1^2\vee \sigma _2^2 \vee \sigma _3^2))R^{\theta +2} \\&-\frac{1}{2}(\mu _1-\frac{(\theta +1)}{2}(\sigma _1^2\vee \sigma _2^2 \vee \sigma _3^2))(S+I)^{\theta +2} +(\widehat{M}c_1\beta +\beta )g'(0)I \\ {}&+\widehat{M}c_1(\mu _1+\frac{\sigma _1^2}{2}) +\mu _1+\mu _3+\tau +\frac{\sigma _1^2}{2}+\frac{\sigma _3^2}{2} +B \\ \le&\widehat{K}_4-\frac{1}{4}(\mu _1-\frac{(\theta +1)}{2}(\sigma _1^2\vee \sigma _2^2 \vee \sigma _3^2))R^{\theta +2}\\ \le&\widehat{K}_4-\frac{1}{4}(\mu _1-\frac{(\theta +1)}{2}(\sigma _1^2\vee \sigma _2^2 \vee \sigma _3^2))\frac{1}{\epsilon ^{2\theta +4}} \end{aligned} \end{aligned}$$

  (54)

  where

  $$\begin{aligned}{} & {} \widehat{K}_4=\sup _{(S,I,R)\in \mathbb {R}^3_+} \Big \{ -\frac{1}{4}(\mu _1-\frac{(\theta +1)}{2}(\sigma _1^2\vee \sigma _2^2 \vee \sigma _3^2))R^{\theta +2}+\mu _1+\mu _3+\tau +B \nonumber \\{} & {} \quad +(\widehat{M}c_1\beta +\beta )g'(0)I+\widehat{M}c_1(\mu _1+\frac{\sigma _1^2}{2})+\frac{\sigma _1^2}{2}+\frac{\sigma _3^2}{2}\nonumber \\{} & {} \quad -\frac{1}{2}(\mu _1-\frac{(\theta +1)}{2}(\sigma _1^2\vee \sigma _2^2 \vee \sigma _3^2))(S+I)^{\theta +2} \Big \} \end{aligned}$$

  (55)

  Consequently, from (44) we can get $LV \le -1$ on $D_6$. It then follows from equations (45), (48), (49), (50), (52) and (54) that for a sufficiently small $\epsilon$, we have

  $$\begin{aligned} LV(S,I,R)\le -1\;\;\; for \;\;all\;\;\;(S,I,R)\in \mathbb {R}^3_+\setminus D \end{aligned}$$

So the condition 1 in Lemma 5 is satisfied.

Now we check condition (2) in Lemma 5. First, the diffusion matrix of the stochastic model (4) is given by

$$\begin{aligned} A(x)=( \lambda _{i,j}(x) )= \begin{pmatrix} \sigma _{1}^{2}S^{2}&{} 0 &{} 0\\ 0 &{} \sigma _{2}^{2}I^{2} &{} 0\\ 0 &{} 0 &{} \sigma _{3}^{2}R^{2} \end{pmatrix} \end{aligned}$$

where $x=((S(t),I(t),R(t))$. We can conclude that

$$\begin{aligned} \sum ^3_{i,j=1}\lambda _{i,j}(x)\xi _i\xi _j= & {} (\sigma _1 S)^2 \xi _1^2+(\sigma _2 I)^2 \xi _2^2+(\sigma _3 R)^2\xi _3^2\\ \ge M |\xi |^2 \end{aligned}$$

for all $\xi =(\xi _1, \xi _2, \xi _3 ) \in \mathbb {R}^3$ and $(S(t),I(t),R(t))\in D_k$

where $\displaystyle M=\min _{(S,I,R)\in D_k}\{\sigma _1^2S^2, \sigma _2^2I^2, \sigma _3^2R^2\}.$

Then the condition 2 in Lemma 5 holds .

This complete the proof that the solution (S(t), I(t), R(t)) of the stochastic model (4) has a unique ergodic stationary distribution. $\square$

6 Conclusions and Numerical Simulations

This paper has been concerned with the stochastic SIRS model with a general nonlinear incidence function for the dynamic behaviors of an infectious disease. We considered a white noise representing changes in the transmission rate resulting from variations in the environment, this allows us to define a stochastic threshold quantity $\mathcal {R}_s,$ which served to explore the extinction and the persistence of the disease. First of all, we have studied the existence, uniqueness and positivity of the global solution to the proposed model by constructing suitable stochastic Lyapunov functions. The proven extinction result shows that the disease dies out almost surely when $\mathcal {R}_s < 1$, on the other hand, we will have disease persistence if $\mathcal {R}_s> 1$. Finally, in order to derive the sufficient criterion for the persistence we proved that the solution of the stochastic model (4) admits a stationary distribution and that it is ergodic by using a result mentioned by Hasminskii [8].

Now, to verify the effectiveness of the theoretical results, we will give some examples with computer simulations using the Euler-Maruyama (EM) method [14] and by choosing the time step size $\Delta t= 2^{-9}$ and the initial value $(S(0);I(0);R(0))= (0.7; 0.1; 0.1)$. For the sake of simplicity, we choose incidence function $g (I) = \frac{I}{1 + I}.$

Example 1

In this example, we consider the the parameters values $\Lambda =0.3$; $\beta =0.45$; $\mu _1=0.2$; $\mu _2=0.3$; $\mu _3=0.4$; $\tau =0.5$; $\lambda =0.4$; $\sigma _1=0.08$; $\sigma _2=0.3$; $\sigma _3=0.2$. In this example, we have $\mathcal {R}_0=0.9642$ and $\mathcal {R}_s =0.9$.

In this case, the condition $\mathcal {R}_s < 1$ is satisfied. By Theorem 2, we know that I(t) will tend to zero, i.e., the disease will disappear. Figure (Fig.1) clearly support this result.

Fig. 1

Trajectories of stochastic and deterministic systems at time $T=100$ and using the parameters values given in Example 1

Example 2

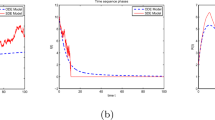
Now, we consider the parameters values $\Lambda =0.5$; $\mu _1=0.2$; $\mu _2=0.3$; $\mu _3=0.4$; $\lambda =0.6$; $\beta =0.45$; $\tau =0.4$; $\sigma 1=0.09$; $\sigma 2=0.2$; $\sigma 3=0.2$.

By computing, we can obtain $\mathcal {R}_0 =1.25$ and $\mathcal {R}_s =1.227$.

In this case, figure (Fig.2) delineates the persistence of the disease. Hence, the numerical simulation supports the analytic result proven in Theorem 1.

Fig. 2

Trajectories of stochastic and deterministic systems at time $t=300$ with the parameters values given in Example 2

Example 3

By choosing the parameters values $\Lambda =0.7$; $\mu _1=0.2$; $\mu _2=0.5$; $\mu _3=0.4$; $\lambda =0.6$; $\beta =0.6$; $\tau =0.5$; $\sigma 1=0.05$; $\sigma 2=0.03$; $\sigma 3=0.02$,we obtain that $\mathcal {R}_s =1.6152$.

By Theorem 3, the solution (S(t), I(t), R(t)) of the system (4) has a unique stationary distribution ergodic stationary distribution as shown in figure (Fig.3) and figure (Fig.4), which indicates that the epidemic disease will persist.

Fig. 3

The histogram of the probability density function of the solutions of model (4) at time $t=1000$ and using the parameter values in Example 3

Fig. 4

Computer simulation and density function of S(t), I(t) and R(t) at time $t=1000$ by using the parameter values given in Example 3

Next, We keep parameters in the above simulations unchanged and only change the time $t= 10000$, the figures (Fig.5) and (Fig.6) show that the solution of the stochastic model (4) admits also a stationary distribution.

Fig. 5

The histogram of the probability density function of the solutions of model (4) using and the parameter values in Example 3

Fig. 6

Trajectories of stochastic and deterministic systems with the parameters values given in Example 3

From the above, we point out that the dynamics of the proposed stochastic model is different from that of the deterministic case due to the effect of stochastic perturbation. This reveals other topics worthy of further investigation in our future work, in order to propose more realistic but complex models.