Nonconstant Steady States in a Predator–Prey System with Density-Dependent Motility

Abstract

We investigate the existence, structure and stability of the nonconstant steady states for a predator–prey system with density-dependent motility under the Neumann boundary condition. By applying the Leray–Schauder degree theory, we show that under certain conditions, a small prey diffusion rate can ensure the existence of the nonconstant steady states, which is verified by numerical simulations. Over 1D domain, we treat prey diffusion rate as a bifurcation parameter and obtain the local and global structure of steady states near the homogeneous steady states with the aid of bifurcation theory and index theory. Moreover, a stability criterion of the bifurcating steady states is also presented. Finally, we give the existence and stability of time-periodic nontrivial solutions.

1 Introduction

Predator–prey interactions are fundamental modules that make up entire complex ecosystems [24, 34], which have been studied extensively in the past decades since the pioneering work by Lotka and Volterra in 1920, see [2, 11, 43, 46] and references therein. These interactions have been investigated widely by various reaction diffusion equations with random diffusion. However, random diffusion is sometimes insufficient for describing animal movements in real world, especially in the foraging for animals with cognition. In reality, predators usually admit a directed movement toward the gradient direction of prey distribution, which is called prey-taxis. In order to model the predator–prey interaction with prey-taxis, Karevia and Odell [22] gave the following general prey-taxis system:

$$\begin{aligned} \left\{ \begin{aligned}&u_{t}=\nabla \cdot (d(v)\nabla u)-\nabla \cdot (u\chi (u, v)\nabla v)+F_1(u,v),\\&v_t=D\Delta v+F_2(u,v), \end{aligned} \right. \end{aligned}$$

(1.1)

where $u=u(x,t)$ and $v=v(x,t)$ are the densities of predators and preys at space x and time t, respectively; $D>0$ is the prey diffusion rate; the term $\nabla \cdot (d(v)\nabla u)$ characterizes the diffusion of u with coefficient d(v); $-\nabla \cdot (u\chi (u, v)\nabla v)$ represents the mobility induced by prey-taxis with coefficient $\chi (u, v)$ which measures the strength of prey-taxis; and the terms $F_1(u,v)$ and $F_2(u,v)$ indicate the predator–prey interaction. In the field experiment, Karevia and Odell [22] used model (1.1) with proper interactions $F_1(u,v)$ and $F_2(u,v)$ to simulate the area-restricted non-random search behavior of the ladybugs and aphids, and they found heterogeneous aggregative patterns. A typical form for $F_1(u,v)$ and $F_2(u,v)$ is

$$\begin{aligned} F_1(u,v)=\gamma uF(u,v)+h(u), \quad F_2(u,v)=f(v)-uF(u,v), \end{aligned}$$

(1.2)

where F(u, v) is the functional response function which represents the ability of the predator to consume its prey; h(u) and f(v) characterize the intra-specific interactions of predators and preys, respectively. In the literature, the functions h(u), f(v) and F(u, v) admit some appropriate forms for special ecological phenomenon. Particularly, the term h(u) is usually defined as $-u(\theta +\alpha u)$ with $\theta >0$ and $\alpha \ge 0$; the prey growth term f(v) has the following typical forms (see [2, 5]):

• (Logistic): $f(v)=rv(1-\frac{v}{K})$;

• (Strong Allee effect): $f(v)=rv(1-\frac{v}{K})(v-m)$;

• (Weak Allee effect): $f(v)=rv(1-\frac{v}{K})-\frac{av}{v+b}$;

where r is the intrinsic growth rate of prey and $K>0$ is the carrying capacity, and $0<\frac{1}{m}, \frac{b^2r}{a}<K$. There are various forms on predator functional response function F(u, v) (see [34, 38]):

• $F(u,v)=F(v)$(prey-dependent):

  $$\begin{aligned}&(\text {Holling l}){:} \ F(v)=v;\quad (\text {Holling ll}): F(v)=\frac{mv}{1+av};\\&(\text {Holling lll}){:} \ F(v)=\frac{v^k}{1+v^k}; \quad (\text {lvlev}): F(v)=c(1-e^{-av}); \end{aligned}$$

• F(u, v) (prey-predator dependent):

  $$\begin{aligned}&(\text {Beddington--DeAngelis}){:} F(u,v)=\frac{\mu u}{a+bu+cv};\\&(\text {Crowley--Martin}){:} F(u,v)=\frac{\mu u}{(a+bu)(a+cv)};\\&(\text {Ratio-dependent}){:} F(u,v)=\frac{cv}{u+mv}; \end{aligned}$$

where a,b,c and m are positive constants, and $k>1$.

On a bounded domain $\Omega$, system (1.1) is usually supplemented by suitable boundary conditions on the boundary surface $\partial \Omega$. Of special interest is the zero Neumann boundary condition:

$$\begin{aligned} \partial _n u=\partial _n v=0, \quad \text {on}\ \partial \Omega , \end{aligned}$$

(1.3)

which means that no flow across the boundary $\partial \Omega$. Meanwhile, an initial condition is also needed, which is given by

$$\begin{aligned} u(x, 0)=u_0(x),\quad v(x, 0)=v_0(x), \quad \text {in} \ \Omega . \end{aligned}$$

(1.4)

After the pioneering work of Kareiva and Odell [22], there exist numerous investigations on (1.1) with interaction (1.2). In the case where d(v) is a constant and $\chi (u,\ v)$ is a nonnegative non-increasing function with respect to v, Lee et al. [25] obtained the existence of traveling wave solutions for (1.1) with $\chi (u,\ v)=\frac{1}{(1+v)^n}, (n=1,2)$ in $x\in {\mathbb {R}}$; in a bounded interval, they Lee et al. [26] also gave some conditions for the occurrence of pattern formation for (1.1) with different F(u, v), f(v) and $\chi (u,\ v)=\chi$ or $\frac{\chi }{v}$; Wu et al. [45] gave the existence of global classical solutions of (1.1) with any dimensional domain under the assumption that $\chi (u,\ v)=\chi$ is small enough; meanwhile, without the smallness of $\chi$, the global existence of classical solutions of (1.1) in two-dimensional domain has been obtained in [16], where the global stability of constant steady state is also studied; over 1D domain, nonconstant positive steady states and pattern formation have been obtained in [44] for any $\chi >0$. In the case where d(v) is a constant but $\chi (u,\ v)=\chi (1-u)$ with $\chi >0$, Ma et al. [31] obtained the existence and stability of nonconstant steady states for a volume-filling chemotaxis model with $F_1(u,v)$ being the logistic growth of cell and $F_2(u, v)=\alpha u-\beta v$ for chemical. In the case where d(v) is a constant but $F_1(u, v)=F_1(v)$ and $\chi (u,\ v)=\chi (u)$ satisfying $\chi (u_m)=0, \chi (u)>0$ for $0\le u< u_m$ with $u_m$ being certain positive number, the global existence results has been investigated in [1, 12, 41] and the existence of nonconstant steady states has been investigated in [27, 42]. For more studies on the global bifurcation and pattern formation of (1.1) with more complex interaction, the reader is referred to the recent papers [3, 30, 47].

Limited work has been done in (1.1) with both d(v) and $\chi (u, v)$ being nonconstants. Recently, for $\chi (u, v)=\chi (v)$ and interaction (1.2) with $h(u)=-u(\theta +\alpha u)$. where $\theta >0$ and $\alpha >0$, Jin and Wang [17] showed the global boundedness of solutions of (1.1) in two-dimensional domain under the condition $\alpha >0$ or $\chi (v)=-d'(v)$, and they also obtained the global stability of constant steady state for (1.1) under different parameter conditions. Several spatiotemporal patterns were also presented in [17]. A three-species predator–prey model with density-dependent motilities has been studied in [36].

However, it should be pointed out that several issues related to (1.1) with nonconstant d(v) are still unclear, such as traveling wave solution and stationary solutions. In this paper, we set $\chi (u,v)=-d'(v)$ and consider the following special case of (1.1), (1.3) and (1.4) with interaction (1.2) in a two-dimensional domain,

$$\begin{aligned} \left\{ \begin{array}{ll} u_{t}=\Delta (d(v)u)+u(\gamma F(v)-\theta ), \quad &{} \hbox {in} \ \Omega \times (0, +\infty ),\\ v_{t}=D\Delta v-uF(v)+f(v), \quad &{} \hbox {in} \ \Omega \times (0, +\infty ),\\ u(x, 0)=u_0(x), v(x, 0)=v_0(x), \quad &{} \hbox {in} \ \Omega \\ \partial _n u=\partial _n v=0, \quad &{} \text {on}\ \partial \Omega . \end{array}\right. \end{aligned}$$

(1.5)

where $\Omega \in {\mathbb {R}}^2$. The main purpose of this paper is to study the existence and structure of nonnegative nonconstant steady states of (1.5). First, we give the following several assumptions on functions d(v), F(v), f(v):

• (A0) d(v) is a smooth function satisfying $d(v)>0$ and $d'(v)< 0$ on $[0,\ +\infty )$;

• (A1) $F(v)\in C^1([0,\ \infty ))$, $F(0)=0$, $F(v)>0$ in $(0,\ \infty )$ and $0\le F'(v)<l$, where $l=\sup _{0\le v}F'(v)<+\infty$;

• (A2) $f:[0,\ \infty )\rightarrow {\mathbb {R}}$ is in $C^1$ with $f(0)=0$ and $f'(0)>0$ which satisfying $f(v)\le \mu v$ for any $v\le 0$ and some $\mu >0$; there exists unique $K>0$ such that $f(K)=0$ and $f(v)<0$ for all $v>K$;

where $'=\frac{d}{dv}$. Define ${\bar{M}}=\max \nolimits _{y\ge 0}f(y)$, then by assumption (A2), we have $0<{\bar{M}}<+\infty$. The assumption $d'(v)<0$ characterizes a common and reasonable biological phenomena that the mobility of predator will be reduced in the area with high prey density, which has been called “density-suppressed motility.” Such movement was first observed and investigated in a biological experiment [28] on E. coli cells and corresponding signal acyl-homoserine lactone which are excreted by E. coli cells themselves, where the movement of E. coli cells will be suppressed by the density of acyl-homoserine lactone. For more studies about single-species model or multiple-species interaction system with the density-suppressed motility, we can refer to Jin et al. [18,19,20], Gao and Guo [10], Fujie and Jiang [9], Jiang et al. [15], Ma et al. [32, 33] and references therein.

Obviously, (1.5) always admits two boundary constant steady states $e_0=(0,\ 0)$ and $e_1=(0,\ K)$. When $\gamma F(K)>\theta$, then (1.5) has a positive homogeneous steady state $e_2=(u^*,\ v^*)$ which satisfying

$$\begin{aligned} u^*=\frac{f(v^*)}{F(v^*)}, \quad F(v^*)=\frac{\theta }{\gamma }. \end{aligned}$$

As a special case, the global boundedness of the classical solutions of (1.5) has been given in [17], where the global dynamics for (1.5) has also been characterized, which is given in the following modified lemma,

Lemma 1.1

Let assumptions $(A0)-(A2)$ hold and (u, v) be the solution of (1.5) with initial value $(u_0,\ v_0)$.

• (1) If the parameters $\theta$, $\gamma$, K satisfying $\gamma F(K)<\theta$, then

  $$\begin{aligned} \Vert u\Vert _{L^\infty }+\Vert v-K\Vert _{L^\infty }\rightarrow 0, \quad t\rightarrow \infty . \end{aligned}$$

• (2) If the parameters $\theta$, $\gamma$, K satisfying $\gamma F(K)>\theta$ and

  $$\begin{aligned} D\ge \max _{0\le v\le K_0} \frac{u^*\Vert F(v)\Vert ^2\Vert d'(v)\Vert ^2}{4\gamma F(v^*)F'(v)d(v)}, \end{aligned}$$

  then

  $$\begin{aligned} \Vert u-u^*\Vert _{L^\infty }+\Vert v-v^*\Vert _{L^\infty }\rightarrow 0, \quad t\rightarrow \infty , \end{aligned}$$

  where $K_0=\max \{\Vert v_0\Vert _\infty ,\ K\}$.

The above lemma implies that no pattern formation will occur for (1.5) with large D. Several numerical studies has been given in [17] to show that (1.5) can produce aggregation patterns, periodic patterns and even chaotic spatiotemporal patterns with some parameter conditions. The first aim of this paper is to give a theoretic condition that ensures the existence of nonconstant steady state of (1.5). Equivalently, we will explore the existence condition of nonconstant positive solutions of the following elliptic problem:

$$\begin{aligned} \left\{ \begin{array}{ll} \Delta (d(v)u)+u(\gamma F(v)-\theta )=0, \quad &{} \hbox {in} \ \Omega ,\\ \Delta v+\frac{1}{D}(f(v)-uF(v))=0, \quad &{} \hbox {in} \ \Omega ,\\ \partial _n u=\partial _n v=0, \quad &{} \text {on}\ \partial \Omega , \end{array} \right. \end{aligned}$$

(1.6)

Set $w=d(v)u$, then we can reformulate (1.6) as

$$\begin{aligned} \left\{ \begin{array}{ll} \Delta w+\frac{w}{d(v)}(\gamma F(v)-\theta )=0, \quad &{} \hbox {in} \ \Omega ,\\ \Delta v+\frac{1}{D}\Big (f(v)-\frac{wF(v)}{d(v)}\Big )=0, \quad &{} \hbox {in} \ \Omega ,\\ \partial _n w=\partial _n v=0, \quad &{} \text {on}\ \partial \Omega . \end{array}\right. \end{aligned}$$

(1.7)

Based on a priori estimate on the solutions of (1.7), we will perform the Leray–Schauder degree theory to (1.7) and obtain a theoretic condition on the existence of nonconstant positive solutions of (1.7). Therefore, the first aim of this paper is achieved. In order to capture more details about nonconstant steady states of (1.5), we further give the structure of steady states near the positive constant steady state of (1.5) with special functions F(v) and f(v) in a one-dimensional domain via bifurcation theory. Specifically, we employ the user-friendly Crandall–Rabinowitz bifurcation theory [39] to get the local existence and structure of nonconstant positive steady states and obtain the global structure of the bifurcation branches by using the global bifurcation theorem of Rabinowitz and the Leray–Schauder degree theory; the linear stability of the local bifurcation branches is investigated by applying perturbation method; and the existence and stability of spatially inhomogeneous periodic solution are also presented.

The rest of this paper is organized as follows. In Sect. 2, we obtain an analytic condition to guarantee the existence of nonconstant steady states to (1.5) (See Theorem 2.1). Section 3 is devoted to the more information on nonconstant steady states to (1.5) with special interaction, including the local and global structure, and linear stability.

Before ending this section, we will give some notations. Let $0=\lambda _0<\lambda _1<\cdots<\lambda _i<\cdots$ satisfying $\lim \limits _{i\rightarrow +\infty } \lambda _i=+\infty$ be the eigenvalues of $-\Delta$ under homogeneous Neumann boundary condition. For each integer $i\ge 0$, $\lambda _i$ has multiplicity $\eta _i\ge 1$ and the eigenspace with respect to $\lambda _i$ has an orthonormal basis $\phi _{ij}, i\ge 0, 1\le j\le \eta _i$. Therefore, the set $\{\phi _{ij}: i\ge 0, 1\le j\le \eta _i\}$ forms a complete orthonormal basis in space $L^2(\Omega )$. Let

$$\begin{aligned} S=\Big \{(\phi , \psi )\in [H^2(\Omega )]^2: \frac{\partial \phi }{\partial n}=\frac{\partial \psi }{\partial n}=0\Big \}, \end{aligned}$$

then

$$\begin{aligned} S=\bigoplus _{i=0}^{\infty }S_i, \quad S_i=\bigoplus _{j=1}^{\eta _i}S_{ij}, \end{aligned}$$

where $S_{ij}=\{c\cdot \phi _{ij}: c\in {\mathbb {R}}^2\}$. We denote the Kernel, the Range of a given linear operator L by KerL, RanL.

2 Existence of Nonconstant Steady States

In this section, we will investigate the stationary problem of (1.5), i.e., in this case, when $\gamma F(K)>\theta$, then (1.7) has a positive constant solution $(w^*,\ v^*)$ which satisfies

$$\begin{aligned} w^*=d(v^*)u^*, \quad F(v^*)=\frac{\theta }{\gamma }. \end{aligned}$$

Lemma 2.1

Assume $\gamma F(K)\ne \theta$ and $(w(x),\ v(x))$ be a nonnegative solution of (1.7) satisfying $v(x)\not \equiv 0$, then there exist two positive constants $\underline{C}$ and ${\overline{C}}$ satisfying $\underline{C}<{\overline{C}}$ such that

$$\begin{aligned} \underline{C}\le w(x), v(x) \le {\overline{C}}, \quad x\in {\bar{\Omega }}. \end{aligned}$$

(2.1)

Proof

Obviously, $w(x)>0$ and $v(x)>0$ for $x\in {\bar{\Omega }}$ in view of strong maximum principle. Applying comparison principle to the second equation of (1.7), then by assumption (A2), we get $v(x)\le K$ for $x\in {\bar{\Omega }}$. Meanwhile, by assumption (A0) and the boundedness of v, we have

$$\begin{aligned} -\Delta (w+\gamma v)&=-\frac{\theta }{d(v)}(w+\gamma v)+\frac{\gamma }{D}f(v)+\frac{\theta }{d(v)}\gamma v \\&\le \frac{\gamma }{D}{\bar{M}}+\frac{\theta }{d(K)}\gamma K-\frac{\theta }{d(0)}(w+\gamma v), \end{aligned}$$

from which we can use comparison principle to get for $x\in {\bar{\Omega }}$,

$$\begin{aligned} w(x)+\gamma v(x)\le \frac{d(0)}{\theta }\Big (\frac{\gamma }{D}{\bar{M}}+\frac{\theta }{d(K)}\gamma K\Big ). \end{aligned}$$

Therefore,

$$\begin{aligned} 0<w(x), v(x)\le \max \Big \{K,\ \frac{d(0)}{\theta }\Big (\frac{\gamma }{D}{\bar{M}}+\frac{\theta }{d(K)}\gamma K\Big )\Big \}:={\bar{C}}, \quad x\in {\bar{\Omega }}. \end{aligned}$$

(2.2)

Next, we will show that w and v have positive lower bound. Let

$$\begin{aligned} L_1(x)=\frac{\gamma F(v)-\theta }{d(v)}, \quad L_2(x)=\frac{1}{Dv}\Big (f(v)-\frac{wF(v)}{d(v)}\Big ), \end{aligned}$$

then

$$\begin{aligned} |L_1(x)|\le \frac{\gamma F(K)+\theta }{d(K)}, \quad |L_2(x)|\le \frac{\mu d(K)+{\bar{C}}l}{Dd(K)}. \end{aligned}$$

Then, we can apply Harnack inequality to get a constant $C_1>0$ depending on $\gamma$, K, $\mu$, $\theta$, l, D and $\Omega$ such that

$$\begin{aligned} \sup _{{\bar{\Omega }}} w(x)\le C_1 \inf _{{\bar{\Omega }}} w(x), \quad \sup _{{\bar{\Omega }}} v(x)\le C_1 \inf _{{\bar{\Omega }}} v(x). \end{aligned}$$

If we can obtain a constant $C_2>0$ such that

$$\begin{aligned} \sup _{{\bar{\Omega }}} w(x)\ge C_2 \quad \text {and} \quad \sup _{{\bar{\Omega }}} v(x)\ge C_2, \end{aligned}$$

(2.3)

then we have (2.1). In fact, using similar arguments in [11, 43], we can obtain such $C_2>0$ satisfying (2.3). Therefore, we can get $\underline{C}>0$ such that $\underline{C}\le w(x), v(x)$ for $x\in {\bar{\Omega }}$, which together with (2.2) implies (2.1). $\square$

Based on Lemma 2.1, in the case where $\gamma F(K)>\theta$, we now turn to investigate the existence of nonconstant positive solutions for (1.7) by applying the Leray–Schauder degree theory [8]. For simplicity of presentation, we set $U=(w, v)$ and $U^*=(w^*,\ v^*)$, and let

$$\begin{aligned} M(U)=\begin{pmatrix} \frac{w}{d(v)}(\gamma F(v)-\theta )\\ \frac{1}{D}(f(v)-\frac{w}{d(v)}F(v)) \end{pmatrix}. \end{aligned}$$

Then, we can rewrite (1.7) as

$$\begin{aligned} \Delta U+M(U)=0, \quad U\in S. \end{aligned}$$

(2.4)

Therefore, the eigenvalue problem associated with the linearized system of (2.4) at $U^*$ is

$$\begin{aligned} \Delta U+M_U(U^*)U=eU, \quad U\in S. \end{aligned}$$

(2.5)

where

$$\begin{aligned} M_U(U^*)=\begin{pmatrix} 0 &{} w^*\frac{\gamma F'(v^*)}{d(v^*)}\\ -\frac{F(v^*)}{d(v^*)D} &{} \frac{L(v^*)}{Dd^2(v^*)} \end{pmatrix}, \end{aligned}$$

(2.6)

and $L(v^*)=f'(v^*)d^2(v^*)-w^*(F'(v^*)d(v^*)-F(v^*)d'(v^*))$. Note that $U=(w, v)\in S$ which can be written as an expansion of all the eigenfunctions to $\lambda _i(0\le i\le +\infty )$, then it is easy to see that the eigenvalues of (2.5) satisfy the following equations,

$$\begin{aligned} e^2+P_i(D)e+Q_i(D)=0, \quad i=0,1,2,3,\ldots , \end{aligned}$$

(2.7)

where

$$\begin{aligned} P_i(D)= & {} 2\lambda _i-\frac{L(v^*)}{Dd^2(v^*)}, \\ Q_i(D)= & {} \lambda _i^2-\frac{L(v^*)}{Dd^2(v^*)}\lambda _i+w^*\frac{\gamma F'(v^*)F(v^*)}{Dd^2(v^*)}, \end{aligned}$$

and for each nonnegative integer i, we let $e^1_i$ and $e_i^2$ be the roots of (2.7). Obviously, if $L(v^*)<0$, then all the eigenvalues of (2.5) admit negative real part which implies $U^*$ is linearly stable.

In the case where $L(v^*)>0$, note that $Q_0(D)>0$, then for $i=1,2,\ldots$, $Q_i(D)<0$ if and only if $D<D_i$, where

$$\begin{aligned} D_i=\frac{1}{\lambda _i}\Big (\frac{L(v^*)}{d^2(v^*)}-\frac{\gamma w^* F'(v^*)F(v^*)}{d^2(v^*)}\frac{1}{\lambda _i}\Big ). \end{aligned}$$

If for some positive integer i, we have $0<D<D_i$, then (2.5) admits two real eigenvalues $e_i^1$ and $e_i^2$ with different signs, which means $U^*$ is linear unstable. Specifically, we have the following lemma,

Lemma 2.2

Assume $L(v^*)>0$.

• (1) There exists minimal $i^c\in \{1,2,\ldots \}$ satisfying $\lambda _{i^c}>\frac{\gamma w^*F'(v^*)F(v^*)}{L(v^*)}$ such that

  • (i) if $i^c=1$, then $D_i>0$ holds for all $i\ge 1$;

  • (ii) if $i^c>1$, then

    $$\begin{aligned} D_i>0 \quad \text {for}\quad i\ge i^c, \quad D_i\le 0 \quad \text {for} \quad 1\le i\le i^c-1. \end{aligned}$$

    Furthermore, let

    $$\begin{aligned} D_{m}=\max _{i\ge i^c} D_i=\frac{1}{\lambda _{i^m}}\Big (\frac{L(v^*)}{d^2(v^*)}-\frac{\gamma w^* F'(v^*)F(v^*)}{d^2(v^*)}\frac{1}{\lambda _{i^m}}\Big ). \end{aligned}$$

    Then, if $0<D<D_m$, (2.5) admits at least one positive eigenvalue with the algebraic multiplicity $\eta _{i^m}$.

• (2) Let $i^c$ be the index in the lemma 2.2(1). If $D>D_m$, then $Q_i(D)>0$ for $i\in \{0, 1, 2, \ldots \}$ and for each nonnegative integer i, (2.7) has two roots with either positive real part or negative real part.

Let

$$\begin{aligned} {\bar{D}}:=\frac{L^2(v^*)}{4\gamma w^*d^2(v^*)F'(v^*)F(v^*)}, \end{aligned}$$

then it is easy to see that ${\bar{D}}$ is the maximum of the following real value function,

$$\begin{aligned} g(x)=x\Big (\frac{L(v^*)}{d^2(v^*)}-\frac{\gamma w^* F'(v^*)F(v^*)}{d^2(v^*)}x\Big ),\quad x\ge 0. \end{aligned}$$

Obviously, we have ${\bar{D}}\ge D_m$ and the equality holds when $g(i^m)={\bar{D}}$. In the following, we will investigate the existence of nonconstant solution of (1.7) for $L(v^*)>0$ and $D\in (0,\ {\bar{D}})$.

In order to apply the topological degree theory, we define

$$\begin{aligned} {\bar{S}}= & {} \Big \{(w, v)\in [C^1({\bar{\Omega }})]^2: \frac{\partial w}{\partial n}=\frac{\partial v}{\partial n}=0\Big \},\\{} & {} \quad {\bar{S}}^+=\{(w, v)\in {\bar{S}}: w\ge 0, v\ge 0\},\\ G(D,\ U)= & {} U-(Id-\Delta )^{-1}(U+M(D,\ U)), \end{aligned}$$

where Id is identity operator and $(Id-\Delta )^{-1}$ is the inverse of operator $Id-\Delta$ in ${\bar{S}}$ with Neumann boundary condition. Equivalently, we can resort to find the zero points of $G(D,\ U)$ in ${\bar{S}}^+$ in order to obtain the positive solutions for (1.7). Note that $G(D,\ \dot{)}$ is compact perturbation of operator Id and $0\not \in (Id-\Delta )^{-1}(\cdot +M(D,\ \cdot ))(\partial {\bar{S}}_0^+)$, where

$$\begin{aligned} {\bar{S}}_0^+=\Big \{(w,\ v)\in S^+: \frac{\underline{C}}{2}\le w(x), v(x)\le 2{\overline{C}},\ x\in {\bar{\Omega }}\Big \}, \end{aligned}$$

then $deg(G(D,\ \cdot ), {\bar{S}}_0^+, 0)$ is well defined and due to the homotopy invariance, it is also constant for $\gamma F(K)>\theta$. It follows from Lemma 1.1 that for large D, operator $G(D, \cdot )$ only has zero point $U^*$, which shows that

$$\begin{aligned} deg(G(D,\ \cdot ), {\bar{S}}_0^+, 0)=index(G(D,\ \cdot ),\ U^*). \end{aligned}$$

(2.8)

A simple computation gives

$$\begin{aligned} G_{U}(D, U^*)=Id-(Id-\Delta )^{-1}(Id+M_{U}(U^*)), \end{aligned}$$

where $M_{U}(U^*)$ is given in (2.6). A well-known theorem [8, Theorem 8.10] about the computation of the Leray–Schauder degree states that if 0 is not an eigenvalue of operator $G_U(D, U^*)$ (i.e., $G_U(D,\ U^*)$ is invertible), then

$$\begin{aligned} index(G(D,\ \cdot ),\ U^*)=(-1)^{\mu }, \end{aligned}$$

(2.9)

where $\mu$ is number of negative eigenvalues of the operator $G_U(D, U^*)$.

Next, we will compute the eigenvalues of $G_U(D,\ U^*)$. Let $\rho$ be the eigenvalue of $G_U(D, U^*)$ with corresponding eigenfunction $\Psi \in {\bar{S}}$, then

$$\begin{aligned} \begin{pmatrix} \rho +(\rho -1)\Delta &{} w^*\frac{\gamma F'(v^*)}{d(v^*)}\\ -\frac{F(v^*)}{d(v^*)D} &{} \rho +(\rho -1)\Delta -\frac{L(v^*)}{Dd^2(v^*)} \end{pmatrix}\Psi =0. \end{aligned}$$

Similar to the process from (2.5) to (2.7), $\rho$ satisfies

$$\begin{aligned}{} & {} (\lambda _i(1-\rho )-\rho )^2-\frac{L(v^*)}{Dd^2(v^*)}(\lambda _i(1-\rho )-\rho )\\{} & {} \quad +w^*\frac{\gamma F'(v^*)F(v^*)}{Dd^2(v^*)}=0, \quad i=0,1,2,\ldots . \end{aligned}$$

It is easy to see that for nonnegative integer i, operator $G_U(D,\ U^*)$ admits two eigenvalues $\rho _i^{\pm }$, where $\rho _i^{\pm }=\frac{\lambda _i-\mu ^{\pm }(D)}{1+\lambda _i}$ with

$$\begin{aligned} \mu ^{\pm }(D)=\frac{L(v^*)}{2Dd^2(v^*)}\pm \sqrt{\frac{L^2(v^*)}{4D^2d^4(v^*)}-\frac{w^*\gamma F(v^*)F'(v^*)}{d^2(v^*)D}}. \end{aligned}$$

Note that $L(v^*)>0$ and $0<D<{\bar{D}}$, then $0<\mu ^{-}<\mu ^{+}$. Furthermore, $\mu ^{+}(D)$ is a monotone decreasing function with respect to D and satisfies

$$\begin{aligned} \lim _{D\rightarrow 0}\mu ^+(D)=+\infty , \quad \lim _{D\rightarrow {\bar{D}}}\mu ^+(D)=\frac{L(v^*)}{2{\bar{D}}d^2(v^*)}:=l_1; \end{aligned}$$

and $\mu ^{-}(D)$ is a monotone increasing function with respect to D and satisfies

$$\begin{aligned} \lim _{D\rightarrow 0}\mu ^-(D)=\frac{w^*\gamma F(v^*)F'(v^*)}{L(v^*)}:=l_2, \quad \lim _{D\rightarrow {\bar{D}}}\mu ^-(D)=\frac{L(v^*)}{2{\bar{D}}d^2(v^*)}. \end{aligned}$$

Due to the positivity of $l_1$ and $l_2$, there exist two positive integers $j_0$, $k_0$ satisfying $j_0<k_0$ and

$$\begin{aligned} \lambda _{j_0}<l_2\le \lambda _{j_0+1}, \quad \lambda _{k_0}<l_1\le \lambda _{k_0+1}. \end{aligned}$$

For $j\in \{0, 1, 2, \ldots , k_0-j_0\}$ and $k\in \{0,1,2,\ldots \}$, we set

$$\begin{aligned} \underline{D}_j= & {} inf\{0<D<{\bar{D}}: \mu ^-(D)>\lambda _{j_0+j}\},\\ {\overline{D}}_k= & {} sup\{0<D<{\bar{D}}: \mu ^+(D)>\lambda _{k_0+k}\}. \end{aligned}$$

Let $\underline{D}_{k_0-j_0+1}={\overline{D}}_0={\bar{D}}$, then the monotonicity of $\mu ^{\pm }(D)$ with respect to D implies

$$\begin{aligned} \underline{D}_0<\underline{D}_1<\cdots<\underline{D}_{k_0-j_0}<\underline{D}_{k_0-j_0+1}, \quad {\overline{D}}_0>{\overline{D}}_1>{\overline{D}}_2>\cdots \rightarrow 0. \end{aligned}$$

Choosing $D^*>{\bar{D}}$ such that (1.7) has a unique solution $U^*$ in ${\bar{S}}_0^+$, then together with lemma 2.2(2), (2.8) and (2.9), we have $deg(G(D,\ \cdot ), {\bar{S}}_0^+, 0)=1$ for $D\ge D^*$. Therefore, it follows from the homotopy invariance that

$$\begin{aligned} deg(G(D,\ \cdot ), {\bar{S}}_0^+, 0)=1 \quad \text {for} \quad D>0. \end{aligned}$$

(2.10)

Theorem 2.1

Assume $L(v^*)>0$ and $0<D<{\bar{D}}$. System (1.5) admits at least one nonconstant steady state if $D\in (\underline{D}_j,\ \underline{D}_{j+1})\cap ({\overline{D}}_{k+1}, \ {\overline{D}}_k)$ for some $j\in \{0, 1, \ldots , k_0-j_0\}$ and $k\in \{0, 1,2 \ldots \}$ satisfying $j_0+k_0+j+k$ is odd.

Proof

If not, then (1.7) has only solution $U^*$ in ${\bar{S}}_0^+$ which implies

$$\begin{aligned} deg(G(D,\ \cdot ), {\bar{S}}_0^+, 0)=index(G(D,\ \cdot ),\ U^*). \end{aligned}$$

Meanwhile, the number of negative eigenvalues of the operator $G_U(D, U^*)$ is $j_0+k_0+j+k+2$. Then, $deg(G(D,\ \cdot ), {\bar{S}}_0^+, 0)=-1$ due to the condition that $j_0+k_0+j+k$ is odd. This contradicts to (2.10). $\square$

Now, we will give some numerical examples to verify Theorem 2.1 in one-dimensional interval $[0,\ 2\pi ]$. Let $\gamma =2$, $\theta =1$ and choose

$$\begin{aligned} d(v)=\frac{1}{1+e^{\frac{1}{10}(v-1)}},\quad F(v)=\frac{v}{\lambda +v},\quad f(v)=\mu v\Big (1-\frac{v}{K}\Big ), \end{aligned}$$

where $K=4$, $\lambda =1$ and $\mu =1$, then $u^*=\frac{3}{2}$, $v^*=1$ and $w^*=\frac{3}{4}$. It is easy to get that

$$\begin{aligned} d'(v)=-\frac{e^{\frac{1}{10}(v-1)}}{10(1+e^{\frac{1}{10}(v-1)})^2}, \quad f'(v)=1-\frac{v}{2}, \quad F'(v)=\frac{1}{(1+v)^2}. \end{aligned}$$

Then, we have

$$\begin{aligned} L(v^*)=0.0219>0, \quad {\bar{D}}=0.0026,\quad l_1=16.85, \quad l_2=8.57. \end{aligned}$$

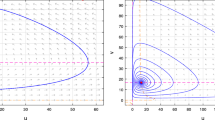
Choose $D=0.002$, then $\mu ^{+}(D)=32.13$ and $\mu ^{-}(D)=11.67$. Therefore, $k_0+j_0+j+k=8+5+1+3=17$, which is odd. As shown in Fig. 1, a nonconstant positive steady state of (1.5) arises and we observe a stable aggregation pattern for (1.5), where both u (blue line) and v (red line) have their own stable aggregation area (see Fig. 1c). When we set $D=0.00065$, then we have $\mu ^{+}(D)=125.58$ and $\mu ^{-}(D)=9.19$, which implies $k_0+j_0+j+k=8+5+1+14=28$, which is even. In this case, although the condition in Theorem 2.1 is not satisfied, we still observe a time-periodic solution for (1.5)(see Fig. 2). Therefore, as indicated in both figures, a stable pattern can appear for the value of D which is close to ${\bar{D}}$, and in the case where the value of D is far away from ${\bar{D}}$, a pattern, which changes in time, may arise.

Fig. 1

Simulations of the solution (u, v) of system (1.5) with $D=0.002$, where the initial value $(u_0, v_0)$ is $\Big (\frac{3}{2},\ 1\Big )+(0.001, 0.001)\cos (x)$. (Color figure online)

Fig. 2

Simulations of the solution (u, v) of system (1.5) with $D=0.00065$, where the initial value $(u_0, v_0)$ is $\Big (\frac{3}{2},\ 1\Big )+(0.001, 0.001)\cos (x)$

3 Bifurcation Analysis

In order to get more details about the nonconstant steady states for (1.1), in this section, we set

$$\begin{aligned} F(v)=\frac{v}{1+v}, \quad \theta =1,\quad f(v)=v\Big (1-\frac{v}{K}\Big ) \end{aligned}$$

and consider the following system in $\Omega =(0,\ l)$ with $l>0$:

$$\begin{aligned} \left\{ \begin{array}{ll} u_{t}=(d(v)u)_{xx}+\frac{\gamma uv}{1+v}-u, \quad &{} x\in (0,\ l),\quad t>0,\\ v_{t}=Dv_{xx}-\frac{uv}{1+v}+v\Big (1-\frac{v}{K}\Big ), \quad &{} x\in (0,\ l),\quad t>0,\\ u(x, 0)=u_0(x), \quad v(x, 0)=v_0(x), \quad &{} x\in (0,\ l) \\ u_x(0,\ t)=u_x(l,\ t)=0, \quad v_x(0,\ t)=v_x(l,\ t)=0 \quad &{} t>0. \end{array} \right. \end{aligned}$$

(3.1)

Here, we will use $D>0$ as a bifurcation parameter. The function d(v) satisfies assumption (A0). Obviously, (3.1) has two boundary steady states $e_0=(0,\ 0)$ and $e_1=(0,\ K)$. If $\gamma >\frac{1+K}{K}$, then (3.1) admits a positive constant steady state $e_2=(u^*,\ v^*)$, where

$$\begin{aligned} u^*=\frac{\gamma (K\gamma -K-1)}{K(\gamma -1)^2}, \quad v^*=\frac{1}{\gamma -1}. \end{aligned}$$

It is easy to check that

$$\begin{aligned} u^*=\frac{(1+v^*)(K-v^*)}{K}. \end{aligned}$$

(3.2)

We first consider the effects of D on the stability of constant steady states of (3.1). Let $({\hat{u}},\ {\hat{v}})$ be an equilibrium of (3.1). Then, the corresponding linear system of (3.1) at $({\hat{u}},\ {\hat{v}})$ is given by

$$\begin{aligned} \left\{ \begin{array}{ll} {\hat{U}}_{t}=d({\hat{v}}){\hat{U}}_{xx}+d'({\hat{v}}){\hat{u}}{\hat{V}}_{xx}+\Big (\frac{\gamma {\hat{v}}}{1+{\hat{v}}}-1\Big ){\hat{U}}+\frac{\gamma {\hat{u}}}{(1+{\hat{v}})^2}{\hat{V}}, \quad &{} x\in (0,\ l),\quad t>0,\\ {\hat{V}}_{t}=D{\hat{V}}_{xx}-\frac{{\hat{v}}}{1+{\hat{v}}}{\hat{U}}+\Big (1-\frac{2{\hat{v}}}{K}-\frac{{\hat{u}}}{(1+{\hat{v}})^2}\Big ){\hat{V}} \quad &{} x\in (0,\ l),\quad t>0,\\ {\hat{U}}(x, 0)={\hat{U}}_0(x), {\hat{V}}(x, 0)={\hat{V}}_0(x), \quad &{} x\in (0,\ l) \\ {\hat{U}}_x(0,\ t)={\hat{U}}_x(l,\ t)=0,\ {\hat{V}}_x(0,\ t)={\hat{V}}_x(l,\ t)=0 \quad &{} t>0. \end{array}\right. \nonumber \\ \end{aligned}$$

(3.3)

where ${\hat{U}}=u-{\hat{u}}$ and ${\hat{V}}=v-{\hat{v}}$. Note that the eigenvalue problem

$$\begin{aligned} \left\{ \begin{array}{ll} -\phi _{xx}=\lambda \phi , \quad &{} x\in (0,\ l),\\ \phi _x=0, \quad &{}x=0,l, \end{array} \right. \end{aligned}$$

has countable many simple eigenvalues with corresponding eigenfunctions which are given by

$$\begin{aligned} \lambda _j=\Big (\frac{\pi j}{l}\Big )^2, \quad \phi _j(x)=\left\{ \begin{array}{ll} 1, \quad &{}j=0, \\ \cos \Big (\frac{\pi jx}{l}\Big ), \quad &{}j>0, \end{array} \right. \end{aligned}$$

where $j\in \{0,1,2,\ldots \}$. Therefore, the solution $({\hat{U}},\ {\hat{V}})$ of (3.3) has the following expansions,

$$\begin{aligned} {\hat{U}}(x, t)=\sum _{j=0}^{\infty }{\hat{c}}_j^1e^{\sigma t}\phi _j(x), \quad {\hat{V}}(x)=\sum _{j=0}^{\infty }{\hat{c}}_j^2e^{\sigma t}\phi _j(x), \end{aligned}$$

(3.4)

where ${\hat{c}}_j,\ j=1,2$, are constants and $\sigma$ is the temporal eigenvalue. Inserting (3.4) into (3.3), we get

$$\begin{aligned}{} & {} \sum _{j=0}^\infty \begin{pmatrix} \sigma +d({\hat{v}})\Big (\frac{\pi j}{l}\Big )^2+1-\frac{\gamma {\hat{v}}}{1+{\hat{v}}} &{} d'({\hat{v}}){\hat{u}}\Big (\frac{\pi j}{l}\Big )^2-\frac{\gamma {\hat{u}}}{(1+{\hat{v}})^2}\\ \frac{{\hat{v}}}{1+{\hat{v}}} &{} \sigma +D\Big (\frac{\pi j}{l}\Big )^2+\Big (\frac{{\hat{u}}}{(1+{\hat{v}})^2}+\frac{2{\hat{v}}}{K}-1\Big ) \end{pmatrix}\\{} & {} \begin{pmatrix} {\hat{c}}^1_j \\ {\hat{c}}^2_j \end{pmatrix}e^{\sigma t}\phi _j(x)=\begin{pmatrix} 0 \\ 0 \end{pmatrix}. \end{aligned}$$

Denote

$$\begin{aligned} A({\hat{u}},\ {\hat{v}})= & {} 1-\frac{\gamma {\hat{v}}}{1+{\hat{v}}}, \quad B({\hat{u}},\ {\hat{v}})=-\frac{\gamma {\hat{u}}}{(1+{\hat{v}})^2},\nonumber \\ C({\hat{u}},\ {\hat{v}})= & {} \frac{{\hat{v}}}{1+{\hat{v}}}, \quad D({\hat{u}},\ {\hat{v}})=\frac{2{\hat{v}}}{K}+\frac{{\hat{u}}}{(1+{\hat{v}})^2}-1, \end{aligned}$$

(3.5)

then $\sigma$ is a root of

$$\begin{aligned} \sigma ^2+{\hat{a}}(j, D, {\hat{u}}, {\hat{v}})\sigma +{\hat{b}}(j, D, {\hat{u}}, {\hat{v}})=0, \quad j\in \{0,1,2,\ldots \}, \end{aligned}$$

(3.6)

where

$$\begin{aligned} {\hat{a}}(j, D, {\hat{u}}, {\hat{v}})&=d({\hat{v}})\Big (\frac{\pi j}{l}\Big )^2+D\Big (\frac{\pi j}{l}\Big )^2+A({\hat{u}},\ {\hat{v}})+D({\hat{u}},\ {\hat{v}}), \\ {\hat{b}}(j, D, {\hat{u}}, {\hat{v}})&=d({\hat{v}})D\Big (\frac{\pi j}{l}\Big )^4+(d({\hat{v}})D({\hat{u}}, {\hat{v}})+DA({\hat{u}}, {\hat{v}})-d'({\hat{v}}){\hat{u}}C({\hat{u}},{\hat{v}}))\Big (\frac{\pi j}{l}\Big )^2 \\&\quad +A({\hat{u}}, {\hat{v}})D({\hat{u}}, {\hat{v}})-B({\hat{u}}, {\hat{v}})C({\hat{u}}, {\hat{v}}). \end{aligned}$$

According to the standard principle of linearized stability( [35]), the homogeneous steady state $({\hat{u}}, {\hat{v}})$ of (3.1) is asymptotically stable if and only if the real parts of all the roots to (3.6) are negative. Thus, it is easy to get the following stability results on $e_0$ and $e_1$.

Lemma 3.1

• (1) $e_0$ is unstable;

• (2) $e_1$ is stable if $0<\gamma <\frac{1+K}{K}$ and unstable if $\gamma >\frac{1+K}{K}$.

Next, in the case where $\gamma >\frac{1+K}{K}$, we will show the effect of D on the dynamical behaviors around $e_2$. Note that

$$\begin{aligned} {\hat{a}}(j, D, e_2)&=d(v^*)\Big (\frac{\pi j}{l}\Big )^2+D\Big (\frac{\pi j}{l}\Big )^2+\frac{v^*(2v^*+1-K)}{K(1+v*)}, \\ {\hat{b}}(j, D, e_2)&=d(v^*)D\Big (\frac{\pi j}{l}\Big )^4\\&\quad +\,\Big (d(v^*)\frac{v^*(2v^*+1-K)}{K(1+v*)}-\frac{d'(v^*)u^*}{\gamma }\Big )\Big (\frac{\pi j}{l}\Big )^2+\frac{K-v^*}{K(1+v^*)}, \end{aligned}$$

then according to assumption (A0), we have that $e_2$ is stable if $\frac{K-1}{2}< v^*<K$. For $v^*=\frac{K-1}{2}$, we have

$$\begin{aligned} {\hat{a}}(0, D, e_2)=0, {\hat{b}}(0, D, e_2)>0 \text {and}\quad {\hat{a}}(j, D, e_2)>0, {\hat{b}}(j, D, e_2)>0 \quad \text {for } j>0, \end{aligned}$$

which implies that spatially homogeneous periodic solutions arise. Therefore, we will investigate the influence of D on spatially inhomogeneous patterns for (3.1) under the condition $0<v^*< \frac{K-1}{2}$. In this case, ${\hat{a}}(0, D, e_2)=\frac{v^*(2v^*+1-K)}{K(1+v*)}<0$, ${\hat{b}}(0, D, e_2)=\frac{K-v^*}{K(1+v^*)}>0$, which implies that $e_2$ is unstable for $0<v^*< \frac{K-1}{2}$. Then, we set for $j\in \{1,2,\ldots \}$,

$$\begin{aligned} D^H_j= & {} \Big (\frac{l}{\pi j}\Big )^2\frac{v^*(K-1-2v^*)}{K(1+v^*)}-d(v^*),\\ D^S_j= & {} \Big (\frac{l}{\pi j}\Big )^2\Big (\frac{d'(v^*)u^*}{\gamma d(v^*)}-\frac{K-v^*}{d(v^*)K(1+v^*)}\Big (\frac{l}{\pi j}\Big )^2-\frac{v^*(2v^*+1-K)}{K(1+v^*)}\Big ) \end{aligned}$$

and give the following two assumptions,

(A3):

$d(v^*)<\Big (\frac{l}{\pi }\Big )^2\frac{v^*(K-1-2v^*)}{K(1+v^*)}$;

(A4):

$-\frac{d'(v^*)}{d(v^*)}<\frac{\gamma v^*(K-1-2v^*)}{K(1+v^*)u^*}$.

It follows from assumption (A3) that the set of j such that $D^H_j>0$, denoted by ${\mathcal {S}}_1$, is nonempty. By assumption (A4), the set of j such that $D^S_j>0$, denoted by ${\mathcal {S}}_2$, is nonempty. We set ${\hat{D}}_*=\max _{j\in {\mathcal {S}}_2}\{D^H_1,\ D^S_j\}$.

Remark 3.1

There exist three cases for the possible occurrence of steady-state bifurcation and Hopf bifurcation.

• (1) If there exists an integer $j_0\ge 1$ such that ${\hat{D}}_*=D_{j_0}^S>D^H_1$, then ${\hat{b}}(j_0, {\hat{D}}_*, e_2)=0$ and the eigenvalues of (3.6) at ${\hat{D}}_*$ are $\sigma ^S_1({\hat{D}}_*, j_0)=0$ and $\sigma ^S_2({\hat{D}}_*, j_0)=-{\hat{a}}(j_0, {\hat{D}}_*, e_2)<0$. This means steady-state bifurcation can occur, and we will study it in the next subsection. Note that $e_2$ is unstable when $0<D<{\hat{D}}_*$, then (3.6) with $D=D_{j}^S$, $j\ne j_0$ admits at least one eigenvalue with positive real part.

• (2) If ${\hat{D}}_*=D^H_1>D_{j}^S$ with $j\in {\mathcal {S}}_2$, then ${\hat{a}}(1, {\hat{D}}_*, e_2)=0$ and ${\hat{b}}(1, {\hat{D}}_*, e_2)>0$. Thus, the eigenvalues of (3.6) at ${\hat{D}}_*$ are $\sigma ^H_{1,2}({\hat{D}}_*, 1)=\pm \sqrt{{\hat{b}}(1, {\hat{D}}_*, e_2)} i$, which implies (3.1) with $D={\hat{D}}_*$ may undergo a Hopf Bifurcation and a time-periodic spatial patterns can arise.

• (3) If ${\hat{D}}_*=D^H_1=D_{j_0}^S$, then (3.6) can admit two zero eigenvalues. Therefore, in this case, (3.1) may experience a codimension-two bifurcation around $e_2$, which is more complicate than steady-state bifurcation and Hopf bifurcation. For our purpose, we assume $D^S_j\ne D^H_j$, $j\in {\mathcal {S}}_1\cup {\mathcal {S}}_2$.

Remark 3.2

Due to the positivity of D, either (A3) or (A4) can ensure possible pattern formation of (3.1) with respect to D.

3.1 Steady-State Bifurcation

3.1.1 Local and Global Bifurcation

We will investigate the nonconstant steady states to (3.1) induced by the steady-state bifurcation. It is easy to see that a nonconstant steady state of (3.1) is also a nonconstant positive solution of the following stationary system,

$$\begin{aligned} \left\{ \begin{array}{ll} (d(v)u)_{xx}+\frac{\gamma uv}{1+v}-u=0, \quad &{} x\in (0,\ l),\\ Dv_{xx}-\frac{uv}{1+v}+v\Big (1-\frac{v}{K}\Big )=0, \quad &{} x\in (0,\ l),\\ u_{x}=v_{x}=0, &{} x=0, l, \end{array} \right. \end{aligned}$$

(3.7)

Therefore, we only focus on the information about the positive solutions of (3.7). Then, $e_2$ is a positive constant solution of (3.7). Meanwhile, it follows from Lemma 2.1 that there exist two positive numbers $\underline{C}$ and ${\overline{C}}$ such that $\underline{C}\le u(x), v(x)\le {\overline{C}}$ for $0\le x\le l$, where $(u(x),\ v(x))$ is a positive solution of (3.7). And according to Lemma 1.1, all the solutions of (3.1) will converge to $e_2$ if $D\ge D_0$, where

$$\begin{aligned} D_0=\frac{K\gamma (\gamma -1)-\gamma }{4(\gamma -1)^2}\max _{0\le v\le K_0}\frac{v^2|d'(v)|^2}{d(v)}, \quad K_0=\max \{\Vert v_0\Vert _{\infty },\ K\}. \end{aligned}$$

Next, regarding $D>0$ as the bifurcation parameter, we will investigate the local and global structure of positive solutions for (3.7). First, we set

$$\begin{aligned} {\mathcal {F}}_1(u,\ v)=\frac{\gamma uv}{1+v}-u,\quad {\mathcal {F}}_2(u,\ v)=\frac{uv}{1+v}-v\Big (1-\frac{v}{K}\Big ), \end{aligned}$$

and let ${\mathcal {F}}$ be the following map from $\Upsilon :=(0,\ +\infty )\times X$ to Y:

$$\begin{aligned} {\mathcal {F}}(D, u, v)=\begin{pmatrix} -[(d(v)u)_{xx}+{\mathcal {F}}_1(u,\ v)] \\ -Dv_{xx}+{\mathcal {F}}_2(u,\ v) \end{pmatrix}, \end{aligned}$$

where

$$\begin{aligned} X=\{(u,\ v): u,\ v\in {W^{2,2}([0,\ l])}, u_x=v_x=0,\ \text {at}\ x=0,\ l\} \end{aligned}$$

with the usual $C^2$ norm and $Y=L^2(0,\ l)\times L^2(0,\ l)$ with inner product

$$\begin{aligned} (z_1,\ z_2)_Y=(u_1,\ u_2)_{L^2(0,\ l)}+(v_1,\ v_2)_{L^2(0,\ l)} \end{aligned}$$

for $z_1=(u_1,\ u_2)\in Y$ and $z_2=(v_1,\ v_2)\in Y$. Therefore, to find the solutions for (3.7), it suffices to investigate the zeros for the map ${\mathcal {F}}$. For any fixed $(D, u_1, v_1)\in \Upsilon$, the Frèchet derivative of ${\mathcal {F}}(D, u, v)$ at $(D, u_1, v_1)$ is given by

$$\begin{aligned}{} & {} {\mathcal {F}}_{(u,\ v)}(D, u_1, v_1)\begin{pmatrix} u \\ v \end{pmatrix}\nonumber \\{} & {} \quad =\begin{pmatrix} -(d'(v_1)u_1v+d(v_1)u)_{xx}+A(u_1, v_1)u+B(u_1, v_1)v \\ -Dv_{xx}+C(u_1, v_1)u+D(u_1, v_1)v \end{pmatrix}, \end{aligned}$$

(3.8)

where $A(u_1, v_1)$, $B(u_1, v_1)$, $C(u_1, v_1)$ and $D(u_1, v_1)$ are given in (3.5). We claim that for any $(u_1,v_1)\in X$ and given $D>0$, the Frèchet derivative ${\mathcal {F}}_{(u,\ v)}(D, u_1, v_1):X\rightarrow Y$ is a Fredholm operator with index zero. In fact, we can rewrite (3.8) as

$$\begin{aligned} {\mathcal {F}}_{(u,\ v)}(D, u_1, v_1)\begin{pmatrix} u \\ v \end{pmatrix}= & {} -\begin{pmatrix} d(v_1) &{} d'(v_1)u_1\\ 0 &{} D \end{pmatrix}\begin{pmatrix} u_{xx} \\ v_{xx} \end{pmatrix}\\{} & {} + \begin{pmatrix} A(u_1, v_1)u+B(u_1, v_1)v \\ C(u_1, v_1)u+D(u_1, v_1)v \end{pmatrix}, \end{aligned}$$

and by Remark 2.5 case 3 in [39], it is easy to obtain that ${\mathcal {F}}_{(u,\ v)}(D, u_1, v_1):X\rightarrow Y$ is elliptic and satisfies Agmon’s condition. Therefore, it follows from Theorem 3.3 and Remark 3.4 in [39] that ${\mathcal {F}}_{(u,\ v)}(D, u_1, v_1):X\rightarrow Y$ is a Fredholm operator with zero index. Note that (3.7) always admit two boundary constant solutions $e_0$ and $e_1$, and when $\gamma >\frac{1+K}{K}$, (3.7) has a positive constant solution $e_2$. A routine analysis shows that $e_0$ is linearly unstable and $e_1$ is linear stable. Hence, we will only find positive nonconstant solutions of (3.7) around $e_2$.

We proceed to look for a potential bifurcation value D by checking the necessary condition $Ker{\mathcal {F}}_{(u,\ v)}(D, e_2)\ne \{0\}$, where

$$\begin{aligned} {\mathcal {F}}_{(u,\ v)}(D, e_2)\begin{pmatrix} u \\ v \end{pmatrix}=\begin{pmatrix} -(d'(v^*)u^*v+d(v^*)u)_{xx}-\frac{\gamma (K-v^*)}{K(1+v^*)}v \\ -Dv_{xx}+\frac{1}{\gamma }u+\frac{v^*(2v^*+1-K)}{K(1+v^*)}v \end{pmatrix}, \end{aligned}$$

(3.9)

in which (3.2) is used. By (3.9), it is obvious that each element in $Ker{\mathcal {F}}_{(u,\ v)}(D, e_2)$ is a solution of the following system

$$\begin{aligned} \left\{ \begin{array}{ll} -d(v^*)u_{xx}-d'(v^*)u^*v_{xx}-\frac{\gamma (K-v^*)}{K(1+v^*)}v=0, \quad &{} x\in (0,\ l), \\ -Dv_{xx}+\frac{1}{\gamma }u+\frac{v^*(2v^*+1-K)}{K(1+v^*)}v=0, \quad &{} x\in (0,\ l), \\ u_{x}=v_{x}=0, \quad &{} x=0, l. \end{array} \right. \end{aligned}$$

(3.10)

In order to show that $Ker{\mathcal {F}}_{(u,\ v)}(D, e_2)\ne \{0\}$, we rewrite the solution (u(x), v(x)) of (3.10) into their eigenexpansions

$$\begin{aligned} u(x)=\sum _{j=0}^{\infty }c_j^1\phi _j(x), \quad v(x)=\sum _{j=0}^{\infty }c_j^2\phi _j(x), \end{aligned}$$

(3.11)

where $c_j^1$ and $c_j^2$, $j=0,1,2,\ldots ,$ are constants. Inserting (3.11) into (3.10), we have

$$\begin{aligned} \sum _{j=0}^\infty {\hat{L}}_j(D, e_2)\begin{pmatrix} c^1_j \\ c^2_j \end{pmatrix}\phi _j=0, \end{aligned}$$

where

$$\begin{aligned} {\hat{L}}_j(D, e_2)=\begin{pmatrix} d(v^*)\Big (\frac{\pi j}{l}\Big )^2 &{} d'(v^*)u^*\Big (\frac{\pi j}{l}\Big )^2-\frac{\gamma (K-v^*)}{K(1+v^*)}\\ \frac{1}{\gamma } &{} D\Big (\frac{\pi j}{l}\Big )^2+\frac{v^*(2v^*+1-K)}{K(1+v^*)} \end{pmatrix}. \end{aligned}$$

It is easy to see that $Ker{\mathcal {F}}_{(u,\ v)}(D, e_2)\ne \{0\}$ if and only if there exists at least an integer $j\ge 0$ such that $(c^1_j,\ c^2_j)$ is nontrivial. Obviously, $c^1_0=c^2_0=0$. Therefore, (3.10) has nontrivial solutions if and only if $D=D_j$, where

$$\begin{aligned} D_j= & {} \Big (\frac{l}{\pi j}\Big )^2\Big (\frac{d'(v^*)u^*}{\gamma d(v^*)}-\frac{K-v^*}{d(v^*)K(1+v^*)}\Big (\frac{l}{\pi j}\Big )^2\nonumber \\{} & {} -\,\frac{v^*(2v^*+1-K)}{K(1+v^*)}\Big )=D^S_j, \quad j=1,2,\ldots . \end{aligned}$$

(3.12)

Under assumption (A4), we can obtain a set ${\mathcal {S}}_2$ such that $D^S_j>0$ for $j\in {\mathcal {S}}_2$. Then for each positive integer $j\in {\mathcal {S}}_2$ such that $D^S_j\ne D^S_k$, $j\ne k$ and $D^S_j\ne D^H_j$, we have that $dim Ker{\mathcal {F}}_{(u,\ v)}(D^S_j, e_2)=1$ and

$$\begin{aligned} Ker({\mathcal {F}}_{u, v}(D^S_j, e_2)=span\{(u^*_j,\ v^*_j)\}, \end{aligned}$$

where

$$\begin{aligned} \left\{ \begin{array}{ll} u^*_j=b_1(j)\phi _j, \quad &{} b_1(j)=-\gamma \Big (D^S_j\Big (\frac{\pi j}{l}\Big )^2+\frac{v^*(2v^*+1-K)}{K(1+v^*)}\Big )>0,\\ v^*_j=\phi _j. \end{array} \right. \end{aligned}$$

(3.13)

Next, we claim that

$$\begin{aligned} {\mathcal {F}}_{(u, v)D}(D, u_1, v_1)(u^*_j,\ v^*_j)|_{D=D^S_j} \not \in Ran({\mathcal {F}}_{u, v}(D^S_j, u_1, v_1)), \end{aligned}$$

(3.14)

where

$$\begin{aligned} {\mathcal {F}}_{(u, v)D}(D, u_1, v_1)(u^*,\ v^*)|_{D=D^S_j}=\begin{pmatrix} 0 \\ \Big (\frac{\pi j}{l}\Big )^2\phi _j \end{pmatrix}. \end{aligned}$$

If not, then there exists a nontrivial pair $(h_1,\ h_2)$ such that

$$\begin{aligned} \left\{ \begin{array}{ll} -d(v^*)h''_1-d'(v^*)u^*h''_2-\frac{\gamma (K-v^*)}{K(1+v^*)}h_2=0, &{} x\in (0,\ l),\\ -D^S_j h''_2+\frac{1}{\gamma }h_1+\frac{v^*(2v^*+1-K)}{K(1+v^*)}h_2=\Big (\frac{\pi j}{l}\Big )^2\phi _j, &{}x\in (0,\ l),\\ h'_1(x)=h'_2(x)=0,&{} x=0,\ l. \end{array} \right. \end{aligned}$$

(3.15)

Note that $\int _0^l \phi ^2_j(x)dx=\frac{l}{2}$, then multiplying both sides of the first two equations in (3.15) by $\phi _j(x)$ and integrating them over $(0,\ l)$, we obtain

$$\begin{aligned} \begin{pmatrix} d(v^*) \Big (\frac{\pi j}{l}\Big )^2 &{} d'(v^*)u^* \Big (\frac{\pi j}{l}\Big )^2-\frac{\gamma (K-v^*)}{K(1+v^*)}\\ \frac{1}{\gamma } &{} D^S_j \Big (\frac{\pi j}{l}\Big )^2+\frac{v^*(2v^*+1-K)}{K(1+v^*)} \end{pmatrix} \begin{pmatrix} \int _0^lh_1\phi _jdx\\ \int _0^lh_2\phi _jdx \end{pmatrix}=\begin{pmatrix} 0\\ \frac{l}{2}\Big (\frac{\pi j}{l}\Big )^2 \end{pmatrix}. \end{aligned}$$

It follows from (3.12) that the coefficient matrix of the above equation is singular, which implies $h_1=h_2=0$. Therefore, we have (3.14).

According to Theorem 4.3 in [39], we obtain that for each positive integer $j\in {\mathcal {S}}_2$ such that $D^S_j\ne D^S_k$, $j\ne k$ and $D^S_j\ne D^H_j$, $(D^S_j, e_2)$ is a bifurcation point in $\Upsilon$. Specifically, there exists a $\delta >0$ such that (3.7) admits a one-parameter family of nonconstant solutions ${\mathcal {C}}_j^*=(D_j(s), u_j(s,x), v_j(s,x))$, $s\in (-\delta ,\ \delta )$, which is bifurcated from $(D^S_j, e_2)$, and $D_j(s), u_j(s,x), v_j(s,x)$ are smooth functions with respect to s and satisfy $(u_j(s,x), v_j(s,x))\in X$,

$$\begin{aligned} \left\{ \begin{array}{l} D_j(0)=D^S_j,\quad u_j(s,x)=u^*+su_j^*(x)+o_1(s),\\ v_j(s,x)=v^*+sv_j^*(x)+o_2(s), \end{array} \right. \end{aligned}$$

with $(o_1(s),\ o_2(s))\in \hat{{\mathcal {Z}}}$, where $\hat{{\mathcal {Z}}}$ is given by

$$\begin{aligned} \hat{{\mathcal {Z}}}=\Big \{(u,\ v)\in X \Big | \int _{0}^L(uu_j^*+vv_j^*)dx=0\Big \}. \end{aligned}$$

Moreover, all nonconstant solutions of (3.7) around $(D^S_j, e_2)$ lie on the curve ${\mathcal {C}}_j^*$. Obviously, there are infinite possible bifurcation values $D^S_j$ and $D^S_j\rightarrow 0$ as $j\rightarrow \infty$.

Furthermore, by applying global bifurcation theorem of Rabinowitz (see Corollary 1.12 in [37]) and the Leray–Schauder degree theory, we will investigate the global information of the bifurcating curve ${\mathcal {C}}_j^*$. We first rewrite (3.7) as

$$\begin{aligned} \left\{ \begin{array}{ll} -u_{xx}=f(u,v), \quad &{} x\in (0,\ l),\\ -v_{xx}=g(u,v), \quad &{} x\in (0,\ l),\\ u_x=v_x=0, \quad &{} x=0, l, \end{array} \right. \end{aligned}$$

(3.16)

where

$$\begin{aligned} g(u,v)= & {} \frac{1}{D}\Big [v\Big (1-\frac{v}{K}\Big )-\frac{uv}{1+v}\Big ], \\ f(u,v)= & {} \frac{1}{d(v)}\Big (\frac{\gamma uv}{1+v}+\ddot{d} (v)v_x^2u-{\dot{d}}(v)g(u,v)u+2{\dot{d}}(v) v_xu_x-u\Big ), \end{aligned}$$

in which $\ddot{d} (v)$, ${\dot{d}}(v)$ denote the second derivative and the first derivative of d(v) with respect to v, respectively. Let ${\bar{u}}=u-u^*$ and ${\bar{v}}=v-v^*$, then (3.16) becomes

$$\begin{aligned} \left\{ \begin{array}{ll} -{\bar{u}}_{xx}=f_0{\bar{u}}+f_1{\bar{v}}+f_2({\bar{u}}, {\bar{v}}), \quad &{} x\in (0,\ l),\\ -{\bar{v}}_{dxx}=g_0{\bar{u}}+g_1{\bar{v}}+g_2({\bar{u}}, {\bar{v}}), \quad &{} x\in (0,\ l),\\ {\bar{u}}_{x}={\bar{v}}_{x}=0,\quad &{} x=0, l, \end{array} \right. \end{aligned}$$

(3.17)

where both $f_2$ and $g_2$ are higher-order terms of ${\bar{u}}$ and ${\bar{v}}$, $f_0=f_u(u^*, v^*)=\frac{d'(v^*)u^*v^*}{Dd(v^*)(1+v^*)}$, $g_0=g_u(u^*, v^*)=-\frac{v^*}{D(1+v^*)}$, $g_1=g_v(u^*, v^*)=\frac{v^*(K-1-2v^*)}{KD(1+v^*)}$ and

$$\begin{aligned} f_1=f_v(u^*, v^*)=\frac{1}{d(v^*)}\Big [\frac{\gamma u^*}{(1+v^*)^2}-\frac{d'(v^*)u^*v^*(K-1-2v^*)}{KD(1+v^*)}\Big ]. \end{aligned}$$

Hence, the constant solution $e_2$ of (3.7) is moved to the zero solution ${\mathcal {O}}=(0,\ 0)$ of (3.17). According to assumptions (A3), we have $f_0<0$ and $g_1>0$. Let $G_1$ and $G_2$ be the inverse operators of $-f_0-\frac{d^2}{dx^2}$ and $g_1-\frac{d^2}{dx^2}$ with homogeneous Neumann boundary condition. Furthermore, set

$$\begin{aligned} {\bar{U}}=\begin{pmatrix} {\bar{u}} \\ {\bar{v}} \end{pmatrix}, \quad M(D)=\begin{pmatrix} 0 &{} f_1G_1\\ g_0G_2 &{} 2g_1G_2 \end{pmatrix}, \quad H(D, {\bar{U}})=\begin{pmatrix} G_1(f_2({\bar{u}},{\bar{v}})) \\ G_2(g_2({\bar{u}},{\bar{v}})) \end{pmatrix}, \end{aligned}$$

then (3.17) is equivalent to the following equation

$$\begin{aligned} {\bar{U}}=M(D){\bar{U}}+H(D,{\bar{U}})\overset{def}{=}K(D,{\bar{U}}), \quad {\bar{U}}\in X. \end{aligned}$$

(3.18)

Note that for any given $D>0$, M(D) is a compact linear operator on X. Furthermore, $H(D,{\bar{U}})=o(\Vert {\bar{U}}\Vert )$ for ${\bar{U}}$ near zero uniformly and $H(D,{\bar{U}})$ is a compact operator on X for D in the closed sub-intervals of $(0,\ +\infty )$. In order to study the global bifurcation for (3.7), we first present the following lemma.

Lemma 3.2

Let $\gamma >\frac{1+K}{K}$ and $0<v^*< \frac{K-1}{2}$. Suppose assumptions (A0) and (A3) hold. If there exists a positive integer $j\in {\mathcal {S}}_2$ such that $D^S_j\ne D^S_k$, $j\ne k$ and $D^S_j\ne D^H_j$, then 1 is an eigenvalue of $M(D^S_j)$ with algebraic multiplicity one.

Proof

Let $\varTheta =\begin{pmatrix} \varphi \\ \psi \end{pmatrix}$, where $\varphi =\sum _{i=0}^{\infty }a_i\phi _i$ and $\psi =\sum _{i=0}^{\infty }b_i\phi _i$, then we consider equation $(M(D_j)-I)\varTheta =0$ which leads to

$$\begin{aligned} \begin{pmatrix} f_0+\frac{d^2}{dx^2} &{} f_1\\ g_0&{} g_1+\frac{d^2}{dx^2} \end{pmatrix}\varTheta =0. \end{aligned}$$

(3.19)

Note that a simple computation shows that (3.19) is same as (3.10) with $D=D^S_j$. Therefore, 1 is an eigenvalue of $M(D^S_j)$ with the unique eigenfunction $\Phi = \begin{pmatrix} b_1(j)\\ 1 \end{pmatrix}\phi _j$, where $b_1(j)$ is defined in (3.13). Hence, $dim ker(M(D^S_j)-I)=1$. Thus, we only need to show that the eigenvalue 1 is simple. Note that the algebraic multiplicity of eigenvalue 1 is defined as the dimension of the generalized null space $\bigcup _{i=1}^{\infty }ker(M(D^S_j)-I)^i$, then it remains to prove that $ker(M(D^S_j)-I) \bigcap Ran(M(D^S_j)-I)=\{0\}$. We first compute $ker(M^*(D^S_j)-I)$, where $M^*(D^S_j)$ is the adjoint of $M(D^S_j)$. To this end, let $(\varphi ,\ \psi )\in ker(M^*(D^S_j)-I)$, then we get

$$\begin{aligned} \left\{ \begin{array}{l} g^j_0G_2(\psi )=\varphi ,\\ f^j_1G_1(\varphi )+2g^j_1G_2(\psi )=\psi , \end{array} \right. \end{aligned}$$

where $g^j_0=-\frac{v^*}{D^S_j(1+v^*)}$, $g^j_1=\frac{v^*(K-1-2v^*)}{KD^S_j(1+v^*)}$ and

$$\begin{aligned} f^j_1=\frac{1}{d(v^*)}\Big [\frac{\gamma u^*}{(1+v^*)^2}-\frac{d'(v^*)u^*v^*(K-1-2v^*)}{KD^S_j(1+v^*)}\Big ]. \end{aligned}$$

Therefore, according to the definitions of $G_1$ and $G_2$, we obtain

$$\begin{aligned} \left\{ \begin{aligned}&-\varphi _{xx}=g_0^j\psi -g_1^j\varphi ,\\&-g_0^j\psi _{xx}=F_{\varphi }\varphi +F_{\psi }\psi , \end{aligned} \right. \end{aligned}$$

(3.20)

where

$$\begin{aligned} F_{\varphi }=f_1^jg_0^j-2g_1^jf_0^j-2(g_1^j)^2, \quad F_{\psi }=2g_0^jg_1^j+g_0^jf_0^j. \end{aligned}$$

Set $\varphi =\sum _{k=0}^{\infty }a_k\phi _k$ and $\psi =\sum _{k=0}^{\infty }b_k\phi _k$, then using (3.20), we get

$$\begin{aligned} \sum _{k=0}^{\infty }L^*_k\begin{pmatrix} a_k \\ b_k \end{pmatrix}\phi _k,\quad L^*_k=\begin{pmatrix} \Big (\frac{\pi k}{l}\Big )^2+g_1^j &{} -g_0^j\\ -F_{\varphi }&{} g_0^j\Big (\frac{\pi k}{l}\Big )^2-F_{\psi } \end{pmatrix}. \end{aligned}$$

It is not difficult to get that $det(L^*_k)=g_0^j\Big (\Big (\frac{\pi k}{l}\Big )^2-\Big (\frac{\pi j}{l}\Big )^2\Big )\Big (\Big (\frac{\pi k}{l}\Big )^2+\Big (\frac{\pi j}{l}\Big )^2-(g_1^j+f_0^j)\Big )$. Due to the assumption that $D^S_k\ne D^S_j$ for $k\ne j$, we have that $\Big (\frac{\pi k}{l}\Big )^2\ne (g_1^j+f_0^j)-\Big (\frac{\pi j}{l}\Big )^2$ for $k\ne j$. Therefore, we can obtain that $det(L^*_k)=0$ if and only if $k=j$ and

$$\begin{aligned} L^*_j=\begin{pmatrix} \Big (\frac{\pi j}{l}\Big )^2+g_1^j &{} -g_0^j\\ 0&{} 0 \end{pmatrix}. \end{aligned}$$

Set $\Phi ^*=\begin{pmatrix} g_0^j\\ \lambda _j+g_1^j \end{pmatrix}\phi _j$, thus space $ker(M^*(D^S_j)-I)$ is generated by $\Phi ^*$. It is easy to see that $(\Phi , \Phi ^*)_Y=\frac{\gamma v^*}{1+v^*}\Big (\frac{l}{\pi j}\Big )^2+\Big (\frac{\pi j}{l}\Big )^2>0$, which implies that $\Phi \notin Ran(M(D^S_j)-I)$. therefore, $ker(M(D^S_j)-I) \bigcap Ran(M(D^S_j)-I)=\{0\}$. The proof is completed. $\square$

Now, we give the following results on the global structure of the bifurcating curve ${\mathcal {C}}_j^*$.

Theorem 3.1

Let $\gamma >\frac{1+K}{K}$ and $0<v^*< \frac{K-1}{2}$. Suppose assumptions (A0) and (A3) hold. If there exists a positive integer $j\in {\mathcal {S}}_2$ such that $j\le \sqrt{\frac{l^2}{2\pi ^{2}}}$, $D^S_j\ne D^S_k$, $j\ne k$ and $D^S_j\ne D^H_j$, then the projection of the bifurcation curve ${\mathcal {C}}_j^*$ onto the D-axis contains the interval $(0,\ D^S_j)$. Moreover, if ${\bar{m}}<\sqrt{\frac{l^2}{2\pi ^{2}}}$, where $D_{{\bar{m}}}=D^*=\max _{j\in {\mathcal {S}}_2}D^S_j$, then system (3.7) admits at least one nonconstant positive solution if $D\in (0,\ D^*)$.

Proof

According to Lemma 3.2, for any $D\in (0,\ D^*)$, where $D\ne D^S_j$ and D lies in a small neighborhood of $D^S_j$, we obtain that the operator $I-M(D):X\rightarrow X$ is bijection, which implies ${\mathcal {O}}$ is an isolated solution of (3.18) for such D. Therefore, in order to apply global bifurcation theory (see Corollary 1.12 in [37]), we shall compute the index of the isolated solution ${\mathcal {O}}$ of $I-K(D,\ \cdot )$, which is given by

$$\begin{aligned} i(I-K(D,\ \cdot ), (D,\ {\mathcal {O}}))=deg(I-M(D),{\mathcal {B}},{\mathcal {O}})=(-1)^p, \end{aligned}$$

where ${\mathcal {B}}$ is a sufficiently small ball with origin ${\mathcal {O}}$ and p is the total number of the algebraic multiplicities of the eigenvalues of M(D) that are large than 1. For our purpose, we need to check that

$$\begin{aligned} i(I-K(D^S_j-{\mathcal {E}},\ \cdot ), (D^S_j-{\mathcal {E}},\ {\mathcal {O}}))\ne i(I-K(D^S_j+{\mathcal {E}},\ \cdot ), (D^S_j+{\mathcal {E}},\ {\mathcal {O}})),\nonumber \\ \end{aligned}$$

(3.21)

with small enough ${\mathcal {E}}>0$, which means that this index must changes as D cross $D^S_j$.

In fact, let ${\bar{\mu }}$ be an eigenvalue of M(D) with an eigenfunction $(\varphi , \psi )$, then we get

$$\begin{aligned} \left\{ \begin{aligned}&-{\bar{\mu }}\varphi _{xx}={\bar{\mu }}f_0\varphi +f_1\psi ,\\&-{\bar{\mu }}\psi _{xx}=g_0\varphi +(2-{\bar{\mu }})g_1\psi . \end{aligned} \right. \end{aligned}$$

(3.22)

Note that $\varphi =\sum _{i=0}^{\infty }a_i\phi _i$ and $\psi =\sum _{i=0}^{\infty }b_i\phi _i$, then (3.22) becomes

$$\begin{aligned} \sum _{i=0}^{+\infty }\begin{pmatrix} {\bar{\mu }}\Big (f_0-\Big (\frac{\pi i}{l}\Big )^2\Big ) &{} f_1\\ g_0&{} (2-{\bar{\mu }})g_1-{\bar{\mu }}\Big (\frac{\pi i}{l}\Big )^2 \end{pmatrix}\begin{pmatrix} a_i \\ b_i \end{pmatrix}\phi _i=0. \end{aligned}$$

It is easy to see that the set of eigenvalues of M(D) is made up of all the zeros of the following characteristic equation for ${\bar{\mu }}$,

$$\begin{aligned} \Big (g_1+\Big (\frac{\pi i}{l}\Big )^2\Big ){\bar{\mu }}^2-2g_1{\bar{\mu }}-\frac{g_0f_1}{\Big (\frac{\pi i}{l}\Big )^2-f_0}=0, \quad i=0,1,2,\ldots . \end{aligned}$$

(3.23)

Let $D=D^S_j$ in (3.23), if ${\bar{\mu }}=1$ is a root of (3.23), then a simple computation shows that

$$\begin{aligned} D^S_j=\Big (\frac{l}{\pi i}\Big )^2\Big (\frac{d'(v^*)u^*}{\gamma d(v^*)}-\frac{K-v^*}{d(v^*)K(1+v^*)}\Big (\frac{l}{\pi i}\Big )^2-\frac{v^*(2v^*+1-K)}{K(1+v^*)}\Big )=D^S_i. \end{aligned}$$

Note that $D^S_k\ne D^S_j$ for $k\ne j$, then $i=j$. Hence, M(D) admits the equal number of eigenvalues which are greater than 1 for all D close to $D^S_j$ and those eigenvalues have the same multiplicities. It is easy to see that (3.23) with $i=j$ has the following roots,

$$\begin{aligned} {\bar{\mu }}_1(D^S_j)=1, \quad {\bar{\mu }}_2(D^S_j)=\frac{g_1^j-\Big (\frac{\pi j}{l}\Big )^2}{g_1^j+\Big (\frac{\pi j}{l}\Big )^2}<1. \end{aligned}$$

Due to the continuous dependence of ${\bar{\mu }}_2$ on parameter D, we know that ${\bar{\mu }}_2(D)<1$ still be true for D close to $D_j$. Note that

$$\begin{aligned} {\bar{\mu }}_1(D)=\frac{2g_1+\sqrt{4g_1^2+{\tilde{M}}(j,\ D)}}{2g_1+2\Big (\frac{\pi j}{l}\Big )^2},\quad {\tilde{M}}(j,\ D)=4\Big (g_1+\Big (\frac{\pi j}{l}\Big )^2\Big )\Big (\frac{g_0f_1}{\Big (\frac{\pi j}{l}\Big )^2-f_0}\Big ), \end{aligned}$$

then a routine computation gives rise to

$$\begin{aligned} \frac{d{\bar{\mu }}_1}{d D}=\frac{2(g_1)_D+\frac{(4g_1^2)_D+({\tilde{M}}(j,\ D))_D}{2\sqrt{4g_1^2+{\tilde{M}}(j,\ D)}}-2\Big (2g_1+\sqrt{4g_1^2+{\tilde{M}}(j,\ D)}\Big )(g_1)_D}{4\Big (g_1+\Big (\frac{\pi j}{l}\Big )^2\Big )^2}, \end{aligned}$$

where $(H)_D$ is the derivative of H with respect to D. By assumption (A3), we have

$$\begin{aligned} f_0< & {} 0,\quad (f_0)_D>0,\quad g_0<0,\quad (g_0)_D>0, \\ f_1> & {} 0,\quad (f_1)_D<0,\quad g_1>0,\quad (g_1)_D<0. \end{aligned}$$

A tedious computation yields $({\tilde{M}}(j,\ D))_D<0$. Note that $4g_1^{j2}+{\tilde{M}}(j,\ D^S_j)=4\Big (\frac{\pi j}{l}\Big )^4$, then

$$\begin{aligned} \begin{aligned}&\frac{d{\bar{\mu }}_1}{d D}|_{D=D^S_j}\\&\quad =\frac{\Big (2-4\Big (\frac{\pi j}{l}\Big )^2\Big )(g_1)_D(D^S_j)+\Big (2\Big (\frac{l}{\pi j}\Big )^2-4\Big )g_1^j(g_1)_D(D^S_j)+\frac{({\tilde{M}}(j,\ D))_D(D^S_j)}{4}\Big (\frac{l}{\pi j}\Big )^2}{4\Big (g^j_1+\Big (\frac{\pi j}{l}\Big )^2\Big )^2}, \end{aligned} \end{aligned}$$

where $H_D(D^S_j)$ denotes the value of the derivative of H with respect to D at $D=D^S_j$. Due to the assumption that $j<\sqrt{\frac{l^2}{2\pi ^2}}$, we have $\frac{d{\bar{\mu }}_1}{d D}|_{D=D^S_j}<0$, which implies that ${\bar{\mu }}_1(D)$ is a decreasing function of D in a small neighborhood of $D^S_j$. Therefore,

$$\begin{aligned} {\bar{\mu }}_1(D^S_j-{\mathcal {E}})>1, \quad {\bar{\mu }}_1(D^S_j+{\mathcal {E}})<1, \end{aligned}$$

from which we get that $M(D^S_j-{\mathcal {E}})$ has exactly one more eigenvalue that is larger then 1, than $M(D_j+{\mathcal {E}})$ does. An argument similar to the one used in Lemma 3.2 shows that that eigenvalue also has algebraic multiplicity one, which means (3.21) is true.

Note systems (3.7) and (3.17) are equivalent, then by above analysis and Corollary 1.12 in [37], we can obtain a conclusion that ${\mathcal {C}}_j^*$ either meets the boundary of $(0,\ D^*)\times X$ or meets $(D^S_k,\ e_2)$ for some $k\in {\mathcal {S}}_2$ and $k\ne j$. By a reflective and periodic extension methods, and using a similar idea in [14, 40, 48], we can show that the first alternative must occur. By Lemma 2.1, the proof of this theorem is completed. $\square$

3.1.2 Stability of Bifurcation Steady States

It follows from the above discussions that under the conditions in Lemma 3.2, we can detect the spatially inhomogeneous steady-state $(u_j(s,x),\ v_j(s,x))$ bifurcating from $(D_j^S,\ e_2)$. Along this direction, we will focus on the turning direction of the bifurcation curve ${\mathcal {C}}_j^*$ and the stability of $(u_j(s,x),\ v_j(s,x))$ by investigating the sign of the eigenvalues of ${\mathcal {F}}_{(u,\ v)}(D_j(s), u_j(s,x), v_j(s,x))$.

Due to the smooth property of d(v) and ${\mathcal {F}}$, together with the fact that functions $D_j(s)$, $u_j(s,x)$ and $v_j(s,x)$ are smooth with respect to s, using [6, Theorem 1.18], we have the following expansions,

$$\begin{aligned} \left\{ \begin{aligned}&D_j(s)=D^S_j+s k_1+s^2k_2+o(s^2),\\&u_j(s, x)=u^*+s b_1(j)\cos \Big (\frac{\pi jx}{l}\Big )+s^2\varphi _1(x)+s^3\varphi _2(x)+o(s^3),\\&v_j(s, x)=v^*+s \cos \Big (\frac{\pi jx}{l}\Big )+s^2\zeta _1(x)+s^3\zeta _2(x)+o(s^3), \end{aligned} \right. \end{aligned}$$

(3.24)

where $b_1(j)$ is defined in (3.13), $(\varphi _i,\ \zeta _i)\in \hat{{\mathcal {Z}}}$ for $i=1,2$, the terms $o(s^3)$ are taken in $C^2-$norm and $k_i$ for $i=1,2$ are constants. Note that

$$\begin{aligned} D_j(s)(v_j(s, x))_{xx}= & {} D_j^S\Big (\cos \Big (\frac{\pi jx}{l}\Big )\Big )_{xx}s\nonumber \\{} & {} +\,\Big (D_j^S(\zeta _1(x))_{xx}+k_1\cos \Big (\frac{\pi jx}{l}\Big )_{xx}\Big )s^2\nonumber \\{} & {} +\,\Big (D_j^S(\zeta _2(x))_{xx}+k_1(\zeta _1(x))_{xx}\nonumber \\{} & {} +\,k_2\cos \Big (\frac{\pi jx}{l}\Big )_{xx}\Big )s^3+o(s^3), \end{aligned}$$

(3.25)

$$\begin{aligned} (d(v_j(s, x))u_j(s, x))_{xx}= & {} A_{11}s+A_{12}s^2+A_{13}s^3+o(s^3), \end{aligned}$$

(3.26)

$$\begin{aligned} {\mathcal {F}}_1(v_j(s, x),\ v_j(s, x))= & {} B_{11}s+B_{12}s^2+B_{13}s^3+o(s^3) \end{aligned}$$

(3.27)

$$\begin{aligned} -{\mathcal {F}}_2(u_j(s, x),\ v_j(s, x))= & {} C_{11}s+C_{12}s^2+C_{13}s^3+o(s^3) \end{aligned}$$

(3.28)

where $A_{1k}$, $B_{1k}$ and $C_{1k}$ with $k=1,2,3$ are given in Appendix 4.1, then using (3.25)–(3.28) in the second equation of (3.7) and collecting all the $s^2-$terms, we get

$$\begin{aligned}{} & {} D^S_j(\zeta _1(x))_{xx}+\frac{v^*(K-2v^*-1)}{K(1+v^*)}\zeta _1(x)-\frac{v^*}{1+v^*}\varphi _1(x) \nonumber \\{} & {} \quad =-k_1\Big (\cos \Big (\frac{\pi jx}{l}\Big )\Big )_{xx}+\Big (\frac{1}{K}+\frac{b_1(j)}{(1+v^*)^2}-\frac{u^*}{(1+v^*)^3}\Big )\cos ^2\Big (\frac{\pi jx}{l}\Big ).\nonumber \\ \end{aligned}$$

(3.29)

Multiplying by $\cos \Big (\frac{\pi jx}{l}\Big )$ both sides of (3.29), and integrating the resulting equation over $(0,\ l)$, we obtain

$$\begin{aligned} \frac{(\pi j)^2}{2l}k_1= & {} \Big (\frac{v^*(K-2v^*-1)}{K(1+v^*)}-D_j^S\Big (\frac{\pi j}{l}\Big )^2\Big )\int _0^l \zeta _1(x)\cos \Big (\frac{\pi jx}{l}\Big )dx\nonumber \\{} & {} -\,\frac{v^*}{1+v^*}\int _0^l \varphi _1(x)\cos \Big (\frac{\pi jx}{l}\Big )dx. \end{aligned}$$

(3.30)

Likewise, applying (3.25)–(3.28) to the first equation of (3.7) and collecting all the $s^2-$terms, we have

$$\begin{aligned}{} & {} d(v^*)(\varphi _1(x))_{xx}+d'(v^*)u^*(\zeta _1(x))_{xx}+\frac{\gamma u^*\zeta _1(x)}{(1+v^*)^2} \nonumber \\{} & {} \quad =-d'(v^*)b_1(j)\Big (\cos ^2\Big (\frac{\pi jx}{l}\Big )\Big )_{xx}-\frac{d''(v^*)u^*}{2}\Big (\cos ^2\Big (\frac{\pi jx}{l}\Big )\Big )_{xx}\nonumber \\{} & {} \quad -\,\frac{\gamma (b_1(j)(1+v^*)-u^*)}{(1+v^*)^3}\cos ^2\Big (\frac{\pi jx}{l}\Big ). \end{aligned}$$

(3.31)

Multiplying by $\cos \Big (\frac{\pi jx}{l}\Big )$ both sides of (3.31), and integrating the resulting equation over $(0,\ l)$, we get

$$\begin{aligned}{} & {} -d(v^*)\Big (\frac{\pi j}{l}\Big )^2\int _0^l \varphi _1(x)\cos \Big (\frac{\pi jx}{l}\Big )dx\nonumber \\{} & {} \quad +\,\Big (\frac{\gamma u^*}{(1+v^*)^2}-d'(v^*)u^*\Big (\frac{\pi j}{l}\Big )^2\Big )\int _0^l \zeta _1(x)\cos \Big (\frac{\pi jx}{l}\Big )dx=0. \end{aligned}$$

(3.32)

Since $(\varphi _i,\ \zeta _i)\in \hat{{\mathcal {Z}}}$ for $i=1,2$, then

$$\begin{aligned} b_1(j)\int _0^l \varphi _1(x)\cos \Big (\frac{\pi jx}{l}\Big )dx+\int _0^l \zeta _1(x)\cos \Big (\frac{\pi jx}{l}\Big )dx=0. \end{aligned}$$

(3.33)

Combining (3.32) and (3.33), we arrive at

$$\begin{aligned} \begin{pmatrix} -d(v^*) \Big (\frac{\pi j}{l}\Big )^2 &{} \frac{\gamma u^*}{(1+v^*)^2}-d'(v^*)u^*\Big (\frac{\pi j}{l}\Big )^2\\ b_1(j) &{} 1 \end{pmatrix} \begin{pmatrix} \int _0^l \varphi _1(x)\cos \Big (\frac{\pi jx}{l}\Big )dx\\ \int _0^l \zeta _1(x)\cos \Big (\frac{\pi jx}{l}\Big )dx \end{pmatrix}=\begin{pmatrix} 0\\ 0 \end{pmatrix}. \end{aligned}$$

(3.34)

Using assumption (A0) and the fact that $b_1(j)>0$, it is easy to see that the determinant of the coefficient matrix in (3.34) is negative, which implies

$$\begin{aligned} \int _0^l \varphi _1(x)\cos \Big (\frac{\pi jx}{l}\Big )dx=\int _0^l \zeta _1(x)\cos \Big (\frac{\pi jx}{l}\Big )dx=0. \end{aligned}$$

(3.35)

Using (3.35) in (3.30), we have $k_1=0$. Therefore, the bifurcation branch ${\mathcal {C}}_j^*$ around $(D_j^S,\ e_2)$ is pitchfork.

Therefore, the stability of ${\mathcal {C}}_j^*$ near $(D_j^S,\ e_2)$ depends on the sign of $k_2$, which has been evaluated in Appendix 4.2, and we give the main result in the following theorem.

Theorem 3.2

Assume that $\gamma >\frac{1+K}{K}$ and $0<v^*< \frac{K-1}{2}$. Suppose assumptions (A0) and (A3) hold, and for positive integer j, k in ${\mathcal {S}}_2$,

$$\begin{aligned} D^S_j\ne D^S_k, \quad j\ne k,\quad \textrm{and} \quad D^S_j\ne D^H_j. \end{aligned}$$

Let ${\mathcal {C}}_j^*$ be the bifurcation curve near $(D_j^S,\ e_2)$ and ${\hat{D}}_*=\max _{j\in {\mathcal {S}}_2}\{D^H_1,\ D^S_j\}$. Then

• (1) if ${\hat{D}}_*=D_{j_0}^S>D_1^H$, then the bifurcation branch ${\mathcal {C}}_{j_0}^*$ near $(D_{j_0}^S,\ e_2)$ is asymptotically stable when $k_2\Big (\Big (\frac{\pi j_0}{l}\Big )^2-x^+\Big )>0$ and unstable when $k_2\Big (\Big (\frac{\pi j_0}{l}\Big )^2-x^+\Big )<0$, where $x^+$ is the only positive root of the following polynomial

  $$\begin{aligned} p(x)=-\gamma d(v^*)x^2-\frac{d'(v^*)u^*}{d(v^*)}x+\frac{\gamma (K-v^*)}{d(v^*)(1+v^*)}; \end{aligned}$$

  (3.36)

  meanwhile, for $j\ne j_0$, ${\mathcal {C}}_{j}^*$ near $(D_{j}^S,\ e_2)$ is always unstable;

• (2) if ${\hat{D}}_*=D_{1}^H>\max _{j\in {\mathcal {S}}_2}D_{j}^S$, then ${\mathcal {C}}_{j}^*$ near $(D_{j}^S,\ e_2)$ is always unstable for $j=1,2,\ldots$.

Proof

To study the stability of ${\mathcal {C}}_{j}^*$ for any given positive integer j, we need to investigate the following eigenvalue problem

$$\begin{aligned} {\mathcal {F}}_{(u,\ v)}(D_j(s), u_j(s, x), v_j(s, x))\begin{pmatrix} u \\ v \end{pmatrix}=\lambda (s)\begin{pmatrix} u \\ v \end{pmatrix}. \end{aligned}$$

(3.37)

Let $s\rightarrow 0$, then (3.37) becomes

$$\begin{aligned} {\mathcal {F}}_{(u,\ v)}(D^S_j, e_2)\begin{pmatrix} u \\ v \end{pmatrix}={\bar{\lambda }}\begin{pmatrix} u \\ v \end{pmatrix}. \end{aligned}$$

(3.38)

According to the discussions in the part (3.1.1), we have that ${\bar{\lambda }}=0$ is a simple eigenvalue of (3.38) and

$$\begin{aligned} Ker({\mathcal {F}}_{u, v}(D^S_j, e_2)=span\{(u^*_j,\ v^*_j)\}, \end{aligned}$$

where $(u^*_j,\ v^*_j)$ is given in (3.13). Multiplying both sides of (3.38) by $\phi _j(x)$, and integrating the result over (0, l), then we get that 0 is a simple eigenvalue of the matrix ${\mathcal {M}}_{j}$, where

$$\begin{aligned} {\mathcal {M}}_{j}=\begin{pmatrix} d(v^*)\Big (\frac{\pi j}{l}\Big )^2 &{} d'(v^*)u^*\Big (\frac{\pi j}{l}\Big )^2-\frac{\gamma (K-v^*)}{K(1+v^*)}\\ \frac{1}{\gamma } &{} D^S_j\Big (\frac{\pi j}{l}\Big )^2+\frac{v^*(2v^*+1-K)}{K(1+v^*)} \end{pmatrix}. \end{aligned}$$

Since ${\hat{D}}_*=D_{j_0}^S>D_1^H$ or ${\hat{D}}_*=D_{j_1}^H>\max _{j\in {\mathcal {S}}_2}D_{j}^S$, it follows from Remark 3.1 that ${\mathcal {M}}_{j}(j\ne j_0)$ always admits an eigenvalue with positive real part. Therefore, it follows from the standard eigenvalue perturbation theory [23] that for $j\ne j_0$ and a small enough s, and the linearized operator ${\mathcal {F}}_{(u,\ v)}(D_j(s), u_j(s, x), v_j(s, x))$ admits an eigenvalue $\lambda (s)$ with positive real part which implies that $(D_j(s), u_j(s, x), v_j(s, x)), \ s\in (-\delta ,\ \delta )$ is unstable.

Next, we will investigate the stability of ${\mathcal {C}}_{j_0}^*$ near $(D_{j_0}^S,\ e_2)$. Since ${\hat{D}}_*=D_{j_0}^S$, then by Remark 3.1, besides a zero eigenvalue, the characteristic polynomial of (3.38) with $j=j_0$ admits one negative eigenvalue. Therefore, for small enough s, we only need to study the sign of $\lambda (s)$ around the zero eigenvalue. According to (3.14) with $D=D^S_{j_0}$, we have that 0 is a simple eigenvalue of ${\mathcal {F}}_{(u,\ v)}(D^S_j, e_2)$. Thus, using Crandall and Rabinowitz [6, Corollary 1.13], we can get two intervals $I_1$, $I_2$ with $D^S_{j_0}\in I_1$, $0\in I_2$ and the following continuously differentiable functions,

$$\begin{aligned} {\widetilde{\lambda }}_1: I_1\rightarrow {\mathbb {R}}, \quad {\widetilde{\lambda }}_2: I_2\rightarrow {\mathbb {R}}, \quad ({\bar{u}}_1, {\bar{v}}_1):I_1\rightarrow X, \quad ({\bar{u}}_2, {\bar{v}}_2):I_2\rightarrow X, \end{aligned}$$

such that

$$\begin{aligned}{} & {} {\mathcal {F}}_{u, v}(D, e_2)\begin{pmatrix} {\bar{u}}_1 \\ {\bar{v}}_1 \end{pmatrix}={\widetilde{\lambda }}_1(D)\begin{pmatrix} {\bar{u}}_1 \\ {\bar{v}}_1 \end{pmatrix}, \end{aligned}$$

(3.39)

$$\begin{aligned}{} & {} {\mathcal {F}}_{u, v}(D(s), u(s,x), v(s,x)))\begin{pmatrix} {\bar{u}}_2 \\ {\bar{v}}_2 \end{pmatrix}={\widetilde{\lambda }}_2(s)\begin{pmatrix} {\bar{u}}_2 \\ {\bar{v}}_2 \end{pmatrix}, \end{aligned}$$

(3.40)

where

$$\begin{aligned} D(0)=D^S_{j_0},\ {\widetilde{\lambda }}_1(D^S_{j_0})={\widetilde{\lambda }}_2(0)=0,\\ ({\bar{u}}_1(D^S_{j_0}), {\bar{v}}_1(D^S_{j_0}))=({\bar{u}}_2(0), {\bar{v}}_2(0))=(u^*_{j_0}, v^*_{j_0}), \end{aligned}$$

and

$$\begin{aligned} ({\bar{u}}_1(D_j), {\bar{v}}_1(D_j))=(b_1(j)\phi _j, \phi _j), \quad ({\bar{u}}_2(s), {\bar{v}}_2(s))-(u^*_{j_0}, v^*_{j_0})\in \hat{{\mathcal {Z}}}. \end{aligned}$$

Furthermore, for any fixed small intervals $I_1$ and $I_2$, ${\widetilde{\lambda }}_1(D)$ and ${\widetilde{\lambda }}_2(s)$ are the only eigenvalues of (3.39) and (3.40), respectively. By Crandall and Rabinowitz [6, Theorem 1.16], for small |s|, the functions ${\widetilde{\lambda }}_2(s)$ and $-s(D_j(s))'\dot{{\widetilde{\lambda }}}_1(D^S_{j_0})$ admit the same zeros, where $\dot{{\widetilde{\lambda }}}_1=\frac{d{\widetilde{\lambda }}_1}{dD}$ and

$$\begin{aligned} \lim _{s\rightarrow 0, {\widetilde{\lambda }}_2(s)\ne 0}\frac{-s(D_j(s))'\dot{{\widetilde{\lambda }}}_1(D^S_{j_0})}{{\widetilde{\lambda }}_2(s)}=1. \end{aligned}$$

(3.41)

Clearly, it follows from (3.41) that ${\widetilde{\lambda }}_2(s)$ and $-s(D_j(s))'\dot{{\widetilde{\lambda }}}_1(D^S_{j_0})$ have the same sign in small neighborhood of $s=0$ for ${\widetilde{\lambda }}_2(s)\ne 0$. Since $k_1=0$, then for small |s|, $sgn(s(D_j(s))')=sgn(k_2)$. Next, we study the sign of $\dot{{\widetilde{\lambda }}}_1(D^S_{j_0})$. In fact, by differentiating (3.39) with respect to D and setting $D=D^S_{j_0}$, we get

$$\begin{aligned} \left\{ \begin{array}{ll} -d(v^*)\dot{u_1}_{xx}-d'(v^*)u^*\dot{v_1}_{xx}-\frac{\gamma (K-v^*)}{K(1+v^*)}\dot{v_1}=\dot{{\widetilde{\lambda }}}_1(D^S_{j_0}) u^*_{j_0}, &{} x\in (0,\ l),\\ -D_{j_0}^S\dot{v_1}_{xx}-v_{1xx}+\frac{1}{\gamma }\dot{u_1}+\frac{v^*(2v^*+1-K)}{K(1+v^*)}\dot{v_1}=\dot{{\widetilde{\lambda }}}_1(D^S_{j_0}) v^*_{j_0}, &{} x\in (0,\ l),\\ \dot{u_1}'_{x}=\dot{v_1}'_{x}=0, &{} x=0, l, \end{array} \right. \qquad \end{aligned}$$

(3.42)

where $\dot{u_1}=\frac{du_1}{dD}|_{D=D^S_{j_0}}$, $\dot{v_1}=\frac{dv_1}{dD}|_{D=D^S_{j_0}}$ and $\dot{{\widetilde{\lambda }}}_1(D^S_{j_0})=\frac{d{\widetilde{\lambda }}_1}{dD}|_{D=D^S_{j_0}}$. Multiplying both sides of (3.42) by $\phi _{j_0}(x)$, and integrating the result over (0, l), we obtain

$$\begin{aligned} \begin{pmatrix} d(v^*)\Big (\frac{\pi j_0}{l}\Big )^2 &{} d'(v^*)u^*\Big (\frac{\pi j_0}{l}\Big )^2-\frac{\gamma (K-v^*)}{K(1+v^*)}\\ \frac{1}{\gamma } &{} D^S_{j_0}\Big (\frac{\pi j_0}{l}\Big )^2+\frac{v^*(2v^*+1-K)}{K(1+v^*)} \end{pmatrix} \begin{pmatrix} \int _0^l\dot{u_1}\phi _{j_0}\\ \int _0^l\dot{v_1}\phi _{j_0} \end{pmatrix}\nonumber \\ =\begin{pmatrix} \dot{{\widetilde{\lambda }}}_1(D^S_{j_0})b_1(j_0)\frac{l}{2} \\ \Big (\dot{{\widetilde{\lambda }}}_1(D^S_{j_0})-\Big (\frac{\pi j_0}{l}\Big )^2\Big )\frac{l}{2} \end{pmatrix}. \end{aligned}$$

(3.43)

It follows from (3.12) that the coefficient matrix of (3.43) is singular. Since (3.43) is solvable, then

$$\begin{aligned} \frac{1}{\gamma d(v^*)\Big (\frac{\pi j_0}{l}\Big )^2}=\frac{\dot{{\widetilde{\lambda }}}_1(D^S_{j_0})-\Big (\frac{\pi j_0}{l}\Big )^2}{\dot{{\widetilde{\lambda }}}_1(D^S_{j_0})b_1(j_0)}, \end{aligned}$$

which gives

$$\begin{aligned} \Big (\frac{l}{\pi j_0}\Big )^2p\Big (\Big (\frac{\pi j_0}{l}\Big )^2\Big )\dot{{\widetilde{\lambda }}}_1(D^S_{j_0})=-\gamma d(v^*)\Big (\frac{\pi j_0}{l}\Big )^4, \end{aligned}$$

(3.44)

where p(x) is given by (3.36). It follows from (3.44) that

$$\begin{aligned} sgn(\dot{{\widetilde{\lambda }}}_1(D^S_{j_0}))=-sgn\Big (\Big (\Big (\frac{\pi j_0}{l}\Big )^2-x^+\Big )\Big ), \end{aligned}$$

where $x^+$ is the only positive root of $p(x)=0$. From (3.41) and the fact that $sgn(s(D_j(s))')=sgn(k_2)$ holds for small |s|, we get that $sgn({\widetilde{\lambda }}_2(s))=sgn\Big (k_2\Big (\Big (\frac{\pi j_0}{l}\Big )^2-x^+\Big )\Big )$. Therefore, the proof of the theorem is now complete. $\square$

The conclusion of Theorem 3.2(1) means that the stable bifurcation branch emanated from $(D^S_j, e_2)$ could only be the one with wave mode number $j=j_0$ such that $D^S_{j_0}={\hat{D}}_*$, which provides a wave mode selection mechanism for system (3.1). Theorem 3.2(2) shows that under certain conditions, the stability of $e_2$ is lost to stable Hopf bifurcation solutions, which will be proved in detail in the next part. However, it is not easy to show whether ${\hat{D}}_*$ is achieved at $D^S_j$ or $D^H_1$, which depends the shapes of functions $D^S(x)$ and $D^H(x)$ satisfying $D^S\Big (\frac{l}{\pi j}\Big )=D^S_j$ and $D^H\Big (\frac{l}{\pi j}\Big )=D^H_j$, where

$$\begin{aligned} \begin{aligned} D^H(x)&=x^2\frac{v^*(K-1-2v^*)}{K(1+v^*)}-d(v^*), \\ D^S(x)&=x^2\Big (\frac{d'(v^*)u^*}{\gamma d(v^*)}-\frac{K-v^*}{d(v^*)K(1+v^*)}x^2-\frac{v^*(2v^*+1-K)}{K(1+v^*)}\Big ). \end{aligned} \end{aligned}$$

3.2 Hopf Bifurcation

From the above discussions, we know that (3.1) has a spatially homogeneous periodic solution when $v^*=\frac{K-1}{2}$. In this subsection, we will investigate spatially inhomogeneous periodic solution for (3.1) when $v^*<\frac{K-1}{2}$. It is easy to see that if $D=D^H_j$ and ${\hat{b}}(j, D^H_j, e_2)>0$, then $e_2$ loses its stability to periodic solution via Hopf bifurcation. Note that when $D^H_j>D^S_j$, ${\hat{b}}(j, D^H_j, e_2)>0$. Therefore, we will prove the existence of Hopf bifurcation of (3.1) under the condition $D^H_j>D^S_j$. First, we denote that

$$\begin{aligned} {\hat{M}}(D)=\begin{pmatrix} -d(v^*)\Big (\frac{\pi j}{l}\Big )^2 &{} -d'(v^*)u^*\Big (\frac{\pi j}{l}\Big )^2+\frac{\gamma (K-v^*)}{K(1+v^*)}\\ -\frac{1}{\gamma } &{} -D\Big (\frac{\pi j}{l}\Big )^2-\frac{v^*(2v^*+1-K)}{K(1+v^*)} \end{pmatrix} \end{aligned}$$

and give the following result about the nontrivial periodic solution for (3.1).

Theorem 3.3

Assume that $\gamma >\frac{1+K}{K}$ and $0<v^*< \frac{K-1}{2}$. Suppose assumptions (A0) and (A4) hold, and for positive integer j, k in ${\mathcal {S}}_1\bigcup {\mathcal {S}}_2$,

$$\begin{aligned} D^H_j\ne D^H_k, \quad j\ne k,\quad \textrm{and} \quad D^S_j< D^H_j. \end{aligned}$$

Then, (3.1) admits a unique one-parameter family of inhomogeneous periodic orbits ${\mathcal {P}}_j^*(s)=(D_j(s), {\textbf{u}}_j(s,x,t), {\mathcal {T}}_j(s)): s\in (-{\bar{\delta }}, {\bar{\delta }})\rightarrow {\mathbb {R}}\times C^2({\mathbb {R}}, X^2) \times {\mathbb {R}}^+$ with constant ${\bar{\delta }}>0$ and

$$\begin{aligned} {\textbf{u}}_j(s,x,t)=(u^*, v^*)+s(E^+_je^{i\kappa _0t}+E^-_je^{-i\kappa _0t})\phi _j(x)+o(s) \end{aligned}$$

where ${\textbf{u}}_j(s,x,t)$ is periodic solution in t with period

$$\begin{aligned} {\mathcal {T}}_j(s)\approx \frac{2\pi }{\kappa _0}, \quad \kappa _0=\sqrt{{\hat{b}}(j, D^H_j, e_2)} \end{aligned}$$

and $\{(E^{\pm }_j, \pm i\kappa _0)\}$ are eigenpairs of ${\hat{M}}(D)$ with $D=D^H_j$; for any $s_1\ne s_2$ in $(-{\bar{\delta }}, {\bar{\delta }})$, ${\mathcal {P}}_j^*(s_1)\ne {\mathcal {P}}_j^*(s_2)$ and all inhomogeneous periodic solutions near $(D^H_j, e_2)$ must lie on the orbit ${\mathcal {P}}_j^*(s), s\in (-{\bar{\delta }}, {\bar{\delta }})$ in the sense that if (3.1) admits a inhomogeneous periodic solution $\bar{{\textbf{U}}}(x,t)$ with period ${\mathcal {T}}$ for some $D\in {\mathbb {R}}$ near ${\mathcal {P}}_j^*(s)$ satisfying

$$\begin{aligned} |D-D^H_j(s)|<\varepsilon , \quad |{\mathcal {T}}-\frac{2\pi }{\kappa _0}|<\varepsilon , \quad \max _{t>0, x\in (0, l)}|\bar{{\textbf{U}}}(x,t)-e_2|<\varepsilon , \end{aligned}$$

for some small $\varepsilon >0$, then $({\mathcal {T}}, D)=({\mathcal {T}}_j(s_0), D^H_j(s_0))$ and $\bar{{\textbf{U}}}(x,t)={\textbf{u}}_j(s_0, x, t+\theta _0)$ for some $s_0\in (-{\bar{\delta }}, {\bar{\delta }})$ and $\theta _0\in [0,\ 2\pi )$.

Proof

This theorem will be proved by applying Liu et al. [29, Theorem 6.1]. Since $D^S_j< D^H_j$ for $j\in {\mathcal {S}}_1\bigcup {\mathcal {S}}_2$, then matrix ${\hat{M}}(D)$ with $D=D^H_j$ admits a pair of purely imaginary eigenvalues $\sigma ^H_{1,2}(D^H_j)=\pm \sqrt{{\hat{b}}(j, D^H_j, e_2)} i$; meanwhile, under the condition that $D^H_j\ne D^H_k$ for $j\ne k$, $\sigma ^H_{1,2}(D^H_j)$ is a pair of simple eigenvalues of ${\hat{M}}(D^H_j)$, which implies that ${\hat{M}}(D^H_j)$ has no eigenvalues of the form $k_*\sqrt{{\hat{b}}(j, D^H_j, e_2)}i$ except $k_*=\pm 1$.

Let $\sigma ^H_{1,2}(D,j)=\sigma _R(D,j)\pm i\sigma _I(D,j)$ be the unique eigenvalues of ${\hat{M}}(D)$ with D near $D^H_j$, where $\sigma _R(D,j)$ and $\sigma _I(D,j)$ satisfy $\sigma _R(D^H_j,j)=0$ and $\sigma _I(D^H_j,j)=\sqrt{{\hat{b}}(j, D^H_j, e_2)}$. According to Liu et al. [29, Theorem 6.1], it is sufficient to show that

$$\begin{aligned} \frac{\partial {\sigma _R (D,j)}}{\partial {D}}\Big |_{D=D^H_j}\ne 0. \end{aligned}$$

(3.45)

Inserting $\sigma ^H_{1,2}(D,j)$ into the characteristic equation of ${\hat{M}}(D)$, collecting the real and imaginary parts, we have

$$\begin{aligned} \sigma _R(D,j)=-\frac{{\hat{a}}(j, D, e_2)}{2}. \end{aligned}$$

Therefore, (3.45) can be verified by differentiating the above equation with respect to D. Hence, this proof is completed by using Liu et al. [29, Theorem 6.1]. $\square$

Theorem 3.3 shows that (3.1) may have inhomogeneous time-periodic solution when $D^H_j>D^S_j$ for positive integer $j\ge 1$; meanwhile, it also presents the explicit expression of oscillation solution with the spatial profile $\phi _j$. However, as mentioned above, it is not easy to verify $D^H_j>D^S_j$, which depends on the shapes of $D^H(x)$ and $D^S(x)$.

We proceed to investigate the stability of ${\mathcal {P}}_j^*(s),\ s\in (-{\bar{\delta }}, {\bar{\delta }})$ obtained in Theorem 3.3. Here, the stability of a periodic solution refers to the formal linearized stability relative to the perturbations from ${\mathcal {P}}_j^*(s)$, which is only in the local sense. We perform the stability analysis under the assumptions in Theorem 3.3 except that ${\hat{D}}_*=D_{1}^H>\max _{j\in {\mathcal {S}}_2}D_{j}^S$. We begin by rewriting (3.1) into the form

$$\begin{aligned} \frac{d {\mathcal {U}}_j}{dt}={\mathcal {P}}(D_j(s), {\mathcal {U}}_j), \end{aligned}$$

(3.46)

where ${\mathcal {U}}_j(s,x,t)=(u_j(s,x,t), v_j(s,x,t))$, $(D_j(s), {\mathcal {U}}_j(s,x,t),{\mathcal {T}}_j(s))$ be the inhomogeneous periodic solution on the curve ${\mathcal {P}}_j^*(s)$ obtained in Theorem 3.3, and

$$\begin{aligned} {\mathcal {P}}(D_j(s), {\mathcal {U}}_j)=\begin{pmatrix} (d(v_j)u_j)_{xx}+ \frac{\gamma u_jv_j}{1+v_j}-u_j\\ D_j(s)v_{xx}-\frac{u_jv_j}{1+v_j}+v_j\Big (1-\frac{v_j}{K}\Big ) \end{pmatrix}. \end{aligned}$$

After differentiating (3.46) with respect to t and writing $\dot{{\mathcal {U}}_j}=\frac{d{\mathcal {U}}_j }{dt}$, we obtain

$$\begin{aligned} \frac{d \dot{{\mathcal {U}}_j}}{dt}={\mathcal {P}}_u(D_j(s), {\mathcal {U}}_j)\dot{{\mathcal {U}}_j}, \end{aligned}$$

from which we can show that ${\mathcal {U}}_j$ admits a Floquet exponent 0 and a Floquet multiplier 1, where ${\mathcal {P}}_u$ denotes the Frèchet derivative with respect to ${\mathcal {U}}$. In order to study the stability of ${\mathcal {U}}_j$, we substitute the perturbed solution ${\mathcal {U}}_j+{\textbf{M}}e^{-lt}$ into (3.46) and get

$$\begin{aligned} \frac{d {\textbf{M}}(s,t)}{dt}={\mathcal {P}}_u(D_j(s), {\mathcal {U}}_j){\textbf{M}}(s,t)+l(s){\textbf{M}}(s,t), \end{aligned}$$

(3.47)

where ${\textbf{M}}$ is a sufficiently small $T-$periodic function. Hence, the eigenvalues of (3.47) determine the stability of the bifurcated periodic solutions around $D_j^H$. The eigenvalue problem of (3.47) with $s=0$ is given by

$$\begin{aligned} {\mathcal {P}}_0(j){\textbf{M}}= l(0){\textbf{M}}, \end{aligned}$$

where

$$\begin{aligned} {\mathcal {P}}_0(j)={\mathcal {P}}_u(D^H_j, e_2)=\begin{pmatrix} d(v^*)\frac{d^2}{dx^2} &{} d'(v^*)u^*\frac{d^2}{dx^2}+\frac{\gamma (K-v^*)}{K(1+v^*)}\\ -\frac{1}{\gamma } &{} D^H_j\frac{d^2}{dx^2}-\frac{v^*(2v^*+1-K)}{K(1+v^*)} \end{pmatrix}. \end{aligned}$$

All the eigenvalues of ${\mathcal {P}}_0(j)$ consist of the eigenvalues of the following matrices,

$$\begin{aligned} {\hat{M}}_k(D_j^H)=\begin{pmatrix} -d(v^*)\Big (\frac{\pi k}{l}\Big )^2 &{} -d'(v^*)u^*\Big (\frac{\pi k}{l}\Big )^2+\frac{\gamma (K-v^*)}{K(1+v^*)}\\ -\frac{1}{\gamma } &{} -D_j^H\Big (\frac{\pi k}{l}\Big )^2-\frac{v^*(2v^*+1-K)}{K(1+v^*)} \end{pmatrix},\quad k=1,2,\ldots . \end{aligned}$$

First, we claim that ${\mathcal {P}}_j^*(s)$ near $D^H_j$ is unstable for $j\ne 1$. According to Remark 3.1, we know that $e_2$ is unstable when $D<{\hat{D}}_*$, which implies that ${\hat{M}}_j(D_j^H)$ has at least one eigenvalue with positive real part. Hence, for $j\ne 1$, ${\mathcal {P}}_0(j)$ admits at least one eigenvalue with positive real part and hence $l(0)<0$. Thus, according to the standard perturbation theory for an eigenvalue with finite multiplicity [13, 23], when $j\ne 1$, $l(s)<0$ for s small enough, which implies that for $j\ne 1$, the bifurcation curves ${\mathcal {P}}_j^*(s)$ near $(D_j^H,e_2)$ are unstable.

Next, we will investigate the stability of the curve ${\mathcal {P}}_1^*(s)$ near $(D_1^H, e_2)$. Using Lemma 2.10 in [7], l(s) is a continuous function with respect to s near the origin. Therefore, the eigenvalues of ${\hat{M}}_1(D)$ are $\sigma ^H_{1,2}(D,j)=\sigma _R(D,j)\pm i\sigma _I(D,j)$ with D near $D_1^H$. Using Theorem 2.13 in [7], we have that for s near 0, l(s) and $sD'_1(s)$ admit the same zeros which implies that l(s) and $-\sigma '_R(D_1^H)sD'_1(s)$ admit the same sign when both l(s) and $-\sigma '_R(D_1^H)sD'_1(s)$ are nonzero, and for $s\rightarrow 0$,

$$\begin{aligned} |l(s)+\sigma '_R(D_1^H)sD'_1(s)|\le |sD'_1(s)|o(1). \end{aligned}$$

According to Theorem 8.2.3 in [13], the periodic bifurcation solutions are orbitally asymptotically stable if $l(s)>0$ and unstable if $l(s)<0$. In view of Theorem 3.3, we have $\frac{\partial {\sigma _R (D,j)}}{\partial {D}}\Big |_{D=D^H_j}<0$. Thus, l(s) and $sD'_1(s)$ have the same sign for |s| small enough, from which we get that when $D^{''}_1(0)\ne 0$, the bifurcating solutions are stable if they appear supercritical and unstable if they appear subcritical. Therefore, the stability of the ${\mathcal {P}}_1^*(s)$ near $(D_1^H, e_2)$ depends on the values of $D'_1(0)$ and $D^{''}_1(0)$ which can be computed by the methods in [4, 21], and we skip these computations for simplicity.

Appendix

1.1 Coefficients in (3.26)–(3.28)

Note that the values of $A_{1k}$, $B_{1k}$ and $C_{1k}$ with $k=1,2,3$ in (3.26)–(3.28) play an important role in the computations of $k_1$ and $k_2$, then by a tedious computation, we can have those values as follows,

$$\begin{aligned} A_{11}&= d(v^*)b_1(j)\Big (\cos \Big (\frac{\pi jx}{l}\Big )\Big )_{xx}+d'(v^*)u^*\Big (\cos \Big (\frac{\pi jx}{l}\Big )_{xx},\\ A_{12}&= d'(v^*)b_1(j)\Big (\cos ^2\Big (\frac{\pi jx}{l}\Big )\Big )_{xx}+\frac{d''(v^*)u^*}{2}\Big (\cos ^2\Big (\frac{\pi jx}{l}\Big )\Big )_{xx} \\&\quad +\,d(v^*)(\varphi _1(x))_{xx}+d'(v^*)u^*(\zeta _1(x))_{xx},\\ A_{13}&= (d'(v^*)b_1(j)+d''(v^*)u^*)\Big (\cos \Big (\frac{\pi jx}{l}\Big )\zeta _1(x)\Big )_{xx} \\&\quad +\,\Big (\frac{d'''(v^*)u^*}{6}+\frac{d''(v^*)b_1(j)}{2}\Big )\Big (\cos ^3\Big (\frac{\pi jx}{l}\Big )\Big )_{xx}\\&\quad +\, d'(v^*)\Big (\cos \Big (\frac{\pi jx}{l}\Big )\varphi _1(x)\Big )_{xx}+d(v^*)(\varphi _2(x))_{xx}+d'(v^*)u^*(\zeta _2(x))_{xx},\\ B_{11}&= \frac{\gamma u^*(1-v^*)}{1+v^*}\cos \Big (\frac{\pi jx}{l}\Big ),\\ B_{12}&= \frac{\gamma u^*\zeta _1(x)}{(1+v^*)^2}+\frac{\gamma b_1(j)+\gamma v^*b_1(j)-\gamma u^*}{(1+v^*)^3}\cos ^2\Big (\frac{\pi jx}{l}\Big ),\\ B_{13}&= \frac{\gamma u^*\zeta _2(x)}{(1+v^*)^2}+\frac{\gamma \varphi _1(x)+\gamma b_1(j)\zeta _1(x)}{(1+v^*)^2}\cos \Big (\frac{\pi jx}{l}\Big ) \\&\quad +\,\Big (\frac{2\gamma u^*+\gamma u^*v^*}{(1+v^*)^4}-\frac{\gamma b_1(j)+2\gamma u^*\zeta _1(x)}{(1+v^*)^3}\Big )\cos ^3\Big (\frac{\pi jx}{l}\Big ),\\ C_{11}&= \frac{Kv^*-\gamma v^{*2}}{K}\cos \Big (\frac{\pi jx}{l}\Big )-\frac{b_1(j)v^*}{1+v^*}\cos \Big (\frac{\pi jx}{l}\Big ),\\ C_{12}&= \frac{v^*(K-2v^*-1)}{K(1+v^*)}\zeta _1(x)+\Big (\frac{u^*}{(1+v^*)^3}\\&\quad -\frac{1}{K}-\frac{b_1(j)}{(1+v^*)^2}\Big )\cos ^2\Big (\frac{\pi jx}{l}\Big )-\frac{\varphi _1(x)v^*}{1+v^*},\\ C_{13}&= \frac{v^*(K-2v^*-1)}{K(1+v^*)}\zeta _2(x)+\Big (\frac{2u^*}{(1+v^*)^3}-\frac{b_1(j)}{(1+v^*)^2}-\frac{2}{K}\Big )\zeta _1(x)\cos \Big (\frac{\pi jx}{l}\Big ) \\&\quad +\,\Big (\frac{-u^*v^*-2u^*}{2(1+v^*)^4}+\frac{b_1(j)}{(1+v^*)^3}\Big )\cos ^3\Big (\frac{\pi jx}{l}\Big )\\&\quad -\frac{\varphi _1(x)}{(1+v^*)^2}\cos \Big (\frac{\pi jx}{l}\Big )-\frac{v^*\varphi _2(x)}{1+v^*}. \end{aligned}$$

1.2 Computation of $k_2$

Since $k_1=0$ in (3.24), then the steady-state bifurcation curve ${\mathcal {C}}_j^*$ around $(D_j^S,\ e_2)$ is pitchfork. Therefore, $k_2$ in (3.24) plays important role in the turning direction and stability of ${\mathcal {C}}_j^*$. The aim of this part is to give a general expression of $k_2$ for each ${\mathcal {C}}_j^*$.

By using (3.25)–(3.28) in the second equation of (3.7) and collecting all the $s^3-$terms, we have

$$\begin{aligned}{} & {} D^S_j(\zeta _2(x))_{xx}+\frac{v^*(K-2v^*-1)}{K(1+v^*)}\zeta _2(x)-\frac{v^*}{1+v^*}\varphi _2(x) \nonumber \\{} & {} \quad =-k_2\Big (\cos \Big (\frac{\pi jx}{l}\Big )\Big )_{xx}-\Big (\frac{2u^*}{(1+v^*)^3}-\frac{b_1(j)}{(1+v^*)^2}-\frac{2}{K}\Big )\zeta _1(x)\cos \Big (\frac{\pi jx}{l}\Big )\nonumber \\{} & {} \qquad +\,\Big (\frac{u^*v^*+2u^*}{2(1+v^*)^4}-\frac{b_1(j)}{(1+v^*)^3}\Big )\cos ^3\Big (\frac{\pi jx}{l}\Big )+\frac{\varphi _1(x)}{(1+v^*)^2}\cos \Big (\frac{\pi jx}{l}\Big ). \end{aligned}$$

(4.1)

Note that

$$\begin{aligned} \int _0^l\cos ^4\Big (\frac{\pi jx}{l}\Big )dx= & {} \frac{3}{8}l,\\ \int _0^l \varphi _1(x)\cos ^2\Big (\frac{\pi jx}{l}\Big )dx= & {} \frac{1}{2}\Big (\int _0^l\varphi _1(x)\cos \Big (\frac{2\pi jx}{l}\Big )dx+\int _0^l\varphi _1(x)dx\Big ), \end{aligned}$$

and

$$\begin{aligned} \int _0^l \zeta _1(x)\cos ^2\Big (\frac{\pi jx}{l}\Big )dx=\frac{1}{2}\Big (\int _0^l\zeta _1(x)\cos \Big (\frac{2\pi jx}{l}\Big )dx+\int _0^l\zeta _1(x)dx\Big ), \end{aligned}$$

then multiplying by $\cos \Big (\frac{\pi jx}{l}\Big )$ both sides of (4.1), and integrating the resulting equation over $(0,\ l)$, we obtain

$$\begin{aligned} \frac{(\pi j)^2}{2l}k_2= & {} D_{11} \int _0^l \varphi _2(x)\cos \Big (\frac{\pi jx}{l}\Big )dx+D_{12}\int _0^l \zeta _2(x)\cos \Big (\frac{\pi jx}{l}\Big )dx\nonumber \\{} & {} +\,D_{13}\int _0^l\varphi _1(x)\cos \Big (\frac{2\pi jx}{l}\Big )dx+D_{14}\int _0^l\zeta _1(x)\cos \Big (\frac{2\pi jx}{l}\Big )dx\nonumber \\{} & {} +\,D_{15}\int _0^l\varphi _1(x)dx+D_{16}\int _0^l\zeta _1(x)dx+D_{17}, \end{aligned}$$

(4.2)

where

$$\begin{aligned} \begin{aligned} D_{11}&=-\frac{v^*}{1+v^*}, \quad D_{12}=\frac{v^*(K-2v^*-1)}{K(1+v^*)}-D_j^S \Big (\frac{\pi j}{l}\Big )^2,\\ D_{13}&=D_{15}=-\frac{1}{2(1+v^*)^2}, \quad D_{14}=D_{16}=\frac{1}{2}\Big (\frac{2u^*}{(1+v^*)^3}-\frac{b_1(j)}{(1+v^*)^2}-\frac{2}{K}\Big ),\\ D_{17}&=\Big (\frac{b_1(j)}{(1+v^*)^3}-\frac{u^*v^*+2u^*}{2(1+v^*)^4}\Big )\frac{l}{8}. \end{aligned} \end{aligned}$$

Therefore, in order to obtain $k_2$, we need to compute the following integral values,

$$\begin{aligned} \begin{aligned}&\int _0^l \varphi _2(x)\cos \Big (\frac{\pi jx}{l}\Big )dx,\quad \int _0^l \zeta _2(x)\cos \Big (\frac{\pi jx}{l}\Big )dx, \quad \int _0^l\varphi _1(x)\cos \Big (\frac{2\pi jx}{l}\Big )dx,\\&\int _0^l\zeta _1(x)\cos \Big (\frac{2\pi jx}{l}\Big )dx, \quad \int _0^l\varphi _1(x)dx, \quad \int _0^l\zeta _1(x)dx. \end{aligned} \end{aligned}$$

Similarly, using (3.25)–(3.28) in the first equation of (3.7) and collecting all the $s^3-$terms, we get

$$\begin{aligned} \begin{aligned}&d(v^*)(\varphi _2(x))_{xx}+d'(v^*)u^*(\zeta _2(x))_{xx}+\frac{\gamma u^*}{(1+v^*)^2}\zeta _2(x)\\&\quad =-d'(v^*)\Big (\cos \Big (\frac{\pi jx}{l}\Big )\varphi _1(x)\Big )_{xx}\\&\quad -(d'(v^*)b_1(j)+d''(v^*)u^*)\Big (\cos \Big (\frac{\pi jx}{l}\Big )\zeta _1(x)\Big )_{xx} \\&\qquad -\,\Big (\frac{d''(v^*)b_1(j)}{2}+\frac{d'''(v^*)u^*}{6}\Big )\Big (\cos ^3\Big (\frac{\pi jx}{l}\Big )\Big )_{xx}\\&\quad -\frac{\gamma \varphi _1(x)+\gamma b_1(j)\zeta _1(x)}{(1+v^*)^2}\cos \Big (\frac{\pi jx}{l}\Big ) \\&\qquad +\,\Big (\frac{\gamma b_1(j)+2\gamma u^*\zeta _1(x)}{(1+v^*)^3}-\frac{2\gamma u^*+\gamma u^*v^*}{(1+v^*)^2}\Big )\cos ^3\Big (\frac{\pi jx}{l}\Big ). \end{aligned} \end{aligned}$$

Then, multiplying by $\cos \Big (\frac{\pi jx}{l}\Big )$ both sides of above equation, and integrating the resulting equation over $(0,\ l)$, we obtain

$$\begin{aligned}{} & {} \Big (\frac{\gamma u^*}{(1+v^*)^2}-d'(v^*)u^*\Big (\frac{\pi j}{l}\Big )^2\Big )\int _0^l \zeta _2(x)\cos \Big (\frac{\pi jx}{l}\Big )dx\nonumber \\{} & {} \quad -\,d(v^*)\Big (\frac{\pi j}{l}\Big )^2\int _0^l \varphi _2(x)\cos \Big (\frac{\pi jx}{l}\Big )dx={\hat{C}}_0, \end{aligned}$$

(4.3)

where

$$\begin{aligned} \begin{aligned} {\hat{C}}_0&=\frac{d'(v^*)(\pi j)^2}{2l^2}\int _0^l \varphi _1(x)dx+\frac{d'(v^*)(\pi j)^2}{2l^2}\int _0^l \varphi _1(x)\cos \Big (\frac{2\pi jx}{l}\Big )dx\\&\quad +\,\frac{(d'(v^*)b_1(j)+d''(v^*)u^*)(\pi j)^2}{2l^2}\int _0^l \zeta _1(x)\Big (1+\cos \Big (\frac{2\pi jx}{l}\Big )\Big )dx \\&\quad +\,\frac{(\pi j)^2(3d''(v^*)b_1(j)+d'''(v^*)u^*}{16l}-\frac{l(\gamma \varphi _1(x)+\gamma b_1(j)\zeta _1(x))}{2(1+v^*)^2} \\&\quad +\,\frac{3l}{8}\Big (\frac{\gamma b_1(j)+2\gamma u^*\zeta _1(x)}{(1+v^*)^3}-\frac{2\gamma u^*+\gamma u^*v^*}{(1+v^*)^2}\Big ). \end{aligned} \end{aligned}$$

Using (4.3) and the fact that $(\varphi _2(x), \zeta _2(x))\in \hat{{\mathcal {Z}}}$, we have

$$\begin{aligned} \begin{pmatrix} -d(v^*) \Big (\frac{\pi j}{l}\Big )^2 &{} \frac{\gamma u^*}{(1+v^*)^2}-d'(v^*)u^*\Big (\frac{\pi j}{l}\Big )^2\\ b_1(j) &{} 1 \end{pmatrix} \begin{pmatrix} \int _0^l \varphi _2(x)\cos \Big (\frac{\pi jx}{l}\Big )dx\\ \int _0^l \zeta _2(x)\cos \Big (\frac{\pi jx}{l}\Big )dx \end{pmatrix}=\begin{pmatrix} {\hat{C}}_0\\ 0 \end{pmatrix}, \end{aligned}$$

which implies

$$\begin{aligned} \int _0^l \varphi _2(x)\cos \Big (\frac{\pi jx}{l}\Big )dx=\frac{E_1}{E_0}, \quad \int _0^l \zeta _2(x)\cos \Big (\frac{\pi jx}{l}\Big )dx=\frac{E_2}{E_0}, \end{aligned}$$

(4.4)

where $E_1={\hat{C}}_0$, $E_2=-b_1(j){\hat{C}}_0$ and

$$\begin{aligned} E_0=-d(v^*) \Big (\frac{\pi j}{l}\Big )^2-b_1(j)\Big (\frac{\gamma u^*}{(1+v^*)^2}-d'(v^*)u^*\Big (\frac{\pi j}{l}\Big )^2\Big ). \end{aligned}$$

Integrating (3.29) and (3.31) over $(0,\ l)$, it is easy to have

$$\begin{aligned} \int _0^l\zeta _1(x)dx= & {} -\frac{l(b_1(j)(1+v^*)-u^*)}{2u^*(1+v^*)},\nonumber \\ \int _0^l\varphi _1(x)dx= & {} -\frac{l(K-2v^*-1)(b_1(j)(1+v^*)-u^*)}{2Ku^*(1+v^*)}\nonumber \\{} & {} -\,\frac{l(1+v^*)}{2v^*}\Big (\frac{1}{K}+\frac{b_1(j)}{(1+v^*)^2}-\frac{u^*}{(1+v^*)^3}\Big ). \end{aligned}$$

(4.5)

Multiplying (3.29) and (3.31) by $\cos \Big (\frac{2\pi jx}{l}\Big )$, and integrating the result over $(0,\ l)$, we obtain

$$\begin{aligned} \begin{pmatrix} -\frac{4d(v^*)(\pi j)^2}{l^2} &{} \frac{\gamma u^*}{(1+v^*)^2}-\frac{4d'(v^*)u^*(\pi j)^2}{l^2}\\ -\frac{v^*}{1+v^*} &{} -\frac{4D_j^S(\pi j)^2}{l^2}+\frac{v^*(K-2v^*-1)}{K(1+v^*)} \end{pmatrix} \begin{pmatrix} \int _0^l \varphi _1(x)\cos \Big (\frac{2\pi jx}{l}\Big )dx\\ \int _0^l \zeta _1(x)\cos \Big (\frac{2\pi jx}{l}\Big )dx \end{pmatrix}=\begin{pmatrix} {\hat{C}}_1\\ {\hat{C}}_2 \end{pmatrix}, \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} {\hat{C}}_1&=\frac{(\pi j)^2}{l}\Big (d'(v^*)b_1(j)+\frac{d''(v^*)u^*}{2}\Big )-\frac{\gamma l(b_1(j)(1+v^*)-u^*)}{4(1+v^*)^3}, \\ {\hat{C}}_2&=\frac{l}{4}\Big (\frac{1}{K}+\frac{b_1(j)}{(1+v^*)^2}-\frac{v^*}{(1+v^*)^3}\Big ). \end{aligned} \end{aligned}$$

Hence,

$$\begin{aligned} \int _0^l \varphi _1(x)\cos \Big (\frac{2\pi jx}{l}\Big )dx=\frac{{\hat{E}}_1}{{\hat{E}}_0}, \quad \int _0^l \zeta _1(x)\cos \Big (\frac{2\pi jx}{l}\Big )dx=\frac{{\hat{E}}_2}{{\hat{E}}_0}, \end{aligned}$$

(4.6)

where

$$\begin{aligned} \begin{aligned} {\hat{E}}_1&={\hat{C}}_1\Big (\frac{v^*(K-2v^*-1)}{K(1+v^*)}-\frac{4D_j^S(\pi j)^2}{l^2}\Big )-{\hat{C}}_2\Big (\frac{\gamma u^*}{(1+v^*)^2}-\frac{4d'(v^*)u^*(\pi j)^2}{l^2}\Big ), \\ {\hat{E}}_2&={\hat{C}}_1\frac{v^*}{1+v^*}-{\hat{C}}_2\frac{4d(v^*)(\pi j)^2}{l^2}, \\ {\hat{E}}_0&=-\frac{4d(v^*)(\pi j)^2}{l^2}\Big (\frac{v^*(K-2v^*-1)}{K(1+v^*)}-\frac{4D_j^S(\pi j)^2}{l^2}\Big ) \\&\quad +\frac{v^*}{1+v^*}\Big (\frac{\gamma u^*}{(1+v^*)^2}-\frac{4d'(v^*)u^*(\pi j)^2}{l^2}\Big ). \end{aligned} \end{aligned}$$

Using (4.4)–(4.6) in (4.2), we can compute $k_2$.