The Effect on the Largest Eigenvalue of Degree-Based Weighted Adjacency Matrix by Perturbations

Abstract

Let G be a connected graph. Denote by $d_i$ the degree of a vertex $v_i$ in G. Let $f(x,y)>0$ be a real symmetric function. Consider an edge-weighted graph in such a way that for each edge $v_iv_j$ of G, the weight of $v_iv_j$ is equal to the value $f(d_i, d_j)$. Therefore, we have a degree-based weighted adjacency matrix $A_f(G)$ of G, in which the (i, j)-entry is equal to $f(d_i,d_j)$ if $v_iv_j$ is an edge of G and is equal to zero otherwise. Let ${\textbf{x}}$ be a positive eigenvector corresponding to the largest eigenvalue $\lambda _1(A_f(G))$ of the weighted adjacency matrix $A_f(G)$. In this paper, we first consider the unimodality of the eigenvector ${\textbf{x}}$ on an induced path of G. Second, if f(x, y) is increasing in the variable x, then we investigate how the largest weighted adjacency eigenvalue $\lambda _1(A_f(G))$ changes when G is perturbed by vertex contraction or edge subdivision. The aim of this paper is to unify the study of spectral properties for the degree-based weighted adjacency matrices of graphs.

1 Introduction

All graphs considered in this paper are simple, finite, undirected and connected. For notation and terminology not defined here, we refer to [2]. Let $G=(V(G), E(G))$ be a graph of order n with vertex set $V(G)=\{v_0,v_1,\ldots ,v_{n-1}\}$ and edge set E(G). If a pair of vertices $v_i$ and $v_j$ are adjacent, then we denote $v_iv_j\in E(G)$. For a vertex $v_i\in V(G)$, let $N_{G}(v_i)$ be the set of neighbors of $v_i$ in G. The degree of the vertex $v_i$, denoted by $d_i$, is equal to $|N_{G}(v_i)|$. The closed neighborhood of $v_i$ in G is the set $N_{G}[v_i]=N_{G}(v_i)\cup \{v_i\}$. If $d_i=1$, then the vertex $v_i$ of G is said to be a pendant vertex. The distance between two vertices $v_i$ and $v_j$ in a graph G is the length of a shortest $v_iv_j$-path in G. If $V(H)\subseteq V(G)$ and $E(H)\subseteq E(G)$, then H is a subgraph of G. Furthermore, if H is a subgraph of G and H contains all the edges $v_iv_j\in E(G)$ for any $v_i,v_j\in V(H)$, then H is an induced subgraph of G. We denote by $K_{1,n-1}$, $P_n$ and $C_n$, respectively, the star, the path and the cycle of order n.

In chemical graph theory, graphical or topological indices are applied to represent chemical structures of molecular graphs and reflect molecular properties. The general form of degree-based topological indices is

$$\begin{aligned} TI(G)=\sum \limits _{v_i v_j \in E(G)}f(d_i,d_j), \end{aligned}$$

where the edge-weight function f(x, y) is a real symmetric with variables $x>0$ and $y>0$, and the value $f(d_i,d_j)$ is the edge-weight of the edge $v_iv_j$ of G. In fact, each index is obtained by summing up the edge-weights of all edges in a molecular graph with edge-weights defined by the function f(x, y), and it maps a molecular graph into a single number. For a symmetric function f(x, y), if the first partial derivative $f_x^{\prime }(x,y)\ge 0$, then f(x, y) is said to be increasing in variable x. There are many important and well-studied indices collected by Gutman [4], as in Table 1. It is not difficult for us to find that the first fourteen edge-weight functions f(x, y) in Table 1 are increasing in variable x. This means that increasing property is very important to study topological indices.

Table 1 Some well-studied chemical indices

In spectral graph theory, a matrix associated with graph G is a critical tool. In 2015, one of the authors Li [8] proposed that if we use a matrix to represent the structure of a molecular graph with edge-weights separately on its edges, it would keep much more structural information than a topological index. Subsequently, matrices defined by topological indices from algebraic viewpoint were studied separately, including the first(second) Zagreb matrix [13], Nirmala matrix [6], Sombor matrix [5] and inverse sum indeg matrix [1].

In 2018, the following definition of the weighted adjacency matrix for a graph with degree-based edge-weights was first published in [3].

Definition 1.1

Let G be a graph of order n and f(x, y) be a real symmetric function. The weighted adjacency matrix $A_f(G)$ is defined as

$$\begin{aligned} (A_f(G))_{ij}= {\left\{ \begin{array}{ll} f(d_i,d_j),&{}\quad v_iv_j\in E(G),\\ 0,&{}\quad otherwise. \end{array}\right. } \end{aligned}$$

We name the eigenvalues of the $n\times n$ matrix $A_{f}(G)$ as the weighted adjacency eigenvalues of a graph G with edge-weight function f(x, y). Because f(x, y) is a real symmetric function, then $A_f(G)$ is a real symmetric matrix, and therefore its eigenvalues are all real. Then the weighted adjacency eigenvalues can be ordered as

$$\begin{aligned} \lambda _1(A_f(G))\ge \lambda _2(A_f(G))\ge \cdots \ge \lambda _n(A_f(G)), \end{aligned}$$

which are always arranged in a non-increasing order and repeated according to their multiplicity. $\lambda _1(A_f(G))$ is the largest weighted adjacency eigenvalue. If we let ${\textbf{x}}=(x_0,x_1,\ldots ,x_{n-1})^T$ be the eigenvector corresponding to $\lambda _1(A_f(G))$, then $A_f(G){\textbf{x}}=\lambda _1(A_f(G)){\textbf{x}}$. Moreover, the vector ${\textbf{x}}$ can be regarded as a function on V(G). For any vertex $v_i$, the entry of ${\textbf{x}}$ corresponding to $v_i$ is denoted by $x_i$.

Up to now, there have been a few articles studying the largest weighted adjacency eigenvalue $\lambda _1(A_f(G))$. Let us list some known results. In 2021, Li and Wang [9] first attempted to study the extremal tree with the largest value of $\lambda _1(A_f(G))$, which is a star or a double star when the symmetric real function f(x, y) is increasing and convex in variable x, and with the smallest value of $\lambda _1(A_f(G))$, which is a path when f(x, y) is a symmetric polynomial with nonnegative coefficients and zero constant term. In 2022, Zheng et al. [14] added a restriction $P^*$ to f(x, y) and they confirmed that star is the unique tree with the largest value of $\lambda _1(A_f(G))$ among all trees of order n. They also obtained the extremal unicyclic graphs with the largest and smallest value of $\lambda _1(A_f(G))$, respectively. Recently, Li and Yang [12] gave some lower and upper bounds for $\lambda _1(A_f(G))$ and characterized the corresponding extremal graphs. In 2022, Li and Yang [10, 11] got uniform interlacing inequalities for the weighted adjacency eigenvalues under some kinds of graph operations, including edge deletion, edge subdivision, vertex deletion and vertex contraction, and examples were given to show that the interlacing inequalities are the best possible for their type when f(x, y) is increasing in variable x. Although, we can get some upper and lower bounds for $\lambda _1(A_f(G))$ from the interlacing inequalities, it cannot be reflected directly that how the largest weighted adjacency eigenvalue $\lambda _1(A_f(G))$ changes when one graph is transformed to another graph. In this paper, we are interested in the impact on the largest weighted adjacency eigenvalue $\lambda _1(A_f(G))$ under two graph perturbations.

Definition 1.2

(Vertex contraction) The contraction of a pair of vertices $u,v\in V(G)$ produces a new graph $G_{\{u,v\}}$, where $V(G_{\{u,v\}})=(V(G){\setminus }\{u,v\})\cup \{s\}$, s is a new vertex with $N_{G_{\{u,v\}}}(s)=\left( N_G(u)\cup N_G(v)\right) {\setminus }\{u,v\}$, and $E(G_{\{u,v\}})=(E(G){\setminus }(\{uz:z\in N_G(u)\}\cup \{vz:z\in N_G(v)\}))\cup \{sz:z\in N_{G_{\{u,v\}}}(s)\}.$

Definition 1.3

(Edge subdivision) The subdivision of an edge $e=v_iv_j\in E(G)$ produces a new graph $G_e$, where $V(G_e)=V(G)\cup \{v_{n}\}$, such that $v_{n}\notin V(G)$, and $E(G_e)=(E(G){\setminus } e)\cup \{v_iv_{n}, v_jv_{n}\}.$

The structure of this paper is as follows. In Sect. 2, we present some known results that will be used in the subsequent sections. In Sect. 3, since the eigenvector ${\textbf{x}}$ corresponding to the largest weighted adjacency eigenvalue $\lambda _1(A_f(G))$ plays an important role in the investigation of $\lambda _1(A_f(G))$, we first study the property of ${\textbf{x}}$ on an induced path of G. Then, the effects on the largest weighted adjacency eigenvalue $\lambda _1(A_f(G))$ perturbed by the vertex contraction and edge subdivision of G are described, respectively, when $f(x,y)>0$ is a real symmetric function and increasing in variable x.

2 Preliminaries

At the very beginning, we state some fundamental results on matrix theory, which will be used in the sequel. Let $A=(a_{ij})_{n\times m}$ and $B=(b_{ij})_{n\times m}$ be two matrices. If $a_{ij}\le b_{ij}$ for all i and j, then we say that $A\le B$. If $A\le B$ and $A\ne B$, then we say that $A<B$.

Lemma 2.1

[7] Let A, B be two $n\times n$ nonnegative symmetric matrices. If $A\le B$, then

$$\begin{aligned} \lambda _1(A)\le \lambda _1(B). \end{aligned}$$

Furthermore, if B is irreducible and $A<B$, then $\lambda _1(A)<\lambda _1(B)$.

The next result plays a very important role in the proof of our main results.

Lemma 2.2

[7] Let A be an $n\times n$ nonnegative matrix and ${\textbf{y}}=(y_0,y_1,\ldots ,y_{n-1})^T$ be a positive vector. If $\alpha ,\beta \ge 0$, such that $\alpha {\textbf{y}}\le A{\textbf{y}}\le \beta {\textbf{y}}$, then

$$\begin{aligned} \alpha \le \lambda _1(A)\le \beta . \end{aligned}$$

If $\alpha {\textbf{y}}<A{\textbf{y}}$, then $\alpha < \lambda _1(A)$; if $A{\textbf{y}}<\beta {\textbf{y}}$, then $\lambda _1(A)<\beta$.

Finally we state the famous Perron–Frobenius theorem.

Lemma 2.3

[2] Let A be an irreducible symmetric matrix with nonnegative entries. Then the largest eigenvalue $\lambda _1(A)$ of A is simple, with a corresponding eigenvector whose entries are all positive.

3 Main Results

In this section, we first study the property of the eigenvector ${\textbf{x}}$ corresponding to the largest weighted adjacency eigenvalue $\lambda _1(A_f(G))$. For a connected graph G, if $f(x,y)>0$ is a real symmetric function, then $A_f(G)$ is an irreducible symmetric matrix with nonnegative entries. From Lemma 2.3, we have a positive eigenvector ${\textbf{x}}$ corresponding to the largest weighted adjacency eigenvalue $\lambda _1(A_f(G))$. The following result says the unimodality of ${\textbf{x}}$ on an induced path of G.

Theorem 3.1

For a connected graph G of order n and a real symmetric function $f(x,y)>0$, let ${\textbf{x}}=(x_0,x_1,\ldots ,x_{n-1})^T$ be a positive eigenvector corresponding to the eigenvalue $\lambda _1(A_f(G))$ and $P_k=v_1v_2\ldots v_k$ be an induced path of G such that $d_i=2$ for $1\le i\le k$. If $\lambda _1(A_f(G))>2f(2,2)$, then the following statements hold.

• (1) If $x_1=x_k$, then

  $$\begin{aligned} x_1>x_2>\cdots >x_{\lfloor \frac{k+1}{2}\rfloor }=x_{\lceil \frac{k+1}{2}\rceil }<\cdots<x_{k-1}<x_k \end{aligned}$$

  and $x_i=x_{k+1-i}$ for $2\le i\le k-1.$

• (2) If $x_1<x_k$, then there is an integer $1\le j\le \lfloor \frac{k+1}{2}\rfloor$ such that

  $$\begin{aligned} x_1>x_2>\cdots >x_j\ge x_{j+1}<\cdots<x_{k-1}<x_k \end{aligned}$$

  or

  $$\begin{aligned} x_1>x_2>\cdots >x_j< x_{j+1}<\cdots<x_{k-1}<x_k. \end{aligned}$$

  Moreover, $x_i<x_{k+1-i}$ for $2\le i\le \lceil \frac{k+1}{2}\rceil -1$.

Proof

Since ${\textbf{x}}$ is a positive eigenvector corresponding to $\lambda _1(A_f(G))$, we have $x_i>0$ for $0\le i\le n-1$. Recall that $P_k=v_1v_2\ldots v_k$ is an induced path of G such that $d_i=2$ for $1\le i\le k$. Hence, it is not difficult to get the following relation:

$$\begin{aligned} \lambda _1(A_f(G))x_i=f(2,2)x_{i-1}+f(2,2)x_{i+1}, \end{aligned}$$

where $2\le i\le k-1.$ This means that

$$\begin{aligned} \frac{\lambda _1(A_f(G))}{f(2,2)}x_i=x_{i-1}+x_{i+1}, \end{aligned}$$

where $2\le i\le k-1.$ Clearly, this is a recurrence relation and the characteristic equation is

$$\begin{aligned} t^2-\frac{\lambda _1(A_f(G))}{f(2,2)}t+1=0. \end{aligned}$$

Since $\lambda _1(A_f(G))>2f(2,2)$, we can deduce that this characteristic equation has two unequal real roots $t_1$ and $t_2$, such that $t_1t_2=1, t_1+t_2>2$. Without loss of generality, we assume that $t_2>1>t_1>0$. The solution of this linear homogeneous recurrence relation with constant coefficients is given by

$$\begin{aligned} x_i=At^i_1+Bt^i_2. \end{aligned}$$

Let $x_1$ and $x_k$ be the initial conditions. We can determine constants A and B from the initial conditions:

$$\begin{aligned} {\left\{ \begin{array}{ll} At_1+Bt_2=x_1,\\ At^k_1+Bt^k_2=x_k. \end{array}\right. } \end{aligned}$$

This implies that

$$\begin{aligned} A=\frac{x_1t^{k+1}_2-x_kt^2_2}{t^k_2-t^{k-2}_1},\quad B=\frac{x_k-x_1t^{k-1}_1}{t^k_2-t^{k-2}_1}. \end{aligned}$$

Because $t_2>1>t_1>0$, it follows that $t^k_2-t^{k-2}_1>0$. We then have

$$\begin{aligned} x_i=\frac{1}{t^k_2-t^{k-2}_1}\left( (x_1t^{k+1}_2-x_kt^2_2)t^i_1+(x_k-x_1t^{k-1}_1)t^i_2\right) \end{aligned}$$

for $1\le i\le k$.

(1) Since $x_1=x_k$, we have

$$\begin{aligned} x_i&=\frac{x_1}{t^k_2-t^{k-2}_1}\left( \left( t^{k+1}_2-t^2_2\right) t^i_1+(1-t^{k-1}_1)t^i_2\right) \\&=\frac{x_1}{t^k_2-t^{k-2}_1}\left( t^{k+1-i}_2-t^{i-2}_1+t^i_2-t^{k-1-i}_1\right) , \end{aligned}$$

where $1\le i\le k$. Furthermore, we can get

$$\begin{aligned} x_{k+1-i}=\frac{x_1}{t^k_2-t^{k-2}_1}\left( t^i_2-t^{k-1-i}_1+t^{k+1-i}_2-t^{i-2}_1\right) . \end{aligned}$$

Hence, for $1\le i\le k$, we have $x_i=x_{k+1-i}$. Now we let

$$\begin{aligned} f(i)&=t^{k+1-i}_2-t^{i-2}_1+t^i_2-t^{k-1-i}_1\\&=t^{k+1-i}_2-\frac{1}{t^{i-2}_2}+t^i_2-\frac{1}{t^{k-1-i}_2}\\&=\frac{t^{k-3+i}_2+t^{2k-2-i}_2-t^{k-1-i}_2-t^{i-2}_2}{t^{k-3}_2}. \end{aligned}$$

Since $t^k_2-t^{k-2}_1>0$ and $x_1>0$, it follows that the monotonicity of f(i) is the same as the monotonicity of $x_i$. Suppose that

$$\begin{aligned} g(i)=t^{k-3+i}_2+t^{2k-2-i}_2-t^{k-1-i}_2-t^{i-2}_2. \end{aligned}$$

Because $t^{k-3}_2>0$, the monotonicity of g(i) is the same as the monotonicity of f(i).

We now consider the monotonicity of g(i). By the first derivative of g(i), it follows that

$$\begin{aligned} g'\left( i\right)&=t^{k-3+i}_2\ln t_2-t^{2k-2-i}_2\ln t_2+t^{k-1-i}_2\ln t_2-t^{i-2}_2\ln t_2\\&=t^{k-1}_2\left( t^{i-2}_2-t^{k-1-i}_2\right) \ln t_2+\left( t^{k-1-i}_2-t^{i-2}_2\right) \ln t_2\\&=\left( t_2^{k-1}-1\right) \left( t^{i-2}_2-t^{k-1-i}_2\right) \ln t_2. \end{aligned}$$

Recalling that $t_2>1$, it follows that $t_2^{k-1}-1>0$ and $\ln t_2>0$. If $i-2>k-1-i$, that is, $i>\frac{k+1}{2}$, then we have $t^{i-2}_2>t^{k-1-i}_2$, hence $g'(i)>0$. This means that $x_i$ is monotonically increasing for $i>\frac{k+1}{2}$. If $i-2<k-1-i$, that is, $i<\frac{k+1}{2}$, then we obtain $t^{i-2}_2<t^{k-1-i}_2$, hence $g'(i)<0$. This means that $x_i$ is monotonically decreasing for $i<\frac{k+1}{2}$. Thus, we conclude that $x_1>x_2>\cdots >x_{\lfloor \frac{k+1}{2}\rfloor }=x_{\lceil \frac{k+1}{2}\rceil }<\cdots<x_{k-1}<x_k$.

(2) We assume that $x_1<x_k$. Otherwise, we can relabel the vertices on $P_k$. Note that

$$\begin{aligned} x_i=\frac{1}{t^k_2-t^{k-2}_1}\left( (x_1t^{k+1}_2-x_kt^2_2)t^i_1+(x_k-x_1t^{k-1}_1)t^i_2\right) , \end{aligned}$$

where $1\le i\le k$. For $2\le i\le \lceil \frac{k+1}{2}\rceil -1$, we have

$$\begin{aligned}&x_{k+1-i}-x_i\\&\quad =\frac{1}{t^k_2-t^{k-2}_1}\Bigg ((x_1t^{k+1}_2-x_kt^2_2)t^{k+1-i}_1+(x_k-x_1t^{k-1}_1)t^{k+1-i}_2\\&\qquad -((x_1t^{k+1}_2-x_kt^2_2)t^i_1+(x_k-x_1t^{k-1}_1)t^i_2)\Bigg )\\&\quad =\frac{1}{t^k_2-t^{k-2}_1}\Bigg (x_1t^i_2-x_kt^{k-i-1}_1+x_kt^{k+1-i}_2-x_1t^{i-2}_1-(x_1t^{k+1-i}_2\\&\qquad -x_kt^{i-2}_1+x_kt^i_2-x_1t^{k-1-i}_1)\Bigg )\\&\quad =\frac{1}{t^k_2-t^{k-2}_1}(x_k-x_1)(t^{k+1-i}_2-t^i_2+t^{i-2}_1-t^{k-i-1}_1). \end{aligned}$$

Since $2\le i\le \lceil \frac{k+1}{2}\rceil -1$, it follows that $t^{k+1-i}_2>t^i_2$ and $t^{i-2}_1>t^{k-i-1}_1$. Recalling that $x_k>x_1$, we obtain $x_{k-i+1}>x_i$ for $2\le i\le \lceil \frac{k+1}{2}\rceil -1$.

Now let us consider a function

$$\begin{aligned} h(i)&=(x_1t^{k+1}_2-x_kt^2_2)t^i_1+(x_k-x_1t^{k-1}_1)t^i_2\\&=x_1t^{k+1-i}_2-x_kt^{2-i}_2+x_kt^i_2-x_1t^{i-k+1}_2. \end{aligned}$$

Because $t^k_2-t^{k-2}_1>0$, it follows that the monotonicity of h(i) is the same as the monotonicity of $x_i$. By the first derivative of h(i), we obtain

$$\begin{aligned} h'(i)&=-x_1t^{k+1-i}_2\ln t_2+x_kt^{2-i}_2\ln t_2+x_kt^{i}_2\ln t_2-x_1t^{i-k+1}_2\ln t_2\\&=(x_k(t^{i}_2+t^{2-i}_2)-x_1(t^{k+1-i}_2+t^{i-k+1}_2))\ln t_2. \end{aligned}$$

Then we consider the following two cases.

Case 1 $i>k+1-i$, that is, $i\ge {\lfloor \frac{k+1}{2}\rfloor }+1$.

We consider the function $l(i)=t^i_2+t^{2-i}_2$. Since $l'(i)=t^i_2(1-t^{2(1-i)}_2)\ln t_2$, the function l(i) is monotonically increasing for $i>1$. This means that $t^{i}_2+t^{2-i}_2>t^{k+1-i}_2+t^{i-k+1}_2$. Because $x_k>x_1$, it follows that $h'(i)>0$ for $i\ge {\lfloor \frac{k+1}{2}\rfloor }+1$. Hence, $x_i$ is monotonically increasing for $i\ge {\lfloor \frac{k+1}{2}\rfloor }+1$. We then have $x_{{\lfloor \frac{k+1}{2}\rfloor }+1}<\cdots<x_{k-1}<x_k$.

Case 2 $i\le k+1-i$, that is, $i\le \lfloor \frac{k+1}{2}\rfloor$.

Now we consider the function

$$\begin{aligned} w(i)=\frac{t^{k+1-i}_2+t^{i-k+1}_2}{t^i_2+t^{2-i}_2}. \end{aligned}$$

By the first derivative of w(i), we have

$$\begin{aligned} w'(i)&=\frac{((-t^{k+1-i}_2+t^{i-k+1}_2)(t^i_2+t^{2-i}_2)-(t^i_2-t^{2-i}_2)(t^{k+1-i}_2+t^{i-k+1}_2))\ln t_2}{(t^i_2+t^{2-i}_2)^2}\\&=\frac{2(t^{3-k}_2-t^{k+1}_2)\ln t_2}{(t^i_2+t^{2-i}_2)^2}. \end{aligned}$$

It is clear that $w'(i)<0$. There are two possibilities.

Subcase 2.1 $\frac{x_k}{x_1}>w(i)$ for $1\le i\le \lfloor \frac{k+1}{2}\rfloor$.

Since w(i) is monotonically decreasing, we have

$$\begin{aligned} h'(i)=(x_k(t^{i}_2+t^{2-i}_2)-x_1(t^{k+1-i}_2+t^{i-k+1}_2))\ln t_2>0 \end{aligned}$$

for $1\le i\le \lfloor \frac{k+1}{2}\rfloor$. This means that $x_i$ is monotonically increasing for $1\le i\le \lfloor \frac{k+1}{2}\rfloor$. Together with Case 1, it follows that $x_1<x_2<\cdots <x_k$.

Subcase 2.2 There exits an integer $1\le i\le \lfloor \frac{k+1}{2}\rfloor$ such that $\frac{x_k}{x_1}\le w(i)$.

Since w(i) is strictly monotonically decreasing, there is only an integer $1\le j\le \lfloor \frac{k+1}{2}\rfloor$ such that $w(j)\ge \frac{x_k}{x_1}$ and $w(j+1)<\frac{x_k}{x_1}$. Thus, we can say that

$$\begin{aligned} h'(i)=(x_k(t^{i}_2+t^{2-i}_2)-x_1(t^{k+1-i}_2+t^{i-k+1}_2))\ln t_2\le 0 \end{aligned}$$

for $1\le i\le j$. This means that $x_i$ is monotonically decreasing for $1\le i\le j$. Furthermore,

$$\begin{aligned} h'(i)=(x_k(t^{i}_2+t^{2-i}_2)-x_1(t^{k+1-i}_2+t^{i-k+1}_2))\ln t_2>0 \end{aligned}$$

for $j+1\le i\le \lfloor \frac{k+1}{2}\rfloor$. This means that $x_i$ is monotonically increasing for $j+1\le i\le \lfloor \frac{k+1}{2}\rfloor$. Together with Case 1, we can conclude that $x_1>x_2>\cdots>x_j> x_{j+1}<\cdots<x_{k-1}<x_k$ or $x_1>x_2>\cdots >x_j\le x_{j+1}<\cdots<x_{k-1}<x_k$. This proof is thus complete. $\square$

In fact, there are many graphs satisfying $\lambda _1(A_f(G))>2f(2,2)$. Here we give a result as follows.

Theorem 3.2

Let $G\ne C_n$ be a connected graph of order n. Assume that $f(x,y)>0$ is a real symmetric function and increasing in variable x. If G contains a cycle, then $\lambda _1(A_f(G))>2f(2,2)$.

Proof

Without loss of generality, we suppose that G has an induced cycle $C_{k+1}=v_0v_1\ldots v_kv_0$. Let B be a $(k+1)\times (k+1)$ matrix, which is obtained by choosing the rows and columns associated with $v_0,v_1,\ldots ,v_k$ from $A_f(G)$. Since $f(x,y)>0$ is an increasing function in variable x, it is clear that $B\ge A_f(C_{k+1})$. From Lemma 2.1, we have $\lambda _1(B)\ge \lambda _1(A_f(C_{k+1}))=2f(2,2)$.

Adding $n-k-1$ zero rows and zero columns to B, we have an $n\times n$ matrix C. Clearly, $\lambda _1(B)=\lambda _1(C)$. Because $G\ne C_n$ and $f(x,y)>0$, it follows that $A_f(G)>C$. Recalling that G is a connected graph, by using Lemma 2.1 again we have $\lambda _1(A_f(G))>\lambda _1(C)=\lambda _1(B)$. Hence, $\lambda _1(A_f(G))>2f(2,2)$. The required result is obtained. $\square$

In fact, for a subgraph H of a connected graph G, if $G\ne H$, using a similar argument in Theorem 3.2, then we can prove that $\lambda _1(A_f(G))>\lambda _1(A_f(H)).$ Next, when $f(x,y)>0$ is a real symmetric function and increasing in variable x, we consider the effect on the largest weighted adjacency eigenvalue $\lambda _1(A_f(G))$ by vertex contraction.

Theorem 3.3

Let G be a connected graph of order n and $H=G_{\{u,v\}}$, where u and v are two distinct vertices of G such that the distance between u and v is at least 3. Assume that $f(x,y)>0$ is a real symmetric function and increasing in variable x. Then

$$\begin{aligned} \lambda _1(A_f(G))< \lambda _1(A_f(H)). \end{aligned}$$

Proof

Since the distance between u and v is at least 3, we have $uv\notin E(G)$ and $N_G(u)\cap N_G(v)=\emptyset$. Without loss of generality, we suppose that $N_G(u)=\{u_1,u_2,\ldots ,u_p\}$ and $N_G(v)=\{v_1,v_2,\ldots ,v_q\}$, where $p,q\ge 1$. Contracting the two vertices u and v, we obtain a new vertex s. Because G is connected, it follows that H is connected. For the weighted adjacency matrix $A_f(H)$, from Lemma 2.3, we have a positive eigenvector ${\textbf{x}}$ corresponding to $\lambda _1(A_f(H))$. That is, $A_f(H){\textbf{x}}=\lambda _1(A_f(H)){\textbf{x}}$. Let n-dimensional vector ${\textbf{y}}$ be an assignment of G satisfying

$$\begin{aligned} {\left\{ \begin{array}{ll} y_u=y_v=x_s,\\ y_w=x_w,&{}w\in V(G){\setminus }\{u,v\}, \end{array}\right. } \end{aligned}$$

where $x_z$ and $y_z$ are the entries of ${\textbf{x}}$ and ${\textbf{y}}$ corresponding to vertex z, respectively. Obviously, the vector ${\textbf{y}}$ is positive. Next we prove $A_f(G){\textbf{y}}<\lambda _1(A_f(H)){\textbf{y}}$.

First, we compare the entry $(A_f(G){\textbf{y}})_u$ to $\lambda _1(A_f(H))y_u$. We have

$$\begin{aligned} (A_f(G){\textbf{y}})_u&=\sum _{i=1}^{p}f(p,d_{u_i})y_{u_i}=\sum _{i=1}^{p}f(p,d_{u_i})x_{u_i}\\&\le \sum _{i=1}^{p}f(p+q,d_{u_i})x_{u_i}\\&<\sum _{i=1}^{p}f(p+q,d_{u_i})x_{u_i}+\sum _{i=1}^{q}f(p+q,d_{v_i})x_{v_i}\\&=\lambda _1(A_f(H))x_s=\lambda _1(A_f(H))y_u. \end{aligned}$$

Since $f(p+q,d_{v_i})>0$ and $x_{v_i}>0$, it follows that $\sum \limits _{i=1}^{q}f(p+q,d_{v_i})x_{v_i}>0$. Thus, the above inequality is strict. Similarly, we have

$$\begin{aligned} (A_f(G){\textbf{y}})_v&=\sum _{i=1}^{q}f(q,d_{v_i})y_{v_i}=\sum _{i=1}^{q}f(q,d_{v_i})x_{v_i}\\&\le \sum _{i=1}^{q}f(p+q,d_{v_i})x_{v_i}\\&<\sum _{i=1}^{q}f(p+q,d_{v_i})x_{v_i}+\sum _{i=1}^{p}f(p+q,d_{u_i})x_{u_i}\\&=\lambda _1(A_f(H))x_s=\lambda _1(A_f(H))y_v. \end{aligned}$$

Because $\sum \limits _{i=1}^{p}f(p+q,d_{u_i})x_{u_i}>0$, this inequality is also strict. For any vertex $w\in V(G){\setminus }(N[u]\cup N[v])$, we have

$$\begin{aligned} (A_f(G){\textbf{y}})_w&=\sum _{z\in N_G(w)}f(d_w,d_z)y_{z}=\sum _{z\in N_{H}(w)}f(d_w,d_z)x_{z}\\&=\lambda _1(A_f(H))x_w=\lambda _1(A_f(H))y_w. \end{aligned}$$

Moreover, for a vertex $u_i$, $1\le i\le p$, we have

$$\begin{aligned} (A_f(G){\textbf{y}})_{u_i}&=\sum _{z\in N_G(u_i){\setminus } u}f(d_{u_i},d_z)y_{z}+f(d_{u_i},p)y_u\\&\le \sum _{z\in N_H(u_i){\setminus } s}f(d_{u_i},d_z)x_z+f(d_{u_i},p+q)x_s\\&=\lambda _1(A_f(H))x_{u_i}=\lambda _1(A_f(H))y_{u_i}. \end{aligned}$$

For a vertex $v_i$, $1\le i\le q$, we have

$$\begin{aligned} (A_f(G){\textbf{y}})_{v_i}&=\sum _{z\in N_G(v_i){\setminus } v}f(d_{v_i},d_z)y_{z}+f(d_{v_i},q)y_v\\&\le \sum _{z\in N_H(v_i){\setminus } s}f(d_{v_i},d_z)x_z+f(d_{v_i},p+q)x_s\\&=\lambda _1(A_f(H))x_{v_i}=\lambda _1(A_f(H))y_{v_i}. \end{aligned}$$

Thus, $A_f(G){\textbf{y}}<\lambda _1(A_f(H)){\textbf{y}}$. From Lemma 2.2, we can conclude that $\lambda _1(A_f(G))<\lambda _1(A_f(H))$. This completes the proof. $\square$

Fig. 1

Graphs $G_1$ and $G_2$

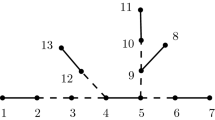
Remark 1 In Theorem 3.3, the condition “the distance between u and v is at least 3" is reasonable. Here are some examples to illustrate the situation. First, we consider that the distance between u and v is 1. Suppose that a connected graph G contains a pendent vertex v. Contracting the vertex v and its neighbor, we can get a graph H. Since H is an induced subgraph of G and $f(x,y)>0$ is increasing in variable x, it follows that $\lambda _1(A_f(G))>\lambda _1(A_f(H))$. In addition, if $G=G_1$(see Fig. 1), contracting $v_1$ and $v_7$, then we can get a graph $G_2$. When $f(x,y)=\sqrt{\lg (xy)}$, by calculation it is not difficult to get that $1.5845\approx \lambda _1(A_f(G_1))>\lambda _1(A_f(G_2))\approx 1.5806$. Second, we consider that the distance between u and v is 2. If $G=K_{1,n-1}$, contracting two pendant vertices, then we have $H=K_{1,n-2}$. Because $f(x,y)>0$ is increasing in variable x, it suffices to prove that $f(1,n-1)\sqrt{n-1}=\lambda _1(A_f(K_{1,n-1}))>\lambda _1(A_f(K_{1,n-2}))=f(1,n-2)\sqrt{n-2}$. Moreover, if $G=G_1$(see Fig. 1), contracting $v_1$ and $v_2$, then we can obtain $K_{1,5}$. When $f(x,y)=(xy)^3$, a short calculation reveals that $307.8474\approx \lambda _1(A_f(G_1))>\lambda _1(A_f(K_{1,5}))\approx 279.5085$.

Finally, we establish the relation between the largest weighted adjacency eigenvalue $\lambda _1(A_f(G))$ and $\lambda _1(A_f(G_e))$, where $f(x,y)>0$ is a real symmetric function and increasing in variable x. Now we introduce the definition of an internal path of a graph G in the first place.

Definition 3.4

Let G be a connected graph of order n. The walk $v_0v_1\ldots v_{k+1}$ is an internal path of G if one of the following holds:

• (i) $k\ge 2$, the vertices $v_0, v_1, \ldots , v_k$ are distinct, $v_{k+1}=v_0$, $v_iv_{i+1}\in E(G)$ where $0\le i\le k$, $d_0\ge 3$ and $d_i=2$ where $1\le i\le k$;

• (ii) $k\ge 0$, the vertices $v_0, v_1, \ldots , v_{k+1}$ are distinct, $v_iv_{i+1}\in E(G)$ where $0\le i\le k$, $d_0\ge 3$, $d_{k+1}\ge 3$ and $d_i=2$ where $1\le i\le k$.

Theorem 3.5

Let G be a connected graph of order n and $H=G_e$. Assume that $f(x,y)>0$ is a real symmetric function and increasing in variable x. Let ${\textbf{x}}=\{x_0,x_1,\ldots ,x_{n-1}\}^T$ be a positive eigenvector corresponding to $\lambda _1(A_f(G))$ and $P_{k+2}=v_0v_1\ldots v_{k+1}$ be an internal path of G such that $x_0\le x_{k+1}$. Then the following statements hold.

• (1) If $G\ne C_n$ and e does not belong to an internal path of G, then

  $$\begin{aligned} \lambda _1(A_f(H))>\lambda _1(A_f(G)). \end{aligned}$$

• (2) If for any vertex $v_i \in N_G(v_0)$, $d_i\ge 2$ and e belongs to an internal path of G, then

  $$\begin{aligned} \lambda _1(A_f(H))<\lambda _1(A_f(G)). \end{aligned}$$

Proof

(1) If $G\ne C_n$ and e does not belong to an internal path of G, then we can get G by deleting a pendent vertex v from H. This means that H has a proper subgraph $H'=H{\setminus } v$ isomorphic to G. Now deleting the row and column associated with v from $A_f(H)$, we get a matrix B. Then, adding a zero row and a zero column to B, we have an $(n+1)\times (n+1)$ matrix C. It is not difficult to verify that $\lambda _1(B)=\lambda _1(C)$. The matrix $A_f(H)-C$ has two same nonnegative nonzero entries f(2, 1) in symmetric place, and all other entries of $A_f(H)-C$ are zero. Since G is connected, $A_f(H)$ is irreducible. Now using Lemma 2.1, we have $\lambda _1(A_f(H))>\lambda _1(C)=\lambda _1(B)$.

Note that the matrix $B-A_f(G)$ has two same nonnegative entries $f(2,2)-f(2,1)$ in symmetric place, and all other entries of $B-A_f(G)$ are zero. Since $f(x,y)>0$ is an increasing function in variable x, we have $B\ge A_f(G)$. Using Lemma 2.1 again, we get $\lambda _1(B)\ge \lambda _1(A_f(G))$. Until now, we can obtain $\lambda _1(A_f(H))>\lambda _1(A_f(G))$.

(2) For convenience, we suppose that $v_{n}$ is the addition vertex which appears in subdividing edge e. Next, we prove the result by discussing the type of the internal path with the edge e.

Case 1 e belongs to an internal path $P_{k+2}=v_0v_1\ldots v_{k+1}$ of type (i).

Let $x_i$ be the entry of ${\textbf{x}}$ corresponding to the vertex $v_i$ of G, where $i=0,1,\ldots ,k$. Since $v_0=v_{k+1}$ and $v_1v_2\ldots v_k$ is an induced path of G, by Theorem 3.1(1), we have $x_i=x_{k+1-i}$ for $1\le i\le k$. Next we consider the following two cases.

Case 1.1 k is even.

We have $x_{\frac{k}{2}}=x_{\frac{k}{2}+1}$. Without loss of generality, we take $e=v_{\frac{k}{2}}v_{\frac{k}{2}+1}$. Let ${\textbf{y}}$ be an $(n+1)$-dimensional vector obtained from ${\textbf{x}}$ by inserting the addition entry $y_{n}=x_{\frac{k}{2}}=x_{\frac{k}{2}+1}$. That is,

$$\begin{aligned} {\left\{ \begin{array}{ll} y_{n}=x_{\frac{k}{2}},\\ y_i=x_i,&{}v_i\in V(G). \end{array}\right. } \end{aligned}$$

Hence, the vector ${\textbf{y}}$ is positive. Then we have

$$\begin{aligned} (A_f(H){\textbf{y}})_{n}&=f(2,2)x_{\frac{k}{2}}+f(2,2)x_{\frac{k}{2}+1}\\&=2f(2,2)x_{\frac{k}{2}}\\&<\lambda _1(A_f(G))x_{\frac{k}{2}}=\lambda _1(A_f(G))y_{n}. \end{aligned}$$

Since e belongs to an internal path of type (i), G has a cycle as an induced subgraph, from Theorem 3.2, we know that the above inequality is strict. For any vertex $v_i\ne v_{n}$, we can easily obtain $(A_f(H){\textbf{y}})_i=\lambda _1(A_f(G))y_i$.

Hence, $A_f(H){\textbf{y}}<\lambda _1(A_f(G)){\textbf{y}}$. Using Lemma 2.2, we get $\lambda _1(A_f(H))<\lambda _1(A_f(G))$.

Case 1.2 k is odd.

We have $x_{\frac{k-1}{2}}=x_{\frac{k+3}{2}}$. Since $\lambda _1(A_f(G))>2f(2,2)$, from Theorem 3.1(1), we obtain $x_{\frac{k-1}{2}}>x_{\frac{k+1}{2}}$. Without loss of generality, we take $e=v_{\frac{k-1}{2}}v_{\frac{k+1}{2}}$. Let vector ${\textbf{y}}$ be obtained from ${\textbf{x}}$ by inserting the addition entry $y_{n}=x_{\frac{k+1}{2}}$. That is,

$$\begin{aligned} {\left\{ \begin{array}{ll} y_{n}=x_{\frac{k+1}{2}},\\ y_i=x_i,&{}v_i\in V(G). \end{array}\right. } \end{aligned}$$

Hence, vector $A_f(H){\textbf{y}}$ differs from $\lambda _1(A_f(G)){\textbf{y}}$ only in the $\frac{k+1}{2}$th and nth entries. Comparing the two corresponding entries in $A_f(H){\textbf{y}}$ and $\lambda _1(A_f(G)){\textbf{y}}$, respectively, we get

$$\begin{aligned} (A_f(H){\textbf{y}})_\frac{k+1}{2}&=f(2,2)y_{n}+f(2,2)x_{\frac{k+3}{2}}\\&=f(2,2)x_{\frac{k+1}{2}}+f(2,2)x_{\frac{k+3}{2}}\\&<f(2,2)x_{\frac{k-1}{2}}+f(2,2)x_{\frac{k+3}{2}}\\&=\lambda _1(A_f(G))x_{\frac{k+1}{2}}=\lambda _1(A_f(G))y_{\frac{k+1}{2}}, \end{aligned}$$

and

$$\begin{aligned} (A_f(H){\textbf{y}})_{n}&=f(2,2)x_{\frac{k-1}{2}}+f(2,2)x_{\frac{k+1}{2}}\\&<f(2,2)x_{\frac{k-1}{2}}+f(2,2)x_{\frac{k-1}{2}}\\&=f(2,2)x_{\frac{k-1}{2}}+f(2,2)x_{\frac{k+3}{2}}\\&=\lambda _1(A_f(G))x_{\frac{k+1}{2}}=\lambda _1(A_f(G))y_{n}. \end{aligned}$$

It follows that $A_f(H){\textbf{y}}<\lambda _1(A_f(G)){\textbf{y}}$. From Lemma 2.2, we get $\lambda _1(A_f(H))<\lambda _1(A_f(G))$.

Case 2 e belongs to an internal path $P_{k+2}=v_0v_1\ldots v_{k+1}$ of type (ii).

Let $x_i$ be the entry of ${\textbf{x}}$ corresponding to the vertex $v_i$ of G, where $i=0,1,\ldots ,k+1$. Let t be the smallest index such that $x_t=\min \{x_0,x_1,\ldots ,x_{k+1}\}$. Because $x_0\le x_{k+1}$, we have $0\le t<k+1$. Without loss of generality, we take $e=v_tv_{t+1}$. Here we still discuss by distinguishing two cases.

Case 2.1 $t>0$.

Since $v_1v_2\ldots v_k$ is an induced path, by Theorem 3.1(2), it follows that $0< t\le \lfloor \frac{k+1}{2}\rfloor$. Furthermore, we have $x_i>x_t$ for $0\le i<t$, and $x_t\le x_{t+1}<x_i$ for $t+1<i\le k+1$. Let ${\textbf{y}}$ be obtained from ${\textbf{x}}$ by inserting the addition entry $y_{n}=x_t$. That is,

$$\begin{aligned} {\left\{ \begin{array}{ll} y_{n}=x_t,\\ y_i=x_i,&{}v_i\in V(G). \end{array}\right. } \end{aligned}$$

We can deduce that $A_f(H){\textbf{y}}$ differs from $\lambda _1(A_f(G)){\textbf{y}}$ only in the tth and nth entries. It is not difficult to get that

$$\begin{aligned} (A_f(H){\textbf{y}})_t&=f(2,d_{t-1})x_{t-1}+f(2,2)y_{n}\\&=f(2,d_{t-1})x_{t-1}+f(2,2)x_t\\&\le f(2,d_{t-1})x_{t-1}+f(2,d_{t+1})x_{t+1}\\&=\lambda _1(A_f(G))x_t=\lambda _1(A_f(G))y_t, \end{aligned}$$

and

$$\begin{aligned} (A_f(H){\textbf{y}})_{n}&=f(2,2)x_{t}+f(2,d_{t+1})x_{t+1}\\&<f(2,d_{t-1})x_{t-1}+f(2,d_{t+1})x_{t+1}\\&=\lambda _1(A_f(G))x_t=\lambda _1(A_f(G))y_{n}. \end{aligned}$$

Thus, $A_f(H){\textbf{y}}<\lambda _1(A_f(G)){\textbf{y}}$. Using Lemma 2.2, we have $\lambda _1(A_f(H))<\lambda _1(A_f(G))$.

Case 2.2 $t=0$.

We take $e=v_0v_1$. According to the choice of t, it follows that $x_0\le x_i$ for $1\le i\le k+1$. For convenience, let S be the set of neighbors of $v_0$ other than $v_1$ in G, and $s=\sum \limits _{v_j\in S}f(d_0,d_j)x_j$, and let R be the set of neighbors of $v_1$ other than $v_0$ in G, and $r=\sum \limits _{v_j\in R}f(d_1,d_j)x_j$.

Subcase 2.2.1 $f(d_0,2)x_0+f(d_1,2)x_1<\lambda _1(A_f(G))x_0$.

Let ${\textbf{y}}$ be obtained from ${\textbf{x}}$ by inserting the addition entry $y_{n}=x_0$, that is,

$$\begin{aligned} {\left\{ \begin{array}{ll} y_{n}=x_0,\\ y_i=x_i,&{}v_i\in V(G). \end{array}\right. } \end{aligned}$$

It is easy to show that vector $A_f(H){\textbf{y}}$ differs from $\lambda _1(A_f(G)){\textbf{y}}$ in at most three entries: 0th, 1th and nth. For the vertex $v_0$, we have

$$\begin{aligned} (A_f(H){\textbf{y}})_0&=f(d_0,2)y_{n}+\sum _{v_j\in S}f(d_0,d_j)x_j\\&=f(d_0,2)x_0+s\\&\le f(d_0,d_1)x_1+s\\&=\lambda _1(A_f(G))x_0=\lambda _1(A_f(G))y_0. \end{aligned}$$

For the vertex $v_1$, we have

$$\begin{aligned} (A_f(H){\textbf{y}})_1&=f(d_1,2)y_{n}+\sum _{v_j\in R}f(d_1,d_j)x_j\\&=f(d_1,2)x_0+r\\&\le f(d_1,d_0)x_0+r\\&=\lambda _1(A_f(G))x_1=\lambda _1(A_f(G))y_1. \end{aligned}$$

For the vertex $v_{n}$, we have

$$\begin{aligned} (A_f(H){\textbf{y}})_{n}&=f(d_0,2)x_0+f(d_1,2)x_1\\&<\lambda _1(A_f(G))x_0=\lambda _1(A_f(G))y_{n}. \end{aligned}$$

It follows that $A_f(H){\textbf{y}}<\lambda _1(A_f(G)){\textbf{y}}$. From Lemma 2.2, we get $\lambda _1(A_f(H))<\lambda _1(A_f(G))$.

Subcase 2.2.2 $f(d_0,2)x_0+f(d_1,2)x_1\ge \lambda _1(A_f(G))x_0$.

Since $\lambda _1(A_f(G))x_0=s+f(d_0,d_1)x_1$, we obtain $s\le f(d_0,2)x_0+f(d_1,2)x_1-f(d_0,d_1)x_1$. Recalling that $f(x,y)>0$ is an increasing function. Then, $f(d_1,2)-f(d_0,d_1)\le 0$ and $f(d_0,2)>0$. Because each entry of ${\textbf{x}}$ is positive, we can get $0<s=\sum \limits _{v_j\in S}f(d_0,d_j)x_j\le f(d_0,2)x_0$. Hence, $\frac{s}{f(d_0,2)}\le x_0$. Now let vector ${\textbf{y}}$ be an assignment of the vertices of G satisfying that

$$\begin{aligned} {\left\{ \begin{array}{ll} y_0=\frac{\lambda _1(A_f(G))x_0-f(d_0,d_1)x_1}{f(d_0,2)},\\ y_{n}=x_0,\\ y_i=x_i,&{}v_i\in V(G){\setminus }\{v_0\}. \end{array}\right. } \end{aligned}$$

Since $s=\lambda _1(A_f(G))x_0-f(d_0,d_1)x_1$, we have $y_0=\frac{s}{f(d_0,2)}$, and then $0<y_0\le x_0$. In addition, ${\textbf{x}}$ is a positive vector, and hence ${\textbf{y}}$ is also a positive vector. Next we prove that the $(n+1)$-dimensional vector ${\textbf{y}}$ satisfies $A_f(H){\textbf{y}}<\lambda _1(A_f(G)){\textbf{y}}$. The vector $A_f(H){\textbf{y}}$ differs from $\lambda _1(A_f(G)){\textbf{y}}$ in at most the following entries. For the vertex $v_0$, we establish that

$$\begin{aligned} (A_f(H){\textbf{y}})_0&=f(d_0,2)y_{n}+\sum _{v_j\in S}f(d_0,d_j)x_j\\&=f(d_0,2)x_0+s\\&\le 2f(d_0,2)x_0\\&\le (d_0-1)f(d_0,2)x_0\\&=\sum _{v_j\in S}f(d_0,2)x_0\\&\le \sum _{v_j\in S}f(d_0,d_j)x_0\\&\le \sum _{v_j\in S}\frac{f(d_0,d_j)}{f(d_0,2)}\cdot f(d_0,d_j)x_0\\&<\sum _{v_j\in S}\frac{f(d_0,d_j)}{f(d_0,2)}\cdot \lambda _1(A_f(G))x_j\\&=\frac{\lambda _1(A_f(G))}{f(d_0,2)}\cdot s=\lambda _1(A_f(G))y_0. \end{aligned}$$

Because the degrees of the neighbors of $v_0$ are at least 2 and $f(x,y)>0$ is increasing, we get $f(d_0,2)\le f(d_0,d_j)$. It follows that the third and fourth inequalities hold. If $v_j\in S$, we have

$$\begin{aligned} f(d_0,d_j)x_0<\sum _{v_k\in N_G(v_j){\setminus } v_0}f(d_k,d_j)x_k+f(d_0,d_j)x_0=\lambda _1(A_f(G))x_j. \end{aligned}$$

Hence, the last inequality is strict. For the vertex $v_1$, we have

$$\begin{aligned} (A_f(H){\textbf{y}})_1&=f(d_1,2)y_{n}+\sum _{v_j\in R}f(d_1,d_j)x_j\\&=f(d_1,2)x_0+r\\&\le f(d_1,d_0)x_0+r\\&=\lambda _1(A_f(G))x_1=\lambda _1(A_f(G))y_1. \end{aligned}$$

For the vertex $v_j\in S$, we have

$$\begin{aligned} (A_f(H){\textbf{y}})_j&=\sum _{v_k\in N_H(v_j){\setminus } v_0}f(d_k,d_j)x_k+f(d_j,d_0)y_0\\&\le \sum _{v_k\in N_G(v_j){\setminus } v_0}f(d_k,d_j)x_k+f(d_j,d_0)x_0\\&=\lambda _1(A_f(G))x_j=\lambda _1(A_f(G))y_j. \end{aligned}$$

For the vertex $v_{n}$, we have

$$\begin{aligned} (A_f(H){\textbf{y}})_{n}&=f(d_0,2)y_0+f(d_1,2)y_1\\&=s+f(d_1,2)x_1\\&\le s+f(d_1,d_0)x_1\\&=\lambda _1(A_f(G))x_0=\lambda _1(A_f(G))y_{n}. \end{aligned}$$

Thus, $A_f(H){\textbf{y}}<\lambda _1(A_f(G)){\textbf{y}}$. By Lemma 2.2, it follows that $\lambda _1(A_f(H))<\lambda _1(A_f(G))$. The proof is now complete. $\square$

Remark 2 In Theorem 3.5 (2), the condition “for any vertex $v_i \in N_G(v_0)$, $d_i\ge 2$" is necessary. Otherwise, there are graphs G and H which do not satisfy $\lambda _1(A_f(H))<\lambda _1(A_f(G))$. For example, when $f(x,y)=\sqrt{\lg (xy)}$, considering $G=G_2$ and $H=G_1$ in Fig. 1, we can have $1.5845\approx \lambda _1(A_f(G_1))>\lambda _1(A_f(G_2))\approx 1.5806$.