Spectral Transformation Associated with a Perturbed $R_I$ Type Recurrence Relation

Abstract

In this work, orthogonal polynomials satisfying $R_I$ type recurrence relation are analyzed when the recurrence coefficients are modified. The structural relationship between the perturbed and the unperturbed polynomials along with the spectral properties and spectral transformation of continued fraction are investigated. It is demonstrated that the transfer matrix method is computationally more efficient than the classical method for obtaining perturbed $R_I$ polynomials. Further, an interesting consequence of co-dilation on the Carathéodary function is presented. Finally, the study of co-recursion and co-dilation in connection to the unit circle is carried out with the help of an illustration. The interlacing and monotonicity of zeros between L-Jacobi polynomials and their perturbed forms are demonstrated.

1 Introduction

Consider the recurrence relation

$$\begin{aligned}&{\mathcal {P}}_{n+1}(z) = (z-c_n){\mathcal {P}}_n(z)-\lambda _n (z-a_n){\mathcal {P}}_{n-1}(z), \quad n\ge 0, \\&\nonumber {\mathcal {P}}_{-1}(z) = 0, \qquad {\mathcal {P}}_0(z) = 1. \end{aligned}$$

(1.1)

It was demonstrated in [25, Theorem 2.1] that if $\lambda _n \ne 0$ and ${\mathcal {P}}_n(a_n)\ne 0$ for $n\ge 1$, then there exists a rational function $\psi _n(z)=\frac{{\mathcal {P}}_n(z)}{\prod _{j=1}^{n}(z-a_j)}$ and a linear functional $\mathfrak {N}$ such that the orthogonality relations

$$\begin{aligned} \mathfrak {N}[a_0] \ne 0, \quad \mathfrak {N}\left[ z^k \psi _n(z) \right] = 0, \quad 0\le k < n, \end{aligned}$$

hold. We can obtain (1.1) by starting with a sequence of rational functions $\psi _n(z)$ that satisfy a three-term recurrence relation and have poles at $\{a_k\}_{k=0}^\infty$. According to [25], the recurrence relation (1.1) is a $R_I$ type recurrence relation, and ${\mathcal {P}}_n(z), n\ge 1$, generated by (1.1) are $R_I$ polynomials. The $R_I$ type recurrence relation (1.1) has several applications such as defining biorthogonal systems of rational functions, studying multipoint rational interpolants or Pade approximation, evaluating some types of beta integrals, and so on.

Note that the infinite continued fraction

(1.2)

becomes finite when $z=a_k$, $k \ge 2$. Following [20], we call it a $R_I$-fraction. Polynomials ${\mathcal {P}}_n(z)$ are the numerator polynomials associated with (1.2). Also, the polynomials of the second kind [25, page 7, equation (2.9)] associated with recurrence relation (1.1) are given by

$$\begin{aligned}&\mathcal {Q}_{n+1}(z) = (z-c_n)\mathcal {Q}_n(z)-\lambda _n (z-a_n)\mathcal {Q}_{n-1}(z), \quad n\ge 1, \\&\nonumber \mathcal {Q}_{0}(z) = 0, \qquad \mathcal {Q}_1(z) = 1, \end{aligned}$$

(1.3)

such that the ratio $\dfrac{\mathcal {Q}_n(z)}{{\mathcal {P}}_n(z)}$ is the n-th convergent of the continued fraction (1.2). The existence of an $m-$function associated with an $R_I$-fraction was established in [25, Theorem 2.3]. The orthogonal Laurent polynomials (OLP) or L-orthogonal polynomials [18] are the $R_I$ polynomials (1.1) when $a_n=0$ and z is real. They satisfy the recurrence

$$\begin{aligned}&{\mathcal {P}}_{n+1}(x) = (x-c_n){\mathcal {P}}_n(x)-\lambda _n x{\mathcal {P}}_{n-1}(x), \quad n\ge 0, \quad x \in \mathbb {R}, \\&\nonumber {\mathcal {P}}_{-1}(x) = 0, \qquad {\mathcal {P}}_0(x) = 1, \end{aligned}$$

(1.4)

where $\{c_n\}_{n \ge 0}$ and $\{\lambda _n\}_{n \ge 0}$ are positive numbers. For more details, we refer to [44] and the references therein. [30] provides a combinatorial interpretation of $R_I$ polynomials. Interested readers may look at [4, 9, 16] for some recent progress related to $R_I$ type recurrence relations and $R_I$ polynomials.

The study of perturbation of the coefficients of a recurrence relation has considerable literature and has been dealt with in numerous ways by many authors. Constructing new sequences by modifying the original sequence is a powerful tool with many applications to theoretical and physical problems.

Orthogonal polynomials on the real line (OPRL) satisfy the recurrence relation

$$\begin{aligned} \mathcal {R}_{n+1}(x) = (x-b_{n})\mathcal {R}_n(x)-\gamma _n \mathcal {R}_{n-1}(x), \quad \mathcal {R}_{-1}(x) = 0, \quad \mathcal {R}_0(x) = 1, \quad n \ge 0. \end{aligned}$$

(1.5)

The case, known as co-recursive, was introduced and studied in [14] by adding a constant to the first coefficient $b_0$. The case of another type of perturbation called co-dilation was presented in [19]. The Stieltjes function and the fourth-order differential equation for the co-dilated polynomials inside the Laguerre-Hahn class were investigated in [20, 40]. The general case, called the generalized co-modification, arising from perturbation of coefficients in (1.5) at any level, was studied in [36] from the point of view of Stieltjes function, fourth-order differential equation, and distribution of zeros. A connection to the Laguerre-Hahn class was also investigated in [36]. The properties of co-modified classical orthogonal polynomials were studied in [40]. Its extension to semi-classical orthogonal polynomials was investigated in [20, 41]. Interlacing properties and some new inequalities for the zeros of co-modified OPRL, called co-polynomials on the real line (COPRL), were studied in [10]. In this direction, finite perturbations were studied in [38]. When the perturbations are large, some information is expected to be lost, which was explored in [31]. For perturbations of recurrence coefficients in the recurrence relations of higher-order and their extensions to Sobolev OPRL, see [32, 33]. Recently, a transfer matrix approach was introduced in [10] to study polynomials perturbed in a generalized co-modified way.

Unlike OPRL, a sequence of monic orthogonal polynomials on the unit circle (OPUC) denoted by $\{\phi _n(z)\}_{n=0}^\infty$ satisfies a first-order recurrence relation (Szegő recurrence)

$$\begin{aligned} \begin{bmatrix} \phi _{n+1}(z) \\ \phi ^*_{n+1}(z) \end{bmatrix}&= T_n(z) \begin{bmatrix} \phi _{n}(z) \\ \phi ^*_{n}(z) \end{bmatrix}, \quad T_n(z) = \begin{bmatrix} z &{} -\overline{\alpha _n} \\ -\alpha _n z &{} 1 \end{bmatrix}, \end{aligned}$$

(1.6)

with initial condition $\phi _0(z)=1$, where $\phi ^*_{n}(z)=z^n \overline{\phi _n(\frac{1}{\bar{z}})}$ is the reversed polynomial, and $T_n(z)$ is the transfer matrix [44]. The elements of the sequence $\{\alpha _n\}_{n=0}^\infty$ where $\alpha _n = -\overline{\phi _{n+1}(0)}$ lie in the unit disc and are known as Schur, reflection, Geronimus or Verblunsky coefficients.

The monic OPUC is completely determined by its reflection coefficients (Verblunsky theorem). This fact motivated the authors in [5] to study polynomials associated with perturbations of Verblunsky coefficients. Again, a transfer matrix approach has been used to study so-called co-polynomials on the unit circle (COPUC). The structural relations and rational spectral transformation for C-functions associated with COPUC are also discussed in [5] (see also [11]).

In this direction, results related to co-recursive of $d-$ orthogonal polynomials [42], co-recursive of $q-$ classical orthogonal polynomials [23], fourth-order difference equation and its factorization for co-dilated and/or co-recursive of classical discrete orthogonal polynomials [24] are available in the literature. For some applications, see [21, 22, 45].

This manuscript aims to study properties of the polynomials that satisfy a recurrence relation as (1.1) with new recurrence coefficients perturbed in a (generalized) co-recursive/co-dilated/co-modified way, i.e.,

$$\begin{aligned} {\mathcal {P}}_{n+1}(z;\mu _k,\nu _k) = (z-c^*_n){\mathcal {P}}_n(z;\mu _k,\nu _k)-\tilde{\lambda }_n (z-a_n){\mathcal {P}}_{n-1}(z;\mu _k,\nu _k), \quad n\ge 1, \end{aligned}$$

(1.7)

with initial conditions ${\mathcal {P}}_0(z) = 1$ and ${\mathcal {P}}_{-1}(z) =0$. In other words, we consider arbitrary single modification of recurrence coefficients as follows:

$$\begin{aligned} c^*_n&= c_n+\mu _k \delta _{n,k}, \quad \mu _k \in \mathbb {R}, \qquad \text {(co-recursive)} \end{aligned}$$

(1.8)

$$\begin{aligned} \tilde{\lambda }_n&= \nu _k^{\delta _{n,k}} \lambda _n, \quad \nu _k>0, \qquad \text {(co-dilated)} \end{aligned}$$

(1.9)

where k is a fixed non-negative integer. The rest of the paper is summarized as follows: Sect. 2 defines co-polynomials of $R_I$ type and analyzes rational spectral transformations associated with the corresponding continued fraction. Structural relations between the perturbed polynomials and the original ones are developed via two methods: the transfer matrix method and the classical matrix method. The computational complexities of both methods for the generation of perturbed $R_I$ polynomials are compared. The obtained results are compared with the obtained results for perturbed $R_{II}$ polynomials in [43], and some interesting conclusions are drawn. Further, the behaviour of zeros of L-orthogonal polynomials and their perturbed versions are studied. Finally, a result for obtaining the parameters of the PPC-fraction corresponding to a perturbed chain sequence is presented. In Sect. 3, an illustration is provided for exploring the effects of co-recursion and co-dilation in the chain sequences on Szegő polynomials, reflection coefficients, and associated measures. L-Jacobi polynomials are used to illustrate interlacing and monotonicity results on zeros numerically.

2 Co-polynomials of $R_I$ Type and Spectral Transformation

2.1 Structural Relations

Perturbing the coefficients $c_n$ and $\lambda _n$ at $n=k$ according to Favard theorem [25, Theorem 2.1] generates a new family of $R_I$ polynomials. A more general situation in the finite case can be any change at any level. The recurrence relation of $R_I$ type for generalised co-modified polynomials are given by

$$\begin{aligned} {\mathcal {P}}_{k+1}(z;\mu _k,\nu _k)&= (z-c_k-\mu _k){\mathcal {P}}_k(z;\mu _k,\nu _k)-\nu _k \lambda _k (z-a_k){\mathcal {P}}_{k-1}(z;\mu _k,\nu _k),\quad n = k,\nonumber \\ {\mathcal {P}}_{n+1}(z;\mu _k,\nu _k)&= (z-c_n){\mathcal {P}}_n(z;\mu _k,\nu _k)-\lambda _n (z-a_n){\mathcal {P}}_{n-1}(z;\mu _k,\nu _k), \quad n \ne k. \end{aligned}$$

(2.1)

The recurrence relation of $R_I$ type for generalised co-recursive polynomials ${\mathcal {P}}_{n+1}(z;\mu _k)$ and for generalised co-dilated polynomials ${\mathcal {P}}_{n+1}(z;\nu _k)$ and their representation in terms of unperturbed ones can be obtained by substituting $\nu _k=1$ and $\mu _k=0$, respectively, in (2.1).

Remark 2.1

Co-polynomials on the real line (COPRL) [10] and co-polynomials on the unit circle (COPUC) [5] are obtained after perturbations in (1.5) and in (1.6). Following a similar terminology, we can refer to the perturbed polynomials introduced above as co-polynomials of $R_I$ type.

Let us introduce

$$\begin{aligned} \mathbb {F}_{n+1}&:= \begin{bmatrix} {\mathcal {P}}_{n+1}(z) &{} -\mathcal {Q}_{n+1}(z)\\ {\mathcal {P}}_{n}(z) &{} -\mathcal {Q}_{n}(z) \end{bmatrix} = \textbf{T}_n \mathbb {F}_{n}, \end{aligned}$$

where$\{\mathcal {Q}_n(z)\}_{n \ge 0}$ are the associated polynomials of second kind that satisfy the recurrence relation (1.4) with initial conditions $\mathcal {Q}_0(z) = 0$ and $\mathcal {Q}_1(z) = 1$. They are monic polynomials of degree $n-1$. Clearly, $\mathbb {F}_{n+1}$ can be written as the product of the transfer matrices

$$\begin{aligned}&\mathbb {F}_{n+1} = \textbf{T}_n \mathbb {F}_{n} = \textbf{T}_n \ldots \textbf{T}_{k+1}\textbf{T}_k \textbf{T}_{k-1} \ldots \textbf{T}_0, \end{aligned}$$

(2.2)

where $\textbf{T}_n$ is the transfer matrix given by

$$\begin{aligned} \textbf{T}_n= \begin{bmatrix} z-c_n &{} -\lambda _n (z-a_n) \\ 1 &{} 0 \end{bmatrix} \quad \textrm{and} \quad \det (\textbf{T}_n)=\lambda _n (z-a_n). \end{aligned}$$

Using matrix notation (2.2), we have

$$\begin{aligned} \mathbb {F}_{n+1}(\mu _k,\nu _k)&= (\textbf{T}_n \ldots \textbf{T}_{k+1})\textbf{T}_k(\mu _k,\nu _k)(\textbf{T}_{k-1} \ldots \textbf{T}_0) \mathbb {F}_{0}, \end{aligned}$$

(2.3)

where

$$\begin{aligned} \textbf{T}_k (\mu _k,\nu _k)&= \begin{bmatrix} z-c_k-\mu _k &{} -\nu _k \lambda _k (z-a_k) \\ 1 &{} 0 \end{bmatrix}. \end{aligned}$$

Further, $\textbf{T}_k (\mu _k,\nu _k)$ can be written as

$$\begin{aligned} \textbf{T}_k (\mu _k,\nu _k)=\textbf{T}_k+\textbf{N}_k, \quad \textbf{N}_k = \begin{bmatrix} -\mu _k &{} -(\nu _k-1) \lambda _k (z-a_k) \\ 0 &{} 0 \end{bmatrix}. \end{aligned}$$

(2.4)

The associated polynomials of order $k+1$, ${\mathcal {P}}^{(k+1)}_{n-k}(x)$, satisfy

$$\begin{aligned} {\mathcal {P}}^{(k+1)}_{n+1}(z) = (z-c_{n+k+1}){\mathcal {P}}^{(k+1)}_n(x)-\lambda _{n+k+1}(z-a_{n+k+1}) {\mathcal {P}}^{(k+1)}_{n-1}(z), \quad n\ge 0, \end{aligned}$$

with initial conditions ${\mathcal {P}}^{(k+1)}_{-1}(z)=0$ and ${\mathcal {P}}^{(k+1)}_{0}(z)=1$. Hence, by Favard’s theorem [25], there exists a moment functional with respect to which ${\mathcal {P}}^{(k+1)}_{n}(z)$ is also a sequence of $R_I$ polynomials. According to the theory of linear difference equations, the two sequences $\{u_n\}_{n \ge 0}$ and $\{v_n\}_{n \ge 0}$ are said to be linearly independent if the Casorati determinant

$$\begin{aligned} D(u_n,v_n)=\begin{array}{|cc|} u_n &{} v_n \\ {u}_{n+1} &{} {v}_{n+1} \end{array} \end{aligned}$$

(2.5)

is different from zero for every n [37]. Since ${\mathcal {P}}^{(k+1)}_{n-k}(z)$ is a solution of the recurrence relation (1.4) with initial conditions ${\mathcal {P}}^{(k+1)}_{-1}(z)=0$ and ${\mathcal {P}}^{(k+1)}_{0}(z)=1$, it is easy to verify that

$$\begin{aligned} \begin{bmatrix} {\mathcal {P}}_{n+1}(z) &{} {\mathcal {P}}^{(k+1)}_{n-k}(z)\\ {\mathcal {P}}_{n}(z) &{} {\mathcal {P}}^{(k+1)}_{n-k-1}(z) \end{bmatrix}&=\textbf{T}_n \begin{bmatrix} {\mathcal {P}}_{n}(z) &{} {\mathcal {P}}^{(k+1)}_{n-k-1}(z)\\ {\mathcal {P}}_{n-1}(z) &{} {\mathcal {P}}^{(k+1)}_{n-k-2}(z) \end{bmatrix}. \end{aligned}$$

Let X denote the set of zeros of ${\mathcal {P}}_{k}(z)$. From the above equality, we get

$$\begin{aligned} D({\mathcal {P}}_{n+1}(z),{\mathcal {P}}^{(k+1)}_{n-k}(z))&= {\mathcal {P}}_{k}(z)\prod _{j=k+1}^{n}\lambda _j(z-a_j), \end{aligned}$$

(2.6)

which means that ${\mathcal {P}}_{n+1}(z)$ and ${\mathcal {P}}^{(k+1)}_{n-k}(z)$ are linearly independent in $\mathbb {C}\backslash X$.

2.2 The Spectral Transformation

The Stieltjes or the Cauchy (also called the Borel [44] ) transform of the orthogonality measure $d\alpha$ is given by

$$\begin{aligned} m_\alpha (z)=\int _\Gamma \dfrac{d\alpha (y)}{z-y}, \quad z \in \mathbb {C}\backslash \Gamma . \end{aligned}$$

(2.7)

An expression analogous to (2.7) for $R_{I}$ polynomials is given in [25, eqn. 2.11, page 7]

$$\begin{aligned} R_{I}(z)= \int _\Gamma \dfrac{d\alpha (y)}{z-y}, \quad z \in \mathbb {C}\backslash \Gamma , \end{aligned}$$

(2.8)

where $\Gamma = \left( \displaystyle \bigcup _{j=1}^{N}\Gamma _j\right) \cup \{z_k\}_{k\ge 0}$. Here, $\{\Gamma _j\}_{j=1}^{N}$ denote the finite number of branch cuts and $\{z_k\}_{k\ge 0}$ be the number of poles of the function at which corresponding continued fraction converges.

Also [25, eqn 2.10] suggests that

(2.9)

and

(2.10)

are the representations of the continued fraction for $\mathcal {R}_{I}(z)$ and its $(k+1)$-th approximant, respectively. Integral transforms are widely used in the literature for studying various special functions, for some recent references in this regard, see [1, 2].

From [15, chapter 4, equation 4.4], we have

(2.11)

The numerator polynomials of the corresponding continued fraction are $A_n$, and the denominator polynomials are $B_n$. Further, by the determinant formula, we obtain

$$\begin{aligned} \det \mathbb {F}_{n+1}= \begin{vmatrix} {\mathcal {P}}_{n+1}(z)&-\mathcal {Q}_{n+1}(z)\\ {\mathcal {P}}_{n}(z)&-\mathcal {Q}_{n}(z) \end{vmatrix} = \prod _{j=1}^{n}\lambda _j (z-a_j), \end{aligned}$$

and hence, $\mathbb {F}_{n+1}$ is non-singular. In what follows, the product $\prod _{j=1}^{n}\lambda _j (z-a_j)$ will be denoted by the short-hand notation $\Lambda _n$. These identities will be used to prove some of the results presented in this manuscript.

Definition 2.1

The $\dot{=}$ notation used in [12] has been adapted for the homography mapping

$$\begin{aligned} r(z)=\dfrac{a(z)u(z)+b(z)}{c(z)u(z)+d(z)}, \quad a(z)d(z)-b(z)c(z) \ne 0. \end{aligned}$$

A pure rational spectral transformation is referred to as the transformation of a function u(z) [12] given by

$$\begin{aligned} r(z) \dot{=} \textbf{A}(z)u(z), \quad \text{ where } \quad \textbf{A}(z) = \begin{bmatrix} a(z) &{} b(z)\\ c(z) &{} d(z) \end{bmatrix}. \end{aligned}$$

A spectral transformation changes the $m-$ function $m_\alpha$ (2.7) into a new $m-$ function $m_\beta$, associated with the measure $d\beta$, which is nothing more than a modification of the original measure $d\alpha$. We call the transformation of $m_\beta$ a pure rational spectral transformation when

$$\begin{aligned} m_\beta \dot{=} A(z) m_\alpha , \end{aligned}$$

where a(z), b(z), c(z) and d(z) are nonzero polynomials.

2.3 Generalized Co-modified $R_I$ Polynomials

Let $\mathcal {R}_{I}(z;\mu _k,\nu _k)$ be the continued fraction related to the co-modified polynomial. Using (2.10), $\mathcal {R}_{I}(z;\mu _k,\nu _k)$ can be written as

(2.12)

Theorem 2.1

$\mathcal {R}_{I}(z;\mu _k,\nu _k)$ defines a rational spectral transformation of $\mathcal {R}_{I}(z)$ as

$$\begin{aligned} \mathcal {R}_{I}(z;\mu _k,\nu _k)~\dot{=}~ \textbf{M}_k(z) \mathcal {R}_{I}(z), \end{aligned}$$

where $\textbf{M}_k$ is the transfer matrix

$$\begin{aligned} \textbf{M}_k = \begin{bmatrix} \hat{\mathcal {S}}_k(z) {\mathcal {P}}_k(z) +\Lambda _k &{} -\mathcal {Q}_k(z)\hat{\mathcal {S}}_k(z)\\ -\mathcal {S}_k(z){\mathcal {P}}_k(z) &{} \Lambda _k+\mathcal {S}_k(z)\mathcal {Q}_k(z) \end{bmatrix}, \end{aligned}$$

and where

$$\begin{aligned} \hat{\mathcal {S}}_k(z)&= -\mu _ k \mathcal {Q}_k(z)-(\nu _k-1)\lambda _k(z-a_k)\mathcal {Q}_{k-1}(z), \\ \mathcal {S}_k(z)&=\mu _k {\mathcal {P}}_k(z)+(\nu _k-1)\lambda _k (z-a_k) {\mathcal {P}}_{k-1}(z). \end{aligned}$$

Proof

First, we will find the relation between the continued fraction $\mathcal {R}_{I}(z;\mu _k,\nu _k)$ associated with the perturbations (1.8) and (1.9) and its $(k+1)$-th approximant $\mathcal {R}_{I}^{k+1}(z)$. The continued fraction expansion (2.12), in comparison with (2.11), gives

$$\begin{aligned}&\mathcal {R}_{I}(z;\mu _k,\nu _k) =\frac{(z-c_{k}-\mu _k-\lambda _{k+1}(z-a_{k+1})\mathcal {R}_{I}^{k+1}(z))\mathcal {Q}_{k}-\nu _k\lambda _{k}(z-a_{k})\mathcal {Q}_{k-1}}{(z-c_{k}-\mu _k-\lambda _{k+1}(z-a_{k+1})\mathcal {R}_{I}^{k+1}(z)){\mathcal {P}}_{k}-\nu _k \lambda _{k}(z-a_{k}){\mathcal {P}}_{k-1}} \nonumber \\&= \frac{\mathcal {Q}_{k+1} -\lambda _{k+1}(z-a_{k+1})\mathcal {R}_{I}^{k+1}(z) \mathcal {Q}_{k}-\mu _k \mathcal {Q}_{k} +(1-\nu _k)\lambda _{k}(z-a_{k})\mathcal {Q}_{k-1}}{{\mathcal {P}}_{k+1} -\lambda _{k+1}(z-a_{k+1})\mathcal {R}_{I}^{k+1}(z) {\mathcal {P}}_{k} -\mu _k {\mathcal {P}}_{k}+(1-\nu _k)\lambda _{k}(z-a_{k}){\mathcal {P}}_{k-1}} \nonumber \\&= \frac{\mathcal {A}(z)\mathcal {R}_{I}^{k+1}(z)+\mathcal {B}(z)}{\mathcal {C}(z)\mathcal {R}_{I}^{k+1}(z)+\mathcal {D}(z)}, \end{aligned}$$

(2.13)

where

$$\begin{aligned}&\mathcal {A}(z) = \lambda _{k+1}(z-a_{k+1}) \mathcal {Q}_{k}, \quad \mathcal {B}(z) = -\mathcal {Q}_{k+1}+\mu _k \mathcal {Q}_{k} +(\nu _k-1)\lambda _{k}(z-a_{k})\mathcal {Q}_{k-1}, \\&\mathcal {C}(z) = \lambda _{k+1}(z-a_{k+1}) {\mathcal {P}}_{k}, \quad \mathcal {D}(z) = -{\mathcal {P}}_{k+1}+\mu _k {\mathcal {P}}_{k} +(\nu _k-1)\lambda _{k}(z-a_{k}){\mathcal {P}}_{k-1}. \end{aligned}$$

Now, looking at Definition 2.1, it can be concluded that $\mathcal {R}_{I}(z;\mu _k,\nu _k)$ is the rational spectral transformation of its $(k+1)$-th approximant $\mathcal {R}_{I}^{k+1}(z)$. Further, putting $\mu _k = 0$ and $\nu _k = 1$ implies $\mathcal {R}_{I}(z)=\mathcal {R}_{I}(z;\mu _k,\nu _k)$, and formula (2.13) takes the form

$$\begin{aligned} \mathcal {R}_{I}(z)&= \frac{\mathcal {Q}_{k+1} -\lambda _{k+1}(z-a_{k+1})\mathcal {R}_{I}^{k+1}(z) \mathcal {Q}_{k}}{ {\mathcal {P}}_{k+1} -\lambda _{k+1}(z-a_{k+1})\mathcal {R}_{I}^{k+1}(z) {\mathcal {P}}_{k}},\nonumber \\&\Longrightarrow \lambda _{k+1}(z-a_{k+1})\mathcal {R}_{I}^{k+1}(z) \mathcal {Q}_{k}-\lambda _{k+1}(z-a_{k+1})\mathcal {R}_{I}^{k+1}(z) {\mathcal {P}}_{k}\mathcal {R}_{I}(z) \nonumber \\&= \mathcal {Q}_{k+1}-{\mathcal {P}}_{k+1}\mathcal {R}_{I}(z), \nonumber \\&\Longrightarrow \lambda _{k+1}(z-a_{k+1})\mathcal {R}_{I}^{k+1}(z)[\mathcal {Q}_{k}-{\mathcal {P}}_{k}\mathcal {R}_{I}(z)] = \mathcal {Q}_{k+1}-{\mathcal {P}}_{k+1}\mathcal {R}_{I}(z), \nonumber \\&\Longrightarrow \lambda _{k+1}(z-a_{k+1})\mathcal {R}_{I}^{k+1}(z)= \frac{{\mathcal {P}}_{k+1}\mathcal {R}_{I}(z)-\mathcal {Q}_{k+1}}{{\mathcal {P}}_{k}\mathcal {R}_{I}(z)-\mathcal {Q}_{k}}. \end{aligned}$$

(2.14)

Now, eliminating $\mathcal {R}_{I}^{k+1}(z)$ from (2.13) and (2.14), we obtain

$$\begin{aligned}&\mathcal {R}_{I}(z;\mu _k,\nu _k) = \frac{\mathcal {A}(z)\mathcal {R}_{I}^{k+1}(z)+\mathcal {B}(z)}{\mathcal {C}(z)\mathcal {R}_{I}^{k+1}(z)+\mathcal {D}(z)}\\&= \dfrac{\lambda _{k+1}(z-a_{k+1}) \mathcal {Q}_{k}\mathcal {R}_{I}^{k+1}(z)-\mathcal {Q}_{k+1}+\mu _k \mathcal {Q}_{k}+(\nu _k-1)\lambda _{k}(z-a_{k})\mathcal {Q}_{k-1} }{\lambda _{k+1}(z-a_{k+1}) {\mathcal {P}}_{k}\mathcal {R}_{I}^{k+1}(z)-{\mathcal {P}}_{k+1}+\mu _k {\mathcal {P}}_{k} +(\nu _k-1)\lambda _{k}(z-a_{k}){\mathcal {P}}_{k-1}} \\&= \frac{\mathcal {Q}_{k}{\mathcal {P}}_{k+1}\mathcal {R}_{I}(z)-\mathcal {Q}_{k}\mathcal {Q}_{k+1}-\mathcal {Q}_{k+1}[{\mathcal {P}}_{k}\mathcal {R}_{I}(z)-\mathcal {Q}_{k}]+\mu _k \mathcal {Q}_{k}[{\mathcal {P}}_{k}\mathcal {R}_{I}(z)-\mathcal {Q}_{k}] +}{{\mathcal {P}}_{k}{\mathcal {P}}_{k+1}\mathcal {R}_{I}(z)-\mathcal {Q}_{k+1}{\mathcal {P}}_{k}-{\mathcal {P}}_{k+1}[{\mathcal {P}}_{k}\mathcal {R}_{I}(z)-\mathcal {Q}_{k}]+\mu _k {\mathcal {P}}_{k}[{\mathcal {P}}_{k}\mathcal {R}_{I}(z)-\mathcal {Q}_{k}] +} \\&\quad \dfrac{+(\nu _k-1)\lambda _{k}(z-a_{k})\mathcal {Q}_{k-1}[{\mathcal {P}}_{k}\mathcal {R}_{I}(z)-\mathcal {Q}_{k}]}{+(\nu _k-1) \lambda _{k}(z-a_{k}) {\mathcal {P}}_{k-1}[{\mathcal {P}}_{k}\mathcal {R}_{I}(z)-\mathcal {Q}_{k}]}\\&= \frac{[-\Lambda _k+\mu _k \mathcal {Q}_{k}{\mathcal {P}}_{k} +(\nu _k-1)\lambda _{k}(z-a_{k})\mathcal {Q}_{k-1}{\mathcal {P}}_{k}]\mathcal {R}_{I}(z)-\mu _k[\mathcal {Q}_{k}]^2-}{[\mu _k[{\mathcal {P}}_{k}]^2+(\nu _k-1)\lambda _{k}(z-a_{k}){\mathcal {P}}_{k-1}{\mathcal {P}}_{k}] \mathcal {R}_{I}(z) - \Lambda _k-\mu _k \mathcal {Q}_{k}{\mathcal {P}}_{k} - } \\&\quad \dfrac{-(\nu _k-1)\lambda _{k}(z-a_{k})\mathcal {Q}_{k-1}\mathcal {Q}_k}{-(\nu _k-1)\lambda _{k}(z-a_{k}){\mathcal {P}}_{k-1}\mathcal {Q}_{k}} \\&=\dfrac{(\textbf{M}_k)_{11}\mathcal {R}_{I}(z)+(\textbf{M}_k)_{12}}{(\textbf{M}_k)_{21}\mathcal {R}_{I}(z)+ (\textbf{M}_k)_{22}}, \end{aligned}$$

where

$$\begin{aligned}&(\textbf{M}_k)_{11} = \Lambda _k- (\nu _k-1)\lambda _{k}(z-a_{k})\mathcal {Q}_{k-1}{\mathcal {P}}_{k}-\mu _k \mathcal {Q}_{k}{\mathcal {P}}_{k}, \\&(\textbf{M}_k)_{12}=(\nu _k-1)\lambda _{k}(z-a_{k})\mathcal {Q}_{k-1}\mathcal {Q}_{k}+\mu _k[\mathcal {Q}_{k}]^2,\\&(\textbf{M}_k)_{21}= -(\nu _k-1)\lambda _{k}(z-a_{k}){\mathcal {P}}_{k-1}{\mathcal {P}}_{k}-\mu _k[{\mathcal {P}}_{k}]^2,\\&(\textbf{M}_k)_{22}= \Lambda _k+(\nu _k-1)\lambda _{k}(z-a_{k}){\mathcal {P}}_{k-1}\mathcal {Q}_{k}+\mu _k \mathcal {Q}_{k}{\mathcal {P}}_{k}. \end{aligned}$$

Now, in the view of Definition 2.1, we obtain the required result. $\square$

The following specific cases of generalized co-recursive and generalized co-dilated $R_I$ polynomials are immediate consequence of results proved earlier in this section.

Remark 2.2

Let $\mathcal {R}_{I}(z;\mu _k)$ be the continued fraction corresponding to co-recursive perturbation (1.8). With $\nu _k = 1$, relation (2.13) reduces to give a relation between $\mathcal {R}_{I}(z;\mu _k)$ and $\mathcal {R}_{I}^{k+1}(z)$.

$$\begin{aligned} \mathcal {R}_{I}(z;\mu _k)&\dot{=} \begin{bmatrix} \lambda _{k+1}(z-a_{k+1}) \mathcal {Q}_{k} &{} -\mathcal {Q}_{k+1}+\mu _k \mathcal {Q}_{k}\\ \lambda _{k+1}(z-a_{k+1}) {\mathcal {P}}_{k} &{} -{\mathcal {P}}_{k+1}+\mu _k \mathcal {Q}_{k} \end{bmatrix} \mathcal {R}_{I}^{k+1}(z). \end{aligned}$$

Remark 2.3

A relation between continued fraction associated with co-recursion (1.8) and its $(k+1)$-th approximant can be given in the following way:

$$\begin{aligned} \mathcal {R}_{I}(z;\mu _k)&\dot{=} \begin{bmatrix} \Lambda _k+\mu _k \mathcal {Q}_{k}{\mathcal {P}}_{k} &{} -\mu _k \mathcal {Q}_{k}^2\\ \mu _k {\mathcal {P}}_{k}^2 &{} \Lambda _k-\mu _k {\mathcal {P}}_{k}\mathcal {Q}_{k} \end{bmatrix} \mathcal {R}_{I}(z). \end{aligned}$$

Remark 2.4

Let $\mathcal {R}_{I}(z;\nu _k)$ be the continued fraction associated with co-dilation (1.9). With $\mu _k = 0$, equation (2.13) reduces to give a relation between $\mathcal {R}_{I}(z;\nu _k)$ and its $(k+1)$-th approximant.

$$\begin{aligned} \mathcal {R}_{I}(z;\nu _k)&\dot{=} \begin{bmatrix} \lambda _{k+1}(z-a_{k+1}) \mathcal {Q}_{k} &{} -\mathcal {Q}_{k+1}+(\nu _k-1)\lambda _{k}(z-a_{k})\mathcal {Q}_{k-1}\\ \lambda _{k+1}(z-a_{k+1}) {\mathcal {P}}_{k} &{} -{\mathcal {P}}_{k+1} +(\nu _k-1)\lambda _{k}(z-a_{k}){\mathcal {P}}_{k-1} \end{bmatrix} \mathcal {R}_{I}^{k+1}(z). \end{aligned}$$

Remark 2.5

A relation between continued fraction associated with co-dilation (1.9) and its $(k+1)$-th approximant can be given in the following way:

$$\begin{aligned} \mathcal {R}_{I}(z;\nu _k) \dot{=}\begin{bmatrix} \Lambda _k+(\nu _k-1)\lambda _{k}(z-a_{k})\mathcal {Q}_{k-1}{\mathcal {P}}_{k} &{} -(\nu _k-1)\lambda _{k}(z-a_{k})\mathcal {Q}_{k-1}\mathcal {Q}_{k}\\ (\nu _k-1)\lambda _{k}(z-a_{k}){\mathcal {P}}_{k-1}{\mathcal {P}}_{k} &{} \Lambda _k-(\nu _k-1)\lambda _{k}(z-a_{k}){\mathcal {P}}_{k-1}\mathcal {Q}_{k} \end{bmatrix} \mathcal {R}_{I}(z). \end{aligned}$$

For additional details regarding rational spectral transformations, see [47].

The next important aspect is the computation of perturbed polynomials from the original ones. This can be achieved in two ways:

• (1) The transfer matrix method

• (2) The classical method.

2.4 The Transfer Matrix Method

The following result is important both from a computational and theoretical standpoint because $\textbf{M}_k$ being a matrix, it is easy to compute the perturbed polynomials ${\mathcal {P}}_{n+1}(z;\mu _k,\nu _k)$ and $\mathcal {Q}_{n+1}(z;\mu _k,\nu _k)$.

Theorem 2.2

The following relation holds in $\mathbb {C}$:

$$\begin{aligned} \Lambda _k \begin{bmatrix} {\mathcal {P}}_{n+1}(z;\mu _k,\nu _{k}) &{} {\mathcal {P}}_{n}(z;\mu _k,\nu _{k}) \\ -\mathcal {Q}_{n+1}(z;\mu _k,\nu _{k}) &{} -\mathcal {Q}_{n}(z;\mu _k,\nu _{k}) \end{bmatrix}&= ~ cof(\textbf{M}_k)(z) \begin{bmatrix} {\mathcal {P}}_{n+1}(z) &{} {\mathcal {P}}_{n}(z)\\ -\mathcal {Q}_{n+1}(z) &{} -\mathcal {Q}_{n}(z) \end{bmatrix}, \end{aligned}$$

where $cof(\cdot )$ is the cofactor matrix operator.

Proof

Let $\mathbb {F}_{n+1}(\mu _k,\nu _k)$ be the polynomial matrix corresponding to co-modified polynomials of $R_{I}$ type. From (2.2), we get

$$\begin{aligned} \mathbb {F}_{n+1}(\mu _k,\nu _k)&= \textbf{T}_n \ldots \textbf{T}_{k+1}\textbf{T}_k (\mu _k,\nu _k) \textbf{T}_{k-1} \ldots \textbf{T}_0 \nonumber \\&=\textbf{T}_n \ldots \textbf{T}_{k+1}\textbf{T}_k \textbf{T}_{k-1} \ldots \textbf{T}_0 (\mathbb {F}_{k+1} )^{-1}\textbf{T}_k (\mu _k,\nu _k)\mathbb {F}_{k} \nonumber \\&= \mathbb {F}_{n+1}(\mathbb {F}_{k+1} )^{-1} \mathbb {F}_{k+1}(\mu _k,\nu _k). \end{aligned}$$

This implies

$$\begin{aligned} \mathbb {F}^T_{n+1}(\mu _k,\nu _k)&=[\mathbb {F}_{k+1}(\mu _k,\nu _k)]^T (\mathbb {F}_{k+1} )^{-T} \mathbb {F}^T_{n+1} . \end{aligned}$$

(2.15)

Since

$$\begin{aligned}{}[\mathbb {F}_{k+1}(\mu _k,\nu _k)]^T= \begin{bmatrix} {\mathcal {P}}_{k+1}(z;\mu _k,\nu _k) &{} {\mathcal {P}}_{k}(z)\\ -\mathcal {Q}_{k+1}(z;\mu _k,\nu _k) &{} -\mathcal {Q}_{k}(z) \end{bmatrix} \end{aligned}$$

(2.16)

and by the determinant formula, $\det (\mathbb {F}_{k+1}) = \Lambda _k$,

$$\begin{aligned} (\mathbb {F}_{k+1})^{-T}&= \frac{1}{\Lambda _k} \begin{bmatrix} -\mathcal {Q}_{k}(z) &{} -{\mathcal {P}}_{k}(z)\\ \mathcal {Q}_{k+1}(z) &{} {\mathcal {P}}_{k+1}(z) \end{bmatrix}. \end{aligned}$$

(2.17)

Using (2.16) and (2.17) in (2.15), we obtain

$\displaystyle [\mathbb {F}_{k+1}(\mu _k,\nu _k)]^T (\mathbb {F}_{k+1} )^{-T}$

$$\begin{aligned}&=\frac{1}{\Lambda _k}\begin{bmatrix} -{\mathcal {P}}_{k+1}(z;\mu _k,\nu _k) \mathcal {Q}_{k}(z)+{\mathcal {P}}_{k}(z)\mathcal {Q}_{k+1}(z) &{} -{\mathcal {P}}_{k+1}(z;\mu _k,\nu _k){\mathcal {P}}_{k}(z)+{\mathcal {P}}_{k}(z){\mathcal {P}}_{k+1}(z)\\ \mathcal {Q}_{k+1}(z;\mu _k,\nu _k)\mathcal {Q}_{k}(z)-\mathcal {Q}_{k}(z)\mathcal {Q}_{k+1}(z) &{} \mathcal {Q}_{k+1}(z;\mu _k,\nu _k){\mathcal {P}}_{k}(z)-\mathcal {Q}_{k}(z){\mathcal {P}}_{k+1}(z) \end{bmatrix} \nonumber \\&= \frac{1}{\Lambda _k} \begin{bmatrix} \Lambda _k +\mathcal {S}_k(z)\mathcal {Q}_k(z) &{} \mathcal {S}_k(z){\mathcal {P}}_k(z) \\ \mathcal {Q}_k(z)\hat{\mathcal {S}}_k(z) &{} \hat{\mathcal {S}}_k(z) {\mathcal {P}}_k(z) +\Lambda _k \end{bmatrix} \nonumber \\&=\frac{1}{\Lambda _k} \begin{bmatrix} (\textbf{M}_k)_{22} &{} -(\textbf{M}_k)_{21}\\ -(\textbf{M}_k)_{12} &{} (\textbf{M}_k)_{11} \end{bmatrix}= \frac{cof(\textbf{M}_k)(z)}{\Lambda _k} \end{aligned}$$

(2.18)

The theorem follows after substituting (2.18) in (2.15).

The former theorem enables the study of the polynomials when finite number of recurrence coefficients are perturbed. In this regard, the following can be proved using techniques given in [5, 43].

Theorem 2.3

Let k, m be two fixed non-negative integers with $m < k$. Then for $n > m$, the following relation holds:

$$\begin{aligned} \prod _{j=m}^{k}\Lambda _j \mathbb {F}_{n+1}(\mu _m,\nu _m,\ldots \mu _k,\nu _k)&= \prod _{j=m}^{k}cof(\textbf{M}_j)(z) \mathbb {F}_{n+1}. \end{aligned}$$

2.5 The Classical Method

A disadvantage of Theorem 2.4 is that it requires the knowledge of associated polynomials, ${\mathcal {P}}^{(k+1)}_{n-k}(z)$ and $\mathcal {Q}^{(k+1)}_{n-k}(z)$, while Theorem 2.2 utilizes already given polynomials ${\mathcal {P}}_{n}(z)$ and $\mathcal {Q}_{n}(z)$ to compute the perturbed polynomials.

Theorem 2.4

The following formulas hold:

$$\begin{aligned} {\mathcal {P}}_{n+1}(z;\mu _k,\nu _k)&={\mathcal {P}}_{n+1}(z), \qquad n< k, \\ {{\mathcal {P}}}_{n+1}(z;\mu _k,\nu _k)&= {\mathcal {P}}_{n+1}(z) - \mathcal {S}_k(z){\mathcal {P}}^{(k+1)}_{n-k}(z), \qquad n \ge k, \\ \text {and} \quad \mathcal {Q}_{n+1}(z;\mu _k,\nu _k)&=\mathcal {Q}_{n+1}(z), \qquad n < k, \\ {\mathcal {Q}}_{n+1}(z;\mu _k,\nu _k)&= \mathcal {Q}_{n+1}(z) + \hat{\mathcal {S}}_k(z)\mathcal {Q}^{(k+1)}_{n-k}(z), \qquad n \ge k, \end{aligned}$$

Proof

Any solution to (2.1) will be a linear combination of two linearly independent solutions, as is clear from the theory of difference equations. From (2.3),

$$\begin{aligned} \begin{bmatrix} {\mathcal {P}}_{n+1}(z;\mu _k,\nu _k) &{} -\mathcal {Q}_{n+1}(z;\mu _k,\nu _k)\\ {{\mathcal {P}}}_{n}(z;\mu _k,\nu _k) &{} -\mathcal {Q}_{n}(z;\mu _k,\nu _k) \end{bmatrix}&= (\textbf{T}_n \ldots \textbf{T}_{k+1})\textbf{T}_k(\mu _k,\nu _k) \begin{bmatrix} {\mathcal {P}}_{k}(z) &{} -\mathcal {Q}_{k}(z)\\ {{\mathcal {P}}}_{k-1}(z) &{} -\mathcal {Q}_{k-1}(z) \end{bmatrix}. \end{aligned}$$

Use of (2.4) implies

$$\begin{aligned}&\begin{bmatrix} {\mathcal {P}}_{n+1}(z;\mu _k,\nu _k) &{} -\mathcal {Q}_{n+1}(z;\mu _k,\nu _k)\\ {{\mathcal {P}}}_{n}(z;\mu _k,\nu _k) &{} -\mathcal {Q}_{n}(z;\mu _k,\nu _k) \end{bmatrix}= (\textbf{T}_n \ldots \textbf{T}_{k+1})(\textbf{T}_k+\textbf{N}_k) \begin{bmatrix} {\mathcal {P}}_{k}(z) &{} -\mathcal {Q}_{k}(z)\\ {{\mathcal {P}}}_{k-1}(z) &{} -\mathcal {Q}_{k-1}(z) \end{bmatrix} \\ =&\begin{bmatrix} {\mathcal {P}}_{n+1}(z) &{} -\mathcal {Q}_{n+1}(z)\\ {{\mathcal {P}}}_{n}(z) &{} -\mathcal {Q}_{n}(z) \end{bmatrix}+ \textbf{T}_n \ldots \textbf{T}_{k+1} \begin{bmatrix} -\mu _k &{} -(\nu _k-1) \lambda _k (z-a_k) \\ 0 &{} 0 \end{bmatrix} \begin{bmatrix} {\mathcal {P}}_{k}(z) &{} -\mathcal {Q}_{k}(z)\\ {{\mathcal {P}}}_{k-1}(z) &{} -\mathcal {Q}_{k-1}(z) \end{bmatrix}\\ =&\begin{bmatrix} {\mathcal {P}}_{n+1}(z) &{} -\mathcal {Q}_{n+1}(z)\\ {{\mathcal {P}}}_{n}(z) &{} -\mathcal {Q}_{n}(z) \end{bmatrix}+ \textbf{T}_n \ldots \textbf{T}_{k+1} \begin{bmatrix} -\mathcal {S}_k(z) &{} -\hat{\mathcal {S}}_k(z)\\ 0 &{} 0 \end{bmatrix}\\&=\begin{bmatrix} {\mathcal {P}}_{n+1}(z) &{} -\mathcal {Q}_{n+1}(z)\\ {{\mathcal {P}}}_{n}(z) &{} -\mathcal {Q}_{n}(z) \end{bmatrix} + \begin{bmatrix} -\mathcal {S}_k(z) {\mathcal {P}}^{(k+1)}_{n-k}(z) &{} -\hat{\mathcal {S}}_k(z)\mathcal {Q}^{(k+1)}_{n-k}(z)\\ -\mathcal {S}_k(z) {\mathcal {P}}^{(k+1)}_{n-k-1}(z) &{} -\hat{\mathcal {S}}_k(z)\mathcal {Q}^{(k+1)}_{n-k-1}(z) \end{bmatrix} \end{aligned}$$

which proves the theorem.

Next, we compare the computational complexity between both approaches to compute perturbed $\mathcal {R}_{I}$ polynomials. Further, a comparative study of complexity involved in the computation of perturbed $\mathcal {R}_{I}$ polynomials (discussed in this work) and perturbed $\mathcal {R}_{II}$ polynomials (discussed in [43]) from both approaches is also provided.

2.6 Comparison of Computational Cost Between the Classical and the Transfer Matrix Method

In this section, we provide details for ${\mathcal {P}}_{4}(x;\mu _0,\nu _0,\mu _1,\nu _1)$ by explicitly counting the multiplication operation (abbreviated as ‘prod’ now onwards) involved. Consider two consecutive perturbations at $k=0$ and $k=1$ in (1.1). In the Transfer matrix method, the following steps are involved:

• (1) Computation of entries of transfer matrices $\textbf{M}_{0}$ and $\textbf{M}_{1}$ and product of these two matrices.

• (2) Multiplication of the first row of the resultant matrix with the column vector $[{\mathcal {P}}_{4}(x),-\mathcal {Q}_{4}(x)]^T$.

Because the multiplication operation is considered to be the most expensive, we only consider counting distinct ‘prod’ among real coefficients. The transfer matrices $\textbf{M}_{0}$ and $\textbf{M}_{1}$ are

$$\begin{aligned} \textbf{M}_{0}= \begin{bmatrix} 0 &{} \mu _0\\ 0 &{} 0 \end{bmatrix}, \quad \textbf{M}_{1} =\begin{bmatrix} a_{11} &{} a_{12}\\ a_{21} &{} a_{22} \end{bmatrix}, \end{aligned}$$

where $a_{11}=\mu _1(x-c_0)+\nu _1\lambda _1(x-a_1)$, $a_{12} = \mu _1(x-c_0)^2+(\nu _1-1)\lambda _1(x-a_1)(x-c_0)$, $a_{21}=-\mu _1$ and $a_{22}=-\mu _1(x-c_0)+\lambda _1(x-a_1)$. In this case, $a_{11}$ involves three distinct ‘prod’, namely $\mu _1c_0$ and $\nu _1\lambda _1$. Similarly, $a_{12}$, $a_{21}$, and $a_{22}$ each have 5, 0, and 0 distinct ‘prod’, respectively (because $\mu _1c_0$ is already computed in $a_{11}$, it will not be counted again). The product $\textbf{M}_{0}\textbf{M}_{1}$

$$\begin{aligned} \textbf{M}_{0}\textbf{M}_{1}= \begin{bmatrix} -\mu _0\mu _1 &{} \mu _0[\mu _1(x-c_0)+\lambda _1(x-a_1)]\\ 0 &{} 0 \end{bmatrix}=\begin{bmatrix} b_{11} &{} b_{12}\\ b_{21} &{} b_{22} \end{bmatrix}, \end{aligned}$$

requires 4 ‘prod’. As ${\mathcal {P}}_{4}(x)$ and $\mathcal {Q}_{4}(x)$ are (known) polynomials of degrees 4 and 3, $b_{11} \times {\mathcal {P}}_{4}(x)$ requires 5 ‘prod’, and $b_{12} \times \mathcal {Q}_{4}(x)$ requires 8 ‘prod’ (since $b_{12}$ in itself is a polynomial of degree 1). As a result, the computation of ${\mathcal {P}}_{4}(x;\mu _0,\nu _0,\mu _1,\nu _1)$ requires a total of 25 ‘prod’.

On the other hand, in the classical method, we have

$$\begin{aligned}&{\mathcal {P}}_{0}(x)=1, \\&{\mathcal {P}}_{1}(x;\mu _0,\nu _0)=(x-c_{0}-\mu _0){\mathcal {P}}_0(x), \\&{\mathcal {P}}_{2}(x;\mu _0,\nu _0,\mu _1,\nu _1)=(x-c_{1}-\mu _1){\mathcal {P}}_1(x;\mu _0,\nu _0)-\nu _1\lambda _{1} (x^2+1){\mathcal {P}}_{0}(x),\\&{\mathcal {P}}_{3}(x;\mu _0,\nu _0,\mu _1,\nu _1)=(x-c_{2}){\mathcal {P}}_2(x;\mu _0,\nu _0,\mu _1,\nu _1)-\lambda _{2} (x^2+1){\mathcal {P}}_{1}(x;\mu _0,\nu _0), \\&{\mathcal {P}}_{4}(x;\mu _0,\nu _0,\mu _1,\nu _1)=(x-c_{3}){\mathcal {P}}_3(x;\mu _0,\nu _0,\mu _1,\nu _1)-\lambda _{3} (x^2+1){\mathcal {P}}_{2}(x;\mu _0,\nu _0,\mu _1,\nu _1). \end{aligned}$$

Substitution can now be used to compute ${\mathcal {P}}_{4}(x;\mu _0,\nu _0,\mu _1,\nu _1)$. In the computation, 42 distinct ‘prod’ are involved. In this case, the Transfer matrix method outperforms the classical method in terms of computational speed. Furthermore, we have compared the methods for higher degree polynomials (see Conclusion 2) and discovered that the difference in the number of ‘prod’ between these two approaches grows even faster.

2.6.1 Conclusions

• (1) Both approaches have been shown to be equally efficient for generating lower-degree polynomials with a single perturbation.

• (2) According to Fig. 1, the classical method requires less computation for ${\mathcal {P}}_{2}(x;\mu _0, \nu _0,\mu _1,\nu _1)$ and ${\mathcal {P}}_{3}(x;\mu _0,\nu _0,\mu _1,\nu _1)$. However, the number of ‘prod’ involved in the computation of higher degree perturbed polynomials (with two consecutive perturbations) by the classical method (blue dashed line) is significantly greater than that involved in Transfer matrix method (solid red line). Furthermore, the growth of ‘prod’ involved in the classical method is non-linear.

• (3) The cost of computing perturbed $\mathcal {R}_{I}$ (solid red line) and $\mathcal {R}_{II}$ (dash-dot magenta line) polynomials (see [43]) from the transfer matrix method is compared in Fig. 1. Observe that, upto degree 4, lesser ‘prod’ are required in the computation of perturbed $\mathcal {R}_{II}$ polynomials than in perturbed $\mathcal {R}_{I}$ polynomials, but after degree 5, the situation reverses, i.e., requiring more ‘prod’ in the computation of perturbed $\mathcal {R}_{I}$ polynomials than in perturbed $\mathcal {R}_{II}$ polynomials.

• (4) It is interesting to note that (see Fig. 1) the complexity of the classical method for computing perturbed $\mathcal {R}_{I}$ (dashed blue line) is higher than that of the perturbed $\mathcal {R}_{II}$ (dotted brown line) polynomials (see [43]).

Table 1 Compuatational cost comparison between the two methods of computing perturbed $\mathcal {R}_{I}$ and $\mathcal {R}_{II}$ polynomials

Fig. 1

Degree of polynomials versus number of ‘prod’ involved in computing perturbed $\mathcal {R}_{I}$ and $\mathcal {R}_{II}$ polynomials

2.7 Inclusion, Interlacing and Monotonicity Properties of Zeros

To discuss the zeros, we consider a special form of $\mathcal {R}_{I}$ type recurrence with $a_n=0$, $\forall ~ n$ and given by (1.4). In the view of recurrence (1.4), Theorem 2.4 implies the following corollary:

Corollary 2.1

The following formulas hold:

$$\begin{aligned} {{\mathcal {P}}}_{n+1}(x;\mu _k,\nu _k)&= {\mathcal {P}}_{n+1}(x) - \mathcal {S}_k(x){\mathcal {P}}^{(k+1)}_{n-k}(x), \qquad n \ge k, \\ \text {and} \quad {\mathcal {Q}}_{n+1}(x;\mu _k,\nu _k)&= \mathcal {Q}_{n+1}(x) + \hat{\mathcal {S}}_k(x)\mathcal {Q}^{(k+1)}_{n-k}(x), \qquad n \ge k, \end{aligned}$$

where $\mathcal {S}_k(x)=\mu _k {\mathcal {P}}_k(x)+(\nu _k-1)\lambda _k x {\mathcal {P}}_{k-1}(x)$ and $\hat{\mathcal {S}}_k(x)=-\mu _k \mathcal {Q}_k(x)-(\nu _k-1)\lambda _k x \mathcal {Q}_{k-1}(x)$.

From (2.6), we get ${\mathcal {P}}_{n+1}(x)$ and ${\mathcal {P}}^{(k+1)}_{n-k}(x)$ are linearly independent.

Remark 2.6

If $\mu _k=0$, then the degree of $\mathcal {S}_k(x)$ is k. Similarly, if $\nu _k=1$, then the degree of $\mathcal {S}_k(x)$ is k. This leads to the conclusion that the degree of $\mathcal {S}_k(x)$ is equal for both co-recursive and co-dilated cases. Note that this is not true for OPRL satisfying TTRR, see [10, Theorem 2.1] (also see [36]).

Theorem 2.5

If ${\mathcal {P}}_{n+1}(x;\mu _k,\nu _k)$ and ${\mathcal {P}}_{n+1}(x)$ share a zero, then that zero will also be shared by $\mathcal {S}_k(x)$.

Proof

Assume ${\mathcal {P}}_{n+1}(x;\mu _k,\nu _k)$ and ${\mathcal {P}}_{n+1}(x)$ share a common zero $\beta$ that is not the zero of $\mathcal {S}_k$. Let Y represent the set of zeros of $\mathcal {S}_k(x)$. Then, because $\beta \in \mathbb {C}\backslash (X \cup Y)$, Theorem 2.4 implies ${\mathcal {P}}^{(k+1)}_{n-k}(\beta )=0$, a violation of the linear independence of ${\mathcal {P}}_{n+1}(x)$ and ${\mathcal {P}}^{(k+1)}_{n-k}(x)$.

Once it is established that ${\mathcal {P}}_{n}(x;\mu _k,\nu _k)$ and ${\mathcal {P}}_{n}(x)$ share some common zeros, the next goal is to find the location in the perturbed polynomial sequence that contains all of the common zeros.

Theorem 2.6

If $c_n$ and $\lambda _{n}$ are constants in (1.4), then the set of zeros of ${\mathcal {P}}_{n}(x)$ and $\mathcal {Q}_{n}(x)$ is the subset of the set of zeros of ${\mathcal {P}}_{2n+1}(x)$ and $\mathcal {Q}_{2n}(x)$, respectively.

Proof

For $c_n=c$ and $\lambda _n=\lambda$, we have $\textbf{T}_{i}= \begin{bmatrix} x-c &{} -\lambda x \\ 1 &{} 0 \end{bmatrix}, \forall ~i$. Hence, we can write

$$\begin{aligned} \textbf{T}_{n}\ldots \textbf{T}_{0}=\textbf{T}_{0}\ldots \textbf{T}_{n} =\begin{bmatrix} {\mathcal {P}}_{n+1}(x) &{} -\lambda x{\mathcal {P}}_{n}(x) \\ \mathcal {Q}_{n+1}(x) &{} -\lambda x\mathcal {Q}_{n}(x) \end{bmatrix}, \end{aligned}$$

where $\textbf{T}_{n}$ (or $\textbf{T}_{0}$) is given by

$$\begin{aligned} \textbf{T}_{n}=\begin{bmatrix} x-c &{} -\lambda x \\ 1 &{} 0 \end{bmatrix} =\begin{bmatrix} {\mathcal {P}}_{1}(x) &{} -\lambda x{\mathcal {P}}_{0}(x) \\ 1 &{} 0 \end{bmatrix} . \end{aligned}$$

Now, from (2.2), we obtain

$$\begin{aligned} \begin{bmatrix} {\mathcal {P}}_{2n+1}(x) &{} -\mathcal {Q}_{2n+1}(x)\\ {{\mathcal {P}}}_{2n}(x) &{} -{\mathcal {Q}}_{2n}(x) \end{bmatrix}&= (\textbf{T}_n \ldots \textbf{T}_{0}) \begin{bmatrix} {\mathcal {P}}_{n}(x) &{} -\mathcal {Q}_{n}(x) \\ {{\mathcal {P}}}_{n-1}(x) &{} -\mathcal {Q}_{n-1}(x) \end{bmatrix}. \end{aligned}$$

(2.19)

Therefore, from (2.19), we get

$$\begin{aligned} \begin{bmatrix} {\mathcal {P}}_{2n+1}(x) &{} -\mathcal {Q}_{2n+1}(x)\\ {{\mathcal {P}}}_{2n}(x) &{} -{\mathcal {Q}}_{2n}(x) \end{bmatrix}&= \begin{bmatrix} {\mathcal {P}}_{n+1}(x) &{} -\lambda x{\mathcal {P}}_{n}(x) \\ \mathcal {Q}_{n+1}(x) &{} -\lambda x\mathcal {Q}_{n}(x) \end{bmatrix} \begin{bmatrix} {\mathcal {P}}_{n}(x) &{} -\mathcal {Q}_{n}(x) \\ {{\mathcal {P}}}_{n-1}(x) &{} -\mathcal {Q}_{n-1}(x) \end{bmatrix}. \\ \Longrightarrow {\mathcal {P}}_{2n+1}(x)&= {\mathcal {P}}_{n}(x)[{\mathcal {P}}_{n+1}(x)-\lambda x {\mathcal {P}}_{n-1}(x)],\\ \mathcal {Q}_{2n}(x)&= \mathcal {Q}_{n}(x)[\mathcal {Q}_{n+1}(x)-\lambda x\mathcal {Q}_{n-1}(x)], \end{aligned}$$

which means ${\mathcal {P}}_{n}(x)$ is a factor of ${\mathcal {P}}_{2n+1}(x)$ and $\mathcal {Q}_{n}(x)$ is a factor of $\mathcal {Q}_{2n}(x)$ and the conclusion follows.

Proposition 2.1

The polynomials ${\mathcal {P}}_{n}(x;\mu _k)$ and ${\mathcal {P}}_{n}(x)$ share k zeros, that are identical to the zeros of ${\mathcal {P}}_{k}(x)$. Furthermore, the set of zeros of ${\mathcal {P}}_{k}(x)$ and $\mathcal {Q}_{k}(x)$ is the subset of the set of zeros of ${\mathcal {P}}_{2k+1}(x)$ and $\mathcal {Q}_{2k}(x)$, respectively, for $c_n=c$ and $\lambda _n=\lambda$.

Proof

The first part follows from Theorem 2.5. Proceeding as in the proof of Theorem 2.6, we obtain

$$\begin{aligned}&\displaystyle \begin{bmatrix} {\mathcal {P}}_{2k+1}(x;\mu _k) &{} -\mathcal {Q}_{2k+1}(x;\mu _k)\\ {{\mathcal {P}}}_{2k}(x;\mu _k) &{} -\mathcal {Q}_{2k}(x;\mu _k) \end{bmatrix}\\&\quad =\textbf{T}_{2k+1} \ldots \textbf{T}_{k+1} \textbf{T}_k(\mu _k,\nu _k=1) \begin{bmatrix} {\mathcal {P}}_{k}(x) &{} -\mathcal {Q}_{k}(x)\\ {{\mathcal {P}}}_{k-1}(x) &{} -{\mathcal {Q}}_{k-1}(x) \end{bmatrix} \\&\quad =\begin{bmatrix} {\mathcal {P}}_{k}(x) &{} -\lambda x{\mathcal {P}}_{k-1}(x) \\ \mathcal {Q}_{k}(x) &{} -\lambda x\mathcal {Q}_{k-1}(x) \end{bmatrix}(\textbf{T}_k+\textbf{N}_k) \begin{bmatrix} {\mathcal {P}}_{k}(x) &{} -\mathcal {Q}_{k}(x)\\ {{\mathcal {P}}}_{k-1}(x) &{} -{\mathcal {Q}}_{k-1}(x) \end{bmatrix}\\&\quad = \begin{bmatrix} {\mathcal {P}}_{k+1}(x)-\mu _k{\mathcal {P}}_{k}(x) &{} -\lambda x{\mathcal {P}}_{k}(x) \\ \mathcal {Q}_{k+1}(x)-\mu _k\mathcal {Q}_{k}(x) &{} -\lambda x\mathcal {Q}_{k}(x) \end{bmatrix} \begin{bmatrix} {\mathcal {P}}_{k}(x) &{} -\mathcal {Q}_{k}(x)\\ {{\mathcal {P}}}_{k-1}(x) &{} -{\mathcal {Q}}_{k-1}(x) \end{bmatrix}. \end{aligned}$$

This implies

$$\begin{aligned}&{\mathcal {P}}_{2k+1}(x;\mu _k) = {\mathcal {P}}_{k}(x)[{\mathcal {P}}_{k+1}(x)- \mu _k {\mathcal {P}}_{k}(x) -\lambda x{\mathcal {P}}_{k-1}(x)] \quad \text{ and } \\&\mathcal {Q}_{2k}(x;\mu _k) = \mathcal {Q}_{k}(x)[\mathcal {Q}_{k+1}(x)- \mu _k \mathcal {Q}_{k}(x) -\lambda x\mathcal {Q}_{k-1}(x)]. \end{aligned}$$

$\square$

Proposition 2.2

For some $n \ge k$, the $k-1$ zeros of ${\mathcal {P}}_{k-1}(x)$ are shared by the co-dilated polynomials ${\mathcal {P}}_{n}(x;\nu _k)$ and the polynomials ${\mathcal {P}}_{n}(x)$. Specifically, for $c_n=c$ and $\lambda _n=\lambda$, the set of zeros of ${\mathcal {P}}_{k-1}(x)$, $\mathcal {Q}_{k-1}(x)$, ${\mathcal {P}}_{k}(x)$ and $\mathcal {Q}_{k}(x)$ is the subset of the set of zeros of ${\mathcal {P}}_{2k-1}(x;\nu _k)$, $\mathcal {Q}_{2k-2}(x;\nu _k)$, ${\mathcal {P}}_{2k+1}(x;\nu _k)$ and $\mathcal {Q}_{2k}(x;\nu _k)$, respectively.

Proof

The first part is a direct consequence of Theorem 2.5. Using the conclusion of Theorem 2.4 and the technique presented in Theorem 2.6, we get

$$\begin{aligned}&\displaystyle \begin{bmatrix} {\mathcal {P}}_{2k-1}(x;\nu _k) &{} -\mathcal {Q}_{2k-1}(x;\nu _k)\\ {{\mathcal {P}}}_{2k-2}(x;\nu _k) &{} -{\mathcal {Q}}_{2k-2}(x;\nu _k) \end{bmatrix}\\&\quad = \textbf{T}_{2k-1} \ldots \textbf{T}_{k+1} \textbf{T}_k(\mu _k=0,\nu _k) \begin{bmatrix} {\mathcal {P}}_{k}(x) &{} -\mathcal {Q}_{k}(x)\\ {{\mathcal {P}}}_{k-1}(x) &{} -{\mathcal {Q}}_{k-1}(x) \end{bmatrix}\\&\quad =\begin{bmatrix} {\mathcal {P}}_{k-2}(x) &{} -\lambda x{\mathcal {P}}_{k-3}(x) \\ \mathcal {Q}_{k-2}(x) &{} -\lambda x\mathcal {Q}_{k-3}(x) \end{bmatrix}(\textbf{T}_k+\textbf{N}_k) \begin{bmatrix} {\mathcal {P}}_{k}(x) &{} -\mathcal {Q}_{k}(x)\\ {{\mathcal {P}}}_{k-1}(x) &{} -{\mathcal {Q}}_{k-1}(x) \end{bmatrix}\\&\quad = \begin{bmatrix} {\mathcal {P}}_{k-1}(x) &{} -\nu _k\lambda x{\mathcal {P}}_{k-2}(x) \\ \mathcal {Q}_{k-1}(x) &{} -\nu _k\lambda x\mathcal {Q}_{k-2}(x) \end{bmatrix} \begin{bmatrix} {\mathcal {P}}_{k}(x) &{} -\mathcal {Q}_{k}(x)\\ {{\mathcal {P}}}_{k-1}(x) &{} -{\mathcal {Q}}_{k-1}(x) \end{bmatrix}. \end{aligned}$$

This implies

$$\begin{aligned}&{\mathcal {P}}_{2k-1}(x;\nu _k) = {\mathcal {P}}_{k-1}(x) [{\mathcal {P}}_{k}(x)-\nu _k\lambda x{\mathcal {P}}_{k-2}(x)] \quad \text{ and }\\&\mathcal {Q}_{2k-2}(x;\nu _k) = \mathcal {Q}_{k-1}(x) [\mathcal {Q}_{k}(x)-\nu _k\lambda x\mathcal {Q}_{k-2}(x)]. \end{aligned}$$

The remaining part of the proposition follows along similar lines. $\square$

Remark 2.7

It should be noted that, for co-recursive polynomials, the set of zeros of ${\mathcal {P}}_{k-1}(x)$ is not contained in the set of zeros of ${\mathcal {P}}_{2k-1}(x;\mu _k)$. However, this fact holds for co-dilated polynomials (see Proposition 2.2). This is due to the fact that a similar calculation for co-recursive polynomials produces

$$\begin{aligned} {\mathcal {P}}_{2k-1}(x;\mu _k)&= {\mathcal {P}}_{k}(x)[{\mathcal {P}}_{k-1}(x)-\mu _k{\mathcal {P}}_{k-2}(x)] -\lambda x{\mathcal {P}}_{k-2}(x){\mathcal {P}}_{k-1}(x). \end{aligned}$$

We need the following result given in [17] to prove our next result.

Theorem 2.7

[17, Lemma 2.1] The zeros $x^{(n)}_j$, $j=1,2, \ldots n$ of ${\mathcal {P}}_n(x)$ are real, simple and positive. Assuming the ordering $x^{(n)}_{j-1} < x^{(n)}_{j}$, we have the interlacing property

$$\begin{aligned} 0< x^{(n+1)}_{1}< x^{(n)}_{1}<x^{(n+1)}_2<x^{(n)}_2< \cdots< x^{(n+1)}_{n}< x^{(n)}_{n} <x^{(n+1)}_{n+1}, \quad n \ge 1. \end{aligned}$$

Theorem 2.8

Let l be the number of non-common zeros between ${\mathcal {P}}_{n}(x;\mu _k)$ and ${\mathcal {P}}_{n}(x)$, $n \ge k$. Suppose $x^{(n)}_j(\mu )$ and $x^{(n)}_j$, $j=1,2, \ldots l$, are the zeros corresponding to ${\mathcal {P}}_{n}(x;\mu _k)$ and ${\mathcal {P}}_{n}(x)$. If $\mu < 0$, then

$$\begin{aligned} x^{(n)}_{1}(\mu )<x^{(n)}_{1}<x^{(n)}_{2}(\mu )< \cdots< x^{(n)}_{l-1}< x^{(n)}_l(\mu ) < x^{(n)}_{l}, \end{aligned}$$

(2.20)

where the role of the zeros $x^{(n)}_j(\mu )$ and $x^{(n)}_j$, $j=1,2, \ldots l$ gets intercharged when $\mu > 0$.

Proof

Since $n \ge k$, using (2.3), (2.4) and (2.5), we can write

$$\begin{aligned}&\begin{array}{|cc|} {\mathcal {P}}_{n+1}(x;\mu _k) &{} {\mathcal {P}}_{n+1}(x) \\ {\mathcal {P}}_{n}(x;\mu _k) &{} {\mathcal {P}}_{n}(x) \end{array} = |\textbf{T}_n \ldots \textbf{T}_{k+1}| \begin{vmatrix} {\mathcal {P}}_{k+1}(x)-\mu _k{\mathcal {P}}_{k}(x)&{\mathcal {P}}_{k+1}(x) \\ {\mathcal {P}}_{k}(x)&{\mathcal {P}}_{k}(x) \end{vmatrix}. \nonumber \\&\Longrightarrow \quad {\mathcal {P}}_{n}(x){\mathcal {P}}_{n+1}(x;\mu _k)-{\mathcal {P}}_{n}(x;\mu _k){\mathcal {P}}_{n+1}(x) = -\mu _k(\lambda _n \ldots \lambda _k)x^{n-k}{\mathcal {P}}^2_{k}(x). \end{aligned}$$

(2.21)

We have $(-1)^j {\mathcal {P}}_{n+1}(x^{(n)}_j)> 0$, $j=1,2, \ldots n$. Recall that $x^{(n)}_j$, $j=1,2, \ldots n$ are the n real zeros corresponding to ${\mathcal {P}}_{n}(x)$. First, consider the case when ${\mathcal {P}}_{n}(x;\mu _k)$ and ${\mathcal {P}}_{n}(x)$ have no common zeros. Now, when $\mu < 0$ and $\{\lambda _{n}\}_{n \ge 1}$ is a positive sequence of real numbers, From Theorem 2.7 and (2.21), we have $-{\mathcal {P}}_{n}(x^{(n)}_j;\mu _k){\mathcal {P}}_{n+1}(x^{(n)}_j) > 0$, which implies

$$\begin{aligned} (-1)^{j+1}{\mathcal {P}}_{n}(x^{(n)}_j;\mu _k) > 0, \quad j \ge 1. \end{aligned}$$

Since the number of real zeros of ${\mathcal {P}}_{n}(x;\mu _k)$ cannot exceed n and ${\mathcal {P}}_{n}(x^{(n)}_1;\mu _k) > 0$, (2.20) follows. For $\mu > 0$, a similar analysis leads to change of sign in (2.21) and subsequently, the result follows.

The case when ${\mathcal {P}}_{n}(x;\mu _k)$ and ${\mathcal {P}}_{n}(x)$ have common zeros is dealt with in a similar manner by excluding such common zeros.

Remark 2.8

In [6], a similar result was proved by transforming the $R_I$ type recurrence relation into a three-term Frobenius type recursion. However, our approach differs because we have not used the Delsarte-Genin mapping discussed in the aforementioned paper. Instead, we have used the positivity of zeros in L-orthogonal polynomials, as demonstrated in [17].

Theorem 2.9

Let $x^{(n)}_j$ and $x^{(n)}_j(\vec {\mu })$, $j=1,2,\ldots ,n$ be the zeros of ${\mathcal {P}}_{n}(x)$ and ${\mathcal {P}}_{n}(x;\vec {\mu })$, respectively, where $\vec {\mu }=(\mu _0,\ldots , \mu _{n-1})$. If $\mu _k > 0$ (or $<0$), $k=0,1,\ldots ,n-1$, then the zeros of ${\mathcal {P}}_{n}(x;\vec {\mu })$ are strictly increasing (or strictly decreasing) functions of $\mu _0,\ldots ,\mu _{n-1}$.

Proof

Let $x^{(n)}_j(\mu _0)$, $j=1,2,\ldots ,n$ be the zeros of ${\mathcal {P}}_{n}(x;\mu _0)$. Then, applying Theorem 2.8 and assuming $\mu _0 > 0$, we get

$$\begin{aligned} x^{(n)}_j < x^{(n)}_j(\mu _0), \quad j=1,2,\ldots ,n. \end{aligned}$$

Now, considering ${\mathcal {P}}_{n}(x;\mu _0)$ as a new sequence of $\mathcal {R}_{I}$ polynomials and perturbing $c_1$ by $\mu _1 > 0$, we have the polynomials ${\mathcal {P}}_{n}(x;\mu _0,\mu _{1})$ whose zeros are $x^{(n)}_j(\mu _0,\mu _{1})$, $j=1,2,\ldots ,n$. Again, applying Theorem 2.8, we obtain

$$\begin{aligned} x^{(n)}_j(\mu _0) < x^{(n)}_j(\mu _0, \mu _1), \quad j=1,2,\ldots ,n. \end{aligned}$$

Repeating same process $n-2$ times, we have

$$\begin{aligned} x^{(n)}_j(\mu _0)< x^{(n)}_j(\mu _0, \mu _1)< \cdots < x^{(n)}_j(\mu _0,\ldots , \mu _{n-1}) \quad j=1,2,\ldots ,n. \end{aligned}$$

To show that the zeros of ${\mathcal {P}}_{n}(x;\vec {\mu })$ are increasing functions of $\mu _k$, $k=0,1,\ldots ,n-1$, we will replace $\mu _k$ by $\mu _k+\epsilon _k$, $\epsilon _k > 0$, $k=0,1,\ldots ,n-1$ and establish that $x^{(n)}_j(\vec {\mu }) < x^{(n)}_j(\vec {\mu },\vec {\epsilon })$, $j=1,2,\ldots ,n$, where $\vec {\epsilon }=(\epsilon _0,\ldots ,\epsilon _{n-1})$ and $x^{(n)}_j(\vec {\mu },\vec {\epsilon })$ be the zeros of polynomial ${\mathcal {P}}_{n}(x;\vec {\mu }, \vec {\epsilon })$. First of all, replacing $\mu _0$ by $\mu _0+\epsilon _0$, the polynomials ${\mathcal {P}}_{n}(x;\vec {\mu }, \epsilon _0)$ are obtained. Proceeding as per the proof of Theorem 2.8, it can be shown that

$$\begin{aligned} x^{(n)}_j(\vec {\mu }) < x^{(n)}_j(\vec {\mu }, \epsilon _0), \quad j=1,2,\ldots ,n. \end{aligned}$$

where $x^{(n)}_j(\vec {\mu }, \epsilon _0)$, $j=1,2,\ldots ,n$ are the zeros of ${\mathcal {P}}_{n}(x;\vec {\mu }, \epsilon _0)$. Further, let $x^{(n)}_j(\vec {\mu }, \epsilon _0, \epsilon _1)$, $j=1,2,\ldots ,n$ be the zeros of polynomial ${\mathcal {P}}_{n}(x;\vec {\mu }, \epsilon _0, \epsilon _1)$ obtained on replacing $\mu _1$ by $\mu _1+\epsilon _1$. From Theorem 2.8, we get

$$\begin{aligned} x^{(n)}_j(\vec {\mu }, \epsilon _0) < x^{(n)}_j(\vec {\mu }, \epsilon _0, \epsilon _1), \quad j=1,2,\ldots ,n. \end{aligned}$$

Using similar argument, we conclude that

$$\begin{aligned} x^{(n)}_j(\vec {\mu })< x^{(n)}_j(\vec {\mu }, \epsilon _0)< x^{(n)}_j(\vec {\mu }, \epsilon _0, \epsilon _1),< \cdots < x^{(n)}_j(\vec {\mu },\vec {\epsilon }) \quad j=1,2,\ldots ,n, \end{aligned}$$

(2.22)

and the proof is complete.

Corollary 2.2

Let $x^{(n)}_j(\mu _k,\mu _{k+1})$, $j=1,2,\ldots ,n$ be the zeros of ${\mathcal {P}}_{n}(x;\mu _k,\mu _{k+1})$ with $\mu _k>0$ and $\mu _{k+1}>0$ obtained by perturbing two consecutive recurrence coefficients. Then for fixed j and $n \ge k$, $x^{(n)}_j(\mu _k,\mu _{k+1})$ are strictly increasing functions of $\mu _k$ and $\mu _{k+1}$. Similarly, the zeros of ${\mathcal {P}}_{n}(x;\mu _k,\mu _{k+1})$ are strictly decreasing functions of $\mu _k$ and $\mu _{k+1}$ whenever $\mu _k<0$ and $\mu _{k+1}<0$.

2.8 Perturbation in the Chain Sequence and Carathéodary Function

Recurrence relation of the form

$$\begin{aligned} {\mathcal {P}}_{n+1}(z) = ((1+i\beta _{n+1})z+(1-i\beta _{n+1})){\mathcal {P}}_{n}(z)- 4d_{n+1}z{\mathcal {P}}_{n-1}(z), \end{aligned}$$

(2.23)

with initial conditions ${\mathcal {P}}_0(z) = 1$ and ${\mathcal {P}}_1(z) = (1+i\beta _{1})z+(1-i\beta _{1})$ are studied extensively in [6, 9] to cite a few. The existence of a unique non-trivial probability measure supported on the unit disc is known since the classical work of Delsarte and Genin, and has recently been revisited using a different technique, i.e., using Markov’s theorem, in [8]. Further, when $\{\beta _n\}_{n=1}^\infty$ is a sequence of real numbers, we have

$$\begin{aligned} \varphi _0(z)=1, \quad \varphi _{n}(z)\prod _{k=1}^{n}(1+i\beta _{k})={\mathcal {P}}_{n}(z)-2(1-m_n){\mathcal {P}}_{n-1}(z), \end{aligned}$$

(2.24)

as the corresponding sequence of monic OPUC where $\{m_n\}_{n=1}^\infty$ is the minimal parameter sequence of the chain sequence $\{d_{n+1}\}_{n=1}^\infty$. Perturbation of co-recursive type in $\beta _n$ is investigated in [6] from the view point of interlacing properties and some new inequalities involving zeros are derived. Note that, under certain restrictions, (2.23) can be viewed as a special case of (1.1). The polynomials ${\mathcal {P}}_{n+1}(z)$ generated by (2.23) are called the para-orthogonal polynomials on the unit circle (POPUC), and the most general results related to zeros of POPUC can be found in [7, 13]. This section aims to study the co-dilation in (2.23) and we will see how a perturbation in the chain sequence $\{d_{n+1}\}_{n \ge 1}$ leads to some interesting consequences in function theory and orthogonal polynomials.

The Hermitian Perron-Carathéodary fractions, or HPC-fractions, arising in the study of the connection between the Szegő polynomials and the continued fractions are given as

(2.25)

and are completely determined by $\delta _{n} \in \mathbb {C}$, where $\delta _{0} \ne 0$ and $\delta _{n} \ne 1$, $n \ge 1$. When $\delta _{0} > 0$ and $|\delta _{n}| < 1$, $n \ge 1$, (2.25) is known as the positive PC fraction (PPC-fraction). Then $\phi _n(z)$ are the odd ordered denominators $\mathcal {Q}_{2n+1}(z)$ and $\phi ^*_n(z)$ are the even ordered denominators $\mathcal {Q}_{2n}(z)$, where $\mathcal {Q}_n(z)$, a polynomial of degree n, is the denominator of $n^{th}$ approximant of PPC-fraction [27]. Having set $\delta _{n}=\phi _n(0)$ as reflection coefficients, the following are the recurrence relations for Szegő polynomials

$$\begin{aligned} \phi ^*_n(z)&= \bar{\delta }_n z\phi _{n-1}(z)+\phi ^*_{n-1}(z), \\ \phi _n(z)&= \delta _n\phi ^*_{n}(z)+(1-|\delta _n|^2)z\phi _{n-1}(z), \quad n \ge 1. \end{aligned}$$

Under the condition

$$\begin{aligned} \delta _{n+1}\delta _{n}=\delta _{n+1}-\delta _{n}, \quad \delta _{0} > 0 ~ \text {and} ~ |\delta _{n}| < 1 , \quad n \ge 1, \end{aligned}$$

(2.26)

the chain sequence $\{d_{n+1}\}_{n \ge 1}$ is such that $d_{n+1}=(1-m_n)m_{n+1}$, where $m_{n}=(1-\delta _n)/2$, $n \ge 1$, is the minimal parameter sequence, i.e.,

$$\begin{aligned} d_{n+1}=\dfrac{1}{4}(1+\delta _{n})(1-\delta _{n+1})=\dfrac{1}{4}(1-2\delta _{n}\delta _{n+1}). \end{aligned}$$

(2.27)

A sequence of para-orthogonal polynomials satisfying

$$\begin{aligned} {\mathcal {P}}_{n+1}(z)&= (z+1){\mathcal {P}}_n(z)-4d_{n+1}z{\mathcal {P}}_{n-1}(z), \quad n \ge 1, \end{aligned}$$

(2.28)

with initial conditions ${\mathcal {P}}_0(z)=1$ and ${\mathcal {P}}_1(z)=z+1$ has been obtained in [3, Proposition 3.1] together with a sequence of Szegő polynomials $\phi _n(z)$ having $\delta _{n} \in \mathbb {R}$ as the reflection coefficients and satisfying (2.26). The Carathéodary function

$$\begin{aligned} \mathcal {C}(z)= \dfrac{1+(1-2\sigma )z}{1-z}, \quad |z|< 1, \quad 0< \sigma <1, \end{aligned}$$

corresponds to a PPC-fraction with the parameter $\delta _n = -\frac{1}{n+\frac{\sigma }{1-\sigma }}$ obeying (2.26).

Now, from (2.27), we have

$$\begin{aligned} \delta _{n+1}= \dfrac{1-4d_{n+1}}{2\delta _{n}}. \end{aligned}$$

Therefore, from the sequence $\{d_{n+1}\}_{n \ge 1}$, the sequence $\{\delta _{n} \}_{n \ge 0}$ can be completely determined. Perturbing (2.28) as (1.9) such that the new sequence $\{d'_{n+1}\}_{n \ge 1}$ is again a positive chain sequence, we get a new sequence of the Szegő polynomials, say $\hat{\phi }_n(z)$ with $\{\hat{\delta }_{n}\}_{n \ge 0}$ as the reflection coefficients. Suppose that the perturbation is for $n=k$, then $d'_{k+1}= \nu _{k+1}d_{k+1}$ and

$$\begin{aligned} \hat{\delta }_{k+1} =\dfrac{1-4d'_{k+1}}{2\hat{\delta }_{k}} = \dfrac{1-4\nu _{k+1}d_{k+1}}{2\hat{\delta }_{k}} ~ \text {and} ~ \hat{\delta }_{n+1} =\dfrac{1-4d_{n+1}}{2\hat{\delta }_{n}}, \quad n > k. \end{aligned}$$

With these $\hat{\delta }_{n}$’s as the parameters of a PPC-fraction, there corresponds a Carathéodary function, say $\mathcal {\hat{C}}(z)$. Observe that the structure of $\mathcal {\hat{C}}(z)$ depends on the choice of $\nu _{k+1}$ and the level at which perturbation is done. This makes it difficult to determine exact form of $\mathcal {\hat{C}}(z)$. However, for some particular cases, we can find its precise form. One such choice is proposed in the next result by summarizing the above details.

Proposition 2.3

Consider the sequence $\{\delta _{n} \}_{n \ge 0}$ of reals under the restriction $\delta _{n+1}\delta _{n}=\delta _{n+1}-\delta _{n}$, $\delta _{0} > 0$ and $|\delta _{n}| < 1$, $n \ge 1$. If $\mathcal {C}(z)$ is the Carathéodory function whose PPC-fraction can be obtained from $\delta _n$, then $\hat{\delta }_{n}$ given as

$$\begin{aligned} \hat{\delta }_{n+1}&= \delta _{n+1}, \hspace{7.9cm} n < k, \\ \hat{\delta }_{k+1}&= \delta _{k+1}+\dfrac{2(1-\nu _{k+1})d_{k+1}}{\delta _{k}}\, , \quad \hat{\delta }_{n+1} =\dfrac{1-4d_{n+1}}{2\hat{\delta }_{n}}, \quad n > k, \end{aligned}$$

gives the PPC-fraction corresponding to Carathéodary function $\mathcal {\hat{C}}(z)$. Further, if $\nu _{k+1}=\dfrac{1+2\delta _{k}\delta _{k+1}}{1-2\delta _{k}\delta _{k+1}}$, then $\hat{\delta }_{k+1}=-\delta _{k+1}$, $n \ge k$. In particular, if $\nu _{2}=\dfrac{1+2\delta _{1}\delta _{2}}{1-2\delta _{1}\delta _{2}}$, then $\hat{\delta }_{n}=-\delta _{n}=\dfrac{1}{n+\frac{\sigma }{1-\sigma }}$, $n \ge 1$ and the corresponding Carathéodary function is given by $1/\mathcal {C}(z)$.

The OPUC with $\{-\delta _{n} \}_{n \ge 0}$ as reflection coefficients and corresponding Carathéodary function has been studied in [39].

3 Illustrative Examples

Example 3.1

Consider the sequence of $R_I$ polynomials generated by the recurrence

$$\begin{aligned} {\mathcal {P}}_{n+1}(z) = \left( z-\dfrac{b-c-n}{b+n}\right) {\mathcal {P}}_{n}(z) -\dfrac{n(n+c-1)}{(b+n-1)(b+n)}z{\mathcal {P}}_{n-1}(z), \end{aligned}$$

(3.1)

with initial conditions ${\mathcal {P}}_{0}(z) = 1$ and ${\mathcal {P}}_1(z) = z-\dfrac{b-c}{b}$.

If $(a)_n$ is the pochhammer symbol and F represents the Gaussian hypergeometric function, use of the contiguous relation

$$\begin{aligned} (c-a)F(a-1,b;c;z)&=(c-2a-(b-a)z)F(a,b;c;z)+a(1-z)\\&\quad \quad F(a+1,b;c;z), \end{aligned}$$

shows that the monic polynomial

$$\begin{aligned} {\mathcal {P}}_{n}(z) = \dfrac{(c)_n}{(b)_n}F(-n,b;c;1-z), \end{aligned}$$

satisfies (3.1) [46]. For $b= \eta +1$ and $c= 2\eta +2$ with $\eta > -1/2$, (3.1) reduces to

$$\begin{aligned} {\mathcal {P}}_{n+1}(z) = (z+1){\mathcal {P}}_{n}(z)-\dfrac{n(2\eta +n+1)}{(\eta +n)(\eta +n+1)}z {\mathcal {P}}_{n-1}(z), \end{aligned}$$

which is of the form (2.23) with $\beta _{n}=0$.

3.1 Co-recursion

It can be easily verified that, for $\eta =0$, the solution of the recurrence

$$\begin{aligned}&{\mathcal {P}}_{n+1}(z) = (z+1){\mathcal {P}}_{n}(z)-z {\mathcal {P}}_{n-1}(z), \end{aligned}$$

(3.2)

is given by

$$\begin{aligned} {\mathcal {P}}_{n}(z)=\dfrac{z^{n+1}-1}{z-1}, \quad n \ge 0. \end{aligned}$$

(3.3)

Now, let us make a perturbation at the beginning of the sequence. If $\mu > 0$, we write ${\mathcal {P}}_1(z) = z+1-\mu$. Consequently, we have

$$\begin{aligned} {\mathcal {P}}_{n+1}(z;\mu ) = {\mathcal {P}}_{n+1}(z)-\mu {\mathcal {P}}_{n}(z). \end{aligned}$$

Note that this is the case for perturbation for $k=0$. Therefore, ${\mathcal {P}}_{0}(z)=1$ and ${\mathcal {P}}^{(0)}_{n}(z)={\mathcal {P}}_{n}$ produce the above relation. If $\mu = 1$, then

$$\begin{aligned} {\mathcal {P}}_{n+1}(z;1)&= {\mathcal {P}}_{n+1}(z)-{\mathcal {P}}_{n}(z) = z^{n+1} . \end{aligned}$$

The polynomial ${\mathcal {P}}_{n+1}(z;1)$ satisfies (3.2) but with perturbed initial conditions ${\mathcal {P}}_{0}(z;1) = 1$, ${\mathcal {P}}_1(z;1) = z$, which shows the validity of our results in Theorem 2.1.

3.2 Co-dilation and Chain Sequences

In this part, we will see the effect of the co-dilation in the chain sequence on the corresponding parameter sequences, Szegő polynomials, reflection coefficients, and associated measures. For $\eta > -1/2$, the positive chain sequence $\{d_{n+1} \}_{n \ge 1}$, where

$$\begin{aligned} d_{n+1}= \dfrac{1}{4} \dfrac{n(2\eta +n+1)}{(\eta +n)(\eta +n+1)}, \end{aligned}$$

has minimal parameter sequence $\{m_{n} \}_{n \ge 0}$, where $m_n=\dfrac{n}{2(\eta +n+1)}$ and a maximal parameter sequence $\{M_{n} \}_{n \ge 0}$, where $M_n=\dfrac{2\eta +n}{2(\eta +n)}$, which makes $\{d_{n+1} \}_{n \ge 1}$ non-SPPCS [4]. Clearly, for $\eta =0$, $\{d_{n+1}=1/4 \}_{n \ge 1}$ is not an SPPCS and its minimal and maximal parameter sequences are given as

$$\begin{aligned} m_{n}=\dfrac{n}{2n+2}, \quad n \ge 0, \quad \textrm{and} \quad M'_{n}=\dfrac{1}{2}, \quad n \ge 0. \end{aligned}$$

The corresponding para-orthogonal polynomials are

$$\begin{aligned} {\mathcal {P}}_n(z)=\dfrac{z^{n+1}-1}{z-1}, \quad n \ge 0, \end{aligned}$$

and hence, the monic OPUC is given by

$$\begin{aligned} \phi _{n}(z)=\dfrac{(n+1)z^{n}+nz^{n-1}+(n-1)z^{n-2}+\ldots +2z+1}{n+1}, \quad n \ge 0, \end{aligned}$$

with $\gamma _{n-1}=-\dfrac{1}{n+1}$ as reflection coefficients and $d\mu (z) = \dfrac{|z-1|^2}{4i\pi z}dz$ as the measure of orthogonality [26].

Consider the co-dilated chain sequence $\{1/2, 1/4, 1/4, \ldots \}$ that results from multiplication of 2 in the first term of the chain sequence $\{1/4, 1/4, 1/4, \ldots \}$. The co-dilated chain sequence is an SPPCS as it is known to have a minimal parameter sequence $\{k'_{n} \}_{n \ge 0}$, where $k'_{0}=0$ and $k'_{n}=1/2$, $n \ge 1$, which is also the maximal parameter sequence. So, from (2.23), the para-orthogonal polynomials in this case are obtained as

$$\begin{aligned} \tilde{{\mathcal {P}}}_n(z)&=z^n+1, \quad n \ge 1. \end{aligned}$$

The reflection coefficients are zero and $\tilde{\phi }_{n}(z)= z^n$ are the Szegő-Chebyshev polynomials with respect to standard Lebesgue measure.

3.3 Behaviour of Zeros

Example 3.2

Let us consider the specialized $R_{I}$ type recurrence relation (1.4) with $c_n = \dfrac{c+n}{a-n-1}$, $n \ge 0$ and $\lambda _n =\dfrac{n(c+n-a)}{(a-n-1)(a-n)}$, $n \ge 1$.

With these values, we have

$$\begin{aligned} {\mathcal {P}}^{(a,c)}_{n+1}(x) = \left( x-\dfrac{c+n}{a-n-1}\right) {\mathcal {P}}^{(a,c)}_n(x)- \dfrac{n(c+n-a)}{(a-n-1)(a-n)} x{\mathcal {P}}^{(a,c)}_{n-1}(x), \quad n\ge 1, \end{aligned}$$

(3.4)

where ${\mathcal {P}}^{(a,c)}_{n}(x)$ are the orthogonal Laurent Jacobi polynomials considered in [18]. It is important to remark some recent contributions especially [28, 29] regarding distribution of zeros of q- Leguerre polynomials and some new hypergeometric type functions. With ${\mathcal {P}}^{(a,c)}_{-1}(x)=0$ and ${\mathcal {P}}^{(a,c)}_{0}(x)=1$, we get the monic polynomials

$$\begin{aligned} {\mathcal {P}}^{(a,c)}_n(x) = \dfrac{(c)_n}{(1-a)_n}F(-n,1-a,1-c-n;x). \end{aligned}$$

It was shown [18] that $c_n$ and $\lambda _n$ are positive when $c>a>N$ or $a<c<1-N$, $n=1,2, \ldots N-1$. This example is used to investigate the behaviour of zeros for the following two cases:

Case I $c>a>N$ and $\mu _k < 0$.

Perturbing the recurrence coefficient $c_n$ such that $c_4 \rightarrow c_4+\mu _4$, where $\mu _4 = -2$ generates a new sequence of polynomials ${\mathcal {P}}_{n}(x;-2)$. Note that ${\mathcal {P}}_{6}(x)$ and ${\mathcal {P}}_{6}(x;-2)$ have no common zeros as shown in Table 2. Clearly, these zeros satisfy the interlacing property in accordance with Theorem 2.8 (see Fig. 2). All the calculations are performed and figures are drawn using Mathematica on a system with an Intel Core i3-6006U CPU @ 2.00 GHz and 8 GB of RAM.

Fig. 2

Zeros of ${\mathcal {P}}_{6}(x)$ (red diamonds) and ${\mathcal {P}}_{6}(x;-2)$ (blue circles) with parameter values $a=11$ and $c=12$. (Color figure online)

Case II $a<c<1-N$ and $\mu _k > 0$.

For this purpose, the recurrence coefficient $c_3$ is perturbed as $c_3 \rightarrow c_3+0.5$, resulting in a new sequence of polynomials ${\mathcal {P}}_{5}(x;0.5)$. The zeros of ${\mathcal {P}}_{5}(x)$ and ${\mathcal {P}}_{5}(x;0.5)$ are listed in Table 3. Now let us look (see Fig. 3) at the location of these zeros. The results follows Theorem 2.8.

Table 2 Zeros of $\mathcal {P}_{6}(x)$ and $\mathcal {P}_{6}(x;\mu _4=-2)$

Table 3 Zeros of $\mathcal {P}_{5}(x)$ and $\mathcal {P}_{5}(x;\mu _3=0.5)$

Fig. 3

Zeros of ${\mathcal {P}}_{5}(x)$ (red diamonds) and ${\mathcal {P}}_{5}(x;0.5)$ (blue circles) with parameter values $a=-12$ and $c=-10$. (Color figure online)

To illustrate Corollary 2.2, the recurrence relation satisfied by L-Jacobi polynomials (3.4) is taken into consideration.

Case I $\mu _k > 0$ and $\mu _{k+1}>0$.

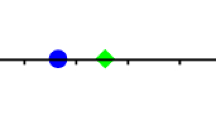
The zeros of perturbed L-Jacobi polynomials ${\mathcal {P}}_{5}(x;\mu _3=0.3,\mu _4=0.4)$ obtained by perturbing two successive terms $c_3$ and $c_4$ are listed in Table 4. These zeros are represented by blue circles in Fig. 4. Now, take $\mu '_k > \mu _k$ and $\mu '_{k+1} > \mu _{k+1}$. The zeros of ${\mathcal {P}}_{5}(x;\mu '_3=0.5,\mu '_4=0.6)$ are plotted with green diamonds. The following point plot states the validity of our result for this case.

Table 4 Zeros of $\mathcal {P}_{5}(x)$, $\mathcal {P}_{5}(x;\mu _3=0.3,\mu _4=0.4)$ and $\mathcal {P}_{5}(x;\mu '_3=0.5, \mu '_4=0.6)$

Case II $\mu _k < 0$ and $\mu _{k+1}<0$.

The zeros of initial L-Jacobi polynomials ${\mathcal {P}}_{6}(x)$ and perturbed ones, i.e., ${\mathcal {P}}_{6}(x;\mu _4=-0.2,\mu _5=-0.25)$ (blue circles) and ${\mathcal {P}}_{6}(x;\mu '_4=-0.7,\mu '_5=-0.8)$ (green diamonds) are plotted in Fig. 5 and given in Table 5. Observe that the result holds in this case as well.

Fig. 4

Zeros of ${\mathcal {P}}_{5}(x;0.3,0.4)$ (blue circles) and ${\mathcal {P}}_{5}(x;0.5,0.6)$ (green diamonds) with parameter values $a=-12$ and $c=-10$. (Color figure online)

Fig. 5

Zeros of ${\mathcal {P}}_{6}(x;-0.2,-0.25)$ (blue circles) and ${\mathcal {P}}_{6}(x;-0.7,-0.8)$ (green diamonds) with parameter values $a=11$ and $c=12$. (Color figure online)

Table 5 Zeros of $\mathcal {P}_{6}(x)$, $\mathcal {P}_{6}(x;\mu _4=- 0.2,\mu _5=-0.25)$ and $\mathcal {P}_{6}(x;\mu '_4=-0.7,\mu '_5=-0.8)$

3.4 Note

Table 6 Zeros of $\mathcal {P}_{6}(x)$ and $\mathcal {P}_{6}(x;\mu _3=-0.5,\nu _3=2.5)$

It has been shown that zeros of co-recursive $R_I$ polynomials and unperturbed polynomials exhibit nice interlacing and monotonicity properties. However, this may not hold in the case of co-modified polynomials. The zeros of ${\mathcal {P}}_{6}(x)$ and ${\mathcal {P}}_{6}(x;-0.5,2.5)$ are listed in Table 6 when a perturbation $c_3 \rightarrow c_3-0.5$ and $\lambda _{3} \rightarrow 2.5\times \lambda _{3}$ is made. Clearly, the zeros do not show any kind of interlacing for this case (see Fig. 6). Similarly, one can check that co-dilated $R_I$ polynomials do not have such a relationship with the unperturbed ones.

Fig. 6

Zeros of ${\mathcal {P}}_{6}(x)$ (red diamonds) and ${\mathcal {P}}_{6}(x;-0.5,2.5)$ (blue circles) with parameter values $a=11$ and $c=12$. (Color figure online)

Remark 3.1

This observation raises the question about the assumptions on $\mu _k$ and $\nu _k$ to be made such that the co-modified (or co-dilated) $R_I$ polynomials do show some interlacing with the unperturbed polynomials. Although, this subject is not dealt with in this manuscript and attracts further research. An idea to proceed in this direction can be found out in [34, 35]

3.5 Open Problem

In Sect. 2.1 and Sect. 2.7, the behaviour of zeros has been discussed for a particular case when $a_n=0$, $c_n \ge 0,$ and $\lambda _{n} > 0$ in recurrence relation (1.1), which corresponds to the L-orthogonal polynomials. It would be interesting to investigate the behaviour of the zeros for the case $a_n \ne 0$. More precisely, we want to know what conditions to impose on the nonzero parameters $a_n$, $\lambda _{n}$, and $c_n$ so that the zeros of the corresponding orthogonal polynomials lie on the real line and then investigate the interlacing relation between the perturbed and the original $R_I$ polynomials. At present, no concrete example is available in the literature for the case $a_n \ne 0$, and results for obtaining these conditions are still open, which, if found, will provide interesting consequences. A potential solution to address these situations can be discovered in [8].