On the 4-Flow Nullity of Graphs

Abstract

The k-flow nullity $n_k(G)$ of a graph G is the minimum number n for which G admits a k-flow $(D,\psi )$ such that there are exactly n edges e with $\psi (e)=0$. Let X and Y be two subgraphs of G. It is proved that $n_4(X\cup Y)\le n_4(X)+n_4(Y)$ if $|E(X)\cap E(Y)|=4$ and the subgraph of G induced by $E(X)\cap E(Y)$ is a connected graph which is not a tree with 2 or 3 leaves.

1 Introduction

All graphs considered are finite and undirected with no loops, possibly with multiple edges. Let G be a graph with vertex set V(G) and edge set E(G). An orientation D of G is an assignment of a direction to each edge of G. For a vertex $v\in V(G)$, we use $D^{+}(v)$ (resp. $D^{-}(v)$) to denote the set of edges of G being endowed orientation with tail (resp. head) at v. Let $\psi$ be an integer valued function on E(G). If $\sum _{e\in D^{+}(v)}\psi (e)=\sum _{e\in D^{-}(v)}\psi (e)$ for every $v\in V(G)$ and $\max \{|\psi (e)|:e\in E(G)\}<k$ for a given positive integer k, then we call $(D, \psi )$ a k-flow of G.

For every k-flow $(D, \psi )$ of G, we call $\textrm{supp}\,\psi :=\{e\in E(G):\psi (e)\ne 0\}$ the support of $\psi$. If $\textrm{supp}\,\psi =E(G)$, then $(D, \psi )$ is said to be nowhere-zero. The k-flow nullity $n_k(G)$ of G is defined as

$$\begin{aligned} n_k(G)=\min \{|E(G)|-|\textrm{supp}~\psi |:(D, \psi )~\text{ is } \text{ a }~k\text{-flow } \text{ of }~G\}. \end{aligned}$$

It is obvious that there is a nowhere-zero k-flow of G if and only if $n_k(G)=0$. For convenience, we specify that the k-flow nullity of an empty graph is 0.

The concept of flows of graphs was introduced by Tutte [9] who discerned the close relationship between nowhere-zero 4-flows of planar graphs and the 4-color conjecture. Subsequently, he proposed three conjectures: the 5-flow [9], 4-flow [10], and 3-flow [1] conjectures. Despite plenty of researches on these conjectures, all of them remain unsolved so far. Using the concept of k-flow nullity, these conjectures are stated as follows: $n_5(G)=0$ if G is a 2-edge-connected graph; $n_4(G)=0$ if G is a 2-edge-connected graph which can not be contracted to the Petersen graph; $n_3(G)=0$ if G is a 4-edge-connected graph.

The best result close to the 5-flow conjecture is that $n_6(G)=0$ for all 2-edge-connected graphs G (proved by Seymour in [7]). In [5], Jaeger proved that $n_4(G)=0$ for every 4-edge-connected graph G and conjectured that $n_3(G)=0$ if G is k-edge-connected for a given k. In [8], Thomassen verified Jaeger’s conjecture by proving that $n_3(G)=0$ provided G is 8-edge-connected. This result was soon extended to 6-edge-connected graphs by Lovász et al. [6]. We refer readers to the monograph [11] by Zhang for more about integer flows.

Consider two subgraphs X and Y of a graph G. The union $X\cup Y$ of X and Y is the graph defined as follows: $V(X\cup Y)=V(X)\cup V(Y)$ and $E(X\cup Y)=E(X)\cup E(Y)$. The intersection $X\cap Y$ of X and Y is the induced subgraph $G[E(X)\cap E(Y)]$. Note that $X\cap Y$ is the empty graph with no vertices if $E(X)\cap E(Y)=\emptyset$. Let G/X be the graph obtained from G by using edge contraction operation to all edges of X and removing all resulting loops. In [2], Catlin proved that if X is a cycle of length at most 4 and $n_4(G/X)=0$, then $n_4(G)=0$. This result implies the following theorem (see also [11, Lemma 3.8.11]).

Theorem 1.1

Let $G=X\cup Y$ where X is a cycle of length at most 4 and $n_4(Y)=0$. Then $n_4(G)=0$.

The above theorem was generalized by the second author and Lu [12] as follows.

Theorem 1.2

Let $G=X\cup Y$ where $n_4(X)=n_4(Y)=0$. Suppose that $|E(X\cap Y)|\le 3$ and $X\cap Y$ is connected if $|E(X\cap Y)|=3$. Then $n_4(G)=0$.

Very recently, the authors [4] proved the following proposition.

Proposition 1.3

Let $G=X\cup Y$ where $n_4(X)=n_4(Y)=0$. Suppose that $|E(X\cap Y)|=3$ and $X\cap Y$ has parallel edges. Then $n_4(G)=0$.

Our main result in this paper is the following theorem which can be seen as a further generalization of Theorem 1.1.

Theorem 1.4

Suppose that G has two subgraphs X and Y satisfying one of the following three conditions:

• (i) $|E(X\cap Y)|\le 2$;

• (ii) $|E(X\cap Y)|=3$ and $X\cap Y$ is connected or $X\cap Y$ admits parallel edges;

• (iii) $|E(X\cap Y)|=4$, $X\cap Y$ is connected and $X\cap Y$ is not a tree with 2 or 3 leaves.

Then $n_4(X\cup Y)\le n_4(X)+n_4(Y)$.

Now, we describe the structure of the paper. In Sect. 2, we introduce the concepts of parity subgraphs and evenly spanning subgraphs which are important tools for dealing with 4-flow problems. In particular, we prove a result (Theorem 2.2) on evenly spanning subgraphs which plays a key role in proving Theorem 1.4. In Sect. 3, we show that $n_4(X\cup Y)=0$ if $n_4(X)=n_4(Y)=0$ and the condition (iii) in Theorem 1.4 holds. In Sect. 4, based on Theorem 1.2 and the result in Sect. 3, we give a proof of Theorem 1.4.

2 Parity Subgraphs and Evenly Spanning Subgraphs

Let G be a graph. The degree $\textrm{deg}_{G}(v)$ of a vertex $v\in V(G)$ is the number of edges of G incident with v. If $\textrm{deg}_{G}(v)$ is odd (resp. even), then v is called an odd (resp. even) vertex of G. By O(G) (resp. ${\bar{O}}(G)$), we denote the set of all odd (resp. even) vertices of G. If ${\bar{O}}(G)=V(G)$, then G is said to be even. A cycle is a connected graph of which every vertex is of degree 2. In particular, it is called a k-cycle if the number of its edges is k. Note that every k-cycle is a simple graph except the 2-cycle.

Let H be a subgraph of G. Set $O_{G}(H):=V(H)\cap O(G)$ and ${\bar{O}}_{G}(H):=V(H)\cap {\bar{O}}(G)$. For convenience, we write $\textrm{deg}_{H}(v)=0$ for all $v\in V(G){\setminus } V(H)$. We call H a parity subgraph of G if $V(H)=V(G)$ and $\textrm{deg}_{G}(v)- \textrm{deg}_{H}(v)$ is an even integer for each vertex $v\in V(G)$. If H is even, $V(H)=V(G)$ and $|O_{G}(K)|$ is an even integer for every connected component K of H, then we call H an evenly spanning subgraph of G.

The first lemma of this section describes the relationship between parity subgraphs and evenly spanning subgraphs.

Lemma 2.1

(Celmins [3]) A subgraph H of a graph G is an evenly spanning subgraph if and only if G has two parity subgraphs X and Y such that $H=X\cup Y$ and $E(X)\cap E(Y)=\emptyset$.

The symmetric difference $X\ominus Y$ of two subgraphs X and Y of a graph G is the subgraph obtained from $X\cup Y$ by removing all edges of $X\cap Y$. Clearly, $X\ominus Y$ is even if X and Y are both even.

The theorem below plays a key role in proving Theorem 1.4.

Theorem 2.2

Let $G=X\cup Y$. Suppose that X has an evenly spanning subgraph $X^{*}$ and Y has an evenly spanning subgraph $Y^{*}$. Let $G^{*}$ be an even subgraph of G such that $E(X^{*}\ominus Y^{*})\subseteq E(G^{*})\subseteq E(X^{*}\cup Y^{*})$. If $V(X\cap Y)$ is contained in a connected component of $G^{*}$, then $G^{*}$ is an evenly spanning subgraph of G.

Proof

Take a connected component H of $G^{*}$. Since $E(X^{*}\ominus Y^{*})\subseteq E(G^{*})\subseteq E(X^{*}\cup Y^{*})$ and $V(X\cap Y)$ is contained in a connected component of $G^{*}$, the subgraph of $X^{*}\cup Y^{*}$ induced by V(H) is a connected component of $X^{*}\cup Y^{*}$. Let $H_1$ be the subgraph of $X^{*}$ induced by $V(H)\cap V(X^{*})$ and $H_2$ be the subgraph of $Y^{*}$ induced by $V(H)\cap V(Y^{*})$. Then $H_1$ and $H_2$ are unions of a number of connected components of $X^{*}$ and $Y^{*}$, respectively.

Since $X^{*}$ is an evenly spanning subgraph of X, we have that $V(X^{*})=V(X)$ and $|O_{X}(H_1)|$ is even. Similarly, $V(Y^{*})=V(Y)$ and $|O_{Y}(H_2)|$ is even. Set $\Delta =O_{X}(H_{1})\cup O_{Y}(H_2)$ and $\Lambda =O_{X}(H_{1})\cap O_{Y}(H_2)$. Then $\textrm{deg}_{X}(u)+\textrm{deg}_{Y}(u)$ is odd if and only if $u\in \Delta -\Lambda$ for all $u\in V(H)$. Since $|\Delta -\Lambda |=|O_{X}(H_{1})|+|O_{Y}(H_2)|-2|\Lambda |$, we have that $|\Delta -\Lambda |$ is an even integer.

Since $V(X\cap Y)$ is contained in a connected component of $G^{*}$, either $O(X\cap Y)\cap V(H)=\emptyset$ or $O(X\cap Y)\subseteq V(H)$. Set $\Pi =O(X\cap Y)\cap O(G)$ and ${\bar{\Pi }}=O(X\cap Y)\cap {\bar{O}}(G)$. Then $|\Pi |-|{\bar{\Pi }}|=|O(X\cap Y)|-2|{\bar{\Pi }}|$. Since the number of odd vertices in a graph is even [1, Corollary 1.1], we have that $|O(X\cap Y)|$ is even. Therefore $|\Pi |-|{\bar{\Pi }}|$ is even. Since $G=X\cup Y$, we get $\textrm{deg}_{G}(u)= \textrm{deg}_{X}(u)+\textrm{deg}_{Y}(u)- \textrm{deg}_{X\cap Y}(u)$ for all $u\in V(G)$. Therefore

$$\begin{aligned} \textrm{deg}_{G}(u)\equiv \left\{ \begin{array}{ll} \textrm{deg}_{X}(u)+\textrm{deg}_{Y}(u)\pmod 2, &{} \hbox {if}~ u\notin O(X\cap Y);\\ \textrm{deg}_{X}(u)+\textrm{deg}_{Y}(u)-1\pmod 2, &{} \hbox {if}~u\in O(X\cap Y). \end{array} \right. \end{aligned}$$

(1)

Recall that $\textrm{deg}_{X}(u)+\textrm{deg}_{Y}(u)$ is odd if and only if $u\in \Delta -\Lambda$ for all $u\in V(H)$. If $O(X\cap Y)\cap V(H)=\emptyset$, by (1) we have $O_{G}(H)=\Delta -\Lambda$. If $O(X\cap Y)\subseteq V(H)$, by (1) we have ${\bar{\Pi }}\subseteq \Delta -\Lambda$, $\Pi \cap (\Delta -\Lambda )=\emptyset$ and $O_{G}(H)=[(\Delta -\Lambda )-{\bar{\Pi }}]\cup \Pi$. For the former, $|O_{G}(H)|$ is an even integer. For the latter, since $|O_{G}(H)|=|[(\Delta -\Lambda )-{\bar{\Pi }}]\cup \Pi |=|\Delta -\Lambda |-|{\bar{\Pi }}|+|\Pi |$, we have that $|O_{G}(H)|$ is also an even integer.

Recalling that $V(X^{*})=V(X)$, $V(Y^{*})=V(Y)$ and $G=X\cup Y$, we have $V(X^{*}\cup Y^{*})=V(G)$. Since $E(X^{*}\ominus Y^{*})\subseteq E(G^{*})\subseteq E(X^{*}\cup Y^{*})$, we get $V(G^{*})=V(G)$. Since $G^{*}$ is an even subgraph of G, it follows that $G^{*}$ is an evenly spanning subgraph of G. $\square$

Corollary 2.3

Let G be a union of two subgraphs X and Y. Suppose that X has an evenly spanning subgraph $X^{*}$ and Y has an evenly spanning subgraph $Y^{*}$. If $X\cap Y=X^{*}\cap Y^{*}$ and $X\cap Y$ is a connected even subgraph of G, then $X^{*}\cup Y^{*}$ is an evenly spanning subgraph of G.

Proof

Since $X^{*}$ and $Y^{*}$ are evenly spanning subgraphs of X and Y, respectively, $X^{*}$ and $Y^{*}$ are both even and $X^{*}\cup Y^{*}$ is a spanning subgraph of G. Since $X\cap Y=X^{*}\cap Y^{*}$ and $X\cap Y$ is a connected even subgraph of G, we have that $V(X\cap Y)$ is contained in a connected component of $X^{*}\cup Y^{*}$ and $X^{*}\cup Y^{*}$ is an even subgraph of G. By Theorem 2.2, $X^{*}\cup Y^{*}$ is an evenly spanning subgraph of G. $\square$

Corollary 2.4

Let G be a union of two subgraphs X and Y. Suppose that X has an evenly spanning subgraph $X^{*}$ and Y has an evenly spanning subgraph $Y^{*}$. If $V(X\cap Y)$ is contained in a connected component of $X^{*}\ominus Y^{*}$, then $X^{*}\ominus Y^{*}$ is an evenly spanning subgraph of G.

Proof

Since $X^{*}$ and $Y^{*}$ are evenly spanning subgraphs of X and Y, respectively, both $X^{*}$ and $Y^{*}$ are even and therefore $X^{*}\ominus Y^{*}$ is an even subgraph of G. Since $V(X\cap Y)$ is contained in a connected component of $X^{*}\ominus Y^{*}$, it follows from Theorem 2.2 that $X^{*}\ominus Y^{*}$ is an evenly spanning subgraph of G. $\square$

The decomposition $G=G_{1}\cup G_{2}\cup \cdots \cup G_{k}$ of a graph G is called a parity decomposition if $G_{1},G_{2},\cdots ,G_{k}$ are all parity subgraphs of G and each pair of them has no common edges.

The next lemma provides a basis for studying 4-flow problems by the method of parity decomposition.

Lemma 2.5

(Zhang [11]) For a graph G, $n_4(G)=0$ if and only if there is a parity decomposition $G=G_{1}\cup G_{2}\cup G_{3}$.

The result below gives a method to construct new parity decompositions from old ones.

Lemma 2.6

Let G be a graph which has two parity subgraphs $P_1$ and $P_2$ such that $E(P_1)\cap E(P_2)=\emptyset$. Let Q be an even subgraph of $P_1\cup P_2$. Then $P_1\ominus Q$ and $P_2\ominus Q$ are two parity subgraphs of G and $E(P_1\ominus Q)\cap E(P_2\ominus Q)=\emptyset$.

Proof

Since $E(Q)\subseteq E(P_1\cup P_2)$ and $E(P_1)\cap E(P_2)=\emptyset$, we get $E(P_1\ominus Q)\cap E(P_2\ominus Q)=\emptyset$. Take an arbitrary $v\in V(G)$. Since Q is even and $\textrm{deg}_{P_1 \ominus Q}(v)=\textrm{deg}_{P_1}(v)+\textrm{deg}_Q(v)-2\textrm{deg}_{P_1\cap Q}(v)$, we have $\textrm{deg}_{P_1 \ominus Q}(v)\equiv \textrm{deg}_{P_1}(v)\pmod 2$. Since $P_1$ is a parity subgraph of G, we get $\textrm{deg}_{P_1}(v)\equiv \textrm{deg}_{G}(v)\pmod 2$. Therefore $\textrm{deg}_{P_1 \ominus Q}(v)\equiv \textrm{deg}_{G}(v)\pmod 2$. Similarly, $\textrm{deg}_{P_2 \ominus Q}(v)\equiv \textrm{deg}_{G}(v)\pmod 2$. It follows that $P_1\ominus Q$ and $P_2\ominus Q$ are two parity subgraphs. $\square$

The following lemma is an immediate corollary of Lemmas 2.1 and 2.5.

Lemma 2.7

Let G be a graph. Then $n_4(G)=0$ if and only if G has an evenly spanning subgraph.

3 For the Case of $n_4(X)=n_4(Y)=0$

Throughout this section. Let $G=X\cup Y$ where $n_4(X)=n_4(Y)=0$ and $|E(X\cap Y)|=4$. Suppose that $X\cap Y$ is a connected graph but not a tree with 2 or 3 leaves. Then $X\cap Y$ is one of the ten graphs listed in Fig. 1.

Fig. 1

$X\cap Y$

By Lemma 2.5, X admits a parity decomposition $X=X_1\cup X_2\cup X_3$ and Y admits a parity decomposition $Y=Y_1\cup Y_2\cup Y_3$. Construct a bipartite graph B with bipartition $\{\{x_1,x_2,x_3\},\{y_1,y_2,y_3\}\}$ as follows: the number of edges between $x_i$ and $y_j$ is equal to $|E(X_i\cap Y_j)|$ where $i,j\in \{1,2,3\}$. Then $|E(B)|=4$ as $|E(X)\cap E(Y)|=4$. By straightforward checking, B is one of the sixteen graphs listed in Fig. 2 up to isomorphism.

Fig. 2

B

We aim to prove $n_4(G)=0$. The proof begins with the following two lemmas.

Lemma 3.1

If $X_i\cap Y$ or $X\cap Y_i$ contains a cycle for some $i\in \{1,2,3\}$, then $n_4(G)=0$.

Proof

It is sufficient to give a proof for the case when $X_1\cap Y$ contains a cycle as the proofs for the other cases are exactly the same. Let C be a cycle of $X_1\cap Y$. Set $X'=X-E(C)$ and $X'_1=X_1-E(C)$. Then $X'$ has the following parity decomposition $X'=X'_1\cup X_2\cup X_3$. By Lemma 2.5, we get $n_4(X')=0$. It is obvious that $G=X'\cup Y$ and $|E(X')\cap E(Y)|\le 2$. By Theorem 1.2, we obtain $n_4(G)=0$. $\square$

Lemma 3.2

If B is the second or third graph in Fig. 2 and $X\cap Y$ is an even graph, then $n_4(G)=0$.

Proof

First consider the case that B is the second graph in Fig. 2. Set $X^{*}=X_2\cup X_3$ and $Y^{*}=Y_1\cup Y_2$. Then $E(X^{*})\cap E(Y^{*})=\emptyset$ and $|E(X^{*}\cup Y^{*})\cap E(X\cap Y)|=3$. By Lemma 2.1, $X^{*}$ and $Y^{*}$ are evenly spanning subgraphs of X and Y, respectively. Since $E(X^{*})\cap E(Y^{*})=\emptyset$, we have that $X^{*}\cup Y^{*}$ is an even subgraph of G. Since $X\cap Y$ is a connected even graph with 4 edges and $|E(X^{*}\cup Y^{*})\cap E(X\cap Y)|=3$, we conclude that $V(X\cap Y)$ is contained in a connected component of $X^{*}\cup Y^{*}$. By Theorem 2.2, $X^{*}\cup Y^{*}$ is an evenly spanning subgraph of G.

Then consider the case that B is the third graph in Fig. 2. Set $X^{*}=X_1\cup X_3$ and $Y^{*}=Y_1\cup Y_3$. Then $X^{*}$ and $Y^{*}$ are evenly spanning subgraphs of X and Y, respectively, $X\cap Y$ is a connected even subgraph of G and $X\cap Y=X^{*}\cap Y^{*}$. By Corollary 2.3, $X^{*}\cup Y^{*}$ is an evenly spanning subgraph of G.

Now we have proved that G has an evenly spanning subgraph if B is the second or third graph in Fig. 2. The conclusion follows from Lemma 2.7. $\square$

The proof of the main result of this section is divided into proofs of the following four lemmas.

Lemma 3.3

If B is not any of the first three graphs in Fig. 2, then $n_4(G)=0$.

Proof

Set $X'=(X_1\cup X_2)\ominus (Y_1\cup Y_3)~ \text{ and }~Y'=(X_1\cup X_3)\ominus (Y_2\cup Y_3)$. By straightforward checking, $G=X'\cup Y'$. Since $X_i$ and $Y_i$ are all parity subgraphs of X and Y respectively, and each pair of them has no common edges where $i\in \{1,2,3\}$, it follows from Lemma 2.1 that all the four graphs $X_1\cup X_2$, $Y_1\cup Y_3$, $X_1\cup X_3$ and $Y_2\cup Y_3$ are even. Therefore $X'$ and $Y'$ are both even graphs. By [11, Theorem 3.1.2], a graph admits a nowhere-zero 4-flow if and only if it is a union of two even graphs. Therefore $n_4(G)=0$. $\square$

Lemma 3.4

If B is the first graph in Fig. 2, then $n_4(G)=0$.

Proof

By Lemma 3.1, $n_4(G)=0$ if $X_1\cap Y$ contains a cycle. Now assume that $X_1\cap Y$ does not contain any cycle. Since $X_1\cap Y=X\cap Y$, we conclude that $X\cap Y$ is the first graph in Fig. 1. Then $|E(C)\cap E(X\cap Y)|\le 2$ for any cycle C of G. Set $E(X\cap Y)=\{e_1,e_2,e_3,e_4\}$. By Lemma 2.1, $X_1\cup X_2$ is an even graph and therefore has a cycle decomposition. Let $H_i$ be the cycle in a cycle decomposition of $X_1\cup X_2$ such that $e_i\in E(H_i)$ where $i\in \{1,2,3,4\}$. If $|E(H_{i_0})\cap \{e_1,e_2,e_3,e_4\}|\ne 1$ for some $i_0\in \{1,2,3,4\}$, then we set $H=H_{i_0}$. If otherwise, then we set $H=H_1\cup H_2$. In either case, we have $|E(H)\cap \{e_1,e_2,e_3,e_4\}|=2$ and H is an even subgraph of G. Set $X'_1=X_1\ominus H$ and $X'_2=X_2\ominus H$. By Lemma 2.6, $X'_1$ and $X'_2$ are two parity subgraphs of X and $E(X'_1)\cap E(X'_2)=\emptyset$. Note that the bipartite graph being associated with the decompositions $X=X'_1\cup X'_2\cup X_3$ and $Y=Y_1\cup Y_2\cup Y_3$ is not any of the first three graphs in Fig. 2. By Lemma 3.3, we have $n_4(G)=0$. $\square$

Lemma 3.5

If B is the second graph in Fig. 2, then $n_4(G)=0$.

Proof

Since B is the second graph in Fig. 2, $X_1\cap Y$ is a graph obtained from $X\cap Y$ by removing an edge. By Lemmas 3.1 and 3.2, it suffices to deal with the case that $X_1\cap Y$ does not contain any cycle and $X\cap Y$ is not even. These two conditions imply that $X\cap Y$ is not any of the last five graphs in Fig. 1. The rest of the proof is divided into three cases.

Case 1 $X\cap Y$ is the first graph in Fig. 1.

In this case, $X_1\cap Y$ is a claw. By Lemma 2.1, $X_1\cup X_2$ is an even graph and therefore has a cycle decomposition. Let C be a cycle of $X_1\cup X_2$ such that $E(C)\cap E(X_1\cap Y)\ne \emptyset$. Then $|E(C)\cap E(X_1\cap Y)|=1~\text{ or }~2$. Therefore the bipartite graph being associated with the parity decompositions $X=(X_1\ominus C)\cup (X_2\ominus C)\cup X_3$ and $Y=Y_1\cup Y_2\cup Y_3$ is not any of the first three graphs in Fig. 2. By Lemma 3.3, we have $n_4(G)=0$.

Case 2 $X\cap Y$ is the second graph in Fig. 1.

Use C to denote the 3-cycle of $X\cap Y$. Since $X_1\cap Y$ does not contain any cycle, the unique common edge of $X_3$ and $Y_3$ is contained in E(C). Therefore the bipartite graph being associated with the parity decompositions $X=(X_1\ominus C)\cup X_2\cup (X_3\ominus C)$ and $Y=Y_1\cup Y_2\cup Y_3$ is not any of the first three graphs in Fig. 2. By Lemma 3.3, we have $n_4(G)=0$.

Case 3 $X\cap Y$ is one of the third to fifth graphs in Fig. 1.

In this case, $X\cap Y$ has a pair of parallel edges, say $e_1$ and $e_2$. Since $X_1\cap Y$ does not contain any cycle, either $E(X_3\cap Y)=\{e_1\}$ or $E(X_3\cap Y)=\{e_2\}$. Without loss of generality, assume $E(X_3\cap Y)=\{e_1\}$. If $e_2\in E(Y_3)$, then $E(X \cap Y_3)=\{e_1,e_2\}$. Therefore $X \cap Y_3$ contains a 2-cycle. By Lemma 3.1, we get $n_4(G)=0$.

Now assume that $e_2\notin E(Y_3)$ and set $E(X \cap Y_3)=\{e_1,e_3\}$. Without loss of generality, assume $e_2\in E(Y_1)$. Then $E(Y_1\cup Y_3)\cap E(X)=\{e_1,e_2,e_3\}$. By Lemma 2.1, $Y_1\cup Y_3$ is even. Since $e_1$ and $e_2$ are parallel edges, $(Y_1\cup Y_3)-\{e_1,e_2\}$ is even and therefore has a cycle decomposition. Let C be a cycle of $(Y_1\cup Y_3)-\{e_1,e_2\}$ such that $e_3\in E(C)$. Then the bipartite graph being associated with the parity decompositions $X=X_1\cup X_2\cup X_3$ and $Y=(Y_1\ominus C)\cup Y_2\cup (Y_3\ominus C)$ is not any of the first three graphs in Fig. 2. By Lemma 3.3, we have $n_4(G)=0$. $\square$

Lemma 3.6

If B is the third graph in Fig. 2, then $n_4(G)=0$.

Proof

By Lemma 3.2, $n_4(G)=0$ if $X\cap Y$ is even. If $X_1\cap Y$ or $X_3\cap Y$ is a 2-cycle, then Lemma 3.1 implies $n_4(G)=0$. Now assume that $X\cap Y$ is not even and neither $X_1\cap Y$ nor $X_3\cap Y$ is a 2-cycle. Then $X\cap Y$ is not any of the last four graphs in Fig. 1. The rest of the proof is divided into three cases.

Case 1 $X\cap Y$ is the first graph in Fig. 1.

In this case, $X_1\cap Y$, $X_3\cap Y$, $X\cap Y_1$ and $X\cap Y_3$ are all pathes of length 2. Set $E(X_1\cap Y)=\{e_1,e_2\}$ and $E(X_3\cap Y)=\{e_3,e_4\}$. Without loss of generality, let $E(X\cap Y_1)=\{e_1,e_4\}$ and $E(X\cap Y_3)=\{e_2,e_3\}$.

If there is a cycle C of $X_1\cup X_3$ (resp. $Y_1\cup Y_3$) such that $|E(C)\cap \{e_1,e_2,e_3,e_4\}|=1$, then the bipartite graph being associated with the parity decompositions $X=(X_1\ominus C)\cup X_2\cup (X_3\ominus C)$ and $Y=Y_1\cup Y_2\cup Y_3$ (resp. $X=X_1\cup X_2\cup X_3$ and $Y=(Y_1\ominus C)\cup Y_2\cup (Y_3\ominus C)$) is not any of the first three graphs in Fig. 2. By Lemma 3.3, we have $n_4(G)=0$.

Now we assume that $|E(C)\cap \{e_1,e_2,e_3,e_4\}|\ne 1$ for any cycle C of $X_1\cup X_3$ (resp. $Y_1\cup Y_3$). Let $C_1$ (resp. $C_2$ ) be a cycle of $X_1\cup X_3$ (resp. $Y_1\cup Y_3$) containing $e_1$. Then $|E(C_1)\cap \{e_2,e_3,e_4\}|=|E(C_2)\cap \{e_2,e_3,e_4\}|=1$. If $E(C_1)\cap \{e_2,e_3,e_4\}=\{e_2\}$ or $\{e_3\}$, then the bipartite graph being associated with the parity decompositions $X=(X_1\ominus C_1)\cup X_2\cup (X_3\ominus C_1)$ and $Y=Y_1\cup Y_2\cup Y_3$ is not any of the first three graphs in Fig. 2. By Lemma 3.3, we have $n_4(G)=0$. Similarly, if $E(C_2)\cap \{e_2,e_3,e_4\}=\{e_4\}$ or $\{e_3\}$, then we get $n_4(G)=0$. If neither of the above two, then $E(C_1)\cap \{e_2,e_3,e_4\}=\{e_4\}$ and $E(C_2)\cap \{e_2,e_3,e_4\}=\{e_2\}$. By straightforward checking, the bipartite graph being associated with the parity decompositions $X=(X_1\ominus C_1)\cup X_2\cup (X_3\ominus C_1)$ and $Y=(Y_1\ominus C_2)\cup Y_2\cup (Y_3\ominus C_2)$ is not any of the first three graphs in Fig. 2. By Lemma 3.3, we have $n_4(G)=0$.

Case 2 $X\cap Y$ is the second graph in Fig. 1.

Use C to denote the 3-cycle of $X\cap Y$. Note that C is contained in $X_1\cup X_3$. By straightforward checking, the bipartite graph being associated with the parity decompositions $X=(X_1\ominus C)\cup X_2\cup (X_3\ominus C)$ and $Y=Y_1\cup Y_2\cup Y_3$ is not any of the first three graphs in Fig. 2. By Lemma 3.3, we have $n_4(G)=0$.

Case 3 $X\cap Y$ is one of the third to sixth graphs in Fig. 1.

In this case, $X\cap Y$ has a pair of parallel edges. Since neither $X_1\cap Y$ nor $X_3\cap Y$ is a 2-cycle, there exist $e_1\in E(X_1\cap Y)$ and $e_2\in E(X_3\cap Y)$ such that $e_1$ is parallel to $e_2$. Set $E(X_1\cap Y)=\{e_1,e_4\}$ and $E(X_3\cap Y)=\{e_2,e_3\}$. Assume that neither $X\cap Y_1$ nor $X\cap Y_3$ is a 2-cycle (if otherwise, then $n_4(G)=0$ follows from Lemma 3.1). Without loss of generality, set $E(X\cap Y_1)=\{e_1,e_3\}$ and $E(X\cap Y_3)=\{e_2,e_4\}$.

Let $H_{1}$ (resp. $H_{2}$) be the connected component of $X_1\cup X_2$ (resp. $Y_1\cup Y_2$) such that $e_4\in E(H_1)$ (resp. $e_3\in E(H_2)$). By Lemma 2.1, $X_1\cup X_2$ and $Y_1\cup Y_2$ are evenly spanning subgraphs of X and Y, respectively. Therefore both $H_{1}$ and $H_{2}$ are even. If $e_1\notin E(H_1)$, then the bipartite graph being associated with the parity decompositions $X=(X_1\ominus H_1)\cup (X_2\ominus H_1)\cup X_3$ and $Y=Y_1\cup Y_2\cup Y_3$ is not any of the first three graphs in Fig. 2. By Lemma 3.3, we have $n_4(G)=0$. Similarly, $n_4(G)=0$ if $e_1\notin E(H_2)$.

Now we assume that $e_1\in E(H_1)\cap E(H_2)$. Since $E(X_1\cup X_2)\cap E(Y_1\cup Y_2)=\{e_1\}$, we get $E(H_1)\cap E(H_2)=\{e_1\}$. Since $H_1$ (or $H_2$) is an even connected graph, $e_1$ is not a cut edge of $H_1$ (or $H_2$). Therefore $H_1\ominus H_2$ is connected and $V(H_1\ominus H_2)=V(H_1\cup H_2)$. Since $e_1,e_3,e_4\in E(H_1\cup H_2)$ and $e_1$ is parallel to $e_2$, we conclude that $V(X\cap Y)\subseteq V(H_1\cup H_2)$. Since $V(H_1\ominus H_2)=V(H_1\cup H_2)$, we have that $V(X\cap Y)$ is contained in a connected component of $(X_1\cup X_2)\ominus (Y_1\cup Y_2)$. Recall that $X_1\cup X_2$ and $Y_1\cup Y_2$ are evenly spanning subgraphs of X and Y, respectively. It follows from Corollary 2.4 that $(X_1\cup X_2)\ominus (Y_1\cup Y_2)$ is an evenly spanning subgraph of G. By Lemma 2.7, we get $n_4(G)=0$. $\square$

The following theorem is our main result in this section, which follows from Lemmas 3.3, 3.4, 3.5 and 3.6 directly.

Theorem 3.7

Let $G=X\cup Y$. Suppose that $|E(X\cap Y)|=4$ and $X\cap Y$ is a connected graph which is not a tree with 2 or 3 leaves. If $n_4(X)=n_4(Y)=0$, then $n_4(G)=0$.

Fig. 3

The Petersen graph and its two subgraphs

Remark 3.8

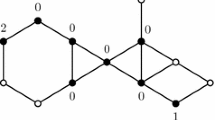
If $X\cap Y$ is a path of length 4, then $n_4(X)=n_4(Y)=0$ does not guarantee $n_4(G)=0$. For example, in Fig. 3, the Petersen graph G is the union of the two subgraphs X and Y. Note that $X\cap Y$ is a path of length 4 and $n_4(X)=n_4(Y)=0$. But $n_4(G)=1$.

Remark 3.9

The problem whether $n_4(X)=n_4(Y)=0$ leads to $n_4(G)=0$ if $X\cap Y$ is a tree with four edges and three leaves remains open.

4 Proof of Theorem 1.4

Assume that G has two subgraphs X and Y satisfying one of the following three conditions:

• (i) $|E(X\cap Y)|\le 2$;

• (ii) $|E(X\cap Y)|=3$ and $X\cap Y$ is connected or $X\cap Y$ admits parallel edges;

• (iii) $|E(X\cap Y)|=4$, $X\cap Y$ is connected and $X\cap Y$ is not a tree with 2 or 3 leaves.

By the definition of flow nullity, there exist subgraphs $X'$ and $Y'$ of X and Y, respectively such that $n_4(X')=n_4(Y')=0$, $|E(X)|=|E(X')|+n_4(X)$ and $|E(Y)|=|E(Y')|+n_4(Y)$. Note that $X'\cap Y'$ is a subgraph of $X\cap Y$. If $X\cap Y$ satisfies conditions (i) or (ii), then so does $X'\cap Y'$. If $X\cap Y$ satisfies conditions (iii), then, by checking the graphs listed in Fig. 1, $X'\cap Y'$ satisfies one of the three conditions (i), (ii) and (iii). By Theorem 1.2, Proposition 1.3 and Theorem 3.7, we get $n_4(X'\cup Y')=0$. It follows that $n_4(X\cup Y)\le |E(X\cup Y)|-|E(X'\cup Y')|$. Note that

$$\begin{aligned} |E(X\cup Y)|= & {} |E(X)|+|E(Y)|-|E(X\cap Y)|, \\ |E(X'\cup Y')|= & {} |E(X')|+|E(Y')|-|E(X'\cap Y')| \end{aligned}$$

and $|E(X'\cap Y')|\le |E(X\cap Y)|$. Therefore

$$\begin{aligned} n_4(X\cup Y)\le (|E(X)|-|E(X')|)+(|E(Y)|-|E(Y')|). \end{aligned}$$

Since $|E(X)|=|E(X')|+n_4(X)$ and $|E(Y)|=|E(Y')|+n_4(Y)$, we get

$$\begin{aligned} n_4(X\cup Y)\le n_4(X)+n_4(Y). \end{aligned}$$