1 Introduction

For any set X and any nonnegative integer i, we adopt the convention that \(\left( {\begin{array}{c}X\\ i\end{array}}\right) \) represents the set of all i-element subsets of X. Surely, \(2^X\) denotes the power set of X, namely \(\bigcup _{i=0}^{|X |}\left( {\begin{array}{c}X\\ i\end{array}}\right) \). A graph G is a pair consisting of its vertex set \({{\,\mathrm{V}\,}}(G)\) and its edge set \({{\,\mathrm{E}\,}}(G)\subseteq \left( {\begin{array}{c}{{\,\mathrm{V}\,}}(G)\\ 2\end{array}}\right) \). For each \(U\subseteq {{\,\mathrm{V}\,}}(G)\), the subgraph G[U] of G induced by U is the graph having U as its vertex set and \(\left( {\begin{array}{c}U\\ 2\end{array}}\right) \cap {{\,\mathrm{E}\,}}(G)\) as its edge set. We call a graph \(G'\) an induced subgraph of G if \(G' = G[U]\) for some \(U\subseteq {{\,\mathrm{V}\,}}(G)\), and we represent this by writing \(G'\lhd G\).

When we refer to a digraph D, we mean a pair comprising its vertex set \({{\,\mathrm{V}\,}}(D)\) and its arc set \({{\,\mathrm{A}\,}}(D)\subseteq {{\,\mathrm{V}\,}}(D)\times {{\,\mathrm{V}\,}}(D)\). For each vertex v of D, we denote by \({{\,\mathrm{N}\,}}_D^{-}(v)\) the set of in-neighbors of v in D. Namely, \({{\,\mathrm{N}\,}}_D^{-}(v) = \{ u\in {{\,\mathrm{V}\,}}(D) : \ (u,v)\in {{\,\mathrm{A}\,}}(D) \}\). We write \({{\,\mathrm{N}\,}}_D^{-}[v] \) for \( {{\,\mathrm{N}\,}}_D^{-}(v)\cup \{v\}\), and call it the closed in-neighborhood of v in D. A digraph is acyclic if it has no directed cycle. Equivalently, a digraph D is acyclic provided it is compatible with a total order < on \({{\,\mathrm{V}\,}}(D)\), i.e., \({{\,\mathrm{N}\,}}_D^-(u) \subseteq \{v : \ v<u\}\) for all \(u\in {{\,\mathrm{V}\,}}(D)\).

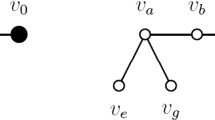
The competition graph (resp. phylogeny graph) of a digraph D, denoted by \({{\,\mathrm{\mathcal {C}}\,}}(D)\) (resp. \({{\,\mathrm{\mathcal {P}}\,}}(D)\)), is the graph with vertex set \({{\,\mathrm{V}\,}}(D)\) in which two different vertices u and v are adjacent if and only if there exists \(w\in {{\,\mathrm{V}\,}}(D)\) such that \(u,v\in {{\,\mathrm{N}\,}}^-_D(w)\) (resp. \(u,v\in {{\,\mathrm{N}\,}}^-_D[w]\)). Let G be a graph. A digraph D is called a competition digraph (resp. phylogeny digraph) for G if D is acyclic and \(G\lhd {{\,\mathrm{\mathcal {C}}\,}}(D)\) (resp. \(G\lhd {{\,\mathrm{\mathcal {P}}\,}}(D)\)). The reader can check that the digraph on the right of Fig. 1 is a phylogeny digraph of the graph on its left. The competition number (resp. phylogeny number) of G, denoted by \(\kappa (G)\) (resp. \({{\,\mathrm{\phi }\,}}(G)\)), is the minimum value of \(|{{\,\mathrm{V}\,}}(D)|- |{{\,\mathrm{V}\,}}(G)|\), where D runs through all competition digraphs (resp. phylogeny digraphs) for G. We name a phylogeny digraph D of G an optimal phylogeny digraph of G provided \(\phi (G)=|{{\,\mathrm{V}\,}}(D)|- |{{\,\mathrm{V}\,}}(G)|\).

Fig. 1
figure 1

The Hamming graph \(\mathrm {H}_{2,2}^1\) and one of its optimal phylogeny digraphs

Full size image

In the study of food webs, Cohen [1] introduced the concept of the competition graph of an acyclic digraph. Roberts [2] showed that every graph can be made into the competition graph of an acyclic digraph by adding some isolated vertices and introduced the definition of competition number. Motivated by problems of phylogenetic tree reconstruction, Roberts and Sheng [3] proposed the notions of phylogeny graph and phylogeny number. Phylogeny graphs are also known as moral graphs [4] in the study of graphical models. The problems of determining the competition number and the phylogeny number of a given graph are both known as NP-complete problems [3, 5, 6].

Let n be a positive integer. We use [n] for the set \(\{1,\ldots ,n\}\). For any two n-tuples \(x = (x_1,\ldots ,x_n)\) and \(y = (y_1,\ldots ,y_n)\), the Hamming distance \({{\,\mathrm{d}\,}}(x,y)\) between x and y is the number of positions in which x and y take different values, i.e., \({{\,\mathrm{d}\,}}(x,y) = |\{ i\in [n] : \ x_i \ne y_i \} |\). Let \(a_1,\ldots ,a_n\) be n positive integers. We write \(\mathrm {Grid}_{a_1,\ldots ,a_n}\) for the set \([a_1]\times \dots \times [a_n]\). For each \(k \in [n]\), define the generalized Hamming graph \(\mathrm {H}_{a_1,\ldots ,a_n}^{k}\) to be the graph with vertex set \(\mathrm {Grid}_{a_1,\ldots ,a_n}\) in which two vertices x and y are adjacent if and only if \({{\,\mathrm{d}\,}}(x,y)\in [ k]\). If \((b_1,\ldots ,b_n)\) is obtained from \((a_1,\ldots ,a_n)\) by a permutation, it is clear that \(\mathrm {H}_{b_1,\ldots ,b_n}^{k}\), \(\mathrm {H}_{a_1,\ldots ,a_n}^{k}\) and \(\mathrm {H}_{a_1,\ldots ,a_n, 1}^{k}\) are pairwise isomorphic. Without loss of generality, we may thus focus on generalized Hamming graphs \(\mathrm {H}_{a_1,\ldots ,a_n}^{k}\) with \(\min _{i\in [n]} a_i\ge 2\). To simplify notation, we often write \(\mathrm {H}_{a_1,\ldots ,a_n}^{k}\) as \(\mathrm {H}_{m: n}^{k}\) when \(a_1=\cdots =a_n=m\).

Hamming graphs and their various generalizations have attracted intense attention in the literature. Mostly often, people name \(\mathrm {H}_{d: n}^{1}\) a Hamming graph and denote it by \(\mathrm {H}(n,d)\) [7,8,9,10]. However, some authors prefer to call all graphs of the form \(\mathrm {H}_{a_1,\ldots ,a_n}^{1}\) Hamming graphs [11] and some may identify generalized Hamming graphs as a much wider class of Cayley graphs on finite abelian groups [12].

We collect below some results of Park and Sano on the competition numbers of generalized Hamming graphs. We remark that Park and Sano stated their results [13, Theorem 4, Theorem 5] only for the equal parameter case. But the reader can check that their proof indeed applies to the general case that p, q, r may not be equal.

Theorem 1

  1. (1)

    [13, Proposition 3] \(\kappa (\mathrm {H}^{1}_{ p }) =1\) for all integers \(p\ge 2\).

  2. (2)

    [13, Theorem 4] \(\kappa (\mathrm {H}^{1}_{ p,q }) =2\) for all integers \(p,q\ge 2\).

  3. (3)

    [13, Theorem 5] \(\kappa (\mathrm {H}^{1}_{ p,q,r }) =6\) for all integers \(p,q,r\ge 2\).

  4. (4)

    [13, Proposition 2] \(\kappa (\mathrm {H}_{2: n}^{1}) = (n-2)2^{n-1}+2\) for all positive integers n.

  5. (5)

    [14, Theorem 1.3] \(\kappa (\mathrm {H}_{3: n}^{1}) = (n-3)3^{n-1}+6\) for all integers \(n \ge 3\).

We add one more observation below on the competition numbers of generalized Hamming graphs.

Theorem 2

\(\kappa (\mathrm {H}_{m,m,m}^{2}) = {\left\{ \begin{array}{ll} 2, &{} \text {if } m = 2; \\ 3, &{} \text {if } m \ge 3. \\ \end{array}\right. } \)

Note that \(\mathrm {H}_{2:n}^{1}\) is just the hypercube graph, which is bipartite and hence has no triangle. Roberts and Sheng declared that \(\phi (G) = |{{\,\mathrm{E}\,}}(G) |- |{{\,\mathrm{V}\,}}(G) |+1\) holds for each triangle-free connected graph G. Accordingly, we have the easy consequence that \(\phi (\mathrm {H}_{2:n}^{1}) = (n-2) 2^{n-1} +1\) for all positive integers n. For each nonnegative integer i, denote by \(\sigma _i\) the ith elementary symmetric polynomial. We now present the main result of this note. It is worth mentioning that Theorem 3 (1) generalizes the above-stated result about \(\phi (\mathrm {H}_{2:n}^{1})\).

Theorem 3

  1. (1)

    \(\phi (\mathrm {H}_{a_1,\ldots ,a_n}^{1}) = \sigma _{n-1}(a_1,\ldots ,a_n) - \sum _{i=0}^{n-1} \sigma _i(a_1-1, \ldots , a_n-1)\) for all integers \(a_1,\ldots ,a_n\ge 2\).

  2. (2)

    \(\phi (\mathrm {H}_{m,m,m}^{2}) = {\left\{ \begin{array}{ll} 1, &{} \text {if } m = 2; \\ 2, &{} \text {if } m \ge 3. \\ \end{array}\right. } \)

  3. (3)

    Let \(n\ge 4\) be an integer. Then, there is an integer m such that \( \phi (\mathrm {H}_{a: n}^{n-1}) = n-1 \) holds whenever \( a \ge m\).

Here is an immediate corollary of Theorems 1, 2 and 3.

Corollary 4

  1. (1)

    \(\phi (\mathrm {H}_{2:n}^{1}) - \kappa (\mathrm {H}_{2:n}^{1}) + 1 = 0\) for all positive integers n.

  2. (2)

    \(\phi (\mathrm {H}_{3:n}^{1}) - \kappa (\mathrm {H}_{3:n}^{1}) + 1 = 2^n-5\) for all integers \(n\ge 3\).

  3. (3)

    \(\phi (\mathrm {H}_{m,m,m}^{2}) - \kappa (\mathrm {H}_{m,m,m}^{2}) + 1 = 0\) for every integer \(m\ge 2\).

  4. (4)

    \(\phi (\mathrm {H}_{ p,q }^{1}) - \kappa (\mathrm {H}_{ p,q }^{1}) + 1 = 0\) for all integers \(p,q\ge 2\).

  5. (5)

    \(\phi (\mathrm {H}_{ p,q,r }^{1}) - \kappa (\mathrm {H}_{ p,q,r }^{1}) + 1 = p+q+r - 6\) for all integers \(p,q,r\ge 2\).

Wu et al. [15] found that the range of the function \(\phi (G) - \kappa (G) + 1\) is the set of all nonnegative integers if we allow G go through all graphs. Xiong et al. [16] further confirmed that for any integer N there exists a connected graph G with \(\phi (G) - \kappa (G) + 1>N\). Eoh et al. [17] showed that for every nonnegative integer N there is a connected graph G satisfying \(\phi (G) - \kappa (G) + 1= N\). Note that Corollary 4 (5) implies that this graph can be simply chosen as the very simple graph \(\mathrm {H}_{2,2,N+2}^{1}\).

For a graph G, we have discussed three parameters, \(\kappa (G)\), \(\phi (G)\) and \(\phi (G) - \kappa (G) + 1\). Can we estimate them for more generalized Hamming graphs? Beyond competition numbers and phylogeny numbers, one can still consider niche numbers [18, 19], double competition numbers [20, 21] and m-step competition numbers [22, 23]. Since Hamming graphs and generalized Hamming graphs are among the most basic combinatorial structures, the estimation of these parameters for them may be a touchstone for us to provoke some unexpected further investigations.

The rest of the paper is organized into four sections. Sect. 2 provides a simple connection between bootstrap process and phylogeny number (Theorem 7). In Sect. 3, we employ linear algebra argument to calculate the percolation number of a special edge clique cover of \(\mathrm {H}_{a_1,\ldots ,a_n}^{k}\) (Theorem 10). We report in Sect. 4 several different upper bound estimates of the phylogeny numbers of generalized Hamming graphs. In Sect. 5, we establish lower bounds of the phylogeny numbers of generalized Hamming graphs in several cases and then close our proof of Theorem 2 and Theorem 3.

2 Bootstrap Process and Phylogeny Number

Let G be a graph. A set \(S\subseteq {{\,\mathrm{V}\,}}(G)\) is a clique of G if G[S] is a complete graph, namely \({{\,\mathrm{E}\,}}(G[S]) = \left( {\begin{array}{c}S\\ 2\end{array}}\right) \). A clique of G is maximal if it is not a subset of any other clique of G. Let \(\mathcal {F}\) be a collection of subsets of \({{\,\mathrm{V}\,}}(G)\). We say that \(\mathcal {F}\) is an edge clique cover of G, denoted by \(\mathcal {F} \vdash G\), if \({{\,\mathrm{E}\,}}(G) = \bigcup _{K \in \mathcal {F}} \left( {\begin{array}{c}K\\ 2\end{array}}\right) \) and \({{\,\mathrm{V}\,}}(G) = \bigcup _{K \in \mathcal {F}} K\). Let D be a digraph. We use the shorthand \(D \Cap G\) for the set

$$\begin{aligned} \Bigl \{ {{\,\mathrm{N}\,}}^-_D[v]\cap {{\,\mathrm{V}\,}}(G) : \ v\in {{\,\mathrm{V}\,}}(D) \Bigr \}\setminus \{\emptyset \}\subseteq 2^{{{\,\mathrm{V}\,}}(G)}\setminus \{\emptyset \}. \end{aligned}$$

Here is a trivial observation.

Lemma 5

([15, Lemma 1 (ii)]) Let D be a digraph and let G be a graph. Then, \(G\lhd {{\,\mathrm{\mathcal {P}}\,}}(D)\) if and only if \((D \Cap G) \vdash G\).

Let \(a_1,\ldots ,a_n\ge 2\) be integers. For every \(x \in \mathrm {Grid}_{a_1,\ldots ,a_n}\) and \(J \subseteq [n]\), define \(\mathrm {Grid}_{a_1,\ldots ,a_n}(x;J)\) to be the set \(\bigl \{ y\in \mathrm {Grid}_{a_1,\ldots ,a_n} : \ x|_{[n] \setminus J} = y|_{[n]\setminus J} \bigr \}\), and call it the \(|J|\)-slice of \(\mathrm {Grid}_{a_1,\ldots ,a_n}\) along the direction J through x. For each \(k\in [n]\), define \(\mathcal {F}_{a_1,\ldots ,a_n}^{k}\) to be the set of all k-slices of \(\mathrm {Grid}_{a_1,\ldots ,a_n}\). Namely,

$$\begin{aligned} \mathcal {F}_{a_1,\ldots ,a_n}^{k} = \Bigl \{ \mathrm {Grid}_{a_1,\ldots ,a_n}(x;J) : \ x\in \mathrm {Grid}_{a_1,\ldots ,a_n}, J\in \left( {\begin{array}{c}[n]\\ k\end{array}}\right) \Bigr \}. \end{aligned}$$

Surely, \(\mathcal {F}_{a_1,\ldots ,a_n}^{k}\) is an edge clique cover of \(\mathrm {H}_{a_1,\ldots ,a_n}^{k}\), i.e., \(\mathcal {F}_{a_1,\ldots ,a_n}^{k} \vdash \mathrm {H}_{a_1,\ldots ,a_n}^{k}\).

Example 1

On the left of Fig. 1 is \(\mathrm {H}_{2,2}^1\). On the right of Fig. 1 is a digraph D which is compatible with the total order \(v_1< v_2< v_3< v_4 < z\). Note that D is an optimal phylogeny digraph for \(\mathrm {H}_{2,2}^1\) and that \(D\Cap \mathrm {H}_{2,2}^1 = \mathcal {F}_{2,2}^1 \cup \bigl \{ \{ v_1 \} \bigr \}\vdash \mathrm {H}_{2,2}^1 \).

Let V be a finite set. A hypergraph on V is a subset \(\mathcal {H} \) of \( 2^{V}\) such that \(V = \bigcup _{e\in \mathcal {H}} e\). Each element \(e \in \mathcal {H}\) is called a hyperedge of \(\mathcal {H}\). Let U be a subset of V. Put \(U_0 = U\). For every nonnegative integer t, let \(U_{t+1} = U_{t} \cup \{ v : \ \exists e \in \mathcal {H} \text{ with } e\setminus U_t = \{ v \} \}\). Let \([U]_{\mathcal {H}}\) denote the set \(\bigcup _{t\ge 0} U_t\). We call the process initiating from \(U_0\) to \([U]_{\mathcal {H}}\) an \(\mathcal {H}\)-bootstrap process and call U an \(\mathcal {H}\)-percolating set if \([U]_{\mathcal {H}} = V\) [24]. The percolation number of \(\mathcal {H}\), denoted by \({{\,\mathrm{m}\,}}(\mathcal {H})\), is defined to be the minimum size of an \(\mathcal {H}\)-percolating set. We write \({{\,\mathrm{\overline{m}}\,}}(\mathcal {H})\) for \(|V |- {{\,\mathrm{m}\,}}(\mathcal {H})\), which is the maximum size of a subset of V whose complement can still be an \(\mathcal {H}\)-percolating set.

Lemma 6

Let G be a graph and let D be a phylogeny digraph for G. Then, \(U=\{ u\in {{\,\mathrm{V}\,}}(G) : \ {{\,\mathrm{N}\,}}_D^-[u] \cap {{\,\mathrm{V}\,}}(G) = \{u\} \}\) is an \(\mathcal {F}\)-percolating set for \(\mathcal {F} = (D\Cap G) \setminus \left( {\begin{array}{c}{{\,\mathrm{V}\,}}(G)\\ 1\end{array}}\right) \).

Proof

By the definition of \(D\Cap G\), U and \({{\,\mathrm{\mathcal {P}}\,}}(D)\), we may assume that \({{\,\mathrm{A}\,}}(D)\cap \bigl (({{\,\mathrm{V}\,}}(D)\setminus {{\,\mathrm{V}\,}}(G) )\times {{\,\mathrm{V}\,}}(G)\bigr )=\emptyset \). It then follows that D is compatible with some total order \(u_1,\ldots ,u_m, v_1,\ldots , v_q, z_1,\ldots ,z_p\) where \(U = \{u_1,\ldots ,u_m\}\), \({{\,\mathrm{V}\,}}(D) \setminus {{\,\mathrm{V}\,}}(G) = \{ z_1,\ldots ,z_p \}\) and \(|{{\,\mathrm{N}\,}}_D^-[v_i] \cap {{\,\mathrm{V}\,}}(G) |\ge 2\) for all \(i\in [q]\). For each \(i\in [q]\), there exists \(e_i \doteq {{\,\mathrm{N}\,}}_D^-[v_i] \cap {{\,\mathrm{V}\,}}(G) \in \mathcal {F}\) such that \(v_i \in e_i \subseteq \{ u_1, \ldots , u_m, v_1, \ldots , v_i \}\). This ensures that U is an \(\mathcal {F}\)-percolating set. \(\square \)

Theorem 7

It holds for every connected graph G that \(\phi (G) = \min _{ \mathcal {F} \vdash G } \left( |\mathcal {F} |- {{\,\mathrm{\overline{m}}\,}}(\mathcal {F}) \right) \).

Proof

Let \(\mathcal {F}\) be an edge clique cover of G. Let U be an \(\mathcal {F}\)-percolating set with \({{\,\mathrm{m}\,}}(\mathcal {F})=|U|\). By the definition of the bootstrap process, we can enumerate \({{\,\mathrm{V}\,}}(G) \setminus U\) as \(v_1,\ldots ,v_{q}\) so that there exists \(e_i\in \mathcal {F}\) satisfying \(v_i \in e_i \subseteq ( U \cup \{ v_1,\ldots ,v_i \} )\) for all \(i\in [q]\). Note that \(q=|{{\,\mathrm{V}\,}}(G) |- |U |={{\,\mathrm{\overline{m}}\,}}(\mathcal {F})\). Put \(p = |\mathcal {F}|- q\) and write \(\mathcal {F} = \{ e_1,\ldots ,e_q, f_1,\ldots ,f_{p} \}\). Let D be the digraph with \({{\,\mathrm{V}\,}}(D) = {{\,\mathrm{V}\,}}(G) \cup \{ z_1,\ldots ,z_{p} \}\) and \({{\,\mathrm{A}\,}}(D)= \bigcup _{i\in [p]} \{ (u, z_i) : \ u\in f_i \} \cup \bigcup _{i\in [q]} \{ (u, v_i) : \ u\in e_i\setminus \{v_i\} \}\). It is easy to check that D is a phylogeny digraph for G. Henceforth, we obtain \(\phi (G) \le |{{\,\mathrm{V}\,}}(D)\setminus {{\,\mathrm{V}\,}}(G) |= p = |\mathcal {F}|- q = |\mathcal {F}|-{{\,\mathrm{\overline{m}}\,}}(\mathcal {F})\).

To end the proof, it remains to find an edge clique cover \(\mathcal {F}\) of G for which \(\phi (G) \ge |\mathcal {F}|-{{\,\mathrm{\overline{m}}\,}}(\mathcal {F})\) happens. This is trivial when \(|{{\,\mathrm{V}\,}}(G)|=1\). We then assume that \(|{{\,\mathrm{V}\,}}(G)|>1\) and hence G contains no isolated vertices.

Let D be an optimal phylogeny digraph for G. Put \(U = \{ u\in {{\,\mathrm{V}\,}}(G) : \ {{\,\mathrm{N}\,}}_D^-[u] \cap {{\,\mathrm{V}\,}}(G) = \{u\} \}\) and \(\mathcal {F} = (D\Cap G) \setminus \left( {\begin{array}{c}{{\,\mathrm{V}\,}}(G)\\ 1\end{array}}\right) \). Note that \(|U |+ |\mathcal {F} |= |{{\,\mathrm{V}\,}}(D) |=|{{\,\mathrm{V}\,}}(G) |+\phi (G)\). Since G has no isolated vertices, it follows from Lemma 5 that \(\mathcal {F} \vdash G\). By Lemma 6, we know that U is an \(\mathcal {F}\)-percolating set. Consequently, we obtain \({{\,\mathrm{\overline{m}}\,}}(\mathcal {F}) \ge |{{\,\mathrm{V}\,}}(G) |-|U |= |{{\,\mathrm{V}\,}}(G) |-( |{{\,\mathrm{V}\,}}(D) |- |\mathcal {F} |)= |\mathcal {F} |- \phi (G)\), as was to be shown. \(\square \)

3 Linear Algebra of Slices

Let \(a_1,\ldots ,a_n\ge 2\) be integers. For each \(x\in \mathrm {Grid}_{a_1,\ldots ,a_n}\), we set \(|x|_1 \) to be \(|\{ i\in [n] : \ x_i = 1 \} |\). For any \(k\in [n]\), let us define

$$\begin{aligned} {{\,\mathrm{Q}\,}}_k^{a_1,\ldots ,a_n} = \{ x\in \mathrm {Grid}_{a_1,\ldots ,a_n} : \ |x|_1 \ge k \}. \end{aligned}$$

Note that the set \({{\,\mathrm{Q}\,}}_k^{a_1,\ldots ,a_n}\) is the so-called \((n-k,n)\)-rainbow sunflower on an n-colored set of type \((a_1,\ldots ,a_n)\) [25, Definition 1.16]. The general rainbow sunflower constructions have been used to construct families of large collapsible rainbow simplicial complexes; see [25, Theorem 2.1].

Lemma 8

\(\mathrm {Grid}_{a_1,\ldots ,a_n} \setminus {{\,\mathrm{Q}\,}}_k^{a_1,\ldots ,a_n}\) is an \(\mathcal {F}_{a_1,\ldots ,a_n}^{k}\)-percolating set.

Proof

For each nonnegative integer t, we set \(U_t = \{ x\in \mathrm {Grid}_{a_1,\ldots ,a_n} : \ |x|_1 < k+t \}\). For each \(x \in \mathrm {Grid}_{a_1,\ldots ,a_n}\) with \(|x|_1 \ge k\), choose J to be a k-subset of \(\{ i\in [n] : \ x_i = 1 \}\) and let \(F = \mathrm {Grid}_{a_1,\ldots ,a_n}(x; J)\) be the k-slice along the direction J through x. Note that \(|y|_1 > |x|_1\) for all \(y\in F \setminus \{x\}\). This implies that \(U_{t+1} = U_{t} \cup \{ x\in \mathrm {Grid}_{a_1,\ldots ,a_n} : \ \exists F \in \mathcal {F}_{a_1,\ldots ,a_n}^{k} \text{ with } F\setminus U_t = \{ x \} \}\) for all nonnegative integers t, and so \([U_0]_{\mathcal {F}_{a_1,\ldots ,a_n}^{k}} = U_{n-k+1} = \mathrm {Grid}_{a_1,\ldots ,a_n}\). In other words, \(U_0 = \mathrm {Grid}_{a_1,\ldots ,a_n} \setminus {{\,\mathrm{Q}\,}}_k^{a_1,\ldots ,a_n}\) is an \(\mathcal {F}_{a_1,\ldots ,a_n}^{k}\)-percolating set. \(\square \)

For any integers \(0\le t\le k\le n\) and \(a_1,\ldots ,a_n\ge 2\), let \(\mathcal {W}_{t,k}^{a_1,\ldots ,a_n}\) designate the \(\mathcal {F}_{a_1,\ldots ,a_n}^{n-t}\times \mathcal {F}_{a_1,\ldots ,a_n}^{n-k}\) (0, 1) matrix whose (X, Y)-entry is 1 if and only if \(X\supseteq Y\). Note that \(\mathcal {W}_{t,k}^{a_1,\ldots ,a_n}\) is referred to as the (t, k)-inclusion matrix of rainbow subsets of an n-colored set of type \((a_1,\ldots ,a_n)\) [26]. We remind the reader that \(\sigma _i\) is the ith elementary symmetric polynomial, as indicated in the paragraph above Theorem 3.

Theorem 9

([26, Theorem 5.2(2)]) For any n integers \(a_1,\ldots ,a_n\ge 2\) and for any integer t with \(0\le t\le n\), the rank of \(\mathcal {W}_{t,n}^{a_1,\ldots ,a_n}\) over any field is \(\sum _{i=0}^t \sigma _i(a_1-1,\ldots ,a_n-1)\).

In light of Theorem 7, to estimate the phylogeny number of a given connected graph G, we should estimate \(|\mathcal {F} |- {{\,\mathrm{\overline{m}}\,}}(\mathcal {F})\) for some “nice” edge clique cover \(\mathcal {F}\) of G. For the graph \(\mathrm {H}_{a_1,\ldots ,a_n}^{k}\), we are now ready to look into its edge clique cover \(\mathcal {F}_{a_1,\ldots ,a_n}^{k}\).

Theorem 10

Let \(a_1,\ldots ,a_n\ge 2\) be n integers. For every \(k\in [n]\), it holds that \({{\,\mathrm{\overline{m}}\,}}(\mathcal {F}_{a_1,\ldots ,a_n}^{k}) = \sum _{i=0}^{n-k} \sigma _{i}(a_1-1,\ldots ,a_n-1)\).

Proof

By Lemma 8, \(\mathrm {Grid}_{a_1,\ldots ,a_n} \setminus {{\,\mathrm{Q}\,}}_k^{a_1,\ldots ,a_n}\) is an \(\mathcal {F}_{a_1,\ldots ,a_n}^{k}\)-percolating set. This implies that \({{\,\mathrm{\overline{m}}\,}}(\mathcal {F}_{a_1,\ldots ,a_n}^{k}) \ge |{{\,\mathrm{Q}\,}}_k^{a_1,\ldots ,a_n} |= \sum _{i=0}^{n-k} \sigma _{i}(a_1-1,\ldots ,a_n-1)\).

On the other hand, let U be a \(\mathcal {F}_{a_1,\ldots ,a_n}^{k}\)-percolating set with \(|U |= {{\,\mathrm{m}\,}}(\mathcal {F}_{a_1,\ldots ,a_n}^{k})\). Enumerate \(\mathrm {Grid}_{a_1,\ldots ,a_n} \setminus U\) as \(x^{(1)},\ldots ,x^{(m)}\) such that for each \(i\in [m]\), there exists \(e^{(i)} \in \mathcal {F}_{a_1,\ldots ,a_n}^{k}\) with \(x^{(i)} \in e^{(i)} \subseteq U \cup \{ x^{(1)}, \ldots , x^{(i)} \}\). Let M be the \(m\times m\) (0, 1) matrix whose (i, j)-entry is 1 if and only if \(x^{(i)} \in e^{(j)}\). Note that M is an upper triangular matrix with all ones along its main diagonal and it is a submatrix of \(\mathcal {W}_{n-k,n}^{a_1,\ldots ,a_n}\). It then follows from Theorem 9 that \({{\,\mathrm{\overline{m}}\,}}(\mathcal {F}_{a_1,\ldots ,a_n}^{k}) = m \le \sum _{i=0}^{n-k} \sigma _{i}(a_1-1,\ldots ,a_n-1)\). \(\square \)

We mention that Theorem 10 can be read as a special case of a more general result of Balogh, Bollobás, Morris, and Riordan [24, Theorem 4]. Before we know of the work of Balogh et al., Wu and Xiong once posed it as a conjecture in 2020 [27, Conjecture 2]. An independent proof of the case \(k=1\) of Theorem 10 has been given by Frankl and Pach [28, Theorem 1]. A generalization of Theorem 10, which is different from Balogh-Bollobás-Morris-Riordan’s Theorem [24, Theorem 4], can be found in [25, Theorem1.13]. Some discussions of related work is present in [25, Remark 1.12].

4 Upper Bounds

Lemma 11

Let \(a_1,\ldots ,a_n\ge 2\) and \(k\in [n]\). Then,

$$\begin{aligned} \phi \left( \mathrm {H}_{a_1,\ldots ,a_n}^{k}\right) \le \sigma _{n-k}(a_1,\ldots ,a_n) - \sum _{i=0}^{n-k} \sigma _i(a_1-1, \ldots , a_n-1). \end{aligned}$$

Proof

By Theorems 7 and 10, we have \(\phi (\mathrm {H}_{a_1,\ldots ,a_n}^{k}) \le |\mathcal {F}_{a_1,\ldots ,a_n}^{k} |- {{\,\mathrm{\overline{m}}\,}}(\mathcal {F}_{a_1,\ldots ,a_n}^{k}) = \sigma _{n-k}(a_1,\ldots ,a_n) - \sum _{i=0}^{n-k} \sigma _i(a_1-1, \ldots , a_n-1)\), completing the proof. \(\square \)

The following three examples indicate three cases in which we can improve the upper bound reported in Lemma 11. In other words, by virtue of Theorem 7, it may happen for \(k\ge 2\) that \(\mathcal {F}=\mathcal {F}_{a_1,\ldots ,a_n}^{k}\) does not minimize the value \(|\mathcal {F} |- {{\,\mathrm{\overline{m}}\,}}(\mathcal {F}) \) for all those \(\mathcal {F} \vdash \mathrm {H}_{a_1,\ldots ,a_n}^{k}\).

Example 2

We consider the following edge clique cover of \(\mathrm {H}_{2,2,2}^{2}\):

$$\begin{aligned} \left\{ \begin{array}{l} K_1 = \{ (1,1,1), (1,2,1), (1,2,2), (1,1,2) \}, \\ K_2 = \{ (1,1,1), (2,2,1), (2,1,2), (2,1,1) \}, \\ K_3 = \{ (1,2,1), (2,2,1), (2,2,2), (2,1,1) \}, \\ K_4 = \{ (1,1,2), (2,2,2), (2,1,2), (2,1,1) \}, \\ K_5 = \{ (2,2,1), (1,2,2), (2,1,2), (2,2,2) \}. \end{array} \right. \end{aligned}$$

Let \(D_1\) be the graph with vertex set \(\mathrm {Grid}_{2,2,2} \cup \{z_1,z_2\}\) such that \({{\,\mathrm{A}\,}}(D_1) = \bigcup _{i\in [5]} A_i\), where

$$\begin{aligned} \left\{ \begin{array}{l} A_1 = \{ (u, z_2) : \ u\in K_1 \}, \\ A_2 = \{ (u, z_1) : \ u\in K_2 \}, \\ A_3 = \{ (u, (1,1,1)) : \ u\in K_3 \}, \\ A_4 = \{ (u, (1,2,1)) : \ u\in K_4 \}, \\ A_5 = \{ (u, (1,1,2)) : \ u\in K_5 \}, \end{array} \right. \end{aligned}$$

and let \(D_2\) be the graph with vertex set \(\mathrm {Grid}_{2,2,2} \cup \{z_1\}\) such that \({{\,\mathrm{A}\,}}(D_2) = \bigcup _{i\in [5]} A'_i\), where

$$\begin{aligned} \left\{ \begin{array}{l} A'_1 = \{ (u, z_1) : \ u\in K_1 \}, \\ A'_2 = \{ (u, (1,1,1)) : \ u\in K_2 \setminus \{ (1,1,1) \} \}, \\ A'_3 = \{ (u, (1,2,1)) : \ u\in K_3 \setminus \{ (1,2,1) \} \}, \\ A'_4 = \{ (u, (1,1,2)) : \ u\in K_4 \setminus \{ (1,1,2) \} \}, \\ A'_5 = \{ (u, (2,2,1)) : \ u\in K_5 \setminus \{ (2,2,1) \} \}. \end{array} \right. \end{aligned}$$

Note that both \(D_1\) and \(D_2\) are compatible with the ensuing total order:

$$\begin{aligned}&(2,2,2)< (1,2,2)< (2,1,2)< (2,2,1)< (2,1,1) \\&\qquad \qquad< (1,1,2)< (1,2,1)< (1,1,1)< z_1 < z_2. \end{aligned}$$

It is not difficult to check that \(\mathrm {H}_{2,2,2}^{2} \lhd {{\,\mathrm{\mathcal {C}}\,}}(D_1)\), \(|{{\,\mathrm{V}\,}}(D_1)|= 10\), \(\mathrm {H}_{2,2,2}^{2} \lhd {{\,\mathrm{\mathcal {P}}\,}}(D_2)\) and \(|{{\,\mathrm{V}\,}}(D_2)|= 9\). This implies that \(\kappa (\mathrm {H}_{2,2,2}^{2}) \le |{{\,\mathrm{V}\,}}(D_1)|-|{{\,\mathrm{V}\,}}(\mathrm {H}_{2,2,2}^{2})|=2\) and \(\phi (\mathrm {H}_{2,2,2}^{2}) \le |{{\,\mathrm{V}\,}}(D_2)|-|{{\,\mathrm{V}\,}}(\mathrm {H}_{2,2,2}^{2})|=1\).

Example 3

Let p be a positive integer and let \( k =2p \). Let m and n be two integers such that \( m \ge 2 \) and \( n \ge (m+1)k \). Consider the generalized Hamming graph \(G=\mathrm {H}_{a_1,\ldots ,a_n}^{k}\) where \(a_i = m\) for all \(i\in [n]\). For each \(v\in {{\,\mathrm{V}\,}}(G)\), let \(K_v=\{ u\in {{\,\mathrm{V}\,}}(G) : \ {{\,\mathrm{d}\,}}(u,v)\le p \}\), which is a clique of G. One can directly check that \(\{ K_v : \ v\in {{\,\mathrm{V}\,}}(G) \} \vdash G\) and that

$$\begin{aligned} \phi (G) \le |\{ K_v : \ v\in {{\,\mathrm{V}\,}}(G) \}|= & {} m^n< \left( {\begin{array}{c}n\\ k\end{array}}\right) m^{n-k} - m^n \\&< \sigma _{n-k}(m,\ldots ,m) - \sum _{i=0}^{n-k} \sigma _i(m-1, \ldots , m-1). \end{aligned}$$

Example 4

Let p be a positive integer and let \( k = 2p + 1 \). Let m and n be two integers satisfying \( m \ge 2 \) and \( n \ge (2 m^3 + 1) k\). Let \(G=\mathrm {H}_{a_1,\ldots ,a_n}^{k}\) where \(a_i = m\) for all \(i\in [n]\). For each \(v\in {{\,\mathrm{V}\,}}(G)\) and \( J \in \left( {\begin{array}{c}[n]\\ p+1\end{array}}\right) \), define \(K_{v,J}\) to be \(\{ u\in {{\,\mathrm{V}\,}}(G) : \ {{\,\mathrm{d}\,}}(u,v)\le p \} \cup \mathrm {Grid}_{a_1,\ldots ,a_n}(J;v) \), which is a clique of G. It is not difficult to verify that \(\{ K_{v,J} : \ v\in {{\,\mathrm{V}\,}}(G), J \in \left( {\begin{array}{c}[n]\\ p+1\end{array}}\right) \} \vdash G\) and that

$$\begin{aligned} \phi (G)\le & {} \left|\left\{ K_{v,J} : \ v\in {{\,\mathrm{V}\,}}(G), J \in \left( {\begin{array}{c}[n]\\ p+1\end{array}}\right) \right\} \right|= \left( {\begin{array}{c}n\\ p+1\end{array}}\right) m^n \\\le & {} (\frac{n-k}{k})^{p}\left( {\begin{array}{c}n\\ p+1\end{array}}\right) m^{n-k} - \left( {\begin{array}{c}n\\ p+1\end{array}}\right) m^n< \left( {\begin{array}{c}n\\ k\end{array}}\right) m^{n-k} - m^n \\< & {} \sigma _{n-k}(m,\ldots ,m) - \sum _{i=0}^{n-k} \sigma _i(m-1, \ldots , m-1). \end{aligned}$$

5 Lower Bounds

Let G be a graph. For each \(v\in {{\,\mathrm{V}\,}}(G)\), let \({{\,\mathrm{N}\,}}_G(v) = \{ u : \ \{u,v\}\in {{\,\mathrm{E}\,}}(G) \}\) and let \({{\,\mathrm{N}\,}}_G[v] = {{\,\mathrm{N}\,}}_G(v) \cup \{v\}\). For any \(v\in {{\,\mathrm{V}\,}}(G)\), we use \(\theta _G(v)\) (resp. \(\theta _G[v]\)) to represent the minimum number of cliques of G whose union contains \({{\,\mathrm{N}\,}}_G (v)\) (resp. \({{\,\mathrm{N}\,}}_G[v]\)).

Lemma 12

Let G be a graph.

  1. (1)

    [6, Proposition 7] \(\kappa (G) \ge \min _{v\in {{\,\mathrm{V}\,}}(G)} \theta _G[v]\).

  2. (2)

    [3, Lemma 18] \(\phi (G) \ge \min _{v\in {{\,\mathrm{V}\,}}(G)} \theta _G(v) - 1\).

  3. (3)

    [15, Lemma 2 (i)] \(\phi (G) - \kappa (G) + 1 \ge 0\).

Proof of Theorem 2

Fix an integer \(m\ge 3\). Note that \(\min _{v\in {{\,\mathrm{V}\,}}(\mathrm {H}_{2,2,2}^{2})} \theta _{\mathrm {H}_{2,2,2}^{2}}[v] = 2\) and that \(\min _{v\in {{\,\mathrm{V}\,}}(\mathrm {H}_{m,m,m}^{2})} \theta _{\mathrm {H}_{m,m,m}^{2}}[v] = 3\). It then follows from Lemma 12 (1) that \(\kappa (\mathrm {H}_{2,2,2}^{2}) \ge 2\) and that \(\kappa (\mathrm {H}_{m,m,m}^{2}) \ge 3\). We already see in Example 2 that \(\kappa (\mathrm {H}_{2,2,2}^{2}) \le 2\); by Lemma 11 and Lemma 12 (3), we find that \(\kappa (\mathrm {H}_{m,m,m}^{2}) \le 3\). \(\square \)

Lemma 13

Let G be a graph and let \(\mathcal {F}\) be the set of all maximal cliques of G. Assume that \(|S_1\cap S_2 |\le 1\) for every \(\{S_1, S_2\}\in \left( {\begin{array}{c}\mathcal {F}\\ 2\end{array}}\right) \). Then, there exists an optimal phylogeny digraph D for G such that \(\Bigl (\left( {\begin{array}{c}{{\,\mathrm{V}\,}}(G)\\ 1\end{array}}\right) \cup \mathcal {F} \Bigr ) \supseteq D\Cap G \supseteq \mathcal {F}\).

Proof

Let \(D'\) be an optimal phylogeny digraph for G. Since \(D'\) is acyclic, it is compatible with a total order \(v_1< \cdots < v_m\) on \({{\,\mathrm{V}\,}}(D')\). For each \(S \in \mathcal {F}\cap \left( {\begin{array}{c}{{\,\mathrm{V}\,}}(G)\\ >1\end{array}}\right) \), define

$$\begin{aligned} \Gamma (S) = \left\{ v\in {{\,\mathrm{V}\,}}(D') : \ {{\,\mathrm{N}\,}}^-_{D'}[v] \cap {{\,\mathrm{V}\,}}(G) \in \left( {\begin{array}{c}S\\ > 1\end{array}}\right) \right\} \not = \emptyset , \end{aligned}$$

and let \(\gamma (S) \) be the maximum element of \(\Gamma (S) \) according to the total order < on \({{\,\mathrm{V}\,}}(D')\). If \(\gamma (S_1) = \gamma (S_2) = v\) for two elements \(S_1\) and \(S_2\) from \(\mathcal {F}\cap \left( {\begin{array}{c}{{\,\mathrm{V}\,}}(G)\\ >1\end{array}}\right) \), then \(S_1\cap S_2\) is a superset of \({{\,\mathrm{N}\,}}^-_{D'}[v] \cap {{\,\mathrm{V}\,}}(G)\), whose size is at least two. Our assumption then forces that \(S_1 = S_2\). Let \(U=\{\gamma (S):\ S \in \mathcal {F}\cap \left( {\begin{array}{c}{{\,\mathrm{V}\,}}(G)\\ >1\end{array}}\right) \}\) and let \(W=\bigcup _{S \in \mathcal {F}\cap \left( {\begin{array}{c}{{\,\mathrm{V}\,}}(G)\\ 1\end{array}}\right) }S\). For each \(w\in W\), it is clear that \({{\,\mathrm{N}\,}}^-_{D'}[w] \cap {{\,\mathrm{V}\,}}(G)= \{w\}\). We thus conclude that \(W\cap U=\emptyset \).

Now let us construct the required digraph D with \({{\,\mathrm{V}\,}}(D)={{\,\mathrm{V}\,}}(D')\) by putting \((v ,u)\in {{\,\mathrm{A}\,}}(D)\) if and only if there exists \(S \in \mathcal {F}\cap \left( {\begin{array}{c}{{\,\mathrm{V}\,}}(G)\\ >1\end{array}}\right) \) such that \(u = \gamma (S)\not =v \in S\).

As D is still compatible with the total order \(v_1< \cdots < v_m\), it is acyclic. In addition, if \(|{{\,\mathrm{N}\,}}^-_{D}[u]\cap {{\,\mathrm{V}\,}}(G)|\ge 2\), we must have \(u\in U\) and \(\bigl ({{\,\mathrm{N}\,}}^-_{D}[u]\cap {{\,\mathrm{V}\,}}(G) \bigr )\in \mathcal {F}\cap \left( {\begin{array}{c}{{\,\mathrm{V}\,}}(G)\\ >1\end{array}}\right) \). For any isolated vertex w of G, from \(W\cap U=\emptyset \) we deduce that \({{\,\mathrm{N}\,}}^-_{D}[w]=\{w\}\). So far, we can see that \(D\Cap G \) must be the set \(\mathcal F\) together with zero or a positive number of singleton sets. Because \(\mathcal {F}\) is surely an edge clique cover of G, an application of Lemma 5 then completes the proof. \(\square \)

Lemma 14

Let \(a_1,\ldots ,a_n\ge 2\) be integers. Then, it holds \(\phi (\mathrm {H}_{a_1,\ldots ,a_n}^{1}) \ge \sigma _{n-1}(a_1,\ldots ,a_n) - \sum _{i=0}^{n-1} \sigma _i(a_1-1, \ldots , a_n-1)\).

Proof

Note that \(\mathcal {F}_{a_1,\ldots ,a_n}^{1}\) is the set of all maximal cliques of \(\mathrm {H}_{a_1,\ldots ,a_n}^{1}\) and that \(|S_1\cap S_2 |\le 1\) for every \(\{S_1, S_2\}\in \left( {\begin{array}{c}\mathcal {F}_{a_1,\ldots ,a_n}^{1}\\ 2\end{array}}\right) \). By virtue of Lemma 13, we can find an optimal phylogeny digraph D for \(\mathrm {H}_{a_1,\ldots ,a_n}^{1}\) satisfying \(( D \Cap \mathrm {H}_{a_1,\ldots ,a_n}^{1} ) \setminus \left( {\begin{array}{c}{{\,\mathrm{V}\,}}(\mathrm {H}_{a_1,\ldots ,a_n}^{1})\\ 1\end{array}}\right) = \mathcal {F}_{a_1,\ldots ,a_n}^{1}\). Put \(W = \{ v\in {{\,\mathrm{V}\,}}(\mathrm {H}_{a_1,\ldots ,a_n}^{1}) : \ {{\,\mathrm{N}\,}}^-_{D}[v] \in \mathcal {F}_{a_1,\ldots ,a_n}^{1} \}\) and \(U = {{\,\mathrm{V}\,}}(\mathrm {H}_{a_1,\ldots ,a_n}^{1}) \setminus W\). Since D is optimal, there is a one-to-one correspondence between \({{\,\mathrm{V}\,}}(D) \setminus U\) and \(\mathcal {F}_{a_1,\ldots ,a_n}^{1}\) such that every \(v\in {{\,\mathrm{V}\,}}(D) \setminus U\) is mapped to \({{\,\mathrm{N}\,}}_D^-[v] \cap {{\,\mathrm{V}\,}}(\mathrm {H}_{a_1,\ldots ,a_n}^{1}) \in \mathcal {F}_{a_1,\ldots ,a_n}^{1}\), yielding that \(|{{\,\mathrm{V}\,}}(D) |=|\mathcal {F}_{a_1,\ldots ,a_n}^{1}|+ |U|\). By Lemma 6, we know that U is an \(\mathcal {F}_{a_1,\ldots ,a_n}^{1}\)-percolating set and so \({{\,\mathrm{\overline{m}}\,}}(\mathcal {F}_{a_1,\ldots ,a_n}^{1})\ge |W|\). Therefore, we have

$$\begin{aligned}&\phi (\mathrm {H}_{a_1,\ldots ,a_n}^{1}) \\&\quad = |{{\,\mathrm{V}\,}}(D) |- |{{\,\mathrm{V}\,}}(\mathrm {H}_{a_1,\ldots ,a_n}^{1}) |\qquad \qquad \qquad \qquad \qquad (D\text { is optimal}) \\&\quad = (|\mathcal {F}_{a_1,\ldots ,a_n}^{1} |+ |U |)- |{{\,\mathrm{V}\,}}(\mathrm {H}_{a_1,\ldots ,a_n}^{1}) |\qquad \qquad ({|{{\,\mathrm{V}\,}}(D) |=|\mathcal {F}_{a_1,\ldots ,a_n}^{1}|+ |U|}) \\&\quad = |\mathcal {F}_{a_1,\ldots ,a_n}^{1}|- |W |\qquad \qquad \qquad \qquad \qquad \qquad \qquad ({W = {{\,\mathrm{V}\,}}(\mathrm {H}_{a_1,\ldots ,a_n}^{1}) \setminus U}) \\&\quad \ge |\mathcal {F}_{a_1,\ldots ,a_n}^{1}|- {{\,\mathrm{\overline{m}}\,}}(\mathcal {F}_{a_1,\ldots ,a_n}^{1}) \qquad \qquad \qquad \qquad \qquad ({{{\,\mathrm{\overline{m}}\,}}(\mathcal {F}_{a_1,\ldots ,a_n}^{1})\ge |W|}) \\&\quad = \sigma _{n-1}(a_1,\ldots ,a_n) - \sum _{i=0}^{n-1} \sigma _i(a_1-1, \ldots , a_n-1), \text {(By Theorem 10 for } k=1\text {)} \end{aligned}$$

finishing the proof. \(\square \)

Lemma 15

The maximum size of cliques in \(\mathrm {H}_{\ell : n}^{n-1}\) is \(\ell ^{n-1}\) when \(\ell \ge n\ge 2\).

Proof

For any integer k, we write \(\left\langle k\right\rangle _\ell \) for the minimum positive integer p such that \(k \equiv p \pmod {\ell }\). For each \((i_1,\ldots ,i_{n-1})\in [\ell ]^{[n-1]}\), let

$$\begin{aligned} S_{i_1,\ldots ,i_{n-1}}= & {} \Bigl \{ \bigl (i_1,\ldots ,i_{n-1}, 1\bigr ), \bigl (\left\langle i_1+1 \right\rangle _\ell , \ldots , \left\langle i_{n-1}+1 \right\rangle _\ell , 2\bigr ),\ldots , \\&\bigl (\left\langle i_1+\ell -1 \right\rangle _\ell , \ldots , \left\langle i_{n-1}+\ell -1 \right\rangle _\ell , \ell \bigr ) \Bigr \}. \end{aligned}$$

It is not hard to see that \(\{ S_{i_1,\ldots ,i_{n-1}} : \ (i_1,\ldots ,i_{n-1})\in [\ell ]^{[n-1]} \}\) gives a partition of \({{\,\mathrm{V}\,}}(\mathrm {H}_{\ell : n}^{n-1})\) into \(\ell ^{n-1}\) nonempty independent sets of \(\mathrm {H}_{\ell : n}^{n-1}\). On the other hand, for the set \(\mathcal {F}_{a_1,\ldots ,a_n}^{n-1}\), where \(a_1 = \cdots = a_n = \ell \), every element in it is a clique of \(\mathrm {H}_{\ell : n}^{n-1}\) of size \(\ell ^{n-1}\). Consequently, the maximum size of cliques of \(\mathrm {H}_{\ell : n}^{n-1}\) is \(\ell ^{n-1}\). \(\square \)

Proof of Theorem 3

Lemma 11 in conjunction with Lemma 14 leads to the first statement.

To verify the second claim, we fix \(m\ge 3\) and observe that \( \theta _{\mathrm {H}_{2,2,2}^{2}}(v) = 2\) for all \(v\in {{\,\mathrm{V}\,}}(\mathrm {H}_{2,2,2}^{2})\) while \(\theta _{\mathrm {H}_{m,m,m}^{2}}(w) = 3\) for all \(w\in {{\,\mathrm{V}\,}}(\mathrm {H}_{m,m,m}^{2})\). This enables us to conclude from Lemma 12 (2) that \(\phi ( \mathrm {H}_{2,2,2}^{2} ) \ge 1\) and that \(\phi ( \mathrm {H}_{m,m,m}^{2} ) \ge 2\). According to Example 2, we obtain \(\phi ( \mathrm {H}_{2,2,2}^{2} ) = 1\). In light of Lemma 11, we have \(\phi ( \mathrm {H}_{m,m,m}^{2} ) = 2\).

Lastly, we turn to the third statement. Let \(P(x) = x^{n} - (x-1)^{n} - 1\) and \(Q(x) = (n-1)(x^{n-1} - 1)\) be two polynomials in a single variable x. Since \(P(x)-Q(x)\) is a monic polynomial in x, we can find a real m so that \(P(\ell )>Q(\ell )\) for all \(\ell >m\). We now fix an integer \(\ell \ge \max \{m,n\}\) and let \(a_1 = \cdots = a_n = \ell \). Applying Lemma 11 for \(k=n-1\), we have \(\phi (\mathrm {H}_{a_1,\ldots ,a_n}^{n-1}) \le n-1\). Our final object thus reduces to proving \(\phi (\mathrm {H}_{a_1,\ldots ,a_n}^{n-1}) \ge n-1\).

Let \(G=\mathrm {H}_{a_1,\ldots ,a_n}^{n-1}\) and let D be an optimal phylogeny digraph for G. Pick \(v\in {{\,\mathrm{V}\,}}(G)\). For every clique K of G, \((K \cap {{\,\mathrm{N}\,}}_G(v))\cup \{v\}\) is a clique in G, which, according to Lemma 15, has size at most \(\ell ^{n-1}\). Henceforth, every clique can cover at most \(\ell ^{n-1}-1\) elements of \({{\,\mathrm{N}\,}}_G(v)\). Note that \(\left|{{\,\mathrm{N}\,}}_G(v) \right|= P(\ell )> Q(\ell )\). By the pigeonhole principle, we need more than \(\frac{Q(\ell )}{\ell ^{n-1}-1}=n-1\) cliques to cover \({{\,\mathrm{N}\,}}_G(v)\). At this moment, we can finish the proof by appealing to Lemma 12 (2). \(\square \)