Duality Results for Fractional Variational Problems and Its Application

Abstract

This article is tendered to discuss the nondifferentiable class of multiobjective variational problems of minimizing a vector of quotients of functionals of curvilinear integral type with cone constraints, and duality theorems are proved under assumptions of higher-order $(F,\alpha ,\rho ,d)$-pseudoconvexity. The value of the objective function of primal cannot exceed the value of dual is shown by giving the weak duality theorem. Moreover, we study the connection between the values of the primal problem and dual problem in strong and converse duality theorems. Also, we have obtained the examples of functionals which are higher-order $(F,\alpha ,\rho ,d)$-pseudoconvex but not higher-order F-pseudoconvex and not $(F,\alpha ,\rho ,d)$-pseudoconvex. We have given a real-world application verifying the weak duality theorem.

1 Introduction

The minimization principle is one of the most general methods for developing mathematical models that govern physical system equilibrium configurations. Also, several well-known numerical integration strategies, such as the efficient finite method, are frequently based on a paradigm of minimization. The investigation of physical and mechanical problems gives rise to the origination of the calculus of variations. It provides efficient ways of studying a curve between the two points that either maximize or minimize an integral, such as for evaluating a curve which produces the smallest area revolution surface whenever revolving around the x-axis. So, we are interested to determine a curve ${\mathfrak {z}}={\mathfrak {z}}(\tau )$ where ${\mathfrak {z}}(c_0)=\alpha ^1$ and ${\mathfrak {z}}(c_1)=\alpha ^2$, the integral

$$\begin{aligned} \int _{c_0}^{c_1}h(\tau ,{\mathfrak {z}}(\tau ),\dot{{\mathfrak {z}}}(\tau ))~\mathrm{d}\tau \end{aligned}$$

is either minimum or maximum for the given functional $h(t,{\mathfrak {z}}(\tau ),\dot{{\mathfrak {z}}}(\tau ))$ having variables $\tau ,{\mathfrak {z}},\dot{{\mathfrak {z}}}$. The solution, i.e., the curve which satisfies the aforesaid, is called the extremal. Nevertheless, calculus of variations has many applications like isoperimetric problems and brachistochrone problems. Applications of various techniques lead to the development of the solution of an individual and also explain the “variational principles” that also have implications in different domains of physics and engineering, from classical mechanics to elementary particles.

The other way of determining the solution gives rise to the concept of duality. In the optimization theory, the various duality models acquire ample space in the literature. Hanson [1] was the first to examine and generalize the relation between mathematical programming and calculus of variation. Further, for a class of variational problems with differential inequality constraints, duality formulation is derived in [2]. Dorn’s [3] pioneering work on the theory of symmetric duality has given impetus to further research. Mond and Hanson [4] worked on the notion of symmetric duality to variational problems.

Frequently, in multiobjective variational programming (MVP) problems, there are many objective functions, including minimization or maximizing. To tackle these types of problems, we define the new objective function as the weighted sum of the multiple objectives. Firstly, Bector and Husain [5] worked on Wolfe and Mond-Weir-type dual models for MVP problems under convexity assumptions. Mishra and Mukherjee [6] proved the duality relations using the parametric approach under concavity suppositions for a class of multiobjective fractional variational problems. The Wolfe and Mond-Weir-type duals for MVP problems under invexity assumptions were formulated in [7]. Mishra et al. [8] studied the nondifferentiable multiobjective variational problems using generalized invexity. Later, Mishra et al. [9] proposed the multiobjective fractional variational symmetric dual problem for a class of nondifferentiable functions and proved duality theorems under generalized invexity assumptions. Kailey and Gupta [10] proposed a pair of symmetric dual problems for a class of nondifferentiable multiobjective fractional variational programs over arbitrary cones and proved the usual duality results under generalized $(F,\alpha ,\rho ,d)$-convexity assumptions.

Second-order duality plays a vital role as it gives better bounds whenever approximation is used. The second-order dual models for variational programming problems were proposed by Chen [11]. Symmetric duality for the second-order variational problem was studied in [12], and duality results were proved under generalized invexity. Further, Jayswal and Jha [13] studied the second-order symmetric duality results for fractional variational programming problems involving cone constraints. Sachdev et al. [14] studied the second-order symmetric dual for MVP problems and proved duality theorems for this pair under the assumptions of $\eta$-bonvexity/ $\eta$-pseudobonvexity. Nevertheless, the problem’s complexity was to enforce researchers to analyze the situations where the objective functions consist of support functions, rendering it nondifferentiable in character. Therefore, Prasad et al. [15] studied the fractional problems for the second-order nondifferentiable functions and defined its symmetric dual formulation over cone constraints. Further, they obtained a comprehensive proof with the help of support function and second-order F-convexity assumptions.

Inspired by the work of [10, 13, 15, 16], we study nondifferentiable class of MVP problems of minimizing a vector of quotients of functionals of curvilinear integral type with cone constraints under assumptions of higher-order $(F,\alpha ,\rho ,d)$-convexity. The paperwork is organized as follows. Few relevant definitions and the concept of $(F,\alpha ,\rho ,d)$-convexity for fractional variational problems are introduced in Sect. 2. Also, we identify a class of nontrivial functionals which are higher-order $(F,\alpha ,\rho ,d)$-pseudoconvex but not higher-order F-pseudoconvex and not $(F,\alpha ,\rho ,d)$-pseudoconvex. The usual duality theorems proved for a ratio dual of a nondifferentiable class consisting a vector of quotients of functionals of curvilinear integral type under higher-order $(F,\alpha ,\rho ,d)$-convexity assumptions in Sect. 3. In Sect. 4, we have given a model of an FMCG company, and for that model we have proved the weak duality theorem hypothesis. Finally, Sect. 5 presents the conclusions of the work.

2 Notation and Preliminaries

Let $\varOmega =[\delta _1,\delta _2]$ be real closed interval and ${\mathcal {C}}_1\subset R^{n_1}$, ${\mathcal {C}}_2\subset R^{n_2}$ denotes the closed convex cones with $\text {int} {\mathcal {C}}_1=\phi =\text {int} {\mathcal {C}}_2$ having positive polars ${\mathcal {C}}_1^*$ and ${\mathcal {C}}_2^*$, respectively. Consider ${\mathcal {W}}(\varOmega ,R^{n_1})$ represents the space of piecewise smooth functions $s:\varOmega \rightarrow R^{n_1}$ with the norm

$$\begin{aligned} \Vert s\Vert =\Vert Ds\Vert _\infty +\Vert s\Vert _\infty , \end{aligned}$$

where the differentiation operator is given by

$$\begin{aligned}&\nu = Ds\\ \Leftrightarrow ~&s(t) = \mu _1 + \int _{\delta _1}^{t} \nu (g)\mathrm{d}g, \end{aligned}$$

where $\mu _1$ is a given boundary value. Similarly, we denote the space of piecewise smooth functions $y:\varOmega \rightarrow R^{n_2}$ as $S(\varOmega ,R^{n_2})$ with the norm as that of space ${\mathcal {W}}(\varOmega ,R^{n_1})$. For each $k\in \kappa = \{ 1,2,...,l\}$, suppose $\phi _1^k(t,s(t),{\dot{s}}(t),y(t),{\dot{y}}(t))$ and $\phi _2^k(t,s(t),{\dot{s}}(t),y(t),{\dot{y}}(t))$, where $s:\varOmega \rightarrow R^{n_1}$ and $y:\varOmega \rightarrow R^{n_2}$, with derivatives ${\dot{s}}$ and ${\dot{y}}$, are twice continuously differentiable functions. We denote the gradient vector of the scalar function $\phi _1^k(t,s,{\dot{s}},y,{\dot{y}})$ with respect to $s,{\dot{s}},y$ and ${\dot{y}}$ as $(\phi _1^k)_s,(\phi _1^k)_{{\dot{s}}},(\phi _1^k)_y$ and $(\phi _1^k)_{{\dot{y}}}$, respectively. Further, we have

$$\begin{aligned} (\phi _1^k)_s=\begin{pmatrix} \dfrac{\partial \phi _1^k}{\partial s^1} \\ \vdots \\ \dfrac{\partial \phi _1^k}{\partial s^{n_1}} \end{pmatrix} ~~~~\text {and}~~~~ (\phi _1^k)_{{\dot{s}}}=\begin{pmatrix} \dfrac{\partial \phi _1^k}{\partial {\dot{s}}^1} \\ \vdots \\ \dfrac{\partial \phi _1^k}{\partial {\dot{s}}^{n_1}} \end{pmatrix}. \end{aligned}$$

Similarly, $(\phi _2^k)_s,(\phi _2^k)_{{\dot{s}}},(\phi _2^k)_y$ and $(\phi _2^k)_{{\dot{y}}}$ denote the gradient vectors of $\phi _2^k(t,s,{\dot{s}},y,{\dot{y}})$ with respect to $s,{\dot{s}},y$ and ${\dot{y}}$, respectively.

The results mentioned below help us to prove Theorem 3.3

$$\begin{aligned} \quad \quad D(\phi _1^k)_{{\dot{y}}}=(\phi _1^k)_{{\dot{y}}t}+(\phi _1^k)_{{\dot{y}}y}{\dot{y}}+(\phi _1^k)_{{\dot{y}}{\dot{y}}}\ddot{y}+(\phi _1^k)_{{\dot{y}}s}{\dot{s}}+(\phi _1^k)_{{\dot{y}}{\dot{s}}}\ddot{s}. \end{aligned}$$

Consequently,

$$\begin{aligned} \dfrac{\partial }{\partial y}D(\phi _1^k)_{{\dot{y}}}&=D(\phi _1^k)_{{\dot{y}}y},~~\dfrac{\partial }{\partial \dot{y}}D(\phi _1^k)_{\dot{y}}=D(\phi _1^k)_{\dot{y}\dot{y}}+(\phi _1^k)_{{\dot{y}}y},~~\dfrac{\partial }{\partial \ddot{y}}D(\phi _1^k)_{\dot{y}}=(\phi _1^k)_{\dot{y}\dot{y}},\\ \dfrac{\partial }{\partial s}D(\phi _1^k)_{{\dot{y}}}&=D(\phi _1^k)_{{\dot{y}}s},~~\dfrac{\partial }{\partial \dot{s}}D(\phi _1^k)_{\dot{y}}=D(\phi _1^k)_{\dot{y}\dot{s}}\\&\quad \, \, +(\phi _1^k)_{{\dot{y}}s},~~\dfrac{\partial }{\partial \ddot{s}}D(\phi _1^k)_{\dot{y}}=(\phi _1^k)_{\dot{y}\dot{s}},\quad k\in \kappa . \end{aligned}$$

Similarly, $D(\phi _2^k)_{{\dot{y}}}$ can be defined.

Consider the following MVP problem: (FVP) Minimize

$$\begin{aligned} \int _{\delta _1}^{\delta _2} h(t,s(t),{\dot{s}}(t)) ~\mathrm{d}t=\bigg (\int _{\delta _1}^{\delta _2}h^1(t,s(t),{\dot{s}}(t))~\mathrm{d}t,\dots ,\int _{\delta _1}^{\delta _2}h^l(t,s(t),{\dot{s}}(t))~\mathrm{d}t \bigg ) \end{aligned}$$

subject to

$$\begin{aligned}&s(\delta _1)=0=s(\delta _2),\\&{\dot{s}}(\delta _1)=0={\dot{s}}(\delta _2),\\ -&\psi (t,s(t),{\dot{s}}(t))\in Q,~~~~ t\in \varOmega , \end{aligned}$$

where $h:\varOmega \times R^{n_1} \times R^{n_1} \rightarrow R^l$ and $\psi :\varOmega \times R^{n_1} \times R^{n_1} \rightarrow R^{n_2}$ are differentiable functions, Q is a closed convex cone in $R^{n_2}$ with $\text {int} Q=\phi$.

The set of feasible solutions of (FVP) is given by

$$\begin{aligned}&{\tilde{S}} = \{s\in {\mathcal {W}}(\varOmega ,R^{n_1}) ~|~ s(\delta _1)=0=s(\delta _2), ~ {\dot{s}}(\delta _1)=0={\dot{s}}(\delta _2),\\&\qquad -\psi (t,s(t),{\dot{s}}(t)) \in Q,~t\in \varOmega \}. \end{aligned}$$

Definition 2.1

[10]. A point $s\in {\tilde{S}}$ is an efficient solution of (FVP), if there does not exist another ${\bar{s}}\in {\tilde{S}}$ such that

$$\begin{aligned} \int _{\delta _1}^{\delta _2} h(t,{\bar{s}}(t),\dot{{\bar{s}}}(t))~\mathrm{d}t \le \int _{\delta _1}^{\delta _2} h(t,s(t),{\dot{s}}(t)) ~\mathrm{d}t. \end{aligned}$$

Definition 2.2

[10]. A point $s\in {\tilde{S}}$ is a weak efficient solution of (FVP), if there does not exist another ${\bar{s}}\in {\tilde{S}}$ such that

$$\begin{aligned} \int _{\delta _1}^{\delta _2} h(t,{\bar{s}}(t),\dot{{\bar{s}}}(t))~\mathrm{d}t< \int _{\delta _1}^{\delta _2} h(t,s(t),{\dot{s}}(t)) ~\mathrm{d}t. \end{aligned}$$

Definition 2.3

[10]. A functional $F:\varOmega \times {\mathcal {W}} \times {\mathcal {W}} \times {\mathcal {W}} \times {\mathcal {W}} \times R^{n_1} \rightarrow R$ is said to be sublinear in its sixth argument, if for all $s,{\dot{s}},a,{\dot{a}} \in {\mathcal {W}}(\varOmega ,R^{n_1})$, satisfy

• (i) $F(t,s,{\dot{s}},a,{\dot{a}}; e + f) \leqq F (t,s,{\dot{s}},a,{\dot{a}}; e) + F(t,s,{\dot{s}},a,{\dot{a}}; f)$, $\forall$ $e, f \in R^{n_1}$;

• (ii) $F(t,s,{\dot{s}},a,{\dot{a}}; \vartheta e) = \vartheta F(t,s,{\dot{s}},a,{\dot{a}}; e)$, for all $\vartheta \in R_+$, and $e \in R^{n_1}$.

Definition 2.4

[10]. Let O be a compact convex set in $R^{n_1}$. The support function ${\hat{S}}(s|O)$ of O is defined by

$$\begin{aligned} {\hat{S}}(s|O)=\text {max}\{s^Tz :z\in O\}. \end{aligned}$$

A support function, being convex and everywhere finite, has a subdifferential, that is, there exists $u \in R^{n_1}$ such that

$$\begin{aligned} {\hat{S}}(z|O) \geqq {\hat{S}}(s|O) + u^T(z-s) ~~ \text {for all}~ z \in O. \end{aligned}$$

The subdifferential of ${\hat{S}}(s|O)$ is given by

$$\begin{aligned} \partial {\hat{S}}(s|O) = \{u\in O :u^Ts={\hat{S}}(s|O)\}. \end{aligned}$$

For any convex set ${\hat{M}} \subset R^{n_1}$, the normal cone to ${\hat{M}}$ at a point $s \in {\hat{M}}$ is defined by

$$\begin{aligned} N_{{\hat{M}}}(s) = \{ z \in R^{n_1} : z^T(u-s) \leqq 0~ \text {for all}~ u \in {\hat{M}} \}. \end{aligned}$$

It can be easily seen that for a compact convex set O, $z \in N_O(s)$ if and only if ${\hat{S}}(z|O)=s^Tz$, or equivalently, $s \in \partial {\hat{S}}(z|O)$.

Definition 2.5

[10]. Let ${\mathcal {A}}$ be a closed convex cone in $R^{n_1}$ with nonempty interior. The positive polar cone ${\mathcal {A}}^*$ of ${\mathcal {A}}$ is defined as

$$\begin{aligned} {\mathcal {A}}^* = \{z:s^Tz\geqq 0, ~\text {for all}~ s \in {\mathcal {A}} \}. \end{aligned}$$

Let F and G be sublinear functionals with respect to sixth argument and $d=(d_1,d_2)$ where $d_1=(d_1^1,d_1^2,\dots ,d_1^l)$ $:\varOmega \times {\mathcal {W}} \times {\mathcal {W}} \times {\mathcal {W}} \times {\mathcal {W}} \rightarrow R^l$, $d_2=(d_2^1,d_2^2,\dots ,d_2^l):\varOmega \times S \times S \times S \times S \rightarrow R^l$. Let $\phi _1=(\phi _1^1,\phi _1^2,\dots ,\phi _1^l):\varOmega \times {\mathcal {W}} \times {\mathcal {W}} \times S \times S \rightarrow R^l$ and $h^k:\varOmega \times {\mathcal {W}} \times {\mathcal {W}} \times S \times S \times R^{n_1} \rightarrow R$ be differentiable functions. Further, assume $\alpha = (\alpha _1,\alpha _2)$ where $\alpha _1 :{\mathcal {W}} \times {\mathcal {W}} \rightarrow R_+ \setminus \{0\}$, $\alpha _2 :S \times S \rightarrow R_+ \setminus \{0\}$ and $\rho = (\rho _1,\rho _2)$, $\rho _1=(\rho _1^1,\rho _1^2,\dots ,\rho _1^l)$, $\rho _2=(\rho _2^1,\rho _2^2,\dots ,\rho _2^l)\in R^l$.

Definition 2.6

For each $k\in \kappa$, $\int _{\delta _1}^{\delta _2}\phi _1^k(t,s(t),{\dot{s}}(t),y(t),{\dot{y}}(t)) \mathrm{d}t$ is said to be higher-order $(F,\alpha _1,\rho _1^k,d_1^k)$-convex at a and ${\dot{a}}$ for fixed y and ${\dot{y}}$ with respect to $h^k$, if for all $(t,a,{\dot{a}},y,{\dot{y}},p^k) \in \varOmega \times {\mathcal {W}} \times {\mathcal {W}} \times S \times S \times R^{n_1}$ and $s,{\dot{s}}~ \in ~ {\mathcal {W}}$, satisfy

$$\begin{aligned}&\int _{\delta _1}^{\delta _2}\Big [ \phi _1^k(t,s,{\dot{s}},y,{\dot{y}})-\phi _1^k(t,a,{\dot{a}},y,{\dot{y}})-h^k(t,a,{\dot{a}},y,{\dot{y}},p^k)\\&\qquad +(p^k)^T\nabla _{p^k}h^k(t,a,{\dot{a}},y,{\dot{y}},p^k)-\rho ^k_1[d^k_1(t,s,{\dot{s}},a,{\dot{a}})]^2\Big ] \mathrm{d}t \\&\quad \geqq \int _{\delta _1}^{\delta _2}F\mathbf ( t,s,{\dot{s}},a,{\dot{a}};\alpha _1(s,a)((\phi _1^k)_s(t,a,{\dot{a}},y,{\dot{y}})-D(\phi _1^k)_{{\dot{s}}}(t,a,{\dot{a}},y,{\dot{y}})\\&\qquad +\nabla _{p^k}h^k(t,a,{\dot{a}},y,{\dot{y}},p^k))\mathbf ) ~\mathrm{d}t. \end{aligned}$$

Definition 2.7

For each $k\in \kappa$, $\int _{\delta _1}^{\delta _2}\phi _1^k(t,s(t),{\dot{s}}(t),y(t),{\dot{y}}(t)) \mathrm{d}t$ is said to be higher-order $(F,\alpha _1,\rho _1^k,d_1^k)$-pseudoconvex at a and ${\dot{a}}$ for fixed y and ${\dot{y}}$ with respect to $h^k$, if for all $(t,a,{\dot{a}},y,{\dot{y}},p^k) \in \varOmega \times {\mathcal {W}} \times {\mathcal {W}} \times S \times S \times R^{n_1}$ and $s,{\dot{s}}~ \in ~ {\mathcal {W}}$, satisfy

$$\begin{aligned}&\int _{\delta _1}^{\delta _2}F\mathbf ( t,s,{\dot{s}},a,{\dot{a}};\alpha _1(s,a)((\phi _1^k)_s(t,a,{\dot{a}},y,{\dot{y}})-D(\phi _1^k)_{{\dot{s}}}(t,a,{\dot{a}},y,{\dot{y}}) \\&\qquad +\nabla _{p^k}h^k(t,a,{\dot{a}},y,{\dot{y}},p^k))\mathbf ) ~\mathrm{d}t\geqq 0\\&\implies \int _{\delta _1}^{\delta _2} \phi _1^k(t,s,{\dot{s}},y,{\dot{y}})~\mathrm{d}t\geqq \int _{\delta _1}^{\delta _2} \mathbf ( \phi _1^k(t,a,{\dot{a}},y,{\dot{y}})+h^k(t,a,{\dot{a}},y,{\dot{y}},p^k)\\&\qquad -(p^k)^T\nabla _{p^k}h^k(t,a,{\dot{a}},y,{\dot{y}},p^k) +\rho ^k_1[d^k_1(t,s,{\dot{s}},a,\dot{a })]^2\mathbf ) ~ \mathrm{d}t. \end{aligned}$$

In this example, we will show that there exists a nontrivial functional which is higher-order $(F,\alpha _1,\rho _1^1,d_1^1)$-pseudoconvex but not F-pseudoconvex.

Example 2.1

Consider $\varOmega =[0,1]$, $n_1=1$, $n_2=1$ and ${\mathcal {W}}$ and S be the space of piecewise smooth functions $s:\varOmega \rightarrow [0,\infty )$ and $y:\varOmega \rightarrow [0,\infty )$, respectively. For $k=1$, define

$$\begin{aligned}&\phi _1^1:\varOmega \times {\mathcal {W}} \times {\mathcal {W}} \times S \times S \rightarrow R ~\text {as}~ \phi _1^1(t,s,{\dot{s}},y,{\dot{y}})=(s^2-s)t,\\&F:\varOmega \times {\mathcal {W}} \times {\mathcal {W}} \times {\mathcal {W}} \times {\mathcal {W}} \times R \rightarrow R ~\text {be defined as}~ F(t,s,{\dot{s}},a,{\dot{a}};\beta )=\\&-\beta (s+a+1)^2,\\&\alpha _1 :{\mathcal {W}} \times {\mathcal {W}} \rightarrow R_+ \setminus \{0\} ~\text {defined as}~\alpha _1(s,a)=\dfrac{1}{(s+a+1)^2},\\&h^1:\varOmega \times {\mathcal {W}}\times {\mathcal {W}}\times S \times S \times R \rightarrow R~\text {defined as}~ h^1(t,a,{\dot{a}},y,{\dot{y}},p^1)=p^1(a^2+a)t,\\&d_1^1:\varOmega \times {\mathcal {W}} \times {\mathcal {W}} \times {\mathcal {W}} \times {\mathcal {W}} \rightarrow R ~\text {defined as}~ d_1^1(t,s,{\dot{s}},a,{\dot{a}})=(s+a)^{1/2},\\&\text {and}\\&\rho _1^1=-4. \end{aligned}$$

Since the inequalities

$$\begin{aligned}&\int _{0}^{1}F\mathbf ( t,s,{\dot{s}},a,{\dot{a}};\alpha _1(s,a)((\phi ^1_1)_s(t,a,{\dot{a}},y,{\dot{y}})-D(\phi ^1_1)_{{\dot{s}}}(t,a,{\dot{a}},y,{\dot{y}})\\&\qquad +\nabla _{p^1}h^1(t,a,{\dot{a}},y,{\dot{y}},p^1))\mathbf ) ~\mathrm{d}t\\&=\int _{0}^{1}(-2at+t-(a^2+a)t)~\mathrm{d}t\geqq 0~\text {for}~s(t)\in {\mathcal {W}}, ~ a(t)=0 ~\text {and}~ p^1\in R \end{aligned}$$

and

$$\begin{aligned}&\int _{0}^{1} (\phi _1^1(t,s,{\dot{s}},y,{\dot{y}}) - \phi _1^1(t,a,{\dot{a}},y,{\dot{y}}) -h^1(t,a,{\dot{a}},y,{\dot{y}},p^1)\\&\qquad +p^1\nabla _{p^1}h^1(t,a,{\dot{a}},y,{\dot{y}},p^1)-\rho ^1_1[d^1_1(t,s,{\dot{s}},a,{\dot{a}})]^2)~ \mathrm{d}t\\&=\int _{0}^{1} (s^2-s)t+4s~\mathrm{d}t\\&=\int _{0}^{1}\psi _1~\mathrm{d}t\geqq 0 \end{aligned}$$

as

$$\begin{aligned} \psi _1 =(s^2-s)t+4s\geqq 0 \end{aligned}$$

(1)

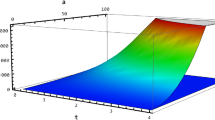
which can be conclude from the graphical representation of (1) shown in Fig. 1 for $s(t)\in [0,N],~t\in [0,1]$, where N is very large number. In general, we can conclude that inequality (1) is true for $s(t)\in [0,\infty ),~ t\in [0,1]$.

Fig. 1

Graph of $\psi _1$ for parametric values $0\le s(t) \le N<\infty$ and $0\le t \le 1$

Therefore the functional $\int _{0}^{1}\phi _1^1(t,s,{\dot{s}},y,{\dot{y}})~\mathrm{d}t$ is higher-order $(F,\alpha _1,\rho _1^1,d_1^1)$-pseudoconvex at $a(t)=0$. But it is not higher-order F- pseudoconvex at $a(t)=0$ as,

$$\begin{aligned}&\int _{0}^{1}F\mathbf ( t,s,{\dot{s}},a,{\dot{a}};((\phi ^1_1)_s(t,a,{\dot{a}},y,{\dot{y}})-D(\phi ^1_1)_{{\dot{s}}}(t,a,{\dot{a}},y,{\dot{y}})\\&\qquad +\nabla _{p^1}h^1(t,a,{\dot{a}},y,{\dot{y}},p^1))\mathbf ) ~\mathrm{d}t\int _{0}^{1}\bigg ( (-2at+t-(a^2+a)t)(s+a+1)^2 \bigg )~\mathrm{d}t\\&=\int _{0}^{1}\psi _2~\mathrm{d}t\geqq 0 \end{aligned}$$

where

$$\begin{aligned} \psi _2 =t(s+1)^2\geqq 0 \end{aligned}$$

(2)

which can be conclude from the graphical representation of inequality (2) shown in Fig. 2 for $s(t)\in [0,N],~t\in [0,1]$, where N is very large number. In general, we can conclude that inequality (2) is true for $s(t)\in [0,\infty ),~ t\in [0,1]$.

Fig. 2

Graph of $\psi _2$ for parametric values $0\le s(t) \le N<\infty$ and $0\le t \le 1$

But

$$\begin{aligned}&\int _{0}^{1} (\phi _1^1(t,s,{\dot{s}},y,{\dot{y}}) - \phi _1^1(t,a,{\dot{a}},y,{\dot{y}}) -h^1(t,a,{\dot{a}},y,{\dot{y}},p^k)\\&\qquad +p^1\nabla _{p^1}h^1(t,a,{\dot{a}},y,{\dot{y}},p^1))~ \mathrm{d}t=\int _{0}^{1} (s^2-s)t~\mathrm{d}t.\\&\text {If we take} ~s(t)=\frac{1}{2}\\&\int _{0}^{1} (s^2-s)t~\mathrm{d}t=-0.125<0. \end{aligned}$$

So, it is not higher-order F- pseudoconvex at $a(t)=0$.

In this example, we will show that there exists a nontrivial functional which is higher-order $(F,\alpha _1,\rho _1^1,d_1^1)$-pseudoconvex but not $(F,\alpha _1,\rho _1^1,d_1^1)$-pseudoconvex.

Example 2.2

Let $\varOmega =[0.004,1]$ and ${\mathcal {W}}$ and S be the space of piecewise smooth functions $s:\varOmega \rightarrow [0,\infty )$ and $y:\varOmega \rightarrow [0,\infty )$, respectively. For $k=1$, define

$$\begin{aligned}&\phi _1^1:\varOmega \times {\mathcal {W}} \times {\mathcal {W}} \times S \times S \rightarrow R ~\text {as}~ \phi _1^1(t,s,{\dot{s}},y,{\dot{y}})=t\exp (-s)+\sin (s)+{\dot{y}},\\&F:\varOmega \times {\mathcal {W}} \times {\mathcal {W}} \times {\mathcal {W}} \times {\mathcal {W}} \times R \rightarrow R ~\text {be defined as}~ F(t,s,{\dot{s}},a,{\dot{a}};\beta )=\beta (s^2+1)^2,\\&\alpha _1 :{\mathcal {W}} \times {\mathcal {W}} \rightarrow R_+ \setminus \{0\} ~\text {defined as}~\alpha _1(s,a)=s^4,\\&h^1:\varOmega \times {\mathcal {W}}\times {\mathcal {W}}\times S \times S \times R \rightarrow R~\text {defined as}~ h^1(t,a,{\dot{a}},y,{\dot{y}},p^1)=-(a^2+1),\\&d_1^1:\varOmega \times {\mathcal {W}} \times {\mathcal {W}} \times {\mathcal {W}} \times {\mathcal {W}} \rightarrow R ~\text {defined as}~ d_1^1(t,s,{\dot{s}},a,{\dot{a}})=s^{1/4}, \\&\text {and}\\&\rho _1^1=-1. \end{aligned}$$

Since this inequality

$$\begin{aligned}&\int _{0.004}^{1}F\mathbf ( t,s,{\dot{s}},a,{\dot{a}};\alpha _1(s,a)((\phi _1^1)_s(t,a,{\dot{a}},y,{\dot{y}})-D(\phi _1^1)_{{\dot{s}}}(t,a,{\dot{a}},y,{\dot{y}})\\&\qquad +\nabla _{p^1}h^1(t,a,{\dot{a}},y,{\dot{y}},p^1))\mathbf ) ~\mathrm{d}t\\&=\int _{0.004}^{1}\big ( (s^2+1)^2s^4(-t\exp (-a)+\cos (a)) \big )~\mathrm{d}t\\&=\int _{0}^{1}\psi _3~\mathrm{d}t\geqq 0, \end{aligned}$$

where

$$\begin{aligned} \psi _3=\left( (s^2+1)^2s^4\left( -t\exp \left( \frac{-1}{2}\right) +\cos \left( \frac{1}{2}\right) \right) \right) \geqq 0. \end{aligned}$$

(3)

which can be conclude from the graphical representation of inequality (3) is shown in Fig. 3 for $s(t)\in [0,N],~t\in [0.004,1]$, where N is very large number. In general, we can conclude that inequality (3) is true for $s(t)\in [0,\infty ),~ t\in [0.004,1]$.

Fig. 3

Graph of $\psi _3$ for parametric values $0\le s(t) \le N<\infty$ and $0.004\le t \le 1$

And

$$\begin{aligned}&\int _{0.004}^{1} (\phi _1^1(t,s,{\dot{s}},y,{\dot{y}}) - \phi _1^1(t,a,{\dot{a}},y,{\dot{y}}) -h^1(t,a,{\dot{a}},y,{\dot{y}},p^1)\\&\qquad +p^1\nabla _{p^1}h^1(t,a,{\dot{a}},y,{\dot{y}},p^1)-\rho ^1_1[d^1_1(t,s,{\dot{s}},a,{\dot{a}})]^2)~ \mathrm{d}t\\&=\int _{0.004}^{1} \bigg (t\exp (-s)+\sin (s)+{\dot{y}}-t\exp (-a)-\sin (a)-{\dot{y}}+(a^2+1)+s^{1/2}\bigg )~\mathrm{d}t\\&=\int _{0.004}^{1} \bigg (t\exp (-s)+\sin (s)-t\exp (-a)-\sin (a)+(a^2+1)+s^{1/2}\bigg ) ~\mathrm{d}t\\&=\int _{0}^{1}\psi _4~\mathrm{d}t\geqq 0 \end{aligned}$$

where

$$\begin{aligned}&\psi _4 =\left( t\exp (-s)+\sin (s)-t\exp \left( \frac{-1}{2}\right) -\sin \left( \frac{1}{2}\right) +\left( \left( \frac{1}{2}\right) ^2+1\right) +s^{1/2}\right) \geqq 0. \end{aligned}$$

(4)

which can be conclude from the graphical representation of inequality (4) is shown in Fig. 4 for $s(t)\in [0,N],~t\in [0.004,1]$, where N is very large number. In general, we can conclude that inequality (4) is true for $s(t)\in [0,\infty ),~ t\in [0.004,1]$.

Fig. 4

Graph of $\psi _4$ for parametric values $0\le s(t) \le N<\infty$ and $0.004\le t \le 1$

Therefore the functional $\int _{0.004}^{1}\phi _1^1(t,s,{\dot{s}},y,{\dot{y}})~\mathrm{d}t$ is higher-order $(F,\alpha _1,\rho _1^1,d_1^1)$-pseudoconvex at $a(t)=1/2$. But it is not $(F,\alpha _1,\rho _1^1,d_1^1)$- pseudoconvex at $a(t)=1/2$ as,

$$\begin{aligned}&\int _{0.004}^{1}F\mathbf ( t,s,{\dot{s}},a,{\dot{a}};\alpha _1(s,a)((\phi _1^1)_s(t,a,{\dot{a}},y,{\dot{y}})-D(\phi _1^1)_{{\dot{s}}}(t,a,{\dot{a}},y,{\dot{y}})\mathbf ) ~\mathrm{d}t\\&\quad =\int _{0.004}^{1}\big ( (s^2+1)^2s^4(-t\exp (-a)+\cos (a)) \big )~\mathrm{d}t\geqq 0~\text {for}~s(t)\in {\mathcal {W}}, ~ a(t)=1/2 \\&\qquad ~\text {and}~ p^1\in R,\\&\text {but}\\&\int _{0.004}^{1} (\phi _1^1(t,s,{\dot{s}},y,{\dot{y}}) - \phi _1^1(t,a,{\dot{a}},y,{\dot{y}}) -\rho ^1_1[d^1_1(t,s,{\dot{s}},a,{\dot{a}})]^2)~ \mathrm{d}t\\&\quad =\int _{0.004}^{1} \bigg (t\exp (-s)+\sin (s)+{\dot{y}}-t\exp (-a)-\sin (a)-{\dot{y}}+s^{1/2}\bigg )~\mathrm{d}t\\&\quad =\int _{0.004}^{1} \bigg (t\exp (-s)+\sin (s)-t\exp (-a)-\sin (a)+s^{1/2}\bigg ) ~\mathrm{d}t\\&\text {If we take}~ s(t)=0.01,~\text {then above expression results as follows}\\&\int _{0.004}^{1} \bigg (t\exp (-0.01)+\sin (0.01)-t\exp (\dfrac{-1}{2})-\sin (\dfrac{1}{2})+(0.01)^{1/2}\bigg ) ~\mathrm{d}t\\&\quad \approx -0.176<0. \end{aligned}$$

Hence the above functional is higher-order $(F,\alpha _1,\rho _1^1,d_1^1)$- pseudoconvex but not $(F,\alpha _1,\rho _1^1,d_1^1)$-pseudoconvex at $a(t)=1/2$.

3 Ratio Dual for a Nondifferentiable Class Consisting a Vector of Quotients of Functionals of Curvilinear Integral Type

(HFVP) Primal Problem

Minimize

$$\begin{aligned}&\dfrac{\int _{\delta _1}^{\delta _2} \{\phi _1(t,s,{\dot{s}},y,{\dot{y}}) + {\hat{S}}(s|B) - y^Tz +h_1(t,s,{\dot{s}},y,{\dot{y}},p)-p^T\nabla _{p}h_1(t,s,{\dot{s}},y,{\dot{y}},p)\}\mathrm{d}t}{\int _{\delta _1}^{\delta _2} \{\phi _2(t,s,{\dot{s}},y,{\dot{y}}) - {\hat{S}}(s|E) + y^Tr +g_1(t,s,{\dot{s}},y,{\dot{y}},p)-p^T\nabla _{p}g_1(t,s,{\dot{s}},y,{\dot{y}},p)\}\mathrm{d}t}\\&=\Bigg ( \dfrac{\int _{\delta _1}^{\delta _2} \{\phi _1^1(t,s,{\dot{s}},y,{\dot{y}}) + {\hat{S}}(s|B^1) - y^Tz^1 +h^1_1(t,s,{\dot{s}},y,{\dot{y}},p^1)-{(p^1)}^T\nabla _{p^1}h^1_1(t,s,{\dot{s}},y,{\dot{y}},p^1)\}\mathrm{d}t,}{\int _{\delta _1}^{\delta _2} \{\phi _2^1(t,s,{\dot{s}},y,{\dot{y}}) - {\hat{S}}(s|E^1) + y^Tr^1 +g^1_1(t,s,{\dot{s}},y,{\dot{y}},p^1)-{(p^1)}^T\nabla _{p^1}g_1^1(t,s,{\dot{s}},y,{\dot{y}},p^1)\}\mathrm{d}t,}\\&\quad \quad \dfrac{\dots ,\int _{\delta _1}^{\delta _2} \{\phi _1^l(t,s,{\dot{s}},y,{\dot{y}}) + {\hat{S}}(s|B^l) - y^Tz^l +h^l_1(t,s,{\dot{s}},y,{\dot{y}},p^l)-{(p^l)}^T\nabla _{p^l}h^l_1(t,s,{\dot{s}},y,{\dot{y}},p^l)\}\mathrm{d}t}{\dots ,\int _{\delta _1}^{\delta _2}\{\phi _2^l(t,s,{\dot{s}},y,{\dot{y}}) - {\hat{S}}(s|E^l) + y^Tr^l +g^l_1(t,s,{\dot{s}},y,{\dot{y}},p^l)-{(p^l)}^T\nabla _{p^l}g_1^l(t,s,{\dot{s}},y,{\dot{y}},p^l)\}\mathrm{d}t} \Bigg ) \end{aligned}$$

Subject to

$$\begin{aligned}&s(\delta _1)=0=s(\delta _2), ~~~~~~~~~~~ y(\delta _1)=0=y(\delta _2),\\&{\dot{s}}(\delta _1)=0={\dot{s}}(\delta _2), ~~~~~~~~~~~ {\dot{y}}(\delta _1)=0={\dot{y}}(\delta _2),\\&-\sum \limits _{k=1}^{l}\lambda _k \Bigg \{ \left[ (\phi _1^k)_y-D(\phi _1^k)_{{\dot{y}}}-z^k + \nabla _{p^k}h^k_1 \right] -\left[ (\phi _2^k)_y-D(\phi _2^k)_{{\dot{y}}}+r^k + \nabla _{p^k}g^k_1 \right] \\&\qquad \dfrac{\check{F}^k(s,y)}{\check{G}^k(s,y)} \Bigg \} \in {\mathcal {C}}^*_2,\quad t\in \varOmega ,\\&y^T\sum \limits _{k=1}^{l}\lambda _k \Bigg \{ \left[ (\phi _1^k)_y-D(\phi _1^k)_{{\dot{y}}}-z^k + \nabla _{p^k}h^k_1 \right] -\left[ (\phi _2^k)_y-D(\phi _2^k)_{{\dot{y}}}+r^k + \nabla _{p^k}g^k_1 \right] \\&\qquad \dfrac{\check{F}^k(s,y)}{\check{G}^k(s,y)} \Bigg \} \geqq 0,\quad t\in \varOmega ,\\&\lambda >0,~~~~~~ s(t)\in {\mathcal {C}}_1,~~~~~~ t\in \varOmega ,\\&z^k\in D^k,~~~~~~ r^k\in H^k,~~~~~~ k\in \kappa . \end{aligned}$$

(HFVD) Dual Problem

Maximize

$$\begin{aligned}&\dfrac{\int _{\delta _1}^{\delta _2} \{\phi _1(t,a,{\dot{a}},b,{\dot{b}}) - {\hat{S}}(b|D) + a^Tw +h_2(t,a,{\dot{a}},b,{\dot{b}},q)-q^T\nabla _{q}h_2(t,a,{\dot{a}},b,{\dot{b}},q)\}\mathrm{d}t}{\int _{\delta _1}^{\delta _2} \{\phi _2(t,a,{\dot{a}},b,{\dot{b}}) + {\hat{S}}(b|H) - a^Tx +g_2(t,a,{\dot{a}},b,{\dot{b}},q)-q^T\nabla _{q}g_2(t,a,{\dot{a}},b,{\dot{b}},q)\}\mathrm{d}t}\\&=\Bigg ( \dfrac{\int _{\delta _1}^{\delta _2} \{\phi _1^1(t,a,{\dot{a}},b,{\dot{b}}) - {\hat{S}}(b|D^1) + a^Tw^1 +h^1_2(t,a,{\dot{a}},b,{\dot{b}},q^1)-{(q^1)}^T\nabla _{q^1}h^1_2(t,a,{\dot{a}},b,{\dot{b}},q^1)\}\mathrm{d}t,}{\int _{\delta _1}^{\delta _2} \{\phi _2^1(t,a,{\dot{a}},b,{\dot{b}}) + {\hat{S}}(b|H^1) - a^Tx^1 +g^1_2(t,a,{\dot{a}},b,{\dot{b}},q^1)-{(q^1)}^T\nabla _{q^1}g_2^1(t,a,{\dot{a}},b,{\dot{b}},q^1)\}\mathrm{d}t,}\\&\quad \quad \dfrac{\dots ,\int _{\delta _1}^{\delta _2} \{\phi _1^l(t,a,{\dot{a}},b,{\dot{b}}) - {\hat{S}}(b|D^l) + a^Tw^l +h^l_2(t,a,{\dot{a}},b,{\dot{b}},q^l)-{(q^l)}^T\nabla _{q^l}h^l_2(t,a,{\dot{a}},b,{\dot{b}},q^l)\}\mathrm{d}t}{\dots ,\int _{\delta _1}^{\delta _2}\{\phi _2^l(t,a,{\dot{a}},b,{\dot{b}}) + {\hat{S}}(b|H^l) - a^Tx^l +g^l_2(t,a,{\dot{a}},b,{\dot{b}},q^l)-{(q^l)}^T\nabla _{q^l}g_2^l(t,a,{\dot{a}},b,{\dot{b}},q^l)\}\mathrm{d}t} \Bigg ) \end{aligned}$$

Subject to

$$\begin{aligned}&a(\delta _1)=0=a(\delta _2), ~~~~~~~~~~~ b(\delta _1)=0=b(\delta _2),\\&{\dot{a}}(\delta _1)=0={\dot{a}}(\delta _2), ~~~~~~~~~~~ {\dot{b}}(\delta _1)=0={\dot{b}}(\delta _2),\\&\sum \limits _{k=1}^{l}\lambda _k \Bigg \{ \left[ (\phi _1^k)_s-D(\phi _1^k)_{{\dot{s}}}+w^k + \nabla _{q^k}h^k_2 \right] -\left[ (\phi _2^k)_s-D(\phi _2^k)_{{\dot{s}}}-x^k + \nabla _{q^k}g^k_2 \right] \\&\qquad \dfrac{\check{M}^k(a,b)}{\check{L}^k(a,b)} \Bigg \} \in {\mathcal {C}}^*_1,\quad t\in \varOmega ,\\&a^T\sum \limits _{k=1}^{l}\lambda _k \Bigg \{ \left[ (\phi _1^k)_s-D(\phi _1^k)_{{\dot{s}}}+w^k + \nabla _{q^k}h^k_2 \right] -\left[ (\phi _2^k)_s-D(\phi _2^k)_{{\dot{s}}}-x^k + \nabla _{q^k}g^k_2 \right] \\&\qquad \dfrac{\check{M}^k(a,b)}{\check{L}^k(a,b)} \Bigg \} \leqq 0,\quad t\in \varOmega ,\\&\lambda >0,~~~~~~ b(t)\in {\mathcal {C}}_2,~~~~~~ t\in \varOmega ,\\&w^k\in B^k,~~~~~~ x^k\in E^k,~~~~~~ k\in \kappa , \end{aligned}$$

where

• (i) $\phi _1^k:\varOmega \times {\mathcal {W}} \times {\mathcal {W}} \times S \times S \rightarrow R_+$, $\phi _2^k:\varOmega \times {\mathcal {W}} \times {\mathcal {W}} \times S \times S \rightarrow R_+/\{0\}$, $h_1^k,g_1^k :\varOmega \times {\mathcal {W}}\times {\mathcal {W}} \times S \times S\times R^{n_2}\rightarrow R$ and $h_2^k,g_2^k :\varOmega \times {\mathcal {W}}\times {\mathcal {W}} \times S \times S\times R^{n_1}\rightarrow R$, $k\in \kappa$, are continuously differentiable functions,

• (ii) $p^k:\varOmega \rightarrow R^{n_2}$ and $q^k:\varOmega \rightarrow R^{n_1}$,

• (iii) $B^k, E^k, D^k$ and $H^k$ are compact convex sets in $R^{n_1}, R^{n_1}, R^{n_2}$ and $R^{n_2}$, respectively.

and

$$\begin{aligned} \check{F}^k(s,y)&=\int _{\delta _1}^{\delta _2} \{\phi _1^k(t,s,{\dot{s}},y,{\dot{y}}) + {\hat{S}}(s|B^k) - y^Tz^k +h^k_1(t,s,{\dot{s}},y,{\dot{y}},p^k)\\&\quad -{(p^k)}^T \nabla _{p^k}h^k_1(t,s,{\dot{s}},y,{\dot{y}},p^k)\}\mathrm{d}t;\\ \check{G}^k(s,y)&=\int _{\delta _1}^{\delta _2} \{\phi _2^k(t,s,{\dot{s}},y,{\dot{y}}) - {\hat{S}}(s|E^k) + y^Tr^k +g^k_1(t,s,{\dot{s}},y,{\dot{y}},p^k)\\&\quad -{(p^k)}^T \nabla _{p^k}g_1^k(t,s,{\dot{s}},y,{\dot{y}},p^k)\}\mathrm{d}t;\\ \check{M}^k(a,b)&=\int _{\delta _1}^{\delta _2} \{\phi _1^k(t,a,{\dot{a}},b,{\dot{b}}) - {\hat{S}}(b|D^k) + a^Tw^k +h^k_2(t,a,{\dot{a}},b,{\dot{b}},q^k)\\&\quad -{(q^k)}^T\nabla _{q^k}h^k_2(t,a,{\dot{a}},b,{\dot{b}},q^k)\}\mathrm{d}t;\\ \check{L}^k(a,b)&=\int _{\delta _1}^{\delta _2} \{\phi _2^k(t,a,{\dot{a}},b,{\dot{b}}) + {\hat{S}}(b|H^k) - a^Tx^k +g^k_2(t,a,{\dot{a}},b,{\dot{b}},q^k)\\&\quad -{(q^k)}^T\nabla _{q^k}g_2^k(t,a,{\dot{a}},b,{\dot{b}},q^k)\}\mathrm{d}t. \end{aligned}$$

Further assume that

$$\begin{aligned} \check{G}^k(s,y)>0, \qquad \check{L}^k(a,b)>0, \qquad \check{F}^k(s,y) \geqq 0, \qquad \check{M}^k(a,b) \geqq 0 \qquad \forall k\in \kappa . \end{aligned}$$

Parametric prospective of above dual formulation

For simplicity, consider

$$\begin{aligned}&m^k=\dfrac{\check{F}^k(s,y)}{\check{G}^k(s,y)}\\&~~~=\dfrac{\int _{\delta _1}^{\delta _2} \{\phi _1^k(t,s,{\dot{s}},y,{\dot{y}}) + {\hat{S}}(s|B^k) - y^Tz^k +h^k_1(t,s,{\dot{s}},y,{\dot{y}},p^k)-{(p^k)}^T\nabla _{p^k}h^k_1(t,s,{\dot{s}},y,{\dot{y}},p^k)\}\mathrm{d}t}{\int _{\delta _1}^{\delta _2} \{\phi _2^k(t,s,{\dot{s}},y,{\dot{y}}) - {\hat{S}}(s|E^k) + y^Tr^k +g^k_1(t,s,{\dot{s}},y,{\dot{y}},p^k)-{(p^k)}^T\nabla _{p^k}g_1^k(t,s,{\dot{s}},y,{\dot{y}},p^k)\}\mathrm{d}t},\\&n^k=\dfrac{\check{M}^k(a,b)}{\check{L}^k(a,b)}\\&~~~=\dfrac{\int _{\delta _1}^{\delta _2} \{\phi _1^k(t,a,{\dot{a}},b,{\dot{b}}) - {\hat{S}}(b|D^k) + a^Tw^k +h^k_2(t,a,{\dot{a}},b,{\dot{b}},q^k)-{(q^k)}^T\nabla _{q^k}h^k_2(t,a,{\dot{a}},b,{\dot{b}},q^k)\}\mathrm{d}t}{\int _{\delta _1}^{\delta _2} \{\phi _2^k(t,a,{\dot{a}},b,{\dot{b}}) + {\hat{S}}(b|H^k) - a^Tx^k +g^k_2(t,a,{\dot{a}},b,{\dot{b}},q^k)-{(q^k)}^T\nabla _{q^k}g_2^k(t,a,{\dot{a}},b,{\dot{b}},q^k)\}\mathrm{d}t}. \end{aligned}$$

Expressing the problems (HFVP) and (HFVD) equivalently as follows.

(SHFVP) Minimize $m=(m^1,m^2,\dots ,m^l)$

subject to

$$\begin{aligned}&s(\delta _1)=0=s(\delta _2), ~~~~~~~~~~~ y(\delta _1)=0=y(\delta _2), \end{aligned}$$

(5)

$$\begin{aligned}&{\dot{s}}(\delta _1)=0={\dot{s}}(\delta _2), ~~~~~~~~~~~ {\dot{y}}(\delta _1)=0={\dot{y}}(\delta _2), \end{aligned}$$

(6)

$$\begin{aligned}&\int _{\delta _1}^{\delta _2} \{\phi _1^k(t,s,{\dot{s}},y,{\dot{y}}) + {\hat{S}}(s|B^k) - y^Tz^k +h^k_1(t,s,{\dot{s}},y,{\dot{y}},p^k)\nonumber \\&\quad -{(p^k)}^T\nabla _{p^k}h^k_1(t,s,{\dot{s}},y,{\dot{y}},p^k)\}\mathrm{d}t \nonumber \\&\quad -m^k\int _{\delta _1}^{\delta _2} \{\phi _2^k(t,s,{\dot{s}},y,{\dot{y}}) - {\hat{S}}(s|E^k) + y^Tr^k+g^k_1(t,s,{\dot{s}},y,{\dot{y}},p^k)-{(p^k)}^T\nonumber \\&\qquad \nabla _{p^k}g_1^k(t,s,{\dot{s}},y,{\dot{y}},p^k)\}\mathrm{d}t =0, \end{aligned}$$

(7)

$$\begin{aligned}&-\sum _{k=1}^{l}\lambda _k \Bigg \{ \left[ (\phi _1^k)_y-D(\phi _1^k)_{{\dot{y}}}-z^k + \nabla _{p^k}h^k_1 \right] \nonumber \\&\qquad -m^k\left[ (\phi _2^k)_y-D(\phi _2^k)_{{\dot{y}}}+r^k + \nabla _{p^k}g^k_1 \right] \Bigg \} \in {\mathcal {C}}^*_2,\quad t\in \varOmega , \end{aligned}$$

(8)

$$\begin{aligned}&y^T\sum _{k=1}^{l}\lambda _k \Bigg \{ \left[ (\phi _1^k)_y-D(\phi _1^k)_{{\dot{y}}}-z^k + \nabla _{p^k}h^k_1 \right] \nonumber \\&\qquad -m^k\left[ (\phi _2^k)_y-D(\phi _2^k)_{{\dot{y}}}+r^k + \nabla _{p^k}g^k_1 \right] \Bigg \} \geqq 0,\quad t\in \varOmega , \end{aligned}$$

(9)

$$\begin{aligned}&\lambda >0,~~~~~~ s(t)\in {\mathcal {C}}_1,~~~~~~ t\in \varOmega , \end{aligned}$$

(10)

$$\begin{aligned}&z^k\in D^k,~~~~~~ r^k\in H^k,~~~~~~ k\in \kappa . \end{aligned}$$

(11)

(SHFVD) Maximize $n=(n^1,n^2,\dots ,n^l)$

subject to

$$\begin{aligned}&a(\delta _1)=0=a(\delta _2), ~~~~~~~~~~~ b(\delta _1)=0=b(\delta _1), \end{aligned}$$

(12)

$$\begin{aligned}&{\dot{a}}(\delta _1)=0={\dot{a}}(\delta _1), ~~~~~~~~~~~ {\dot{b}}(\delta _1)=0={\dot{b}}(\delta _1), \end{aligned}$$

(13)

$$\begin{aligned}&\int _{\delta _1}^{\delta _2} \{\phi _1^k(t,a,{\dot{a}},b,{\dot{b}}) - {\hat{S}}(b|D^k) + a^Tw^k +h^k_2(t,a,{\dot{a}},b,{\dot{b}},q^k)-{(q^k)}^T\nonumber \\&\qquad \nabla _{q^k}h^k_2(t,a,{\dot{a}},b,{\dot{b}},q^k)\}\mathrm{d}t \nonumber \\&\quad -n^k\int _{\delta _1}^{\delta _2} \{\phi _2^k(t,a,{\dot{a}},b,{\dot{b}}) + {\hat{S}}(b|H^k) - a^Tx^k+g^k_2(t,a,{\dot{a}},b,{\dot{b}},q^k)-{(q^k)}^T\nonumber \\&\qquad \nabla _{q^k}g_2^k(t,a,{\dot{a}},b,{\dot{b}},q^k)\}\mathrm{d}t=0, \end{aligned}$$

(14)

$$\begin{aligned}&\sum _{k=1}^{l}\lambda _k \Bigg \{ \left[ (\phi _1^k)_s-D(\phi _1^k)_{{\dot{s}}}+w^k + \nabla _{q^k}h^k_2 \right] \nonumber \\&\qquad -n^k\left[ (\phi _2^k)_s-D(\phi _2^k)_{{\dot{s}}}-x^k + \nabla _{q^k}g^k_2 \right] \Bigg \} \in {\mathcal {C}}^*_1,\quad t\in \varOmega , \end{aligned}$$

(15)

$$\begin{aligned}&a^T\sum _{k=1}^{l}\lambda _k \Bigg \{ \left[ (\phi _1^k)_s-D(\phi _1^k)_{{\dot{s}}}+w^k + \nabla _{q^k}h^k_2 \right] \nonumber \\&\qquad -n^k\left[ (\phi _2^k)_s-D(\phi _2^k)_{{\dot{s}}}-x^k + \nabla _{q^k}g^k_2 \right] \Bigg \} \leqq 0,\quad t\in \varOmega , \end{aligned}$$

(16)

$$\begin{aligned}&\lambda >0,~~~~~~ b(t)\in {\mathcal {C}}_2,~~~~~~ t\in \varOmega , \end{aligned}$$

(17)

$$\begin{aligned}&w^k\in B^k,~~~~~~ x^k\in E^k,~~~~~~ k\in \kappa . \end{aligned}$$

(18)

In the above-simplified problem (SHFVP) and (SHFVD), m and n are nonnegative. Let M denotes the set of feasible solutions of (SHFVP) and N denotes the set of feasible solutions of (SHFVD). In the subsequent analysis, usual theorems of duality in terms of (SHFVP) and (SHFVD) will be discussed and applied equally to (HFVP) and (HFVD).

Theorem 3.1

(Weak Duality). Let $(s,y,m,\lambda ,z,r,p) \in M$ and $(a,b,n,\lambda ,w,x,q) \in N$. Let the sublinear functionals $F:\varOmega \times {\mathcal {W}} \times {\mathcal {W}} \times {\mathcal {W}} \times {\mathcal {W}} \times R^{n_1} \rightarrow R$ and $G:\varOmega \times S \times S \times S \times S \times R^{n_2} \rightarrow R$ satisfy the following conditions:

$$\begin{aligned}&F(t,s,{\dot{s}},a,{\dot{a}};e)+\alpha _1^{-1}e^Ta \geqq 0, ~~ \forall ~~e \in {\mathcal {C}}_1^*,~~ t\in \varOmega , \end{aligned}$$

(19)

$$\begin{aligned}&G(t,b,{\dot{b}},y,{\dot{y}};f)+\alpha _2^{-1}f^Ty \geqq 0,~~ \forall ~~f \in {\mathcal {C}}_2^*,~~ t\in \varOmega . \end{aligned}$$

(20)

Suppose that

• (i) $\sum \limits _{k=1}^{l} \lambda _k \int _{\delta _1}^{\delta _2} \{(\phi _1^k(t,\cdot ,\cdot ,b,{\dot{b}})+(\cdot )^Tw^k)-n^k(\phi _2^k(t,\cdot ,\cdot ,b,{\dot{b}})-(\cdot )^Tx^k) \} \mathrm{d}t$ is higher-order $(F,\alpha _1,\rho _1,d_1)$-pseudoconvex at a and ${\dot{a}}$ with respect to $\sum \limits _{k=1}^{l}\lambda _k \{h_2^k-n^kg_2^k\}$ and $q^k \in R^{n_1}$ for fixed b and ${\dot{b}}$,

• (ii) $\sum \limits _{k=1}^{l} \lambda _k \int _{\delta _1}^{\delta _2} \{-(\phi _1^k(t,s,{\dot{s}},\cdot ,\cdot )+(\cdot )^Tz^k)+m^k(\phi _2^k(t,s,{\dot{s}},\cdot ,\cdot )+(\cdot )^Tr^k) \} \mathrm{d}t$ is higher-order $(G,\alpha _2,\rho _2,d_2)$-pseudoconvex at y and ${\dot{y}}$ with respect to $\sum \nolimits _{k=1}^{l}\lambda _k \{-h_1^k+m^kg_1^k\}$ and $p^k\in R^{n_2}$ for fixed s and ${\dot{s}}$,

• (iii) either (a) $\sum \nolimits _{k=1}^{l} \lambda _k\int _{\delta _1}^{\delta _2}\Big ( \rho _1^k\left[ d_1^k(t,s,{\dot{s}},a,{\dot{a}}) \right] ^2 + \rho _2^k\left[ d_2^k(t,b,{\dot{b}},y,{\dot{y}}) \right] ^2\Big )\mathrm{d}t \geqq 0$ or (b) $\rho _1^k \geqq 0 ~~ \& ~~\rho _2^k \geqq 0,$ $\forall k\in \kappa$,

• (iv) $\int _{\delta _1}^{\delta _2} (\phi _2^k(t,s,{\dot{s}},b,{\dot{b}})-{\hat{S}}(s|E^k) + b^Tr^k)~\mathrm{d}t > 0,~\forall k\in \kappa$.

Then

$$\begin{aligned} m\nleq n. \end{aligned}$$

(21)

Proof

Suppose, to the contrary, that (21) is not true, i.e., $m\le n$ i.e., for all $k\in \kappa$, $m^k\leqq n^k$ and $m^j < n^j$, for some $j\in \kappa$, then from $\lambda >0$ and hypothesis (iv) we get

$$\begin{aligned}&\sum _{k=1}^{l}\lambda _k(m^k-n^k)\int _{\delta _1}^{\delta _2}(\phi _2^k(t,s,{\dot{s}},b,{\dot{b}})-{\hat{S}}(s|E^k)+b^Tr^k)~\mathrm{d}t <0. \end{aligned}$$

(22)

As $(s,y,m,\lambda ,z,r,p)$ is feasible for the primal problem (SHFVP) and $(a,b,n,\lambda ,w,x,q)$ is feasible for the dual problem (SHFVD), $\alpha _1(s,a) > 0$, by dual constraint (15), the vector $e=\alpha _1(s,a)\sum _{k=1}^{l}\lambda _k \bigg \{ [ (\phi _1^k)_s-D(\phi _1^k)_{{\dot{s}}}$ $+w^k + \nabla _{q^k}h^k_2 ] -n^k\left[ (\phi _2^k)_s-D(\phi _2^k)_{{\dot{s}}}-x^k + \nabla _{q^k}g^k_2 \right] \bigg \} \in {\mathcal {C}}^*_1, t\in \varOmega$. So from (19), we obtain

$$\begin{aligned}&F\Bigg (t,s,{\dot{s}},a,{\dot{a}};\alpha _1(s,a)\sum _{k=1}^{l}\lambda _k \bigg \{ \left[ (\phi _1^k)_s-D(\phi _1^k)_{{\dot{s}}}+w^k + \nabla _{q^k}h^k_2 \right] \\&\qquad -n^k\Big [ (\phi _2^k)_s-D(\phi _2^k)_{{\dot{s}}}-x^k + \nabla _{q^k}g^k_2 \Big ] \bigg \}\Bigg ) \\&\quad \geqq -a^T\sum _{k=1}^{l}\lambda _k \bigg \{ \left[ (\phi _1^k)_s-D(\phi _1^k)_{{\dot{s}}}+w^k + \nabla _{q^k}h^k_2 \right] \\&\qquad -n^k\left[ (\phi _2^k)_s-D(\phi _2^k)_{{\dot{s}}}-x^k + \nabla _{q^k}g^k_2 \right] \bigg \}\\&\quad \geqq 0 ~~ (\text {by dual constraint} (16)). \end{aligned}$$

By using sublinearity of F and $\lambda _k > 0$, $k\in \kappa$, we get

$$\begin{aligned}&\sum _{k=1}^{l}\lambda _kF\Bigg (t,s,{\dot{s}},a,{\dot{a}};\alpha _1(s,a) \bigg \{ \left[ (\phi _1^k)_s-D(\phi _1^k)_{{\dot{s}}}+w^k + \nabla _{q^k}h^k_2 \right] \\&\qquad -n^k\Big [ (\phi _2^k)_s-D(\phi _2^k)_{{\dot{s}}}-x^k + \nabla _{q^k}g^k_2 \Big ] \bigg \}\Bigg )\geqq 0, \end{aligned}$$

which implies

$$\begin{aligned}&\sum _{k=1}^{l}\lambda _k\int _{\delta _1}^{\delta _2}F\Bigg (t,s,{\dot{s}},a,{\dot{a}};\alpha _1(s,a) \bigg \{ \left[ (\phi _1^k)_s-D(\phi _1^k)_{{\dot{s}}}+w^k + \nabla _{q^k}h^k_2 \right] \nonumber \\&\quad -n^k\big [ (\phi _2^k)_s-D(\phi _2^k)_{{\dot{s}}}-x^k+ \nabla _{q^k}g^k_2 \big ] \bigg \}\Bigg )~\mathrm{d}t\geqq 0. \end{aligned}$$

(23)

From (23), using higher-order $(F,\alpha _1,\rho _1,d_1)$-pseudoconvexity of $\sum _{k=1}^{l} \lambda _k \int _{\delta _1}^{\delta _2} \{(\phi _1^k(t,\cdot ,\cdot ,b,{\dot{b}})+(\cdot )^Tw^k)-n^k(\phi _2^k(t,\cdot ,\cdot ,b,{\dot{b}})-(\cdot )^Tx^k) \} \mathrm{d}t$ at a and ${\dot{a}}$ with respect to $\sum _{k=1}^{l}\lambda _k \{h_2^k-n^kg_2^k\}$ for fixed b and ${\dot{b}}$, we have

$$\begin{aligned}&\sum _{k=1}^{l} \lambda _k \int _{\delta _1}^{\delta _2} \{ (\phi _1^k(t,s,{\dot{s}},b,{\dot{b}})+s^Tw^k) -n^k (\phi _2^k(t,s,{\dot{s}},b,{\dot{b}})-s^Tx^k)\}~\mathrm{d}t\nonumber \\&\quad -\sum _{k=1}^{l} \lambda _k \int _{\delta _1}^{\delta _2} \{ (\phi _1^k(t,a,{\dot{a}},b,{\dot{b}})+a^Tw^k) \nonumber \\&\quad -n^k (\phi _2^k(t,a,{\dot{a}},b,{\dot{b}}) -a^Tx^k)\}~\mathrm{d}t- \sum _{k=1}^{l} \lambda _k \int _{\delta _1}^{\delta _2} \{ h_2^k(t,a,{\dot{a}},b,{\dot{b}},q^k)\nonumber \\&\quad -n^k g_2^k(t,a,{\dot{a}},b,{\dot{b}},q^k)\}~\mathrm{d}t +\sum _{k=1}^{l} \lambda _k \int _{\delta _1}^{\delta _2} \{ (q^k)^T\nabla _{q^k}h_2^k(t,a,{\dot{a}},b,{\dot{b}},q^k)\nonumber \\&\quad - n^k (q^k)^T\nabla _{q^k}g_2^k(t,a,{\dot{a}},b,{\dot{b}},q^k)\}\mathrm{d}t \geqq \sum _{k=1}^{l} \lambda _k \rho ^k_1 \int _{\delta _1}^{\delta _2} (d_1^k(t,s,{\dot{s}},a,{\dot{a}})^2\mathrm{d}t. \end{aligned}$$

(24)

Using $s^Tw^k \leqq {\hat{S}}(s|B^k),~ w^k\in B^k$ and $s^Tx^k \leqq {\hat{S}}(s|E^k),~ x^k\in E^k$, $k\in \kappa$, in the above inequality, we obtain

$$\begin{aligned}&\sum _{k=1}^{l} \lambda _k \int _{\delta _1}^{\delta _2} \{ (\phi _1^k(t,s,{\dot{s}},b,{\dot{b}})+{\hat{S}}(s|B^k)) -n^k (\phi _2^k(t,s,{\dot{s}},b,{\dot{b}})-{\hat{S}}(s|E^k))\}~\mathrm{d}t\\&\qquad - \sum _{k=1}^{l} \lambda _k \int _{\delta _1}^{\delta _2} \{ (\phi _1^k(t,a,{\dot{a}},b,{\dot{b}})+a^Tw^k) -n^k (\phi _2^k(t,a,{\dot{a}},b,{\dot{b}}) -a^Tx^k)\}~\mathrm{d}t\\&\qquad - \sum _{k=1}^{l} \lambda _k \int _{\delta _1}^{\delta _2} \{ h_2^k(t,a,{\dot{a}},b,{\dot{b}},q^k) -n^k g_2^k(t,a,{\dot{a}},b,{\dot{b}},q^k)\}~\mathrm{d}t\\&\qquad + \sum _{k=1}^{l} \lambda _k \int _{\delta _1}^{\delta _2} \{ (q^k)^T\nabla _{q^k}h_2^k(t,a,{\dot{a}},b,{\dot{b}},q^k) - n^k (q^k)^T\nabla _{q^k}g_2^k(t,a,{\dot{a}},b,{\dot{b}},q^k)\}\mathrm{d}t\\&\quad \geqq \sum _{k=1}^{l} \lambda _k \rho ^k_1 \int _{\delta _1}^{\delta _2} (d_1^k(t,s,{\dot{s}},a,{\dot{a}})^2\mathrm{d}t. \end{aligned}$$

Using equation (14) along with $b^Tr^k \leqq {\hat{S}}(b|H^k), r^k \in H^k, n^k\geqq 0, \lambda _k > 0, \forall k,$ in the above inequality we have

$$\begin{aligned}&\sum _{k=1}^{l} \lambda _k \int _{\delta _1}^{\delta _2} \{ (\phi _1^k(t,s,{\dot{s}},b,{\dot{b}})+{\hat{S}}(s|B^k)-{\hat{S}}(b|D^k)) -n^k (\phi _2^k(t,s,{\dot{s}},b,{\dot{b}}) \nonumber \\&\quad -{\hat{S}}(s|E^k)+b^Tr^k)\}~\mathrm{d}t\geqq \sum _{k=1}^{l} \lambda _k \rho ^k_1 \int _{\delta _1}^{\delta _2} (d_1^k(t,s,{\dot{s}},a,{\dot{a}})^2\mathrm{d}t. \end{aligned}$$

(25)

By constraint (8), $\alpha _2(b,y)>0$, taking vector $b=-\alpha _2(b,y)\sum _{k=1}^{l}\lambda _k \bigg \{ \left[ (\phi _1^k)_y-D(\phi _1^k)_{{\dot{y}}}-z^k + \nabla _{p^k}h^k_1 \right]$ $-m^k[ (\phi _2^k)_y$ $-D(\phi _2^k)_{{\dot{y}}}+r^k + \nabla _{p^k}g^k_1 ] \bigg \} \in {\mathcal {C}}^*_2, ~ t\in \varOmega$, and using (20), we get

$$\begin{aligned}&G\Bigg (t,b,{\dot{b}},y,{\dot{y}};-\alpha _2(b,y)\sum _{k=1}^{l}\lambda _k \bigg \{ \left[ (\phi _1^k)_y-D(\phi _1^k)_{{\dot{y}}}-z^k + \nabla _{p^k}h^k_1 \right] \\&\qquad -m^k\Big [ (\phi _2^k)_y-D(\phi _2^k)_{{\dot{y}}}+r^k + \nabla _{p^k}g^k_1 \Big ] \bigg \}\Bigg ) \\&\quad \geqq y^T \sum _{k=1}^{l}\lambda _k \bigg \{ \left[ (\phi _1^k)_y-D(\phi _1^k)_{{\dot{y}}}-z^k + \nabla _{p^k}h^k_1 \right] \\&\qquad -m^k\left[ (\phi _2^k)_y-D(\phi _2^k)_{{\dot{y}}}+r^k + \nabla _{p^k}g^k_1 \right] \bigg \} \\&\quad \geqq 0 ~~~~ (\text {using Primal Constraint} (9). \end{aligned}$$

Now sublinearity of G and $\lambda _k>0,~k\in \kappa$, gives

$$\begin{aligned}&\sum _{k=1}^{l}\lambda _kG\Bigg (t,b,{\dot{b}},y,{\dot{y}};-\alpha _2(b,y) \bigg \{ \left[ (\phi _1^k)_y-D(\phi _1^k)_{{\dot{y}}}-z^k + \nabla _{p^k}h^k_1 \right] \\&\qquad -m^k\Big [ (\phi _2^k)_y-D(\phi _2^k)_{{\dot{y}}}+r^k + \nabla _{p^k}g^k_1 \Big ] \bigg \}\Bigg ) \geqq 0, \end{aligned}$$

which implies

$$\begin{aligned}&\sum _{k=1}^{l}\lambda _k\int _{\delta _1}^{\delta _2}G\Bigg (t,b,{\dot{b}},y,{\dot{y}};-\alpha _2(b,y) \bigg \{ \left[ (\phi _1^k)_y-D(\phi _1^k)_{{\dot{y}}}-z^k + \nabla _{p^k}h^k_1 \right] \nonumber \\&\quad -m^k\left[ (\phi _2^k)_y-D(\phi _2^k)_{{\dot{y}}}+r^k + \nabla _{p^k}g^k_1 \right] \bigg \}\Bigg )~\mathrm{d}t \geqq 0. \end{aligned}$$

(26)

From above and using hypothesis (ii), we get

$$\begin{aligned}&\sum _{k=1}^{l} \lambda _k \int _{\delta _1}^{\delta _2} \{ (-\phi _1^k(t,s,{\dot{s}},b,{\dot{b}})+b^Tz^k) +m^k (\phi _2^k(t,s,{\dot{s}},b,{\dot{b}})+b^Tr^k)\}~\mathrm{d}t \nonumber \\&\qquad - \sum _{k=1}^{l} \lambda _k \int _{\delta _1}^{\delta _2} \{ (-\phi _1^k(t,s,{\dot{s}},y,{\dot{y}})+y^Tz^k)+m^k (\phi _2^k(t,s,{\dot{s}},y,{\dot{y}}) +y^Tr^k)\}~\mathrm{d}t \nonumber \\&\qquad - \sum _{k=1}^{l} \lambda _k \int _{\delta _1}^{\delta _2} \{ -h_1^k(t,s,{\dot{s}},y,{\dot{y}},p^k)+m^k g_1^k(t,s,{\dot{s}},y,{\dot{y}},p^k)\}~\mathrm{d}t \nonumber \\&\qquad +\sum _{k=1}^{l} \lambda _k \int _{\delta _1}^{\delta _2} \{ -(p^k)^T\nabla _{p^k}h_1^k(t,s,{\dot{s}},y,{\dot{y}},p_1^k) + m^k (p^k)^T\nabla _{p^k}g_1^k(t,s,{\dot{s}},y,{\dot{y}},p^k)\}\mathrm{d}t \nonumber \\&\quad \geqq \sum _{k=1}^{l} \lambda _k \rho ^k_2 \int _{\delta _1}^{\delta _2} (d_2^k(t,b,{\dot{b}},y,{\dot{y}})^2\mathrm{d}t. \end{aligned}$$

(27)

From (7) and $b^Tz^k\leqq {\hat{S}}(b|D^k), ~z^k \in D^k, \lambda _k>0,~ \forall k$, equation (27) becomes

$$\begin{aligned}&\sum _{k=1}^{l} \lambda _k \int _{\delta _1}^{\delta _2} \{ (-\phi _1^k(t,s,{\dot{s}},b,{\dot{b}})-{\hat{S}}(s|B^k)+{\hat{S}}(b|D^k)) +m^k (\phi _2^k(t,s,{\dot{s}},b,{\dot{b}})\nonumber \\&\qquad -{\hat{S}}(s|E^k)+b^Tr^k)\}~\mathrm{d}t \geqq \sum _{k=1}^{l} \lambda _k \rho ^k_2 \int _{\delta _1}^{\delta _2} (d_2^k(t,b,{\dot{b}},y,{\dot{y}})^2\mathrm{d}t. \end{aligned}$$

(28)

Adding (25) and (28) and using hypothesis (iii), we get

$$\begin{aligned} \sum _{k=1}^{l}\lambda _k(m^k-n^k)\int _{\delta _1}^{\delta _2}(\phi _2^k(t,s,{\dot{s}},b,{\dot{b}})-{\hat{S}}(s|E^k)+b^Tr^k)~\mathrm{d}t \geqq 0. \end{aligned}$$

(29)

This contradicts (22). Hence the result. $\square$

Theorem 3.2

(Weak Duality). Let $(s,y,m,\lambda ,z,r,p) \in M$ and $(a,b,n,\lambda ,w,x,q) \in N$. Let the sublinear functionals $F:\varOmega \times {\mathcal {W}} \times {\mathcal {W}} \times {\mathcal {W}} \times {\mathcal {W}} \times R^{n_1} \rightarrow R$ and $G:\varOmega \times S \times S \times S \times S \times R^{n_2} \rightarrow R$ satisfy the following conditions:

$$\begin{aligned}&F(t,s,{\dot{s}},a,{\dot{a}};e)+\alpha _1^{-1}e^Tu \geqq 0, ~~ \forall ~~e \in {\mathcal {C}}_1^*,~~ t\in \varOmega , \\&G(t,b,{\dot{b}},y,{\dot{y}};f)+\alpha _2^{-1}f^Ty \geqq 0,~~ \forall ~~f \in {\mathcal {C}}_2^*,~~ t\in \varOmega . \end{aligned}$$

Suppose that

• (i) $\int _{\delta _1}^{\delta _2} \{(\phi _1^k(t,\cdot ,\cdot ,b,{\dot{b}})+(\cdot )^Tw^k)-n^k(\phi _2^k(t,\cdot ,\cdot ,b,{\dot{b}})-(\cdot )^Tx^k) \} \mathrm{d}t$ is higher order $(F,\alpha _1,\rho _1,d_1)$-convex at a and ${\dot{a}}$ with respect to $\{h_2^k-n^kg_2^k\}$ and $q^k \in R^{n_1}$ for fixed b and ${\dot{b}}$,

• (ii) $\int _{\delta _1}^{\delta _2} \{-(\phi _1^k(t,s,{\dot{s}},\cdot ,\cdot )-(\cdot )^Tz^k)+m^k(\phi _2^k(t,s,{\dot{s}},\cdot ,\cdot )+(\cdot )^Tr^k) \} \mathrm{d}t$ is higher order $(G,\alpha _2,\rho _2,d_2)$-convex at y and ${\dot{y}}$ with respect to $\{-h_1^k+m^kg_1^k\}$ and $p^k\in R^{n_2}$ for fixed s and ${\dot{s}}$,

• (iii) either (a) $\sum \nolimits _{k=1}^{l} \lambda _k\int _{\delta _1}^{\delta _2}\Big ( \rho _1^k\left[ d_1^k(t,s,{\dot{s}},a,{\dot{a}}) \right] ^2 + \rho _2^k\left[ d_2^k(t,b,{\dot{b}},y,{\dot{y}}) \right] ^2\Big )\mathrm{d}t \geqq 0$ or (b) $\rho _1^k \geqq 0 ~~ \& ~~\rho _2^k \geqq 0,~ k\in \kappa$,

• (iv) $\int _{\delta _1}^{\delta _2} (\phi _2^k(t,s,{\dot{s}},b,{\dot{b}})-{\hat{S}}(s|E^k) + b^Tr^k)~\mathrm{d}t > 0,~\forall k\in \kappa$.

Then

$$\begin{aligned} m\nleq n. \end{aligned}$$

Proof

It follows on the lines of Theorem 3.1. $\square$

Any problem, say (SHFVD), in which $\lambda$ is fixed to be ${\bar{\lambda }}$ will be denoted by $\text {(SHFVD)}_{{\bar{\lambda }}}$.

For simplicity, the following notations are used in Theorem 3.3,

$$\begin{aligned}&\quad \quad \phi _1^k=\phi _1^k(t,s,{\dot{s}},y,{\dot{y}}),~~~~~~~~~~~~~\phi _2^k=\phi _2^k(t,s,{\dot{s}},y,{\dot{y}}),\\&\quad \quad h^k_1=h^k_1(t,s,{\dot{s}},y,{\dot{y}},p^k),~~~~~~~~g^k_1=g^k_1(t,s,{\dot{s}},y,{\dot{y}},p^k),~~~~ \text {for every} ~~k\in \kappa . \end{aligned}$$

Theorem 3.3

(Strong Duality Theorem). Assume (${\bar{s}},{\bar{y}},{\bar{m}},{\bar{\lambda }},{\bar{z}},{\bar{r}},{\bar{p}}$) is a weakly efficient solution for (SHFVP). Further, suppose that

• (i) The Hessian matrices $\nabla _{p^kp^k}h^k_1-{\bar{m}}^k\nabla _{p^kp^k}g^k_1$ are nonsingular matrices,

• (ii) The set of vectors $\big \{ \left[ (\phi _1^k)_y-D(\phi _1^k)_{{\dot{y}}}-{\bar{z}}^k + \nabla _{p^k}h^k_1 \right] -{\bar{m}}^k\left[ (\phi _2^k)_y-D(\phi _2^k)_{{\dot{y}}}+{\bar{r}}^k + \nabla _{p^k}g^k_1 \right] \big \}$ are linearly independent,

• (iii) $\nabla _{y}h^k_1(t,{\bar{s}},\dot{{\bar{s}}},{\bar{y}},\dot{{\bar{y}}},0)=0$, $\nabla _{{\dot{s}}}h^k_1(t,{\bar{s}},\dot{{\bar{s}}},{\bar{y}},\dot{{\bar{y}}},0)=0,$ $\nabla _{{\dot{y}}}h^k_1(t,{\bar{s}},\dot{{\bar{s}}},{\bar{y}},\dot{{\bar{y}}},0)=0$, $\nabla _{\ddot{s}}h^k_1(t,{\bar{s}},\dot{{\bar{s}}},{\bar{y}},\dot{{\bar{y}}},0)=0,$ $\nabla _{\ddot{y}}h^k_1(t,{\bar{s}},\dot{{\bar{s}}},{\bar{y}},\dot{{\bar{y}}},0)=0$, $\nabla _{p^k}h^k_1(t,{\bar{s}},\dot{{\bar{s}}},{\bar{y}},\dot{{\bar{y}}},0)\!=0$, $\nabla _{s}h^k_1(t,{\bar{s}},\dot{{\bar{s}}},{\bar{y}},\dot{{\bar{y}}},0)=\nabla _{q^k}h^k_2(t,{\bar{s}},\dot{{\bar{s}}},{\bar{y}},\dot{{\bar{y}}},0)$, $\nabla _{y}g^k_1(t,{\bar{s}},\dot{{\bar{s}}},{\bar{y}},\dot{{\bar{y}}},0)=0$, $\nabla _{{\dot{s}}}g^k_1(t,{\bar{s}},\dot{{\bar{s}}},{\bar{y}},\dot{{\bar{y}}},0)=0,$ $\nabla _{{\dot{y}}}g^k_1(t,{\bar{s}},\dot{{\bar{s}}},{\bar{y}},\dot{{\bar{y}}},0)=0$, $\nabla _{\ddot{s}}g^k_1(t,{\bar{s}},\dot{{\bar{s}}},{\bar{y}},\dot{{\bar{y}}},0)=0,$ $\nabla _{\ddot{y}}g^k_1(t,{\bar{s}},\dot{{\bar{s}}},{\bar{y}},\dot{{\bar{y}}},0)=0$, $\nabla _{p^k}g^k_1(t,{\bar{s}},\dot{{\bar{s}}},{\bar{y}},\dot{{\bar{y}}},0)\!=0$, $\nabla _{s}g^k_1(t,{\bar{s}},\dot{{\bar{s}}},{\bar{y}},\dot{{\bar{y}}},0)=\nabla _{q^k}g^k_2(t,{\bar{s}},\dot{{\bar{s}}},{\bar{y}},\dot{{\bar{y}}},0)$.

Then

• (i) there exist ${\bar{w}}^k \in B^k$, ${\bar{x}}^k \in E^k,~k\in \kappa$, such that $({\bar{s}},{\bar{y}},{\bar{m}},{\bar{w}},{\bar{x}},{\bar{q}}=0)$ is feasible for $\text {(SHFVD)}_{{\bar{\lambda }}}$, and

• (ii) the objective values of (SHFVP) and $\text {(SHFVD)}_{{\bar{\lambda }}}$ are equal.

Furthermore, if the hypotheses of weak duality theorem are satisfied for all feasible solutions of $\text {(SHFVP)}_{{\bar{\lambda }}}$ and $\text {(SHFVD)}_{{\bar{\lambda }}}$, then $({\bar{s}},{\bar{y}},{\bar{m}},{\bar{w}},{\bar{x}},{\bar{q}}=0)$ is an efficient solution of $\text {(SHFVD)}_{{\bar{\lambda }}}$.

Proof

Since (${\bar{s}},{\bar{y}},{\bar{m}},{\bar{\lambda }},{\bar{z}},{\bar{r}},{\bar{p}}$) is weakly efficient solution of (SHFVP), by Fritz John optimality conditions [17], then there exist $\alpha \in R^l_+, \beta \in R^l$, piecewise smooth functions $\gamma (t) :\varOmega \rightarrow {\mathcal {C}}_2,~~ \xi (t):\varOmega \rightarrow R_+$ and $\delta \in R^l_+$ such that

$$\begin{aligned} {\tilde{M}}&= \sum _{k=1}^{l}\alpha ^k{\bar{m}}^k+\sum _{k=1}^{l}\beta ^k \bigg [(\phi _1^k + {\hat{S}}({\bar{s}}|B^k) - {\bar{y}}^T{\bar{z}}^k +h^k_1-{({\bar{p}}^k)}^T\nabla _{p^k}h^k_1) \\&\quad - {\bar{m}}^k(\phi _2^k - {\hat{S}}({\bar{s}}|E^k) + {\bar{y}}^T{\bar{r}}^k+g^k_1 -{({\bar{p}}^k)}^T\nabla _{p^k}g^k_1) \bigg ]\\&\quad + (\gamma - \xi {\bar{y}})^T \bigg [ \sum _{k=1}^{l}{\bar{\lambda }}_k \big \{ \left[ (\phi _1^k)_y-D(\phi _1^k)_{{\dot{y}}}-{\bar{z}}^k + \nabla _{p^k}h^k_1 \right] \\&\quad -{\bar{m}}^k\big [ (\phi _2^k)_y -D(\phi _2^k)_{{\dot{y}}}+{\bar{r}}^k+\nabla _{p^k}g^k_1 \big ] \big \} \bigg ] -\delta ^T{\bar{\lambda }} \end{aligned}$$

satisfies the conditions given below at (${\bar{s}},{\bar{y}},{\bar{m}},{\bar{\lambda }},{\bar{z}},{\bar{r}},{\bar{p}}) :$

$$\begin{aligned}&\big [{\tilde{M}}_s-D{\tilde{M}}_{{\dot{s}}}+D^2{\tilde{M}}_{\ddot{s}} \big ](s(t)-{\bar{s}}(t)) \geqq 0, ~~~ \forall ~ s(t)\in {\mathcal {C}}_1,~~~~t\in \varOmega , \end{aligned}$$

(30)

$$\begin{aligned}&{\tilde{M}}_y-D{\tilde{M}}_{{\dot{y}}}+D^2{\tilde{M}}_{\ddot{y}} = 0, ~~~~ t\in \varOmega , \end{aligned}$$

(31)

$$\begin{aligned}&{\tilde{M}}_\lambda = 0, ~~~~t\in \varOmega , \end{aligned}$$

(32)

$$\begin{aligned}&{\tilde{M}}_m=0,~~~~t\in \varOmega , \end{aligned}$$

(33)

$$\begin{aligned}&{\tilde{M}}_p=0,~~~~t\in \varOmega , \end{aligned}$$

(34)

$$\begin{aligned}&\int _{\delta _1}^{\delta _2} \beta ^k \bigg [ (\phi _1^k + {\hat{S}}({\bar{s}}|B^k) - {\bar{y}}^T{\bar{z}}^k +h^k_1-{({\bar{p}}^k)}^T\nabla _{p^k}h^k_1)-{\bar{m}}^k(\phi _2^k - {\hat{S}}({\bar{s}}|E^k) \nonumber \\&\qquad + {\bar{y}}^T{\bar{r}}^k +g^k_1- {({\bar{p}}^k)}^T\nabla _{p^k}g^k_1) \bigg ] ~\mathrm{d}t =0, \quad k\in \kappa , ~t\in \varOmega , \end{aligned}$$

(35)

$$\begin{aligned}&\gamma ^T\left[ \sum _{k=1}^{l}{\bar{\lambda }}_k ((\phi _1^k)_y-D(\phi _1^k)_{{\dot{y}}}-{\bar{z}}^k + \nabla _{p^k}h^k_1 ) -{\bar{m}}^k( (\phi _2^k)_y-D(\phi _2^k)_{{\dot{y}}}+{\bar{r}}^k + \nabla _{p^k}g^k_1 )\right] \nonumber \\&\qquad =0,\quad t\in \varOmega , \end{aligned}$$

(36)

$$\begin{aligned}&\xi {\bar{y}}^T\left[ \sum _{k=1}^{l}{\bar{\lambda }}_k ((\phi _1^k)_y-D(\phi _1^k)_{{\dot{y}}}-{\bar{z}}^k + \nabla _{p^k}h^k_1 ) -{\bar{m}}^k( (\phi _2^k)_y-D(\phi _2^k)_{{\dot{y}}}+{\bar{r}}^k + \nabla _{p^k}g^k_1 )\right] \nonumber \\&\qquad =0,\quad t\in \varOmega , \end{aligned}$$

(37)

$$\begin{aligned}&\delta ^T{\bar{\lambda }}=0, \end{aligned}$$

(38)

$$\begin{aligned}&{\hat{S}}({\bar{s}}|B^k)={\bar{s}}^T\eta ^k,~~\eta ^k\in B^k,~~k\in \kappa , \end{aligned}$$

(39)

$$\begin{aligned}&{\hat{S}}({\bar{s}}|E^k)={\bar{s}}^T\theta ^k,~~\theta ^k\in E^k,~~k\in \kappa , \end{aligned}$$

(40)

$$\begin{aligned}&\beta ^k{\bar{y}}^T+[\gamma -\xi {\bar{y}}]{\bar{\lambda }}_k\in N_{D^k}({\bar{z}}^k), \end{aligned}$$

(41)

$$\begin{aligned}&{\bar{m}}^k[\beta ^k{\bar{y}}^T+(\gamma -\xi {\bar{y}}){\bar{\lambda }}_k]\in N_{H^k}({\bar{r}}^k), \end{aligned}$$

(42)

$$\begin{aligned}&(\alpha ,\beta ,\gamma ,\xi ,\delta )\ne 0,~~t\in \varOmega . \end{aligned}$$

(43)

Conditions (30)−(43) are valid for the entire interval $\varOmega$, except at the vertices of $({\bar{s}},{\bar{y}},{\bar{m}},{\bar{\lambda }},{\bar{z}},{\bar{r}},{\bar{p}})$, where (30) and (31) hold for unique right- and left-hand limits. The piecewise smooth functions $\gamma$ and $\xi$ are continuously differentiable except possibly of the corners of $({\bar{s}},{\bar{y}},{\bar{m}},{\bar{\lambda }},{\bar{z}},{\bar{r}},{\bar{p}})$.

Now equations (30)−(34) along with the observations on $D(\phi _1^k)_{{\dot{y}}}$ and $D(\phi _2^k)_{{\dot{y}}}$, $k\in \kappa$, from Sect. 2, become

$$\begin{aligned}&\Bigg [\sum _{k=1}^{l}\beta ^k \Big [(\phi _1^k)_s + \eta ^k +(h^k_1-{({\bar{p}}^k)}^T\nabla _{p^k}h^k_1)_s - {\bar{m}}^k((\phi _2^k)_s -\theta ^k+(g^k_1-{({\bar{p}}^k)}^T\nabla _{p^k}g^k_1)_s)\nonumber \\&\quad -D((\phi _1^k)_{{\dot{s}}}+(h^k_1-{({\bar{p}}^k)}^T\nabla _{p^k}h^k_1)_{{\dot{s}}}-{\bar{m}}^k((\phi _2^k)_{{\dot{s}}} +(g^k_1-{({\bar{p}}^k)}^T\nabla _{p^k}g^k_1)_{{\dot{s}}}))\nonumber \\&\quad +D^2((h^k_1-{({\bar{p}}^k)}^T\nabla _{p^k}h^k_1)_{\ddot{s}}- {\bar{m}}^k((g^k_1-{({\bar{p}}^k)}^T\nabla _{p^k}g^k_1)_{\ddot{s}})) \Big ] \nonumber \\&\quad + (\gamma - \xi {\bar{y}})^T\bigg [\sum _{k=1}^{l}{\bar{\lambda }}_k \{ (\phi _1^k)_{ys}-D(\phi _1^k)_{{\dot{y}}s} + (\nabla _{p^k}h^k_1)_s-{\bar{m}}^k( (\phi _2^k)_{ys}-D(\phi _2^k)_{{\dot{y}}s}\nonumber \\&\quad + (\nabla _{p^k}g^k_1)_s)\}\bigg ]-D\bigg [ (\gamma - \xi {\bar{y}})^T\Big [\sum _{k=1}^{l}{\bar{\lambda }}_k \{ (\phi _1^k)_{y{\dot{s}}}-D(\phi _1^k)_{{\dot{y}}{\dot{s}}}-(\phi _1^k)_{{\dot{y}}s} \nonumber \\&\quad + (\nabla _{p^k}h^k_1)_{{\dot{s}}} -{\bar{m}}^k( (\phi _2^k)_{y{\dot{s}}}-D(\phi _2^k)_{{\dot{y}}{\dot{s}}}-(\phi _2^k)_{{\dot{y}}s} + (\nabla _{p^k}g^k_1)_{{\dot{s}}})\} \Big ]\bigg ]\nonumber \\&\quad +D^2\bigg [ (\gamma - \xi {\bar{y}})^T\Big [\sum _{k=1}^{l}{\bar{\lambda }}_k \{ -(\phi _1^k)_{{\dot{y}}{\dot{s}}}+ (\nabla _{p^k}h^k_1)_{\ddot{s}} -{\bar{m}}^k( -(\phi _2^k)_{{\dot{y}}{\dot{s}}} + (\nabla _{p^k}g^k_1)_{\ddot{s}})\} \Big ]\bigg ]\Bigg ]\nonumber \\&\qquad (s(t)-{\bar{s}}(t)) \geqq 0,~\forall s(t)\in {\mathcal {C}}_1,~t\in \varOmega , \end{aligned}$$

(44)

$$\begin{aligned}&\sum _{k=1}^{l}\beta ^k \Big [(\phi _1^k)_y - {\bar{z}}^k +(h^k_1-{({\bar{p}}^k)}^T\nabla _{p^k}h^k_1)_y - {\bar{m}}^k((\phi _2^k)_y + {\bar{r}}^k +(g^k_1-{({\bar{p}}^k)}^T\nabla _{p^k}g^k_1)_y) \nonumber \\&\quad -D((\phi _1^k)_{{\dot{y}}} +(h^k_1-{({\bar{p}}^k)}^T\nabla _{p^k}h^k_1)_{{\dot{y}}}-{\bar{m}}^k((\phi _2^k)_{{\dot{y}}}+(g^k_1-{({\bar{p}}^k)}^T\nabla _{p^k}g^k_1)_{{\dot{y}}}))\nonumber \\&\quad +D^2((h^k_1-{({\bar{p}}^k)}^T\nabla _{p^k}h^k_1)_{\ddot{y}} - {\bar{m}}^k((g^k_1-{({\bar{p}}^k)}^T\nabla _{p^k}g^k_1)_{\ddot{y}}))\Big ]\nonumber \\&\quad + (\gamma - \xi {\bar{y}})^T\bigg [\sum _{k=1}^{l}{\bar{\lambda }}_k \{ (\phi _1^k)_{yy}-D(\phi _1^k)_{{\dot{y}}y} + (\nabla _{p^k}h^k_1)_y-{\bar{m}}^k( (\phi _2^k)_{yy}-D(\phi _2^k)_{{\dot{y}}y}\nonumber \\&\quad + (\nabla _{p^k}g^k_1)_y)\}\bigg ]-\xi \bigg [ \sum _{k=1}^{l}{\bar{\lambda }}_k ( \{ (\phi _1^k)_y-D(\phi _1^k)_{{\dot{y}}}-{\bar{z}}^k+ \nabla _{p^k}h^k_1 \} -{\bar{m}}^k( (\phi _2^k)_y-D(\phi _2^k)_{{\dot{y}}}\nonumber \\&\quad +{\bar{r}}^k + \nabla _{p^k}g^k_1 ) ) \bigg ]-D\bigg [ (\gamma - \xi {\bar{y}})^T\Big [\sum _{k=1}^{l}{\bar{\lambda }}_k \{ (\phi _1^k)_{y{\dot{y}}}-D(\phi _1^k)_{{\dot{y}}{\dot{y}}}-(\phi _1^k)_{{\dot{y}}y} + (\nabla _{p^k}h^k_1)_{{\dot{y}}}\nonumber \\&\quad -{\bar{m}}^k( (\phi _2^k)_{y{\dot{y}}} -D(\phi _2^k)_{{\dot{y}}{\dot{y}}} -(\phi _2^k)_{{\dot{y}}y}+ (\nabla _{p^k}g^k_1)_{{\dot{y}}})\} \Big ]\bigg ] \nonumber \\&\quad +D^2\bigg [ (\gamma - \xi {\bar{y}})^T\Big [\sum _{k=1}^{l}{\bar{\lambda }}_k \{ -(\phi _1^k)_{{\dot{y}}{\dot{y}}}+ (\nabla _{p^k}h^k_1)_{\ddot{y}}-{\bar{m}}^k( -(\phi _2^k)_{{\dot{y}}{\dot{y}}} + (\nabla _{p^k}g^k_1)_{\ddot{y}})\} \Big ]\bigg ]= 0,\nonumber \\&\qquad ~~~t\in \varOmega , \end{aligned}$$

(45)

$$\begin{aligned}&(\gamma - \xi {\bar{y}})^T \Big [ \left[ (\phi _1^k)_y-D(\phi _1^k)_{{\dot{y}}}-{\bar{z}}^k + \nabla _{p^k}h^k_1 \right] -{\bar{m}}^k\left[ (\phi _2^k)_y-D(\phi _2^k)_{{\dot{y}}}+{\bar{r}}^k + \nabla _{p^k}g^k_1 \right] \Big ] \nonumber \\&\qquad -\delta ^k=0,~k\in \kappa ,~~t\in \varOmega , \end{aligned}$$

(46)

$$\begin{aligned}&\alpha ^k-\beta ^k(\phi _2^k - {\hat{S}}({\bar{s}}|E^k) + {\bar{y}}^T{\bar{r}}^k +g^k_1-{({\bar{p}}^k)}^T\nabla _{p^k}g_1^k)-(\gamma - \xi {\bar{y}})^T [{\bar{\lambda }}_k((\phi _2^k)_y\nonumber \\&\qquad -D(\phi _2^k)_{{\dot{y}}}+{\bar{r}}^k+ \nabla _{p^k}g^k_1) ]=0, \quad k\in \kappa ,~~t\in \varOmega , \end{aligned}$$

(47)

$$\begin{aligned}&\big ((\gamma - \xi {\bar{y}}){\bar{\lambda }}_k-\beta ^k{\bar{p}}^k\big )\Big [ \nabla _{p^kp^k}h^k_1-{\bar{m}}^k\nabla _{p^kp^k}g^k_1\Big ]=0,~~k\in \kappa ,~~t\in \varOmega , \end{aligned}$$

(48)

As $\delta \geqq 0$ and ${\bar{\lambda }}>0$, (38) gives

$$\begin{aligned} \delta = 0. \end{aligned}$$

(49)

Consequently (46) becomes

$$\begin{aligned}&(\gamma - \xi {\bar{y}})^T \Big [ \left[ (\phi _1^k)_y-D(\phi _1^k)_{{\dot{y}}}-{\bar{z}}^k + \nabla _{p^k}h^k_1 \right] -{\bar{m}}^k\Big [ (\phi _2^k)_y-D(\phi _2^k)_{{\dot{y}}}+{\bar{r}}^k\nonumber \\&\quad + \nabla _{p^k}g^k_1 \Big ] \Big ]=0,~~\forall k\in \kappa ,~~t\in \varOmega . \end{aligned}$$

(50)

Since from hypothesis (i), $\nabla _{p^kp^k}h^k_1-{\bar{m}}^k\nabla _{p^kp^k}g^k_1$ are nonsingular, from (48), we get

$$\begin{aligned} (\gamma - \xi {\bar{y}})^T{\bar{\lambda }}_k=\beta ^k{\bar{p}}^k,~~~k\in \kappa , \end{aligned}$$

(51)

Now by hypothesis (ii) and (50), we get

$$\begin{aligned} \gamma - \xi {\bar{y}}=0, \end{aligned}$$

(52)

From Eqs. (51) and (52), we get

$$\begin{aligned} \beta ^k{\bar{p}}^k=0, ~~~k\in \kappa . \end{aligned}$$

(53)

As $\beta ^k\in R$ and ${\bar{p}}^k\in R^{n_2}$, this implies either

$$\begin{aligned} \beta ^k=0~~ \text {or}~~ {\bar{p}}^k=0, ~~~k\in \kappa . \end{aligned}$$

(54)

Hence from equation (45), (52), (54) and hypothesis (iii), we have

$$\begin{aligned}&\sum _{k=1}^{l}(\beta ^k -\xi {\bar{\lambda }}_k)\Big [(\phi _1^k)_y -D(\phi _1^k)_{{\dot{y}}} - {\bar{z}}^k +\nabla _{p^k}h^k_1 - {\bar{m}}^k((\phi _2^k)_y-D(\phi _2^k)_{{\dot{y}}} + {\bar{r}}^k +\nabla _{p^k}g^k_1)\Big ]\nonumber \\&\quad =0,~~k\in \kappa . \end{aligned}$$

(55)

Using assumption (ii) and (55), we have

$$\begin{aligned}&\beta ^k=\xi {\bar{\lambda }}_k, ~~k\in \kappa \nonumber \\ \text {i.e.,}~~&\beta =\xi {\bar{\lambda }} \end{aligned}$$

(56)

If $\beta ^k=0$ for some $k\in \kappa$, from (56) $\xi =0$, ${\bar{\lambda }}>0$ implies $\beta ^k=0$ for all $k \in \kappa$, (52) implies $\gamma =0$, and using (52), (47) implies $\alpha =0$. Using (49), $(\alpha ,\beta ,\gamma ,\xi ,\delta )=0$, contradicting equation (43).

Thus $\beta ^k\ne 0$ $\forall ~k\in ~\kappa$, i.e., $\beta \ne 0$. Hence equation (53) implies

$$\begin{aligned} {\bar{p}}^k=0~~ \text {for all}~~ k. \end{aligned}$$

(57)

By (52), (57), $k\in \kappa$, hypothesis (iii) and ${\bar{\lambda }}>0$, (44) and (45) become

$$\begin{aligned}&\sum _{k=1}^{l}\beta ^k \Big [(\phi _1^k)_s + \eta ^k -D(\phi _1^k)_{{\dot{s}}} +\nabla _{s}h^k_1 - {\bar{m}}^k((\phi _2^k)_s -\theta ^k-D(\phi _2^k)_{{\dot{s}}} +\nabla _{s}g^k_1)\Big ]\nonumber \\&\quad (s(t)-{\bar{s}}(t))\geqq 0,~t\in \varOmega , \end{aligned}$$

(58)

and

$$\begin{aligned}&\sum _{k=1}^{l}(\beta ^k-\xi {\bar{\lambda }}_k) \Big [(\phi _1^k)_y - {\bar{z}}^k -Df_{{\dot{y}}}^k+ \nabla _{p^k}h^k_1 - {\bar{m}}^k((\phi _2^k)_y + {\bar{r}}^k -Dg_{{\dot{y}}}^k+ \nabla _{p^k}g^k_1)\Big ]\nonumber \\&\quad =0, ~t\in \varOmega , \end{aligned}$$

(59)

respectively. Similarly from hypothesis (ii), from (59), we have

$$\begin{aligned} \beta ^k=\xi {\bar{\lambda }}_k \quad \text {or}\quad \beta =\xi {\bar{\lambda }}. \end{aligned}$$

(60)

Since $\beta \ne 0$ and ${\bar{\lambda }}>0$ implies $\xi \ne 0$ that is $\xi >0$. From (52) we have

$$\begin{aligned} {\bar{y}}=\dfrac{\gamma }{\xi }\in {\mathcal {C}}_2, ~t\in \varOmega . \end{aligned}$$

(61)

From (57), (60), hypothesis (iii) and $\xi >0$, equation (58) implies

$$\begin{aligned}&\sum _{k=1}^{l}{\bar{\lambda }}_k \Big [(\phi _1^k)_s + \eta ^k -D(\phi _1^k)_{{\dot{s}}} +\nabla _{q^k}h^k_2 - {\bar{m}}^k((\phi _2^k)_s -\theta ^k-D(\phi _2^k)_{{\dot{s}}} +\nabla _{q^k}g^k_2)\Big ]\nonumber \\&\quad (s(t)-{\bar{s}}(t))\geqq 0,~t\in \varOmega , \end{aligned}$$

(62)

Let $s(t)\in {\mathcal {C}}_1$, then $s(t)+{\bar{s}}(t)\in {\mathcal {C}}_1$, $t\in \varOmega$, so from (62) we have

$$\begin{aligned}&\sum _{k=1}^{l}{\bar{\lambda }}_k \Big [(\phi _1^k)_s + \eta ^k -D(\phi _1^k)_{{\dot{s}}} +\nabla _{q^k}h^k_2 - {\bar{m}}^k((\phi _2^k)_s -\theta ^k-D(\phi _2^k)_{{\dot{s}}} +\nabla _{q^k}g^k_2)\Big ]\\&\quad s(t)\geqq 0,~t\in \varOmega , \end{aligned}$$

that is

$$\begin{aligned}&\sum _{k=1}^{l}{\bar{\lambda }}_k \Big [(\phi _1^k)_s + \eta ^k -D(\phi _1^k)_{{\dot{s}}} +\nabla _{q^k}h^k_2 - {\bar{m}}^k((\phi _2^k)_s -\theta ^k-D(\phi _2^k)_{{\dot{s}}} +\nabla _{q^k}g^k_2)\Big ]\nonumber \\&\quad \in {\mathcal {C}}_1^*,~t\in \varOmega . \end{aligned}$$

(63)

Also, let $s(t)=0$ and $s(t)=2{\bar{s}}(t)$, simultaneously in equation (62), we have

$$\begin{aligned}&{\bar{s}}(t)^T\sum _{k=1}^{l}{\bar{\lambda }}_k \Big [(\phi _1^k)_s + \eta ^k -D(\phi _1^k)_{{\dot{s}}} +\nabla _{q^k}h^k_2 - {\bar{m}}^k((\phi _2^k)_s -\theta ^k-D(\phi _2^k)_{{\dot{s}}} +\nabla _{q^k}g^k_2)\Big ]\nonumber \\&\quad = 0,~t\in \varOmega . \end{aligned}$$

(64)

Further, equations (41), (52) and (60) with $\xi >0$, $t\in \varOmega$ give

$$\begin{aligned}&\quad \quad {\bar{\lambda }}_k{\bar{y}}\in N_{D^k}({\bar{z}}^k), ~ \text {for}~k\in \kappa ,\\&\text {or}\quad {\bar{y}}\in N_{D^k}({\bar{z}}^k), ~ \text {using} ~{\bar{\lambda }}_k>0. \end{aligned}$$

Since $D^k$ is compact convex set in $R^{n_2}$, ${\bar{y}}^T{\bar{z}}^k={\hat{S}}({\bar{y}}|D^k)$, $k\in \kappa$.

Also, from (42), (52), (60) with $\xi >0$, $t\in \varOmega$, we have for $k\in \kappa$

$$\begin{aligned}&\quad \quad {\bar{m}}^k{\bar{\lambda }}_k{\bar{y}}\in N_{H^k}({\bar{r}}^k),\\&\text {or}\quad {\bar{y}}\in N_{H^k}({\bar{r}}^k), ~ \text {using} ~{\bar{\lambda }}_k>0. \end{aligned}$$

Since $H^k$ is compact convex set in $R^{n_2}$, ${\bar{y}}^T{\bar{r}}^k={\hat{S}}({\bar{y}}|H^k)$, $k\in \kappa$.

Therefore, from (61), (63), (64), it shows that $({\bar{s}},{\bar{y}},{\bar{m}},{\bar{w}}=\eta ,{\bar{x}}=\theta ,{\bar{q}}=0)$ is feasible solution for the dual problem $\text {(SHFVD)}_{{\bar{\lambda }}}$. Thus (SHFVP) and $\text {(SHFVD)}_{{\bar{\lambda }}}$ have equal objectives values (i.e., ${\bar{m}}={\bar{n}}$).

If $({\bar{s}},{\bar{y}},{\bar{m}},{\bar{w}},{\bar{x}},{\bar{q}}=0)$ is not an efficient solution of $\text {(SHFVD)}_{{\bar{\lambda }}}$, then there exists $({\bar{a}},{\bar{b}},{\bar{n}},{\bar{w}},{\bar{x}},{\bar{q}}=0)$ feasible for $\text {(SHFVD)}_{{\bar{\lambda }}}$ such that

$$\begin{aligned} {\bar{m}}\le {\bar{n}}, \end{aligned}$$

which is contradiction to weak duality theorem (Theorem 3.1 or 3.2). Thus $({\bar{s}},{\bar{y}},{\bar{m}},{\bar{w}},{\bar{x}},{\bar{q}}=0)$ is an efficient solution of $\text {(SHFVD)}_{{\bar{\lambda }}}$. This completes the proof. $\square$

Theorem 3.4

(Converse Duality Theorem). Assume (${\bar{a}},{\bar{b}},{\bar{n}},{\bar{\lambda }},{\bar{w}},{\bar{x}},{\bar{q}}$) be a weakly efficient solution for (SHFVD). Further, suppose that

• (i) The Hessian matrices $\nabla _{q^kq^k}h^k_2-{\bar{n}}^k\nabla _{q^kq^k}g^k_2$ are nonsingular matrices,

• (ii) The set of vectors $\big \{ \left[ (\phi _1^k)_s-D(\phi _1^k)_{{\dot{s}}}+{\bar{w}}^k + \nabla _{q^k}h^k_2 \right] -{\bar{n}}^k\left[ (\phi _2^k)_s-D(\phi _2^k)_{{\dot{s}}}-{\bar{x}}^k + \nabla _{q^k}g^k_2 \right] \big \}$ are linearly independent,

• (iii) $\nabla _{s}h^k_2(t,{\bar{a}},\dot{{\bar{a}}},{\bar{b}},\dot{{\bar{b}}},0)=0$, $\nabla _{{\dot{y}}}h^k_2(t,{\bar{a}},\dot{{\bar{a}}},{\bar{b}},\dot{{\bar{b}}},0)=0,$ $\nabla _{{\dot{s}}}h^k_2(t,{\bar{a}},\dot{{\bar{a}}},{\bar{b}},\dot{{\bar{b}}},0)=0,$ $\nabla _{\ddot{y}}h^k_2(t,{\bar{a}},\dot{{\bar{a}}},{\bar{b}},\dot{{\bar{b}}},0)=0,$ $\nabla _{\ddot{s}}h^k_2(t,{\bar{a}},\dot{{\bar{a}}},{\bar{b}},\dot{{\bar{b}}},0)$, $\nabla _{q^k}h^k_2(t,{\bar{a}},\dot{{\bar{a}}},{\bar{b}},\dot{{\bar{b}}},0)=0$, $\nabla _{y}h^k_2(t,{\bar{a}},\dot{{\bar{a}}},{\bar{b}},\dot{{\bar{b}}},0)=\nabla _{p^k}h^k_1(t,{\bar{a}},\dot{{\bar{a}}},{\bar{b}},\dot{{\bar{b}}},0)$, $\nabla _{s}g^k_2(t,{\bar{a}},\dot{{\bar{a}}},{\bar{b}},\dot{{\bar{b}}},0)=0$, $\nabla _{{\dot{y}}}g^k_2(t,{\bar{a}},\dot{{\bar{a}}},{\bar{b}},\dot{{\bar{b}}},0)=0$, $\nabla _{{\dot{s}}}g^k_2(t,{\bar{a}},\dot{{\bar{a}}},{\bar{b}},\dot{{\bar{b}}},0)=0$, $\nabla _{\ddot{y}}g^k_2(t,{\bar{a}},\dot{{\bar{a}}},{\bar{b}},\dot{{\bar{b}}},0)=0$, $\nabla _{\ddot{s}}g^k_2(t,{\bar{a}},\dot{{\bar{a}}},{\bar{b}},\dot{{\bar{b}}},0)=0$, $\nabla _{q^k}g^k_2(t,{\bar{a}},\dot{{\bar{a}}},{\bar{b}},\dot{{\bar{b}}},0)\!=0$, $\nabla _{y}g^k_2(t,{\bar{a}},\dot{{\bar{a}}},{\bar{b}},\dot{{\bar{b}}},0)=\nabla _{p^k}g^k_2(t,{\bar{a}},\dot{{\bar{a}}},{\bar{b}},\dot{{\bar{b}}},0)$.

Then

• (i) there exist ${\bar{z}}^k \in D^k$, ${\bar{r}}^k \in H^k,~k\in \kappa$, such that $({\bar{a}},{\bar{b}},{\bar{n}},{\bar{z}},{\bar{r}},{\bar{p}}=0)$ is feasible for $\text {(SHFVP)}_{{\bar{\lambda }}}$, and

• (ii) the objective values of (SHFVD) and $\text {(SHFVP)}_{{\bar{\lambda }}}$ are equal.

Furthermore, if the hypotheses of weak duality theorem are satisfied for all feasible solutions of $\text {(SHFVP)}_{{\bar{\lambda }}}$ and $\text {(SHFVD)}_{{\bar{\lambda }}}$, then $({\bar{a}},{\bar{b}},{\bar{n}},{\bar{z}},{\bar{r}},{\bar{p}}=0)$ is an efficient solution of $\text {(SHFVP)}_{{\bar{\lambda }}}$.

Proof

It follows on the lines of Theorem 3.3. $\square$

4 Application of Weak Duality Theorem

Suppose there is an FMCG company interested in manufacturing a new product and wishes to minimize its production schedule over a period of 1 year. Its production schedule is given by

$$\begin{aligned}&\text {(EHFVP)~min}~~\dfrac{\int _{0}^{1}s^2+y+3~\mathrm{d}t}{\int _{0}^{1}y+3~\mathrm{d}t}\\&\qquad \text {Subject to}\\&\qquad s(0)=0=s(1),~~y(0)=0=y(1),\\&\qquad {\dot{s}}(0)=0={\dot{s}}(1), ~~~ {\dot{y}}(0)=0={\dot{y}}(1),\\&\qquad -\bigg (1-\dfrac{\int _{0}^{1}s^2+y+3~\mathrm{d}t}{\int _{0}^{1}y+3~\mathrm{d}t}\bigg )\geqq 0, \\&\qquad y\bigg (1-\dfrac{\int _{0}^{1}s^2+y+3~\mathrm{d}t}{\int _{0}^{1}y+3~\mathrm{d}t}\bigg )\geqq 0,\\&\text { where } s:\varOmega \rightarrow [0,\infty ] \text { and } y:\varOmega \rightarrow [0,\infty ] \text { are smooth functions.}. \end{aligned}$$

For this model, we will verify the weak duality theorem. Further, we simplified problem (EHFVP) using parametric prospective defined below.

$$\begin{aligned}&\text {(SEHFVP)~min}~~m^1\\&\qquad \text {Subject to}\\&\qquad s(0)=0=s(1),~~y(0)=0=y(1),\\&\qquad {\dot{s}}(0)=0={\dot{s}}(1), ~~~ {\dot{y}}(0)=0={\dot{y}}(1),\\&\qquad \int _{0}^{1}s^2+y+3~\mathrm{d}t-m^1\int _{0}^{1}y+3~\mathrm{d}t=0,\\&\qquad -\bigg (1-m^1\bigg )\geqq 0,\\&\qquad y\bigg (1-m^1\bigg )\geqq 0,\\&\qquad s(t)\in [0,\infty ],~~~~~~ t\in [0,1]. \end{aligned}$$

For its dual, consider the higher-order functions as:

$$\begin{aligned}&\qquad h_2(t,s,{\dot{s}},y,{\dot{y}},q)=q^2,\\&\qquad g_2(t,s,{\dot{s}},y,{\dot{y}},q)=0. \end{aligned}$$

Consequently, the dual of the above problem (SEHFVP) is given below.

$$\begin{aligned}&\text {(SEHFVD)~max}~~n^1\\&\qquad \text {Subject to}\\&\qquad a(0)=0=a(1),~~b(0)=0=b(1),\\&\qquad {\dot{a}}(0)=0={\dot{a}}(1), ~~~ {\dot{b}}(0)=0={\dot{b}}(1),\\&\qquad \int _{0}^{1}(a^2+b+3-q^2)~\mathrm{d}t-n^1\int _{0}^{1}b+3~\mathrm{d}t=0,\\&\qquad \bigg (2a+2q\bigg )\geqq 0,\\&\qquad a\bigg (2a+2q\bigg )\leqq 0,\\&\qquad b(t)\in [0,\infty ],~~~~~~ t\in [0,1], \end{aligned}$$

where

$$\begin{aligned}&n_1=n_2=1,~l=1,~\phi _1^1=s^2+y+3,~\phi _2^1=y+3,~B^1=E^1=D^1=H^1=0,\\&m^1=\dfrac{\check{F}^k(s,y)}{\check{G}^k(s,y)}=\dfrac{\int _{0}^{1}s^2+y+3~\mathrm{d}t}{\int _{0}^{1}y+3~\mathrm{d}t},\\&n^1=\dfrac{\check{M}^k(a,b)}{\check{L}^k(a,b)}=\dfrac{\int _{0}^{1}a^2+b+3-q^2~\mathrm{d}t}{\int _{0}^{1}b+3~\mathrm{d}t}. \end{aligned}$$

We can easily verify that $(s,y,m^1,\lambda ,z,r,p)=(t(t-1),0,m^1,1,0,0,t)$ and $(a,b,n^1,\lambda ,w,x,q)=(0,t,n^1,1,0,0,t)$ are the feasible solutions of (SEHFVP) and (SEHFVD), respectively, where $m^1=\dfrac{91}{90}$ and $n^1=\dfrac{19}{21}$.

Now, we will show that it satisfies the weak duality assumptions. For that, assume that $F(t,s,{\dot{s}},y,{\dot{y}};\alpha _1)=\alpha _1(s+y+1)$, $G(t,s,{\dot{s}},y,{\dot{y}};\alpha _2)=\alpha _2(s+y+1)^2$, where $\alpha _1(s,a)=\dfrac{1}{s+a+1}$, $\alpha _2(s,y)=\dfrac{1}{(s+y+1)^2}$. Also, $d_1(t,s,{\dot{s}},a,{\dot{a}})=(s+a)$, $d_2(t,y,{\dot{y}},b,{\dot{b}})=y^2$, $\rho _1=\dfrac{1}{7}$, and $\rho _2=\dfrac{1}{10}$

• (i) $\int _{0}^{1}(s^2+b+3)-n^1(b+3)~\mathrm{d}t$ is higher-order $(F,\alpha _1,\rho _1,d_1)$-pseudoconvex at $a(t)=0$ with respect to $q^2$ for fixed $b(t)=t$. We have

  $$\begin{aligned}&\int _{0}^{1}F\mathbf ( t,s,{\dot{s}},a,{\dot{a}};\alpha _1(s,a)(2a+2q)\mathbf ) ~\mathrm{d}t=\int _{0}^{1}2a+2q~\mathrm{d}t\geqq 0\\&\implies \int _{0}^{1} s^2+b+3-n^1(b+3)-a^2-b-3+n^1(b+3)-q^2\\&\qquad +2q^2-\dfrac{1}{7}(s+a)^2~\mathrm{d}t\\&=\int _{0}^{1}s^2+q^2-\dfrac{1}{7}(s+a)^2~\mathrm{d}t\geqq 0. \end{aligned}$$

• (ii) Similarly, we can show $\int _{0}^{1}-(s^2+b+3)+m^1(b+3)~\mathrm{d}t$ is higher-order $(G,\alpha _2,\rho _2,d_2)$-pseudoconvex at $y(t)=0$ for fixed $s(t)=t(t-1)$.

• (iii) $\int _{0}^{1}\Big ( \rho _1\left[ d_1(t,s,{\dot{s}},a,{\dot{a}}) \right] ^2 + \rho _2\left[ d_2(t,b,{\dot{b}},y,{\dot{y}}) \right] ^2\Big )\mathrm{d}t\geqq 0.$

• (iv) $\int _{0}^{1}b+3~\mathrm{d}t\geqq 0.$

Further,

$$\begin{aligned}&F(t,s,{\dot{s}},a,{\dot{a}};e)+\alpha _1^{-1}e^Ta \geqq 0, ~~ \forall ~~e \in [0,1],\\&G(t,b,{\dot{b}},y,{\dot{y}};f)+\alpha _2^{-1}f^Ty \geqq 0,~~ \forall ~~f \in [0,1]. \end{aligned}$$

Since all hypothesis of Theorem (3.1) is satisfied, we can conclude that $m\nleq n$, that is, $\dfrac{91}{90}\nleq \dfrac{19}{21}.$

5 Conclusion

A ratio dual of multiobjective higher-order variational symmetric dual programs involving support functions with cone constraints has been formulated. Duality theorems under higher-order $(F,\alpha ,\rho ,d)$-pseudoconvexity assumptions have also been established to relate the values of the primal problem and dual problem. We identify a class of functionals lying exclusively in the class of higher-order $(F,\alpha ,\rho ,d)$ pseudoconvexity and not in class of higher-order F-pseudoconvexity and $(F,\alpha ,\rho ,d)$-pseudoconvexity. A real-world application of FMCG company is given to validate the results of the weak duality theorem. However, it is difficult but fascinating to see whether this work can be applied to arbitrary cones.