An EPQ Model for Delayed Deteriorating Items with Two-Phase Production Period, Exponential Demand Rate and Linear Holding Cost

Abstract

The economic production quantity (EPQ) model for delayed deteriorating items considering two-phase production periods, exponential demand rate and linearly increasing function of time holding cost is proposed to solve a production problem similar to the one caused by the Covid-19 pandemic. Without shortages, the necessary and sufficient conditions for optimality of this model are characterized through a theorem and lemmas while a solution methodology based on differential calculus is adopted. This paper determines the best replenishment cycle length corresponding to the optimal total variable cost and production quantity of imperfect production industry. To illustrate this model, a numerical experiment is conducted. The results demonstrate that a higher carrying charge decreases the production quantity and a longer demanding period decreases the total variable cost of an industry with a distracted production period. Finally, managerial insights are discussed using sensitivity analysis and future research directions are exposed.

1 Introduction

Inventory refers to a physical stock of goods as well as economic resources that are reserved for the smooth, efficient and effective functioning of the business. An economic order quantity (EOQ) model is an inventory control model that determines the optimal quantity to be ordered to meet a deterministic demand over a predetermined period of time to either minimize cost or maximize profit. An economic production quantity (EPQ) determines the optimal quantity to be produced so as to meet a deterministic demand to minimize cost or maximize profit. Thus, the EPQ model is an offshoot of the well-known EOQ paradigm.

The basic EOQ model was developed by [1] and assumed a constant demand rate, items do not deteriorate and no stock out condition. This is a feature of a static environment, while in today’s dynamic environment most things are not constant. However, the demand rate of many products may always be in a dynamic state as ages of inventories have negative impacts on demand due to loss of quality, spoilage, loss of market potential and depletion. The EPQ model has been widely applied in exercise. However, there are some additional concepts in the assumption of the traditional EPQ model and several researchers. Many researchers have modified the basic EOQ/EPQ models by considering some more realistic features such as time-dependent demand, shortages and deterioration.

The first attempt to modify the basic EOQ model for the case of a time-varying demand rate was made in [2]. Later, [3] developed a heuristic approach for selecting lot size quantities in the general case of a deterministic time varying-demand rate and discrete opportunities for replenishment. Many inventory models, as in [4,5,6,7,8] and so on, are developed on the assumption that the demand rate of items varies linearly with time. However, the assumption of a linear demand rate reduces the applicability of the above models because it assumed a steady rise or fall in the demand rate per unit time which is rarely seen to occur for so many products. The demand for items such as some industrial products, seasonal goods, cloth materials, cars and mobile phones is either asymptotically normally distributed or time-dependent quadratic demand. As such, inventory models considering accelerated/retarded rise or fall in demand rate, which is represented by a quadratic function of time, are needed. Consequently, some researchers study inventory systems with a time quadratic demand rate as seen in [9] which investigates an EOQ model over a finite time horizon for an item with a time-dependent quadratic demand rate with shortages under permissible delay in payments. Subsequent [10] developed an inventory model for a two-parameter Weibull distributed deterioration rate with quadratic time-varying demand and shortages, then [11] minimize the average system cost on an EOQ model for a time-proportional deteriorating item with quadratic demand rate where shortage occurs in every cycle. Justifiably, [12] modified an inventory model for a deteriorating item having quadratic time-dependent demand under trade credit policy. Later [13] provided an optimal inventory replenishment policy for a deteriorating item assuming time-quadratic demand and partially time-dependent backlog with shortages in every cycle. Khanra et al. [14], Mishra [15], Uthayakumar and Karuppasamy [16], Dari and Sani [17], Priya and Senbagam [18], Babangida and Baraya [19] among others follows where quadratic demand rate are considered.

However, in real life, an exponentially availing situation of demand rate of items (i.e., the demand for face-mask, hand sanitizer and safety kits during the Covid-19 Pandemic) normally occur and this situation can best be represented by the exponential demand rate. Whenever some new attractive products launch in a supermarket or some seasonal items at beginning of the season like winter, the demand for such products is increasing depending upon the rate of purchase. Therefore, an exponential demand is more realistic than other types of demand. An inventory replenishment policy for instantaneous deteriorating items with time-dependent exponential declining market demand rate is initially discussed in [20]. Likewise, [21] discussed production policies for deteriorating items with time-dependent exponential declining market demand rate, then an inventory model for deteriorating items with exponentially declining demand rate is established in [22]. In [23], an inventory model for deteriorating items with exponentially declining demand rate is derived with time-dependent linear holding cost. Also, an inventory model for non-instantaneous deteriorating goods with time-dependent exponential declining demand rate is developed by [24] considering shortages that are fully backlogged. Tripathi et al. [25] developed an inventory model with exponential time-dependent demand and time-dependent deterioration. Shortages are allowed. The demand rate and the unit production cost are both considered proportional to each other. Later, [26] provided a manufacturing inventory model with preservation technology and shortages considering exponentially increasing function of time demand rate where the production rate is demand dependent. Consequently, [27] developed a two-phase production inventory model with a constant production rate considering exponential demand rate and time-dependent deterioration.

Many authors developed an inventory model for time-dependent deterioration, at the same time, some other authors considered items that start deteriorating upon production, that is why [28] studied an inventory replenishment policy for instantaneous deteriorating items with time-dependent quadratic demand rate and shortages assuming zero lead time while deteriorated items are not repaired or replaced during a giving cycle. Also, EPQ models which jointly determine the optimal inventory and marketing policy for the production inventory system of deteriorating items under inflationary conditions with demand as a function of insertions in media are developed in [29], under the assumption that the marginal effect of advertisement on sales is proportional to the unrealized potential of the market. In similar manner, an EPQ model for deteriorating items in which the demand rate is a function of the selling price and the production rate is considered as demand dependent is derived in [30] where shortages are allowed and partially backlogged, then [31] considered an EPQ model for deteriorating items with the growth of demand and shortages, where the optimal cycle time (which minimizes the total cost) and the optimal amount of shortage if it is allowed are determined. More current assumptions are considered when [32] established an EPQ model for deteriorating and meliorating items with stochastic inflation, variable demand rate in the warehouse and permissible delay in payments. Shortages are allowed and partially backlogged. The demand rate is assumed to be dependent on the selling price and permissible delay in payment. The demand rate increases as the delay in payment increases and decreases as the selling price increases. Later, [33] considered an EPQ model for deteriorating items with constant, linear and quadratic holding cost, where a comparative study between constant, linear and quadratic holding costs is carried out. Trade credit policy is considered in [34] when establishing an EPQ model for deteriorating substitute items. Similarly, some related studies on inventory models with the assumption that the deterioration starts immediately after the items are produced can be found in [35, 36] and so on.

Instantaneous deterioration is only realistic for some certain items. Inventories such as computers, photographic films, televisions, some industrial products and so on have a span of maintaining originality or quality and deterioration in that case sets in after that span which means they undergo decay over time. In [37], an EPQ model for items that exhibit a delay in deterioration with constant demand rate and reliability consideration is developed. Subsequently, [38] developed an EPQ model for non-instantaneous deteriorating items, where the demand rate is exponential, the production rate is a function of the demand rate, holding cost varies with time, partially deteriorated items are sold with a discount rate from the original one and the items which are completely deteriorated are superfluous. Shortages are not allowed to occur. Moreover, some related studies on inventory models for non-instantaneous deteriorating items under various assumptions can be found in [17, 19, 39] and so on.

Most of the inventory models assumed that the holding cost of items when they are held in stock is constant. However, this is not generally the case, the holding cost of many items may be in a dynamic state. The cost of storing perishable items when more storage facilities and services are needed is always high, i.e., the cost of holding items such as fruits etc., in the stock is higher when better-preserving facilities are used to maintain the freshness and to prevent spoilage, and consequently this lower deterioration rate. Moreover, sometimes holding cost increases due to inflation, bank interest, hiring charge and so on. Thus, considering inventory models for time-varying holding cost is of great importance. This results in the establishment of an inventory model for deteriorating items with price dependent demand rate and time-varying holding cost with shortages that are completely backlogged in [40]. Later, [41] presented an EPQ model for delayed deteriorating items with stock-dependent demand rate and linear time-dependent holding cost. In the same trend, [42] developed an EOQ model for delayed deteriorating items with linear time-dependent holding cost. Also, the order quantity models for instantaneous deteriorating items with constant, linearly increasing function of time and quadratic holding costs are developed in [43], where a comparative study is carried out between constant, linear and quadratic holding costs with shortages. In [44], an integrated replenishment model for deteriorating items with multiple market demand rate under volume flexibility is established, the deterioration rate depends upon the quality level and time and follows a two-parameter Weibull distribution and holding cost is assumed to be a linearly increasing function of time. Also, some related studies on inventory models with time-varying holding cost can be found in [45,46,47,48] and so on.

Table 1 Comparison of some existing literature on production inventory models

Any situation similar to the Covid-19 pandemic would make it necessary to consider linear holding cost due to the accelerated production rate that occurred upon predicting that measures such as border closure, movement control order and the total lock-down would be taken by the government of the country affected. Upon predicting that these measures would be taken, the producers may change the production rate in either of negative or positive direction depending on the nature of the products. For local products with less life span, the production rate has to be reduced to avoid losses while for globally use with longer life span products and some items that their demand is at an exponential rate (such as past-food wrapping materials, facemasks, hand wash sanitizer and so on), the production rate needs to be accelerated before these measures are imposed to avoid shortages. The production rate of this kind is conditional and little work is found where it is considered in the study of inventory systems, where it exists [49, 50], the change in production is not instantaneous and the demand rate is not exponential. As such, this research tries to solve the production problem caused by the instantaneous sudden change in production rate by providing an EPQ model for non-instantaneous deteriorating items with conditional production rate, exponential demand rate and linearly time-dependent holding cost (Table 1).

2 Notations and Assumptions

Table 2 contains the notation used in this paper.

Table 2 Notations

The proposed model is developed based on the following modified assumptions adopted from [49] with addition of 2, 4, 9 and 10:

• 1. Instantaneous production.

• 2. Instantaneous change of production rate.

• 3. Unconstrained supplies capital.

• 4. Shortages not allowed.

• 5. After inspection, all defective items are discarded.

• 6. Production exceed demand during inventory build-up.

• 7. It is assumed that the inventory build-up period splits in two phases with different production rates which is a function defined as

  $$\begin{aligned} f(t)=\left\{ \begin{array}{ll} \rho ;&{}\quad 0\le t \le P_1\\ a\rho ;&{}\quad P_{1}\le t\le P_{2} \end{array}\right. , \end{aligned}$$

  where $a\in \{(0, 1)\cup (1, 2)\}$.

• 8. The demand rates $\lambda$ and $\lambda _2$ (during inventory build-up and within deterioration period, respectively) are assumed to be constant.

• 9. The demand rate $\lambda _1$ (after production but before deterioration starts) is assumed to be a exponential function of time defined as $\lambda _1 = \alpha e^{\beta t}$, where $\lambda _1 = \alpha$ at the point production stopped and $0\le \beta < 1$.

• 10. The hold cost per unit item is assumed to be linear function of time defined as $C_{H} = c_{1}+c_{2}t.$

• 11. The time borders of the inventory system are finite. That is, $P_1\le P_2 \le P_3 \le P.$

• 12. It is unreasonable to have deterioration continuously up to 1 year, so it is assumed that $P - P_{3}<1.$

3 Modeling

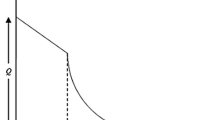
As shown in Fig. 1, the inventory level varies with time due to both conditional production rate, different demand rates and deterioration. Production start at a time $t = 0$ with a rate $\rho$ which change at time $t = P_1$, while the constant demand rate during the time interval $[0, P_1]$ is $\lambda$ and the inventory attains a level $X_1$ at a rate $\rho -\lambda$. Instantly, the production rate changes to $a \rho$ at time $t = P_1$ and the inventories continue accumulating at a rate $a \rho -\lambda$ up to the time $t = P_2$ when the inventories attained its maximum level $X_2$. Production stopped at time $t = P_2$ and the demand within the time interval $[P_2, P_3]$ is an exponential function of time ($\lambda _1=\alpha e^{\beta t}$). The inventory drops to level $X_3$ at time $t = P_3$ when deterioration sets-in. During the time interval $[P_{3}, P]$, the inventories continue dropping due to both constant demand rate $\lambda _{2}$ and deterioration up to the time $t = P$ when the inventories completely drop to zero.

Fig. 1

The inventory system of delayed deteriorating items

The governing differential equations that described the situation of the inventory system above are:

$$\begin{aligned} \frac{\mathrm{d}X(t)}{\mathrm{d}t}&= \rho -\lambda ;&0\le t\le P_1. \end{aligned}$$

(1)

$$\begin{aligned} \frac{\mathrm{d}X_{1}(t)}{\mathrm{d}t}&= a \rho -\lambda ;&P_1\le t\le P_2. \end{aligned}$$

(2)

$$\begin{aligned} \frac{\mathrm{d}X_{2}(t)}{\mathrm{d}t}&= -\lambda _{1}=-\alpha e^{\beta t};&P_2\le t\le P_3. \end{aligned}$$

(3)

$$\begin{aligned} \frac{\mathrm{d}X_{3}(t)}{\mathrm{d}t} +\theta X(t)_{3}&= -\lambda _2;&P_3\le t\le P_4. \end{aligned}$$

(4)

The solution of the differential equation (D.E) Eq. (1) that described the situation within the time interval $[0, P_1]$ is given below

$$\begin{aligned} X(t) = (\rho -\lambda )t + c\quad (\hbox {where}\quad c\quad \hbox {is constant}). \end{aligned}$$

(5)

Apply the boundary conditions $X(0)=0$ and $X(P_1)=X_{1}$ in Eq. (5)

$$\begin{aligned} X_{1}&= (\rho -\lambda ){P_1}. \end{aligned}$$

(6)

$$\begin{aligned} X(t)&= (\rho -\lambda )t. \end{aligned}$$

(7)

The solution of the D.E (2) which described the situation in $[P_1-P_2]$ is

$$\begin{aligned} X_{1}(t)=(a \rho -\lambda )t + c_{1}\quad (\hbox {where}\quad c_{1}\quad \hbox {is constant}), \end{aligned}$$

(8)

using the boundary conditions $X_{1}(P_1)=X_1$, and $X_{1}(P_2)=X_2$ in Eq. (8),

$$\begin{aligned} X_{1}(t)=(a \rho -\lambda )(t-{P_1})+(\rho -\lambda )P_{1};\quad P_{1}\le t \le P_{2}. \end{aligned}$$

(9)

The solution for the D.E (3) that described the situation within $[P_2, P_3]$ is

$$\begin{aligned} X_{2}(t)=-\frac{\alpha }{\beta }e^{\beta t} + c_{2}\quad (\hbox {where}\quad c_{2}\quad \hbox {is constant}), \end{aligned}$$

(10)

using the boundary conditions $X_{2}(P_2) = X_2$ and $X_{2}(P_3) = X_3$ in (10)

$$\begin{aligned} X_{2}(t)=\frac{\alpha }{\beta }\left( e^{\beta P_{3}} - e^{\beta t}\right) + X_{3}. \end{aligned}$$

(11)

Using the method of Integrating Factor, the solution of D.E (4) which described the situation within $[P_3, P]$ is:

$$\begin{aligned} X_{3}(t)=\frac{-\lambda _{2}}{\theta }+c_{3}e^{-\theta t}\quad (\hbox {where}\quad c_{3}\quad \hbox {is constant}), \end{aligned}$$

(12)

using the boundary conditions $X_{3}(P_3)=X_{3}$ and $X_{3}(P)=0$ in Eq. (10), the equations below are obtained

$$\begin{aligned} X_{3}(t)&= \frac{-\lambda _{2}}{\theta }+\left( X_{3}+\frac{\lambda _{2}}{\theta }\right) e^{\theta (P_{3}-t)}. \end{aligned}$$

(13)

$$\begin{aligned} X_{3}&= \frac{\lambda _{2}}{\theta }\left( e^{\theta (P-P_{3})}-1\right) . \end{aligned}$$

(14)

Substitute Eq. (14) into Eqs. (11) and (13) to get

$$\begin{aligned} X_{2}(t)&= \frac{\alpha }{\beta }\bigg (e^{\beta P_{3}}-e^{\beta t}\bigg ) + \frac{\lambda _{2}}{\theta }\left( e^{\theta (P-P_{3})}-1\right) \quad P_{2}\le t \le P_{3}. \end{aligned}$$

(15)

$$\begin{aligned} X_{3}(t)&= \frac{\lambda _{2}}{\theta }\left( e^{\theta (P-t)}-1\right) \quad P_{3}\le t \le P. \end{aligned}$$

(16)

4 Analytical Formulation

The inventory holding cost H associated with the carrying charge of all inventories and costs of storage of the total inventory from production until the sales of the last item is a multiple of inventory’s carrying charge per unit item, costs per unit item and the total number of item involved, obtained as:

$$\begin{aligned} H&= \pi C_{H}\left[ \int ^{P_1}_{0}X(t)\mathrm{d}t+\int ^{P_2}_{P_1}X_{1}(t)\mathrm{d}t+\int ^{P_3}_{P_2}X_{2}(t)\mathrm{d}t+\int ^{P}_{P_3}X_{3}(t)\mathrm{d}t\right] \nonumber \\&= \pi (c_{1}+c_{2}t)\bigg [\int ^{P_1}_{0}(\rho -\lambda )t\mathrm{d}t\,+\,\int ^{P_2}_{P_2}\bigg ((a \rho -\lambda )(t-{P_1})+(\rho -\lambda )P_{1}\bigg )\mathrm{d}t \nonumber \\&\quad +\,\int ^{P_3}_{P_2}\Bigg (\frac{\alpha }{\beta }\bigg (e^{\beta P_{3}}-e^{\beta t}\bigg ) + \frac{\lambda _{2}}{\theta }(e^{\theta (P-P_{3})}-1)\Bigg )\mathrm{d}t \nonumber \\&\quad +\, \int ^{P}_{P_3}\frac{\lambda _{2}}{\theta }(e^{\theta (P-t)}-1)\mathrm{d}t\bigg ] \nonumber \\&= \pi \Bigg [c_{1}\bigg [\frac{(\rho -\lambda )}{2}t^{2}\bigg |^{P_1}_{0}\,+\,\bigg ((a \rho -\lambda )\bigg (\frac{t^{2}}{2}-P_{1}t\bigg )+(\rho -\lambda )P_{1}t\bigg )\bigg |^{P_2}_{P_1} \nonumber \\&\quad +\, \bigg (\frac{\alpha }{\beta }\bigg (te^{\beta P_{3}}-\frac{1}{\beta }e^{\beta t}\bigg )+\frac{\lambda _{2}t}{\theta }(e^{\theta (P-P_{3})}-1)\bigg )\bigg |^{P_{3}}_{P_{2}}+\frac{\lambda _{2}}{\theta }\bigg (-\frac{1}{\theta }e^{\theta (P-t)}-t\bigg )\bigg |^{P}_{P_{3}}\bigg ] \nonumber \\&\quad +\,c_{2}\Bigg [\frac{\rho -\lambda }{3}t^{3}\bigg |^{P_1}_{0}+\bigg ((a \rho -\lambda )\Bigg (\frac{t^{3}}{3}-\frac{P_{1}t^{2}}{2}\Bigg )+\frac{(\rho -\lambda )}{2}P_{1}t^{2}\bigg )\bigg |^{P_2}_{P_1} \nonumber \\&\quad +\,\bigg (\frac{\alpha }{\beta }(\frac{t^{2}}{2}e^{\beta P_{3}}-\frac{t}{\beta }e^{\beta t}+\frac{1}{\beta ^{2}}e^{\beta t})+\frac{\lambda _{2}t^{2}}{2 \theta }(e^{\theta (P-P_{3})}-1)\bigg )\bigg |^{P_3}_{P_2} \nonumber \\&\quad +\frac{\lambda _{2}}{\theta }\bigg (\frac{-t}{\theta }e^{\theta (P-t)}+\frac{1}{\theta ^{2}}e^{\theta (P-t)}-\frac{t^{2}}{2}\bigg )^{P}_{P_3}\Bigg ]\Bigg ] \nonumber \\ H&= \pi \Bigg [c_{1}\Bigg [\frac{(\rho -\lambda )}{2}P^{2}_{1}+\frac{a \rho -\lambda }{2}(P_{2}-P_{1})^{2}+(\rho -\lambda )P_{1}(P_{2}-P_{1})+\frac{\alpha }{\beta }e^{\beta P_{2}} \nonumber \\&\quad +\frac{\alpha }{\beta }\bigg ((P_{3}-P_{2})-\frac{1}{\beta }\bigg )e^{\beta P_{3}}+\frac{\lambda _{2}}{\theta }\bigg (\frac{1}{\theta }+(P_{3}-P_{2})\bigg )\bigg (e^{\theta (P-P_{3})}-1\bigg ) \nonumber \\&\quad -\,\frac{\lambda _{2}}{\theta }(P-P_{3})\Bigg ]+c_{2}\bigg [\frac{(\rho -\lambda )}{3}P^{3}_{1}+\frac{a \rho -\lambda }{6}(2P^{3}_{2}-3P_{1}P^{2}_{2}+P^{3}_{1}) \nonumber \\&\quad +\frac{(\rho -\lambda )}{2}P_{1}(P^{2}_{2}-P^{2}_{1})+\frac{\alpha }{\beta }\bigg (\frac{P^{2}_{3}-P^{2}_{2}}{2}-\frac{P_{3}}{\beta }+\frac{1}{\beta ^{2}}\bigg )e^{\beta P_{3}} \nonumber \\&\quad +\frac{\alpha }{\beta ^{2}}(P_{2}-\frac{1}{\beta })e^{\beta P_{2}}+\frac{\lambda _2}{\theta }\bigg (\frac{P^{2}_{3}-P^{2}_{2}}{2}-\frac{1}{\theta ^{2}}\bigg )(e^{\theta (P-P_{3})}-1) \nonumber \\&\quad +\frac{\lambda _{2}}{\theta ^{2}}P_{3}e^{\theta (P-P_{3})}-\frac{\lambda _{2}}{\theta ^{2}}P-\frac{\lambda _{2}}{2\theta }(P^{2}-P^{2}_{3})\bigg ]\Bigg ]. \end{aligned}$$

(17)

The number of deteriorated inventories $N_{d}$ is the positive difference between the number of the remaining inventories at the time deterioration starts and the number of items demanded from the beginning to the end of the deterioration period, which is determined as

$$\begin{aligned} N_{d}=\frac{\lambda _{2}}{\theta }\left( e^{\theta (P-P_{3})}-1\right) -\lambda _{2}(P-{P_3}) \end{aligned}$$

(18)

4.1 Total Variable Cost

The total variable cost Z is the sum of setup cost A, holding cost H and deterioration cost $CN_{d}$, which is

$$\begin{aligned} Z=A+CN_d+H. \end{aligned}$$

The total variable cost per unit time is the total variable cost divided by cycle length, given by

$$\begin{aligned} Z(P)&= \frac{\hbox {Total variable cost}}{\hbox {Production cycle length}} \nonumber \\&= \frac{A}{P}\,+\,\frac{CN_{d}}{P}\,+\,\frac{H}{P}\nonumber \\ Z(P)&= \frac{A}{P}\,+\,\frac{C}{P}\left[ \frac{\lambda _{2}}{\theta }\left( e^{\theta (P-P_{3})}-1\right) -\lambda _{2}(P-{P_3})\right] +\frac{\pi }{P}\Bigg [c_{1}\bigg [\frac{(\rho -\lambda )}{2}P^{2}_{1}\nonumber \\&\quad +\frac{a \rho -\lambda }{2}(P_{2}-P_{1})^{2}+(\rho -\lambda )P_{1}(P_{2}-P_{1})+\frac{\alpha }{\beta }e^{\beta P_{2}} \nonumber \\&\quad +\frac{\alpha }{\beta }\left( (P_{3}-P_{2})-\frac{1}{\beta }\right) e^{\beta P_{3}}+\frac{\lambda _{2}}{\theta }\left( \frac{1}{\theta }+(P_{3}-P_{2})\right) (e^{\theta (P-P_{3})}-1) \nonumber \\&\quad -\frac{\lambda _{2}}{\theta }(P-P_{3})\bigg ]+c_{2}\bigg [\frac{(\rho -\lambda )}{3}P^{3}_{1}+\frac{a \rho -\lambda }{6}\big (2P^{3}_{2}-3P_{1}P^{2}_{2}+P^{3}_{1}\big ) \nonumber \\&\quad +\frac{(\rho -\lambda )}{2}P_{1}\big (P^{2}_{2}-P^{2}_{1}\big )+\frac{\alpha }{\beta }\left( \frac{P^{2}_{3}-P^{2}_{2}}{2}-\frac{P_{3}}{\beta }+\frac{1}{\beta ^{2}}\right) e^{\beta P_{3}} \nonumber \\&\quad +\frac{\alpha }{\beta ^{2}}(P_{2}-\frac{1}{\beta })e^{\beta P_{2}}+\frac{\lambda _2}{\theta }\left( \frac{P^{2}_{3}-P^{2}_{2}}{2}-\frac{1}{\theta ^{2}}\right) (e^{\theta (P-P_{3})}-1) \nonumber \\&\quad +\frac{\lambda _{2}}{\theta ^{2}}P_{3}e^{\theta (P-P_{3})}-\frac{\lambda _{2}}{\theta ^{2}}P-\frac{\lambda _{2}}{2\theta }\big (P^{2}-P^{2}_{3}\big )\bigg ]\Bigg ]. \end{aligned}$$

(19)

To obtain the value of the best cycle length P that minimizes the total variable cost, the derivative of Z(P) with respect to P needs to be equal to zero, i.e., $\frac{\mathrm{d}Z(P)}{P}=0$ (necessary condition) and $\frac{d^{2}Z(P)}{P^{2}}>0$ (sufficient condition for optimality of P).

For the necessary condition of optimality,

$$\begin{aligned} \frac{\mathrm{d}Z(P)}{\mathrm{d}P}&= \frac{-A}{P^{2}}-\frac{C}{P^{2}} \left[ \frac{\lambda _{2}}{\theta }\left( e^{\theta (P-P_{3})}-1\right) - \lambda _{2}(P-{P_3})\right] -\frac{\pi }{P^{2}}\Bigg [c_{1} \bigg [\frac{(\rho -\lambda )}{2}P^{2}_{1}\nonumber \\&\quad +\frac{a \rho -\lambda }{2}(P_{2}-P_{1})^{2}+(\rho -\lambda )P_{1}(P_{2}-P_{1})+\frac{\alpha }{\beta }e^{\beta P_{2}} \nonumber \\&\quad +\frac{\alpha }{\beta }\left( (P_{3}-P_{2})-\frac{1}{\beta }\right) e^{\beta P_{3}}+\frac{\lambda _{2}}{\theta }\left( \frac{1}{\theta }+(P_{3}-P_{2})\right) \left( e^{\theta (P-P_{3})}-1\right) \nonumber \\&\quad -\frac{\lambda _{2}}{\theta }(P-P_{3})\bigg ]+c_{2} \bigg [\frac{(\rho -\lambda )}{3}P^{3}_{1}+\frac{a \rho -\lambda }{6}(2P^{3}_{2}-3P_{1}P^{2}_{2}+P^{3}_{1}) \nonumber \\&\quad +\frac{(\rho -\lambda )}{2}P_{1}(P^{2}_{2}-P^{2}_{1})+\frac{\alpha }{\beta }\left( \frac{P^{2}_{3}-P^{2}_{2}}{2}-\frac{P_{3}}{\beta }+\frac{1}{\beta ^{2}}\right) e^{\beta P_{3}} \nonumber \\&\quad +\frac{\alpha }{\beta ^{2}}(P_{2}-\frac{1}{\beta })e^{\beta P_{2}}+\frac{\lambda _2}{\theta }\left( \frac{P^{2}_{3}-P^{2}_{2}}{2}-\frac{1}{\theta ^{2}}\right) (e^{\theta (P-P_{3})}-1) \nonumber \\&\quad +\frac{\lambda _{2}}{\theta ^{2}}P_{3}e^{\theta (P-P_{3})}-\frac{\lambda _{2}}{\theta ^{2}}P-\frac{\lambda _{2}}{2\theta }(P^{2}-P^{2}_{3}) \bigg ]\Bigg ]+\frac{C}{P}\left( \lambda _{2}e^{\theta (P-P_{3})}-\lambda _2 \right) \nonumber \\&\quad +\frac{\pi }{P}\Bigg [c_{1}\left[ \lambda _{2}\left( \frac{1}{\theta }+(P_{3}-P_{2})\right) e^{\theta (P-P_{3})}-\frac{\lambda _{2}}{\theta }\right] \nonumber \\&\quad + c_{2}\left[ \lambda _{2}\left( \frac{P^{2}_{3}-P^{2}_{2}}{2}-\frac{1}{\theta ^{2}}\right) e^{\theta (P-P_{3})}+\frac{\lambda _{2}}{\theta }P_{3}e^{\theta (P-P_{3})}\right. \nonumber \\&\quad \left. -\frac{\lambda _{2}}{\theta ^{2}}-\frac{\lambda _{2}}{\theta }P\right] \Bigg ] \nonumber \\&=\frac{-A}{P^{2}}-\frac{C\lambda _{2}}{P^{2}}\left[ \left( \frac{1}{\theta }-P\right) e^{\theta (P-P_{3})}+P_{3}-\frac{1}{\theta }\right] -\frac{\pi }{P^{2}}\Bigg [c_{1}\bigg [\frac{(\rho -\lambda )}{2}P^{2}_{1}\nonumber \\&\quad +\frac{a \rho -\lambda }{2}(P_{2}-P_{1})^{2}+(\rho -\lambda )P_{1}(P_{2}-P_{1})+\frac{\alpha }{\beta }e^{\beta P_{2}} \nonumber \\&\quad +\frac{\alpha }{\beta }\left( (P_{3}-P_{2})-\frac{1}{\beta }\right) e^{\beta P_{3}}+\frac{\lambda _{2}}{\theta }\left( \frac{1}{\theta }+(P_{3}-P_{2})\right) (e^{\theta (P-P_{3})}-1) \nonumber \\&\quad -P\lambda _{2}\left( \frac{1}{\theta }+(P_{3}-P_{2})\right) e^{\theta (P-P_{3})}+\frac{\lambda _{2}}{\theta }P_{3}\bigg ]+ c_{2}\bigg [\frac{(\rho -\lambda )}{3}P^{3}_{1} \nonumber \\&\quad +\frac{a \rho -\lambda }{6}(2P^{3}_{2}-3P_{1}P^{2}_{2}+P^{3}_{1})+\frac{(\rho -\lambda )}{2}P_{1}(P^{2}_{2}-P^{2}_{1}) \nonumber \\&\quad +\frac{\alpha }{\beta }\left( \frac{P^{2}_{3}-P^{2}_{2}}{2}-\frac{P_{3}}{\beta }+\frac{1}{\beta ^{2}}\right) e^{\beta P_{3}}+\frac{\alpha }{\beta ^{2}}(P_{2}-\frac{1}{\beta })e^{\beta P_{2}} \nonumber \\&\quad +\frac{\lambda _2}{\theta }\left( \frac{P^{2}_{3}-P^{2}_{2}}{2}-\frac{1}{\theta ^{2}}\right) (e^{\theta (P-P_{3})}-1)+\frac{\lambda _{2}}{2\theta }(P^{2}+P^{2}_{3}) \nonumber \\&\quad -\lambda _{2} P\left( \frac{P^{2}_{3}-P^{2}_{2}}{2}-\frac{1}{\theta ^{2}}\right) e^{\theta (P-P_{3})} + \frac{\lambda _{2}}{\theta }\left( \frac{1}{\theta }-P\right) P_{3}e^{\theta (P-P_{3})}\bigg ]\Bigg ] \end{aligned}$$

(20)

applying the approximate value of the exponential power using Maclaurin Series Expansion, which are $e^{\theta (P-P_{3})}\approx 1+\theta (P-P_{3}),$ $e^{\beta P_{2}}\approx 1+\beta P_{2}$ and $e^{\beta P_{3}}\approx 1+\beta P_{3}$ we have

$$\begin{aligned} \frac{\mathrm{d}Z(P)}{\mathrm{d}P}&= \frac{-A}{P^{2}}-\frac{C}{P^{2}}\bigg (\theta \lambda _{2}P(P_{3}-P)\bigg )\,-\,\frac{\pi }{P^{2}}\Bigg [c_{1}\bigg [\frac{(\rho -\lambda )}{2}P^{2}_{1} \nonumber \\&\quad +\frac{a \rho -\lambda }{2}(P_{2}-P_{1})^{2}+(\rho -\lambda )P_{1}(P_{2}-P_{1})+\frac{\alpha }{\beta }(1-P_{2})\nonumber \\&\quad +\alpha \bigg (P_{2}+P_{3}(P_{3}-P_{2})\bigg )-\frac{\alpha }{\beta ^{2}}-\lambda _{2}P_{3}\left( \frac{1}{\theta }+(P_{3}-P_{2})\right) \nonumber \\&\quad +\lambda _{2}PP_{3}\theta \left( \frac{1}{\theta }+(P_{3}-P_{2})\right) -\lambda _{2}P^{2}\theta \left( \frac{1}{\theta }+(P_{3}-P_{2})\right) \nonumber \\&\quad +\frac{\lambda _{2}}{\theta }P_{3}\bigg ]+ c_{2}\bigg [\frac{(\rho -\lambda )}{3}P^{3}_{1}+\frac{a \rho -\lambda }{6}(2P^{3}_{2}-3P_{1}P^{2}_{2}+P^{3}_{1}) \nonumber \\&\quad +\frac{(\rho -\lambda )}{2}P_{1}(P^{2}_{2}-P^{2}_{1}) - \frac{\alpha }{2\beta }(P^{2}_{3}-P^{2}_{2})+ \frac{\alpha }{2}P_{3}\left( P^{2}_{3}-P^{2}_{2}\right) \nonumber \\&\quad +\lambda _{2}\bigg (\left( \frac{P^{2}_{3}-P^{2}_{2}}{2}-\frac{1}{\theta ^{2}}\right) \theta + P_{3}\bigg )P_{3}P-\lambda _{2}\bigg (\bigg (\frac{P^{2}_{3}-P^{2}_{2}}{2} \nonumber \\&\quad -\frac{1}{\theta ^{2}}\bigg )\theta +P_{3}-\frac{1}{2\theta }\bigg )P^{2}-\lambda _{2}P_{3}\bigg (\frac{P^{2}_{3}-P^{2}_{2}}{2}-\frac{2}{\theta ^{2}}+\frac{1}{2\theta }P_{3}\bigg )\bigg ]\Bigg ] \end{aligned}$$

(21)

Simplify and setting (21) to zero,

$$\begin{aligned} \frac{\mathrm{d}Z(P)}{\mathrm{d}P}&= - A + \bigg [C\theta \lambda _{2}+\pi c_{1}\lambda _{2}\left( \frac{1}{\theta }+(P_{3}-P_{2})\right) \theta \nonumber \\&\quad +\pi c_{2}\lambda _{2}\bigg (\left( \frac{P^{2}_{3}-P^{2}_{2}}{2}-\frac{1}{\theta ^{2}}\right) +P_{3}-\frac{1}{2\theta }\bigg )\bigg ]P^{2}-\bigg [C\lambda _{2}\theta P_{3}\theta \nonumber \\&\quad +\pi c_{1}\lambda _{2}P_{3}\theta \left( \frac{1}{\theta }+(P_{3}-P_{2})\right) +\pi c_{2}\lambda _{2}\bigg (\left( \frac{P^{2}_{3}-P^{2}_{2}}{2}-\frac{1}{\theta ^{2}}\right) \theta \nonumber \\&\quad + P_{3}\bigg )P_{3}\bigg ]P-\pi \Bigg [c_{1}\bigg [\frac{(\rho -\lambda )}{2}P^{2}_{1}+\frac{a \rho -\lambda }{2}(P_{2}-P_{1})^{2}\nonumber \\&\quad +(\rho -\lambda )P_{1}(P_{2}-P_{1})+\frac{\alpha }{\beta }(1-\frac{1}{\beta })+\alpha P_{2}(1-\frac{1}{\beta })\nonumber \\&\quad +P_{3}(\alpha -\lambda _{2})(P_{3}-P_{2})\bigg ]+ c_{2}\bigg [\frac{(\rho -\lambda )}{3}P^{3}_{1}\nonumber \\&\quad +\frac{a \rho -\lambda }{6}(2P^{3}_{2}-3P_{1}P^{2}_{2}+P^{3}_{1})+\frac{(\rho -\lambda )}{2}P_{1}(P^{2}_{2}-P^{2}_{1}) \nonumber \\&\quad - \frac{\alpha }{2\beta }(P^{2}_{3}-P^{2}_{2}) + \frac{\alpha }{2}P_{3}\left( P^{2}_{3}-P^{2}_{2}\right) \nonumber \\&\quad -\lambda _{2}P_{3}\bigg (\frac{P^{2}_{3}-P^{2}_{2}}{2}-\frac{2}{\theta ^{2}}+\frac{1}{2\theta }P_{3}\bigg )\bigg ]\Bigg ]. \nonumber \\&= MP^{2}-LP-F=0 \end{aligned}$$

(22)

where

$$\begin{aligned} M&= C\theta \lambda _{2}+\pi c_{1}\lambda _{2}\left( \frac{1}{\theta }+(P_{3}-P_{2})\right) \theta \\&\quad +\pi c_{2}\lambda _{2}\bigg (\bigg (\frac{P^{2}_{3}-P^{2}_{2}}{2}-\frac{1}{\theta ^{2}}\bigg )\theta +P_{3}-\frac{1}{2\theta }\bigg ). \\ L&= C\lambda _{2}\theta P_{3}+\pi c_{1}\lambda _{2}P_{3}\theta \left( \frac{1}{\theta }+(P_{3}-P_{2})\right) \\&\quad +\pi c_{2}\lambda _{2}\bigg (\bigg (\frac{P^{2}_{3}-P^{2}_{2}}{2}-\frac{1}{\theta ^{2}}\bigg )\theta + P_{3}\bigg )P_{3}. \\ F&= \pi \Bigg [c_{1}\bigg [\frac{(\rho -\lambda )}{2}P^{2}_{1}+\frac{a \rho -\lambda }{2}(P_{2}-P_{1})^{2}+(\rho -\lambda )P_{1}(P_{2}-P_{1}) \\&\quad +\frac{\alpha }{\beta }(1-\frac{1}{\beta })+\alpha P_{2}(1-\frac{1}{\beta })+P_{3}(\alpha -\lambda _{2})(P_{3}-P_{2})\bigg ]+ c_{2}\bigg [\frac{(\rho -\lambda )}{3}P^{3}_{1} \\&\quad +\frac{a \rho -\lambda }{6}(2P^{3}_{2}-3P_{1}P^{2}_{2}+P^{3}_{1})+\frac{(\rho -\lambda )}{2}P_{1}(P^{2}_{2}-P^{2}_{1}) - \frac{\alpha }{2\beta }(P^{2}_{3}-P^{2}_{2}) \\&\quad + \frac{\alpha }{2}P_{3}\left( P^{2}_{3}-P^{2}_{2}\right) - \lambda _{2}P_{3}\bigg (\frac{P^{2}_{3}-P^{2}_{2}}{2}-\frac{2}{\theta ^{2}}+ \frac{1}{2\theta }P_{3}\bigg )\bigg ]\Bigg ]+A. \end{aligned}$$

Theorem 1

If $P_{1}\le P_{2}\le P_{3}\le 1$, $c_{1}>\frac{c_{2}}{\theta }$, $\lambda _{2} \le \alpha$, $P^{2}_{2}\ge P^{3}_{3}$, $\theta <1$, $\beta <1$ and $A \ge \pi \bigg (\frac{\alpha }{\beta }\bigg (\frac{c_{1}}{\beta }+\frac{c_{2}}{2}P^{2}_{3}\bigg )+\frac{c_{2}a\rho }{2}P_{2} P^{2}_{1}\bigg )$ then $M, L, F \in \Re ^{+}$ (see “Appendix A” for the proof).

Lemma 4.1

With the hypotheses of Theorem 1, the optimal cycle length is

$$\begin{aligned} P^*=\frac{1}{2M}\Bigg (L+\left( L^{2}+4MF\right) ^{\frac{1}{2}}\Bigg ). \end{aligned}$$

(23)

(See “Appendix B” for the proof).

Lemma 4.2

The total cost function Z(P) is a convex function of P, iff the hypotheses of Theorem 1 are valid.

(See “Appendix C” for the proof).

EPQ is the sum of total demand within production periods, total demand after production before deterioration starts, total demand after the deterioration starts and the total number of deteriorated items.

$$\begin{aligned} \hbox {EPQ}&= \lambda (P_1) + \lambda (P_{2}-P_{1}) + \lambda _{1}(P_{3}-P_{2}) + \lambda _{2}(P-P_{3}) + d(P_{3})\nonumber \\&= \lambda (P_1) + \lambda (P_{2}-P_{1}) + \int ^{P_{3}}_{P_{2}}\alpha e^{\beta t}\mathrm{d}t + \lambda _{2}(P-P_{3})\nonumber \\&\quad + \frac{\lambda _{2}}{\theta }\left( e^{\theta (P-P_{3})}-1\right) - \lambda _{2}(P-P_{3}) \nonumber \\&= \lambda (P_1) + \lambda (P_{2}-P_{1}) + \frac{\alpha }{\beta }\left( e^{\beta P_{3}}-e^{\beta P_{2}}\right) +\frac{\lambda _{2}}{\theta }\left( e^{\theta (P-P_{3})}-1\right) \nonumber \\ \Longrightarrow \hbox {EPQ}^{*}&= \lambda (P_2) + \frac{\alpha }{\beta }\left( e^{\beta P_{3}}-e^{\beta P_{2}}\right) +\frac{\lambda _{2}}{\theta }\left( e^{\theta (P-P_{3})}-1\right) . \end{aligned}$$

(24)

5 Numerical Experiments

The model developed in this work is illustrated by performing the following numerical experiments. Some of the parameter values presented in Table 3 are adopted from [17, 49] in addition to the values of parameters absent in their work which were also obtained optimally.

Table 3 Experiment parameters

5.1 Results

The problem described in this work is solved by substituting the parameter values presented in Table 3 in Eqs. (19), (23) and (24), the optimal values of the total variable cost, the best cycle length and economic production quantity are obtained and presented in Table 4.

Table 4 Optimal Solution

5.2 Comparison

The proposed model is derived from the existing ones, as such, the results can be compared with those using the same data for the numerical experiment to prove the optimality of the proposed model in this work (Table 5).

The proposed model in comparison with the existing models having the same objective and using the same data, it is discovered that the total variable cost obtained in this work is far minimum to that obtained in [17, 49]. Similarly, the production quantity obtained in this work within a less than 1 year cycle $(P<1)$ is maximum to that obtained in [17] with a cycle of more than one and half years $(P>1.5)$. Also, maximum to the production quantity obtained in [49] within a cycle of more than 1 year $(P>1)$. As such, the proposed model in this work is perfectly better.

Table 5 Comparison table

Table 6 Sensitivity analysis

Though the total variable cost obtained in [50] is minimum, it is less realistic to produce 8115.56 units in a cycle length closer to one and half years $(P\longrightarrow 1.5)$ if compared to the quantity of 83,995.12 units determined by the proposed model in a cycle of less than 1 year $(P<1)$. Assuming the cycle length of the proposed model is approaching that determined in [50], taking into account that, the demanding nature of the proposed model is an exponentially increasing function of time, then the total variable cost should have also been minimized. As such, the proposed model is an improved one here.

5.3 Sensitivity Analysis

The sensitivity analysis on the numerical solutions obtained and presented in Table 4 is performed to show the effects of varying some model’s parameter values on the optimal solutions, such effects can be observed as presented in Table 6. Also, the graphical representations of these effects are presented below.

Fig. 2

Effect of change in A on Z and EPQ

Fig. 3

Effect of change in C on Z and EPQ

Fig. 4

Effect of change in $\rho$ on Z and EPQ

Fig. 5

Effect of change in $\lambda$ on Z and EPQ

Fig. 6

Effect of change in $\pi$ on Z and EPQ

Fig. 7

Effect of change in $\theta$ on Z and EPQ

Fig. 8

Effect of change in $P_{3}$ on Z and EPQ

• 1. Both the total variable cost per unit time Z(P) and the economic production quantity (EPQ) increase as the setup cost (A) rises (see Fig. 2). In practice, any change in the setup cost has an impact on the total variable cost. The setup cost (A), on the other hand, has a significant impact on economic production. Manufacturers must investigate the setup cost scenario and compare the effects of total variable cost and EPQ. They should ensure the highest possible setup cost in order to maximize profit while minimizing overall variable costs.

• 2. The total variable cost per unit time Z(P) increases when the unit cost per item (C) rises, while the economic production quantity (EPQ) decreases, as shown in Fig. 3. The higher the unit cost, the higher the total variable cost, it stands to reason. The economic production quantity (EPQ) will decrease as a result. To minimize overall variable costs and maximize profit, the manufacturer should ensure that the cost per unit item is as low as possible.

• 3. The total variable cost Z(P) and the economic production quantity (EPQ) both increase slightly as the initial production rate ($\rho$) increases (see Fig. 4). Any change in production rate, of course, has an effect on both the total variable cost and the EPQ. However, the increase in EPQ is slightly greater. As a result, in order to maximize profit, the manufacturer should ensure the highest initial production rate possible, because the direction of the subsequent one cannot be predicted.

• 4. The total variable cost Z(P) drops when the demand during the production period ($\lambda$) rises while the economic production quantity (EPQ) rises (see Fig. 5). In practice, increasing demand during manufacturing generates an increase in production, resulting in the highest EPQ. Higher demand during production, on the other hand, lowers the holding cost of the items produced, lowering the total variable cost. This suggests that during the inventory build-up period, the advertisement and implementation of an appropriate marketing strategy be ensured.

• 5. The total variable cost per unit time Z(P) and the economic production quantity (EPQ) rises when the inventory carrying charge ($\pi$) increases (see Fig. 6). Because the inventory carrying charge ($\pi$) is one of the independent variables in the total variable cost function, and the higher the inventory carrying charge, the higher the total variable cost, this must be the case in practice. To achieve the best overall variable cost, manufacturers must guarantee that the carrying fee is kept to a bare minimum.

• 6. The total variable cost per unit time Z(P) increases as the deterioration rate ($\theta$) rises, but the economic production quantity (EPQ) falls (see Fig. 7). This is usually the case because as the rate of deterioration rises, so does the cost of deterioration, which raises the total variable cost. Furthermore, because the rate of deterioration is high, fewer items will be ordered, reducing demand and, as a result, the EPQ. Manufacturers must therefore seek all conceivable strategies to reduce the deterioration rate in order to maximize EPQ for maximum profit and minimize total variable cost.

• 7. The total variable cost per unit time Z(P) decreases when the purely demanding period (P3) grows, but the economic production quantity (EPQ) increases (see Fig. 8). This is very usual, since as the period of the demand is high, the deterioration period is short, lowering the cost of deterioration and lowering the overall variable cost. Similarly, the EPQ rises as the number of products sought rises. As a result, in order to maximize EPQ while lowering total variable cost, manufacturers must ensure that things have a longer life cycle in order to extend the demanding period.

6 Conclusion

This research investigated the optimal cycle length that optimizes the total variable cost and production quantity of an imperfect production industry of non-instantaneous deteriorating goods in which the inspection processes are imperfect with a distracted production period considering linear holding cost and exponential demand rate. The rationale for considering an exponential demand instead of a linear demand or a quadratic demand has been explained at the beginning $\lambda _1 = \alpha e^{\beta t}$; $\alpha >0$, $\beta \ne 0$. Production inventory modelers have considered many different types of production rates but so far the conditional production rate of a nature considered in this work is not visible. The best cycle length which minimizes the total variable cost is determined and proved optimal to the existing models numerically. The result shows that the proposed model is main for industries of non-instantaneous deteriorating goods on a special case for distracted productions period and rate. It also proved that an increase in $\lambda _{1}$ decreases Z and increases EPQ which shows that a new strategic marketing plan needs to be proposed for deterioration at the instance of change in production rate. The findings indicate that instant maximum production rate and possible minimum cost per unit item are required at the point instantaneous change of production rate occurs while extra care is needed on the combinatorial production formula when the cycle length is suddenly distracted. For optimality reasons, similar work can be proposed with shortage considering two or more dependent variables, also the same model could be proposed under trade credit policy.

Appendices

Appendix A: Proof of Theorem 1

Suppose

$$\begin{aligned} c_{1}\ge \frac{c_{2}}{\theta } \end{aligned}$$

(A1)

$$\begin{aligned} M&= C\theta \lambda _{2}+\pi c_{1}\lambda _{2}\left( \frac{1}{\theta }+(P_{3}-P_{2})\right) \theta \nonumber \\&\quad + \pi c_{2}\lambda _{2}\bigg (\bigg (\frac{P^{2}_{3}-P^{2}_{2}}{2}-\frac{1}{\theta ^{2}}\bigg )\theta +P_{3}-\frac{1}{2\theta }\bigg )\nonumber \\&= \lambda _{2}\left[ C\theta +\pi \left( c_{1} + c_{1}\theta (P_{3}-P{2})+ c_{2}P_{3}-\frac{c_{2}}{2\theta }+ \frac{c_{2}(P^{2}_{3}-P^{2}_{2})\theta }{2}-\frac{c_{2}}{\theta }\right) \right] \nonumber \\&= \lambda _{2}\left[ C\theta +\pi \left( c_{1} -\frac{3c_{2}}{2\theta }+\theta \left( c_{1}(P_{3}-P{2})+ \frac{c_{2}(P^{2}_{3}-P^{2}_{2})}{2}\right) +c_{2}P_{3}\right) \right] \end{aligned}$$

(A2)

since $c_{1}>\frac{c_{2}}{\theta }$ then

$$\begin{aligned} c_{1}\ge \frac{3c_{2}}{2\theta } \end{aligned}$$

(A3)

substitute (A3) in (A2)

$$\begin{aligned} M= \lambda _{2}\left[ C\theta +\pi \theta \left( c_{1}(P_{3}-P{2}) + \frac{c_{2}(P^{2}_{3}-P^{2}_{2})}{2}\right) +\pi c_{2}P_{3}\right] >0 \end{aligned}$$

hence

$$\begin{aligned} M>0 \end{aligned}$$

now,

$$\begin{aligned} L&= C\lambda _{2}\theta P_{3}+\pi c_{1}\lambda _{2}P_{3}\theta \left( \frac{1}{\theta }+(P_{3}-P_{2})\right) \nonumber \\&\quad +\pi c_{2}\lambda _{2}\bigg (\bigg (\frac{P^{2}_{3}-P^{2}_{2}}{2}-\frac{1}{\theta ^{2}}\bigg )\theta + P_{3}\bigg )P_{3}\nonumber \\&= \lambda _{2}\bigg (C\theta P_{3}+\pi c_{1}P_{3}+\pi c_{1}\theta P_{3}(P_{3}-P_{2}) \nonumber \\&\quad +\frac{\pi c_{2}P_{3}(P^{2}_{3}-P^{2}_{2})\theta }{2}-\frac{\pi c_{2}P_{3}}{\theta }+\pi c_{2}P^{2}_{3}\bigg ) \nonumber \\&= \lambda _{2}P_{3}\bigg (C\theta +\pi \bigg ( c_{1}-\frac{c_{2}}{\theta }+c_{1}\theta (P_{3}-P_{2})+\frac{c_{2}(P^{2}_{3}-P^{2}_{2})\theta }{2}+ c_{2}P_{3}\bigg )\bigg ) \end{aligned}$$

(A4)

substitute (A1) in (A4)

$$\begin{aligned} L&= P_{3}\lambda _{2}\bigg [C\theta +\pi \theta \bigg (c_{1}(P_{3}-P_{2})+\frac{c_{2}(P^{2}_{3}-P^{2}_{2})}{2}\bigg )+ c_{2}\pi P_{3}\bigg ] \\&= P_{3}M \end{aligned}$$

since $M>0$ then $P_{3}M>0$ hence

$$\begin{aligned} L>0 \end{aligned}$$

Next suppose $P_{1}\le P_{2}\le P_{3}\le 1$, $\lambda _{2} \le \alpha$, $P^{2}_{2}\ge P^{3}_{3}$, $\theta <1$, $\beta <1$ and

$$\begin{aligned} A&\ge \pi \bigg (\frac{\alpha }{\beta }\left( \frac{c_{1}}{\beta }+\frac{c_{2}}{2}P^{2}_{3}\right) +\frac{c_{2}a\rho }{2}P_{2} P^{2}_{1}\bigg ) \end{aligned}$$

(A5)

$$\begin{aligned} F&= \pi \Bigg [c_{1}\bigg [\frac{(\rho -\lambda )}{2}P^{2}_{1}+\frac{a \rho -\lambda }{2}(P_{2}-P_{1})^{2}+(\rho -\lambda )P_{1}(P_{2}-P_{1})\nonumber \\&\quad +\frac{\alpha }{\beta }\bigg (1-\frac{1}{\beta }\bigg )+\alpha P_{2}\bigg (1-\frac{1}{\beta }\bigg )+P_{3}(\alpha -\lambda _{2})(P_{3}-P_{2})\bigg ]+ c_{2}\bigg [\frac{(\rho -\lambda )}{3}P^{3}_{1} \nonumber \\&\quad +\frac{a \rho -\lambda }{6}(2P^{3}_{2}-3P_{1}P^{2}_{2}+P^{3}_{1})+\frac{(\rho -\lambda )}{2}P_{1}(P^{2}_{2}-P^{2}_{1}) - \frac{\alpha }{2\beta }(P^{2}_{3}-P^{2}_{2}) \nonumber \\&\quad + \frac{\alpha }{2}P_{3}\left( P^{2}_{3}-P^{2}_{2}\right) -\lambda _{2}P_{3}\bigg (\frac{P^{2}_{3}-P^{2}_{2}}{2}-\frac{2}{\theta ^{2}}+\frac{1}{2\theta }P_{3}\bigg )\bigg ]\Bigg ]+A \nonumber \\ F&= \pi \Bigg [c_{1}\bigg [\frac{(\rho -\lambda )}{2}P^{2}_{1}+\frac{a \rho -\lambda }{2}(P_{2}-P_{1})^{2}+(\rho -\lambda )P_{1}(P_{2}-P_{1})\nonumber \\&\quad +\alpha \bigg (P_{2}+\frac{1}{\beta }\bigg )\bigg (1-\frac{1}{\beta }\bigg )+P_{3}(\alpha -\lambda _{2})(P_{3}-P_{2})\bigg ] \nonumber \\&\quad + c_{2}\bigg [\frac{(\rho -\lambda )}{3}P^{3}_{1}+\frac{a \rho -\lambda }{6}(2P^{3}_{2}-3P_{1}P^{2}_{2}+P^{3}_{1}) \nonumber \\&\quad +\frac{(\rho -\lambda )}{2}P_{1}\bigg (P^{2}_{2}-P^{2}_{1}\bigg ) + \frac{\alpha }{2}\bigg (P_{3}-\frac{1}{\beta }\bigg )(P^{2}_{3}-P^{2}_{2}) \nonumber \\&\quad + \frac{2\alpha }{\theta ^{2}}P_{3}-\frac{\lambda _{2}}{2}P_{3}\bigg (P^{2}_{3}-P^{2}_{2}+\frac{1}{\theta }P_{3}\bigg )\bigg ]\Bigg ]+A \end{aligned}$$

(A6)

The Binomial Expansion of $(P_{2}-P_{1})^{3}$ is

$$\begin{aligned} (P_{2}-P_{1})^{3} = P^{3}_{2}-3P^{2}_{2}P_{1}+3P_{2}P^{2}_{1}-P^{3}_{1} \end{aligned}$$

thus

$$\begin{aligned} 2P^{3}_{2} - 3P^{2}_{2}P_{1} + P^{3}_{1} = (P_{2}-P_{1})^{3} + P^{3}_{2}+2P^{3}_{1} - 3P_{2}P^{2}_{1} \end{aligned}$$

(A7)

Substitute (A7) in (A6)

$$\begin{aligned} F&= \pi \Bigg [c_{1}\bigg [\frac{(\rho -\lambda )}{2}P^{2}_{1}+\frac{a \rho -\lambda }{2}(P_{2}-P_{1})^{2}+(\rho -\lambda )P_{1}(P_{2}-P_{1})\nonumber \\&\quad +\alpha \bigg (P_{2}+\frac{1}{\beta }\bigg )-\frac{\alpha }{\beta }\bigg (P_{2}+\frac{1}{\beta }\bigg )+P_{3}(\alpha -\lambda _{2})(P_{3}-P_{2})\bigg ] \nonumber \\&\quad + c_{2}\bigg [\frac{(\rho -\lambda )}{3}P^{3}_{1}+\frac{a \rho -\lambda }{6}\bigg ((P_{1}-P_{1})^{3}+P^{3}_{2}+2P^{3}_{1}\bigg )-\frac{(a\rho -\lambda )}{2}P_{2}P^{2}_{1} \nonumber \\&\quad +\frac{(\rho -\lambda )}{2}P_{1}(P^{2}_{2}-P^{2}_{1}) + \frac{\alpha }{2}P_{3}(P^{2}_{3}-P^{2}_{2})-\frac{\alpha }{2\beta }(P^{2}_{3}-P^{2}_{2}) \nonumber \\&\quad -\frac{\lambda _{2}}{2}P_{3}(P^{2}_{3}-P^{2}_{2})+ \frac{2\lambda _{2}}{\theta ^{2}}P_{3}-\frac{\lambda _{2}}{2\theta }P^{2}_{3}\bigg ]\Bigg ]+A \end{aligned}$$

(A8)

$$\begin{aligned} F&= A+\pi \Bigg [c_{1}\bigg [\frac{(\rho -\lambda )}{2}P^{2}_{1}+\frac{a \rho -\lambda }{2}(P_{2}-P_{1})^{2}+(\rho -\lambda )P_{1}(P_{2}-P_{1})\nonumber \\&\quad +\alpha \bigg (P_{2}+\frac{1}{\beta }\bigg )+P_{3}(\alpha -\lambda _{2})(P_{3}-P_{2})-\frac{\alpha }{\beta }(P_{2}+\frac{1}{\beta })\bigg ]+ c_{2}\bigg [\frac{(\rho -\lambda )}{3}P^{3}_{1} \nonumber \\&\quad +\frac{a \rho -\lambda }{6}\bigg ((P_{1}-P_{1})^{3}+P^{3}_{2}+2P^{3}_{1}\bigg )+\frac{\lambda }{2}P_{2}P^{2}_{1}+\frac{(\rho -\lambda )}{2}P_{1}\bigg (P^{2}_{2}-P^{2}_{1}\bigg ) \nonumber \\&\quad -\frac{a\rho }{2}P_{2}P^{2}_{1} + \frac{\alpha }{2}P_{3}\bigg (P^{2}_{3}-P^{2}_{2}\bigg )-\bigg (\frac{\alpha }{2\beta }+\frac{\lambda _{2}}{2}P_{3}\bigg )\bigg (P^{2}_{3}-P^{2}_{2}\bigg ) + \frac{\lambda _{2}}{\theta }\bigg (\frac{2}{\theta }-\frac{1}{2}P^{2}_{3}\bigg )\bigg ]\Bigg ] \nonumber \\&= A +\pi \Bigg [c_{1}\bigg [\frac{(\rho -\lambda )}{2}P^{2}_{1}+\frac{a \rho -\lambda }{2}(P_{2}-P_{1})^{2}+(\rho -\lambda )P_{1}(P_{2}-P_{1})\nonumber \\&\quad +\alpha \bigg (P_{2}+\frac{1}{\beta }\bigg )+P_{3}(\alpha -\lambda _{2})(P_{3}-P_{2})-\frac{\alpha }{\beta }\bigg (P_{2}+\frac{1}{\beta }\bigg )\bigg ]+ c_{2}\bigg [\frac{(\rho -\lambda )}{3}P^{3}_{1} \nonumber \\&\quad +\frac{a \rho -\lambda }{6}\bigg ((P_{1}-P_{1})^{3}+P^{3}_{2}+2P^{3}_{1}\bigg )+\frac{\lambda }{2}P_{2}P^{2}_{1} \nonumber \\&\quad +\frac{(\rho -\lambda )}{2}P_{1}\bigg (P^{2}_{2}-P^{2}_{1}\bigg )-\frac{a\rho }{2}P_{2}P^{2}_{1} \nonumber \\&\quad + \frac{\alpha }{2}P_{3}(P^{2}_{3}-P^{2}_{2})+P^{2}_{2}\bigg (\frac{\alpha }{2\beta }+\frac{\lambda _{2}}{2}P_{3}\bigg )-P^{2}_{3}\bigg (\frac{\alpha }{2\beta }+\frac{\lambda _{2}}{2}P_{3}\bigg ) + \frac{\lambda _{2}}{2\theta }\bigg (\frac{4}{\theta }-P^{2}_{3}\bigg )\bigg ]\Bigg ] \nonumber \\&= \pi \Bigg [c_{1}\bigg [\frac{(\rho -\lambda )}{2}P^{2}_{1}+\frac{a \rho -\lambda }{2}(P_{2}-P_{1})^{2}+(\rho -\lambda )P_{1}(P_{2}-P_{1})\nonumber \\&\quad +P_{3}(\alpha -\lambda _{2})(P_{3}-P_{2})+\frac{\alpha }{\beta }(1-P_{2})+\alpha P_{2}\bigg ]+ c_{2}\bigg [\frac{(\rho -\lambda )}{3}P^{3}_{1}\nonumber \\&\quad +\frac{a \rho -\lambda }{6}\bigg ((P_{1}-P_{1})^{3}+P^{3}_{2}+2P^{3}_{1}\bigg )+\frac{\lambda }{2}P_{2}P^{2}_{1} \nonumber \\&\quad +\frac{(\rho -\lambda )}{2}P_{1}(P^{2}_{2}-P^{2}_{1}) + \frac{\alpha }{2}P_{3}(P^{2}_{3}-P^{2}_{2}) + \frac{1}{2}\bigg (\frac{\alpha }{\beta }P^{2}_{2}-\lambda _{2}P^{3}_{3}\bigg ) \nonumber \\&\quad + \frac{\alpha }{2\beta }P_{3}P^{2}_{2} + \frac{\lambda _{2}}{2\theta }\bigg (\frac{4}{\theta }-P^{2}_{3}\bigg )\bigg ]\Bigg ]-\pi \left( \frac{\alpha }{\beta }\bigg (\frac{c_{1}}{\beta }+\frac{c_{2}}{2}P^{2}_{3}\bigg )+\frac{c_{2}a\rho }{2}P_{2}P^{2}_{1}\right) +A \end{aligned}$$

(A9)

substitute (A5) in (A9)

$$\begin{aligned} F&= \pi \Bigg [c_{1}\bigg [\frac{(\rho -\lambda )}{2}P^{2}_{1}+\frac{a \rho -\lambda }{2}(P_{2}-P_{1})^{2}+(\rho -\lambda )P_{1}(P_{2}-P_{1})\nonumber \\&\quad + P_{3}(\alpha -\lambda _{2})(P_{3}-P_{2})+\alpha \left( \frac{1}{\beta }(1-P_{2})+P_{2}\right) \bigg ]+ c_{2}\bigg [\frac{(\rho -\lambda )}{3}P^{3}_{1} \nonumber \\&\quad +\frac{a \rho -\lambda }{6}\bigg ((P_{1}-P_{1})^{3}+P^{3}_{2}+2P^{3}_{1}\bigg )+\frac{\lambda }{2}P_{2}P^{2}_{1}+\frac{(\rho -\lambda )}{2}P_{1}(P^{2}_{2}-P^{2}_{1}) \nonumber \\&\quad + \frac{\alpha }{2}P_{3}\left( P^{2}_{3}+P^{2}_{2}\bigg (\frac{1}{\beta }-1\bigg )\right) + \frac{1}{2}\bigg (\frac{\alpha }{\beta }P^{2}_{2}-\lambda _{2}P^{3}_{3}\bigg ) + \frac{\lambda _{2}}{2\theta }\bigg (\frac{4}{\theta }-P^{2}_{3}\bigg )\bigg ]\Bigg ] \end{aligned}$$

(A10)

since $P_{1}\le P_{2}\le P_{3}\le 1$, $\lambda _{2} \le \alpha$, $P^{2}_{2}\ge P^{3}_{3}$, $\theta <1$, $\beta <1$ then $F>0$ hence

$$\begin{aligned} M, L, F \in \Re ^{+} \end{aligned}$$

Appendix B: Proof of Lemma 4.1

The quadratic equation (22) has two different solutions namely $P^{*}_{(+)}$ and $P^{*}_{(-)}$ and presented below

$$\begin{aligned} P^{*}_{(+)}=\frac{1}{2M}\Bigg (L+\left( L^{2}+4MF\right) ^{\frac{1}{2}}\Bigg ), \end{aligned}$$

and

$$\begin{aligned} P^{*}_{(-)}=\frac{1}{2M}\Bigg (L-\left( L^{2}+4MF\right) ^{\frac{1}{2}}\Bigg ). \end{aligned}$$

From the hypothesis of Theorem 1,

$$\begin{aligned} \Bigg (L+\left( L^{2}+4MF\right) ^{\frac{1}{2}}\Bigg )\;\;\ge \;\;0, \end{aligned}$$

while

$$\begin{aligned} \Bigg (L-\left( L^{2}+4MF\right) ^{\frac{1}{2}}\Bigg )\;\;\le \;\;0, \end{aligned}$$

thus,

$$\begin{aligned} \frac{1}{2M}\Bigg (L-\left( L^{2}+4MF\right) ^{\frac{1}{2}}\Bigg )\;\;\le \;\;0 \end{aligned}$$

since the cycle length is always positive, the best cycle length that optimizes both the total variable cost and EPQ is

$$\begin{aligned} P^*=P^{*}_{(+)} \end{aligned}$$

hence

$$\begin{aligned} P^* = \frac{1}{2M}\Bigg (L+\left( L^{2}+4MF\right) ^{\frac{1}{2}}\Bigg ) \end{aligned}$$

$\square$

Appendix C: Proof of Lemma 4.2

Re-differentiating (21)

(C11)

Since $P>0$ and Theorem 1 shows that $L>0$ and $F>0$. Thus, $\frac{L}{P^{2}}>0$ and $\frac{2F}{P^{3}}>0$ then

$$\begin{aligned} \frac{d^{2}Z(P)}{\mathrm{d}P^{2}}>0, \end{aligned}$$

hence, the sufficient condition from the optimality of P is satisfied. $\square$