1 Introduction

Nonlinear evolution equations play an extremely important role as the object of study for many mathematical physicists in numerous fields, such as mathematics, plasma physics and fluid mechanics and so on [1,2,3]. In the general case, the nonlinear evolution equations are local, and in recent years many scholars have started to study nonlocal nonlinear equations in order to better model the type of interaction of the solutions. For example, nonlocal Fokas–Lenells equation [4], nonlocal Davey–Stewartson equation [5], nonlocal Gerdjikov–Ivanov equation [6], nonlocal Gross–Pitaevskii equation [7, 8]. In addition, the variable coefficient nonlocal equations have gradually started to be studied [9,10,11], which have more general solutions than the constant coefficient equations. There are also a number of methods for solving nonlocal equations, including Darboux transformation [12,13,14], inverse scattering method [15, 16], Hirota bilinear method [17, 18], etc.

Among the many nonlocal equations, the best known and most important is the nonlocal nonlinear Schrödinger (NNLS) equation [19],

$$\begin{aligned} i{u_t}(x,t) = {u_{xx}}(x,t) \pm 2u(x,t){u^*}( - x,t)u(x,t), \end{aligned}$$
(1.1)

where \(^*\) denotes complex conjugation and the nonlocal equation is presented by Ablowitz and Musslimani. After this, many scholars began to investigate the generalization of the NNLS equation. For example, general soliton solutions of the reverse-time NNLS equation were studied in literature [20] using the Darboux transformation; the reverse space-time NNLS equation was studied in literature [21] using the inverse scattering transform method. There are also studies of the solutions to the NNLS equation [22,23,24].

In this paper, based on some of Ablowitz’s points in [19], we deduce the variable coefficient nonlocal Newell–Whitehead equation

$$\begin{aligned} i{q_t}(x,t) + \delta (t){q^2}(x,t)q( - x, - t) + \frac{1}{2}\delta (t){q_{xx}}(x,t) + 2\delta (t)q(x,t) = 0, \end{aligned}$$
(1.2)

by a symmetry reduction. Further we construct the Darboux transformation of this equation as well as exact solutions [25,26,27]. Nonlocal symmetries and group invariant solutions of the coupled variable coefficient NW equation are studied in literature [28]. A review of the literature shows that the variable coefficient nonlocal NW equation has not been investigated.

The paper is structured as follows: in Sect. 2, the variable coefficient nonlocal NW equation is derived with the help of the Lax pair and a symmetry reduction. In Sect. 3, we describe the Darboux transformation method in detail and give the formula for the n-fold Darboux transformation. In Sect. 4, exact solutions of the nonlocal NW equation with variable coefficient is obtained using onefold Darboux transformation. Soliton solutions are given for special values of the coefficient function, such as kinked soliton solution, periodic soliton solution, etc. A short conclusion is given in Sect. 5.

2 Nonlocal NW Equation with Variable Coefficient

In this section, we will describe how to construct the nonlocal NW equation with variable coefficient. The Lax pair for Eq. (1.2) is shown below,

$$\begin{aligned} \begin{array}{l} {\phi _x} = U\phi ,\\ {\phi _t} = V\phi , \end{array} \end{aligned}$$
(2.1)

where \(\phi = {({\phi _1}(x,t),{\phi _2}(x,t))^T}\). The matrices U and V are dependent on the functions q(x, t), r(x, t) and the parameter \(\lambda \),

$$\begin{aligned} U = \left( {\begin{array}{*{20}{c}} { - i\lambda }&{}{q(x,t)}\\ {r(x,t)}&{}{i\lambda } \end{array}} \right) ,\,\,\,\,V = \left( {\begin{array}{*{20}{c}} A&{}B\\ C&{}{ - A} \end{array}} \right) , \end{aligned}$$
(2.2)

and A, B, C have the form of

$$\begin{aligned} \begin{array}{l} A = \delta (t)\left( { - i{\lambda ^2} - \dfrac{1}{2}iqr + i} \right) ,\\ B = \delta (t)\left( {\lambda q + \dfrac{1}{2}i{q_x}} \right) ,\\ C = \delta (t)\left( {\lambda r - \dfrac{1}{2}i{r_x}} \right) . \end{array} \end{aligned}$$
(2.3)

The compatibility condition \({U_t} - {V_x} + \left[ {U,V} \right] = 0\) gives us the following system

$$\begin{aligned} \begin{array}{l} {q_t}(x,t) = i\delta (t)\left( { - q{{(x,t)}^2}r(x,t) + \dfrac{1}{2}{q_{xx}}(x,t) + 2q(x,t)} \right) ,\\ {r_t}(x,t) = i\delta (t)\left( {q(x,t)r{{(x,t)}^2} - \dfrac{1}{2}{r_{xx}}(x,t) - 2r(x,t)} \right) , \end{array} \end{aligned}$$
(2.4)

make a symmetry reduction

$$\begin{aligned} r(x,t) = - q( - x, - t). \end{aligned}$$
(2.5)

When \(a(t) = \frac{1}{2}\delta (t),b(t) = 2\delta (t),c(t) = - \delta (t)\) and \(u = q = - {r^*}\), and \({r^*}\) denotes the complex conjugate, the coupled variable coefficient NW equation (2.4) can be reduced to the following form of the variable coefficient NW equation

$$\begin{aligned} i{u_t} = a(t){u_{xx}} + b(t)u - c(t){u^3}. \end{aligned}$$

Under the action of (2.5), we can rewrite (2.4) in the following form

$$\begin{aligned} \begin{array}{l} {q_t}(x,t) = i\delta (t)\left( {q{{(x,t)}^2}q( - x, - t) + \dfrac{1}{2}{q_{xx}}(x,t) + 2q(x,t)} \right) ,\\ {q_t}(x,t) = i\delta ( - t)\left( {q{{(x,t)}^2}q( - x, - t) + \dfrac{1}{2}{q_{xx}}(x,t) + 2q(x,t)} \right) . \end{array} \end{aligned}$$
(2.6)

It is easy to observe that if the two equations in (2.6) are to be equal, it must be satisfied that \(\delta (t)\) is an even function, i.e.

$$\begin{aligned} \delta (t) = \delta ( - t). \end{aligned}$$
(2.7)

Then, the integrable variable coefficient nonlocal NW Eq. (1.2) can be obtained from the system (2.6).

3 Darboux Transformation

The Darboux transformation is a very essential method for solving the exact solutions of integrable nonlinear equations [29, 30], not only for local equations but also for nonlocal equations. A detailed description of how to build the Darboux transformation of Eq. (1.2) is given in this section.

First of all, we choose the gauge transformation

$$\begin{aligned} {\phi ^{[1]}} = {T^{[1]}}\phi , \end{aligned}$$
(3.1)

then Eq. (2.1) can be transformed into the following form

$$\begin{aligned} \begin{array}{l} \phi _x^{[1]} = {U^{[1]}}{\phi ^{[1]}},\\ \phi _t^{[1]} = {V^{[1]}}{\phi ^{[1]}}, \end{array} \end{aligned}$$
(3.2)

where

$$\begin{aligned} \begin{array}{l} {U^{[1]}} = (T_x^{[1]} + {T^{[1]}}U){({T^{[1]}})^{ - 1}},\\ {V^{[1]}} = (T_x^{[1]} + {T^{[1]}}V){({T^{[1]}})^{ - 1}}. \end{array} \end{aligned}$$
(3.3)

Next, it is essential to find the matrix \({T^{[1]}}\) such that matrices \({U^{[1]}},{V^{[1]}}\) and U, V have the same forms. At the same time, the old potentials q, r in U and V are mapped to the new potentials \({q^{[1]}},{r^{[1]}}\) in \({U^{[1]}}\) and \({V^{[1]}}\).

Suppose

$$\begin{aligned} {T^{[1]}} = \left( {\begin{array}{*{20}{c}} {\lambda + {b_{11}}}&{}{{b_{12}}}\\ {{b_{21}}}&{}{\lambda + {b_{22}}} \end{array}} \right) , \end{aligned}$$
(3.4)

where \({b_{ij}},(i,j = 1,2)\) are functions on x and t.

Substituting Eq. (3.4) into Eq. (3.3) and combining the \(\lambda \) coefficients of the same power, we can obtain the relationship between the new potentials and the old potentials,

$$\begin{aligned} \begin{array}{l} {q^{[1]}}(x,t) = 2i{b_{12}}(x,t) + q(x,t),\\ {r^{[1]}}(x,t) = - 2i{b_{21}}(x,t) + r(x,t). \end{array} \end{aligned}$$
(3.5)

According to the symmetry reduction Eq. (2.5), one can obtain

$$\begin{aligned} {b_{21}}(x,t) = {b_{12}}( - x, - t). \end{aligned}$$
(3.6)

Now, we assume that \(f({\lambda _j}) = {\left( {{f_1}({\lambda _j}),{f_2}({\lambda _j})} \right) ^T},g({\lambda _j}) = {\left( {{g_1}({\lambda _j}),{g_2}({\lambda _j})} \right) ^T}\) are the two basic solutions of (2.1), and combining this with the gauge transformation (3.1), the constants \({\gamma _j},(j = 1,2)\) exist satisfying

$$\begin{aligned} {\lambda _j} + {b_{11}}(x,t) + {\alpha _j}{b_{12}}(x,t) = 0,\,\,\,\,\,{\alpha _j}({\lambda _j} + {b_{22}}(x,t)) + {b_{21}}(x,t) = 0, \end{aligned}$$
(3.7)

with

$$\begin{aligned} {\alpha _j} = \frac{{{g_2}({\lambda _j}){\gamma _j} + {f_2}({\lambda _j})}}{{{g_1}({\lambda _j}){\gamma _j} + {f_1}({\lambda _j})}},\,\,(j = 1,2). \end{aligned}$$
(3.8)

The coefficient determinant of (3.7) is made nonzero by choosing the appropriate \({\lambda _j},{\gamma _j}(j = 1,2)\). Thus, it is known that \({b_{ij}},(i,j = 1,2)\) are uniquely determined with (3.7). By calculation, Eq. (3.4) can be rewritten as

$$\begin{aligned} {T^{[1]}} = \left( {\begin{array}{*{20}{c}} {\lambda - \dfrac{{{\alpha _1}{\lambda _2} - {\lambda _1}{\alpha _2}}}{{{\alpha _1} - {\alpha _2}}}}&{}{\dfrac{{{\lambda _2} - {\lambda _1}}}{{{\alpha _1} - {\alpha _2}}}}\\ {\dfrac{{{\alpha _1}{\alpha _2}({\lambda _1} - {\lambda _2})}}{{{\alpha _1} - {\alpha _2}}}}&{}{\lambda - \dfrac{{{\alpha _1}{\lambda _1} - {\alpha _2}{\lambda _2}}}{{{\alpha _1} - {\alpha _2}}}} \end{array}} \right) . \end{aligned}$$
(3.9)

The calculation from Eqs. (2.1) and (3.8) shows that \({\alpha _j},(j = 1,2)\) satisfies the following form

$$\begin{aligned} \begin{array}{l} {\alpha _{jx}} = - \alpha _j^2q + 2i{\lambda _j}{\alpha _j} + r,\\ {\alpha _{jt}} = \dfrac{1}{2}\delta (t)\left( { - i{q_x} - 2{\lambda _j}q} \right) \alpha _j^2 + \dfrac{1}{2}\delta (t)\left( {2iqr + 4i\lambda _j^2 - 4i} \right) {\alpha _j} + \dfrac{1}{2}\delta (t)\left( {2{\lambda _j}r - i{r_x}} \right) . \end{array}\nonumber \\ \end{aligned}$$
(3.10)

Next we will show that the \({V^{[1]}}\) to be determined in Eq. (3.2) has the same form as V. Assuming \({T^{ - 1}} = {(\det T)^{ - 1}}{T^*}\), and

$$\begin{aligned} ({T_x} + \mathrm{TV}){T^*} = \left( {\begin{array}{*{20}{c}} {{f_{11}}(\lambda )}&{}{{f_{12}}(\lambda )}\\ {{f_{21}}(\lambda )}&{}{{f_{22}}(\lambda )} \end{array}} \right) , \end{aligned}$$
(3.11)

we can obtain \({f_{ij}}(i,j = 1,2)\) as cubic or quartic polynomial with respect to \(\lambda \). Based on Eq. (3.10), we obtained above it is easy to prove that \({\lambda _j}(j = 1,2)\) are the roots of \({f_{ij}}(i,j = 1,2)\). So (3.11) can be rewritten as

$$\begin{aligned} \left( {{T_x} + \mathrm{TV}} \right) {T^*} = (\det T)P(\lambda ), \end{aligned}$$
(3.12)

where \(P(\lambda )\) has the following form,

$$\begin{aligned} P(\lambda ) = \left( {\begin{array}{*{20}{c}} {{\lambda ^2}P_{11}^2 + \lambda P_{11}^1 + P_{11}^0}&{}{\lambda P_{12}^1 + P_{12}^0}\\ {\lambda P_{21}^1 + P_{21}^0}&{}{{\lambda ^2}P_{22}^2 + \lambda P_{22}^1 + P_{22}^0} \end{array}} \right) , \end{aligned}$$
(3.13)

with \(P_{ij}^k(i,j = 1,2,k = 0,1,2)\) not being the functions on \(\lambda \). Therefore, Eq. (3.12) is also equivalent to

$$\begin{aligned} {T_x} + \mathrm{TV} = P(\lambda )T. \end{aligned}$$
(3.14)

Through combining the coefficients of the same order \(\lambda \) in Eq. (3.14) and making them equal to zero, we can obtain the following system,

$$\begin{aligned} \begin{array}{l} {\lambda ^3}:\,\,\,\, - i\delta (t) - P_{11}^2 = 0,\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,i\delta (t) - P_{22}^2 = 0,\\ {\lambda ^2}:\,\,\,\, - i\delta (t){b_{11}} - {b_{11}}P_{11}^2 - P_{11}^1 = 0,\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,i\delta (t){b_{22}} - {b_{22}}P_{22}^2 - P_{22}^1 = 0,\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,i\delta (t){b_{12}} + \delta (t)q - {b_{12}}P_{11}^2 - P_{12}^1 = 0,\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\, - i\delta (t){b_{21}} + \delta (t)r - {b_{21}}P_{11}^2 - P_{21}^1 = 0,\\ {\lambda ^1}:\,\,\,\,\,\delta (t)\left( { - \dfrac{1}{2}iqr + i} \right) + \delta (t)r{b_{12}} - {b_{11}}P_{11}^1 - {b_{21}}P_{12}^1 - P_{11}^0 = 0,\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\delta (t)\left( {\dfrac{1}{2}iqr - i} \right) + \delta (t)q{b_{21}} - {b_{12}}P_{21}^1 - {b_{22}}P_{22}^1 - P_{22}^0 = 0,\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\delta (t)q{b_{11}} + \dfrac{1}{2}i\delta (t){q_x} - {b_{12}}P_{11}^1 - {b_{22}}P_{12}^1 - P_{12}^0 = 0,\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\delta (t)r{b_{22}} - \dfrac{1}{2}i\delta (t){r_x} - {b_{12}}P_{21}^1 - {b_{22}}P_{22}^1 - P_{22}^0 = 0,\\ {\lambda ^0}:\,\,\,\,\dfrac{{\partial {b_{11}}(x,t)}}{{\partial x}} + \delta (t){b_{11}}\left( { - \dfrac{1}{2}iqr + i} \right) - \dfrac{1}{2}i\delta (t){r_x}{b_{12}} - {b_{11}}P_{11}^0 - {b_{21}}P_{12}^0 = 0,\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{{\partial {b_{21}}(x,t)}}{{\partial x}} + \delta (t){b_{21}}\left( { - \dfrac{1}{2}iqr + i} \right) - \dfrac{1}{2}i\delta (t){r_x}{b_{22}} - {b_{11}}P_{21}^0 - {b_{21}}P_{22}^0 = 0,\\ \,\,\,\,\,\,\,\,\,\,\,\,\dfrac{{\partial {b_{12}}(x,t)}}{{\partial x}} + \delta (t){b_{12}}\left( {\dfrac{1}{2}iqr - i} \right) + \dfrac{1}{2}i\delta (t){q_x}{b_{11}} - {b_{12}}P_{11}^0 - {b_{22}}P_{12}^0 = 0,\\ \,\,\,\,\,\,\,\,\,\,\,\,\dfrac{{\partial {b_{22}}(x,t)}}{{\partial x}} + \delta (t){b_{22}}\left( {\dfrac{1}{2}iqr - i} \right) + \dfrac{1}{2}i\delta (t){q_x}{b_{21}} - {b_{12}}P_{21}^0 - {b_{22}}P_{22}^0 = 0, \end{array} \end{aligned}$$
(3.15)

solving (3.15) for this system of overdetermined equations, we get

$$\begin{aligned} \begin{array}{l} P_{11}^2 = - i\delta (t),\,\,P_{22}^2 = i\delta (t),\,\,P_{11}^1 = P_{22}^1 = 0,\\ P_{12}^1 = 2i\delta (t){b_{12}} + \delta (t)q = \delta (t){q^{[1]}},\\ P_{21}^1 = - 2i\delta (t){b_{21}} + \delta (t)r = \delta (t){r^{[1]}},\\ P_{11}^0 = - \dfrac{1}{2}i\delta (t)qr + i\delta (t) + \delta (t)r{b_{12}} - 2i\delta (t){b_{12}}{b_{21}} - \delta (t)q{b_{21}}\\ \,\,\,\,\,\,\,\,\,\, = - \dfrac{1}{2}i\delta (t){q^{[1]}}{r^{[1]}} + i\delta (t),\\ P_{22}^0 = \dfrac{1}{2}i\delta (t)qr - i\delta (t) - \delta (t)r{b_{12}} + 2i\delta (t){b_{12}}{b_{21}} + \delta (t)q{b_{21}}\\ \,\,\,\,\,\,\,\,\,\, = \dfrac{1}{2}i\delta (t){q^{[1]}}{r^{[1]}} - i\delta (t),\\ P_{12}^0 = \delta (t)q{b_{11}} + \dfrac{1}{2}i\delta (t){q_x} - 2i\delta (t){b_{12}}{b_{22}} - \delta (t)q{b_{22}}\\ \,\,\,\,\,\,\,\,\,\, = \dfrac{1}{2}i\delta (t)q_x^{[1]},\\ P_{21}^0 = \delta (t)r{b_{22}} - \dfrac{1}{2}i\delta (t){r_x} + 2i\delta (t){b_{21}}{b_{11}} - \delta (t)r{b_{11}}\\ \,\,\,\,\,\,\,\,\,\, = - \dfrac{1}{2}i\delta (t)r_x^{[1]}. \end{array} \end{aligned}$$
(3.16)

Based on the above facts, we can get the following the proposition.

Proposition 1

The matrix \({V^{[1]}}\) determined by Eq. (3.2) has the form as V. Namely,

$$\begin{aligned} {V^{[1]}} = \left( {\begin{array}{*{20}{c}} {\delta (t)\left( { - i{\lambda ^2} - \dfrac{1}{2}i{q^{[1]}}{r^{[1]}} + i} \right) }&{}{\delta (t)\left( {\lambda {q^{[1]}} + \dfrac{1}{2}iq_x^{[1]}} \right) }\\ {\delta (t)\left( {\lambda {r^{[1]}} - \dfrac{1}{2}ir_x^{[1]}} \right) }&{}{\delta (t)\left( {i{\lambda ^2} + \dfrac{1}{2}i{q^{[1]}}{r^{[1]}} - i} \right) } \end{array}} \right) , \end{aligned}$$
(3.17)

where the transformation relationships between q, r and \({q^{[1]}},{r^{[1]}}\) are given in Eqs. (3.5).

Similarly to the above proof, we can obtain that \({U^{[1]}}\) and U have the same form.

Proposition 2

The matrix \({U^{[1]}}\) determined by Eq. (3.2) has the form as U. Namely,

$$\begin{aligned} U = \left( {\begin{array}{*{20}{c}} { - i\lambda }&{}{{q^{[1]}}}\\ {{r^{[1]}}}&{}{i\lambda } \end{array}} \right) , \end{aligned}$$
(3.18)

where the transformation relationships between q, r and \({q^{[1]}},{r^{[1]}}\) are given in Eqs. (3.5).

Finally, we can derive the n-fold Darboux transformation of the nonlocal NW equation with variable coefficient.

$$\begin{aligned} {\phi ^{[n]}} = {T_n}(\lambda )\phi = {T^{[n]}}(\lambda ){T^{[n - 1]}} \cdots {T^{[k]}}(\lambda ) \cdots {T^{[1]}}(\lambda )\phi , \end{aligned}$$
(3.19)

where

$$\begin{aligned} {T^{[k]}} = \left( {\begin{array}{*{20}{c}} {\lambda - \dfrac{{{\alpha _{2k - 1}}{\lambda _{2k}} - {\lambda _{2k - 1}}{\alpha _{2k}}}}{{{\alpha _{2k - 1}} - {\alpha _{2k}}}}}&{}{\dfrac{{{\lambda _{2k}} - {\lambda _{2k - 1}}}}{{{\alpha _{2k - 1}} - {\alpha _{2k}}}}}\\ {\dfrac{{{\alpha _{2k - 1}}{\alpha _{2k}}\left( {{\lambda _{2k - 1}} - {\lambda _{2k}}} \right) }}{{{\alpha _{2k - 1}} - {\alpha _{2k}}}}}&{}{\lambda - \dfrac{{{\alpha _{2k - 1}}{\lambda _{2k - 1}} - {\alpha _{2k}}{\lambda _{2k}}}}{{{\alpha _{2k - 1}} - {\alpha _{2k}}}}} \end{array}} \right) , \end{aligned}$$
(3.20)

and

$$\begin{aligned} \begin{array}{l} {\alpha _j} = \dfrac{{g_2^{[k - 1]}({\lambda _j}){\gamma _j} + f_2^{[k - 1]}({\lambda _j})}}{{g_1^{[k - 1]}({\lambda _j}){\gamma _j} + f_1^{[k - 1]}({\lambda _j})}}\,\,\,\left( {j = 2k - 1,k = 1,2, \cdots ,n} \right) ,\\ {f^{[k]}}(\lambda ) = {\left( {f_1^{[k]}(\lambda ),f_2^{[k]}(\lambda )} \right) ^T} = {T^{[k]}}(\lambda ){f^{[k - 1]}}({\lambda _1},{\lambda _2}, \cdots {\lambda _{2k}}),\\ {g^{[k]}}(\lambda ) = {\left( {g_1^{[k]}(\lambda ),g_2^{[k]}(\lambda )} \right) ^T} = {T^{[k]}}(\lambda ){g^{[k - 1]}}({\lambda _1},{\lambda _2}, \cdots {\lambda _{2k}}), \end{array} \end{aligned}$$
(3.21)

and subject to the following constraint,

$$\begin{aligned} b_{21}^{[k]}(x,t) = b_{12}^{[k]}( - x, - t), \end{aligned}$$
(3.22)

so that we obtain the following conclusion

$$\begin{aligned} {q^{[n]}}(x,t) = 2i\sum \limits _{k = 1}^n {b_{12}^{[k]}(x,t) + q(x,t).} \end{aligned}$$
(3.23)

Unlike the local variable coefficient NW equation, the Darboux transformation of the variable coefficient nonlocal NW equation has a constraint of (3.22).

4 Onefold Darboux Transformation

In this section, we will use the Darboux transformation to give the exact solutions of Eq. (1.2). As a special example, we choose the seed solutions \(q = r = 0\) of Eq. (1.2), then Lax pair satisfies the following equations,

$$\begin{aligned} \begin{array}{l} {\phi _{1x}} = - i\lambda {\phi _1},\\ {\phi _{2x}} = i\lambda {\phi _2},\\ {\phi _{1t}} = - i\delta (t)\left( {{\lambda ^2} - 1} \right) {\phi _1},\\ {\phi _{2t}} = i\delta (t)\left( {{\lambda ^2} - 1} \right) {\phi _2}, \end{array} \end{aligned}$$
(4.1)

solving the above system (4.1), we can obtain

$$\begin{aligned} \begin{array}{l} f\left( {x,t;\lambda } \right) = {\left( {{e^{ - i\left( {{\lambda ^2}\int {\delta (t)\mathrm{d}t + \lambda x - \int {\delta (t)\mathrm{d}t} } } \right) }},0} \right) ^T},\\ g\left( {x,t;\lambda } \right) = {\left( {0,{e^{i\left( {{\lambda ^2}\int {\delta (t)\mathrm{d}t + \lambda x - \int {\delta (t)\mathrm{d}t} } } \right) }}} \right) ^T}. \end{array} \end{aligned}$$
(4.2)

According to (3.8) and (4.2), it is possible to obtain

$$\begin{aligned} {\alpha _j} = {\gamma _j}{e^{2i\left( {\lambda _j^2\int {\delta (t)\mathrm{d}t} + {\lambda _j}x - \int {\delta (t)\mathrm{d}t} } \right) }},\,\,\,(j = 1,2), \end{aligned}$$
(4.3)

and

$$\begin{aligned} \begin{array}{l} {b_{12}}(x,t) = \dfrac{{{\lambda _1} - {\lambda _2}}}{{{\gamma _2}{e^{2i{a_2}}} - {\gamma _1}{e^{2i{a_1}}}}},\\ {b_{21}}(x,t) = - \dfrac{{{\gamma _1}{\gamma _2}({\lambda _1} - {\lambda _2}){e^{2i({a_1} + {a_2})}}}}{{{\gamma _2}{e^{2i{a_2}}} - {\gamma _1}{e^{2i{a_1}}}}}, \end{array} \end{aligned}$$
(4.4)

with

$$\begin{aligned} \begin{array}{l} {a_1} = \lambda _1^2\int {\delta (t)\mathrm{d}t + {\lambda _1}x - \int {\delta (t)\mathrm{d}t} } ,\\ {a_2} = \lambda _2^2\int {\delta (t)\mathrm{d}t + {\lambda _2}x - \int {\delta (t)\mathrm{d}t} } . \end{array} \end{aligned}$$

Under constraint condition \({b_{21}}(x,t) = {b_{12}}( - x, - t)\), we can get \({\gamma _j}(j = 1,2)\) needs to satisfy

$$\begin{aligned} \gamma _1^2 = 1,\,\,\gamma _2^2 = 1. \end{aligned}$$

So we can get the new solution in this case as

$$\begin{aligned} {q^{[1]}} = \dfrac{{2i({\lambda _1} - {\lambda _2})}}{{{\gamma _2}{e^{2i{a_2}}} - {\gamma _1}{e^{2i{a_1}}}}}, \end{aligned}$$
(4.5)

where \({a_1} = \lambda _1^2\int {\delta (t)\mathrm{d}t + {\lambda _1}x - \int {\delta (t)\mathrm{d}t} } ,{a_2} = \lambda _2^2\int {\delta (t)\mathrm{d}t + {\lambda _2}x - \int {\delta (t)\mathrm{d}t} } \).

Next, we assign different values to \(\delta (t)\) in order to better analyse the variable coefficient nonlocal NW equation.

Case 1: When \(\delta (t) = 1\), then we get

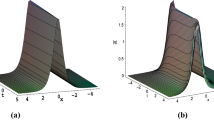
$$\begin{aligned} {q^{[1]}} = \dfrac{{2i({\lambda _1} - {\lambda _2})}}{{{\gamma _2}{e^{2i\left( {\lambda _2^2t + {\lambda _2}x - t} \right) }} - {\gamma _1}{e^{2i\left( {\lambda _1^2t + {\lambda _1}x - t} \right) }}}}. \end{aligned}$$
(4.6)

At this point, solution (4.6) is the solution to the nonlocal NW equation with constant coefficients.

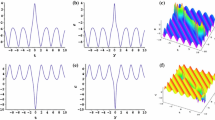
Case 2: When \(\delta (t) = \cos (t)\), then we get

$$\begin{aligned} {q^{[1]}} = \dfrac{{2i\left( {{\lambda _1} - {\lambda _2}} \right) }}{{{\gamma _2}{e^{2i{a_2}}} + {\gamma _1}{e^{2i{a_1}}}}}, \end{aligned}$$
(4.7)

where \({a_1} = \lambda _1^2\sin (t) + {\lambda _1}x - \sin (t),{a_2} = \lambda _2^2\sin (t) + {\lambda _2}x - \sin (t)\). At this point, solution (4.7) is the solution to the variable coefficient nonlocal NW equation when \(\delta (t) = \cos (t)\). Then, in order to see the structure of the solution more intuitively, we show the 3D plots of solution (4.6) and solution (4.7) for different parameters in Figs. 1, 2, and 3.

Fig. 1
figure 1

kink soliton solution of the variable coefficient nonlocal NW equation with the parameters \({\lambda _1} = 0.99,{\lambda _2} = 2.28i,{\gamma _1} = - 1,{\gamma _2} = 1\). a \(\delta (t) = 1\). b \(\delta (t) = \cos (t)\)

Full size image
Fig. 2
figure 2

Interaction solution of the variable coefficient nonlocal NW equation with the parameters \({\lambda _1} = 0.1,{\lambda _2} = 0.9+0.34i,{\gamma _1} = - 1,{\gamma _2} = -1\). a \(\delta (t) = 1\). b \(\delta (t) = \cos (t)\)

Full size image
Fig. 3
figure 3

Interaction solution of the variable coefficient nonlocal NW equation with the parameters \({\lambda _1} = 1.1 + 0.1i,{\lambda _2} = 1.9,{\gamma _1} = - 1,{\gamma _2} = 1\). a \(\delta (t) = 1\). b \(\delta (t) = \cos (t)\)

Full size image

It is worth noting that the choice of \(\delta (t)\) is not unique, as long as the condition for even function is met, for example, \(\delta (t) = {t^2},\delta (t) = \cosh (t)\), etc. When we choose different types of functions, we can obtain different types of interaction solutions. So based on the above results, it is clear that more exact solutions can be constructed for the nonlocal NW equation with variable coefficient.

5 Conclusions

In this article, we derive the variable coefficient nonlocal NW equation using symmetry reduction and Lax pair and study the nonlocal NW equation with variable coefficient for the first time. On this basis, the Darboux transformation method for the nonlocal NW equation with variable coefficient is described in detail and an n-fold Darboux transformation formula is given. Exact solution of the nonlocal NW equation with variable coefficient are obtained by means of onefold Darboux transformation. Soliton solutions are given for special values of the coefficient function, including kink soliton solution, periodic soliton solution, etc. Finally, images are used to show the structural features of the solutions visually.