Monochromatic Vertex-Disconnection Colorings of Graphs

Abstract

Let G be a vertex-colored connected graph. A subset U of the vertex set of G is called monochromatic, if all vertices of U are assigned the same color. The vertex-colored graph G is called monochromatic vertex-disconnected if for any two distinct vertices x and y, there is a monochromatic vertex-subset S of G such that x and y belong to different components of $G-S$ if x and y are nonadjacent, and if x and y are adjacent, then x or y has the same color as S and x and y belong to distinct components of $(G-xy)-S$. The monochromatic vertex-disconnection number of a connected graph G, denoted by $\mathrm{mvd}(G)$, is defined as the maximum number of colors that are allowed to make G monochromatic vertex-disconnected. The concept is inspired by the concepts of rainbow vertex-disconnection number $\mathrm{rvd}(G)$ and monochromatic disconnection number $\mathrm{md}(G)$. In this paper, we present some sufficient conditions for a connected graph G to have $\mathrm{mvd}(G)=1$ and show that almost all graphs have monochromatic vertex-disconnection number 1. Moreover, we present Nordhaus–Gaddum-type results for the new parameter $\mathrm{mvd}(G)$. At last, we investigate the monochromatic vertex-disconnection numbers for four graph products.

1 Introduction

Let G be a finite and undirected graph with vertex set V(G) and edge set E(G). We use m(G) and n(G) to denote the number of vertices and the number of edges of G, respectively, or simply m and n if there is no confusion. For a positive integer k, let [k] denote the set $\{1,2,\cdots , k\}$ of positive integers. For a vertex v of G, we use $d_G(v)$ to denote the degree of v. We use $C_n$ to denote a cycle of length n. If $n=2k+1$, then we call $C_n$ an odd cycle; otherwise, we call $C_n$ an even cycle. Let $P_t$ denote a path with t vertices. If $P_t$ is an $\{x,y\}$-path, we call x and y the end vertices of $P_t$. For undefined notation and terminology, we refer to the book [1].

An edge-coloring of G is a mapping f: $E(G)\rightarrow [k]$, where [k] denotes the set of colors. For $u,v\in V(G)$, a $\{u,v\}$-edge-cut is defined as an edge subset S of G such that u and v are contained in different components of $G-S$, and we say that S separates u and v. Moreover, if every edge of S is assigned with a distinct color, then S is called a $\{u,v\}$-rainbow-cut. An edge-coloring of G is called a rainbow disconnection coloring, if for any two vertices, there is a rainbow-cut separating them. The rainbow disconnection number of a connected graph G, denoted by rd(G), is defined as the minimum number of colors that are needed in a rainbow disconnection coloring of G, which was introduced by Chartrand et al. in [7]. For more relevant results, readers can be referred to [3,4,5,6, 10].

A vertex-coloring of G is a mapping $f'$: $V(G)\rightarrow [k']$, where $[k']$ denotes the set of colors. For $x,y\in V(G)$, an $\{x,y\}$-vertex-cut is defined as a vertex subset $S'$ of G such that x and y belong to different components of $G-S'$ if x and y are nonadjacent, and if x and y are adjacent, then x and y belong to distinct components of $(G-xy)-S'$. In this case, we also say that $S'$ separates x and y. Moreover, if all vertices of $S'$ are assigned with different colors when x and y are nonadjacent, and all vertices of $S'\cup \{x\}$ or $S'\cup \{y\}$ are assigned with different colors when x and y are adjacent, then $S'$ is called an $\{x,y\}$-rainbow vertex-cut. A vertex-coloring of G is called a rainbow vertex-disconnection coloring, if for any two vertices, there is a rainbow vertex-cut separating them. The rainbow vertex-disconnection number of a connected graph G, denoted by rvd(G), is defined as the minimum number of colors are needed in a rainbow vertex-disconnection coloring of G, which was introduced by Bai et al. in [2]. Readers can be referred to [8, 14] for more relevant results.

Contrary to the concepts of rainbow disconnection coloring and rainbow vertex-disconnection coloring, monochromatic versions of these concepts can be naturally introduced. Li et al. in [11] firstly introduced and studied the monochromatic disconnection colorings. Consider an edge-coloring of G and $x,y\in V(G)$. An $\{x,y\}$-edge-cut $S'$ is called a monochromatic-cut if all edges of $S'$ are assigned the same color. An edge-coloring of G is called a monochromatic disconnection coloring if for any two vertices of V(G), there is a monochromatic-cut separating them. The monochromatic disconnection number of a connected graph G, denoted by md(G), is defined as the maximum number of colors that are allowed in a monochromatic disconnection coloring of G. More results for the monochromatic disconnection number of graphs, we refer to [12, 13]. Inspired by rainbow vertex-disconnection coloring and monochromatic disconnection coloring, now we introduce a new definition, the monochromatic vertex-disconnection coloring (MVD-coloring for short). Consider a vertex-coloring f of G, and $u,v\in V(G)$. A $\{u,v\}$-vertex-cut S is called a monochromatic vertex-cut if all vertices of S are assigned with the same color if u and v are nonadjacent, and if u and v are adjacent, then all vertices of $S\cup \{u\}$ or $S\cup \{v\}$ are assigned with the same color. An MVD-coloring of G is a vertex-coloring such that any two vertices have a monochromatic vertex-cut. The monochromatic vertex-disconnection number (MVD-number, for short) of a connected graph G, denoted by mvd(G), is defined as the maximum number of colors that are allowed for an MVD-coloring of G. An MVD-coloring f is called an extremal MVD-coloring if it uses mvd(G) colors.

The MVD-number (MVD-coloring) is not only a natural combinatorial parameter, but can also be applied in logistics transportation, computer network and many other fields. For example, in the process of logistics transportation, we often need to intercept illegal goods, such as smuggled drugs and explosives. We intercept the goods on some road it may pass through. In order to save the output of manpower, we need to use the application model of MVD coloring.

Consider cities as vertices, and if there is a transport road between two cities, we assign an edge between the two vertices. The resulting graph is denoted by G. Besides, each city has a marking instrument and a scanning instrument that receives a fixed frequency. Therefore, each vertex is assigned a color according to the frequency that received by the corresponding city. Suppose that the illegal goods are transported from city x to city y. Because the illegal goods will be marked by the marking instrument when passing through city x, if x and y are not adjacent, then we can get feedback through the scanning instrument of each city on the vertex-cut between x and y, and so they need the same frequency, that is, the corresponding vertices are assigned the same color. Then police can obtain the transportation route of illegal goods, and immediately assign policemen to intercept illegal goods; if x and y are adjacent, we also need to consider the feedback of the scanning instrument in y, that is, the fixed frequency of the scanning machine in y must be the same as that on the $\{x,y\}$-vertex-cut of $G-xy$. Furthermore, if the fixed frequency of the scanning instrument of city x can also feedback whether the illegal goods are transported directly on the road xy, then this situation corresponds to a monochromatic vertex-cut of x and y in the graph G. If the interception is unsuccessful, then continue the next interception. Therefore, a monochromatic vertex-cut is required between any two vertices. In order to improve the accuracy, we require that the more types of scanning machines, the better, that is, the more frequencies, the better, but the premise is to ensure that there is a monochromatic vertex-cut between any two different cities. Therefore, in this problem, the maximum number of types of scanning machines that we need is the MVD-number of the corresponding graph G.

A block B of G is a maximal subgraph of G without a cut-vertex. If $B=e=uv$, then we call B trivial; otherwise, we call B nontrivial. Moreover, if $d_G(u)=1$, then u is called a pendent vertex, uv is called a pendent edge, of G. Let f be an MVD-coloring of G and U be a subset of V(G). Then, let f(U) and |f(U)| be the set and the number of colors used on U under f; especially, if v is a vertex of G, then f(v) is the color assigned on v. Furthermore, if H is a connected subgraph of G, then f(H) and |f(H)| are the set and the number of colors used on the set of vertex in H under f. Besides, we put the vertices with the same color together to form a vertex-subset and call it a color class. Obviously, f contains |f| color classes.

Let G be a graph without loops. For any edge $e=uv$ of G, if e has parallel edges, then we delete all its parallel edges but e and obtain an underlying graph $G'$ of G. Since a vertex-subset $V'$ of G is a vertex-cut of two vertices in V(G) if and only if $V'$ is a vertex-cut of the two corresponding vertices in $V(G')$, we have the following result.

Proposition 1.1

Let G be a graph without loops and $G'$ be an underlying graph of G. Then, $\mathrm{mvd}(G)=\mathrm{mvd}(G')$.

If G has several connected components, then the following result is clear.

Proposition 1.2

If G is a graph with t components $G_1, G_2,\cdots , G_t$, then $\mathrm{mvd}(G)=\sum \limits _{i=1}^{t}\mathrm{mvd}(G_i)$.

2 Some Basic Results

In this section, we first present some basic and useful results or tools.

Let G be a connected graph with at least two blocks. A vertex-coloring of G is an MVD-coloring if and only if it is an MVD-coloring restricted on each block of G. Then, we have the following theorem.

Theorem 2.1

If G has b blocks $B_1,B_2,\cdots ,B_b$, then $\mathrm{mvd}(G)=\sum \limits _{i=1}^{b}\mathrm{mvd}(B_i)-(b-1)$.

Proposition 2.1

If G is a cycle $C_n$, then $\mathrm{mvd}(G)=\lfloor \frac{n}{2}\rfloor$. Besides, if G is a unicyclic graph with cycle C, then $\mathrm{mvd}(G)=n-\lceil \frac{n(C)}{2}\rceil$.

Proof

If G is a unicyclic graph with cycle C, then every vertex of $V(G)\setminus V(C)$ is assigned a new distinct color under any extremal MVD-colorings. By Theorem 2.1, we only need to prove that $\mathrm{mvd}(G)=\lfloor \frac{n}{2}\rfloor$ if G is a cycle.

Let $G=C_n=v_1v_2\cdots v_{n-1}v_nv_1$ and $r=\lfloor \frac{n}{2}\rfloor$. For $i\in [r]$ and $j\in [n]$, if $j\equiv i$(mod r), we assign $v_j$ with color i. Then, this is obviously an MVD-coloring of G, and thus, $\mathrm{mvd}(G)\ge r$.

Next we show that $\mathrm{mvd}(C_n)\le r$. To the contrary, suppose $\mathrm{mvd}(C_n)>r$. Then, there is an MVD-coloring f such that $f(C_n)\ge r+1$. So there is a vertex $v_i$ of $V(C_n)$ such that $v_i$ is assigned the unique color. Since G is a cycle, there are two distinct vertices u and v adjacent to $v_i$. Then, there is no monochromatic vertex-cut separating u and v, a contradiction. $\square$

Proposition 2.2

If $G=K_{n_1,n_2}$ is a complete bipartite graph with $n_1,n_2\ge 2$, then $\mathrm{mvd}(G)=2$.

Proof

Suppose $V_1$ and $V_2$ are the bipartition of V(G). Consider a vertex-coloring f of G such that $f(V_1)=\{1\}$, $f(V_2)=\{2\}$. It is not hard to verify that f is an MVD-coloring of G, and so $\mathrm{mvd}(G)\ge 2$. For any two vertices u and v of $V_1$, $V_2$ is the minimal vertex-cut of them, and thus, all vertices of $V_2$ are assigned the same color. Similarly, all vertices of $V_1$ are assigned the same color. Thus, $\mathrm{mvd}(G)\le 2$. So, $\mathrm{mvd}(G)=2$. $\square$

Corollary 2.1

Suppose G is a graph obtained by adding an edge e on two nonadjacent vertices of a complete bipartite graph $K_{n_1,n_2}$ with $n_1,n_2\ge 2$. Then, $\mathrm{mvd}(G)=1$.

Proposition 2.3

Let H be a subgraph of G and f be an MVD-coloring of G. Then, f is an MVD-coloring of H.

Proof

Let $f'$ be a vertex-coloring by restricting f on H. For any two vertices x and y of V(H), if S is a monochromatic vertex-cut separating x and y in G under f, then $S\cap V(H)$ is a monochromatic vertex-cut separating x and y in H under $f'$; otherwise, there is a path P with length at least two connecting x and y in $H\setminus S$, and so P is in $G\setminus S$, a contradiction. $\square$

Lemma 2.1

If H is a connected spanning subgraph of G, then $\mathrm{mvd}(H)\ge \mathrm{mvd}(G)$.

Proof

Suppose f is an extremal MVD-coloring of G. By Proposition 2.3, f is an MVD-coloring restricted on H. From the definition of MVD-number, we have $\mathrm{mvd}(H)\ge \mathrm{mvd}(G)$. $\square$

Theorem 2.2

Let G be a connected graph on n vertices. Then, $\mathrm{mvd}(G)\le n$, where equality holds if and only if G is a tree.

Proof

Since every connected graph G has a spanning tree T, by Theorem 2.1, $\mathrm{mvd}(T)=n$. Combining with Lemma 2.1, we have $\mathrm{mvd}(G)\le \mathrm{mvd}(T)=n$. On the other hand, if G is connected, $\mathrm{mvd}(G)=n$ and G is not a tree, then G contains at least one cycle. By Proposition 2.1 and Lemma 2.1, we have $\mathrm{mvd}(G)<n-1$, a contradiction. $\square$

Lemma 2.2

Let $H=\bigcup \limits _{i=1}^{r}H_i$. If $\bigcap \limits _{i\in [r]}V(H_i)\ne \emptyset$ and $\mathrm{mvd}(H_i)=1$ for any $i\in [r]$, then $\mathrm{mvd}(H)=1$.

Proof

Suppose f is an MVD-coloring of H such that $|f(H)|\ge 2$. Then, there exist two vertices v and w of H, such that $f(v)=1$ and $f(u)=2$. From the definition of $H_i$, suppose $v\in V(H_1)$ and $u\in V(H_2)$. By Proposition 2.3, f is also an MVD-coloring restricted on $H_1$ and $H_2$ and $\mathrm{mvd}(H_1)=\mathrm{mvd}(H_2)=1$. Then, all vertices of $H_1$ are colored 1 and all vertices of $H_2$ are colored 2, which contradicts $\bigcap \limits _{i\in [r]}V(H_i)\ne \emptyset$. $\square$

Lemma 2.3

Let G be a connected graph. Suppose $v\in V(G)$ and v is neither a cut-vertex nor a pendent vertex of G. Then, $\mathrm{mvd}(G)\le \mathrm{mvd}(G-v)$.

Proof

We can obtain the above lemma by deducing directly from the following Claim.

Claim 1

Suppose $v\in V(G)$ and v is neither a cut-vertex nor a pendent vertex. Then, for any extremal MVD-coloring f of G, $f(G)\setminus f(G-v)=\emptyset$.

Proof

Suppose that $f(v)\notin f(G-v)$ but $f(v)\in f(G)$. Since $v\in V(G)$ and v is neither a cut-vertex nor a pendent vertex, v is contained in at least one cycle C of G. Furthermore, suppose that the neighbors of v on C are u and w. Consider the monochromatic vertex-cut S of u and w. Then, S must contain v, but v is the only vertex with color f(v). Then, there is no monochromatic vertex-cut separating u and w, a contradiction. $\square$

From Claim 1, $\mathrm{mvd}(G)=|f(G)|\le |f(G-v)|\le \mathrm{mvd}(G-v)$, completing the proof of Lemma 2.3. $\square$

Theorem 2.3

Let G be a k-connected graph with n vertices, where k is a positive integer. Then, $\mathrm{mvd}(G)\le \lfloor \frac{n}{k}\rfloor$.

Proof

If G is a connected graph with a cut-vertex, then $\mathrm{mvd}(G)\le n$ is obvious, by Theorem 2.2, when the equality holds only if G is a tree.

If G is a k-connected graph with $k\ge 2$, suppose f is an extremal MVD-coloring of G. Then, we claim that there are at least k vertices contained in each color class under f. Suppose that $V'$ is a color class of f and $v\in V'$. Then, we need to prove that $|V'|\ge n$. Since G is k-connected with $k\ge 2$, there are at least two neighbors of v, say u, w. Consider the monochromatic vertex-cut between u and w. Then, the color of monochromatic vertex-cut that separating u and w is f(v). If u and w are adjacent, then the color of u or w is f(v). Besides, there are at least $k-1$ internally disjoint paths with length at least two connecting u and w. In order to separating u and w, each of the above paths has at least one vertex assigned with color f(v). So we find k vertices with color f(v). If u and w are nonadjacent, similarly, we can also find that there are at least k vertices assigned with color f(v). Consequently, $|V'|\ge k$. Due to the arbitrariness of the selection of $V'$, it follows that each color class contains at least k vertices. As a result, we complete the proof. $\square$

By Theorem 2.2 and Proposition 2.1, the upper bound is sharp when $k\le 2$.

3 Graphs with MVD-Number 1

In this section, we are going to characterize some graphs with MVD-number 1 and to show that for almost all graphs G, we have $\mathrm{mvd}(G)=1$.

Proposition 3.1

Let G be a connected graph. If any two vertices of V(G) have at least two common neighbors, then $\mathrm{mvd}(G)=1$.

Proof

We can easily see the above proposition by the following claim.

Claim 2

Let u and v be two vertices of a connected graph G such that they have at least two common neighbors. Then, for any MVD-colorings of G, u and v are assigned the same color.

Proof

Suppose u and v have two common neighbors x and y. Then, uxv and uyv are two internally disjoint $\{u,v\}$-paths. So, xuy and xvy are two internally disjoint $\{x,y\}$-paths. Therefore, u and v are assigned the identical color for any MVD-colorings. $\square$

For any two vertices u and v of G, fixing the vertex u, by the claim above, we can obtain our proposition by arbitrary selection of v. $\square$

Corollary 3.1

For any integer $n\ge 3$, $\mathrm{mvd}(K_n)=1$.

Next we define a relation $\theta$ on V(G) as follows. For two vertices u and v, we say $u\theta v$ if there exists a sequence $G_1,\cdots ,G_t$ of subgraphs in G such that $\mathrm{mvd}(G_j)=1$ for all $j\in [t]$, $u\in V(G_1)$ and $v\in V(G_t)$ and $|V(G_i)\cap V(G_{i+1})|\ge 1$ for any $i\in [t-1]$. It is not hard to verify that $\theta$ has the symmetric, reflexive, and transitive properties. So, $\theta$ is a equivalence relation on V(G).

We call G a closure on V(G), if $u\theta v$ holds for any two vertices u and v of V(G).

Lemma 3.1

If G is a closure on V(G), then $\mathrm{mvd}(G)=1$.

Proof

Since G is a closure on V(G), then G is connected. Suppose $\mathrm{mvd}(G)\ge 2$ and f is an extremal MVD-coloring of G. Then, there are two vertices $v_1$ and $v_2$ of V(G) such that $f(v_1)\ne f(v_2)$. Since G is a closure on V(G), there is a sequence $G_1,\cdots ,G_t$ of subgraphs in G such that $\mathrm{mvd}(G_j)=1$ for all $j\in [t]$, $v_1\in V(G_1)$ and $v_2\in V(G_t)$ and $|V(G_i)\cap V(G_{i+1})|\ge 1$ for any $i\in [t-1]$. So, there is at least one common vertex of $G_i$ and $G_{i+1}$ for $i\in [t]$. Then all vertices of $V(G_i)$ and $V(G_{i+1})$ are assigned the same color, that is, $f(G_i)=f(G_{i+1})$. Therefore, $f(G_1)=\cdots =f(G_{i+1})=1$. Thus, $\mathrm{mvd}(G)=1$. $\square$

Proposition 3.2

If G is a connected graph and every edge of E(G) is contained in a subgraph $G'$ with $\mathrm{mvd}(G')=1$, then $\mathrm{mvd}(G)=1$.

Proof

In order to show $\mathrm{mvd}(G)=1$, it is sufficient to show that G is a closure on V(G). Choose any two vertices u and v of V(G). If u and v are adjacent, then uv is contained in a same subgraph $G'$ with $\mathrm{mvd}(G')=1$. If u and v are not adjacent, since G is connected, then there is a path P connecting them, and every edge of P is contained in a subgraph with monochromatic vertex-disconnection number 1. So, G is a closure on V(G). $\square$

Next we will give several specific graphs with MVD-number 1. We say $H\vee v$ is the join of v and H, where $v\notin V(H)$, which means that there is an edge connecting v and each vertex of H. A triangular graph is a connected graph with every edge in a triangle. Then, we have the following result.

Theorem 3.1

If G satisfies one of the following conditions, then $\mathrm{mvd}(G)=1$.

• 1) $G=H\vee v$, where H contains no isolated vertices.

• 2) $G=K_{n_1,\cdots ,n_k}$ is a complete multipartite graph with $k\ge 3$.

• 3) $G=H^2$, where H is a connected graph with order at least 3 and $H^2$ denotes the square graph of H.

• 4) G is a 2-connected chordal graph.

• 5) $G\in \{H,L(H)\}$ satisfies that H is a triangular graph with order $n\ge 3$, where L(H) is the line graph of H.

Proof

For 1), choose any edge $e=xy$ of G. If $x,y\in V(H)$, then xyv is a triangle; if $x\in V(H)$ and $y=v$, since there is no isolated vertices in H, there exists $w\in V(H)$ such that $xw\in E(H)$, and so xvw is a triangle. Thus, each edge of G is contained in a triangle, and by Proposition 3.2, $\mathrm{mvd}(G)=1$.

For 2), let $V_1,V_2,\cdots ,V_k$ be the vertex-partition of G with $k\ge 3$. If there is a part $V_i$ ($i\in [k]$) such that $|V_i|=1$, similar to the proof of 1), then $\mathrm{mvd}(G)=1$. Otherwise, for any two vertices of V(G), we can easily find their two common neighbors, and by Proposition 3.1, $\mathrm{mvd}(G)=1$.

For 3), we prove the result by induction on n(H). when $n(H)=3$, H is a $P_3$ or a $K_3$. Then, $H^2=K_3$, and so $\mathrm{mvd}(G)=1$. When $n(H)\ge 4$, let T be a spanning tree of H and v be a leaf of T. Then, $T^2-v=(T-v)^2$. Since v is neither a cut-vertex nor a pendent vertex of $T^2$, by Lemma 2.3, $\mathrm{mvd}(T^2)\le \mathrm{mvd}((T-v)^2)=1$. Because $T^2$ is a spanning tree of $H^2$, $\mathrm{mvd}(H^2)\le \mathrm{mvd}(T^2)$. So, $\mathrm{mvd}(G)=1$.

Observe that if there are two vertices $u,v\in V(G)$ such that the length of a path connecting u and v is larger than 2 (say k), then $\mathrm{mvd}(H^k)=1$.

For 4), recall that a chordal graph is defined as a simple graph contains no induced cycle of length four or larger. If G is a 2-connected chordal graph, then every edge of E(G) is contained in a triangle, and so $\mathrm{mvd}(G)=1$.

For 5), the line graph of a triangular graph is a triangular graph. By the definition of triangular graph, $\mathrm{mvd}(H)=\mathrm{mvd}(L(H))=1$. $\square$

Furthermore, we get the following result.

Theorem 3.2

For almost all graphs G, $\mathrm{mvd}(G)=1$.

Proof

Consider the random graphs $G(n,\frac{1}{2})$. By Proposition 3.1, $\mathrm{mvd}(G)=1$ if any two vertices have at least two common neighbors. So it is sufficient to show that it is almost certain that there are at least two common neighbors for any two vertices in $G(n,\frac{1}{2})$. For any two vertices u, v of V(G), let A be the event that w is a common neighbor of u and v, and ${\overline{A}}$ be the event that w is not a common neighbor of u and v, where $w\in V(G)\setminus \{u,v\}$. Then $P_r(A)=\frac{1}{2}\cdot \frac{1}{2}=\frac{1}{4}$, and $P_r({\overline{A}})=1-P_r(A)=\frac{3}{4}$.

Let ${\mathcal {A}}$ be the event that there is a pair of vertices in G that has at most one common neighbor, and let ${\mathcal {A}}_{u,v}$ denote the event that vertices u and v have at most one common neighbor. Then,

$$\begin{aligned}P_r({\mathcal {A}})&=P_r\left( \bigcup \limits _{u\ne v}{\mathcal {A}}_{u,v}\right) \le \sum \limits _{u\ne v}P_r({\mathcal {A}}_{u,v})\\&=\left( {\begin{array}{c}n\\ 2\end{array}}\right) \left[ \left( \frac{3}{4}\right) ^{n-2}+(n-2)\left( \frac{3}{4}\right) ^{n-3}\cdot \left( \frac{1}{4}\right) \right] \\&<n^3\left( \frac{3}{4}\right) ^{n-4}\rightarrow 0, as~n\rightarrow \infty .\\ \end{aligned}$$

This implies that for almost all graphs G, any two vertices of G have at least two common neighbors, and therefore, by Proposition 3.1, almost surely $\mathrm{mvd}(G)=1$. $\square$

4 The Nordhaus–Gaddum-Type Results

In this section, we consider the Nordhaus–Gaddum-type results for the MVD-number. For convenience, we assume that our graph G and the complement ${\overline{G}}$ are simple and connected in advance, and so $n\ge 4$. We first introduce the following definition and a useful lemma.

Definition 4.1

A deletable vertex of a connected graph G is a vertex which is not a cut-vertex of G.

Lemma 4.1

[11] Let G and ${\overline{G}}$ be connected graphs of order at least 5. Then, there is a vertex $x\in V(G)$ such that x is a deletable vertex of both G and ${\overline{G}}$.

Theorem 4.1

Suppose G and ${\overline{G}}$ are connected graphs. Then, $\mathrm{mvd}(G)+\mathrm{mvd}({\overline{G}})\le n+2$ for $n\ge 5$, $\mathrm{mvd}(G)+\mathrm{mvd}({\overline{G}})\ge 2$ for $n\ge 7$. Furthermore, these bounds are sharp.

Proof

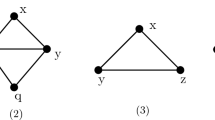
It is obvious that $\mathrm{mvd}(G)+\mathrm{mvd}({\overline{G}})\ge 2$ for $n\ge 7$, since G and ${\overline{G}}$ are connected. Then, we need to explain $\mathrm{mvd}(G)+\mathrm{mvd}({\overline{G}})\le n+2$ for $n\ge 5$. We prove it by induction on n. When $n=5$, by symmetry there are five cases for $\{G, {\overline{G}}\}$ to be considered, as shown in Fig. 1.

Fig. 1

Five cases of $\{G, {\overline{G}}\}$ with $n=5$

Observe that $\mathrm{mvd}(G)+\mathrm{mvd}({\overline{G}})\le 7$ for all five cases with $n=5$, and when $\{G, {\overline{G}}\}=\{G_1, \overline{G_1}\}$, $\mathrm{mvd}(G)+\mathrm{mvd}({\overline{G}})= 7$.

When $n\ge 6$, by Lemma 4.1, for connected graphs G and ${\overline{G}}$, there is a deletable vertex, say v. Let $G'=G-v$. Then, $G'$ and $\overline{G'}$ are two connected graphs, by induction hypothesis, $\mathrm{mvd}(G')+\mathrm{mvd}(\overline{G'})\le n+1$. Let f be an extremal MVD-coloring of G. Since $n\ge 5$, $\max \{d_G(v), d_{{\overline{G}}}(v)\}\ge 2$. Suppose $d_G(v)=t\ge 2$. Then, v is neither a cut-vertex nor a pendent vertex of G. By Lemma 2.3, $\mathrm{mvd}(G)\le \mathrm{mvd}(G')$. If $d_{{\overline{G}}}(v)\ge 2$, $\mathrm{mvd}({\overline{G}})\le \mathrm{mvd}(\overline{G'})$ also holds. Then, $\mathrm{mvd}(G)+\mathrm{mvd}({\overline{G}})\le \mathrm{mvd}(G')+\mathrm{mvd}(\overline{G'})\le n+1$. If $d_{{\overline{G}}}(v)=1$, $\mathrm{mvd}({\overline{G}})=\mathrm{mvd}(\overline{G'})+1$, then $\mathrm{mvd}(G)+\mathrm{mvd}({\overline{G}})\le \mathrm{mvd}(G')+\mathrm{mvd}(\overline{G'})+1\le n+2$.

Now we show that the upper bound is tight for $n\ge 5$. For any integer n with $n\ge 5$, let $B_n$ be a spanning tree of $K_n$ with $\Delta (B_n)=n-2$. Then, $\mathrm{mvd}(B_n)=n$, and $\overline{B_n}$ is a graph obtained by adding a pendent edge to one vertex of $K_{n-1}^-$ with minimum degree. By 1) of Theorem 3.1 and Theorem 2.1, $\mathrm{mvd}(\overline{B_n})=2$. Thus, $\mathrm{mvd}(B_n)+\mathrm{mvd}(\overline{B_n})=n+2$.

Next we show that the lower bound is tight for $n\ge 7$. Let $V(K_n)=A\cup B$ and $0\le |A|-|B|\le 1$. Consider the complete bipartite graph $K_{|A|,|B|}$. Since $n\ge 7$, assume $A=\{u_1,u_2,u_3,u_4,\cdots ,u_{|A|}\}$ and $B=\{v_1,v_2, \cdots , v_{|B|}\}$. Let $D_n=G[A,B]\cup \{u_2u_3\}\setminus \{v_1u_1,v_1u_4\}$. Then, $\overline{D_n}=K_{|A|}^-\cup K_{|B|}\cup \{vu_1,vu_4\}$, where $D_n$ and $\overline{D_n}$ are shown in Fig. 2.

Fig. 2

Extremal graphs of $\{D_n, \overline{D_n}\}$ with $\mathrm{mvd}(D_n)+\mathrm{mvd}(D_n)=2$ for $n\ge 7$

Suppose f is an extremal MVD-coloring of $D_n$. Consider $v_1$ and $v_2$ of B in $D_n$. Since every vertex of A is their common neighbors, $|f(A)|=1$, say $f(A)=\{1\}$. Similarly, we have $|f(B)|=1$. Since $v_1u_2u_3$ is a triangle, $f(v_1)=f(u_2)=f(u_3)$. Therefore, $f(A)=f(B)=\{1\}$. Then, $\mathrm{mvd}(D_n)=1$. Next we consider the MVD-number of $\overline{D_n}$. Since $\overline{D_n}(A)=K_{|A|}^-$, $\overline{D_n}(B)=K_{|B|}$ and $u_1u_4v_1$ is a triangle, by Theorem 3.1$\mathrm{mvd}(\overline{D_n}(A))=\mathrm{mvd}(\overline{D_n}(B))=\mathrm{mvd}(u_1u_4v_1)=1$. Then, G is a closure on V(G), and from Lemma 3.1, $\mathrm{mvd}(\overline{D_n})=1$. $\square$

Remark

Note that the upper bounds of $\mathrm{mvd}G)+\mathrm{mvd}({\overline{G}})$ for $n\le 6$ and the lower bounds of $\mathrm{mvd}(G)+\mathrm{mvd}({\overline{G}})$ for $n=4$ have not been given.

When $n=4$, $G={\overline{G}}=P_4$, then $\mathrm{mvd}(G)=\mathrm{mvd}({\overline{G}})=4$, and so $\mathrm{mvd}(G)+\mathrm{mvd}({\overline{G}})=8$.

When $n=5$, as shown in Fig. 1, if $\{G,{\overline{G}}\}=\{G_3,\overline{G_3}\}$, we get the minimum value 4 of $\mathrm{mvd}(G)+\mathrm{mvd}({\overline{G}})$.

When $n=6$, $m(G)+m({\overline{G}})=15$. To get the lower bound of $\mathrm{mvd}(G)+\mathrm{mvd}({\overline{G}})$, by symmetry there are three cases to be considered. If $m(G)=5$ and $m({\overline{G}})=10$, G is a tree, then $\mathrm{mvd}(G)+\mathrm{mvd}({\overline{G}})\ge 7$. If $m(G)=6$ and $m({\overline{G}})=9$, then G is a unicyclic graph and the length of the unique cycle is at most 6. By Proposition 2.1, $\mathrm{mvd}(G)+\mathrm{mvd}({\overline{G}})\ge 4$, and the equality holds when the unique cycle is $C_6$ or $C_5$. If $m(G)=7$ and $m({\overline{G}})=8$, suppose G has r blocks. When $r=1$, there are three cases to consider, as depicted in Fig. 3.

Fig. 3

Three cases of $\{G, {\overline{G}}\}$ with a block for $n=6$

For all three cases of $\{G, {\overline{G}}\}$ with one block, we have $\mathrm{mvd}(G)+\mathrm{mvd}({\overline{G}})\ge 3$, and when $\{G, {\overline{G}}\}=\{G_1, \overline{G_1}\}$, the equality holds.

When $r=2$, then G is isomorphic to one of the four graphs shown in Fig. 4.

Fig. 4

Four cases of G with two blocks for $n=6$

For each graph of the four cases, $\mathrm{mvd}(G)=2$. Together with $\mathrm{mvd}({\overline{G}})\ge 1$, we have $\mathrm{mvd}(G)+\mathrm{mvd}({\overline{G}})\ge 3$.

When $r\ge 3$, since $n=6$ and $m=7$, $m=n+1$, then G is a bicyclic graph. It is easy to verify that there are at most 3 blocks in G, and then $r=3$. Suppose ${\mathcal {C}}$ is the set of vertices on the cycles of G. Then, $4\le |{\mathcal {C}}|\le 6$. If $|{\mathcal {C}}|=4$, ${\mathcal {C}}=\{K_4^-\}$, and there are two trivial blocks added on some vertices of $K_4^-$. Then, $\mathrm{mvd}(G)=3$ by Theorem 2.1. So, $\mathrm{mvd}(G)+\mathrm{mvd}({\overline{G}})\ge 4$. If $|{\mathcal {C}}|=5$, then the graph G is depicted in Fig. 5a, and so $\mathrm{mvd}(G)=2$ and $\mathrm{mvd}(G)+\mathrm{mvd}({\overline{G}})\ge 3$. If $|{\mathcal {C}}|=6$, then the graph G is shown in Fig. 5b, and so $\mathrm{mvd}(G)=2$ and $\mathrm{mvd}(G)+\mathrm{mvd}({\overline{G}})\ge 3$.

Fig. 5

Some graphs of G with three blocks for $n=6$

Thus, $\mathrm{mvd}(G)+\mathrm{mvd}({\overline{G}})\ge 3$ when $n=6$.

For convenience of reading, we sum up the lower bounds and upper bounds of $\mathrm{mvd}(G)+\mathrm{mvd}({\overline{G}})$ for $n\ge 4$ in Table 1.

Table 1 Bounds of $\mathrm{mvd}(G)+\mathrm{mvd}({\overline{G}})$ for $n\ge 4$

Next we study the bounds of $\mathrm{mvd}(G)\cdot \mathrm{mvd}({\overline{G}})$.

Theorem 4.2

Suppose G and ${\overline{G}}$ are connected graphs of order $n\ge 4$. Then, $\mathrm{mvd}(G)\cdot \mathrm{mvd}({\overline{G}})=16$ when $n=4$, $4\le \mathrm{mvd}(G)\cdot \mathrm{mvd}({\overline{G}})\le 10$ when $n=5$, $2\le \mathrm{mvd}(G)\cdot \mathrm{mvd}({\overline{G}})\le 12$ when $n=6$, and $1\le \mathrm{mvd}(G)\cdot \mathrm{mvd}({\overline{G}})\le 2n$ when $n\ge 7$. Moreover, these bounds are tight.

Proof

Let G and ${\overline{G}}$ be connected. When $n=4$, $G={\overline{G}}=P_4$, then $\mathrm{mvd}(G)\cdot \mathrm{mvd}({\overline{G}})=16$. When $n=5$, as shown in Fig. 1, $4\le \mathrm{mvd}(G)\cdot \mathrm{mvd}({\overline{G}})\le 10$. If $\{G, {\overline{G}}\}=\{G_3,\overline{G_3}\}$, then $\mathrm{mvd}(G)\cdot \mathrm{mvd}({\overline{G}})=4$. If $\{G, {\overline{G}}\}=\{G_1,\overline{G_1}\}$, then $\mathrm{mvd}(G)\cdot \mathrm{mvd}({\overline{G}})=10$. When $n=6$, since $3\le \mathrm{mvd}(G)+ \mathrm{mvd}({\overline{G}})\le 8$, $\mathrm{mvd}(G)\cdot \mathrm{mvd}({\overline{G}})\le 2$, and one pair of $\{G,{\overline{G}}\}$ achieving the lower bound of $\mathrm{mvd}(G)\cdot \mathrm{mvd}({\overline{G}})$ is $\{G_3,\overline{G_3}\}$, which is shown in Fig. 3,

Next we show that the upper bound of $\mathrm{mvd}(G)\cdot \mathrm{mvd}({\overline{G}})$ is 2n for $n\ge 5$. We mainly proceed by induction on n. When $n=5$, by above analyses, $\mathrm{mvd}(G)\cdot \mathrm{mvd}({\overline{G}})\le 10=2n$. When $n>5$, by Lemma 4.1, there is a vertex w such that w is deletable for G and ${\overline{G}}$, i.e., $G-w$ and ${\overline{G}}-w$ are connected. Now we distinguish two cases to discuss.

Case 1

$d_G(w)\ge 2$ and $d_{{\overline{G}}}(w)\ge 2$.

Then, w is neither a cut-vertex nor a pendent vertex of G and ${\overline{G}}$. From Lemma 4.1, $\mathrm{mvd}(G)\le \mathrm{mvd}(G-w)$ and $\mathrm{mvd}({\overline{G}})\le \mathrm{mvd}({\overline{G}}-w)$. So, $\mathrm{mvd}(G)\cdot \mathrm{mvd}({\overline{G}})\le \mathrm{mvd}(G-w)\cdot \mathrm{mvd}({\overline{G}}-w)$. When $n\ge 6$, by the induction hypothesis,

$$\begin{aligned} \mathrm{mvd}(G)\cdot \mathrm{mvd}({\overline{G}})\le \mathrm{mvd}(G-w)\cdot \mathrm{mvd}({\overline{G}}-w)\le 2(n-1)<2n. \end{aligned}$$

Case 2

$d_G(w)=1$ and $d_{{\overline{G}}}(w)=n-2$.

Suppose $wu\in E(G)$. Then, w is adjacent to every vertex of $V(G)\setminus \{w,u\}$ in ${\overline{G}}$. Therefore, ${\overline{G}}-u=w\vee (G-\{w,u\})$. If ${\overline{G}}-\{u,w\}$ contains no isolated vertices, by 1) of Theorem 3.1, $\mathrm{mvd}({\overline{G}}-u)=1$, and so $\mathrm{mvd}({\overline{G}})=1$. Otherwise, suppose there are j isolated vertices $s_1,\cdots ,s_j$ contained in ${\overline{G}}-\{u,w\}$. By Theorem 2.1, $\mathrm{mvd}({\overline{G}}-u)=1+j$. Since ${\overline{G}}-v$ is connected, every vertex $s_i$ with $i\in [j]$ is adjacent to u. Then, $\{w,u\}$ and $\{s_1,\cdots ,s_j\}$ form a vertex-bipartition of a complete bipartite graph $\overline{G'}$ of ${\overline{G}}$, $\mathrm{mvd}(\overline{G'})=2$ and the colors assigned on u and w are identical. By Theorem 2.1 and 1) of Theorem 3.1, $\mathrm{mvd}({\overline{G}})=2$. Since $\mathrm{mvd}(G)\le n$, $\mathrm{mvd}(G)\cdot \mathrm{mvd}({\overline{G}})\le 2n$. The graphs $B_n$ and $\overline{B_n}$ defined in the proof of Theorem 4.1 satisfy $\mathrm{mvd}(G)\cdot \mathrm{mvd}({\overline{G}})=2n$, and so the upper bound is tight.

Now we consider the lower bound of $\mathrm{mvd}(G)\cdot \mathrm{mvd}({\overline{G}})$ for $n\ge 7$. Since $\mathrm{mvd}(G)+\mathrm{mvd}({\overline{G}})\ge 2$ for $n\ge 7$, $\mathrm{mvd}(G)\cdot \mathrm{mvd}({\overline{G}})\ge 1$. The graphs $D_n$ and $\overline{D_n}$ defined in the proof of Theorem 4.1 satisfy $\mathrm{mvd}(G)\cdot \mathrm{mvd}({\overline{G}})=1$ for $n\ge 7$, and so the lower bound is tight.

For ease of reading, we summarize the lower bounds and upper bounds of $\mathrm{mvd}(G)\cdot \mathrm{mvd}({\overline{G}})$ for $n\ge 4$ in Table 2.

$\square$

Table 2 Bounds of $\mathrm{mvd}(G)\cdot \mathrm{mvd}({\overline{G}})$ for $n\ge 4$

5 Results for Four Kinds of Graph Products

In this section, we mainly consider the MVD-coloring of four kinds of graph products: cartesian product, strong product, lexicographic product, and direct product. Suppose G and H are two simple connected graphs with vertex sets $V(G)=\{v_1,\cdots ,v_{n_1}\}$ and $V(H)=\{u_1,\cdots ,u_{n_2}\}$. Then, the concepts of the four kinds of graph products on G and H are defined as follows:

Definition 5.1

The Cartesian product of G and H is the graph $G\square H$ with vertex set $V(G\square H)=V(G)\times V(H)$ and edge set $E(G\square H)$ being the set of all pairs $(v_i, u_j)(v_s, u_t)$ for $i,s\in [n_1]$ and $j,t\in [n_2]$, such that either $v_iv_s\in E(G)$ and $u_s=u_t$, or $u_ju_t\in E(H)$ and $v_i=v_s$.

The direct product of G and H is the graph $G\times H$ with $V(G\times H)=V(G)\times V(H)$ and edge set $E(G\times H)=\{(v_i, u_j)(v_s, u_t): v_iv_s\in E(G) ~and~ u_ju_t\in E(G)~ for~ i,s\in [n_1]~ and~ j,t\in [n_2]\}$.

The strong product of G and H is the graph $G\boxtimes H$ whose vertex set is $V(G\boxtimes H)=V(G)\times V(H)$ and whose edge set $E(G\boxtimes H)$ is the union of edge sets of the Cartesian and the direct product.

The lexicographic product (or composition) of G and H is the graph $G\circ H$ with vertex set $V(G\circ H)=V(G)\times V(H)$ in which $(v_i, u_j)$ is adjacent to $(v_s, u_t)$ if and only if either $v_iv_s\in E(G)$, or $v_i=v_s$ and $u_ju_t\in E(H)$, where $i,s\in [n_1]$ and $j,t\in [n_2]$.

We first consider the MVD-number of Cartesian product of G and H. Some useful lemmas are shown as follows.

Lemma 5.1

Suppose G and H are two connected graphs. If v is a vertex of G, then $\mathrm{mvd}(G\square H)\le \mathrm{mvd}((G-v)\square H)$.

Proof

For convenience, let $v=v_1$. To the contrary, suppose $\mathrm{mvd}(G\square H)> \mathrm{mvd}((G-v)\square H)$. Assume f is an extremal MVD-coloring of $G\square H$. By Proposition 2.3, f is an MVD-coloring of $(G-v)\square H$, since $(G-v)\square H$ is a subgraph of $G\square H$. From the definition of Cartesian product, $G\square H$ is composed of its pairwise disjoint and distinct subgraphs $v_1\square H,v_2\square H,\cdots ,v_{n_1}\square H$ by connecting edges between corresponding pairs of vertices. Then, there is a vertex $(v_1,u_i)$ such that $f((v_1,u_i))$ is contained in $f(v_1\square H)$ but not in $f(v_j\square H)$ for each integer $j\ge 2$. Since G and H are connected, $v_1$ has at least one neighbor in G, say $v'$, and $u_i$ has at least one neighbor in H, write $u'$. Then, $vv'u'u_i$ is a 4-cycle in $G\square H$. By the definition of f, f is not an MVD-coloring of $vv'u'u_i$, which contradicts with Proposition 2.3. $\square$

Corollary 5.1

If v is a vertex of G and u is a vertex H, then $\mathrm{mvd}(G\square H)\le \mathrm{mvd}((G-v) \square (H-u))$.

Proof

Since v is a vertex of G, by Lemma 5.1, $\mathrm{mvd}(G\square H)\le \mathrm{mvd}((G-v) \square H)$. Because $u\in V(H)$, $\mathrm{mvd}((G-v) \square H)\le \mathrm{mvd}((G-v) \square (H-u))$. Thus, $\mathrm{mvd}(G\square H)\le \mathrm{mvd}((G-v) \square (H-u))$.

$\square$

Lemma 5.2

[9] Cartesian product of bipartite graphs is a bipartite graph.

Lemma 5.3

• (1) $\mathrm{mvd}(P_s\square P_t)=2$ for any two integers s and t with $s,t \ge 2$;

• (2) $\mathrm{mvd}(C_{2k+1}\square P_2)=1$ for any positive integer k.

Proof

For (1), any 4-cycle $C_4$ has two kinds of MVD-colorings on it: Each vertex is assigned with a same color 1, or its vertices are assigned with the colors 1 and 2, alternatively. Since every edge of $P_s\square P_t$ is contained in a 4-cycle and there is no cut-vertex and pendent vertex in $P_s\square P_t$, we have $\mathrm{mvd}(P_s\square P_t)\le 2$. Note that the proper 2-coloring of any connected bipartite graph is an MVD-coloring of this graph, and so $\mathrm{mvd}(P_s\square P_t)=2$.

For (2), suppose to the contrary, there is an MVD-coloring $f'$ such that $|f'(C_{2k+1}\square P_2)|=2$. Suppose $C_{2k+1}=v_1v_2\cdots v_{2k+1}v_1$ and $P_2=u_1u_2$. Then, $V(C_{2k+1}\square P_2)=\{(v_i,u_j),i\in [2k+1]~and~ j\in [2]\}$. By Proposition 2.3, there are two adjacent vertices (for convenience, write $(v_1,u_1)$ and $(v_2,u_1)$) of $u_1\square C_{2k+1}$ that are colored with the same color, say 1. Then, $(v_1,u_2)$ and $(v_2,u_2)$ are assigned the color 1. By the assumption, suppose i is the minimum integer such that $(v_i,u_1)$ or $(v_i,u_2)$ are colored with a distinct color, say 2, under $f'$. If $f'(v_i,u_1)=f'(v_i,u_2)=2$ or $f'(v_i,u_1)=2\ne f'(v_i,u_2)$, then $f'$ is not an MVD-coloring of the 4-cycle formed by the vertices $(v_{i-1},u_1), (v_{i-1},u_2),(v_i,u_1)$ and $(v_i,u_2)$, a contradiction to Proposition 2.3. Therefore, $\mathrm{mvd}(C_{2k+1}\square P_2)=1$. $\square$

Theorem 5.1

Suppose G and H are two connected graphs. Then, we have the two following results.

• (1) If both G and H are bipartite, then $\mathrm{mvd}(G\square H)=2$,

• (2) If one of G and H is non-bipartite, then $\mathrm{mvd}(G\square H)=1$.

Proof

For (1), since both G and H are bipartite, by Lemma 5.2, $G\square H$ is a bipartite graph. Then, we can find a complete bipartite graph $G'$ which contains $G\square H$ as a spanning subgraph. By Proposition 2.2 and Lemma 2.1, $\mathrm{mvd}(G\square H)\ge \mathrm{mvd}(G')=2$. On the other hand, since G is connected, then we can find a spanning tree T of G. We delete in turn the leaves of T or the new tree until the new tree is a path. Suppose the final path we obtain is $P'$. Analogically, we can get a path of H through the above operation, write $P^*$. Together with Lemma 2.1, Corollary 5.1 and (1) of Lemma 5.3, we have $\mathrm{mvd}(T\square H)\le \mathrm{mvd}(P'\square P^*)=2$. Thus, $\mathrm{mvd}(G\square H)=2$.

For (2), suppose $C_{2t+1}$ is an odd cycle of G. We contract $C_{2t+1}$ into a vertex $u_0$, and let $G'$ be the new graph. Then, $G'$ is connected and so we can find a spanning tree $T'$ of $G'$. We delete in turn the leaves of $T'$ or the new tree until the remaining vertex is $u_0$. Finally, we restore $u_0$, and get the graph $C_{2t+1}$. Since H is connected, we can find a spanning tree $T''$ of H. We delete in turn the leaves of $T''$ or the new tree until the new tree is $P_2$. Combining with Lemma 2.1, Corollary 5.1 and (2) of Lemma 5.3, we have $\mathrm{mvd}(G\square H)\le \mathrm{mvd}(C_{2t+1}\square P_2)=1$. So, $\mathrm{mvd}(G\square H)=1$. $\square$

For any three connected graphs $G_1$, $G_2$ and $G_3$, since $G_1\square G_2\square G_3=(G_1\square G_2)\square G_3$, the following results are clearly true.

Corollary 5.2

Suppose $G_1,G_2,\cdots ,G_k$ are k connected graphs of orders at least 2. Then, we have the two following results.

• (1) If each graph $G_i$ is bipartite for $i\in [k]$, then $\mathrm{mvd}(G_1\square \cdots \square G_k)=2$,

• (2) If at least one of $G_1,G_2,\cdots ,G_k$ is non-bipartite, then $\mathrm{mvd}(G_1\square \cdots \square G_k)=1$.

In the following, we consider the MVD-number of the strong product of two graphs G and H.

Lemma 5.4

If $s\ge 2$ and $t\ge 2$, then $P_s\boxtimes P_t$ is a closure on $V(P_s\boxtimes P_t)$.

Proof

We proceed the proof by induction on $s+t$. When $s=2$ and $t=2$, then $P_s\boxtimes P_t=K_4$, so we are done. Suppose $s+t\ge 5$ and $s,t\ge 2$. Let $P_s=v_1v_2\cdots v_s$ and $P_t=u_1u_2\cdots u_t$. Suppose $P=P_s-v_s$. By the induction hypothesis, $P\boxtimes P_t$ is a closure on $V(P\boxtimes P_t)$, and $\{v_{s-1}v_s\}\boxtimes P_t$ is also a closure on $V(\{v_{s-1}v_s\}\boxtimes P_t)$. Since $P\boxtimes P_t$ and $\{v_{s-1}v_s\}\boxtimes P_t$ contain a common vertex $(u_{s-1},v_t)$, $P_s\boxtimes P_t$ is a closure on $V(P_s\boxtimes P_t)$. $\square$

Theorem 5.2

For two connected graphs G and H of orders at least 2, we have $\mathrm{mvd}(G\boxtimes H)=1$.

Proof

We only need to show that $G\boxtimes H$ is a closure on $V(G\boxtimes H)$. Suppose $V(G)=\{x_1,\cdots ,x_s\}$ and $V(H)=\{y_1,\cdots ,y_t\}$. For any two distinct vertices $(x_a,y_b)$ and $(x_c,y_d)$ of $G\boxtimes H$, we need to find a closure containing them. If $a\ne c$ and $b\ne d$, then there is a path $P_{ac}$ in G connecting $x_a$ and $x_c$, and there is also a path $P_{bd}$ in H connecting $y_b$ and $y_d$. Thus, $P_{ac}\boxtimes P_{bd}$ is a subgraph in $G\boxtimes H$ that contains $(x_a,y_b)$ and $(x_c,y_d)$. Together with Lemma 5.4, $P_{ac}\boxtimes P_{bd}$ is a closure on $V(P_{ac}\boxtimes P_{bd})$. If $a\ne c$ and $b=d$, then there is a path $P_{ac}$ in G connecting $x_a$ and $x_c$. Since H is connected and $n(H)\ge 2$, there is a vertex $y'$ in H adjacent to $y_1$. By Lemma 5.4, $P_{ac}\boxtimes \{y_1y'\}$ is a closure on $V(P_{ac}\boxtimes \{y_1y'\})$ that contains $(x_a,y_b)$ and $(x_c,y_d)$. If $a=c$ and $b\ne d$, analogically, we can also find a closure containing $(x_a,y_b)$ and $(x_c,y_d)$. Due to the arbitrary selection of the two vertices $(x_a,y_b)$ and $(x_c,y_d)$, $G\boxtimes H$ is a closure on $V(G\boxtimes H)$. $\square$

Proposition 5.1

[12] Suppose G and H are connected graphs. Then, $G\boxtimes H$ is a connected spanning subgraph of $G\circ H$.

Combining with Lemma 2.3, we can easily obtain the following theorem.

Theorem 5.3

Suppose G and H are connected graphs. Then, $\mathrm{mvd}(G\circ H)=1$.

For the MVD-number of the direct product $G\times H$ of two connected graphs G and H, we need some known tools as follows.

Proposition 5.2

[15] For two connected graphs G and H, $G\times H$ is connected if and only if at least one of G, H is not bipartite.

Definition 5.2

[12] Suppose G is a connected graph and $V'=\{v_1,v_2,\cdots ,v_t\}$ is a vertex subset of G. Let $G=G_0$ and $G_i=G_{i-1}-v_i$ for $i\in [t]$. We call a vertex sequence $\gamma =(v_1,v_2,\cdots ,v_t)$ a softer layer of G if the degree of $v_i$ in $G_{i-1}$ is at least 2 and $G_i$ is connected for $i\in [t]$.

From Lemma 2.3, we can deduce the following lemma directly.

Lemma 5.5

Suppose G is connected and the vertex sequence $\gamma =(v_1,v_2,\cdots ,v_t)$ is a softer layer of G. Then, $\mathrm{mvd}(G)\le \mathrm{mvd}(G_t)$.

Lemma 5.6

Let $G'$ be a connected subgraph of a connected graph G, and H be a connected graph with $\delta (H)\ge 2$. If at least one of $G',H$ is not bipartite, then $\mathrm{mvd}(G\times H)\le \mathrm{mvd}(G'\times H)$.

Proof

We proceed the proof by induction on the value of $n(G)-n(G')$. If $n(G)-n(G')=0$, then $G'$ is a spanning subgraph of G, and so $G'\times H$ is a spanning subgraph of $G\times H$. Since at least one of $G'$ and H are not bipartite, $G\times H$ and $G'\times H$ are connected by Proposition 5.2. By Lemma 2.1, $\mathrm{mvd}(G\times H)\le \mathrm{mvd}(G'\times H)$.

Now we assume $n(G)-n(G')\ge 1$. Since $G'$ is a connected subgraph of G, there is a spanning tree T with a leaf v, such that $v\notin V(G')$. Let ${\hat{G}}=G-v$. Then, ${\hat{G}}$ is a connected subgraph of G which contains $G'$ as a subgraph. Since ${\hat{G}}\times H$ is connected and $n({\hat{G}})-n(G')\le n(G)-n(G')$, by induction, $\mathrm{mvd}({\hat{G}}\times H)\le \mathrm{mvd}(G'\times H)$. Let $V(H)=\{u_1,u_2,\cdots ,u_n\}$ and let $G\times H_{i}=G\times H-\{(v,u_1),(v,u_2),\cdots ,(v,u_i)\}$ for $i\in [n]$. Furthermore, suppose $S=\{(v,u_i): i\in [n]\}$. Then, S is an independent set of $G\times H$, and $G\times H-S={\hat{G}}\times H$. For each element $(v,u_i)$ of S, since $\delta (H)\ge 2$, $u_i$ has two neighbors in $H_{i-1}$, write $u_{i1}, u_{i_2}$. Similarly, let $v'$ be one of the neighbors of v in G. Then, $(v',u_{i1})$ and $(v',u_{i2})$ are two neighbors of $(v,u_i)$ in $G\times H_{i-1}$. Then, each vertex $(v,u_i)$ of S has at least two neighbors in $G\times H_{i-1}$. Therefore, the vertex sequence $((v,u_1),(v,u_2),\cdots ,(v,u_n))$ is a soft layer of $G\times H$. By Lemma 5.5, $\mathrm{mvd}(G\times H)\le \mathrm{mvd}({\hat{G}}\times H)\le \mathrm{mvd}(G'\times H)$. Consequently, $\mathrm{mvd}(G\times H)\le \mathrm{mvd}(G'\times H)$. $\square$

Theorem 5.4

Let $G'$ and $H'$ be connected subgraphs of two connected graphs G and H, respectively, satisfying that either $\delta (H)\ge 2$ and $\delta (G')\ge 2$, or $\delta (G)\ge 2$ and $\delta (H')\ge 2$. If at least one of $G',H'$ is not bipartite, then $\mathrm{mvd}(G\times H)\le \mathrm{mvd}(G'\times H')$.

Proof

We only need to prove the case that $\delta (H)\ge 2$ and $\delta (G')\ge 2$. Since at least one of $G'$ and $H'$ is not bipartite, at least one of G, H is not bipartite, and so are $G'$ and H. Then, $G\times H$, $G'\times H$ and $G'\times H'$ are connected by Proposition 5.2. Since $\delta (H)\ge 2$, by Lemma 5.6, $\mathrm{mvd}(G\times H)\le \mathrm{mvd}(G'\times H)$. Analogously, since $\delta (G')\ge 2$, we have $\mathrm{mvd}(G'\times H)\le \mathrm{mvd}(G'\times H')$. Therefore, $\mathrm{mvd}(G\times H)\le \mathrm{mvd}(G'\times H')$.

Symmetrically, for the case that $\delta (G)\ge 2$ and $\delta (H')\ge 2$, we can also obtain $\mathrm{mvd}(G\times H)\le \mathrm{mvd}(G'\times H')$. $\square$

Definition 5.3

[12] For a non-bipartite graph G, the odd girth of G, denoted by $g_o(G)$, is the minimum value of the lengths of all odd cycles of G. If G is a bipartite graph, we set $g_o(G)=+\infty$, which is because a bipartite graph has no odd cycle.

Corollary 5.3

Let G and H be two connected graphs without pendent edges, and at least one of them is not bipartite. Then, $\mathrm{mvd}(G\times H)\le \min \{g_o(G), g_o(H)\}$.

Proof

For convenience, suppose G contains an odd cycle $C_o$ such that $n(C_o) =\min \{g_o(G), g_o(H)\}$. Since there is no pendent edges in H, suppose H contains a cycle $C'$. By Theorem 5.4, $\mathrm{mvd}(G\times H)\le \mathrm{mvd}(C_o\times C')$. By Lemma 5.6, $\mathrm{mvd}(C\times C')\le \mathrm{mvd}(C_o\times P_2)$. Since $C_o\times P_2=C_{2\cdot n(C_o)}$, we have $\mathrm{mvd}(C_o\times P_2)=n(C_o)$. Thus, $\mathrm{mvd}(G\times H)\le \min \{g_o(G), g_o(H)\}$. $\square$

Lemma 5.7

If G is a bipartite graph, then $G\times K_n$ is also a bipartite graph.

Proof

Suppose $V_1=\{u_{11},u_{12},\cdots ,u_{1a}\}$ and $V_2=\{u_{21},u_{22},\cdots ,u_{2b}\}$ are the bipartition of V(G). Let $V(K_n)=\{v_1,v_2,\cdots ,v_n\}$. Then, two vertices $(u_{ij},v_p)$ and $(u_{st},v_q)$ of $G*K_n$ are adjacent if $i\ne s$, $u_{ij}u_{st}\in E(G)$ and $p\ne q$. Therefore, $V_1'=\{(u_{1i},v_j):i\in [a]~ and ~j\in [n]\}$ and $V_2'=\{(u_{2i},v_j):i\in [b]~ and~ j\in [n]\}$ form a bipartition of $V(G\times K_n)$ and there are no edges that connects any two vertices of $V_1'$ and $V_2'$, respectively. Thus, $G\times K_n$ is a bipartite graph with vertex-bipartition $V_1'$ and $V_2'$. $\square$

Since a subgraph of a bipartite graph is also bipartite, if G is a bipartite graph and H is a connected non-bipartite graph, then $G\times H$ is also a bipartite graph.

Lemma 5.8

• (1) $\mathrm{mvd}(P_3\times K_3)=2$.

• (2) $\mathrm{mvd}(P_2\times K_q)=2$ for $q\ge 4$.

• (3) $\mathrm{mvd}(K_3\times C_{2k+1})=1$ for $k\ge 1$.

Proof

For (1), since $P_3$ is a bipartite graph, together with Lemma 5.7, Proposition 2.2 and Proposition 2.3, we have $\mathrm{mvd}(P_3\times K_3)\ge 2$. Let $P_3=u_1u_2u_3$ and $V(K_3)=\{v_1,v_2,v_3\}$. For ease of understanding and stating, we depict $P_3\times K_3$ in Fig. 6a, and let $x_i^j=(u_i,v_j)$ for $i\in [3]$ and $j\in [3]$. Then, the unique unlabeled vertex is $x_2^2$.

Fig. 6

$P_3\times K_3$ and $P_2\times K_4$

Suppose f is an extremal MVD-coloring of $P_3\times K_3$. In Fig. 6a, since $x_2^1x_1^3x_2^2x_3^3$ is a 4-cycle, $x_2^1$ and $x_2^2$ ($x_1^3$ and $x_3^3$) have two common distinct neighbors, and so $f(x_2^1)=f(x_2^2)$ and $f(x_1^3)=f(x_3^3)$. Similarly, since $x_1^1x_2^2x_3^1x_2^3$ is a 4-cycle, $x_2^1$ and $x_2^3$ have two common distinct neighbors, and so $f(x_2^1)=f(x_2^3)$ and $f(x_1^1)=f(x_3^1)$. Thus, $f(x_2^1)=f(x_2^2)=f(x_2^3)$. Similarly, we have $f(x_1^2)=f(x_3^2)$, because $x_2^1x_1^2x_2^3x_3^2$ is a 4-cycle in $P_3\times K_3$. Suppose to the contrary, $|f|\ge 3$. Then, at least one color of $\{f(x_1^1),f(x_1^2),f(x_1^3)\}$ is different from the other two. Without loss of generality, suppose $f(x_1^1)\ne f(x_1^2)$ and $f(x_1^2)=f(x_1^3)$. Then, $f(x_2^1)\ne f(x_1^1)\ne f(x_1^2)$. However, there is no monochromatic vertex-cuts separating $x_2^2$ and $x_2^3$ under f, a contradiction. Analogically, for the other cases, we can also get a contradiction. Thus, $\mathrm{mvd}(P_3\times K_3)=2$.

For (2), since $P_2$ is a bipartite graph, together with Lemma 5.7, Proposition 2.2 and Proposition 2.3, we have $\mathrm{mvd}(P_2\times K_q)\ge 2$ for $q\ge 4$. On the other hand, since $K_4$ is a subgraph of $K_n$ for $n\ge 4$, by Lemma 5.6, we only need to show $\mathrm{mvd}(P_2\times K_4)\le 2$. Let $P_2=a_1a_2$ and $V(K_4)=\{b_1,b_2,b_3,b_4\}$. For ease of understanding and stating, we depict $P_2\times K_4$ in Fig. 6b, and let $y_i^j=(a_i,b_j)$ for $i\in [2]$ and $j\in [4]$. Suppose g is an extremal MVD-coloring of $P_2\times K_4$. For $y_1^1$ and $y_1^2$, since $y_2^3$ and $y_2^4$ are two common neighbors of them, we have $g(y_1^1)=g(y_1^2)$. Then, consider $y_1^3$ and $y_1^4$. Since $y_2^1$ and $y_2^2$ are two common neighbors of them, we have $g(y_1^3)=g(y_1^4)$. Similarly, for $y_1^2$ and $y_1^3$, since $y_2^1$ and $y_2^4$ are two common neighbors of them, we have $g(y_1^2)=g(y_1^3)$. Therefore, $g(y_1^1)=g(y_1^2)=g(y_1^3)=g(y_1^4)$. Analogically, we obtain $g(y_2^1)=g(y_2^2)=g(y_2^3)=g(y_2^4)$. Then, $|g(P_2\times K_4)|\le 2$. Therefore, $\mathrm{mvd}(P_2\times K_4)=2$. Consequently, $\mathrm{mvd}(P_2\times K_q)=2$ for $q\ge 4$.

For (3), suppose $V(K_3)=\{u_1,u_2,u_3\}$ and $V(C_{2k+1})=\{v_1,v_2,\cdots ,v_{2k+1}\}$. Let $V_i=\{(u_1,v_i),(u_2,v_i),(u_3,v_i)\}$ for $i\in [2k+1]$. Then, $V_1,V_2,\cdots ,V_{2k+1}$ form a partition of $V(K_3\times C_{2k+1})$. Suppose f is an extremal MVD-coloring of $K_3\times C_{2k+1}$. Since $K_3\times P_{2k+1}$ is a subgraph of $K_3\times C_{2k+1}$, from the proof of (1), we have $|f(V_1)|=|f(V_2)|=\cdots =|f(V_{2k+1})|=1$ and $|f(K_3\times C_{2k+1})|\le 2$ due to Proposition 2.3. To the contrary, suppose $f(K_3\times C_{2k+1})\ge 2$. Then, $f(K_3\times C_{2k+1})=2$. Since $2k+1$ is odd, there is a positive integer p such that $f(V_p)=f(V_{p+1})$. Let $i'$ be the minimum integer (module $2k+1$) larger than $p+1$ such that $f(V_{i'})\ne f(V_p)$. Consider any two vertices u and v of $V_{i'-1}$. From the definition of direct product, u and v are not adjacent. Then, we need to delete some vertices of $V_{i'-2}$ and $V_{i'}$ to separate them. Since $f(V_{i'-2})\ne f(V_{i'})$, there is no monochromatic vertex-cuts separating u and v under f, which contradicts with Proposition 2.3. Therefore, $\mathrm{mvd}(K_3\times C_{2k+1})=1$ for $k\ge 1$. $\square$

Corollary 5.4

Let G be a connected graph and $H=K_n$ $(n\ge 3)$. Then, we have the two following results.

• (1) If G is a bipartite graph except $\mathrm{mvd}(K_3\times P_2)=3$, then $\mathrm{mvd}(G\times H)=2$.

• (2) If G is non-bipartite, then $\mathrm{mvd}(G\times H)=1$.

Proof

For (1), suppose G is a connected bipartite graph. By Lemma 5.7, $G\times H$ is a bipartite graph. Together with Proposition 2.3 and 2.2, we have $\mathrm{mvd}(G\times H)\ge 2$. On the other hand, when $G=P_2$ and $H=K_3$, $G\times H=C_6$, we have $\mathrm{mvd}(G\times H)=mvd(C_6)=3$. When $n(G)\ge 3$ and $n(H)=3$, by Lemma 5.6 and (1) of 5.8 we have $\mathrm{mvd}(G\times H)\le \mathrm{mvd}(P_3\times K_3)=2$. Then, $\mathrm{mvd}(G\times H)=2$. When $n(G)\ge 2$ and $n(H)\ge 4$, by Lemma 5.6 and (2) of 5.8 we have $\mathrm{mvd}(G\times H)\le \mathrm{mvd}(P_2\times K_n)=2$. Then, $\mathrm{mvd}(G\times H)=2$.

For (2), suppose G is a connected non-bipartite graph. Then, G contains an odd cycle, say $C_{2k+1}$, where $k\ge 1$. Combining with Theorem 5.4 and (3) of Lemma 5.8, we have $\mathrm{mvd}(G\times H)\le \mathrm{mvd}(K_3\times C_{2k+1})=1$. Therefore, $\mathrm{mvd}(G\times H)=1$. $\square$

For more general case, we have the following result.

Corollary 5.5

Let H be a connected graph without pendent edges and with at least one triangle. Then

• (1) if G is a connected bipartite graph and contains an even cycle, then $\mathrm{mvd}(G\times H)=2$.

• (2) If G is a non-bipartite graph, then $\mathrm{mvd}(G\times H)=1$.

Proof

For (1), since G is a bipartite, by Lemma 5.7 we have $G\times H$ is bipartite. So, $\mathrm{mvd}(G\times H)\ge 2$. From the definition of G, there are some pendent edges in G. Then, we obtain a graph $G'$ by deleting all pendent edges of G one by one, and $G'$ is a connected bipartite graph with $\delta (G)\ge 2$. By Theorem 5.4 and Corollary 5.4, we have $\mathrm{mvd}(G\times H)\le \mathrm{mvd}(G'\times K_3)=2$. Thus, $\mathrm{mvd}(G\times H)\le 2$. So, $\mathrm{mvd}(G\times H)=2$.

For (2), since G is not bipartite, G contains a odd cycle, say $C_{2k+1}$. Because $\delta (H)\ge 2$, by Theorem 5.4 and (3) of Lemma 5.8 we have $\mathrm{mvd}(G\times H)\le \mathrm{mvd}(K_3\times C_{2k+1})=1$. Thus, $\mathrm{mvd}(G\times H)=1$. $\square$

As one can see, for the former three products, Cartesian product, strong product and lexicographic product (or composition), we have completely got the exact values of their MVD-numbers. Only for the last product, direct product, we have not completely solved the problem. To completely solve it, further work of more detailed structural analysis needs to be done.