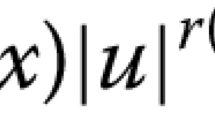Existence and Multiplicity of Positive Solutions to a p-Kirchhoff-Type Equation

Abstract

In this paper, a p-Kirchhoff-type elliptic equation involving a positive parameter $\lambda$ is considered. Existence, nonexistence and multiplicity of weak solutions are obtained by the fibering maps and the mountain pass lemma. We use the nonlinear generalized Rayleigh quotient to characterize two extremal values $\lambda _0^*$ and $\lambda ^*$. The parameter $\lambda _0^*$ is characterized for which the energy functional has nonnegative energy for the local minimum when $\lambda \ge \lambda _0^*$. The parameter $\lambda ^*$ is characterized for which the problem has no nonzero solution when $\lambda >\lambda ^*$. Moreover, the asymptotic behavior of the solutions is also studied when $\lambda \downarrow 0$.

1 Introduction

In this paper, we are concerned with the following p-Kirchhoff-type elliptic equation:

$$\begin{aligned} \ \ \ \ \ \ \ \ \ \ \ \ {\left\{ \begin{array}{ll} -M\left( \int _{\Omega }|\nabla u|^p\mathrm {d}x\right) \Delta _{p}u=|u|^{q-2}u, &{}x\in \Omega ,\\ u(x)=0, &{}x\in \partial \Omega ,\\ \end{array}\right. } \end{aligned}$$

(1.1)

where $\Omega \subset {\mathbb {R}}^{n}$ is a bounded domain with smooth boundary $\partial \Omega$, $1<p,q<p^{*}$, $p^{*}$ is the Sobolev conjugate of p, i.e., $p^*=\frac{np}{n-p}$ when $p<n$ and $p^*=\infty$ when $p\ge n$; $M(s)=a+\lambda s^{p-1}$ where a is a positive constant and $\lambda$ is a positive parameter; $\Delta _pu=\mathrm {div}(|\nabla u |^{p-2}\nabla u )$ is the standard p-Laplace operator.

The following p-Kirchhoff elliptic equation, a natural generalization of the equation in (1.1),

$$\begin{aligned} {\left\{ \begin{array}{ll} -\Big (a+b\left( \int _{\Omega }|\nabla u|^p\mathrm {d}x\right) ^{p-1}\Big )\Delta _{p}u=f(x, u),\quad &{}x\in \Omega ,\\ u(x)=0,\quad &{} x\in \partial \Omega , \end{array}\right. } \end{aligned}$$

(1.2)

is closely related to the stationary version of the wave-type Kirchhoff equation

$$\begin{aligned} u_{tt}-\left( a+b\left( \int _{\Omega }|\nabla u|^p\mathrm {d}x\right) ^{p-1}\right) \Delta _{p}u=f(t,x, u). \end{aligned}$$

(1.3)

When $n=1$ and $p=2$, (1.3) was first proposed by Kirchhoff [14] to describe the transversal oscillations of a stretched string, where u denotes the displacement of the string, f stands for the external force, a represents the initial tension and b is related to the intrinsic properties of the string (see [11]).

Problem (1.2) is usually referred to as being nonlocal, since the presence of the term $M(\int _{\Omega }|\nabla u|^p\mathrm {d}x)\Delta _{p}u$ means that the equation is no longer a point-wise identity. When one considers the existence of weak solutions to problem (1.2), the main difficulty caused by this nonlocal term is that generally one can not deduce from $u_n\rightharpoonup u$ weakly in $W_0^{1,p}(\Omega )$ the convergence $M(\int _{\Omega }|\nabla u_n|^p\mathrm {d}x) \Delta _{p}u_n\rightharpoonup M(\int _{\Omega }|\nabla u|^p\mathrm {d}x)\Delta _{p}u$ in $W^{-1,p'}(\Omega )$. In the past few years, the existence and multiplicity of weak solutions to problem (1.2) with different kinds of nonlinearities have been investigated extensively by applying various techniques such as perturbation method, variational methods, the mountain pass lemma, the Nehari manifold approach, genus theory and Morse theory. We refer the interested reader to [1, 2, 5, 6, 8,9,10, 13, 15,16,17,18, 20,21,23, 28, 29, 32] and the references therein for the study of Kirchhoff equations with one or more of the above-mentioned methods.

In [7], Chen et al. discussed the existence of solutions to problem (1.2) with $p=2$ and $f(x, u)=\lambda f(x)|u|^{q-2}u+g(x)|u|^{p-2}u$, where $f,\ g \in C(\Omega )$ are sign-changing weight functions, and the parameters $a,\ b, \ \lambda > 0$, $1<q<2<p<2^*$($2^*=\frac{2n}{n-2}$, if $n\ge 3$, $2^*=\infty$, if $n=1, 2$). By using the Nehari manifold and the fibering maps, they obtained the existence of multiple positive solutions to problem (1.2). When $p=2$ and $f(x, u)=|u|^{\gamma -2}u$ with $\gamma \in (2.4)$, Silva [30] investigated the existence and multiplicity of weak solutions to problem (1.2) in a bounded smooth domain $\Omega \subset {\mathbb {R}}^3$. After defining two variational numbers, he obtained the existence of a local minimum and a mountain pass-type solution by using the fibering maps and the mountain pass lemma.

There are also some works concerning the existence and multiplicity of weak solutions to problem (1.2) for general $p>1$. For example, Silva et al. [31] considered the existence and multiplicity of weak solutions to problem (1.2) with $a=1$, $b=0$ and $f(x,u)=\lambda |u|^{q-2}u+f(x)|u|^{r-2}u$, where the parameters $a,\ b, \ \lambda > 0$, $1<q<p<r<p^*$ and $f\in L^\infty (\Omega )$ is a sign-changing weight function. By using the Nehari manifold and the fibering maps, they showed the existence of two positive solutions on some interval $(0,\lambda ^*+\varepsilon )$, where $\lambda ^*$ can be characterized variationally. Li et al. [17] dealt with problem (1.2) with $f(x, u)=\lambda f(x)|u|^{q-2}u+g(x)|u|^{r-2}u$ and $1<q<p<r\le p^*$, where $f,\ g \in C(\Omega )$ are sign-changing weight functions and the parameters $a,\ b, \ \lambda >0$. They showed, under certain conditions, that problem (1.2) admits multiple nontrivial nonnegative solutions by applying the variational method. Moreover, by using the concentration compactness principle [19], the existence of weak solutions with critical exponent was also proved.

Recently, Il’yasov [12] came up with a fact that the extreme values of the parameter $\lambda$ for the Nehari manifold method can be found through the critical values of a corresponding nonlinear generalized Rayleigh quotient. Since the nonlinear generalized Rayleigh quotient is one of the main tools in this paper, let us explain in a more detailed way its main idea. Let $\Phi _\lambda : W\rightarrow {\mathbb {R}}$ be a Fréchet-differentiable functional, where W is a Banach space, $\Phi _\lambda =T(u)-\lambda G(u)$ and $\lambda \in {\mathbb {R}}$. For simplicity, we assume that $\langle D_uG(u),u\rangle \ne 0$, where $\langle \ ,\ \rangle$ denotes the dual pairing between W and its dual space. Consider the equation of variational form

$$\begin{aligned} D_u\Phi _\lambda (u)=D_uT(u)-\lambda D_uG(u)=0,\ u\in W. \end{aligned}$$

(1.4)

The Nehari manifold associated with (1.4) is defined as follows by

$$\begin{aligned} N_{\lambda }=\{u\in W\backslash \{0\}: \langle D_{u}\Phi _\lambda (u),u\rangle =0 \}. \end{aligned}$$

A natural idea to solve (1.4) is to consider the constrained minimization problem in the Nehari manifold $N_\lambda$. Then, by the Lagrange multiplier rule, we know that the sufficient condition for the local minimizer $u\in N_\lambda$ to be a solution of (1.4) is that $D_{uu}\Phi _\lambda (u)(u,u)\ne 0$. Since this sufficient condition usually depends on the parameter $\lambda$, this raises the question of how to find these extremes such that the sufficient condition may hold only when $\lambda$ belongs to some interval. Solving (1.4) with respect to $\lambda =: r(u)$, we obtain the following functional $r(u)=\frac{\langle D_uT(u),u\rangle }{\langle D_uG(u),u\rangle }$, $u\in W\backslash \{0\}$, which is termed as the nonlinear generalized Rayleigh quotient. Note that u belongs to $N_\lambda$ if and only if it lies on the level set $r(u)=\lambda$. Using this fact, we compute the following main identity $\langle D_ur(u),u\rangle =\frac{ D_{uu}\Phi _\lambda (u)(u,u)}{\langle D_uG(u),u\rangle }$, $\forall \ u\in N_\lambda$, which means, in particular, that the sufficient condition holds if and only if $\langle D_ur(u),u\rangle \ne 0$. Notice that $\langle D_ur(u),u\rangle = \dfrac{\partial r(tu)}{\partial t} \Big |_{t=1}$. These reasonings lead us to the main idea: The extreme values of the Nehari manifold method can be found by means of studying the critical values of the fibered nonlinear generalized Rayleigh quotient r(tu), $t\in {\mathbb {R}}^+$, $u\in W\backslash \{0\}$. It is worthy pointing out that the extremal values are not the first time to be mentioned and can be found, for example, in [26].

The main purpose of this paper is to extend the main results in [30] to p-Kirchhoff elliptic problem (1.1). To be a little more precise, we study the existence and multiplicity of weak solutions to (1.1) by using the Nehari manifold ( [24, 25])), the fibering maps ( [27]) and the mountain pass lemma. We discuss how the Nehari manifold changes as $\lambda$ changes and show the relationship between the existence results for positive solutions of the problem and the properties of the Nehari manifold. For this, the nonlinear generalized Rayleigh quotient, a different one from that used in [30], is introduced to characterize two extremal parameters $\lambda _0^*<\lambda ^*$. The parameter $\lambda _0^*$ is characterized for which the solution has nonnegative energy for the local minimum when $\lambda \ge \lambda _0^*$. The parameter $\lambda ^*$ is characterized for which problem (1.1) admits no nontrivial solution when $\lambda >\lambda ^*$, and the maximal interval for problem (1.1) to have positive solutions is $\lambda \in (0,\lambda ^*]$. When $\lambda \in (0,\lambda ^*]$, by using standard minimization techniques, one can easily minimize the energy functional associated with (1.1) over the Nehari manifold, and a local minimizer $u_\lambda >0$ follows immediately. Furthermore, if $\lambda \in (0,\lambda _0^*)$, then $I_\lambda (u_\lambda )<0$, while $I_{\lambda _0^*}(u_{\lambda _0^*})=0$ and if $\lambda \in (\lambda _0^*,\lambda ^*]$, then $I_\lambda (u_\lambda )>0$. To find the second solution, the same approach no longer applies. So we use the first local minimal solution $u_\lambda$ to construct the geometric structure of the mountain pass. Then, we can conclude that problem (1.1) admits a mountain pass-type solution when $\lambda \in (0,\lambda _0^*+\varepsilon )$ for some $\varepsilon >0$. Moreover, we also study the asymptotic behavior of the solutions when $\lambda \downarrow 0$.

The rest of this paper is organized as follows. In Sect. 2, we give some notations and definitions and introduce some necessary lemmas. The main results of this paper are also stated in this section. In Sect. 3, we give the detailed proof of the main results. In Sect. 4, we make a conclusion.

2 Preliminaries

In order to state our main results precisely, we first introduce some notations and definitions and give some basic properties. Throughout this paper, we denote by $\Vert \cdot \Vert _{p}$ the $L^p(\Omega )$ norm for $1\le p\le \infty$. The Sobolev space $W_{0}^{1,p}(\Omega )$ will be equipped with the norm $\Vert u\Vert :=\Vert u\Vert _{W_{0}^{1,p}(\Omega )}=\Vert \nabla u\Vert _p$, which is equivalent to the full one due to Poincaré’s inequality. $W^{-1,p'}(\Omega )$ is its dual space, where $\frac{1}{p}+\frac{1}{p'}=1$. We use $\rightarrow$ and $\rightharpoonup$ to denote the strong and weak convergence in Banach space, respectively. For any $r\in (1,p^*]$, we use $S_r>0$ to denote the embedding constant from $W_{0}^{1,p}(\Omega )$ to $L^r(\Omega )$, i.e.,

$$\begin{aligned} \Vert u\Vert _r\le S_r\Vert u\Vert ,\quad \forall \ u\in W_{0}^{1,p}(\Omega ). \end{aligned}$$

In this paper, we consider weak solutions to problem (1.1) in the following sense.

Definition 2.1

$\mathbf (Weak \ solution)$ A function $u\in W_{0}^{1,p}(\Omega )$ is called a weak solution to problem (1.1), if for every $\varphi \in W_{0}^{1,p}(\Omega )$, it holds that

$$\begin{aligned} M\Big (\int _{\Omega }|\nabla u|^p\mathrm {d}x\Big )\int _{\Omega }|\nabla u|^{p-2}\nabla u\nabla \varphi \mathrm {d}x-\int _{\Omega }| u|^{q-2}u\varphi \mathrm {d}x=0. \end{aligned}$$

(2.1)

We define the energy functional associated with problem (1.1) by

$$\begin{aligned} I_{\lambda }(u)=\frac{a}{p}\Vert u\Vert ^p+\frac{\lambda }{p^2}\Vert u\Vert ^{p^2}-\frac{1}{q}\Vert u\Vert _q^q,\ \forall \ u\in W_{0}^{1,p}(\Omega ). \end{aligned}$$

(2.2)

Since $1<q<p^*$, it can be directly verified that $I_\lambda (u)$ is a $C^1$ functional in $W_{0}^{1,p}(\Omega )$. Noticing that $I_\lambda (u)=I_\lambda (|u|)$, we may assume that $u\ge 0$ in the sequel.

For each $\lambda >0$ and $u\in W_{0}^{1,p}(\Omega )\setminus \{0\}$, define the fibering maps $\phi _{\lambda ,u}(t)$: $(0,+\infty )\rightarrow {\mathbb {R}}$ by

$$\begin{aligned} \phi _{\lambda ,u}(t)=I_{\lambda }(tu). \end{aligned}$$

So for each $\lambda >0$, consider the Nehari set

$$\begin{aligned} \begin{aligned} N_{\lambda }&=\{u\in W_{0}^{1,p}(\Omega )\backslash \{0\}: \langle I_{\lambda }'(u),u\rangle =0 \} \\&=\{u\in W_{0}^{1,p}(\Omega )\backslash \{0\}: \phi _{\lambda ,u}'(1)=0 \}. \end{aligned} \end{aligned}$$

Here $\langle \ ,\ \rangle$ denotes the pairing between $W^{-1,p}(\Omega )$ and $W_0^{1,p}(\Omega )$. We split $N_{\lambda }$ into three parts:

$$\begin{aligned} \begin{aligned} N_{\lambda }^{+}&=\{u\in N_{\lambda }: \phi _{\lambda ,u}''(1)>0\},\\ N_{\lambda }^{-}&=\{u\in N_{\lambda }: \phi _{\lambda ,u}''(1)<0\},\\ N_{\lambda }^{0}&=\{u\in N_{\lambda }: \phi _{\lambda ,u}''(1)=0\}, \end{aligned} \end{aligned}$$

which corresponds to local minima, local maxima and points of inflexion of the fibering maps, respectively.

We then present the following two lemmas. The first one shows that the critical points of the energy functional $I_{\lambda }$ on the Nehari manifold $N_{\lambda }$ are “usually” (if they are not in $N_{\lambda }^{0}$) the weak solutions to problem (1.1). The second one describes some basic properties of $I_{\lambda }$ and $N_{\lambda }$.

Lemma 2.1

If $u\in N_{\lambda }^{+}\cup N_{\lambda }^{-}$ is a critical point of $I_{\lambda }\Big |_{N_{\lambda }^{+}\cup N_{\lambda }^{-}}$, then u is a critical point of $I_{\lambda }$ in $W_{0}^{1,p}(\Omega )$ and hence a solution to problem (1.1).

Proof

Similar proof can be found in [3]. $\square$

Lemma 2.2

There holds

(i) $I_\lambda (u)$ is weakly lower semi-continuous in $W_{0}^{1,p}(\Omega )$.

(ii) If $1<p<q<p^2$ or $1<q<p<p^2$, then $I_\lambda (u)$ is coercive in $W_{0}^{1,p}(\Omega )$. If $1<p<p^2<q$, $I_\lambda (u)$ is not coercive in $W_{0}^{1,p}(\Omega )$, but it is coercive on $N_{\lambda }$.

(iii) $N_\lambda$ is a closed set.

Proof

(i), (iii) and the first part of (ii) are obvious. If $1<p<p^2<q$, $u\in N_{\lambda }$, we have

$$\begin{aligned} a\Vert u\Vert ^p+\lambda \Vert u\Vert ^{p^2}-\Vert u\Vert _q^{q}=0, \end{aligned}$$

which implies that

$$\begin{aligned} \begin{aligned} I_{\lambda }(u)&=\frac{a}{p}\Vert u\Vert ^p+\frac{\lambda }{p^2}\Vert u\Vert ^{p^2}-\frac{1}{q}\Vert u\Vert _q^{q}\\&=\left( \frac{1}{p}-\frac{1}{q}\right) a\Vert u\Vert ^p+\left( \frac{1}{p^2}-\frac{1}{q}\right) \lambda \Vert u\Vert ^{p^2}\\&=\Vert u\Vert ^p\left[ \left( \frac{1}{p}-\frac{1}{q}\right) a+\left( \frac{1}{p^2}-\frac{1}{q}\right) \lambda \Vert u\Vert ^{p^2-p}\right] . \end{aligned} \end{aligned}$$

Therefore, $I_\lambda (u)$ is coercive on $N_{\lambda }$. The proof is complete. $\square$

Next, we state the mountain pass lemma which helps us to obtain the second solution.

Lemma 2.3

$\mathbf (Mountain \ Pass\ Lemma)$ Assume that X is a Banach space, $I:X\rightarrow {\mathbb {R}}$ is a $C^1$ functional satisfying the $(PS)_c$ condition, c is a real number, and there exist $R>0$ and $d>0$ such that

(i) $I(u)\ge R>0$ if $\Vert u\Vert =d$;

(ii) There exists a ${\overline{u}}\in X$ such that $\Vert {\overline{u}}\Vert >d$ and $I({\overline{u}})<R$.

Let

$$\begin{aligned} c=\inf _{\gamma \in \Gamma }\max _{t\in [0,1]}I(\gamma (t)), \end{aligned}$$

and

$$\begin{aligned} \Gamma =\{\gamma \in C([0,1],X): \gamma (0)=0, \gamma (1)={\overline{u}}\}, \end{aligned}$$

then there exists a $u\in X$, $\Vert u\Vert >d$, such that $I(u)=c\ge R>0$ and $I'(u)=0$.

We end this section with the main results of this paper which can be summarized in the following theorems.

Theorem 2.1

Suppose that $1<p<q<p^2$. Then, there exist parameters $0<\lambda _0^*<\lambda ^*$ and a positive constant $\varepsilon$ such that

(1) For each $\lambda \in (0,\lambda ^*]$, problem (1.1) has a positive solution $u_\lambda$ which is a global minimizer for $I_\lambda$ for $\lambda \in (0,\lambda _0^*]$, while $u_\lambda$ is a local minimizer for $I_\lambda$ when $\lambda \in (0,\lambda ^*]$. Moreover, $I''_\lambda (u_\lambda )(u_\lambda ,u_\lambda )>0$ for $\lambda \in (0,\lambda ^*)$ and $I''_{\lambda ^*}(u_{\lambda ^*})(u_{\lambda ^*},u_{\lambda ^*})=0$.

(2) For each $\lambda \in (0,\lambda _0^*+\varepsilon )$, problem (1.1) has a positive solution $w_\lambda$ which is a mountain pass-type critical point for $I_\lambda$.

(3) If $\lambda \in (0,\lambda _0^*)$, then $I_\lambda (u_\lambda )<0$, while $I_{\lambda _0^*}(u_{\lambda _0^*})=0$ and if $\lambda \in (\lambda _0^*,\lambda ^*]$, then $I_\lambda (u_\lambda )>0$.

(4) $I_\lambda (w_\lambda )>0$, $I_\lambda (w_\lambda )>I_\lambda (u_\lambda )$ for each $\lambda \in (0,\lambda _0^*+\varepsilon )$.

(5) If $\lambda >\lambda ^*$, then the only solution $u\in W_0^{1,p}(\Omega )$ to problem (1.1) is $u = 0$.

Theorem 2.2

Suppose that $1<p<q<p^2$. Then, $I_\lambda (u_\lambda )\rightarrow -\infty$ and $\Vert u_\lambda \Vert \rightarrow \infty$ as $\lambda \downarrow 0$.

Theorem 2.3

Suppose that $1<p<p^2<q$. Then, for any $\lambda >0$, there exists a mountain pass-type solution $w_\lambda \in W_0^{1,p}(\Omega )\backslash \{0\}$ such that $I_\lambda (w_\lambda )>0$.

Theorem 2.4

Suppose that $1<q<p<p^2$. Then, for any $\lambda >0$, $I_\lambda$ has a global minimizer $u_\lambda$ with $I_\lambda (u_\lambda )<0$.

3 Proofs of the Main Results

Since the geometric properties of the fibering map $\phi _{\lambda ,u}(t)$ differ when q belongs to different intervals, we shall divide it into three cases to consider the existence and multiplicity of weak solutions to problem (1.1).

3.1 $The \ Case \ 1<p<q<p^2$.

The structure of the Nehari manifold $N_\lambda$ is closely related to the graph of the fibering maps. Therefore, we first describe some fundamental properties of the fibering maps.

Proposition 3.1

For each $\lambda >0$ and $u\in W_{0}^{1,p}(\Omega )\backslash \{0\}$, there are only three possibilities for the graph of $\phi _{\lambda ,u}(t)$

(i) The function $\phi _{\lambda ,u}(t)$ has two critical points, namely $0<t_{\lambda }^{-}(u)<t_{\lambda }^{+}(u)$. Moreover, $t_{\lambda }^{-}(u)$ is a local maximum with $\phi _{\lambda ,u}''(t_{\lambda }^{-}(u))<0$ and $t_{\lambda }^{+}(u)$ is a local minimum with $\phi _{\lambda ,u}''(t_{\lambda }^{+}(u))>0$;

(ii) The function $\phi _{\lambda ,u}(t)$ has only one critical point at $t=t_{\lambda }(u)$. Moreover, $\phi _{\lambda ,u}''(t_{\lambda }(u))=0$ and $\phi _{\lambda ,u}(t)$ is increasing;

(iii) The function $\phi _{\lambda ,u}(t)$ is increasing and has no critical point.

Proof

For any fixed $u\in W_{0}^{1,p}(\Omega )\backslash \{0\}$, we have

$$\begin{aligned} \phi _{\lambda ,u}'(t)=t^{p-1}\big (a\Vert u\Vert ^p+\lambda t^{p^2-p}\Vert u\Vert ^{p^2}-t^{q-p}\Vert u\Vert _q^{q}\big ) :=t^{p-1}g(t), \quad t>0. \end{aligned}$$

(3.1)

Direct computation shows that

$$\begin{aligned} \begin{aligned} g'(t)=t^{q-p-1}\big ((p^2-p)\lambda t^{p^2-q}\Vert u\Vert ^{p^2}-(q-p)\Vert u\Vert _q^q\big ),\\ \end{aligned} \end{aligned}$$

which implies that there exists a unique $T_0(u)>0$ such that $g'(T_0(u))=0$. Moreover, $g'(t)<0$ for $t\in (0,T_0(u))$ and $g'(t)>0$ for $t\in (T_0(u),\infty )$, which means that g(t) is decreasing on $(0,T_0(u))$, increasing on $(T_0(u),\infty )$, and achieves its minimum at $T_0(u)$. Since $g(0)>0$ and $g(t)\rightarrow +\infty$ as $t\rightarrow +\infty$, the discussion of the graph of $\phi _{\lambda ,u}(t)$ will be divided into three cases, depending on the sign of $g(T_0(u))$.

(i) If $g(T_0(u))<0$, then $g(t)=0$ has two roots $0<t_{\lambda }^{-}(u)<t_{\lambda }^{+}(u)$, which means that $\phi '_{\lambda ,u}(t_{\lambda }^{-}(u))=\phi '_{\lambda ,u}(t_{\lambda }^{+}(u))=0$, by (3.1). When $t\in (0,t_{\lambda }^{-}(u))\cup (t_{\lambda }^{+}(u),\infty )$, $\phi '_{\lambda ,u}(t)>0$ and $\phi _{\lambda ,u}(t)$ is increasing on $(0,t_\lambda ^-(u))\cup (t_\lambda ^+(u),\infty )$; when $t\in (t_\lambda ^-(u),t_\lambda ^+(u))$, $\phi '_{\lambda ,u}(t)<0$ and $\phi _{\lambda ,u}(t)$ is decreasing on $(t_\lambda ^-(u),t_\lambda ^+(u))$. Moreover, $t_{\lambda }^{-}(u)$ is a local maximum with $\phi _{\lambda ,u}''(t_{\lambda }^{-}(u))<0$ and $t_{\lambda }^{+}(u)$ is a local minimum with $\phi _{\lambda ,u}''(t_{\lambda }^{+}(u))>0$.

(ii) If $g(T_0(u))=0$, then $g(t)\ge 0$ and $g(t)=0$ has only one root $t_{\lambda }(u)=T_0(u)>0$, which means that $\phi '_{\lambda ,u}(t_{\lambda }(u))=0$. Therefore, $\phi _{\lambda ,u}'(t)\ge 0$ and $\phi _{\lambda ,u}(t)$ is increasing on $(0,\infty )$. Moreover, from (3.1) it follows that $\phi ''_{\lambda ,u}(t_{\lambda }(u))=0$.

(iii) If $g(T_0(u))>0$, then g(t) is positive for all $t>0$ and so is $\phi _{\lambda ,u}'(t)$. Hence, $\phi _{\lambda ,u}(t)$ is increasing and has no critical point. The proof is complete. $\square$

Next, let us explore how the structure of the fibering map $\phi _{\lambda ,u}(t)$ changes with respect to the parameter $\lambda$, by considering the monotonicity and the extreme values of $\phi _{\lambda ,u}(t)$.

Firstly, similarly to [4], we introduce the nonlinear generalized Rayleigh quotients R(u), $R_0(u)$ : $W_{0}^{1,p}\backslash \{0\}\rightarrow {\mathbb {R}}$ by

$$\begin{aligned} R(u)= & {} \frac{1}{\Vert u\Vert ^{p^2}}\Big (\Vert u\Vert _q^{q}-a\Vert u\Vert ^{p}\Big ),\\ R_0(u)= & {} \frac{p^2}{\Vert u\Vert ^{p^2}}\Big (\frac{1}{q}\Vert u\Vert _q^{q}-\frac{a}{p}\Vert u\Vert ^{p}\Big ). \end{aligned}$$

As a consequence, for each $u\in W_{0}^{1,p}\backslash \{0\}$, we have

(i) $R(u)=\lambda$ if, and only if, $\langle I_\lambda '(u), u\rangle =0$;

(ii) $R_0(u)=\lambda$ if, and only if, $I_\lambda (u)=0$.

Secondly, we consider the corresponding fibering Rayleigh quotients

$$\begin{aligned} r(t)\triangleq R(tu)= & {} \frac{1}{\Vert u\Vert ^{p^2}}\left( t^{q-p^2}\Vert u\Vert _q^{q}-at^{p-p^2}\Vert u\Vert ^{p}\right) , \end{aligned}$$

(3.2)

$$\begin{aligned} r_0(t)\triangleq R_0(tu)= & {} \frac{p^2}{\Vert u\Vert ^{p^2}}\left( \frac{1}{q}t^{q-p^2}\Vert u\Vert _q^{q}-\frac{a}{p}t^{p-p^2}\Vert u\Vert ^{p}\right) . \end{aligned}$$

(3.3)

Fix $u\in W_0^{1,p}(\Omega )\backslash \{0\}$. By simple analysis, we see that $r(t)\rightarrow -\infty$ as $t\rightarrow 0$, $r(t)\rightarrow 0^+$ as $t\rightarrow +\infty$ and there exists a unique $t(u)>0$ such that r(t) is increasing for $t\in (0,t(u))$, decreasing for $t\in (t(u),\infty )$, and r(t) achieves its maximum at t(u), where $t(u)=\Big (\frac{(p^2-p)a\Vert u\Vert ^{p}}{(p^2-q)\Vert u\Vert _q^{q}}\Big )^{\frac{1}{q-p}}$. Thus, we obtain the following nonlinear generalized Rayleigh $\lambda$-quotient:

$$\begin{aligned} \lambda (u)\triangleq r_{\mathrm{max}}=r(t(u))=C_{a,p,q}\left( \frac{\Vert u\Vert _{q}}{\Vert u\Vert }\right) ^{q\frac{p^2-p}{q-p}}, \end{aligned}$$

(3.4)

where

$$\begin{aligned} C_{a,p,q}=a\left( \frac{q-p}{p^2-q}\right) \left( a\frac{p^2-p}{p^2-q}\right) ^{\frac{p-p^2}{q-p}}. \end{aligned}$$

Similarly, the function $r_0(t)$ achieves its global maximum at $t_0(u)= \Big (aq\frac{p-1}{p^2-q}\frac{\Vert u\Vert ^p}{\Vert u\Vert _{q}^q}\Big )^{\frac{1}{q-p}}$, and the corresponding nonlinear generalized Rayleigh $\lambda$-quotient is given by

$$\begin{aligned} \lambda _0(u)\triangleq r_{0\mathrm{max}}=r_0(t_0(u))= C_{0,a,p,q}\lambda (u), \end{aligned}$$

(3.5)

where

$$\begin{aligned} C_{0,a,p,q}=p\left( \frac{p}{q}\right) ^{\frac{p^2-p}{q-p}}<1. \end{aligned}$$

Obviously, $0<\lambda _0(u)<\lambda (u)$ for any $u\in W_0^{1,p}(\Omega )\backslash \{0\}$.

Let us now reveal the relationship between the fibering map $\phi _{\lambda ,u}(t)$ and the corresponding fibering Rayleigh quotients. Since

$$\begin{aligned} \phi _{\lambda ,u}'(t)=t^{p-1}\big (a\Vert u\Vert ^p+\lambda t^{p^2-p}\Vert u\Vert ^{p^2}-t^{q-p}\Vert u\Vert _q^{q}\big ) :=t^{p-1}g(t), \end{aligned}$$

$\phi _{\lambda ,u}'(t)=0$ is equivalent to $g(t)=0$. From (3.2), one sees that the necessary and sufficient condition for $g(t)=0$ to have a solution is $\lambda =r(t)$. Similarly, let $h(t)=\frac{a}{p}\Vert u\Vert ^p+\frac{\lambda }{p^2} t^{p^2-p}\Vert u\Vert ^{p^2}-\frac{1}{q}t^{q-p}\Vert u\Vert _q^{q}$, then $\phi _{\lambda ,u}(t)=t^{p}h(t)$. Therefore, $\phi _{\lambda ,u}(t)=0$ is equivalent to $h(t)=0$, and the necessary and sufficient condition for $h(t)=0$ to have a solution is $\lambda =r_0(t)$. In conclusion, $\lambda (u)$ is the unique parameter $\lambda >0$ for which the fibering map $\phi _{\lambda ,u}$ has a critical point with second derivative zero at t(u). $\lambda _{0}(u)$ is the unique parameter $\lambda >0$ for which the fibering map $\phi _{\lambda ,u}$ has a critical point with zero energy at $t_{0}(u)$.

According to what has been mentioned above, the following geometrical interpretation for the functionals $\lambda (u)$ and $\lambda _0(u)$ can be given.

Proposition 3.2

Fix $u\in W_{0}^{1,p}(\Omega )\backslash \{0\}$. Let $\lambda (u)$ and $\lambda _0(u)$ be given in (3.4) and (3.5), respectively. Then,

(i) If $0<\lambda <\lambda (u)$, then the graph of $\phi _{\lambda ,u}$ satisfies (i) of Proposition 3.1. Moreover, if $0<\lambda <\lambda _{0}(u)$, then $\inf _{t>0}\phi _{\lambda ,u}(t)=\phi _{\lambda ,u}(t_{\lambda }^{+}(u)) <0$; if $\lambda =\lambda _{0}(u)$, then $\inf _{t>0}\phi _{\lambda ,u}(t)=\phi _{\lambda ,u}(t_{\lambda }^{+}(u)) =0$; if $\lambda >\lambda _{0}(u)$, then $\phi _{\lambda ,u}(t_{\lambda }^{+}(u)) >0$ and $\inf _{t>0}\phi _{\lambda ,u}(t)=\phi _{\lambda ,u}(0) =0$.

(ii) If $\lambda =\lambda (u)$, then the graph of $\phi _{\lambda ,u}$ satisfies (ii) of Proposition 3.1.

(iii) If $\lambda >\lambda (u)$, then the graph of $\phi _{\lambda ,u}$ satisfies (iii) of Proposition 3.1.

Proof

(i) When $0<\lambda <\lambda (u)$, the line $y=\lambda$ and the graph of r(t) has two points of intersection $0<t_\lambda ^-<t_\lambda ^+$. For $t\in (0,t_\lambda ^-)\cup (t_\lambda ^+,\infty )$, we have $\lambda >r(t)$, so $\phi '_{\lambda ,u}(t)>0$ and $\phi _{\lambda ,u}(t)$ is increasing on $(0,t_\lambda ^-)\cup (t_\lambda ^+,\infty )$; for $t\in (t_\lambda ^-,t_\lambda ^+)$, we have $\lambda <r(t)$, so $\phi '_{\lambda ,u}(t)<0$ and $\phi _{\lambda ,u}(t)$ is decreasing on $(t_\lambda ^-,t_\lambda ^+)$.

Moreover, when $\lambda \in (0,\lambda _0(u))$, there exists a $t'>0$ such that $\lambda <r_0(t')$, i.e., $\phi _{\lambda ,u}(t')<0$, which implies that $\inf _{t>0}\phi _{\lambda ,u}(t)=\phi _{\lambda ,u}(t_{\lambda }^{+}) <0$. When $\lambda =\lambda _0(u)$, we have $\lambda \ge r_0(t)$, $\forall \ t>0$. Therefore, $\inf _{t>0}\phi _{\lambda ,u}(t)=\phi _{\lambda ,u}(t_{\lambda }^{+})=0$. When $\lambda \in (\lambda _0(u),\infty )$, we have $\lambda >r_0(t)$, which means that $\phi _{\lambda ,u}(t)>0$, $\forall \ t>0$. So we have $\inf _{t>0}\phi _{\lambda ,u}(t)=\phi _{\lambda ,u}(0)=0$.

(ii) When $\lambda =\lambda (u)$, the line $y=\lambda$ and the graph of r(t) has one point of intersection $t_\lambda >0$, which means that $\phi '_{\lambda ,u}(t_\lambda )=0$. Moreover, for any $t\ne t_\lambda$, one has $\phi '_{\lambda ,u}(t)>0$ and $\phi _{\lambda ,u}(t)$ is increasing on $(0,\infty )$. Therefore, the graph of $\phi _{\lambda ,u}$ satisfies (ii) of Proposition 3.1.

(iii) When $\lambda >\lambda (u)$, the line $y=\lambda$ and the graph of r(t) have no point of intersection. Thus, $\lambda >r(t)$ and $\phi _{\lambda ,u}(t)$ is strictly increasing on $(0,\infty )$, i.e., the graph of $\phi _{\lambda ,u}$ satisfies (iii) of Proposition 3.1. The proof is complete. $\square$

Then, we give the definition of the nonlinear generalized Rayleigh $\lambda$-extremal values

$$\begin{aligned} \lambda ^*= & {} \sup _{u\in W_{0}^{1,p}(\Omega )\backslash \{0\}}\lambda (u)=\sup _{u\in W_{0}^{1,p}(\Omega )\backslash \{0\}}\sup _{t>0}r(t), \end{aligned}$$

(3.6)

$$\begin{aligned} \lambda _{0}^*= & {} \sup _{u\in W_{0}^{1,p}(\Omega )\backslash \{0\}}\lambda _{0}(u)=\sup _{u\in W_{0}^{1,p}(\Omega )\backslash \{0\}}\sup _{t>0}r_0(t), \end{aligned}$$

(3.7)

the main properties of which are summarized in the following propositions.

Proposition 3.3

There holds $\lambda _{0}^*<\lambda ^*<\infty$. Moreover, there exists a $u\in W_{0}^{1,p}(\Omega )\backslash \{0\}$ such that $\lambda (u)=\lambda ^*$ and $\lambda _{0}(u)=\lambda _{0}^*$, i.e., both $\lambda _{0}^*$ and $\lambda ^*$ are attained.

Proof

Indeed, from (3.4), (3.5) and the Sobolev embedding, we have $0<\lambda _{0}^*,\ \lambda ^*<\infty$. Obviously, $\lambda (u)$ is 0-homogeneous, that is $\lambda (tu) = \lambda (u)$ for each $t>0$. Without loss of generality, we may assume that there exists a sequence $\{u_n\}\subset W_{0}^{1,p}(\Omega )\backslash \{0\}$ such that $\Vert u_{n}\Vert =1$ and $\lambda (u_{n})\rightarrow \lambda ^*$ as $n\rightarrow \infty$. From the Sobolev embedding, it follows that there exists a $u\in W_{0}^{1,p}(\Omega )$ such that $u_{n}\rightharpoonup u$ in $W_{0}^{1,p}(\Omega )$, $u_{n}\rightarrow u$ in $L^s(\Omega )$, $1\le s<p^*$, and point-wise a.e. in $\Omega$ as $n\rightarrow \infty$. From (3.4), we know $u\ne 0$. Otherwise, $u_{n}\rightarrow 0$ in $L^s(\Omega )$ as $n\rightarrow \infty$. Then, $\lambda (u_{n})\rightarrow 0$ as $n\rightarrow \infty$, which is impossible. From the weakly lower semi-continuity,

$$\begin{aligned} \lambda ^*=\limsup _{n\rightarrow \infty }\lambda (u_{n})&=C_{a,p,q}\limsup _{n\rightarrow \infty }\Big (\frac{\Vert u_n\Vert _{q}}{\Vert u_n\Vert }\Big )^{\frac{pq(p-1)}{q-p}} \\&\quad \le C_{a,p,q}\frac{\limsup \limits _{n\rightarrow \infty }\Vert u_{n}\Vert _{q}^{\frac{pq(p-1)}{q-p}}}{\liminf \limits _{n\rightarrow \infty }\Vert u_{n}\Vert ^{\frac{pq(p-1)}{q-p}}}\le \lambda (u). \end{aligned}$$

From the definition of $\lambda ^*$, we know $\lambda ^*\ge \lambda (u)$. So $\lambda ^*=\lambda (u)$ and $u_{n}\rightarrow u$ in $W_{0}^{1,p}(\Omega )$ as $n\rightarrow \infty$. Since $\lambda _{0}(u)=C_{0,a,p,q}\lambda (u)$ and $C_{0,a,p,q}<1$, it follows that $\lambda _{0}^*=\lambda _{0}(u)$ and $\lambda _{0}^*<\lambda ^*$. The proof is complete. $\square$

As a consequence of Proposition 3.3, we can obtain the following results.

Proposition 3.4

There holds

(i) For each $\lambda \in (0,\lambda ^*)$, $N_{\lambda }^{+}$ and $N_{\lambda }^{-}$ are non-empty. If $\lambda >\lambda ^*$, then $N_{\lambda }=\emptyset$.

(ii) For each $\lambda \in (0,\lambda _{0}^*)$, there exists a $u\in W_{0}^{1,p}(\Omega )\backslash \{0\}$ such that $I_{\lambda }(u)<0$. If $\lambda \ge \lambda _{0}^*$, then $\inf _{t>0}\phi _{\lambda ,u}(t)=0$ for each $u\in W_{0}^{1,p}(\Omega )\backslash \{0\}$.

Proof

(i) From Propositions 3.3 and 3.2, we know there exists a $u\in W_{0}^{1,p}(\Omega )\backslash \{0\}$ such that $\lambda ^*=\lambda (u)$ and $\phi _{\lambda ,u}$ satisfies (i) of Proposition 3.1 for each $\lambda \in (0,\lambda ^*)$. So $t_{\lambda }^-(u)u\in N_{\lambda }^-$ and $t_{\lambda }^+(u)u\in N_{\lambda }^+$, which implies that $N_{\lambda }^{+}$ and $N_{\lambda }^{-}$ are non-empty. Suppose that $\lambda >\lambda ^*$, we have $\lambda >\lambda ^*\ge \lambda (u)$ for any $u\in W_{0}^{1,p}(\Omega )\backslash \{0\}$. So $\phi _{\lambda ,u}$ satisfies (iii) of Proposition 3.1, and hence $N_{\lambda }=\emptyset$.

(ii) From Proposition 3.3, there exists a $u\in W_{0}^{1,p}(\Omega )\backslash \{0\}$ such that $\lambda _{0}^*=\lambda _{0}(u)$. Therefore, we know from (i) of Proposition 3.2 that there exists a $t>0$ such that $I_{\lambda }(tu)<0$ for each $\lambda \in (0,\lambda _{0}^*)$. When $\lambda \ge \lambda _{0}^*$, one has $\lambda \ge \lambda _{0}^*\ge \lambda _{0}(u)$ for any $u\in W_{0}^{1,p}(\Omega )\backslash \{0\}$. So from Proposition 3.2, we have $\inf _{t>0}\phi _{\lambda ,u}(t)=0$. The proof is complete. $\square$

From the definition of $\lambda ^*$, the following conclusion can be drawn directly.

Corollary 3.1

For each $\lambda >\lambda ^*$, $I_{\lambda }$ does not have any critical points other than $u=0$.

Proposition 3.5

For each $\lambda \in (0,\lambda ^*]$, there exists an $r>0$ which does not depend on $\lambda$ such that $\Vert u\Vert \ge r$ for any $u\in N_{\lambda }$.

Proof

When $u\in N_{\lambda }$, from Sobolev embedding, we obtain

$$\begin{aligned} \begin{aligned} 0&=a\Vert u\Vert ^p+\lambda \Vert u\Vert ^{p^2}-\Vert u\Vert _{q}^q\ge a\Vert u\Vert ^p+\lambda \Vert u\Vert ^{p^2}-S_q^q\Vert u\Vert ^q\\&\ge a\Vert u\Vert ^p-S_q^q\Vert u\Vert ^q=\Vert u\Vert ^p(a-S_q^q\Vert u\Vert ^{q-p}). \end{aligned} \end{aligned}$$

Hence, $a-S_q^q\Vert u\Vert ^{q-p}\le 0$. So there exists an $r>0$ such that $\Vert u\Vert \ge r$. This ends the proof. $\square$

To show that the local minimizer of the functional $I_{\lambda }$ is a solution to problem (1.1), the following energy estimate is needed.

Proposition 3.6

For each $\lambda \in (0,\lambda ^*]$, there holds

$$\begin{aligned} I_{\lambda }(u)=\frac{(q-p)^2(p-1)}{p^2q(p^2-q)}\frac{a^2}{\lambda },\ \forall \ u\in N_{\lambda }^0. \end{aligned}$$

Proof

If $u\in N_{\lambda }^0$, then

$$\begin{aligned} \ \ \ \ \ \ \ \ \ \ \ \ {\left\{ \begin{array}{ll} \phi _{\lambda ,u}'(1)=a\Vert u\Vert ^p+\lambda \Vert u\Vert ^{p^2}-\Vert u\Vert _{q}^q=0,\\ \phi _{\lambda ,u}''(1)=(p-1)a\Vert u\Vert ^p+(p^2-1)\lambda \Vert u\Vert ^{p^2}-(q-1)\Vert u\Vert _{q}^q=0, \end{array}\right. } \end{aligned}$$

from which it follows that

$$\begin{aligned} \Vert u\Vert =\Big [\frac{(q-p)a}{(p^2-q)\lambda }\Big ]^\frac{1}{p}. \end{aligned}$$

(3.8)

Substituting (3.8) into $I_{\lambda }(u)$, we have

$$\begin{aligned} \begin{aligned} I_{\lambda }(u)&=\frac{a}{p}\Vert u\Vert +\frac{\lambda }{p^2}\Vert u\Vert ^{p}-\frac{1}{q}\Vert u\Vert _q^{q}\\&=\frac{(q-p)^2(p-1)}{p^2q(p^2-q)}\frac{a^2}{\lambda }. \end{aligned} \end{aligned}$$

The proof is complete. $\square$

We give some variational properties related to $\phi _{\lambda ,u}(t)$.

Lemma 3.1

For each $\lambda \in (0,\lambda ^*)$, there holds

(i) Suppose that $\{u_{n}\}\subset W_0^{1,p}(\Omega )$ is a Palais–Smale sequence at the level c for $I_{\lambda }$, where c is a real number, that is $I_{\lambda }(u_{n})\rightarrow c$ in ${\mathbb {R}}$ and $I'_{\lambda }(u_{n})\rightarrow 0$ in $W^{-1,p'}(\Omega )$, as $n\rightarrow \infty$. Then, there exists a $u\in W_0^{1,p}(\Omega )$ such that $u_{n}\rightarrow u$ in $W_0^{1,p}(\Omega )$, as $n\rightarrow \infty$.

(ii) There exist $M>0$ and $\rho >0$ such that when $\Vert u\Vert =\rho$,

$$\begin{aligned} I_{\lambda }(u)\ge M, \ and \lim _{M\rightarrow 0}\rho =0. \end{aligned}$$

Proof

(i) From (ii) of Lemma 2.2, we see that $\{u_{n}\}$ is bounded in $W_{0}^{1,p}(\Omega )$. Therefore, there exists a subsequence, still denoted by $\{u_{n}\}$, such that $u_{n}\rightharpoonup u$ in $W_{0}^{1,p}(\Omega )$, $u_{n}\rightarrow u$ in $L^s(\Omega )$, $1\le s<p^*$, and point-wise a.e. in $\Omega$ as $n\rightarrow \infty$. Since $\lim \limits _{n\rightarrow \infty }I'_{\lambda }(u_{n})=0$, it holds, $\forall \ \varphi \in W_{0}^{1,p}(\Omega )$ that

$$\begin{aligned} \begin{aligned} 0=&\lim _{n\rightarrow \infty }\langle I'_{\lambda }(u_{n}), \varphi \rangle \\ =&\lim _{n\rightarrow \infty }\Big [(a+\lambda \Vert u_{n}\Vert ^{p^2-p})\int _{\Omega }|\nabla u_{n}|^{p-2}\nabla u_{n}\nabla \varphi \mathrm {d}x-\int _{\Omega }| u_{n}|^{q-2}u_{n}\varphi \mathrm {d}x\Big ]. \end{aligned} \end{aligned}$$

Take $\varphi =u_{n}-u$, from Hölder’s inequality, we conclude that

$$\begin{aligned} |\int _{\Omega }| u_{n}|^{q-2}u_{n}(u_{n}-u)\mathrm {d}x|\le \Vert u_{n}\Vert _{q}^{q-1}\Vert u_{n}-u\Vert _{q}\rightarrow 0, \ n\rightarrow \infty . \end{aligned}$$

So

$$\begin{aligned} \lim _{n\rightarrow \infty }(a+\lambda \Vert u_{n}\Vert ^{p^2-p})\int _{\Omega }|\nabla u_{n}|^{p-2}\nabla u_{n}\nabla (u_{n}-u)\mathrm {d}x=0, \end{aligned}$$

which guarantees that

$$\begin{aligned} \int _{\Omega }|\nabla u_{n}|^{p-2}\nabla u_{n}\nabla (u_{n}-u)\mathrm {d}x\rightarrow 0,\ as \ n\rightarrow \infty , \end{aligned}$$

(3.9)

since both a and $\lambda$ are positive.

On the other hand, from the weak convergence of $u_n\rightharpoonup u$ in $W_{0}^{1,p}(\Omega )$ as $n\rightarrow \infty$, we conclude that

$$\begin{aligned} \int _{\Omega }|\nabla u|^{p-2}\nabla u\nabla (u_{n}-u)\mathrm {d}x\rightarrow 0,\ as\ n\ \rightarrow \infty . \end{aligned}$$

(3.10)

Combining (3.9) with (3.10) and recalling the following basic inequality in ${\mathbb {R}}^{n}$

$$\begin{aligned}&\big (|\xi |^{p-2}\xi -|\eta |^{p-2}\eta ,\ \xi -\eta \big )\ge C_p|\xi -\eta |^p, \ p\ge 2,\\&\big (|\xi |^{p-2}\xi -|\eta |^{p-2}\eta ,\ \xi -\eta \big )\ge C_p|\xi -\eta |^2\big (|\xi |+|\eta |\big )^{p-2}, \ 1<p< 2, \end{aligned}$$

we get $\nabla u_{n}\rightarrow \nabla u$ in $L^p(\Omega )$ as $n\rightarrow \infty$, i.e., $u_{n}$ converges strongly to u in $W_0^{1,p}(\Omega )$. Here, $C_p$ is a positive constant and $( \ ,\ )$ is the inner product in ${\mathbb {R}}^n$.

(ii) From Sobolev embedding, we have

$$\begin{aligned} \begin{aligned} I_{\lambda }(u)&=\frac{a}{p}\Vert u\Vert ^p+\frac{\lambda }{p^2}\Vert u\Vert ^{p^2}-\frac{1}{q}\Vert u\Vert _q^{q}\ge \frac{a}{p}\Vert u\Vert ^p+\frac{\lambda }{p^2}\Vert u\Vert ^{p^2}-\frac{S_q^q}{q}\Vert u\Vert ^{q}\\&\ge \frac{a}{p}\Vert u\Vert ^p-\frac{S_q^q}{q}\Vert u\Vert ^{q}=\Vert u\Vert ^p\Big (\frac{a}{p}-\frac{S_q^q}{q}\Vert u\Vert ^{q-p}\Big ), \end{aligned} \end{aligned}$$

which implies the results of (ii) directly. The proof is complete. $\square$

In the following, we will prove our main results by a series of lemmas.

Lemma 3.2

For each $\lambda \in (0,\lambda _{0}^*)$, $I_\lambda$ has a global minimizer $u_\lambda \ne 0$, and $I_\lambda (u_\lambda )<0$.

Proof

From Sobolev embedding, we have $\forall \ u\in W_{0}^{1,p}(\Omega )$,

$$\begin{aligned} \begin{aligned} I_{\lambda }(u)&=\frac{a}{p}\Vert u\Vert ^p+\frac{\lambda }{p^2}\Vert u\Vert ^{p^2}-\frac{1}{q}\Vert u\Vert _q^{q}\ge \frac{a}{p}\Vert u\Vert ^p+\frac{\lambda }{p^2}\Vert u\Vert ^{p^2}-\frac{S_q^q}{q}\Vert u\Vert ^{q}\\&\ge \frac{\lambda }{p^2}\Vert u\Vert ^{p^2}-\frac{S_q^q}{q}\Vert u\Vert ^{q}=\Vert u\Vert ^q\Big (\frac{\lambda }{p^2}\Vert u\Vert ^{p^2-q}-\frac{S_q^q}{q}\Big ), \end{aligned} \end{aligned}$$

which implies $I_{\lambda }(u)$ is bounded from below in $W_{0}^{1,p}(\Omega )$, and $\inf \limits _{u\in W_{0}^{1,p}(\Omega )}I_{\lambda }(u)<0$ by (i) of Proposition 3.2. Let $\{u_{n}\}$ be a minimizing sequence of $I_\lambda$ in $W_{0}^{1,p}(\Omega )$, i.e., $I_{\lambda }(u_{n})\rightarrow \inf \limits _{u\in W_{0}^{1,p}(\Omega )}I_{\lambda }(u)$ as $n\rightarrow \infty$. It follows from (ii) of Lemma 2.2 that $\{u_{n}\}$ is bounded in $W_{0}^{1,p}(\Omega )$. Therefore, we can assume that $u_{n}\rightharpoonup u$ in $W_{0}^{1,p}(\Omega )$, $u_{n}\rightarrow u$ in $L^s(\Omega )$, $1\le s<p^*$, and point-wise a.e. in $\Omega$ as $n\rightarrow \infty$. Then, by the weak lower semi-continuity of $I_\lambda$ in $W_{0}^{1,p}(\Omega )$ we conclude that

$$\begin{aligned} I_{\lambda }(u)\le \liminf _{n\rightarrow \infty }I_{\lambda }(u_{n})=\lim _{n\rightarrow \infty }I_{\lambda }(u_{n})=\inf _{u\in W_{0}^{1,p}(\Omega )}I_{\lambda }(u)\le I_{\lambda }(u). \end{aligned}$$

Hence, $I_{\lambda }(u)=\inf \limits _{u\in W_{0}^{1,p}(\Omega )}I_{\lambda }(u)<0$, and $u\ne 0$. Let $u_{\lambda }\equiv u$, then the proof is complete. $\square$

Lemma 3.3

When $\lambda =\lambda _{0}^*$, $I_{\lambda _{0}^*}$ has a global minimizer $u_{\lambda _{0}^*}\ne 0$, and $I_{\lambda _{0}^*}(u_{\lambda _{0}^*})=0$.

Proof

Choose a sequence $\{\lambda _{n}\}\subset (0,\lambda _0^*)$ such that $\lambda _{n}\uparrow \lambda _0^*$, as $n\rightarrow \infty$. For each n take $u_n\equiv u_{\lambda _n}$, where $u_{\lambda _n}$ is given in Lemma 3.2. From $I_{\lambda _{n}}(u_n)<0$ and (ii) of Lemma 2.2, one sees that $\{u_n\}$ is bounded. Therefore, we can assume that $u_{n}\rightharpoonup u$ in $W_{0}^{1,p}(\Omega )$, $u_{n}\rightarrow u$ in $L^s(\Omega )$, $1\le s<p^*$, and point-wise a.e. in $\Omega$, as $n\rightarrow \infty$. So we conclude that

$$\begin{aligned} I_{\lambda _0^*}(u)\le \liminf _{n\rightarrow \infty }I_{\lambda _n}(u_{n})\le 0. \end{aligned}$$

(3.11)

On the other hand, from Proposition 3.4, we know $I_{\lambda _0^*}(u)\ge 0$, which, together with (3.11), implies that $I_{\lambda _0^*}(u)=\lim \limits _{n\rightarrow \infty }I_{\lambda _n}(u_{n})=0$, and $u_n\rightarrow u$ in $W_{0}^{1,p}(\Omega )$ as $n\rightarrow \infty$. Noticing that $u\in N_{\lambda _{0^*}}$, we obtain $u\ne 0$ from Proposition 3.5. Let $u_{\lambda _{0^*}}\equiv u$, then the proof is complete. $\square$

From Proposition 3.3 and the definitions of $\lambda _0(u)$ and $\lambda (u)$, the following remark is obvious.

Remark 3.1

$\lambda _0(u_{\lambda _0^*})=\lambda _0^*$ and $\lambda (u_{\lambda _0^*})=\lambda ^*$.

When $\lambda >\lambda _0^*$, we need the following definition to show the existence of local minimizers. For $\lambda \in (0,\lambda ^*)$, define

$$\begin{aligned} {\widehat{I}}_{\lambda }=\inf _{u\in N_\lambda ^+\bigcup N_\lambda ^0}I_{\lambda }(u). \end{aligned}$$

Remark 3.2

From Lemmas 3.2 and 3.3, we conclude that

$$\begin{aligned} {\widehat{I}}_{\lambda }=\inf _{u\in W_0^{1,p}(\Omega )}I_{\lambda }(u),\ \forall \ \lambda \in (0,\lambda _0^*]. \end{aligned}$$

Before going further, we need some properties of the functions $t_\lambda ^-(u)$ and $t_\lambda ^+(u)$, given in Proposition 3.2.

Proposition 3.7

There holds

(i) The function $(0,\lambda ^*)\ni \lambda \mapsto t_\lambda ^+(u_{\lambda _0^*})$ is continuous and decreasing; the function $(0,\lambda ^*)\ni \lambda \mapsto t_\lambda ^-(u_{\lambda _0^*})$ is continuous and increasing.

(ii) $\lim _{\lambda \uparrow \lambda ^*}t_\lambda ^+(u_{\lambda _0^*}) =\lim _{\lambda \uparrow \lambda ^*}t_\lambda ^-(u_{\lambda _0^*})=t(u_{\lambda _0^*})$.

Proof

(i) It follows from $\lambda <\lambda ^*=\lambda (u_{\lambda _0^*})$ and Proposition 3.2 that the graph of $\phi _{\lambda ,u_{\lambda _0^*}}(t)$ satisfies (i) of Proposition 3.1. Thus, the functions $t_\lambda ^+(u_{\lambda _0^*})$ and $t_\lambda ^-(u_{\lambda _0^*})$ are well defined. Let $t_\lambda ^+\equiv t_\lambda ^+(u_{\lambda _0^*})$, $t_\lambda ^-\equiv t_\lambda ^-(u_{\lambda _0^*})$. One has $\phi '_{\lambda ,u_{\lambda _0^*}}(t_\lambda ^+)=0$ and $\phi ''_{\lambda ,u_{\lambda _0^*}}(t_\lambda ^+)>0$ for each $\lambda \in (0,\lambda ^*)$. From the implicit function theorem, it follows that $(0,\lambda ^*)\ni \lambda \mapsto t_\lambda ^+(u_{\lambda _0^*})$ is $C^1$ and that

$$\begin{aligned} \dfrac{\partial t_\lambda ^+}{\partial \lambda }=-\frac{t_\lambda ^{+(p^2-1)}\Vert u_{\lambda _0^*}\Vert ^{p^2}}{(p-1)at_\lambda ^{+(p-2)}\Vert u_{\lambda _0^*}\Vert ^p+(p^2-1)\lambda t_\lambda ^{+(p^2-2)}\Vert u_{\lambda _0^*}\Vert ^{p^2}-(q-1)t_\lambda ^{+(q-2)}\Vert u_{\lambda _0^*}\Vert _{q}^q}<0. \end{aligned}$$

Therefore, $t_\lambda ^+(u_{\lambda _0^*})$ is decreasing. Similarly, we see that the function $(0,\lambda ^*)\ni \lambda \mapsto t_\lambda ^-(u_{\lambda _0^*})$ is continuous and increasing.

(ii) From the definitions of $t_\lambda ^+(u_{\lambda _0^*})$ and $t_\lambda ^-(u_{\lambda _0^*})$, we have

$$\begin{aligned} \ \ \ \ \ \ \ \ \ \ \ \ {\left\{ \begin{array}{ll} \phi _{\lambda ,u_{\lambda _0^*}}'(t_\lambda ^+)=0,\\ \phi _{\lambda ,u_{\lambda _0^*}}''(t_\lambda ^+)>0, \end{array}\right. } \end{aligned}$$

(3.12)

and

$$\begin{aligned} \ \ \ \ \ \ \ \ \ \ \ \ {\left\{ \begin{array}{ll} \phi _{\lambda ,u_{\lambda _0^*}}'(t_\lambda ^-)=0,\\ \phi _{\lambda ,u_{\lambda _0^*}}''(t_\lambda ^-)<0, \end{array}\right. } \end{aligned}$$

(3.13)

By (i) and $0<t_\lambda ^-<t_\lambda ^+$, we can assume that $t_\lambda ^+\rightarrow t^+$, $t_\lambda ^-\rightarrow t^-$, as $\lambda \uparrow \lambda ^*$, and $0<t^-\le t^+<\infty$. Let $\lambda \uparrow \lambda ^*$ in (3.12) and (3.13), one has

$$\begin{aligned} \ \ \ \ \ \ \ \ \ \ \ \ {\left\{ \begin{array}{ll} \phi _{\lambda ^*,u_{\lambda _0^*}}'(t^+)=0,\\ \phi _{\lambda ^*,u_{\lambda _0^*}}''(t^+)\ge 0, \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} \ \ \ \ \ \ \ \ \ \ \ \ {\left\{ \begin{array}{ll} \phi _{\lambda ^*,u_{\lambda _0^*}}'(t^-)=0,\\ \phi _{\lambda ^*,u_{\lambda _0^*}}''(t^-)\le 0, \end{array}\right. } \end{aligned}$$

We claim that $t^-=t^+$. Otherwise, $t^-<t^+$ and therefore $\phi _{\lambda ^*,u_{\lambda _0^*}}(t)$ have two critical points $t^-$ and $t^+$ . But since $\lambda (u_{\lambda _0^*})=\lambda ^*$, we know $\phi _{\lambda ^*,u_{\lambda _0^*}}(t)$ has only one critical point $t(u_{\lambda _0^*})$, a contradiction. Thus, (ii) is true and the proof is complete. $\square$

Proposition 3.8

For each $\lambda \in (\lambda _0^*,\lambda ^*)$, there holds

$$\begin{aligned} {\widehat{I}}_{\lambda }<\frac{(q-p)^2(p-1)}{p^2q(p^2-q)}\frac{a^2}{\lambda }. \end{aligned}$$

Proof

From Proposition 3.7, we know that $t_\lambda ^-(u_{\lambda _0^*})<t_{\lambda ^*}(u_{\lambda _0^*})<t_\lambda ^+(u_{\lambda _0^*})$ for each $\lambda \in (\lambda _0^*,\lambda ^*)$. This, together with Proposition 3.6, implies

$$\begin{aligned} \begin{aligned} {\widehat{I}}_{\lambda }&\le I_\lambda (t_\lambda ^+(u_{\lambda _0^*})u_{\lambda _0^*})<I_{\lambda }(t_{\lambda ^*}(u_{\lambda _0^*})u_{\lambda _0^*})<I_{\lambda ^*}(t_{\lambda ^*}(u_{\lambda _0^*})u_{\lambda _0^*})\\&=\frac{(q-p)^2(p-1)}{p^2q(p^2-q)}\frac{a^2}{\lambda ^*} <\frac{(q-p)^2(p-1)}{p^2q(p^2-q)}\frac{a^2}{\lambda },\ \forall \ \lambda \in (\lambda _0^*,\lambda ^*). \end{aligned} \end{aligned}$$

The proof is complete. $\square$

Lemma 3.4

For each $\lambda \in (\lambda _0^*,\lambda ^*)$, there exists a $u_{\lambda }\in N_\lambda ^+$ such that $I_{\lambda }(u_{\lambda })= \widehat{I_{\lambda }}>0$.

Proof

Assume that $\{u_n\}\subset N_\lambda ^+\bigcup N_\lambda ^0$ satisfying $I_{\lambda }(u_n)\rightarrow {\widehat{I}}_{\lambda }$ as $n\rightarrow \infty$. From Lemma 2.2, $\{u_n\}$ is bounded. Therefore, there exists a $u\in W_{0}^{1,p}(\Omega )$ such that $u_{n}\rightharpoonup u \ in\ W_{0}^{1,p}(\Omega )$, $u_{n}\rightarrow u\ in\ L^s(\Omega )$, $1\le s<p^*$, and point-wise a.e. in $\Omega$ as $n\rightarrow \infty$. From Proposition 3.5, we conclude that $u\ne 0$. We claim that $u_{n}\rightarrow u$ in $W_{0}^{1,p}(\Omega )$ as $n\rightarrow \infty$. Otherwise,

$$\begin{aligned} \phi _{\lambda ,u}'(1)=a\Vert u\Vert ^p+\lambda \Vert u\Vert ^{p^2}-\Vert u\Vert _{q}^q<\liminf _{n\rightarrow \infty }(a\Vert u_n\Vert ^p+\lambda \Vert u_n\Vert ^{p^2}-\Vert u_n\Vert _{q}^q)=0, \end{aligned}$$

which implies that the fibering map $\phi _{\lambda ,u}$ satisfies (i) of Proposition 3.1 and $t_\lambda ^-(u)<1<t_\lambda ^+(u)$. From this and the weak lower semi-continuity of $I_{\lambda }$, we conclude that

$$\begin{aligned} I_{\lambda }(t_\lambda ^+(u)u)<I_{\lambda }(u)\le \liminf _{n\rightarrow \infty }I_{\lambda }(u_{n})={\widehat{I}}_{\lambda }, \end{aligned}$$

which is a contradiction since $t_\lambda ^+(u)u\in N_{\lambda }^+$. Therefore, $u_{n}\rightarrow u$ in $W_{0}^{1,p}(\Omega )$ as $n\rightarrow \infty$, $u\in N_\lambda ^+\bigcup N_\lambda ^0$ and $I_\lambda (u)={\widehat{I}}_{\lambda }$. The case $u\in N_\lambda ^0$ can be excluded by combining Propositions 3.6 with 3.8. Moreover, from $\lambda >\lambda _0^*\ge \lambda _0(u)$ and Proposition 3.2, we have ${\widehat{I}}_\lambda >0$. Then, the conclusion of this lemma follows by letting $u_\lambda \equiv u$. $\square$

The above conclusions can be summarized into the following proposition.

Proposition 3.9

For each $\lambda \in (0,\lambda ^*)$, $I_\lambda$ has a local minimizer $u_\lambda \in N_\lambda ^+$. Moreover, if $\lambda \in (0,\lambda _0^*)$, then $I_\lambda (u_\lambda )<0$ while $I_{\lambda _0^*}(u_{\lambda _0^*})=0$ and if $\lambda \in (\lambda _0^*,\lambda ^*)$, then $I_\lambda (u_\lambda )>0$.

To show the existence of weak solutions to problem (1.1) when $\lambda =\lambda ^*$, we need some properties of ${\widehat{I}}_\lambda$ for $\lambda \in (0,\lambda ^*)$.

Proposition 3.10

The function ${\widehat{I}}_\lambda$ is continuous and increasing with respect to $\lambda$ on $(0,\lambda ^*)$.

Proof

Firstly, we prove that ${\widehat{I}}_\lambda$ is increasing on $(0,\lambda ^*)$. Suppose that $\lambda<\lambda '<\lambda ^*$. By Lemmas 3.2–3.4, there exists a $u_{\lambda '}$ such that $I_{\lambda '}(u_{\lambda '})=\inf _{u\in N_{\lambda '}^+\bigcup N_{\lambda '}^0}I_{\lambda '}(u)$. Obviously, the fibering map $\phi _{\lambda ',u_{\lambda '}}$ satisfies (i) of Proposition 3.1 (since it has a local minimizer). Consequently, $\lambda '<\lambda (u_{\lambda '})$. Since $\lambda<\lambda '<\lambda (u_{\lambda '})$, $\phi _{\lambda ,u_{\lambda '}}$ also satisfies (i) of Proposition 3.1 and then

$$\begin{aligned} {\widehat{I}}_\lambda \le I_\lambda (t_\lambda ^+(u_{\lambda '})u_{\lambda '})<I_\lambda (t_{\lambda '}^+(u_{\lambda '})u_{\lambda '}) =I_\lambda (u_{\lambda '})<I_{\lambda '}(u_{\lambda '})={\widehat{I}}_{\lambda '}, \end{aligned}$$

that is ${\widehat{I}}_\lambda$ is increasing on $(0,\lambda ^*)$.

Next, we prove the continuity. Suppose that $\lambda _n\uparrow \lambda \in (0,\lambda ^*)$ and choose $u_n\equiv u_{\lambda _n}$ such that ${\widehat{I}}_{\lambda _n}= I_{\lambda _n}(u_{n})$ and $I'_{\lambda _n}(u_{n})=0$ for each $n\in {\mathbb {N}}$. We claim that $u_{n}\rightarrow u$ in $W_{0}^{1,p}(\Omega )$ as $n\rightarrow \infty$. Otherwise,

$$\begin{aligned} \phi _{\lambda ,u}'(1)=a\Vert u\Vert ^p+\lambda \Vert u\Vert ^{p^2}-\Vert u\Vert _{q}^q<\liminf _{n\rightarrow \infty }(a\Vert u_n\Vert ^p+\lambda _n\Vert u_n\Vert ^{p^2}-\Vert u_n\Vert _{q}^q)=0, \end{aligned}$$

which implies that the fibering map $\phi _{\lambda ,u}$ satisfies (i) of Proposition 3.1 and $t_\lambda ^-(u)<1<t_\lambda ^+(u)$. From this and the weak lower semi-continuity of $I_{\lambda }$, we conclude that

$$\begin{aligned} I_{\lambda }(t_\lambda ^+(u)u)<I_{\lambda }(u)\le \liminf _{n\rightarrow \infty }I_{\lambda _n}(u_{n})=\liminf _{n\rightarrow \infty }{\widehat{I}}_{\lambda _n}. \end{aligned}$$

Since ${\widehat{I}}_{\lambda }$ is increasing, ${\widehat{I}}_{\lambda _n}<{\widehat{I}}_{\lambda }$ for each n. Therefore, $I_{\lambda }(t_\lambda ^+(u)u)<\liminf _{n\rightarrow \infty }{\widehat{I}}_{\lambda _n}\le {\widehat{I}}_{\lambda }$, which is a contradiction since $t_\lambda ^+(u)u\in N_{\lambda }^+$. Therefore, $u_{n}\rightarrow u$ in $W_{0}^{1,p}(\Omega )$ when $n\rightarrow \infty$ as claimed. By the monotonicity of ${\widehat{I}}_{\lambda }$ and the strong convergence of $u_{n}$ to u, one obtains ${\widehat{I}}_{\lambda _n}\rightarrow {I}_{\lambda }(u)\le {\widehat{I}}_{\lambda }$ as $n\rightarrow \infty$. Recalling the definition of ${\widehat{I}}_{\lambda }$ and the fact that $u\in N_\lambda ^+$, one sees that ${I}_{\lambda }(u)={\widehat{I}}_{\lambda }$, i.e., ${\widehat{I}}_{\lambda _n}\rightarrow {\widehat{I}}_{\lambda }$ as $\lambda _n\uparrow \lambda$.

Now suppose that $\lambda _n\downarrow \lambda \in (0,\lambda ^*)$. Since ${\widehat{I}}_{\lambda }$ is increasing, we can assume that ${\widehat{I}}_{\lambda _n}>{\widehat{I}}_{\lambda }$ for each n and $\lim _{n\rightarrow \infty }{\widehat{I}}_{\lambda _n}\ge {\widehat{I}}_\lambda$. Choose $u_{\lambda }$ such that ${\widehat{I}}_{\lambda }={\widehat{I}}_\lambda (u_\lambda )$ and observe that ${\widehat{I}}_\lambda \le \lim _{n\rightarrow \infty }{\widehat{I}}_{\lambda _n}\le \lim _{n\rightarrow \infty }I_{\lambda _n}(t_{\lambda _n}^+(u_{\lambda })u_{\lambda })=I_{\lambda }(t_{\lambda }^+(u_{\lambda })u_{\lambda })=I_{\lambda }(u_{\lambda })={\widehat{I}}_{\lambda }$. Here, we have used the fact that $t_{\lambda }^+$ is continuous with respect to $\lambda$. The proof is complete. $\square$

Proposition 3.11

When $\lambda =\lambda ^*$, problem (1.1) admits a solution $u_{\lambda ^*}\in N_{\lambda ^*}^0$ such that $I_{\lambda ^*}(u_{\lambda ^*})= {\widehat{I}}_{\lambda ^*}>0$ and $I''_{\lambda ^*}(u_{\lambda ^*})(u_{\lambda ^*},u_{\lambda ^*})=0$.

Proof

Fix a $\beta >0$ such that $\lambda _0^*+\beta <\lambda ^*$. Choose a sequence $\lambda _n\in (\lambda _0^*+\beta ,\lambda ^*)$, $\lambda _n\uparrow \lambda ^*$ and a corresponding sequence $u_n\equiv u_{\lambda _n}\in N_{\lambda _n}^+$ such that $I_{\lambda _n}(u_n)={\widehat{I}}_{\lambda _n}$, and $I'_{\lambda _n}(u_n)=0$ for each $n\in N$. It follows from Proposition 3.10 that $I_{\lambda _n}(u_n)={\widehat{I}}_{\lambda _n}>{\widehat{I}}_{\lambda _0^*+\beta }>0$. From the proof of Proposition 3.8, we have

$$\begin{aligned} {\widehat{I}}_{\lambda _n}<\frac{(q-p)^2(p-1)}{p^2q(p^2-q)}\frac{a^2}{\lambda ^*},\ \forall \ n\in N. \end{aligned}$$

Combining the above inequality, the coerciveness of $I_{\lambda _n}$ in $W_0^{1,p}(\Omega )$ with the assumption that $\lambda _n\uparrow \lambda ^*$ as $n\rightarrow \infty$ we see that $\{u_n\}$ is bounded in $W_0^{1,p}(\Omega )$. As before, we claim that $u_n\rightarrow u$ in $W_0^{1,p}(\Omega )$ as $n\rightarrow \infty$. Otherwise, we would have $\phi _{\lambda ^*,u}'(1)<\liminf _{n\rightarrow \infty } \phi _{\lambda _n,u_n}'(1)=0$, and hence $\lambda ^*<\lambda (u)$, which is a contradiction since $\lambda ^*\ge \lambda (u)$ for any $u\in W_0^{1,p}(\Omega )$. Therefore,

$$\begin{aligned} I_{\lambda ^*}(u)=\lim _{n\rightarrow \infty }I_{\lambda _n}(u_n)=\lim _{n\rightarrow \infty }{\widehat{I}}_{\lambda _n}>0, \end{aligned}$$

which implies that $u\ne 0$. Letting $n\rightarrow \infty$ in $I'_{\lambda _n}(u_n)=0$, it follows that $I'_{\lambda ^*}(u)=0$, i.e., u is a weak solution to problem (1.1). Moreover, from the definition of $\lambda ^*$ we also obtain that $I''_{\lambda ^*}(u)(u,u)=0$. Set $u_{\lambda ^*}\equiv u$, then the proof is complete. $\square$

From now on, we show the existence of the second solution to problem (1.1) which is a mountain pass type.

Lemma 3.5

Given $\delta \in (0,M)$, where $M>0$ is the constant given in Lemma 3.1, there exists an $\varepsilon _\delta >0$ such that

$$\begin{aligned} 0<{\widehat{I}}_\lambda \le \delta ,\ \forall \ \lambda \in (\lambda _0^*,\lambda _0^*+\varepsilon _\delta ). \end{aligned}$$

Proof

The inequality ${\widehat{I}}_\lambda >0$ follows from Lemma 3.4. Obviously, the fibering map $\phi _{\lambda _0^*,u_{\lambda _0^*}}$ satisfies (i) of Proposition 3.1 (since it has a local minimizer). It follows from Proposition 3.2 that $\lambda _0^*<\lambda (u_{\lambda _0^*})$. Hence, there exists an $\varepsilon _1>0$ such that $\lambda _0^*+\varepsilon _1<\lambda (u_{\lambda _0^*})$. For each $\lambda \in (\lambda _0^*,\lambda _0^*+\varepsilon _1)$, applying Proposition 3.2 again, one sees that $\phi _{\lambda ,u_{\lambda _0^*}}$ satisfies (i) of Proposition 3.1. Hence, there exists a $t_\lambda ^+(u_{\lambda _0^*})>0$ such that $t_\lambda ^+(u_{\lambda _0^*})u_{\lambda _0^*}\in N_\lambda ^+$. From (i) of Proposition 3.7, we have $t_\lambda ^+(u_{\lambda _0^*})\rightarrow t_{\lambda _0^*}^+(u_{\lambda _0^*})=1$ as $\lambda \downarrow \lambda _0^*$. This, together with Lemma 3.3, guarantees that

$$\begin{aligned} {\widehat{I}}_\lambda \le I_\lambda (t_\lambda ^+(u_{\lambda _0^*})u_{\lambda _0^*})\rightarrow I_{\lambda _0^*}(t_{\lambda _0^*}^+(u_{\lambda _0^*})u_{\lambda _0^*})=I_{\lambda _0^*}(u_{\lambda _0^*})=0,\ \lambda \downarrow \lambda _0^*. \end{aligned}$$

Consequently, there exists an $\varepsilon _2> 0$ such that ${\widehat{I}}_\lambda <\delta$ for each $\lambda \in (\lambda _0^*,\lambda _0^*+\varepsilon _2)$. If we set $\varepsilon _\delta =\min \{\varepsilon _1,\varepsilon _2\}$, then the conclusion of this lemma follows. $\square$

Proposition 3.12

There exists an $\varepsilon >0$ such that for each $\lambda \in (0,\lambda _0^*+\varepsilon )$, one can find an $w_\lambda \in W_0^{1,p}(\Omega )$ such that $I_\lambda (w_\lambda )=c_\lambda$ and $I'_\lambda (w_\lambda )=0$. Moreover, $c_\lambda >0$ and $c_\lambda >{\widehat{I}}_\lambda$.

Proof

For the moment, we choose $\rho < r$ in Lemma 3.1 and take $M>0$ correspondingly. Here, r is the positive constant determined in Proposition 3.5. Let $\varepsilon _\sigma$ be given in Lemma 3.5 and denote it by $\varepsilon$ for simplicity. Set

$$\begin{aligned} \ \ \ \ \ \ \ \ \ \ \ \ {\left\{ \begin{array}{ll} {\overline{u}}_\lambda =u_{\lambda _0^*}, \ if \ \lambda \in (0,\lambda _0^*],\\ {\overline{u}}_\lambda =u_\lambda , \ if \ \lambda \in (\lambda _0^*,\lambda _0^*+\varepsilon ).\\ \end{array}\right. } \end{aligned}$$

Noticing that ${\overline{u}}_\lambda =u_{\lambda _0^*}\in N_{\lambda _0^*}$ for $\lambda \in (0,\lambda _0^*]$ and ${\overline{u}}_\lambda =u_\lambda \in N_\lambda$ for $\lambda \in (\lambda _0^*,\lambda _0^*+\varepsilon )$, we have $\Vert {\overline{u}}_\lambda \Vert \ge r$, by Proposition 3.5.

Define

$$\begin{aligned} c_\lambda =\inf _{\gamma \in \Gamma _\lambda }\max _{t\in [0,1]}I_\lambda (\gamma (t)), \end{aligned}$$

where

$$\begin{aligned} \Gamma _\lambda =\{\gamma \in C([0,1],W_0^{1,p}(\Omega )): \gamma (0)=0, \gamma (1)={\overline{u}}_\lambda \}. \end{aligned}$$

It is easily seen that when $\lambda \in (0,\lambda _0^*]$, $I_\lambda ({\overline{u}}_\lambda )=I_\lambda (u_{\lambda _0^*})\le I_{\lambda _0^*}(u_{\lambda _0^*})=0<M$; when $\lambda \in (\lambda _0^*,\lambda _0^*+\varepsilon )$, $I_\lambda ({\overline{u}}_\lambda )=I_\lambda (u_{\lambda })={\widehat{I}}_\lambda<\delta < M$, by Lemma 3.5. Therefore, we have

$$I_\lambda (u)\ge M>\max \{I_\lambda (0),I_\lambda ({\overline{u}})\}, \text {if}\ \Vert u\Vert =\rho ,$$

which is the desired the mountain pass geometry.

This, together with Lemma 3.1, implies that there exists an $w_\lambda \in W_0^{1,p}(\Omega )$ such that $I_\lambda (w_\lambda )=c_\lambda \ge M>0$, and $I'_\lambda (w_\lambda )=0$. When $\lambda \in (0,\lambda _0^*)$, we have $c_\lambda>0>{\widehat{I}}_\lambda$; when $\lambda \in (\lambda _0^*, \lambda _0^*+\varepsilon )$, we have $c_\lambda \ge M>{\widehat{I}}_\lambda$. The proof is complete. $\square$

Now, we are ready to prove Theorems 2.1 and 2.2.

Proof of Theorem 2.1

The existence of $u_\lambda$ and $\omega _\lambda$ follows from Propositions 3.9 and 3.12. The item (4) is a consequence of Proposition 3.12. Item (5) can be proved by using the fact that every critical point of $I_\lambda$ lies in $N_\lambda$ and Corollary 3.1. $\square$

Proof of Theorem 2.2

Fix $u\in W_0^{1,p}(\Omega )\backslash \{0\}$, choose $\lambda \in (0,\lambda _0(u))$. It follows from Proposition 3.2 that the fibering map $\phi _{\lambda ,u}$ satisfies (i) of Proposition 3.1. Since

$$\begin{aligned} \lim _{t\rightarrow \infty }\Big (\frac{a}{p}t^p\Vert u\Vert ^p-\frac{1}{q}t^q\Vert u\Vert _q^{q}\Big )=-\infty , \end{aligned}$$

we know for any $K>0$, there exists a large enough $t_0>0$, such that $\frac{a}{p}t_0^p\Vert u\Vert ^p-\frac{1}{q}t_0^q\Vert u\Vert _q^{q}<-K$. For $t_0>0$ given above, there holds

$$\begin{aligned} \phi _{\lambda ,u}(t_0)\rightarrow \frac{a}{p}t_0^p\Vert u\Vert ^p-\frac{1}{q}t_0^q\Vert u\Vert _q^{q},\ as\ \lambda \downarrow 0. \end{aligned}$$

Hence, for given small enough $\varepsilon >0$, there exists a $\sigma >0$, such that $\phi _{\lambda ,u}(t_0)<\frac{a}{p}t_0^p\Vert u\Vert ^p-\frac{1}{q}t_0^q\Vert u\Vert _q^{q}+\varepsilon <-K+\varepsilon$ for $\lambda \in (0,\sigma )$. Therefore, for any $M:=-K+\varepsilon _0<0$, there exists $\sigma >0$ given above, such that $\phi _{\lambda ,u}(t_0)<M$ for $\lambda \in (0,\sigma )$. And from the fact that $\phi _{\lambda ,u}(t_0)\ge \phi _{\lambda ,u}(t_\lambda ^+(u))=I_\lambda (t_\lambda ^+(u)u)\ge \inf _{u\in W_0^{1,p}(\Omega )}I_\lambda (u)={\widehat{I}}_\lambda$, we know ${\widehat{I}}_\lambda =I_\lambda (u_\lambda )\rightarrow -\infty$ as $\lambda \downarrow 0$. And it is clear that $\Vert u_\lambda \Vert \rightarrow \infty$ as $\lambda \downarrow 0$. The proof of Theorem 2.2 is complete. $\square$

3.2 $The \ Case \ 1<p<p^2<q$.

We shall prove that problem (1.1) admits a mountain pass-type solution when $1<p<p^2<q$, by showing that the energy functional $I_\lambda (u)$ satisfies the mountain pass geometry around 0. Indeed, for fixed $u\in W_0^{1,p}(\Omega )\setminus \{0\}$ and $\lambda >0$, we have

$$\begin{aligned} \lim _{t\rightarrow 0}\frac{\phi _{\lambda ,u}(t)}{t^p}=\frac{a}{p}\Vert u\Vert ^p>0, \end{aligned}$$

and

$$\begin{aligned} \lim _{t\rightarrow \infty }\phi _{\lambda ,u}(t)=-\infty , \end{aligned}$$

which directly imply the following lemma.

Lemma 3.6

For each $\lambda >0$, there exist two positive constants R and d such that

(i) $I_\lambda (u)\ge R$ if $\Vert u\Vert =d$;

(ii) There exists a ${\overline{u}}\in W_0^{1,p}(\Omega )$ such that $\Vert {\overline{u}}\Vert >d$ and $I_\lambda ({\overline{u}})<R$.

With the help of Lemma 3.6, we can now prove Theorem 2.3.

Proof of Theorem 2.3

Firstly, we need to prove that the functional $I_\lambda$ satisfies the $(PS)_c$ condition. Assume that $\{u_{n}\}\subset W_0^{1,p}(\Omega )$ is a Palais–Smale sequence at level c for $I_{\lambda }$, where c is a real number, that is $I_{\lambda }(u_{n})\rightarrow c$ in ${\mathbb {R}}$ and $I'_{\lambda }(u_{n})\rightarrow 0$ in $W^{-1,p'}(\Omega )$, as $n\rightarrow \infty$. We claim that $\{u_{n}\}$ is bounded in $W_0^{1,p}(\Omega )$. Otherwise, we would have

$$\begin{aligned} \begin{aligned} c+1+o(1)\Vert u_n\Vert&\ge I_{\lambda }(u_n)-\frac{1}{q}\langle I'_{\lambda }(u_n),u_n\rangle \\&=(\frac{1}{p}-\frac{1}{q})a\Vert u\Vert ^p+(\frac{1}{p^2}-\frac{1}{q})\lambda \Vert u\Vert ^{p^2}, \end{aligned} \end{aligned}$$

which is a contradiction. Hence, $\{u_{n}\}$ is bounded in $W_0^{1,p}(\Omega )$. By applying the argument similar to the proof of Lemma 3.1, we conclude that $I_\lambda$ satisfies the $(PS)_c$ condition. Then, it follows from the mountain pass lemma that problem (1.1) admits a solution $w_\lambda \in W_0^{1,p}(\Omega )\backslash \{0\}$ such that $I_\lambda (w_\lambda )>0$. The proof is complete. $\square$

3.3 $The \ Case \ 1<q<p<p^2$.

Theorem 2.4 can be proved by using direct variational method. More precisely, we shall show that the energy functional is bounded from below in the whole space $W_{0}^{1,p}(\Omega )$, which, combined with the coerciveness and weakly lower semi-continuity of $I_\lambda$, implies that the minimizer of $I_\lambda$ is a weak solution of problem (1.1).

Proof of Theorem 2.4

From Sobolev embedding, we see, $\forall \ u\in W_{0}^{1,p}(\Omega )\backslash \{0\}$, that

$$\begin{aligned} \begin{aligned} I_{\lambda }(u)&=\frac{a}{p}\Vert u\Vert ^p+\frac{\lambda }{p^2}\Vert u\Vert ^{p^2}-\frac{1}{q}\Vert u\Vert _q^{q}\\&\ge \frac{\lambda }{p^2}\Vert u\Vert ^{p^2}-\frac{S_q^q}{q}\Vert u\Vert ^{q}\\&=\Vert u\Vert ^q\Big (\frac{\lambda }{p^2}\Vert u\Vert ^{p^2-q}-\frac{S_q^q}{q}\Big ), \end{aligned} \end{aligned}$$

which implies $I_{\lambda }(u)$ is bounded from below in $W_{0}^{1,p}(\Omega )$. From

$$\begin{aligned} \lim _{t\rightarrow 0}\frac{\phi _{\lambda ,u}(t)}{t^q}=-\frac{1}{q}\Vert u\Vert _q^q<0, \end{aligned}$$

we know $\inf \limits _{u\in W_{0}^{1,p}(\Omega )}I_{\lambda }(u)<0$. Let $\{u_{n}\}\subset W_{0}^{1,p}(\Omega )$ be a minimizing sequence for $I_{\lambda }(u)$ in $W_{0}^{1,p}(\Omega )$. By the coerciveness of $I_{\lambda }(u)$ (see Lemma 2.2), we know that $\{u_{n}\}$ is bounded in $W_{0}^{1,p}(\Omega )$. And therefore, we can assume that $u_{n}\rightharpoonup u$ in $W_{0}^{1,p}(\Omega )$, $u_{n}\rightarrow u$ in $L^s(\Omega )$, $1\le s<p^*$, and point-wise a.e. in $\Omega$ as $n\rightarrow \infty$. Since $I_\lambda$ is weakly lower semi-continuous, one has

$$\begin{aligned} I_{\lambda }(u)\le \liminf _{n\rightarrow \infty }I_{\lambda }(u_{n})=\lim _{n\rightarrow \infty }I_{\lambda }(u_{n})=\inf _{u\in W_{0}^{1,p}(\Omega )}I_{\lambda }(u)\le I_{\lambda }(u). \end{aligned}$$

Therefore, $I_{\lambda }(u)=\inf _{u\in W_{0}^{1,p}(\Omega )}I_{\lambda }(u)<0$. Let $u_\lambda \equiv u$, then the proof is complete. $\square$

4 Conclusion

In this paper, we study the existence, nonexistence and multiplicity of weak solutions to a p-Kirchhoff elliptic equation with a real parameter $\lambda$ and a power-type nonlinearity. We showed that the problem admits at least two positive solutions for some $\lambda >0$, a local minimum and a mountain pass-type solution. Two extremal parameters $0<\lambda _0^*<\lambda ^*$ are characterized such that problem (1.1) admits only trivial solution when $\lambda >\lambda ^*$, and the local minimum has nonnegative energy when $\lambda >\lambda _0^*$. In conclusion, we extend the existence, nonexistence and multiplicity results for Kirchhoff equations to p-Kirchhoff equations. Moreover, the method we use to characterize the extremal parameters is different from that used in [30].