1 Introduction

In this work, a new flexible extension of the Chen (C) distribution is derived using the compound Burr X family (Abouelmagd et al. [3]) called the compound Burr X Chen (CBC) distribution. The hazard rate function (HRF) of the new Chen extension can be "decreasing-constant-increasing (bathtub)", "monotonically increasing", "upside down constant-increasing", "monotonically decreasing", "upside down" and "J shape". However, the HRF function of the Chen distribution has only "monotonically increasing" and "bathtub (U)" shapes. The density of the CBC distribution accommodates the "unimodal right skewed", "unimodal left skewed", "bimodal right skewed" and "bimodal left skewed" shapes with different shapes. A random variable (RV) Z has a Chen distribution (see Chen [11]) with parameters \(\beta _{2}>0\) and \(\beta _{1}>0\) (write \(Z\sim \)Chen (\(\beta _{1},\beta _{2}\))) if Z has cumulative distribution function (CDF) given by

$$\begin{aligned} W_{\beta _{1},\beta _{2}}\left( \mathtt {z}\right) =1-\mathrm{exp}\left\{ \beta _{2} \left[ 1-\mathrm{exp}\left( \mathtt {z}^{\beta _{1}}\right) \right] \right\} |_{ \mathtt {z}>0}. \end{aligned}$$
(1)

For \(\beta _{2}=1\), the Chen distribution reduces to the standard one parameter Chen distribution. The HRF of the Chen model has a "bathtub" shape when \(\beta _{1}<1\) and has "monotonically increasing" failure rate function when \(\beta _{1}\ge 1\). Chen [11] compared the Chen distribution with many other distributions and showed that the Chen distribution has some merits. Recently, Chaubey and Zhang [10] presented two propositions studying PDF of the exponentiated Chen (Ex-C) model. The first proposition shows that the PDF shapes are either "decreasing" or "unimodal". The second proposition concludes that the HRF shapes are either "increasing" or "bathtub". Chaubey and Zhang [10] also addressed the problem of estimation of parameters of the Ex-C distribution, focusing on the maximum likelihood estimation method. Dey et al. [15] addressed various mathematical properties and estimation methods for the Ex-C model. They described different estimation methods such as the method of maximum likelihood estimation, percentile estimation, ordinary least square and weighted least square estimation, Cramér-von Mises estimation, maximum product of spacings estimation, Anderson–Darling and right-tail Anderson-Darling estimation. The CDF of the compound Burr X (CBX-G) family is defined as

(2)

where

For \(\gamma =1\), the CBX-G family reduces to the standard compound Rayleigh G (CR-G) family. Inserting (1) into (2), the CDF of the compound Burr X Chen (CBC) distribution can be expressed as

(3)

where

$$\begin{aligned} \varvec{\psi }_{{\beta _{1}},{\beta _{2}}}(\mathtt {z})=\frac{1-\mathtt {O}_{{\beta _{1}},{\beta _{2}}}\left( \mathtt {z}\right) }{\mathtt {O}_{{\beta _{1}},{\beta _{2}}}\left( \mathtt {z}\right) } \end{aligned}$$

and

For \(\gamma =1\), the CBC distribution reduces to the compound Rayleigh Chen distribution. For \(\beta _{2}=1\), the CBC distribution reduces to the two-parameter compound Burr X Chen distribution. For \(\gamma =\beta _{2}=1\), the CBC distribution reduces to the one-parameter standard compound Rayleigh Chen distribution. The new CDF in (3) can be used for presenting a new discrete Chen distribution for modeling the count data (see Aboraya et al. [2], Ibrahim et al. [28], Chesneau et al. [36] and Yousof et al. [50] for more details). The corresponding probability density function (PDF) of (3) can be derived as

(4)

where \({{{\underline{\varvec{V}}}}}=\left( {\gamma },\beta _{1},\beta _{2}\right) . \) For simulating the CBC model, the following quantile function can be used

$$\begin{aligned} \mathtt {Z}_{\upsilon }=\left( \ln \left[ 1-\frac{1}{{\beta _{2}}}\ln \left( -\left\{ -\ln \left[ 1-\hbar _{\gamma }\left( \upsilon \right) \right] \right\} ^{\frac{1}{2}}\right) \right] \right) ^{\frac{1}{\beta _{1}}}, \end{aligned}$$
(5)

where

$$\begin{aligned} \hbar _{\gamma }\left( \upsilon \right) =\left( -\ln \left\{ 1-\upsilon \left[ {1}-\mathrm{exp}{(-1)}\right] \right\} \right) ^{\frac{1}{\gamma }},0\le \upsilon \le 1. \end{aligned}$$

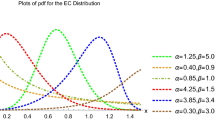
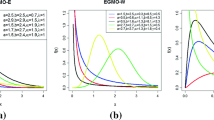
For exploring the flexibility of the new CBC PDF, we present Fig. 1 which shows the wide flexibility of the new PDF of the CBC model. Based on Fig. 1, we note that the new CBC PDF can be "unimodal right skewed", "unimodal left skewed", "bimodal right skewed" and "bimodal left skewed" with different shapes. Analogously, Fig. 2 is presented for exploring the flexibility of the HRF of the CBC model. Based on Fig. 2, we note that the new CBC HRF can be "decreasing-constant-increasing (bathtub)", "monotonically increasing", "upside down constant-increasing", "monotonically decreasing", "J-HRF" and "upside down".

Fig. 1
figure 1

Some PDF Plots

Full size image
Fig. 2
figure 2

Some HRF Plots

Full size image

We are motivated to define and study the CBC for the following reasons:

  • The new PDF in (4) can be "unimodal right skewed", "unimodal left skewed", "bimodal right skewed" and "bimodal left skewed" with different shapes (see Fig. 1).

  • The HRF of the CBC model can be "decreasing-constant-increasing (bathtub)", "monotonically increasing", "upside down constant-increasing", "monotonically decreasing", "J-HRF" and "upside down" (see Fig. 2).

  • In reliability analysis, the CBC model may be chosen as the best probabilistic model, especially in modeling the right heavy tail bimodal asymmetric real data and left heavy tail bimodal asymmetric real data.

2 Linear Representation

Consider the power series

$$\begin{aligned} \mathrm{exp}\left( \frac{\tau _{1}}{\tau _{2}}\right) =\sum \limits _{\tau _{3}=0}^{\infty }\frac{1}{\tau _{3}!}\left( \frac{\tau _{1}}{\tau _{2}} \right) ^{\tau _{3}}|_{\tau _{2}>0}. \end{aligned}$$
(6)

Applying (5) to (4), then (4) can be written as

(7)

If \(\left| \frac{\tau _{1}}{\tau _{2}}\right| <1\) and \(\tau _{3}>0\) is a real non-integer, the following power series holds

$$\begin{aligned} \left( 1-\frac{\tau _{1}}{\tau _{2}}\right) ^{\tau _{3}}=\overset{\infty }{ \underset{\tau _{4}=0}{\sum }}\frac{\left( -1\right) ^{\tau _{4}}\,\Gamma \left( 1+\tau _{3}\right) }{\tau _{4}!\,\Gamma \left( 1+\tau _{3}-\tau _{4}\right) }\,\left( \frac{\tau _{1}}{\tau _{2}}\right) ^{\tau _{4}}.~ \end{aligned}$$
(8)

Applying (8) to (7) we have

(9)

Applying the power series to the term \(\mathrm {exp }\left[ -\left( j+1\right) \varvec{\psi }_{{\beta _{1}},{\beta _{2}}}^{2}(\mathtt {z})\right] ,\) Equation (9) becomes

(10)

Consider the series expansion

$$\begin{aligned} \left( 1-\frac{\tau _{1}}{\tau _{2}}\right) ^{-\tau _{3}}\text { }|_{\left( \left| \frac{\tau _{1}}{\tau _{2}}\right| <1,~\tau _{3}>0\right) }= \overset{\infty }{\underset{v=0}{\sum }}\frac{\Gamma \left( \tau _{3}+v\right) }{v!\Gamma \left( \tau _{3}\right) }\left( \frac{\tau _{1}}{ \tau _{2}}\right) ^{v}. \end{aligned}$$
(11)

Applying the expansion in (11) to (10) for the term , Equation (10) becomes

This can be written as

(12)

where

$$\begin{aligned} {C}_{\upsilon ,v}=\,\frac{2\gamma \left( -1\right) ^{\upsilon }\Gamma \left( 3+2\upsilon +v\right) }{\upsilon !v!\left[ {1}-\mathrm{exp}{(-1)}\right] \Gamma \left( 2\upsilon +3\right) \varvec{\varepsilon }}\overset{\infty }{\underset{ \nu ,j=0}{\sum }}\frac{\left( -1\right) ^{\nu +j}\,\Gamma \left( \gamma \left( \nu +1\right) \right) \left( j+1\right) ^{\upsilon }}{j!\,\Gamma \left( \gamma \left( \nu +1\right) -j\right) },\, \end{aligned}$$

and

$$\begin{aligned} h_{\varvec{\varepsilon }{,}\beta _{1},\beta _{2}}(\mathtt {z})=\varvec{ \varepsilon }w_{{\beta _{1}},{\beta _{2}}}\left( \mathtt {z}\right) \left[ W_{{\beta _{1}},{\beta _{2}}}\left( \mathtt {z}\right) \right] ^{\varvec{ \varepsilon }-1}, \end{aligned}$$

which is the PDF of the Ex-C model with power parameter \(\varvec{\varepsilon }>0\).

Equation (12) reveals that the density of Z can be expressed as a linear mixture of Ex-C densities. So, several mathematical properties of the new family can be obtained from those of the Ex-C distribution. Similarly, the CDF of the CBC model can also be expressed as a mixture of Ex-C CDFs given by

$$\begin{aligned} F_{{{{\underline{\varvec{V}}}}}}\left( \mathtt {z}\right) =\overset{\infty }{ \underset{\upsilon ,v=0}{\sum }}{C}_{\upsilon ,v}~H_{\varvec{\varepsilon } {,}\beta _{1},\beta _{2}}\left( \mathtt {z}\right) , \end{aligned}$$
(13)

where

$$\begin{aligned} H_{\varvec{\varepsilon ,}\beta _{1},\beta _{2}}(\mathtt {z})=\left[ W_{{\beta _{1}},{\beta _{2}}}\left( \mathtt {z}\right) \right] ^{\varvec{\varepsilon }}, \end{aligned}$$

is the CDF of the Ex-C family with power parameter \(\varvec{\varepsilon }>0\) . Due to Dey et al. [15], the shape of the PDF of the Ex-C distribution may be characterized as follows: for \(\varvec{\varepsilon }<\) 1,  \(1>\beta _{1}\), \(h_{\varvec{\varepsilon }{,}\beta _{1},\beta _{2}}(\mathtt {z})\) is a monotonically decreasing density, for \(\varvec{\varepsilon } >1,\) \(\beta _{1}\) > 1, \(h_{\varvec{\varepsilon }{,}\beta _{1},\beta _{2}}( \mathtt {z})\) is a unimodal (upside down) density and for \(\varvec{ \varepsilon }<1,\) \(\beta _{1}\) > 1 and \(\varvec{\varepsilon >}1\), \( 1>\beta _{1}\), \(h_{\varvec{\varepsilon }{,}\beta _{1},\beta _{2}}( \mathtt {z})\) is unimodal (upside down) or monotonically decreasing density. Chaubey and Zhang [10] presented a proof that the failure behaviors of the Ex-C distribution are, respectively, bathtub (\(\varvec{\varepsilon }<1\), \( \beta _{1}<1\)), monotonically increasing (\(\varvec{\varepsilon }>1\), \(\beta _{1}\) \(>1\)), monotonically increasing or bathtub (\(\varvec{\varepsilon } <1,\beta _{1}>1\) and \(\varvec{\varepsilon }>1,\beta _{1}<1\)). In this regard, two theorems related to the Ex-C model are presented below:

Theorem 1

Let Z be a RV having the Ex-C distribution with parameters \(\beta _{1},\beta _{2}\) and power parameter \(\varvec{\varepsilon } \). Then using the transformation

$$\begin{aligned} t=\left[ G_{\beta _{1},\beta _{2}}\left( \mathtt {z}\right) \right] ^{\frac{1 }{\varvec{\varepsilon }}}, \end{aligned}$$

the \(s^{\text {th}}\) ordinary moment of Z is given by

$$\begin{aligned} \mu _{s,Z}^{\prime }={\mathbb {E}}\left[ Z^{s}\right] =\beta _{1}\sum _{p,q=0}^{+\infty }\varvec{\varepsilon }_{p}\left( \frac{s}{\beta _{1}}\right) \varvec{\varepsilon }_{q}\left( \frac{s}{\beta _{1}}+p\right) \frac{\left( -1\right) ^{\frac{2s}{\beta _{1}}+p}}{\beta _{2}^{\frac{2s}{ \beta _{1}}+p}\left[ \beta _{1}\left( \varvec{\varepsilon }+p+q\right) +s \right] }, \end{aligned}$$

where \(\varvec{\varepsilon }_{p}\left( \frac{s}{\beta _{1}}\right) \) is the coefficient of \(\left[ \frac{1}{\beta _{2}}\log \left( 1-t\right) \right] ^{ \frac{2s}{\beta _{1}}+p}\) in the expansion of

$$\begin{aligned} \left\{ \sum _{\hbar _{1}=1}^{+\infty }\frac{1}{\hbar _{1}}\left[ \frac{1}{ \beta _{2}}\log \left( 1-t\right) \right] \right\} ^{\frac{s}{\beta _{1}}}, \end{aligned}$$

and \(\varvec{\varepsilon }_{q}\left( \frac{s}{\beta _{1}}+p\right) \) is the coefficient of \(t^{p+q+\frac{s}{\beta _{1}}}\) in the expansion of

$$\begin{aligned} \left( \sum _{\hbar _{2}=1}^{+\infty }\frac{t^{\hbar _{2}}}{\hbar _{2}} \right) ^{\frac{s}{\beta _{1}}+p}. \end{aligned}$$

Theorem 2

Let Z be a RV having the Ex-C distribution. Then, the \(s^{\text {th}}\) conditional moment can be derived as

See Dey et al. [15] and Balakrishnan and Cohen [9] for more details.

3 Mathematical and Statistical Properties

3.1 Moments

Based on Theorem 1, the \(s{\text {th}}\) ordinary moment of the CBC model can then be expressed as

$$\begin{aligned} \mu _{s,\mathtt {z}}^{\prime }={\mathbb {E}}\left[ Z^{s}\right] = \varvec{\varepsilon }\beta _{1}\overset{+\infty }{\underset{\upsilon ,v,p,q=0 }{\sum }}{C}_{\upsilon ,v}\varvec{\varepsilon }_{p}\left( \frac{s}{\beta _{1}}\right) \varvec{\varepsilon }_{q}\left( \frac{s}{\beta _{1}}+p\right) \frac{\left( -1\right) ^{\frac{2s}{\beta _{1}}+p}}{\beta _{2}^{\frac{2s}{ \beta _{1}}+p}\left[ \beta _{1}\left( \varvec{\varepsilon }+p+q\right) +s \right] }. \end{aligned}$$
(14)

In particular, the first four raw moments can be derived as:

$$\begin{aligned}&\mu _{1,Z}^{\prime }=\varvec{\varepsilon }\beta _{1}\overset{+\infty }{ \underset{\upsilon ,v,p,q=0}{\sum }}{C}_{\upsilon ,v}\varvec{\varepsilon } _{p}\left( \beta _{1}^{-1}\right) \varvec{\varepsilon }_{q}\left( \beta _{1}^{-1}+p\right) \frac{\left( -1\right) ^{\frac{2}{\beta _{1}}+p}}{\beta _{2}^{\frac{2}{\beta _{1}}+p}\left[ \beta _{1}\left( \varvec{\varepsilon } +p+q\right) +1\right] }, \\&\mu _{2,Z}^{\prime }=\varvec{\varepsilon }\beta _{1}\overset{+\infty }{ \underset{\upsilon ,v,p,q=0}{\sum }}{C}_{\upsilon ,v}\varvec{\varepsilon } _{p}\left( \frac{2}{\beta _{1}}\right) \varvec{\varepsilon }_{q}\left( \frac{ 2}{\beta _{1}}+p\right) \frac{\left( -1\right) ^{\frac{2}{\beta _{1}}+p}}{ \beta _{2}^{\frac{2}{\beta _{1}}+p}\left[ \beta _{1}\left( \varvec{ \varepsilon }+p+q\right) +2\right] }, \\&\mu _{3,Z}^{\prime }=\varvec{\varepsilon }\beta _{1}\overset{+\infty }{ \underset{\upsilon ,v,p,q=0}{\sum }}{C}_{\upsilon ,v}\varvec{\varepsilon } _{p}\left( \frac{3}{\beta _{1}}\right) \varvec{\varepsilon }_{q}\left( \frac{ 3}{\beta _{1}}+p\right) \frac{\left( -1\right) ^{\frac{6}{\beta _{1}}+p}}{ \beta _{2}^{\frac{6}{\beta _{1}}+p}\left[ \beta _{1}\left( \varvec{ \varepsilon }+p+q\right) +3\right] }, \end{aligned}$$

and

$$\begin{aligned} \mu _{4,Z}^{\prime }=\varvec{\varepsilon }\beta _{1}\overset{+\infty }{ \underset{\upsilon ,v,p,q=0}{\sum }}{C}_{\upsilon ,v}\varvec{\varepsilon } _{q}\left( \frac{4}{\beta _{1}}\right) \varvec{\varepsilon }_{q}\left( \frac{ 4}{\beta _{1}}+p\right) \frac{\left( -1\right) ^{\frac{8}{\beta _{1}}+p}}{ \beta _{2}^{\frac{8}{\beta _{1}}+p}\left[ \beta _{1}\left( \varvec{ \varepsilon }+p+q\right) +4\right] }. \end{aligned}$$

The variance, cumulants, \(n{\text {th}}\) central moment, skewness, kurtosis and dispersion index can be numerically evaluated from the ordinary moments using well-known relationships.

3.2 The Conditional Moments

For the increasing failure rate models, it is also of interest to know what \({\mathbb {E}}\left( Z^{s}|Z>\mathtt {z}\right) \) is. It can be easily seen that

(15)

In particular,

and

3.3 Mean Residual Life

The mean residual life (MRL) is the expected remaining life, \(Z-\mathtt {z}\), given that the item has survived to time \(\mathtt {z}\). Thus, in life testing situations, the expected additional lifetime given that a component has survived until time \(\mathtt {z}\) is called the MRL. Since the MRL function is the expected remaining life, \(\mathtt {z}\) must be subtracted, yielding

where

Then using (12), we get

3.4 Mean Past Lifetime

In a real life situation, where systems often are not monitored continuously, one might be interested in getting inference more about the history of the system, for example, when the individual components have failed. Assume now that a component with lifetime \(\mathtt {z}\) has failed at or some time before \(\mathtt {z}\), \(\mathtt {z}\ge 0\). Consider the conditional random variable \(\mathtt {z}-Z|Z\le \mathtt {z}\). This conditional random variable shows, in fact, the time elapsed from the failure of the component given that its lifetime is less than or equal to \( \mathtt {z}\). Hence, the mean past lifetime (MPL) of the component can be defined as

Then using (11) and (12), we get

4 Copula

In this Section, we shall derive some bivariate CBC type distributions using some common copulas such as the Farlie-Gumbel-Morgenstern (FGM) copula (Morgenstern [43], Gumbel (1958) and Gumbel [23]), modified FGM copula (Rodriguez-Lallena and Ubeda-Flores [45]), Renyi’s entropy (Pougaza and Djafari [44]), Ali-Mikhail-Haq copula (Ali et al. [5]) and Clayton copula (see Elgohari and Yousof ([16, 17]), Elgohari and Yousof [18], Elgohari et al. [19], Ali et al. ([6, 7]), Shehata and Yousof ([46, 47]), Shehata et al. [48] and Aboraya et al. [1]). The Multivariate CBC (M-CBC) type is also presented under the Clayton copula. Future works may be allocated to the study of the new bivariate models. First, consider the joint CDF of the FGM copula, where

$$\begin{aligned} {\Im }_{\varvec{\tau }}(\varvec{\xi },\varvec{\zeta })=\varvec{\xi } \varvec{\zeta }\left( 1+\varvec{\tau }\varvec{\xi }^{\cdot }\varvec{\zeta } ^{\cdot }\right) |_{\varvec{\xi }^{\cdot }=1-\varvec{\xi },\ \varvec{\zeta } ^{\cdot }=1-\varvec{\zeta }} \end{aligned}$$

and the marginal function

$$\begin{aligned} \varvec{\xi }=F_{1},\varvec{\zeta }=F_{2},\varvec{\tau }\in \left( -1,1\right) \end{aligned}$$

is a dependence parameter and for every \(\varvec{\xi },\) \(\zeta \)\( \in \left( 0,1\right) \), \({\Im }(\varvec{\xi },0)={\Im }(0,\) \(\zeta \)\()=0\) which is "grounded minimum" and \({\Im }( \varvec{\xi },1)=\varvec{\xi }\) and \({\Im }(1,\) \(\zeta \)\()=\) \(\zeta \) which is "grounded maximum", \({\Im }\left( \varvec{ \xi }_{1},\varvec{\zeta }_{1}\right) +{\Im }\left( \varvec{\xi }_{2}, \varvec{\zeta }_{2}\right) -{\Im }\left( \varvec{\xi }_{1},\varvec{ \zeta }_{2}\right) -{\Im }\left( \varvec{\xi }_{2},\varvec{\zeta } _{1}\right) \ge 0\).

4.1 Via FGM Family

A copula is continuous in \(\varvec{\xi }\) and \(\zeta \); actually, it satisfies the stronger Lipschitz condition, where

$$\begin{aligned} |{\Im }\left( \varvec{\xi }_{2},\varvec{\zeta }_{2}\right) -\mathrm { \Im }\left( \varvec{\xi }_{1},\varvec{\zeta }_{1}\right) |\le |\varvec{\xi } _{2}-\varvec{\xi }_{1}|+|\varvec{\zeta }_{2}-\varvec{\zeta }_{1}|. \end{aligned}$$

For \(0\le \varvec{\xi }_{1}\le \varvec{\xi }_{2}\le 1\) and \(0\le \) \(\zeta \)\(_{1}\le \) \(\zeta \)\(_{2}\le 1,\) we have

$$\begin{aligned} \Pr \left( \varvec{\xi }_{1}\le \varvec{\xi }\le \varvec{\xi }_{2},\varvec{ \zeta }_{1}\le \varvec{\zeta }\le \varvec{\zeta }_{2}\right) ={\Im } \left( \varvec{\xi }_{1},\varvec{\zeta }_{1}\right) +{\Im }\left( \varvec{\xi }_{2},\varvec{\zeta }_{2}\right) -{\Im }\left( \varvec{ \xi }_{1},\varvec{\zeta }_{2}\right) -{\Im }\left( \varvec{\xi }_{2}, \varvec{\zeta }_{1}\right) \ge 0. \end{aligned}$$

Then, setting

$$\begin{aligned} \varvec{\xi }^{\cdot }=1-F_{_{{{{\underline{\varvec{V}}}}}_{1}}}(w_{1})|_{\left[ \varvec{\xi }^{\cdot }=\left( 1-\varvec{\xi }\right) \in \left( 0,1\right) \right] } \end{aligned}$$

and

$$\begin{aligned} \varvec{\zeta }^{\cdot }=1-F_{_{{{{\underline{\varvec{V}}}}}_{2}}}(w_{2})|_{\left[ \varvec{\zeta }^{\cdot }=(1-\varvec{\zeta })\in \left( 0,1\right) \right] }, \end{aligned}$$

we can then obtain the joint CDF of the CBC. The joint PDF can then be derived from

$$\begin{aligned} \hbar _{\varvec{\tau }}(\mathtt {z},y)=1+\varvec{\tau \xi }^{\cdot }\varvec{ \zeta }^{\cdot }|_{\left( \varvec{\xi }^{\cdot }=1-2\varvec{\xi }\text { and }\varvec{\zeta }^{\cdot }=1-2\varvec{\zeta }\right) }. \end{aligned}$$

4.2 Via Modified FGM Family

The modified FGM copula is defined as

$$\begin{aligned} {\Im }_{\varvec{\tau }}(\varvec{\xi },\varvec{\zeta })=\varvec{\xi \zeta }+\varvec{\tau }\mathfrak {D}_{\varvec{\xi }}\mathfrak {I}_{\varvec{ \zeta }}|_{\varvec{\tau }\in \left( -1,1\right) }, \end{aligned}$$

where \(\mathfrak {D}_{\varvec{\xi }}\) and \(\mathfrak {I}_{\varvec{\zeta }}\) are two continuous functions on (0, 1) with \(\mathfrak {D}\left( 0\right) = \mathfrak {D}\left( 1\right) =\mathfrak {I}\left( 0\right) =\mathfrak {I}\left( 1\right) =0.\) Let

$$\begin{aligned}&c_{1}\left( \mathfrak {D}_{\varvec{\xi }}\right) =\inf \left\{ \mathfrak {D}_{ \varvec{\xi }}:\frac{\partial }{\partial \varvec{\xi }}\mathfrak {D}_{\varvec{ \xi }}\right\} |_{\varvec{\Lambda }_{1,\varvec{\xi }}}<0,c_{2}\left( \mathfrak {D}_{\varvec{\xi }}\right) =\sup \left\{ \mathfrak {D}_{\varvec{\xi } }:\frac{\partial }{\partial \varvec{\xi }}\mathfrak {D}_{\varvec{\xi } }\right\} |_{\varvec{\Lambda }_{1,\varvec{\xi }}}<0, \\&c_{3}\left( \mathfrak {I}_{\varvec{\zeta }}\right) =\inf \left\{ \mathfrak {I} _{\varvec{\zeta }}:\frac{\partial }{\partial \varvec{\zeta }}\mathfrak {I}_{ \varvec{\zeta }}\right\} |_{\varvec{\Lambda }_{2,\varvec{\zeta } }}>0,c_{4}\left( \mathfrak {I}_{\varvec{\zeta }}\right) =\sup \left\{ \mathfrak {I}_{\varvec{\zeta }}:\frac{\partial }{\partial \varvec{\zeta }} \mathfrak {I}_{\varvec{\zeta }}\right\} |_{\varvec{\Lambda }_{2,\varvec{\zeta }}}>0. \end{aligned}$$

Then,

$$\begin{aligned} 1\le \min \left\{ c_{1}\left( \mathfrak {D}_{\varvec{\xi }}\right) c_{2}\left( \mathfrak {D}_{\varvec{\xi }}\right) ,c_{3}\left( \mathfrak {I}_{ \varvec{\zeta }}\right) c_{4}\left( \mathfrak {I}_{\varvec{\zeta }}\right) \right\} <\infty , \end{aligned}$$

where

$$\begin{aligned}&\varvec{\xi }\frac{\partial }{\partial \varvec{\xi }}\mathfrak {D}_{\left( \varvec{\xi }\right) }=\frac{\partial }{\partial \varvec{\xi }}\mathfrak {D}_{ \varvec{\xi }}-\mathfrak {D}_{\left( \varvec{\xi }\right) }, \\&\varvec{\Lambda }_{1,\varvec{\xi }}=\left\{ \varvec{\xi }:\varvec{\xi }\in \left( 0,1\right) |\frac{\partial }{\partial \varvec{\xi }}\mathfrak {D}_{ \varvec{\xi }}\text { exists}\right\} \text { and }\varvec{\Lambda }_{2, \varvec{\zeta }}=\left\{ \varvec{\zeta }:\varvec{\zeta }\in \left( 0,1\right) |\frac{\partial }{\partial \varvec{\zeta }}\mathfrak {I}_{\varvec{ \zeta }}\text { exists}\right\} . \end{aligned}$$

4.2.1 Type-I

Consider the following functional forms for both \(\mathfrak {D}_{\varvec{\xi } }\) and \(\mathfrak {I}_{\varvec{\zeta }}\). Then, the bivariate version (Type-I) can be derived from \({\Im }_{\varvec{\tau }}(\varvec{\xi }, \varvec{\zeta })=\varvec{\xi }\varvec{\zeta }+\varvec{\tau }\mathfrak {D}_{ \varvec{\xi }}\mathfrak {I}_{\varvec{\zeta }}|_{\varvec{\tau }\in \left( -1,1\right) }.\)

4.2.2 Type-II

Let \(\mathfrak {D}_{\left( \varvec{\xi }\right) }^{\cdot }\) and \(\mathfrak {I} _{\left( \varvec{\zeta }\right) }^{\cdot }\) be two functional forms satisfying all the conditions stated earlier where

$$\begin{aligned} \mathfrak {D}_{\left( \varvec{\xi }\right) }^{\cdot }|_{\left( \varvec{\tau } _{1}>0\right) }=\varvec{\xi }^{\varvec{\tau }_{1}}\left( 1-\varvec{\xi } \right) ^{1-\varvec{\tau }_{1}}, \end{aligned}$$

and \(\mathfrak {I}_{\left( \varvec{\zeta }\right) }^{\cdot }|_{\left( \varvec{\tau }_{2}>0\right) }=\) \(\zeta \)\(^{\varvec{\tau }_{2}}\left( 1-\varvec{\zeta }\right) ^{1-\varvec{\tau }_{2}}.\) Then, the corresponding bivariate version (Type-II) can be derived from

$$\begin{aligned} {\Im }_{\varvec{\tau },\varvec{\tau }_{1},\varvec{\tau }_{2}}(\varvec{ \xi },\varvec{\zeta })=\varvec{\xi }\varvec{\zeta }\left[ 1+\varvec{\tau } \mathfrak {D}_{\left( \varvec{\xi }\right) }^{\cdot }\text { }\mathfrak {I} _{\left( \varvec{\zeta }\right) }^{\cdot }\right] . \end{aligned}$$

4.2.3 Type-III

Let \(\mathfrak {D}\left( \varvec{\xi }\right) =\varvec{\xi }\left[ \log \left( 1+\varvec{\xi }^{\cdot }\right) \right] \) and \(\mathfrak {I}\left( \varvec{\zeta }\right) =\) \(\zeta \)\(\left[ \log \left( 1+\varvec{ \zeta }^{\cdot }\right) \right] \) for all \(\mathfrak {D}\left( \varvec{\xi } \right) \) and \(\mathfrak {I}\left( \varvec{\zeta }\right) \) which satisfy all the conditions stated earlier. In this case, one can also derive a closed form expression for the associated CDF of the bivariate version (Type- III) from \({\Im }_{\varvec{\tau }}(\varvec{\xi },\varvec{ \zeta })=\varvec{\xi }\varvec{\zeta }\left( 1+\varvec{\tau }\mathfrak {D} \left( \varvec{\xi }\right) \text { }\mathfrak {I}\left( \varvec{\zeta } \right) \right) .\)

4.3 Bivariate CBC and M-CBC Type via Clayton Copula

The Clayton copula can be considered as

$$\begin{aligned} {\Im }(\varvec{\zeta }_{1},\varvec{\zeta }_{2})=\left[ \left( 1/ \varvec{\zeta }_{1}\right) ^{\varvec{\tau }}+\left( 1/\varvec{\zeta } _{2}\right) ^{\varvec{\tau }}-1\right] ^{-\varvec{\tau }^{-1}}|_{\varvec{ \tau }\in \left( 0,\infty \right) }. \end{aligned}$$

Setting \(\zeta \)\(_{1}=F_{{{{\underline{\varvec{V}}}}}_{1}}(\varvec{\zeta } _{1})\) and \(\zeta \)\(_{2}=F_{{{{\underline{\varvec{V}}}}}_{2}}(\varvec{ \zeta }_{2})\), the bivariate CBC type can be derived from

4.4 Bivariate CBC Type via Renyi’s Copula

Using the theorem of Pougaza and Djafari [44], the Renyi’s copula can be directly derived from

$$\begin{aligned} {\Im }(\mathtt {z},y)=yF_{{{{\underline{\varvec{V}}}}}_{1}}\left( \mathtt {z} \right) +\mathtt {z}F_{{{{\underline{\varvec{V}}}}}_{2}}\left( y\right) -\mathtt {z} y, \end{aligned}$$

4.5 Bivariate CBC type via Ali-Mikhail-Haq Copula

Following Ali et al. ([5]), the joint CDF of the archimedean Ali-Mikhail-Haq copula under the stronger Lipschitz condition can be expressed as

$$\begin{aligned} \mathrm {\Im }(\varvec{\zeta }_{1},\varvec{\zeta }_{2})=\frac{\varvec{\zeta } _{1}\varvec{\zeta }_{2}}{1-\varvec{\rho }\overline{\varvec{\zeta }_{1}} \overline{\varvec{\zeta }_{2}}}|_{\varvec{\tau }\in \left( -1,1\right) }, \end{aligned}$$

sitting \(\overline{\varvec{\varsigma }_{1}}=1-F_{_{{{{\underline{\varvec{V}}}}} _{1}}}(w_{1})\) and \(\overline{\varvec{\varsigma }_{2}}=1-F_{{{{\underline{\varvec{{V}}}}}_{2}}}(w_{2})\) we can derive the joint CDF of the bivariate CBC model. The corresponding joint PDF of the archimedean Ali–Mikhail–Haq copula can then be expressed as

$$\begin{aligned} h(\varvec{\varsigma }_{1},\varvec{\varsigma }_{2})=\frac{1-\varvec{\tau }+2 \varvec{\tau }\frac{\varvec{\zeta }_{1}\varvec{\zeta }_{2}}{1-\varvec{\rho } \overline{\varvec{\zeta }_{1}}\overline{\varvec{\zeta }_{2}}}}{\left[ 1- \varvec{\tau }\overline{\varvec{\zeta }_{1}}\overline{\varvec{\zeta }_{2}} \right] ^{2}}|_{\varvec{\tau }\in \left( -1,1\right) }. \end{aligned}$$

5 Parameter Estimation

Let \(Z_{1},...,Z_{n}\) be a random sample of size n from (4), then the log-likelihood function of (4) without constant terms is given by

The maximum likelihood estimates (MLEs) are obtained by solving the following nonlinear systems of equations

$$\begin{aligned} \frac{\partial }{\partial \gamma }\ell \left( {{{\underline{\varvec{V}}}}}\right) =0,\frac{\partial }{\partial \beta _{2}}\ell \left( {{{\underline{\varvec{V}}}}} \right) =0,\frac{\partial }{\partial \beta _{1}}\ell \left( {{\underline{\varvec{{V}}}}}\right) =0. \end{aligned}$$

6 Applications

In this section, two real data sets are analyzed and considered for showing applicability of the CBC model. The new CBC model is compared with many common competitive models under the Akaike Information Criterion (AIC), the Bayesian Information Criterion (BIC), the Cramér–von Mises (CVM), the Anderson–Darling (AD) and Kolmogorov–Smirnov (KS) (corresponding p-value). The following competitive models are considered: the Gamma-Chen distribution (GC) (Alzaatreh et al. [8]), the Beta-Chen distribution (BC) (Eugene et al. [20]), Marshall-Olkin Chen distribution (MOC) (Jose [33]), the Kumaraswamy Chen distribution (KC) (Cordeiro and de Castro [12]), the Transmuted Chen (TC) (Khan et al. [34]), the Transmuted Exponentiated Chen (TEx-C) (Khan et al. [35]), the Extended Chen (EC) and the standard Chen distribution have been selected for comparison in two examples. However many other useful applications can be found in Korkmaz et al. [36], Yousof et al. [50] and Ibrahim et al. [27]. The parameters of models have been estimated by the MLE method. The first data set is called the relief times of 20 patients data (see Gross and Clark (1975)). This second data set is called the minimum flow data which was presented by Cordeiro et al. [13] and include 38 observations.

Table 1 Comparing models under the relief times data
Full size table
Table 2 The MLEs and SEs for the relief times data
Full size table
Table 3 Comparing models under the minimum flow data
Full size table
Table 4 The MLEs and SEs for the minimum flow data
Full size table

Table 1 lists statistics for comparing the competitive models under the relief times data. Table 2 gives the MLEs and their corresponding standard errors (SEs) for the relief times data. Table 3 lists statistics for comparing the competitive models under the minimum flow data. Table 4 gives the MLEs and SEs for the minimum flow data. Based on Table 1, it is noted that the CBC model provides the best results: AIC=40.13, BIC=44.11, CVM=0.048, AD=0.281, K.S=0.130 and P Value=0.886. Table 3 gives the MLEs (SEs) for the relief times data. Based on Table 3, it is noted that the CBC model provides the best results: AIC=390.02, BIC= 396.57, CVM=0.07, AD= 0.48, K.S= 0.11 and P-Value=0.708. Figure 3 gives box plots. Figure 4 gives quantile-quantile (Q-Q) plots. Figure 5 shows the total time in test (TTT) plots. Figure 6 gives nonparametric Kernel density estimation (NKDE) plots. The box plot shows that relief times data has one extreme value (see Fig. 3 left panel) and the minimum flow data has one extreme value (see Fig. 3 right panel). The Q-Q plots ensure the results obtained by the box plots. The dashed line in all the Q-Q plots refers to the safe boundaries for the standard errors. The TTT plot shows that the HRFs for the relief times data is "monotonically increasing" (Fig. 5 left panel) and the HRFs for the relief times data is "monotonically increasing" (see Fig. 5 right panel). The NKDE plot shows that the KDE is "asymmetric bimodal density" with right tail (see Fig. 6 left panel) and the KDE of minimum flow data is “asymmetric bimodal" density (see Fig. 6 right panel). Figure 7 gives the estimated-PDF (E-PDF), estimated-CDF (E-CDF), Probability-Probability (P-P), estimated-HRF (E-HRF) and the Kaplan-Meier plot for the relief times data. Figure 8 gives the E-PDF, E-CDF, P-P, E-HRF and the Kaplan-Meier plot for the minimum flow data. According to Figs 7 and 8,the new model showed a very close fit to the empirical functions in modeling the relief times and minimum flow data sets.

Fig. 3
figure 3

Box plots

Full size image
Fig. 4
figure 4

Q-Q plots

Full size image
Fig. 5
figure 5

TTT plots

Full size image
Fig. 6
figure 6

NKDE plots

Full size image
Fig. 7
figure 7

P-P, E-PDF, E-CDF, E-HRFand Kaplan-Meier plot for the relief times data

Full size image
Fig. 8
figure 8

P-P, E-PDF, E-CDF, E-HRF and Kaplan-Meier plot for the minimum flow data

Full size image

7 Conclusions

A novel flexible compound extension of Chen distribution which accommodates "decreasing-constant-increasing (bathtub)", "monotonically increasing", "upside down constant-increasing", "monotonically decreasing", " J failure rate" and "upside down" is defined and studied. The new model is motivated by its wide applicability in modeling the "unimodal right skewed", "unimodal left skewed", "bimodal right skewed" and "bimodal left skewed" real data. The new density can be "unimodal right skewed", "unimodal left skewed" and "bimodal right skewed" with different shapes. Relevant statistical properties of the novel model are derived such as conditional moments, mean residual life and mean past lifetime. Some bivariate type extensions are derived using some common copulas such as the Farlie-Gumbel-Morgenstern, Ali-Mikhail-Haq copula, modified Farlie-Gumbel-Morgenstern copula, Renyi entropy copula and Clayton copula. The method of maximum likelihood estimation is considered for estimating the model parameters. Two real data sets are analyzed for illustrating wide applicability of the novel model. The new model is compared with many common competitive Chen extensions such as the the Beta-Chen, Gamma-Chen , Marshall-Olkin Chen, the Transmuted Chen, the Extended Chen, the Transmuted exponentiated Chen, the Kumaraswamy Chen and the standard Chen distribution. The comparison is performed under some well-known goodness-of-fit statistic criteria including the Akaike Information criterion, Bayesian Information criterion, Cramér-von Mises criterion, Anderson-Darling criterion, Kolmogorov-Smirnov test and its corresponding p value.

As a potential future work, we may consider many new useful goodness-of-fit tests for the right censored distributional validation such as the Nikulin-Rao-Robson goodness test and the Bagdonavičius-Nikuli test as recently performed by Goual et al. ([24, 26]), Yadav et al. [49], Ibrahim et al. [29], Goual and Yousof ([25]), Mansour et al. ([37,38,39,40,41,42]) and Aidi et al. [4], among others.