Autoregressive Time Series Analysis of Variance with Skew Normal Innovations

Abstract

Independence and normality of observations for each level of the classification variables are two fundamental assumptions in traditional analysis of variance (ANOVA), whereas in many real applications the data violate seriously from these assumptions. Accordingly, in these situations using this traditional theory leads to unappealing results. We consider time series ANOVA by assuming a skew normal distribution for innovations. We provide iterative closed forms for the maximum likelihood estimators and construct asymptotic confidence intervals for them. A simulation study and a real data example are used to evaluate the efficiency and applicability of the proposed model for analyzing skew-symmetric time series data.

1 Introduction

The ANOVA is a frequently used statistical methodology for analyzing data in which one or more response variables are considered under various situations specified by one or more factors (explanatory classification variables). The aim of this technique is to discover and model the significant differences between the means of three or more independent populations by splitting total variability of response observations into the systematic (between the classification variables) and non-systematic variability (within the classification variables). As it is highlighted by some authors, e.g., Gelman [13], ANOVA is an extremely important method in exploratory and confirmatory data analysis. It is often the starting step for many statistical surveys about different populations that helps researcher to verify the effective factors on response variables. There are numerous applications for ANOVA in various disciplines such as agriculture, engineering, economics, public health and social sciences. This seminal technique was firstly developed by Fisher in 1920s. Reitz [25] was the first who used ANOVA in educational researches. The seminal books of Fisher [12], Cochran and Cox [11], Cox [10], Snedecor and Cochran [29] and Montgomery [24], among others, have been provided a set of comprehensive useful references about ANOVA. Regarding the above-mentioned references, the validity of ANOVA depends on some fundamental assumptions where the most important of them are: (i) independence of observations for each group, (ii) independence of groups under consideration, (iii) normality of observations for each group and (iv) homogeneity of observations variance for different groups. Lund et al. [22] studied the problem of dependency in ANOVA for time series data and also proposed a new test statistic for autocorrelated data to use one-way ANOVA. Senoglu and Tiku [27] showed the effect of non-normality on the test statistic while working with two-way classification model. A number of studies take a part in the literature which are based on time series data in ANOVA. See, for example, Górecki and Smaga [14] and Liu et al. [21]. The idea in this article is to use a flexible skew-symmetric distribution, to handle the non-normality of data in ANOVA when the observations are timely dependent. In this direction, we used a member of the Skew Normal (SN) distribution which is a class of skew-symmetric distributions with highly flexibility for analyzing abnormal observations and includes the normal as a special case. Since Azzalini [2] where the first univariate version of the distribution introduced, much research effort has been focused on developing similar new families of distributions or generalizing an existing one. See, for example, Azzalini [3] and Henze [17] for discussion on univariate and Azzalini and Dalla-Valle [5], Azzalini and Capitanio [4], Branco and Dey [8] and Sahu et al. [26] for multivariate case. In addition, various applications of SN distribution have been discussed in the literature; for example, Cancho et al. [9] and Arellano-Valle et al. [1] discussed SN regression analysis, Lin and Lee [20] considered the SN mixed effect model and Lachos et al. [18] demonstrated analyzing censored data under SN distribution. In the context of the time series data, there has been a progressive interest in using SN distribution for data analysis. A non-Gaussian autoregressive (AR) model with epsilon skew normal innovations has been introduced by Bondon [7] and also the method of moments and maximum likelihood (ML) estimators of the model parameters and their corresponding limiting have been provided in it. Following Bondon [7], Sharafi and Nematollahi [28] considered SN distribution for the innovations. The semiparametric analysis of the nonlinear AR(1) model with skew-symmetric innovations has been investigated by Hajrajabi and Fallah [15]. Hajrajabi and Fallah [16] discussed the classical and Bayesian estimation of the AR(1) model with skew-symmetric innovations from a parametric point of view. More recently, Maleki et al. [23] provided the expectation conditional maximization either (ECME) algorithm for multivariate scale mixture of skew normal (SMSN) distributions in vector autoregressive (VAR) models. In this paper, we develop a time series ANOVA model under the SN distribution. We have used a version of the SN distribution which introduced by Sahu et al. [26] and Azzalini [2]. This family of SN distributions is more tractable than others specially in maximum likelihood (ML) estimation of the parameters via expectation–maximization (EM) algorithm. This paper is organized as follows. The theoretical foundation of the proposed model is presented in Sect. 2. We also discuss the maximum likelihood estimation of the model, in this section. In Sect. 3, we use the asymptotic properties of the maximum likelihood estimators to construct the confidence interval for the model coefficients. A simulation study is worked out in order to assess the model in various situations, in Sect. 4. In Sect. 5, real world data are analyzed to explain the applicability and performance of the proposed theory.

2 The Proposed Model

There are many designs for an ANOVA model such as complete random design, randomized complete block design, split plot, Latin squares and Greco-Latin. On the other hand, the factors in an ANOVA model may indicate to fixed or random effects. For a fixed effect model, the levels of factors are all the levels of interest, while for a random effect model a subset of randomly selected levels from all possible levels are considered in order to generalize the results to the whole levels. In what follows, for the sake of brevity, we assume that there are a single factor and a single response variable. We also assume that the factor indicates fixed effects. Consider an autoregressive time series one-way ANOVA model, for R treatment and T observations, of the form

$$\begin{aligned} Y_{it}=\mu _0+\tau _i+\sum _{j=1}^{p}\phi _{ij}Y_{it-j}+a_{it},\ \ i=1,\ldots ,R;\ t=p+1,\ldots ,T, \end{aligned}$$

(1)

where $Y_{it}$ denotes the t-th observation in the i-th treatment, p is order of autoregressive model, $\mu _0$ is the overall mean of the observations and $\tau _i$ is the specific effect of the i-th treatment. The constraint $\sum _{i=1}^{R}\tau _i=0$ is imposed to the effects of treatments. The main purposes of the ANOVA are usually to estimate the treatment means and to test hypotheses about them. In traditional theory of the ANOVA, the model innovations and consequently the responses are assumed to be normal and mutually independent random variables, whereas these assumptions does not appear to be feasible in many situations especially when the observations indicate to asymmetry and dependent data.

Considering the Sahu et al. [26] skew normal (SSN) distribution with scale parameter $\sigma ^2$ and skewness parameter $\lambda$ for the innovations, $a_{it}$, the model (1) could be written as

$$\begin{aligned} Y_{it}|Y_{it-1},\ldots ,Y_{it-p}\sim & {} \hbox {SSN}(\mu _{it}-{\sqrt{2/\pi }}\lambda ,\sigma ^2,\lambda ), \nonumber \\&\quad i=1,\ldots ,R;\;\; t=p+1,\ldots ,T, \end{aligned}$$

(2)

where

$$\begin{aligned} \mu _{it}= \mu _0+\tau _i+\Phi _{i1}Y_{it-1}+\cdots +\Phi _{ip}Y_{it-p}. \end{aligned}$$

Hence, the conditional distribution of response variable is of the form

$$\begin{aligned} f_{SN}(y_{it}| y_{it-1},\ldots ,y_{it-p},{\varvec{\nu }})= & {} 2\phi \left( y_{it};\mu _{it}-{\sqrt{\frac{2}{\pi }}}\lambda ,\sigma ^2+\lambda ^2\right) \Phi \nonumber \\&\left( \frac{\lambda }{\sigma }\frac{(y_{it}-\mu _{it}+{\sqrt{\frac{2}{\pi }}}\lambda )}{(\sigma ^2+\lambda ^2)^{\frac{1}{2}}}\right) , \end{aligned}$$

(3)

where ${\varvec{\nu }}=({\varvec{\theta }}, {\varvec{\tau }}, {\varvec{\Phi }})$ with ${\varvec{\theta }}=(\mu _0,\sigma ^2,\lambda )$, ${\varvec{\tau }}=(\tau _1,\ldots ,\tau _{R-1})$ and ${\varvec{\Phi }}=({\varvec{\Phi }}_1,\ldots ,{\varvec{\Phi }}_{R})$ such that ${\varvec{\Phi }}_i=(\Phi _{i1},\ldots ,\Phi _{ip}),\ i=1,\ldots ,R$. Also $\phi (\cdot )$ and $\Phi (\cdot )$ denote the density and cumulative distribution function of the normal distribution, respectively. Given data ${\varvec{y}}=(y_{p+1},\ldots ,y_n)$, the conditional likelihood function of the model (2) is given by

$$\begin{aligned}&L({\varvec{\theta }}, {\varvec{\tau }}, {\varvec{\Phi }}|{\varvec{y}})\nonumber \\&\quad = \prod _{i=1}^{R}\prod _{t=p+1}^{T}f_{SN}(Y_{it}| y_{it-1},\ldots ,y_{it-p},{\varvec{\nu }})\nonumber \\&\quad =\prod _{i=1}^{R}\prod _{t=2}^{T}2\phi \left( y_{it};\mu _{it}-{\sqrt{\frac{2}{\pi }}}\lambda ,\sigma ^2+\lambda ^2\right) \Phi \left( \frac{\lambda }{\sigma } \frac{\left( y_{it}-\mu _{it}+{\sqrt{\frac{2}{\pi }}}\lambda \right) }{(\sigma ^2+\lambda ^2)^{\frac{1}{2}}}\right) . \end{aligned}$$

(4)

As it can be seen, due to the complexity of likelihood function (4), there are no analytical form for the ML estimators of the model parameters. Therefore, we provide an EM algorithm to compute the numerical values of these estimators. For this purpose we used the following lemma about stochastic representation of the skew normal distribution as a mixture of half-normal (HN) and normal distribution. We refer the reader to Barr et al. [6] for more details.

Lemma 1

If $Y_t|U_t=u_t\sim N(\mu +\lambda u_t,\sigma ^2)$ and $U_t\sim HN(0,1)$, then $Y_t$ distributed as $SSN(\mu , \sigma ^2,\lambda )$. Also, the joint density of $(Y_t,U_t)$ and conditional distribution of $U_t|Y_t$ are given, respectively, by

$$\begin{aligned} f_{Y_t,U_t}(y_t,u_t)= & {} \frac{1}{\pi \sigma }\exp \left\{ \frac{-1}{2\sigma ^2}(y_t-\mu -\lambda s_t)^2-\frac{u_t^2}{2}\right\} \end{aligned}$$

and

$$\begin{aligned} U_t|Y_t=y_t\sim \mathrm{HN}\left( \frac{\lambda }{\sigma ^2+\lambda ^2}(y_t-\mu ),\frac{\sigma ^2}{\sigma ^2+\lambda ^2}\right) . \end{aligned}$$

Also, we have

$$\begin{aligned} E(U_t|Y_t=y_t)= & {} \eta _{t}+\jmath \delta _{t},\nonumber \\ E(U_t^2|Y_t=y_t)= & {} \eta _{t}^2+\jmath ^2+\jmath \delta _{t}\eta _{t}, \end{aligned}$$

where $\eta _{t}=\frac{\lambda }{\sigma ^2+\lambda ^2}(y_{t}-\mu )$, $\jmath ^2 =\frac{\sigma ^2}{\sigma ^2+\lambda ^2}$ and $\delta _{t} =\frac{\phi (\frac{\eta _{t}}{ \jmath })}{\Phi (\frac{ \eta _{t}}{\jmath })}$.

By using Lemma 1, the model (2) can be written as a mixture of half-normal (HN) and normal distribution as: $Y_{it}|U_{it}=u_{it}\sim N(\mu _{it}-{\sqrt{\frac{2}{\pi }}}\lambda +\lambda u_{it},\sigma ^2)$ with considering $U_{it}\sim HN(0,1)$. Therefore, the joint distribution of incomplete and missing data $(Y_{it},U_{it})$ as the complete data are

$$\begin{aligned} f_{(Y_{it},U_{it})}(y_{it},u_{it})= & {} \frac{1}{{\pi \sigma }} \exp \Bigg \{-\frac{1}{2\sigma ^2}\Bigg [\left( y_{it}-\mu _{it} -\lambda \left( u_{it}-{\sqrt{\frac{2}{\pi }}}\right) \right) ^2+\sigma ^2 u_{it}^2\Bigg ]\Bigg \}.\nonumber \\ \end{aligned}$$

(5)

Considering (5), the complete likelihood and log-likelihood functions are obtained to be

$$\begin{aligned} L_c({\varvec{\theta }}, {\varvec{\tau }}, {\varvec{\Phi }}|{\varvec{y}},{\varvec{u}})= & {} \prod _{i=1}^{R}\prod _{t=p+1}^{T}f_{(Y_{it},U_{it})}(y_{it},u_{it})\\= & {} ({{\pi \sigma }})^{-R(T-p)}\exp \Bigg \{\sum _{i=1}^{R}\sum _{t=p+1}^{T}H_{it}\Bigg \}, \end{aligned}$$

and

$$\begin{aligned} \ell _{c}({\varvec{\theta }}, {\varvec{\tau }}, {\varvec{\Phi }}|{\varvec{y}},{\varvec{u}})= & {} -(R(T-p))\log ({{\pi \sigma }})-\frac{1}{2}\sum _{i=1}^{R}\sum _{t=p+1}^{T}H_{it}, \end{aligned}$$

respectively, where

$$\begin{aligned} H_{it}= & {} (Y_{it}-\mu _{it})^2-2\lambda \left( Y_{it}-\mu _{it}+{\sqrt{\frac{2}{\pi }}}\lambda \right) u_{it}+(\lambda ^2+\sigma ^2)u_{it}^2\\&+2 {\sqrt{\frac{2}{\pi }}}\lambda (Y_{it}-\mu _{it})+\frac{2\lambda ^2}{\pi }. \end{aligned}$$

2.1 The EM Algorithm

In this section, an EM algorithm is developed to estimated the proposed model parameters. In E step, the conditional expectation of complete data log likelihood given incomplete data are obtained to be

$$\begin{aligned} E[\ell _{c}({\varvec{\nu }})|{\varvec{y}}]=-(R(T-p))\log (\pi \sigma )-\frac{(n-1)}{2}\sum _{i=1}^{R}\sum _{t=p+1}^{T}\hat{H_{it}}, \end{aligned}$$

(6)

where

$$\begin{aligned} \hat{H_{it}}= & {} (Y_{it}-\mu _{it})^2-2\lambda \left( Y_{it}-\mu _{it}+ {\sqrt{\frac{2}{\pi }}}\lambda \right) {\hat{u}}_{it}+(\lambda ^2+\sigma ^2){\hat{u}}_{it}^2\\&+2 {\sqrt{\frac{2}{\pi }}}\lambda (Y_{it}-\mu _{it})+\frac{2\lambda ^2}{\pi }, \end{aligned}$$

with, according to Lemma 1,

$$\begin{aligned} {\hat{u}}_{it}= & {} E(U_{it}|Y_{it}=y_{it})=\eta _{t}+\jmath \delta _{t},\\ {\hat{u}}_{it}^2= & {} E(U_{it}^2|Y_{it}=y_{it})=\eta _{t}^2+\jmath ^2+\jmath \delta _{t}\eta _{t}, \end{aligned}$$

where $\eta _{it}=\frac{\lambda }{\sigma ^2+\lambda ^2}(y_{it}-\mu _{it}+{\sqrt{\frac{2}{\pi }}}\lambda )$, $\jmath ^2=\frac{\sigma ^2}{\sigma ^2+\lambda ^2}$ and $\delta _{it}=\frac{\phi (\frac{\eta _{it}}{ \jmath })}{\Phi (\frac{ \eta _{it}}{\jmath })}$. In M step, the algorithm finds values in parameter space that maximize the conditional expectation (6). Given the values of parameters in iteration j, the updated estimates of the model parameters in $(j+1)$-th iteration are obtained to be:

$$\begin{aligned} \hat{\mu _0}^{(j+1)}= & {} \frac{1}{R(T-p)}\left[ \sum _{i=1}^{R}\sum _{t=p}^{T}\left( y_{it}-{\hat{\tau }}_i^{(j)}-\sum _{k=1}^{p}{\hat{\Phi }}_{ik}^{(j)}y_{it-k}-{\hat{\lambda }}^{(j)}{\hat{u}}_{it}+ {\sqrt{\frac{2}{\pi }}}{\hat{\lambda }}^{(j)}\right) \right] ,\nonumber \\ {\hat{\lambda }}^{(j+1)}= & {} \frac{\sum _{i=1}^{R}\sum _{t=p+1}^{T}\left[ \left( {\hat{u}}_{it}- {\sqrt{\frac{2}{\pi }}}\right) \left( y_{it}-{\hat{\mu }}_{it}^{(j)}\right) \right] }{\sum _{i=1}^{R}\sum _{t=p+1}^{T}\left[ {\hat{u}}_{it}^2-2 {\sqrt{\frac{2}{\pi }}}{\hat{u}}_{it}+\frac{2}{\pi }\right] },\nonumber \\ {\hat{\sigma }}^{2(j+1)}= & {} \frac{1}{R(T-p)}\left[ \sum _{i=1}^{R}\sum _{t=p+1}^{T}\left[ \left( y_{it}-{\hat{\mu }}_{it}^{(j)}\right) ^2-2{\hat{\lambda }}^{(j)}\left( y_{it}-{\hat{\mu }}_{it}^{(j)}+ {\sqrt{\frac{2}{\pi }}}{\hat{\lambda }}^{(j)}\right) {\hat{u}}_{it}\right. \right. \nonumber \\&\left. \left. +{\hat{\lambda }}^{2(j)}{\hat{u}}_{it}^2+2 {\sqrt{\frac{2}{\pi }}}{\hat{\lambda }}^{(j)}\left( y_{it}-{\hat{\mu }}_{it}^{(j)}\right) +\frac{2{\hat{\lambda }}^{2(j)}}{\pi }\right] \right] ,\nonumber \\ \hat{\tau _i}^{(j+1)}= & {} \frac{1}{(T-p)}\sum _{t=p}^{T}\left[ y_{it}-{\hat{\tau }}_0^{(j)}-\sum _{k=1}^{p}{\hat{\Phi }}_{ik}^{(j)}y_{it-k} -{\hat{\lambda }}^{(j)}{\hat{u}}_{it}+ {\sqrt{\frac{2}{\pi }}}{\hat{\lambda }}^{(j)}\right] ,\nonumber \\&\quad i=1,\ldots ,R.\nonumber \\ {\hat{\Phi }}_{ih}^{(j+1)}= & {} \frac{1}{\sum _{t=p}^{T}y_{it-h}^2}\left[ \sum _{t=p+1}^{T}y_{it-h}\left( y_{it}-{\hat{\mu }}_0^{(j)}-{\hat{\tau }}_i^{(j)}-{\hat{\lambda }}^{(j)}{\hat{u}}_{it}+ {\sqrt{\frac{2}{\pi }}}{\hat{\lambda }}^{(j)}\right) \right. \nonumber \\&-\left. \sum _{m\ne h}^{T}\sum _{t=p+1}^{T}{\hat{\Phi }}_{im}^{(j)}y_{it-m}y_{it-h}\right] ,\ \ i=1,\ldots ,R,\ \ h=1,\ldots ,p. \end{aligned}$$

(7)

The E and M steps are repeated alternately until a convergence rule holds. See Hajrajabi and Fallah [15] for more details.

3 Asymptotic Confidence Intervals

Since there is no closed form expression for the ML estimators of parameters in proposed model, computing the exact distribution of these estimators is not possible. In this section, the asymptotic distribution of ML estimators are used to construct asymptotic confidence intervals for the parameters.

According to the fundamental asymptotic properties of ML estimators (see, for example, Lehmann [19], p. 525), we have asymptotically normal (AN) distribution as follows,

$$\begin{aligned} {{\hat{{\varvec{\theta }}}}}_\mathrm{ML}\sim & {} \hbox {AN}({\varvec{\theta }},{\varvec{I}}^{-1}({\varvec{\theta }})),\\ {{\hat{{\varvec{\tau }}}}}_\mathrm{ML}\sim & {} \hbox {AN}({\varvec{\tau }},{\varvec{I}}^{-1}({\varvec{\tau }})),\\ {{\hat{{\varvec{\Phi }}}}}_\mathrm{ML}\sim & {} \hbox {AN}({\varvec{\Phi }},{\varvec{I}}^{-1}({\varvec{\Phi }})), \end{aligned}$$

where

$$\begin{aligned} {\varvec{I}}({\varvec{\theta }})= & {} \left[ \begin{array}{ccc} I(\mu _0)&{}\quad I(\mu _0,\lambda )&{}\quad I(\mu _0,\sigma ^2)\\ I(\lambda ,\mu _0)&{}\quad I(\lambda )&{}\quad I(\lambda ,\sigma ^2)\\ I(\sigma ^2,\mu _0)&{}\quad I(\sigma ^2,\lambda )&{}\quad I(\sigma ^2)\\ \end{array}\right] , \\ {\varvec{I}}({\varvec{\tau }})= & {} \left[ \begin{array}{ccc} I(\tau _{1})&{}\quad \ldots &{}\quad \ldots \\ \ldots &{}\quad I(\tau _{2})&{}\quad \ldots \\ \vdots &{}\quad \ddots &{}\quad \vdots \\ \ldots &{}\quad \ldots &{}\quad I(\tau _{R}) \end{array}\right] , \end{aligned}$$

and

$$\begin{aligned} {\varvec{I}}({\varvec{\Phi }})=({\varvec{I}}({\varvec{\Phi }}_1),\ldots ,{\varvec{I}}({\varvec{\Phi }}_{R})), \end{aligned}$$

with

$$\begin{aligned} {\varvec{I}}({\varvec{\Phi }}_i)=\left[ \begin{array}{cccc} I(\Phi _{i1})&{}\quad I(\Phi _{i1},\Phi _{i2})&{}\quad \ldots &{}\quad I(\Phi _{i1},\Phi _{ip})\\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ I(\Phi _{ip},\Phi _{i1})&{}\quad I(\Phi _{ip},\Phi _{i2})&{}\quad \ldots &{}\quad I(\Phi _{ip}) \end{array}\right] , \end{aligned}$$

for $i=1,\ldots ,R$. Letting ${\varvec{\nu }}=({\varvec{\theta }},{\varvec{\tau }},{\varvec{\Phi }})$, the general Fisher information matrix of model given by

$$\begin{aligned} {\varvec{I}}({\varvec{\theta }},{\varvec{\tau }},{\varvec{\Phi }})=\left( \begin{array}{ccc} {\varvec{I}}({\varvec{\theta }}) &{}\quad {\varvec{I}}({\varvec{\theta }},{\varvec{\tau }}) &{}\quad {\varvec{I}}({\varvec{\theta }},{\varvec{\Phi }})\\ {\varvec{I}}({\varvec{\tau }},{\varvec{\theta }})&{}\quad {\varvec{I}}({\varvec{\tau }}) &{}\quad {\varvec{I}}({\varvec{\tau }},{\varvec{\Phi }}) \\ {\varvec{I}}({\varvec{\Phi }},,{\varvec{\theta }}) &{}\quad {\varvec{I}}({\varvec{\Phi }},{\varvec{\tau }}) &{}\quad {\varvec{I}}({\varvec{\Phi }})\\ \end{array} \right) \end{aligned}$$

could be written as

$$\begin{aligned} {\varvec{I}}({\varvec{\nu }},{\varvec{\nu }}^{'})= & {} -E\left[ \frac{\partial ^{2}{\ell }({\varvec{\nu }}|{\varvec{y}})}{\partial \varvec{{\varvec{\nu }}}\partial {\varvec{\nu }}^{'}}\right] \\= & {} -E\left[ \sum _{i=1}^{R}\sum _{t=p+1}^{T}\frac{\partial ^{2}{\ell _{it}}}{\partial \varvec{{\varvec{\nu }}}\partial {\varvec{\nu }}^{'}}\right] . \end{aligned}$$

where

$$\begin{aligned} \ell _{it}= & {} \log {f_\mathrm{SN}(Y_{it}| y_{it-1},\ldots ,y_{it-p},{\varvec{\theta }}, {\varvec{\tau }}, {\varvec{\Phi }})}\\= & {} \log 2-\frac{1}{2}\log 2\pi -\frac{1}{2}\log Q^{'} -\frac{p_{it}}{2}+\log \Phi (m_{it}), \end{aligned}$$

with $Q^{'}=\sigma ^2+\lambda ^2$ and

$$\begin{aligned} p_{it}= & {} \frac{\left( y_{it}-\mu _{it}+{\sqrt{\frac{2}{\pi }}}\right) ^2}{Q^{'}},\\ m_{it}= & {} \frac{\lambda }{\sigma } \frac{\left( y_{it}-\mu _{it}+{\sqrt{\frac{2}{\pi }}}\right) }{Q^{{'}^{\frac{1}{2}}}}. \end{aligned}$$

Also, the second-order derivations of the log-likelihood function with respect to the parameters are given by

$$\begin{aligned} \frac{\partial ^{2}\ell _{it}}{\partial {\varvec{\nu }}\partial {\varvec{\nu }}^{\prime }}= -\frac{1}{2}\frac{\partial ^2\log Q^{'}}{\partial {\varvec{\nu }}\partial {\varvec{\nu }}^{\prime }}-\frac{1}{2}\frac{\partial ^2 p_{it}}{\partial {\varvec{\nu }}\partial {\varvec{\nu }}^{\prime }}+\frac{\partial ^2\log \Phi (m_{it})}{\partial {\varvec{\nu }}\partial {\varvec{\nu }}^{\prime }}, \end{aligned}$$

(8)

where

$$\begin{aligned} \frac{\partial ^2\log \Phi (m_{it})}{\partial {\varvec{\nu }}\partial {\varvec{\nu }}^{\prime }}= & {} \delta _{\Phi }(k_{ij})\Big (\frac{\partial ^2 m_{it}}{\partial {\varvec{\nu }}\partial {\varvec{\nu }}^{\prime }}\Big )+\Delta _{\Phi }({m_{it}})\Big (\frac{\partial m_{it}}{\partial {\varvec{\nu }}}\Big )\Big (\frac{\partial m_{it}}{\partial {\varvec{\nu }}}\Big )'. \end{aligned}$$

with $\delta _{\Phi (s)}=\dfrac{\phi (s)}{\Phi (s)}$ and $\Delta _{\phi }(s)=\delta _{\Phi (s)}(s+\delta _{\Phi (s)})$. The computational details of the second-order derivation of parameters in Eq. (8) are straightforward, see Appendix A. For example, we have

$$\begin{aligned} I(\mu _0)= & {} -E\left[ \sum _{i=1}^{R}\sum _{t=p+1}^{T}\frac{\partial ^{2}{\ell _{it}}}{\partial \varvec{\mu }_0^2}\right] \\= & {} -E\left[ \sum _{i=1}^{R}\sum _{t=p+1}^{T}-\frac{1}{2}\frac{\partial ^2\log Q^{'}}{\partial {\varvec{\nu }}\partial {\varvec{\nu }}^{\prime }}-\frac{1}{2}\frac{\partial ^2 p_{it}}{\partial {\varvec{\nu }}\partial {\varvec{\nu }}^{\prime }}+\frac{\partial ^2\log \Phi (m_{it})}{\partial {\varvec{\nu }}\partial {\varvec{\nu }}^{\prime }}\right] \\= & {} \frac{1}{2}\sum _{i=1}^{R}\sum _{t=p+1}^{T}E\left[ \frac{\partial ^2\log Q^{'}}{\partial {\varvec{\nu }}\partial {\varvec{\nu }}^{\prime }}+\frac{\partial ^2 p_{it}}{\partial {\varvec{\nu }}\partial {\varvec{\nu }}^{\prime }}\right] -E\left[ \frac{\partial ^2\log \Phi (m_{it})}{\partial {\varvec{\nu }}\partial {\varvec{\nu }}^{\prime }}\right] \\= & {} \frac{R(T-p)}{Q^{'}}-\left( \frac{\lambda }{\sigma Q^{{'}^{\frac{1}{2}}}}\right) ^2 \sum _{i=1}^{R}\sum _{t=p+1}^{T} E[\Delta _\phi (m_{it})]. \end{aligned}$$

Thus, the asymptotic $(1-\alpha )\%$ confidence intervals for the model parameters are given by:

$$\begin{aligned} \Big ({{\hat{{\varvec{\theta }}}}}_\mathrm{ML}-Z_{1-\frac{\alpha }{2}}{\sqrt{{\varvec{I}}^{-1}}({{\hat{{\varvec{\theta }}}}}_\mathrm{ML})},&\quad {{\hat{{\varvec{\theta }}}}}_\mathrm{ML}+Z_{1-\frac{\alpha }{2}} {\sqrt{{\varvec{I}}^{-1}({{\hat{{\varvec{\theta }}}}}}_\mathrm{ML})}\Big ),\nonumber \\ \Big ({{\hat{{\varvec{\tau }}}}}_\mathrm{ML}-Z_{1-\frac{\alpha }{2}}{\sqrt{{\varvec{I}}^{-1}({{\hat{{\varvec{\tau }}}}}}_\mathrm{ML})},&\quad {{\hat{{\varvec{\tau }}}}}_\mathrm{ML}+Z_{1-\frac{\alpha }{2}}\sqrt{{\varvec{I}}^{-1}({{\hat{{\varvec{\tau }}}}}_\mathrm{ML})}\Big ),\nonumber \\ \Big ({{\hat{{\varvec{\Phi }}}}}_\mathrm{ML}-Z_{1-\frac{\alpha }{2}}{\sqrt{{\varvec{I}}^{-1}({{\hat{{\varvec{\Phi }}}}}}_\mathrm{ML})},&\quad {{\hat{{\varvec{\Phi }}}}}_\mathrm{ML}+Z_{1-\frac{\alpha }{2}} {\sqrt{{\varvec{I}}^{-1}}({{\hat{{\varvec{\Phi }}}}}_\mathrm{ML})}\Big ). \end{aligned}$$

(9)

As it can be seen in Eq. (9), in Fisher information matrices the ML estimators of parameters are substituted by their corresponding consistent estimators according to large sample theory. See, for example, Lehmann [19] for more details.

4 Simulation Study

In this section, we perform a simulation study to evaluate the proposed methodology. We simulated the data from the model in Eq. (2) where

$$\begin{aligned} \mu _{it}= \tau _0+\tau _i+\Phi _{i1}Y_{it-1},\ \ T=50, 100, 200, 400, \end{aligned}$$

(10)

with $R=3$, $(\mu _0, \sigma ^2)=(0.1, 0.1)$, $(\tau _1, \tau _2, \tau _3)=(1, 2, -3)$ and $(\Phi _{11}, \Phi _{21}, \Phi _{31})=(0.1, 0.9, 0.3)$. In order to evaluate the ability of the proposed model with both symmetric and asymmetric structures, time series data are simulated by considering different values for the skewness parameter $\lambda$ in the set of $\{-2, 0, 2\}$. For assessing the effects of number of observations on ML estimators, we consider a range of variations for T in the set of $\{50, 100, 200, 400\}$. The expected value, relative bias, $\hbox {RB}=E(\frac{{\hat{{\varvec{\nu }}}}}{{\varvec{\nu }}})-1$, and the root of mean squares error (RMSE) of the ML estimator under the above conditions are computed and the results are presented in Table 1. In all computations, the number of repetitions is fixed in 1000. As it can be seen, there exist some negligible biases in estimates of parameters. Also the values of RMSE decreases when the number of observations increases indicating to consistency of the ML estimators.

Table 1 Expected value, relative bias and RMSE of the ML estimators of model parameters

We also considered a situation in which one may vanish the skewness of the data and use a usual normal model. In Table 2, the relative efficiency (RE) of the estimators for the normal (N) model to their counterparts for the skew normal model for different number of observations is computed as $\hbox {RE}({\hat{{\varvec{\nu }}}}_\mathrm{N},{\hat{{\varvec{\nu }}}}_\mathrm{SSN})=\frac{\text {MSE}({\hat{{\varvec{\nu }}}}_\mathrm{SSN})}{\text {MSE}({\hat{{\varvec{\nu }}}}_\mathrm{N})}$. The results indicate the considerably more efficiency of the skew normal in comparison with the normal model, due to the skewed structure of the simulated data for ($\lambda =-\,2, 2$). As it is expected, for $\lambda =0$, there are no significant differences between the values of MSE for the normal and skew normal models.

Table 2 RE of the estimators for the normal model to their counterparts for the skew normal model for different values of $\lambda$ and number of observations

5 Real Example

In this section, we report some empirical results based on the analysis of the daily returns of the Mellat, Saderat and Ansar bank stock of Iran from 01/01/2014 to 01/14/2015 for 222 observations. These data are available at www.tsetmc.com. The descriptive statistics of the daily returns presented for the observations of each bank in Table 3 indicate to the negative skewness of data.

Table 3 Descriptive statistics of the daily return series for the Mellat, Saderat and Ansar bank stock of Iran

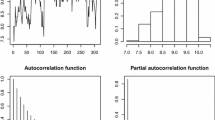
The box plot and the histogram of the observations for three banks presented in Fig. 1 (left and middle panels) indicate unimodality and left-skewed structure of data. Also, partial autocorrelation function (PACF) for three banks is shown in Fig. 1 (right panel) that indicate the dependency degree of observations in order one.

Fig. 1

Box plot (right), the histogram (middle) and the PACF (left) for the Mellat bank (up), Saderat bank (middle) and Ansar bank (down)

The ML estimates of model parameters and their asymptotic confidence interval (ACI) are presented in Table 4.

Table 4 ML estimates and asymptotic confidence interval (ACI) of the skew normal model parameters along with the corresponding values for the normal model

As given in Table 4, the estimates of $\Phi _{11}$ appear to be statistically nonsignificant at the 5% level based on the ACI in both skew normal and normal models. Therefore, the model can be simplified by dropping this nonsignificant parameter. The ML estimates of the reduced model parameters and their asymptotic confidence intervals are presented in Table 5. It is seen that all the estimates are significant at the 5% level.

Table 5 ML estimates and asymptotic confidence interval (ACI) of the skew normal model parameters along with the corresponding values for the normal model after dropping $\Phi _{11}$

We compute the RMSE of prediction defined by $\hbox {RMSEP}={\sqrt{\frac{1}{n-1}\sum _{t=2}^{n}(y_t-\hat{y_t}})^2}$ in order to assess the predictive power of the models and also the AIC and BIC criteria for two models that are provided in Table 6.

Table 6 Goodness-of-fit criteria

The results indicate that the skew normal model has better fit to the data than the normal model. We also check the residuals of model by using Ljung–Box goodness-of-fit test for significant serial correlations. The results show the model appears to be adequate in describing the data.

6 Conclusion

We proposed an ANOVA time series model with assuming the skew normal distribution for innovations in situations that the observations show a serious violation from normality assumption. In these cases, the skew normal family of distributions due to its flexibility can be used for data analysis. The ML approach is used to estimate the parameters of proposed model via the EM algorithm. The simulation results and the empirical application on the daily returns of the Mellat, Saderat and Ansar bank stock of Iran indicated the performance of the proposed method. Also, proposed methodology could be extended to multivariate ANOVA models (MANOVA).

Appendix A

In this appendix, we provide details of the computation for the second-order derivation of parameters in Eq. (8). Letting $a_{it}=y_{it}-m_{it}+{\sqrt{\frac{2}{\pi }}}$, we have:

The second-order derivations correspond to $\mu _0$:

$$\begin{aligned} \frac{\partial ^{2}{\log Q^{'}}}{\partial \mu _0^2}= & {} 0,\quad \frac{\partial ^{2}p_{it}}{\partial \mu _0^2}=\frac{2}{Q^{'}},\quad \frac{\partial m_{it}}{\partial \mu _0}= -\frac{\lambda }{\sigma {Q^{{{'}}{\frac{1}{2}}}}}, \quad \frac{\partial ^{2}m_{it}}{\partial \mu _0^2}=0,\\ \frac{\partial ^{2}{\log Q^{'}}}{\partial \mu _0\partial \lambda }= & {} 0, \quad \frac{\partial ^{2}p_{it}}{\partial \mu _0\partial \lambda }=\frac{-2\left[ {\sqrt{\frac{2}{\pi }}}Q^{'}-2\lambda a_{it}\right] }{Q^{{'}2}},\\ \frac{\partial ^{2}m_{it}}{\partial \mu _0\partial \lambda }= & {} -\frac{\sigma [Q^{{'}{\frac{1}{2}}}-\lambda ^2Q^{{'}{\frac{-1}{2}}} ]}{\sigma ^2 Q^{'}},\\ \frac{\partial ^{2}{\log Q^{'}}}{\partial \mu _0\partial \tau _i}= & {} 0,\quad \frac{\partial ^{2}p_{it}}{\partial \mu _0\partial \tau _i}=\frac{2}{Q^{'}}\quad \frac{\partial ^{2}m_{it}}{\partial \mu _0\partial \tau _i}=0,\\ \frac{\partial ^{2}{\log Q^{'}}}{\partial \mu _0\partial \phi _{ik}}= & {} 0,\quad \frac{\partial ^{2}p_{it}}{\partial \mu _0\partial \phi _{ik}}=\frac{2}{Q^{'}}y_{it-k},\quad \frac{\partial ^{2}m_{it}}{\partial \mu _0\partial \phi _{ik}}=0,\\ \frac{\partial ^{2}p_{it}}{\partial \mu _0\partial \sigma ^2}= & {} 0\quad \frac{\partial ^{2}p_{it}}{\partial \mu _0\partial \sigma ^2}=\frac{2}{Q^{{'}2}}a_{it},\quad \frac{\partial ^{2}m_{it}}{\partial \mu _0\partial \sigma ^2} =\frac{\lambda }{2}(\sigma ^2 Q^{'})^{-\frac{3}{2}}(2\sigma ^2+\lambda ^2). \end{aligned}$$

The second-order derivations correspond to $\lambda$:

$$\begin{aligned} \frac{\partial ^{2}{\log Q^{'}}}{\partial \lambda ^2}= & {} 2,\\ \frac{\partial ^{2}p_{it}}{\partial \lambda ^2}= & {} \frac{1}{Q^{{'}4}}\left[ \left[ \frac{4}{\pi }Q^{'}+4{\sqrt{\frac{2}{\pi }}}\lambda a_{it}-2\left( a_{it}^2+2{\sqrt{\frac{2}{\pi }}}\lambda \right) \right] Q^{{'}2}\right. \\&\left. -8\lambda Q^{'}\left[ {\sqrt{\frac{2}{\pi }}}a_{it}Q^{'}-\lambda a_{it}^2\right] \right] ,\\ \frac{\partial m_{it}}{\partial \lambda }= & {} \frac{1}{Q^{'}\sigma ^2}\left[ \left[ a_{it}+{\sqrt{\frac{2}{\pi }}}\lambda \right] (Q^{'}\sigma ^2)^{\frac{1}{2}}-\sigma (Q^{'})^{-\frac{1}{2}}\lambda ^2 a_{it}\right] ,\\ \frac{\partial ^{2}m_{it}}{\partial \lambda ^2}= & {} \frac{1}{\sigma ^4 Q^{{'}2}}\left[ \left[ 2{\sqrt{\frac{2}{\pi }}}\sigma Q^{{'}{\frac{1}{2}}}+\sigma \lambda Q^{{'}{-\frac{1}{2}}}\left( a_{it}+{\sqrt{\frac{2}{\pi }}}\lambda \right) \right. \right. \\&\left. -\sigma \left( Q^{{'}{-\frac{3}{2}}}\lambda ^3+2\lambda Q^{{'}{-\frac{1}{2}}}\right) a_{it}+{\sqrt{\frac{2}{\pi }}}\sigma Q^{{'}{-\frac{1}{2}}}\lambda ^2\right] Q^{'}\sigma ^2\\&\left. -2\sigma ^2\lambda \left[ Q^{{'}{\frac{1}{2}}}\sigma (a_{it}+{\sqrt{\frac{2}{\pi }}}\lambda )-\sigma Q^{{'}{-\frac{1}{2}}}\lambda ^2 a_{it}\right] \right] ,\\ \frac{\partial ^{2}{\log Q^{'}}}{\partial \lambda \partial \sigma ^2}= & {} 0,\quad \frac{\partial ^{2}p_{it}}{\partial \lambda \partial \sigma ^2}=\frac{1}{Q^{{'}4}} \left[ 2a_{it}{\sqrt{\frac{2}{\pi }}}Q^{{'}2}-2Q^{'}\left[ 2a_{it}{\sqrt{\frac{2}{\pi }}}Q^{'}-2\lambda a_{it}^2\right] \right] ,\\ \frac{\partial ^{2}m_{it}}{\partial \lambda \partial \sigma ^2}= & {} \frac{1}{\sigma ^4 Q^{{'}2}}\left[ \left[ \frac{1}{2}(\sigma ^2 Q^{{'}){-\frac{1}{2}}}(2\sigma ^2+\lambda ^2)a_{it}-\frac{1}{4}a_{it}\lambda ^2 Q^{{'}{-2}}\right] \sigma ^2 Q^{'}\right. \\&\left. -(Q^{'}+\sigma ^2)\left[ \left( a_{it}+{\sqrt{\frac{2}{\pi }}}\lambda \right) (\sigma ^2 Q^{'})^{\frac{1}{2}}- \sigma \lambda ^2 Q^{{'}{-\frac{1}{2}}} a_{it}\right] \right] \\ \frac{\partial ^{2}{\log Q^{'}}}{\partial \lambda \partial \tau _i}= & {} 0,\quad \frac{\partial ^{2}p_{it}}{\partial \lambda \partial \tau _i}=\frac{2}{Q^{'}}\left[ - {\sqrt{\frac{2}{\pi }}}Q^{'}+4\lambda a_{it}\right] ,\\ \frac{\partial ^{2}m_{it}}{\partial \lambda \partial \tau _i}= & {} \frac{1}{\sigma ^2Q^{'}}\left[ \sigma Q^{{'}{-\frac{1}{2}}}\lambda ^2-(\sigma ^2 Q^{'})^{\frac{1}{2}}\right] ,\\ \frac{\partial ^{2}{\log Q^{'}}}{\partial \lambda \partial \phi _{ik}}= & {} 0,\quad \frac{\partial ^{2}p_{it}}{\partial \lambda \partial \phi _{ik}}=\frac{1}{Q^{{'}2}}\left[ -2{\sqrt{\frac{2}{\pi }}}y_{it-k}Q^{'}+4\lambda a_{it} y_{it-k}\right] ,\\ \frac{\partial ^{2}m_{it}}{\partial \lambda \partial \phi _{ik}}= & {} \frac{1}{\sigma ^2Q^{'}}\left[ -y_{it-k}(\sigma ^2 Q^{'})^{\frac{1}{2}}+\sigma \lambda ^2 Q^{{'}{-\frac{1}{2}}}y_{it-k}\right] ,\\ \end{aligned}$$

The second-order derivations correspond to $\sigma ^2$:

$$\begin{aligned} \frac{\partial ^{2}{\log Q^{'}}}{\partial \sigma ^{22}}= & {} 0,~~~~~~~ \frac{\partial ^{2}p_{it}}{\partial \sigma ^{22}}=2Q^{{'}{-3}}a_{it}^2,\\ \frac{\partial m_{it}}{\partial \sigma ^2}= & {} -\frac{\lambda }{2 }a_{it}Q^{{'}{-\frac{3}{2}}}(2\sigma ^2+ \lambda ^2 ),\\ \frac{\partial ^{2}m_{it}}{\partial \sigma ^{22}}= & {} -\frac{\lambda }{2} a_{it}\left[ -\frac{3}{2} Q^{{'}{-\frac{5}{2}}}(2\sigma ^2+ \lambda ^2)+2Q^{{'}{-\frac{3}{2}}}\right] ,\\ \frac{\partial ^{2}{\log Q^{'}}}{\partial \sigma ^2\partial \tau _i}= & {} 0,~~~~~~~ \frac{\partial ^{2}p_{it}}{\partial \sigma ^2\partial \tau _i}=\frac{2}{Q^{{'}2}} a_{it},~~~~~~~~~~\frac{\partial ^{2}m_{it}}{\partial \sigma ^2\partial \tau _i}=\frac{\lambda }{2}Q^{{'}{-\frac{3}{2}}}(2\sigma ^2+ \lambda ^2 ),\\ \frac{\partial ^{2}{\log Q^{'}}}{\partial \sigma ^2\partial \phi _{ik}}= & {} 0,~~~~~\frac{\partial ^{2}p_{it}}{\partial \sigma ^2\partial \phi _{ik}}=\frac{2}{Q^{{'}2}}a_{it}y_{it-k},\\ \frac{\partial ^{2}m_{it}}{\partial \sigma ^2\partial \phi _{ik}}= & {} \frac{\lambda }{2}Q^{{'}{-\frac{3}{2}}}(2\sigma ^2+ \lambda ^2)y_{it-k}.\\ \end{aligned}$$

The second-order derivations correspond to $\tau _i$:

$$\begin{aligned} \frac{\partial ^{2}{\log Q^{'}}}{\partial \tau _i^2}= & {} 0,~~~~~~~ \frac{\partial ^{2}p_{it}}{\partial \tau _i^2}=-\frac{2}{Q^{'}},~~~~~~~\frac{\partial m_{it}}{\partial \tau _i}= -\frac{\lambda }{\sigma Q^{{'}{\frac{1}{2}}}}, ~~~~~~~\frac{\partial ^{2}m_{it}}{\partial \tau _i^2}=0,\\ \frac{\partial ^{2}{\log Q^{'}}}{\partial \tau _i\partial \phi _{ik}}= & {} 0,~~~~~~~\frac{\partial ^{2}p_{it}}{\partial \tau _i\partial \Phi _{ik}}=\frac{2}{Q^{'}}y_{it-k},~~~~~~~\frac{\partial ^{2}m_{it}}{\partial \tau _i\partial \Phi _{ik}}=0,\\ \frac{\partial ^{2}{\log Q^{'}}}{\partial \tau _i\partial \tau _j}= & {} \frac{\partial ^{2}p_{it}}{\partial \tau _i\partial \tau _j}=\frac{\partial ^{2}m_{it}}{\partial \tau _i\partial \tau _j}=0,~~~~~~i\ne j=1,\ldots ,R. \end{aligned}$$

The second-order derivations correspond to $\phi _{ik},~~~~k=1,\ldots ,p$:

$$\begin{aligned} \frac{\partial ^{2}{\log Q^{'}}}{\partial \phi _{ik}^2}= & {} 0,~~~~~~~\frac{\partial ^{2}p_{it}}{\partial \phi _{ik}^2}=-\frac{2}{Q^{'}}a_{it}y_{it-k},\\ \frac{\partial m_{it}}{\partial \phi _{ik}}= & {} -\frac{\lambda }{\sigma Q^{{'}{\frac{1}{2}}}}y_{it-k}, ~~~~~~~\frac{\partial ^{2}m_{it}}{\partial \phi _{ik}^2}=0,\\ \frac{\partial ^{2}{\log Q^{'}}}{\partial \phi _{ij}\partial \phi _{ik}}= & {} 0,~~~~~~~\frac{\partial ^{2}p_{it}}{\partial \phi _{ij}\partial \phi _{ik}}\frac{2}{Q^{'}}y_{it-j}y_{it-k},\\ \frac{\partial ^{2}m_{it}}{\partial \phi _{ij}\partial \phi _{ik}}= & {} 0,~~~j=1,\ldots ,p.\\ \end{aligned}$$