Isolation of the Diamond Graph

Abstract

A graph is H-free if it contains no H as a subgraph. The diamond graph is the graph obtained from $K_4$ by deleting one edge. We prove that if G is a connected graph with order $n\ge 10$, then there exists a subset $S\subseteq V(G)$ with $|S|\le n/5$ such that the subgraph induced by $V(G)\setminus N[S]$ is diamond-free, where N[S] is the closed neighborhood of S. Furthermore, the bound is sharp.

1 Introduction

Let G be a finite simple graph with vertex set V(G) and edge set E(G). The order and the size of a graph G, denoted by |V(G)| and |E(G)|, are its number of vertices and edges, respectively. For a subset $S\subseteq V(G)$, the neighborhood of S is the set $N_G(S)=\{u\in V(G)\setminus S\mid uv\in E(G), v\in S\}$ and closed neighborhood of S is the set $N_G[S]=N_G(S)\cup S$. Thus, $N_G(v)$ and $N_G[v]$ denote the neighborhood and closed neighborhood of $v\in V(G)$, respectively. The degree of v is $d_G(v)=|N_G(v)|$. If the graph G is clear from the context, we will omit it as the subscript. $\delta (G)$ and $\Delta (G)$ denote the minimum and maximum degree of a graph G, respectively. Denote by G[S] the subgraph of G induced by $S \subseteq V(G)$. For terminology and notations not explicitly described in this paper, readers can refer to related books [1, 9].

Given graphs G and H, the notation $G + H$ means the disjoint union of G and H. Then tG denotes the disjoint union of t copies of G. For graphs, we will use equality up to isomorphism, so $G = H$ means that G and H are isomorphic. A graph is H-free if it does not contain H as a subgraph. $\kappa (G)$ and $\gamma (G)$ denote the connectivity and domination number of a graph G, respectively. $P_n, C_n, K_n$ and $K_{p,q}$ stand for the path, cycle, complete graph of order n and complete bipartite graph with partition sets of p and q vertices, respectively.

Let G be a graph and $\mathcal {F}$ a family of connected graphs. A subset $S\subseteq V(G)$ is called an $\mathcal {F}$-isolating set of G if $G-N[S]$ contains no subgraph isomorphic to any $F \in \mathcal {F}$. The minimum cardinality of an $\mathcal {F}$-isolating set of a graph G will be denoted $\iota (G,\mathcal {F})$ and called the $\mathcal {F}$-isolation number of G. When $\mathcal {F}=\{H\}$, we simply write $\iota (G,H)$ for $\iota (G,\{H\})$.

The definition of isolation set is a natural extension of the commonly defined dominating set, which was introduced by Caro and Hansberg [5]. Indeed, if $\mathcal {F}= \{K_1\}$, then an $\mathcal {F}$-isolating set coincides with a dominating set and $\iota (G,\mathcal {F})=\gamma (G)$. A classical result of Ore [7] is that the domination number of a graph G with order n and $\delta (G)\ge 1$ is at most $\frac{n}{2}$. In other words, if G is a connected graph of order $n\ge 2$, then $\iota (G,K_1)\le \frac{n}{2}$. Caro and Hansberg [5] focused mainly on $\iota (G,K_2)$ and $\iota (G,K_{1,k+1})$ and gave some basic properties, examples concerning $\iota (G,\mathcal {F})$ and the relation between $\mathcal {F}$-isolating sets and dominating sets. They [5] proved that if G is a connected graph of order $n\ge 3$ that is not a $C_5$, then $\iota (G,K_2)\le \frac{n}{3}$. Since then, Borg [2] showed that if G is a connected graph of order n, then $\iota (G,\{C_k : k\ge 3\})\le \frac{n}{4}$ unless G is $K_3$. After that, Borg, Fenech and Kaemawichanurat [3] proved that if G is a connected graph of order n, then $\iota (G,K_k)\le \frac{n}{k+1}$ unless G is $K_k$, or $k = 2$ and G is $C_5$. Both the bounds are sharp. Then Zhang and Wu [11] gave the result that if G is a connected graph of order n, then $\iota (G,P_3)\le \frac{2n}{7}$ unless $G\in \{P_3,C_3,C_6\}$, and this bound can be improved to $\frac{n}{4}$ if $G\notin \{P_3,C_7,C_{11}\}$ and the girth of G is at least 7. For more research on isolating sets, refer to [4, 6, 8, 10, 12].

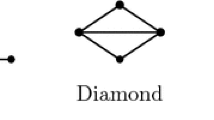
The diamond graph is the graph obtained from $K_4$ by deleting one edge (see Fig. 1). The book graph with p pages, denoted by $B_p$, is the graph that consists of p triangles sharing a common edge. Obviously, $B_2$ is the diamond graph. For the convenience of expression, we use $B_2$ to represent the diamond graph in the sequel.

Fig. 1

Diamond graph

Fig. 2

The 4-regular graph of order 9 Y

In this paper, we consider the isolation number of the diamond graph in a connected graph of a given order.

Theorem 1

If G is a connected graph of order n, then, unless G is the diamond graph, $K_4$, or Y,

$$\begin{aligned} \iota (G,B_2)\le \frac{n}{5}, \end{aligned}$$

where Y is shown in Fig. 2.

2 Main Results

From the proof of Theorem 3.8 in this paper [5], we obtain Lemma 2 and give an example that satisfies the lemma, see Fig. 3. The minimum cardinality of a $B_2$-isolating set of the graph H of order 15 is 3.

Lemma 2

There exists a connected graph G of order n such that $\iota (G,B_2)= \frac{n}{5}$.

Fig. 3

The graph H

We start with two lemmas that will be used repeatedly.

Lemma 3

[2, 11] If G is a graph, $\mathcal {F}$ is a set of connected graphs, $A\subseteq V(G)$ and $B \subseteq N[A]$, then

$$\begin{aligned} \iota (G,\mathcal {F})\le |A|+ \iota (G-B,\mathcal {F}). \end{aligned}$$

In particular, if $A=\{v\}$ and $B=N[A]$, then $\iota (G,\mathcal {F})\le 1+ \iota (G-N[v],\mathcal {F})$.

Lemma 4

[2, 11] Let $\mathcal {F}$ be a family of connected graphs. If $G_1,\ldots ,G_k$ are the distinct components of a graph G, then

$$\begin{aligned} \iota \left( G,\mathcal {F}\right) =\sum _{i=1}^{k}\iota \left( G_i,\mathcal {F}\right) . \end{aligned}$$

For any graph G, let $A,B\subseteq V(G)$ and $A\cap B=\phi$. Denote by E(A, B) the set of edges of G with one end in A and the other end in B and $e(A,B)=|E(A,B)|$. We abbreviate $E(\{x\},B)$ to E(x, B) and $e(\{x\},B)$ to e(x, B).

Now, we first prove Theorem 1 when the order $n\le 9$.

Lemma 5

Let G be a connected graph of order $n\le 9$. Then $\iota (G,B_2)\le \frac{n}{5}$ except for $G\in \{B_2,K_4,Y\}$.

Proof

Let G be a connected graph of order n. The result is trivial if $n \le 4$ or $\iota (G, B_2) = 0$. Suppose $5\le n\le 9$ and $\iota (G, B_2) \ge 1$. Then we need to show that G has a $B_2$-isolating set S with $|S|=1$ except for $G=Y$.

Since $\iota (G, B_2) \ge 1$, it follows G contains $B_2$ and $\Delta (G)\ge 3$. Let $x\in V(G)$ such that $d(x)=\Delta (G)$. Of course, $S=\{x\}$ is a $B_2$-isolating set of G if $G-N[x]$ is $B_2$-free. Otherwise, it implies that $n=8$ with $\Delta (G)= 3$ or $n=9$ with $3\le \Delta (G)\le 4$. We distinguish two cases.

Case 1 $\Delta (G)= 3$ and $n=8$ or 9

Let $u\in V(G)$ such that $d(u)=3$ and $G[N[u]]=B_2$. If $G-N[u]$ is $B_2$-free, then $\iota (G, B_2) = 1\le \frac{n}{5}$. So, suppose that $G-N[u]$ contains $B_2$. For $n=8$, obviously, $G-N[u]=B_2$. Since G is a connected graph and $\Delta (G)= 3$, there is an edge $e=yz$ with $y\in N(u)$ and $z\in V(G)\setminus N[u]$. It is easy to check that $\{y\}$ or $\{z\}$ is a $B_2$-isolating set of G. Hence, $\iota (G, B_2)=1 \le \frac{n}{5}$. Now we prove the case of $n=9$. Let us consider a copy H of $B_2$ in $G-N[u]$ and let w be the remaining vertex of $G-N[u]-V(H)$. If there is an edge $e=yz$ with $y\in N(u)$ and $z\in V(H)$, then $\{y\}$ or $\{z\}$ is a $B_2$-isolating set of G. Otherwise, w is a cut vertex of G and $G-N[w]$ is $B_2$-free. Hence, $\iota (G, B_2)=1 \le \frac{n}{5}$.

Case 2 $\Delta (G)= 4$ and $n=9$

Let $u\in V(G)$ such that $d(u)=4$ and let $F=G-N[u]$. We have $\iota (G, B_2)=1$ if F is $B_2$-free. Assume that F contains $B_2$. Since $|V(F)|=4$, then $F=B_2$ or $F=K_4$. The vertices are labeled as shown in Fig. 4. We distinguish two subcases.

Fig. 4

The labels of the vertices for Case 2

Fig. 5

The labels of the vertices for Subcase 2.2

Subcase 2.1 $F=K_4$. Note that $e(N(u),V(F))\ne 0$. Without loss of generality, suppose $u_1$ is adjacent to v. If $G-N[v]$ is $B_2$-free, $\iota (G, B_2)=1$. Otherwise, $G-N[v]=K_4$ or $B_2$ since $|V(G)\setminus N[v]|=4$. For $G-N[v]=K_4$, we have $G-\{u,u_1,v\}$ is $B_2$-free. Thus, $\{u_1\}$ is a $B_2$-isolating set of G and $\iota (G, B_2) \le \frac{n}{5}$. For $G-N[v]=B_2$, $G-\{u,u_1,v\}$ contains $B_2$ if and only if $u_2$ or $u_4$ is adjacent to at least two vertices of $\{v_1,v_2,v_3\}$. Now we have $\{u_2\}$ or $\{u_4\}$ is a $B_2$-isolating set of G, and hence, $\iota (G, B_2) \le \frac{n}{5}$.

Subcase 2.2 $F=B_2$. The proof for this case is similar to Subcase 2.1. First suppose F has a vertex of degree 3 that is adjacent to one vertex of N(u). Without loss of generality, suppose v, $d_{F}(v)=3$, is adjacent to $u_1$. Then we have $\iota (G, B_2)=1$ if $G-N[v]$ is $B_2$-free. Otherwise, $G-N[v]$ contains $B_2$. For $G-N[v]=K_4$, by the proof of Subcase 2.1, $\iota (G, B_2) \le \frac{n}{5}$. For $G-N[v]=B_2$, $G-\{u,u_1,v\}$ contains $B_2$ when one of the following four cases is true. (1)$u_2v_1\in E(G)$, $u_2v_2\in E(G)$ and $u_3v_1\in E(G)$. (2)$u_2v_2\in E(G)$, $u_2v_3\in E(G)$ and $u_3v_3\in E(G)$. (3)$u_3v_1\in E(G)$, $u_4v_1\in E(G)$ and $u_4v_2\in E(G)$. (4)$u_3v_3\in E(G)$, $u_4v_2\in E(G)$ and $u_4v_3\in E(G)$. Figure 5 shows that the proof methods of the above four cases are similar. So let us just consider the first case. Note that $G-N[u_2]$ contains $B_2$ if and only if $G[u_1,u_4,v_3]=K_3$. Observe that $G=Y$.

Next suppose that only the vertices of degree 2 of F are adjacent to the vertices of N(u). Suppose $v_1$, $d_{F}(v_1)=2$, is adjacent to $u_1$. Then $\iota (G, B_2)=1$ if $G-\{u,u_1,v_1\}$ is $B_2$-free. Otherwise, since $e(v,N(u))=e(v_2,N(u))=0$, we have $G[u_2,u_3,u_4,v_3]$ contains $B_2$ as a subgraph. Recall that $\Delta (G)= 4$, then $G[u_2,u_3,u_4,v_3]=B_2$. Moreover, $G-N[v_3]$ is $B_2$-free. Thus, $\iota (G, B_2) \le \frac{n}{5}$.

Hence, in all cases we obtain $\iota (G, B_2) \le \frac{n}{5}$ with $n\le 9$ except for $\iota (B_2, B_2)=1$, $\iota (K_4, B_2)=1$ and $\iota (Y, B_2)=2$. $\square$

Next, we prove Theorem 1 when $\Delta (G)= 3$.

Lemma 6

Let G be a connected graph of order n. $\iota (G',B_2)=\iota (G,B_2)$ if

• (1) $G'$ is obtained from G by attaching one edge to any vertex of G,

• (2) $G'$ is obtained from G by identifying one vertex of a triangle and a vertex of G,

• (3) $G'$ is obtained from $G+K_3$ by adding an edge joining a vertex of $K_3$ and a vertex of G.

Proof

(1) Let S be a minimum $B_2$-isolating set of G. Then, clearly, S is a $B_2$-isolating set of $G'$, and thus, $\iota (G',B_2)\le \iota (G,B_2)$. Let $S'$ be a minimum $B_2$-isolating set of $G'$ and let x be the vertex of $V(G')\setminus V(G)$. Note that $S'\setminus \{x\}$ is a $B_2$-isolating set of G. Thus, $\iota (G,B_2)\le \iota (G',B_2)$. Now the both inequalities imply the result.

(2) and (3) can be proved similarly as (1). $\square$

Lemma 7

Let G be a connected graph of order n. If $\Delta (G)= 3$, then

$$\begin{aligned} \iota (G,B_2)\le \frac{n}{5} \end{aligned}$$

except for $G\in \{B_2,K_4\}$.

Proof

Let G be a connected graph of order n with $\Delta (G)= 3$. The proof is by induction on n. By Lemma 5, the result is trivial if $n \le 9$ or $\iota (G,B_2)=0$. Thus, suppose that $n\ge 10$ and $\iota (G,B_2)\ge 1$. Since G contains $B_2$, it follows that there exists at least one vertex $u\in V(G)$ such that $d(u)=3$ and $G[N[u]]=B_2$. Let $N(u)=\{u_1,u_2,u_3\}$ and let $u_2$ be the another vertex of the $B_2$ with degree 3. As G is connected and $\Delta (G)= 3$, then either $d(u_1)=3$ or $d(u_3)=3$. We distinguish the following two cases.

Case 1 $d(u_1)=3$ and $d(u_3)=2$ or $d(u_1)=2$ and $d(u_3)=3$

Without loss of generality, suppose $d(u_1)=3$ and $d(u_3)=2$. Let $w\in V(G-N[u])$ and w is adjacent to $u_1$. Define $G'=G-N[u]-w$. Note that $|V(G')|=n-5 \ge 5$. Clearly, $\{u_1\}$ is a $B_2$-isolating set of G if $G'$ is $B_2$-free. Suppose $G'$ contains $B_2$. If $G'$ is connected, by the induction hypothesis, $\iota (G',B_2)\le \frac{n-5}{5}$. Then by Lemmas 3 and 4, we have $\iota (G,B_2)\le |\{u_1\}|+\iota (G',B_2)\le 1+\frac{n-5}{5}=\frac{n}{5}$.

Suppose that $G'$ is disconnected. It is easy to check that $d(w)=3$ and $G'$ has exactly two components. Let $G'=G_1+G_2$. If $G_1\ne B_2$ and $G_2\ne B_2$, the union of a minimum $B_2$-isolating set of $G_1$, a minimum $B_2$-isolating set of $G_2$ and $\{u_1\}$ is a $B_2$-isolating set of G. By the induction hypothesis and Lemma 4,

$$\begin{aligned} \iota (G,B_2)\le 1+\iota (G_1,B_2)+\iota (G_2,B_2)\le 1+\frac{|V(G_1)|}{5}+\frac{|V(G_2)|}{5}=\frac{n}{5}. \end{aligned}$$

If $G_1= B_2$ and $G_2= B_2$, we have $n=13$. Observe that $\{w\}$ is a $B_2$-isolating set of G. Hence, $\iota (G,B_2)\le \frac{n}{5}$. So, it remains to consider the case of exactly one of $\{G_1,G_2\}$ is isomorphic to $B_2$. Suppose that $G_1=B_2$ and $G_2\ne B_2$. Let $w_1$ be the neighbor of w in $G_2$ and let $G''=G'-V(G_1)-w_1$. Note that $|V(G'')|=n-10$.

Fig. 6

The graph when G” is disconnected

If $G''$ is connected and $G''\ne B_2$, by the induction hypothesis, $\iota (G'',B_2)\le \frac{n-10}{5}$. Then the union of $\{w\}$ and a minimum $B_2$-isolating set of $G''$ is a $B_2$-isolating set of G. Thus, $\iota (G,B_2)\le 1+\frac{n-10}{5}\le \frac{n}{5}$. Observe that $n=14$ and $\{w,w_1\}$ is a $B_2$-isolating set of G when $G''= B_2$. We also have $\iota (G,B_2)\le \frac{n}{5}$. Suppose that $G''$ is disconnected. Recall that $\Delta (G)= 3$, then $d(w_1)=3$ and $G''$ has exactly two components. Let $G''=G'_1 + G'_2$ (see Fig. 6). Now let us consider the components $G'_1$ and $G'_2$. If $G'_1\ne B_2$ and $G'_2\ne B_2$, then the union of a minimum $B_2$-isolating set of $G'_1$, a minimum $B_2$-isolating set of $G'_2$ and $\{w\}$ is a $B_2$-isolating set of G. Thus, by Lemmas 3, 4 and the induction hypothesis,

$$\begin{aligned} \iota (G,B_2)\le 1+\iota (G'_1,B_2)+\iota (G'_2,B_2)\le 1+\frac{|V(G'_1)|}{5}+\frac{|V(G'_2)|}{5}\le \frac{n}{5}. \end{aligned}$$

If $G'_1= B_2$ and $G'_2= B_2$, we have $n=18$ and $\{w,w_1\}$ is a $B_2$-isolating set of G. Hence, $\iota (G,B_2)\le \frac{n}{5}$. So, it remains to consider the case of exactly one of $\{G'_1,G'_2\}$ is isomorphic to $B_2$. Suppose that $G'_1=B_2$ and $G'_2\ne B_2$. Note that the union of a minimum $B_2$-isolating set of $G'_2$, the neighbor of $w_1$ in $G'_1$ and $\{w\}$ is a $B_2$-isolating set of G. Therefore, $\iota (G,B_2)\le 1+1+ \frac{|V(G'_2)|}{5}\le \frac{n}{5}$. This completes the proof of Case 1.

Case 2 $d(u_1)=3$ and $d(u_3)=3$

If $N(u_1)=N(u_3)$, denote $G^*=G\setminus (N[u_1]\cup \{u_3\})$. Then $G^*$ is connected and $|V(G^*)|=n-5 \ge 5$ since $\Delta (G)= 3$ and $n\ge 10$. Observe that the union of $\{u_1\}$ and a minimum $B_2$-isolating set of $G^*$ is a $B_2$-isolating set of G. Hence, by the induction hypothesis, $\iota (G,B_2)\le 1+\frac{|V(G^*)|}{5}=\frac{n}{5}$. Otherwise, there exist two vertices $w,z\in V(G)$ such that $u_1$ is adjacent to w and $u_3$ is adjacent to z.

We first prove $G-N[u]$ is connected. Let $G'=G-N[u]-w$. Note that this case differs from Case 1 only in that there is an edge between $u_3$ and $G'$. By Lemma 6 and the proof of Case 1, we have $\iota (G,B_2)\le \frac{n}{5}$. Therefore, we omit the proof. Next we treat $G-N[u]$ is disconnected. Since $\Delta (G)=3$, then $G-N[u]$ contains exactly two components and w and z belong to different components. Define $G-N[u]=G_{w}+G_{z}$, where $G_{w}$ contains w and $G_{z}$ contains z. Obviously, if $G_{w}=B_2$ or $G_{z}=B_2$, the union of $\{u_1\}$ and a minimum $B_2$-isolating set of $G_{z}$ or the union of $\{u_3\}$ and a minimum $B_2$-isolating set of $G_{w}$ is a $B_2$-isolating set of G, respectively. Hence, $\iota (G,B_2)\le \frac{n}{5}$. So, suppose that $G_{w}\ne B_2$ and $G_{z}\ne B_2$. Let $G'=G-V(G_{z})-N[u]-w$. By Lemma 6 (3), we have $\iota (G_z,B_2)=\iota (G[V(G_z)\cup \{u,u_2,u_3\}],B_2)$. Similarly, using the same method of Case 1, we have $\iota (G,B_2)\le \frac{n}{5}$. This completes the proof of Lemma 7. $\square$

So far, it remains to consider Theorem 1 when $\Delta (G)\ge 4$.

Lemma 8

The connected graph Y of order 9 has the following properties:

• (1) $\kappa (Y)=4$,

• (2) $\Delta (Y)=\delta (Y)=4$,

• (3) for any two vertices $u,v \in V(Y)$, $|N(u)\cap N(v)|\le 2$,

• (4) for any vertex $u\in V(Y)$, there exists a vertex $v\in V(Y)\setminus \{u\}$ such that the graph induced by $V(Y)\setminus (\{u\}\cup N[v])$ is $P_3$.

Proof

It is easy to check these properties of the graph Y (see Fig. 2). $\square$

Lemma 9

[5, 11] Let G be a graph on n vertices and $\mathcal {F}$ a family of connected graphs and let $A\cup B$ be a partition of V(G). Then

$$\begin{aligned} \iota (G,\mathcal {F})\le \iota (G[A],\mathcal {F}) + \gamma (G[B]). \end{aligned}$$

Lemma 10

Let G be a connected graph of order n. If $\Delta (G)\ge 4$, then

$$\begin{aligned} \iota (G,B_2)\le \frac{n}{5} \end{aligned}$$

except for $G=Y$.

Proof

Let G be a connected graph of order n with $\Delta (G)\ge 4$. The proof is by induction on n. By Lemma 5, the result is trivial if $n \le 9$ or $\iota (G,B_2)=0$. Thus, suppose that $n\ge 10$ and $\iota (G,B_2)\ge 1$. Denote by $d(u)=\Delta (G)$ and $H=G-N[u]$. Obviously, $\iota (G,B_2)=1$ if H is $B_2$-free. If $H=B_2$ or $K_4$, $\iota (G,B_2)\le 1+1= 2\le \frac{n}{5}$ for $n\ge 10$. If $H=Y$, then $\Delta (G)\ge 5$. Hence, we have $n\ge 15$ and $\iota (G,B_2)\le 1+\iota (Y,B_2)=3 \le \frac{n}{5}$. Suppose that $H\ne B_2, K_4,Y$. By Lemmas 3, 7 and the induction hypothesis, it is easy to check that $\iota (G,B_2)\le \frac{n}{5}$ when H is connected. Therefore, let $H=G_1+ G_2+ \cdots + G_k$ with $k\ge 2$ and $|V(G_i)|=n_i$ for $i=1,2,\ldots ,k$. If H does not contain $B_2, K_4$ or Y as a component, by Lemmas 3, 4, 7 and the induction hypothesis, we have

$$\begin{aligned} \iota (G,B_2)\le |\{u\}|+\sum _{i=1}^{k}\iota (G_i,B_2)\le 1+\frac{n_1}{5}+\frac{n_2}{5}+\cdots +\frac{n_k}{5}=\frac{n-\Delta (G)+4}{5}. \end{aligned}$$

Since $\Delta (G)\ge 4$, then $\iota (G,B_2)\le \frac{n}{5}$.

Next suppose that at least one component of H is $B_2, K_4$ or Y. We sort the components of H in the order of $K_4$, Y, $B_2$ with one vertex of degree 3 of $B_2$ is adjacent to one vertex of N(u), $B_2$ with only vertices of degree 2 of $B_2$ are adjacent to vertices of N(u) and others. Then $G_1$ is isomorphic to $K_4$, Y, or $B_2$. Let $N(u)=\{u_1,u_2,\ldots ,u_{\Delta (G)}\}$. Since G is connected, without loss of generality, suppose $N(u_1)\cap V(G_1)\ne \phi$. Denote $G^*=G-u_1-V(G_1)$. Obviously, $|V(G^*)|\ge 5$.

Case 1 $G^*$ is connected.

Subcase 1.1 $G_1=K_4$. If $G^*= Y$, we have $n=14$ and $\Delta (G)= 5$. By Lemma 8 (4), there exists a vertex $v\in V(G^*)$ such that the graph induced by $G^*-u-N[v]$ is $P_3$. Since $\Delta (G)= 5$, we have $\{u_1,v\}$ is a $B_2$-isolating set of G, and hence, $\iota (G,B_2)\le 2 \le \frac{n}{5}$. If $G^*\ne Y$, by the induction hypothesis and Lemma 7, $\iota (G^*,B_2)\le \frac{n-5}{5}$. Then, by Lemma 9, $\iota (G,B_2)\le \gamma (G[V(G_1)\cup \{u_1\}])+\iota (G^*,B_2)\le 1+\frac{n-5}{5}=\frac{n}{5}$.

Subcase 1.2 $G_1=Y$. Let x be a neighbor of $u_1$ in $V(G_1)$. If $G^*= Y$, we have $n=19$ and $\Delta (G)= 5$. Then, by Lemma 8 (4), there exist a vertex $v_1\in V(G^*)$ such that the graph induced by $G^*-u-N[v_1]$ is $P_3$ and a vertex $v_2\in V(G_1)$ such that the graph induced by $G_1-x-N[v_2]$ is $P_3$. Then $\{v_1,u_1,v_2\}$ is a $B_2$-isolating set of G and $\iota (G,B_2)\le 3\le \frac{n}{5}$. If $G^*\ne Y$, similar to Subcase 1.1, $\iota (G,B_2)\le \gamma (G[V(G_1)\cup \{u_1\}])+\iota (G^*,B_2)\le 2+\frac{n-10}{5}=\frac{n}{5}$.

Subcase 1.3 $G_1=B_2$ and there is one vertex of degree 3 of $V(G_1)$ is adjacent to $u_1$. Let x be a neighbor of $u_1$ in $V(G_1)$ and $d_{G[V(G_1)]}(x)=3$. If $G^*= Y$, we have $n=14$ and $\Delta (G)= 5$. Then, similarly, there exists $v\in V(G^*)$ such that $G^*-u-N[v]=P_3$. Define $P=P_3$. If $G^*-N[u_1]-N[v]$ has no $B_2$, then $\iota (G,B_2)\le 2\le \frac{n}{5}$. Otherwise, let $N(x)=\{x_1,x_2,x_3\}$ and let $d_{G[V(G_1)]}(x_2)=3$. Observe that $G^*-N[u_1]-N[v]$ contains $B_2$ if and only if $e(V(P),x_1)=3$ or $e(V(P),x_3)=3$. Assume that $e(V(P),x_3)=3$, then $d(x_3)=5$. By Lemma 8 (1), $G-(N[x_3]\setminus \{x\})$ is a connected graph of order 9. Since $G-(N[x_3]\setminus \{x\})\ne Y$, by Lemmas 3 and 5,

$$\begin{aligned} \iota (G,B_2)\le |\{x_3\}|+ \iota (G-(N[x_3]\setminus \{x\}),B_2)\le 1+1\le \frac{n}{5}. \end{aligned}$$

If $G^*\ne Y$, similar to Subcase 1.1, $\iota (G,B_2)\le \gamma (G[V(G_1)\cup \{u_1\}])+\iota (G^*,B_2)\le 1+\frac{n-5}{5}=\frac{n}{5}$.

Subcase 1.4 $G_1=B_2$ and only vertices of degree 2 of $V(G_1)$ are adjacent to $u_1$. Let x be a neighbor of $u_1$ in $V(G_1)$ and $d_{G[V(G_1)]}(x)=2$ and Let $d_{G[V(G_1)]}(x_2)=2$. Note that the two remaining vertices of $V(G_1)\setminus \{x,x_2\}$ have degrees of 3 in G. First we prove the case of $u_1\in N(x_2)$ and the case of $u_1\notin N(x_2)$ and $|N(x_2)\cap N(u)|\le 1$ . If $G^*= Y$, we have $n=14$ and $\Delta (G)= 5$. By Lemma 8 (4), there exists $v\in V(G^*)$ such that $G^*-u-N[v]=P_3$. Since $\Delta (G)= 5$, then $\{u_1,v\}$ is a $B_2$-isolating set of G and $\iota (G,B_2)\le 2 \le \frac{n}{5}$. If $G^*\ne Y$, by the induction hypothesis, Lemmas 6 (1) and 7, $\iota (G,B_2)\le 1+\frac{n-5}{5}=\frac{n}{5}$. It remains the case of $u_1\notin N(x_2)$ and $|N(x_2)\cap N(u)|\ge 2$, we will deal with it later.

Case 2 $G^*$ is disconnected.

It implies that $E(V(G_i),N(u))=E(V(G_i),u_1)$ for some $i\in \{2,3,\ldots ,k\}$. Let us denote the components satisfying $E(V(G_i),N(u))=E(V(G_i),u_1)$ as $G_{11},G_{12},\ldots ,G_{1t}$, $t\ge 1$. Let $G_u$ be the component contains u in $G^*$. Then $G^*=G_{11}+G_{12}+\cdots +G_{1t}+G_u$. Assume that there are $s_1B_2$, $s_2K_4$ and $s_3Y$ in $\{G_{11},G_{12},\ldots ,G_{1t}\}$.

Subcase 2.1 $G_1=K_4$. Let x be a neighbor of $u_1$ in $V(G_1)$ and let $N(x)=\{x_1,x_2,x_3\}$. It is easy to check that $\iota (G,B_2)\le 1+\frac{|V(G_{11})|}{5}+\cdots +\frac{|V(G_{1t})|}{5}+\frac{|V(G_u)|}{5}=\frac{n}{5}$ if $G_{11},G_{12},\ldots ,G_{1t},G_u\notin \{B_2,K_4,Y\}$. If $G_u=K_4$, then $\Delta (G)=4$. Hence, by Lemmas 3, 4, 7 and the induction hypothesis,

$$\begin{aligned}&\iota (G,B_2)\le |\{u_1\}|+\sum _{i=1}^{t}\iota \left( G_{1i}-N[u_1],B_2\right) \le 1+s_3\\&\quad +\frac{n-(5+4+4s_1+4s_2+9s_3)}{5}\le \frac{n}{5}. \end{aligned}$$

If $G_u=B_2$, then $\Delta (G)=4$. Note that $G[N[u]\cup V(G_1)]-\{u,u_1,x\}$ contains $B_2$ if and only if $e(u_2,\{x_1,x_2,x_3\})= 2$ or $e(u_4,\{x_1,x_2,x_3\})= 2$. Without loss of generality, suppose $e(u_2,\{x_1,x_2,x_3\})= 2$. Then $d(u_2)=4$ and $G-N[u_2]$ is a connected graph of order $n-5$ or the union of a connected graph of order $n-6$ and an isolated vertex. By Lemma 8, $G-N[u_2]$ does not contain Y as an induced subgraph. Hence, by the induction hypothesis and Lemma 7,

$$\begin{aligned} \iota (G,B_2)\le |\{u_2\}|+\iota (G-N[u_2],B_2)\le 1+\frac{n-5}{5}=\frac{n}{5}. \end{aligned}$$

If $G_u=Y$, by Lemma 8 (4), there exists $v\in V(G_u)$ such that $G_u-u-N[v]=P_3$. Note that $\Delta (G)=5$, then

$$\begin{aligned}&\iota (G,B_2)\le |\{u_1,v\}|+\sum _{i=1}^{t}\iota \left( G_{1i}-N[u_1],B_2\right) \le 2+s_3\\&\quad +\frac{n-(5+9+4s_1+4s_2+9s_3)}{5}\le \frac{n}{5}. \end{aligned}$$

Suppose $G_u\ne B_2,K_4,Y$. Then at least one of $\{s_1,s_2,s_3\}$ is not less than one. Obviously,

$$\begin{aligned}&\iota (G,B_2)\le |\{u_1\}|+\sum _{i=1}^{t}\iota \left( G_{1i}-N[u_1],B_2\right) + \iota (G_{u},B_2)\le 1+s_3\\&\quad +\frac{n-(5+4s_1+4s_2+9s_3)}{5}\le \frac{n}{5} \end{aligned}$$

when $e(V(G_u),V(G_1)\setminus \{x\})=0$. For $e(V(G_u),V(G_1)\setminus \{x\})>0$, $G[V(G_u)\cup \{u_1\}\cup V(G_1)]-\{u_1,x\}\ne B_2,K_4$. If $G[V(G_u)\cup \{u_1\}\cup V(G_1)]-\{u_1,x\}=Y$, by Lemma 8 (4), there exists v such that $G[V(G_u)\cup \{u_1\}\cup V(G_1)]-\{u_1,x,u\}- N[v]=P_3$. Then we have

$$\begin{aligned}&\iota (G,B_2)\le |\{u_1,v\}|+\sum _{i=1}^{t}\iota \left( G_{1i}-N[u_1],B_2\right) \le 2+s_3\\&\quad +\frac{n-(2+9+4s_1+4s_2+9s_3)}{5}\le \frac{n}{5}. \end{aligned}$$

Otherwise,

$$\begin{aligned}&\iota (G,B_2)\le |\{u_1\}|+\iota \left( G[V(G_u)\cup V(G_1)\setminus \{x\}],B_2\right) +\sum _{i=1}^{t}\iota \left( G_{1i}-N[u_1],B_2\right) \\&\le 1+s_3+\frac{n-(2+4s_1+4s_2+9s_3)}{5}\le \frac{n}{5}. \end{aligned}$$

Subcase 2.2 $G_1=Y$. Note that none of the components of H is $K_4$. It follows that $s_2=0$. Let x be a neighbor of $u_1$ in $V(G_1)$. It is easy to check that $\iota (G,B_2)\le 2+\frac{|V(G_{11})|}{5}+\cdots +\frac{|V(G_{1t})|}{5}+\frac{|V(G_u)|}{5}=\frac{n}{5}$ if $G_{11},G_{12},\ldots ,G_{1t},G_u\notin \{B_2,K_4,Y\}$. Since $\Delta (G)\ge 5$, we have $G_u\ne B_2,K_4$. If $G_u=Y$, then $\Delta (G)=5$. Similar to the proofs of Subcase 1.2 and Subcase 2.1, we have

$$\begin{aligned} \iota (G,B_2)\le 3+\sum _{i=1}^{t}\iota (G_{1i}-N[u_1],B_2)\le 3+s_3+\frac{n-(19+4s_1+9s_3)}{5}\le \frac{n}{5}. \end{aligned}$$

Suppose $G_u\ne Y$. Then at least one of $\{s_1,s_3\}$ is not less than one. If $e(V(G_u),V(G_1)\setminus \{x\})=0$, we have

$$\begin{aligned}&\iota (G,B_2)\le \iota (G_1+u_1,B_2)+\iota (G_u,B_2)+\sum _{i=1}^{t}\iota (G_{1i}-N[u_1])\le 2+s_3\\&\quad +\frac{n-(10+4s_1+9s_3)}{5}\le \frac{n}{5}. \end{aligned}$$

Otherwise,

$$\begin{aligned}&\iota (G,B_2)\le |\{u_1\}|+\iota (G[V(G_u)\cup V(G_1)\setminus \{x\}],B_2)+\sum _{i=1}^{t}\iota (G_{1i}-N[u_1],B_2)\\&\le 1+s_3+\frac{n-(2+4s_1+9s_3)}{5}\le \frac{n}{5} \end{aligned}$$

since the component of $G[V(G_1)\cup \{u_1\}\cup V(G_u)]-\{u_1,x\}$ is not $B_2,K_4$ or Y.

Subcase 2.3 $G_1=B_2$ and there is one vertex of degree 3 of $V(G_1)$ is adjacent to $u_1$. Note that none of the components of H is $K_4$ or Y. It follows that $s_2=s_3=0$. Let x be a neighbor of $u_1$ in $V(G_1)$ and $d_{G[V(G_1)]}(x)=3$. It is easy to check that $\iota (G,B_2)\le \frac{n}{5}$ if $G_{11},G_{12},\ldots ,G_{1t},G_u\notin \{B_2,K_4,Y\}$. If $G_u=K_4$, by the proof of the case of $G_u=B_2$ in Subcase 2.1, we have $\iota (G,B_2)\le \frac{n}{5}$. If $G_u=B_2$, then $\Delta (G)=4$. Let $N(x)=\{x_1,x_2,x_3\}$ and let $d_{G[V(G_1)]}(x_2)=3$. Define $G'=G[V(G_u)\cup \{u_1\}\cup V(G_1)]-\{u,u_1,x\}$. Note that $G'$ contains $B_2$ when one of the following four cases is true. (1)$u_2x_1\in E(G)$, $u_2x_2\in E(G)$ and $u_3x_1\in E(G)$. (2)$u_2x_2\in E(G)$, $u_2x_3\in E(G)$ and $u_3x_3\in E(G)$. (3)$u_3x_1\in E(G)$, $u_4x_1\in E(G)$ and $u_4x_2\in E(G)$. (4)$u_3x_3\in E(G)$, $u_4x_2\in E(G)$ and $u_4x_3\in E(G)$. We can see that the proof methods of the above four cases are similar. So let us just consider the first case. Then $G-N[u_2]$ is a connected graph with order $n-5$ or the union of a connected graph with order $n-6$ and a isolated vertex. By Lemma 8, $G-N[u_2]$ does not contain Y as an induced subgraph. Thus,

$$\begin{aligned} \iota (G,B_2)\le |\{u_2\}|+\iota (G-N[u_2],B_2)\le \frac{n}{5}. \end{aligned}$$

If $G_u=Y$, we have $\Delta (G)=5$. By Lemma 8 (4), there exists $v\in V(G_u)$ such that $G_u-u-N[v]=P_3$. Denote $P=P_3$. Then $G[V(G_u)\cup \{u_1\}\cup V(G_1)]-\{u,u_1,x\}-N[v]$ contains $B_2$ if and only if $e(x_1,V(P))=3$ or $e(x_3,V(P))=3$. Suppose $e(x_1,V(P))=3$. Then $d(x_1)=5$. By Lemma 8 (1), $G-N[x_1]\setminus \{x\}$ is a connected graph with order $n-5$ and $G-N[x_1]\setminus \{x\}\ne Y$. Therefore,

$$\begin{aligned} \iota (G,B_2)\le |\{x_1\}|+\iota (G-(N[x_1]\setminus \{x\}),B_2)\le \frac{n}{5}. \end{aligned}$$

Next suppose $G_u\notin \{B_2,K_4,Y\}$. Then $s_1\ge 1$. Obviously,

$$\begin{aligned} \iota (G,B_2)\le |\{u_1\}|+\iota (G_u,B_2)+\sum _{i=1}^{t}\iota (G_{1i}-N[u_1],B_2)\le 1+\frac{n-5-4s_1}{5}< \frac{n}{5} \end{aligned}$$

when $e(V(G_u),V(G_1)\setminus \{x\})=0$. If $e(V(G_u),V(G_1)\setminus \{x\})>0$, then $G[V(G_1)\cup \{u_1\}\cup V(G_u)]-\{u_1,x\}\ne B_2,K_4$. If $G[V(G_1)\cup \{u_1\}\cup V(G_u)]-\{u_1,x\}=Y$, by Lemma 8 (4), there exists v such that $G[V(G_1)\cup \{u_1\}\cup V(G_u)]-\{u,u_1,x\}-N[v]=P_3$. Then we have

$$\begin{aligned} \iota (G,B_2)\le |\{u_1,v\}|+\sum _{i=1}^{t}\iota (G_{1i}-N[u_1],B_2)\le 2+\frac{n-(2+9+4s_1)}{5}< \frac{n}{5}. \end{aligned}$$

Otherwise, $\iota (G,B_2)\le |\{u_1\}|+\iota (G-u_1-x,B_2)\le 1+\frac{n-(2+4s_1)}{5}< \frac{n}{5}$.

Subcase 2.4 $G_1=B_2$ and only vertex of degree 2 of $V(G_1)$ is adjacent to $u_1$. Let x be a neighbor of $u_1$ in $V(G_1)$ and $d_{G[V(G_1)]}(x)=2$ and Let $d_{G[V(G_1)]}(x_2)=2$. Note that the two remaining vertices of $V(G_1)\setminus \{x,x_2\}$ have degrees of 3 in G. First we prove the case of $u_1\in N(x_2)$ and the case $u_1\notin N(x_2)$ and $|N(x_2)\cap N(u)|= 1$. It is easy to check that $\iota (G,B_2)\le \frac{n}{5}$ if $G_2,\ldots ,G_t,G_u\notin \{B_2,K_4,Y\}$. If $G_u=B_2$ or $K_4$, then $\Delta (G)\le 4$, and hence,

$$\begin{aligned} \iota (G,B_2)\le |\{u_1\}|+\sum _{i=1}^{t}\iota (G_{1i}-N[u_1],B_2)\le 1+\frac{n-9-4s_1}{5}< \frac{n}{5}. \end{aligned}$$

If $G_u=Y$, by Lemma 6 (3), $\iota (G_u,B_2)=\iota (V(G_u)\cup (V(G_1)\setminus \{x\}),B_2)$. Furthermore, by Lemma 8 (4), there exists $v\in V(G_u)$ such that $G_u-u-N[v]=P_3$. Then

$$\begin{aligned} \iota (G,B_2)\le |\{u_1,v\}|+\sum _{i=1}^{t}\iota (G_{1i}-N[u_1],B_2)\le 2+\frac{n-5-9-4s_1}{5}< \frac{n}{5}. \end{aligned}$$

Suppose $G_u\ne B_2,K_4,Y$. Then $s_1\ge 1$. We have $\iota (G,B_2)\le |\{u_1\}|+\frac{n-5-4s_1}{5}< \frac{n}{5}$. It remains the case of $u_1\notin N(x_2)$ and $|N(x_2)\cap N(u)|\ge 2$.

In the end, we deal with the case of $u_1\notin N(x_2)$ and $|N(x_2)\cap N(u)|\ge 2$, whether $G^*$ is connected or not. Assume that $u_2,u_3\in N(x_2)$. Denote by $G''=G-\{u_2,u_3,x_1,x_2,x_3\}$. Obviously, if $G''$ is connected, then $G''\notin \{B_2,K_4,Y\}$ and we have $\iota (G,B_2)\le 1+ \frac{n-5}{5}=\frac{n}{5}$. If $G''$ is disconnected, it implies that $E(V(G_i),N(u))=E(V(G_i),\{u_2,u_3\})$ for some $i\in \{2,3,\ldots ,k\}$. Let us denote the components satisfying $E(V(G_i),N(u))=E(V(G_i),\{u_2,u_3\})$ as $G''_{11},G''_{12},\ldots ,G''_{1t}$, $t\ge 1$ and let $G''_u$ be the component contains u in $G''$. Then $G''=G''_{11}+G''_{12}+\cdots +G''_{1t}+G''_u$. Clearly, $G''_u\ne K_4$. By Lemma 8 (3), $G''_u\ne Y$. And from the proof of above Subcase 2.4, we have $\iota (G,B_2)\le \frac{n}{5}$ if any component of $\{G''_{11},G''_{12},\ldots ,G''_{1t}\}$ is $B_2$. In other words, $G''_{1i}\notin \{B_2,K_4,Y\}$ for $i\in \{1,\ldots ,t\}$. Now, we distinguish two cases. If $G''_u\ne B_2$, then

$$\begin{aligned} \iota (G,B_2)\le |\{x_2\}|+\iota (G''_u,B_2)+\sum _{i=1}^{t}\iota (G''_{1i},B_2)\le 1+\frac{n-5}{5}=\frac{n}{5}. \end{aligned}$$

If $G''_u=B_2$, then $\Delta (G)=4$. Note that $|V(G''_u)\cup N[x_2]|=9$ and $\{u_2\}$ is a $B_2$-isolating set of $G[V(G''_u)\cup N[x_2]]$. Hence,

$$\begin{aligned} \iota (G,B_2)\le |\{u_2\}|+\iota (G-(V(G''_u)\cup N[x_2]\setminus \{u_3\}),B_2)\le 1+\frac{n-8}{5}<\frac{n}{5}. \end{aligned}$$

This completes the proof of Lemma 10. $\square$

Proof of Theorem 1

From Lemma 2, we can see that the bound is sharp. It is easy to check that the result of Theorem 1 is true when $\Delta (G)\le 2$. Combining the results in Lemmas 5, 7, 10, we obtain Theorem 1. $\square$