A Strategy for Isolator in the Toucher–Isolator Game on Trees

Abstract

The Toucher–Isolator game was introduced recently by Dowden, Kang, Mikalački and Stojaković. Two players, Toucher and Isolator, alternately claim an edge from a graph, where Toucher plays first. Toucher aims to touch as many vertices as possible, and Isolator aims to minimize the number of vertices that are so touched. Among trees with n vertices, they showed that the star is the best choice for Isolator and they asked for the most suitable tree for Toucher. Later, Räty showed that the answer is the path with n vertices. We give a simple alternative proof of this result. The method to determine where Isolator should play is by breaking down the gains and losses in each move of both players.

1 Introduction

A Maker–Breaker game, introduced by Erdős and Selfridge [3] in 1973, is a positional game played on the complete graph $K_n$ with n vertices, by two players: Maker and Breaker, who alternately claim an edge from the remaining graph, where Maker plays first. Maker wins if she can build a particular structure (e.g., a clique [1, 6], a perfect matching [9, 11] or a Hamiltonian cycle [9, 10]) from her claimed edges, while Breaker wins if he can prevent this. There are several variants of Maker–Breaker games, many of which are studied recently (see [4, 5, 7, 8]). The Toucher–Isolator game, introduced by Dowden, Kang, Mikalački and Stojaković [2] in 2019, is a quantitative version of a Maker–Breaker game played on a finite graph by two players: Toucher and Isolator, who alternately claim an edge from the remaining graph, where Toucher plays first. A vertex is touched if it is incident to at least one edge claimed by Toucher, and a vertex is untouched if all edges incident to it are claimed by Isolator. The score of the game is the number of untouched vertices at the end of the game when all edges have been claimed. Toucher aims at minimizing the score, while Isolator aims at maximizing the score. For a graph G, let u(G) be the score of the game on G when both players play optimally.

The above-mentioned authors gave general upper and lower bounds for u(G), leaving the asymptotic behavior of $u(C_n)$ and $u(P_n)$ as the most interesting unsolved cases, where $C_n$ is a cycle with n vertices and $P_n$ is a path with n vertices. Later in 2019, Räty [12] determined the exact values of $u(C_n)$ and $u(P_n)$, showing that

$$\begin{aligned} u(C_n)=\left\lfloor \dfrac{n+1}{5}\right\rfloor \quad {\hbox {and}} \quad u(P_n)=\left\lfloor \dfrac{n+3}{5}\right\rfloor . \end{aligned}$$

Moreover, the first set of authors showed that for any tree T with $n\ge 3$ vertices,

$$\begin{aligned} \dfrac{n+2}{8}\le u(T)\le \dfrac{n-1}{2}, \end{aligned}$$

where the upper bound is tight when T is a star, but the only tight example they found for the lower bound is a path with six vertices. Therefore, they asked whether there is an infinite family of tight examples for the lower bound, or if it can be improved for large n.

Later in 2020, Räty [13] improved the lower bound for u(T) by showing that the path $P_n$ is the most suitable tree with n vertices for Toucher.

Theorem 1

Let T be a tree with $n\ge 3$ vertices. Then,

$$\begin{aligned} u(T)\ge \left\lfloor \dfrac{n+3}{5}\right\rfloor . \end{aligned}$$

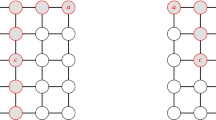
In this paper, we give a simple new proof of this theorem. The argument proceeds as follows. The strategy for Isolator is that he claims an edge which immediately creates an untouched vertex in every move for as long as he can (see Fig. 1: left). When no such an edge exists, we modify the graph before the game continues. The edges claimed by Isolator and their corresponding untouched vertices can be deleted as their disappearance does not change the touched/untouched status of any vertex (see Fig. 1: middle). Observe that the leaves of the remaining tree are touched otherwise Isolator would have claimed the edge incident to it. Then, we delete the edges e claimed by Toucher one by one and, in order to keep the game equivalent to the original game, we replace the edges $u_1v,\dots ,u_tv$ sharing a vertex v with e by new edges $u_1v_1,\dots ,u_tv_t$ keeping their respective Toucher/Isolator status, where the new vertices $v_1,\dots ,v_t$ are considered touched. The resulting graph is a forest all of whose leaves are considered touched (see Fig. 1: right).

Therefore, this motivates us to study the non-leaf Isolator-Toucher game on a forest F which is a variant of the Toucher–Isolator game on F where Isolator plays first. The score of the game is the number of untouched vertices which are not leaves of F, at the end of the game. The aim of Toucher is to minimize the score, while the aim of Isolator is to maximize the score. We remark that this game is inspired by the proof of the lower bound for $u(P_n)$ in [12]. Our main lemma gives a lower bound for the minimum score $\alpha (m,k,\ell )$ of the non-leaf Isolator-Toucher game on F when both players play optimally, among all forests F with m edges, k components, and $\ell$ leaves.

Fig. 1

Strategy for Isolator in the Toucher–Isolator game on a tree and the modification of the graph, where the red dashed and blue dotted edges are Toucher and Isolator edges, respectively

Lemma 2

For non-negative integers m, k and $\ell$,

$$\begin{aligned} \alpha (m,k,\ell )\ge \left\lfloor \dfrac{m+4k-3\ell +4}{5}\right\rfloor . \end{aligned}$$

The strategy for Isolator in the non-leaf Isolator-Toucher game is that, for as long as he can, he claims edges inducing a connected subgraph so that, in every move except the first one, an untouched vertex is created, and then, he repeats in a different part of the forest. The key step is to determine which part of the forest is the most profitable for Isolator to play in. We do this by breaking down the gains and losses in each move of both players.

The rest of this paper is organized as follows. Section 2 is devoted to proving Lemma 2 and then applying it to prove Theorem 1. In Sect. 3, we give some concluding remarks and mention related interesting questions.

2 Proofs

Before proving Lemma 2 and Theorem 1, we give some definitions necessary for the proofs and make observations regarding how to modify the graph after deleting some edges, to keep the game equivalent to the original game, and how much Isolator gains in each move of both players.

For convenience, we first give some names to vertices and edges in a forest. A leaf is a vertex of degree 1. A small vertex is a vertex of degree 2. A big vertex is a vertex of degree at least 3. A big edge is an edge incident to a big vertex. A leaf edge is an edge incident to a leaf. An internal vertex of a subgraph is a vertex adjacent to no vertex outside the subgraph.

We also give some names to paths in a forest. A path component is a component of the forest which is a path. A branch is a path such that the non-endpoint vertices are internal and both endpoints are big. A twig is a path such that the non-endpoint vertices are internal and one endpoint is a leaf while the other is big.

Finally, we define some game related terms. A Toucher edge is an edge claimed by Toucher. An Isolator edge is an edge claimed by Isolator. An Isolator subgraph is a subgraph whose edges are Isolator edges. An Isolator path is an Isolator subgraph which is either a path component, a branch or a twig. A partially played graph is a graph where each edge is either a Toucher edge, an Isolator edge or an unclaimed edge.

Now we show how a partially played graph should be modified after deleting a Toucher edge or an Isolator subgraph, in order to keep the game equivalent to the original game. For a partially played graph G with a Toucher edge uv, we define $G\circleddash uv$ to be the partially played graph obtained from G by

• (i) deleting the vertices u and v, and all edges incident to them,

• (ii) adding new vertices $u_1,\dots ,u_{d(u)-1}$ and joining $u_i$ to $u'_i$ where $N(u)\setminus \{v\}=\{u'_1,\dots ,u'_{d(u)-1}\}$ such that if $uu'_i$ has been claimed by a player, then we let $u_iu'_i$ be claimed by the same player,

• (iii) adding new vertices $v_1,\dots ,v_{d(v)-1}$ and joining $v_i$ to $v'_i$ where $N(v)\setminus \{u\}=\{v'_1,\dots ,v'_{d(v)-1}\}$ such that if $vv'_i$ has been claimed by a player, then we let $v_iv'_i$ be claimed by the same player,

where N(x) and d(x) denote the neighborhood and degree of vertex x, respectively.

Fig. 2

Partially played graph $G\circleddash uv$, where the red dashed and blue dotted edges are Toucher and Isolator edges, respectively

For a partially played graph G with an Isolator subgraph H, we define $G\circleddash H$ to be the partially played graph obtained from G by deleting the edges of H and the internal vertices of H.

Fig. 3

Partially played graph $G\circleddash H$, where H is the subgraph induced by the set of Isolator edges, and the red dashed and blue dotted edges are Toucher and Isolator edges, respectively

Proposition 3

• (i) The non-leaf Isolator-Toucher game on a partially played graph G with a Toucher edge e is equivalent to that on $G\circleddash e$.

• (ii) The Toucher–Isolator game on a partially played graph G with an Isolator subgraph H with r internal vertices is equivalent to that on $G\circleddash H$ with an extra score of r. The non-leaf Isolator-Toucher game on a partially played graph G with the Isolator subgraph H with r non-leaf internal vertices is equivalent to that on $G\circleddash H$ with an extra score of r.

• (iii) The score of the non-leaf Isolator-Toucher game on a partially played graph G when both players play optimally is equal to that on $G-U$, where U is the set of vertices of path components of length 1 in G.

Proof

(i):

Clearly, there is a bijection between the edges of $G-e$ and $G\circleddash e$. The endpoints of the Toucher edge e in the game on G and the new leaves in the game on $G\circleddash e$ are not counted in the score of each game.

(ii):

Clearly, there is a bijection between the edges of $G-E(H)$ and $G\circleddash H$. Deleting an Isolator edge does not change the touched/untouched status of its endpoints. An extra score of r comes from the (non-leaf) internal vertices on H.

(iii):

A player gains nothing by claiming a path component of length 1 because its vertices are leaves which are not counted in the score.

$\square$

Next, in order to determine which part of the forest is the most profitable for Isolator to play in, it is useful to calculate the changes in the number of edges, components and leaves of the forest when deleting a Toucher edge or an Isolator path. Moreover, deleting path components of length 1 also produces a profit.

Table 1 Profit of deleting a Toucher edge

Table 2 Profit of deleting an Isolator path

Table 3 Profit of deleting q path components of length 1

Proposition 4

• (i) Let G be a partially played graph which is a forest with m edges, k components and $\ell$ leaves, and let uv be a Toucher edge in G. Suppose $G\circleddash uv$ is a forest with $m+\varDelta (m)$ edges, $k+\varDelta (k)$ components and $\ell +\varDelta (\ell )$ leaves. Then, the change in $m+4k-3\ell$ is as in Table 1 and the profit $p_T(G,uv)=\varDelta (m+4k-3\ell )+3$ is non-negative.

• (ii) Let G be a partially played graph which is a forest with m edges, k components and $\ell$ leaves, and let P be an Isolator path of length $r+1$ in G. Suppose $G\circleddash P$ is a forest with $m+\varDelta (m)$ edges, $k+\varDelta (k)$ components and $\ell +\varDelta (\ell )$ leaves. Then, the change in $m+4k-3\ell$ is as in Table 2 and the profit $p_I(G,P)=\varDelta (m+4k-3\ell )+r-1$ is non-negative.

• (iii) Let G be a partially played graph which is a forest with m edges, k components, $\ell$ leaves and let U be a set of vertices of q path components of length 1. Suppose $G-U$ is a forest with $m+\varDelta (m)$ edges, $k+\varDelta (k)$ components and $\ell +\varDelta (\ell )$ leaves. Then, the change in $m+4k-3l$ is as in Table 3 and the profit $p_L(G,U)=\varDelta (m+4k-3\ell )$ is equal to q.

Proof

The calculation steps are shown in the tables. The profit $p_T(G,uv)\ge 0$ since the term $+3$ in the definition of $p_T(G,uv)$ comes from $(-1)$ times the minimum value of $\varDelta (m+4k-3\ell )$ in Table 1. The profit $p_I(G,P)\ge 0$ since the term $+(r-1)$ in the definition of $p_I(G,uv)$ comes from $(-1)$ times the minimum value of $\varDelta (m+4k-3\ell )$ in Table 2. $\square$

We are now ready to prove our main lemma which provides a lower bound for $\alpha (m,k,\ell )$ of the non-leaf Isolator-Toucher game on a forest.

Proof of Lemma 2

We use induction on the number of edges m in a forest. Let F be a forest with n vertices, m edges, k components, $\ell$ leaves, a small vertices and b big vertices. First, we suppose that all path components have lengths at most 2, all branches have lengths at most 2, and all twigs have lengths 1. In this case, we shall show that $\left\lfloor \frac{m+4k-3\ell +4}{5}\right\rfloor \le 0$, and so there is nothing to prove. Indeed, since $\sum _{v\in F}d(v)=2m=2(n-k)$, we have $\ell +2a+\sum _{d(v)\ge 3}d(v)=2\ell +2a+2b-2k$. Then, $\ell =\sum _{d(v)\ge 3}d(v)-2b+2k$ and so $\ell \ge b+2k$. Since every edge in a non-path component is adjacent to a big vertex and every path component contains at most 2 edges, it follows that

$$\begin{aligned} m\le \displaystyle \displaystyle \sum _{d(v)\ge 3}d(v)+2k=\ell +2b\le 3\ell -4k \end{aligned}$$

as required.

Now, we suppose that there is either a path component of length at least 3, a branch of length at least 3, or a twig of length at least 2.

Isolator’s strategy is to keep claiming consecutive edges, for as long as he can, to form an Isolator path. Therefore, he only plays within a path component, a branch or a twig, say P. We label the edges of P by $e_1, e_2,\dots , e_s$, respectively, starting from a big edge (if exists). Note that we shall use this convention to label any path component, branch or twig in this proof. Assuming he has claimed the edges $e_t, e_{t+1},\dots , e_{t+r}$, he then claims $e_{t-1}$ or $e_{t+r+1}$ if it is available; otherwise, he stops. That is, he stops if ($t=1$ or $e_{t-1}$ is a Toucher edge) and ($t+r=s$ or $e_{t+r+1}$ is a Toucher edge).

Suppose Isolator stops with edges $e_t, e_{t+1},\dots , e_{t+r}$. Then, these edges form a path Q. So far, both players have claimed $r+1$ edges each since Isolator plays first, and the score is r since Isolator creates an untouched vertex in every move except the first one. We note that the case where Toucher has claimed only r edges because all edges had been claimed can be proved similarly. Let G be the partially played graph at this step. If $f_1,\dots ,f_{r+1}$ are the Toucher edges in G, then let $G_1=G\circleddash f_1\circleddash \dots \circleddash f_{r+1}$ be a forest with $m_1$ edges, $k_1$ components and $\ell _1$ leaves, let $G_2=G_1\circleddash Q$ be a forest with $m_2$ edges, $k_2$ components and $\ell _2$ leaves, and let $G_3=G_2-U$ be a forest with $m_3$ edges, $k_3$ components and $\ell _3$ leaves, where U is the set of vertices of path components of length 1 in $G_2$.

By Proposition 3, the game on G is equivalent to the game on $G_1$ which is equivalent to the game on $G_2$ with an extra score of r, and the score of the game on $G_2$ when both players play optimally is equal to that on $G_3$. Therefore, it follows that

$$\begin{aligned} \alpha (m,k,\ell )&\ge r+\alpha (m_3,k_3,\ell _3) \\&\ge r+\left\lfloor \dfrac{m_3+4k_3-3\ell _3+4}{5}\right\rfloor \quad \text {(by the induction hypothesis)} \\&= r+\left\lfloor \dfrac{m+4k-3\ell +4}{5}+\dfrac{\varDelta _1(m+4k-3\ell )}{5}\right. \\&\quad \left. +\dfrac{\varDelta _2(m+4k-3\ell )}{5} +\dfrac{\varDelta _3(m+4k-3\ell )}{5} \right\rfloor \\&= r+\left\lfloor \dfrac{m+4k-3\ell +4}{5}+\dfrac{\sum _{i=0}^{r} (-3+p_T(G\circleddash f_1\circleddash \dots \circleddash f_{i},f_{i+1}))}{5}\right. \\&\quad \left. +\dfrac{-r+1+p_I(G_1,Q)}{5}+\dfrac{p_{L}(G_2,U)}{5}\right\rfloor \\&\quad \text {(by Proposition }~4 \text { since }Q\text { is an Isolator path in }G_1) \\&= r+\left\lfloor \dfrac{m+4k-3\ell +4}{5}+\dfrac{-3(r+1)+p_T}{5}+\dfrac{-r+1+p_I}{5}+\dfrac{p_{L}}{5}\right\rfloor \\&=\left\lfloor \dfrac{m+4k-3\ell +4}{5}+\dfrac{r+p_T+p_I+p_{L}-2}{5}\right\rfloor , \end{aligned}$$

where

$$\begin{aligned} \varDelta _1(m+4k-3\ell )&=(m_1+4k_1-3\ell _1)-(m+4k-3\ell ), \\ \varDelta _2(m+4k-3\ell )&=(m_2+4k_2-3\ell _2)-(m_1+4k_1-3\ell _1), \\ \varDelta _3(m+4k-3\ell )&=(m_3+4k_3-3\ell _3)-(m_2+4k_2-3\ell _2), \\ p_T&=\sum p_T(G\circleddash f_1\circleddash \dots \circleddash f_{i},f_{i+1}), \\ p_I&=p_I(G_1,Q)\text { and }\, p_L=p_L(G_2,U). \end{aligned}$$

Therefore, it suffices to show that $r+p_T+p_I+p_{L}\ge 2$. Since every term in the sum $r+\sum p_T(G\circleddash f_1\circleddash \dots \circleddash f_{i},f_{i+1})+p_I+p_{L}$ is non-negative by Proposition 4, we shall find a subset of terms whose sum is at least 2. Recall that there is either a path component of length at least 3, a branch of length at least 3 or a twig of length at least 2. The proof is divided into five cases.

Case 1 There is a path component of length 3.

Isolator claims the edge $e_2$ in his first move. If Toucher claims the leaf edge $e_1$ or $e_3$ in some move, then $p_T\ge 2$ by Proposition 4. Otherwise, Isolator claims the edges $e_1$ and $e_3$, hence $r=2$.

Case 2 There is a path component of length at least 4.

Isolator claims the edge $e_3$ in his first move. If Toucher claims the leaf edge $e_1$ in some move, then $p_T\ge 2$ by Proposition 4. If Toucher claims the edge $e_2$ in some move (but not $e_1$), then $G_2$ has a path component $e_1$ of length 1 and so $p_{L}\ge 1$ by Proposition 4. Clearly, $r\ge 1$, hence it follows that $r+p_{L}\ge 2$. Otherwise, Isolator claims the edges $e_1$ and $e_2$, hence $r\ge 2$.

Case 3 There is a branch of length at least 3.

Isolator claims the edge $e_2$ in his first move. If Toucher claims the big edge $e_1$ in some move, then $p_T\ge 1$ by Proposition 4. Clearly, $r\ge 1$, hence it follows that $r+p_T\ge 2$. If Toucher claims the edge $e_3$ in some move, then $p_I\ge 1$ by Proposition 4 since Isolator claims the big edge $e_1$. Clearly, $r=1$, hence it follows that $r+p_I\ge 2$. Otherwise, Isolator claims the edges $e_1$ and $e_3$, hence $r\ge 2$.

Case 4 There is a twig of length 2.

Isolator claims the edge $e_1$ in his first move. If Toucher claims the leaf edge $e_2$ in some move, then $p_T\ge 2$ by Proposition 4. Otherwise, Isolator claims the edge $e_2$, hence $p_I\ge 1$ by Proposition 4 since Isolator claims the big edge $e_1$. Clearly, $r=1$, hence it follows that $r+p_I\ge 2$.

Case 5 There is a twig of length at least 3.

Isolator claims the edge $e_2$ in his first move. If Toucher claims the big edge $e_1$ in some move, then $p_T\ge 1$ by Proposition 4. Clearly, $r\ge 1$, hence it follows that $r+p_T\ge 2$. If Toucher claims the edge $e_3$ in some move, then $p_I\ge 1$ by Proposition 4 since Isolator claims the big edge $e_1$. Clearly, $r=1$, it follows that $r+p_I\ge 2$. Otherwise, Isolator claims the edges $e_1$ and $e_3$, hence $r\ge 2$.

This completes the proof of Lemma 2. $\square$

We now prove Theorem 1 which improves the lower bound for u(T) of the Toucher–Isolator game, by applying the result on the non-leaf Isolator-Toucher game in Lemma 2.

Proof of Theorem 1

Let T be a tree with $m\ge 2$ edges and $\ell$ leaves. We shall show that

$$\begin{aligned} u(T)\ge \left\lfloor \dfrac{m+4}{5}\right\rfloor . \end{aligned}$$

For a partially played graph G, a meta-leaf in G is a leaf in the graph obtained from G by deleting all Isolator edges, and a meta-leaf edge in G is an edge incident to a meta-leaf in G.

Isolator’s strategy is to keep claiming an edge which produces a new untouched vertex in every move, i.e., he claims a meta-leaf edge in the current partially played graph if it is available, otherwise he stops (see Fig. 1: left). That is, he stops when all meta-leaf edges are Toucher edges. We note that he always obtains a score of one in every move because if he claims the edge uv where u is a meta-leaf, then all already played edges incident to u are Isolator edges, and so u becomes untouched. If the process stops after Isolator’s move, i.e., all edges have been claimed by both players, then Isolator obtains a score of $\left\lfloor \frac{m}{2}\right\rfloor \ge \left\lfloor \frac{m+4}{5}\right\rfloor$, as required. Therefore, we may assume that the process stops after Toucher’s move, and in particular, $m\ge 3$.

Suppose Isolator stops after r moves. Let G be the partially played graph at this step. Then, G has $r+1$ Toucher edges and r Isolator edges since Toucher plays first. Let H be the Isolator subgraph of G formed by all Isolator edges, and let $G_1=G\circleddash H$ be a forest with $m_1$ edges, $k_1$ components and $\ell _1$ leaves (see Fig. 1: middle). Since Isolator claimed only meta-leaf edges and all meta-leaf edges in G are Toucher edges, $G_1$ is a tree all of whose leaves are touched, and $k_1=1$. By $m\ge 3$, each leaf of $G_1$ is incident to a distinct Toucher edge, and so $r+1\ge \ell _1$. Let $f_1,\dots ,f_{r+1}$ be the Toucher edges in G, and let $G_2=G_1\circleddash f_1\circleddash \dots \circleddash f_{r+1}$ be the forest with $m_2$ edges, $k_2$ components and $\ell _2$ leaves (see Fig. 1: right).

By Proposition 3 and the fact that the leaves in $G_1$ are touched, the Toucher–Isolator game on G where Isolator plays first is equivalent to the non-leaf Isolator-Toucher game on $G_1$ which is equivalent to the non-leaf Isolator-Toucher game on $G_2$ with an extra score of r. Therefore, it follows that

$$\begin{aligned} u(T)&\ge r+\alpha (m_2,k_2,\ell _2)\\&\ge r+\left\lfloor \dfrac{m+4(1)-3\ell +4}{5}+\dfrac{\varDelta _1(m+4k-3\ell )}{5}\right. \\&\quad \left. +\dfrac{\varDelta _2(m+4k-3\ell )}{5}\right\rfloor \quad \text {(by Lemma }2)\\&= r+\left\lfloor \dfrac{m+4-3\ell +4}{5}+\dfrac{(m_1-m)+4(k_1-1)-3(\ell _1-\ell )}{5}\right. \\&\quad \left. +\dfrac{\sum _{i=0}^{r} (-3+p_T(G_1\circleddash f_1\circleddash \dots \circleddash f_{i},f_{i+1}))}{5}\right\rfloor \\&\ge r+\left\lfloor \dfrac{m-3\ell +8}{5}+\dfrac{(-r)+4(0)-3(\ell _1-\ell )}{5}\right. \\&\quad \left. +\dfrac{-3(r+1)+2\ell _1}{5}\right\rfloor \\&\quad \text {(by Proposition } ~4 \text { since }G_1\text { has }\ell _1\text { leaf edges}) \\&=\left\lfloor \dfrac{m+r-\ell _1+5}{5}\right\rfloor \\&\ge \left\lfloor \dfrac{m+4}{5}\right\rfloor , \quad {(r+1\ge \ell _1)} \end{aligned}$$

where

$$\begin{aligned} \varDelta _1(m+4k-3\ell )&=(m_1+4k_1-3\ell _1)-(m+4-3\ell ), \\ \varDelta _2(m+4k-3\ell )&=(m_2+4k_2-3\ell _2)-(m_1+4k_1-3\ell _1). \end{aligned}$$

$\square$

3 Concluding remarks

As a result of Theorem 1, for any tree T with $n\ge 3$ vertices,

$$\begin{aligned} u(P_n)\le u(T)\le u(S_n), \end{aligned}$$

where $S_n$ is a star with n vertices. Moreover, Theorem 1 implies that, for a forest with k trees, $u(F)\ge \sum _{i=1}^{k}\left\lfloor \frac{n_i+3}{5}\right\rfloor$, where $n_i$ is the number of vertices of the $i^{\text {th}}$ tree in F because, in each move, Isolator can play optimally on the tree Toucher just played. However, the lower bound of $\left\lfloor \frac{n+3k}{5}\right\rfloor$ is not possible because for example, $u(kP_3)=k$ where $kP_3$ is the disjoint union of k copies of $P_3$. Many interesting questions about the Toucher–Isolator game are still open (see [2]). For example, find a 3-regular graph G with n vertices that maximizes u(G). Dowden, Kang, Mikalački and Stojaković showed that the largest proportion of untouched vertices for a 3-regular graph is between $\frac{1}{24}$ and $\frac{1}{8}$.