Abstract
In the present paper, we devote our aspiration to some initial and final value problems for a class of space-fractional diffusion equation with time-dependent diffusivity factor. For the initial value problem (IVP), we investigate the stability of the solution concerning the data and the fractional order. For the final value problem, we prove the ill-posedness and suggest a filter method to regularize the problem. Explicit convergence rate of Hölder type is established. Finally, several numerical examples based on the finite difference approximation and the discrete Fourier transform are performed to demonstrate the effectiveness of the proposed method.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In recent decades, the fractional calculus has become a very bewitching area to researchers due to its challenges and convincing applications in the real world. Besides the common applications of fractional calculus which are now very famous in engineering, the reader may refer to [35] for an updated collection of applications of fractional calculus in the real world including the field of physics, signal and image processing, biology, environmental science, economic, etc. Comparing to the model using the ordinary derivative, the fractional model can be more adequate thanks to the advantages of the memory effect of the fractional derivative. However, this memory effect (or nonlocality) at the same time yields much more difficulties in solving these models (see for instance [48, 49]) for a discussion on the difficulty of the model with fractional derivative).
The space-fractional diffusion equation (SFDE) is derived by replacing the standard Laplacian by its fractional version defined as (1.2). In physical terms, space-fractional diffusion is obtained if one replaces the Gaussian statistics of the classical Brownian motion with a stable probability distribution, resulting in a Levy flight (see [3, 11, 13, 31]). It appears in many practical applications such as in the theory of viscoelasticity and viscoplasticity (mechanics), in the modeling of polymers and proteins (biochemistry), in the transmission of ultrasound waves (electrical engineering), and in the modeling of human tissue under mechanical loads (medicine). The forward problem for SFDE which is a well-posed one, has been studied deeply in recent years (see [9, 12, 29, 32, 37, 41] and the references given there). In comparison with the forward problem, the backward problem for SFDE is usually more difficult to solve because of its ill-posedness. Backward problem for diffusion equation has many applications in practice such as the hydrology [25], material science [28], groundwater contamination [34], image processing [4, 44]. The backward problem here is understood in the following sense: Given the data at the terminal time T, the aspiration is to reconstruct the historical distribution at an earlier time \(t<T\). Particularly, we studied the following backward problem
where \(0< \alpha \le 1\) is the fractional parameter, \(\lambda (t)\) is the time-dependent diffusivity, g(x) is the final data, \(\ell (x,t)\) is the source function and the fractional Laplacian is defined pointwise by
Here, P.V. stands for the principle value
The forward model associated with problem (1.1) is model (2.1) where the data is given at initial time \(t=0\), i.e., \(u(x,0)=\varphi (x)\). Unlike the constant diffusivity which is commonly used in the study of the diffusion equation, the diffusivity in this paper is non-constant, but a time-dependent function. The time-dependent diffusion coefficient appears in many phenomena. For instance, it appears in the diffusion of the population of photogenerated species in organic semiconductors [27], the methane diffusion phenomena in [5], the transient dynamics of diffusion-controlled bimolecular reactions in liquids [24], the hydrodynamic diffusion phenomena [30] and so on. The advantage of non-constant diffusivity was studied very carefully by experiment in [8, 10, 26, 42].
The model (1.1) generalizes some of the previous ones. Particularly, the backward heat conduction problem (BHCP) can be obtained from (1.1) by setting \(\alpha := 1\). The BHCP is a classical ill-posed problem that has been studied extensively for decades. In fact, there is a vast literature on the BHCP including the classical works in [2, 7, 14, 15, 19, 23, 36, 39, 43]. In the current paper, we are more interested in the fractional case of \(0< \alpha <1\) where it is called the backward problem for the space-fractional diffusion equation. The seminal works in this problem refer to Zheng and Zhang in [48,49,50] in which they have studied the problem (1.1) with \(\ell := 0\) and \(\lambda :=1\). It was mentioned in [48] that problem is ill-posed in the sense of Hadamard. However, proof of this conclusion has not been yet provided. In [22], the authors extended the work in [48,49,50] by investigating the problem (1.1) with \(\lambda := 1\). Again, the ill-posedness was also claimed without proof in [22]. Other remarkable works related to problem (1.1) including its nonlinear cases and the Riesz–Feller diffusion cases can be found in [18, 20, 38, 40, 45, 46].
One of the objectives of this paper is to supplement the theory of problem (1.1) by providing detailed proof of its ill-posedness which is not trivial. As a next step, we propose a filter-type regularization method to achieve reliable approximations to the solution of the problem. We emphasize that problem (1.1) is more difficult to deal with, compared to its homogenous or classical versions. The difficulties naturally arise from the nonlocality of fractional derivative and nonzero right-hand side. The nonlocality will make the finite difference matrix is not spare while the nonzero right-hand side makes the problem is more complicated. Here, inspired by the convolution regularization method for the classical backward diffusion equation (\(\alpha = 1\)) in [33], we proposed a filter method basing on the Fourier transform to achieve Hölder approximations to the solution of the investigated problem. Another important part of this paper is devoted to some regularity results of the forward problem (2.1). It is important to observe the forward problem because there always exist relations between forward and backward problems. For instance, using some properties of the forward problem, one may explain or derive the nature of the imposed condition on the backward one. In the current paper, using regularity results of the forward problem, we provide some explanation on the nature of the a priori assumption imposed to the problem in order to establish the Hölder error estimate.
The rest of this paper is divided into four sections. In Sect. 2, we establish some regularity results of the associated forward problem including the fractional parameter-continuity property. Section 3 is devoted to the analysis of the ill-posed structure of problem (1.1) and its treatment by the filter regularization method. The convergence rate is also presented in this section. Section 4 provides two numerical examples, mainly based on the finite difference scheme and the discrete Fourier transform, to illustrate the theoretical results. Finally, we end up this paper by Sect. 5 summarizing the achievements obtained in the paper.
2 Some Regularity Results for the Forward Problem
Throughout this paper, we assume that there exists two positive numbers \(\mathrm {M}_1\) and \(\mathrm {M}_2\) such that
for all \(t \in \left[ {0,T} \right] \). This assumption is quite natural since the diffusivity is usually positive and finite. We begin this section by introducing some notations that are needed for the analysis in the next sections. We always denote \(\left\| {\cdot } \right\| = {\left\| {\cdot } \right\| _{{L^2}({\mathbb {R}})}}\) the standard \(L^2\)-norm. The Fourier transform of a function g will be defined as
and its inversion
For \(s>0\), \({\mathbf{{H}}^s}\left( {\mathbb {R}}\right) \) stands for the standard Sobolev space
For a Banach space X, we denote by \(L^p \left( 0,T;X \right) \) and \(C\left( {[0,T];X} \right) \) the Banach space of real functions \(u:\left[ {0,T} \right] \rightarrow X\) measurable, such that
In this section, we present some properties of the forward problem associated with problem (1.1), i.e., the following problem
For ease of presentation, we refer problem (2.1) with respect to the fractional order \(\alpha \) as problem \((FP_\alpha )\). It is clear that problem \((FP_1)\) stands for the classical forward diffusion problem. Put
Taking the Fourier transform with respect to the space variables for both sides of (2.1), we get
Then, we obtain
The solution of (2.1) is then written as
Using this representation, we establish the following result concerning the continuity of the solution of (2.1) with respect to the fractional parameter. This type of result may be called the parameter continuity result (see [6]).
Theorem 2.1
Let v be the solution of classical diffusion problem \((FP_1)\) and \(v_\alpha \) be the solution of problem \((FP_\alpha )\). Assume that \(\ell \in {L^2}(0,T;{\mathbf{{H}}^{3 - 2\alpha }}({\mathbb {R}}))\) and the initial data \(\varphi \in {{\mathbf {H}}^{3 - 2\alpha }}({\mathbb {R}})\), then there exists a positive constant \({{\mathcal {K}}}:={{\mathcal {K}}}[\varphi ,\ell ]\) such that
Proof
From v be the solution of problem \((FP_1)\), and \(v_\alpha \) be the solution of problem \((FP_\alpha )\), we have
By directly computation, and Hölder inequality, one has
To obtain a stability estimate with respect to the fractional parameter \(\alpha \), the idea is now to evaluate the inside exponential-difference term of \({{\mathcal {I}}}_1\) and \({{\mathcal {I}}}_2\). To do so, let us denote
We have the following cases.
Case 1: \(\xi \in {{\mathbb {D}}_1}\). Using the Lagrange mean value theorem for \(f(x) = {e^{ - x}},x \ge 0\), there exists a positive point \({\xi _1} \in \left[ {{{\left| \xi \right| }^{2\alpha }}\left( {\Lambda (t) - \Lambda (s)} \right) ,{{\left| \xi \right| }^2}\left( {\Lambda (t) - \Lambda (s)} \right) } \right] \) such that
Again, by using Lagrange mean value theorem one more time, but for \(g(\alpha ) = {a^\alpha },a \ge 1\), there exists a positive number \({\alpha _1} \in [0 ,2-2\alpha ]\) such that
Since \(0 \le \log x \le x\) for all \( x \ge 1\), we can write that
Case 2: \(\xi \in {{\mathbb {D}}_2}\). By adapting the same procedure as in Case 1, there exists a positive point \({\xi _2} \in \left[ {{{\left| \xi \right| }^2}\left( {\Lambda (t) - \Lambda (s)} \right) ,{{\left| \xi \right| }^{2\alpha }}\left( {\Lambda (t) - \Lambda (s)} \right) } \right] \) such that
Once again, by the Lagrange mean value theorem, there exists a positive \({\alpha _2} \in [2\alpha ,2]\) such that
Therefore,
Thus, we arrive the following estimates
By combining (2.2), (2.3) and (2.4), we arrive at the final estimate
where \({{\mathcal {K}}}: = {{\mathcal {K}}}[\varphi ,\ell ] = 2\sqrt{2} \left( 1+\Lambda (T)\right) \left( {{{\left\| \varphi \right\| }_{{{\mathbf {H}}^{3 - 2\alpha }}({\mathbb {R}})}} + \sqrt{T} {{\left\| \ell \right\| }_{{L^2}(0,T;{{\mathbf {H}}^{3 - 2\alpha }}({\mathbb {R}}))}}} \right) \). The proof is complete. \(\square \)
Next, we present some properties of the solution of \((FP_\alpha )\).
Theorem 2.2
The following statements hold:
-
a.
For \(0 \le p \le \alpha \), if \({\varphi } \in L^2\left( {\mathbb {R}}\right) \) and \( \ell \in {L^2}\left( {0,T;{L^2 }\left( {\mathbb {R}}\right) } \right) \), then \({v_\alpha }\left( {\cdot ,t} \right) \in {\mathbf{{H}}^{p }}\left( {\mathbb {R}}\right) \) for all \(0 < t \le T\) and
$$\begin{aligned} {\left\| {{v_\alpha }( \cdot ,t)} \right\| _{{\mathbf{{H}}^p}\left( {\mathbb {R}}\right) }} \le {{{\mathcal {D}}}}(t)\left( {\left\| \varphi \right\| + {{\left\| \ell \right\| }_{{L^2}\left( {0,T;{L^2}\left( {\mathbb {R}}\right) } \right) }}} \right) , \end{aligned}$$where \({{\mathcal {D}}}\) is a positive function depends on t defined by
$$\begin{aligned} {{{\mathcal {D}}}}(t) = 2\max \left\{ {\sqrt{\frac{{1 + t{\mathrm{{M}}_\mathrm{{1}}}}}{{t{\mathrm{{M}}_\mathrm{{1}}}}}} ,\sqrt{\frac{T}{{\mathrm{{2}}{\mathrm{{M}}_\mathrm{{1}}}}} + {T^2}} } \right\} . \end{aligned}$$ -
b.
For \(q\ge 0\), if \({\varphi } \in {\mathbf{{H}}^q}\left( {\mathbb {R}}\right) \) and \( \ell \in {L^2}\left( {0,T;{\mathbf{{H}}^q }\left( {\mathbb {R}}\right) } \right) \), then \({v_\alpha } \in {L^\infty }\left( {0,T;{\mathbf{{H}}^q}\left( {\mathbb {R}}\right) } \right) \). More precisely,
$$\begin{aligned} {\left\| {{v_\alpha }} \right\| _{{L^\infty }\left( {0,T;{\mathbf{{H}}^q}\left( {\mathbb {R}}\right) } \right) }} \le \sqrt{2}\max \left\{ {1 ,T} \right\} \left( {{{\left\| \varphi \right\| }_{{\mathbf{{H}}^q}\left( {\mathbb {R}}\right) }} + {{\left\| \ell \right\| }_{{L^2}\left( {0,T;{\mathbf{{H}}^q}\left( {\mathbb {R}}\right) } \right) }}} \right) . \end{aligned}$$ -
c.
If \({\varphi } \in {L^2}\left( {\mathbb {R}}\right) \) and \( \ell \in {L^2}\left( {0,T;{{\mathbf {H}}^\alpha }\left( {\mathbb {R}}\right) } \right) \), then \(v_\alpha \in C\left( {\left( {0,T} \right] ,{L^2}\left( {\mathbb {R}}\right) } \right) \cap {L^\infty }\left( {0,T;{L^2 }\left( {\mathbb {R}}\right) } \right) .\)
-
d.
If \({\varphi } \in {{\mathbf {H}}^{2\alpha }}\left( {\mathbb {R}}\right) \) and \( \ell \in {L^2}\left( {0,T;{{\mathbf {H}}^\alpha }\left( {\mathbb {R}}\right) } \right) \), then \(v_\alpha \in C\left( {\left[ {0,T} \right] ,{L^2}\left( {\mathbb {R}}\right) } \right) \cap {L^\infty }\left( {0,T;{{\mathbf {H}}^\alpha }\left( {\mathbb {R}}\right) } \right) .\)
Proof
a.) Since \({\left\| {{v_\alpha }( \cdot ,t)} \right\| _{{\mathbf{{H}}^p}\left( {\mathbb {R}}\right) }} \le {\left\| {{v_\alpha }( \cdot ,t)} \right\| _{{\mathbf{{H}}^\alpha }\left( {\mathbb {R}}\right) }}\) for all \(0 \le p \le \alpha \), it suffices to prove the part a of the theorem for \(p=\alpha \). By Hölder inequality , we see that
Since \(\Lambda (t) \ge {\mathrm{{M}}_\mathrm{{1}}}t \) for all \(0<t\le T\), we can write that
which means that \({v_\alpha }\left( {\cdot ,t} \right) \in {\mathbf{{H}}^{\alpha }}\left( {\mathbb {R}}\right) \) for all \(t \in \left( {0,T} \right] \). The above estimate can be rewritten as
The part (a) of this theorem is proved.
b.) For \(q \ge 0\), we have
The right-hand side of (2.5) is independent of t, we conclude that \({v_\alpha } \in {L^\infty }\left( {0,T;{\mathbf{{H}}^q}\left( {\mathbb {R}}\right) } \right) \). Moreover, (2.5) also implies that
The part (b) is proved.
c.) By applying the result of part (b) with \(q=0\), we conclude that \({v_\alpha } \in {L^\infty }\left( {0,T;{L^2}\left( {\mathbb {R}}\right) } \right) \). Now we will prove that \(v_\alpha \in C\left( {\left( {0,T} \right] ,{L^2}\left( {\mathbb {R}}\right) } \right) \). For \({t_0} \in \left( {0,T} \right] \), let us evaluate the limit \(\mathop {\lim }\limits _{t \rightarrow t_0^ + } \left\| {{{\widehat{v}}_\alpha }( \cdot ,t) - {{{\widehat{v}}}_\alpha }( \cdot ,{t_0})} \right\| \). We have
Since \(1 - {e^{ - x}} \le x\) for all \(x\ge 0\), it yields that
Then, we can assert that
In view of the Hölder inequality, one has
The remaining task is now to find a bound for \(\left\| {{\mathcal {I}}}_5 \right\| \). In fact, we have
Having disposed of this preliminary step, we can now return to the main estimate
In the same manner, we can prove that \(\mathop {\lim }\limits _{t \rightarrow t_0^ - } \left\| {{v_\alpha }( \cdot ,t) - {v_\alpha }( \cdot ,{t_0})} \right\| = 0\) for all \(t_0\in \left( 0,T\right] \). It implies that
This leads to \(v_\alpha \in C\left( {\left( {0,T} \right] ;{L^2}\left( {\mathbb {R}}\right) } \right) \cap {L^\infty }\left( {0,T;{L^2 }\left( {\mathbb {R}}\right) } \right) \) as claimed.
d.) Applying the result of part b for \(q=\alpha \) which arrives at \({v_\alpha } \in {L^\infty }\left( {0,T;{\mathbf{{H}}^\alpha }\left( {\mathbb {R}}\right) } \right) .\) The remain task is to solve \(\mathop {\lim }\limits _{t \rightarrow {0^ + }} \left\| {{v_\alpha }( \cdot ,t) - {v_\alpha }( \cdot ,0)} \right\| = 0\). For \({{\mathcal {I}}}_4\) and \({{\mathcal {I}}}_5\), the estimate is the same with part (c). The rest is to re-evaluate \({{\mathcal {I}}}_3\). We have
This leads to \(\mathop {\lim }\limits _{t \rightarrow {0^ + }} \left\| {{v_\alpha }( \cdot ,t) - {v_\alpha }( \cdot ,0)} \right\| = 0\). The theorem is completely proved. \(\square \)
3 The Ill-Posedness and Regularization Method for the Backward Problem
This section is devoted to the investigation of the backward problem (1.1) which is the main result of the current paper. Using the same Fourier technique as in Sect. 2, after some elementary calculations, we get
Thus, the exact solution of backward problem (1.1) is obtained by the inverse Fourier transform
Let us take a look at the formula (3.2). It is not difficult to see that (3.2) contains the quantity \({e^{{{\left| \xi \right| }^{2\alpha }}\Lambda (T)}}\) which will go to infinity as \(|\xi |\) tends to infinity. Thus, the solution of problem (1.1) is unstable at the high frequencies of \(\xi \). As a result, the ill-posedness appears. This property is quite consistent with the classical case \(\alpha =1\). To be more precise, we present the following theorem.
Theorem 3.1
The backward problem (1.1) is ill-posed in the Hadamard’s sense.
Proof
The following example demonstrates the ill-posedness of (1.1). For any \(n\in {\mathbb {N}}\) and \(n\ge 2\). Define \({\Omega _n}: = \left\{ {\xi \in {\mathbb {R}};1 \le \xi \le n } \right\} \), let \(g _n \in L^2\left( {\mathbb {R}}\right) \), \({\ell _n} \in {L^2}\left( {0,T;{L^2}\left( {\mathbb {R}} \right) } \right) \) be the measured data such that
where \(\gamma \in \left( 0,1\right) \).
Using Parseval’s identity, we see that
Let u and \(u_n\) be two solutions of problem (1.1) correspond to the data \(\left( {g,\ell } \right) \) and \(\left( {{g_n},{\ell _n}} \right) \), respectively, i.e.,
We know that
This leads to
This proves the ill-posedness of the backward problem (1.1). The proof of this theorem is complete. \(\square \)
As in Theorem 3.1, the solution of backward problem (1.1) is unstable with respect to the data. Thus, there is a demand for the regularization method to mitigate the impact of this ill-posedness. Otherwise, the standard calculation may fail to describe the solution. In addition, the final data in practice is obtained by measurement which always contains error. To model this impact, for a noise level \(\delta \), let us denote that measure data of \(\left( {g,\ell } \right) \) by \(\left( {{g_\delta },{\ell _\delta }} \right) \) and \(\left( {{g_\delta },{\ell _\delta }} \right) \) is naturally required to satisfy the following error bound
As previously mentioned, there are exponential growths in the solution leading to the ill-posedness. Therefore, if one successfully control these growths, then the ill-posedness will be overcome. For the regularization method in the unbounded domain, the convolution regularization introduced in [33, 47] is proved a very effective method. This method may be simply considered as a very interesting application of the convolution properties of Fourier transform. In the current paper, we propose a filter approach which is originally inspired by the convolution regularization in [33, 47]. Rather than dealing with an approximate problem in form of a convolution operator as in [33, 47]. Based on Parseval’s equation, it is equivalent to modifying problem 1 to be equivalent to modifying the Fourier problem of problem 1. In particular, we directly use the filter called \({{\mathbb {F}}}_{\mu ,\beta }\) to regularize the problem (1.1). To be more precise, for \(\mu > 0,\beta \ge 0\) the \({{\mathbb {F}}}_{\mu ,\beta }\) is defined by
Using this filter, we consider the following regularized Fourier problem
Using the same technique as in Sect. 2, the solution of problem (3.4) is obtained by
Equivalently,
To perform the convergence analysis between the regularized and exact solution, we first present the following auxiliary results.
Lemma 3.1
Let \(\beta , r, a>0\). Then, we have
Proof
Applying inequality \(\left( a_1+a_2\right) ^p\le 2^p\left( a_1^p+a_2^p\right) \) for all \(a_1,a_2,p>0.\) We see that
By direct computation, we know that
Hence,
The proof is completed. \(\square \)
Lemma 3.2
Let \(\alpha >0\), and \(0<a<b\). Then, we have
Proof
Consider the following function \(f_2\left( x \right) = \frac{{{x^a}}}{{1 + \alpha {x^b}}}\) for \(x>0\). Then,
which completes the proof Lemma 3.2. \(\square \)
Use Lemmas 3.1 and 3.2, we have the following proposition which is very important for the proof of next theorems.
Proposition 3.1
The following inequality holds
where \(p> 0\).
Proof
By Lemma 3.1, one has
which completes the proof. \(\square \)
Proposition 3.2
The following inequality holds
Proof
In case \( \vartheta \ge 1\), the proof is obvious. In the remaining case, using Lemma 3.2, one has
The proof is completed. \(\square \)
Now, we are in a position to present the convergence estimate. The first result reads as follows.
Theorem 3.2
Let \({v_1 }\) and \({v_2 }\) be two solution of regularized problem (3.4) correspond to the data \(\left( {g_1,\ell _1 } \right) \) and \(\left( {g_2,\ell _2 } \right) \), respectively, then we have
Proof
We have
In view of Parseval’s identity, Lemma 3.2, one has
The proof is complete. \(\square \)
Next, we proceed to show the convergence rate between the regularized and the exact solution. The most important theorem in this section can be stated as follows.
Theorem 3.3
Let \(\delta \in \left( 0,1\right) \). Assume that there exist constants \(p, \mathbf{{E}}_0\) such that the exact solution satisfy the following a priori bound
where \(p>0\), and \( {{{\mathbf {E}}}_0} > \delta {\left( {\frac{p}{{2\alpha \left( {\Lambda \left( T \right) + \beta } \right) }}} \right) ^{\frac{p}{{2\alpha }}}}\). Let the measure data \(\left( {{g_\delta },{\ell _\delta }} \right) \) satisfy (3.3). Let u be the solution of backward problem (1.1) and \(u_{\mu ,\beta }^\delta \) be the solution of the regularized problem (1.1). If the regularization parameter \(\mu , \beta \) is selected by
then for \(0 \le t < T\), the following convergence estimate holds
Proof
Let \(u_{\mu ,\beta }\) be as in (3.6) which corresponds to the exact data, i.e.,
From the triangle inequality, one has
First, we evaluate \({\mathcal {J}}_1\). Using Theorem 3.2, and (3.8) , we obtain
The remaining task is to estimate \({\mathcal {J}}_2\). In fact, we have
By Proposition 3.1, (3.8), and (3.7), we arrive at the following estimates
Plugging (3.11), (3.12) into (3.10), we get the conclusion (3.9). The theorem is proved. \(\square \)
Theorem 3.4
Let \(\delta \in \left( 0,1\right) \). Assume that there exist constants \(\vartheta , \mathbf{{E}}_1\) such that the exact solution satisfies the following a priori bound
where \(\vartheta ,{{{\mathbf {E}}}_1}>0\). Let the measure data the measured data \({g_\delta }\) and the noisy source \({\ell _\delta }\) satisfy (3.3). If the regularization parameter \(\mu , \beta \) are selected by
then for \(0 \le t < T\), the following convergence estimate holds
Proof
Similarly as Theorem 3.3, we know that
By Proposition 3.2, one has
The proof is completed. \(\square \)
Some comments on the a priori bound (3.7). It is well known in the regularization theory that to obtain the convergence rate between the regularized and exact solution, one needs some a priori information on the exact solution. In the present paper, we use an a priori condition as in (3.7). Let \(\varphi \) be the initial status of problem (1.1). At the initial time \(t=0\), the a priori condition (3.7) is equivalent to the assumption that \(\varphi \in {\mathbf{{H}}^p}\left( {\mathbb {R}}\right) \). However, for \(t>0\) and \(0\le p \le \alpha \), it follows from Theorem 2.2 (part a) that one just needs \(\varphi \in L^2({\mathbb {R}})\) and the source function \(\ell \) belongs to \({L^2}\left( {0,T;{L^2}\left( {\mathbb {R}}\right) } \right) \) to result \(u(\cdot ,t) \in {\mathbf{{H}}^p}\left( {\mathbb {R}}\right) \). Hence, the a priori condition (3.7) is not a very strict condition. Therefore, from our point of view, the technique in this paper is applicable to a wide class of functions.
4 The Numerical Illustration
In this section, we will illustrate theoretical results in Sect. 3 through some specific numerical examples. In fact for numerical purposes, we are usually interested in the bounded domain. In this spirit, let L be a positive number, we consider in this section the numerical solution of the following backward problem
For the fractional diffusion model, it is very difficult to find an analytical solution of the problem (4.1). Thus, we are not going to find an analytical solution of (4.1) in this section. Instead, a fully discrete scheme will be adapted to derive an approximation of (4.1). To do so, let us consider the initial problem associated with problem (1.1), i.e., the following problem
Since (4.2) is a well-posed problem, a finite difference scheme will be very effective to numerically solve (4.2). We use the following simulation strategy:
-
Step 1: Using the finite difference scheme to solve (4.2). After this step, one may obtain the final data \(g(x):=u(x,T)\).
-
Step 2: Perturbing the final data to obtain the measured final data
$$\begin{aligned} {g^\varepsilon }({x}) = u({x},T)\left( {1 + \varepsilon \mathrm {rand()}} \right) ,\end{aligned}$$(4.3)where the command rand() returns the random value in (0, 1).
-
Step 3: Using (3.5) to construct the Fourier transform of the regularized solution. In this step, the discrete Fourier transform will be adapted.
-
Step 4: Using the inverse discrete Fourier transform to obtain the regularized solution.
For the finite difference scheme in step 1, we follow the well-known scheme proposed in [21]. For other numerical methods dealing with the fractional Laplacian, the reader may refer to [1, 16, 17]. Denote N and M the number of grid points in the space and time interval, respectively. Let \(\left\{ {{x_j}} \right\} _{j = 0}^N\) be a space-discretization of \([-L,L]\) with the mesh size \(h=\frac{2L}{N}\) and \(\left\{ {{t_m}} \right\} _{m = 0}^{M}\) be a time-discretization of [0, T] with the mesh size \(\rho =\frac{T}{M}\). Let \(u_j^m\) be the finite difference approximation to \(u(x_j,t_m)\). We have:
-
For \(0\le m \le M\), due to the boundary condition, one has
$$\begin{aligned} u_0^m = u_N^m = 0. \end{aligned}$$ -
For \(m=0\), thanks the initial condition of (4.2), for \(0 \le j \le N \), we have
$$\begin{aligned} u_j^0 = \varphi ({x_j}).\end{aligned}$$(4.4) -
For \(1 \le m \le M\) and \(1 \le j \le N-1\), we use the following forward scheme
$$\begin{aligned} \begin{aligned}&u_j^{m + 1} = u_j^m\\&\quad - \frac{{\rho {\lambda _{m+1}}}}{{2\cos \left( {\alpha \pi } \right) {h^\alpha }}}\left( {\sum \limits _{k = 0}^{j + 1} {{{( - 1)}^k}\left( {\begin{array}{*{20}{l}} {2\alpha }\\ k \end{array}} \right) u_{j + 1 - k}^n} + \sum \limits _{k = 0}^{N - j + 1} {{{( - 1)}^k}\left( {\begin{array}{*{20}{l}} {2\alpha }\\ k \end{array}} \right) u_{j - 1 + k}^n} } \right) \\&\quad + \rho \ell \left( {{x_j},{t_{m+1}}} \right) \end{aligned}\nonumber \!\!\!\!\!\\ \end{aligned}$$(4.5)
where \(\lambda _m=\lambda (t_m)\).
Denote \(U^m_{j}=u^\varepsilon ({x_j,t_m})\) the regularized solution with respects to the noisy data \(g^\varepsilon \), the following discrete error measure will be calculated
Here, \({{\mathcal {E}}}(t_m)\) and \({{\mathcal {R}}}_{{\mathcal {E}}}(t_m)\) denote the discrete root mean square error and the relative root mean square error at time \(t_m\). Fixing \(L = 10, T = 1, N = 100, M = 100, \lambda (t)=2t+1\), let us consider the following examples.
Example 1
In this example, we work with a smooth initial data. For \(\alpha = 0.6\), the initial data and source term in example 1 are given by
Example 2
In this example, we work with a non-smooth initial data. For \(\alpha = 0.9\), the initial data and source term in example 2 are given by
With the data as in these example, we have Figs. 1 and 2 and Tables 1 and 2.
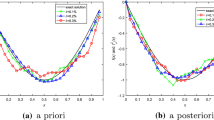
Example 1 with \(\alpha =0.6\): The exact solution (solid line) and regularized solution with \(\varepsilon =10^{-1}\) (asterisk line) and \(\varepsilon =10^{-2}\) (circle line) at various points of time
Example 2 with \(\alpha =0.9\): The exact solution (solid line) and regularized solution with \(\varepsilon =10^{-1}\) (asterisk line) and \(\varepsilon =10^{-2}\) (circle line) at various points of time
5 Conclusion
In this paper, the forward and backward problems associated with space-fractional diffusion equations are investigated. In particular, we derived some regularity results for the forward problem. Next, we provided detailed proof of the ill-posedness of the backward problem and further proposed a regularization method to achieve Hölder approximation to the exact solution. As a potential future work, we wish to study a more general model where the diffusivity factor can be a more general function. For example, \(\lambda := \lambda (x,t)\) or \(\lambda := \lambda (x,t,u)\).
References
Acosta, G., Borthagaray, J.P.: A fractional Laplace equation: regularity of solutions and finite element approximations. SIAM J. Numer. Anal. 55(2), 472–495 (2017)
Ames, K.A., Payne, L.E.: Continuous dependence on modeling for some well-posed perturbations of the backward heat equation. J. Inequal. Appl. 3(1), 51–64 (1999)
Benson, D.A., Meerschaert, M.M., Revielle, J.: Fractional calculus in hydrologic modeling: a numerical perspective. Adv. Water Resources 51, 479–497 (2013)
Carasso, A.S., Sanderson, J.G., Hyman, J.M.: Digital removal of random media image degradations by solving the diffusion equation backwards in time. SIAM J. Numer. Anal. 15(2), 344–367 (1978)
Cheng-Wu, L., Hong-Lai, X., Cheng, G., Wen-biao, L.: Modeling and experiments for the time-dependent diffusion coefficient during methane desorption from coal. J. Geophys. Eng. 15(2), 315–329 (2018)
Dang, D.T., Nane, E., Nguyen, D.M., Tuan, N.H.: Continuity of solutions of a class of fractional equations. Potential Anal. 49(3), 423–478 (2018)
Dang, D.T., Nguyen, H.T.: Regularization and error estimates for nonhomogeneous backward heat problems. Electron. J. Differ. Equ. No. 4, 10 (2006)
Dudko, O.K., Berezhkovskii, A.M., Weiss, G.H.: Time-dependent diffusion coefficients in periodic porous materials. J. Phys. Chem. B 109(45), 21296–21299 (2005)
Ervin, V.J., Heuer, N., Roop, J.P.: Numerical approximation of a time dependent, nonlinear, space-fractional diffusion equation. SIAM J. Numer. Anal. 45(2), 572–591 (2007)
Giestas, M., Joyce, A., Pina, H.: The influence of non-constant diffusivities on solar ponds stability. Int. J. Heat Mass Transf. 40(18), 4379–4391 (1997)
Gorenflo, R., Mainardi, F.: Random walk models for space-fractional diffusion processes. Fract. Calc. Appl. Anal. 1(2), 167–191 (1998)
Gorenflo, R., Mainardi, F.: Random walk models approximating symmetric space-fractional diffusion processes. In: Problems and Methods in Mathematical Physics, pp. 120–145. Springer (2001)
Hanyga, A.: Multidimensional solutions of space-fractional diffusion equations. R. Soc. Lond. Proc. Ser. A Math. Phys. Eng. Sci. 457(2016), 2993–3005 (2001)
Hào, D.N., Van Duc, N.: Stability results for the heat equation backward in time. J. Math. Anal. Appl. 353(2), 627–641 (2009)
Hào, D.N., Van Duc, N., Sahli, H.: A non-local boundary value problem method for parabolic equations backward in time. J. Math. Anal. Appl. 345(2), 805–815 (2008)
Hao, Z., Zhang, Z.: Optimal regularity and error estimates of a spectral Galerkin method for fractional advection-diffusion-reaction equations. SIAM J. Numer. Anal. 58(1), 211–233 (2020)
Huang, Y., Oberman, A.: Numerical methods for the fractional Laplacian: a finite difference-quadrature approach. SIAM J. Numer. Anal. 52(6), 3056–3084 (2014)
Karimi, M., Moradlou, F., Hajipour, M.: Regularization technique for an inverse space-fractional backward heat conduction problem. J. Sci. Comput. 83(2), Paper No. 37, 29 (2020)
Khanh, T.Q., Van Hoa, N.: On the axisymmetric backward heat equation with non-zero right hand side: regularization and error estimates. J. Comput. Appl. Math. 335, 156–167 (2018)
Khieu, T.T., Vo, H.-H.: Recovering the historical distribution for nonlinear space-fractional diffusion equation with temporally dependent thermal conductivity in higher dimensional space. J. Comput. Appl. Math. 345, 114–126 (2019)
Liu, Q., Liu, F., Turner, I., Anh, V.: Approximation of the Lévy-Feller advection-dispersion process by random walk and finite difference method. J. Comput. Phys. 222(1), 57–70 (2007)
Minh, T.L., Khieu, T.T., Khanh, T.Q., Vo, H.-H.: On a space fractional backward diffusion problem and its approximation of local solution. J. Comput. Appl. Math. 346, 440–455 (2019)
Miranker, W.L.: A well posed problem for the backward heat equation. Proc. Am. Math. Soc. 12, 243–247 (1961)
Morita, A., Bagchi, B.: Time dependent diffusion coefficient and the transient dynamics of diffusion controlled bimolecular reactions in liquids: a mode coupling theory analysis. J. Chem. Phys. 110(17), 8643–8652 (1999)
Payne, L.E.: Improperly posed problems in partial differential equations. Society for Industrial and Applied Mathematics, Philadelphia, Pa., 1975. Regional Conference Series in Applied Mathematics, No. 22
Petersen, J.S., Mack, C.A., Sturtevant, J.L., Byers, J.D., Miller, D.A.: Nonconstant diffusion coefficients: short description of modeling and comparison to experimental results. In: Advances in Resist Technology and Processing XII, vol. 2438, pp. 167–181. International Society for Optics and Photonics (1995)
Rais, D., Mensik, M., Paruzel, B., Toman, P., Pfleger, J.: Concept of the time-dependent diffusion coefficient of polarons in organic semiconductors and its determination from time-resolved spectroscopy. J. Phys. Chem. C 122(40), 22876–22883 (2018)
Renardy, M., Hrusa, W.J., Nohel, J.A.: Mathematical problems in viscoelasticity, volume 35 of Pitman Monographs and Surveys in Pure and Applied Mathematics. Longman Scientific & Technical, Harlow (1987)
Saadatmandi, A., Dehghan, M.: A tau approach for solution of the space fractional diffusion equation. Comput. Math. Appl. 62(3), 1135–1142 (2011)
Schurr, J.M.: Time-dependent diffusion coefficients. J. Chem. Phys. 74(2), 1428–1430 (1981)
Seshadri, V., West, B.J.: Fractal dimensionality of Lévy processes. Proc. Nat. Acad. Sci. USA 79(14), 4501–4505 (1982)
Shen, S., Liu, F.: Error analysis of an explicit finite difference approximation for the space fractional diffusion equation with insulated ends. ANZIAM J. 46(C):C871–C887 (2004/05)
Shi, C., Wang, C., Wei, T.: Convolution regularization method for backward problems of linear parabolic equations. Appl. Numer. Math. 108, 143–156 (2016)
Skaggs, T.H., Kabala, Z.J.: Recovering the history of a groundwater contaminant plume: method of quasi-reversibility. Water Resources Res. 31(11), 2669–2673 (1995)
Sun, H.G., Zhang, Y., Baleanu, D., Chen, W., Chen, Y.Q.: A new collection of real world applications of fractional calculus in science and engineering. Commun. Nonlinear Sci. Numer. Simul. 64, 213–231 (2018)
Tautenhahn, U., Schröter, T.: On optimal regularization methods for the backward heat equation. Z. Anal. Anwendungen 15(2), 475–493 (1996)
Tian, W.Y., Zhou, H., Deng, W.: A class of second order difference approximations for solving space fractional diffusion equations. Math. Comput. 84(294), 1703–1727 (2015)
Trong, D.D., Hai, D.N.D., Minh, N.D.: Stepwise regularization method for a nonlinear Riesz-Feller space-fractional backward diffusion problem. J. Inverse Ill-Posed Probl. 27(6), 759–775 (2019)
Trong, D.D., Tuan, N.H.: A nonhomogeneous backward heat problem: regularization and error estimates. Electron. J. Differ. Equ. pages No. 33, 14 (2008)
Tuan, N.H., Hai, D.N.D., Long, L.D., Nguyen, V.T., Kirane, M.: On a Riesz-Feller space fractional backward diffusion problem with a nonlinear source. J. Comput. Appl. Math. 312, 103–126 (2017)
Wang, H., Basu, T.S.: A fast finite difference method for two-dimensional space-fractional diffusion equations. SIAM J. Sci. Comput. 34(5), A2444–A2458 (2012)
Wu, J., Berland, K.M.: Propagators and time-dependent diffusion coefficients for anomalous diffusion. Biophys. J. 95(4), 2049–2052 (2008)
Xiong, X.-T., Chu-Li, F., Qian, Z.: Two numerical methods for solving a backward heat conduction problem. Appl. Math. Comput. 179(1), 370–377 (2006)
Xiong, X., Li, J., Wen, J.: Some novel linear regularization methods for a deblurring problem. Inverse Probl. Imaging 11(2), 403–426 (2017)
Yang, F., Li, X.-X., Li, D.-G., Wang, L.: The simplified Tikhonov regularization method for solving a Riesz-Feller space-fractional backward diffusion problem. Math. Comput. Sci. 11(1), 91–110 (2017)
Zheng, G.H., Wei, T.: Two regularization methods for solving a Riesz-Feller space-fractional backward diffusion problem. Inverse Probl. 26(11), 115017, 22 (2010)
Zheng, G.-H.: Solving the backward problem in Riesz-Feller fractional diffusion by a new nonlocal regularization method. Appl. Numer. Math. 135, 99–128 (2019)
Zheng, G.-H., Zhang, Q.-G.: Recovering the initial distribution for space-fractional diffusion equation by a logarithmic regularization method. Appl. Math. Lett. 61, 143–148 (2016)
Zheng, G.-H., Zhang, Q.-G.: Determining the initial distribution in space-fractional diffusion by a negative exponential regularization method. Inverse Probl. Sci. Eng. 25(7), 965–977 (2017)
Zheng, G.-H., Zhang, Q.-G.: Solving the backward problem for space-fractional diffusion equation by a fractional Tikhonov regularization method. Math. Comput. Simul. 148, 37–47 (2018)
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Theodore E. Simos.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Luan, T.N., Khanh, T.Q. Determination of Initial Distribution for a Space-Fractional Diffusion Equation with Time-Dependent Diffusivity. Bull. Malays. Math. Sci. Soc. 44, 3461–3487 (2021). https://doi.org/10.1007/s40840-021-01118-7
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40840-021-01118-7