1 Introduction

Graphs \(G=(V(G),E(G))\) considered in this paper are simple and connected. For general theoretic notations, we follow Bondy and Murty [2]. For \(W\subseteq V(G)\), by \(G-W\) and G[W] we mean the subgraphs induced by \(V(G)-W\) and W, respectively. For H, a subgraph of a graph G, let V(H) denote the set of vertices of H. For \(v \in V(G)\), let \(N_{H}(v)\) denote the set, and \(d_{H}(v)\) denote the number, of neighbors of v in H. Let \(N_{H}[u]=N_{H}(u)\cup \{u\}\). Throughout this paper, the path and cycle with n vertices are denoted by \(P_{n}\) and \(C_{n}\), respectively.

A graph polynomial is an algebraic object associated with a graph that is usually invariant at least under graph isomorphism. In general, various aspects of combinatorial information concerning a graph are stored in the coefficients of a specific graph polynomial, e.g., Tutte polynomial, chromatic polynomial, matching polynomial, independence polynomial, and so on.

For a graph G, let \(s_{k}\), \(\alpha (G)\) denote the number of independent sets of cardinality k, the independence number of G, respectively, with the convention that \(s_{0} =1\). The polynomial

$$\begin{aligned} I(G;x)=\sum _{k=0}^{\alpha }=s_{0}+s_{1}x+\cdots + s_{\alpha }x^{\alpha }, ~ \alpha =\alpha (G), \end{aligned}$$

is called the independence polynomial of G [7].

The independence polynomial of graphs has a long and rich history, dating back to the paper by Harary and Gutman [7] in 1983. Since then, numbers of properties of the independence polynomial have been presented (see the survey [12] for instance). The value of independence polynomial at some specific points can show some enumerative information of a graph, for example, \(I(G;1)=s_{0}+s_{1}+s_{2}+\ldots \ldots +s_{\alpha }=f(G)\) equals the number of independent sets of G, where f(G) is known as the Fibonacci number of G, which is also called a Merrifield–Simmons index by chemists [8, 15]; \(I(G;-1)=s_{0}-s_{1}+s_{2}+\ldots \ldots + (-1)^{\alpha }\cdot s_{\alpha }\) equals the difference of the numbers of independent sets of even and odd sizes.

Classical question about the independence polynomial concerns its computation. In general, determining the independence polynomial of a graph is a very difficult problem, since evaluating \(\alpha (G)\) is an NP-complete problem [5]. Indeed, only a few of graphs are available. Hence, it makes sense to search for classes of graphs that allow its efficient computation. For \(P_{n}\) and \(C_{n}\), it has been shown by Hopkins and Staton [9] that \(I(P_{n};x)=\sum _{j=0}^{\lfloor (n+1)/2\rfloor }\left( {\begin{array}{c}n+1-j\\ j\end{array}}\right) \cdot x^{j}\) and \(I(C_{n};x)=1+\sum _{j=1}^{\lfloor n/2\rfloor }\frac{n}{j}\left( {\begin{array}{c}n-1-j\\ j-1\end{array}}\right) \cdot x^{j}\). Based on this result, Levit et al. presented the following results.

Proposition 1.1

[14] For \(n\ge 1\), the following equalities hold:

(i):

\(I(P_{3n-2};-1)=0,~I(P_{3n-1};-1)=I(P_{3n};-1)=(-1)^n\);

(ii):

\(I(C_{3n};-1)=2\cdot (-1)^n,~I(C_{3n+1};-1)=(-1)^n,~ I(C_{3n+2};-1)= (-1)^{n+1}.\)

Recently, many more researchers have focused on the independence polynomial of composite graphs. Rosenfeld [16] obtained several formulae expressing the independence polynomials of two sorts of the rooted product of graphs. Gutman [6] proposed explicit expression for the independence polynomial of the corona of two graphs. Motivated by Gutman’s result, Song et al. [17]determined exact independence polynomials of several well-covered graphs. Lass [11] gave Mehler formulae for the independence polynomial of claw-free graphs.

Another interesting question is to find upper bounds on the value of independence polynomial at some specific points. Estes, Staton and Wei [4] provided a bound on the value of independence polynomial at \(\frac{-1}{k}\) for k-degenerate graphs. Engström [1] proved a well-known result regarding the upper bound on \(|I(G;-1)|\) of a given graph G: \(|I(G;-1)| \le 2^{\phi (G)}\), where \(\phi (G)\) is the decycling number of G, namely the minimum number of vertices that have to be deleted in order to turn G into a forest. Levit and Mandrescu [13] gave a simple proof for Engström’s result, and they conjectured that for every positive integer k and integer q with \(|q|\le 2^{k}\), there is a connected graph G with \(\phi (G)=k\) and \(I(G;-1)=q\). Cutler and Kahl [3] confirmed the conjecture. Levit and Mandrescu [14] also presented an elementary proof for the result: \(|I(G;-1)| \le 2^{\beta (G)}\). Here, \(\beta (G)\) is the cyclomatic number of G, which can be easily computed: \(\beta (G)= |E(G)|-|V(G)|+p\) where p is the number of connected components of G.

The purpose of the present article is to improve the upper bound \(2^{\phi (G)}\). For brevity, we say that a cycle is a \(\tilde{3}\)-cycle if its length is divisible by 3, otherwise a non-\(\tilde{3}\)-cycle. From the proposition above, one may see that for a graph G, its independence polynomial at -1 has relation with its non-\(\tilde{3}\)-cycles. Motivated by this, we improve the bound \(2^{\phi (G)}\) on \(|I(G;-1)|\) by considering the existences of non-\(\tilde{3}\)-cycles in graphs.

Theorem 1.1

If G contains a non-\(\tilde{3}\)-cycle, then

$$\begin{aligned} |I(G;-1)|\le 2^{\beta (G)}-\beta (G). \end{aligned}$$

One may readily see that this upper bound on \(|I(G;-1)|\) is an improvement on the bound \(2^{\phi (G)}\) since there are infinitely many graphs satisfying \(\beta (G)=\phi (G)\) and containing non-\(\tilde{3}\)-cycles. Meanwhile, comparing with the simple expression of \(\beta (G)\), computing the parameter \(\phi (G)\) is an NP-complete problem [10].

A natural question following from Theorem 1.1 is whether the number of \(\tilde{3}\)-cycles or non-\(\tilde{3}\)-cycles could determine the upper bound on \(|I(G;-1)|\) for some specific graphs. Theorem 1.2 will answer this question in some sense.

Theorem 1.2

If all cycles of G are pairwise disjoint, then \(|I(G;-1)|\le 2^{k}\), where k is the number of \(\tilde{3}\)-cycles of G.

Compared with the previous results in the literature, Theorem 1.2 raises a new perspective on estimating the independence polynomial at -1 for many special graphs

As we all know, the independence number of a graph is closely related to its minimum degree. Thus, it is of interest to check whether minimum degree of a graph G affects the upper bound on \(|I(G;-1)|\) or not. A typical result is the following theorem.

Theorem 1.3

Let G be a graph with \(\beta (G)\ge 2\). If G contains no vertices of degree 1, then \(|I(G;-1)|\le 2^{\beta (G)}-1\).

Again taking the existence of non-\(\tilde{3}\)-cycle into account, we get the following result.

Theorem 1.4

Let G be a graph with non-\(\tilde{3}\)-cycles. If G contains no vertices of degree 1, then \(|I(G;-1)|\le 2^{\beta (G)-1}\).

We remark that these two theorems imply that for a graph G, both its minimum degree and non-\(\tilde{3}\)-cycles affect the upper bound on \(|I(G;-1)|\).

2 The proofs of Main Results

In this section, we shall prove our main results. In order to compute the independence polynomial of a graph, we need the following two tools which are commonly known and very useful in calculating independence polynomials of graphs. In fact, these tools could reduce the calculations to smaller graphs. The first tool can be applied to the independence polynomials of disjoint graphs.

Theorem 2.1

[7] Let \(G_{1}\) and \(G_{2}\) be two disjoint graphs. If \(G= G_{1} \cup G_{2}\), then

$$\begin{aligned}I(G;x)=I(G_{1};x)\cdot I(G_{2};x).\end{aligned}$$

Remark 2.1

Using this result, one can easily get that \(I(G;-1)=0\) if G contains an isolated vertex. Therefore, we assume from now on that all graphs stated in this paper contain no isolated vertices.

The next result provides a recurrence which allows us to decompose the independence polynomial of a graph vertex by vertex.

Theorem 2.2

[7] If \(u\in V(G)\), then

$$\begin{aligned} I(G;x)=I(G-u;x)+x \cdot I(G-N_{G}[u];x). \end{aligned}$$

Corollary 2.1

If \(u\in V(G)\), then

$$\begin{aligned} I(G;-1)=I(G-u;-1)- I(G-N_{G}[u];-1). \end{aligned}$$

Corollary 2.2

If u is a vertex of degree 1 and \(v= N_{G}(u)\), then

$$\begin{aligned} I(G;-1)=(-1)\cdot I(G-N_{G}[v];-1). \end{aligned}$$

Let u be a vertex of degree 1, we call the deletion of \(N_{G}[v]\) from G the vertex-elimination operation, where \(\{v\}=N_{G}(u)\). Indeed, there is no change in the absolute value of the independence polynomials at -1 under the vertex-elimination operation. Based on the vertex-elimination operation, it is easy to count the independence polynomials at -1 of forests.

Proposition 2.1

[13] \(I(T;-1)\in \{-1,0,1 \}\) for each forest T.

Finally, we introduce an inequality that will be frequently used in this paper.

Theorem 2.3

[14] \(|I(G;-1)|\le 2^{\beta (G)}\) for every graph G.

We now put all of the above together to prove our main theorems.

Proof of Theorem 1.1

We prove it by induction on \(\beta (G)\). From Proposition 2.1, the statement clearly holds for \(\beta (G)=0\). Now consider the case \(\beta (G)=1\). If G contains no vertices of degree 1, then G is a cycle. By Proposition 1.1, the statement is true. Otherwise, we perform the vertex-elimination operation on G repeatedly until the resulting graph \(G_{1}\) either has no vertices of degree 1 or is a forest. Of course, in each case above, \(|I(G_{1}; -1)|\le 1\) holds. By Corollary 2.2,

$$\begin{aligned} |I(G ;-1)|=|I(G_{1} ;-1)|\le 1=2^{1}-1. \end{aligned}$$

Assume that \(\beta (G)=k+1 \ge 2\). There are two cases that must be handled.

Case 1 There are intersecting cycles in G.

Choose a vertex u of G such that \(\beta (G-u)\le k-1\). By Corollary 2.1 and Theorem 2.3,

$$\begin{aligned} |I(G;-1)|&\le |I(G-u;-1)|+|I(G-N_{G}[u];-1)|\\&\le 2 \cdot 2^{k-1}=2^{k}\le 2^{k+1}-(k+1). \end{aligned}$$

Case 2 All cycles of G are pairwise disjoint.

We further consider two subcases.

Subcase 2.1 G contains a \(\tilde{3}\)-cycle.

Let C be a \(\tilde{3}\)-cycle of G. We choose a vertex u in C. By the induction hypothesis, \(|I(G-u;-1)| \le 2^{k}-k\). If \(\beta (G-N_{G}[u])\le k-1\), Theorem 2.3 implies that \(|I(G-N_{G}[u];-1)|\le 2^{k-1}\). Using Corollary 2.1, we derive that

$$\begin{aligned} |I(G;-1)|&\le |I(G-u;-1)|+|I(G-N_{G}[u];-1)|\\&\le 2^{k}-k +2^{k-1} \le 2^{k+1}-(k+1). \end{aligned}$$

Otherwise, removing \(N_{G}[u]\) from G destroys only one cycle, that is C. Then, by the induction hypothesis, \(|I(G-u;-1)|\le 2^{k}-k\) and \(|I(G-N_{G}[u];-1)| \le 2^{k}-k\). Thereby,

$$\begin{aligned} |I(G;-1)|&\le |I(G-u;-1)|+|I(G-N_{G}[u];-1)|\\&\le 2^{k}-k+2^{k}-k \le 2^{k+1}-(k+1). \end{aligned}$$

Subcase 2.2 G contains no \(\tilde{3}\)-cycles.

Obviously, all cycles of G are non-\(\tilde{3}\)-cycles. Select a vertex u belonging to a cycle of G. According to our induction hypothesis,

$$\begin{aligned} |I(G;-1)|&\le |I(G-u;-1)|+|I(G-N_{G}[u];-1)|\\&\le 2^{k}-k+2^{k}-k \le 2^{k+1}-(k+1). \end{aligned}$$

The proof is completed. \(\square \)

Now, we are ready to prove Theorem 1.2 by the procedure used in the proof of Theorem 1.1.

Proof of Theorem 1.2

As we did in Theorem 1.1, we prove it by induction on \(\beta (G)\).

Let us first consider the case \(\beta (G)=1\). If G contains a \(\tilde{3}\)-cycle, then \(|I(G;-1)|\le 2^{1}\), due to Theorem 2.3. Otherwise, Theorem 1.1 yields that \(|I(G;-1)|\le 2^{1}-1=2^{0}\). Thereby, the statement is true in the base case.

Now assume that \(\beta (G)=k+1 \ge 2\) and m is the number of \(\tilde{3}\)-cycles of G. There are two cases to be treated.

Case 1 G has no vertices of degree 1.

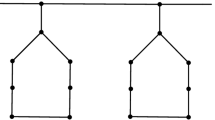
It should be point out that a tree is obtained by shrinking each cycle of G to a single vertex, since all cycles of G are pairwise disjoint. Therefore, we choose a cycle C such that C has only one vertex with degree 3 in G, say u (see Fig. 1). If C is a \(\tilde{3}\)-cycle, then the numbers of \(\tilde{3}\)-cycles in both \(G-u\) and \(G-N_{G}[u]\) are not more than \(m-1\). By induction hypothesis,

$$\begin{aligned} |I(G;-1)|\le |I(G-u;-1)| + |I(G-N_{G}[u];-1)|\le 2^{m-1}+2^{m-1}=2^{m}. \end{aligned}$$

Otherwise, C is a non-\(\tilde{3}\)-cycle. Then, Proposition 1.1 assures that \(I(C-u;-1) \cdot I(C-N_{C}[u];-1)=0\). Without loss of generality, we may assume that \(I(C-u;-1)=0\). Thus,

$$\begin{aligned}&|I(G;-1)|\le |I(G-u;-1)| + |I(G-N_{G}[u];-1)|\\&\quad =|I(G-C;-1)\cdot I(C-u;-1) | +|I(G-(C \cup N_{G}[u]);-1) \\&\qquad \times \cdot I(C - N_{C}[u];-1) |\\&\quad \le |I(G-(C \cup N_{G}[u]);-1)|. \end{aligned}$$

Let \(m_{1}\) be the number of \(\tilde{3}\)-cycle in \(G-(C \cup N_{G}[u]\)). Obviously, \(m_{1}\le m\). Using the induction hypothesis, we deduce that \(|I(G-(C \cup N_{G}[u]);-1)| \le 2^{m_{1}}.\) It is clear that \(|I(G;-1)|\le 2^{m}.\)

Fig. 1
figure 1

The cycle with a vertex of degree 3

Full size image

Case 2 G contains a vertex of degree 1.

We perform the vertex-elimination operation on G repeatedly until the resulting graph \(G_{1}\) either has no vertices of degree 1 or has cyclomatic number fewer than \(k+1\). Combining Case 1 and induction hypothesis, we derive that \(|I(G;-1)|=|I(G_{1};-1)|\le 2^{m} \). This finishes the proof. \(\square \)

In the rest of this section, we shall finish the proofs of Theorem 1.3 and 1.4 mainly by employing the ideas in Theorems 1.1 and 1.2. For brevity, we first build up Theorem 1.4.

Proof of Theorem 1.4

Also, we establish it by induction on \(\beta (G)\). For \(\beta (G)=1\), the statement is true, according to Proposition 1.1. Now, assume that G is a graph with \(\beta (G)=k+1 \ge 2\). .

The proof has been divided into two cases.

Case 1 G has intersecting cycles.

We choose a vertex u such that \(\beta (G-u)\le k-1\). It follows that

$$\begin{aligned} |I(G;-1)|\le |I(G-u;-1)| + |I(G-N_{G}[u];-1)|\le 2 \cdot 2^{k-1}=2^{k}=2^{k+1-1}. \end{aligned}$$

Case 2 All cycles of G are pairwise disjoint.

As we have seen, shrinking every cycle of G to a single vertex leads to a tree. Based on this, we choose a cycle C having exactly one vertex of degree 3 such that \(G-C\) contains a non-\(\tilde{3}\)-cycle. Let u be such that vertex. Then,

$$\begin{aligned} |I(G;-1)|\le |I(G-u;-1)| + |I(G-N_{G}[u];-1)|. \end{aligned}$$

We only need to prove that \(|I(G-u;-1)| \le 2^{k-1}\) and \(|I(G-N_{G}[u];-1)| \le 2^{k-1}\). Here, we first prove the first inequality. Since \(G-u=(G-C)\cup (C-u)\) and \(|I(C-u;-1)| \le 1\), it is sufficient to prove that \(|I(G-C;-1)|\le 2^{k-1}\). Let \(G_{1}=G-C\). If there are no vertices of degree 1 in \(G_{1}\), then \(|I(G_{1};-1)|\le 2^{k-1}\) since \(\beta (G_{1})\le k\). Otherwise, we repeatedly perform the vertex-elimination operation on \(G_{1}\) until the resulting graph \(G_{2}\) either has cyclomatic number smaller than k or has no vertices of degree 1. It follows that

$$\begin{aligned} |I(G_{2};-1)|\le 2^{k-1},~\mathrm {i.e.},~|I(G_{1};-1)|\le 2^{k-1}. \end{aligned}$$

Similarly, \(|I(G-C-N[u];-1)|\le 2^{k-1}\). Consequently,

$$\begin{aligned} I(G;-1)\le 2^{k-1}+2^{k-1}=2^{(k+1)-1}. \end{aligned}$$

\(\square \)

Proof of Theorem 1.3

We shall prove this theorem by induction on \(\beta (G)\) as well. We first consider the case of \(\beta (G)=2\). There is nothing to prove for the case that there are two intersecting cycles in G. If all cycles are disjoint, then G is obtained by adding a path to two disjoint cycles, say \(C_{l}\), \(C_{k}\), as depicted in Fig. 2.

Fig. 2
figure 2

The graph with cyclomatic number 2

Full size image

Let \(G-u=G_{1}\cup G_{2}\) and \(G-N_{G}[u]=G_{3}\cup G_{4}\) with \(G_{1}=C_{l}-u\), \(G_{2}=G-C_{l}\) and \(G_{3}=C_{l}-N_{C_{l}}[u]\), \(G_{4}=G-(C_{l}\cup N_{G}[u])\). By Corollary 2.1, Theorem 2.1 and Proposition 1.1,

$$\begin{aligned} I(G;-1)&=I(G-u;-1)-I(G-N[u];-1)\\&=I(G_{1};-1)\cdot I(G_{2};-1)-I(G_{3};-1)\cdot I(G_{4};-1)\\&\le |I(G_{2};-1)|+|I(G_{4};-1)|. \end{aligned}$$

Furthermore, suppose that the (u, v)-path contains \(m+2\) vertices with \(m\ge 0\). It follows that

$$\begin{aligned} I(G_{2};-1)&=I(G_{2}-v;-1)-I(G_{2}-N_{G_{2}}[v];-1)\\&=I(P_{k-1};-1)\cdot I(P_{m};-1)-I(P_{k-3};-1)\cdot I(P_{m-1};-1), \end{aligned}$$

and

$$\begin{aligned} I(G_{4};-1)=I(P_{k-1};-1)\cdot I(P_{m-1};-1)-I(P_{k-3};-1)\cdot I(P_{m-2};-1). \end{aligned}$$

Table 1 implies that \(I(G_{2};-1)\) and \(I(G_{4};-1)\) cannot equal 2 at the same time, as well as \(-2\). We conclude that

$$\begin{aligned} |I(G;-1)|\le 4, \end{aligned}$$

which shows that our Theorem holds \(\beta (G)=2\). The proof of the case \(\beta (G)\ge 3\) is similar to that of Theorem 1.4, so we omit it here.

k

m

\(I(G_{2};-1)\)

\(I(G_{4};-1)\)

3i

3j

\(2\cdot (-1)^{i+j}\)

\((-1)^{i+j}\)

3i

\(3j+1\)

\((-1)^{i+j}\)

\(2\cdot (-1)^{i+j}\)

3i

\(3j+2\)

\((-1)^{i+j}\)

\((-1)^{i+j}\)

\(3i+1\)

3j

\((-1)^{i+j}\)

\((-1)^{i+j}\)

\(3i+1\)

\(3j+1\)

0

0

\(3i+1\)

\(3j+2\)

\((-1)^{i+j+1}\)

0

\(3i+2\)

3j

\((-1)^{i+j+1}\)

0

\(3i+2\)

\(3j+1\)

\((-1)^{i+j+1}\)

\((-1)^{i+j+1}\)

\(3i+2\)

\(3j+1\)

\((-1)^{i+j+1}\)

\((-1)^{i+j+1}\)

\(3i+2\)

\(3j+2\)

0

\((-1)^{i+j+1}\)

\(\square \)