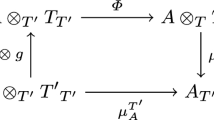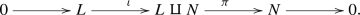On the Homological Classification of Semigroups with Local Units

Abstract

In this paper, we study homological classification of semigroups with local units depending on properties around projectivity and flatness of acts over them, the results form a new progress in this research area. First, we show that Hom functors and tensor functors in the category of acts over semigroups are left and right exact, respectively. Then we characterize semigroups with local units over which all acts have some property with respect to (principal) weak flatness and torsion freeness of acts. Finally, we establish relationships between several different properties and Rees short exact sequence of acts.

1 Introduction

S-acts are proved to be very useful tool in the study of monoids from the external action, and their theory is used in many fields of mathematics like computer science, algebraic automata theory, coding theory, etc. (see [1,2,3,4,5]). From a computer scientist’s view point, an S-act is a semiautomation, that is, an automaton having only input and there is no output. In algebraic sense, an S-act over a monoid S is a nonadditive generalization of an R-module over a ring R with identity, and its theory gives rise to the nonadditive homological algebra of monoids. It is natural to formulate questions of homological classification for monoids.

In accordance with the theory of rings and modules, the collection of results characterizing monoids by properties of their associated S-acts is called homological classification of monoids. The different so-called flatness properties (projectivity, flatness, weak flatness, principal weak flatness, torsion freeness etc.) have been widely used in the homological classification of monoids (see, for example, [6,7,8,9,10]) and are usually connected with preservation properties of Hom functors and tensor functors (from the category of S-acts into the category of sets). It is worth noting that this research is mainly aimed at characterizing semigroups with identity (namely monoids) by studying flatness properties of acts. But, in fact, there are many classes of semigroups without identity. This would lead us to think about the problem ‘how to use existing results and methods of the S-act theory to research the characteristics of semigroups without identity’.

A first step was made by Talwar [12] in 1995. He extended the notion of projective acts from monoids to semigroups with local units and gave the structure of projective S-acts in the category of unitary S-acts for such a semigroup S. And then, Chen [13] introduced the concept of exact sequence for S-acts and studied projectivity in the category of S-acts for a semigroup S via exactness of Hom functors. In 2011, Lawson [14] assembled some results on projectives in the category of closed S-acts (called firm S-acts by Laan, etc., in [15]) by using a technique similar to that of [12] and obtained some algebraic characterizations of Morita equivalence of semigroups with local units. Recently, Irannezhad and Madanshekaf [16] further extended the results of [13] to posemigroups. In this paper, we continue to study projective acts and investigate homological classification of semigroups with local units by projectivity of their cyclic acts.

The main purpose of this paper is to develop homological classification theory for semigroups S with local units by using flatness properties of firm S-acts, which may be an important way to address the above problem. As is known to all, for any monoid S, the mapping $A\otimes _{S} S\rightarrow A$, $a\otimes s\mapsto as$, is an isomorphism for every right S-act A. But this isomorphism is not true in general for semigroups without identity (see Example 2.3 of [15]). Using this isomorphism, Lawson [14] constructed the category of firm acts and studied effectively Morita equivalence of semigroups with local units. We observe that the category of firm acts has several properties that are similar to the category of all acts (see, for example, [14, 15, 17, 18]). In particular, if S is a monoid the category of firm S-acts coincides with the category of all S-acts. More importantly, when we describe internal properties of semigroups S with local units by flatness properties (flatness, weak flatness, principal weak flatness) of their acts one needs the natural isomorphisms. For these reasons, we consider the category of firm acts. In our eyes, the results in the present paper are convincing enough to claim that firm acts are the natural environment to study homological classification of semigroups S with local units.

The outline of this paper is as follows. In Sect. 3, we ascertain when two elements of the tensor product of S-acts are equal and discuss the exactness of Hom functors and tensor product functors in the category of S-acts for semigroups S. In Sect. 4, we study in detail homological classification for semigroups S with local units by flatness properties of S-acts. We give descriptions of semigroups with local units over which the cyclic (one-element) act is projective in the category of unitary acts. In analogy to the case of monoids, we introduce flatness of acts and related properties for semigroups and characterize semigroups with local units by these properties in the category of firm acts. In Sect. 5, we establish relationships between various types of flatness properties and Rees short exact sequence of acts, and the known results are generalized.

2 Definitions and Preliminaries

We start with some basic definitions. Throughout the text, S stands for the semigroup and E(S) the set of all idempotents of S. A semigroup S is said to have local units if for each $s\in S$ there exist idempotents (not necessarily unique) $e, f\in E(S)$ such that $es = s = sf$. A semigroup S is said to have common weak right local units if for every $s, t\in S$ there exists $u\in S$ such that $s = su$ and $t = tu$. Semigroups with common weak left local units are defined dually. A semigroup S is said to be left reversible if for any $s, t\in S$, there exist $u, v\in S$ such that $su=tv$. Right reversible semigroups are defined dually.

A nonempty set A is called a right S-act (or right act over S), if there exists a mapping $A\times S\rightarrow A$, $(a, s)\mapsto as$, such that $a(st) = (as)t$ for all $a\in A$ and all $s, t\in S$. A right S-act A is denoted $A_{S}$. Analogously, we define a left S-act A and write $_{S}A$. The one-element right S-act $\{\theta \}_{S}$ is shortly denoted by $\Theta _{S}$. A mapping $f:A_{S}\rightarrow B_{S}$ is called a homomorphism of right S-acts or just an S-homomorphism, if $f(as)=f(a)s$ for all $a\in A_{S}$ and $s\in S$. All right S-acts together with the S-homomorphisms form the category of right S-acts which we shall denote by Act-S. In this way, the categories S-Act and Set of left S-acts and sets are obtained. We note that for a family $\{P_{i}|~ i\in I\}$ of right S-acts, the product $\prod _{i\in I} P_{i}$ and the coproduct $\coprod _{i\in I} P_{i}$ in Act-S exist, being, respectively, isomorphic to the cartesian product and the disjoint union of the sets $P_{i}$, with a suitable action of S.

A right S-act A is called unitary if $AS = A$. If S is a semigroup with local units then this implies that for each $a\in A$ there exists $e\in E(S)$ such that $ae = a$. All unitary right S-acts together with the S-homomorphisms form a full subcategory of Act-S, which is denoted by UAct-S. Particularly, if S is a monoid with identity 1, then as in the case for rings with identity, we say that a right S-act A is unital if $a1 = a$ for all $a\in A_{S}$. Note that if S is a monoid, then the concepts of unital and unitary coincide.

Let $A_{S}$ be an S-act. An equivalence relation $\rho$ on $A_{S}$ is called a congruence on $A_{S}$ if $a\rho a'$ implies that $(as)\rho (a's)$ for $a, a'\in A_{S}$, $s\in S$. The factor set $A_{S}/\rho = \{[a]_{\rho }~|~a\in A\}$ becomes an S-act with the action $[a]_{\rho }s = [as]_{\rho }$ for every $a\in A_{S}$, $s\in S$ which is called the factor act of $A_{S}$ by $\rho$. Moreover, the canonical surjection $\pi _{\rho }: A_{S}\rightarrow A_{S}/\rho$ given by $\pi _{\rho }(a) = [a]_{\rho }$ is a homomorphism called a canonical epimorphism. Any subact $B_{S}\subseteq A_{S}$ defines the Rees congruence $\rho _{B}$ on $A_{S}$, by setting $a\rho _{B} a'$ if and only if $a = a'$ or $a, a'\in B$. We denote the resulting factor act by A/B and call it the Rees factor act of $A_{S}$ by the subact $B_{S}$.

As is known to all, Hom functors and tensor functors are important in homological algebra (see, for example, [20]). The tensor functor arises from the concept of tensor product in the category of S-acts.

Definition 1

( [12])For a right S-act $A_{S}$ and a left S-act $_{S}B$, the tensor product $A\otimes _{S} B$ of $A_{S}$ and $_{S}B$ is a solution of the usual universal problem: that is, $A\otimes _{S} B$ = $(A\times B)/\sigma$, where $\sigma$ is the equivalence relation on the set $A\times B$ generated by

$$\begin{aligned} \Sigma = \{((as, b),(a, sb))~|~a\in A, b\in B, s\in S\}. \end{aligned}$$

We denote the $\sigma$-class of (a, b) by $a\otimes b$.

For a fixed object $A\in$ Act-S, we define the tensor functor $A\otimes _{S} -$ as follows:

$$\begin{aligned} A\otimes _{S} -:~\mathbf{S-Act}&\longrightarrow \mathbf{Sets},\\ _{S}B&\longmapsto A\otimes _{S} B, \end{aligned}$$

and if $f :~_{S}B\rightarrow _{S}\!\!B'$ is an S-homomorphism, then

$$\begin{aligned} (A\otimes _{S} -)(f)=1_{A}\otimes _{S} f:~A\otimes _{S} B&\longrightarrow A\otimes _{S} B',\\ a\otimes b&\longmapsto a\otimes f(b), \end{aligned}$$

where $1_{A}$ is the identity homomorphism on A. If $_{S}A_{R}$ and $_{R}B_{T}$ are biacts, then $_{S}A\otimes _{R} N_{T}$ is an S-T-biact in a natural way.

Let A be a fixed object in S-Act. Then we obtain a Hom functor $Hom_{S}(A, -)$ as follows:

$$\begin{aligned} Hom_{S}(A, -):~\mathbf{S-Act}&\longrightarrow \mathbf{Sets},\\ _{S}B&\longmapsto Hom_{S}(A, B), \end{aligned}$$

and if $f :~_{S}B\rightarrow _{S}\!\!B'$ is an S-homomorphism, then

$$\begin{aligned} Hom_{S}(A, -)(f)=f_{*}:~Hom_{S}(A, B)&\longrightarrow Hom_{S}(A, B'),\\ g&\longmapsto fg. \end{aligned}$$

For other definitions and terminologies not mentioned in this paper, the reader is referred to [6, 7, 9, 11,12,13].

3 Exactness of the Hom and Tensor Functors

As we shall see, homological algebra allows us to study a semigroup S by investigating objects in its category of S-acts, and some objects are investigated by the behavior of the Hom and tensor functors. So in this section, we discuss the exactness of Hom and tensor functors in the category of S-acts.

The following definition of short exact sequence of S-acts for semigroups first appeared in [13].

Let S be a semigroup with a zero 0. An element $\theta \in A_{S}$ is called a fixed element of $A_{S}$ if $\theta s =\theta$ for all $s\in S$. It follows that $\theta s =\theta$ and $a 0=\theta$, for all $s\in S$ and $a\in A$, and we shall call $\theta$ the zero of $A_{S}$ and also denote by 0. From now on, 0 will show the zero of acts. Let L and M be S-acts, and let $f:~L\rightarrow M$ be an S-homomorphism. Then denote by

$$\begin{aligned} ker f = \{(l_{1}, l_{2})\in L\times L~|~f(l_{1}) = f(l_{2})\}~\text{ and }~{\mathcal {K}}_{Imf} = (Imf\times Imf)\cup 1_{M}, \end{aligned}$$

where $1_{M}$ is the identity congruence on M. It is clear that both kerf and ${\mathcal {K}}_{Imf}$ are congruences on L and M, respectively, and $f(L)\cong L/kerf$ as S-acts. We recall that the sequence

of S-acts is exact at M if $kerg = {\mathcal {K}}_{Imf}$. If the sequence

(1)

of S-acts is exact at L, M and N, then it is called a Rees short exact sequence. We note that if the sequence (1) is a Rees short exact sequence, then it is easy to show that f is a monomorphism, g is an epimorphism and $gf = 0$. As in the case of modules, the sequence (1) is called left(right) split if there exists an S-homomorphism $f': M\rightarrow L$ ($g': N \rightarrow M$) such that $f'f = 1_{L}$($gg' = 1_{N}$), where $1_{L}$($1_{N}$) is the identity map on L(N). For every subact L of M, it is clear that

is a Rees short exact sequence, where i is the inclusion and $\pi$ is the canonical homomorphism.

To accomplish goals, we need to know when two elements $a\otimes b$ and $a'\otimes b'$ in tensor product $A\otimes _{S}B$ are equal.

Lemma 2

Let $A\in$ UAct-S and $B\in$ S-Act. Then $a\otimes b= a'\otimes b'$ for $a, a'\in A$ and $b, b'\in B$ if and only if there exist $a_1, \ldots , a_n\in A$, $b_2, \ldots , b_n\in B$, $s_1, t_1, \ldots , s_n, t_n\in S$ such that

$$\begin{aligned} \begin{array}{rclcrcl} a &{} = &{} a_1s_1 &{} &{} &{} &{} \\ a_1t_1 &{} = &{} a_2s_2 &{} &{} s_1b &{} = &{} t_1b_2 \\ a_2t_2 &{} = &{} a_3s_3 &{} &{} s_2b_2 &{} = &{} t_2b_3 \\ &{} \cdots &{} &{} &{} &{} \cdots &{} \\ a_nt_n &{} = &{} a' &{} &{} s_nb_n &{} = &{} t_nb'. \end{array} \end{aligned}$$

Proof

Define a relation $\rho$ on $A\times B$ so that $(a, b)\rho (a', b')$ for any $a, a'\in A$ and $b, b'\in B$ if and only if the elements $a_1, \ldots , a_n\in A$, $b_2, \ldots , b_n\in B$, $s_1, t_1, \ldots , s_n, t_n\in S$, required in the statement, exist. We shall show that $\rho$ is an equivalence relation on $A\times B$.

Since A is a unitary right S-act, for any $a\in A=AS$, we can find $a_{1}\in A$ and $u\in S$ such that $a=a_{1}u$. Thereby we have

$$\begin{aligned} \begin{array}{rclcrcl} a &{} = &{} a_1\cdot u &{} &{} &{} &{} \\ a_1\cdot u &{} = &{} a &{} &{} u\cdot b &{} = &{} u\cdot b, \end{array} \end{aligned}$$

this means that $(a, b)\rho (a, b)$, i.e., $\rho$ is reflexive.

It is easy to check that the relation $\rho$ is symmetric. Now we show that $\rho$ is transitive. Suppose that $(a, b)\rho (a', b')$ and $(a', b')\rho (a'', b'')$ for any $a, a', a''\in A$ and $b, b', b''\in B$. For $a'\in A$, there exist $a'_{n}\in A$ and $u\in S$ such that $a'=a'_{n}u$, so we get

$$\begin{aligned} \begin{array}{rclcrcl} a &{} = &{} a_1s_1 &{} &{} &{} &{} \\ a_1t_1 &{} = &{} a_2s_2 &{} &{} s_1b &{} = &{} t_1b_2 \\ a_2t_2 &{} = &{} a_3s_3 &{} &{} s_2b_2 &{} = &{} t_2b_3 \\ &{} \cdots &{} &{} &{} &{} \cdots &{} \\ a_nt_n &{} = &{} (a'=)a'_n\cdot u &{} &{} s_nb_n &{} = &{} t_nb',\\ a'_n\cdot u(=a') &{} = &{} a'_1u_1 &{} &{}u\cdot b' &{}= &{}u\cdot b' \\ a'_1v_1 &{} = &{} a'_2u_2 &{} &{} u_1b' &{} = &{} v_1b'_2 \\ a'_2v_2 &{} = &{} a'_3u_3 &{} &{} u_2b'_2 &{} = &{} v_2b'_3 \\ &{} \cdots &{} &{} &{} &{} \cdots &{} \\ a'_mv_m &{} = &{} a'' &{} &{} u_mb'_m &{} = &{} v_mb'', \end{array} \end{aligned}$$

this implies $(a, b)\rho (a'', b'')$. Hence $\rho$ is an equivalence relation.

For any $((as, b), (a, sb))\in \Sigma$, we have

$$\begin{aligned} \begin{array}{rclcrcl} as &{} = &{} a_1u\cdot s=a_1\cdot us &{} &{} &{} &{} \\ a_1\cdot u &{} = &{} a &{} &{} us\cdot b &{} = &{} u\cdot sb, \end{array} \end{aligned}$$

so $(as, b)\rho (a, sb)$, it follows that $\sigma \subseteq \rho$. On the other hand, if $(a, b)\rho (a', b')$, then

$$\begin{aligned} (a, b)&=(a_{1}s_{1}, b)\sigma (a_{1}, s_{1}b)=(a_{1}, t_{1}b_{2})\sigma (a_{1}t_{1},b_{2})=(a_{2}s_{2}, b_{2})\sigma (a_{2}, s_{2}b_{2})\\&=\cdots =(a_{n}s_{n}, b_{n})\sigma (a_{n}, s_{n}b_{n})=(a_{n}, t_{n}b')\sigma (a_{n}t_n,b')=(a', b'). \end{aligned}$$

Hence $(a, b)\sigma (a', b')$ which means that $\rho \subseteq \sigma$. Thus we have $\rho = \sigma$. The proof is complete. $\square$

It follows immediately form this lemma that if $B=S$ and $a\otimes s= a'\otimes s'$ in $A\otimes _{S}S$, then $as=a's'$.

We are now ready to prove one of the main results of this section.

Theorem 3

(Right Exactness) Let S be a semigroup with a zero, and $A\in$ UAct-S. Let

(2)

be a Rees short exact sequence of left S-acts. Then

is a Rees short exact sequence of sets.

Proof

According to the definition of exactness, the proof is divided into three steps.

(i) $ker(1\otimes g)\subseteq {\mathcal {K}}_{Im(1\otimes f)}$. Let $(a\otimes m, a'\otimes m')\in ker(1\otimes g)$ with $a\otimes m\ne a'\otimes m'$, for $a, a'\in A$, $m, m'\in M$. Then

$$\begin{aligned} a\otimes g(m)=(1\otimes g)(a\otimes m)=(1\otimes g)(a'\otimes m')=a'\otimes g(m') \end{aligned}$$

in $A\otimes _{S}N$. Thus by Lemma 2 there exists an S-tossing

$$\begin{aligned} \begin{array}{rclcrcl} a &{} = &{} a_1s_1 &{} &{} &{} &{} \\ a_1t_1 &{} = &{} a_2s_2 &{} &{} s_1g(m) &{} = &{} t_1n_2 \\ a_2t_2 &{} = &{} a_3s_3 &{} &{} s_2n_2 &{} = &{} t_2n_3 \\ &{} \cdots &{} &{} &{} &{} \cdots &{} \\ a_kt_k &{} = &{} a' &{} &{} s_kn_k &{} = &{} t_kg(m'), \end{array} \end{aligned}$$

where $a_1, \ldots , a_k\in A$, $n_2, \ldots , n_k\in N$, $s_1, \ldots , s_k, t_1, \ldots , t_k\in S$. Since g is an epimorphism, there exist $m_{i}, i=2, \cdots , k$, such that $g(m_{i})=n_{i}, i=2, \cdots , k$, and so we can compute that

$$\begin{aligned} g(s_{1}m)=s_{1}g(m)=t_{1}n_{2}=t_{1}g(m_{2})=g(t_{1}m_{2}). \end{aligned}$$

This implies $(s_{1}m, t_{1}m_{2})\in kerg= {\mathcal {K}}_{Imf}$. Continuing in this manner we can obtain that $(s_{k}m_{k}, t_{k}m')\in {\mathcal {K}}_{Imf}$ and $(s_{i}m_{i}, t_{i}m_{i+1})\in {\mathcal {K}}_{Imf}, i=2, \cdots , k-1$. Using the definition of ${\mathcal {K}}_{Imf}$, if $s_{1}m= t_{1}m_{2}$, $s_{k}m_{k}= t_{k}m'$, and $s_{i}m_{i}= t_{i}m_{i+1}$, $i=2, \cdots , k-1$, it follows that $a\otimes m = a'\otimes m'$ in $A\otimes _{S} M$, a contradiction. Thus, we may assume without loss of generality that $(s_{i}m_{i}, t_{i}m_{i+1}), (s_{j}m_{j}, t_{j}m_{j+1})\in Imf\times Imf$ for some $i, j\in \{i=2, \cdots , k-1\}$ (i and j can be equal). In this case we can find $l_{i}, l_{j+1}\in L$ with $f(l_{i})=s_{i}m_{i}$ and $f(l_{j+1})=t_{j}m_{j+1}$. Hence we calculate that

$$\begin{aligned} a\otimes m&=a_{1}s_{1}\otimes m=a_{1}\otimes s_{1}m=a_{1}\otimes t_{1}m_{2}=a_{1}t_{1}\otimes m_{2}=a_{2}s_{2}\otimes m_{2}\\&=\cdots =a_{i}s_{i}\otimes m_{i}=a_{i}\otimes s_{i}m_{i}=a_{i}\otimes f(l_{i})=(1\otimes f)(a_{i}\otimes l_{i}). \end{aligned}$$

Similarly, we also get $a'\otimes m'=(1\otimes f)(a_{j}\otimes l_{j+1})$. This means that $(a\otimes m, a'\otimes m')\in {\mathcal {K}}_{Im(1\otimes f)}$.

(ii) ${\mathcal {K}}_{Im(1\otimes f)}\subseteq ker(1\otimes g)$. If $(a\otimes m, a'\otimes m')\in Im(1\otimes f)\times Im(1\otimes f)$ with $a\otimes m\ne a'\otimes m'$, for $a, a'\in A$, $m, m'\in M$, then there exist $l, l'\in L$ such that $a\otimes m=(1\otimes f)(a\otimes l)$ and $a'\otimes m'=(1\otimes f)(a'\otimes l')$. From the exactness of the sequence (2), it follows that

$$\begin{aligned} (1\otimes g)(a\otimes m)&=(1\otimes g)(1\otimes f)(a\otimes l)=(1\otimes gf)(a\otimes l)=(1\otimes 0)(a\otimes l)\\&=(1\otimes gf)(a'\otimes l')=(1\otimes g)(1\otimes f)(a'\otimes l')=(1\otimes g)(a'\otimes m'). \end{aligned}$$

This shows that $(a\otimes m, a'\otimes m')\in ker(1\otimes g)$.

(iii) $1\otimes g$ is surjective. For any $a\otimes n\in A\otimes _{S}N$, since g is an epimorphism, there exists $m\in M$ such that $g(m)=n$. So we have $(1\otimes g)(a\otimes m)=a\otimes g(m)=a\otimes n$, as desired. $\square$

The following example shows the tensor functor is not left exactness.

Example 4

Let $S=Z$, $A=Z/2Z\in$ Act-Z. Then we can get a Rees short exact sequence of left Z-acts

However, one can show that

is not a Rees short exact sequence of sets. This is because $[1]\otimes 5= [2]\otimes 5$ in $A\otimes Q$, but $[1]\otimes 5\ne [2]\otimes 5$ in $A\otimes Z$.

The following theorem says that the Hom functor is a left exact functor.

Theorem 5

(Left Exactness) Let S be a semigroup with a zero 0, and $A\in {\mathbf{S-UAct}}$. Let

(3)

be a Rees short exact sequence of left S-acts. Then

is a Rees short exact sequence of sets.

Proof

There are three things to check.

(i) $kerg_{*}\subseteq {\mathcal {K}}_{Imf_{*}}$. Assume that $(u, v)\in kerg_{*}$ with $u\ne v$, for $u, v\in Hom_{S}(A, M)$. Then $g_{*}(u)=g_{*}(v)$, namely, $gu(x)=gv(x)$ for all $x\in A$. It follows that $(u(x), v(x))\in kerg= {\mathcal {K}}_{Imf}$ for all $x\in A$. If $u(x)= v(x)$ for all $x\in A$, then $u=v$, which is a contradiction. Thus, $(u(x), v(x))\in Imf\times Imf$, which implies $f(l)=u(x)$ and $f(l')=v(x)$ for some $l, l'\in L$. Since f is injective, the elements l and $l'$ are unique. Hence the function $h:~A\rightarrow L$, given by $h(x)=l$ if $f(l)=u(x)$, is well-defined. Since $u(sx)=su(x)=sf(l)=f(sl)$, we have $h(sx)=sl=sh(x)$, that is, h is a left S-homomorphism. But $f_{*}(h)=fh$ and $fh(x)=f(l)=u(x)$ for all $x\in A$. This shows that $f_{*}(h)=u$. A similar argument shows that $f_{*}(i)=v$ for some left S-homomorphism $i:~A\rightarrow L$. Thus $(u, v)\in {\mathcal {K}}_{Imf_{*}}$, as required.

(ii) ${\mathcal {K}}_{Imf_{*}}\subseteq kerg_{*}$. If $(u, v)\in Imf_{*}\times Imf_{*}$ with $u\ne v$ for $u, v\in Hom_{S}(A, M)$, then there are $u_{1}, v_{1}\in Hom_{S}(A, L)$ with $f_{*}(u_{1})=fu_{1}=u$ and $f_{*}(v_{1})=fv_{1}=v$. But it follows that $g_{*}(u)=gu=gfu_{1}=0$ from exactness of the sequence (3). Similarly, we also get $g_{*}(v)=0$, so $(u, v)\in kerg_{*}$, and we are done.

(iii) $f_{*}$ is injective. Let $f_{*}(u)=f_{*}(v)$ for $u, v\in Hom_{S}(A, L)$. Then $fu=fv$, i.e., $fu(x)= fv(x)$ for all $x\in A$. Since f is injective, we have $u(x)= v(x)$ for all $x\in A$, that is, $u=v$. The proof is complete. $\square$

We note from [13, Corollary 4.4] that the fact says that for any semigroup S and $P\in$ S-UAct the functor $Hom(P, -)$ is an exact functor if and only if $P \cong Se$ for some $e\in E(S)$. It follows from this fact and the above theorem that, in general, the functor $Hom(A, -)$ is not right exact for an arbitrary unitary S-act A. Also, it can be easily observed from [12, Theorem 2.9] that, in S-UAct for a semigroup S with local units, an object P is projective if and only if the functor $Hom(P, -)$ preserves epimorphisms, and an object P is projective and indecomposable if and only if the functor $Hom(P, -)$ is exact.

4 On Homological Classification of Semigroups

In this section, we consider the question of homological classification of a semigroup with local units by flatness properties of acts.

4.1 Projectivity of Acts in the Category UAct-S

It is known that projective acts are one of the most important objects in homological algebra of monoids, and they also play an important role in the Morita theory of semigroups. In this subsection, we shall study projectivity in the category UAct-S for a semigroup S with local units in order to get characterizations of projective cyclic acts in the category UAct-S.

Throughout the following, we shall assume that S is a semigroup with local units unless otherwise stated.

Recall that $P\in$ Act-S is called projective [12] if given any diagram

of S-acts and S-homomorphisms with p surjective there exists an S-homomorphism $g: P \rightarrow M$ such that the triangle is commutative.

We start with a characterization of projective cyclic acts in the category UAct-S. In what follows, we need the following result.

Lemma 6

([12, Proposition 2.6]) In the category UAct-S, the following statements are equivalent.

• (1) An S-act P is projective.

• (2) Every S-epimorphism $M\rightarrow P$ is a retract.

Proposition 7

Let $A\in$ UAct-S and $a\in A$. The cyclic right S-act aS is projective if and only if there exists $e\in E(S)$ such that $ae=a$, and $ax=ay$ implies $ex=ey$ for $x, y\in S$.

Proof

Necessity. Suppose that the cyclic right subact aS of A is projective. Then by Lemma 6, the S-epimorphism $f: S\rightarrow aS$, $s\mapsto as$, $s\in S$, is a retract. Hence there exists an S-homomorphism $g: aS\rightarrow S$ such that $fg=1_{aS}$. Set $g(a)=e\in S$. Then we have $a=fg(a)=f(e)=ae$, and

$$\begin{aligned} e^{2}=g(a)g(a)=g(a)e=g(ae)=g(a)=e. \end{aligned}$$

Now $ax=ay$, $x, y\in S$, implies that

$$\begin{aligned} ex=g(a)x=g(ax)=g(ay)=g(a)y=ey. \end{aligned}$$

Sufficiency. Assume that there exists an idempotent $e\in E(S)$ such that $ae=a$, and for any $x, y\in S$, $ax=ay$ implies $ex=ey$. From the assumption it follows that the mapping $g: aS\rightarrow eS$ with $g(as)=es$ for any $s\in S$ is an S-homomorphism, and it is surjective. Since $ae=a$ and $es=et$ for any $s, t\in S$, imply that

$$\begin{aligned} as=aes=aet=at, \end{aligned}$$

this shows the mapping g is also injective, and so $aS\cong eS$. Hence aS is projective by Lemma 2.4 of [12]. $\square$

If $\sigma$ is a right congruence on S, then we can define a binary relation $\sigma _{e}$, $e\in E(S)$, on S by

$$\begin{aligned} x\sigma _{e} y~\Longleftrightarrow ~(ex)\sigma (ey). \end{aligned}$$

It is easy to see that $\sigma _{e}$ is also a right congruence on S, and $(ex)\sigma _{e} x$ for every $x\in S$.

Proposition 8

Let $\sigma$ be a right congruence on S. Then the following statements are equivalent.

• (1) $S/\sigma _{e}$, $e\in E(S)$, is projective.

• (2) There exists $t \in S$ such that $t\sigma _{e} e$, and for any $x, y\in S$, $x\sigma _{e} y$ implies $etx=ety$.

Proof

$(1)\Rightarrow (2)$ Suppose $S/\sigma _{e}$ is projective for some idempotent $e\in E(S)$. Then the S-epimorphism $f: eS\rightarrow S/\sigma _{e}$, $es\mapsto [s]_{\sigma _{e}}$, is a retract by Lemma 6. It follows that there exists an S-homomorphism $g: S/\sigma _{e}\rightarrow eS$ such that $fg=1_{S/\sigma _{e}}$. Set $g([e]_{\sigma _{e}})=et$, $t\in S$. Then in $S/\sigma _{e}$ we have

$$\begin{aligned}{}[e]_{\sigma _{e}}=fg([e]_{\sigma _{e}})=f(et)=[t]_{\sigma _{e}}, \end{aligned}$$

that is $e\sigma _{e} t$. Now let $x, y\in S$ be such that $[x]_{\sigma _{e}}=[y]_{\sigma _{e}}$. Then we get

$$\begin{aligned} etx=g([e]_{\sigma _{e}})x=g([ex]_{\sigma _{e}})=g([x]_{\sigma _{e}})=g([y]_{\sigma _{e}})=g([ey]_{\sigma _{e}})=g([e]_{\sigma _{e}})y=ety. \end{aligned}$$

$(2)\Rightarrow (1)$ Assume that there exists an element $t\in S$ satisfying the condition (2). Define a mapping $g: S/\sigma _{e}\rightarrow eS$ by $g([s]_{\sigma _{e}})=ets$ for any $s\in S$. Since $[x]_{\sigma _{e}}=[y]_{\sigma _{e}}$ we have $x\sigma _{e} y$, and so by assumption, $etx=ety$, which proves that g is well-defined. Clearly, g is an S-homomorphism. Now consider the S-epimorphism $f: eS\rightarrow S/\sigma _{e}$, $es\mapsto [s]_{\sigma _{e}}$. Since for any $x\in S$, we can compute that

$$\begin{aligned} fg([x]_{\sigma _{e}})=f(etx)=f(et)x=[t]_{\sigma _{e}}x=[e]_{\sigma _{e}}x=[ex]_{\sigma _{e}}=[x]_{\sigma _{e}}. \end{aligned}$$

Hence $fg=1_{S/\sigma _{e}}$, which shows that f is a retract. Notice that eS is projective we get $S/\sigma _{e}$ is projective by Proposition 1.7.30 of [6]. $\square$

In particular, if S is a monoid, and $e\in E(S)$ is taken as the identity element 1 of S in the above proposition, we immediately obtain the following result.

Corollary 9

([8, Lemma 2.2.3]) Let $\sigma$ be a right congruence on a monoid S. Then the following statements are equivalent.

• (1) $S/\sigma$ is projective.

• (2) There exists $t \in S$ such that $t\sigma 1$, and for any $x, y\in S$, $x\sigma y$ implies $tx=ty$.

Next we formulate necessary and sufficient conditions for projectivity of principal right ideals.

Definition 10

We say that an element s of a semigroup S is called left e-cancellable for an idempotent $e\in S$ if $s = se$, and $sx = sy$ implies $ex = ey$ for $x, y\in S$. A semigroup S is called a right PP semigroup if every element $s\in S$ is left e-cancellable for some idempotent $e\in S$. Note that all regular semigroups are right PP semigroups.

For principal right ideals, Proposition 7 yields the following result.

Corollary 11

Let $s\in S$. Then the principal right ideal sS is projective if and only if s is left e-cancellable for some idempotent $e\in S$.

From Corollary 11, one obtains the following

Theorem 12

All principal right ideals of S are projective if and only if S is a right PP semigroup.

The analog for projective principal right ideals of a monoid S is presented in [6] (see Theorem 4.11.15).

In the following theorem, we give a characterization of right PP semigroups in an important special case. For the sake of completeness, we give the proof which is similar to that of [6, Theorem 4.11.16].

Theorem 13

A semigroup S with local units is a right PP semigroup with central idempotents if and only if S is a semilattice of left cancellative monoids.

Proof

Necessity. Let S be a right PP semigroup with central idempotents and let

$$\begin{aligned} S_{e} =\{a\in S~|~a~\text{ is } \text{ left } \text{ e-cancellable }\}. \end{aligned}$$

Notice that any element of S is left e-cancellable for some idempotent $e\in S$ by Theorem 12, we have $S =\bigcup _{e\in E}S_{e}$ where E the set of idempotents of S. Suppose that $e, f\in E$ and $a\in S_{e}\cap S_{f}$. Then $a = ae$ and $a = af$. From $a= ae$ and left f-cancellability of a, we get $f = fe$. Analogously from $a = af$ and left e-cancellability of a we get $e = ef$. Since idempotents commute $e = f$ follows. Hence

$$\begin{aligned} S =\dot{\bigcup _{e\in E}}S_{e}. \end{aligned}$$

Now let $e, f\in E$, $a\in S_{e}$, $b\in S_{f}$. Then $a = ae$, $b = bf$ and $(ab)(ef) =aebf = ab$. Moreover, if $(ab)s = (ab)t$, $s, t\in S$ then $a(bs) = a(bt)$ and left e-cancellability of a implies $b(es) =e(bs) = e(bt) = b(et)$. Now left f-cancellability of b implies $(ef)s=f(es)= f(et)=(ef)t$. This means that $ab\in S_{ef}$. Analogously one gets $ba\in S_{ef}$. Hence for any $e\in E$ the subset $S_{e}$ is a submonoid of S with identity e and S is a semilattice of the submonoids $S_{e}$, $e\in E$.

Finally suppose that $ca = cb$ for some elements $a, b, c\in S_{e}$, $e\in E$. By left e-cancellability of c we have then $ea = eb$ or $a = b$. Hence $S_{e}$ is left cancellative for any $e\in E$.

Sufficiency. Let S be a semilattice of left cancellative monoids $S\alpha$, $\alpha \in I$, let $e_{\alpha }$ be the identity of $S_{\alpha }$ and c an arbitrary element of S.

Take $c\in S_{\gamma }$, $\gamma \in I$. Then $ce_{\gamma } = c$. Suppose $ca = cb$ for $a\in S_{\alpha }$, $b \in S_{\beta }$, $\alpha , \beta \in I$. Let $\delta \in I$ be such that $ca\in S_{\delta }$. Then $e_{\gamma }e_{\alpha } = e_{\gamma }e_{\beta } = e_{\delta }$. Since

$$\begin{aligned} (ce_{\delta })(e_{\gamma }a) = ce_{\delta }a = cae_{\delta } = ca = cb = cbe_{\delta } = ce_{\delta }b = (ce_{\delta })(e_{\gamma }b), \end{aligned}$$

where $ce_{\delta }, e_{\gamma }a, e_{\gamma }b\in S_{\delta }$ and since by assumption $S_{\delta }$ is left cancellative, one obtains $e_{\gamma }a = e_{\gamma }b$. Hence S is a right PP semigroup. $\square$

Finally, we give a condition under which the one-element act is projective.

Proposition 14

The one-element act $\Theta _{S}$ is a projective right S-act if and only if S contains a left zero.

Proof

Suppose $\Theta _{S}=\{\theta \}$ is projective and consider the epimorphism $\pi : S_{S}\rightarrow \Theta _{S}$. Using Lemma 6 we get a homomorphism $\psi : \Theta _{S}\rightarrow S_{S}$ such that $\pi \psi = 1_{\Theta _{S}}$. Now $\psi (\theta )$ is a left zero of S.

The converse follows from Lemma 2.4 of [12]. $\square$

4.2 Flatness of Acts in the Category FAct-S

We note from Example 4 that, the tensor functor in general does not preserve monomorphisms. In this subsection, we shall consider when the tensor functor preserves monomorphisms. To this end, we introduce the following definitions for semigroups which are same as the case for monoids.

Definition 15

For any semigroup S, definitions of flatness, weak flatness and principal weak flatness are formulated as follows:

• An S-act $A_{S}$ is called flat, if the functor $A_{S}\otimes -$ preserves monomorphisms.

• An S-act $A_{S}$ is called weakly flat, if the functor $A_{S}\otimes -$ preserves all embeddings of left ideals into S.

• An S-act $A_{S}$ is called principally weakly flat, if the functor $A_{S}\otimes -$ preserves all embeddings of principal left ideals into S.

It is a well-known fact that in the category of S-acts for a monoid S there exists the canonical isomorphism $A\otimes _{S} S\cong A$ (see [6, Proposition 2.5.13]), which plays important roles on studying the homological classification of monoids and Morita equivalence of acts. However, this fact cannot hold for a semigroup with local units in general. Therefore Lawson [14] introduced the definition of closed acts, which were called ‘firm acts’ in [15].

Definition 16

( [15]) Let S be a semigroup. We say that a right S-act $A_{S}$ is firm if the mapping

$$\begin{aligned} \mu _{A}:~A\otimes _{S} S\rightarrow A,\ \ a\otimes s\mapsto as \end{aligned}$$

is bijective. A semigroup S is called firm if it is firm as a right (or, equivalently, left) S-act.

The category of all firm right S-acts is denoted by FAct-S. Obviously, $A_{S}$ is unitary if and only if the mapping $\mu _{A}$ is surjective. Hence, for any semigroup S, FAct-S is a subcategory of UAct-S. In particular, if S is a semigroup with common right weak local units, then these categories coincide. In this subsection, we consider S-acts in the category FAct-S.

To present classification results, we start with general properties around principal weak flatness and weak flatness.

Lemma 17

Let S be a semigroup, and $A\in$ FAct-S. Then A is principally weakly flat if and only if $as= a's$ for $a, a'\in A$, $s\in S$ implies $a\otimes s = a'\otimes s$ in the tensor product $A\otimes _{S} Ss$.

Proof

Note that $a\otimes s= a'\otimes s$ for $a, a'\in A$, $s\in S$ in the tensor product $A\otimes _{S} S$ if and only if $as=a's$ in A since A be a firm right S-act. And then the result is easy to obtain from Definition 15. $\square$

Similarly, we also have the following

Lemma 18

Let S be a semigroup, and $A\in$ FAct-S. Then A is weakly flat if and only if $as= a's'$ for $a, a'\in A$, $s, s'\in S$ implies $a\otimes s = a'\otimes s'$ in the tensor product $A\otimes _{S} (Ss\cup Ss')$.

The following characterizations of (principal) weak flatness for left PP semigroups are parallel with relative results of left PP monoids; we shall therefore present them without proof.

Theorem 19

Let S be a left PP semigroup, and $A\in$ FAct-S. Then A is principally weakly flat if and only if, for every $a, a'\in A$ and $s\in S$, $as = a's$ implies that there exists $e\in E(S)$ such that $es=s$ and $ae= a'e$.

Proof

The proof is similar to that of [6, Theorem 3.10.16] $\square$

Theorem 20

Let S be a left PP semigroup, and $A\in$ FAct-S. Then A is weakly flat if and only if, for every $a, a'\in A$ and $s, s'\in S$, $as = a's'$ implies that there exist $a''\in A$, $u, v\in S$, $e, f\in E(S)$ such that $es=s$, $fs'=s'$, $ae= a''u$, $a'f= a''v$ and $us=vs'$.

Proof

The proof is similar to that of [6, Theorem 3.11.9]. $\square$

Now we establish one of our main results.

Theorem 21

Let S be a semigroup with local units. In the category FAct-S, the following statements are equivalent.

• (1) All S-acts are principally weakly flat.

• (2) All finitely generated S-acts are principally weakly flat.

• (3) All cyclic S-acts are principally weakly flat.

• (4) S is a regular semigroup.

Proof

The implications $(1)\Rightarrow (2)\Rightarrow (3)$ are obvious.

$(3)\Rightarrow (4)$. Let $s\in S$. If $s=s^{2}$ we are done. Now we assume that $s\ne s^{2}$. Since S is a semigroup with local units, there exists an idempotent $e\in S$ such that $s =es$. By $\lambda$, we denote the smallest congruence on S generated by $(s, s^{2})$. Obviously, $[e]\otimes s= [e]\otimes s^{2}$ in $S/\lambda \otimes S$. By assumption, the cyclic act $S/\lambda$ is principally weakly flat, so we have $[e]\otimes s= [e]\otimes s^{2}$ in $S/\lambda \otimes Ss$. This implies that there exist $u_{1}, \cdots , u_{n}\in S/\lambda$, $s_{1}, \cdots , s_{n}, t_{1},\cdots , t_{n}\in S$, $v_{2},\cdots , v_{n}\in Ss$, such that

$$\begin{aligned} \begin{array}{rclcrcl} [e] &{} = &{} u_{1}s_{1} &{} &{} &{} &{} \\ u_{1}t_{1} &{} = &{} u_{2}s_{2} &{} &{} s_{1}s &{} = &{} t_{1}v_{2} \\ u_{2}t_{2} &{} = &{} u_{3}s_{3} &{} &{} s_{2}v_{2} &{} = &{} t_{2}v_{3} \\ &{} \cdots &{} &{} &{} &{} \cdots &{} \\ u_{n}t_{n} &{} = &{} [e] &{} &{} s_{n}v_{n} &{} = &{} t_{n}s^{2}. \end{array} \end{aligned}$$

Set $u_{i}=[w_{i}]\in S/\lambda$, $i= 1,\cdots , n$. Then $(e, w_{1}s_{1})$, $(w_{1}t_{1}, w_{2}s_{2})$, $\ldots , (w_{n}t_{n}, e)\in \lambda$. If $e=w_{1}s_{1}$, $w_{1}t_{1}= w_{2}s_{2}, \ldots , w_{n}t_{n}= e$, we can easily obtain that $s=s^{2}$, which is a contradiction. Now we assume $e=w_{1}s_{1}$, $w_{1}t_{1}= w_{2}s_{2}, \ldots , w_{i-1}t_{i-1}= w_{i}s_{i}$, but $w_{i}t_{i}\ne w_{i+1}s_{i+1}$. Then there exists $t\in S$ such that $w_{i}t_{i}\in st$, and so we get

$$\begin{aligned} s=es=w_{1}s_{1}s=w_{1}t_{1}v_{2}=\cdots =w_{i-1}t_{i-1}v_{i}=w_{i}s_{i}v_{i}=w_{i}t_{i}v_{i+1}=stv_{i+1}\in sSs. \end{aligned}$$

This means that s is a regular element of S.

$(4)\Rightarrow (1)$. Let A be a firm right S-act and $as = a's$ for $a,a'\in A$, $s\in S$. Since S is regular there exists $s'\in S$ such that $ss's= s$. Now we have the following equalities

$$\begin{aligned} a\otimes s= a\otimes ss's= as\otimes s's= a's\otimes s's=a'\otimes ss's=a'\otimes s \end{aligned}$$

in $A\otimes _{S} Ss$ and so A is principally weakly flat by Lemma 17. $\square$

Next we characterize semigroups over which all right S-acts are weakly flat in FAct-S. For this, we need the following propositions.

Proposition 22

Let S be a semigroup, and $A\in$ FAct-S. Then A is weakly flat if and only if it is principally weakly flat and satisfies Condition

$\mathrm {(W)}$ If $as = a's'$ for $a, a'\in A$, $s, s'\in S$, then there exist $a''\in A$, $u\in Ss\cap Ss'$, such that $as = a's' = a''u$.

Proof

The proof is similar to that of [6, Theorem 3.11.4]. $\square$

When S be a regular semigroup, the characterization of weak flatness is simpler.

Proposition 23

Let S be a regular semigroup, and $A\in$ FAct-S. Then A is weakly flat if and only if for every $s, t\in S$ and $a\in A$, $as=at$ implies that there exists $z\in Ss\cap St$, such that $as=at=az$.

Proof

Necessity. Let $as=at$ for $s, t\in S$ and $a\in A$. From Proposition 22, it follows that there exist $a''\in A$, $u\in Ss\cap Ss'$, such that $as = at = a''u$. Let $u'$ be the element inverse to u, since S is a regular semigroup. Set $z=su'u$. Then $z\in Ss\cap Ss'$, and $az=asu'u=a''uu'u=a''u=as = at$, as required.

Sufficiency. Suppose that A is a right S-act satisfying the assumption conditions. Since S is regular, A is principally weakly flat by Theorem 21. We shall show that A also satisfies Condition (W). Assume that $as = a't$ for $a, a'\in A$, $s, t\in S$. Put $a''=as = a't$, and let $s'$ and $t'$ be elements inverse to s and t, respectively. Then we have $a''=as=ass's=a''s's=a''t't$. By assumption, there exists $z\in Ss's\cap St't$ such that $a''s's=a''t't=a''z$. Hence $as=a't=a''z$, and so A is weakly flat by Proposition 22. $\square$

Theorem 24

Let S be a semigroup with local units. In the category FAct-S the following statements are equivalent.

• (1) All S-acts are weakly flat.

• (2) All finitely generated S-acts are weakly flat.

• (3) All cyclic S-acts are weakly flat.

• (4) S is regular and satisfies Condition

$\mathrm {(R)}$ For any $s, t\in S$, there exists $z\in Ss\cap St$, such that $z\rho (s, t)s$.

Proof

The implications $(1)\Rightarrow (2)\Rightarrow (3)$ are obvious.

$(3)\Rightarrow (4)$. Regularity of S follows from Theorem 21. For any $s, t\in S$, since S is a semigroup with local units, there exist idempotents $e, f\in S$ such that $s =es$ and $t=ft$. We denote by $\rho =\rho (s, t)$ the smallest congruence on S generated by (s, t). Then $s\rho t$, i.e., $[e]s=[f]t$. Since $S/\rho$ is weakly flat by assumption, Proposition 22 implies the existence of elements $w\in S$, $z'\in Ss\cap St$ such that $[e]s=[f]t=[w]z'$. Putting $z=wz'$ we have $z\in Ss\cap St$ and $[s]=[es]=[e]s=[w]z'=[z]$. This implies $(s, z)\in \rho$, that is, we have Condition (R).

$(4)\Rightarrow (1)$. Suppose that A is any right S-act. Then A is principally weakly flat by Theorem 21. Let $as = at$, for $a\in A$, $s, t\in S$. Now define a congruence $\lambda$ on S by

$$\begin{aligned} x\lambda y\ \ \Longleftrightarrow \ \ ax=ay. \end{aligned}$$

Clearly, $(s, t)\in \lambda$, and of course $\rho (s, t)\subseteq \lambda$. From (4) it follows that there exists $z\in Ss\cap St$, such that $z\rho (s, t)s$. Hence $(z, s)\in \lambda$, and so $as = at=az$. Thus A is weakly flat by Proposition 23. $\square$

In particular, Theorem 24 yields the following result for commutative regular semigroups.

Corollary 25

Let S be a commutative regular semigroup. Then all S-acts are weakly flat.

Now we shall consider the special case of idempotent semigroups. Recall that an idempotent semigroup (or a band) S is called left regular if $st = sts$ for any $s, t\in S$ (see [6, Remark 1.3.45]).

Proposition 26

Let S be an idempotent semigroup. In the category FAct-S the following statements are equivalent.

• (1) All S-acts are weakly flat.

• (1) S is left regular.

Proof

The proof is similar to that of [6, IV, Proposition 7.6]. $\square$

So far, we have not yet been able to characterize semigroups with local units over which all acts are flat by using elements and ideals of semigroups. But we can obtain the partial result concerning the commutative situation. To do so we need the following lemma.

Lemma 27

Let S be a semigroup, and $A\in$ FAct-S. Then A is flat if and only for any left S-act B, $a\otimes b= a'\otimes b'$ for $a, a'\in A$, $b, b'\in B$ in $A\otimes B$ implies $a\otimes b = a'\otimes b'$ in $A\otimes (Sb\cup Sb')$.

Proof

It is a routine matter. $\square$

Theorem 28

Let S be a commutative semigroup with local units. In the category FAct-S the following statements are equivalent.

• (1) All S-acts are flat.

• (2) All finitely generated S-acts are flat.

• (3) All cyclic S-acts are flat.

• (4) S is regular.

Proof

The implications $(1)\Rightarrow (2)\Rightarrow (3)$ are obvious.

$(3)\Rightarrow (4)$. Note that flatness implies weak flatness. The regularity of S follows from Theorem 24.

$(4)\Rightarrow (1)$. Suppose that S is a commutative regular semigroup. Then all cyclic S-acts are weakly flat by Theorem 24 and Corollary 25. Let $A = aS$ be a cyclic weakly flat S-act, let B be any left S-act, $b, b'\in B$, and $a\otimes b = a\otimes b'$ in $A\otimes B$. We need to only show that this equality holds in $A\otimes (Sb\cup Sb')$ by Lemma 27. By assumption there exist $b_{1}, b_{2}, \ldots , b_n\in B$, $s_1, t_1, \ldots , s_n, t_n\in S$ such that

$$\begin{aligned} \begin{array}{rclcrcl} &{} &{} &{} &{} b &{} = &{} s_1 b_1 \\ as_1 &{} = &{} at_1 &{} &{} t_1b_1 &{} = &{} s_2 b_2 \\ as_2 &{} = &{} at_2 &{} &{} t_2b_2 &{} = &{} s_3 b_3 \\ &{} \cdots &{} &{} &{} &{} \cdots &{} \\ as_n &{} = &{} at_n &{} &{} t_nb_n &{} = &{} b'. \end{array} \end{aligned}$$

For each $i\in \{1, \ldots , n\}$, there exist $u_{i}, v_{i}\in S$ such that $u_{i}s_{i}=v_{i}t_{i}$, and $as_{i} = at_{i}= au_{i}s_{i}=av_{i}t_{i}$ by Proposition 22. Since S is a semigroup with local units, there exist $e, f\in E(S)$ such that $b = eb$, $b' = fb'$. For convenience let $v_{0} = e$, $s_{n+1} = f$ and $b_{n+1} = b'$. We use induction on i to prove for each $i\in \{1, \ldots , n\}$, $v_{i}\cdots v_{1}s_{i+1}b_{i+1}\in Sb$ and $a\otimes v_{i-1}\cdots v_{1}s_{i}b_{i}=a\otimes v_{i}\cdots v_{1}s_{i+1}b_{i+1}$ in $aS\otimes Sb$.

If $i = 1$ then, since $b = s_{1}b_{1}$ and $as_{1} = (au_{1})s_{1}$, it follows that $a\otimes b = au_{1}\otimes b$ in $aS\otimes Sb$. Hence we get

$$\begin{aligned} a\otimes v_{0}s_{1}b_{1} = a\otimes b = au_{1}\otimes b = a\otimes u_{1}s_{1}b_{1} = a\otimes v_{1}t_{1}b_{1}=a\otimes v_{1}s_{2}b_{2} \end{aligned}$$

in $aS\otimes Sb$ as required. Now assume the result is true for a particular i $(1\le i\le n)$. Since $v_{i}\cdots v_{1}s_{i+1}b_{i+1}=(v_{i}\cdots v_{1}s_{i+1})b_{i+1}$ and $a(v_{i}\cdots v_{1}s_{i+1})=(as_{i+1})(v_{i}\cdots v_{1})=(au_{i+1}s_{i+1})(v_{i}\cdots v_{1})=(au_{i+1})(v_{i}\cdots v_{1}s_{i+1})$, we can obtain that

$$\begin{aligned} a\otimes (v_{i}\cdots v_{1}s_{i+1}b_{i+1})=au_{i+1}\otimes (v_{i}\cdots v_{1}s_{i+1}b_{i+1}) \end{aligned}$$

in $aS\otimes S(v_{i}\cdots v_{1}s_{i+1}b_{i+1})$, hence, in $aS\otimes Sb$. Furthermore,

$$\begin{aligned}&u_{i+1}v_{i}\cdots v_{1}s_{i+1}b_{i+1}=v_{i}\cdots v_{1}(u_{i+1}s_{i+1})b_{i+1}\\ =~&v_{i}\cdots v_{1}(v_{i+1}t_{i+1})b_{i+1}=v_{i+1}v_{i}\cdots v_{1}s_{i+2}b_{i+2}, \end{aligned}$$

and the conclusion follows easily.

Now, calculating in $aS\otimes Sb$,

$$\begin{aligned} a\otimes b&= a\otimes v_{1}s_{2}b_{2}=\cdots =a\otimes v_{n-1}\cdots v_{1}s_{n}b_{n}\\&=a\otimes v_{n}\cdots v_{1}s_{n+1}b_{n+1}=a\otimes v_{n}\cdots v_{1}b'. \end{aligned}$$

Dually, $a\otimes b'= a\otimes u_{n}\cdots u_{1}b$ in $aS\otimes Sb'$. Moreover,

$$\begin{aligned} u_{n}\cdots u_{1}b&=u_{n}\cdots u_{2}(u_{1}s_{1})b_{1}=u_{n}\cdots u_{2}v_{1}t_{1}b_{1}=u_{n}\cdots u_{2}v_{1}s_{2}b_{2}\\&=v_{1}u_{n}\cdots u_{2}s_{2}b_{2}=v_{1}u_{n}\cdots u_{3}v_{2}t_{2}b_{2}\\&=\cdots =v_{n-1}\cdots v_{1}v_{n}t_{n}b_{n}=v_{n}\cdots v_{1}b'. \end{aligned}$$

Therefore $a\otimes b = a\otimes b'$ in $aS\otimes (Sb\cup Sb')$. This completes the proof. $\square$

The following two statements are easy consequences of definitions.

Proposition 29

Let S be a semigroup. Then

• (1) $\Theta _{S}$ is principally weakly flat.

• (2) $\Theta _{S}$ is (weakly) flat if and only if S is right reversible.

Next, we continue to do research properties of acts connected with projectivity. The weakest of such properties is torsion freeness.

Definition 30

We call a right S-act $A_{S}$ torsion free if, for any $a, a'\in A$ and any right cancellable element $c\in S$, there exists an idempotent $e\in S$ such that $c =ec$, and the equality $ac= a'c$ implies $ae =a'e$.

We say that an element s of a semigroup S is right e-invertible for an idempotent $e\in S$ if $s = es$ and there exists $s'\in S$ such that $ss' = e$. It is obvious that the condition of the definition is satisfied for any right cancellable element which is right e-invertible.

Proposition 31

Let S be a semigroup with local units and I a proper right ideal of S. Then the Rees factor act S/I is torsion free if and only if for every $s\in S$ and every right cancellable element c of S, there exists an idempotent $e\in S$ such that $c =ec$, and $sc\in I$ implies $se\in I$.

Proof

Necessity. Assume $sc\in I$ for $s, c\in S$, where c is a right cancellable element of S. Since S is a semigroup with local units, for the element c, we can find $e\in E(S)$ with $c =ec$. Form $sc\in I$ it follows that $scc\in I$. Then $[s]c = [sc] = [scc]= [sc]c$. Since S/I is torsion free, we have $[s]e = [sc]e$. This implies that $se\in I$.

Sufficiency. Suppose $[s]c = [t]c$, $s, t, c\in S$, c a right cancellable element. Then there exists $e\in E(S)$ such that $c =ec$ because S has local units. If $sc, tc\in I$ then by assumption $se, te\in I$ which means $[s]e=[se]=[te]= [t]e$. If $sc = tc$, then of course $s = t$ and so $[s]e = [t]e$. Thus S/I is torsion free. $\square$

In what follows, we shall use the above proposition to answer so-called homological questions, for which semigroups are all acts torsion free.

Theorem 32

Let S be a semigroup with local units. In the category FAct-S, the following statements are equivalent.

• (1) All S-acts are torsion free.

• (2) All cyclic S-acts are torsion free.

• (3) All Rees factor acts of S are torsion free.

• (4) Every right cancellable element of S is right e-invertible for some idempotent $e\in S$.

Proof

The implications $(1)\Rightarrow (2)\Rightarrow (3)$ are obvious.

$(3)\Rightarrow (4)$. Let $c\in S$ be a right cancellable element. Then there exists an idempotent $e\in S$ such that $c =ec$. By assumption, the Rees factor act S/cS is torsion free. Since $ec=c\in cS$, Proposition 31 implies $e\in cS$. Hence c is right e-invertible.

$(4)\Rightarrow (1)$. Suppose that A is a right S-act and $ac=a'c$ for a right cancellable element $c\in S$ and $a, a'\in A$. Since S is a semigroup with local units, there exists an idempotent $e\in S$ such that $c =ec$. Then by assumption c is right e-invertible, we have $ae = a'e$. This shows that A is torsion free. $\square$

From the proof of this theorem, we observe that Theorem 32 also holds in the category Act-S.

Corollary 33

([6, Theorem 4.6.1]) For any monoid S, the following statements are equivalent.

• (1) All right S-acts are torsion free.

• (2) All cyclic right S-acts are torsion free.

• (3) All right Rees factor acts of S are torsion free.

• (4) Every right cancellable element of S is right invertible.

Later on in this section, we clarify the relationship between properties defined in Definitions 15 and 30 and projectivity. We begin to investigate the relationship between projectivity and flatness. To reach this goal, we need the following result. Consider an S-monomorphism $f: A\rightarrow B$ in the category Act-S. Then f is called a retraction if there exists an S-homomorphism $g: B\rightarrow A$ with $gf = 1_{A}$.

Lemma 34

Let A be a subact of an act $B_{S}$, and let the inclusion $A\rightarrow B$ be a retraction. If B is flat, then A is also flat.

Proof

Let $g: B\rightarrow A$ be such that $g|_{A}= 1_{A}$. Suppose that C is a subact of a left S-act $_{S}D$, and that $a\otimes c=a'\otimes c'$ in $A\otimes D$ for $c, c'\in C$, $a, a'\in A$. Then the equality $a\otimes c=a'\otimes c'$ holds in $B\otimes D$. Since B is flat, the equality $a\otimes c=a'\otimes c'$ also holds in $B\otimes C$. Hence we get

$$\begin{aligned} a\otimes c=(g\otimes 1_{C})(a\otimes c)=(g\otimes 1_{C})(a'\otimes c')=a'\otimes c' \end{aligned}$$

in $A\otimes B$. This shows that the mapping $A\otimes C\rightarrow A\otimes D$ is a monomorphism, and thus A is flat. $\square$

Proposition 35

Let S be a semigroup with local units. Then every projective S-act is flat.

Proof

For an arbitrary idempotent $e\in E(S)$, note that the inclusion $eS\hookrightarrow S$ is a retraction. From the firmness of the S-act $S_{S}$, it follows that S is flat, and so, by Lemma 34, eS is flat. Now let P be a projective S-act. Then by Corollary 2.10 of [12] $P\cong \coprod _{i\in I}e_{i}S$, $e_{i}\in E(S)$. Further, from Proposition 2.5.14 of [6] we obtain that P is flat. $\square$

In what follows, we describe the relationship between torsion freeness and principal weak flatness.

Proposition 36

Let S be a semigroup with local units. Then every principally weakly flat firm S-act is torsion free.

Proof

Let A be a principally weakly flat firm right S-act and let $ac= a'c$ for $a, a'\in A$ and for a right cancellable element $c\in S$. Then $a\otimes c = a'\otimes c$ in the tensor product $A\otimes _{S} Sc$ by Lemma 17. Hence we have an S-tossing

$$\begin{aligned} \begin{array}{rclcrcl} a &{} = &{} a_1s_1 &{} &{} &{} &{} \\ a_1t_1 &{} = &{} a_2s_2 &{} &{} s_1c &{} = &{} t_1c \\ a_2t_2 &{} = &{} a_3s_3 &{} &{} s_2c &{} = &{} t_2c \\ &{} \cdots &{} &{} &{} &{} \cdots &{} \\ a_nt_n &{} = &{} a' &{} &{} s_nc &{} = &{} t_nc, \end{array} \end{aligned}$$

where $s_{1}, \cdots , s_{n}, t_{1},\cdots , t_{n}\in S$, $a_{1},\cdots , a_{n}\in S$. Since c is right cancellable and $ec=c$ for some idempotent $e\in S$ we have $s_{i}e = t_{i}e$, $i=1,\cdots , n$. Using the left equalities from the S-tossing we get

$$\begin{aligned} ae=a_{1}s_{1}e=a_{1}t_{1}e=a_{2}s_{2}e=\cdots = a_{n}s_{n}e= a_{n}t_{n}e=a'e. \end{aligned}$$

Thus A is torsion free. $\square$

Now applying these two propositions and Definition 15, we obtain the following implications.

Proposition 37

Let S be a semigroup with local units. In the category FAct-S, we have the following implications:

$$\begin{aligned} projective {\Rightarrow } flat {\Rightarrow } weakly \, flat {\Rightarrow } principally \, weakly \, flat {\Rightarrow } torsion free. \end{aligned}$$

Note that these implications in Proposition 37 are strict. Implication projective $\Rightarrow$ flat is strict by Example 38. Implication flat $\Rightarrow$ weakly flat is strict by Example 3.12.20 of [6]. Implication weakly flat $\Rightarrow$ principally weakly flat is strict by Proposition 29. Implication principally weakly flat $\Rightarrow$ torsion free is strict by Example 3.10.13 of [6].

Example 38

Let $S = \{1, e, 0\}$ where $e^{2}= e$, $K_{S} = \{e, 0\}$. Consider the Rees factor right S-act S/K. Since S is a commutative semigroup with local units, S/K is flat by Theorem 28. However, it is not projective by Corollary 9, since $e\rho _{K} 0$, but $e\ne 0$.

5 Rees Short Exact Sequence and Flatness Properties

In this section, we shall extend the theory of Rees short exact sequence of acts over monoids to semigroups with local units. We consider conditions under which a Rees short exact sequence of acts is left and right split, respectively, and investigate relationships between different types of flatness and Rees short exact sequence.

The following proposition is proved in exactly the same manner as is the module case (see Proposition 2.72 of [20]).

Proposition 39

(Five Lemma) Let S be a semigroup. Consider a commutative diagram of S-acts with exact rows.

• (1) If $\alpha _{2}$ and $\alpha _{4}$ are monomorphisms and $\alpha _{1}$ is an epimorphism, then $\alpha _{3}$ is monomorphism.

• (2) If $\alpha _{2}$ and $\alpha _{4}$ are epimorphisms and $\alpha _{5}$ is monomorphism, then $\alpha _{3}$ is an epimorphism.

• (3) If $\alpha _{2}$ and $\alpha _{4}$ are isomorphism, $\alpha _{1}$ is an epimorphism and $\alpha _{5}$ is monomorphism, then $\alpha _{3}$ is isomorphism.

Proof

A diagram chase. $\square$

Throughout the following, we shall assume that S is a semigroup with a zero 0.

Proposition 40

Let

(4)

be a Rees short exact sequence of S-acts. Then the following statements are equivalent.

• (1) The sequence (4) is right split.

• (2) f(L) is a direct summand of M.

• (3) The sequence (4) is isomorphic to the Rees short exact sequence

  

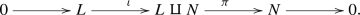
Proof

The technique used in [19, Theorem 2.5] will be employed. $\square$

Now we present relationships between different types of flatness and Rees short exact sequence. We begin our investigation with the weakest of flatness properties.

Proposition 41

Let S be a semigroup with local units. Let

be a Rees short exact sequence of right S-acts. If both L and N are torsion free, then M is torsion free.

Proof

Let $mc = m'c$ for $m, m'\in M$ and $c\in S$ a right cancellable element of S. Since S is a semigroup with local units, there exists an idempotent $e\in E(S)$ such that $c = ec$. Applying torsion freeness of N to the equality $g(m)c = g(m')c$, we get $g(m)e = g(m')e$, and so $(me, m'e)\in kerg = {\mathcal {K}}_{Imf}$. If $me = m'e$, then the result follows. Otherwise, there exist $l, l'\in L$, such that $f(l) = me$ and $f(l') = m'e$. Hence we obtain that

$$\begin{aligned} f(lc) = f(l)c = mec =mc= m'c = m'ec =f(l')c = f (l'c). \end{aligned}$$

Since f is a monomorphism, $lc = l'c$ and as L is torsion free, we have $le = l'e$. Thus $me = m'e$, i.e., M is torsion free. $\square$

Proposition 42

Let S be a semigroup with local units. Let

be a Rees short exact sequence of right firm S-acts. If both L and N are principally weakly flat, then M is also principally weakly flat.

Proof

Suppose that $ms = m's$ for $m, m\in M$, $s\in S$. Then we have $g(m)s = g(m')s$ in N. Using firmness of N we have $g(m)\otimes s = g(m')\otimes s$ in $N\otimes S$. Since N is principally weakly flat, the equality $g(m)\otimes s = g(m')\otimes s$ holds in $N\otimes Ss$. So there exists an S-tossing

$$\begin{aligned} \begin{array}{rclcrcl} g(m) &{} = &{} b_1s_1 &{} &{} &{} &{} \\ b_1t_1 &{} = &{} b_2s_2 &{} &{} s_1s &{} = &{} t_1s \\ b_2t_2 &{} = &{} b_3s_3 &{} &{} s_2s &{} = &{} t_2s \\ &{} \cdots &{} &{} &{} &{} \cdots &{} \\ b_nt_n &{} = &{} g(m') &{} &{} s_ns &{} = &{} t_ns, \end{array} \end{aligned}$$

where $b_1, \ldots , b_n\in N$, $s_1, \ldots , s_n, t_1, \ldots , t_n\in S$. Since g is an S-epimorphism, there exists $m_{i}\in M$ such that $g(m_{i}) = b_{i}$ for every i $(1\le i\le n)$. Thus

$$\begin{aligned} \begin{array}{rclcrcl} g(m) &{} = &{} g(m_{1})s_1 &{} &{} &{} &{} \\ g(m_{1})t_1 &{} = &{} g(m_{2})s_2 &{} &{} s_1s &{} = &{} t_1s \\ g(m_{2})t_2 &{} = &{} g(m_{3})s_3 &{} &{} s_2s &{} = &{} t_2s \\ &{} \cdots &{} &{} &{} &{} \cdots &{} \\ g(m_{n})t_n &{} = &{} g(m') &{} &{} s_ns &{} = &{} t_ns. \end{array} \end{aligned}$$

(5)

For $m, m'\in M$, we have $m=me$, $m'=m'f$ for some $e, f\in E(S)$, since S is a semigroup with local units. Take $m_{0} = m$, $t_{0} = e$, $m_{n+1} = m'$, $s_{n+1} = f$. Then $(m_{i}t_{i}, m_{i+1}s_{i+1})\in kerg = {\mathcal {K}}_{Imf}$, $(0\le i\le m)$. If $m_{i}t_{i}=m_{i+1}s_{i+1}$ for every i $(0\le i\le m)$, then we can obtain $m\otimes s = m'\otimes s$ in $M\otimes Ss$, which implies that M is principally weakly flat. Otherwise, suppose that l is the smallest index such that $(m_{l}t_{l}, m_{l+1}s_{l+1})\in (Imf\times Imf)$ and k is the largest index such that $(m_{k}t_{k}, m_{k+1}s_{k+1})\in (Imf\times Imf)$. Then there exist $a_{l}, a_{k+1}\in L$ such that $f(a_{l})= m_{l}t_{l}$ and $f(a_{k+1})= m_{k+1}s_{k+1}$. Thus we have

$$\begin{aligned} f(a_{l}s)&= f(a_{l})s= m_{l}t_{l}s = m_{l}s_{l}s = m_{l-1}t_{l-1}s\\&= \cdots = m_{1}t_{1}s= m_{1}s_{1}s= ms= m's= m_{n}t_{n}s = m_{n}s_{n}s = m_{n-1}t_{n-1}s\\&= \cdots = m_{k+1}s_{k+1}s=f (a_{k+1})s= f (a_{k+1}s). \end{aligned}$$

Since f is an S-monomorphism, $a_{l}s = a_{k+1}s$. From principal weak flatness of L, it follows that $a_{l}\otimes s = a_{k+1}\otimes s$ in $L\otimes Ss$. Thus there exists an S-tossing

$$\begin{aligned} \begin{array}{rclcrcl} a_{l} &{} = &{} \alpha _1u_1 &{} &{} &{} &{} \\ \alpha _1v_1 &{} = &{} \alpha _2u_2 &{} &{} u_1s &{} = &{} v_1s \\ \alpha _2v_2 &{} = &{} \alpha _3u_3 &{} &{} u_2s &{} = &{} v_2s \\ &{} \cdots &{} &{} &{} &{} \cdots &{} \\ \alpha _zv_z &{} = &{} a_{k+1} &{} &{} u_zs &{} = &{} v_zs, \end{array} \end{aligned}$$

where $\alpha _1, \ldots , \alpha _z\in L$, $u_1, v_1, \ldots , u_z, v_z\in S$. Then applying S-tossing (5) we can computer that

$$\begin{aligned} m\otimes s&= m_{1}s_{1}\otimes s = m_{1}\otimes s_{1}s = m_{1} \otimes t_{1}s = m_{1}t_{1}\otimes s =\cdots = m_{l}t_{l}\otimes s \\&= f(a_{l})\otimes s = f(\alpha _{1})u_{1}\otimes s = f(\alpha _{1})\otimes u_{1}s = f(\alpha _{1})\otimes v_{1}s = f(\alpha _{1})v_{1}\otimes s\\&= \cdots = f(\alpha _{z})v_{z}\otimes s= f(a_{k+1})\otimes s = m_{k+1}s_{k+1}\otimes s = m_{k+1}\otimes s_{k+1}s\\&= m_{k+1}\otimes t_{k+1}s = m_{k+1}t_{k+1}\otimes s = \cdots = m_{n}t_{n}\otimes s = m'\otimes s \end{aligned}$$

in $M\otimes Ss$, and so M is principally weakly flat. $\square$

Similarly one proves the case of (weak) flatness of acts.

Proposition 43

Let

be a left split Rees short exact sequence of right S-acts. If L, N are (weakly) flat right S-acts, then M is (weakly) flat.

Finally we investigate with projectivity of acts.

Proposition 44

Let S be a semigroup with local units. Let

(6)

be a Rees short exact sequence of right S-acts. If both L and N are projective, then M is also projective.

Proof

From projectivity of N it follows that there exists an S-homomorphism $g': N\rightarrow M$, such that $gg' = 1_{N}$. By Proposition 40, the sequence (6) is isomorphic to

Therefore $M\cong L\amalg N$. Since L and N are projective, M is also projective by [12, Proposition 2.7]. $\square$

6 Conclusion

The aim of this paper is to develop homological classification theory for semigroups with local units. We show that Hom functors and tensor functors in the category of acts over semigroups are left and right exact functors, respectively (see Theorems 3 and 5). Our main result presents characterizations of semigroups with local units, and the main tool in our work is different types of flatness in the category of firm acts (see, for example, Theorems 21, 24, 28, 32). It should be noted that when semigroups with local units are monoids, we can obtain the corresponding classification results for monoids (see, for example, Theorems 4.6.1, 4.6.6, 4.7.5 of [6]). This suffices to show that our new approach is scientific and reasonable. In addition, we define a new class of semigroups called PP semigroups and give conditions for semigroups with local units to be these semigroups by projectivity in the category of unitary acts (see Theorem 12). Moreover, we also investigate conditions under which flatness properties of right acts L and N in the Rees short exact sequence can be transferred to M (see Sect. 5). The obtained results may also be applied in various fields such as graph theory, algebraic automata theory, theory of machines, theory of formal languages, information theory, data bases, theory of communications and electronic circuits.