A Description of Ad-nilpotent Elements in Semiprime Rings with Involution

Abstract

In this paper, we study ad-nilpotent elements in Lie algebras arising from semiprime associative rings R free of 2-torsion. With the idea of keeping under control the torsion of R, we introduce a more restrictive notion of ad-nilpotent element, pure ad-nilpotent element, which is a only technical condition since every ad-nilpotent element can be expressed as an orthogonal sum of pure ad-nilpotent elements of decreasing indices. This allows us to be more precise when setting the torsion inside the ring R in order to describe its ad-nilpotent elements. If R is a semiprime ring and $a\in R$ is a pure ad-nilpotent element of R of index n with R free of t and $\left( {\begin{array}{c}n\\ t\end{array}}\right)$-torsion for $t=[\frac{n+1}{2}]$, then n is odd and there exists $\lambda \in C(R)$ such that $a-\lambda$ is nilpotent of index t. If R is a semiprime ring with involution $*$ and a is a pure ad-nilpotent element of ${{\,\mathrm{Skew}\,}}(R,*)$ free of t and $\left( {\begin{array}{c}n\\ t\end{array}}\right)$-torsion for $t=[\frac{n+1}{2}]$, then either a is an ad-nilpotent element of R of the same index n (this may occur if $n\equiv 1,3 \,(\text {mod } 4)$) or R is a nilpotent element of R of index $t+1$, and R satisfies a nontrivial GPI (this may occur if $n\equiv 0,3 \,(\text {mod } 4)$). The case $n\equiv 2 \,(\text {mod } 4)$ is not possible.

1 Introduction

Herstein’s theory of rings, which started in 1954 in [19] (see also the influential works [20, 32]), is the study of nonassociative objects in associative prime and semiprime rings perhaps with involution or in rings with well-behaved idempotents that provide a context rich enough for the theory to be satisfactorily developed. Among the main contributors, apart from Herstein itself, we can also cite Posner, Lanski, Montgomery, Martindale and Miers, and Brešar and Beidar.

Herstein’s theory developed into several similar but different branches: the study of sets with an additional nonassociative structure, as Lie and Jordan ideals (e.g., [31]), culminating in the development of GPI theory [5]; the study of special conditions (e.g., commuting map) on special maps (e.g., generalized derivations) over special sets (e.g., Jordan ideals), in which strong knowledge is gained about the map or the ring (e.g., commutativity) through the a priori weaker properties of the map (e.g., [7, 15, 25, 33]); and the determination of the structure of nonassociative maps, as Lie homomorphisms and derivations (e.g., [2,3,4]), culminating in the development of the theory of functional identities [6]. It is to this last branch of Herstein’s theory that our paper belongs, centering on the structure of nilpotent derivations, which have been broadly studied since the 1960s. In 1963, Herstein proved that for any ad-nilpotent element a of index n in a simple ring R of characteristic zero or greater than n, there exists some $\lambda$ in the center of R such that $a-\lambda$ is nilpotent. Furthermore, he showed that the index of nilpotence of such element is not greater than $[\frac{n+1}{2}]$, see [21, Theorem in p. 84]. Herstein’s result was extended by Martindale and Miers in 1983 ([28, Corollary 1]) to prime rings of characteristic greater than n by making use of the extended centroid of R. In 1978, Kharchenko obtained in [23] an important result: All algebraic derivations of prime rings of characteristic zero are inner for certain elements in an overring; he extended this result to torsion-free semiprime rings in 1979, see [24]. In 1983, Chung and Luh stated that the index of nilpotence of a nilpotent derivation on a semiprime ring of characteristic zero is always odd (see [12, 13]), and in 1984 Chung, Kobayashi and Luh [14] proved that if R is semiprime and $\mathrm{char}\, R = p > 2$ then the index of nilpotence of a nilpotent derivation is of the form $n=a_sp^s+a_{s+1}p^{s+1}+\dots +a_lp^l$ where $0 \le s \le l$, the $a_i$ are nonnegative integers less than p, $a_s$ is odd, and $a_{s+1},\dots , a_l$ are even. Moreover, Chung in 1985 proved, for prime rings of characteristic zero, that a nilpotent derivation is inner and induced by a nilpotent element of an overring, see [11]. In 1992, with different techniques, Grzeszczuk showed that any nilpotent derivation in a semiprime ring with minimal restrictions on its characteristic is an inner derivation in a semiprime subring of the right Martindale ring of quotients of R and is induced by a nilpotent element in such subring, see [18, Corollary 8] and its generalization by Chuang and Lee in [10, §3].

Two important examples of Lie algebras appear when working with rings R with involution $*$, the Lie algebra of skew-symmetric elements $K:={{\,\mathrm{Skew}\,}}(R,*)$ and the derived Lie algebra $[K,K]/([K,K]\cap Z(R))$. The nilpotent derivations of the skew-symmetric elements of prime rings with involution were studied by Martindale and Miers in the 1990s. In this case, if R has zero characteristic and is not an order in a 4-dimensional central simple algebra, for every inner derivation ${{\,\mathrm{ad}\,}}_a$ with ${{\,\mathrm{ad}\,}}_a^n=0$ there exists an element $\lambda$ in the extended centroid of R such that either $(a-\lambda )^{[\frac{n+1}{2}]}=0$ or the involution is of the first kind and $a^{[\frac{n+1}{2}]+1}=0$, see [29, Main Theorem]. This result was partially extended to semiprime rings by Lee in 2018. In his main result, he proved that if R is semiprime with involution and has no n!-torsion, then for any $a\in K$ with ${{\,\mathrm{ad}\,}}_a^n(K)=0$ there exist $\lambda$ and a symmetric idempotent $\epsilon$ in the extended centroid of R such that $(\epsilon a-\lambda )^{[\frac{n+1}{2}]+1}=0$, see [26, Theorem 1.5].

The main goal of this paper is to deepen into the description of ad-nilpotent elements of K for semiprime rings. In the spirit of Martindale and Miers’ result [29, Main Theorem], we will obtain different results about the form of an ad-nilpotent element of K of index n depending on the equivalence class of n modulo 4. To get such results in the semiprime context, we introduce a new concept, that of pure ad-nilpotence. We say that an ad-nilpotent element a of index n in $L:=R^-$ or K is pure if $\lambda a$ remains ad-nilpotent of the same index for every $\lambda$ in the extended centroid such that $\lambda a\ne 0$. This is just a technical condition, since every ad-nilpotent element of $R^-$ can be expressed as an orthogonal sum of pure ad-nilpotent elements of the central closure ${\hat{R}}$ of R with decreasing indices of ad-nilpotence.

As a first step, we focus on ad-nilpotent elements of R. In this case, under the hypothesis of pure ad-nilpotence, the condition on the torsion of the ring can be weakened when compared with the result of Lee in [26, Theorem 1.3]:

Theorem 4.4 Let R be a semiprime ring with no 2-torsion, and let $a\in R$ be a pure ad-nilpotent element of R of index n. Let $t:=[\frac{n+1}{2}]$ and suppose that R is free of $n\atopwithdelims ()t$-torsion and t-torsion. Then n is odd and there exists $\lambda \in C(R)$ such that $a-\lambda$ is nilpotent of index $\frac{n+1}{2}$.

When dealing with ad-nilpotent elements of K, we can again split them into orthogonal sums of pure ad-nilpotent elements in ${{\,\mathrm{Skew}\,}}({\hat{R}},*)$ with decreasing indices. We study each of these pure pieces and get precise descriptions of them depending on the equivalence class of their indices of ad-nilpotence modulo 4.

Theorem 5.6 Let R be a semiprime ring with involution $*$ and free of 2-torsion, let ${\hat{R}}$ be its central closure, and let $a\in K$ be a pure ad-nilpotent element of K of index $n>1$. If R is free of $\left( {\begin{array}{c}n\\ t\end{array}}\right)$-torsion and t-torsion for $t:=[\frac{n+1}{2}]$ then:

• (1)   If $n\equiv 0 \,(\text {mod } 4)$ then $a^{t+1}=0$, $a^t\ne 0$ and $a^tKa^t=0$. Moreover, there exists an idempotent $\epsilon \in H(C(R),*)$ such that $\epsilon a=a$ and the ideal generated by $a^t$ is essential in $\epsilon {\hat{R}}$. In addition $\epsilon {\hat{R}}$ satisfies the GPI $a^txa^tya^t=a^tya^txa^t$ for every $x,y\in \epsilon {\hat{R}}$.

• (2)   If $n\equiv 1 \,(\text {mod } 4)$ then there exists $\lambda \in {{\,\mathrm{Skew}\,}}(C(R),*)$ such that $(a-\lambda )^t=0$ (a is an ad-nilpotent element of R of index n).

• (3)   It is not possible that $n\equiv 2 \,(\text {mod } 4)$.

• (4)   If $n\equiv 3 \,(\text {mod } 4)$ then there exists an idempotent $\epsilon \in H(C(R),*)$ making $a=\epsilon a+(1-\epsilon )a\in {\hat{R}}$ such that:

  (4.1):

    If $\epsilon a\ne 0$ then $\epsilon a^{t+1}=0$, $\epsilon a^t\ne 0$ and $\epsilon a^tk\epsilon a^{t-1}=\epsilon a^{t-1}k\epsilon a^t$ for every $k\in {{\,\mathrm{Skew}\,}}({\hat{R}}, *)$. The ideal generated by $\epsilon a^t$ is essential in $\epsilon {\hat{R}}$ and $\epsilon {\hat{R}}$ satisfies the GPI $a^txa^tya^t=a^tya^txa^t$ for every $x,y\in \epsilon {\hat{R}}$.

  (4.2):

    If $(1-\epsilon )a\ne 0$ then there exists $\lambda \in {{\,\mathrm{Skew}\,}}(C(R),*)$ such that $((1-\epsilon )a-\lambda )^t=0$ ($(1-\epsilon )a$ is a pure ad-nilpotent element of ${\hat{R}}$ of index n).

In particular, for all $n>1$ there exists $\lambda \in {{\,\mathrm{Skew}\,}}(C(R),*)$ such that $(a-\lambda )^{t+1}=0$, $(a-\lambda )^{t-1}\ne 0$.

From these two results describing pure ad-nilpotent elements of R and of K we easily recover Lee’s results [26, Theorem 1.3 and Theorem 1.5]. Furthermore, we also describe ad-nilpotent elements of Lie algebras of the form R/Z(R) and $K/(K\cap Z(R))$, and of their derived Lie algebras $[R, R]/([R, R]\cap Z(R))$ and $[K, K]/([K, K]\cap Z(R))$.

2 Preliminaries

In this paper, we will be dealing with rings R with or without involution $*$, free of 2-torsion. When R has an involution $*$, we will consider the subsets of skew-symmetric elements $K:={{\,\mathrm{Skew}\,}}(R,*)$ and symmetric elements $H:=H(R,*)$. We will also be dealing with Lie algebras. As usual, a Lie algebra L over a ring of scalars $\Phi$ is a $\Phi$-module with an anticommutative bilinear product $[\ , \ ]$ satisfying the Jacobi identity. Recall that the adjoint map determined by any $x\in L$ is ${{\,\mathrm{ad}\,}}_x(y):=[x,y]$ for every $y\in L$. Typical examples of Lie algebras come from the associative setting: if R is an associative algebra over a ring of scalars $\Phi$, then R with product $[x,y]:=x y-y x$ is a Lie algebra denoted by $R^-$, and if R has an involution $*$ then K is a Lie subalgebra of $R^-$.

2.1 A ring R is semiprime (resp. $*$-semiprime) if for every nonzero ideal (resp. $*$-ideal) I of R, $I^2:=\{\sum _i x_iy_i\ \vert \ x_i,y_i\in I\}\ne 0$, and it is prime (resp. $*$-prime) if $IJ:=\{\sum _i x_iy_i\ \vert \ x_i\in I, y_i\in J\}\ne 0$ for every pair of nonzero ideals (resp. $*$-ideals) I, J of R. It is well known that a ring R is prime if and only if $aRb\ne 0$ for arbitrary nonzero elements $a,b\in R$, and it is semiprime if and only if it is nondegenerate, i.e., $aRa\ne 0$ for every nonzero element $a\in R$. Moreover, if R has an involution, the notions of semiprimeness and $*$-semiprimeness coincide.

An ideal $I_\alpha$ of a ring R (resp. with involution $*$) is prime (resp. $*$-prime) if $R/I_\alpha$ is a prime (resp. $*$-prime) ring. If R is a semiprime ring then there exists a family of prime ideals $\{I_\alpha \}_{\alpha \in \Delta }$ such that $\bigcap _{\alpha \in \Delta } I_\alpha =\{0\}$ and therefore R can be seen as a subdirect product of prime rings. Similarly, if R is a semiprime ring with involution $*$, there exists a family of $*$-prime ideals $\{I_\alpha \}_{\alpha \in \Delta }$ such that $\bigcap _{\alpha \in \Delta } I_\alpha =\{0\}$ and therefore R can be seen as a subdirect product of $*$-prime rings.

Moreover, if R is semiprime and free of n-torsion then the intersection of all prime ideals $I_\alpha$ such that $R/I_\alpha$ is free of n-torsion is zero (notice that the intersection of all prime ideals $I_{\alpha }$ such that $R/I_{\alpha }$ has n-torsion contains the essential ideal nR). With the same argument, we also have that semiprime rings without m and n-torsion are subdirect products of prime rings with no m nor n-torsion.

2.2 Given an ideal I of R, the annihilator of I in R is the set ${{\,\mathrm{Ann}\,}}_R(I):=\{z\in R\ \vert \ zI=Iz=0\}.$ The annihilator of an ideal I of R is an ideal of R. Moreover, when R is semiprime ${{\,\mathrm{Ann}\,}}_R(I)=\{z\in R\ \vert \ zIz=0\}$ and an ideal I of R is essential (for every nonzero ideal J of R, $I\cap J\ne 0$) if and only if ${{\,\mathrm{Ann}\,}}_R(I)=0$.

2.3 Given a ring R, we define a permissible map of R as a pair (I, f) where I is an essential ideal of R and f is a homomorphism of right R-modules. For permissible maps (I, f) and (J, g) of R, define a relation $\equiv$ by $(I,f)\equiv (J,g)$ if there exists an essential ideal K of R, contained in $I\cap J$, such that $f(x)=g(x)$ for all $x\in K$. It is easy to see that this is an equivalence relation. The quotient set $Q_{m}^r(R)$ will be called the right Martindale ring of quotients of R. If R is a semiprime ring, then $Q_{m}^r(R)$ has a ring structure coming from the addition of homomorphisms and from the composition of restrictions of homomorphisms, see [5, Chapter 2]:

• $[I,f]+[J,g]:=[I\cap J,f+g]$,

• $[I,f]\cdot [J,g]:=[(I\cap J)^2,f\circ g]$.

Note that if R is a semiprime ring then the map $f:R\rightarrow Q_{m}^r(R)$ defined by $f(r):=[R,\lambda _r]$, where $\lambda _r:R\rightarrow R$ is defined by $\lambda _r(x):=rx$, is a monomorphism of associative rings, i.e., R can be considered as a subring of its right Martindale ring of quotients. Moreover every subring S of $Q_{m}^r(R)$ which contains R is semiprime because every nonzero ideal of S has nonzero intersection with R.

The symmetric Martindale ring of quotients of R is defined as

$$\begin{aligned} Q_m^s(R):=\{q\in Q_{m}^r(R)\vert \ \exists \text { an essential ideal } I\hbox { of }R\hbox { such that } qI+Iq\subset R\} \end{aligned}$$

(if R has an involution one can replace the filter of essential ideals by the filter of essential $*$-ideals in the definition of the symmetric Martindale ring of quotients, see [1, p. 858-859].) If R is semiprime then $Q^s_m(R)$, which is a subring of $Q^r_m(R)$ containing R, is also a semiprime ring.

When R has an involution $*$, this involution can be extended to $Q_m^s(R)$ as follows: for any $q\in Q_m^s(R)$, let I be an essential $*$-ideal such that $qI+Iq\subset R$. Then $q^*:=[I,f]$ where $f(y):=(y^* q)^*$ for any y in the essential $*$-ideal I (see [5, Proposition 2.5.4]).

The extended centroid C(R) of a semiprime ring R is defined as the center of $Q_m^s(R)$. The extended centroid of a prime ring is a field (see [5, p. 70]), the set of symmetric elements of the extended centroid of a $*$-prime ring is again a field (see [1, Theorem 4(a)]), and the extended centroid of a semiprime ring is a commutative and unital von Neumann regular ring (see [5, Theorem 2.3.9(iii)]). In particular, if R is semiprime, C(R) is a semiprime ring without nilpotent elements.

The central closure of R, denoted by ${\hat{R}}$, is defined as the unital subring of $Q_m^s(R)$ generated by R and C(R), i.e., ${\hat{R}}:=C(R)R+C(R)$, and can be seen as a C(R)-algebra. Therefore we can consider R contained in ${\hat{R}}$. Moreover, since ${\hat{R}}$ contains R and is contained in $Q_m^s(R)$, if R is semiprime then ${\hat{R}}$ is semiprime. The ring ${\hat{R}}$ is centrally closed, i.e., it coincides with its central closure. In particular, its center equals its extended centroid, $Z({\hat{R}})=C({\hat{R}})$.

If R is a centrally closed semiprime ring, then $R^-$ is a Lie algebra over the ring of scalars C(R); if in addition R has an involution $*$, then K is a Lie algebra over $H(C(R),*)$.

2.4  If R is a centrally closed $*$-prime ring without 2-torsion and ${{\,\mathrm{Skew}\,}}(C(R),*)\ne 0$, then for any $0\ne \lambda \in {{\,\mathrm{Skew}\,}}(C(R),*)$ we have $R=H+K=\lambda ^2 H +K\subseteq \lambda K+K\subseteq R$ because $0\ne \lambda ^2$ is invertible, so $R=\lambda K+ K$ for every $0\ne \lambda \in {{\,\mathrm{Skew}\,}}(C(R),*)$. This occurs in particular when R is $*$-prime but not prime, because in this situation there exists a nonzero ideal I of R such that $I\cap I^*= 0$, and so we can define a nonzero skew element $\lambda :I\oplus I^*\rightarrow R$ in C(R) given by $\lambda (x+y):=x-y$.

2.5  ([9, 2.10]) Since the extended centroid C(R) of a semiprime ring R is von Neumann regular, given an element $\lambda \in C(R)$ there exists $\lambda '\in C(R)$ such $\lambda \lambda '\lambda =\lambda$ and $\lambda '=\lambda '\lambda \lambda '$. Let us define $\epsilon _\lambda :=\lambda \lambda '$. Then $\epsilon _\lambda$ is an idempotent of C(R) satisfying $\epsilon _\lambda \lambda =\lambda$. If R has no k-torsion for some $k\in \mathbb {N}$, then for $k=k\cdot 1\in C(R)$ there exists a unique $k'\in C(R)$ such that $k k' k=k$, so $k(k'k-1)=0$ and $k'k=1$, i.e., $k'=\frac{1}{k}\in C(R)$. In particular, throughout this paper $\frac{1}{2}\in C(R)$ because R will always be a semiprime ring without 2-torsion.

Moreover, if R is a semiprime ring without 2-torsion with involution $*$ and $\lambda \in {{\,\mathrm{Skew}\,}}(C(R),*)$, then $-\lambda =\lambda ^*=(\lambda \lambda '\lambda )^*=\lambda \lambda '^*\lambda$, which implies that $\lambda '$ can be taken in ${{\,\mathrm{Skew}\,}}(C(R),*)$ (indeed, replace $\lambda '$ by $\frac{1}{2} (\lambda '-\lambda '^*)$). In this case, $\epsilon _\lambda =\lambda \lambda '\in H(C(R),*)$ is a symmetric idempotent of C(R).

Lemma 2.6

([9, Lemma 2.11]) Let $(R,*)$ be a semiprime ring with involution free of 2-torsion and let $a\in R$. If there exist $\lambda$ and $\mu \in C(R)$ such that $a-\lambda$ and $a-\mu$ are nilpotent then $\lambda =\mu$. Moreover, if $a\in K$ and $\lambda \in C(R)$ is such that $a-\lambda$ is nilpotent, then $\lambda \in {{\,\mathrm{Skew}\,}}(C(R),*)$.

Proof

If $a-\lambda$ and $a-\mu$ are nilpotent elements of the central closure ${\hat{R}}$ of R, $a-\lambda -(a-\mu )=\mu -\lambda$ is a nilpotent element in the semiprime commutative ring C(R). Therefore $\lambda =\mu$. Now, if $a\in K$ and $a-\lambda$ is nilpotent then $(a-\lambda )^*=-(a+\lambda ^*)$ is nilpotent and therefore $a+\lambda ^*$ is nilpotent, which implies that $\lambda =-\lambda ^*\in {{\,\mathrm{Skew}\,}}(C(R),*)$. $\square$

We will use the following two results due to Beidar, Martindale and Mikhalev.

Theorem 2.7

([30, Theorem 2(a)]) Let R be a prime ring. Let $a_i,b_i\in R$ for $i=1,2,\dots , n$ with $b_1\ne 0$ be such that $\sum _{i=1}^n a_ixb_i=0$ for every $x\in R$. Then there exist $\lambda _i\in C(R)$ for $i=2,\dots , n$ such that $a_1=\sum _{i=2}^n \lambda _i a_i$ in ${\hat{R}}$.

Theorem 2.8

([5, Theorem 2.3.3]) Let R be a semiprime ring and let $a_1,a_2,\dots ,a_n\in R$. If $a_1\not \in \sum _{i=2}^n C(R)a_i$ in ${\hat{R}}$ then there exist $r_j,s_j\in R$ for $j=1,2,\dots , m$ such that $\sum _{j=1}^m r_ja_1s_j\ne 0$ and $\sum _{j=1}^m r_ja_ks_j=0$ for $k=2,\dots , n$.

The next corollary can be found in [9]. For the sake of completeness, we include its proof here.

Corollary 2.9

Let R be a semiprime ring. Let $a_i,b_i\in R$ for $i=1,2,\dots , n$ be such that ${{\,\mathrm{Id}\,}}_R(a_1)\subset {{\,\mathrm{Id}\,}}_R(b_1)$ and $\sum _{i=1}^n a_ixb_i=0$ for every $x\in R$. Then there exist $\lambda _i\in C(R)$ for $i=2,\dots , n$ such that $a_1=\sum _{i=2}^n \lambda _i a_i$ in ${\hat{R}}$.

Proof

By Theorem 2.8, if $a_1\not \in \sum _{i=2}^n C(R)a_i$ there exist $r_j,s_j\in R$, $j=1,\dots ,m$, such that $\sum _{j=1}^m r_ja_1s_j\ne 0$ and $\sum _{j=1}^m r_ja_ks_j=0$ for $k=2,3,\dots , n$. Replace x by $s_jx$ and multiply $\sum _{i=1}^n a_ixb_i=0$ on the left by $r_j$. We have

$$\begin{aligned} 0=\sum _{i=1}^n \sum _{j=1}^m r_ja_is_jxb_i=\sum _{j=1}^m r_ja_1s_jxb_1, \end{aligned}$$

which implies that the ideal generated by $\sum _{j=1}^m r_ja_1s_j$ is orthogonal to the ideal generated by $b_1$, and therefore, since ${{\,\mathrm{Id}\,}}_R(a_1)\subset {{\,\mathrm{Id}\,}}_R(b_1)$, the ideal generated by $\sum _{j=1}^m r_ja_1s_j$ has zero square, a contradiction because R is semiprime. $\square$

The following proposition is an easy generalization of [5, Theorem 2.3.9(i)].

Proposition 2.10

Let R be a centrally closed semiprime ring free of 2-torsion. For any subset $V\subset R$, there exists a unique idempotent $\epsilon \in C(R)$ such that $\epsilon v = v$ for all $v\in V$, the annihilator in C(R) of V is ${{\,\mathrm{Ann}\,}}_{C(R)}(V) = (1 -\epsilon ) C(R)$, the annihilator in R of the ideal generated by V is ${{\,\mathrm{Ann}\,}}_R({{\,\mathrm{Id}\,}}_R(V)) =(1 - \epsilon )R$, and the ideal generated by V is essential in $\epsilon R$. Moreover, when R has an involution $*$ and $V\subset H$ or $V\subset K$, then $\epsilon \in H(C(R),*)$.

Proof

The first part of the proof follows as in [5, Theorem 2.3.9(i)] with the obvious changes. Let $V\subset H$ or $V\subset K$, and consider the unique idempotent $\epsilon \in C(R)$ such that $\epsilon v = v$ for all $v\in V$, the annihilator in C(R) of V is ${{\,\mathrm{Ann}\,}}_{C(R)}(V) = (1 -\epsilon ) C(R)$ and the annihilator in R of the ideal generated by V is ${{\,\mathrm{Ann}\,}}_R({{\,\mathrm{Id}\,}}_R(V)) =(1 - \epsilon )R$. When R has an involution, we can decompose $\epsilon =\epsilon _k+\epsilon _h$ with $\epsilon _k\in {{\,\mathrm{Skew}\,}}(C(R),*)$ and $\epsilon _h\in H(C(R),*)$. We have that $\epsilon v=v$ implies $\epsilon _k v=0$. Therefore, $\epsilon _k\in {{\,\mathrm{Ann}\,}}_{C(R)}(V)=(1-\epsilon )C(R)$, i.e., $\epsilon _k \epsilon =0$ and $\epsilon _k^2=\epsilon _k\epsilon _h=0$ and therefore $\epsilon =\epsilon ^2=(\epsilon _k+\epsilon _h)^2=\epsilon _h^2\in H(C(R),*)$. $\square$

Lemma 2.11

Let R be a centrally closed semiprime algebra and let $\{\nu _i\}_{i\in I}$ be a family of idempotent elements in C(R). Suppose there exists a family $\{\lambda _{i}\}_{i\in I}$ of elements in C(R) such that for every $i,j\in I$, $\lambda _{i} \nu _i\nu _j=\lambda _{j} \nu _i\nu _j$. Then there exists $\lambda \in C(R)$ such that $\lambda \nu _i=\lambda _{i} \nu _i$ for every $i\in I$. Moreover, if the ideal generated by the family $\{\nu _i\}_{i\in I}$ is essential in R, such $\lambda$ is unique.

Proof

Let us consider the ideal $S =\sum R\nu _i$ generated by the family of idempotents $\{\nu _i\}_{i\in I}$ and the essential ideal $T =S\oplus {{\,\mathrm{Ann}\,}}_R(S)$. Define $\lambda :T\rightarrow R$ by

$$\begin{aligned} \lambda \left( \sum x_i\nu _i+z\right) :=\sum \lambda _ix_i\nu _i. \end{aligned}$$

Let us prove that $\lambda$ is well defined and an element in C(R). If $\sum x_i\nu _i+z=0$ then $\sum x_i\nu _i=0=z$ and for every $\nu _k$, we have

$$\begin{aligned} \left( \sum \lambda _i x_i\nu _i\right) \nu _k=\sum \lambda _k x_i\nu _i \nu _k=\lambda _k\left( \sum x_i\nu _i\right) \nu _k=0. \end{aligned}$$

Therefore $\sum \lambda _i x_i\nu _i\in S\cap {{\,\mathrm{Ann}\,}}_R(S)=0$ which proves that $\lambda$ is well defined. By construction $[T, \lambda ] \in C(R)$. Moreover, if the ideal S generated by the family $\{\nu _i\}_{i\in I}$ is essential, ${{\,\mathrm{Ann}\,}}_R(S)=0$ and $[S, \lambda ]\in C(R)$ is uniquely defined. $\square$

3 Pure Ad-nilpotent Elements

Recall that an element a in a Lie algebra L is ad-nilpotent of index n if ${{\,\mathrm{ad}\,}}_a^n(L)=0$ and ${{\,\mathrm{ad}\,}}_a^{n-1}(L)\ne 0$.

3.1.

• (i) Let us consider $R^-$: we say that an element a is a pure ad-nilpotent element of $R^-$ of index n if for every $\lambda \in C(R)$ with $\lambda a\ne 0$, $\lambda a$ is ad-nilpotent in ${\hat{R}}^-$ of index n, where ${\hat{R}}$ is the central closure of R.

• (ii) Let us consider K: we say that an element a is a pure ad-nilpotent element of K of index n if for every $\lambda \in H(C(R)),*)$ with $\lambda a\ne 0$, $\lambda a$ is ad-nilpotent in ${{\,\mathrm{Skew}\,}}({\hat{R}},*)$ of index n, where ${\hat{R}}$ is the central closure of R.

Lemma 3.2

If R is a semiprime ring and a is an ad-nilpotent element of R of index n, the following conditions are equivalent:

• (i) a is a pure ad-nilpotent element of $R^-$.

• (ii) ${{\,\mathrm{Id}\,}}_R({{\,\mathrm{ad}\,}}_a^{n-1}(R))$ is an essential ideal of ${{\,\mathrm{Id}\,}}_R(a)$.

• (iii) ${{\,\mathrm{Ann}\,}}_R({{\,\mathrm{Id}\,}}_R({{\,\mathrm{ad}\,}}_a^{n-1}(R)))={{\,\mathrm{Ann}\,}}_R({{\,\mathrm{Id}\,}}_R(a))$.

Proof

Suppose that R is semiprime and centrally closed (otherwise, substitute R by its central closure ${\hat{R}}$).

(i) $\Rightarrow$ (ii). Let us consider $V=\{{{\,\mathrm{ad}\,}}_a^{n-1}x \ |\ x\in R\}$. By Proposition 2.10 there exists $e\in C(R)$ such that $ev=v$ for every $v\in V$ and ${{\,\mathrm{Ann}\,}}_R({{\,\mathrm{Id}\,}}_R(V))=(1-e)R$. Suppose that $(1-e)a\ne 0$. By hypothesis $(1-e)a$ is ad-nilpotent of index n, hence $0\ne {{\,\mathrm{ad}\,}}_{(1-e)a}^{n-1}(R)=(1-e){{\,\mathrm{ad}\,}}_a^{n-1}(R)=0$, a contradiction. So $ea=a$ and ${{\,\mathrm{Ann}\,}}_{{{\,\mathrm{Id}\,}}_R(ea)}({{\,\mathrm{Id}\,}}_R({{\,\mathrm{ad}\,}}_a^{n-1}(R)))\subset {{\,\mathrm{Ann}\,}}_R({{\,\mathrm{Id}\,}}_R({{\,\mathrm{ad}\,}}_a^{n-1}(R)))=(1-e)R$ must be zero, i.e., ${{\,\mathrm{Id}\,}}_R({{\,\mathrm{ad}\,}}_a^{n-1}(R))$ is essential in ${{\,\mathrm{Id}\,}}_R(ea)$.

(ii)$\Rightarrow$ (iii). This holds in general if I and J are ideals of R with I essential in J: $0={{\,\mathrm{Ann}\,}}_J(I)={{\,\mathrm{Ann}\,}}_R(I)\cap J$ implies ${{\,\mathrm{Ann}\,}}_R(I) J=0$, so ${{\,\mathrm{Ann}\,}}_R(I)\subset {{\,\mathrm{Ann}\,}}_R(J)$.

(iii) $\Rightarrow$ (i). Let $\lambda \in C(R)$ be such that $\lambda a \ne 0$. Clearly ${{\,\mathrm{ad}\,}}_{\lambda a}^n(R)=0$. Suppose that ${{\,\mathrm{ad}\,}}_{\lambda a}^{n-1}(R)=0$: then $\lambda ^{n-1}{{\,\mathrm{ad}\,}}_a^{n-1}(R)=0$, so $\lambda ^{n-1}\in {{\,\mathrm{Ann}\,}}_R({{\,\mathrm{Id}\,}}_R({{\,\mathrm{ad}\,}}_a^{n-1}(R)))={{\,\mathrm{Ann}\,}}_R({{\,\mathrm{Id}\,}}_R(a))$, which is not possible because R is semiprime and $\lambda a\ne 0$. $\square$

Lemma 3.3

Let R be a centrally closed semiprime ring with involution $*$ and no 2-torsion, and let $a\in K$ be a pure ad-nilpotent element of K of index n. If there exists $\lambda \in H(C(R),*)$ such that $\lambda a$ is ad-nilpotent of R of index n, then $\lambda a$ is a pure ad-nilpotent element of R of index n.

Proof

Let us see that for every $\mu \in C(R)$ with $\mu \lambda a\ne 0$, the element $\mu \lambda a$ has index of ad-nilpotency in R equal to n. Suppose that there exists $\mu \in C(R)$ with ${{\,\mathrm{ad}\,}}_{\mu \lambda a}^{n-1}R=0$, and let us prove that $\mu \lambda a=0$:

We have that $\mu ^{n-1}{{\,\mathrm{ad}\,}}_{\lambda a}^{n-1}R={{\,\mathrm{ad}\,}}_{\mu \lambda a}^{n-1}R=0$, so $\mu {{\,\mathrm{ad}\,}}_{\lambda a}^{n-1}R=0$ because C(R) is regular von Neumann. In particular, $\mu {{\,\mathrm{ad}\,}}_{\lambda a}^{n-1}H=\mu {{\,\mathrm{ad}\,}}_{\lambda a}^{n-1}K=0$. Since $\mu =\mu _h+\mu _k$, we have that $\mu _h{{\,\mathrm{ad}\,}}_{\lambda a}^{n-1}R=\mu _k{{\,\mathrm{ad}\,}}_{\lambda a}^{n-1}R=0$.

From $0=\mu _h^{n-1}{{\,\mathrm{ad}\,}}_{\lambda a}^{n-1}R={{\,\mathrm{ad}\,}}_{\mu _h \lambda a}^{n-1}R$, we get that $\mu _h \lambda a$ index of ad-nilpotency in K lower than n, implying $\mu _h \lambda a=0$ because a is a pure ad-nilpotent element of K.

From $0=(\mu _k^2)^{n-1}{{\,\mathrm{ad}\,}}_{\lambda a}^{n-1}R={{\,\mathrm{ad}\,}}_{\mu _k^2 \lambda a}^{n-1}R$ we get that $\mu _k^2 \lambda a$ has index of ad-nilpotency in K lower than n, so again $\mu _k^2 \lambda a=0$ (because a is a pure ad-nilpotent element of K), and by regularity of C(R), $\mu _k \lambda a=0$.

This implies $\mu \lambda a=0$. $\square$

The next proposition shows that every ad-nilpotent of $R^-$ and of K can be expressed as an orthogonal sum of pure ad-nilpotent elements of decreasing indices.

Proposition 3.4

Let R be a centrally closed semiprime ring and let $a\in R$ be an ad-nilpotent element of $R^-$ of index n. There exists a family of orthogonal idempotents $\{\epsilon _i\}_{i=1}^k\subset C(R)$ such that $a=\sum _{i=1}^k \epsilon _ia$ with $\epsilon _ia$ a pure ad-nilpotent element of index $n_i$ in $\epsilon _iR$ for $n=n_1>n_2>\cdots > n_k$.

Similarly, if R has an involution $*$ and a is an ad-nilpotent element of K of index n, then there exists a family of orthogonal idempotents $\{\epsilon _i\}_{i=1}^k\subset H(C(R),*)$ such that $a=\sum _{i=1}^k \epsilon _ia_i$ with $\epsilon _ia$ a pure ad-nilpotent element of index $n_i$ in ${{\,\mathrm{Skew}\,}}(\epsilon _iR,*)$ for $n=n_1>n_2>\cdots > n_k$.

Proof

Let us prove the result for Lie algebras of skew-symmetric elements. We will proceed by induction on n. If $n=1$ there is nothing to prove. Let us suppose that the result is true for every ad-nilpotent element of index less than n and let $a\in K$ be an ad-nilpotent element of index $n\ge 3$. Let us consider $V=\{{{\,\mathrm{ad}\,}}_a^{n-1}x \ |\ x\in K\}$. By Proposition 2.10 there exists $\epsilon \in H(C(R),*)$ such that $\epsilon v=v$ for every $v\in V$ and ${{\,\mathrm{Ann}\,}}_R({{\,\mathrm{Id}\,}}_R(V))=(1-\epsilon )R$. Then $a=\epsilon a+(1-\epsilon )a$.

Clearly, by construction $(1-\epsilon )a$ is ad-nilpotent of index less than n in K: for every $x\in K$, ${{\,\mathrm{ad}\,}}_{(1-\epsilon )a}^{n-1}x=(1-\epsilon ){{\,\mathrm{ad}\,}}_{a}^{n-1}x={{\,\mathrm{ad}\,}}_{a}^{n-1}x-\epsilon {{\,\mathrm{ad}\,}}_{a}^{n-1}x=0$.

Let us prove that $\epsilon a$ is pure ad-nilpotent of index n in ${{\,\mathrm{Skew}\,}}(\epsilon R,*)$. For any $\lambda \in H(C(R),*)$ such that $\lambda \epsilon a\ne 0$, $\lambda \epsilon a$ is ad-nilpotent of index n: clearly ${{\,\mathrm{ad}\,}}_{\lambda \epsilon a}^{n} ({{\,\mathrm{Skew}\,}}(\epsilon R,*))=0$ and if ${{\,\mathrm{ad}\,}}_{\lambda \epsilon a}^{n-1} ({{\,\mathrm{Skew}\,}}(\epsilon R,*))= 0$ then $\lambda ^{n-1}\epsilon \in {{\,\mathrm{Ann}\,}}_R({{\,\mathrm{Id}\,}}_R(V))=(1-\epsilon )R$, which leads to a nilpotent ideal generated by the nonzero element $\lambda \epsilon a$, a contradiction with the semiprimeness of R.

Apply now the induction hypothesis to $(1-\epsilon )a$ and the Lie algebra of skew-symmetric elements ${{\,\mathrm{Skew}\,}}((1-\epsilon )R,*)$. $\square$

4 Ad-nilpotent Elements of R

In this section, we are going to prove that every nilpotent inner derivation is induced by a nilpotent element, generalizing to semiprime rings Herstein’s result [21, Theorem in p. 84] for simple rings. This result was already proved by Grzeszczuk ([18, Corollary 8]). Our techniques are rather elementary and, by adding the hypothesis of pure ad-nilpotence, we can describe such elements with less restrictions on the torsion of the ring.

Lemma 4.1

Let R be a semiprime ring and let $a\in R$ be a nilpotent element. Suppose that there exist some $\lambda _i\in \mathbb {Z}$, $i=0,\dots , n$, such that

$$\begin{aligned} \sum _{i=0}^{n}\lambda _i a^i [x,y] a^{n-i}=0 \end{aligned}$$

for all $x,y\in R$. Then for every $i=0,\dots , n$ we have $\lambda _i a^{\max (i, n-i)}=0$. In particular, each term in the identity above is zero.

Proof

First, let us suppose that R is prime and suppose that $a\ne 0$ has index of nilpotence s. If the lemma is not satisfied, there exists some k with $\lambda _k a^{\max (k, n-k)}\ne 0$. In particular, $\max (k, n-k)< s$. Let us multiply the expression $\sum _{i=0}^{n}\lambda _i a^i [x,y] a^{n-i}$ by $a^{s-1-k}$ on the left and by $a^{s-1-(n-k)}$ on the right, so that

$$\begin{aligned} 0=a^{s-1-k}\left( \sum _{i=0}^{n}\lambda _i a^i [x,y] a^{n-i} \right) a^{s-1-(n-k)}=\lambda _k a^{s-1}[x,y]a^{s-1} \end{aligned}$$

for every $x,y\in R$. Hence $\lambda _k a^{s-1}xy a^{s-1}= \lambda _k a^{s-1}yx a^{s-1}$ for every $x,y\in R$. Since $a^{s-1}\ne 0$ for every $x\in R$, we have by Theorem 2.7 that there exists $\alpha _x\in C(R)$ such that $\lambda _k a^{s-1}x=\alpha _x\lambda _k a^{s-1}$. Multiplying this last expression by a on the right, we get $\lambda _k a^{s-1}xa=0$ for every $x\in R$. By primeness of R we get that either $a^{s-1}=0$ or $\lambda _ka=0$, leading to a contradiction.

If R is semiprime then R is a subdirect product of prime quotients $R/I_\alpha$ with $\bigcap _\alpha I_\alpha =0$. For any $\alpha$ and any i, by the prime case $\lambda _i a^{\max (i, n-i)}\in I_\alpha$, so $\lambda _i a^{\max (i, n-i)}=0$. $\square$

Lemma 4.2

Every nilpotent element of a ring R is ad-nilpotent. If a has index of nilpotence s and index of ad-nilpotence n, then $n\le 2s-1$. If R is semiprime then $n\ge s$, and if in addition R is free of $\left( {\begin{array}{c}n\\ t\end{array}}\right)$-torsion for $t:=[\frac{n+1}{2}]$, then $s=t$ and $n=2s-1$.

Proof

Since $a^s=0$, for every $x\in R$ we have

$$\begin{aligned} {{\,\mathrm{ad}\,}}_a^{2s-1}x=\sum _{i=0}^{2s-1} \left( {\begin{array}{c}2s-1\\ i\end{array}}\right) (-1)^{2s-1-i} a^ixa^{2s-1-i}=0 \end{aligned}$$

because if $i<s$ then $2s-1-i\ge s$. Therefore $n\le 2s-1$.

Suppose now that R is semiprime and let us see that $n\ge s$: if on the contrary

$$\begin{aligned} {{\,\mathrm{ad}\,}}_a^{s-1}x=\sum _{i=0}^{s-1} \left( {\begin{array}{c}s-1\\ i\end{array}}\right) (-1)^{s-1-i} a^ixa^{s-1-i}=0 \end{aligned}$$

for every $x\in R$, focusing on the first summand of this expression ($(-1)^{s-1}xa^{s-1}$) we get that $a^{s-1}=0$ by Lemma 4.1, a contradiction.

Moreover, since for every $x\in R$ we have $0={{\,\mathrm{ad}\,}}_a^n(x)=\sum _{i=0}^{n} \left( {\begin{array}{c}n\\ i\end{array}}\right) (-1)^{n-i} a^ixa^{n-i}$, again by Lemma 4.1$\left( {\begin{array}{c}n\\ t\end{array}}\right) a^t=0$ for $t:=[\frac{n+1}{2}]$. If R is free of $\left( {\begin{array}{c}n\\ t\end{array}}\right)$-torsion, then $a^t=0$ so $t\ge s$, i.e., $n\ge 2s-1$, and therefore, $n=2s-1$ (equivalently, $s=t$). $\square$

The next example shows that all possible cases in the lemma above can be realized: Let p be an odd prime number and R a prime ring with characteristic p. If $a\in R$ is a nilpotent element of index $s\in \{\frac{p+1}{2},\dots , p$}, then a is ad-nilpotent of index p. In particular, there are no ad-nilpotent elements of index between $p+1$ and $2p-1$, and a nilpotent element of index p is ad-nilpotent of the same index p.

Proposition 4.3

Let R be a prime ring and let $a\in R$ be an ad-nilpotent element of $R^-$ of index n. Let $\overline{\mathbb {F}}$ denote the algebraic closure of the field $\mathbb {F}:=C(R)$ and $\overline{R}:={\hat{R}}\otimes \overline{\mathbb {F}}$. Then:

• (1) There exists $\mu \in \overline{\mathbb {F}}$ such that $a-\mu$ is a nilpotent element of ${\overline{R}}$.

• (2) If R is free of $n\atopwithdelims ()t$-torsion for $t:=[\frac{n+1}{2}]$ then n is odd and the index of nilpotence of $a-\mu$ is ${n+1\over 2}$. If in addition R is free of t-torsion then $\mu \in C(R)$.

Proof

• (1) Since R is prime, $\mathbb {F}=C(R)$ is a field and $\overline{R}$ is a centrally closed prime ring (see [5, pp. 445–446]). From

  $$\begin{aligned} 0={{\,\mathrm{ad}\,}}_a^n x=\sum _{i=0}^n {n\atopwithdelims ()i} (-1)^{n-i} a^ixa^{n-i} \end{aligned}$$

  for every $x\in R$ we have, by Theorem 2.7, that a seen as an element of ${\hat{R}}$ is an algebraic element over $\mathbb {F}$ of degree not greater than n. Let us consider the minimal polynomial $p(X)\in \mathbb {F}[X]$ of a. Let $\overline{\mathbb {F}}$ be the algebraic closure of $\mathbb {F}$ and let $\mu _1,\dots ,\mu _t\in \overline{\mathbb {F}}$ be the roots of p(X) in $\overline{\mathbb {F}}$, i.e., $p(X)=(X-\mu _1)^{k_1}\cdots (X-\mu _t)^{k_t}\in \overline{\mathbb {F}}[X]$.

  Let us prove that p(X) has only one root in $\overline{\mathbb {F}}$ and therefore $p(X)=(X-\mu )^k\in {\mathbb {F}}[X]$, whence $a-\mu$ is nilpotent in ${\overline{R}}$: Suppose on the contrary that p(X) has different roots $\mu _1,\dots , \mu _t$, $t>1$, and define $q_i(X):=p(X)/(X-\mu _i)$ for every i. Since p(X) is the minimal polynomial of a, $q_i(a)\ne 0$ in ${\overline{R}}$. Note that $(a-\mu _i)q_i(a)=p(a)=0$ and therefore $aq_i(a)=\mu _iq_i(a)$. Now, since we are in the prime case, there exists $y\in R$ such that $q_1(a)yq_2(a)\ne 0$ and therefore ${{\,\mathrm{ad}\,}}_a(q_1(a)yq_2(a))=aq_1(a)yq_2(a)-q_1(a)yq_2(a)a=(\mu _1-\mu _2)q_1(a)yq_2(a)\ne 0$. This means that $q_1(a)yq_2(a)$ is an eigenvector of the linear map ${{\,\mathrm{ad}\,}}_a$ associated to the eigenvalue $\mu _1-\mu _2$; hence, it is an eigenvector of ${{\,\mathrm{ad}\,}}_a^2$ associated to $(\mu _1-\mu _2)^2$, etc. This is a contradiction because both $q_1(a)yq_2(a)$ and each power of $(\mu _1-\mu _2)$ are nonzero, while ${{\,\mathrm{ad}\,}}_a$ is nilpotent. Therefore $t=1$, $p(X)=(X-\mu )^{k}\in \mathbb {F}[X]$ and $(a-\mu )^k=0$.

• (2) Let us consider $b:=a-\mu \in {\overline{R}}$, which is ad-nilpotent of index n. Let us see that n is odd: Suppose on the contrary that $n=2m$. Then

  $$\begin{aligned} 0={{\,\mathrm{ad}\,}}_a^n x={{\,\mathrm{ad}\,}}_b^n x=\sum _{i=0}^n \left( {\begin{array}{c}n\\ i\end{array}}\right) (-1)^{n-i} b^ixb^{n-i} \end{aligned}$$

  implies by Lemma 4.1 that $\left( {\begin{array}{c}n\\ m\end{array}}\right) b^m=0$ and, since ${\overline{R}}$ is free of $\left( {\begin{array}{c}n\\ m\end{array}}\right)$-torsion, that $b^m=0$. Substituting in ${{\,\mathrm{ad}\,}}_b^{n-1} x=\sum _{i=0}^{n-1} \left( {\begin{array}{c}n-1\\ i\end{array}}\right) (-1)^{n-1-i} b^ixb^{n-1-i}$ we get that ${{\,\mathrm{ad}\,}}_b^{n-1}x=0$ for every $x\in R$, a contradiction.

  Therefore n is odd and $a-\mu$ is nilpotent of ${\overline{R}}$ of index $t:=\frac{n+1}{2}$ by Lemma 4.2. Moreover, since the coefficient of degree $t-1$ of $p(X)=(X-\mu )^t\in \mathbb {F}[X]$ is $-t\mu \in \mathbb {F}$, if R is free of t-torsion then $\mu \in \mathbb {F}$, i.e., there exists $\mu \in C(R)$ such that $a-\mu$ is nilpotent of index $t=\frac{n+1}{2}$.

$\square$

In the following theorem, we get the description of the pure ad-nilpotent elements of $R^-$. In its proof, Proposition 4.3 is primarily used to find that any ad-nilpotent element $a\in R$ of index n forces $[a,[{{\,\mathrm{ad}\,}}_a^{n-1}x,[{{\,\mathrm{ad}\,}}_a^{n-1}x,y]]]=0$ for every $x,y\in R$. If $2, 3,\dots , r$ were invertible in R for $r\ge n+[\frac{n}{2}]+1$, this identity would directly follow from the proof of [17, Theorem 2.3].

Theorem 4.4

Let R be a semiprime ring with no 2-torsion, let ${\hat{R}}$ be its central closure, and let $a\in R$ be a pure ad-nilpotent element of $R^-$ of index n. Put $t:=[\frac{n+1}{2}]$, and suppose that R is free of $n\atopwithdelims ()t$-torsion and t-torsion. Then n is odd and there exists $\lambda \in C(R)$ such that $a-\lambda \in {\hat{R}}$ is nilpotent of index $\frac{n+1}{2}$.

Proof

Let us suppose that R is a prime ring and, without loss of generality, that it is centrally closed. Consider $\mu \in C(R)$ as given by Proposition 4.3. Putting $b:=a-\mu$, we know that $b^t=0$ for $t:={n+1\over 2}$, hence for every $x,y\in R$ we have

$$\begin{aligned} ({{\,\mathrm{ad}\,}}_a^{n-1}x) ({{\,\mathrm{ad}\,}}_a^{n-1}x)&=({{\,\mathrm{ad}\,}}_b^{n-1}x)({{\,\mathrm{ad}\,}}_b^{n-1}x)=0,\hbox { and}\\ [a,[{{\,\mathrm{ad}\,}}_a^{n-1}x,[{{\,\mathrm{ad}\,}}_a^{n-1}x,y]]]&= [b,[{{\,\mathrm{ad}\,}}_b^{n-1}x,[{{\,\mathrm{ad}\,}}_b^{n-1}x,y]]]\\&=-2{{n-1} \atopwithdelims (){t-1}}{{n-1}\atopwithdelims (){t-1}}\\ {}&[b,b^{t-1}xb^{t-1}yb^{t-1}xb^{t-1}]=0. \end{aligned}$$

If R is semiprime, R is a subdirect product of prime rings (without $n\atopwithdelims ()t$ and t-torsion) and in any of these prime quotients

$$\begin{aligned} \overline{({{\,\mathrm{ad}\,}}_a^{n-1}x)({{\,\mathrm{ad}\,}}_a^{n-1}x)}=\overline{0}\hbox { and } \overline{[a,[{{\,\mathrm{ad}\,}}_a^{n-1}x,[{{\,\mathrm{ad}\,}}_a^{n-1}x,y]]]}={\overline{0}}, \end{aligned}$$

which imply that

$$\begin{aligned} ({{\,\mathrm{ad}\,}}_a^{n-1}x)({{\,\mathrm{ad}\,}}_a^{n-1}x)=0, \hbox { and } [a,[{{\,\mathrm{ad}\,}}_a^{n-1}x,[{{\,\mathrm{ad}\,}}_a^{n-1}x,y]]]=0 \end{aligned}$$

for every $x,y\in R$. For every $x\in R$, let $z_x:={{\,\mathrm{ad}\,}}_a^{n-1}x$. By the identity above,

$$\begin{aligned} 0=\frac{1}{2}[a,[z_x,[z_x,y]]]=-az_xyz_x+z_xyz_xa. \end{aligned}$$

Therefore, since ${{\,\mathrm{Id}\,}}_R(z_xa)\subset {{\,\mathrm{Id}\,}}_R(z_x)$, by Corollary 2.9 there exists $\lambda _x\in C(R)$ such that $z_xa=\lambda _x z_x$ and by Proposition 2.10 there exists $\epsilon _x\in C(R)$ such that $\epsilon _xz_x=z_x$ and ${{\,\mathrm{Ann}\,}}_R({{\,\mathrm{Id}\,}}_R(z_x))=(1-\epsilon _x)R$. Therefore

$$\begin{aligned} 0&=z_x{{\,\mathrm{ad}\,}}_a^n y=z_x\left( \sum _{i=0}^n \left( {\begin{array}{c}n\\ i\end{array}}\right) (-1)^{n-i} a^iya^{n-i}\right) =\sum _{i=0}^n \left( {\begin{array}{c}n\\ i\end{array}}\right) (-1)^{n-i} z_x a^iya^{n-i}\\&=\sum _{i=0}^n \left( {\begin{array}{c}n\\ i\end{array}}\right) (-1)^{n-i} z_x \lambda _x^iya^{n-i}= z_x y\left( \sum _{i=0}^n \left( {\begin{array}{c}n\\ i\end{array}}\right) (-1)^{n-i}\lambda _x^ia^{n-i}\right) =z_xy(a-\lambda _x)^n \end{aligned}$$

for every $y\in R$, whence $(a-\lambda _x)^n\in {{\,\mathrm{Ann}\,}}_R({{\,\mathrm{Id}\,}}_R(z_x))$. So $\epsilon _x(a-\lambda _x)^n=0$. Now, for every $x,x'\in R$ there exist $\lambda _x,\lambda _{x'}\in C(R)$ and idempotents $\epsilon _x,\epsilon _{x'}\in C(R)$ such that $0=(\epsilon _x\epsilon _{x'}a-\epsilon _x\epsilon _{x'}\lambda _x)^n=(\epsilon _x\epsilon _{x'}a-\epsilon _x\epsilon _{x'}\lambda _{x'})^n$, so $\epsilon _x\epsilon _{x'}\lambda _x=\epsilon _x\epsilon _{x'}\lambda _{x'}$ by Lemma 2.6. By Lemma 2.11 there exists $\lambda \in C(R)$ such that $\epsilon _x\lambda =\epsilon _x\lambda _x$ for every $x\in R$. Then for every $x\in R$, we have $z_x(a-\lambda )^n=\epsilon _xz_x(a-\lambda _x)^n=0$, so $0=\epsilon _x z_x {{\,\mathrm{ad}\,}}_a^n y=z_x y (a-\lambda )^n$ for every $y\in R$ thus $(a-\lambda )^n\in {{\,\mathrm{Ann}\,}}_R({{\,\mathrm{Id}\,}}_R(z_x))$ (see 2.2). Moreover $\bigcap _{x\in R}{{\,\mathrm{Ann}\,}}_R({{\,\mathrm{Id}\,}}_R(z_x))={{\,\mathrm{Ann}\,}}_R({{\,\mathrm{Id}\,}}_R({{\,\mathrm{ad}\,}}_a^{n-1}(R)))$ by definition of $z_x$, and ${{\,\mathrm{Ann}\,}}_R({{\,\mathrm{Id}\,}}_R({{\,\mathrm{ad}\,}}_a^{n-1}(R)))={{\,\mathrm{Ann}\,}}_R({{\,\mathrm{Id}\,}}_R(a))$ because a is pure (Lemma 3.2(iii)). Finally, let $\epsilon \in C(R)$ be such that $\epsilon a=a$ and ${{\,\mathrm{Ann}\,}}_R({{\,\mathrm{Id}\,}}_R(a))=(1-\epsilon )R$. Then $\epsilon (a-\lambda )^n=(a-\epsilon \lambda )^n=0$ because it is contained in $(1-\epsilon )R$.

Hence $a-\epsilon \lambda$ is nilpotent in addition to being ad-nilpotent of index n. Put $t:=[\frac{n+1}{2}]$ and take any prime quotient without t and $n\atopwithdelims ()t$-torsion in which $\overline{a-\epsilon \lambda }$ is still ad-nilpotent of index n. By Proposition 4.3(2), we get that n must be odd and $\overline{a-\epsilon \lambda }$ is nilpotent of index t. Since in any prime quotient $(\overline{a-\epsilon \lambda })^{t}={\bar{0}}$ by Proposition 4.3(2), we have that t is the index of nilpotence of $a-\epsilon \lambda$. $\square$

Lee’s description of ad-nilpotent elements of $R^-$ is recovered when the hypothesis of being pure is removed.

Corollary 4.5

([26, Theorem 1.3]) Let R be a semiprime ring, let ${\hat{R}}$ be its central closure, let $a\in R$ be an ad-nilpotent element of $R^-$ of index n, and suppose that R is free of n!-torsion. Then n is odd and there exists $\lambda \in C(R)$ such that $a-\lambda \in {\hat{R}}$ is nilpotent of index ${\frac{n+1}{2}}$.

Proof

Suppose without loss of generality that R is centrally closed, i.e., $R={\hat{R}}$.

By Proposition 3.4, there exists a family of orthogonal idempotents $\{\epsilon _i\}_{i=1}^k\subset C(R)$ such that $a=\sum _{i=1}^k \epsilon _ia$ with $\epsilon _ia$ a pure ad-nilpotent element of index $n_i$ ($n=n_1>n_2>\cdots$) of $R\epsilon _i$. Then by Theorem 4.4 there exists a family of scalars $\{\lambda _i\}_{i=1}^k\subset C(R)$ such that $(\epsilon _ia-\lambda _i)^{t_i}=0$ for $t_i:=[\frac{n_i+1}{2}]$. Hence $\lambda =\sum _{i=1}^{n}\epsilon _i\lambda _i$ satisfies the claim. $\square$

Interesting Lie algebras associated to simple rings R are the quotient algebras $[R,R]/([R,R]\cap Z(R))$, which are simple unless R has 2-torsion and is 4-dimensional over its center ([22, Theorem 1.13]). Let us study ad-nilpotent elements in these algebras.

Lemma 4.6

([27, Lemma 4.6]) Let R be a semiprime ring and let $a\in R$ be such that ${{\,\mathrm{ad}\,}}_a^n(R)\subset Z(R)$. Then ${{\,\mathrm{ad}\,}}_a^n(R)=0$.

Proof

For every $x\in R$, we have

$$\begin{aligned} 0=[{{\,\mathrm{ad}\,}}_a^n(xa),x]=[({{\,\mathrm{ad}\,}}_a^nx)a,x]=({{\,\mathrm{ad}\,}}_a^nx)[a,x]. \end{aligned}$$

Therefore $0={{\,\mathrm{ad}\,}}_a^{n-1}(({{\,\mathrm{ad}\,}}_a^n x)[a,x])=({{\,\mathrm{ad}\,}}_a^n x)^2$ which implies, since R is semiprime and ${{\,\mathrm{ad}\,}}_a^nx\in Z(R)$, that ${{\,\mathrm{ad}\,}}_a^nx=0$. $\square$

Lemma 4.7

Let R be a semiprime ring, let $L:=[R,R]/([R,R]\cap Z(R))$ and let ${\overline{a}}:=a+([R,R]\cap Z(R))\in L$ be an ad-nilpotent element of L of index n. Then a is an ad-nilpotent element of index n in $R^-$.

Proof

For every $x\in R$, ${{\,\mathrm{ad}\,}}_a^{n+1}x={{\,\mathrm{ad}\,}}_a^{n}([a,x])\in {{\,\mathrm{ad}\,}}_a^n([R,R])\subset Z(R)$ so, by Lemma 4.6, ${{\,\mathrm{ad}\,}}_a^{n+1}x=0$ for every $x\in R$, i.e., a is ad-nilpotent in $R^-$ of index n or $n+1$.

Let us suppose that R is prime. Then, by Proposition 4.3, there exists $\mu \in \overline{\mathbb {F}}$, the algebraic closure of $\mathbb {F}:=C(R)$, such that $a-\mu$ is nilpotent in $R\otimes \overline{{\mathbb {F}}}$ of some index s. Moreover, by Lemma 4.2, $s\le n+1$. Put $b:=a-\mu$. Then

$$\begin{aligned} 0={{\,\mathrm{ad}\,}}_a^n([x,y])={{\,\mathrm{ad}\,}}_b^n([x,y])=\sum _{i=0}^{n} \left( {\begin{array}{c}n\\ i\end{array}}\right) (-1)^{n-i} b^i[x,y]b^{n-i} \end{aligned}$$

for every $x,y\in R$. By Lemma 4.1, for every $k\in \{0,1,\dots , [\frac{n+1}{2}]\}$ we have $\left( {\begin{array}{c}n\\ k\end{array}}\right) b^{\max (k,n-k)}=0$, so

$$\begin{aligned} {{\,\mathrm{ad}\,}}_a^n x={{\,\mathrm{ad}\,}}_b^n x=\sum _{i=0}^n \left( {\begin{array}{c}n\\ i\end{array}}\right) (-1)^{n-i} b^ixb^{n-i}=0, \end{aligned}$$

i.e., a is an ad-nilpotent element of $R^-$ of index n.

Finally, since ${\overline{a}}$ is ad-nilpotent of index not greater than n in any prime quotient, a is an ad-nilpotent element of $R^-$ of index n when R is semiprime. $\square$

In particular, from these last two lemmas we get that if R is semiprime then $[R,R]/([R,R]\cap Z(R))$ and R/Z(R) are nondegenerate Lie algebras (see [22, Sublemma in p. 5]).

Corollary 4.8

Let R be a semiprime ring, let ${\hat{R}}$ be its central closure, and let $L:=[R,R]/([R,R]\cap Z(R))$ or $L:=R/Z(R)$. If $\overline{a}\in L$ is an ad-nilpotent element of L of index n and R is free of n!-torsion, then n is odd and there exists $\lambda \in C(R)$ such that $a-\lambda \in {\hat{R}}$ is nilpotent of index $\frac{n+1}{2}$.

Proof

If $L= [R,R]/([R,R]\cap Z(R))$ the result follows by Lemma 4.7 and Corollary 4.5. If $L=R/Z(R)$ the result follows by Lemma 4.6 and Corollary 4.5. $\square$

5 Ad-nilpotent Elements of K

In this section, we focus on semiprime rings R with involution $*$ and their set of skew-symmetric elements K. As in the previous section, we will first describe the pure ad-nilpotent elements of K and then remove the hypothesis of being pure by decomposing each ad-nilpotent element into a sum of pure ad-nilpotent elements of decreasing indices.

The following lemma collects some results about $*$-identities. Item (1) is [22, Remark on p. 43] (with a different proof), item (2) is a generalization of [29, Lemma 5], and item (3) is a generalization of [9, Lemma 5.2].

Lemma 5.1

Let R be a semiprime ring with involution $*$ and free of 2-torsion. Let $k\in K$ and $h\in H$. Then:

• (1) $kKk=0$ implies $k=0$.

• (2) $hKh=0$ implies $hRh\subset H(C(R),*)h$. In particular, R satisfies

  $$\begin{aligned} hxhyh=hyhxh \quad \hbox { for every }x,y\in R, \end{aligned}$$

  and if ${{\,\mathrm{Id}\,}}_R(h)$ is essential then ${{\,\mathrm{Skew}\,}}(C(R),*)=0$.

• (3) $hKh=0$ and $hKk=0$ imply $hRk=0$. In particular, if ${{\,\mathrm{Id}\,}}_R(h)$ is essential then $k=0$, while if $h\in {{\,\mathrm{Id}\,}}_R(k)$ then $h=0$ (resp. if $k\in {{\,\mathrm{Id}\,}}_R(h)$ then $k=0$).

• (4) $k[K,K]k=0$ and $k^2=0$ imply $k=0$.

Proof

We can suppose without loss of generality that $R={\hat{R}}$, i.e., R is centrally closed.

• (1) Take $x\in R$. Note that $k(x-x^*)k=0$, so that $kxk=kx^*k$. Then

  $$\begin{aligned} k(xkx)k&= k(xkx)^*k = -kx^*kx^*k = -(kx^*k)x^*k = -kxkx^*k \\&= -kx(kx^*k) = -kxkxk \end{aligned}$$

  and so we have $kxkxk=0$ since R is free of 2-torsion. Therefore $kxkxkyk=0$ for every $y\in R$, hence

  $$\begin{aligned} 0 = -kxk(xky)k = -kxk(xky)^*k = kxky^*kx^*k = kxkykxk, \end{aligned}$$

  so $(kxk)R(kxk)=0$ and $kxk=0$ since R is semiprime. Now $kRk=0$ implies, again by semiprimeness, that $k=0$.

• (2) If $h=0$ then the claim is trivially fulfilled, so assume $h\ne 0$. Take $x,y\in R$. Note that $h(x-x^*)h = 0$ and therefore $hxh = hx^*h$. Then

  $$\begin{aligned} 0 = h(xhy-(xhy)^*)h = hxhyh - hy^*hx^*h = hxhyh - (hy^*h)x^*h = \end{aligned}$$
  $$\begin{aligned} = hxhyh - hy(hx^*h) = hxhyh -hyhxh = (hxh)yh - hy(hxh), \end{aligned}$$

  i.e., $hxhyh=hyhxh$. By Corollary 2.9, since $h\ne 0$ and ${{\,\mathrm{Id}\,}}_R(hxh)\subseteq {{\,\mathrm{Id}\,}}_R(h)$, for each $x\in R$ there exists $\mu _x\in C(R)$ such that $hxh=\mu _x h$. Hence $0\ne hRh\subset C(R)h$. Moreover, since $hx^*h = hxh$, $2hxh =hxh+hx^*h= (\mu _x+\mu _x^*)h\in H(C(R),*)h$, so $hRh\subseteq H(C(R),*)h$.

  Let us suppose that ${{\,\mathrm{Id}\,}}_R(h)$ is essential in R and let us show that ${{\,\mathrm{Skew}\,}}(C(R),*)=0$: Take $\lambda \in {{\,\mathrm{Skew}\,}}(C(R),*)$ and $y\in R$. Then $(\lambda h)y(\lambda h) = \lambda h(y\lambda ) h = \lambda \mu _{\lambda y}h\in K$ for some $\mu _{\lambda y}\in H(C(R),*)$. On the other hand, $(\lambda h)y(\lambda h) =\lambda ^2 hyh=\lambda ^2\mu _y h\in H$ for some $\mu _{y}\in H(C(R),*)$. Therefore $(\lambda h)y(\lambda h)=0$ for every $y\in R$, and by semiprimeness of R, $\lambda h=0$, so $\lambda =0$ because ${{\,\mathrm{Id}\,}}_R(h)$ is essential.

• (3) Suppose first that R is $*$-prime and, without loss of generality, that it is centrally closed. If R is not prime then there is $\lambda \in {{\,\mathrm{Skew}\,}}(C(R),*)$ such that $R=K+\lambda K$ (see 2.4), hence $hKh=0$ implies $hRh=0$ and $h=0$ since R is semiprime, so trivially $hRk=0$. Now assume R is prime. Since $R=H+K$ we only need to show that $hHk=0$. Let $x\in H$ and $y\in R$. Then

  $$\begin{aligned} 0&= h(x ky-(x ky)^*) h = hx ky h + hy^* kx h = hx ky h + hy kx h \end{aligned}$$

  since $h(y^*-y)k=0$ for every $y\in R$. By Corollary 2.9, since ${{\,\mathrm{Id}\,}}_{R }( hx k)\subset {{\,\mathrm{Id}\,}}_{R }( h)$, for each $x\in R$ there exists $\mu _x\in C(R )$ such that $hx k=\mu _x h$. If $\mu _x=0$ then $hxk=0$ and we are done. Otherwise, $0=hxkxk=\mu _xhxk=\mu _x^2h$, hence $h=0$ and we are also done.

  Suppose now that R is semiprime. Then there exists a family of $*$-prime ideals $\{I_\alpha \}_{\alpha \in \Delta }$ such that $\bigcap _{\alpha \in \Delta } I_\alpha =0$. In each $*$-prime quotient $R/I_\alpha$, we have ${\bar{h}} R/I_\alpha {\bar{k}}={\bar{0}}$, so $hRk\subset I_\alpha$ for all $\alpha$, hence $hRk=0$.

• (4) Since $k^2=0$ and $k[K,K]k=0$, for all $x,y\in K$ we get

  

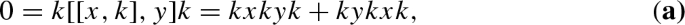
  thus $kxkyk=-kykxk$ and $2kxkxk=0$ for all $x\in K$, hence $kxkxk=0$ since R is free of 2-torsion. Now, by (a),

  $$\begin{aligned} 0=(kxkxk)yk = kx(kxkyk)= - kxkykxk \end{aligned}$$

  for all $x,y\in K$. Thus $(kxk)K(kxk)=0$ for all $x\in K$, $kKk=0$ and $k=0$ by item (1) applied twice. $\square$

Remark 5.2

Let R be a semiprime ring with involution such that $R=H+K$ (in particular this is true when R is centrally closed and has no 2-torsion by 2.5). Then every $x\in R$ can be expressed as $x=x_h+x_k$ with $x_h\in H$ and $x_k\in K$. If $a\in K$ is an ad-nilpotent element of K of index n, then for every $x\in R$

$$\begin{aligned} {{\,\mathrm{ad}\,}}_a^n(ax+xa)&={{\,\mathrm{ad}\,}}_a^n(ax_k+x_ka)+{{\,\mathrm{ad}\,}}_a^n(ax_h+x_ha)\\&=a{{\,\mathrm{ad}\,}}_a^n(x_k)+{{\,\mathrm{ad}\,}}_a^n(x_k)a+{{\,\mathrm{ad}\,}}_a^n(ax_h+x_ha)=0, \end{aligned}$$

since $ax_h+x_ha\in K$. On the other hand, expanding this expression,

$$\begin{aligned} 0={{\,\mathrm{ad}\,}}_a^n(ax+xa)=(-1)^nxa^{n+1}+\sum _{i=1}^{n} \left( \left( {\begin{array}{c}n\\ i\end{array}}\right) -\left( {\begin{array}{c}n\\ i-1\end{array}}\right) \right) (-1)^{n-i} a^ixa^{n+1-i}+a^{n+1}x. \end{aligned}$$

Observe that a nilpotent element in K is ad-nilpotent of both K and R, but its index of ad-nilpotence in R may be higher than the one found in K. In the following proposition, we describe the ad-nilpotent elements of K of index n that are already nilpotent of certain index s. The description depends on the equivalence class of the index of ad-nilpotence modulo 4 and relates the index of nilpotence to the index of ad-nilpotence.

Proposition 5.3

Let R be a semiprime ring with involution $*$ and free of 2-torsion, let ${\hat{R}}$ be its central closure, and let $a\in K$ be a nilpotent element of index of nilpotence s. Then a is ad-nilpotent in R. If the index of ad-nilpotence of a in K is n and R is free of $\left( {\begin{array}{c}n\\ t\end{array}}\right)$-torsion for $t:=[\frac{n+1}{2}]$, then:

• (1) If $n\equiv 0\ ({{\,\mathrm{mod}\,}}4)$ then $s=t+1$ and $a^{t}Ka^{t}=0$.

• (2) If $n\equiv 1\ ({{\,\mathrm{mod}\,}}4)$ then $s=t$ and the index of ad-nilpotence of a in R is also n.

• (3) The case $n\equiv 2\ ({{\,\mathrm{mod}\,}}4)$ is not possible.

• (4) If $n\equiv 3\ ({{\,\mathrm{mod}\,}}4)$ then there exists an idempotent $\epsilon \in C(R)$ such that $\epsilon a^t=a^t$. Moreover, when we write $a=\epsilon a+(1-\epsilon )a$, we have:

  (4.1):

  If $0\ne \epsilon a\in {\hat{R}}$ then $\epsilon a$ is nilpotent of index $t+1$, $\epsilon a^t=a^t$ generates an essential ideal in $\epsilon {\hat{R}}$ and $(\epsilon a)^{t-1}k(\epsilon a)^{t}= (\epsilon a)^{t}k(\epsilon a)^{t-1}$ for every $k\in {{\,\mathrm{Skew}\,}}({\hat{R}},*)$.

  (4.2):

  If $0\ne (1-\epsilon )a\in {\hat{R}}$, then the index of ad-nilpotence of $(1-\epsilon )a$ in ${\hat{R}}$ is not greater than n, and $(1-\epsilon )a^t=0$.

Furthermore, if a is a pure ad-nilpotent element of K then in (2) and in (4.2) we obtain pure ad-nilpotent elements of R (respectively of ${\hat{R}}$) of index n.

Proof

Let us suppose without loss of generality that $R={\hat{R}}$, i.e., R is centrally closed.

Let $a\in K$ be a nilpotent element of index of nilpotence s. Then a is ad-nilpotent of K of a certain index n. If we apply Lemma 4.1 to the second formula obtained in Remark 5.2, we get that all the monomials appearing in it are zero. We will now focus on certain monomials depending on the parity of n.

$\bullet$ If n is even, $n=2t$. Let us see that $s=t+1$: on the one hand, for any $x\in R$ we know that

$$\begin{aligned} \left( \left( {\begin{array}{c}n\\ t\end{array}}\right) -\left( {\begin{array}{c}n\\ t-1\end{array}}\right) \right) (-1)^t a^{t}xa^{t+1}=0 \end{aligned}$$

and, since $\left( {\begin{array}{c}n\\ t\end{array}}\right) -\left( {\begin{array}{c}n\\ t-1\end{array}}\right)$ is a divisor of $2\left( {\begin{array}{c}n\\ t\end{array}}\right)$ and R is free of $2\left( {\begin{array}{c}n\\ t\end{array}}\right)$-torsion, we have that $a^{t}xa^{t+1}=0$ for all x. Therefore $a^{t+1}=0$ by semiprimeness, hence $s\le t+1$. On the other hand, if $s=t$ then $a^{t}=0$ and ${{\,\mathrm{ad}\,}}_a^{2t-1}(R)=0$, a contradiction.

Let us see that $n\equiv 0\ ({{\,\mathrm{mod}\,}}4)$: For any $k\in K$,

$$\begin{aligned} 0={{\,\mathrm{ad}\,}}_a^{2t}(k)=\sum _{i=1}^{2t} \left( {\begin{array}{c}2t\\ i\end{array}}\right) (-1)^{2t-i} a^ika^{2t-i}=\left( {\begin{array}{c}2t\\ t\end{array}}\right) (-1)^ta^tka^t, \end{aligned}$$

so $a^tka^t=0$ for every $k\in K$, which implies that t has to be even, since otherwise $a^t\in K$ and $a^tKa^t=0$ imply $a^t=0$ by Lemma 5.1(1), a contradiction. We have shown that, if n is even, $n\equiv 2\ ({{\,\mathrm{mod}\,}}4)$ is not possible.

$\bullet$ If n is odd, $n=2t-1$, and for any $x\in R$,

$$\begin{aligned} \left( \left( {\begin{array}{c}n\\ t-1\end{array}}\right) -\left( {\begin{array}{c}n\\ t-2\end{array}}\right) \right) a^{t-1}xa^{t+1}=0. \end{aligned}$$

Since $\left( {\begin{array}{c}n\\ t-1\end{array}}\right) -\left( {\begin{array}{c}n\\ t-2\end{array}}\right)$ is a divisor of $2\left( {\begin{array}{c}n\\ t\end{array}}\right)$ and R is free of $2\left( {\begin{array}{c}n\\ t\end{array}}\right)$-torsion, we have that $a^{t-1}xa^{t+1}=0$ for all x. Therefore $a^{t+1}=0$ by semiprimeness, hence $s\le t+1$. On the other hand $s>t-1$ since otherwise ${{\,\mathrm{ad}\,}}_a^{2t-2}(R)=0$, a contradiction.

If $a^t=0$ then a is already an ad-nilpotent element of R of index n. In this case, $n\equiv 1\ ({{\,\mathrm{mod}\,}}4)$ or $n\equiv 3\ ({{\,\mathrm{mod}\,}}4)$ by Proposition 4.3(2). Furthermore, if a is pure in K then a is pure in R by Lemma 3.3.

Suppose from now on that $a^t\ne 0$. Let us show that $n\equiv 3\ ({{\,\mathrm{mod}\,}}4)$. By Proposition 2.10, there exists an idempotent $\epsilon \in H(C(R),*)$ such that $\epsilon a^t=a^t$ and ${{\,\mathrm{Ann}\,}}_R({{\,\mathrm{Id}\,}}_R(a^t))=(1-\epsilon )R$ (so $a^t=\epsilon a^t$ generates an essential ideal in $\epsilon R$). Notice that $\epsilon a\ne 0$ (otherwise $0=(\epsilon a)^t=\epsilon a^t=a^t$, a contradiction). For every $k\in K$, we have

$$\begin{aligned} 0&={{\,\mathrm{ad}\,}}_{\epsilon a}^{n}k=\sum _{i=1}^{n} \left( {\begin{array}{c}n\\ i\end{array}}\right) (-1)^{n-i} \epsilon a^ika^{n-i}=\\&=\left( {\begin{array}{c}n\\ t-1\end{array}}\right) (-1)^{t} \epsilon a^{t-1}ka^{t}+\left( {\begin{array}{c}n\\ t\end{array}}\right) (-1)^{t-1} \epsilon a^{t}ka^{t-1}=\\&=\left( {\begin{array}{c}n\\ t\end{array}}\right) (-1)^{t-1}(- \epsilon a^{t-1}ka^{t}+ \epsilon a^{t}ka^{t-1}). \end{aligned}$$

Since R has no $\left( {\begin{array}{c}n\\ t\end{array}}\right)$-torsion, $\epsilon a^{t-1}ka^{t}=\epsilon a^{t}ka^{t-1}$ for every $k\in K$. Moreover, multiplying by a on the right we get $\epsilon a^{t}ka^{t}= a^{t}ka^{t}=0$, so $a^{t}Ka^{t}=0$, which by Lemma 5.1(1) is only possible if $a^t\ne 0$ is symmetric, hence t is even and $n\equiv 3\ ({{\,\mathrm{mod}\,}}4)$.

If $(1-\epsilon )a\ne 0$ then ${{\,\mathrm{ad}\,}}_{(1-\epsilon )a}^{2t-1}(R)=0$ and $(1-\epsilon )a$ is an ad-nilpotent element of R of index not greater than $2t-1$.

If a is a pure ad-nilpotent element of index n in K then $(1-\epsilon )a$ is ad-nilpotent of K of index n and therefore $(1-\epsilon )a^{t-1}\ne 0$. From this, the index of ad-nilpotence of $(1-\epsilon )a$ in R must be $n=2t-1$. Then by Lemma 3.3$(1-\epsilon )a$ is a pure ad-nilpotent element of R of index n. $\square$

Remark 5.4

Let $a\in K$ be a nilpotent element of index s. If we denote its index of ad-nilpotence in K by n, we obtain from Proposition 5.3 that, under the right torsion hypothesis, $2s-3\le n\le 2s-1$ and $\frac{n+1}{2}\le s\le \frac{n+3}{2}$.

Proposition 5.5

Let R be a semiprime ring with involution $*$ and free of 2-torsion, let ${\hat{R}}$ be its central closure, and let $a\in K$ be a pure ad-nilpotent element of K of index $n>1$. Then:

• (1) There exists an idempotent $\epsilon \in H(C(R),*)$ such that $(1-\epsilon )a$ is an ad-nilpotent element of ${\hat{R}}$ of index $\le n$ and $\epsilon a$ is nilpotent with ${{\,\mathrm{ad}\,}}_{\mu \epsilon a}^n ({\hat{R}})\ne 0$ for every $\mu \in C(R)$ such that $\mu \epsilon a\ne 0$.

• (2) Moreover, if a is pure ad-nilpotent in K and R is free of $\left( {\begin{array}{c}n\\ t\end{array}}\right)$-torsion and t-torsion for $t:=[\frac{n+1}{2}]$, when we write $a=\epsilon a+(1-\epsilon )a$ we have:

  • (2.1) If $\epsilon a\ne 0$ then $\epsilon a$ is nilpotent of index $t+1$.

  • (2.2) If $(1-\epsilon )a\ne 0$ then $(1-\epsilon )a$ is pure ad-nilpotent in ${\hat{R}}$ of index n. In this case, n is odd and there exists $\lambda \in {{\,\mathrm{Skew}\,}}(C(R),*)$ such that $((1-\epsilon )a-\lambda )^{t}=0$.

Proof

Notice that $n\ge 3$ since ${{\,\mathrm{ad}\,}}_a^2(K)=0$ implies $a\in Z(R)$ by [16, Corollary 4.8] and so ${{\,\mathrm{ad}\,}}_a(K)=0$, which is not possible because $n>1$ by hypothesis.

(1) Let us suppose first that R is a $*$-prime ring and, without loss of generality, that it is centrally closed.

(1.a) Case 1: ${{\,\mathrm{ad}\,}}_a^n(R)=0$ and we get the claim for the idempotent $\epsilon =0$.

(1.b) Case 2: ${{\,\mathrm{ad}\,}}_a^n(R)\ne 0$ implies that there are no nonzero skew elements $\lambda$ in C(R), since otherwise (by 2.4) $R=K+\lambda K$ would imply ${{\,\mathrm{ad}\,}}_a^n(R)=0$; in particular R is prime. Since ${{\,\mathrm{ad}\,}}_a^n(K)=0$, by the second formula of Remark 5.2 and Corollary 2.9, a is an algebraic element of R over the field $\mathbb {F}:=C(R)$. Let us consider the minimal polynomial $p(X)\in \mathbb {F}[X]$ of a. Let $\overline{\mathbb {F}}$ be the algebraic closure of C(R) and let $\mu _1,\dots ,\mu _t\in \overline{\mathbb {F}}$ such that $p(X)=(X-\mu _1)^{k_1}\cdots (X-\mu _t)^{k_t}$. Let $q_1(X):=p(X)/(X-\mu _1)$, so $q_1(a)a=\mu _1q_1(a)$. Now, for any $x\in R\otimes \overline{\mathbb {F}}$,

$$\begin{aligned} 0&={{\,\mathrm{ad}\,}}_a^n(ax+xa)q_1(a)\\ {}&=a\sum _{i=0}^n\left( {\begin{array}{c}n\\ i\end{array}}\right) (-1)^{n-i} a^ixa^{n-i}q_1(a)+\sum _{i=0}^n\left( {\begin{array}{c}n\\ i\end{array}}\right) (-1)^{n-i} a^ixa^{n-i}aq_1(a)\\&= a\sum _{i=0}^n\left( {\begin{array}{c}n\\ i\end{array}}\right) (-1)^{n-i} a^ix\mu _1^{n-i}q_1(a)+\sum _{i=0}^n\left( {\begin{array}{c}n\\ i\end{array}}\right) (-1)^{n-i} a^ix\mu _1^{n-i}\mu _1q_1(a)\\&= a\sum _{i=0}^n\left( {\begin{array}{c}n\\ i\end{array}}\right) (-1)^{n-i} a^i\mu _1^{n-i}xq_1(a)+\sum _{i=0}^n\left( {\begin{array}{c}n\\ i\end{array}}\right) (-1)^{n-i} a^i\mu _1^{n-i}\mu _1xq_1(a)\\&= a(a-\mu _1)^nxq_1(a)+(a-\mu _1)^n\mu _1xq_1(a)=(a-\mu _1)^n(a+\mu _1)xq_1(a) \end{aligned}$$

and therefore, since $R\otimes \overline{\mathbb {F}}$ is a centrally closed prime ring (see [5, pp. 445–446]), $(a-\mu _1)^n(a+\mu _1)=0$. If $\mu _1=0$, then a is nilpotent of index at most $n+1$. If $\mu _1\ne 0$, since the involution is of the first kind on R, it extends to $R\otimes \overline{\mathbb {F}}$ via $(r\otimes \lambda )^*:=r^*\otimes \lambda$, hence $0=((a-\mu _1)^n)^*(a+\mu _1)^*=(a^*-\mu _1)^n(a^*+\mu _1)=(-a-\mu _1)^n(-a+\mu _1)$ implies $(a+\mu _1)^n(a-\mu _1)=0$. From the conditions $(a-\mu _1)^n(a+\mu _1)=0$ and $(a+\mu _1)^n(a-\mu _1)=0$ we obtain $p(X)=(X-\mu _1)(X+\mu _1)$. Thus $a^2=\mu _1^2$, but then ${{\,\mathrm{ad}\,}}_a^3(k)=4\mu _1^2[a,k]$ for every $k\in K$, a contradiction with $n\ge 3$.

Let us study the semiprime case, and suppose without loss of generality that R is centrally closed: If a is already ad-nilpotent in R of index n, take $\epsilon =0$ and the claim holds. Suppose from now on that ${{\,\mathrm{ad}\,}}_a^n(R)\ne 0$. By Proposition 2.10 let $\epsilon \in H(C(R),*)$ be an idempotent such that $\epsilon {{\,\mathrm{ad}\,}}_a^n(x)={{\,\mathrm{ad}\,}}_a^n(x)$ for every $x\in R$, ${{\,\mathrm{Ann}\,}}_R({{\,\mathrm{Id}\,}}_R({{\,\mathrm{ad}\,}}_a^n(R)))=(1-\epsilon )R$ and ${{\,\mathrm{Ann}\,}}_{C(R)}({{\,\mathrm{ad}\,}}_a^n(R))=(1-\epsilon )C(R)$. Then ${{\,\mathrm{ad}\,}}_{(1-\epsilon )a}^n(R)=(1-\epsilon ){{\,\mathrm{ad}\,}}_{a}^n(R)=0$.

Let us study the element $\epsilon a$: First notice that ${{\,\mathrm{ad}\,}}_{\mu \epsilon a}^nR\ne 0$ for every $\mu$ such that $\mu \epsilon a\ne 0$, since otherwise $\mu \epsilon {{\,\mathrm{ad}\,}}_a^n(R)={{\,\mathrm{ad}\,}}_{\mu \epsilon a}^nR=0$ implies $\mu \epsilon \in {{\,\mathrm{Ann}\,}}_{C(R)}({{\,\mathrm{ad}\,}}_a^n(R))=(1-\epsilon )C(R)$ and hence $\mu \epsilon =0$, a contradiction. Let us see that $\epsilon a$ is nilpotent. Since R is semiprime, the intersection of all $*$-prime ideals of R is zero. Consider the essential $*$-ideal $S:={{\,\mathrm{Id}\,}}_R({{\,\mathrm{ad}\,}}_a^n(R))\oplus {{\,\mathrm{Ann}\,}}_R({{\,\mathrm{Id}\,}}_R({{\,\mathrm{ad}\,}}_a^n(R)))={{\,\mathrm{Id}\,}}_R({{\,\mathrm{ad}\,}}_a^n(R))\oplus (1-\epsilon )R$. Let us consider the families

$$\begin{aligned} \Delta _1:=\{I\triangleleft ^*R\ |\ R/I \hbox { is }*\hbox {-prime and }S\not \subset I \} \end{aligned}$$

and

$$\begin{aligned} \Delta _2:=\{I\triangleleft ^*R\ |\ R/I \hbox { is }*\hbox {-prime and }S\subset I\}. \end{aligned}$$

Since $S\subset \bigcap _{I\in \Delta _2} I$ and S is essential, $\bigcap _{I\in \Delta _1} I=0$ and R is a subdirect product of R/I with $I\in \Delta _1$. Let us see that in any $*$-prime quotient $\epsilon a$ is nilpotent of index not greater than $n+1$. Take $I\in \Delta _1$ and consider ${\bar{R}}:=R/I$. We may have two cases:

• If ${\overline{\epsilon }}={\overline{0}}$ then $\overline{\epsilon a}={\overline{0}}$.

• If ${\overline{\epsilon }}\ne {\overline{0}}$ then $\overline{\epsilon }={\overline{1}}\in R/I$ and $\overline{1-\epsilon }=\overline{0}$, so $(1-\epsilon )R\subset I$. Moreover, ${{\,\mathrm{ad}\,}}_{\overline{\epsilon a}}^n(R/I)\ne {\overline{0}}$ since otherwise ${{\,\mathrm{ad}\,}}_{\overline{\epsilon a}}^n(R/I)={\overline{0}}$ would imply $S\subset I$, a contradiction. Let us see that R/I is prime: if R/I is $*$-prime and not prime there would exist a nonzero skew element $\lambda$ in C(R/I), which implies that $R/I={{\,\mathrm{Skew}\,}}(R/I,*)\oplus \lambda {{\,\mathrm{Skew}\,}}(R/I,*)$ (see 2.4), so ${{\,\mathrm{ad}\,}}_{\overline{\epsilon a}}^n(R/I)={{\,\mathrm{ad}\,}}_{\overline{\epsilon a}}^n({{\,\mathrm{Skew}\,}}(R/I,*)\oplus \lambda {{\,\mathrm{Skew}\,}}(R/I, *))=0$, a contradiction. So R/I is a prime ring with involution and ${{\,\mathrm{ad}\,}}_{\overline{\epsilon a}}^n(R/I))\ne {\overline{0}}$ which implies that $\overline{\epsilon a}$ is nilpotent of index not greater than $n+1$.

In conclusion, for any $I\in \Delta _1$ we have $\epsilon a^{n+1}\in I$ and therefore $\epsilon a^{n+1}=0$.

(2) Suppose now that a is a pure element of K of index n and R is free of $2\left( {\begin{array}{c}n\\ t\end{array}}\right)$-torsion and free of t-torsion for $t:=[\frac{n+1}{2}]$. If a is already ad-nilpotent of R of index n then a is pure in R by Lemma 3.3 and we can use Theorem 4.4 to find that n is odd and there exists $\lambda \in {{\,\mathrm{Skew}\,}}(C(R),*)$ such that $(a-\lambda )^{t}=0$. Otherwise write $a=\epsilon a+(1-\epsilon )a$ as before. Since $\epsilon a$ is nilpotent and ad-nilpotent of K of index n (because we are assuming that a is pure in K), $\epsilon a$ is nilpotent of index $t+1$ (it has index t or $t+1$ by Proposition 5.3, but ${{\,\mathrm{ad}\,}}_{\epsilon a}^n(R)\ne 0$). Moreover, $(1-\epsilon )a$ is a pure ad-nilpotent element of R of index n (if it is nonzero, its index of ad-nilpotence cannot be lower than n since $(1-\epsilon )a$ is ad-nilpotent in K of index n), and we can apply Theorem 4.4 and Lemma 2.6 to get that n is odd and there exists $\lambda \in {{\,\mathrm{Skew}\,}}(C(R),*)$ such that $((1-\epsilon )a-\lambda )^{t}=0$. $\square$

Theorem 5.6

Let R be a semiprime ring with involution $*$ and free of 2-torsion, let ${\hat{R}}$ be its central closure, and let $a\in K$ be a pure ad-nilpotent element of K of index $n>1$. If R is free of $\left( {\begin{array}{c}n\\ t\end{array}}\right)$-torsion and t-torsion for $t:=[\frac{n+1}{2}]$ then:

• (1) If $n\equiv 0 \,(\text {mod } 4)$ then $a^{t+1}=0$, $a^t\ne 0$ and $a^tKa^t=0$. Moreover, there exists an idempotent $\epsilon \in H(C(R),*)$ such that $\epsilon a=a$ and the ideal generated by $a^t$ is essential in $\epsilon {\hat{R}}$. In addition $\epsilon {\hat{R}}$ satisfies the GPI $a^txa^tya^t=a^tya^txa^t$ for every $x,y\in \epsilon {\hat{R}}$.

• (2) If $n\equiv 1 \,(\text {mod } 4)$ then there exists $\lambda \in {{\,\mathrm{Skew}\,}}(C(R),*)$ such that $(a-\lambda )^t=0$ (a is an ad-nilpotent element of R of index n).

• (3) It is not possible that $n\equiv 2 \,(\text {mod } 4)$.

• (4) If $n\equiv 3 \,(\text {mod } 4)$ then there exists an idempotent $\epsilon \in H(C(R),*)$ making $a=\epsilon a+(1-\epsilon )a\in {\hat{R}}$ such that:

  (4.1):

  If $\epsilon a\ne 0$ then $\epsilon a^{t+1}=0$, $\epsilon a^t\ne 0$ and $\epsilon a^tk\epsilon a^{t-1}=\epsilon a^{t-1}k\epsilon a^t$ for every $k\in {{\,\mathrm{Skew}\,}}({\hat{R}}, *)$. The ideal generated by $\epsilon a^t$ is essential in $\epsilon {\hat{R}}$ and $\epsilon {\hat{R}}$ satisfies the GPI $a^txa^tya^t=a^tya^txa^t$ for every $x,y\in \epsilon {\hat{R}}$.

  (4.2):

  If $(1-\epsilon )a\ne 0$ then there exists $\lambda \in {{\,\mathrm{Skew}\,}}(C(R),*)$ such that $((1-\epsilon )a-\lambda )^t=0$ ($(1-\epsilon )a$ is a pure ad-nilpotent element of ${\hat{R}}$ of index n).

In particular, for all $n>1$ there exists $\lambda \in {{\,\mathrm{Skew}\,}}(C(R),*)$ such that $(a-\lambda )^{t+1}=0$, $(a-\lambda )^{t-1}\ne 0$.

Proof

We can suppose without loss of generality that $R={\hat{R}}$, i.e., R is centrally closed. By Proposition 5.5, there exists an idempotent $\epsilon \in H(C(R),*)$ such that $\epsilon {{\,\mathrm{ad}\,}}_a^n x={{\,\mathrm{ad}\,}}_a^n x$ for every $x\in R$ and ${{\,\mathrm{Ann}\,}}_R({{\,\mathrm{Id}\,}}_R({{\,\mathrm{ad}\,}}_a^n (R)))=(1-\epsilon )R$, and moreover:

• If $\epsilon a\ne 0$, it is nilpotent of index $t+1$ and ad-nilpotent of K of index n. By Proposition 5.3, this may happen if either $n\equiv 0\,(\text {mod } 4)$, in which case $a^{t+1}=0$, $a^t\ne 0$, $a^tKa^t=0$ and $(1-\epsilon )a=0$ (because $(1-\epsilon )a$ is ad-nilpotent of R and its index cannot be even), or $n\equiv 3\,(\text {mod } 4)$. The case $n\equiv 1\,(\text {mod } 4)$ is not possible because $\epsilon a^t\ne 0$.

• If $(1-\epsilon )a\ne 0$ then $(1-\epsilon )a$ is a pure ad-nilpotent element of R, n is odd and there exists $\lambda \in {{\,\mathrm{Skew}\,}}(R,*)$ with $((1-\epsilon )a-\lambda )^t=0$. By Proposition 5.3, this may happen if either $n\equiv 1\,(\text {mod } 4)$ (in this case $\epsilon a=0$) or $n\equiv 3 \,(\text {mod } 4)$. The decomposition $(1-\epsilon )a-\lambda =a_1+a_2$ given by Proposition 5.3(4) occurs with $a_1=0$ since otherwise the index $t+1$ of $a_1$ would contradict $((1-\epsilon )a-\lambda )^t=0$.

In the particular case of $n\equiv 3\,(\text {mod } 4)$ with $\epsilon a\ne 0$, the idempotent $\epsilon _1$ produced in Proposition 5.3(4) for the nilpotent element $\epsilon a$ satisfies $\epsilon _1\epsilon a^t=\epsilon a^t$, so $(1-\epsilon _1)\epsilon \in {{\,\mathrm{Ann}\,}}_R({{\,\mathrm{Id}\,}}_R({{\,\mathrm{ad}\,}}_a^n (R)))=(1-\epsilon )R$, thus $\epsilon _1\epsilon =\epsilon$ and $\epsilon a^t=\epsilon _1\epsilon a^t$ generates an essential ideal in $\epsilon R$. On the other hand, we know from Proposition 5.5 that $(\epsilon a)^{t-1}k(\epsilon a)^{t}=(\epsilon a)^{t}k(\epsilon a)^{t-1}$ for every $k\in K$; in particular $(\epsilon a)^{t}K(\epsilon a)^{t}=0$. Therefore, by Lemma 5.1(2) the identity

$$\begin{aligned} a^txa^tya^t=a^tya^txa^t \end{aligned}$$

holds in $\epsilon R$.

In the particular case of $n\equiv 0\,(\text {mod } 4)$, the idempotent $\epsilon$ produced in Proposition 5.5 satisfies $\epsilon a^txa^t=\epsilon a^t$ for every $x\in R$ and ${{\,\mathrm{Ann}\,}}_{R}{{\,\mathrm{Id}\,}}_{R}(a^tRa^t)=(1-\epsilon )R$. On the other hand, $(1-\epsilon )a$ must be zero because ${{\,\mathrm{ad}\,}}_{(1-\epsilon )a}^n (R)=0$ and a is a pure ad-nilpotent element (so $a=\epsilon a$). Therefore, the ideal generated by $a^t$ in $\epsilon R$ is essential in $\epsilon R$ and the identity $a^txa^tya^t=a^tya^txa^t$ holds in $\epsilon R$ by Lemma 5.1(2). $\square$

Remark 5.7

It is worth noting that in the semiprime case, when $n\equiv 3 \,(\text {mod } 4)$ there can exist elements a with two nonzero parts $\epsilon a$ and $(1-\epsilon )a$ behaving as in Theorem 5.6(4.1) and Theorem 5.6(4.2). This is no longer true in the prime case, see [29, Main Theorem].

In the next corollary, we recover Lee’s main result by taking into account that every ad-nilpotent element can be expressed as a sum of pure ad-nilpotent elements of decreasing indices.

Corollary 5.8

([26, Theorem 1.5]) Let R be a semiprime ring with involution $*$ and free of n!-torsion, let ${\hat{R}}$ be its central closure, and let $a\in K$ be an ad-nilpotent element of K of index n. Then there exist $\lambda \in {{\,\mathrm{Skew}\,}}(C(R),*)$ and an idempotent $\epsilon \in H(C(R),*)$ such that $(\epsilon a-\lambda )^{t+1}=0$ and $(\epsilon a-\lambda )^{t-1}\ne 0$ for $t:=[\frac{n+1}{2}]$, and $(1-\epsilon ){\hat{R}}$ is a PI-algebra satisfying the standard identity $S_4$.

Proof

We can suppose without loss of generality that $R={\hat{R}}$, i.e., R is centrally closed. By Proposition 3.4, there exists a family of orthogonal symmetric idempotents $\{\epsilon _i\}_{i=1}^k$ of the extended centroid such that $a=\sum _{i=1}^k \epsilon _ia$, with $\epsilon _ia$ a pure ad-nilpotent element of index $n_i$ ($n=n_1>n_2>\dots$) of ${{\,\mathrm{Skew}\,}}(\epsilon _iR,*)$. If $n_k=1$ then $\epsilon _{k}a$ can be decomposed as $\epsilon _ka=\epsilon _{k1}a+(1-\epsilon _{k1})a$, where $\epsilon _{k1}a\in Z(R)$ and $(1-\epsilon _{k1})R$ is a PI-algebra satisfying the standard identity $S_4$ by [9, Theorem 4.2(i),(ii) and (*)]. The claim follows now from Theorem 5.6. $\square$

Let us extend this last result to Lie algebras of the form $K/(K\cap Z(R))$ and $[K,K]/([K,K]\cap Z(R))$.

Corollary 5.9

Let R be a semiprime ring with involution free of n!-torsion, let ${\hat{R}}$ be its central closure, and consider the Lie algebra $L:=K/(K\cap Z(R))$. If ${\bar{a}}$ is an ad-nilpotent element of L of index n, then there exist $\lambda \in {{\,\mathrm{Skew}\,}}(C(R),*)$ and an idempotent $\epsilon \in H(C(R),*)$ such that $(\epsilon a-\lambda )^{t+1}=0$ and $(\epsilon a-\lambda )^{t-1}\ne 0$ for $t:=[\frac{n+1}{2}]$, and $(1-\epsilon ){\hat{R}}$ is a PI-algebra that satisfying the standard identity $S_4$.

Proof

Let us prove that ${{\,\mathrm{ad}\,}}_a^n(K)\subset Z(R)$ implies ${{\,\mathrm{ad}\,}}_a^n(K)=0$: Suppose first that R is $*$-prime and, without loss of generality, centrally closed. If ${{\,\mathrm{ad}\,}}_a^n(K)\ne 0$, there would exist $0\ne \lambda \in {{\,\mathrm{ad}\,}}_a^n(K)\cap Z(R)$, so $R=K+\lambda K$ by 2.4 and hence ${{\,\mathrm{ad}\,}}_a^n(R)\subset Z(R)$, which implies by Lemma 4.6 that ${{\,\mathrm{ad}\,}}_a^n(R)=0$, a contradiction. The same result follows for semiprime rings because they can be expressed as subdirects product of $*$-prime quotients.

The claim follows now from Corollary 5.8. $\square$

Now we turn to Lie algebras of the form $[K,K]/([K,K]\cap Z(R))$. We first need a technical lemma.

Lemma 5.10

Let R be a semiprime ring with involution $*$ and $a\in K$ be such that ${{\,\mathrm{ad}\,}}_a^n([K,K])\subset Z(R)$, $n>1$. If R is free of $(n+1)!$-torsion then ${{\,\mathrm{ad}\,}}_a^n(K)=0$.

Proof

Let us first suppose that R is a $*$-prime ring and, without loss of generality, that it is centrally closed. If ${{\,\mathrm{Skew}\,}}(C(R),*)\ne 0$ then $R=K+\lambda K$ for any $0\ne \lambda \in {{\,\mathrm{Skew}\,}}(C(R),*)$ (see 2.4); thus ${{\,\mathrm{ad}\,}}_a^n([R,R])\subset Z(R)$, and by Lemma 4.7a is an ad-nilpotent element of R of index n. Otherwise ${{\,\mathrm{Skew}\,}}(C(R),*)=0$, in which case R must be prime and $K\cap Z(R)=0$, so ${{\,\mathrm{ad}\,}}_a^n([K,K])=0$. From ${{\,\mathrm{ad}\,}}_a^{n+1}K\subset {{\,\mathrm{ad}\,}}_a^n([K,K])=0$ and ${{\,\mathrm{Skew}\,}}(C(R),*)=0$, we get from Proposition 5.5 that a is a nilpotent element of R. Let s be its index of nilpotence. If ${{\,\mathrm{ad}\,}}_a^nK=0$ we are done; suppose it is not and let us compare the index of ad-nilpotence of a in K with its index of nilpotence s (see Proposition 5.3) to get a contradiction:

(a) If $n+1\equiv 0 \ ({{\,\mathrm{mod}\,}}4)$ then $s={n+3\over 2}$ and $a^{s-1}Ka^{s-1}=0$. From $\left( {\begin{array}{c}n\\ s-2\end{array}}\right) =\left( {\begin{array}{c}n\\ s-1\end{array}}\right)$ we get, for every $x\in R$, that ${{\,\mathrm{ad}\,}}_a^n x=(-1)^{s-1}\left( {\begin{array}{c}n\\ s-2\end{array}}\right) \left( a^{s-2}xa^{s-1}-a^{s-1}xa^{s-2}\right)$. Then, for every $k, k'\in K$,

$$\begin{aligned}&2({{\,\mathrm{ad}\,}}_a^nk)k'({{\,\mathrm{ad}\,}}_a^nk)\\ {}&\quad =2\left( {\begin{array}{c}n\\ s-2\end{array}}\right) \left( {\begin{array}{c}n\\ s-2\end{array}}\right) \left( a^{s-2}ka^{s-1}k'a^{s-2}ka^{s-1}+ a^{s-1}ka^{s-2}k'a^{s-1}ka^{s-2} \right) \\&\quad =2\left( {\begin{array}{c}n\\ s-2\end{array}}\right) \left( {\begin{array}{c}n\\ s-2\end{array}}\right) a^{s-2}k(a^{s-1}k'a^{s-2}-a^{s-2}k'a^{s-1})ka^{s-1}+\\&\qquad +2\left( {\begin{array}{c}n\\ s-2\end{array}}\right) \left( {\begin{array}{c}n\\ s-2\end{array}}\right) a^{s-1}k(a^{s-2}k'a^{s-1}-a^{s-1}k'a^{s-2})ka^{s-2}\\&\quad =2(-1)^{s-2}\left( {\begin{array}{c}n\\ s-2\end{array}}\right) (a^{s-2}k ({{\,\mathrm{ad}\,}}_a^nk') ka^{s-1} - a^{s-1}k({{\,\mathrm{ad}\,}}_a^nk')ka^{s-2})\\&\quad =(-1)^{s-2}\left( {\begin{array}{c}n\\ s-2\end{array}}\right) (a^{s-2}{{\,\mathrm{ad}\,}}_k^2 ({{\,\mathrm{ad}\,}}_a^nk')a^{s-1}-a^{s-1}{{\,\mathrm{ad}\,}}_k^2 ({{\,\mathrm{ad}\,}}_a^nk')a^{s-2})\\&\quad ={{\,\mathrm{ad}\,}}_a^n({{\,\mathrm{ad}\,}}_k^2({{\,\mathrm{ad}\,}}_a^n k'))\in {{\,\mathrm{ad}\,}}_a^n([K,K])=0 \end{aligned}$$

because $a{{\,\mathrm{ad}\,}}_a^n k=0=({{\,\mathrm{ad}\,}}_a^n k)a$, $a^{s-1}Ka^{s-1}=0$ and $s\ge 3$ implies $a^{s-1}a^{s-2}=0$. Therefore $({{\,\mathrm{ad}\,}}_a^n k)K({{\,\mathrm{ad}\,}}_a^n k)=0$ and hence ${{\,\mathrm{ad}\,}}_a^n k=0$ for every $k\in K$ by Lemma 5.1(1).

(b) If $n+1\equiv 1\ ({{\,\mathrm{mod}\,}}4)$ then $s={n\over 2}+1$. For every $x\in R$, ${{\,\mathrm{ad}\,}}_a^n x=(-1)^{s-1}\left( {\begin{array}{c}n\\ s-1\end{array}}\right) a^{s-1}xa^{s-1}$. Then, for every $k,k'\in K$,

$$\begin{aligned} 2({{\,\mathrm{ad}\,}}_a^n k)k'({{\,\mathrm{ad}\,}}_a^nk)&=2\left( {\begin{array}{c}n\\ s-1\end{array}}\right) \left( {\begin{array}{c}n\\ s-1\end{array}}\right) a^{s-1}ka^{s-1}k'a^{s-1}ka^{s-1}\\&=\left( {\begin{array}{c}n\\ s-1\end{array}}\right) \left( {\begin{array}{c}n\\ s-1\end{array}}\right) a^{s-1}{{\,\mathrm{ad}\,}}_k^2(a^{s-1}k'a^{s-1})a^{s-1}\\&={{\,\mathrm{ad}\,}}_a^n ({{\,\mathrm{ad}\,}}_k^2({{\,\mathrm{ad}\,}}_a^n k'))\in {{\,\mathrm{ad}\,}}_a^n([K,K])=0 \end{aligned}$$

because $a^{s-1}a^{s-1}=0$. Therefore $({{\,\mathrm{ad}\,}}_a^n k)K({{\,\mathrm{ad}\,}}_a^n k)=0$ and hence ${{\,\mathrm{ad}\,}}_a^n k=0$ for every $k\in K$ by Lemma 5.1(1).

(c) The case $n+1\equiv 2 \ ({{\,\mathrm{mod}\,}}4)$ is not possible.

(d) If $n+1\equiv 3 \ ({{\,\mathrm{mod}\,}}4)$ then, by primeness of R, either $s=\frac{n}{2}+2$ and $a^{s-2}ka^{s-1}=a^{s-1}ka^{s-2}$ for every $k\in K$ (case (4.1) in Theorem 5.6) or $s\le \frac{n}{2}+1$ (case (4.2) in Theorem 5.6).

(d.1) Suppose $s=\frac{n}{2}+2$ and $a^{s-2}ka^{s-1}=a^{s-1}ka^{s-2}\,\, \mathbf (1)$ for every $k\in K$. For convenience write $\alpha :=\left( {\begin{array}{c}n\\ s-3\end{array}}\right)$, $\beta :=\left( {\begin{array}{c}n\\ s-2\end{array}}\right)$ and observe that $\alpha \ne \beta$ (since $n\ne 2s-5$). For every $k,k'\in K$, we have

Multiplying on the left by a and applying (1) to the second term afterwards,

$$\begin{aligned} 0&=a{{\,\mathrm{ad}\,}}_a^n([k,k'])=\alpha a^{s-2}[k,k']a^{s-1}- \beta a^{s-1}[k,k']a^{s-2}=\\&=\alpha a^{s-2}[k,k']a^{s-1}-\beta a^{s-2}[k,k']a^{s-1} =(\alpha -\beta )a^{s-2}[k,k']a^{s-1}, \end{aligned}$$

which gives $a^{s-2}[k,k']a^{s-1}=0$ (3) since R is free of $(\alpha -\beta )$-torsion. Now we study two separate cases:

If $n=2$ then $s=3$ and $a\in K$ satisfies ${{\,\mathrm{ad}\,}}_a^3(K)=0$ and $a^2\ne 0, a^3=0$, so it is a Clifford element (see [8]). Since R is free of 2, 3-torsion there is a twin element $b\in K$ of a such that $aba=a$ and $a^2b^2a^2=a^2$ ([8, p. 289 and Proposition 3.7(6)]). Then, by (3),

$$\begin{aligned} 0=a[[b,a],b]a^2= 2(aba)ba^2 - a^2b^2a^2 -ab^2a^3 = 2aba^2 -a^2 = a^2, \end{aligned}$$

a contradiction.

If $n>2$ then $n\ge 6$ and $s\ge 5$, so $2s-4>s$ and $(a^{s-2})^2=0$. We see that

for every $k_1,k_1',k_2,k_2'\in K$: from (2) we can write $\beta a^{s-2}[k_2,k_2']a^{s-2}$ as a linear combination of $a^{s-1}[k,k']a^{s-3}$ and $a^{s-3}[k,k']a^{s-1}$, so (4) follows since R is free of $\beta$-torsion and $a^{s-2}[k_1,k_1']a^{s-1}=0=a^{s-1}[k_1,k_1']a^{s-2}$ by (3) and (1). Since for each $k_1,k_1'\in K$ we have that $b:=a^{s-2}[k_1,k_1']a^{s-2}\in K$ is such that $b^2=0$ and $b[K,K]b=0$ by (4), by Lemma 5.1(4) we get $b=0$ for each $k_1,k_1'\in K$, so $a^{s-2}[K,K]a^{s-2}=0$, and $a^{s-2}=0$ again by Lemma 5.1(4), a contradiction.

(d.2) Suppose $s \le \frac{n}{2}+1$. In this case, the proof follows as in (b): ${{\,\mathrm{ad}\,}}_a^n x=(-1)^{\frac{n}{2}}\left( {\begin{array}{c}n\\ \frac{n}{2}\end{array}}\right) a^{\frac{n}{2}}xa^{\frac{n}{2}}$ for every $x\in R$, $({{\,\mathrm{ad}\,}}_a^n k)K({{\,\mathrm{ad}\,}}_a^n k)=0$ and hence ${{\,\mathrm{ad}\,}}_a^n k=0$ for every $k\in K$ by Lemma 5.1(1).

In any case ${{\,\mathrm{ad}\,}}_a^n(K)=0$. Finally, the semiprime case follows because R is a subdirect product of $*$-prime rings. $\square$

From this lemma and Corollary 5.8 we get:

Corollary 5.11

Let R be a semiprime ring with involution $*$, let ${\hat{R}}$ be its central closure, and consider the Lie algebra $L:=[K,K]/(Z(R)\cap [K,K])$. If ${\bar{a}}$ is an ad-nilpotent element of L of index $n>1$ and R is free of $(n+1)!$-torsion then there exist $\lambda \in {{\,\mathrm{Skew}\,}}(C(R),*)$ and an idempotent $\epsilon \in H(C(R),*)$ such that $(\epsilon a-\lambda )^{t+1}=0$ and $(\epsilon a-\lambda )^{t-1}\ne 0$ for $t:=[\frac{n+1}{2}]$, and $(1-\epsilon ){\hat{R}}$ is a PI-algebra satisfying the standard identity $S_4$.