Algebraic Tensor Products Revisited: Axiomatic Approach

Abstract

This is an expository paper on tensor products where the standard approaches for constructing concrete instances of algebraic tensor products of linear spaces, via quotient spaces or via linear maps of bilinear maps, are reviewed by reducing them to different but isomorphic interpretations of an abstract notion, viz. the universal property, which is based on a pair of axioms.

1 Introduction

The purpose of this paper is to offer a brief and unified review with an expository flavor on the common realizations of algebraic tensor products (either via quotient space or via linear maps of bilinear maps) by reversing the presentation order. In other words, this exposition focuses on the approach where the so-called universal property is taken as an axiomatic starting point, rather than as a theorem for a specific realization. This leads to the abstract notion of algebraic tensor products of linear spaces (the pre-crossnorm stage), where the concrete standard forms are shown to be interpretations of the axiomatic formulation.

The origin of a systematic presentation of tensor products in book form dates back to Schatten’s 1950 monograph [21], where the notion of direct product of linear spaces was given in terms of formal products (which match what its now called tensor product space and single tensors) and their symbols in the form of finite sum of formal products. This followed a Kronecker product-like notion on finite-dimensional spaces given in Weyl’s 1931 book [23, Chapter V]. Grothendieck’s fundamental work in the 1950s has been unified and updated by Diestel, Fourie, and Swart in 2008 [3]. See also Pisier’s 2012 exposition [17]. In Grothendieck’s pioneering work, the notion of tensor product space was essentially given in terms of the dual of the linear space of bilinear forms (or, more generally, the linear space of linear maps of bilinear maps). The same way of defining tensor product also appears in Halmos’s 1958 book on finite-dimensional vector spaces [5, Section 24] (although the formal products variant is also mentioned as a possible alternative). Another representative along this line (dual of the linear space of bilinear forms) is Ryan’s 2002 book on tensor products of Banach spaces [20].

On the other hand, a different but still usual approach for defining tensor product relies on quotient spaces of free linear spaces (equivalent to the linear space of formal linear combinations) of Cartesian products of linear spaces$.\!$ This has been sometimes referred to as algebraic tensor product (although the previous approach is equally algebraic). See, e.g., [1, pp. 22–25], [22, Section 3.4], and [19, Chapter 14] for a linear space version and [15, Section IX.8] and [14, Section XVI.1]) for a module version.

The present paper is organized as follows. Notation, terminology, and auxiliary results are brought together in Sect. 2. This is split into three parts :  formal linear combination, quotient space, and bilinear maps. Tensor products are axiomatically defined in Sect. 3, and common properties shared by the concrete formulations are obtained from such an abstract formulation. The usual realizations, viz. the quotient space and linear maps of bilinear maps, are individually inferred from Definition 3.1 and are considered in Sects. 4 and 5.

2 Notation, Terminology, and Auxiliary Results

Let ${{\mathcal {X}}}$ and ${{\mathcal {Y}}}$ be linear spaces over the same field ${{\mathbb {F}}}$, and let ${{\mathcal {L}}}[{{{\mathcal {X}}},{{\mathcal {Y}}}}]$ denote the linear space over ${{\mathbb {F}}}$ of all linear transformations from ${{\mathcal {X}}}$ to ${{\mathcal {Y}}}$. For ${{{\mathcal {X}}}={{\mathcal {Y}}}}$, write ${{\mathcal {L}}}[{{\mathcal {X}}}]={{\mathcal {L}}}[{{\mathcal {X}}},{{\mathcal {X}}}]$, which is the algebra of all linear transformations of ${{\mathcal {X}}}$ into itself. The kernel ${{{\mathcal {N}}}(L)=L^{-1}({\{0\}})}$ and range ${{{\mathcal {R}}}(L)=L({{\mathcal {X}}})}$ of ${L\in {{\mathcal {L}}}[{{\mathcal {X}}},{{\mathcal {Y}}}]}$ are linear manifolds of ${{\mathcal {X}}}$ and ${{\mathcal {Y}}}$, respectively. A linear transformation ${L\in {{\mathcal {L}}}[{{\mathcal {X}}},{{\mathcal {Y}}}]}$ is injective if ${{\mathcal {N}}}(L)={\{0\}}$ and surjective if ${{\mathcal {R}}}(L)={{\mathcal {Y}}}$. By an isomorphism (or an algebraic isomorphism, or a linear space isomorphism), we mean an invertible (i.e., injective and surjective) linear transformation. Two linear spaces ${{\mathcal {X}}}$ and ${{\mathcal {Y}}}$ are isomorphic (notation ${{{\mathcal {X}}}\cong {{\mathcal {Y}}}}$) if there is an isomorphism between them. For the particular case of ${{{\mathcal {Y}}}={{\mathbb {F}}}}$, the elements of ${{\mathcal {L}}}[{{{\mathcal {X}}},{{\mathbb {F}}}}]$ are referred to as linear functionals or linear forms, and the linear space ${{\mathcal {L}}}[{{{\mathcal {X}}},{{\mathbb {F}}}}]$ of all linear functionals on ${{\mathcal {X}}}$ is referred to as the algebraic dual of ${{\mathcal {X}}}$, denoted by ${{\mathcal {X}}}^\sharp$ (i.e., ${{{\mathcal {X}}}^\sharp ={{\mathcal {L}}}[{{{\mathcal {X}}},{{\mathbb {F}}}}]})$. For an arbitrary linear transformation ${L\in {{\mathcal {L}}}[{{\mathcal {X}}},{{\mathcal {Y}}}]}$, consider the linear transformation ${L^\sharp \in \!{{\mathcal {L}}}[{{\mathcal {Y}}}^\sharp \!,{{\mathcal {X}}}^\sharp ]}$ defined by ${L^\sharp g=g L\in {{\mathcal {X}}}^\sharp }$ for every ${g\in \!{{\mathcal {Y}}}^\sharp }\!$ (i.e., ${(L^\sharp g)(x)=g(Lx)\in {{\mathbb {F}}}}$ for every ${g\in \!{{\mathcal {Y}}}^\sharp }$ and every ${x\in \!{{\mathcal {X}}}}$—we use both notations gL or ${g\circ L}$ for composition). This ${L^\sharp \in \!{{\mathcal {L}}}[{{\mathcal {Y}}}^\sharp \!,{{\mathcal {X}}}^\sharp ]}$ is the algebraic adjoint of ${L\in {{\mathcal {L}}}[{{\mathcal {X}}},{{\mathcal {Y}}}]}$.

The next subsections summarize not only notation and terminology, but also auxiliary results that will be required in Sects. 4 and 5.

2.1 Formal Linear Combination

Let S be an arbitrary nonempty set and let ${{\mathbb {F}}}$ be a field. Consider the linear space ${{\mathbb {F}}}^S\!$ of all scalar-valued functions ${f\!:S\rightarrow {{\mathbb {F}}}}$ on S. Let $\#$ stand for cardinality and consider the set

of all functions ${f\!:S\rightarrow {{\mathbb {F}}}}$ which vanish everywhere on the complement of some finite subset A of S (which depends on f). This is a linear manifold of ${{\mathbb {F}}}^S\!$, and so is itself a linear space over ${{\mathbb {F}}}$. For each ${s\in S}$, take the characteristic function ${e_s={^{_{\textstyle \chi }}}_{\{s\}}\!:S\rightarrow {{\mathbb {F}}}}$ of the singleton ${\{s\}\subseteq S}$. As is readily verified the set

Thus, an arbitrary vector , being a scalar-valued function taking nonzero values only over a finite subset $\{s_i\}_{i=1}^n$ of S, has a unique expansion with ${\alpha _i\in {{\mathbb {F}}}}$:

The linear space is called the free linear space generated by S. Since $\#\{e_s\}_{s\in S}=$ $\#S$ (i.e., each element s from the set S is in a one-to-one correspondence with each function $e_s$ from the Hamel basis ${{\mathbb {S}}}$ for the function space ), then ${\dim {{{{\mathcal {S}}}\!\!\!\!/}}=\#{{\mathbb {S}}}=\#S}$. This sets a natural identification $\approx$ such that ${s\approx e_s}$ and so $S\approx {{\mathbb {S}}}$, which in turn leads to a natural identification for an arbitrary linear combination in ,

$$\begin{aligned} \mathop {\sum }_{i=1}^n\alpha _ie_{s_i}\approx \mathop {\sum }_{i=1}^n\alpha _is_i, \end{aligned}$$

where ${\sum }_{i=1}^n\alpha _is_i$ is referred to as a formal linear combination of points ${s_i\in S}$ (although addition or scalar multiplication is not directly defined on the set S), the collection of which is the linear space of formal linear combinations from S. So any function f in the linear space is identified with a formal linear combination of points in S, and the set S that generates the free linear space is identified with the Hamel basis ${{\mathbb {S}}}$ for In this sense, the set S may be regarded as a subset of , and a function f in may be regarded as a formal linear combination. Thus, write

2.2 Quotient Space

Let ${{\mathcal {M}}}$ be a linear manifold of a linear space ${{\mathcal {X}}}$ over a field ${{\mathbb {F}}}$, let $[x]=x+{{\mathcal {M}}}$ denote the coset of ${x\in {{\mathcal {X}}}}$ modulo ${{\mathcal {M}}}$, and let ${{\mathcal {X}}}/{{\mathcal {M}}}$ stand for the quotient space of ${{\mathcal {X}}}$ modulo ${{\mathcal {M}}}$, which is the linear space over ${{\mathbb {F}}}$ of all cosets [x] modulo ${{\mathcal {M}}}$ for every ${x\in {{\mathcal {X}}}}$. Consider the quotient map (or the natural quotient map) ${\pi \!:{{\mathcal {X}}}\rightarrow {{\mathcal {X}}}/{{\mathcal {M}}}}$ of the linear space ${{\mathcal {X}}}$ onto the linear space ${{\mathcal {X}}}/{{\mathcal {M}}}$, defined by

$$\begin{aligned} \pi (x)=[x]=x+{{\mathcal {M}}}\,\;\;\hbox {for every}\;\; x\in {{\mathcal {X}}}, \end{aligned}$$

which is a surjective linear transformation according to the usual definition of addition and scalar multiplication in ${{\mathcal {X}}}/{{\mathcal {M}}}$.

Proposition 2.1

Universal Property. Let ${{\mathcal {X}}}$ and ${{\mathcal {Z}}}$ be linear spaces over the same field, let ${{\mathcal {M}}}$ be a linear manifold of ${{\mathcal {X}}}$, consider the quotient space ${{{\mathcal {X}}}/{{\mathcal {M}}}}$, and take the natural quotient map ${\pi \! :{{\mathcal {X}}}\rightarrow {{\mathcal {X}}}/{{\mathcal {M}}}}$. If ${L\in {{\mathcal {L}}}[{{\mathcal {X}}},{{\mathcal {Z}}}]}$ and if ${{{\mathcal {M}}}\subseteq {{\mathcal {N}}}(L)}$, then there exists a unique ${\widehat{L}\in {{\mathcal {L}}}[{{\mathcal {X}}}/{{\mathcal {M}}},{{\mathcal {Z}}}]}$ such that

$$\begin{aligned} L=\widehat{L}\circ \pi . \end{aligned}$$

In other words, the diagram

commutes, which means the quotient map $\pi$ factors the linear transformation L through ${{\mathcal {X}}}/{{\mathcal {M}}}$. Moreover, in this case ${{{\mathcal {N}}}(\widehat{L})={{\mathcal {N}}}(L)/{{\mathcal {M}}}}$ and ${{{\mathcal {R}}}(\widehat{L})={{\mathcal {R}}}(L)}$.

Proof

See, e.g., [19, Theorem 3.4, 3.5]. (For a module version see, e.g., [15, Theorem V.4.7]; for a normed space version see, e.g., [16, Theorem 1.7.13].) $\square$

Remark 2.1

Let ${{\mathcal {M}}}$ be linear a manifold of a linear space ${{\mathcal {X}}}$. A set $\{[\hbox {e}_\delta ]\}_{\delta \in \Delta }$ of cosets modulo ${{\mathcal {M}}}$ (with each $\hbox {e}_\delta$ in ${{\mathcal {X}}}$) is a Hamel basis for the linear space ${{\mathcal {X}}}/{{\mathcal {M}}}$ if and only if $\{\hbox {e}_\delta \}_{\delta \in \Delta }$ is a Hamel basis for some algebraic complement of ${{\mathcal {M}}}$ (see, e.g., [12, Remark A.1(b)]). Hence, every Hamel basis $\{e_\gamma \}_{\gamma \in \varGamma }$ for ${{\mathcal {X}}}$ is such that $\{[\hbox {e}_\gamma ]\}_{\gamma \in \varGamma }$ includes a Hamel basis for ${{\mathcal {X}}}/{{\mathcal {M}}}$. Since the quotient map ${\pi \!:{{\mathcal {X}}}\rightarrow {{\mathcal {X}}}/{{\mathcal {M}}}}$ is surjective, the image $\pi (E_{{\mathcal {X}}})$ of an arbitrary Hamel basis $E_{{\mathcal {X}}}$ for ${{\mathcal {X}}}$ includes a Hamel basis $E_{{{\mathcal {X}}}/{{\mathcal {M}}}}$ for ${{\mathcal {X}}}/{{\mathcal {M}}}$ (i.e., $E_{{{\mathcal {X}}}/{{\mathcal {M}}}}\subseteq \pi (E_{{\mathcal {X}}}))$. Therefore,

$$\begin{aligned} {\mathrm{span\,}}\pi (E_{{\mathcal {X}}})={{\mathcal {X}}}/{{\mathcal {M}}}\quad \hbox {for every Hamel basis}\, E_{{\mathcal {X}}}\, \hbox {for}\, {{\mathcal {X}}}, \end{aligned}$$

and so every element [x] of ${{\mathcal {X}}}/{{\mathcal {M}}}$ can be written as a (finite) linear combination of images under $\pi$ of elements of an arbitrary Hamel basis for ${{\mathcal {X}}}$.

2.3 Bilinear Maps

Let ${{\mathcal {X}}}$, ${{\mathcal {Y}}}$, ${{\mathcal {Z}}}$ be nonzero linear spaces over a field ${{\mathbb {F}}}$. Take the Cartesian product ${{{\mathcal {X}}}{\times }{{\mathcal {Y}}}}$ (no algebraic structure imposed on ${{{\mathcal {X}}}{\times }{{\mathcal {Y}}}}$ besides the fact that both ${{\mathcal {X}}}$ and ${{\mathcal {Y}}}$ are linear spaces). A bilinear map ${\phi \!:{{\mathcal {X}}}{\times }{{\mathcal {Y}}}\rightarrow {{\mathcal {Z}}}}$ is a function from the Cartesian product ${{{\mathcal {X}}}{\times }{{\mathcal {Y}}}}$ of linear spaces to a linear space ${{\mathcal {Z}}}$ whose sections are linear transformations. Precisely, let $\phi ^y\!=\phi (\cdot ,y)={\phi |_{{{\mathcal {X}}}{\times }\{y\}}\!:{{\mathcal {X}}}\!\rightarrow {{\mathcal {Z}}}}$ be the y-section of $\phi$ and let $\phi _x\!=\phi (x,\cdot )={\phi |_{\{x\}{\times }{{\mathcal {Y}}}}\!:{{\mathcal {Y}}}\rightarrow {{\mathcal {Z}}}}$ be the x-section of $\phi$. These functions $\phi ^y$ and $\phi _x$ are linear transformations: $\phi ^y={\phi (\cdot ,y)\in {{\mathcal {L}}}[{{\mathcal {X}}},{{\mathcal {Z}}}]}$ for each y in ${{\mathcal {Y}}}$ and $\phi _x={\phi (x,\cdot )\in {{\mathcal {L}}}[{{\mathcal {Y}}},{{\mathcal {Z}}}]}$ for each x in ${{\mathcal {X}}}$. Let ${{\mathcal {Z}}}^S\!$ denote the linear space over the same field ${{\mathbb {F}}}$ of all ${{\mathcal {Z}}}$-valued functions on a set S, and let

$$\begin{aligned} b[{{\mathcal {X}}}{\times }{{\mathcal {Y}}},{{\mathcal {Z}}}] =\big \{\phi \in {{\mathcal {Z}}}^{{{\mathcal {X}}}{\times }{{\mathcal {Y}}}}\!\!:\phi \;\hbox {is bilinear}\big \} \end{aligned}$$

stand for the collection of all ${{\mathcal {Z}}}$-valued bilinear maps on ${{{\mathcal {X}}}{\times }{{\mathcal {Y}}}}.$ The particular case of ${{\mathcal {Z}}}={{\mathbb {F}}}$ yields a bilinear functional ${\phi \!:{{\mathcal {X}}}{\times }{{\mathcal {Y}}}\rightarrow {{\mathbb {F}}}}$, also referred to as a bilinear form. Bilinearity of elements $\phi$ in $b[{{\mathcal {X}}}{\times }{{\mathcal {Y}}},{{\mathcal {Z}}}]$ ensures $b[{{\mathcal {X}}}{\times }{{\mathcal {Y}}},{{\mathcal {Z}}}]$ is a linear manifold of the linear space ${{\mathcal {Z}}}^{{{\mathcal {X}}}{\times }{{\mathcal {Y}}}}\!$, thus a linear space over ${{\mathbb {F}}}$ itself. Let $R(\phi )=\phi ({{\mathcal {X}}}{\times }{{\mathcal {Y}}})$ denote the range of ${\phi \in b[{{\mathcal {X}}}{\times }{{\mathcal {Y}}},{{\mathcal {Z}}}]}$, which in general is not a linear manifold of ${{\mathcal {Z}}}$.

As a composition of linear transformations is a linear transformation, a composition of a bilinear map with a linear transformation is a bilinear map. Also, a restriction of a bilinear map to a Cartesian product of linear manifolds is again a bilinear map (as a consequence of the definitions of linear manifold and of bilinear map).

Proposition 2.2

Let ${{{\mathcal {X}}},{{\mathcal {Y}}},{{\mathcal {Z}}}}$ be linear spaces over the same field ${{\mathbb {F}}}$, and let ${{\mathcal {M}}}$ and ${{\mathcal {N}}}$ be nonzero linear manifolds of ${{\mathcal {X}}}$ and ${{\mathcal {Y}}}.$ If ${\phi \!:{{\mathcal {M}}}{\times }{{\mathcal {N}}}\rightarrow {{\mathcal {Z}}}}$ is a bilinear map, then there exists a bilinear extension ${\widehat{\phi }\!:{{\mathcal {X}}}{\times }{{\mathcal {Y}}}\rightarrow {{\mathcal {Z}}}}$ of $\phi$ defined on the whole Cartesian product ${{{\mathcal {X}}}{\times }{{\mathcal {Y}}}}$ of the linear spaces ${{\mathcal {X}}}$ and ${{\mathcal {Y}}}$.

Sketch of Proof. Every linear transformation on a linear manifold of a linear space has a linear extension to the whole space, whose proof is an application of Zorn’s Lemma (see, e.g., [10, Theorem 2.9]). If a bilinear map is the product of two (algebra-valued) linear maps, then the proof is an application of the linear case. A proof for the general bilinear case follows an argument similar to the linear case. $\square$

Bilinear maps can also be extended by factoring them by the natural bilinear map through a tensor product space (see, e.g., [6, p. 101]). Indeed, Proposition 3.3 will say that ${b[{{\mathcal {X}}}{\times }{{\mathcal {Y}}},{{\mathcal {Z}}}]\cong {{\mathcal {L}}}[{{\mathcal {X}}}\otimes {{\mathcal {Y}}},{{\mathcal {Z}}}]}$, where ${{{\mathcal {X}}}\otimes {{\mathcal {Y}}}}$ stands for tensor product, and this ensures bilinear extension out of linear extension. It is, however, advisable to have the above extension result independently of the notion of tensor product.

3 Tensor Product of Linear Spaces: Axiomatic Theory

Definition 3.1

Let ${{\mathcal {X}}}$ and ${{\mathcal {Y}}}$ be nonzero linear spaces over the same field ${{\mathbb {F}}}.$ A tensor product of ${{\mathcal {X}}}$ and ${{\mathcal {Y}}}\,$ is a pair ${({{\mathcal {T}}},\theta )}$ consisting of a linear space ${{\mathcal {T}}}$ over ${{\mathbb {F}}}$ and a bilinear map ${\theta \!:{{\mathcal {X}}}{\times }{{\mathcal {Y}}}\rightarrow {{\mathcal {T}}}}$ fulfilling the following two axioms.

• (a) The bilinear map ${\theta \in b[{{\mathcal {X}}}{\times }{{\mathcal {Y}}},{{\mathcal {T}}}]}$ is such that its range $R(\theta )$ spans ${{\mathcal {T}}}$.

• (b) If ${\phi \in b[{{\mathcal {X}}}{\times }{{\mathcal {Y}}},{{\mathcal {Z}}}]}$ is an arbitrary bilinear map into a linear space ${{\mathcal {Z}}}$ over ${{\mathbb {F}}}$, then there is a linear transformation ${\varPhi \in {{\mathcal {L}}}[{{\mathcal {T}}},{{\mathcal {Z}}}]}$ for which

  $$\begin{aligned} \phi =\varPhi \circ \theta . \end{aligned}$$

That is, the diagram

commutes, and so $\theta$ factors every bilinear map through ${{\mathcal {T}}}.$ The linear space ${{\mathcal {T}}}$ is referred to as a tensor product space of ${{\mathcal {X}}}$ and ${{\mathcal {Y}}}$ associated with $\theta$, and $\theta$ is referred to as the natural bilinear map (or simply the natural map) associated with ${{\mathcal {T}}}$.

There are different interpretations of tensor products. For instance, the quotient space and the linear maps of bilinear maps formulations are examples of common procedures for building tensor products. These will be shown to be isomorphic, and will be exhibited in the next two sections. So the existence of tensor products will be postponed until then. Definition 3.1 is our starting point for providing these interpretations. A similar start has been considered, for instance, in [14, Section XVI.1] and [19, Chapter 14] for the quotient space formulation, in [24, Section 1.4] and [4, Chapter1] for both formulations, and in [7, Section 1.6] and [2, Section 2.2] for the linear maps of bilinear maps formulation aiming at tensor norms.

The value $\theta (x,y)$ of the natural bilinear map ${\theta \!:{{\mathcal {X}}}{\times }{{\mathcal {Y}}}\rightarrow {{\mathcal {T}}}={\mathrm{span\,}}\theta ({{\mathcal {X}}}{\times }{{\mathcal {Y}}})}$ associated with ${{\mathcal {T}}}$ at a pair (x, y) in ${{{\mathcal {X}}}{\times }{{\mathcal {Y}}}}$ is denoted by ${x\otimes y}$,

$$\begin{aligned} x\otimes y=\theta (x,y)\,\in \,{{\mathcal {T}}}\quad \;\hbox {for every}\;\quad (x,y)\in {{\mathcal {X}}}{\times }{{\mathcal {Y}}}, \end{aligned}$$

and ${x\otimes y}$ is called a single tensor (or a decomposable element, or a single tensor product of x and y) in the tensor product space ${{\mathcal {T}}}.$ Take ${(x,y)\in {{\mathcal {X}}}{\times }{{\mathcal {Y}}}}$ and ${\alpha \in {{\mathbb {F}}}}$ arbitrary. Since $\theta$ is bilinear, then ${\alpha (x\otimes y)}={(\alpha x)\otimes y} ={x\otimes (\alpha y)}$ for any ${\alpha \in {{\mathbb {F}}}}.$ So a multiple of a single tensor is again a single tensor, and the representation of a nonzero single tensor is not unique. Proofs for the next two propositions are straightforward form Definition 3.1 and thus omitted.

Proposition 3.1

An element of a tensor product space is represented as a finite sum of single tensors (and such a representation is not unique):

$$\begin{aligned} \digamma \in {{\mathcal {T}}}\quad \iff \quad \digamma =\mathop {\sum }_i x_i\otimes y_i \quad ({{a\, finite\, sum}}). \end{aligned}$$

Proposition 3.2

If ${{\mathcal {T}}}$ is a tensor product space, then the linear transformation ${\varPhi \in {{\mathcal {L}}}[{{\mathcal {T}}},{{\mathcal {Z}}}]}$ associated with each ${\phi \in b[{{\mathcal {X}}}{\times }{{\mathcal {Y}}},{{\mathcal {Z}}}]}$ as in Definition 3.1 is unique.

The natural bilinear map $\theta$ associated with a tensor product space ${{\mathcal {T}}}$ is unique and, conversely, ${{\mathcal {T}}}$ associated with $\theta$ is unique. This is shown in the next theorem and its corollary$.\!$ From now on, all linear spaces anywhere are over the same field ${{\mathbb {F}}}$.

Theorem 3.1

Let ${{\mathcal {X}}}$ and ${{\mathcal {Y}}}$ be linear spaces. Let ${({{\mathcal {T}}},\theta )}$ and ${({{\mathcal {T}}}',\theta ')}$ be tensor products of ${{\mathcal {X}}}$ and ${{\mathcal {Y}}}.$ Then there is a unique isomorphism ${\varTheta \in {{\mathcal {L}}}[{{\mathcal {T}}}',{{\mathcal {T}}}]}$ such that ${\varTheta \circ \theta '=\theta }.$ That is, such that the following diagram commutes:

Proof

Let ${({{\mathcal {T}}},\theta )}$ and ${({{\mathcal {T}}}'\!,\theta ')}$ be tensor products of ${{\mathcal {X}}}$ and ${{\mathcal {Y}}}.$ For any bilinear map ${\phi \!:{{\mathcal {X}}}{\times }{{\mathcal {Y}}}\rightarrow {{\mathcal {Z}}}}$ into a linear space ${{\mathcal {Z}}}$, there are linear transformations ${\varPhi \!:{{\mathcal {T}}}\!\rightarrow {{\mathcal {Z}}}}$ and ${\varPhi '\!:{{\mathcal {T}}}'\!\rightarrow {{\mathcal {Z}}}}$ such that ${\phi =\varPhi \circ \theta }={\varPhi '\!\circ \theta '}\!$ (Definition 3.1), which means the diagrams

commute. Since ${\theta '\!:{{\mathcal {X}}}{\times }{{\mathcal {Y}}}\rightarrow {{\mathcal {T}}}'}\!$ and ${\theta \!:{{\mathcal {X}}}{\times }{{\mathcal {Y}}}\rightarrow {{\mathcal {T}}}}$ are bilinear maps, then there are linear transformations ${\varTheta '\!:{{\mathcal {T}}}\!\rightarrow {{\mathcal {T}}}'}\!$ and ${\varTheta \!:{{\mathcal {T}}}'\!\rightarrow {{\mathcal {T}}}}\!$ such that ${\theta '\!=\varTheta '\!\circ \theta }$ and ${\theta =\varTheta \!\circ \theta '}\!$ (Definition 3.1 again), which means the diagrams

commute. Therefore,

$$\begin{aligned} \theta '\!=(\varTheta '\!\circ \varTheta )\circ \theta ' \quad \;\hbox {and}\;\quad \theta =(\varTheta \circ \varTheta ')\circ \theta . \end{aligned}$$

Let $I_S$ denote the identity function on an arbitrary set S. By the above equations,

$$\begin{aligned} \varTheta '\!\circ \varTheta |_{R(\theta ')}=I_{R(\theta ')}\!:R(\theta ')\rightarrow R(\theta ') \quad \;\hbox {and}\;\quad \varTheta \circ \varTheta '|_{R(\theta )}=I_{R(\theta )}\!:R(\theta )\rightarrow R(\theta ). \end{aligned}$$

Since $\varTheta$ and $\varTheta '$ are linear transformations (and so are their compositions), and since ${\mathrm{span\,}}R(\theta )={{\mathcal {T}}}$ and ${\mathrm{span\,}}R(\theta ')={{{\mathcal {T}}}'}$ by Definition 3.1, then we get

$$\begin{aligned} \varTheta '\!\circ \varTheta =\varTheta '\!\circ \varTheta |_{{\mathrm{span\,}}\!R(\theta ')} =I_{{\mathrm{span\,}}\!R(\theta ')}=I_{{{\mathcal {T}}}'}, \\ \varTheta \circ \varTheta '=\varTheta \circ \varTheta '|_{{\mathrm{span\,}}\!R(\theta )} =I_{{\mathrm{span\,}}\!R(\theta )}=I_{{\mathcal {T}}}. \end{aligned}$$

Hence, $\varTheta$ and $\varTheta '\!$ are the inverse of each other, and are unique by Proposition 3.2. $\square$

Corollary 3.1

A tensor product of linear spaces is unique up to an isomorphism in the following sense. If ${({{\mathcal {T}}},\theta )}$ and ${({{\mathcal {T}}}'\!,\theta ')}$ are tensor products of the same pair of linear spaces, then ${({{\mathcal {T}}},\theta )}={(\varTheta {{\mathcal {T}}}'\!,\varTheta \theta ')}$ for an isomorphism $\varTheta$ in ${{{\mathcal {L}}}[{{\mathcal {T}}}',{{\mathcal {T}}}]}.$ In particular, two tensor product spaces of the same pair of linear spaces coincide if and only if the natural bilinear maps coincide.

Proof

This is an immediate consequence of Theorem 3.1. $\square$

A tensor product for a given pair of linear spaces is unique up to an isomorphism by Corollary 3.1. Then for a given pair ${({{\mathcal {X}}},{{\mathcal {Y}}})}$ of linear space, it is common to write

$$\begin{aligned} {{\mathcal {T}}}={{\mathcal {X}}}\otimes {{\mathcal {Y}}}\end{aligned}$$

for the tensor product space, and ${({{\mathcal {X}}}\otimes {{\mathcal {Y}}},\theta )}$ for the tensor product, of ${{\mathcal {X}}}$ and ${{\mathcal {Y}}}$.

Proposition 3.3

Take an arbitrary triple ${({{\mathcal {X}}},{{\mathcal {Y}}},{{\mathcal {Z}}})}$ of linear spaces. The linear spaces $b[{{{\mathcal {X}}}{\times }{{\mathcal {Y}}},{{\mathcal {Z}}}}]$ and ${{\mathcal {L}}}[{{{\mathcal {T}}},{{\mathcal {Z}}}]}$ are isomorphic:

$$\begin{aligned} b[{{{\mathcal {X}}}{\times }{{\mathcal {Y}}},{{\mathcal {Z}}}}]\cong {{\mathcal {L}}}[{{{\mathcal {X}}}\otimes {{\mathcal {Y}}},{{\mathcal {Z}}}}]. \end{aligned}$$

Proof

Take any ${\varPhi \in {{\mathcal {L}}}[{{\mathcal {T}}},{{\mathcal {Z}}}]}.$ The composition ${\varPhi \circ \theta \!:{{\mathcal {X}}}{\times }{{\mathcal {Y}}}\rightarrow {{\mathcal {Z}}}}$ lies in $b[{{{\mathcal {X}}}{\times }{{\mathcal {Y}}},{{\mathcal {Z}}}}]$ since $\theta$ is bilinear and $\varPhi$ is linear. Let ${C_\theta \!:{{\mathcal {L}}}[{{\mathcal {T}}},{{\mathcal {Z}}}]\rightarrow b[{{\mathcal {X}}}{\times }{{\mathcal {Y}}},{{\mathcal {Z}}}]}$ be defined by

$$\begin{aligned} C_\theta (\varPhi )=\varPhi \circ \theta \,\in \,b[{{\mathcal {X}}}{\times }{{\mathcal {Y}}},{{\mathcal {Z}}}] \quad \;\hbox {for every}\,\quad \varPhi \in {{\mathcal {L}}}[{{\mathcal {T}}},{{\mathcal {Z}}}]. \end{aligned}$$

For every $\phi$ in $b[{{{\mathcal {X}}}{\times }{{\mathcal {Y}}},{{\mathcal {Z}}}}]$, there is one and only one $\varPhi$ in ${{\mathcal {L}}}[{{{\mathcal {T}}},{{\mathcal {Z}}}}]$ for which ${\phi =\varPhi \circ \theta }$ according to Proposition 3.2. Then $C_\theta$ is injective and surjective, and so invertible. Since it is readily verified that $C_\theta$ is linear, then $C_\theta$ is an isomorphism. $\square$

Thus, a crucial property of a tensor product ${({{\mathcal {T}}},\theta )}$ is to linearize bilinear maps (via factorization by $\theta$ through ${{\mathcal {T}}}$) in the sense of in Proposition 3.3. In particular,

$$\begin{aligned} ({{\mathcal {X}}}\otimes {{\mathcal {Y}}})^\sharp \cong b[{{\mathcal {X}}}{\times }{{\mathcal {Y}}},{{\mathbb {F}}}]. \end{aligned}$$

Theorem 3.2

Let ${{{\mathcal {T}}}={{\mathcal {X}}}\otimes {{\mathcal {Y}}}}$ be a tensor product space of ${{\mathcal {X}}}$ and ${{\mathcal {Y}}},$ let E and D be nonempty subsets of ${{\mathcal {X}}}$ and ${{\mathcal {Y}}}$, respectively, and set

$$\begin{aligned} \top _{\!E,D} =\big \{x\otimes y\in {{\mathcal {X}}}\otimes {{\mathcal {Y}}}\!:\,x\in E\;\hbox {and}\;\,y\in D\big \}. \end{aligned}$$

• (a) If ${\mathrm{span\,}}E={{\mathcal {X}}}$ and ${\mathrm{span\,}}D={{\mathcal {Y}}}$, then ${{\mathrm{span\,}}\!\top _{\!E,D}={{\mathcal {X}}}\otimes {{\mathcal {Y}}}}$.

• (b) If E and D are linearly independent, then $\top _{\!E,D}$ is linearly independent.

Therefore, if E is a Hamel basis for ${{\mathcal {X}}}$ and D is a Hamel basis for ${{\mathcal {Y}}}$, then $\top _{\!E,D}\!$ is a Hamel basis for ${{{\mathcal {T}}}={{\mathcal {X}}}\otimes {{\mathcal {Y}}}}$.

Proof

• (a) Take an arbitrary element $\digamma ={\sum }_{i=1}^nx_i\otimes y_i$ from ${{{\mathcal {X}}}\otimes {{\mathcal {Y}}}}.$ If ${{\mathrm{span\,}}E={{\mathcal {X}}}}$ and ${{\mathrm{span\,}}D={{\mathcal {Y}}}}$, then consider any expansion of each ${x_i\in {{\mathcal {X}}}}$ in terms of vectors $e_{i,j}$ from E and any expansion of each ${y_i\in {{\mathcal {Y}}}}$ in terms of vectors $d_{i,k}$ from D. Since ${x\otimes y=\theta (x,y)}$ for each pair ${(x,y)\in {{\mathcal {X}}}{\times }{{\mathcal {Y}}}}$, and since ${\theta \!:{{\mathcal {X}}}{\times }{{\mathcal {Y}}}\rightarrow {{\mathcal {X}}}\otimes {{\mathcal {Y}}}}$ is bilinear,

  $$\begin{aligned} \digamma =\mathop {\sum }_{i=1}^n \left( \mathop {\sum }_{j=1}^m\beta _j e_{i,j}\otimes \mathop {\sum }_{k=1}^\ell \gamma _k d_{i,k}\right) =\mathop {\sum }_{i,j,k}^{n,m,\ell }\beta _j\gamma _k(e_{i,j}\otimes d_{i,k}). \end{aligned}$$

  Thus, $\digamma$ lies in ${\mathrm{span\,}}\!\top _{\!E,D}.$ Then ${{{\mathcal {X}}}\otimes {{\mathcal {Y}}}\subseteq {\mathrm{span\,}}\!\top _{\!E,D}}.$ So ${{\mathrm{span\,}}\!\top _{\!E,D}={{\mathcal {X}}}\otimes {{\mathcal {Y}}}}$.

• (b) Let $E'\!=\{e_j\}_{j=1}^m$ and $D'\!=\{d_k\}_{k=1}^\ell$ be arbitrary nonempty finite linearly independent subsets of E and D, respectively, and consider the linear manifolds

  $$\begin{aligned} {{\mathcal {M}}}={\mathrm{span\,}}E'\!={\mathrm{span\,}}\{e_j\}_{j=1}^m\subseteq {{\mathcal {X}}}\quad \hbox {and}\quad {{\mathcal {N}}}={\mathrm{span\,}}D'\!={\mathrm{span\,}}\{d_k\}_{k=1}^\ell \subseteq {{\mathcal {Y}}}. \end{aligned}$$

  Set ${{\mathcal {Z}}}={{\mathcal {L}}}[{{\mathbb {F}}}^m\!,{{\mathbb {F}}}^\ell ]$, identified with the linear space of all ${\ell {\times }m}$ matrices of entries in ${{\mathbb {F}}}.$ Take ${\phi \!:{{\mathcal {M}}}{\times }{{\mathcal {N}}}\rightarrow {{\mathcal {Z}}}}$ given for ${u=\sum _{j=1}^m\beta _je_j\in {{\mathcal {M}}}}$ and ${v=\sum _{k=1}^\ell \gamma _kd_k\in {{\mathcal {N}}}}$ by

  $$\begin{aligned} \phi (u,v)=\big (\beta _j\gamma _k\big )\in {{\mathcal {Z}}}\quad \;\hbox {for}\;\quad j=1,\dots ,m \;\;\hbox {and}\;\; k=1,\dots ,\ell , \end{aligned}$$

  where $\big (\beta _j\gamma _k\big )$ is the ${\ell {\times }m}$ matrix whose entries are the products $\beta _j\gamma _k$ of the coefficients of the unique expansion of arbitrary vectors ${u\in {{\mathcal {M}}}}$ and ${v\in {{\mathcal {N}}}}$ in terms of the linearly independent sets $E'\!$ and $D'\!.$ It is readily verified that ${\phi \!:{{\mathcal {M}}}{\times }{{\mathcal {N}}}\!\rightarrow {{\mathcal {Z}}}}$ is a bilinear map. Thus, consider the linear transformation ${\varPhi \!:{{\mathcal {M}}}\otimes {{\mathcal {N}}}\!\rightarrow {{\mathcal {Z}}}}$ such that $\phi ={\varPhi \circ \theta }$ according to axiom (b) in Definition 3.1. So $\phi ({u,v})=\varPhi \,(\theta ({u,v}))=\varPhi ({u\otimes v})$ for every $u=\sum _{j=1}^m\beta _je_j$ in ${{\mathcal {M}}}$ and every $v=\sum _{k=1}^\ell \gamma _kd_k$ in ${{\mathcal {N}}}$. In particular,

  $$\begin{aligned} \varPhi (e_j\otimes d_k)=\phi (e_j,d_k)=\Pi _{j,k}, \end{aligned}$$

  where ${\Pi _{j,k}\in {{\mathcal {Z}}}}$ is the ${\ell {\times }m}$ matrix whose entry at position j, k is 1 and all other entries are 0. These matrices form a linearly independent set in ${{\mathcal {Z}}}.$ (In fact, $\{\Pi _{j,k}\}_{j,k=1}^{m,\ell }\!$ is the canonical Hamel basis for ${{\mathcal {Z}}}$.) Take any pair of integers ${k',j'}$ and suppose ${e_{j'}\otimes d_{k'}}$ is a linear combination of the remaining single tensors $\{{e_j\otimes d_k}\}_{j,k\in I'}$ with $I'=\{{j,k=1\;\hbox {to}\;\,m,\ell }\!:\,{j\ne j',k\ne k'}\}$, say

  $$\begin{aligned} e_{j'}\otimes d_{k'} ={\sum }_{j,k\in I'}\delta _{j,k}(e_j\otimes d_k). \end{aligned}$$

  Then, as ${\varPhi \!:{{\mathcal {M}}}\otimes {{\mathcal {N}}}\rightarrow {{\mathcal {Z}}}}$ is linear,

  $$\begin{aligned} \Pi _{j',k'}=\varPhi (e_{j'}\otimes d_{k'}) =\mathop {\sum }_{j,k\in I'}\delta _{j,k}\varPhi (e_j\otimes d_k) =\mathop {\sum }_{j,k\in I'}\delta _{j,k}\Pi _{j,k}, \end{aligned}$$

  and so ${\delta _{j,k}=0}$ for every ${j,k\in I'}$ since $\{\Pi _{j,k}\}_{j,k=1}^{m,\ell }\!$ is linearly independent in ${{\mathcal {Z}}}.$ Hence, $\{e_j\otimes d_k\}_{j,k=1}^{m,\ell }\!$ is linearly independent in $\top _{\!E,D}.$ In other words,

  $$\begin{aligned} \top _{\!E'\!,D'}\! =\{x\otimes y\in {{\mathcal {X}}}\otimes {{\mathcal {Y}}}\!:\,x\in E'\;\hbox {and}\;\,y\in D'\} \end{aligned}$$

  is a finite linearly independent subset of $\top _{\!E,D}$ whenever $E'$ and $D'$ are finite linearly independent subsets of E and D. Thus, if E and D are linearly independent subsets of ${{\mathcal {X}}}$ and ${{\mathcal {Y}}}$, then every finite subset of each of them is trivially linearly independent, and so is every finite subset of $\top _{\!E,D}$ as we saw above. But if every finite subset of $\top _{\!E,D}$ is linearly independent, then so is $\top _{\!E,D}$ (see, e.g., [10, Proposition 2.3]). $\square$

Corollary 3.2

$\dim ({{\mathcal {X}}}\otimes {{\mathcal {Y}}})=\dim {{\mathcal {X}}}\cdot \dim {{\mathcal {Y}}}$.

Proof

If E and D are Hamel basis for ${{\mathcal {X}}}$ and ${{\mathcal {Y}}}$, then $\top _{\!E,D}$ is a Hamel basis for ${{\mathcal {T}}}$ by Theorem 3.2. Also $\top _{\!E,D} ={\big \{x\otimes y\in {{\mathcal {X}}}\otimes {{\mathcal {Y}}}\!:\,x\in E\;\hbox {and}\;\,y\in D\big \}}$ is in a one-to-one correspondence with ${E{\times }D}$ as E and D are linearly independent. Since $\#({E{\times }D})=$ ${\#E\cdot \#D}$ by definition of product of cardinal numbers (see, e.g., [10, Problem 1.30]), then $\#\top _{\!E,D}={\#E\cdot \#D}.$ Thus follows the claimed dimension identity. $\square$

A straightforward consequence of the dimension identity of Corollary 3.2 is this. Tensor product is commutative up to an isomorphism:

$$\begin{aligned} {{\mathcal {X}}}\otimes {{\mathcal {Y}}}\cong {{\mathcal {Y}}}\otimes {{\mathcal {X}}}. \end{aligned}$$

Next we identify a special type of linear manifold of a tensor product space.

Proposition 3.4

Let ${{\mathcal {X}}}$ and ${{\mathcal {Y}}}$ be linear spaces. Suppose ${{\mathcal {M}}}$ and ${{\mathcal {N}}}$ are linear manifolds of ${{\mathcal {X}}}$ and ${{\mathcal {Y}}}$, respectively. Let ${({{\mathcal {X}}}\otimes {{\mathcal {Y}}},\theta )}$ be a tensor product. Set ${{{\mathcal {M}}}\otimes {{\mathcal {N}}}}=$ ${\mathrm{span\,}}R(\theta |_{{{\mathcal {M}}}{\times }{{\mathcal {N}}}}).$ Then ${{{\mathcal {M}}}\otimes {{\mathcal {N}}}}$ is a linear manifold of the tensor product space ${{{\mathcal {X}}}\otimes {{\mathcal {Y}}}}$ and ${({{\mathcal {M}}}\otimes {{\mathcal {N}}},\vartheta )}$ is a tensor product with ${\vartheta =\theta |_{{{\mathcal {M}}}{\times }{{\mathcal {N}}}}}$.

Proof

Consider Definition 3.1. Let ${({{\mathcal {X}}}\otimes {{\mathcal {Y}}},\theta )}$ be a tensor product. Take any bilinear map ${\phi \!:{{\mathcal {X}}}{\times }{{\mathcal {Y}}}\rightarrow {{\mathcal {Z}}}}.$ Let ${\varPhi \!:{{\mathcal {X}}}\otimes {{\mathcal {Y}}}\rightarrow {{\mathcal {Z}}}}$ be the linear transformation such that

$$\begin{aligned} \phi =\varPhi \circ \theta . \end{aligned}$$

Let ${{\mathcal {M}}}$ and ${{\mathcal {N}}}$ be linear manifolds of ${{\mathcal {X}}}$ and ${{\mathcal {Y}}}.$ Take the restriction $\theta |_{{{\mathcal {M}}}{\times }{{\mathcal {N}}}}$ of the natural bilinear map $\theta$ to the Cartesian product ${{{\mathcal {M}}}{\times }{{\mathcal {N}}}\subseteq {{\mathcal {X}}}{\times }{{\mathcal {Y}}}}$ so that

$$\begin{aligned} \theta |_{{{\mathcal {M}}}{\times }{{\mathcal {N}}}}\!:{{\mathcal {M}}}{\times }{{\mathcal {N}}}\rightarrow R(\theta |_{{{\mathcal {M}}}{\times }{{\mathcal {N}}}}) \subseteq {\mathrm{span\,}}R(\theta |_{{{\mathcal {M}}}{\times }{{\mathcal {N}}}})\subseteq {\mathrm{span\,}}R(\theta )={{\mathcal {X}}}\otimes {{\mathcal {Y}}}, \end{aligned}$$

which is a bilinear map. Now consider the restriction $\phi |_{{{\mathcal {M}}}{\times }{{\mathcal {N}}}}$ of the arbitrary bilinear map ${\phi \!:{{\mathcal {X}}}{\times }{{\mathcal {Y}}}\rightarrow {{\mathcal {Z}}}}$ to ${{{\mathcal {M}}}{\times }{{\mathcal {N}}}}$, which is again a bilinear map for which

$$\begin{aligned} \phi |_{{{\mathcal {M}}}{\times }{{\mathcal {N}}}} =(\varPhi \circ \theta )|_{{{\mathcal {M}}}{\times }{{\mathcal {N}}}} =\varPhi \circ \theta |_{{{\mathcal {M}}}{\times }{{\mathcal {N}}}} =\varPhi |_{{\mathrm{span\,}}\!R(\theta |_{{{\mathcal {M}}}{\times }{{\mathcal {N}}}})}\circ \theta |_{{{\mathcal {M}}}{\times }{{\mathcal {N}}}}, \end{aligned}$$

where ${\varPhi |_{{\mathrm{span\,}}\!R(\theta |_{{{\mathcal {M}}}{\times }{{\mathcal {N}}}})}}$ is the restriction of the linear transformation ${\varPhi \!:{{\mathcal {X}}}\otimes {{\mathcal {Y}}}\rightarrow {{\mathcal {Z}}}}$ to the linear manifold ${\mathrm{span\,}}R(\theta |_{{{\mathcal {M}}}{\times }{{\mathcal {N}}}})$, again a linear transformation. Proposition 2.2 says that every bilinear map ${\psi \!:{{\mathcal {M}}}{\times }{{\mathcal {N}}}\rightarrow {{\mathcal {Z}}}}$ is of the form ${\phi |_{{{\mathcal {M}}}{\times }{{\mathcal {N}}}}\!:{{\mathcal {M}}}{\times }{{\mathcal {N}}}\rightarrow {{\mathcal {Z}}}}$ for some bilinear map ${\phi \!:{{\mathcal {X}}}{\times }{{\mathcal {Y}}}\rightarrow {{\mathcal {Z}}}}.$ Thus, for every bilinear map ${\psi \!:{{\mathcal {M}}}{\times }{{\mathcal {N}}}\rightarrow {{\mathcal {Z}}}}$ there is a linear transformation ${\varPhi |_{{\mathrm{span\,}}\!R(\theta |_{{{\mathcal {M}}}{\times }{{\mathcal {N}}}})}\!:{\mathrm{span\,}}R(\theta |_{{{\mathcal {M}}}{\times }{{\mathcal {N}}}})\rightarrow {{\mathcal {Z}}}}$ such that

$$\begin{aligned} \phi =\varPhi |_{{\mathrm{span\,}}\!R(\theta |_{{{\mathcal {M}}}{\times }{{\mathcal {N}}}})}\circ \theta |_{{{\mathcal {M}}}{\times }{{\mathcal {N}}}}. \end{aligned}$$

Set ${{\mathcal {M}}}\otimes {{\mathcal {N}}}={\mathrm{span\,}}R(\theta |_{{{\mathcal {M}}}{\times }{{\mathcal {N}}}})\subseteq {{\mathcal {X}}}\otimes {{\mathcal {Y}}}$, a linear manifold of the linear space ${{{\mathcal {X}}}\otimes {{\mathcal {Y}}}}$, and $\vartheta =\theta |_{{{\mathcal {M}}}{\times }{{\mathcal {N}}}}$, the bilinear restriction of the bilinear $\theta .$ Thus, by Definition 3.1

$$\begin{aligned} {({{\mathcal {M}}}\otimes {{\mathcal {N}}},\vartheta )} \hbox {is a tensor product}. \end{aligned}$$

Therefore, ${{{\mathcal {M}}}\otimes {{\mathcal {N}}}}$ stands for the tensor product space of linear manifolds ${{\mathcal {M}}}$ and ${{\mathcal {N}}}$ of the linear spaces ${{\mathcal {X}}}$ and ${{\mathcal {Y}}}$ according to Corollary 3.1 and Proposition 3.4.

Definition 3.2

A linear manifold $\Upsilon \!$ of a tensor product space ${{{\mathcal {T}}}={{\mathcal {X}}}\otimes {{\mathcal {Y}}}}$ is regular if ${\Upsilon \!={{\mathcal {M}}}\otimes {{\mathcal {N}}}}$ for some linear manifolds ${{\mathcal {M}}}$ and ${{\mathcal {N}}}$ of the linear spaces ${{\mathcal {X}}}$ and ${{\mathcal {Y}}}.$ Otherwise $\Upsilon$ is called irregular.

The next characterization of regular linear manifolds is straightforward from Theorem 3.2. For a collection of properties of regular linear manifolds, see [9, 11].

Proposition 3.5

A nonzero linear manifold $\Upsilon$ of ${{{\mathcal {X}}}\otimes {{\mathcal {Y}}}}$ is regular if and only if

$$\begin{aligned} \Upsilon ={\mathrm{span\,}}\!\top _{\!E'\!,D'} \end{aligned}$$

for some nonempty subsets ${E'\subseteq E}$ and ${D'\subseteq D}$ for Hamel bases E and D for ${{\mathcal {X}}}$ and ${{\mathcal {Y}}}$ , respectively.

The concept of tensor product of linear transformations is given as follows.

Definition 3.3

Let ${{{\mathcal {X}}},{{\mathcal {Y}}},{{\mathcal {V}}},{{\mathcal {W}}}}$ be linear spaces and consider the tensor product spaces ${{{\mathcal {X}}}\otimes {{\mathcal {Y}}}}$ and ${{{\mathcal {V}}}\otimes {{\mathcal {W}}}}.$ Let ${A\in {{\mathcal {L}}}[{{\mathcal {X}}},{{\mathcal {V}}}]}$ and ${B\in {{\mathcal {L}}}[{{\mathcal {Y}}},{{\mathcal {W}}}]}$ be linear transformations. For each ${\sum _{i=1}^nx_i\otimes y_i}$ in ${{{\mathcal {X}}}\otimes {{\mathcal {Y}}}}$, set

$$\begin{aligned} (A\otimes B)\mathop {\sum }_{i=1}^nx_i\otimes y_i =\mathop {\sum }_{i=1}^nAx_i\otimes By_i \,\;\hbox {in}\;\; {{\mathcal {V}}}\otimes {{\mathcal {W}}}. \end{aligned}$$

This defines a map ${A\otimes B}$ of the linear space ${{{\mathcal {X}}}\otimes {{\mathcal {Y}}}}$ into the linear space ${{{\mathcal {V}}}\otimes {{\mathcal {W}}}}$, which is referred to as the tensor product of the transformations A and B, or the tensor product transformation ${A\otimes B}$.

Proposition 3.6

Take ${A\in {{\mathcal {L}}}[{{\mathcal {X}}},{{\mathcal {V}}}]}$ and ${B\in {{\mathcal {L}}}[{{\mathcal {Y}}},{{\mathcal {W}}}]}$.

• (a) In fact, ${A\otimes B}$ in Definition 3.3 defines a linear transformation,

  $$\begin{aligned} A\otimes B\in {{\mathcal {L}}}[{{\mathcal {X}}}\otimes {{\mathcal {Y}}},{{\mathcal {V}}}\otimes {{\mathcal {W}}}], \end{aligned}$$

  and $(A\otimes B)\digamma$ does not depend on the representation ${{\sum }_{i=1}^nx_i\!\otimes \!y_i}$ of ${\digamma \!\in {{\mathcal {X}}}\otimes {{\mathcal {Y}}}}$.

• (b) The map $\theta \!:{{\mathcal {L}}}[{{\mathcal {X}}},{{\mathcal {V}}}]{\times }{{\mathcal {L}}}[{{\mathcal {Y}}},{{\mathcal {W}}}]\rightarrow {{\mathcal {L}}}[{{\mathcal {X}}}\otimes {{\mathcal {Y}}},{{\mathcal {V}}}\otimes {{\mathcal {W}}}]$ defined by

  $$\begin{aligned} \theta (A,B)=A\otimes B \quad \;\hbox {for every}\;\quad (A,B)\in {{\mathcal {L}}}[{{\mathcal {X}}},{{\mathcal {V}}}]{\times }{{\mathcal {L}}}[{{\mathcal {Y}}},{{\mathcal {W}}}], \end{aligned}$$

  with $A\otimes B\in {{\mathcal {L}}}[{{\mathcal {X}}}\otimes {{\mathcal {Y}}},{{\mathcal {V}}}\otimes {{\mathcal {W}}}]$ as in $(\hbox {a})$, is bilinear.

• (c) Set

  $$\begin{aligned} {{\mathcal {L}}}[{{\mathcal {X}}},{{\mathcal {V}}}]\otimes {{\mathcal {L}}}[{{\mathcal {Y}}},{{\mathcal {W}}}] \,=\,{\mathrm{span\,}}R(\theta )\,\subseteq \,{{\mathcal {L}}}[{{\mathcal {X}}}\otimes {{\mathcal {Y}}},{{\mathcal {V}}}\otimes {{\mathcal {W}}}]. \end{aligned}$$

  Then ${({{\mathcal {L}}}[{{\mathcal {X}}},{{\mathcal {V}}}]\otimes {{\mathcal {L}}}[{{\mathcal {Y}}},{{\mathcal {W}}}],\theta )}$ is a tensor product of ${{{\mathcal {L}}}[{{\mathcal {X}}},{{\mathcal {V}}}]}$ and ${{{\mathcal {L}}}[{{\mathcal {Y}}},{{\mathcal {W}}}]}$.

• (d) The transformation ${A\otimes B\in {{\mathcal {L}}}[{{\mathcal {X}}}\otimes {{\mathcal {Y}}},{{\mathcal {V}}}\otimes {{\mathcal {W}}}]}$ in $(\mathrm{a})$ coincides with a single tensor in the tensor product space ${{{\mathcal {L}}}[{{\mathcal {X}}},{{\mathcal {V}}}]\otimes {{\mathcal {L}}}[{{\mathcal {Y}}},{{\mathcal {W}}}]}\!:$

  $$\begin{aligned} A\otimes B\,\in \,{{\mathcal {L}}}[{{\mathcal {X}}},{{\mathcal {V}}}]\otimes {{\mathcal {L}}}[{{\mathcal {Y}}},{{\mathcal {W}}}] \,\subseteq \,{{\mathcal {L}}}[{{\mathcal {X}}}\otimes {{\mathcal {Y}}},{{\mathcal {V}}}\otimes {{\mathcal {W}}}]. \end{aligned}$$

Proof

Items (a), (b), (d) are readily verified. Item (c) goes as follows. Note that

$$\begin{aligned} {\mathrm{span\,}}R(\theta )= & {} {\mathrm{span\,}}\big \{A\otimes B\in {{\mathcal {L}}}[{{\mathcal {X}}}\otimes {{\mathcal {Y}}},{{\mathcal {V}}}\otimes {{\mathcal {W}}}] \!:A\in {{\mathcal {L}}}[{{\mathcal {X}}},{{\mathcal {V}}}]\;\,B\in {{\mathcal {L}}}[{{\mathcal {Y}}},{{\mathcal {W}}}]\big \} \\= & {} \!\left\{ \mathop {\sum }_{i=1}^n A_i\!\otimes B_i\!\in \!{{\mathcal {L}}}[{{\mathcal {X}}}\otimes {{\mathcal {Y}}},{{\mathcal {V}}}\otimes {{\mathcal {W}}}] \!:A\!\in \!{{\mathcal {L}}}[{{\mathcal {X}}},{{\mathcal {V}}}],\,B\!\in \!{{\mathcal {L}}}[{{\mathcal {Y}}},{{\mathcal {W}}}],\,n\!\in \!{{\mathbb {N}}}]\right\} . \end{aligned}$$

For each bilinear map ${\phi \!:{{\mathcal {L}}}[{{\mathcal {X}}},{{\mathcal {V}}}]{\times }{{\mathcal {L}}}[{{\mathcal {Y}}},{{\mathcal {W}}}]\rightarrow {{\mathcal {Z}}}}$, take ${\varPhi \!:{\mathrm{span\,}}R(\theta )\rightarrow {{\mathcal {Z}}}}$ defined by

$$\begin{aligned} \varPhi \left( \mathop {\sum }_{i=1}^n\!A_i\otimes B_i\right) =\mathop {\sum }_{i=1}^n \phi (A_i,B_i)\,\in \,{{\mathcal {Z}}}\quad \hbox {for every}\quad \mathop {\sum }_{i=1}^n\!A_i\otimes B_i\in {\mathrm{span\,}}R(\theta ). \end{aligned}$$

Since $\phi$ is bilinear, it is easy to show that $\varPhi$ is linear: ${\varPhi \in {{\mathcal {L}}}[{\mathrm{span\,}}R(\theta ),{{\mathcal {Z}}}]}.$ Moreover, for every ${(A,B)\in {{\mathcal {L}}}[{{\mathcal {X}}},{{\mathcal {V}}}]{\times }{{\mathcal {L}}}[{{\mathcal {Y}}},{{\mathcal {W}}}]}$

$$\begin{aligned} (\varPhi \circ \theta )(A,B)=\varPhi \big (\theta (A,B)\big )=\varPhi (A\otimes B)=\phi (A,B). \end{aligned}$$

Thus, $\phi =\varPhi \circ \theta$, equivalently, the diagram

commutes. Therefore, $({\mathrm{span\,}}R(\theta ),\theta )$ satisfies the axioms of Definition 3.1. $\square$

The particular case of ${{{\mathcal {V}}}={{\mathcal {W}}}={{\mathbb {F}}}}$ is worth noticing. In this case,

$$\begin{aligned} {{\mathcal {L}}}[{{\mathcal {X}}},{{\mathcal {V}}}]= & {} {{\mathcal {L}}}[{{\mathcal {X}}},{{\mathbb {F}}}]={{\mathcal {X}}}^\sharp , \quad {{\mathcal {L}}}[{{\mathcal {Y}}},{{\mathcal {W}}}]={{\mathcal {L}}}[{{\mathcal {Y}}},{{\mathbb {F}}}]={{\mathcal {Y}}}^\sharp \quad \hbox {and} \\ {{\mathcal {L}}}[{{\mathcal {X}}}\otimes {{\mathcal {Y}}},{{\mathcal {V}}}\otimes {{\mathcal {W}}}]= & {} {{\mathcal {L}}}[{{\mathcal {X}}}\otimes {{\mathcal {Y}}},{{\mathbb {F}}}\otimes {{\mathbb {F}}}] ={{\mathcal {L}}}[{{\mathcal {X}}}\otimes {{\mathcal {Y}}},{{\mathbb {F}}}]=({{\mathcal {X}}}\otimes {{\mathcal {Y}}})^\sharp . \end{aligned}$$

Indeed, $\dim ({{{\mathbb {F}}}\otimes {{\mathbb {F}}}})=\dim {{\mathbb {F}}}=1$ by Corollary 3.2. So write ${{{\mathbb {F}}}\otimes {{\mathbb {F}}}}={{\mathbb {F}}}$ for ${{{\mathbb {F}}}\otimes {{\mathbb {F}}}}\cong {{\mathbb {F}}}$ as usual. Since ${{{\mathcal {L}}}[{{\mathcal {X}}},{{\mathcal {V}}}]\otimes {{\mathcal {L}}}[{{\mathcal {Y}}},{{\mathcal {W}}}]\subseteq {{\mathcal {L}}}[{{\mathcal {X}}}\otimes {{\mathcal {Y}}},{{\mathcal {V}}}\otimes {{\mathcal {W}}}]}$ by Proposition 3.6(c), then

$$\begin{aligned} {{\mathcal {X}}}^\sharp \otimes {{\mathcal {Y}}}^\sharp \subseteq ({{\mathcal {X}}}\otimes {{\mathcal {Y}}})^\sharp . \end{aligned}$$

Basic results on tensor product transformations are given next. Most are straightforward or readily verified: Properties (a,b) are trivial since ${A\otimes B}$ is a single tensor, (c,d) are straightforward by definition of ${A\otimes B}$, and (e,f) are readily verified for the regular linear manifolds ${{{\mathcal {N}}}(A)\otimes {{\mathcal {N}}}(B)}$ and ${{{\mathcal {R}}}(A)\otimes {{\mathcal {R}}}(B)}.$ For the nonreversible inclusion in (f), see, e.g., [13]. Item (g) says :  tensor product of linear transformations is commutative up to isomorphisms, which means ${A\otimes B}$ and ${B\otimes A}$ are isomorphically equivalent in the sense that ${\Pi _2(A\otimes B)=(B\otimes A)\Pi _1}$ for isomorphisms ${\Pi _1\!:{{\mathcal {X}}}\otimes {{\mathcal {Y}}}\rightarrow {{\mathcal {Y}}}\otimes {{\mathcal {X}}}}$ and ${\Pi _2\!:{{\mathcal {V}}}\otimes {{\mathcal {W}}}\rightarrow {{\mathcal {W}}}\otimes {{\mathcal {V}}}}$ (whose existence follows from the fact that ${{{\mathcal {X}}}\otimes {{\mathcal {Y}}}}\cong {{{\mathcal {Y}}}\otimes {{\mathcal {X}}}}$ as a consequence of Corollary 3.2). We prove (h) below.

Proposition 3.7

Let ${{{\mathcal {V}}},{{\mathcal {W}}},{{\mathcal {X}}},{{\mathcal {Y}}},{{\mathcal {X}}}',{{\mathcal {Y}}}'}$ be linear spaces. Take ${A,A_1,A_2\in {{\mathcal {L}}}[{{\mathcal {X}}},{{\mathcal {V}}}]}$ $\,{B,B_1,B_2\!\in {{\mathcal {L}}}[{{\mathcal {Y}}},{{\mathcal {W}}}]}$, $\,{C\in {{\mathcal {L}}}[{{\mathcal {X}}}',{{\mathcal {X}}}]}$, $\,{D\in {{\mathcal {L}}}[{{\mathcal {Y}}}',{{\mathcal {Y}}}]}$ and also ${\alpha ,\beta \in {{\mathbb {F}}}}.$ Then

• (a) $\;{\alpha \,\beta \,(A\otimes B)} ={\alpha A\otimes \beta B} ={\alpha \,\beta A\otimes B} ={A\otimes \alpha \,\beta B}$,

• (b) $\;{(A_1+A_2)\otimes (B_1+B_2)} ={A_1\otimes B_1}+{A_2\otimes B_1} +{A_1\otimes B_2}+{A_2\otimes B_2}$,

• (c) $\;{AC\otimes BD}={(A\otimes B)\,(C\otimes D)}$,

• (d)  If A and B are invertible, then so is ${A\otimes B}$ and ${(A\otimes B)^{-1}} ={A^{-1}\otimes B^{-1}}$,

• (e) $\;{{{\mathcal {R}}}(A)\otimes {{\mathcal {R}}}(B)={{\mathcal {R}}}(A\otimes B)}$,

• (f) $\;{{{\mathcal {N}}}(A)\otimes {{\mathcal {N}}}(B)\subsetneqq {{\mathcal {N}}}(A\otimes B)}$,

• (g) $\;{A\otimes B\cong B\otimes A}$.

• (h) $\;{(A\otimes B)^\sharp }={A^\sharp \otimes B^\sharp \!}$.

Proof

(h) Take ${A\in {{\mathcal {L}}}[{{\mathcal {X}}},{{\mathcal {V}}}]}$, ${B\in {{\mathcal {L}}}[{{\mathcal {Y}}},{{\mathcal {W}}}]}$, ${A^\sharp \in {{\mathcal {L}}}[{{\mathcal {V}}}^\sharp ,{{\mathcal {X}}}^\sharp ]}$, ${B^\sharp \in {{\mathcal {L}}}[{{\mathcal {W}}}^\sharp ,{{\mathcal {Y}}}^\sharp ]}.$ Consider the single tensors ${A\otimes B}$ in ${{{\mathcal {L}}}[{{\mathcal {X}}},{{\mathcal {V}}}]\otimes {{\mathcal {L}}}[{{\mathcal {Y}}},{{\mathcal {W}}}]}\subseteq {{{\mathcal {L}}}[{{\mathcal {X}}}\otimes {{\mathcal {Y}}},{{\mathcal {V}}}\otimes {{\mathcal {W}}}]}$ and ${A^\sharp \otimes B^\sharp }$ in ${{{\mathcal {L}}}[{{\mathcal {V}}}^\sharp ,{{\mathcal {X}}}^\sharp ]\otimes {{\mathcal {L}}}[{{\mathcal {W}}}^\sharp ,{{\mathcal {Y}}}^\sharp ]} \subseteq {{{\mathcal {L}}}[{{\mathcal {V}}}^\sharp \otimes {{\mathcal {W}}}^\sharp ,{{\mathcal {X}}}^\sharp \otimes {{\mathcal {Y}}}^\sharp ]}$, and the algebraic adjoint ${(A\otimes B)^\sharp }$ in ${{{\mathcal {L}}}[({{\mathcal {Y}}}\otimes {{\mathcal {W}}})^\sharp ,({{\mathcal {X}}}\otimes {{\mathcal {V}}})^\sharp ]}.$ Take an arbitrary ${f\otimes g\in {{\mathcal {V}}}^\sharp \otimes {{\mathcal {W}}}^\sharp }\subseteq ({{\mathcal {V}}}\otimes {{\mathcal {Y}}})^\sharp .$ By definition of tensor product transformation and of algebraic adjoint

$$\begin{aligned} (A^\sharp \otimes B^\sharp )(f\otimes g) =A^\sharp f\otimes B^\sharp g =fA\otimes gB \;\in \;{{\mathcal {X}}}^\sharp \otimes {{\mathcal {Y}}}^\sharp \subseteq ({{\mathcal {X}}}\otimes {{\mathcal {Y}}})^\sharp , \end{aligned}$$

(*)

$$\begin{aligned} (A\otimes B)^\sharp (f\otimes g)=(f\otimes g)(A\otimes B) \;\in \; ({{\mathcal {X}}}\otimes {{\mathcal {Y}}})^\sharp . \end{aligned}$$

(**)

Claim.       $(f\otimes g)(A\otimes B) =fA\otimes gB \;\in \;{{\mathcal {X}}}^\sharp \otimes {{\mathcal {Y}}}^\sharp \subseteq ({{\mathcal {X}}}\otimes {{\mathcal {Y}}})^\sharp .$

Proof

Take an arbitrary single tensor ${x\otimes y}$ in ${{{\mathcal {X}}}\otimes {{\mathcal {Y}}}}$, and an arbitrary single tensor ${A\otimes B}$ in ${{{\mathcal {L}}}[{{\mathcal {X}}},{{\mathcal {V}}}]\otimes {{\mathcal {L}}}[{{\mathcal {Y}}},{{\mathcal {W}}}]}.$ By definition of tensor product transformation, ${(A\otimes B)(x\otimes y)}={Ax\otimes By}$, a single tensor in ${{{\mathcal {V}}}\otimes {{\mathcal {W}}}}.$ Next take an arbitrary single tensor ${f\otimes g}$ in ${{{\mathcal {V}}}^\sharp \otimes {{\mathcal {W}}}^\sharp }={{{\mathcal {L}}}[{{\mathcal {V}}},{{\mathbb {F}}}]\otimes {{\mathcal {L}}}[{{\mathcal {W}}},{{\mathbb {F}}}]}$ so that, by definition of tensor product transformation, ${(f\otimes g)(Ax\otimes By)}={fAx\otimes gBy\in {{\mathbb {F}}}\otimes {{\mathbb {F}}}={{\mathbb {F}}}}.$ On the other hand, since ${fA\in {{\mathcal {X}}}^\sharp }={{\mathcal {L}}}[{{{\mathcal {X}}},{{\mathbb {F}}}}]$ and ${gB\in {{\mathcal {Y}}}^\sharp }={{\mathcal {L}}}[{{{\mathcal {Y}}},{{\mathbb {F}}}}]$, then (definition of tensor product transformation), ${(fA\otimes gB)(x\otimes y)}={fAx\otimes gBy\in {{\mathbb {F}}}\otimes {{\mathbb {F}}}={{\mathbb {F}}}}$. Summing up:

$$\begin{aligned} (f\otimes g)(A\otimes B)(x\otimes y) =(f\otimes g)(Ax\otimes By) =fAx\otimes gBy =(fA\otimes gB)(x\otimes y) \end{aligned}$$

for every ${x\otimes y\in {{\mathcal {X}}}\otimes {{\mathcal {Y}}}}.$ Thus, $({f\otimes g})({A\otimes B})\digamma =({f\otimes g})({A\otimes B})\sum _i{x_i\otimes y_i} =\sum _i({f\otimes g})({A\otimes B})({x_i\otimes y_i}) =\sum _i({fA\otimes gB})({x_i\otimes y_i}) =({fA\otimes gB})\sum _i{x_i\otimes y_i} =({fA\otimes gB})\digamma$ for every ${\digamma \in {{\mathcal {X}}}\otimes {{\mathcal {Y}}}}$, and hence,

$$\begin{aligned} (f\otimes g)(A\otimes B)={fA\otimes gB} \end{aligned}$$

in ${{{\mathcal {X}}}^\sharp \otimes {{\mathcal {Y}}}^\sharp }={{{\mathcal {L}}}[{{{\mathcal {X}}},{{\mathbb {F}}}]\otimes {{\mathcal {L}}}[{{\mathcal {Y}}},{{\mathbb {F}}}}]} \subseteq {{\mathcal {L}}}[{{{\mathcal {X}}}\otimes {{\mathcal {Y}}},{{\mathbb {F}}}}]=({{{\mathcal {X}}}\otimes {{\mathcal {Y}}})^\sharp }$. $\square$

Then by $(*)$, $(**)$ and the above claim

$$\begin{aligned} (A^\sharp \otimes B^\sharp )(f\otimes g)=(A\otimes B)^\sharp (f\otimes g) \end{aligned}$$

for every single tensor ${f\otimes g\in {{\mathcal {X}}}^\sharp \otimes {{\mathcal {Y}}}^\sharp }.$ Thus, by a similar argument

$$\begin{aligned} A^\sharp \otimes B^\sharp =(A\otimes B)^\sharp \end{aligned}$$

in ${{\mathcal {L}}}[{{{\mathcal {X}}}^\sharp \otimes {{\mathcal {Y}}}^\sharp ,{{\mathbb {F}}}}]=({{{\mathcal {X}}}^\sharp \otimes {{\mathcal {Y}}}^\sharp })^\sharp$, concluding the proof of (g). $\square$

4 An Interpretation via Quotient Space

Let ${{\mathcal {X}}}$ and ${{\mathcal {Y}}}$ be nonzero linear spaces over a field ${{\mathbb {F}}}.$ Take the Cartesian product $S={{{\mathcal {X}}}{\times }{{\mathcal {Y}}}}$ of ${{\mathcal {X}}}$ and ${{\mathcal {Y}}}.$ Consider the notation and terminology of Sect. 2.1. Thus, is the free linear space generated by S (i.e., the linear space of all functions ${f\!:{{\mathcal {X}}}{\times }{{\mathcal {Y}}}\rightarrow {{\mathbb {F}}}}$ that vanish everywhere on the complement of some finite subset of ${{{\mathcal {X}}}{\times }{{\mathcal {Y}}}}$), and ${{\mathbb {S}}}= {\{e_{(x,y)}\}_{(x,y)\in S}}$ is the Hamel basis for consisting of characteristic functions $e_{(x,y)}={^{_{\textstyle \chi }}}_{\{(x,y)\}}={{^{_{\textstyle \chi }}}_{\{x\}}{^{_{\textstyle \chi }}}_{\{y\}}\!:{{{\mathcal {X}}}{\times }{{\mathcal {Y}}}}\rightarrow {{\mathbb {F}}}}$ of all singletons at each pair of vectors (x, y) in the Cartesian product $S={{{\mathcal {X}}}{\times }{{\mathcal {Y}}}}.$ With the identification $\approx$ of Sect. 2.1 still in force, take the sums of elements from ${{\mathbb {S}}}$ whose double indices have one common entry and consider the following differences.

• (i)    $e_{(x_1+x_2,y)}-e_{(x_1,y)}-e_{(x_2,y)} \,\approx \, (x_1\!+x_2\,,y)-(x_1\,,y)-(x_2\,,y)$,

• (ii)    $e_{(x,y_1+x_2)}-e_{(x,y_1)}-e_{(x,y_2)} \,\approx \, (x\,,y_1\!+y_2)-(x\,,y_1)-(x\,,y_2)$,

• (iii)    $e_{(\alpha x,y)}-\alpha \,e_{(x,y)} \,\approx \, (\alpha x,y)-\alpha (x,y)$,

• (iv)    $e_{(x,\alpha y)}-\alpha \,e_{(x,y)} \,\approx \, (x,\alpha y)-\alpha (x,y)$,

for every ${x,x_1,x_2\in {{\mathcal {X}}}}$, every ${y,y_1,y_2\in {{\mathcal {Y}}}}$, and every ${\alpha \in {{\mathbb {F}}}}.$ The above differences are not null. If they were, then we could identify a bilinear rule on the ordered pairs ${(x,y)\in {{\mathcal {X}}}{\times }{{\mathcal {Y}}}}.$ Thus, look at equivalence classes $[e_{(x,y)}]$ of characteristic functions $e_{(x,y)}\!$ in , gathering those differences at the origin of a quotient space as follows. Take the linear manifold ${{\mathcal {M}}}\!$ of generated by the differences in (i)–(iv), viz.

$$\begin{aligned}&{{\mathcal {M}}}={\mathrm{span\,}}\big \{ e_{(x_1+x_2,y)}-e_{(x_1,y)}-e_{(x_2,y)}\,, \quad e_{(x,y_1+x_2)}-e_{(x,y_1)}-e_{(x,y_2)}\,, \\&\quad e_{(\alpha x,y)}-\alpha \,e_{(x,y)}\,, \quad e_{(x,\alpha y)}-\alpha \,e_{(x,y)}\,\big \}. \end{aligned}$$

Take the quotient space of modulo ${{\mathcal {M}}}$, consider the natural quotient map

and define a map

on ${S={{\mathcal {X}}}{\times }{{\mathcal {Y}}}}$ as follows. For every ${(x,y)\in {{\mathcal {X}}}{\times }{{\mathcal {Y}}}}$, set $\theta (x,y)=\pi (e_{(x,y)}).$ Therefore,

$$\begin{aligned} \theta (S)=\pi ({{\mathbb {S}}}). \end{aligned}$$

The Hamel basis ${{{\mathbb {S}}}=\,}\{e_{(x,y)}\}_{(x,y)\in S}$ for the linear space generated by S is naturally identified with S itself, and so the domain of $\theta$ is identified with the domain of the restriction $\pi |_{{{\mathbb {S}}}}$ of the natural quotient map $\pi$ to ${{\mathbb {S}}}$, that is, ${S\approx {{\mathbb {S}}}}.$ Since they also coincide pointwise, then $\theta$ is naturally identified with $\pi |_{{{\mathbb {S}}}}.$ So write

$$\begin{aligned} \theta =\pi |_{{{\mathbb {S}}}} \quad \;\hbox {for}\;\quad \theta \approx \pi |_{{{\mathbb {S}}}}. \end{aligned}$$

Elements of which are images of the map are denoted by ${x\otimes y}$, and again referred to as single tensors or decomposable elements:

$$\begin{aligned} x\otimes y=\theta (x,y)=\pi (e_{(x,y)})=[e_{(x,y)}] \quad \;\hbox {for every}\;\quad (x,y)\in {{\mathcal {X}}}{\times }{{\mathcal {Y}}}. \end{aligned}$$

Theorem 4.1

    is a tensor product of ${{\mathcal {X}}}$ and ${{\mathcal {Y}}}$.

Proof

Consider the axioms (a) and (b) in Definition 3.1.

(a$_1$) By definition of ${{\mathcal {M}}}$, the differences in (i) to (iv) lie in Thus, with $\theta (x,y)=\pi (e_{(x,y)})=[e_{(x,y)}]$ it follows that is a bilinear map.

(a$_2$) Since ${{\mathbb {S}}}=$ $\{e_{(x,y)}\}_{(x,y)\in {{\mathcal {X}}}{\times }{{\mathcal {Y}}}}$ is a Hamel basis for the linear space , then (cf. Remark 2.1). Thus, as $R(\theta )=R(\pi |_{{{\mathbb {S}}}})$,

(b) Take a bilinear map ${\phi \!:{{\mathcal {X}}}{\times }{{\mathcal {Y}}}\rightarrow {{\mathcal {Z}}}}$ into a linear space ${{\mathcal {Z}}}$ and consider a transformation $\widetilde{\Phi }$ on the free linear space generated by the Cartesian product ${{{\mathcal {X}}}{\times }{{\mathcal {Y}}}}$,

defined by

which is clearly linear. Moreover, since ${\widetilde{\Phi }(e_{(x_i,y_i)})=\phi (x,y)}$, then

$$\begin{aligned} \widetilde{\Phi }({{\mathbb {S}}})=\phi (S). \end{aligned}$$

Again, since ${{{\mathbb {S}}}\approx S={{\mathcal {X}}}{\times }{{\mathcal {Y}}}}$, then $\widetilde{\Phi }|_{{{\mathbb {S}}}}$ is naturally identified with $\phi .$ So write

$$\begin{aligned} \widetilde{\Phi }|_{{{\mathbb {S}}}}=\phi . \end{aligned}$$

Furthermore, since ${\phi \!:{{\mathcal {X}}}{\times }{{\mathcal {Y}}}\rightarrow {{\mathcal {Z}}}}$ is bilinear, then $\widetilde{\Phi }$ evaluated at the differences in (i) to (iv) is null. Hence, the linear manifold ${{\mathcal {M}}}$ of is such that ${\widetilde{\Phi }({{\mathcal {M}}})=0}.$ That is, ${{{\mathcal {M}}}\subseteq {{\mathcal {N}}}(\widetilde{\Phi })}.$ Thus, by Proposition 2.1 there exists a unique linear transformation

such that ${\widetilde{\Phi }=\varPhi \circ \pi }.$ Therefore, restricting to and since , we get $\phi =\widetilde{\Phi }|_{{{\mathbb {S}}}}=(\varPhi \circ \pi )|_{{{\mathbb {S}}}} =\varPhi |_{{\mathrm{span\,}}\!{{\mathcal {R}}}(\pi )}\circ \pi |_{{{\mathbb {S}}}}=\varPhi \circ \theta .$ Equivalently, the diagrams

commute. Identifying again ${S\approx {{\mathbb {S}}}}$ (thus regarding $S={{\mathcal {X}}}{\times }{{\mathcal {Y}}}$ as a subset of and writing $\theta =\pi |_S$ for $\theta =\pi |_{{{\mathbb {S}}}}$ and $\phi =\widetilde{\Phi }|_S$ for $\phi =\widetilde{\Phi }|_{{{\mathbb {S}}}}$), then the diagram

commutes. Therefore, the pair satisfies the axioms of Definition 3.1. $\square$

5 An Interpretation via Linear Map of Bilinear Maps

Let ${{\mathcal {X}}}$ and ${{\mathcal {Y}}}$ be nonzero linear spaces over the same field ${{\mathbb {F}}}$, take the Cartesian product ${{{\mathcal {X}}}{\times }{{\mathcal {Y}}}}$ of ${{\mathcal {X}}}$ and ${{\mathcal {Y}}}$, and consider the linear space $b[{{\mathcal {X}}}{\times }{{\mathcal {Y}}},{{\mathcal {F}}}]$ of all bilinear maps into an arbitrary but fixed linear space ${{\mathcal {F}}}$ over ${{\mathbb {F}}}.$ Associated with each pair ${(x,y)\in {{\mathcal {X}}}{\times }{{\mathcal {Y}}}}$, consider a transformation ${x\otimes y\!:b[{{\mathcal {X}}}{\times }{{\mathcal {Y}}},{{\mathcal {F}}}]\rightarrow {{\mathcal {F}}}}$ defined by

$$\begin{aligned} (x\otimes y)(\psi )=\psi (x,y)\,\in \,{{\mathcal {F}}}\quad \;\hbox {for every}\;\quad \psi \in b[{{\mathcal {X}}}{\times }{{\mathcal {Y}}},{{\mathcal {F}}}]. \end{aligned}$$

This again is referred to as a single tensor and as is readily verified ${x\otimes y}$ is a linear transformation on the linear space of bilinear maps,

$$\begin{aligned} x\otimes y\in {{\mathcal {L}}}[\,b[{{\mathcal {X}}}{\times }{{\mathcal {Y}}},{{\mathcal {F}}}],{{\mathcal {F}}}]. \end{aligned}$$

Thus, the term linear maps of bilinear maps means that this approach to tensor product focuses explicitly on the linearization of bilinear maps. Take the collection

$$\begin{aligned} \top _{\!{{\mathcal {X}}},{{\mathcal {Y}}},\,{{\mathcal {F}}}}=\big \{x\otimes y\in {{\mathcal {L}}}[\,b[{{\mathcal {X}}}{\times }{{\mathcal {Y}}},{{\mathcal {F}}}],{{\mathcal {F}}}] \!:\,x\in {{\mathcal {X}}}\;\hbox {and}\;\,y\in {{\mathcal {Y}}}\big \} \end{aligned}$$

of all single tensors. Consider its span, ${{\mathrm{span\,}}\!\top _{\!{{\mathcal {X}}},{{\mathcal {Y}}},\,{{\mathcal {F}}}}\subseteq {{\mathcal {L}}}[\,b[{{\mathcal {X}}}{\times }{{\mathcal {Y}}},{{\mathcal {F}}}],{{\mathcal {F}}}]}$, which is a linear manifold of the linear space ${{\mathcal {L}}}[\,b[{{\mathcal {X}}}{\times }{{\mathcal {Y}}},{{\mathcal {F}}}],{{\mathcal {F}}}]$, and define a map

$$\begin{aligned} \theta \!:{{\mathcal {X}}}{\times }{{\mathcal {Y}}}\rightarrow \!\top _{\!{{\mathcal {X}}},{{\mathcal {Y}}},\,{{\mathcal {F}}}}\subseteq {\mathrm{span\,}}\!\top _{\!{{\mathcal {X}}},{{\mathcal {Y}}},\,{{\mathcal {F}}}} \end{aligned}$$

as follows: for each pair ${(x,y)\in {{\mathcal {X}}}{\times }{{\mathcal {Y}}}}$ set

$$\begin{aligned} \theta (x,y)=x\otimes y. \end{aligned}$$

Theorem 5.1

${({\mathrm{span\,}}\!\top _{\!{{\mathcal {X}}},{{\mathcal {Y}}},\,{{\mathcal {F}}}},\theta )}$ is a tensor product of ${{\mathcal {X}}}$ and ${{\mathcal {Y}}}$.

Proof

Take an arbitrary linear space ${{\mathcal {F}}}$. Consider axioms (a), (b) in Definition 3.1.

(a$_1$):

$\theta (x,y)$ is a linear transformation, ${\theta (x,y)\in {{\mathcal {L}}}[b[{{\mathcal {X}}}{\times }{{\mathcal {Y}}},{{\mathcal {F}}}],{{\mathcal {F}}}]}$ for each (x, y) in ${{{\mathcal {X}}}{\times }{{\mathcal {Y}}}}$, which is given by ${\theta (x,y)(\psi )=\psi (x,y)\in {{\mathcal {F}}}}$ for every ${\psi \in b[{{\mathcal {X}}}{\times }{{\mathcal {Y}}},{{\mathcal {F}}}]}.$ Then bilinearity of $\psi$ is transferred to $\theta .$ Hence, ${\theta \in b[{{\mathcal {X}}}{\times }{{\mathcal {Y}}},{\mathrm{span\,}}\!\top _{\!{{\mathcal {X}}},{{\mathcal {Y}}},\,{{\mathcal {F}}}}]}$.

(a$_2$):

Since ${\theta (x,y)=x\otimes y}$, then $R(\theta )=\top _{\!{{\mathcal {X}}},{{\mathcal {Y}}},\,{{\mathcal {F}}}}$, and so ${{\mathrm{span\,}}R(\theta )={\mathrm{span\,}}\!\top _{\!{{\mathcal {X}}},{{\mathcal {Y}}},\,{{\mathcal {F}}}}}$.

(b):

An arbitrary element $\digamma$ of the linear space ${\mathrm{span\,}}\!\top _{\!{{\mathcal {X}}},{{\mathcal {Y}}},\,{{\mathcal {F}}}}$ is a linear combination of single tensors, thus lying in ${{\mathcal {L}}}[\,b[{{\mathcal {X}}}{\times }{{\mathcal {Y}}},{{\mathcal {F}}}],{{\mathcal {F}}}].$ Since $\theta$ is bilinear, then every $\digamma$ in ${\mathrm{span\,}}\!\top _{\!{{\mathcal {X}}},{{\mathcal {Y}}},\,{{\mathcal {F}}}}$ is a finite sum of single tensors ${x\otimes y=\theta (x,y)}$:

$$\begin{aligned} \digamma =\mathop {\sum }_ix_i\otimes y_i\,\in \, {\mathrm{span\,}}\!\top _{\!{{\mathcal {X}}},{{\mathcal {Y}}},\,{{\mathcal {F}}}}\,\subseteq \,{{\mathcal {L}}}[\,b[{{\mathcal {X}}}{\times }{{\mathcal {Y}}},{{\mathcal {F}}}],{{\mathcal {F}}}]. \end{aligned}$$

Given an arbitrary bilinear map ${\phi \in b[{{\mathcal {X}}}{\times }{{\mathcal {Y}}},{{\mathcal {Z}}}]}$ into any linear space ${{\mathcal {Z}}}$, consider the transformation ${\varPhi \!:{\mathrm{span\,}}\!\top _{\!{{\mathcal {X}}},{{\mathcal {Y}}},\,{{\mathcal {F}}}}\rightarrow {{\mathcal {Z}}}}$ defined by

$$\begin{aligned} \varPhi (\digamma )=\mathop {\sum }_i\phi (x_i,y_i)\,\in \,{{\mathcal {Z}}}\quad \;\hbox {for every}\;\quad \digamma =\mathop {\sum }_ix_i\otimes y_i\,\in \,{\mathrm{span\,}}\!\top _{\!{{\mathcal {X}}},{{\mathcal {Y}}},\,{{\mathcal {F}}}}. \end{aligned}$$

As is readily verified, this is a linear transformation: ${\varPhi \in {{\mathcal {L}}}[{\mathrm{span\,}}\!\top _{\!{{\mathcal {X}}},{{\mathcal {Y}}},\,{{\mathcal {F}}}},{{\mathcal {Z}}}]}.$ Also,

$$\begin{aligned} (\varPhi \circ \theta )(x,y)=\varPhi \big (\theta (x,y)\big )=\varPhi (x\otimes y)=\phi (x,y) \end{aligned}$$

for every ${(x,y)\in {{\mathcal {X}}}{\times }{{\mathcal {Y}}}}.$ Hence, $\phi =\varPhi \circ \theta$, leading to the commutative diagram

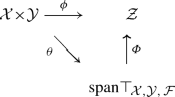
and therefore, the pair $({\mathrm{span\,}}\!\top _{\!{{\mathcal {X}}},{{\mathcal {Y}}},\,{{\mathcal {F}}}},\theta )$ satisfies the axioms of Definition 3.1. $\square$

This interpretation, where single tensors are defined as linear transformations of bilinear maps, is specially tailored to highlight the central property of tensor products as a tool to linearize bilinear maps according to Proposition 3.3.

An important particular case refers to linear and bilinear forms by setting ${{\mathcal {F}}}={{\mathbb {F}}}.$ In this case, single tensors are linear forms of bilinear forms,

$$\begin{aligned} x\otimes y\in \!\top _{\!{{\mathcal {X}}},{{\mathcal {Y}}},\,{{\mathbb {F}}}}\,\subseteq \,{{\mathcal {L}}}[b[{{\mathcal {X}}}{\times }{{\mathcal {Y}}},{{\mathbb {F}}}],\,{{\mathbb {F}}}] =b[{{\mathcal {X}}}{\times }{{\mathcal {Y}}},\,{{\mathbb {F}}}]^\sharp , \end{aligned}$$

in the algebraic dual of $b{[{{\mathcal {X}}}{\times }{{\mathcal {Y}}},{{\mathbb {F}}}]}.$ Particularizing still further, besides setting ${{\mathcal {F}}}={{\mathbb {F}}}$, replace the above linear space ${b[{{\mathcal {X}}}{\times }{{\mathcal {Y}}},{{\mathbb {F}}}]}$ by the following subset of it:

$$\begin{aligned} b_{{{\mathcal {X}}}^\sharp {\times }{{\mathcal {Y}}}^\sharp }[{{\mathcal {X}}}{\times }{{\mathcal {Y}}},{{\mathbb {F}}}] =\big \{{\psi \in b[{{\mathcal {X}}}{\times }{{\mathcal {Y}}},{{\mathbb {F}}}]}\!:{\psi (x,y)=\mu (x)\,\nu (y)} \;\;\hbox {for}\;\; {(\mu ,\nu )\in {{\mathcal {X}}}^\sharp {\times }{{\mathcal {Y}}}^\sharp }\big \}, \end{aligned}$$

consisting of products of linear forms $\mu \in {{\mathcal {X}}}^\sharp ={{\mathcal {L}}}[{{\mathcal {X}}},\,{{\mathbb {F}}}]$ and $\nu \in {{\mathcal {Y}}}^\sharp ={{\mathcal {L}}}[{{\mathcal {Y}}},\,{{\mathbb {F}}}].$ The set $b_{{{\mathcal {X}}}^\sharp {\times }{{\mathcal {Y}}}^\sharp }[{{\mathcal {X}}}{\times }{{\mathcal {Y}}},{{\mathbb {F}}}]$ is not a linear manifold of $b[{{\mathcal {X}}}{\times }{{\mathcal {Y}}},\,{{\mathbb {F}}}].$ Define single tensors as before. To each ${(x,y)\in {{\mathcal {X}}}{\times }{{\mathcal {Y}}}}$ associate a function ${x\otimes y\!:b_{{{\mathcal {X}}}^\sharp {\times }{{\mathcal {Y}}}^\sharp }[{{\mathcal {X}}}{\times }{{\mathcal {Y}}},{{\mathbb {F}}}]\rightarrow {{\mathbb {F}}}}$ defined for every ${\psi \in b_{{{\mathcal {X}}}^\sharp {\times }{{\mathcal {Y}}}^\sharp }[{{\mathcal {X}}}{\times }{{\mathcal {Y}}},{{\mathbb {F}}}]}$ by

$$\begin{aligned} (x\otimes y)(\mu ,\nu )=(x\otimes y)(\psi )=\psi (x,y)=\mu (x)\,\nu (y) \quad \;\hbox {for every}\;\quad (\mu ,\nu )\in {{\mathcal {X}}}^\sharp {\times }{{\mathcal {Y}}}^\sharp . \end{aligned}$$

The difference between this and the previous procedure is due to the fact that single tensors are not linear transformations (or linear forms) any longer as their domain $b_{{{\mathcal {X}}}^\sharp {\times }{{\mathcal {Y}}}^\sharp }[{{\mathcal {X}}}{\times }{{\mathcal {Y}}},{{\mathbb {F}}}]$ is not a linear space. However, as is readily verified they can be regarded as bilinear forms on the Cartesian product of the linear spaces ${{\mathcal {X}}}^\sharp \!$ and ${{\mathcal {Y}}}^\sharp$:

$$\begin{aligned} x\otimes y\in b[{{\mathcal {X}}}^\sharp {\times }{{\mathcal {Y}}}^\sharp ,{{\mathbb {F}}}]=b[{{\mathcal {L}}}[{{\mathcal {X}}},{{\mathbb {F}}}]{\times }{{\mathcal {L}}}[{{\mathcal {Y}}},{{\mathbb {F}}}],\,{{\mathbb {F}}}]. \end{aligned}$$

Thus, take the collection $\top '_{\!{{\mathcal {X}}}\!,{{\mathcal {Y}}}}$ of all these single tensors

$$\begin{aligned} \top '_{\!{{\mathcal {X}}}\!,{{\mathcal {Y}}}}=\big \{ x\otimes y\in b[{{\mathcal {X}}}^\sharp {\times }{{\mathcal {Y}}}^\sharp ,{{\mathbb {F}}}] \!:\,x\in {{\mathcal {X}}}\;\hbox {and}\;\,y\in {{\mathcal {Y}}}\big \}, \end{aligned}$$

and consider its span, ${\mathrm{span\,}}\!\top '_{\!{{\mathcal {X}}}\!,{{\mathcal {Y}}}}$, which is now a linear manifold of the linear space $b[{{\mathcal {X}}}^\sharp {\times }{{\mathcal {Y}}}^\sharp ,{{\mathbb {F}}}]$ of all bilinear forms of pairs of linear forms. As before, define a map ${\theta '\!:{{\mathcal {X}}}{\times }{{\mathcal {Y}}}\rightarrow \top '_{\!{{\mathcal {X}}}\!,{{\mathcal {Y}}}}\subseteq {\mathrm{span\,}}\!\top '_{\!{{\mathcal {X}}}\!,{{\mathcal {Y}}}}}$ for each pair ${(x,y)\in {{\mathcal {X}}}{\times }{{\mathcal {Y}}}}$ by

$$\begin{aligned} \theta '(x,y)=x\otimes y. \end{aligned}$$

Now the value of $\theta '$ at ${(x,y)\in {{\mathcal {X}}}{\times }{{\mathcal {Y}}}}$ is a bilinear form, ${\theta '(x,y)\in b[{{\mathcal {X}}}^\sharp {\times }{{\mathcal {Y}}}^\sharp ,{{\mathbb {F}}}]}$, which is given by ${\theta '(x,y)(\mu ,\nu )=\mu (x)\,\nu (y)\in {{\mathbb {F}}}}$ for every ${(\mu ,\nu )\in {{\mathcal {X}}}^\sharp {\times }{{\mathcal {Y}}}^\sharp }$.

Corollary 5.1

${({\mathrm{span\,}}\!\top '_{\!{{\mathcal {X}}}\!,{{\mathcal {Y}}}},\theta ')}$ is a tensor product of ${{\mathcal {X}}}$ and ${{\mathcal {Y}}}$.

Proof

Consider the proof of Theorem 5.1. Replace ${{\mathcal {F}}}$ by ${{\mathbb {F}}}$ so that ${{{\mathcal {L}}}[b[{{\mathcal {X}}}{\times }{{\mathcal {Y}}},{{\mathcal {F}}}],{{\mathcal {F}}}]}$ is replaced by ${{{\mathcal {L}}}[b[{{\mathcal {X}}}{\times }{{\mathcal {Y}}},{{\mathbb {F}}}],\,{{\mathbb {F}}}]}.$ Then replace the linear space ${b[{{\mathcal {X}}}{\times }{{\mathcal {Y}}},\,{{\mathbb {F}}}]}$ by the subset $b_{{{\mathcal {X}}}^\sharp {\times }{{\mathcal {Y}}}^\sharp }[{{\mathcal {X}}}{\times }{{\mathcal {Y}}},\,{{\mathbb {F}}}]$, still keeping the same definition of single tensors, so that $\top _{\!{{\mathcal {X}}},{{\mathcal {Y}}},\,{{\mathcal {F}}}}\subseteq {{{\mathcal {L}}}[\,b[{{\mathcal {X}}}{\times }{{\mathcal {Y}}},{{\mathcal {F}}}],{{\mathcal {F}}}]}$ is replaced by $\top '_{\!{{\mathcal {X}}}\!,{{\mathcal {Y}}}}\subseteq {b[{{\mathcal {L}}}[{{\mathcal {X}}},{{\mathbb {F}}}]{\times }{{\mathcal {L}}}[{{\mathcal {Y}}},{{\mathbb {F}}}],\,{{\mathbb {F}}}]}.$ Again, ${\theta '\!:\!{{\mathcal {X}}}{\times }{{\mathcal {Y}}}\rightarrow {\mathrm{span\,}}\!\top '_{\!{{\mathcal {X}}},{{\mathcal {Y}}},\,{{\mathcal {F}}}}}$ is a bilinear map with ${{\mathrm{span\,}}R(\theta ')=\!\top '_{\!{{\mathcal {X}}},{{\mathcal {Y}}},\,{{\mathcal {F}}}}}.$ Thus, the argument in the proof of Theorem 5.1 still holds, associating with each bilinear map ${\phi \!:{{\mathcal {X}}}{\times }{{\mathcal {Y}}}\rightarrow {{\mathcal {Z}}}}$ the same linear transformation $\varPhi$ into ${{\mathcal {Z}}}$ now acting on ${\mathrm{span\,}}\!\top '_{\!{{\mathcal {X}}}\!,{{\mathcal {Y}}}}$. $\square$

Remark 5.1

Here is a common and useful example of such a particular case (with ${{{\mathbb {F}}}={{\mathbb {C}}}}).$ Let ${{\mathcal {X}}}$ and ${{\mathcal {Y}}}$ be complex Hilbert spaces with inner products ${\langle \,\cdot \,;\cdot \,\rangle _{{\mathcal {X}}}}$ and ${\langle \,\cdot \,;\cdot \,\rangle _{{\mathcal {Y}}}}$, which are sesquilinear forms (not bilinear forms). Algebraic duals ${{\mathcal {X}}}^\sharp$ and ${{\mathcal {Y}}}^\sharp$ are now naturally replaced by topological duals ${{\mathcal {X}}}^*$ and ${{\mathcal {Y}}}^*$ of continuous linear functionals. A single tensor for each ${(x,y)\in {{\mathcal {X}}}{\times }{{\mathcal {Y}}}}$ is usually defined in this case by

$$\begin{aligned} (x\otimes y)(u,v)=\langle x\,;u\rangle _{{\mathcal {X}}}\,\langle y\,;v\rangle _{{\mathcal {Y}}}\quad \;\hbox {for every}\;\quad (u,v)\in {{\mathcal {X}}}{\times }{{\mathcal {Y}}}. \end{aligned}$$

(See, e.g., [18, Section II.4] and [8].) The Riesz representation theorem for Hilbert spaces says that $\mu$ lies in ${{\mathcal {X}}}^*\!$ and $\nu$ lies in ${{\mathcal {Y}}}^*\!$ if and only if ${\mu (\cdot )=\langle \,\cdot \,;u\rangle _{{\mathcal {X}}}}$ and $\nu (\cdot )=$ $\langle \,\cdot \,;v\rangle _{{\mathcal {Y}}}$ for some u in ${{\mathcal {X}}}$ and v in ${{\mathcal {Y}}}.$ Thus, identify ${\mu \in {{\mathcal {X}}}^*}$ and ${\nu \in {{\mathcal {Y}}}^*}$ with ${u\in {{\mathcal {X}}}}$ and ${v\in {{\mathcal {Y}}}}$ such that the pair ${(u,v)\in {{\mathcal {X}}}{\times }{{\mathcal {Y}}}}$ is identified with the pair ${(\mu ,\nu )\in {{\mathcal {X}}}^*{\times }{{\mathcal {Y}}}^*}\!.$ Then a single tensor ${x\otimes y}$ associated with a pair ${(x,y)\in {{\mathcal {X}}}{\times }{{\mathcal {Y}}}}$ is in fact a bilinear form ${x\otimes y\!:{{\mathcal {X}}}^*{\times }{{\mathcal {Y}}}^*\rightarrow {{\mathbb {C}}}}$ in ${b[{{\mathcal {X}}}^*{\times }{{\mathcal {Y}}}^*,{{\mathbb {C}}}]}$, which is equivalently written as

$$\begin{aligned} (x\otimes y)(\mu ,\nu )=\mu (x)\,\nu (y) \quad \;\hbox {for every}\;\quad (\mu ,\nu )\in {{\mathcal {X}}}^*{\times }{{\mathcal {Y}}}^*. \end{aligned}$$

6 Final Remarks

6.1 Multiple Tensor Products

It is clear how the preceding arguments (in Sects. 3, 4, 5) can be naturally extended to cover the notion of an algebraic tensor product of a finite collection $\{{{\mathcal {X}}}_i\}_{i=1}^n$ of linear spaces over the same field, yielding a tensor product space $\bigotimes _{i=1}^n\!{{\mathcal {X}}}_i$ of a finite number of linear spaces. This is based on the notions of multiple Cartesian products $\prod _{i=1}^n\!{{\mathcal {X}}}_i$, n-tuples, and multilinear maps as a natural extension of Cartesian product of two linear spaces, ordered pairs, and bilinear maps. All results in Sects. 3, 4 and 5 remain true (essentially with the same statement, following similar arguments) if extended to such multiple tensor products. To extend a result on tensor product from a pair of linear spaces to an n-tuple (or to an $\infty$-tuple) may be a relevant task. Sometimes this is a simple job (achieved by induction) but not always. On the other hand, what may also not be always simple is the other way round: When a notion is initially defined for an n-tuple, it may be wise to go down to a pair to see clearly what is really going on.

6.2 Tensor Products of Banach Spaces

We have been dealing with algebraic tensor products ${{{\mathcal {X}}}\otimes {{\mathcal {Y}}}}$ of linear spaces ${{\mathcal {X}}}$ and ${{\mathcal {Y}}}.$ A natural follow-up is to equip the underlying linear space ${{{\mathcal {X}}}\otimes {{\mathcal {Y}}}}$ with a norm and advance the theory of tensor products to Banach spaces. So a new starting point is to equip ${{{\mathcal {X}}}\otimes {{\mathcal {Y}}}}$ with a suitable norm. If ${{\mathcal {X}}}$ and ${{\mathcal {Y}}}$ are Banach spaces and ${{\mathcal {X}}}^*$ and ${{\mathcal {Y}}}^*$ are their duals, then let ${x\otimes y}$ and ${f\otimes g}$ be single tensors in the tensor product spaces ${{{\mathcal {X}}}\otimes {{\mathcal {Y}}}}$ and ${{{\mathcal {X}}}^*\!\otimes {{\mathcal {Y}}}^*}\!.$ A norm $\Vert \cdot \Vert$ on ${{{\mathcal {X}}}\otimes {{\mathcal {Y}}}}$ is a reasonable crossnorm if, for every ${x\in {{\mathcal {X}}}}$, ${y\in {{\mathcal {Y}}}}$, ${f\in {{\mathcal {X}}}^*}$, ${g\in {{\mathcal {X}}}^*}$,

• (a) $\;\Vert x\otimes y\Vert \le \Vert x\Vert \,\Vert y\Vert$,

• (b) $\;{f\otimes g}$ lies in $({{\mathcal {X}}}\otimes {{\mathcal {Y}}})^*\!$,  and $\Vert f\otimes g\Vert _*\le \Vert f\Vert \,\Vert g\Vert$    (where $\Vert \cdot \Vert _*$ is the norm on the dual $({{\mathcal {X}}}\otimes {{\mathcal {Y}}})^*$ when $({{\mathcal {X}}}\otimes {{\mathcal {Y}}})$ is equipped with the norm in (a)),

so that ${{{\mathcal {X}}}^*\otimes {{\mathcal {Y}}}^*\subseteq ({{\mathcal {X}}}\otimes {{\mathcal {Y}}})^*}\!.$ It can be verified that (i) the above norm inequalities become identities, and (ii) when restricted to ${{{\mathcal {X}}}^*\otimes {{\mathcal {Y}}}^*}$ the norm $\Vert \cdot \Vert _*$ on ${({{\mathcal {X}}}\otimes {{\mathcal {Y}}})^*}$ is again a reasonable crossnorm (with respect to the second dual ${({{\mathcal {X}}}\otimes {{\mathcal {Y}}})^{**}}).$ Two special norms on ${{{\mathcal {X}}}\otimes {{\mathcal {Y}}}}$ are the so-called injective ${\Vert \cdot \Vert _{_\vee }}$ and projective $\Vert \cdot \Vert _{_\wedge }$ norms,

$$\begin{aligned}&\Vert \digamma \Vert _{_\vee } =\sup _{\Vert f\Vert \le 1,\,\Vert g\Vert \le 1,\;f\in {{\mathcal {X}}}^*\!,\,g\in {{\mathcal {Y}}}*} \left| \mathop {\sum }_if(x_i)\,g(y_i)\right| , \\&\quad \Vert \digamma \Vert _{_\wedge } =\inf _{\{x_i\}_i,\,\{y_i\}_i,\;\digamma =\mathop {\sum }\limits _{i}x_i\otimes y_i} {\sum }_i\Vert x_i\Vert \,\Vert y_i\Vert , \end{aligned}$$

for every ${\digamma ={\sum }_ix_i\otimes y_i\in {{\mathcal {X}}}\otimes {{\mathcal {Y}}}}.$ It can be shown that (iii) these are reasonable crossnorms, and (iv) a norm $\Vert \cdot \Vert$ on ${{{\mathcal {X}}}\otimes {{\mathcal {Y}}}}$ is a reasonable crossnorm if and only if

$$\begin{aligned} \Vert \digamma \Vert _{_\vee }\le \Vert \digamma \Vert \le \Vert \digamma \Vert _{_\wedge } \quad \hbox {for every}\;\quad \digamma \in {{\mathcal {X}}}\otimes {{\mathcal {Y}}}. \end{aligned}$$

Anyhow, equipped with any reasonable crossnorm, a tensor product space ${{{\mathcal {X}}}\otimes {{\mathcal {Y}}}}$ of a pair of Banach spaces ${{\mathcal {X}}}$ and ${{\mathcal {Y}}}$ is not necessarily complete. Thus, one takes the completion ${{{\mathcal {X}}}\widehat{\otimes }{{\mathcal {Y}}}}$ of ${{{\mathcal {X}}}\otimes {{\mathcal {Y}}}}.$ For the theory of the Banach space ${{{\mathcal {X}}}\widehat{\otimes }{{\mathcal {Y}}}}$, the reader is referred, for instance, to [2, 3, 7, 20]. If ${{\mathcal {X}}}$ and ${{\mathcal {Y}}}$ are Hilbert spaces, then ${{{\mathcal {X}}}\widehat{\otimes }{{\mathcal {Y}}}}$ becomes a Hilbert space when one takes the reasonable crossnorm on ${{{\mathcal {X}}}\otimes {{\mathcal {Y}}}}$ that naturally comes from the inner products in ${{\mathcal {X}}}$ and ${{\mathcal {Y}}}$ as in Remark 5.1, by setting ${\langle x_1\otimes y_1,x_2\otimes y_2\rangle _{{{\mathcal {X}}}\otimes {{\mathcal {Y}}}}} ={\langle x_1\otimes x_2\rangle _{{\mathcal {X}}}\,\langle y_1\otimes y_2\rangle _{{\mathcal {Y}}}}$ (see, e.g., [8, 18, 22]).