Abstract
We consider normalized analytic function f on the open unit disk for which either \(Ref(z)/g(z)>0\), \(|f(z) /g(z) - 1|<1\) or \(Re(1-z^2) f(z) /z>0\) for some analytic function g with \(Re(1-z^2) g(z) /z>0\). We have obtained the radii for these functions to belong to various subclasses of starlike functions. The subclasses considered include the classes of starlike functions of order \(\alpha \), lemniscate starlike functions and parabolic starlike functions.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Let \(\mathbb {D}_r:= \{z \in \mathbb {C}: |z| < r\}\) be an open disk of radius r centered at the origin and \(\mathbb {D}= \mathbb {D}_1\) be the open unit disk in \(\mathbb {C}\). For any two classes \(\mathcal {G}\) and \(\mathcal {H}\) of analytic functions defined on the unit disk \(\mathbb {D}\), the \(\mathcal {H}\)-radius for the class \(\mathcal {G}\), denoted by \(\mathcal {R}_{\mathcal {H}}(\mathcal {G})\) (or just \(\mathcal {R}_{\mathcal {H}}\) if the class \(\mathcal {G}\) is understood in the context), is the largest radius \(\rho \le 1\) such that \(f\in \mathcal {G}\) implies the function \(f_r\), defined by \(f_r(z)=f(rz)/r\), belongs to class \(\mathcal {H}\) for all \(0< r< \rho \). Among the radius problems for various subclasses of analytic functions, one direction of study focuses on obtaining the radius for classes consisting of functions characterized by ratio of the function f and another function g, where g is a function belonging to some special subclass of \(\mathcal {A}\) of all analytic functions on \(\mathbb {D}\) normalized by \(f(0)=0=f'(0)-1\). MacGregor [11, 12] obtained the radius of starlikeness for the class of functions \(f \in \mathcal {A}\) satisfying either \(Re(f(z)/g(z))>0\) or \(|f(z)/g(z)-1|<1\) for some \(g \in \mathcal {K}\). Ali et al. [2] estimated several radii for classes of functions satisfying either (i) \(Re(f(z)/g(z))>0\), where \(Re(g(z)/z)>0\) or \(Re(g(z)/z)>1/2\); (ii) \(|f(z)/g(z)-1|<1\), where \(Re(g(z)/z)>0\) or g is convex; (iii) \(|f'(z)/g'(z)-1|<1\), where \(Reg'(z)>0\). The work is further investigated in [7, 20]. These classes are related to the Caratheodory class \(\mathcal {P}\) consisting of all analytic functions p with \(p(0)=1\) and \(Rep(z)>0\) for all \(z \in \mathbb {D}\).
Motivated by the aforesaid studies, we consider the following three classes \(\mathcal {K}_1\), \(\mathcal {K}_2\), and \(\mathcal {K}_3\) defined by
and
and estimate the radius for the functions in the classes \(\mathcal {K}_1\), \(\mathcal {K}_2\), and \(\mathcal {K}_3\) to belong to various subclasses of starlike functions which we discuss below.
Let the functions f and F be analytic on \(\mathbb {D}\). The function f is subordinate to F, written \(f\prec F\), provided \(f=F\circ w\) for some analytic self-mapping w of the unit disk \( \mathbb {D}\) that fixes the origin. Subordination is very useful in the study of subclasses of univalent functions. For instance, the concept of Hadamard product and subordination was used in [16] to introduce the class of all functions f satisfying \(z{(k_\alpha * f)'}/{(k_\alpha * f)}\prec h\), where \(k_\alpha (z)= z/(1-z)^{\alpha }\), \(\alpha \in \mathbb {R}\), \(f \in \mathcal {A}\) and h is a convex function. Later in 1989, Shanmugam [22] studied the class \(\mathcal {S}_g^*(h)\) of all functions \(f\in {\mathcal {A}}\) satisfying \(z(f*g)'/(f*g) \prec h\), where h is a convex function and g is a fixed function in \(\mathcal {A}\). By replacing g with the functions \(z/(1-z)\) and \(z/(1-z)^2\), we get the subclasses \(\mathcal {S}^*(h)\) and \(\mathcal {K}(h)\) of Ma-Minda starlike and convex functions, respectively. In 1992, Ma and Minda [10] studied the distortion, growth, covering and coefficient estimates for these functions with the weaker assumption of starlikeness on h. These classes unify several subclasses of starlike and convex functions. When h is the mapping of \(\mathbb {D}\) onto the right half-plane, the classes \(\mathcal {S}^*(h)\) and \(\mathcal {K}(h)\) reduce to the classes \(\mathcal {S}^*\) and \(\mathcal {K}\) of starlike and convex functions, respectively. For \(h(z)=(1+Az)/(1+Bz)\), with \(-1 \le B <A \le 1\), the classes become \(\mathcal {S}^*[A,B]\) and \(\mathcal {K}[A,B]\) of Janowski starlike and Janowski convex functions, respectively. For \(A= 1- 2 \alpha \) and \(B = -1\) where \(0 \le \alpha < 1\), these subclasses become \(\mathcal {S}^*(\alpha )\) of the starlike functions of order \(\alpha \) and \(\mathcal {K}(\alpha )\) of convex functions of order \(\alpha \), respectively, introduced by Robertson [18]. For \(h (z)= \sqrt{1+z}\), the class \(\mathcal {S}^*(h)\) becomes the class \(\mathcal {S}^*_{L} \) of the lemniscate starlike functions introduced and studied by Sokól and Stankiewicz [24, 25]; analytically, \(f \in \mathcal {S}^*_{L}\) if \(|(z f'(z)/f(z))^2-1|<1\).
Mendiratta et al. [14, 15] studied the classes \(\mathcal {S}^*_e = \mathcal {S}^*(e^z)\) and \(\mathcal {S}^*_{RL} = \mathcal {S}^*(h_{RL})\), where
Indeed, a function f belongs to \(\mathcal {S}^*_e\) or to \( \mathcal {S}^*_{RL}\) if \(z f'(z)/f(z)\), respectively, belongs to \(\{ w \in \mathbb {C}: |\log w|<1\}\) or \(\{ (w - \sqrt{2})^2 -1 < 1 \}\). Sharma et al. [23] defined and studied the class of functions defined by \(\mathcal {S}^*_c = \mathcal {S}^* (h_c(z))\), where \(h_c(z) = 1 + (4/3) z + (2/3) z^2\); a function \(f\in \mathcal {S}^*_c\) if \(z f'(z)/f(z)\in \{ x + i y : (9 x^2 + 9 y^2 -18 x + 5)^2 -16 (9x^2 + 9 y^2 -6 x +1) = 0 \}\). Cho et al. [4] defined and studied the class \(\mathcal {S}^*_{\sin } = \mathcal {S}^*(1 + \sin z)\). Raina and Sokol [17] defined the class  , where
, where  and
and  consists of functions for which \(z f'(z)/f(z)\) lies in the leftmoon region defined by
consists of functions for which \(z f'(z)/f(z)\) lies in the leftmoon region defined by  . Another particular case is the class \(\mathcal {S}^*_R = \mathcal {S}^*(h_R)\) studied in [8], where \(h_R(z) = 1+ (zk + z^2)/(k^2 - kz)\) and \(k = \sqrt{2} + 1\). The subclass \(\mathcal {S}_{P} \) of parabolic starlike functions (see the survey [19] or [1, 6, 9, 13]) consists of all normalized analytic functions f with \(zf'(z)/f(z)\) lying in the parabolic region \((Im(w))^2< 2 Re(w)-1\).
. Another particular case is the class \(\mathcal {S}^*_R = \mathcal {S}^*(h_R)\) studied in [8], where \(h_R(z) = 1+ (zk + z^2)/(k^2 - kz)\) and \(k = \sqrt{2} + 1\). The subclass \(\mathcal {S}_{P} \) of parabolic starlike functions (see the survey [19] or [1, 6, 9, 13]) consists of all normalized analytic functions f with \(zf'(z)/f(z)\) lying in the parabolic region \((Im(w))^2< 2 Re(w)-1\).
2 Radius Results
The first theorem gives the various radii of starlikeness for the class \(\mathcal {K}_1\) which consists of functions \(f \in \mathcal {A}\) satisfying \(Re(f(z)/g(z)) > 0\) for some \(g \in \mathcal {A}\) satisfying \(Re((1-z^2)g(z)/z) >0\). Note that the functions \(f_1,\ g_1: \mathbb {D}\rightarrow \mathbb {C}\) defined by
satisfy
This means the function \(f_1 \in \mathcal {K}_1\) and so \(\mathcal {K}_1\ne \emptyset \). Further we will see that this function \(f_1\) serves as an extremal function for many radii problems studied here.
Theorem 1
For the class \(\mathcal {K}_1\), the following results hold:
-
1.
For \(0 \le \alpha <1\), the \(\mathcal {S}^*(\alpha )\)-radius is the smallest positive real root of the equation \(r^4(1+\alpha ) - 4 r^3-2 r^2 -4 r +(1-\alpha )=0\).
-
2.
The \(\mathcal {S}^*_L\)-radius is \(\mathcal {R}_{\mathcal {S}^*_L}= (\sqrt{5}-2)/(\sqrt{2}+1) \approx 0.0977826\).
-
3.
The \(\mathcal {S}_{P}\)-radius \(\mathcal {R}_{\mathcal {S}_{P}} \approx 0.116675\) is the smallest positive real root of the equation \( 3 r^4 - 8r^3 -4 r^2 -8 r +1 = 0 \).
-
4.
The \(\mathcal {S}^*_{e}\)-radius \(\mathcal {R}_{\mathcal {S}^*_{e}} \approx 0.144684\) is the smallest positive real root of the equation \((2r^2 +4 r +4 r^3 -1-r^4)e = r^4 - 1 \).
-
5.
The \(\mathcal {S}^*_{c}\)-radius \(\mathcal {R}_{\mathcal {S}^*_{c}} \approx 0.15182\) is the smallest positive real root of the equation \( 4 r^4 - 12 r^3 - 6 r^2 - 12 r + 2 = 0 \).
-
6.
The
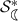 -radius
-radius 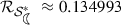 is the smallest positive real root of the equation \( 4 r^3 + 2 r^2 + 4 r + \sqrt{2}(1- r^4) = 2 \).
is the smallest positive real root of the equation \( 4 r^3 + 2 r^2 + 4 r + \sqrt{2}(1- r^4) = 2 \). -
7.
The \(\mathcal {S}^*_{\sin }\)-radius is \(\mathcal {R}_{\mathcal {S}^*_{\sin }}= (-2+\sqrt{4+ \sin {1}(2+ \sin {1})})/(2+ \sin {1}) \approx 0.185835\).
-
8.
The \(\mathcal {S}^*_{RL}\)-radius \(\mathcal {R}_{\mathcal {S}^*_{RL}} \approx 0.0687813\) is the smallest positive real root of the equation
$$\begin{aligned} 4r^2\left( 2r^2 + r + 2\right) ^2= & {} \left( 1-r^4\right) \sqrt{ \left( \sqrt{2}-1 \right) + \left( \sqrt{2}-2\right) r^4} \\&- 2\left( \sqrt{2}-1 + \left( \sqrt{2}-2\right) r^4\right) . \end{aligned}$$ -
9.
The \(\mathcal {S}^*_{R}\)-radius \(\mathcal {R}_{\mathcal {S}^*_{R}} \approx 0.0419413\) is the smallest positive real root of the equation \( 4 r^3 + 2 r^2 + 4 r - r^4 -1 = 2 (1- \sqrt{2})(1- r^4) \).
We would use the following lemmas in order to prove our results:
Lemma 1
([3, Lemma 2.2, p. 4]) For \(0<a<\sqrt{2}\), let \(r_a\) be given by
Then \(\{w: |w-a|< r_a \} \subseteq \{w: |w^2-1|<1\}\).
Lemma 2
([22, Lemma 1, p. 321]) For \(a> 1/2\), let \(r_a\) be given by
Then \(\{w: |w-a|< r_a \} \subseteq \{w: Rew > |w-1|\} = \varOmega _{p}\). Here, \(\varOmega _{p}\) is a parabolic region which is symmetric with respect to the real axis and vertex at (1/2, 0).
Lemma 3
([15, Lemma 2.2, p. 368]) For \( e^{-1}< a < e\), let \(r_a\) be given by
Then \(\{w: |w-a|< r_a \} \subseteq \{w: |\log w|<1\} = \varOmega _e\), which is the image of the unit disk \(\mathbb {D}\) under the exponential function.
Lemma 4
([23, Lemma 2.5, p. 926]) For \( 1/3< a < 3\), let \(r_a\) be given by
Then \(\{w: |w-a|< r_a \} \subseteq \varOmega _c\). Here \(\varOmega _c\) is the region bounded by the cardioid \(\{x+ i y: (9x^2+9y^2-18x+5)^2 - 16 (9 x^2+ 9 y^2 -6x + 1) = 0 \}\).
Lemma 5
([4, Lemma 3.3, p. 7]) For \( 1 - \sin 1< a < 1+ \sin 1 \), let \(r_a= \sin 1 - |a-1|\). Then \(\{w: |w-a|< r_a \} \subseteq \varOmega _{sin}\). Here \(\varOmega _{sin}\) is the image of \(\mathbb {D}\) under the function \(1+ \sin z\).
Lemma 6
([5, Lemma 2.1, p. 3]) For \( \sqrt{2}-1< a < \sqrt{2}+1\), let \(r_a= 1 - |\sqrt{2}-a|\). Then  .
.
Lemma 7
([8, Lemma 2.2, p. 202]) For \( 2 (\sqrt{2}-1)< a < 2\), let \(r_a\) be given by
Then \(\{w: |w-a|< r_a \} \subseteq \varOmega _R\), where \(\varOmega _R\) is the image of \(\mathbb {D}\) under the function \(1+ ((z k + z^2)/(k^2 -k z))\), \(k= \sqrt{2}+1\).
Lemma 8
([14, Lemma 3.2, p. 10]) For \( 0< a < \sqrt{2}\), let \(r_a\) be given by
Then \(\{w: |w-a|< r_a \} \subseteq \{ w: Rew >0, |(w- \sqrt{2})^2-1|< 1 \}= \varOmega _{RL}\).
Lemma 9
([21, Lemma 2, p. 240]) Let \(0 \le \alpha < 1\). If the function \( p(z) = 1 + b_n z^n + b_{n+1} z^{n+1} + \cdots \) is analytic and satisfies \( Rep(z) > \alpha \) for \(z\in \mathbb {D}\), then
With all these tools, we are ready to give the proof of our first result.
Proof of Theorem 1
Let the function \(f \in \mathcal {K}_1\) and the function \(g: \mathbb {D} \rightarrow \mathbb {C}\) be chosen such that
Let us define the functions \(p_1, p_2: \mathbb {D}\rightarrow \mathbb {C}\) by
Then, by Eq. (2), the functions \(p_1\) and \(p_2\) are in \(\mathcal {P}\). Equation (3) yields
A differentiation of the above equation and a simple computation shows that
It can be easily proved that the bilinear transform \(w= (1+z^2)/(1-z^2)\) maps the disk \(|z|\le r\) onto the disk \(\{w\in \mathbb {C}:|w-(1+r^4)/(1-r^4)| \le 2r^2/(1-r^4)\}\), and hence
Now, by Lemma 9, for \(p \in \mathcal {P}(\alpha ) := \{ p \in \mathcal {P} : Rep(z) > \alpha , z \in \mathbb {D}\}\), we have
By using equations (4), (5) and (6), it follows that the function \(f \in \mathcal {K}_1\) satisfies
In order to solve the radius problems for \(f \in \mathcal {K}_1\), we are interested in computing the value of r for which the disk in (7) is contained in the corresponding regions. The classes we are considering here are all subclasses of starlike functions, and therefore, we first determine the radius of starlikeness for the class \(\mathcal {K}_1\). From (7), we have
for \(|z|\le r <\rho \) where \(\rho =1+\sqrt{2}-\sqrt{2 \left( 1+\sqrt{2}\right) }\approx 0.216845\) is the smallest positive root of the equation \(r^4 - 4 r^3 - 2 r^2 -4r + 1=0\). For the function \(f_1\) defined in (1), we have
At \(z := \rho i\), we have \(zf'_1(z)/f_1(z)= 0\), thereby proving that the radius of starlikeness for \(\mathcal {K}_1\) is \(\rho \). It is pertinent to remark that the radii that we are going to estimate here will be less than \(\rho =1+\sqrt{2}-\sqrt{2 \left( 1+\sqrt{2}\right) }\).
-
1.
In order to compute \(R_ {\mathcal {S}^*(\alpha )}\), we estimate the value of \(r \in (0,1)\) satisfying
$$\begin{aligned} Re\frac{z f'(z)}{f(z)} \ge \frac{r^4 - 4 r^3 - 2 r^2 -4r + 1}{1-r^4} > \alpha . \end{aligned}$$If we denote by \(\rho \) the smallest positive root of the equation \(r^4(1+\alpha ) - 4 r^3-2 r^2 -4 r +(1-\alpha )=0\), then we have \({\text {Re}} (z f'(z)/f(z))> \alpha \), \(z \in \mathbb {D}_{\rho }\) for every function \(f \in \mathcal {K}_1\). Since, for the function \(f_1 \in \mathcal {K}_1\) defined by (1), we have
$$\begin{aligned} \frac{\rho i f_1'(\rho i)}{f_1( \rho i)}= \frac{1-4\rho -2\rho ^2-4\rho ^3+\rho ^4}{1-\rho ^4}= \alpha , \end{aligned}$$it follows that the number \(\rho \) is the biggest positive real number having the property \({\text {Re}} (z f'(z)/f(z))> \alpha \), \(z \in \mathbb {D}_{\rho }\) for every \(f \in \mathcal {K}_1\). Consequently, the number \(\rho = \mathcal {R}_{\mathcal {S}^*(\alpha )}\) is the radius of starlikeness of order \(\alpha \) for \(\mathcal {K}_1\).
-
2.
We use Lemma 1 to compute the lemniscate starlike radius for \(\mathcal {K}_1\). Using (7) and writing \(w= zf'(z)/f(z)\), \(a = (1+r^4)/(1-r^4)\), \(r_a= 2r (2 r^2 + r + 2)/(1-r^4)\), we have
$$\begin{aligned} |w-a|= \left| \frac{z f'(z)}{f(z)} - \frac{1+r^4}{1-r^4} \right| \le \frac{2r (2 r^2 + r + 2)}{1-r^4}=r_a. \end{aligned}$$(8)Let \(\rho = (\sqrt{5}-2)/(\sqrt{2}+1)\), which is the smallest positive real root of the equation \((1+\sqrt{2})r^4 + 4r^3 + 2r^2 + 4r + 1 - \sqrt{2} = 0\). For \(0 \le r < 1\), we have \(a \ge 1\). Also, \(a < \sqrt{2}\) for \(r < \root 4 \of {(\sqrt{2}-1)/(\sqrt{2}+1)} \approx 0.1715\). Thus, for \(0\le r< \root 4 \of {(\sqrt{2}-1)/(\sqrt{2}+1)}\), we have \(2\sqrt{2}/3<a<\sqrt{2}\). By Lemma 1, we see that the disk \(\{w:|w-a|<r_a\}\) lies inside the lemniscate region \(\{w:|w^2-1|<1\}\), or equivalently
$$\begin{aligned} \left| \left( \frac{z f'(z)}{f(z)}\right) ^2 -1 \right| < 1, \end{aligned}$$if \(r_a\le \sqrt{2}-a\) for \(0\le r<\rho \). The inequality \(r_a\le \sqrt{2}-a\) holds for \(0\le r<\rho \), as we have
$$\begin{aligned} a+r_a= \frac{2r \left( 2 r^2 + r + 2\right) }{1-r^4} + \frac{1+r^4}{1-r^4}< \frac{2\rho \left( 2 \rho ^2 + \rho + 2\right) }{1-\rho ^4} + \frac{1+\rho ^4}{1-\rho ^4}=\sqrt{2}. \end{aligned}$$(9)Consider the functions \(f, g: \mathbb {D}\rightarrow \mathbb {C}\) defined by
$$\begin{aligned} f(z) = \frac{z(1-z)}{(1+z)^3} \quad \text {and}\quad g(z)= \frac{z}{(1+z)^2}. \end{aligned}$$(10)Then, f is in \(\mathcal {K}_1\) as
$$\begin{aligned} Re\frac{f(z)}{g(z)} = Re\frac{1-z^2}{z}g(z) = Re\frac{1- z}{1+ z} >0. \end{aligned}$$Now, for \(z := - \rho = - \mathcal {R}_{\mathcal {S}^*_{L}}\), we have
$$\begin{aligned} \frac{zf'(z)}{f(z)}=\frac{\rho ^2 +4 \rho +1}{1-\rho ^2}= \frac{\rho ^4 +4 \rho ^3+2\rho ^2+4\rho +1}{1-\rho ^4} = \sqrt{2} \end{aligned}$$and thus
$$\begin{aligned} \left| \left( \frac{zf'(z)}{f(z)}\right) ^2 -1 \right| =1. \end{aligned}$$Consequently, the number \(\mathcal {R}_{\mathcal {S}^*_L}\) is the radius of lemniscate starlikeness of the class \(\mathcal {K}_1\).
-
3.
We use Lemma 2 to compute the parabolic starlike radius of the class \(\mathcal {K}_1\). Again, let \(a = (1+r^4)/(1-r^4)\), which is larger than or equal to 1 for \(0 \le r < 1\). Note that
$$\begin{aligned} a = \frac{1 + r^4}{1 - r^4} = \frac{3}{2}\;\, \Leftrightarrow \;\, r= \left( \frac{1}{5} \right) ^{1/4} \approx 0.66874. \end{aligned}$$Since the radius we are looking for would be less than 0.216845, we only consider the case \(1/2 < a \le 3/2\) in Lemma 2. The required radius is the largest \(r>0\) satisfying the inequality
$$\begin{aligned} \frac{2r(2r^2 + r + 2)}{1-r^4} \le \frac{1 + r^4}{1-r^4} - \frac{1}{2} , \end{aligned}$$and it is the number \(\rho \), where \(\rho \) is the smallest positive real root of the equation \(3 r^4-8 r^3 -4 r^2 -8 r +1= 0\). For the function \(f_1 \in \mathcal {K}_1\) defined in (1), as shown previously, we have at \(z = ir\),
$$\begin{aligned} F(r) = \frac{z f_1'(z)}{f_1(z)}\bigg |_{z = ir} = \frac{1- 4r - 2 r^2 -4 r^3 +r^4}{1- r^4}. \end{aligned}$$Then,
$$\begin{aligned} \left| F(r)- 1 \right|&= \left| \frac{2r (r^3-2r^2-r-2)}{1-r^4}\right| . \end{aligned}$$For \(z := \rho i = i\mathcal {R}_{\mathcal {S}_{P}}\), we have
$$\begin{aligned} Re\frac{z f'_1(z)}{f_1(z)}&= \frac{1+ \rho ^4 - 4 \rho ^3 -2\rho ^2- 4\rho }{1- \rho ^4} \\&= \frac{2 \rho (2+\rho +2\rho ^2-\rho ^3)}{1 -\rho ^4}= \left| \frac{zf_1'(z)}{f_1(z)}- 1 \right| . \end{aligned}$$Consequently, the number \(\mathcal {R}_{\mathcal {S}_{P}}\) is the radius of parabolic starlikeness of the class \(\mathcal {K}_1\).
-
4.
By using Lemma 3 and the argument similar to the above, we see that the exponential starlike radius \(R_{\mathcal {S}^*_e}\) for the class \(\mathcal {K}_1\) is the smallest positive real root of the equation \((4 r^3 +2 r^2 + 4 r -1 -r^4)e = r^4 -1\). Consider the function \(f_1\) defined in (1). For \(z := \rho i = i{\mathcal {R}}_{\mathcal {S}^*_e}\), we have
$$\begin{aligned} \left| \log \frac{zf'_1(z)}{f_1(z)} \right| = \left| \log \frac{1 + \rho ^4 - 4\rho ^3 - 2 \rho ^2 - 4\rho }{1 - \rho ^4}\right| =1. \end{aligned}$$Thereby proving that the number \(\mathcal {R}_{\mathcal {S}^*_{e}}\) is the \(\mathcal {S}^*_e\)-radius of the class \(\mathcal {K}_1\).
-
5.
By using Lemma 4, and similar argument as before, the \(\mathcal {S}^*_c\)-radius \(\mathcal {R}_{\mathcal {S}_c^*}\) for \(\mathcal {K}_1\) is the smallest positive real root of the equation \(2 r^4 - 6 r^3 - 3 r^2 - 6 r +1 = 0\).
For the function \(f_1\) defined in (1), we have at \(z := \rho i = i \mathcal {R}_{\mathcal {S}^*_c}\),
$$\begin{aligned} \frac{zf'_1(z)}{f_1(z)} = \frac{1 + \rho ^4 - 4\rho ^3 - 2 \rho ^2 - 4\rho }{1 - \rho ^4} =\frac{1}{3}=h_c(-1)\in \partial h_c(\mathbb {D}), \end{aligned}$$where \(h_c(z) = 1 + (4/3)z + (2/3)z^2\), as given on page 3. This shows that \(\mathcal {R}_{\mathcal {S}^*_c}\) is the \( \mathcal {S}^*_c\)-radius for the class \(\mathcal {K}_1\) (see Fig. 1).
-
6.
To determine the \(\hbox {-}\mathrm{radius}\),
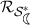 , we will use Lemma 6. After some computations following the idea above, it can be shown that
, we will use Lemma 6. After some computations following the idea above, it can be shown that 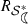 is the smallest positive real root of the equation \(4 r^3 + 2 r^2 + 4r = 2 -\sqrt{2}(1-r^4)\). For the function \(f_1\) defined in (1), at
is the smallest positive real root of the equation \(4 r^3 + 2 r^2 + 4r = 2 -\sqrt{2}(1-r^4)\). For the function \(f_1\) defined in (1), at 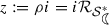 , we have $$\begin{aligned} \left| \left( \frac{zf_1'(z)}{f_1(z)}\right) ^2-1 \right|&= \left| \left( \frac{1+ \rho ^4 - 4 \rho ^3 - 2 \rho ^2 - 4 \rho }{1-\rho ^4}\right) ^2 -1 \right| \\ {}&= 2\left| \frac{1+ \rho ^4 - 4 \rho ^3 - 2 \rho ^2 - 4 \rho }{1-\rho ^4} \right| = 2 \left| \frac{zf_1'(z)}{f_1(z)} \right| . \end{aligned}$$
, we have $$\begin{aligned} \left| \left( \frac{zf_1'(z)}{f_1(z)}\right) ^2-1 \right|&= \left| \left( \frac{1+ \rho ^4 - 4 \rho ^3 - 2 \rho ^2 - 4 \rho }{1-\rho ^4}\right) ^2 -1 \right| \\ {}&= 2\left| \frac{1+ \rho ^4 - 4 \rho ^3 - 2 \rho ^2 - 4 \rho }{1-\rho ^4} \right| = 2 \left| \frac{zf_1'(z)}{f_1(z)} \right| . \end{aligned}$$Consequently, the number
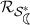 is the
is the 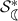 -radius of the class \(\mathcal {K}_1\).
-radius of the class \(\mathcal {K}_1\). -
7.
In order to find the \(\mathcal {S}^*_{\sin }\)-radius for function \(f \in \mathcal {K}_1\), we make use of Lemma 5. Similarly as above, with \(a = {(1+r^4)}/{(1-r^4)} >1\), it can be shown by arguing similarly as above that the \(\mathcal {S}^*_{\sin }\)-radius is the smallest positive real root of the equation \((2 + \sin {1})r^4 + 4r^3 + 2r^2 + 4r - \sin {1} = 0\).
For the function \(f_1\) defined in (1), we have at \(z := \rho = \mathcal {R}_{\mathcal {S}^*_{\sin }}\),
$$\begin{aligned} \frac{zf'_1(z)}{f_1(z)} = \frac{1 + \rho ^4 + 4\rho ^3 + 2 \rho ^2 + 4\rho }{1 - \rho ^4} =1+\sin 1=h_{\sin }(1)\in \partial h_{\sin }(\mathbb {D}). \end{aligned}$$This shows that \(\mathcal {R}_{\mathcal {S}^*_{\sin }}\) is the \( \mathcal {S}^*_{\sin }\) -radius for the class \(\mathcal {K}_1\) (see Fig. 2).
-
8.
In order to compute the \(\mathcal {S}^*_{RL}\)-radius for the class \(\mathcal {K}_1\), we use Lemma 8. As \(\sqrt{2}/3 \le a = {(1+ r^4)}/{(1- r^4)} < \sqrt{2}\) for \(r < \root 4 \of {(\sqrt{2} -1)/(\sqrt{2} +1)} \approx 0.6435942529\), a computation using Lemma 8 shows that the \(\mathcal {S}^*_{RL}\) -radius is the smallest positive real root of the equation
$$\begin{aligned} 4r^2\left( 2r^2 + r + 2\right) ^2= & {} \left( 1-r^4\right) \sqrt{ \left( \sqrt{2}-1 \right) + \left( \sqrt{2}-2\right) r^4}\\&- 2\left( \sqrt{2}-1 + \left( \sqrt{2}-2\right) r^4\right) . \end{aligned}$$For the function \( f \in \mathcal {K}_1\) given by (10), at \( z := - \rho = - {\mathcal {R}}_{\mathcal {S}^*_{RL}}\), we have \(zf'(z)/f(z)=(\rho ^2 -4 \rho +1)/(1-\rho ^2) = \sqrt{2}\) and therefore at \(z = -\rho \),
$$\begin{aligned} \left| \left( \frac{zf'(z)}{f(z)} - \sqrt{2} \right) ^2 -1 \right| = \left| \left( \frac{1- 4\rho + \rho ^2}{1- \rho ^2} - \sqrt{2} \right) ^2 -1 \right| = 1. \end{aligned}$$Hence the result.
-
9.
Since \(2 (\sqrt{2}-1) < a = {(1+ r^4)}/{(1- r^4)}\le \sqrt{2}\) for \(r \le \root 4 \of {(\sqrt{2} -1)/(\sqrt{2} +1)}\), by using Lemma 7, it can be shown that the \(\mathcal {S}_R\)-radius is obtained by solving the equation
$$\begin{aligned} \left( 2\sqrt{2} - 1\right) r^4 - 4r^3 - 2r^2 - 4r + \left( 3 - 2\sqrt{2}\right) =0. \end{aligned}$$For the function \(f_1\) defined in (1), the sharpness of the radius obtained can be seen from Fig. 3.
Indeed, for the function \(f_1\) defined in (1), we have at \(z := \rho i = i\mathcal {R}_{\mathcal {S}^*_R}\) that
$$\begin{aligned} \frac{zf'_1(z)}{f_1(z)} = \frac{1 + \rho ^4 - 4\rho ^3 - 2 \rho ^2 - 4\rho }{1 - \rho ^4} = 2\sqrt{2} -2 =h_R(-1)\in \partial h_R(\mathbb {D}). \end{aligned}$$Here, \(h_R(z)= 1+ (zk + z^2)/(k^2 - kz)\), where \(k = \sqrt{2} + 1\). Consequently, \(\mathcal {R}_{\mathcal {S}^*_R}\) is the \(\mathcal {S}^*_R\)-radius for \(\mathcal {K}_1\). \(\square \)
Our next result gives various radii of starlikeness for the class \(\mathcal {K}_2\), which consists of functions \(f \in \mathcal {A}\) satisfying \(|(f(z)/g(z))-1|<1\) for some \(g \in \mathcal {A}\) and \(Re((1-z^2)g(z)/z) >0\). Consider the functions \(f_2\), \(g_2: \mathbb {D}\rightarrow \mathbb {C}\) defined by
Clearly,
Therefore, the function \(f_2\) is in \(\mathcal {K}_2\) and this shows \(\mathcal {K}_2\ne \emptyset \). Note that this function \(f_2\) would serve as an extremal function for several radii-problems that we study here.
Theorem 2
For \(f \in \mathcal {K}_2\), the following results hold:
-
1.
For \(0 \le \alpha <1\), the \(\mathcal {S}^*(\alpha )\) radius is the smallest positive real root of the equation \( \alpha r^4 -3r (r^2 + r + 1) + (1- \alpha )=0\).
-
2.
The \(\mathcal {S}^*_L\) radius is \(\mathcal {R}_{\mathcal {S^*_L}}\ge (\sqrt{2}-1)/(\sqrt{2}+2) \approx 0.12132\).
-
3.
The \(\mathcal {S}_{P}\) radius is
$$\begin{aligned} \mathcal {R}_{\mathcal {S}_{P}} = \frac{3+\sqrt{17}}{2}-\sqrt{\frac{11+3 \sqrt{17}}{2}} \approx 0.1432698. \end{aligned}$$ -
4.
The \(\mathcal {S}^*_{e}\) radius \(\mathcal {R}_{\mathcal {S}^*_{e}} \approx 0.174887\) is the smallest positive real root of the equation \((3 r^3 + 3 r^2 + 3 r -1)e + 1 - r^4 = 0\).
-
5.
The \(\mathcal {S}^*_{c}\) radius \(\mathcal {R}_{\mathcal {S}^*_{c}} \approx 0.182815\) is the smallest positive real root of the equation \( 9 r^3 + 9 r^2 + 9 r - 2 - r^4 = 0 \).
-
6.
The
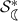 radius
radius 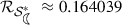 is the smallest positive real root of the equation \( r^4 (1- \sqrt{2}) + 3 r^3 + 3 r^2 + 3 r = 2 - \sqrt{2}\).
is the smallest positive real root of the equation \( r^4 (1- \sqrt{2}) + 3 r^3 + 3 r^2 + 3 r = 2 - \sqrt{2}\). -
7.
The \(\mathcal {S}^*_{\sin }\) radius is \(\mathcal {R}_{\mathcal {S}^*_{\sin }}= \sin {1}/(3+ \sin {1}) \approx 0.219049\).
-
8.
The \(\mathcal {S}^*_{R}\) radius \(\mathcal {R}_{\mathcal {S}^*_{R}} \approx 0.0541073\) is the smallest positive real root of the equation \( 2 r^4 + 3 r^3 + 3 r^2 + 3 r - 3 + 2 \sqrt{2}(1- r^4) =0 \).
-
9.
The \(\mathcal {S}^*_{RL}\) radius \(\mathcal {R}_{\mathcal {S}^*_{RL}} \) is at least the smallest positive real root of the equation
$$\begin{aligned}&{\left( 1- r^4\right) \left\{ \left( 1- r^4\right) ^2 - \left( \sqrt{2}- 1 - \left( \sqrt{2} + 1\right) r^4 \right) ^2 \right\} ^{1/2} } \\&\quad = \left( r^4 + 3r^3 + 3r^2 + 3r\right) ^2 +\left( 1- r^4\right) ^2 - \left( \sqrt{2} - 1 - \left( \sqrt{2} + 1\right) r^4 \right) ^2. \end{aligned}$$
Proof
Let \(f \in \mathcal {K}_2\) and the function \(g: \mathbb {D} \rightarrow \mathbb {C}\) be chosen such that
Note that \(| {f(z)}/{g(z)}-1|< 1 \) holds if and only if \(Re(g(z)/f(z)) > 1/2\). Let define \(p_1, p_2: \mathbb {D}\rightarrow \mathbb {C}\) as
Then, by equations (12) and (13), \(p_1 \in \mathcal {P}\) and \(p_2 \in \mathcal {P}(1/2)\). Equation (13) also yields
A simple computation shows that
By using equations (5), (6) and (14), it can be proven that the function f maps the disk \(|z|\le r\) onto the disk
From (15), we get
for all \(0\le r<\rho \) where \(\rho \approx 0.253077\) is the root of the equation \(3 r ( r^2 + r + 1)=1\). For the function \(f_2\) defined in (11), we have
At \(z := i\rho \), we have \(zf_2'(z)/f_2(z)=0\), thereby proving that \( \rho \) is the radius of starlikeness for the class \(\mathcal {K}_2\). The classes we are considering here are all subclasses of starlike functions; hence, all the radii we estimate here will be less than \(\rho \approx 0.253077\).
-
1.
In order to compute \(R_ {\mathcal {S}^*(\alpha )}\), we determine \(\rho \in [0,1]\) satisfying
$$\begin{aligned} Re\frac{z f'(z)}{f(z)} \ge \frac{1 - 3 r ( r^2 + r + 1)}{(1-r^4)} > \alpha \end{aligned}$$for all \(0\le r <\rho \). If we denote by \(\rho \) the smallest positive root of the equation \(\alpha r^4 - 3 r ( r^2 + r + 1) +(1-\alpha )=0\), then, for every \(f \in \mathcal {K}_2\), we have \({\text {Re}} (z f'(z)/f(z))> \alpha \), \(z \in \mathbb {D}_r\), \(0\le r<\rho \). Since, for \(f_2 \in \mathcal {K}_2\) defined by (11), we have
$$\begin{aligned} \frac{\rho i f'_2(i \rho )}{f_2(i \rho )}= \frac{1 - 3 \rho - 3 \rho ^2 - 3 \rho ^3}{1- \rho ^4}= \alpha \end{aligned}$$it follows that \(\rho \) is the largest positive real number such that \({\text {Re}} (z f'(z)/f(z))> \alpha \), \(z \in \mathbb {D}_{\rho }\) for every \(f \in \mathcal {K}_2\). Consequently, \(\rho = \mathcal {R}_{\mathcal {S}^*(\alpha )}\) is the radius of starlikeness of order \(\alpha \) for the class \(\mathcal {K}_2\).
-
2.
We would use Lemma 1 to compute the lemniscate starlike radius for \(\mathcal {K}_2\). So, let \(a = (1 + r^4)/(1-r^4)\). Then \(1 \le a < \infty \) for \(r\in [0,1)\), and \(a < \sqrt{2}\) when \(r < \left( \left( \sqrt{2} - 1\right) /\left( \sqrt{2} + 1\right) \right) ^{1/4}\). Using (15), we see that the function \(f\in \mathcal {K}_2\) satisfies
$$\begin{aligned} \left| \frac{z f'(z)}{f(z)} - \frac{1+r^4}{1-r^4} \right| \le \frac{r (r^3 + 3 r^2 + 3 r + 3)}{1-r^4}. \end{aligned}$$(16)The inequality
$$\begin{aligned} \frac{r \left( r^3 + 3 r^2 + 3 r + 3\right) }{1-r^4} \le \sqrt{2} - \frac{1+r^4}{1-r^4} \end{aligned}$$holds for \(0 \le r \le \rho \) where \(\rho = (\sqrt{2} -1)/(\sqrt{2} + 2) \approx 0.12132\) is the smallest positive real root of the equation
$$\begin{aligned} \left( \sqrt{2} + 2\right) r^4 - 4r^3 - 2r^2 - 4r + \left( 3 - 2\sqrt{2}\right) = 0. \end{aligned}$$Then by Lemma 1, the lemniscate starlike radius \(\mathcal {R}_{\mathcal {S}^*_L}\) for \(f \in \mathcal {K}_2\) is at least \(\rho \).
-
3.
We use Lemma 2 to compute the parabolic starlike radius for \(\mathcal {K}_2\). For \(a = (1 + r^4)/(1-r^4)\), we have \(a \le 3/2\) if \(r \le (1/5)^{1/4} \approx 0.668740305\). To apply Lemma 2, we need
$$\begin{aligned} \frac{r (r^3 + 3 r^2 + 3 r + 3)}{1-r^4} \le \frac{1+r^4}{1-r^4} - \frac{1}{2}, \end{aligned}$$and this holds for \(0\le r \le \rho \), where
$$\begin{aligned} \rho = \frac{3+\sqrt{17}}{2}-\sqrt{\frac{11+3 \sqrt{17}}{2}} \approx 0.1432698 \end{aligned}$$is the smallest positive real root of the equation
$$\begin{aligned} r^4 - 6r^3 - 6r^2 - 6r + 1 = 0. \end{aligned}$$Consider the function \(f_2 \in \mathcal {K}_2\) defined in (11). As shown previously, at \(z := i r \), we have
$$\begin{aligned} \frac{z f_2'(z)}{f_2(z)} = \frac{1 - 3 r - 3 r^2 - 3 r^3}{1- r^4}. \end{aligned}$$Thus,
$$\begin{aligned} \left| \frac{zf_2'(z)}{f_2(z)}- 1 \right|&= \left| \frac{r (3 + 3 r + 3 r^2 - r^3)}{1 - r^4}\right| \end{aligned}$$For \(z := i \rho \), we have
$$\begin{aligned} Re\frac{z f_2'(z)}{f_2(z)}&= \frac{1 - 3 \rho - 3 \rho ^2 - 3 \rho ^3}{1- \rho ^4} \\&=\frac{\rho (3 + 3 \rho + 3 \rho ^2 - \rho ^3)}{1 - \rho ^4}= \left| \frac{zf_2'(z)}{f_2(z)}- 1 \right| . \end{aligned}$$Consequently, \( \mathcal {R}_{\mathcal {S}_P}=\rho \) is the radius of parabolic starlikeness for \(\mathcal {K}_2\).
-
4.
For the \(\mathcal {S}_e\)-radius of \(f\in \mathcal {K}_2\), we will use Lemma 3. For \(a = (1 + r^4)/(1-r^4)\), \(0\le r <1\), we have \(a < e\) for \(r < [(e-1)/(e+1)]^{1/4} \approx 0.82449\). Since \(a \le \frac{1}{2}(e + e^{-1})\) for \(r < [(e-1)/(e+1)]^{2} \approx 0.213552\), we can apply Lemma 3 provided
$$\begin{aligned} \frac{r \left( r^3 + 3 r^2 + 3 r + 3\right) }{1-r^4} \le \frac{1+r^4}{1-r^4} - \frac{1}{e}. \end{aligned}$$This inequality holds for \(0\le r\le \rho \), where \(\rho \approx 0.174887\) is the smallest positive real root of the equation
$$\begin{aligned} r^4 - e(3r^3 + 3r^2 + 3r) + e - 1 = 0. \end{aligned}$$For the function \(f_2\) defined in (11), we have, at \(z=\rho i\),
$$\begin{aligned} \left| \log \frac{zf'_2(z)}{f_2(z)} \right| = \left| \log \frac{1 - 3 \rho - 3 \rho ^2 - 3 \rho ^3}{1- \rho ^4}\right| =1, \end{aligned}$$hence proving that \( \mathcal {R}_{\mathcal {S}_e}=\rho \) is the exponential starlike radius obtained for the class \(\mathcal {K}_2\).
-
5.
By using Lemma 4, it can be proven similarly as above that the \(\mathcal {S}^*_c\)-radius \(\mathcal {R}_{\mathcal {S}^*_c}\) for the class \(\mathcal {K}_2\) is the smallest positive real root \(\rho \approx 0.182815\) of the equation \(9 r^3 + 9 r^2 + 9 r - 2 - r^4 = 0\). For the function \(f_2\) defined in (11), for \(z := i\rho = i \mathcal {R}_{\mathcal {S}^*_c}\),
$$\begin{aligned} \frac{zf'_2(z)}{f_2(z)} = \frac{1 -3 \rho - 3 \rho ^2 -3 \rho ^3}{1 - \rho ^4} =\frac{1}{3}=h_c(-1)\in \partial h_c(\mathbb {D}), \end{aligned}$$as illustrated in Fig. 4.
-
7.
The \(\hbox {-}\mathrm{radius}\)
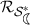 for the class \(\mathcal {K}_2\) is the smallest positive real root of the equation \(r^4 (1- \sqrt{2}) + 3 r^3 + 3 r^2 + 3 r = 2 - \sqrt{2}\). This can be obtained by considering the inequality $$\begin{aligned} \frac{3 r^3 +3 r^2 + 3 r - 1}{1- r^4} \le 1- \sqrt{2} \end{aligned}$$
for the class \(\mathcal {K}_2\) is the smallest positive real root of the equation \(r^4 (1- \sqrt{2}) + 3 r^3 + 3 r^2 + 3 r = 2 - \sqrt{2}\). This can be obtained by considering the inequality $$\begin{aligned} \frac{3 r^3 +3 r^2 + 3 r - 1}{1- r^4} \le 1- \sqrt{2} \end{aligned}$$and then use Lemma 6. For the function \(f_2\) defined in (11), at
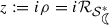 , we have $$\begin{aligned} \left| \left( \frac{zf_2'(z)}{f_2(z)}\right) ^2 - 1 \right|&= \left| \left( \frac{1 - 3 \rho - 3 \rho ^2 - 3 \rho ^3}{1- \rho ^4}\right) ^2 -1 \right| \\&= 2\left| \frac{1 - 3 \rho - 3 \rho ^2 - 3 \rho ^3}{1- \rho ^4} \right| = 2 \left| \frac{zf_2'(z)}{f_2(z)} \right| . \end{aligned}$$
, we have $$\begin{aligned} \left| \left( \frac{zf_2'(z)}{f_2(z)}\right) ^2 - 1 \right|&= \left| \left( \frac{1 - 3 \rho - 3 \rho ^2 - 3 \rho ^3}{1- \rho ^4}\right) ^2 -1 \right| \\&= 2\left| \frac{1 - 3 \rho - 3 \rho ^2 - 3 \rho ^3}{1- \rho ^4} \right| = 2 \left| \frac{zf_2'(z)}{f_2(z)} \right| . \end{aligned}$$Therefore,
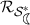 is the
is the 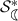 -radius for \(\mathcal {K}_2\).
-radius for \(\mathcal {K}_2\). -
8.
In order to find the \(\mathcal {S}^*_{\sin }\)-radius for the function \(f \in \mathcal {K}_2\), we make use of Lemma 5. It is easy to see that \( 1 - \sin 1< a = {(1+r^4)}/{(1-r^4)} < 1+ \sin 1 \) for \(r < [(\sin {1})/(2 + \sin {1})]^{1/4}\). Since \(a>1\), consider
$$\begin{aligned} \frac{r (r^3 + 3 r^2 + 3 r + 3)}{1-r^4} \le \sin 1 - \left( \frac{1+r^4}{1-r^4} - 1\right) . \end{aligned}$$Then the \(\mathcal {S}^*_{\sin }\)-radius, \(\mathcal {R}_{\mathcal {S}^*_{\sin }} (\approx 0.219049)\), is the smallest positive real root of the equation
$$\begin{aligned} (3 + \sin {1})r^4 + 3r(r^2 + r +1) = \sin {1}. \end{aligned}$$For the function \(f_2\) defined in (11), the radius obtained is shown in Fig. 5.
-
9.
We use Lemma 7 in order to compute the \(\mathcal {S}^*_R\) -radius for the class \(\mathcal {K}_2\). Since \(2 (\sqrt{2}-1) < a = {(1+ r^4)}/{(1- r^4)}\le \sqrt{2}\) for \(r < [(\sqrt{2} - 1)/(\sqrt{2} + 1)]^{1/4} \approx 0.64359\), by Lemma 7, we consider
$$\begin{aligned} \frac{r(r^3 + 3 r^2 +3 r + 3)}{1-r^4} \le \frac{1 + r^4}{1 - r^4} - 2(\sqrt{2} - 1). \end{aligned}$$Then the \(\mathcal {S}^*_R\) -radius for \(\mathcal {K}_2\) can be computed to be \(\mathcal {R}_{\mathcal {S}^*_{R}} \approx 0.0541073\). The radius obtained for the function \(f_2\) defined in (11) is illustrated in Fig. 6.
Indeed, for the function \(f_2\) defined in (11), we have at \(z := i\rho = i \mathcal {R}_{\mathcal {S}^*_R}\),
$$\begin{aligned} \frac{zf'_2(z)}{f_2(z)} = \frac{1 - 3 \rho - 3 \rho ^2 -3 \rho ^3}{1 - \rho ^4} =2 \sqrt{2} - 2=h_R(-1)\in \partial h_R(\mathbb {D}). \end{aligned}$$This shows that \(\mathcal {R}_{\mathcal {S}^*_R}\) is the \(\mathcal {S}^*_R\)-radius for the class \(\mathcal {K}_2\).
-
10.
Finally, for the \(\mathcal {S}^*_{RL}\)-radius, \(\mathcal {R}_{\mathcal {S}^*_{RL}}\), for the class \(\mathcal {K}_2\), by Lemma 8, the value of \(\mathcal {R}_{\mathcal {S}^*_{RL}} \approx 0.0870259\) is obtained from solving the equation
$$\begin{aligned}&{(1- r^4) \left\{ (1- r^4)^2 - \left( \left( \sqrt{2} - 1\right) - \left( \sqrt{2} + 1\right) r^4 \right) ^2 \right\} ^{1/2} } \\&\quad = \left( r^4 + 3r^3 + 3r^2 + 3r\right) ^2 +\left( 1- r^4\right) ^2 - \left( \left( \sqrt{2} - 1\right) - \left( \sqrt{2} + 1\right) r^4 \right) ^2. \end{aligned}$$\(\square \)
The following last theorem aims at computing the various radii of starlikeness for the function \(f \in \mathcal {K}_3\) that satisfies \(Re((1-z^2)f(z)/z) >0\). Consider the function \(f_3: \mathbb {D}\rightarrow \mathbb {C}\) defined by
Clearly,
Therefore, the function \(f_3 \in \mathcal {K}_3\) and \(\mathcal {K}_3\ne \emptyset \). This function \(f_3\) would serve as an extremal function for various radius problems in the following theorem.
Theorem 3
For \(f \in \mathcal {K}_3\), the following results hold:
-
1.
For \(0 \le \alpha <1\), the \(\mathcal {S}^*(\alpha )\) radius is the smallest positive real root of the equation \( (1+\alpha ) r^4 - 2 r (r^2 + r + 1) + (1- \alpha )=0\).
-
2.
The \(\mathcal {S}^*_L\) radius is \({R}_{\mathcal {S_L}}= (\sqrt{2}-1)/(\sqrt{2}+1) \approx 0.171573\).
-
3.
The \(\mathcal {S}_{P}\) radius \(\mathcal {R}_{\mathcal {S}_{P}} \approx 0.2021347\) is the smallest positive real root of the equation \( 4 r^3 + 4 r^2 + 4 r -1 - 3r^4 = 0\).
-
4.
The \(\mathcal {S}^*_{e}\) radius \(\mathcal {R}_{\mathcal {S}^*_{e}} \approx 0.244259\) is the smallest positive real root of the equation \((2 r^3 + 2 r^2 + 2 r -1 - r^4)e + 1 - r^4 = 0\).
-
5.
The \(\mathcal {S}^*_{c}\) radius \(\mathcal {R}_{\mathcal {S}^*_{c}} \approx 0.254726\) is the smallest positive real root of the equation \( 3 r^3 + 3 r^2 + 3 r - 1 - 2 r^4 = 0 \).
-
6.
The
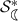 radius
radius 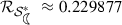 is the smallest positive real root of the equation \( 2 r^3 + 2 r^2 + 2 r - \sqrt{2} r^4 = 2 - \sqrt{2}\).
is the smallest positive real root of the equation \( 2 r^3 + 2 r^2 + 2 r - \sqrt{2} r^4 = 2 - \sqrt{2}\). -
7.
The \(\mathcal {S}^*_{\sin }\) radius is \(\mathcal {R}_{\mathcal {S}^*_{\sin }}= \sin {1}/(2 + \sin {1}) \approx 0.296139\).
-
8.
The \(\mathcal {S}^*_{R}\) radius \(\mathcal {R}_{\mathcal {S}^*_{R}} \approx 0.0790749\) is the smallest positive real root of the equation \( r^4 + 2 r^3 + 2 r^2 + 2 r -3 + 2 \sqrt{2} (1 - r^4)=0 \).
-
9.
The \(\mathcal {S}^*_{RL}\) radius \(\mathcal {R}_{\mathcal {S}^*_{RL}} \) is at least the smallest positive real root of the equation
$$\begin{aligned}&{\left( 1- r^4\right) \left\{ (1- r^4)^2 - \left( \left( \sqrt{2} - 1\right) - \left( \sqrt{2} + 1\right) r^4 \right) ^2 \right\} ^{1/2} }\\&\quad = \left( 2r^3+2r^2+2r\right) ^2 +\left( 1- r^4\right) ^2 - \left( \left( \sqrt{2} - 1\right) - \left( \sqrt{2} + 1\right) r^4 \right) ^2. \end{aligned}$$
Proof
Let the function f be in \(\mathcal {K}_3\). Then
Define the function \(p: \mathbb {D}\rightarrow \mathbb {C}\) by
Therefore, by Eq. (18), we have \(p \in \mathcal {P}\) and
Differentiating the above equation and then multiplying by z/f(z), we get
By using Eqs. (5), (6) and (20), we can prove that the function f maps the disk \(|z|\le r\) onto the disk
In order to solve radius problems, we are interested in computing the value of r for which the disk in (21) is contained in the corresponding regions. Again the classes we are considering here are all subclasses of starlike functions and, therefore, are defined by the quantity \(z f'(z)/f(z)\) lying in some region in the right half plane. In particular, for f to be in \(\mathcal {S^*}\), we need
The last inequality holds for all \(0\le r \le \rho \), where \(\rho =(1 + \sqrt{5})/2 - \sqrt{ (1 + \sqrt{5})/2}\approx 0.346014\). Thus the function \(f \in \mathcal {K}_3\) is starlike in \(|z|< \rho \approx 0.346014\). For the function \(f_3\) defined in (17), we have
At \(z := i\rho \), we have \(zf'_3(z)/f_3(z)=0\), thereby proving that \(\rho \) is the radius of starlikeness for the class \(\mathcal {K}_3\).
With this, now all the radii we estimate here shall be less than \(\rho \approx 0.346014\).
-
1.
To determine the radius \(\mathcal {R}_{\mathcal {S}^*(\alpha )}\) of starlikeness of order \(\alpha \), we estimate the value of \(r \in [0,1]\) satisfying
$$\begin{aligned} Re\frac{z f'(z)}{f(z)} \ge \frac{1 + r^4 - 2 r \left( r^2 + r + 1\right) }{1-r^4}> \alpha . \end{aligned}$$If we denote by \(\rho \) the smallest positive root of the equation \((1 + \alpha ) r^4 - 2 r ( r^2 + r + 1) +(1-\alpha )=0 \), then we have \({\text {Re}} (z f'(z)/f(z))> \alpha \), \(z \in \mathbb {D}_{\rho }\) for every \(f \in \mathcal {K}_3\).
Since, for \(f_3 \in \mathcal {K}_3\) defined by (17), we have
$$\begin{aligned} \frac{\rho i f_3'(i \rho )}{f_3(i \rho )}= \frac{1 - 2 r - 2 r^2 - 2 r^3 + r^4}{1- r^4}= \alpha , \end{aligned}$$it follows that \(\rho \) is the biggest positive real number satisfying \({\text {Re}} (z f'(z)/f(z))> \alpha \), \(z \in \mathbb {D}_{\rho }\) for every \(f \in \mathcal {K}_3\). Consequently, \(\rho = \mathcal {R}_{\mathcal {S}^*(\alpha )}\) is the radius of starlikeness of order \(\alpha \) for the class \(\mathcal {K}_3\).
-
2.
We can use Lemma 1 to compute the lemniscate starlike radius for \(\mathcal {K}_3\). For \(a = (1 + r^4)/(1-r^4)\), we have \(a < \sqrt{2}\) when \(r < \left( \left( \sqrt{2} - 1\right) /\left( \sqrt{2} + 1\right) \right) ^{1/4}\approx 0.643594\). By (15) and Lemma 1, we need to determine \(\rho \) such that
$$\begin{aligned} \frac{2r \left( r^2 + r + 1\right) }{1-r^4} \le \sqrt{2} - \frac{1+r^4}{1-r^4}, \end{aligned}$$for \(0\le r <\rho \). The required \(\rho \approx 0.1715728753\) is clearly the smallest positive real root of the equation
$$\begin{aligned} \left( \sqrt{2} + 1\right) r^4 + 2r^3 + 2r^2 + 2r + \left( 1 - \sqrt{2}\right) = 0. \end{aligned}$$Consider the function \(\hat{f_3}: \mathbb {D}\rightarrow \mathbb {C}\) defined by
$$\begin{aligned} \hat{ f_3}(z) = \frac{z}{(1+z)^2}. \end{aligned}$$(23)Clearly,
$$\begin{aligned} Re\frac{1-z^2}{z}\hat{f_3}(z) = Re\frac{1 - z}{1+ z} >0. \end{aligned}$$So \(\hat{f_3} \in \mathcal {K}_3\). Also
$$\begin{aligned} \left| \left( \frac{z\hat{f_3}'(z)}{\hat{f_3}(z)}\right) ^2 -1 \right| = \left| \left( \frac{1 - z}{1 + z}\right) ^2 -1 \right| . \end{aligned}$$Now, for \(z := -\rho = -{\mathcal {R}_{\mathcal {S}^*_L}}\), we have \((1 - z)/(1 + z) = \sqrt{2}\) and
$$\begin{aligned} \left| \left( \frac{z\hat{f_3}'(z)}{\hat{f_3}(z)}\right) ^2 -1 \right| = \left| \left( \sqrt{2}\right) ^2 -1 \right| =1, \end{aligned}$$Consequently, \(\rho \) is the radius of lemniscate starlikeness for \(\mathcal {K}_3\).
-
3.
For the parabolic starlike radius of the class \(\mathcal {K}_3\), we would use Lemma 2. For \(r \le (1/5)^{1/4}\approx 0.66874\), we have \(a= {(1+r^4)}/{(1-r^4)}\le 3/2\). By Lemma 2, we need to find \(\rho \) such that
$$\begin{aligned} \frac{ 2 r ( r^2 + r + 1)}{1-r^4} \le \frac{1+r^4}{1-r^4} -\frac{1}{2}, \end{aligned}$$(24)for \(0\le r <\rho \). Clearly, \(\rho \approx 0.2021347\) is the smallest positive real root of the equation \(3r^4 - 4 r^3 - 4 r^2 - 4 r + 1 = 0\). For the function \(f_3\) defined in (17), as shown previously, at \(z := i r\), we have
$$\begin{aligned} \frac{z f_3'(z)}{f_3(z)} = \frac{1 - 2 r - 2 r^2 - 2 r^3 + r^4}{1- r^4}. \end{aligned}$$Hence, for \(z := i \rho = i \mathcal {R}_{\mathcal {S}_P}\), we have
$$\begin{aligned} Re\frac{z f'_3(z)}{f_3(z)}&= \frac{1 - 2 \rho - 2 \rho ^2 - 2 \rho ^3 + \rho ^4}{1- \rho ^4} \quad (= 0.5)\\&= \frac{2 \rho (1 + \rho + \rho ^2 - \rho ^3)}{1 - \rho ^4}= \left| \frac{zf_3'(z)}{f_3(z)}- 1 \right| , \end{aligned}$$thus illustrates that \(\rho = \mathcal {R}_{\mathcal {S}_P}\) is the radius of parabolic starlikeness for the function \(f_3\). Therefore, the \(\mathcal {S}_P\)-radius for \(\mathcal {K}_3\) is \( \rho \approx 0.2021347\).
-
4.
By using Lemma 3 and considering
$$\begin{aligned} \frac{2 r ( r^2 + r + 1)}{(1-r^4)} \le \frac{1+r^4}{1-r^4} -\frac{1}{e}, \end{aligned}$$it can be proven similarly as above that the exponential starlike radius \(\mathcal {R}_{\mathcal {S}^*_e}\) for the class \(\mathcal {K}_3\) is the smallest positive real root \(\rho \) of the equation \((2 r^3 + 2 r^2 + 2 r -1 - r^4)e + 1 - r^4 = 0\). Again, for the function \(f_3\) given in (17), at \(z := i \rho = i \mathcal {R}_{\mathcal {S}_e^*}\), we have
$$\begin{aligned} \left| \log \frac{zf'_3(z)}{f_3(z)} \right| = \left| \log \frac{1 - 2 \rho - 2 \rho ^2 - 2 \rho ^3 + \rho ^4}{1- \rho ^4}\right| =1, \end{aligned}$$thereby proving that \(\mathcal {R}_{\mathcal {S}^*_e}\) is the radius of exponential starlikeness for the class \(\mathcal {K}_3\).
-
5.
For the \(\mathcal {S}^*_c\)-radius for the class \(\mathcal {K}_3\), we use Lemma 4 by considering
$$\begin{aligned} \frac{2 r ( r^2 + r + 1)}{1-r^4} \le \frac{1+r^4}{1-r^4} -\frac{1}{3}. \end{aligned}$$Then it can be proven similarly as above that \(\mathcal {R}_{\mathcal {S}^*_c}\) is the smallest positive real root \(\rho \approx 0.254726 \) of the equation
$$\begin{aligned} 3 r^3 + 3 r^2 + 3 r - 1- 2 r^4 = 0. \end{aligned}$$For the function \(f_3\) defined in (17), the radius obtained is shown in Fig. 7.
Indeed, for the function \(f_3\), we have at \(z := i \rho \) that
$$\begin{aligned} \frac{zf'_3(z)}{f_3(z)} = \frac{1 - 2 \rho - 2\rho ^2 -2 \rho ^3 +\rho ^4}{1 - \rho ^4} =\frac{1}{3}=h_c(-1)\in \partial h_c(\mathbb {D}). \end{aligned}$$ -
6.
By using a similar argument as above, the
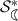 -radius for the class \(\mathcal {K}_3\) is the smallest positive real root \(\rho \) of the equation $$\begin{aligned} 2 r^3 + 2 r^2 + 2 r - \sqrt{2} r^4 = 2 - \sqrt{2}. \end{aligned}$$
-radius for the class \(\mathcal {K}_3\) is the smallest positive real root \(\rho \) of the equation $$\begin{aligned} 2 r^3 + 2 r^2 + 2 r - \sqrt{2} r^4 = 2 - \sqrt{2}. \end{aligned}$$In fact, by Lemma 6, it follows that
$$\begin{aligned} \frac{2 r \left( r^2 + r + 1\right) }{1- r^4} \le 1- \sqrt{2} + \frac{1 + r^4}{1 - r^4} \end{aligned}$$for all \(0\le r <\rho \). For the function \(f_3\) defined in (17), at \(z := i\rho \), we have
$$\begin{aligned} \left| \left( \frac{zf_3'(z)}{f_3(z)}\right) ^2-1 \right|&= \left| \left( \frac{1 - 2 \rho - 2 \rho ^2 - 2 \rho ^3 + \rho ^4}{1- \rho ^4}\right) ^2 -1 \right| \\ {}&= 2\left| \frac{1 - 2 \rho - 2 \rho ^2 - 2 \rho ^3 + \rho ^4}{1- \rho ^4} \right| = 2 \left| \frac{zf_3'(z)}{f_3(z)} \right| . \end{aligned}$$Therefore, \(\rho \) is the
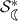 -radius for the class \(\mathcal {K}_3\).
-radius for the class \(\mathcal {K}_3\). -
7.
In order to find the \(\mathcal {S}^*_{\sin }\)-radius for the function \(f \in \mathcal {K}_3\), we make use of Lemma 5, where we would consider
$$\begin{aligned} \frac{2 r ( r^2 + r + 1)}{(1-r^4)} \le \sin 1 - \frac{2 r^4}{1-r^4}. \end{aligned}$$The \(\mathcal {S}^*_{\sin }\)-radius, \(\mathcal {R}_{\mathcal {S}^*_{\sin }}\), is smallest positive real root of the equation
$$\begin{aligned} 2r(r^3 + r^2 + r + 1) = (\sin {1})(1 - r^4). \end{aligned}$$For the function \(\hat{ f_3} \in \mathcal {K}_3\) defined in (23), it can be seen from Fig. 8
that the radius obtained is the biggest positive real number having the property \(z f'(z)/f(z) \prec 1+ \sin {z}\) for every \(f \in \mathcal {K}_3\).
-
8.
We use Lemma 7 to compute the \(\mathcal {S}^*_R\)-radius for the class \(\mathcal {K}_3\). By considering
$$\begin{aligned} \frac{2 r \left( r^2 + r + 1\right) }{1-r^4} \le \frac{1 + r^4}{1 - r^4} - 2\left( \sqrt{2} - 1\right) , \end{aligned}$$we would obtain \(\mathcal {R}_{\mathcal {S}^*_{R}}\) to be given by the smallest positive real root \(\rho \) of the equation
$$\begin{aligned} \left( 2\sqrt{2} - 1\right) r^4 - 2r\left( r^2 + r + 1\right) + \left( 3 - 2\sqrt{2}\right) = 0. \end{aligned}$$For the function \(f_3\) defined in (17), the radius obtained is shown as in Fig. 9.
Indeed, for the function \(f_3\), we have at \(z := i \rho \),
$$\begin{aligned} \frac{zf'_3(z)}{f_3(z)} = \frac{1 - 2 \rho - 2\rho ^2 -2 \rho ^3 + \rho ^4}{1 - \rho ^4} = 2 \sqrt{2}-2=h_R(-1)\in \partial h_R(\mathbb {D}). \end{aligned}$$Consequently, \(\mathcal {R}_{\mathcal {S}^*_c}\) is the \(\mathcal {S}^*_c\)-radius for the class \(\mathcal {K}_3\).
-
9.
Lastly, the \(\mathcal {S}^*_{RL}\)-radius for the class \(\mathcal {K}_3\) is obtained by using Lemma 8 and from the equation
$$\begin{aligned}&{\left( 1- r^4\right) \left\{ (1- r^4)^2 - \left( \left( \sqrt{2} - 1\right) -\left( \sqrt{2} + 1\right) r^4 \right) ^2 \right\} ^{1/2} }\\&\quad = \left( 2r^3+2r^2+2r\right) ^2 +\left( 1- r^4\right) ^2 - \left( \left( \sqrt{2} - 1\right) - \left( \sqrt{2} + 1\right) r^4 \right) ^2. \end{aligned}$$\(\square \)
References
Ali, R.M., Ravichandran, V.: Uniformly convex and starlike functions. Ramanujan Math. Newsl. 21(1), 16–30 (2011)
Ali, R.M., Jain, N.K., Ravichandran, V.: On the radius constants for classes of analytic functions. Bull. Malays. Math. Sci. Soc. (2) 36(1), 23–38 (2013)
Ali, R.M., Jain, N.K., Ravichandran, V.: Radii of starlikeness associated with the lemniscate of Bernoulli and the left-half plane. Appl. Math. Comput. 218(11), 6557–6565 (2012)
Cho, N.E., Kumar, V., Kumar, S.S., Ravichandran, V.: Radius problems for starlike functions associated with the sine function. Bull. Iran. Math. Soc. 45(1), 213–232 (2019)
Gandhi, S., Ravichandran, V.: Starlike functions associated with a lune. Asian-Eur. J. Math. 10(4), 1750064, 12 (2017)
Gangadharan, A., Ravichandran, V., Shanmugam, T.N.: Radii of convexity and strong starlikeness for some classes of analytic functions. J. Math. Anal. Appl. 211(1), 301–313 (1997)
Kanaga, R., Ravichandran, V.: Starlikeness for certain close-to-star functions, Hacettepe J. Math. Stat. to appear
Kumar, S., Ravichandran, V.: A subclass of starlike functions associated with a rational function. Southeast Asian Bull. Math. 40(2), 199–212 (2016)
Ma, W.C., Minda, D.: Uniformly convex functions. Ann. Polon. Math. 57(2), 165–175 (1992)
Ma, W.C., Minda, D.: A unified treatment of some special classes of univalent functions. In: Proceedings of the Conference on Complex Analysis (Tianjin: 157–169. Conf. Proc. Lecture Notes Anal., I, Int. Press, Cambridge, MA (1992)
MacGregor, T.H.: The radius of univalence of certain analytic functions. Proc. Am. Math. Soc. 14, 514–520 (1963)
MacGregor, T.H.: The radius of univalence of certain analytic functions. II. Proc. Am. Math. Soc. 14, 521–524 (1963)
Madaan, V., Kumar, A., Ravichandran, V.: Radii of starlikeness and convexity of some entire functions. Bull. Malays. Math. Sci. Soc. to appear. https://doi.org/10.1007/s40840-020-00925-8
Mendiratta, R., Nagpal, S., Ravichandran, V.: A subclass of starlike functions associated with left-half of the lemniscate of Bernoulli. Int. J. Math. 25(9), 1450090, 17 pp (2014)
Mendiratta, R., Nagpal, S., Ravichandran, V.: On a subclass of strongly starlike functions associated with exponential function. Bull. Malays. Math. Sci. Soc. 38(1), 365–386 (2015)
Padmanabhan, K.S., Parvatham, R.: Some applications of differential subordination. Bull. Austral. Math. Soc. 32(3), 321–330 (1985)
Raina, R.K., Sokół, J.: Some properties related to a certain class of starlike functions. C. R. Math. Acad. Sci. Paris 353(11), 973–978 (2015)
Robertson, M.S.: Certain classes of starlike functions. Michigan Math. J. 32(2), 135–140 (1985)
Rønning, F.: A survey on uniformly convex and uniformly starlike functions. Ann. Univ. Mariae Curie-Skłodowska Sect. A 47, 123–134 (1993)
Sebastian, A., Ravichandran, V.: Radius of starlikeness of certain analytic functions, Math. Slovaca to appear
Shah, G.M.: On the univalence of some analytic functions. Pac. J. Math. 43, 239–250 (1972)
Shanmugam, T.N., Ravichandran, V.: Certain properties of uniformly convex functions. In: Computational Methods and Function Theory 1994 (Penang), 319–324, Ser. Approx. Decompos., 5, World Sci. Publ., River Edge
Sharma, K., Jain, N.K., Ravichandran, V.: Starlike functions associated with a cardioid. Afr. Mat. 27(5–6), 923–939 (2016)
Sokól, J., Stankiewicz, J.: Radius of convexity of some subclasses of strongly starlike functions. Zeszyty Nauk. Politech. Rzeszowskiej Mat. No. 19, 101–105 (1996)
Sokól, J.: Radius problems in the class \(\cal{S}^*_{L}\). Appl. Math. Comput. 214(2), 569–573 (2009)
Acknowledgements
The first author gratefully acknowledges support from USM research university grant 1001.PMATHS.8011101. The authors are thankful to all the three referees for their useful comments.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Rosihan M. Ali.
Dedicated to Prof. K. G. Subramanian on the occasion of his 72nd birthday.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Lee, S.K., Khatter, K. & Ravichandran, V. Radius of Starlikeness for Classes of Analytic Functions. Bull. Malays. Math. Sci. Soc. 43, 4469–4493 (2020). https://doi.org/10.1007/s40840-020-01028-0
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40840-020-01028-0



 -radius
-radius  is the smallest positive real root of the equation
is the smallest positive real root of the equation 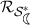 , we will use Lemma
, we will use Lemma 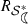 is the smallest positive real root of the equation
is the smallest positive real root of the equation 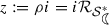 , we have
, we have 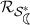 is the
is the 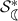 -radius of the class
-radius of the class 

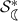 radius
radius 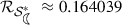 is the smallest positive real root of the equation
is the smallest positive real root of the equation 
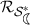 for the class
for the class 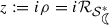 , we have
, we have 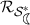 is the
is the 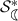 -radius for
-radius for 


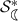 radius
radius 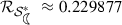 is the smallest positive real root of the equation
is the smallest positive real root of the equation 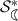 -radius for the class
-radius for the class 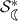 -radius for the class
-radius for the class 

